Significance
The problem of generating and navigating high-dimensional free energy surfaces is a significant challenge in the study of complex systems. The approach introduced represents an advance in this area, and its ability to generate and organize the key features of a high-dimensional free energy surface, i.e., its landmarks, with high efficiency impacts numerous problems in the materials and biomolecular sciences for which prediction of optimal structures is key. These include polypeptide and nucleic acid structure and crystal design and structure prediction. Moreover, as the algorithm targets the free energy surface, candidate structures can be ranked based on their relative free energies, which is not possible with algorithms that target only the bare potential energy surface.
Keywords: free energy surface, stochastic optimization, activation–relaxation, machine learning, network representation
Abstract
Coarse graining of complex systems possessing many degrees of freedom can often be a useful approach for analyzing and understanding key features of these systems in terms of just a few variables. The relevant energy landscape in a coarse-grained description is the free energy surface as a function of the coarse-grained variables, which, despite the dimensional reduction, can still be an object of high dimension. Consequently, navigating and exploring this high-dimensional free energy surface is a nontrivial task. In this paper, we use techniques from multiscale modeling, stochastic optimization, and machine learning to devise a strategy for locating minima and saddle points (termed “landmarks”) on a high-dimensional free energy surface “on the fly” and without requiring prior knowledge of or an explicit form for the surface. In addition, we propose a compact graph representation of the landmarks and connections between them, and we show that the graph nodes can be subsequently analyzed and clustered based on key attributes that elucidate important properties of the system. Finally, we show that knowledge of landmark locations allows for the efficient determination of their relative free energies via enhanced sampling techniques.
Understanding the conformational equilibria of complex systems remains a significant challenge in the computational molecular sciences. Whether one is interested in predicting biomolecular structure, generating and thermodynamically ranking the polymorphs of molecular crystals, or studying the phase behavior of complex materials, the very large number of degrees of freedom renders such problems highly nontrivial. Often the most important conformational states in a system can be characterized in terms of a subset of collective degrees of freedom or “collective variables” (CVs), and the problem of mapping out the conformational equilibria amounts to generating the marginal probability distribution in these CVs, from which the associated free energy surface (FES) can be generated. Unfortunately, due to the existence of many minima on the potential energy surface separated by high barriers, transitions from basin to basin on this surface are rare, so that the FES cannot be generated on any reasonable timescale using standard molecular dynamics (MD) or Monte Carlo (MC) methods. Various enhanced sampling approaches have been devised to accelerate the exploration of such “rough” or “frustrated” energy landscapes to generate such FESs, either by elevating the temperature in the subspace of the CVs (1–3) or by applying a bias potential on the FES (4–7) as in the popular metadynamics approach (4, 5). Recently, we have shown that these two classes of methods can be effectively combined (8), and others have shown that various types of free energy dynamics are possible (9).
Although it is often claimed that a low-dimensional manifold involving the selected CVs and embedded in the full phase space could capture the most important processes in complex systems (10, 11), the problem of identifying the relevant CVs that characterize this low-dimensional surface remains unsolved in general. In particular, the chosen CVs must describe a manifold of slow motions in the system. Although considerable effort has been devoted to this subject (11–13), most of the methods proposed require prior knowledge of the system, which necessitates sufficient sampling of the global configurational distribution. Moreover, quantifying different conformational equilibria might require different numbers of CVs, indicating that assigning a constant dimensionality to the low-dimensional manifold is inadequate (14). One simple solution is to use a large number of CVs for the system, which may contain some redundancy yet are sufficient to incorporate the important slow modes. When this is done, one is necessarily faced with the problem of describing a high-dimensional free energy surface (HDFES). Despite the advent of robust enhanced sampling techniques capable of exploring HDFESs (8, 15, 16), significant difficulties remain in the study of such surfaces, including the characterization and representation of a function of many variables. In fact, the low free energy regions on an HDFES possess a “spider’s web” structure that occupies a relatively small fraction of the surface (16). Thus, enhanced sampling methods designed to sample the surface uniformly could spend too much time in uninteresting, relatively high free energy regions. Even if a well-sampled HDFES is available, fitting it to some model functional form (8) and/or visualizing the samples in a low-dimensional space (16) are nontrivial problems. Interestingly, the spider’s web structure indicates that the most interesting parts of the HDFES are the minima and the transition paths connecting them. As long as minima and saddles are located on an HDFES, relative free energy differences can be calculated and transition paths can be constructed. Therefore, the minima and saddle points are important “landmarks” on an HDFES, and locating these landmarks becomes a threshold for further analysis of the surface.
An obvious way to locate landmarks is to apply a searching algorithm on an analytically represented HDFES. However, difficulties in complete sampling and high-dimensional fitting become obstacles in such an approach. In this paper, we develop a strategy for locating landmarks on an HDFES “on the fly” by direct optimization. Various optimization approaches, such as the dimer method (17–19), the activation–relaxation technology (ART) (20, 21), and discrete path sampling (22), have achieved considerable success in locating minima and saddles on potential energy surfaces. However, the problem of locating such landmarks on an HDFES has received significantly less attention. It is worth noting that, in general, the complexity of a frustrated system described by a particular potential energy function can be reduced by integrating out uninteresting degrees of freedom and obtaining the FES, a surface that encodes information about important conformational states. Because the FES is determined by the expectation of an indicator function, the optimization algorithm proposed here belongs to the general class of stochastic approximations, which is a family of optimization algorithms for objective functions that can be estimated only via noisy observations. Such algorithms have been successful in the field of electrical engineering, specifically in adaptive signal processing (23), are the basis for stochastic gradient descent methods that are widely used in machine learning (24), and have recently been used to optimize a biasing potential (25) in metadynamics. As our algorithm is designed to navigate HDFESs that are multiscale in nature, the algorithm falls within the general framework of multiscale modeling, specifically heterogenous multiscale modeling (HMM) (26) or the “equation-free” approach (27). We show that the optimization algorithm can be tailored to suit the features of the FES, which are generated on the fly using machine-learning methods; this constitutes a significant difference from algorithms that operate on potential energy surfaces. The use of ART leads to a global search algorithm on the HDFES. We term the resulting approach the stochastic activation–relaxation technique (START). Once the landmarks are located, we show that they may be subsequently used as inputs to an enhanced sampling calculation to obtain, quantitatively, their associated free energies, a procedure that is of considerably greater efficiency than attempting to converge the full HDFES from scratch via enhanced sampling (with no a priori knowledge of the location of the landmarks). Finally, we address the problem of representing the HDFES explored by START by introducing a graph-based approach in which all of the landmarks obtained are colored vertices and connections between them are the edges. We then show that the graph nodes can be analyzed and clustered based on suitably chosen attributes to reveal archetypical configurations of the system.
Stochastic Approximation on an HDFES
Consider a system of N particles with coordinates interacting through a potential . We introduce a set of n CVs given by functions , which we assume capture the slow, collective motions of the system. We take the CVs as inputs and do not discuss here how they are generally chosen. The marginal probability distribution , where , gives the probability that , ,…, and and is defined to be , where , is Boltzmann’s constant, and T is the temperature of the system. The variables are referred to as “coarse-grained” variables. Representing the product of δ-functions as the limit of a product of Gaussians (2, 3), we obtain
| [1] |
C and are overall normalization constants. The parameters determine the width and height of the Gaussians, and for finite , the approximate marginal distribution converges to the true distribution weakly as (28). The FES associated with this marginal distribution is , whereas the gradient and Hessian are expressed, respectively, in terms of the expectation or sample mean and sample covariance matrix of the quantity , i.e., (8), and (29), where is the covariance matrix of . The probability distribution for calculating these expectations is the canonical distribution in Eq. 1 with fixed s. The samples come from molecular dynamics or Monte Carlo simulations with a restraint on s. These estimators, denoted by and , exhibit low-amplitude noise whenever finite-time averaging is used. This is the main difference between the optimization on a potential energy surface and a FES. However, the noise is a necessary component in the START algorithm.
Starting from one point on an HDFES, neither minimum nor saddle optimization algorithms can guarantee a complete search of the minima/saddles on the surface. Here, we obtain a global search strategy by combining two protocols iteratively: A saddle optimization approach allows the system to escape a local minimum, and minimum optimization allows the system to relax from a saddle. In the latter, s is updated according to
| [2] |
There are various ways to locate an index-1 saddle point on a potential energy surface, including ART, the dimer method, descrete path sampling, and gentlest ascent dynamics (GAD) (30, 31). As we have recently extended GAD to index-1 saddle searching on FESs (29), we now choose this scheme as the saddle optimization method in the START protocol. The optimization equations in this scheme are
| [3a] |
| [3b] |
Here, and is the same step size as in Eq. 2. The vector is a modification of the force such that an index-1 saddle becomes an attractor of s if n is close to the eigenvector of H with the minimum eigenvalue. The second equation evolves n to the required eigenvector. The parameter γ controls the “sensitivity” of n to a change in H, thus providing a means of damping the noise in H. This type of optimization algorithm most closely fits the HMM framework; i.e., Eqs. 2, 3a, and 3b can be viewed as macroscopic solvers for the coarse-grained variables. Information needed for these solvers can come from any microscopic approach capable of delivering the required constrained averages that produce and . Although the present study employs molecular dynamics for this task, stochastic dynamics or Monte Carlo could work equally well.
Note that in Eqs. 2 and 3a, the step size is constant, and the force (F or ) is normalized. This contrasts with traditional stochastic approximations in which the gradient of an objective function is typically unnormalized, and a step size in the kth step of the optimization is chosen to decay as . In the present scheme, we choose to be sufficiently small so that when multiplied by the normalized force ( or ), s will not evolve too rapidly when or is large. In this way, we avoid large jumps in s and thus avoid a long equilibration phase in the restrained simulations. Note also that in traditional stochastic approximations, when k is large, will be small, and s will advance more slowly than desired. By contrast, START with a constant step size and normalized force guarantees the efficiency of the optimization. When the step size is constant, however, s does not converge to a point; rather, the trajectory of s generates a cluster around a minimum/saddle (32) (see Fig. 2). Such a cluster formed during a minimum/saddle optimization can be extracted by a clustering algorithm (Materials and Methods), and landmarks will be covered by clusters. The exact location of each landmark is then determined by investigating the FES at the cluster. The local FES can be constructed from sampled within the cluster. In START, we approximate this local FES by a quadratic function, , where is a symmetric matrix. Suppose there are M points with in a cluster. The parameters in A and are estimated by minimizing the objective function (8). This is a quadratic programming problem with a unique solution. The landmark point, either a minimum or a saddle, is a critical point with zero gradient on that can be resolved by solving a set of linear equations . The matrix is actually the Hessian at the landmark, estimated by this local fitting, from which the properties of the landmark, e.g., the eigenvalues and eigenvectors of the Hessian, can be determined.
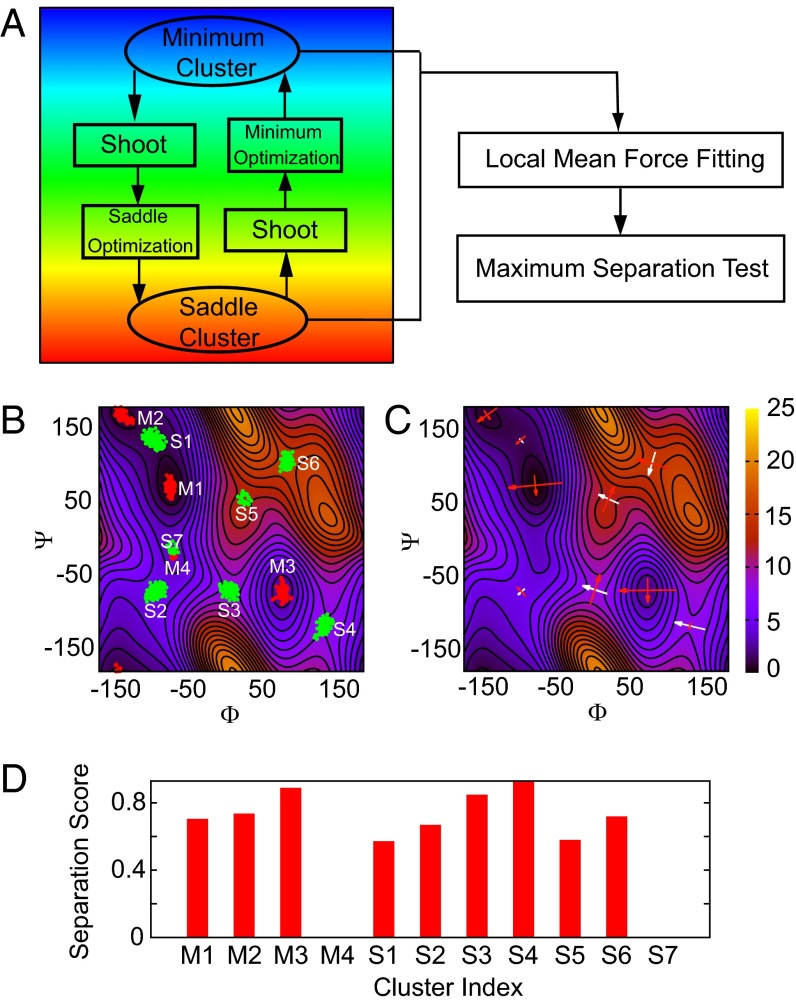
Fig. 2.
(A) Flowchart of the START procedure. First, an optimization is performed to drive the system to the nearest minimum from an initial configuration. Following this, a trajectory is shot along a random direction for several steps. A saddle optimization is then started and terminated if it is converged. Finally, a trajectory is shot again along another random direction, and a new minimum optimization is initiated. One such loop, including one minimum and saddle point optimization, is considered an iteration. All clusters are then sent to a local mean force fitting and maximum separation testing for identifying and locating landmarks. (B) Samples from the START simulation are aggregated as clusters. Red samples are minima candidates and green samples are saddle candidates. (C) The eigenvectors of each minimum/saddle are two perpendicular arrows crossing at the exact location of the minimum/saddle. The length of an arrow is proportional to the magnitude of the corresponding eigenvalue, and the color indicates the sign of the eigenvalue: Red is positive, and white is negative. (D) The scores (l) of the maximum separation test clearly prove that the M4 and S7 clusters are flat regions rather than true minima/saddles.
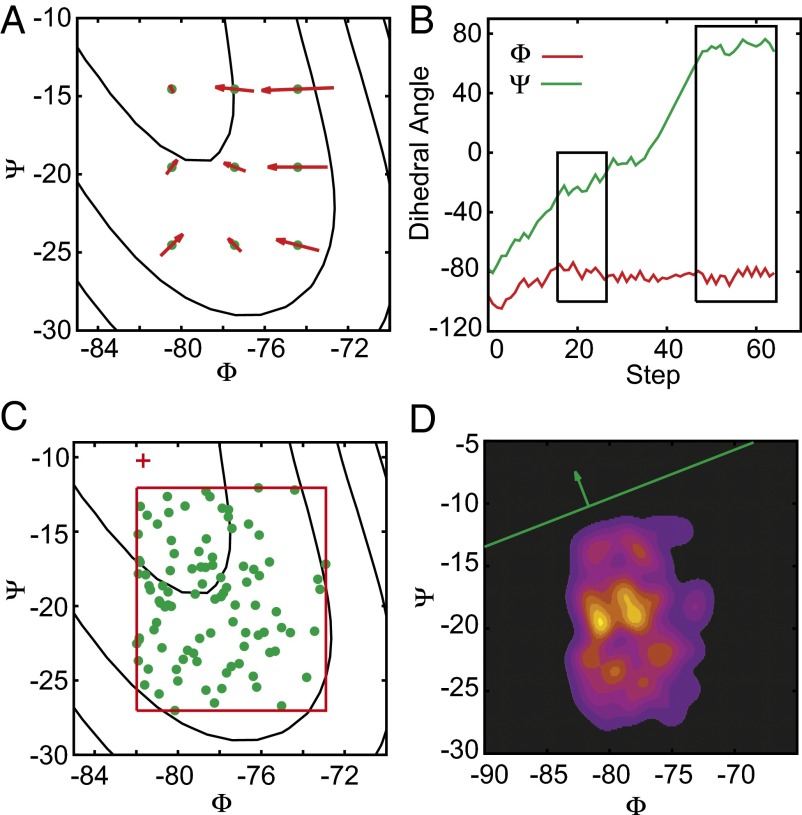
A cluster can also form in a flat region (not a minimum or saddle) on the FES during an optimization. The reason for this is that in such a region, the mean force is small along several directions, and the noisy nature of F and H causes a minimum/saddle optimization trajectory to remain in the region for a considerable period, thereby generating a cluster, before it is able to diffuse out. We illustrate this phenomenon using the alanine dipeptide in vacuum. The Ramachandran map, i.e., the FES as a function of the dihedral angles Φ and Ψ, exhibits a very flat region (proved by studying the converged mean force in Fig. 1A), corresponding to M4 in Fig. 2, that does not contain any landmarks. Fig. 1B shows one minimum optimization trajectory passing through this region: It wanders in this region (left box) for a relatively long period before finally diffusing out to a minimum (right box), thus forming a cluster (our criterion for cluster formation is described in Materials and Methods). When this happens, the optimization halts prematurely, and this cluster is then fed into the minimum/saddle analysis described above. Fig. 1C shows the resulting cluster around M4 together with the fitted critical point (landmark). We thus see that the fitted critical point is separated from the cluster centroid; i.e., it can be located at the edge or even outside the cluster. Inspired by the idea of support vector machines (SVMs), an algorithm that we term the “maximum separation test” is designed to screen out these false landmarks by quantifying the degree to which a point is “at the edge,” “near the center,” or “outside” of a cluster. Let w be the normal vector of a hyperplane through a fitted critical point. The number of samples on one side of the hyperplane is a function , where is the Heaviside step function (0–1 loss function), is the coordinate of the mth point in the cluster, and is the coordinate of the fitted critical point. If we define , the hyperplane with as its normal vector, called the “plane of maximum separation,” should have a minimum number of points on one side and a maximum on the other. Numerically, is replaced by the cumulative distribution of a Gaussian with SD σ, and we obtain the plane of maximum separation by minimizing . We then use the ratio as an indicator of the location of a critical point relative to the cluster: The ratio l will be approximately unity if the critical point lies close to the center of the cluster, will decrease if the critical point shifts to the edge of the cluster, and will be approximately zero if the critical point lies outside the cluster. Fig. 1D shows the plane of maximum separation with all points located on one side. The l score in this case is very small (Fig. 2D), and the fitted critical point should be excluded as a false landmark. The consistency of this result with our observations in Fig. 1 A and D highlights the utility of the maximum separation test.
Fig. 1.
A flat region (M4, Fig. 2) on the Ramachandran plot of the alanine dipeptide in vacuum is studied in detail. (A) A benchmark study proves that this region is not a minimum. The red arrows are the mean force at the green lattice points. (B) One minimum optimization trajectory passes through this range and ultimately forms a cluster at another minimum. (C) Samples in this flat region are the green points, and the background FES is from a 10-ns UFED (8) simulation. The red cross is the fitted critical point. (D) The starting point of the green arrow is the fitted critical point. The green line is the plane of maximum separation and the green arrow is its normal vector. The convolved samples are plotted as the colored density distribution in the background. The light yellow color indicates the largest density and the black color shows the low-density regions.
A flowchart of the START procedure is shown in Fig. 2A. The initial shooting move before each optimization, like the initial shifting of one atom in the activation–relaxation technique (20, 21), forces s to leave a landmark more quickly, thus increasing the overall efficiency. Instead of shooting along a random direction, other strategies, such as shooting along the direction of the Hessian eigenvector with the smallest eigenvalue, can be used (29). The clusters from the clustering algorithm are shown in Fig. 2B for an alanine dipeptide example. Fig. 2D plots the l scores of all of the clusters. Most of these clusters have large scores except for M4 and S7, indicating that these two clusters do not pass the maximum separation test and are, therefore, flat regions on the FES. After local mean force fitting and maximum separation tests, the locations of minima/saddles and the eigenvectors of the Hessians at these points are determined and are plotted in Fig. 2C. The locations of the landmarks match the shape of the FES from a 10-ns benchmark simulation using the unified free energy dynamics (UFED) method (8) (background FES of Fig. 2 B and C) and are also consistent with those in previous studies (33).
Results
Alanine Tripeptide.
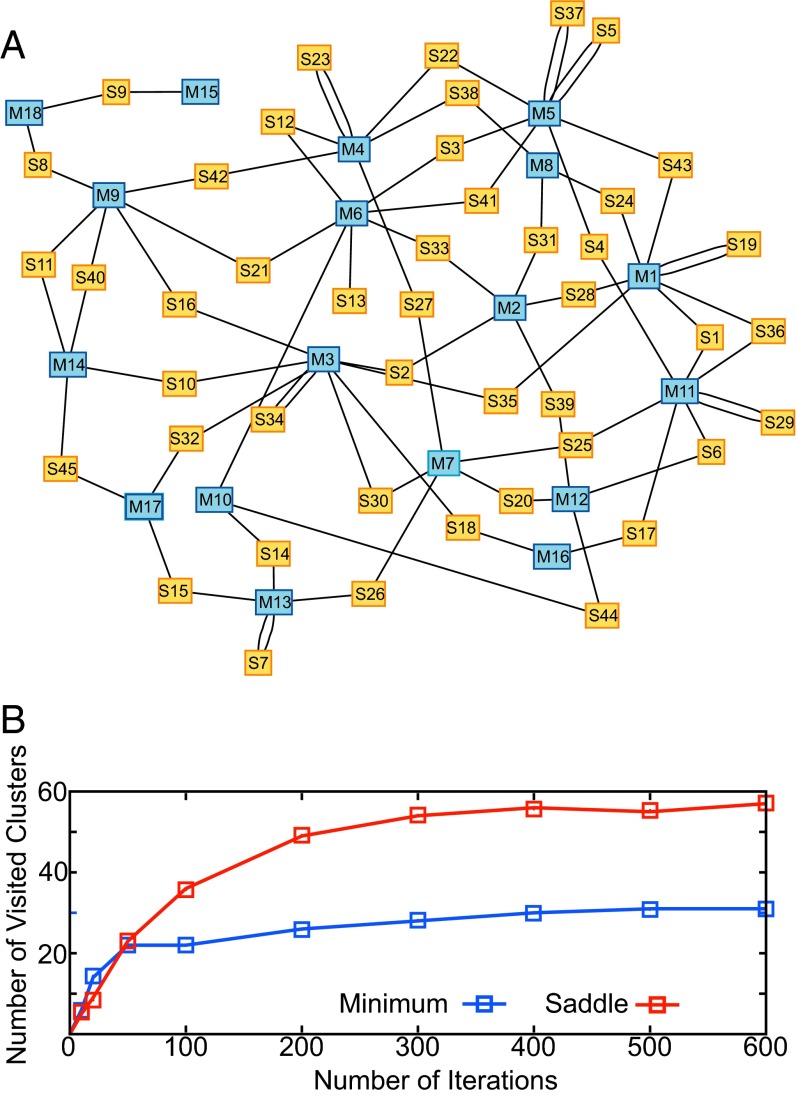
The alanine dipeptide illustrated in Fig. 2 serves as a simple, illustrative example for the START algorithm. However, because the FES can also be generated via numerous enhanced sampling methods, and the locations of minima and saddles can be read off directly from the FES (8, 34), we consider next the alanine tripeptide in vacuum to provide an example of a nontrivial four-dimensional FES. It is instructive to test START on such a system. The two pairs of Ramanchandral angles are the most flexible CVs for this problem. To search as many minima and saddles as possible, 600 START iterations are used, and the total simulation time is nearly 150 ns. Local mean force fitting, followed by maximum separation testing, was applied to generate the critical points, eigenvalues, eigenvectors, and l scores. Eighteen minima (M1–M18) and 45 saddles (S1–S45) were selected (SI Appendix). Seventeen minima found in this study also show up in the previously reported UFED study (8), and one extra minimum, M14, is found. However, this minimum lies close to S40 and possesses a correspondingly small Hessian eigenvalue (SI Appendix), indicating that this minimum is shallow. With the information of all minima and saddles, it is possible to set up a network or graph connecting all metastable configurations. The network consisting of all possible conformational changes through various saddle points is exhibited in Fig. 3A. Blue and yellow vertices correspond to minima and saddles, respectively.
Fig. 3.
(A) A network representing the four-dimensional FES of an alanine tripeptide in vacuum. The CVs are the four Ramachandran dihedral angles of two residues. Each blue box represents a minimum and each yellow box represents a saddle. Generally, each saddle relaxes into two different minima, and two edges are drawn to connect the saddle with these minima, as shown. However, due to the periodicity of the CVs, some saddles, such as S5, S7, S19, S29, S37, and S44, can relax to one minimum only via two different pathways. This situation arises when dihedral angles are used as CVs and is not expected to occur for nonperiodic CVs. (B) The number of clusters after clustering in the START protocol increases with the number of iterations. Most of the minima/saddles are explored within the first 300 iterations.
Fig. 3B shows the number of clusters obtained as a function of the number of iterations. The number of clusters visited increases rapidly at the beginning and more slowly thereafter because the probability of finding a previously visited cluster increases during the START search procedure. After roughly 300 iterations, START has identified nearly all of the minima and most of the saddles. The subsequent 300 iterations simply provide additional mean force samples, which improves the accuracy of the local mean force fitting.
Met-Enkephalin.
Met-enkephalin (Tyr-Gly-Gly-Phe-Met) is a pentapeptide well known as an endogenous ligand of the opioid receptors and distributed throughout the central nervous system. For this small peptide, we used the full set of 10 Ramachandran angles as CVs. In terms of these CVs, the FES is nontrivial (15, 16). Thus, this system provides a very challenging 10-dimensional FES to test the ability of START. Our simulations used 6,905 START iterations (3.5 μs). After locally fitting the FES around a landmark to a quadratic form and testing all clusters by the maximum separation test, 1,081 minima and 1,431 saddles are located (SI Appendix). Saddles connecting to one minimum due the periodicity of the CVs are excluded here because they provide no information on conformational changes.
Similiar to Fig. 3A, a network representation with all minima and saddles as vertices can be constructed for this example. Viewing this network is clearly nontrivial. However, groups of landmarks may share structural similarities on a more coarse-grained level, and the 10 chosen CVs could exhibit structural redundancy. We therefore use the five α-carbon atoms to distinguish structural archetypes. The similarity between two different landmarks is based on the root-mean-square deviation (rmsd) of these α-carbon atoms. The network can be organized by grouping landmarks based on structural similarity, which here is achieved using the sketch-map method (16). The sketch map is a variation of multidimensional scaling that seeks a meaningful dimensional reduction of a high-dimensional configuration space while retaining the cluster structure in the low-dimensional representation (details in Materials and Methods). As shown in Fig. 4A, similar landmarks are clustered, and three regions indicate three major classes of structures. The ability to explore various folded and unfolded structures clearly proves that START is powerful as a global search tool on an HDFES. The locations of the landmarks generated by START are now used as inputs into an enhanced sampling calculation to obtain the free energies of these landmarks. Several enhanced sampling algorithms can be used to estimate the free energies of the landmarks. Here, we use driven adiabatic free energy dynamics (d-AFED)/temperature-accelerated MD (TAMD) (2, 3) to evaluate free energies of the landmarks because of d-AFED’s ability to sweep rapidly over the free energy landscape and quickly generate free energies at the START landmark locations. The same CVs as in START are used in the d-AFED run (details in Materials and Methods). The free energies of landmarks from a 500-ns d-AFED simulation are shown in Fig. 4B. In fact, the first 200 ns of the d-AFED simulation are already sufficient to select quantitatively the low free energy landmarks (<8 kcal/mol) to within 1 kcal/mol (Fig. 4C). Thus, it should be clear that having this information available a priori is considerably more efficient than searching for the landmarks from scratch via the enhanced sampling procedure.
Fig. 4.
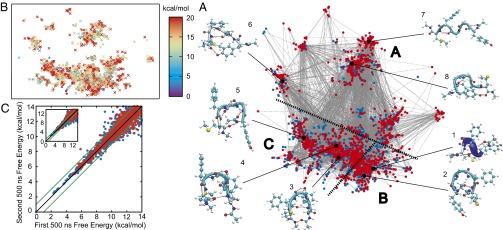
Met-enkephalin in vacuum has been studied by START with the 10 Ramachandran dihedral angles as CVs. (A) The network of all landmarks. Each blue dot denotes a minimum, and each red dot corresponds to a saddle. The coordinates of the vertices are generated by the sketch-map algorithm (16). Every saddle is connected with two minima via solid gray lines. Three major classes of configurations are labeled “A,” “B,” and “C” and divided by black dashed lines. Region A includes all landmarks associated with “unfolded” or “extended” structures. Examples are structures 6, 7, and 8, as shown. Region B corresponds to helical structures, e.g., structures 1 ( helix) and 2. Region C mainly contains hairpin-like conformations. There are β-hairpin structures with various turns: a γ-turn for structure 3 and a β-turn for structure 4; and there are other “U”-shaped structures, e.g., structure 5. Various stable structures (folded and unfolded) indicate the diversity of metastable configurations that were sampled by START. (B) Landmark free energies are estimated from a 500-ns d-AFED/TAMD simulation. A circle denotes a minimum, and a cross corresponds to a saddle. All landmarks with free energies higher than 20 kcal/mol are shown in red. (C) The correlation between landmark free energies from two independent 500-ns d-AFED simulations. Blue dots represent minima, and red dots represent saddles. A point close to the black diagonal indicates that the two free energy values are close. Two green lines represent a ±1 kcal/mol error. The Inset shows the same correlation from two independent 250-ns d-AFED simulations.
Conclusion and Perspective
A robust and efficient approach for searching minima and saddles (landmarks) on an HDFES, START, has been introduced. START provides a strategy for analyzing HDFESs and circumventing the difficulties of uniform sampling and global construction of the HDFES. We used the alanine tripeptide and met-enkaphlin examples to show that START is a powerful tool for the global exploration of an HDFES and for the fast and accurate pinning down of exact locations of landmarks. Although our examples were performed in the gas phase, it is important to note that, since the START algorithm targets the FES in selected CVs, these systems could just as well have been performed in explicit solvent, a feature that distinguishes START from methods that directly target the potential energy surface. If the main goal of a study is to explore the FES, including identifying important configurations such as folded structures in proteins and polymorphs of molecular crystals and computing free energy differences between them, the landmarks located by START are important inputs. The saddles located by START can also be used to construct a good initial guess for subsequent searching of transition paths connecting the two minima on the FES with methods such as the nudged-elastic band approach (17) or the string method (35). The relative free energies of all (or some) landmarks could be easily evaluated by other enhanced sampling methods once the landmarks are located. A network or graph containing all of the landmarks can be constructed as a representation of the HDFES. This network, which also specifies connections between saddles and minima as the edges in the graph, provides important information for studying mechanisms of conformational changes in the system. A related representation was proposed to set up a network for organic reactions (36). In the present scheme, our graph representation allows us to apply graph analysis methods on the HDFES in which the vertices are characterized by a set of key features or molecular structural similarity, so that important properties of the system can be subsequently revealed and elucidated. In a manner that is similar to building a stationary point database in discrete path sampling (22), landmarks located by START, together with their free energies and the graph representation, can also be used for further kinetic studies.
Materials and Methods
Two test systems, here the alanine di- and tripeptides and met-enkaphalin in vacuum, are studied by the START algorithm. Samples for and required by START are generated from restrained molecular dynamics simulations with fixed . All simulations were performed using the PINY_MD (37) package with the CHARMM22 (38) force field. The reversible multiple time-step algorithm r-RESPA (39) was used to integrate the equations of motion, with a 1.0-fs time step for nonbonded interactions and a 0.5-fs time step for intramolecular interactions. The Nosé–Hoover chain algorithm was used with chain length 2 to maintain an average temperature of 300 K. The CVs in all three examples were taken to be the Ramachandran dihedral angles, and the coupling constant κ for the restrained simulations was 278.2 kcal⋅mol−1⋅rad−2. The simulation time for each restrained simulation was 1 ps for the alanine di- and tripeptides. In the met-enkaphalin example, the simulation time for each restrained simulation was 1 ps for optimizing to minima, whereas the simulation time was 10 ps for saddle optimizations. In all three cases, the step size is chosen as 6.0° (0.105 rad). A minimum/saddle optimization was regarded as converged when the trajectory remained in a box with side length 23° (0.4 rad) for 20 steps for the alanine dipeptide, 30 steps for the alanine tripeptide, and 40 steps for met-enkaphalin. Before minimum/saddle optimizations, the system was shot out along a random direction for 5 steps. The initial direction of n in GAD was chosen to be the same as this random shooting direction. In the saddle optimization, the parameter for the alanine dipeptide and the alanine tripeptide, and for the met-enkaphalin due to the very high dimensionality of the FES.
The density-based spatial clustering for applications with noise (DBSCAN) (40) is suitable for analyzing and classifying the clusters generated in the two optimization steps of the START protocol. The DBSCAN algorithm begins with an arbitrary unvisited sample point on the FES and a count of the number of neighboring points in the sample whose Euclidean distance from the sample point is not larger than some specified value r. If the number of neighboring sample points is larger than some lower bound p, a new cluster is assigned. Otherwise, the point is considered “noise.” When a new cluster is assigned, DBSCAN combines all of the neighboring points (neighborhood) within the distance r, together with their neighborhood, provided the points are not noisy points. The cluster growth continues until no points remain (that are not designated as noise) that can be assigned to the cluster. Unlike clustering methods such as k-means and Gaussian mixture models, DBSCAN requires no initial guess of the number or shape of the clusters. In this study, the radius of the neighborhood r is 0.122 rad or 7.0° and the lower bound is . In the following maximum separation test, the l score, above which a cluster passes the test, is 0.2 in the alanine tripeptide example and 0.25 (for minima) and 0.11 (for saddles) in the met-enkaphalin example.
In the met-enkaphalin example, the objective function of the sketch map is (16), where is the Euclidian distance of two different landmarks in the projected 2D space. is the rmsd between two averaged structures in terms of α-carbon atoms. Switching functions and follow the general formula (16). The values of a and b are 3.0 and 9.0 for and 2.0 and 2.0 for . The parameter σ is 0.5 Å in both cases. The optimization strategy follows that in ref. 16. In the d-AFED simulation, the temperature of s is 800 K, and the mass is 168.0 Å2⋅rad−2 times the mass of the proton. The other simulation parameters are the same as those prescribed before. Independent samples are taken from the trajectories every 1 ps. These samples are convoluted with a homogeneous Gaussian kernel with a variance of 20° to generate a probability distribution of s, and landmark free energies can be evaluated following the method in ref. 3.
Supplementary Material
Acknowledgments
M.E.T. and M.C. acknowledge support from the National Science Foundation Grant CHE-1301314. M.C. also acknowledges the Margaret and Herman Sokol Doctoral Fellowship in the Sciences.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1418241112/-/DCSupplemental.
References
- 1.Rosso L, et al. On the use of the adiabatic molecular dynamics technique in the calculation of free energy profiles. J Chem Phys. 2002;116:4389–4402. [Google Scholar]
- 2.Maragliano L, Vanden-Eijnden E. A temperature accelerated method for sampling free energy and determining reaction pathways in rare events simulations. Chem Phys Lett. 2006;426(1–3):168–175. [Google Scholar]
- 3.Abrams JB, Tuckerman ME. Efficient and direct generation of multidimensional free energy surfaces via adiabatic dynamics without coordinate transformations. J Phys Chem B. 2008;112(49):15742–15757. doi: 10.1021/jp805039u. [DOI] [PubMed] [Google Scholar]
- 4.Laio A, Parrinello M. Escaping free-energy minima. Proc Natl Acad Sci USA. 2002;99(20):12562–12566. doi: 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bonomi M, Parrinello M. Enhanced sampling in the well-tempered ensemble. Phys Rev Lett. 2010;104(19):190601. doi: 10.1103/PhysRevLett.104.190601. [DOI] [PubMed] [Google Scholar]
- 6.Darve E, Rodríguez-Gómez D, Pohorille A. Adaptive biasing force method for scalar and vector free energy calculations. J Chem Phys. 2008;128(14):144120. doi: 10.1063/1.2829861. [DOI] [PubMed] [Google Scholar]
- 7.Hénin J, Fiorin G, Chipot C, Klein ML. Exploring multidimensional free energy landscapes using time-dependent biases on collective variables. J Chem Theory Comput. 2010;6(1):35–47. doi: 10.1021/ct9004432. [DOI] [PubMed] [Google Scholar]
- 8.Chen M, Cuendet MA, Tuckerman ME. Heating and flooding: A unified approach for rapid generation of free energy surfaces. J Chem Phys. 2012;137(2):024102. doi: 10.1063/1.4733389. [DOI] [PubMed] [Google Scholar]
- 9.Morishita T, Itoh SG, Okumura H, Mikami M. Free-energy calculation via mean-force dynamics using a logarithmic energy landscape. Phys Rev E Stat Nonlin Soft Matter Phys. 2012;85(6 Pt 2):066702. doi: 10.1103/PhysRevE.85.066702. [DOI] [PubMed] [Google Scholar]
- 10.Piana S, Laio A. Advillin folding takes place on a hypersurface of small dimensionality. Phys Rev Lett. 2008;101(20):208101. doi: 10.1103/PhysRevLett.101.208101. [DOI] [PubMed] [Google Scholar]
- 11.Das P, Moll M, Stamati H, Kavraki LE, Clementi C. Low-dimensional, free-energy landscapes of protein-folding reactions by nonlinear dimensionality reduction. Proc Natl Acad Sci USA. 2006;103(26):9885–9890. doi: 10.1073/pnas.0603553103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tenenbaum JB, de Silva V, Langford JC. A global geometric framework for nonlinear dimensionality reduction. Science. 2000;290(5500):2319–2323. doi: 10.1126/science.290.5500.2319. [DOI] [PubMed] [Google Scholar]
- 13.Coifman RR, et al. Geometric diffusions as a tool for harmonic analysis and structure definition of data: Diffusion maps. Proc Natl Acad Sci USA. 2005;102(21):7426–7431. doi: 10.1073/pnas.0500334102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rohrdanz MA, Zheng W, Maggioni M, Clementi C. Determination of reaction coordinates via locally scaled diffusion map. J Chem Phys. 2011;134(12):124116. doi: 10.1063/1.3569857. [DOI] [PubMed] [Google Scholar]
- 15.Tribello GA, Ceriotti M, Parrinello M. A self-learning algorithm for biased molecular dynamics. Proc Natl Acad Sci USA. 2010;107(41):17509–17514. doi: 10.1073/pnas.1011511107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ceriotti M, Tribello GA, Parrinello M. From the cover: Simplifying the representation of complex free-energy landscapes using sketch-map. Proc Natl Acad Sci USA. 2011;108(32):13023–13028. doi: 10.1073/pnas.1108486108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Henkelman G, Uberuaga BP, Jónsson H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J Chem Phys. 2000;113(22):9901–9904. [Google Scholar]
- 18.Henkelman G, Jónsson H. A dimer method for finding saddle points on high dimensional potential surfaces using only first derivatives. J Chem Phys. 1999;111(15):7010–7022. [Google Scholar]
- 19.Munro LJ, Wales DJ. Defect migration in crystalline silicon. Phys Rev B. 1999;59:3969–3980. [Google Scholar]
- 20.Barkema GT, Mousseau N. Event-based relaxation of continuous disordered systems. Phys Rev Lett. 1996;77(21):4358–4361. doi: 10.1103/PhysRevLett.77.4358. [DOI] [PubMed] [Google Scholar]
- 21.Malek R, Mousseau N. Dynamics of Lennard-Jones clusters: A characterization of the activation-relaxation technique. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 2000;62(6 Pt A):7723–7728. doi: 10.1103/physreve.62.7723. [DOI] [PubMed] [Google Scholar]
- 22.Wales DJ. Discrete path sampling. Mol Phys. 2002;100(20):3285–3305. [Google Scholar]
- 23.Widrow B, Stearns SD. Adaptive Signal Processing. Prentice-Hall; Upper Saddle River, NJ: 1985. [Google Scholar]
- 24.Bottou L. Stochastic learning. In: Bousquet O, von Luxburg U, editors. Advanced Lectures on Machine Learning, Lecture Notes in Artificial Intelligence, LNAI 3176. Springer; Berlin: 2004. pp. 146–168. [Google Scholar]
- 25.Valsson O, Parrinello M. Variational approach to enhanced sampling and free energy calculations. Phys Rev Lett. 2014;113(9):090601. doi: 10.1103/PhysRevLett.113.090601. [DOI] [PubMed] [Google Scholar]
- 26.E W, Engquist B. The heterogeneous multiscale methods. Commun Math Sci. 2002;1(1):87–132. [Google Scholar]
- 27. Gear WC, et al. (2003) Equation-free, coarse-grained multiscale computation: Enabling macroscopic simulators to perform system-level analysis. Commun Math Sci 1(4):715–762.
- 28.Maragliano L, Fischer A, Vanden-Eijnden E, Ciccotti G. 2006. String method in collective variables: Minimum free energy paths and isocommittor surfaces. J Chem Phys 125(2):024106. [DOI] [PubMed]
- 29. Samanta A, Chen M, Yu T-Q, Tuckerman M, E W (2014) Sampling saddle points on a free energy surface. J Chem Phys 140(16):164109. [DOI] [PubMed]
- 30.E W, Zhou X. The gentlest ascent dynamics. Nonlinearity. 2011;24(6):1831–1842. [Google Scholar]
- 31.Samanta A, E W. 2012. Atomistic simulations of rare events using gentlest ascent dynamics. J Chem Phys 136(12):124104.
- 32.Borkar VS. Stochastic Approximation: A Dynamical Systems Viewpoint. Cambridge Univ Press; New York: 2008. [Google Scholar]
- 33.Strodel B, Wales DJ. Free energy surfaces from an extended harmonic superposition approach and kinetics for alanine dipeptide. Chem Phys Lett. 2008;466(4–6):105–115. [Google Scholar]
- 34.Rosso L, Abrams JB, Tuckerman ME. Mapping the backbone dihedral free-energy surfaces in small peptides in solution using adiabatic free-energy dynamics. J Phys Chem B. 2005;109(9):4162–4167. doi: 10.1021/jp045399i. [DOI] [PubMed] [Google Scholar]
- 35.E W, Ren W, Vanden-Eijnden E. String method for the study of rare events. Phys Rev B. 2002;66:052301. doi: 10.1021/jp0455430. [DOI] [PubMed] [Google Scholar]
- 36.Rappoport D, Galvin CJ, Zubarev DYu, Aspuru-Guzik A. Complex chemical reaction networks from heuristics-aided quantum chemistry. J Chem Theory Comput. 2014;10(3):897–907. doi: 10.1021/ct401004r. [DOI] [PubMed] [Google Scholar]
- 37.Tuckerman ME, et al. Exploiting multiple levels of parallelism in molecular dynamics based calculations via modern techniques and software paradigms on distributed memory computers. Comput Phys Commun. 2000;128:333–376. [Google Scholar]
- 38.MacKerell AD, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102(18):3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 39.Tuckerman ME, Martyna GJ, Berne BJ. Reversible multiple time scale molecular dynamics. J Chem Phys. 1992;97:1990–2001. [Google Scholar]
- 40.Ester M, Kriegel H-p, Jörg S, Xu X. 1996. A density-based algorithm for discovering clusters in large spatial databases with noise. Proceedings of 2nd International Conference on Knowledge Discovery and Data Mining (KDD-96), eds Simoudis E, Han J, Fayyad U (AAAI Press, Menlo Park, CA), pp 226–231.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.