Electron crystallography of ultrathin 3D protein crystals: Atomic model with charges

Significance

Electron crystallography has the potential to analyze crystals of membrane proteins and macromolecular complexes too small or too thin for X-ray crystallography, as electrons are scattered four to five orders of magnitude more strongly than X-rays. Electron crystallography yields Coulomb potential maps, rather than electron density maps as X-rays do, providing information on charged states of amino acids and metals. Here we present such Coulomb potential maps at 3.4-Å and 3.2-Å resolution, respectively, of Ca²⁺-ATPase and catalase obtained from crystals of just a few layers thick. These maps demonstrate that it is indeed possible to build atomic models from such crystals and charge information is included, often critical in understanding protein function.

Abstract

Membrane proteins and macromolecular complexes often yield crystals too small or too thin for even the modern synchrotron X-ray beam. Electron crystallography could provide a powerful means for structure determination with such undersized crystals, as protein atoms diffract electrons four to five orders of magnitude more strongly than they do X-rays. Furthermore, as electron crystallography yields Coulomb potential maps rather than electron density maps, it could provide a unique method to visualize the charged states of amino acid residues and metals. Here we describe an attempt to develop a methodology for electron crystallography of ultrathin (only a few layers thick) 3D protein crystals and present the Coulomb potential maps at 3.4-Å and 3.2-Å resolution, respectively, obtained from Ca²⁺-ATPase and catalase crystals. These maps demonstrate that it is indeed possible to build atomic models from such crystals and even to determine the charged states of amino acid residues in the Ca²⁺-binding sites of Ca²⁺-ATPase and that of the iron atom in the heme in catalase.

Protein atoms scatter electrons four to five orders of magnitude more strongly than they do X-rays, thus allowing individual protein molecules to be imaged by electron microscopy (1). Although not fully exploited so far, electron protein crystallography has great potential and indeed has yielded superb high-resolution (∼2.0-Å resolution) atomic structures from 2D crystals (2). However, electron crystallography of 3D crystals is problematic, as stacking of even a few layers makes diffraction patterns discrete in all directions, and methods developed for conventional electron crystallography of 2D crystals (3) are not useful (SI Appendix, Fig. S1A, Left). This problem can be overcome, however, as Gonen and coworkers demonstrated (4, 5), by rotating the crystal to spatially integrate the intensities of diffraction spots as in X-ray crystallography (SI Appendix, Fig. S1A, Right) or, in certain cases, even combining simple tilt series.

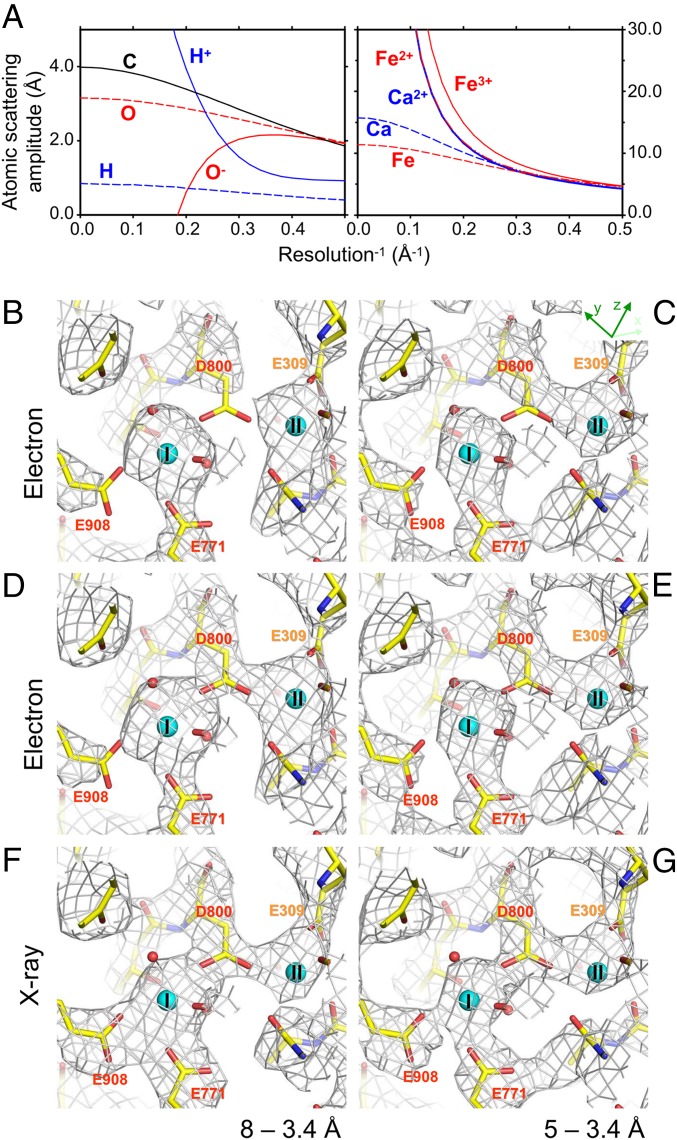
Another important feature of electron scattering is that the diffraction pattern formed by elastically scattered electrons is directly related to the distribution of Coulomb potential. This is in marked contrast to X-rays, which, because they are scattered by electrons, yield an electron density map. Coulomb potential maps may be more difficult to interpret, compared with electron density maps by X-ray crystallography, as the appearance of the same residues may differ depending on their charged state, resolution, and surrounding environment (Fig. 1 and SI Appendix, Fig. S2), but they provide unique information, not attainable by X-rays (6). Theoretical potential maps (F_calc maps; Fig. 1 B–E) calculated from an atomic model of Ca²⁺-ATPase (7) using scattering factors for 300-keV electrons highlight these features. For instance, densities of acidic residues are absent or weak when lower-resolution data are included in the map calculation (Fig. 1 B and C). In contrast, when calculated using scattering factors for X-rays, the densities of the same residues appear more or less identical irrespective of the resolution range (Fig. 1 F and G). These features of Coulomb potential maps result from the fact that atomic scattering factors for electrons vary considerably over a range of spatial frequency depending on the charged state (Fig. 1A) and can become close to zero or even negative (e.g., for O⁻, Fig. 1A). An advantageous consequence is that it is possible to determine experimentally the charged states of protein residues and metals. As proteins use metals of different ionic states for many purposes, notably for catalysis and electron transfer, information on the charged state of metals and amino acid residues can be critical in understanding protein function.

Fig. 1.

Atomic scattering factors and theoretical maps. (A) Atomic scattering factors for 300-keV electrons based on values from International Tables for Crystallography (14), except for H⁺ (taken from ref. 15). Scattering factors for X-rays are provided in SI Appendix, Fig. S2. (B–G) Theoretical Coulomb potential (B–E) and electron density (F and G) maps around the Ca²⁺-binding site of Ca²⁺-ATPase, calculated for 8- to 3.4-Å (B, D, and F) and 5- to 3.4-Å (C, E, and G) resolution and contoured at 1.0 σ (B–E) or 1.2 σ (F and G). Viewed from the cytoplasmic side approximately perpendicular to the membrane. Superimposed is the atomic model of Ca²⁺-ATPase derived from that determined by X-ray (PDB ID code 1SU4) (7) and refined in this study. Cyan spheres represent bound Ca²⁺ (I and II). For the potential maps (B–E), standard charges are assigned to all titratable residues (except for Asp-800 in D and E, treated as a neutral residue) and calculated using the scattering factors for 300-keV electrons. Note that appearances of some charged residues vary substantially depending on the resolution range in the Coulomb potential maps (compare B and C or D and E), but are nearly identical in the electron density maps (F and G).

Here we present the Coulomb potential maps at 3.4-Å and 3.2-Å resolution, respectively, of Ca²⁺-ATPase and catalase obtained from ultrathin (just a few layers thick) crystals using a new electron diffractometer (SI Appendix, Fig. S1B). These maps demonstrate that it is indeed possible to build atomic models from such crystals and even to determine the charged states of amino acid residues in the Ca²⁺-binding sites of Ca²⁺-ATPase and that of the iron atom in the heme in catalase.

Results and Discussion

Data Collection and Structure Determination.

The design of the newly developed diffractometer is shown in SI Appendix, Fig. S1B. A high-precision rotary encoder installed in the goniometer and a simple Faraday cup integrated into the condenser lens aperture continuously monitor the stage rotation (tilt) angle and incident beam current, respectively, and control the opening and closing of the shutter. The goniometer stage is rotated during exposure to spatially integrate intensities of diffraction spots but only in one direction to minimize the effect of backlash. An energy filter (8) that passes only zero-loss (i.e., unscattered and elastically scattered) electrons is mandatory, as only elastically scattered electrons form diffraction patterns directly related to the distribution of Coulomb potential. Energy filtering also largely reduces background noise arising from inelastically scattered electrons, in particular, by amorphous ice surrounding the crystal (9, 10). For building atomic models with highly diffracting crystals (e.g., those of lysozyme), rotation diffraction patterns obtained with a conventional microscope by continuous specimen tilting and image acquisition (4) or combining even simple tilt series (5) could be enough. Nevertheless, our method is highly advantageous particularly in generating accurate potential maps of weakly diffracting crystals, such as those of membrane proteins.

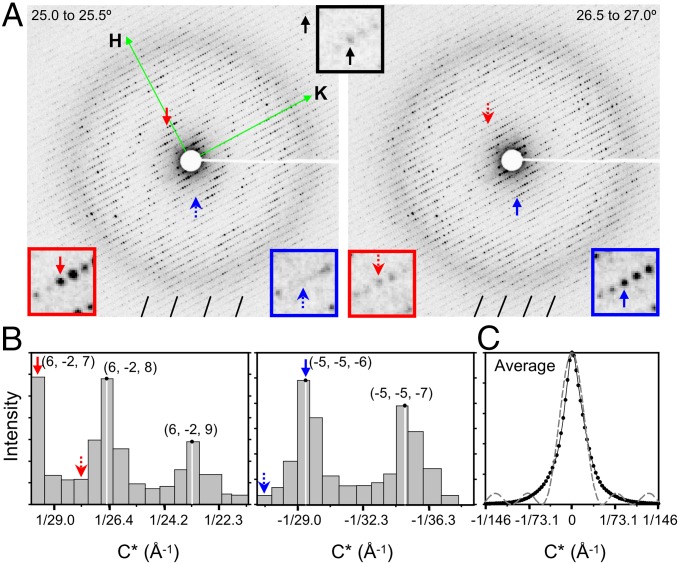
Using the electron diffractometer, we collected rotation series of diffraction patterns from ultrathin protein crystals of Ca²⁺-ATPase (7) from rabbit skeletal muscle sarcoplasmic reticulum (SR) and catalase (11) from bovine liver. These plate-like protein crystals were a few tens of micrometers wide and <0.15 μm thick and embedded in amorphous ice on electron microscope grids (SI Appendix, Fig. S3 A and B). Electron diffraction patterns thus obtained are clear (Fig. 2A) and extend beyond 2-Å resolution with catalase crystals. Diffraction spots are clearly resolved even in frames with large rotation (tilt) angles (SI Appendix, Fig. S3 C and D). A total of 10–30 frames can be recorded of each field at 0.5° or 1.0° intervals. Such series of diffraction patterns (Movie S1) show well-separated spots in all directions, despite rather large c-axis dimensions [Ca²⁺-ATPase, 147 Å (7); catalase, 206 Å (12)]. Reflecting the very large Ewald sphere for 300-keV electrons (λ = 0.02 Å as opposed to ∼1.0 Å used in conventional X-ray crystallography), Laue zones (bars in Fig. 2 A and B), corresponding to lunes in X-ray diffraction patterns, are evident only in frames with small rotation (tilt) angles. A new set of programs was developed for indexing, refinement of crystal lattice and orientation parameters, and integration of intensity using 3D profile fitting (SI Appendix, Fig. S4 A and B). From the profile of diffraction spots along the Z* axis, the number of layers that makes up the crystals can be estimated (four or five in this case). A total of 99 rotation series for Ca²⁺-ATPase and 58 for catalase were merged, resulting in completeness of 67.5% for Ca²⁺-ATPase and 72.9% for catalase with high redundancy. Due to a limitation of the goniometer stage (maximum tilt angle of ∼60°), completeness is limited to the level achieved unless assisted by symmetry. Nevertheless, the resultant Coulomb potential maps were of good quality and proved to be informative.

Fig. 2.

Electron diffraction of an ultrathin catalase crystal. (A) Two frames of a rotation series. Rotation (tilt) angles covered are 25.0–25.5° (Left) and 26.5–27.0° (Right). Approximately 0.03 electrons per Ų are used for each frame. Diffraction spots are visible at least to 2.4-Å resolution (black arrow and Inset at the Top Center). Note that layers of diffraction spots (Laue zones) appear almost straight (bars at Bottom) due to the short wave length of 300-keV electron (0.02 Å). Red and blue boxes enclose parts of diffraction patterns around the reflection (6, −2, 7) (red arrows) and (−5, −5, −6) (blue arrows), respectively. A full set of the frames that constitute this rotation series is provided as Movie S1. (B) Intensity profiles of selected diffraction spots with the same (H and K) indices plotted along the C* axis (c = 206 Å). The arrows correspond to those in A. Each bar corresponds to one rotational frame. Vertical white lines indicate the peak positions estimated by quadratic interpolation over three successive frames. (C) The average spot profile (rocking curve; solid line with points) corrected for mosaic spread (∼0.2° with this crystal), representing the square of Laue function. From this curve, the thickness of the crystal is estimated to be four to five layers. Broken curve represents the square of Laue function for four layers.

The structures were solved by molecular replacement starting from the atomic models of Ca²⁺-ATPase (7) and catalase (13) obtained by X-ray crystallography. Atomic scattering factors for 300-keV electrons were used (14, 15), assuming standard charged states for all titratable residues. The models were refined against the electron diffraction data ranging from 8 to 3.4 Å for Ca²⁺-ATPase and from 8 to 3.2 Å for catalase, because, at lower resolution, the effects of charged states are pronounced, and theoretical scattering factors calculated for ionized atoms in gas phase (14) would be inappropriate for applying to atoms in protein (Fig. 1A). Data and refinement statistics are provided in SI Appendix, Table S1 and Fig. S5A. Distribution of merged diffraction spots is displayed in SI Appendix, Fig. S5B.

Coulomb Potential Maps of Ca²⁺-ATPase.

SR Ca²⁺-ATPase SERCA1a is an integral membrane protein of ∼110 kDa and transports Ca²⁺ into the SR lumen against a concentration gradient by hydrolyzing ATP. X-ray crystallography of Ca²⁺-ATPase in different physiological states has revealed that large conformational changes occur during Ca²⁺ transport (7, 16–19). Ca²⁺-ATPase has two high-affinity Ca²⁺-binding sites (I and II, Fig. 1 B–G) in the transmembrane region, formed by a cluster of acidic amino acid residues.

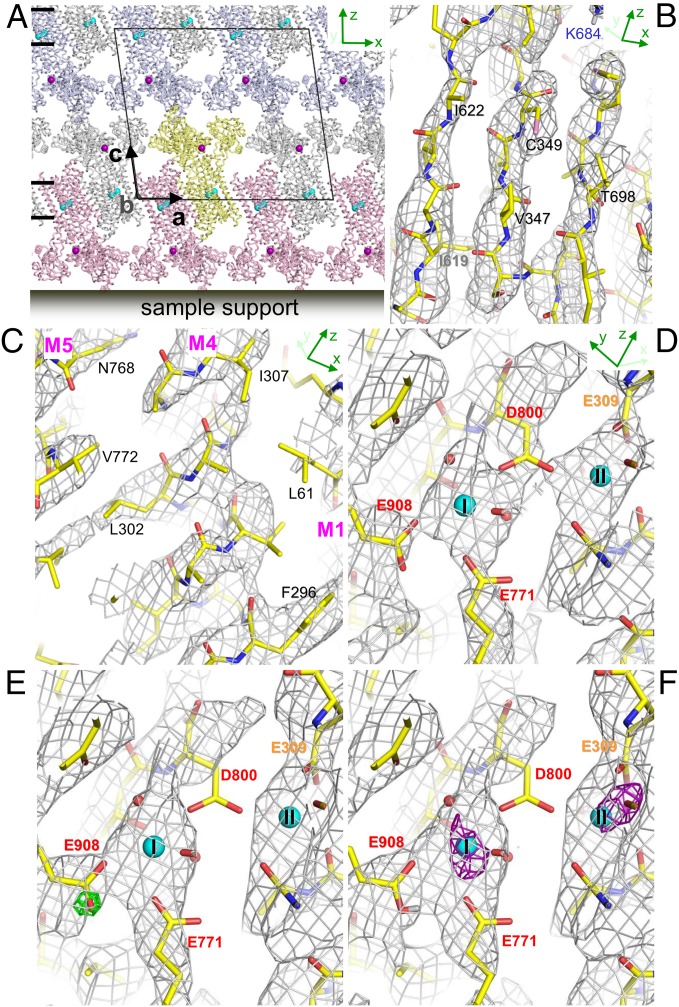
Ca²⁺-ATPase yields thin crystals comprising a stack of 2D crystals in the presence of millimolar Ca²⁺ (7) (Fig. 3A). By changing the crystallization conditions, the thickness can be made thin enough (<0.1 µm) for electron diffraction or thick enough (>10 µm) for X-ray crystallography (7). The Coulomb potential map calculated from the merged diffraction data at 20- to 3.4-Å resolution clearly resolved β-strands around the ATP binding site (Fig. 3B) and transmembrane helices (Fig. 3C). The continuity of density appeared better in this resolution range, although refinement statistics were slightly worse when low-resolution data were included. Coulomb potential maps around the Ca²⁺-binding sites, calculated from 8- to 3.4-Å (Fig. 3 E and F) or 5- to 3.4-Å resolution data (Fig. 3D), show well resolved side chains but different features. For instance, the density for the carboxyl group of Asp-800 is absent in the 8- to 3.4-Å resolution map (Fig. 3 E and F), but present in the 5- to 3.4-Å resolution map (Fig. 3D). This is the expected behavior of a negatively charged residue according to the theoretical maps (Fig. 1 B and C). Continuum electrostatic calculations (20) indeed show that the carboxyl of Asp-800 has the lowest pK_a (<3) of the binding residues, corresponding to a protonation probability of <1%.

Fig. 3.

Crystal packing and Coulomb potential maps of Ca²⁺-ATPase. (A) A preferred orientation of the crystals of Ca²⁺-ATPase (7) with respect to the sample support. Short bars on the Left indicate approximate positions of lipid bilayers. (B and C) A Coulomb potential (σ_A-weighted 2 |F_obs| − |F_calc|) map around the ATP binding site (B) and that of the transmembrane region (C), contoured at 1 σ and overlaid with the atomic model refined in this study. Calculated from 20- to 3.4-Å resolution data with missing cone. Antiparallel β-strands around the phosphorylation site (B) and three transmembrane helices (M1, M4, and M5) near the Ca²⁺ binding sites (C) are clearly resolved. (D–F) Coulomb potential (σ_A-weighted 2|F_obs| − |F_calc|) maps around the Ca²⁺-binding sites, contoured at 1 σ and superimposed on the atomic model. (D) Calculated from 5- to 3.4-Å resolution data with missing cone. (E) Calculated from 8- to 3.4-Å resolution data with a difference (σ_A-weighted |F_obs| − |F_calc|) map (green; contoured at 3.5 σ) overlaid. (F) The same as in E, but calculated with Glu-908 protonated. No significant difference is observed in the density map around Glu-908. If the structure factor for neutral Ca (Fig. 1A) is used, two large positive peaks of 4.3 σ and 4.5 σ appear at sites I and II, respectively, in the difference (|F_obs| − |F_calc|) map (purple nets in F, contoured at 3.5 σ). Small cyan spheres (I and II) represent two bound Ca²⁺ (A and D–F) and the purple sphere Na⁺ (A).

As many acidic residues cluster to form the transmembrane Ca²⁺-binding sites, the pK_as of the carboxyl groups may be highly perturbed. The maps for Glu-908, expected to be protonated to form a hydrogen bond with Glu-771 (20), show distinctly different behavior, displaying positive density at the carboxyl group in both 8- to 3.4-Å and 5- to 3.4-Å resolution maps. Furthermore, the |F_obs| − |F_calc| map calculated from 8- to 3.4-Å resolution data shows a well-defined positive peak of 3.8 σ at the oxygen atom closer to Glu-771 (Fig. 3E), if a negatively charged carboxyl is assumed. This feature is consistent between two data subsets randomly selected from the full dataset (SI Appendix, Fig. S6). The experimental map is well explained if the Glu-908 carboxyl has no charge (Fig. 3F; the peak decreases to 2.3 σ). These observations provide experimental support for electrostatic calculations that indicate that the Glu-908 side chain is protonated (20). Composite omit maps also show consistent features for both Asp-800 and Glu-908 (SI Appendix, Fig. S7 A and B).

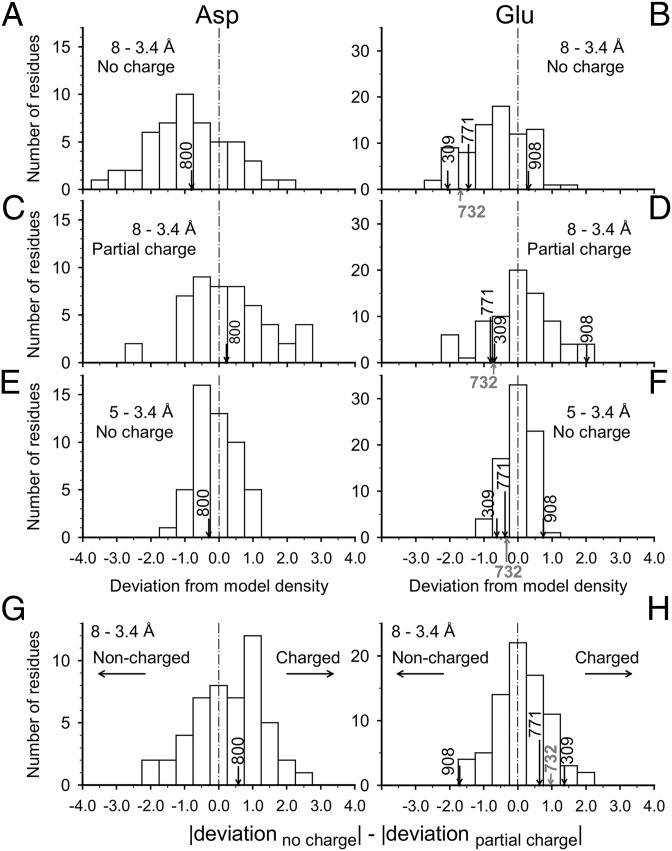
Differences in the appearance of charged residues in Coulomb potential maps at different resolutions may be expected to be more pronounced in the transmembrane region, as the dielectric constant here must be substantially lower than those in regions of the protein outside the membrane. However, Glu-732 in the Na⁺-binding site on the cytoplasmic P-domain also shows the same behavior (SI Appendix, Fig. S8), indicating that the resolution-dependent phenomenon does not depend on a low dielectric. Indeed, the statistics calculated over the entire molecule confirm, more objectively, the difference in appearance of acidic residues. For instance, if all residues are treated as electroneutral, distinct large deviations become apparent with the side chains of only Asp and Glu in the |F_obs| − |F_calc| map (SI Appendix, Fig. S9A). Such deviations (almost) disappear when standard partial charges are assigned to all titratable residues (SI Appendix, Fig. S9B) or low-resolution terms that are sensitive to the difference in atomic scattering factor due to different charged states are excluded from map calculation (SI Appendix, Fig. S9C). Histograms of the deviations of Asp and Glu show clearly that the distribution is offset from zero when no charges are assumed (Fig. 4 A and B), whereas it is better centered but extended toward positive (i.e., likely to be protonated) when standard partial charges are assigned (Fig. 4 C and D). If low-resolution terms are excluded, histograms have narrower distributions, more or less centered around zero (Fig. 4 E and F). As an objective measure of charged/noncharged state, it seems useful to calculate the difference between the deviations from the models (i.e., no charge and partial charges assigned; Fig. 4 G and H). If the map does not show significant change between the two models, this figure becomes close to zero. Of the four Glu residues examined here, only Glu-908 shows a large negative value, indicating that this residue, and only this residue, is highly likely to be protonated (Fig. 4H). In contrast, Asp-800 shows a positive value, like most of the Glu residues (Fig. 4G).

Fig. 4.

Deviation from model density of the side chains of acidic residues in the difference (σ_A-weighted |F_obs| − |F_calc|) Coulomb potential map of Ca²⁺-ATPase. The densities in the difference map are averaged within the van der Waals radius of side chain atoms in each amino acid residue, using CNS (30) with a modified script program. (A–F) Histograms of the deviation for Asp (A, C, and E) and Glu (B, D, and F). All residues are treated as not charged (A, B, E, and F), or partial charges are assigned to all titratable residues (C and D) in the atomic models used for F_calc. Resolution ranges are 8 to 3.4 Å (A–D) and 5 to 3.4 Å (E and F). (G and H) Histograms of difference in deviation (absolute number) from model density between the two |F_obs| − |F_calc| maps, in which no or partial charges are given to all titratable residues [i.e., difference between A and C (G) or B and D (H)]; calculated for the Asp and Glu side chains using the data from 8- to 3.4-Å resolution. In these histograms, noncharged residues go to the Left side and charged residues to the Right. Arrows indicate the acidic residues in the Ca²⁺-binding site (Figs. 1 B–G and 3 D–F) and the one acidic residue in the Na⁺-binding site (Glu-732; SI Appendix, Fig. S8).

This kind of analysis can be extended, at least in theory, to assign partial charges to individual residues. The deviations from model density indeed vary almost linearly according to the partial charges assigned to the carboxyl groups (SI Appendix, Fig. S10). With Asp-800, the deviation becomes zero when a standard partial charge of approximately −0.5 is assigned to both of the carboxyl oxygen atoms. Glu-908 also exhibits an expected behavior but still shows some deviation with zero charge. Therefore, at present, the difference maps appear to be useful only for qualitative measure of charged/noncharged state (Fig. 4 G and H and SI Appendix, Fig. S11 G and H).

The Coulomb potential map should also be able to distinguish the charge of bound calcium. Although the appearance of the map does not change much, if we assume no charge for the bound calcium, the |F_obs| − |F_calc| map exhibits large positive densities around the two calcium atoms (purple nets in Fig. 3F), indicating that both bound calciums are indeed positively charged.

Coulomb Potential Maps of Catalase.

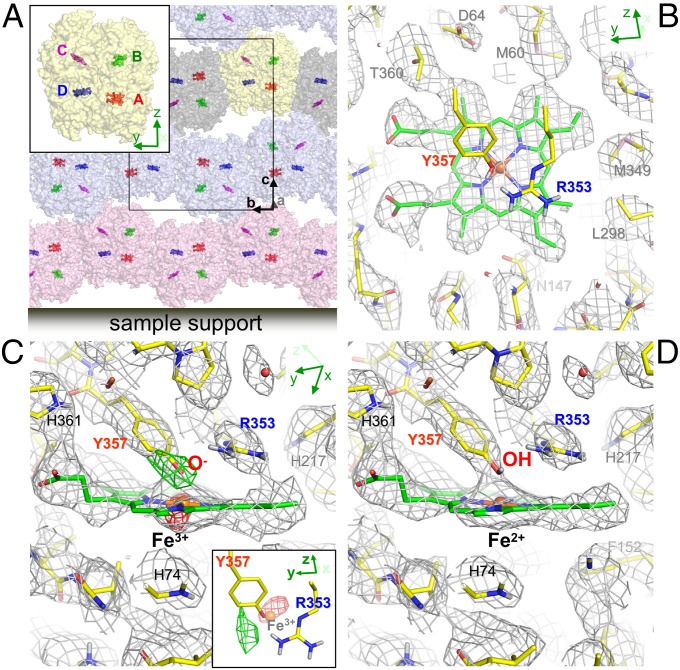
Catalase is a heme-binding enzyme and decomposes toxic hydrogen peroxide (H₂O₂) into H₂O and O₂. Bovine liver catalase is composed of four identical subunits of ∼60 kDa each. Every subunit contains one heme with Fe (III) as the catalytic center. For some time it has been known that the plate-like crystals of catalase yield superb electron diffraction patterns (11), but they are too thin for X-ray crystallography (21). The crystals sit on the substrate through the a–b plane with only one preferred orientation (Fig. 5A). The asymmetric unit of the crystal contains one tetramer (Fig. 5A), indicating that noncrystallographic symmetry (NCS) can be used, at least partially, for overcoming the problem of a missing cone. Indeed, NCS averaging substantially improved the Coulomb potential map of catalase (SI Appendix, Fig. S12). As a result, the coordination of the heme is well resolved at 3.2-Å resolution (Fig. 5B). Here again, the charged states of Asp and Glu residues are clearly resolved (SI Appendix, Figs. S9D and S11), even though catalase is a soluble protein.

Fig. 5.

Crystal packing and Coulomb potential maps of catalase. (A) A preferred orientation of catalase tetramers on the sample support. The c axis becomes parallel to the incident electron beam when the specimen stage is at zero tilt. The asymmetric unit contains one tetramer (Inset). Carbon backbones of hemes are shown in sticks. (B–D) Coulomb potential maps (σ_A-weighted 2 |F_obs| − |F_calc| maps) around the heme binding site of subunit A (red in A) overlaid with the atomic model refined in this study. Calculated from 8- to 3.2-Å resolution data with missing cone, but with NCS averaging. (B) Viewed from the proximal side of the heme. Calculated assuming Fe (II) and nonionized Tyr-357. No map is overlaid for Arg-353 and Tyr-357 for clarity. (C) Viewed from the direction roughly parallel to the heme ring. Calculated assuming Fe (III) and negatively charged Tyr-357. A difference Fourier (σ_A-weighted |F_obs| − |F_calc|) map shows a large negative peak of −3.9 σ (red; contoured at −3.0 σ) around the iron atom and a positive peak of 4.0 σ (green; contoured at 3.0 σ) around the hydroxyl group of Tyr-357. Inset shows the peaks with the iron atom and Arg-353 and Tyr-357, viewed from the same direction as in B. (D) The same as in C, but calculated for Fe (II) and nonionized Tyr-357. The peaks around the iron atom and the hydroxyl group of Tyr-357 become small in a |F_obs| − |F_calc| map (SI Appendix, Table S2). Gray nets are contoured at 1.3 σ.

The iron atom of catalase is in the ferric state (III) (e.g., ref. 22), stabilized by the ionized phenolic oxygen of Tyr-357, stabilized in turn by Arg-353, at an unusually short distance (2.0 Å) from the iron atom (23). However, the |F_obs| − |F_calc| Coulomb potential map calculated assuming Fe (III) and ionized phenolic oxygen, shows a large negative peak of −3.9 σ at the iron atom and a prominent positive peak of +4.0 σ near the phenolic oxygen of Tyr-357 (Fig. 5C). The size of these peaks is reduced if the charged state for the iron atom is lowered and a hydrogen is placed at the phenolic oxygen (Fig. 5D and SI Appendix, Table S2). The unexpected contrary charged states may be due to radiation damage. X-ray radiation often reduces the valence of metal ions (24, 25) even at a safe dose, without damaging the atomic coordination. Indeed, the difference map calculated from diffraction data derived from the first five frames in the rotation series, instead of the later 10–30 frames, shows a weaker −2.9 σ peak at the iron atom. Clearly, electron crystallography provides important information on the charged state of metal and amino acid residues, but caution needs to be exercised regarding the effects of radiation damage.

Along this line, it may be noted that a recent report showed density loss of negatively charged residues upon ∼20 e⁻/Ų and ∼30 e⁻/Ų exposures (26). The question may then arise: Does the weaker density of the Asp and Glu side chains in the Coulomb potential map reflect radiation damage? The answer must be negative, as the total dose in each rotation series is less than 2 e⁻/Ų and the map using only the first five frames (instead of the whole 10–30 frames) shows the same features.

Conclusion

In summary, Coulomb potential maps contain unique and possibly critical information on the charged states of amino acid residues and metals. Whereas the strong interactions of electrons with protein atoms impose a limit on the thickness of the crystals, simple pipetting often breaks down crystals into suitable sizes for electron crystallography. It should be emphasized that electron crystallography of 3D protein crystals is still in its infancy. For instance, the resolution range presently used for refinement is rather narrow considering the good merging statistics, and substantial improvement in the assignment of partial charges and atomic scattering factors would be beneficial. See SI Appendix, SI Discussion for details of technical aspects.

Materials and Methods

Sample Preparation and Data Collection.

Crystals of Ca²⁺-ATPase were prepared as described (7) with slight modifications. Briefly, thin crystals were grown by dialyzing the mixture of purified protein and phospholipid (phosphatidylcholine) against crystallization buffer containing 0.8 M sodium propionate, 3% (vol/vol) polyethylene glycol 2000 (PEG2000), 25% (vol/vol) glycerol, 20 mM CaCl₂, 1 mM MgCl₂, 2.5 mM NaN₃, and 20 mM Mes, pH 6.1, at 4 °C for a few weeks. Small thin crystals of bovine catalase were obtained by incubation in potassium/sodium phosphate buffer, pH 5.3, at 4 °C for approximately a month (11). A few microliters of crystal solution were applied onto a carbon-coated copper grid and the grid was rapidly frozen by blotting off excess solution and plunging it into liquid ethane. The frozen-hydrated samples were examined at ∼90 K in a Hitachi EF-3000SE electron microscope, equipped with a high-precision rotary encoder, an in-column γ-type energy filter (8), and a Schottky emission gun operated at an accelerating voltage of 300 kV (SI Appendix, Fig. S1B). The precision in reading tilt angles is better than 0.001°. An energy slit was adjusted to select only electrons with energy loss less than 10 eV. Diffraction patterns with zero-energy loss were recorded on a slow-scan charge coupled device camera (TVIPS TemCam-F224HD; 2,048 × 2,048 pixels) with a thick scintillator. The data acquisition program (RoED) synchronizes the stage rotation and opening/closing of the rotary shutter of the microscope. The goniometer stage is rotated (i.e., tilted) during exposure to spatially integrate intensities of diffraction spots, but in only one direction to minimize the effect of backlash. A total of 10–40 frames were collected from one crystal, each frame usually covered 0.5–1° rotation during 1- to 3-s exposure. The total dose per frame was 0.01–0.05 electrons per Ų. The camera length was ∼3.45 m. The thickness of crystals used was estimated to be 700 ∼ 1,500 Å as described (10).

Structure Determination.

Individual rotation diffraction series were processed with a newly developed set of programs including a graphical user interface program XQED (SI Appendix, Fig. S4 A and B). Diffraction spots were extracted by 2D profile fitting (27) (EDINT program) and the direction of the rotation axis was estimated first so that consistent intervals could be assigned for as many diffraction spots as possible over successive CCD frames (SPINDLEAXIS program). Then, extracted data were subjected to postrefinement of lattice parameters, including the crystal direction, the direction of the rotation axis, and positional displacements due to Ewald spheres (LATOPT program). The mosaic spread was first estimated from broadening of reflections against resolution shells in each frame (EDINT), and determined in merging a rotational series with LATOPT. Most of the dataset gave cell parameters close to those determined by X-ray crystallography (Ca²⁺-ATPase) (7) or powder diffraction (catalase) (12). The longest cell dimension of the catalase crystal (206 Å) differs by ∼20 Å from that of the crystals of P2₁2₁2₁ symmetry (186 Å; Protein Data Bank ID code 3NWL) (13). Outliers were excluded at this stage. We measured radiation damage as the decay of average I/σ of reflections in each frame, and included CCD frames into a merge until the ratio of the average I/σ became <0.6 of that in the first frame. Each frame was first scaled according to the incident beam current monitored with the Faraday cup on the condenser aperture (SI Appendix, Fig. S1B), and partially recorded spots were integrated by 3D profile fitting with the weight of I/σ (LATOPT). Then, datasets from different crystals were merged with Scalepack (28). The crystal structures were determined by molecular replacement starting from an atomic model of Ca²⁺-ATPase (1SU4) (7) and an atomic model of catalase (3NWL) (13) using Phaser (29). The solutions were unique and of high scores with no packing clashes. The models were refined against the electron diffraction data at higher than 8-Å resolutions using CNS (30) with a restraint on hydrogen bonds (31) and Refmac (32). The atomic scattering factors for 300-keV electrons were derived from International Tables for Crystallography (14) except for H⁺ (adopted from ref. 15); the scattering factors for partially ionized atoms were estimated by a linear combination of those for a neutral and fully ionized atom. Partial charges were assigned to side chain atoms in all titratable residues (Asp, Glu, Arg, and Lys) and His at neutral pH, because crystals of Ca²⁺-ATPase were obtained at pH 6.1 and those of catalase at pH 5.3. These parameters were incorporated into CNS (30) and Refmac (32). The quality of the models was examined with Procheck (33). Ramachandran statistics [favored, allowed, generously allowed, and disallowed (in percent)] were: 82.5, 16.8, 0.6, and 0.1 for the model of Ca²⁺-ATPase; 77.1, 21.7, 1.1, and 0.2 for the model of catalase. Refinement statistics are shown in SI Appendix, Table S1 and Fig. S5A. NCS averaging was carried out using DM (34). Structure figures in Figs. 1 B–G, 3 and 5 and SI Appendix, Figs. S6–S8 and S12 were prepared with PyMol (PyMOL Molecular Graphics System, Schrödinger).