Abstract
For many communicable diseases, knowledge of the underlying contact network through which the disease spreads is essential to determining appropriate control measures. When behavior change is the primary intervention for disease prevention, it is important to understand how to best modify network connectivity using the limited resources available to control disease spread. We describe and compare four algorithms for selecting a limited number of links to remove from a network: two “preventive” approaches (edge centrality, R0 minimization), where the decision of which links to remove is made prior to any disease outbreak and depends only on the network structure; and two “reactive” approaches (S-I edge centrality, optimal quarantining), where information about the initial disease states of the nodes is incorporated into the decision of which links to remove. We evaluate the performance of these algorithms in minimizing the total number of infections that occur over the course of an acute outbreak of disease. We consider different network structures, including both static and dynamic Erdős-Rényi random networks with varying levels of connectivity, a real-world network of residential hotels connected through injection drug use, and a network exhibiting community structure. We show that reactive approaches outperform preventive approaches in averting infections. Among reactive approaches, removing links in order of S-I edge centrality is favored when the link removal budget is small, while optimal quarantining performs best when the link removal budget is sufficiently large. The budget threshold above which optimal quarantining outperforms the S-I edge centrality algorithm is a function of both network structure (higher for unstructured Erdős-Rényi random networks compared to networks with community structure or the real-world network) and disease infectiousness (lower for highly infectious diseases). We conduct a value-of-information analysis of knowing which nodes are initially infected by comparing the performance improvement achieved by reactive over preventive strategies. We find that such information is most valuable for moderate budget levels, with increasing value as disease spread becomes more likely (due to either increased connectedness of the network or increased infectiousness of the disease).
Keywords: Infectious disease control, optimal quarantining, edge centrality, R0 minimization, value of information
1. Introduction
Despite remarkable progress in the past century, infectious diseases continue to cause millions of deaths worldwide every year (Fauci, 2001; Morens et al., 2004; Arias and Murray, 2009). A variety of approaches can be used to prevent such diseases and control their spread, including vaccination, treatment, changing risk behaviors, and quarantining. However, implementation of these measures is often constrained by limited budgets, time, and/or personnel, necessitating difficult decisions about how to best allocate these scarce resources to prevent disease spread.
The way in which individuals and populations come into contact with each other influences how a disease spreads as well as which control measures are most effective. These contact patterns can be represented as a contact network, with nodes representing individuals (or groups of individuals) and links representing contacts that have the potential for disease transmission from one node to another. Different aspects of network structure have been demonstrated to influence the severity of an epidemic and the speed and extent of its spread (Ganesh et al., 2005; Chakrabarti et al., 2008; Youssef and Scoglio, 2011; Watts and Strogatz, 1998; Newman and Watts, 1999; Moore and Newman, 2000; Jackson and Rogers, 2007; May and Lloyd, 2001; Pastor-Satorras and Vespignani, 2001, 2002a; Eames, 2008; Miller, 2009; Newman, 2003; House and Keeling, 2011). For example, for the same average number of contacts, an epidemic is more likely to occur in networks with highly heterogeneous contact distributions (Jackson and Rogers, 2007; May and Lloyd, 2001; Pastor-Satorras and Vespignani, 2001, 2002a). This is illustrated in the extreme in so-called “scale-free” networks, where a small number of highly-connected nodes act as hubs that facilitate rapid, near-unstoppable disease spread (Pastor-Satorras and Vespignani, 2001, 2002a). In contrast, diseases spread more slowly and less diffusely in highly clustered networks (Eames, 2008; Miller, 2009; Newman, 2003; House and Keeling, 2011); though a disease may quickly spread locally within a densely connected cluster, it is less likely to escape the cluster and cause a global outbreak in the network.
Given the importance of network structure to disease spread, it is natural to consider whether and how network information can be used to design more effective disease control interventions. A variety of analyses have shown that interventions that make use of network information outperform those that do not (Pastor-Satorras and Vespignani, 2002b; Eubank et al., 2004; Miller and Hyman, 2007; Hartvigsen et al., 2007; Salathé and Jones, 2010; Marcelino and Kaiser, 2009). For example, Miller and Hyman (2007) compared different vaccination strategies in a simulation model of person-to-person contact in Portland, Oregon. They found that vaccinating individuals with the greatest number of unvaccinated contacts was more effective than random vaccination or vaccinating nodes with the highest number of contacts. Marcelino and Kaiser (2009) investigated flight cancellation as a means of preventing disease spread between cities over the global air travel network. They showed that canceling individual flight routes with the greatest edge centrality (a measure of a link's importance in maintaining the connectivity of the network) was more effective than simply shutting down airports with the greatest number of flights.
Prior work on how to use network information to target interventions in a population has primarily focused on vaccinating critical nodes in the network to prevent disease spread (Pastor-Satorras and Vespignani, 2002b; Eubank et al., 2004; Miller and Hyman, 2007; Hartvigsen et al., 2007). However, for many diseases, including hepatitis C, HIV, many sexually transmitted infections, and emerging influenza strains, a vaccine does not currently exist and behavior change remains the primary intervention. In such cases, a network-based intervention might instead focus on the interactions between nodes that are particularly critical to disease spread.
A number of link removal approaches have been proposed. These can be broadly classified along two dimensions. The first is whether an approach is preventive or reactive. A preventive strategy seeks to modify the network prior to an outbreak to make the network less conducive to disease spread (Marcelino and Kaiser, 2009; Bishop and Shames, 2011), while a reactive strategy assumes that the disease is detected prior to intervention and information about which nodes are initially infected is used to guide how links should be removed to prevent further disease spread (Enns et al., 2012). In general, one would expect reactive strategies to outperform preventive strategies because of the availability of additional information. However, it is unclear under what conditions this additional information is most valuable and when it is unnecessary. The second dimension is whether a strategy is rank-based or optimization-based. Rank-based strategies remove links in order of a link's “importance” to the network, which may be measured in terms of a link's betweenness centrality (Girvan and Newman, 2002; Marcelino and Kaiser, 2009), bridgeness (Cheng et al., 2010), or a variety of other metrics (Borgatti and Everett, 2006; De Meo et al., 2012). In contrast, optimization-based strategies consider link removal more holistically and identify a specific set of links to remove, which will change depending on the link removal budget (Bishop and Shames, 2011; Enns et al., 2012). Because there is no closed-form expression for the expected number of infections over the course of a disease outbreak in a contact network, optimization-based strategies must instead be formulated in terms of surrogate objective functions relating to network structure. The characterization of optimization-based strategies has therefore focused on establishing the algorithm's performance in inducing the desired change in network structure. A systematic evaluation of the impact of optimization-based link removal strategies on the expected number of infections during an outbreak has not yet been done.
In this paper, we compare four approaches to link removal, spanning the four possible combinations of the preventive/reactive and rank-based/optimization-based dimensions. In previous work, we described an optimization-based approach to quarantining infected nodes through link removal under resource constraints and evaluated its performance in separating initially infected and susceptible nodes in a static scenario (Enns et al., 2012). In this paper, we evaluate this optimal quarantining approach and other link removal algorithms as interventions to minimize the expected number of infections over the course of a stochastically evolving epidemic. In contrast to our prior work, where we only considered whether a susceptible node could become infected, not the likelihood of infection, this analysis incorporates the differential risks of infection faced by susceptible nodes based on their position in the network relative to those initially infected as well as the possibility of an outbreak dying out due to random chance.
In Section 2, we outline the link removal problem and describe the four link removal algorithms with their underlying rationale. In Section 3, we simulate acute outbreaks of disease for a variety of disease characteristics and contact network structures (including stochastically evolving networks) and compare the performance of the link removal approaches in terms of the expected final outbreak size as a function of the number of links that can be removed. We evaluate the value of (perfect) surveillance information – that is, the value of knowing which nodes are initially infected – by comparing the relative performance of reactive vs. preventive strategies. We also consider algorithm performance in the case of imperfect surveillance information. Based on the results of these experiments, in Section 4, we conclude with a summary of the network, disease, and budgetary conditions under which different link removal approaches perform best and surveillance information is most valuable.
2. Link removal algorithms
We consider a population of size N interacting through a contact network, represented by an undirected N × N adjacency matrix, A, where Aij = 1 if node i and node j are connected (meaning that individual i can transmit disease to individual j); otherwise, Aij = 0. Because we consider the case of an undirected network and symmetric disease transmission, if Aij = 1 then Aji = 1. We assume that a disease is introduced at time t = 0, with a small number of nodes initially infected. We model outbreaks of an acute, immunity-conferring disease using a susceptible-infected-recovered (SIR) model, where susceptible nodes become infected at a rate β per infected contact and infected nodes recover at a rate δ. Nodes in the recovered health state are no longer infectious nor can they be re-infected with the disease. We represent the health states of the population at time t with an N × 1 vector, st, where
| (1) |
We assume that A is fully known and that the objective is to minimize the expected number of infections by removing up to K links, with K being the link removal budget, from the contact network. We consider reactive and preventive link removal approaches. For preventive approaches, the decision of how to remove links is made prior to any disease outbreak and depends only on the network structure, while reactive approaches incorporate information about the initial disease states of the nodes (s0) into the decision of which links to remove. Note that the link removal problem is trivial for reactive algorithms if the link removal budget is sufficient to completely disconnect all infected nodes from the network. Thus, we restrict our analysis to scenarios of relatively constrained budgets. We also characterize link removal algorithms as either rank- or optimization-based. Rank-based approaches remove links in order of some measure of “importance”, while optimization-based approaches holistically identify a set of K links to remove to optimize a given objective function. We consider four link removal algorithms, one for each combination of characteristics: removing links in order of edge centrality (preventive, rank-based), removing links in order of susceptible-infected (S-I) edge centrality (reactive, rank-based), R0 minimization (preventive, optimization-based), and optimal quarantining (reactive, optimization-based).
2.1. Rank-based approaches to link removal
Edge centrality
Edge betweenness centrality is the most commonly used measure of a link's importance in a network, given by
| (2) |
where σ(i, j|e)/σ(i, j) is the fraction of shortest paths between nodes i and j passing over link e (Girvan and Newman, 2002). It essentially reflects the total number of shortest paths between nodes in the network that rely on a given link. Thus, links with higher edge betweenness centrality are generally more important to maintaining the connectivity of the network than edges with low centrality. We consider a preventive, rank-based link removal algorithm that removes the K links with the greatest edge betweeness centrality from the network.
S-I edge centrality
Instead of measuring the importance of links in maintaining all shortest paths in the network, a reactive approach is to measure the importance of links to only those shortest paths between susceptible and initially infected nodes. This yields a modified centrality measure, susceptible-infected (S-I) edge betweenness centrality, given by
| (3) |
where again σ(i, j|e)/σ(i, j) is the fraction of shortest paths between nodes i and j passing over link e, but we sum only over the shortest paths between infected and susceptible nodes (Enns et al., 2012). This reactive, rank-based algorithm thus involves removing the K links with the greatest S-I edge betweenness centrality.
2.2. Optimization-based approaches to link removal
While rank-based approaches to link removal are intuitive and relatively efficient to compute, they are ultimately greedy algorithms that may miss interdependencies captured by more global approaches. Therefore, we also evaluate the efficacy of optimization-based approaches that holistically consider the removal of links. Because there is no closed-form expression for the expected number of infections over the course of a disease outbreak in a contact network, optimization problems must be formulated in terms of surrogate objective functions. We consider two approaches: a preventive link removal algorithm proposed by Bishop and Shames (2011) that minimizes the basic reproductive number of the contact network, R0, and a reactive, optimal quarantining algorithm proposed by Enns et al. (2012) that seeks to completely disconnect as many susceptible nodes as possible from initially infected nodes.
R0 minimization
The basic reproductive number, R0, is a commonly used epidemiological quantity and represents the average number of secondary infections that would occur if a single infected individual were introduced into a fully susceptible population. For a given disease and population, if R0 < 1, then the pathogen cannot sustain itself and we expect that it will die out before infecting many individuals. However, if R0 > 1, it is expected that the number of infections will grow rapidly, resulting in a widespread epidemic (Anderson and May, 1991). For an SIR disease model and a given contact network, it has been shown that
| (4) |
where β is the transmission rate, δ is the recovery rate, and λ1(A) is the maximum eigenvalue of the contact adjacency matrix, A (Ganesh et al., 2005; Chakrabarti et al., 2008; Youssef and Scoglio, 2011).
Exploiting the relationship between R0 and a network's structure, Bishop and Shames (2011) formulated a convex optimization problem to identify which links to remove in order to minimize the maximum eigenvalue of the adjacency matrix (and thus the R0 of the population). They construct the following optimization problem, P1a:
| (5) |
| (6) |
| (7) |
| (8) |
where A is the original adjacency matrix, K is the maximum number of links to be removed, and à is the modified adjacency matrix resulting from link removal. The semi-definite constraint (6) requires the maximum eigenvalue of à to be less than γ (the quantity being minimized). Constraints (7) and (8) ensure that à can only be formed through the removal of at most K links from A (assuming that A is undirected, so the removal of the link Aij also includes the removal of Aji). Because of the Boolean constraint (8), the above optimization problem cannot be easily solved. Therefore, Bishop and Shames (2011) relaxed the last constraint, resulting in the following convex optimization problem, P1b:
| (9) |
| (10) |
| (11) |
| (12) |
The solution to P1b is the optimal attenuation of edges that minimizes the maximum eigenvalue of Ã. As an approximate solution to the original problem P1a, they identify the edges corresponding to the K largest attenuations, |Aij − Ãij|, as the set of edges to be removed. For any given link removal budget K, they demonstrated that this algorithm reduces the maximum eigenvalue of A more than if links are removed randomly; however, they did not directly investigate the effects of R0 minimization on disease spread or the expected number of infections as we do here.
Optimal quarantining
An alternative, reactive optimization-based approach is the quarantining algorithm proposed by Enns et al. (2012). They formulated an optimization problem to identify links to remove from a network such that as many susceptible nodes as possible are completely disconnected from infected nodes (and thus no longer at risk for infection) given a link removal budget, K. They do so by defining a two-way partitioning problem, where nodes are assigned to one of two sets such that the “cost” of the partition is minimized and at most K links cross the partition. The two sets can be disconnected by removing all links crossing the partition. They define the partition cost such that all infected nodes are assigned to the same set with as few susceptible nodes as is feasible given the link removal constraint. They define the cost matrix, W, as:
| (13) |
where s0 is the vector describing the initial health states of nodes in the network at t = 0, α > 0 is the cost of assigning a susceptible node and an infected node to the same set, and β > 0 is the cost savings of assigning two infected nodes to the same set (β ≫ α to ensure that assigning all infected nodes to the same set is prioritized). The minimization problem can be written as a quadratically-constrained quadratic program (QCQP), P2a:
| (14) |
| (15) |
| (16) |
where A is the adjacency matrix and x is the set assignment vector. Constraint (15) ensures that at most K links cross the partition. The binary constraint (16) ensures that each node is assigned to exactly one set (xi ∈ {1, −1}), but also results in P2a being non-convex.
Rewriting the problem as
| (17) |
| (18) |
| (19) |
| (20) |
and relaxing the final constraint, they defined the semi-definite program (SDP), P2b:
| (21) |
| (22) |
| (23) |
| (24) |
which is convex and can be solved using standard SDP solvers. The solution to P2b, provides both a lower bound on the optimal partition cost of the original QCQP, P2a, and can also be used to identify a feasible, near-optimal set assignment vector, x*, through a randomized sampling heuristic (Enns et al., 2012; Aspremont and Boyd, 2003). The links to be removed are those connecting nodes in opposite sets. Enns et al. evaluated the optimality of their algorithm on small networks compared to the optimal partition found through exhaustive search as well as the extent of quarantining achieved on larger networks compared to removing links in order of different edge centrality measures. However, they did not evaluate the impact of their optimal quarantining algorithm on the expected final outbreak size in the context of stochastic disease spread.
3. Performance of link removal algorithms
We estimated the expected number of infections over the course of an outbreak in a given network A for each link removal algorithm as a function of the number of links removed as follows (also see Algorithm 1): We simulated outbreaks starting with a random 10% of nodes initially infected. For each network, A, we pre-generated and stored 300 sets of initially infected nodes. We used the same initial infection set for all link removal algorithms and budget levels. For each set, we determined the set of links to be removed from the network A for different link removal budgets, K = 0 to Kmax, using the specified link removal algorithm. We generated a modified network, Ã, with these links removed. We simulated a disease spreading over à using a Susceptible-Infected-Recovered (SIR) model with infection rate β per contact per unit time and recovery rate δ per unit time (see Algorithm 2). We simulated disease spread until no infected nodes remained, either because all nodes became infected (and then recovered) or because the disease died out. We repeated this process 100 times to capture stochastic effects and calculated the average number of nodes that became infected over the course of the outbreak. We then averaged this result over all 300 infection patterns to estimate the overall expected proportion of the population to become infected in that network A for each link removal budget, K = 0 to Kmax. All simulations were implemented in Matlab R2012b (Mathworks, Natick, MA) and optimization problems were solved using CVX (Grant and Boyd, 2011). Code is available from the authors upon request.
We evaluated the performance of the four link removal algorithms in preventing infections for a variety of network structures: Erdős-Rényi random networks with varying levels of connectivity; a real-world network of residential hotels connected through injection drug use; a meta-community network (four highly connected communities with a small number of links between them); and dynamic Erdős-Rény random networks with varying link turnover rates. We also considered the value of surveillance information (knowing which nodes are initially infected) and the performance of the link removal algorithms in the face of imperfect surveillance information, modeled as errors in the detection of initially infected nodes. Our findings are summarized in Table 1 and described in detail in Sections 3.1-3.6.
Table 1.
Summary of key findings.
| Network type | Budget level | Variable | Optimal strategy | Value of information |
|---|---|---|---|---|
| Connectivity | ||||
|
| ||||
| Erdős-Rényi random networks | Low | Any | S-I centrality | Low |
| High | Low | Quarantine | High | |
| High | Moderate to High | S-I centrality or Quarantine | High | |
|
| ||||
| Infectivity | ||||
|
| ||||
| Hotel network | Low | Low to Moderate | S-I centrality | Low |
| Low | High | Quarantine | High | |
| High | Any | Quarantine | High | |
|
| ||||
| Meta-community network | Low | S-I centrality | High | |
| Moderate | N/A | Quarantine | Low | |
| High | Quarantine | High | ||
|
|
| Algorithm 1 Evaluating performance of link removal algorithms for a given network A and 300 sets of initially infected nodes, ℐ. |
|
|
| for each link removal algorithm do |
| for K = 0 to Kmax do |
| for m = 1 to 300 do |
| s0(i) = 1 ∀ i ∈ ℐm |
| s0(i) = 0 ∀ i ∉ ℐm |
| % Identify set of links to remove, ℒ, according to link removal algorithm, f(·). % |
| ℒ = f(A, s0, K) |
| Ã = A |
| Ãij = Ãji = 0 ∀ (i, j) ∈ ℒ |
| for n = 1 to 100 do |
| Simulate disease spread with network à and initial heath state vector, s0 (see Algorithm 2). Returns final outbreak size, ninf. |
| Ninf (n) = ninf |
| end for |
| end for |
| return |
| end for |
| Plot P̄inf (K) as function of link removal budget K to generate result plots. |
| end for |
|
|
|
|
| Algorithm 2 Simulating disease spread for a given network, A, and initial infection status of the population, s0. |
|
|
| t=0 |
| while st(i) = 1 for some i ∈ {1, …, N} do |
| t =t + 1 |
| % Infection of susceptible nodes % |
| for all i ∈ {i|st−1(i) = 0} do |
| {Count number of infected contacts} |
| Set st(i) = 1 with probability p(i) = 1 − e−Cinf(i) β |
| end for |
| % Recovery of infected nodes % |
| for all j ∈ {j|st−1(j)1} do |
| Set st(j) = −1 with probability q = 1 − e−δ |
| end for |
| end while |
| return ninf {Final outbreak size} |
|
|
3.1. Erdős-Rényi random networks
We first considered the performance of the algorithms on Erdős-Rényi random networks of 50 nodes. We generated these networks by randomly connecting any pair of nodes with probability p. We generated networks with p = 0.2 (20% of all possible links in the network exist), 0.4 and 0.8 to explore how changes in network connectivity affect the performance of the link removal algorithms. We simulated a disease with β/δ = 0.125. Without link removal, the basic reproductive number, R0, of such a disease was 1.3, 2.5, and 5.0 for networks with p equal to 0.2, 0.4, and 0.8, respectively. For each network, we randomly infected 5 nodes (10% initial prevalence) and simulated disease spread until the disease died out. For each network, we averaged results over 300 random sets of initially infected nodes.
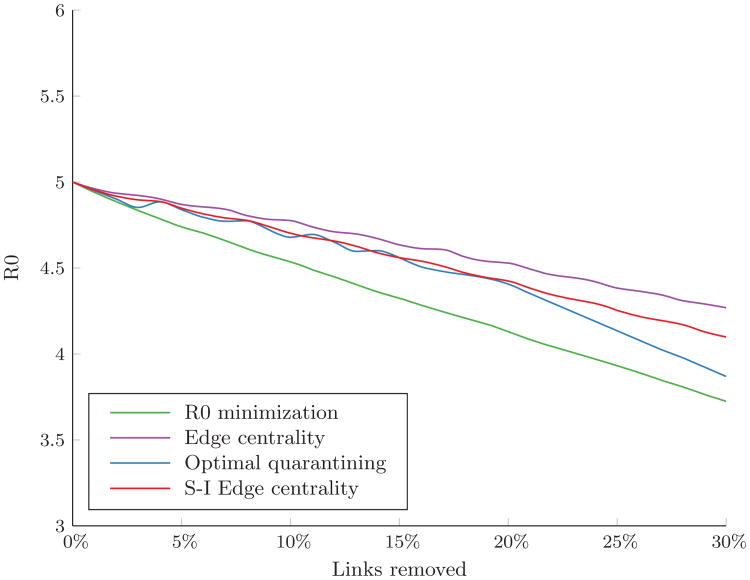
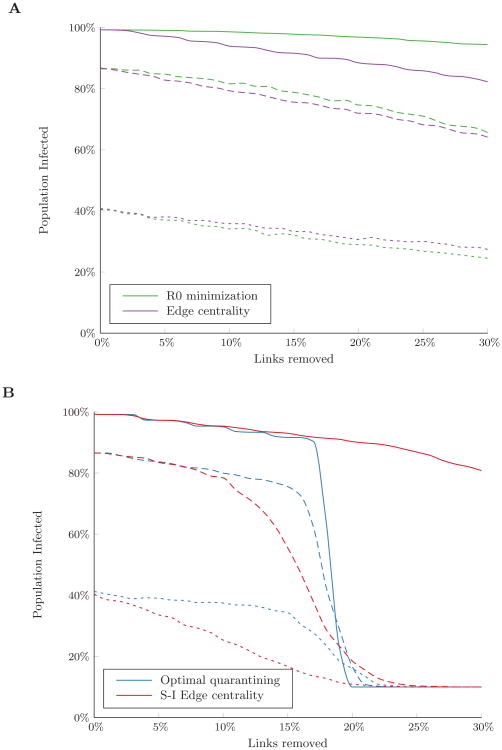
Figure 1 shows how R0 changes as links are removed under the different link removal algorithms. As expected, the R0 minimization approach achieved the greatest reduction in R0 for any given link removal budget. However, minimizing R0 had little impact on the final outbreak size, even with a link removal budget of up to 30% of links in the network (Figure 2A). Removing links in order of edge centrality performed slightly better in reducing the expected number of infections in the highly connected network (p = 0.8); however, as network connectivity decreased, both preventive algorithms had similar effects on the final outbreak size.
Figure 1.
The basic reproductive number, R0, in an Erdős-Rényi random network with p = 0.80 as a function of the number of links removed.
Figure 2.
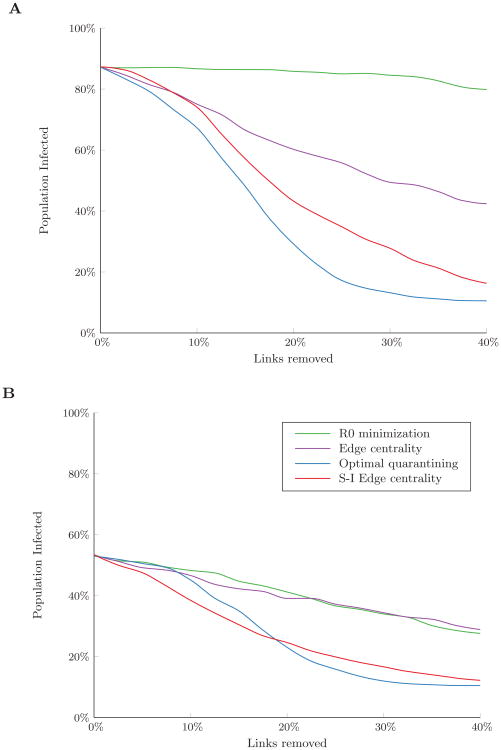
Percent of the population infected over the course of an outbreak under (A) preventive and (B) reactive link removal strategies in Erdős-Rényi random networks with varying levels of connectivity: p = 0.8 (solid line), p = 0.4 (dashed line), p = 0.2 (dotted line). Disease spread was simulated with β/δ = 0.125 and 10% of nodes initially infected. Results are the average of 300 random sets of initially infected nodes.
Reactive approaches, which make use of initial node health state information, significantly outperformed preventive link removal approaches (Figure 2B). The greatest gains resulted when the link removal budget exceeded 20% of the links in the network and nearly all susceptible nodes could be disconnected from infected nodes under the optimal quarantining approach. Below this budget threshold, however, optimal quarantining had little impact on the expected number of infections. This is likely because the quarantining algorithm relies on completely disconnecting susceptible nodes to prevent infections. When the network is unstructured and budgets are small, there is no efficient way to disconnect a substantial number of nodes from the network. Instead, removing links in order of S-I edge centrality resulted in the fewest number of infections for networks with low to moderate connectivity (p = 0.2 and p = 0.4) by increasing infected-susceptible path lengths in the network and making it more likely for an infection to die out before a substantial number of infections occur. This strategy had little impact for networks with high connectivity (p = 0.8), where disease spread was much more efficient. In such cases, only when the budget was sufficient to allow infected nodes to be completely quarantined could a substantial number of infections be averted.
3.2. Residential hotel network
To extend our analysis beyond stylized network models and provide an example of a real-world application, we next considered the performance of link removal algorithms in a network of residential hotels in Winnipeg, Canada connected through injection drug use (Wylie et al., 2007). This analysis allowed us to evaluate the efficacy of link removal strategies in a realistic setting. We note that this network represents only a single instance of an empirical network structure and our findings for this network may have limited generalizability to other real-world contexts.
The network consisted of 49 residential hotels identified in a survey of users of injection drugs as locations of drug use. Two residential hotels were considered to be connected if at least one person reported injecting drugs at both locations. Of the 49 residential hotels identified in the survey, 38 formed the largest connected component. We simulated the spread of a disease over the connected component with β/δ = 0.5 (yielding R0 ≈ 5). We simulated outbreaks for 300 different sets of 4 initially infected nodes (∼ 10% of nodes). In this network, an infected node (hotel) represents the prevalence of disease among the hotel's residents exceeding some threshold.
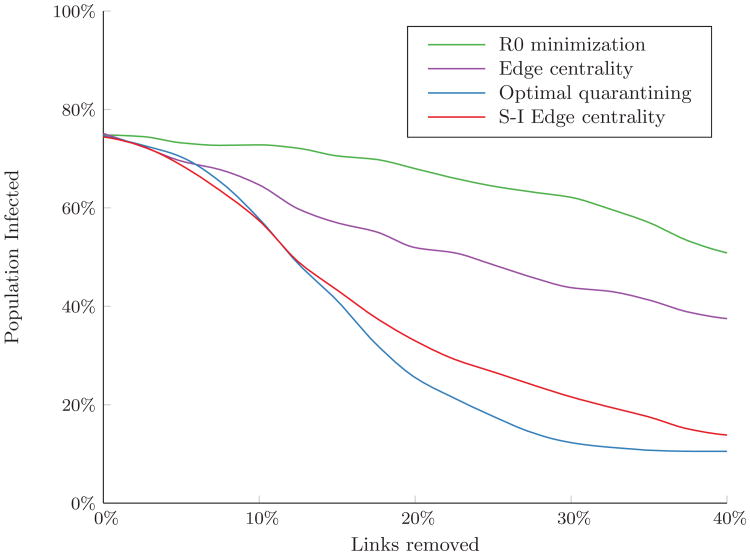
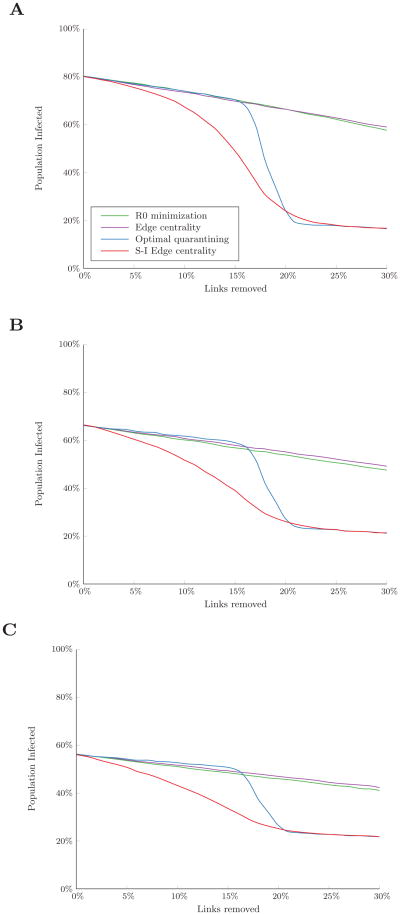
Among preventive strategies, removing links in order of edge centrality outperformed R0 minimization for all link removal budget levels (Figure 3). However, as for the case of Erdős-Rényi random networks, preventive link removal strategies resulted in much larger outbreaks than did reactive strategies. Among reactive strategies, for small link removal budgets, removing links in order of S-I edge centrality resulted in fewer infections than the optimal quarantining approach. This is because when budgets are small, few susceptible nodes can be completely separated from the network and quarantining has little effect. In contrast, removing links with high S-I edge centrality increases path lengths between infected and susceptible nodes, making it more likely that the disease will die out before a large fraction of the network becomes infected. However, once the link removal budget was sufficiently large (greater than 12% of links in the network), a substantial number of susceptible nodes could be disconnected from the network. By reducing the risk of infection of these nodes to zero, optimal quarantining resulted in the fewest number of infections.
Figure 3.
Percent of the population infected over the course of an outbreak in the residential hotel network. Simulated with β/δ = 0.5 (R0 ≈ 5) and 10% of nodes initially infected. Results are the average of 300 random sets of initially infected nodes.
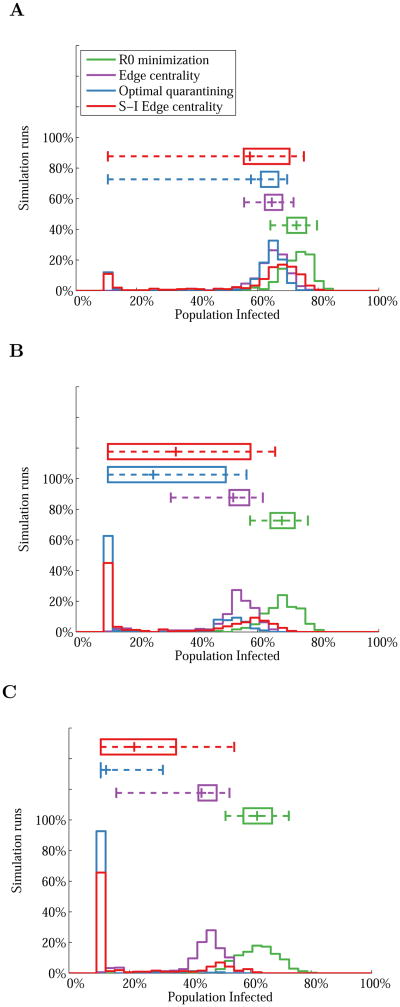
Further insight into link removal performance can be gained by examining how the distribution of final outbreak sizes over the 300 sets of initially infected nodes changes with the link removal budget under each link removal algorithm. The distributions of final outbreak sizes in the residential hotel network for link removal budgets of 10%, 20%, and 30% of links in the network are shown in Figure 4. For both reactive strategies, we find that reductions in the average outbreak size with an increasing link removal budget are achieved by completely eliminated disease spread (beyond the initial set of infected nodes) for an increasing number of scenarios. For scenarios where disease spread is not eliminated, the final outbreak size remains largely unchanged, resulting in bi-modal distributions and wide variability. However, as budgets increase, we find that this variability is reduced, especially for the optimal quarantining algorithm, as the shift to small outbreak sizes increases. We also note that the R0 minimization algorithm has little impact on the distribution of outbreak sizes, and results in only small shifts towards smaller final outbreak sizes as the link removal budget increases.
Figure 4.
Distribution of the final outbreak sizes over 300 random sets of initially infected nodes in the residential hotel network with link removal budgets of (A) K = 10%, (B) K = 20%, and (C) K = 30%. Disease spread was simulated with β/δ = 0.5 (R0 ≈ 5). Average values are indicated by ‘+’ and box plots show interquartile ranges and 95% intervals.
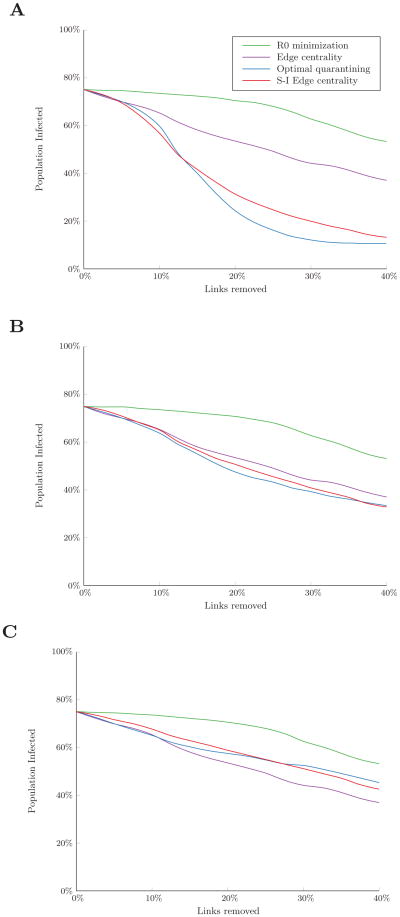
We also compared the performance of the link removal algorithms for varying levels of disease infectiousness, β. When β was double the base case value (β/δ = 1), optimal quarantining (reducing the risk of infection to zero for as many nodes as possible) was the most effective strategy for all budget levels (Figure 5A), as the disease was sufficiently infectious that increasing path lengths had little effect on its probability of spread. However, when β was half the base case value (β/δ = 0.25), the disease was less infectious and more likely to die out. Increasing path lengths between nodes had a greater impact on final outbreak size, and the budget threshold at which optimal quarantining outperforms removing high S-I edge centrality links increased to 20% of links in the network (Figure 5B).
Figure 5.
Percent of the population infected over the course of an outbreak in the residential hotel network for a disease with (A) increased infectiousness (β/δ = 1) and (B) decreased infectiousness (β/δ = 0.25). Simulated with 10% of nodes initially infected. Results are the average of 300 random sets of initially infected nodes.
3.3. Networks with Community Structure
Community structure, where nodes interact within tightly knit groups with only sparse connections between groups, arises in a variety of contexts. For example, community structure is observed in the interactions within human and social animal communities, where individuals self-organize into cliques, core groups, or modular sub-populations (Aral, 2000; Jolly and Wylie, 2002; Griffin and Nunn, 2012); in the interactions between distinct social or territorial groups in a shared environment (Pitt et al., 2008; Craft et al., 2011); and in population interactions over a heterogeneous landscape (or patches) (Hanski, 1998; Smith, 2007). The existence of loosely connected sub- or meta-populations within a network has been shown to influence disease dynamics, with “bridging” individuals or populations playing a particularly crucial role in facilitating disease spread from one sub-population to another (Grenfell and Harwood, 1997; Girvan and Newman, 2002; Salathé and Jones, 2010; Kitchovitch and Liò, 2011; Griffin and Nunn, 2012).
To construct a network exhibiting community structure, we first generated four equally-sized sub-populations of 25 nodes. Each sub-population formed its own Erdős-Rényi random network, with two of the sub-populations exhibiting low connectivity (p = 0.2) and the other two exhibiting high connectivity (p = 0.6). In each sub-population, four “bridging” nodes were each randomly connected to a node in one of the other sub-populations. We considered scenarios where outbreaks began in one of the highly connected sub-populations. We simulated a disease with β/δ = 0.34 (resulting in R0 ≈ 5) with 10% of nodes initially infected.
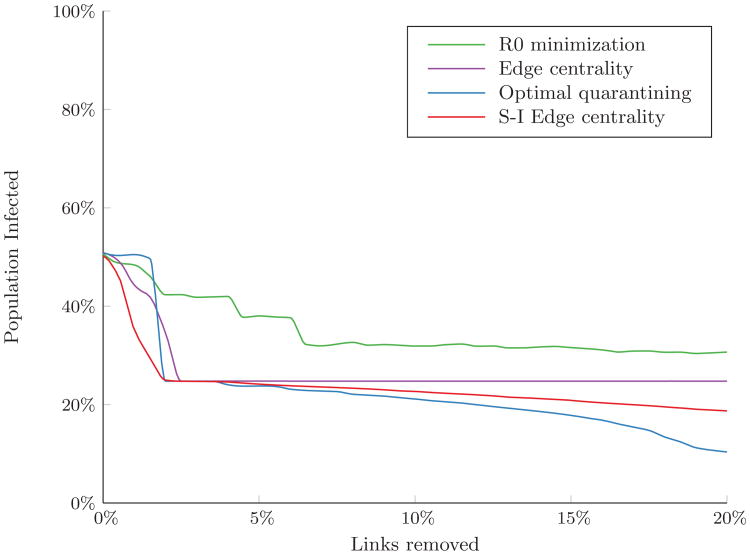
Removing links to minimize R0 had the least impact on the expected number of infections, whereas removing links in order of edge centrality or S-I edge centrality achieved a steady decrease in infections until reaching a plateau when more than 2% of links could be removed (Figure 6). This was also the smallest link removal budget for which the optimal quarantining algorithm was first able to achieve a substantial reduction in the expected number of infections. At this budget level, the majority of bridging links between the sub-populations could be removed, completely disconnecting fully susceptible communities from the infected sub-population. Only when the budget became much larger (10% of links) could a sufficient number of links within the infected sub-population be disconnected, resulting in further decreases in the number of infections under the optimal quarantining and S-I edge centrality strategies.
Figure 6.
Percent of the population infected over the course of an outbreak in a network exhibiting community structure with four sub-populations. Simulated with β/δ = 0.34 (R0 ≈ 5) and 10% of nodes initially infected. Results are the average of 300 random sets of initially infected nodes in one of the highly connected sub-populations.
The structural relationship of this network to its maximum eigenvalue illustrates why minimizing R0 has little effect on the number of infections. The maximum eigenvalue of the overall adjacency matrix is approximately equal to the largest of the maximum eigenvalues of the four sub-populations, meaning it will be driven by the maximum eigenvalue of the more connected communities. To minimize this maximum eigenvalue, links within the most connected communities will be removed, while the particular significance of links between communities to disease transmission is ignored. Thus, the R0 minimization algorithm does not take advantage of the efficiency of disconnecting loosely linked communities to prevent widespread infection, but instead focuses on reducing the local infection rates within the most connected communities.
3.4. Dynamic networks
In the previous examples, we considered outbreaks in static networks; that is, networks that do not change over the course of the outbreak. However, depending on the timescale of the disease's dynamics and the type of contact(s) relevant for its transmission, this may be an unrealistic assumption. Network dynamics can have an important and complex influence on epidemic outcomes, in some cases facilitating and in other cases hindering disease spread depending on a complex interplay of contact turnover rates, transmission and recovery rates, and structural features of the network (Fefferman and Ng, 2007; Vernon and Keeling, 2009; Volz and Meyers, 2009; Taylor et al., 2012; Sloot et al., 2013; Gulyás and Kampis, 2013).
We evaluated the performance of the link removal algorithms in dynamic Erdő-Rényi random networks. Using the dynamic network framework described by Gulyás et al. (2013) and Gulyás and Kampis (2013), we simulated outbreaks in networks with different rates of link turnover, determined by the rate of link acquisition. We set the rate of link termination such that it balanced the process of link formation to maintain the same number of links in the network, on average, over time. We assumed that the link termination and formation rates were constant over time and that new links formed randomly between nodes. In applying link removal algorithms to these now dynamic networks, we assumed that links selected for removal by the algorithm would be both removed and prevented from re-forming.
We varied the rate of link acquisition in multiples of the recovery rate, δ, to explore the performance of link removal in cases where network dynamics were similar to and faster than disease dynamics (and, in particular, the infectious period). The performance of link removal algorithms for a dynamic Erős-Rényi random network with p = 0.40 and β/δ = 0.125 (as in Section 3.1) is presented in Figure 7 for turnover rates equal to δ, 5δ, and 10δ. Without link removal (K = 0%), we observed that in the Erős-Rényi random network, link turnover resulted in interrupted disease spread compared to the static case, with decreasing final outbreak sizes as the turnover rate increased. These results are consistent with other studies of epidemic outcomes as a function of network dynamics (Fefferman and Ng, 2007; Gulyás et al., 2013). The relative performance of the four link removal algorithms is similar to the static case: reactive algorithms vastly outperform preventive ones and removing links in order of S-I edge centrality achieved the smallest outbreak sizes for small link removal budgets, while optimal quarantining averts a substantial number of infections once the link removal budget exceeds a threshold (K = 20% in this case). Beyond this threshold, the final outbreak size under S-I edge centrality and optimal quarantining algorithms reaches a plateau. Compared to the static case, we find that this plateau level increases with the link turnover rate. Though reactive link removal algorithms initially disconnect infected nodes from susceptible ones for large budget levels, the likelihood that these infected nodes form new links to susceptible nodes before they recover increases with the link turnover rate, allowing the disease to spread beyond those initially infected.
Figure 7.
Percent of the population infected over the course of an outbreak in a dynamic Erdős-Rényi random network (with p = 0.40) with varying rates of link turnover. Shown for link formation rates of (A) δ; (B) 5δ; and (C) 10δ, where δ = 0.1 is recovery rate of infected nodes. Simulated with β/δ = 0.125 and 10% of nodes initially infected. Results are the average of 300 random sets of initially infected nodes.
3.5. Value of surveillance information
Reactive strategies outperform preventive strategies because they use additional information about the network, namely which nodes are initially infected, to identify which links to remove. This additional information might be available if, for example, a surveillance program was in place prior to an outbreak. However, surveillance requires an investment of resources. Using our link removal analysis, we can estimate the value of surveillance information, which could be used to evaluate whether the value of a surveillance system justifies its cost. For a given network, disease, and link removal budget, we computed the value of surveillance information as the difference in expected number of infections under the best preventive strategy and the best reactive strategy. We considered the cases of perfect surveillance information where the infection status of all nodes is known before link removal begins (this section) and imperfect surveillance information (next section).
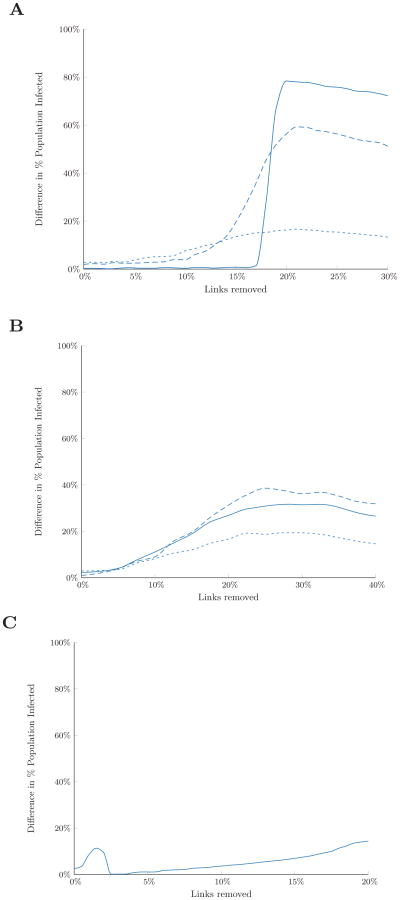
In general, we found that the value of (perfect) surveillance information was higher when the disease was more likely to spread, either because the network was more densely connected or because the disease was more infectious (Figures 8A and 8B). For Erdős-Rényi random networks, the value of surveillance information was low when the link removal budget was small; in this case, none of the link removal algorithms had much effect on disease spread. The value of information in random networks increased substantially once the budget was large enough to disconnect infected nodes from the majority of the susceptible population. In contrast, in networks exhibiting community structure, the value of surveillance information was relatively high for small budgets (Figure 8C): even though only a small number of links could be removed, knowing which community was experiencing the initial outbreak meant that reactive link removal algorithms could prioritize breaking the few links connecting the infected community to the rest of the network. The decrease in value of surveillance information came when the budget was sufficiently large to disconnect all communities (infected or not) from each other. Since all the “bridging” links between communities have high edge centrality, the preventive edge centrality algorithm was breaking more and more of these links as the budget increased, eventually converging to the solution of the two reactive strategies when all such bridging links could be removed.
Figure 8.
Expected value-of-information (in terms of potential infections averted) of knowing which nodes are initially infected, measured as the difference in expected number of infections under the best preventive strategy and the best reactive strategy. Shown for (A) Erdős-Rényi random networks with varying levels of connectivity: p = 0.8 (solid line), p = 0.4 (dashed line), p = 0.2 (dotted line); (B) the residential hotel network with varying levels of infectiousness: base (solid), high (dashed), and low (dotted); and (C) a network exhibiting community structure. Results are based on the average of 300 simulations with 10% of nodes initially infected.
3.6. Imperfect surveillance information
We also evaluated the performance of the link removal algorithms for the case of imperfect surveillance information; that is, when there is error in the detection of infected nodes. We modeled this by introducing an “observed” initial health state vector, ŝ0, which we constructed by applying a false negative rate, pFN, and a false positive rate, pFP to the true initial health state vector, s0. For an initial prevalence of 10%, this yielded pFN(0.1)(N) infected nodes that were wrongly thought to be uninfected (false negatives) and pFP(0.9)(N) uninfected nodes that were mistakenly observed to be infected in ŝ0 (false positives). We applied the link removal algorithms using the observed health states, ŝ0, to identify links to remove. We then simulated the spread of disease over the modified network using the true initial health states, s0.
We varied pFN to explore how the level of false negatives affects algorithm performance. We selected pFP to balance the false negative rate so that the total number of “observed” infected nodes was equal to the total number of truly infected nodes (pFN(0.1)(N) = pFP(0.9)(N)). Results are presented in Figure 9 for the residential hotel network, with false negative rates of 0% (perfect information), 25%, and 50%. We observed that imperfect surveillance information drastically reduces the effectiveness of the reactive strategies. For a false negative rate of 25% or greater, the edge centrality, S-I edge centrality and optimal quarantining approaches led to similar outbreak sizes. At a false negative rate of 50%, removing links in order of betweenness centrality, without using initial node health state information, was the optimal strategy for all budget levels, indicating that at this error level the imperfect surveillance information is more misleading than it is helpful in targeting link removal efforts.
Figure 9.
Percent of the population infected over the course of an outbreak in the residential hotel network with varying levels of error in the identification of initially infected nodes. Shown for (A) perfect information; (B) a 25% false negative rate; and (C) a 50% false negative rate. Simulated with β/δ = 0.5 (R0 ≈ 5) and 10% of nodes initially infected. Results are the average of 300 random sets of initially infected nodes.
4. Discussion
We compared four approaches to removing links from a contact network to prevent disease spread. We evaluated the expected number of infections using these link removal algorithms as a function of the number of links to be removed in different network structures (random, real-world, community-structured, and dynamic) and for different levels of disease infectiousness. Though the performance of the different algorithms will always depend on the complex interplay between network structure, disease characteristics, and budget size, our findings suggest several general themes.
We consistently found that reactive algorithms, which make use of the knowledge of which nodes are initially infected, resulted in fewer infections than preventive approaches, though the magnitude of the difference was dependent on the specific network, disease, and budget level. In our value-of-information analysis, we found that knowing which nodes were initially infected was most valuable when infected nodes, or the community/cluster containing the infected nodes, could be disconnected from the network. For Erdős-Rényi random networks and the residential hotel network, we observed that the value of this information was low for very small or very large budgets, with a peak value at some moderately sized budget. For small budgets, few links can be removed and no strategy will have much impact on disease spread; for large budgets, so much of the network can be disconnected that disease spread will be hindered no matter which specific links are removed. However, at moderate budget levels, disease spread can be prevented, but only if specific, critical links are removed. Networks exhibiting community structure were an exception: knowing which community contained initially infected nodes was valuable at small budget levels because only a small number of links needed to be removed to disconnect the infected community from the others. The value of this information declined once the budget was sufficiently large to disconnect all communities from each other, as even the preventive edge centrality algorithm identified inter-community links as critical to remove.
We also noted that surveillance information, if erroneous, can be harmful. In the residential hotel network, we found that the effectiveness of reactive link removal algorithms was reduced as error rates in the detection of initially infected nodes increased. For high rates of misidentification (a 50% false negative rate), both reactive algorithms in fact performed worse that removing links in order of edge betweenness centrality. Reactive algorithms prioritize connections to infected nodes; however, in the presence of imperfect information about a node's initial health status, resources aimed at nodes observed to be infected may be misplaced, and more general approaches to reducing the conductivity of the network may be more effective at preventing disease spread.
Interestingly, optimization-based link removal algorithms did not always outperform greedy, rank-based algorithms. This is perhaps not surprising, as the objective functions of these optimization problems are formulated in terms of specific structural modifications to the network and not directly related to the expected number of infections. Thus, in our context, the performance of an optimization-based link removal algorithm depends on the appropriateness of the hypothesized structural modification for impeding disease spread. This point was aptly illustrated by the R0 minimization algorithm. Though the R0 minimization algorithm achieved the greatest reduction in the maximum eigenvalue of the contact network for a given budget (Figure 1), this structural modification did not translate into a substantial reduction in the expected number of infections of the course of the outbreak. For all the cases we considered, R0 minimization was dominated by removing links in order of edge centrality. Though R0 has a strong theoretical relationship to the initial trajectory of an outbreak, it did not prove to be a good surrogate for the final outbreak size in stochastically evolving outbreaks. Other related measures may prove to be better predictors of outbreak size, such as the eigenvector corresponding to the maximum eigenvalue of the adjacency matrix, as proposed by Youssef and Scoglio (2011). However, an appropriate formulation of a convex objective function for the minimization of an eigenvector is not immediately apparent.
Among reactive approaches, whether removing links in order of S-I edge centrality (rank-based) or optimal quarantining (optimization-based) resulted in the smallest outbreak depended on the network, disease, and budget. For all the cases considered, we observed the same pattern: the S-I edge centrality algorithm performed best for small budgets; however, once the budget exceeded some threshold, optimal quarantining resulted in the fewest number of infections. We can explain this pattern in terms of the differences in underlying approaches of these algorithms to preventing disease spread. The S-I edge centrality algorithm increases path lengths between infected and susceptible nodes, increasing the probability that a disease will die out before spreading throughout the network; in contrast, the optimal quarantining algorithm fully disconnects susceptible nodes from those initially infected, completely eliminating the risk of infection in disconnected nodes. When budgets are small, few nodes can be fully disconnected from the network, and a quarantining strategy will have little effect; thus, increasing path lengths and increasing the probability of the disease dying out is the best strategy. As the budget increases, however, more and more nodes can be disconnected through quarantining and eventually eliminating the risk of infection will outperform merely reducing it. Disease infectiousness also played an important role in determining the optimal strategy, as we saw that the more infectious the disease, the lower the budget threshold at which quarantining outperformed the S-I edge centrality algorithm. For highly infectious diseases, the probability of disease spread is still high, even with increased path lengths in the network (consider the extreme case when β = ∞ and the probability that a node will infect its contacts is 1). In such cases, fully separating susceptible nodes from the network is the only effective way to prevent infection, making optimal quarantining the most effective strategy.
The two rank-based algorithms considered in this analysis are based on betweenness centrality (and variations thereof) as a measure of a link's importance to the network. Though less studied than node centrality, a number of other edge centrality metrics have been proposed, such as bridgeness (Cheng et al., 2010), k-path centrality (De Meo et al., 2012) and others. Moderate correlation between centrality metrics has been noted (Valente et al., 2009); however, it is possible that other centrality metrics may better reflect a link's importance to disease transmission than betweenness centrality. Which edge centrality metric best reflects a link's role in disease transmission will likely depend on the type of network structure and level of disease infectiousness. The association between different edge centrality metrics and disease spread warrants further investigation.
In our analysis, we did not consider issues of disease persistence or conditions for establishing endemicity. Our analysis focused on link removal as a strategy to contain an acute outbreak of an immunity-conferring disease (following an SIR model) in a closed, finite population. Under these conditions, indefinite disease persistence cannot be maintained: either all nodes in the network will become infected, exhausting the susceptible population, or infected nodes will at some point fail to transmit the disease before recovering, eliminating the source of further infection. Thus, questions of disease persistence are beyond the scope of this analysis.
The contact networks to which we apply the link removal algorithms are relatively small, on the order of 50 to 100 nodes. At these dimensions, finite network effects may have influenced the simulated disease dynamics, potentially leading to different conclusions than if the algorithms had been applied to larger networks (Noël et al., 2009). However, the applicability of link removal as a disease control strategy becomes questionable as networks become large, as individual links may no longer be the relevant unit of intervention. Instead, we might expect that link removal strategies would be applied hierarchically to large networks, first considering the connections between meta-communities, followed by the sub-structure within communities, and so on. The optimization-based algorithms, as implemented, can be applied to networks on the order of hundreds of nodes, though computational demands increase as networks become larger and/or denser. However, because these algorithms rely only on standard convex optimization solvers, they could be extended to larger problems using more sophisticated implementations that leverage large-scale convex optimization techniques (Fujisawa et al., 2007; Zheng et al., 2012).
We assumed perfect knowledge of the contact network. Developing robust link removal algorithms for situations when network information is incomplete or uncertain is an important next step. Complete information about a contact network is rarely available and collecting such information is resource-intensive. Understanding which aspects of network structure are most influential in determining the optimal disease control response could make it more feasible to include network considerations into ongoing surveillance programs. For example, risk behavior surveillance surveys could elicit certain features of a population's contact structure from individual respondents (e.g., average number of contacts or perceived clustering among contacts), without needing to map out an entire network. These issues are topics of future research.
Acknowledgments
This research was funded by the National Institute on Drug Abuse (Grant Number DA-R01-15612). The authors thank Dr. John Wylie for providing access to the Winnipeg network dataset. The authors also acknowledge computational resources provided by the Minnesota Supercomputing Institute.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Eva A. Enns, Email: eenns@umn.edu.
Margaret L. Brandeau, Email: brandeau@stanford.edu.
References
- Anderson R, May R. Infectious Diseases of Humans: Dynamics and Control. Oxford University Press; Oxford: 1991. [Google Scholar]
- Aral S. Behavioral aspects of sexually transmitted diseases: core groups and bridge populations. Sex Transm Dis. 2000;27(6):327–28. doi: 10.1097/00007435-200007000-00005. [DOI] [PubMed] [Google Scholar]
- Arias C, Murray B. Antibiotic-resistant bugs in the 21st century – a clinical super-challenge. New Engl J Med. 2009;360(5):439–43. doi: 10.1056/NEJMp0804651. [DOI] [PubMed] [Google Scholar]
- Aspremont A, Boyd S. EE364b Course Notes. Stanford University; 2003. Relaxations and randomized methods for nonconvex QCQPs. [Google Scholar]
- Bishop A, Shames I. Link operations for slowing the spread of disease in complex networks. EPL. 2011;95(1):18005. [Google Scholar]
- Borgatti S, Everett M. A graph-theoretic perspective on centrality. Soc Networks. 2006;28(4):466–484. [Google Scholar]
- Chakrabarti D, Wang Y, Wang C, Leskovec J, Faloutsos C. Epidemic thresholds in real networks. ACM Trans Inform Syst Secur. 2008;10(4):1–26. [Google Scholar]
- Cheng XQ, Ren FX, Shen HW, Zhang ZK, Zhou T. Bridgeness: a local index on edge significance in maintaining global connectivity. J Stat Mech. 2010;2010(10):P10011. [Google Scholar]
- Craft M, Volz E, Packer C, Meyers L. Disease transmission in territorial populations: the small-world network of serengeti lions. J R Soc Interface. 2011;8(59):776–86. doi: 10.1098/rsif.2010.0511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Meo P, Ferrara E, Fiumara G, Ricciardello A. 2012. A novel measure of edge centrality in social networks. Knowl-Based Syst. 2012 Jun;30:136–150. [Google Scholar]
- Eames K. Modelling disease spread through random and regular contacts in clustered populations. Theor Pop Bio. 2008;73(1):104–11. doi: 10.1016/j.tpb.2007.09.007. [DOI] [PubMed] [Google Scholar]
- Enns E, Mounzer J, Brandeau M. Optimal link removal for epidemic mitigation: a two-way partitioning approach. Mat Biosci. 2012;235(2):138–47. doi: 10.1016/j.mbs.2011.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eubank E, Guclu H, Kumar V, Marathe M, Srinivasan A, Toroczkai Z, Wang N. Modelling disease outbreaks in realistic urban social networks. Nature. 2004 May;429:180–4. doi: 10.1038/nature02541. [DOI] [PubMed] [Google Scholar]
- Fauci A. Infectious diseases: considerations for the 21st century. Clin Infect Dis. 2001;32(5):675–85. doi: 10.1086/319235. [DOI] [PubMed] [Google Scholar]
- Fefferman N, Ng K. How disease models in static networks can fail to approximate disease in dynamic networks. Phys Rev E. 2007;76(3) doi: 10.1103/PhysRevE.76.031919. [DOI] [PubMed] [Google Scholar]
- Fujisawa K, Nakata K, Yamashita M, Fukuda M. SDPA Project: Solving large-scale semidefinite programs. J OR Soc Japan. 2007;50(4):278–298. [Google Scholar]
- Ganesh A, Massoulie L, Towsley D. The effect of network topology on the spread of epidemics. Proc 24th Ann Joint Conf IEEE Computer and Communications Societies. IEEE; Miami. 2005. pp. 1455–66. [Google Scholar]
- Girvan M, Newman M. Community structure in social and biological networks. PNAS. 2002;99(12):7821–6. doi: 10.1073/pnas.122653799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grant M, Boyd S. CVX: Matlab software for disciplined convex programming, version 1.21. 2011 Apr; http://cvxr.com/cvx.
- Grenfell B, Harwood J. (Meta)population dynamics of infectious disease. Trends Ecol Evol. 1997;12(10):395–99. doi: 10.1016/s0169-5347(97)01174-9. [DOI] [PubMed] [Google Scholar]
- Griffin R, Nunn C. Community structure and the spread of infectious disease in primate social networks. Evol Ecol. 2012;26(4):779. [Google Scholar]
- Gulyás L, Kampis G. Spreading processes on dynamically changing contact networks. Eur Phys J Special Topics. 2013;222(6):1359–76. [Google Scholar]
- Gulyás L, Kampis G, Legendi R. Elementary models of dynamic networks. Eur Phys J Special Topics. 2013;222(6):1311–33. [Google Scholar]
- Hanski I. Metapopulation dynamics. Nature. 1998;396(6706):41–9. [Google Scholar]
- Hartvigsen G, Dresch J, Zielinski A, Macula A, Leary C. Network structure, and vaccination strategy and effort interact to affect the dynamics of influenza epidemics. J Theor Biol. 2007;246(2):205–13. doi: 10.1016/j.jtbi.2006.12.027. [DOI] [PubMed] [Google Scholar]
- House T, Keeling M. Epidemic prediction and control in clustered populations. J Theor Biol. 2011;272(1):1–7. doi: 10.1016/j.jtbi.2010.12.009. [DOI] [PubMed] [Google Scholar]
- Jackson M, Rogers B. Relating network structure to diffusion properties through stochastic dominance. BE J Theor Econ. 2007;7(1):1–13. [Google Scholar]
- Jolly A, Wylie J. Gonorrhoea and chlamydia core groups and sexual networks in manitoba. Sex Transm Infect. 2002;78(Suppl 1):i145–51. doi: 10.1136/sti.78.suppl_1.i145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitchovitch S, Liò P. Community structure in social networks: Applications for epidemiological modelling. PloS One. 2011;6:e22220. doi: 10.1371/journal.pone.0022220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcelino J, Kaiser M. Reducing influenza spreading over the airline network. PLoS Curr Influenza. 2009 doi: 10.1371/currents.RRN1005. RRN1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- May R, Lloyd A. Infection dynamics on scale-free networks. Phys Rev E. 2001;64(6):1–4. doi: 10.1103/PhysRevE.64.066112. [DOI] [PubMed] [Google Scholar]
- Miller J. Spread of infectious disease through clustered populations. J R Soc Interface. 2009;6(41):1121–34. doi: 10.1098/rsif.2008.0524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller J, Hyman J. Effective vaccination strategies for realistic social networks. Physica A. 2007;386(2):780–85. [Google Scholar]
- Moore C, Newman M. Epidemics and percolation in small-world networks. Phys Rev E. 2000;5 Pt B(61):5678–82. doi: 10.1103/physreve.61.5678. [DOI] [PubMed] [Google Scholar]
- Morens D, Folkers G, Fauci A. The challenge of emerging and re-emerging infectious diseases. Nature. 2004;430(6996):242–9. doi: 10.1038/nature02759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman M. Properties of highly clustered networks. Phys Rev E. 2003;68(2):1–6. doi: 10.1103/PhysRevE.68.026121. [DOI] [PubMed] [Google Scholar]
- Newman M, Watts D. Scaling and percolation in the small-world network model. Phys Rev E. 1999;60(6):7332–42. doi: 10.1103/physreve.60.7332. [DOI] [PubMed] [Google Scholar]
- Noël PA, Davoudi B, Brunham R, Dubé L, Pourbohloul B. Time evolution of epidemic disease on finite and infinite networks. Phys Rev E. 2009;79(2):026101. doi: 10.1103/PhysRevE.79.026101. [DOI] [PubMed] [Google Scholar]
- Pastor-Satorras R, Vespignani A. Epidemic spreading in scale-free networks. Phys Rev Lett. 2001;86(14):3200–3. doi: 10.1103/PhysRevLett.86.3200. [DOI] [PubMed] [Google Scholar]
- Pastor-Satorras R, Vespignani A. Epidemic dynamics in finite size scale-free networks. Phys Rev E. 2002a;65(3):1–4. doi: 10.1103/PhysRevE.65.035108. [DOI] [PubMed] [Google Scholar]
- Pastor-Satorras R, Vespignani A. Immunization of complex networks. Phys Rev E. 2002b;65(3):1–8. doi: 10.1103/PhysRevE.65.036104. [DOI] [PubMed] [Google Scholar]
- Pitt J, Larivière S, Messier F. Social organization and group formation of raccoons at the edge of their distribution. J Mammal. 2008;89(3):646–53. [Google Scholar]
- Salathé M, Jones J. Dynamics and control of diseases in networks with community structure. PLoS Comput Biol. 2010;6(4):e1000736. doi: 10.1371/journal.pcbi.1000736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sloot P, Kampis G, Gulyás L. Advances in dynamic temporal networks: Understanding the temporal dynamics of complex adaptive networks. Eur Phys J Special Topics. 2013;222(6):1287–93. [Google Scholar]
- Smith M. Territories, corridors, and networks: a biological model for the premodern state. Complexity. 2007;12(4):28–35. [Google Scholar]
- Taylor M, Taylor T, Kiss I. Epidemic threshold and control in a dynamic network. Phys Rev E. 2012;85(1):016103. doi: 10.1103/PhysRevE.85.016103. [DOI] [PubMed] [Google Scholar]
- Valente T, Coronges K, Lakon C, Costenbader E. How correlated are network centrality measures? Connect (Tor) 2009;28(1):16–26. [PMC free article] [PubMed] [Google Scholar]
- Vernon M, Keeling M. Representing the UK's cattle herd as static and dynamic networks. Proc R Soc B. 2009;276(1656):469–76. doi: 10.1098/rspb.2008.1009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volz E, Meyers L. Epidemic thresholds in dynamic contact networks. J R Soc Interface. 2009;6(32):233–41. doi: 10.1098/rsif.2008.0218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts D, Strogatz S. Collective dynamics of ‘small-world’ networks. Nature. 1998;393(6684):440–42. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- Wylie J, Shah L, Jolly A. Incorporating geographic settings into a social network analysis of injection drug use and bloodborne pathogen prevalence. Health Place. 2007;13(3):617–28. doi: 10.1016/j.healthplace.2006.09.002. [DOI] [PubMed] [Google Scholar]
- Youssef M, Scoglio C. An individual-based approach to SIR epidemics in contact networks. J Theor Biol. 2011;283(1):136–44. doi: 10.1016/j.jtbi.2011.05.029. [DOI] [PubMed] [Google Scholar]
- Zheng Y, Yan Y, Liu S, Huang X, Xu W. An efficient approach to solve the large-scale semidefinite programming problems. Math Probl Eng. 2012;2012(2012):1–12. [Google Scholar]