Comparison of Optical and MR-Based Tracking

Abstract

Purpose

This study aims to provide a first comparison of the accuracy of two real-time motion tracking systems in the MR environment: MR-based PROspective Motion Correction (PROMO) and optical Moiré Phase Tracking (MPT).

Methods

Five subjects performed eight predefined head rotations about 8° ± 3° while being simultaneously tracked with PROMO and MPT. Structural images acquired immediately before and after each tracking experiment were realigned with SPM8 to provide a reference measurement.

Results

Mean signed errors (MSEs) in MPT tracking relative to SPM8 were less than 0.3 mm and 0.2° in all 6 degrees of freedom, and MSEs in PROMO tracking ranged up to 0.2 mm and 0.3°. MPT and PROMO significantly differed from SPM8 in y-translation and y-rotation values (p<0.05). Maximum absolute errors ranged up to 2.8 mm and 2.1° for MPT, and 2.2 mm and 2.9° for PROMO.

Conclusion

This study presents the first in vivo comparison of MPT and PROMO tracking. Our data shows that two methods yielded similar performances (within 1 mm and 1° standard deviation) relative to reference image registration. Tracking errors of both systems were larger than offline tests. Future work is required for further comparison of two methods in vivo with higher precision.

INTRODUCTION

Subject motion during brain MRI scans is a major cause of image artifacts, and hence results in inefficient use of scanner time, due to the need to repeat scans. Such concerns are particularly acute with subjects who are uncooperative or unable to remain still, for instance, pediatric subjects or those who are in pain. Motion causes inaccurate encoding of k-space data and affects spin-excitation history, and consequently results in image artifacts such as ghosting or blurring.

A range of methods have been developed to measure rigid head motion in six degrees of freedom (DOF) and compensate for it during or after MR scanning. Retrospective motion correction approaches attempt to eliminate motion artifacts after data acquisition. They reconcile the inconsistencies in the data by co-registration of multiple image volumes or using navigator data (1) or special trajectories (2). Retrospective approaches can mitigate in-plane motion artifacts, but they commonly fail to correct the influence of through-plane motion on spin excitation history.

Alternatively, prospective motion correction approaches are based on continuous measurement of head motion and adjusting scan parameters in real-time (3). Head motion can be tracked by MR navigators (4-7), optical systems (8-12), or other methods (13). MR navigators involve customization of vendor sequences, require sufficient unused time in the host sequence, and are commonly acquired once per repetition time (TR) only. Optical systems utilize one (10,11) or more (8,14-16) cameras, and one or more markers affixed to subjects’ head or jaw. Motion parameters are derived from the motion of the marker(s) using a calibrated camera system. Optical systems are characterized by a high sampling rate (up to 100 frames per second) and do not interfere with the MR measurement process, but require careful calibration to register camera and MR coordinate systems.

The quality of prospective motion correction relies on the quality of the tracking data, but the tracking accuracy of MR-based and optical systems has not previously been compared. Both MR-based adaptive motion correction, specifically PROspective MOtion correction (PROMO) (5,6,17) and optical tracking using Moiré Phase Tracking (MPT) recently became available on our scanner (6). Therefore, we performed a study to compare their motion detection accuracy in comparison to image registration (18,19).

METHODS

MR-Based Prospective Motion Correction (PROMO)

PROMO uses a set of rapid, low-resolution, low-flip angle navigator images in conjunction with a Kalman filter algorithm to estimate head pose (5). Each navigator set consists of three orthogonal images, one each in the axial, transverse and coronal orientations. Brain masks are applied to all navigator images before motion estimation. At the start of each scan, 18 “training” navigator sets are acquired to determine optimal placement of the masks. These training sets are automatically registered to a proton density-weighted brain atlas in order to accurately project the (pre-defined) brain masks onto the three navigator planes. The masks eliminate portions of the navigator image that can move non-rigidly with respect to the brain, such as the neck and jaw (5,6).

After the “training” portion is complete (~6 sec), a single navigator set is designated as the reference set, and subsequent sets are registered to this reference. Navigator sets are acquired during unused time in the host sequence, typically “fill time” after data acquisition to allow for relaxation. Rigid-body parameters are estimated from each navigator set by an extended Kalman filter. This scheme is essentially a standard least-squares image registration, but with a tunable smoothing parameter (set to 1×10⁻¹⁰) to account for dynamics (5). Our PROMO implementation platform acquired three navigator sets (i.e., three sets of three orthogonal spiral navigator images) for each TR to improve estimation accuracy (5). The navigators had 10 × 10 mm in-plane resolution with slice thickness 5 mm and flip angle was 7°. Each navigator set took approximately 47 ms to acquire. With an additional 125 ms per set for spiral reconstruction, motion estimation and delivery of feedback, the effective sampling rate was approximately 2 Hz (1/516 ms).

While PROMO can be used as a stand-alone sequence for testing purposes, we used an existing PROMO implementation as part of a double spin echo “point-resolved spectroscopy” (PRESS) sequence [TR =3000 ms / echo time (TE) =30 ms / acquisition time (TA) =48 s / voxel size=20 × 20 × 20 mm / 10 averages]. This ensures realistic time constraints and relaxation effects (20).

Moiré-Phase-Tracking (MPT) System

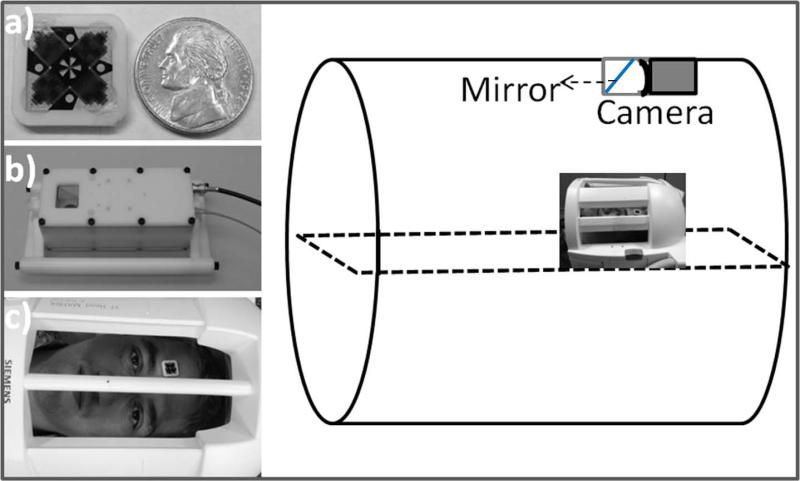
The MPT motion tracking system consists of a digital camera customized for the MR-environment and a passive MPT target (10,21). The camera operated at 80 frames per second, and includes a white LED for target illumination and a mirror (35 × 35 mm) inside a delrin housing (Figure 1). The 15 × 15 × 1.2 mm MPT target allows accurate tracking of 6-DOF motions with a single camera (Figure 1) (22,23).

FIG. 1.

Experimental setup of the Moiré Phase Tracking system. The photographs show the 15×15 mm MPT target next to a nickel (a), MR-compatible in-bore camera (b) and a subject with an MPT marker attached onto his forehead (c).

To assess the accuracy of MPT outside the scanner, a two-axis precision rotary table was used to present controlled motion. The test included tracking hardware and software identical to that used in the MR scanner, and a camera-marker geometry comparable to the in-scanner geometry. A constellation of 242 poses spanning 360° of target axial rotation, 5-35° of tilt out of the image plane and 100 mm of translation were acquired. 181 poses were used to calibrate the test-bench configuration and 61 poses were used to measure MPT accuracy. These controlled motion experiments yielded MPT measurement accuracies of 0.001 mm, 0.106 mm and 0.001 mm corresponding to X, Y and Z MRI coordinates, and better than 0.07° in all three rotations (one standard deviation).

During the scan, the target is fixed to a subject's head using double-sided tape in the area above the eyebrows. Images collected by the camera are transmitted to a processor unit outside the scanner room and analyzed to extract position and orientation information. The motion parameters are broadcast to the control unit of the scanner, where the position and orientation of the imaging volume are updated. The time from image capture to feedback reception (“latency”) is approximately 40 ms. The MR sequence requires an additional 2 ms to receive the feedback, convert them to MR frames, and update the scan parameters.

The MPT system requires an accurate transformation from the camera to the MRI coordinate frame. Therefore, a cross-calibration procedure that uses tracking data and Prospective Acquisition Correction (PACE) motion estimation (24) was performed prior to the experiment (12,25). The procedure is briefly as follows: An MPT marker was attached to a structural phantom. The phantom was imaged at approximately 10 different positions with relative orientations of about 15° between scans. Phantom motion was tracked by the MPT system and the PACE algorithm (24) was used to compute the pose differences (movements) in the MR reference frame. A least-squares optimization algorithm was applied to the two sets of measurements to calculate the optimal transformation matrix between the two coordinate systems (camera and MRI). Errors in cross-calibration of the MPT system are estimated to be within 0.2 mm and 0.2°. Based on a first-order analysis of propagation of camera calibration errors (26), and given head movements of up to 8 mm and 8° for test scans, the upper bound for residual tracking errors (after motion correction) due to miscalibration was estimated to be 0.03° and 0.06 mm (using equations [16] and [19] in reference (26)).

Subjects and Experimental Setup for Simultaneous Tracking

Five healthy subjects provided verbal and written informed consent as approved by the local Institutional Review Board. Scanning was done on a 3 T TIM TRIO (Siemens Healthcare, Erlangen, Germany) scanner with a 12-channel head coil. The protocol comprised eight PROMO-supplemented PRESS scans [TR=3000 ms, TA=48 s] interleaved with isotropic T1-weighted structural images (gradient echo) [TR=7 ms, TE=3.77 ms, FA=15°, FOV: 256 × 256 mm, 128 × 128 matrix, Partial Fourier (Slice & Phase): 6/8, Slice Thickness=2 mm, Acquisition time 26 s].

During each PRESS scan, subjects carried out one of the eight following movements (speed < 1 mm/s and < 1°/s): 1) head rotation toward subject's right about 5° (scanner Z-rotation); 2) reverse Z-rotation; 3) head rotation toward subject's left; 4) reverse Z-rotation; 5) head nodding toward chest about 5° (X rotation); 6) reverse X-rotation; 7) head nodding toward subject's superior; and 8) reverse X-rotation. Subjects were instructed to stay motionless between the scans. PROMO and MPT tracking data were collected simultaneously during each PRESS scan. Moreover, MPT tracking was enabled throughout the experiment to detect possible subject motion during the GRE scans. The MPT sampling rate was 80 Hz. PROMO motion estimates were obtained every TR. Temporal synchronization of the two data sets was realized by tagging MPT data packets at the beginning of each PROMO navigator, using the trigger signal from the scanner. MPT data coinciding with the last PROMO navigator in each TR cycle constituted MPT tracking.

Head poses at the k-space centers of pre- and post GRE scans were estimated using MPT tracking data. The unintentional motion between the center of the GRE acquisition and the PRESS acquisition was determined. If it is larger than 1 mm or 1 degree in any of the 6-DOF, image registration results were considered unreliable, and the affected data were discarded. Due to substantial motion during GRE scans, five X-rotation data were not included in the statistical analysis. The average motion during the remaining GRE acquisitions were 0.18±0.18, 0.14±0.11, 0.21±0.19 (x, y, and z-translation), and 0.23±0.22, 0.14±0.12, 0.18±0.14 (x, y, and z-rotation). In the graphs, MPT measures of head position and orientation at the centers of pre- and post-GRE acquisitions are shown 16 s before time zero (t=-16 s) and 10 s after the end of the PRESS acquisition (t=49 s) to illustrate residual motions. The asymmetry in k-space centers results from acquiring GRE scans with partial Fourier (6/8). The measurement (black cross) at t=49 s in the Figures below represents the net motion from pre-GRE center to post-GRE center based on MPT data and is shown to better interpret and discuss the results, since the net motion would tend to match the SPM8 measurement (red circle) if unintentional motion happened during GRE acquisitions. This is because motion estimation by realignment of motion-corrupted GREs is expected to match MPT estimation of motion from pre-GRE center to post-GRE center, unless other potential errors dominate.

The GRE images were skull-stripped using FSL (27) to improve registration and were registered using SPM8 (18) realign function, which applies a least-squares method and rigid-body spatial transformation. The default parameters were chosen in realignment, which includes a Gaussian smoothing kernel of 5 mm and 2^nd degree B-Spline interpolation to the images before the transformation estimation. The registration parameters produced by SPM8 yielded a pose difference that was converted to MR coordinates and used as a reference for comparison with PROMO and MPT estimates of the head motion. Tracking errors for PROMO and MPT were calculated by comparing six motion parameters at the end of the spectroscopy scan with those of the SPM8 registration parameters. The mean-signed-error (MSE), mean-absolute-error (MAE), maximum-absolute-error (MaxAE), and standard deviation (STD) for each motion parameter were calculated for each experiment. One-sample t-tests were used to determine if signed tracking errors (relative to SPM8) and the MPT and PROMO difference (MPT-PROMO) differed significantly from zero. Paired t-tests were performed on the signed tracking errors of MPT and PROMO to determine whether the two methods differ in accuracy. Moreover, correlation coefficients and linear regression parameters were calculated to compare the 6-DOF motion parameters measured by MPT and PROMO with the corresponding parameters measured by SPM8 for X-rotation and Z-rotation experiments separately.

RESULTS

Table 1 summarizes the MSE, MAE, MaxAE and standard deviations of MPT and PROMO tracking errors relative to the SPM8 registration. MSEs of MPT tracking were less than 0.3 mm and 0.2° in all 6-DOF, whereas MSEs of PROMO tracking ranged up to approximately 0.2 mm and 0.3°. One-sample t-tests on MPT tracking errors relative to SPM8 yielded significance in difference in T_y , whereas PROMO tracking errors (relative to SPM8) were significant for the R_y measurements (p<0.05). Differences between MPT and PROMO errors were significant in T_y (Table 1, Column 3). Likewise, paired t-tests between MPT and PROMO showed a significant difference in the T_y measurement (P<0.05). MAEs for both MPT and PROMO tracking errors were within 1 mm and 1°. MaxAEs ranged up to approximately 2.8 mm and 2.1° for MPT and 2.2 mm and 2.9° for PROMO. Paired t-tests between MAEs of MPT and PROMO yielded significance in the T_z measurement.

Table 1.

The mean-signed error (MSE), mean-absolute-error (MAE), and maximum-absolute-error (MaxAE) and standard deviations of MPT and PROMO tracking errors and their differences across 40 experiments. Asterisks and dagger indicate statistical significance (P<0.05) from one sample and paired t-tests, respectively.

	MPT - SPM	PROMO - SPM	MPT - PROMO
	MSE±STD / MAE±STD MaxAE	MSE±STD / MAE±STD MaxAE	MSE±STD / MAE±STD MaxAE
Tx (mm)	0.01+0.50 / 0.38+0.31 1.19	0.10+0.50 / 0.39+0.33 1.50	−0.09+0.64 / 0.48+0.42 1.45
Ty (mm)	−0.23*+0.53 / 0.46+0.35 1.38	0.17+0.74 / 0.53+0.53 2.21	−0.40*†+0.78 / 0.72+0.49 1.81
Tz (mm)	−0.01+1.10 / 0.85+0.71 2.76	0.01+0.51 / 0.39+0.31 1.10	−0.02+1.25 / 0.87†+0.89 3.71
Rx (°)	0.05+0.68 / 0.51+0.48 1.68	0.11+0.97 / 0.63+0.74 2.92	−0.07+1.19 / 0.88+0.80 2.95
Ry (°)	0.04+0.85 / 0.67+0.52 2.08	−0.23*+0.63 / 0.48+0.47 1.96	0.27*+1.03 / 0.85+0.63 2.43
Rz (°)	−0.13+0.53 / 0.44+0.30 1.24	−0.03+0.56 / 0.43+0.35 1.26	−0.10+0.59 / 0.43+0.41 1.72

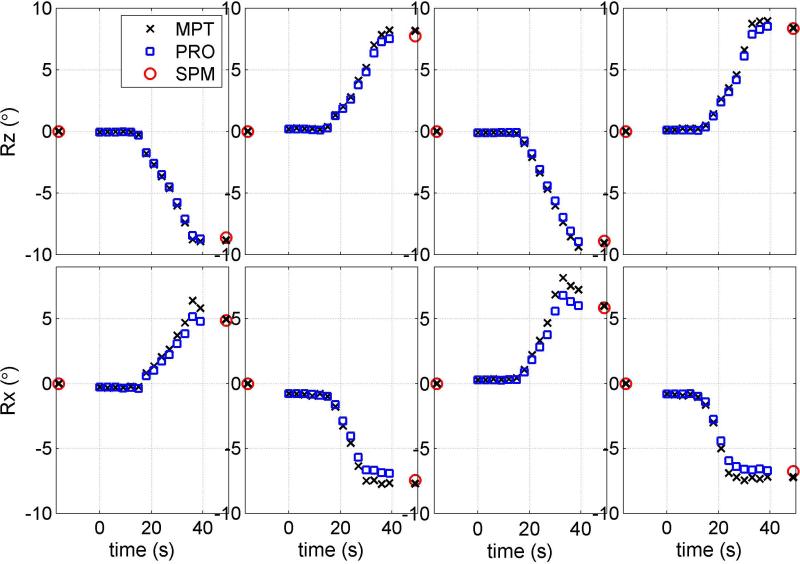
Figures 2-4 show simultaneously acquired motion trajectories of PROMO (blue square) and MPT (black cross) and reference SPM8 measurement of net motion (red circle). The black crosses at approximately 16 s before the zero point and 10 s after the PRESS acquisition are MPT measurements corresponding to the centers of pre- and post-GRE acquisitions. MPT values at pre- and post-GRE centers are expected to match with MPT values at the beginning (t=0) and the end (t=39 s) of PRESS if there is no unintentional motion during GRE acquisitions. The measurement (black cross) at t=49 s indicates the net motion from pre-GRE center to post-GRE center based on MPT data.

FIG. 2.

Motion trajectories for 8 movements that one subject performed during PRESS acquisitions: four Z-rotations (top row) and four X-rotations (bottom row). In each cell, rotation (R_z or R_x) estimates of MPT (letter x) and PROMO (blue squares) are compared to image registration parameters (red circle). MPT estimates of R_x and R_y at GRE centers are shown at times t=-16 s and t=49 s.

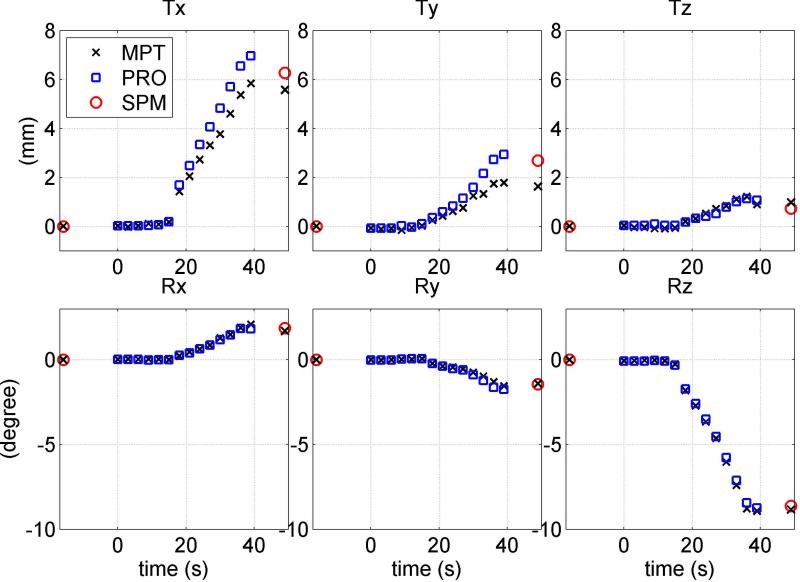
FIG. 4.

Motion trajectories for a representative X-rotation performed by one subject. Three translation (top row) and three rotation measurements (bottom row) of MPT (letter x) and PROMO (squares) are compared to image registration parameters (circle). MPT estimates of pose at GRE centers are shown at times t=-16 s and t=49 s. This figure illustrates involuntary motion during pre- and post-GRE acquisitions resulting in overestimation of MPT in R_x measurement. The MPT measurement from pre-GRE center to post-GRE center (black cross at t=49 s) matches better with SPM8 (red circle).

Figure 2 displays the trajectories for the eight movements that one subject performed. The top row shows the results of four Z-rotations and the bottom row shows the results of four X-rotations. In this example, MPT and PROMO agrees with SPM8 to within 1 mm and 1° for the four Z-rotations. No unintentional motion is observed during pre- or post-GRE acquisitions in Z-rotations according to MPT. On the other hand, MPT overestimates the rotation in comparison to SPM8 in the first and third X-rotations, while PROMO matches it well. However, PROMO underestimates the motion while MPT performs relatively better in the second and fourth Z-rotations. Some involuntary motion is observed during the post-GRE scan for the first X-rotation and during pre-GRE scans for the second and fourth X-rotations. Net motion from the center of pre-GRE acquisition to the center of post-GRE acquisition by MPT (black cross at t=49 s) is a better match than MPT data (t=39 s) at the end of the PRESS acquisition.

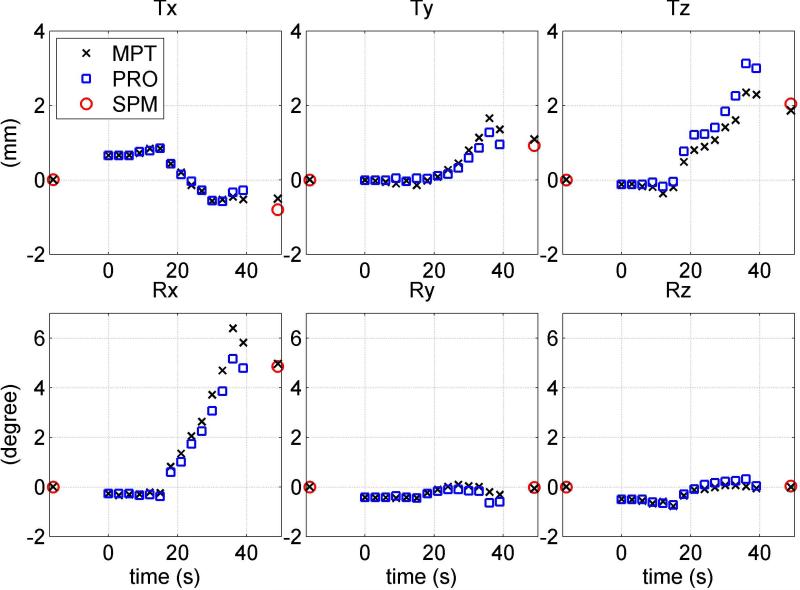
Figures 3 and 4 display three translations and three rotations for representative Z- and X-rotations performed by the same subject. For Z-rotation (Figure 3), MPT and PROMO yield results that match SPM to within 1 mm/degree for all 6-DOF. PROMO overestimates T_x and T_y measurements, while MPT underestimates them. Unintentional motion (within 1 mm) is observed in post-GRE acquisition in T_x and T_y measurements. MPT estimation of net motion between GRE acquisition centers do not agree with SPM8. In Figure 4, PROMO is in agreement with image registration to within 1° for R_x , while MPT overestimates it by about 1.2°. However, involuntary motion is observed during pre-GRE and particularly post-GRE acquisitions. MPT estimation of net motion between the centers of pre- and post-GRE acquisition (black cross at t=49 s) matches relatively better with SPM8 measurement of net motion in all DOF.

FIG. 3.

Motion trajectories for a representative Z-rotation movement performed by one subject. Three translation measurements (top row) and three rotation measurements (bottom row) of MPT (letter x) and PROMO (squares) are compared to image registration parameters (circle). MPT estimates of pose at GRE centers are shown at times t=-16 s and t=49 s.

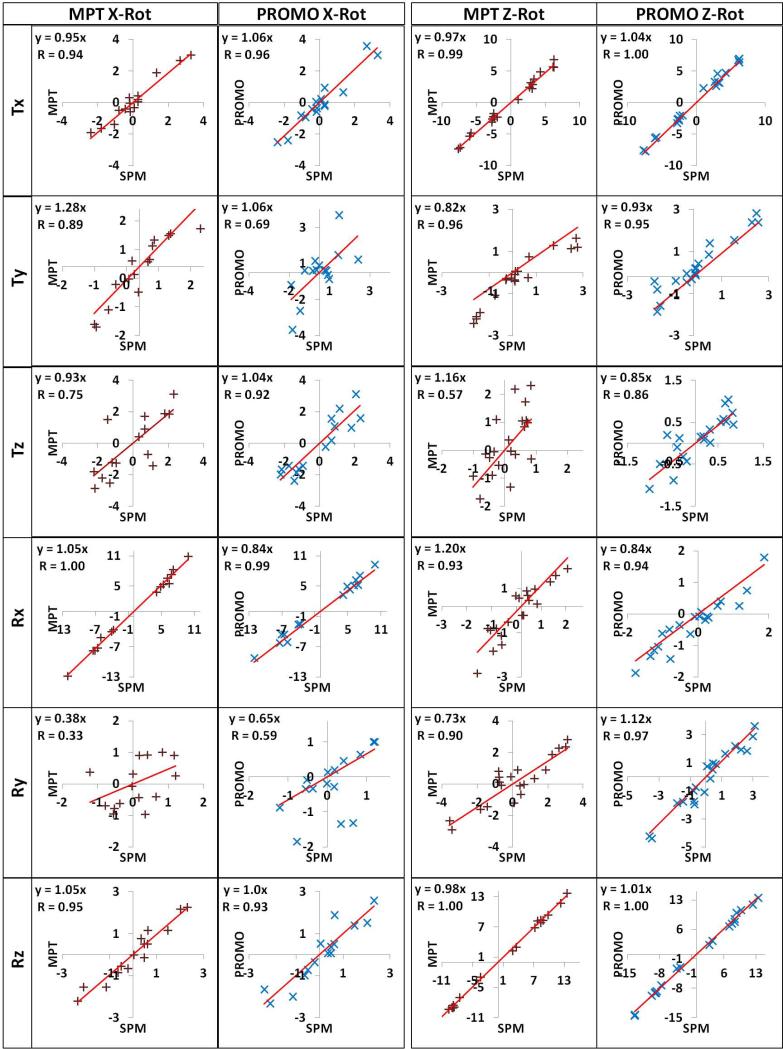
Table 2 presents the correlation coefficients and the slopes of linear regressions for all 6-DOF. For Z-rotation experiments, a linear fit of MPT vs. SPM8 in R_z yielded a slope of 0.98; for PROMO vs. SPM8 the slope was 1.01 (Figure 5). The relationship between the two tracking methods and SPM8 in R_x was more divergent for the X-rotation experiments, with slopes of 1.05 (MPT vs. SPM8) and 0.84 (PROMO vs. SPM8) (Figure 5). Similarly the R_x slopes in Z-rotation experiments were 1.20 and 0.84 for MPT and PROMO. Motion measurements of MPT and PROMO were generally highly correlated with the SPM8 measurements (Table 2). However, both tracking systems yielded low correlations against SPM8 for R_y measurements during X-rotations and T_z measurements during Z-rotations, most likely since the ranges of R_y and T_z motions in the associated experiments were small (within ~1°).

Table 2.

Correlation coefficients (CC) and slopes of the linear regressions for a given tracking method and SPM8 are given for the six degrees of freedom for X- and Z-rotation experiments.

			Tx	Ty	Tz	Rx	Ry	Rz
X-rot	MPT	CC Slope	0.94 0.95	0.89 1.28	0.75 0.93	1.00 1.05	0.33 0.38	0.95 1.05
	PRO	CC Slope	0.96 1.06	0.69 1.06	0.92 1.04	0.99 0.84	0.59 0.65	0.93 1.00
Z-rot	MPT	CC Slope	0.99 0.97	0.96 0.82	0.57 1.16	0.93 1.20	0.90 0.73	1.00 0.98
	PRO	CC Slope	1.00 1.04	0.95 0.93	0.86 0.85	0.94 0.84	0.97 1.12	1.00 1.01

FIG. 5.

Scatter plots of 6-DOF measurements for the X-rotation experiments (left half) and Z-rotation experiments (right half), with linear fit. Correlation coefficients (R) and linear fit function (with intercept fixed at 0) are shown on the graphs.

DISCUSSION

Two primary conclusions can be derived from this comparison study of MPT and PROMO. First, both methods provide sub-millimeter and less than 1° tracking accuracies when image registration is used as a reference (Table 1, mean absolute errors). Second, tracking errors of both systems are notably larger for in vivo scans than offline tests and simulations would suggest (Table 1, maximum absolute errors).

Since subjects performed Z-rotation (head shaking) and X-rotation (head nodding), the discussion will mainly focus on the primary rotation angles: R_z and R_x that represent the largest motion. The three measurements (SPM, MPT, and PROMO) agreed well on the Z-rotation experiments, particularly in R_z (slope 0.98, Table 2) and T_x (slope 0.97, Table 2), which is associated with largely Z-rotations. However, there were some discrepancies in the other DOFs (Table 2), primarily due to low range of motion (Figure 5). The discrepancies in T_x and T_y in Figure 3 might be a combination of involuntary translation during post-GRE acquisition, low range of motion particularly for T_y, and other effects.

Conversely, MPT, PROMO, and image registration showed larger discrepancies for the X-rotation experiments. The primary rotation angle (R_x) measured by MPT and PROMO differed from SPM8 by approximately 5% and -16%, respectively (Table 2). Given that MPT shows 0.1 mm and 0.1° accuracy on benchmark tests, and simulations with PROMO indicate a 0.3 mm steady-state accuracy, this suggests several practical difficulties with prospective motion correction. The discrepancies among three methods, particularly overestimation by MPT during nodding motion can be due to the residual involuntary motion during “before” or “after” structural scan. During X-rotation experiments, subjects rotated their heads in the superior or inferior direction by approximately 10°. However, the rotated head orientation was relatively difficult to maintain perfectly compared to Z-rotation. Based on MPT tracking, most subjects moved back slightly towards the original orientation during GRE acquisition (Figure 2, 1^st and 3^rd X-rotations). We discarded five X-rotation experiments due to large involuntary movement (>1 mm/degree) during GRE scans and thereby confined the involuntary motion to approximately 0.2±0.2 mm/degrees. Unintentional motion during post-GRE acquisition is seen in Figure 4. Of note, MPT estimation of net motion between the acquisition centers of pre- and post-GRE scans (black cross at t=49 s) matches well with image registration (red circle). The involuntary motion may explain the significant deviations in T_y (Table 1, p<0.05 & Table 2, MPT slope: 1.28) and T_z (Table 1) measurements by MPT and PROMO since an error in X-rotation largely affects T_y and T _z measures, while having almost no effect on T_x.

The second explanation for the discrepancies in nodding type motion, and particularly for PROMO's underestimation (Table 2) as illustrated in the second X-rotation in Figure 2, might be the motion-by-magnetic field interactions causing distortions in PROMO navigator images. Specifically, motion-induced susceptibility changes in the sinus region can alter the appearance of susceptibility-induced signal loss artifacts. Given that PROMO navigator voxels are 1 cm, even a subtle change in the intensity of a few voxels may affect PROMO estimates. Since an X-rotation changes the orientation of air-tissue interfaces relative to B0, we expect larger motion-associated PROMO image distortions (and hence errors) in X-rotation experiments compared to Z-rotation experiments (28). Of note, underestimation by PROMO is not seen in the first and third X-rotations in Figure 2, although it is reported about -16% in Table 2. However, the X-rotation was rather low in these examples (approximately 5 degrees), which would tend to attenuate the absolute error. Moreover, the significance in PROMO tracking errors in T_y (Table 1, p<0.05) can be the result of aforementioned reasons and the low range of R_y (within 2°) as seen in Figure 5.

There are two types of potential error sources in MPT tracking that might account for the discrepancies with image registration. The first one is the cross-calibration (26). Unlike PROMO, MPT data are intrinsically obtained in the camera coordinate frame and are transformed into the scanner frame using a calibration; therefore, errors in the transformation matrix may lead to tracking errors. However, with estimated upper bounds of 0.03° and 0.06 mm, residual tracking errors are most likely not the predominant source of inconsistencies between MPT and image registration. Of note, to minimize the effects of cross-calibration errors and possibly eliminate the need for the cross-registration step, Aksoy et al. (29) proposed a combination of prospective optical motion correction with retrospective entropy-based auto-focusing (30). Incorporation of this procedure could improve optimization of the cross-calibration. The second potential source of error in MPT tracking, or in fact any system that uses a marker, is the fixation of the target. The literature shows a variety of fixation techniques, including mouthpiece (9), sports goggles (10), and headbands (11,31); however, all can have fixation issues. In this study, we taped the target directly to the subjects’ head above the eyebrows. The MPT target was well tolerated by subjects, in part due to its light weight. The marker is assumed to have a fixed position relative to the skull and brain, but this may not hold true during facial movements. Furthermore, the friction between the back of the head and the coil could subtly shift the scalp relative to the brain during motion. Since this study was performed on motivated volunteers, who were instructed to keep their faces motionless, we believe that the effect of unwanted skin motion was minimal, but such effects are difficult to assess quantitatively. However, it is difficult to discern how slight, presumably random, alterations in marker fixation would cause a systematic discrepancy of 7% between MPT and SPM8 measures. These considerations highlight the fact that practical difficulties make the tracking errors of both systems markedly larger in realistic in vivo scans than offline tests and simulations would suggest.

Tracking of head motion based on PROMO presents a separate set of problems. Since the tracking quality of PROMO relies on the quality of the navigator images, effects such as scanner instabilities or motion-dependent off-resonance effects that degrade the navigator images may also corrupt rigid-body motion estimates. The overestimation of PROMO in the second and fourth Z-rotations in Figure 2 might be related to quality of navigator images in such relatively large motions (~10°). Moreover, sudden motions cannot be accurately detected by PROMO due to its low sampling rate. The higher sampling rate of MPT compared to PROMO allows for more accurate motion detection in cases of fast motions. Additionally, the Kalman filter used by PROMO to reduce measurement noise may additionally smooth out sudden changes in motion parameters. The PROMO measurement errors presented here are somewhat larger than those reported by White et al (5). This may be due to the use of five navigator sets in the original PROMO implementation, which may result in more stable motion estimation. Additionally, the accuracy of PROMO in real-world situations will depend in a complicated way on the nature of the host sequence, and on the amount of available free time (which restricts the allowable PROMO imaging parameters).

While optical tracking may suffer from errors such as cross-calibration or difficulties with target fixation, the MPT system also offers unique advantages for motion estimation compared to PROMO and other MR-based tracking systems. First, its high sampling rate allows detection of faster movements. Second, the MPT system (and potentially other external tracking systems) demands only a few milliseconds time in the sequence to update gradients and RF pulses, and does not interfere with the MR measurement. Therefore, it can be implemented with essentially all available MR sequences. Third, the number of measurements and adjustments within a single MR excitation is not restricted to one. Herbst et al. (32) reported that a quasi-continuous update of gradients using MPT tracking data is possible, allowing correction of motion-induced gradient moment errors during diffusion imaging. Likewise, Gumus et al. demonstrated that motion-induced gradient moment errors in DTI scans can be eliminated by dynamically applying small correction gradients immediately prior to the readout (21). Fourth, the MPT tracking updates can be placed anywhere in the pulse sequence without interfering with the imaging experiment or relaxation status of the spins. Conversely, the major advantages of MR-based tracking systems, such as PROMO, is that they do not necessitate additional equipment such as a camera or target, and directly track the tissue of issue (i.e., MR navigators do not suffer from marker fixation issues).

This study has two limitations. First, the tracking results reported are the accuracies of PROMO and MPT in comparison to SPM8 image registration for steady-state head pose. Thus, possible inaccuracies in the SPM8 registration algorithm set a limitation for the evaluation of both methods. The SPM realignment algorithm (19) was reported to be highly accurate (with an error below 0.5 mm in 3 directions) (33), yielding better motion estimation than the alternative Automatic Image Registration (AIR) algorithm (34). To increase the accuracy of SPM8 realignment, we also used isotropic resolution (2×2×2 mm) in GRE acquisitions. The second limitation of this study is the residual subject motion during GRE scans. To avoid subject motion during structural scans, we kept the scan time for the reference GRE scans as short as possible (26 s). Additionally, we used MPT data during GRE scans to detect large motions and eliminated data sets with large involuntary motion during GRE scans, confining the involuntary motion to 0.2±0.2 mm/degrees. After these efforts, we defined image registration as the gold standard for our experiments. However, inadvertent motion during structural scans can impair the registration accuracy of SPM8. Thus, the discrepancy between the tracking systems and image registration can partly be due to the imperfect realignment of structural scans corrupted by residual unwanted subject motion. Of note, instead of discarding the data with unwanted motion, we also had the option of freezing the motion during GREs using MPT data. However, this approach might introduce bias towards eliminating errors relative to MPT and was therefore not implemented. Likewise, the use of MPT to detect motion during structural scans might be objectionable, since the purpose of the study is to compare MPT with PROMO. However, this is not a real limitation because MPT data during GRE acquisitions were only used to discard motion-corrupted data, whereas subjects were supposed to be stationary. Therefore, the effect of this action is same on both MPT and PROMO, and aided to select quality structural data for the MPT and PROMO comparison.

This study highlights the fact that an independent method to evaluate prospective motion correction in the MR environment is needed. The motion simulator approach by Prieto et al. (35) could be an extremely useful tool in making reproducible movements in the MR environment and provide a gold standard for real-time motion tracking studies. However, PROMO was designed to track the human brain and may not perform best in phantom experiments, since it particularly uses initial acquisitions to mask the brain and exclude non-rigid parts such as jaw or neck. Therefore, the ideal comparison of PROMO and MPT correction may involve their relative improvements on image or spectral quality. However, the design of such an experiment is challenging since reproducible motion is required to fairly compare both systems and it is difficult for even well-trained subjects to perform exactly the same movement twice. Therefore, the current paper compares tracking accuracy of the two systems.

In conclusion, we simultaneously tested two very different approaches to real-time motion tracking on human subjects in the MRI environment and found that both methods yielded similar performance in terms of accuracy (sub-millimeter and less than 1°) when image registration were used as reference. Tracking errors were measured larger than offline tests indicating the effect of practical difficulties in real-life experiments. This study provides the first in vivo comparison of optical and navigator based tracking systems in literature. Future work is required to further compare two methods with higher precision.