Temporal and spatial assessments of minimum air temperature using satellite surface temperature measurements in Massachusetts, USA

Abstract

Although meteorological stations provide accurate air temperature observations, their spatial coverage is limited and thus often insufficient for epidemiological studies. Satellite data expand spatial coverage, enhancing our ability to estimate near surface air temperature (Ta). However, the derivation of Ta from surface temperature (Ts) measured by satellites is far from being straightforward. In this study, we present a novel approach that incorporates land use regression, meteorological variables and spatial smoothing to first calibrate between Ts and Ta on a daily basis and then predict Ta for days when satellite Ts data were not available. We applied mixed regression models with daily random slopes to calibrate Moderate Resolution Imaging Spectroradiometer (MODIS) Ts data with monitored Ta measurements for 2003. Then, we used a generalized additive mixed model with spatial smoothing to estimate Ta in days with missing Ts. Out-of-sample tenfold cross-validation was used to quantify the accuracy of our predictions. Our model performance was excellent for both days with available Ts and days without Ts observations (mean out-of-sample R²=0.946 and R²=0.941 respectively). Furthermore, based on the high quality predictions we investigated the spatial patterns of Ta within the study domain as they relate to urban vs. non-urban land uses.

1. Introduction

Air temperature measurements are of great importance for epidemiological studies. Recently, it has been shown that variation in ambient minimum air temperature is correlated with human morbidity and mortality, especially for cardiovascular diseases (Basu et al., 2008; Medina-Ramón et al., 2006; Zanobetti and Schwartz, 2008). Furthermore, minimum temperature is considered a better predictor of excess mortality compared to mean or maximum temperature (Saez et al., 1995; Zanobetti and Schwartz, 2008). In addition, near-surface air temperature (Ta) and relative humidity are the most relevant variables to disease vector monitoring and the prediction of disease incidences.

In the thermal infrared region of spectra, satellite sensors measure top of the atmosphere radiances, from which surface brightness temperatures are derived using Planck’s Law (Dash et al., 2002). In order to compute land surface temperature (Ts), these brightness temperatures are further corrected for: (1) atmospheric effects, including absorption, upward emission, and downward irradiance reflected from the surface (Franc and Cracknell, 1994); and (2) spectral emissivity, aiming to account for the roughness properties of the land surface, the amount and nature of vegetation cover, and the thermal properties and moisture content of the soil (Friedl, 2002).

Whereas Ta measurements provide spot data of a selected point or route, remotely sensed Ts data have been widely used to retrieve a spatially continuous view of the land Ts. In this regard, the ability to cover large areas simultaneously on a repeated basis is a significant advantage of satellite observations over conventional climatic methods. Although the genesis and temporal dynamics of surface and air temperatures have dissimilarities, they are nevertheless related (Oke, 1995; Voogt and Oke, 1997). Ts modulates the air temperature of the lower layer of urban atmosphere, and is a key factor in determining surface radiation and energy exchange and human comfort in the cities (Voogt and Oke, 1998). In addition, the physical properties of various types of urban surfaces, their albedo, thermal properties, street geometry, traffic loads, and anthropogenic activities are important factors that determine Ts in the urban environments (Chudnovsky et al., 2004). However, the derivation of near surface Ta from satellite information is not straightforward due to the dissimilarity in the genesis and temporal dynamics of both variables.

Several studies have shown correlations between Ta and Ts when thermal data were obtained from a distance of 3 m (Stoll and Brazel, 1992) or acquired by air-borne sensors at high spatial resolutions (Saaroni et al., 2000; Yang et al., 1994). Recently, several studies correlated between daytime Ts satellite observations and Ta at ground meteorological stations across non-urban areas. For example, Fu et al. (2011) applied linear regression to estimate air temperature of an alpine meadow on the Northern Tibetan Plateau. They estimated at heights of 1.5–2.1 m by using Moderate Resolution Imaging Spectroradiometer (MODIS) data, showing that Ts data were accurate enough to estimate daily minimum and nighttime mean Ta using linear regression (R²>0.55, p<0.01). Vancutsem et al. (2010) explored the possibility of retrieving high-resolution Ta data from the MODIS nighttime surface temperature over different ecosystems in Africa (with Ts–Ta) centered at 0 °C, a mean absolute error (MAE)=1.73 °C and a standard deviation=2.4 °C. Another approach to estimate air temperature is based on the correlation between Ts and spectral satellite-derived Normalized Difference Vegetation Index (NDVI), denoted in the literature often as the Temperature-Vegetation Index (TVX) (Goward et al., 1994; Prihodko and Goward, 1997). In contrast, in the urban environment, since 1989 most papers have reported a qualitative description of thermal patterns. This includes the spatial distribution and magnitude of Urban Heat Islands across the city as well as simple correlations between Ts and land-use and land-cover types (Voogt and Oke, 2003). Importantly, as highlighted in the recent review by Weng (2009), a precise transfer function between Ts and the near ground Ta is not yet available although energy balance models try to provide this capability. For example, thermal remote sensing coupling with urban climate models of the atmosphere is applied to the study of urban surface energy models (Friedl, 2002; Voogt and Oke, 2003).

Generally, correlations of surface temperature with air temperature are superior at night (Dousset, 1989) when microscale advection is reduced. During day hours, due to the influence of the direct solar illumination, additional factors are apparent leading to a more complex interaction between Ta and Ts: satellite–sun geometry, surface geometry, sky view factor, thermal properties of the underlined surfaces and weather conditions.

In this paper we hypothesized that the Ts–Ta relationship varies daily; therefore, in order to use available cloud-free Ts data, it is necessary to calibrate on a daily basis using ground Ta measurements. The underlying assumption is that the effect of time-varying parameters (e.g., surface reflectance, soil moisture, land use and land cover characteristics, vapor pressure gradients, the vegetation–soil interaction and surface winds) that influence the Ts–Ta relationship can be taken into account by using daily available calibrations. Furthermore, we present a novel approach that incorporates land use regression, meteorological variables and spatial smoothing to predict Ta for grid cells when satellite Ts measures are not available. We pursue the use of night time satellite data for estimating daily minimum temperatures. Finally, based on our model we examined the spatial pattern of Ta behavior for 2003 in the study domain.

2. Methods

2.1. Study domain

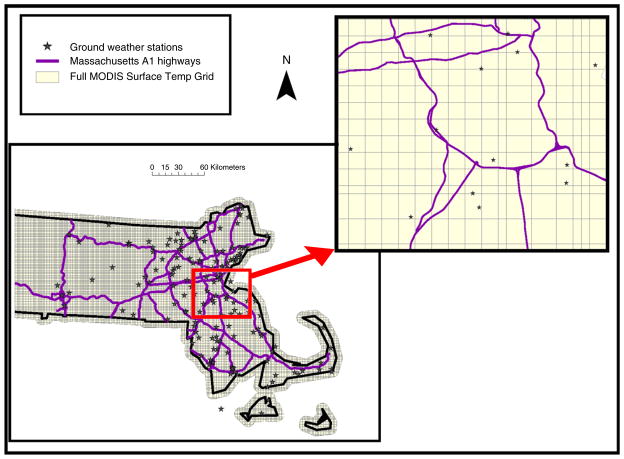
The spatial domain of our study included the state of Massachusetts (MA), USA (Fig. 1). The state of MA is located on the northeastern coast of US and has an area of 27,340 km². MA has a population of 6,349,097 according to the 2000 census (USCB, 2000). Approximately two thirds of the state’s population lives in Greater Boston, most of which is either urban or suburban. MA had an average annual air temperature of 9.26 °C during 2003 (NCDC, 2010). Importantly, there are significant climatic differences between its eastern and western sections. Specifically, MA has cold winters and moderately warm summers. The mountainous regions in the west (the Berkshires) have both the coldest winters and the coolest summers. MA has diverse land use and land types including many urban areas, rural hill towns, forests, small farms, rivers, lakes, mountainous regions and an eastern sea shoreline.

Fig. 1.

Map of the study area showing the full surface temperature grid and all air temperature monitor station across Massachusetts.

2.2. Surface temperature and emissivity data

The satellite data used in this study, are the land surface temperatures (Ts) at a 1 km spatial resolution derived from the Moderate Resolution Imaging Spectroradiometer (MODIS) sensors on board the Terra satellite. We used Terra nighttime Land Surface Temperature and Emissivity (MOD11_L2) product (Wan, 2006, 2008; Wan et al., 2002). The MODIS Ts is derived from two thermal infrared band channels, i.e., 31 (10.78–11.28 μm) and 32 (11.77–12.27 μm) using the split-window algorithm (Wan, 2008) which corrects for atmospheric effects and emissivity using a look-up table based on global land surface emissivity in the TIR region (Thermal Infra-Red, MODIS channels 31–32 or 10,000–12,500 nm) (Snyder et al., 1998). Emissivity is an additional parameter that influences the Ts measurements. First, it causes a reduction of surface-emitted radiance. In addition, the anisotropy of reflectivity and emissivity may reduce or increase the total radiance from the surface (Prata, 1994). Emissivity is a function of wavelength, and is not only controlled by water content, chemical composition, structure, and roughness (Snyder et al., 1998), but it can vary significantly with plant species, areal density, and growth (Snyder et al., 1998). Surface emissivity values are available in MOD11_L2 product in MODIS bands 31 and 32 and they are assigned based on land cover types (Wan, 2006).

The MODIS derived radiometric temperature corrected for atmospheric transmission was further corrected with spectral emissivity to account for the kinetic temperature of the object based on the following (Eq. 1) (Jensen, 2009):

$${\mathrm{T}}_{\text{kin}}={\mathrm{T}}_{\text{rad}}/{{\text{Emmisivity}}_{(\mathrm{\lambda })}}^{1/4}$$ (1)

where T_kin is related to the true kinetic temperature (and further denoted here as Ts) and T_rad is the radiant temperature of an object recorded by a remote sensor.

The nighttime Ts generally presents good correlations with ground measurements across most of the sites in the USA, with absolute biases less than 0.8 °C and RMSEs less than 1.7 °C (Wan, 2008). Importantly, the errors in the MOD11_L2 product weakly depend on the sensor view zenith angle and are independent of surface air temperature, humidity, wind speed, and soil moisture (Wang et al., 2008). A serious limitation of the thermal satellite remote sensing techniques is the requirement for clear skies in order to derive accurate readings of Ts making cloud cover. To that end we identified clear sky observations using the current best available cloud mask algorithm flagged in the MODIS data (Ackerman et al., 1998). More details about MODIS Ts data can be found in previous papers by Wan (Wan, 2008; Wang et al., 2008).

To assure that ground Ta measurements represent the Ts at the time of satellite overpass (10:30 pm local time), we correlated between Ta minimal during a day, and Ts from Terra. We did not collect Ts from the Aqua platform.

2.3. Meteorological data

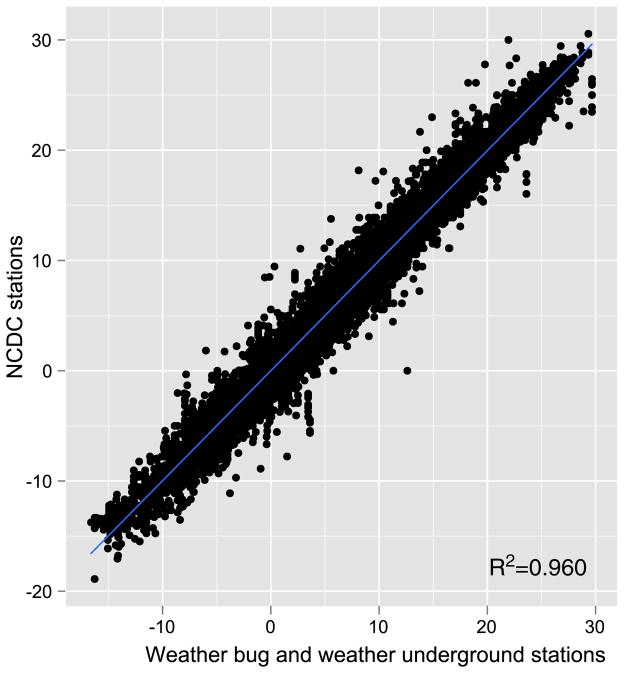
Daily data for Ta and wind speed across MA for 2003 were obtained from four different sources: The National Climatic Data Center (NCDC), US Environmental Protection Agency (EPA), WeatherBug Professional (WB), and Weather Underground Inc. (WU). NCDC and EPA are government agencies and have been collecting meteorological data close to a century now, while the latter two (WB and WU) have been established after 2000. WB is a commercial provider of weather information services, while WU is a network of personal weather stations. All of the above sources have been used in multiple studies in the past few years (Rosenzweig et al., 2006; Von Klot et al., 2008, 2009; Wellenius et al., 2006). To validate the WU and WB stations compared to the more traditional NCDC and EPA sources we have matched each of the WB and WU stations to the closest NCDC weather service station within 10 km, and computed the correlations. The average correlation (R²) was 0.960, suggesting that the use of WB and WU stations is unlikely to be imprecise (see Fig. 2).

Fig. 2.

A scatter plot of the correlation between the weather underground/weatherbug stations and NCDC stations.

We obtained mean, minimum and maximum daily temperatures from the NCDC, EPA, WB and WU from January to December 2003 and removed outliers and extreme values suggestive of coding or measurement errors (extreme temperature values that do not naturally occur due to measurement error such as reported temperature values of over 50 °C or below −40 °C). There were 164 daily monitors operating across MA during the study period (see Fig. 1). Since there was no hourly temperature reading available for all stations, we choose minimum Ta as the closest indicator for nighttime temperature. We used wind speed data from only three available sources: NCDC, EPA and WU and thus used ordinary kriging to interpolate the missing data for each 1×1 km grid cell.

2.4. Spatial predictors of air temperature

Initially we tested the daily correlation between Ta and Ts. In addition, to improve the prediction ability of the final constructed model other potential predictors we expected, a priori, to have a physical influence on Ta were considered for inclusion in the model (traffic density etc.). All the potential predictors were initially included in the model. The only variable that was removed was traffic density, which was much less plausible than impervious surfaces, etc. in the first place, and this was because it was not significant in the model. The following variables were statistically significant and thus were used in our final models: emissivity, percent of impervious surfaces, elevation and NDVI.

2.4.1. Percent of impervious surfaces

These data were obtained through the 2001 national land cover data (NLCD) Multi-Resolution Land Characteristics Consortium (MRLC) (Homer et al., 2004). Data were obtained as raster files with 30 m cell size. Percent of impervious surfaces included all sub categories for developed areas.

2.4.2. Elevation

These data were obtained through the National Elevation Dataset (NED) (Maune, 2007). NED is distributed by the U.S. Geological Survey (USGS) and provides seamless raster elevation data of the conterminous United States. NED is distributed in geographic coordinates at a resolution of 1 arc sec. MA has notable elevation differences between its eastern and western parts. Therefore, elevation was used as a spatial predictor since generally the higher the elevation the lower the air temperature.

2.4.3. NDVI

Satellite-derived Normalized Difference Vegetation Index (NDVI) data have been shown to be a temporal indicator of the vegetation growth rate, its onset, end, peak and duration of vegetation greenness, and also the periodicity of the photosynthetic activity (Reed et al., 1994; Yang et al., 1994). The rationale for using two wavelengths to calculate NDVI is the sensitivity of leaf pigments to red light (RED-wavelengths centered at 660 nm) and high reflectance of leaf structure at near-infrared (NIR-wavelengths ranging from 700 to 1100 nm) (Jensen, 2007; Tucker, 1979) (Eq. 2):

$$\text{NDVI}=\left({\mathrm{\rho }}^{\text{NIR}}-{\mathrm{\rho }}^{\text{RED}}\right)/\left({\mathrm{\rho }}^{\text{NIR}}+{\mathrm{\rho }}^{\text{RED}}\right).$$ (2)

We used monthly vegetation index products (MOD13A3) at a 1 km spatial resolution because NDVI remains relatively constant during each month.

2.5. Statistical methods

To estimate Ta in each grid cell on each day we first calibrated the Ts measurements for each day using grid cells for which both Ta measurements and Ts values were available (stage 1). This stage 1 model was then used to predict Ta in grid cells without Ta measurements but with available Ts measurements (stage 2). Since Ts values are often missing due to cloud cover or retrieval errors, the stage 2 model failed to provide predictions for many grid cell–day combinations. To estimate Ta when no Ts data are available we fit a third model that takes advantage of the association of grid cell Ts values with Ta monitoring located elsewhere and the association with Ts values in neighboring grid cells (stage 3). Importantly, since daily Ta for the whole of MA varies considerably between different geographical regions, MA was divided into three regions: eastern MA, central MA and west MA. The daily mean Ta was calculated for each region.

First a mixed model regression with day-specific random intercepts and Ts slopes was performed (stage 1). At each day we estimate a separate slope in the relationship between Ta and Ts that captures its temporal variability. Specifically we fitted the model (Eq. 3):

$${\text{Ta}}_{\text{ij}}=\left(\mathrm{\alpha }+{\mathrm{u}}_{\mathrm{j}}\right)+\left({\mathrm{\beta }}_1+{\mathrm{v}}_{\mathrm{j}}\right){\text{Ts}}_{\text{ij}}+{\mathrm{\beta }}_2\text{Wind}{\text{Speed}}_{\text{ij}}+{\mathrm{\beta }}_3{\text{Elevation}}_{\mathrm{i}}+{\mathrm{\beta }}_4{\text{NDVI}}_{\text{ik}}+{\mathrm{\beta }}_5\text{Impervious}{\text{surfaces}}_{\mathrm{i}}+{\mathrm{\epsilon }}_{\text{ij}}\left({\mathrm{u}}_{\mathrm{j}}{\mathrm{v}}_{\mathrm{j}}\right)~[(\text{oo}),\mathit{\sum }]$$ (3)

where: Ta_ij is the measured Ta at a spatial site i on a day j; α and u_j are the fixed and random (site specific) intercepts, respectively, Ts_ij is the Ts value in the grid cell corresponding to site i on a day j; β₁ and v_j are the fixed and random slopes, respectively. Wind Speed_ij, and NDVI_ik are the values in the grid cells corresponding to site i on a day j (or month k for NDVI). Elevationi and Impervious surfacesi are the means in grid cells corresponding to site i. Finally, Σ is an unstructured variance–covariance matrix for the random effects and ε_ij is the error term at site i on a day j.

To validate our model, the dataset was repeatedly randomly divided into 90% and 10% splits. Predictions for the held-out 10% of the data were made from the model fit of the remaining 90% of the data. The process was repeated ten times and cross-validated R² values were computed. To test for bias we regressed the measured Ta values against the predicted values in each site on each day. Temporal R² was calculated by regressing delta Ta against delta predicted where: delta Ta is the difference between the actual Ta in place i at time t and the annual mean Ta at that location, and delta predicted is defined similarly for the predicted values generated from the model. Spatial R² was calculated by regressing the annual mean Ta against the mean predicted Ta at place i. In the next stage (stage 2), we used the same stage 1 model to predict Ta in grid cells where Ts data is available but Ta monitoring data is not. Finally in stage 3, we estimated the daily Ta for all grid cells in the study domain for days when Ts data were unavailable using stage 2 data. To capture the ability of neighboring cells to fill in the cells with missing Ts values, we regressed the predicted Ta in each cell on each day against the mean of the Ta measurements on that day in each region (the average Ta measured at all the available Ta measurements on each day) and a smooth function of latitude and longitude, with random cell-specific intercepts and slopes. To allow for temporal variations in the spatial correlation, a separate spatial surface (a thin plate spline) was fit for each two-month period. In contrast to the first stage, the third stage model includes a cell specific random slope and intercept that captures the spatial variability for each cell relative to the average in that region (Eq. 4):

$${\text{PredTa}}_{\text{ij}}=(\mathrm{\alpha }+{\mathrm{u}}_{\mathrm{i}})+({\mathrm{\beta }}_1+{\mathrm{v}}_{\mathrm{i}}){\text{mTa}}_{\text{jr}}+\text{Smooth}{(\mathrm{X},\mathrm{Y})}_{\mathrm{k}(\mathrm{j})}+\text{Bimon}+{\mathrm{\epsilon }}_{\text{ij}}\left({\mathrm{u}}_{\mathrm{j}}{\mathrm{v}}_{\mathrm{i}}\right)~\left[(\mathrm{o}\mathrm{o}),{\mathrm{\Omega }}_{\mathrm{\beta }}\right]$$ (4)

where: PredTa_ij is the predicted Ta at a spatial site i on a day j from the first prediction model; mTa_jr is the mean Ta across the specific region on a day j; α and u_i are the fixed and random intercepts, respectively; β₁ and v_i are the fixed and random slopes, respectively. The smoothing of X,Y is a thin plate spline fit of the latitude and longitude, which is similar to kriging, but it allows greater spatial anisotropy, k(j) denotes the two-month period in which day j falls (that is, a separate spatial smooth was fit for each two-month period), and Bimon (bi-monthly period) is an indicator for each two month period. Using this final model, we again performed cross-validation to estimate the goodness of fit.

We also tested how the performance of our models compared to using traditional spatial smoothing of monitored values (kriging). All modeling was done in R statistical software version 2.12.2.

3. Results

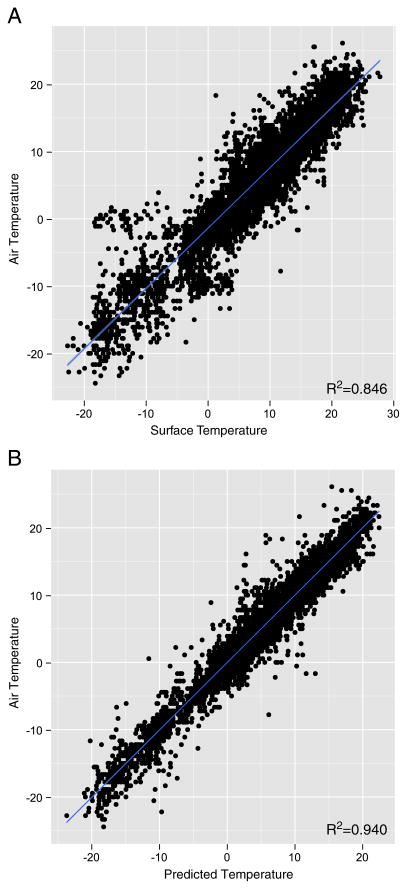
The upper panel of Fig. 3 presents a scatter plot of the Ta–Ts relationship before the stage 1 calibration whereas the relationship between the predicted out of sample Ta vs the actual Ta is shown in the lower panel of Fig. 3. These results show how by using the daily calibration approach we can improve the fit from a R² of 0.848 to a R² of 0.949 (P<0.001).

Fig. 3.

A scatter plot of the air temperature–surface temperature relationship before (A) and after (B) the daily 2003 calibrations.

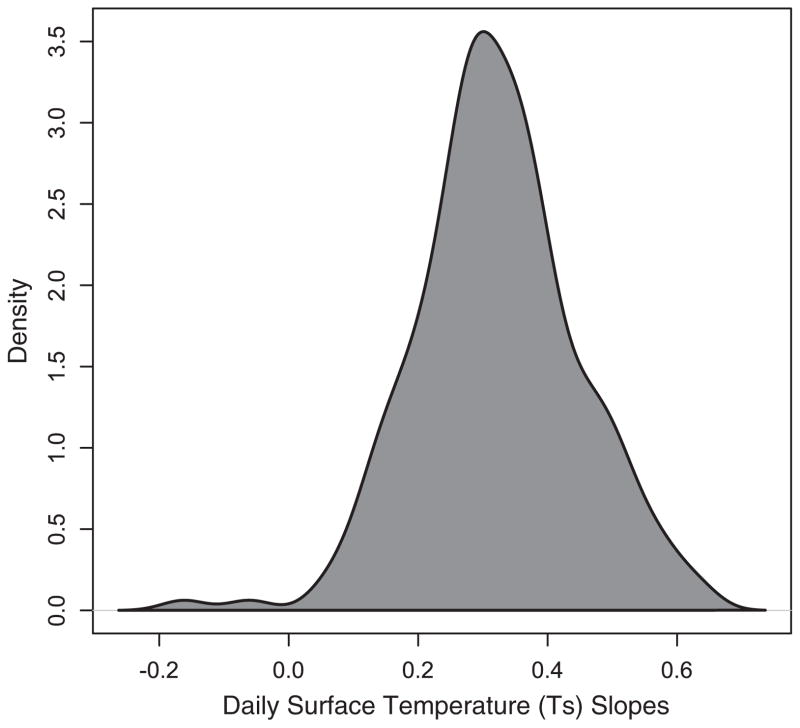
Fig. 4 presents the daily distribution of random slopes of Ts in 2003. It also shows the difference of the day specific slopes from the average slope. As can be seen the relationship between Ta and Ts varies daily which is why the stage 1 calibration model is necessary.

Fig. 4.

A density plot exhibiting the daily variation of surface temperature slopes by time for 2003.

The first stage models all revealed very high out-of-sample fits with a mean out of sample R² of 0.949 (P<0.001), and as expected a highly significant association between Ta and the main explanatory variable—Ts (Table 1). The spatial and temporal out of sample results also presented very high fits (Table 1). For the spatial model the mean out-of-sample R² was 0.960 and for the temporal model the mean out-of-sample R² was 0.800 (P<0.001). We found no bias in our cross validation results (slope of observed vs. predicted=1.00).

Table 1.

Prediction accuracy—cross validated R² for all Ta prediction models for 2003.

	R2
Overall R2	0.949***
Spatial R2	0.960***
Temporal R2	0.800***
Gamm R2	0.947***

^*Indicates a 0.1 significance level.

^**Indicates a 0.05 significance level.

^***Indicates a 0.01 significance level.

Stage 3 models also performed well with a mean out-of-sample R² of 0.947 (P<0.001), which is extremely high considering that these were days with neither ground Ta data nor satellite Ts data in the grid cells being predicted.

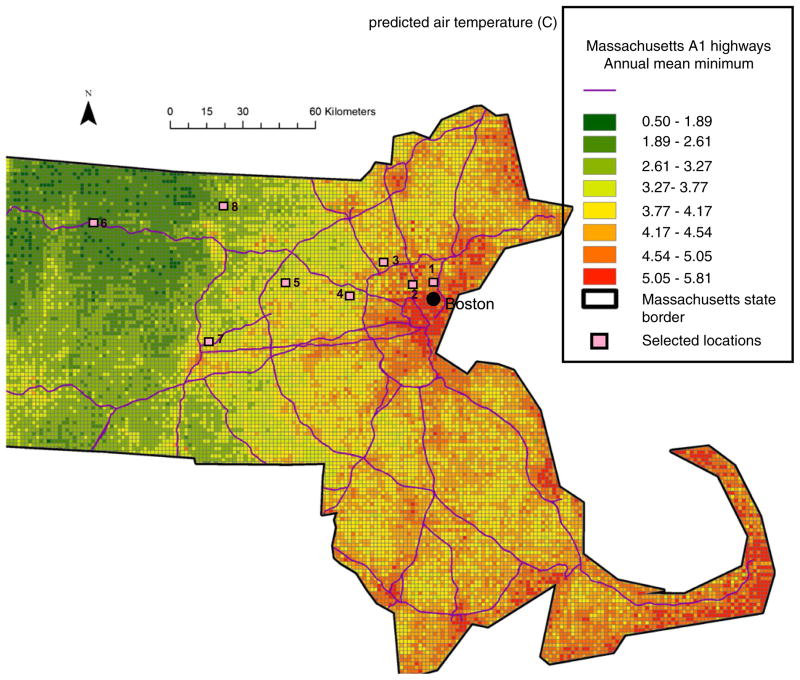
Fig. 5 shows the spatial pattern of predicted Ta values from the Ts models, averaged over the entire study period. Mean predicted minimum Ta values for 2003 ranged from 0.5 to 5.8 °C. Generally urban areas appear warmer than the surrounding areas. To explore these differences we analyzed Ta from eight different representative sites covering an area of 4×4 km² (highlighted in Fig. 5 by rectangles). The results are shown in Fig. 6.

Fig. 5.

Mean air temperature in each 10×10 km grid during 2003 predicted by the surface temperature models.

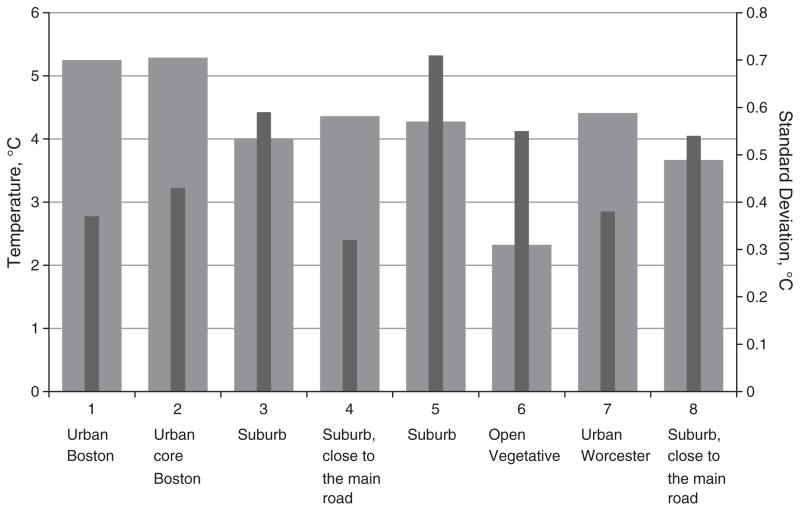
Fig. 6.

Selected 4×4 km representative regions exploring differences in predicted annual mean air temperature between regions. The box represents the predicted air temperature while the whisks represent the standard deviation.

As it can be seen in Fig. 6, there are temperature changes between the rural open and the built-up areas. There is a noticeable change between urban area yearly mean Ta (e.g. point 2 predicted Ta=5.2 °C) and vegetative open space areas (e.g. point 6-predicted Ta=2.3 °C). In addition, sampled suburban areas located near main roads exhibited higher temperature of 0.4–0.5 °C compared to the inner part. Also there is a great variability in standard deviation (SD) among all sampled areas suggesting the local influence of different wind patterns and urban canyon geometry on the measured Ta.

The kriging model resulted as expected in a much lower R² compared to the R² of our combined model (0.30 versus 0.95 respectively).

4. Discussion

In this paper we assessed Ta across MA during the year 2003 based on MODIS Ts data. There are several important key features differentiating our study from previous studies (Fu et al., 2011; Saaroni et al., 2000; Vancutsem et al., 2010; Yang et al., 1994). First and foremost, the use of daily Ts–Ta calibrations allows a better assessment of space–time interactions than models that include only spatially resolved time invariant land use terms. Indeed, this daily calibration approach exhibits the differences in short-term temperature values between grid cells. Most importantly, our model predicts temperature values for days when satellite Ts is unavailable (extensive cloud coverage, snow etc.). For example, in epidemiology such data could be used to assess the acute effects (short-term) of temperature (heat waves, cold spells), and chronic effects (long-term) of temperature, or combines the acute and chronic effects. As shown in our analysis, Ts can be reliably used to predict Ta if modeled appropriately.

Although Vancutsem et al. (2010) found relatively good correlation between night Ts and minimum Ta for vegetative and non-urban land cover types, six stations exhibited higher variability between measured and predicted values. This was explained by the following factors: (i) site location near the sea or lake; (ii) directional effects due to the angular anisotropy of emissivity; and (iii) temperature variability in mountainous areas (e.g., difference of spatial scales, point vs. areal average). Moreover, the differences were also related to location and seasonal changes. Because different variables can influence the Ts–Ta relationship we applied a mixed effects model approach. The underlying assumption was that the effect of time-varying parameters influencing the Ts–Ta relationship (e.g., relative humidity, surface properties, land cover type, location) can be taken into account using daily calibrations. In this regard, to the best of our knowledge our models are the first to cover both vast urban and rural areas across MA, USA with high prediction accuracy for all sites.

Our predicted mean values across MA for the year 2003 are in a good agreement with the recorded annual mean minimum temperatures. For example, in central Boston the annual mean difference between measured (NCDC, 2010) and predicted Ta was 0.2 °C (5.4°–5.6 °C respectively). In the semi-rural area of Fitchburg, MA there was a slightly higher difference of 0.6 °C (3.8°–3.2 °C respectively). Since our model could be used in studies on the acute effects of temperature we sampled the same points for a representative day in the summer (12.08.2003). In central Boston the daily difference between measured and predicted Ta was 0.54 °C (21.85°–21.24 °C respectively). In the semi-rural area of Fitchburg, MA there was a slightly higher difference of 0.15 °C (19.85°–19.70 °C respectively). There is a 2 °C difference between urban and sub urban areas.

We ran a cluster analysis and found a significant clustering (P<0.001) around metropolitan areas (Boston, Worcester) and around coastal areas which is to be expected. Urban areas tend to show higher temperature values compared to rural areas due to well-known factors such as the urban heat island (UHI) (Kim, 1992) etc. Areas closer to the shoreline also tend to exhibit warmer temperatures compared to inland areas since shoreline areas are kept warmer by the water’s effect on the air (Pieri et al., 2011).

Based on our model results, the accuracy of estimating Ta was independent of the other covariates (NDVI, wind speed etc.). However, all covariates were found to be significant (n=5305, Akaike information criterion—AIC=30566.86, P<0.001) and therefore were included in our final model. Our results (as shown in Fig. 5) present high variability in SD values. This can be explained by air temperature spatial variability at the micro-scale level within selected locations (e.g. within points 1–8). In this regard, ground meteorological stations are unable to capture this variability, which is needed for epidemiological studies. However, the ability to estimate this variability is also available through the use of urbanized surface energy balance models that are used within the suite of weather forecasting models (Barry and Chorley, 2003; Friedl, 2002; Voogt and Oke, 2003). Furthermore, urban and densely populated areas exhibit a lower SD than the open rural and vegetation.

It is important to stress out that our prediction models were designed to use only night MODIS Ts for several key reasons. First, health effect studies examining the association between hot days and mortality suggest that the main predictor is minimum temperature. This is because people are more susceptible to the stress posed on the respiratory and circulatory systems when there is no sufficient nighttime cooling (Saez et al., 1995; Zanobetti and Schwartz, 2008). Furthermore, during nighttime, the Earth surface behaves almost as an isothermal and homogeneous surface. In contrast, during daytime there is a significant directional anisotropy effect which is due to differences in sun illumination vs. satellite viewing geometry, and different shading effects within pixels, giving rise to temperature differences as much as 20 °C (Wan and Dozier, 1996).

To the best of our knowledge, all previous epidemiological research studying the association between temperature and health effect have all used one central meteorological station to assign temperature exposure (Halonen et al., 2010; McMichael et al., 2008; O’Neill et al., 2003). This introduces exposure error, and likely biases the effect estimates downward (Zeger et al., 2000). In this regard, predicting nighttime temperature exposures with fine spatial and temporal resolutions will be critical for improving the accuracy in future epidemiological studies. In addition these models could be useful in other fields such as in urban planning, where development of adaptation strategies is necessary.

Although the minimum Ta may be expected near dawn (in most but not all cases), we are correlating Ts which overpasses at 10:30 pm local time with Ta at a different time. The empirical question is whether the use of daily calibration, which captures day to day differences in the association between Ts at one time and Ta several hours later, is sufficient to provide good predictive power. The answer is yes. Our out of sample R² is very high. Had the predictive power been poor, we may have needed to revisit that choice, but in the event it was very good, and so we continued to predict the temperature that seemed most relevant for health studies.

There are a few limitations of the present study that need to be pointed out. For one since we use daily calibrations in this model, this requires a large amount of daily Ta stations which are not always available in other areas. This model would not be transferable in areas without sufficient Ta monitors. However there is nothing special about New England regarding the number of NCDC or WB/WU stations, and this information is available all over the US, as well as in Europe. In addition, MODIS satellite data only go back to March 2000 and thus historical observations are not possible. The spatial resolution of 1×1 km is not as high as that of the multispectral sensors (e.g., Landsat 60 m and ASTER 90 m). However, these sensors have poor temporal resolutions which are roughly every 2 weeks. Finally, our approach should be used to assess daytime temperatures using daytime Ts. Although only the Terra satellite was used in this analysis, we do plan on incorporating the Aqua satellite in future studies and extending the model to a wider geographic area, and more years.

5. Conclusion

In summary, we have clearly demonstrated how Ts can be used reliably to predict daily Ta even in non-retrieval days. These results could be used in various studies such as health effect studies, urban climate and urban planning studies etc.

Abbreviations

Ts

Surface temperature

Ta

Air temperature

MODIS

Moderate Resolution Imaging Spectroradiometer

MA

Massachusetts