The Chronnectome: Time-Varying Connectivity Networks as the Next Frontier in fMRI Data Discovery

Abstract

Recent years have witnessed a rapid growth of interest in moving functional magnetic resonance imaging (fMRI) beyond simple scan-length averages and into approaches that capture time-varying properties of connectivity. In this Perspective we use the term “chronnectome” to describe metrics that allow a dynamic view of coupling. In the chronnectome, coupling refers to possibly time-varying levels of correlated or mutually informed activity between brain regions whose spatial properties may also be temporally evolving. We primarily focus on multivariate approaches developed in our group and review a number of approaches with an emphasis on matrix decompositions such as principle component analysis and independent component analysis. We also discuss the potential these approaches offer to improve characterization and understanding of brain function. There are a number of methodological directions that need to be developed further, but chronnectome approaches already show great promise for the study of both the healthy and the diseased brain.

1. Dynamic Connectivity: A Rapidly Growing Field

The human connectome is of great current interest and has received renewed attention recently with the NIH-funded human connectome projects (http://www.neuroscienceblueprint.nih.gov/connectome/), which focus on generating a large amount of functional and structural data from a variety of brain imaging modalities, and the BRAIN initiative (http://www.whitehouse.gov/share/brain-initiative), which focuses on developing new technologies to provide more detailed access to connectivity information within the brain. The connectome is a term that is used primarily to describe the wiring diagram of the brain (Sporns et al., 2005). However, we would suggest that a wiring diagram absent of function is unlikely to be a sufficient tool to understand how the brain works, even in relatively simple systems, due to the impact of modulatory effects and issues like the numbers and kinds of membrane currents in each of the neurons (Bargmann and Marder, 2013).

The term “connectome” has now been nuanced in multiple ways including scale (e.g., micro, meso, macro) and modality (e.g., structure, function). For both structure and function, one can also consider a spectrum of different scales of change in connectivity (slow, fast). It is also possible to consider the impact of disease on the healthy connectome, in order to derive characteristic signatures of connectivity that maybe specific to certain brain illnesses (Calhoun et al., 2012). One of the key aspects of the “omic” expansion of terminology in our view is that such categorizations describe objects or states that are not random and can be categorized into collections of objects that describe some useful features of function, structure, or dynamics, various aspects of which may interact with disease. Thus, genomics, metabolomics, proteomics, connectomics, and our introduction of chronnectomics all have the common goal of providing a canonical set of descriptors that can be drawn upon to understand the healthy and diseased human organism. The term chronnectome is used to describe a focus on identifying time-varying, but reoccurring, patterns of coupling among brain regions. Of note, the term “dynome” has also recently been introduced (Koppell et al., 2014); however, the focus of the dynome is on time-varying (oscillatory) activity whose basic characteristics (frequency, phase, amplitude, etc.) are generally assumed to be static. The chronnectome is a model of the brain in which nodal activity and connectivity patterns are changing in fundamental ways through time. In the context of this paper, “dynamics” is thus referring to intrinsic non-stationarities rather than to the behavior of model oscillators with effectively static activation and coupling parameters. Thus the chronnectome, as we define it, is making the specific assumption that the dynamics are nonstationary in interesting ways, whereas the dynome does not make any such assumption.

Spontaneous fluctuations are a hallmark of neural signals. To date, macro functional human connectome work has largely been based on functional connectivity maps derived from functional magnetic resonance imaging (fMRI) data. However, such maps are most commonly derived from an fMRI experiment spanning from 5 to 30 min and represent an implicit assumption that the functional connectivity (or chronnectome) over this period of time is relatively static. This assumption was challenged in work focused on time-varying multivariate connectivity patterns (Sakoğlu et al., 2010) and in other work focused on time-frequency analysis methods (Chang and Glover, 2010). Since then, multiple chronnectomic studies have appeared (for a recent review, see Hutchison et al., 2013a). The brain itself is clearly highly dynamic, but the chronnectome refers not to the dynamics within a single region, but rather to the dynamics in the connectivity (coupling) among two or more regions. The concept of dynamic connectivity also has been used in various ways in the field, including (static) functional connectivity, regional (but detailed) modeling of the dynamic changes between a small number of regions with many parameters (typically assuming the same response for each stimulus [Friston et al., 2003] or at rest [Havlicek et al., 2011], so-called effective [dynamic] connectivity), or time-varying whole brain functional connectivity patterns (Allen et al., 2014). In the following, we focus on the whole-brain approaches in this work rather than approaches that focus on only a few regions.

The most fundamental element of the chronnectome is its dynamic view of coupling (e.g., connectivity) in which two or more regions or sets of regions, all possibly evolving spatially in time, are coupled with connective strengths measured as explicit functions of time. This can include temporal coupling (i.e., traditional connectivity), spatial coupling, or spatiotemporal coupling. The time dependence ranging from slow (years) to fast (milliseconds) is also a useful property. In addition, the property of scale (micro, macro, or meso) is important (for fMRI data we are at the macro scale). Another property is modality—e.g., structural MRI, diffusion, functional MRI, electroencephalography (EEG), magnetoencephalography (MEG), or even genetics. Finally, the chronnectome may vary as a function of condition (e.g., health, disease, behavior). These are just a few examples.

Because there are multiple ways to define connectome (e.g., a neuron-level wiring diagram, a set of possibly modulatory factors on said diagram, a statistical summary of many-to-many macroscopic connectivity, etc.), it is important to provide a definition of the term as it is being used in the local context. This is also true of the term “network,” which can refer to diagrams based on graph metrics, unthresholded correlation maps, diffusion tract tracing, or regional brain image covariation among subjects (Erhardt et al., 2011a). In this work we focus upon whole-brain (statistical) connectivity patterns assessed within the relatively faster time-scale of the macro functional connectome (i.e., seconds versus minutes) as measured by fMRI. Note that there is also extensive work in EEG/MEG microstates on the scale of milliseconds, which is relevant but will not be fully reviewed here (Koenig et al., 2002; Musso et al., 2010; Pascual-Marqui et al., 1995).

Based on the rapid increase in journal papers focused on dynamic connectivity (Allen et al., 2014; Calhoun et al., 2013b; Chang and Glover 2010; Hutchison et al., 2013a; Hutchison et al., 2013b; Keilholz 2014; Keilholz et al., 2013; Leonardi et al., 2013; Sakoğlu et al., 2010), including recent work showing that metastable states correspond to stages of consciousness (Hudson et al., 2014), the fMRI community has quickly grasped that assessment of functional connectivity has been limited by the assumption of spatial and temporal stationarity throughout the measurement period. Existing approaches have demonstrated the importance of studying the chronnectome using analyses based on windowed (or gradually tapered) correlations between regions of interest (Di and Biswal, 2013; Kucyi and Davis, 2014; Lindquist et al., 2014; Zalesky et al., 2014) or between temporally coherent networks captured with multivariate approaches (Allen et al., 2014; Damaraju et al., 2014; Sakoğlu et al., 2010), change-point analysis (Cribben et al., 2012), or time-frequency analyses (Chang and Glover, 2010). Multivariate methods in particular have proven quite powerful for both identifying intrinsic connectivity networks and for evaluating dependencies among these networks either in time (Allen et al., 2011; Jafri et al., 2008) or in space (Ma et al., 2011).

In the subsequent sections we first provide examples of different chronnectomic approaches that emphasize various aspects of connectivity that change in time (e.g., temporal coupling, spatial coupling, and graph metrics) in addition to discussing the importance and need for validation. Next, we highlight a bit more the underlying assumptions and approaches for defining a connectivity “state” and the considerable differences that result followed by a higher-order approach that shows promise in unifying some of this information. Finally, we give specific examples of how chronnectomic work from our group has been applied to study mental illness, demonstrating the importance of the chronnectome in assessing the impact of mental illness on the brain. Underscoring this is data showing important differences in dynamic connectivity related to various mental illnesses, including schizophrenia and bipolar disorder. Such an approach provides new hope that we can find powerful biomarkers from fMRI data that are probably currently getting “diluted” through the use of an average connectivity map. Finally, we briefly mention some newer additional approaches that show promise for the future followed by some broader closing comments.

2. Identifying Connectivity States

Here we review several key approaches that have been used to identify dynamic states. The chronnectomic field is relatively young, but there are multiple ways to evaluate different aspects of changes in brain connectivity over time. In this section we start with the most common approach, which is to characterize changes in correlation over time (i.e., temporal coupling) assuming fixed regions. Next, we discuss an approach that models changes in the spatial patterns over time (i.e., spatial coupling). In the third section we discuss graphical models that can reconfigure in time. Each of these approaches provides a useful perspective and highlights different aspects of how brain connectivity is changing over time. Finally, we discuss the important topic of validating the various approaches. It is critical to understand how robust each approach is to noise and to understand their limitations.

2.1. Dynamic Functional Network Connectivity

One of the first proposed approaches to characterize chronnectomic changes is called dynamic functional network connectivity (Sakoğlu et al., 2010). In this, an approach called group independent component analysis (ICA) (Calhoun and Adalı 2012) is used to parcellate the brain into networks, each of which has its own characteristic time course. Next, time-varying changes among component time courses, called functional network connectivity (FNC) (Jafri et al., 2008), is captured by calculating cross-correlations between brain networks (components) over time using a tapered windowing (Allen et al., 2014; Sakoğlu et al., 2010). An example of this can be seen in Figure 1 in which group ICA is run on multiple subjects, followed by selection of components of interest and estimation of among-component time course correlations. Following this, a k-means clustering is performed (one of several methods that have been proposed) on the time series of correlation patterns to identify connectivity “state” matrices (these can be thought of as average patterns that subjects tend to return to during the course of the experiment). These can then be summarized based on the patterns of connectivity within each state as well as high-level summaries such as the dwell time each individual subject spends in each state (Allen et al., 2014). A similar approach, except using regions of interest instead of components, has been used to show that sleep states can be predicted based on their connectivity pattern at a given time (Larson-Prior et al., 2011; Tagliazucchi and Laufs, 2014). This is quite exciting, as it suggests that these state patterns may be useful for prediction. They also appear to be useful for characterizing disease, and an example of this appears in a recent paper focused on schizophrenia (Damaraju et al., 2014). One striking finding is that patterns that appear to characterize disease are only present in some of the states, and thus they are best estimated with a chronnectomic approach.

Figure 1. Dynamic Functional Network Connectivity: An Approach to Identify Time-Varying Patterns of Connectivity from fMRI Data.

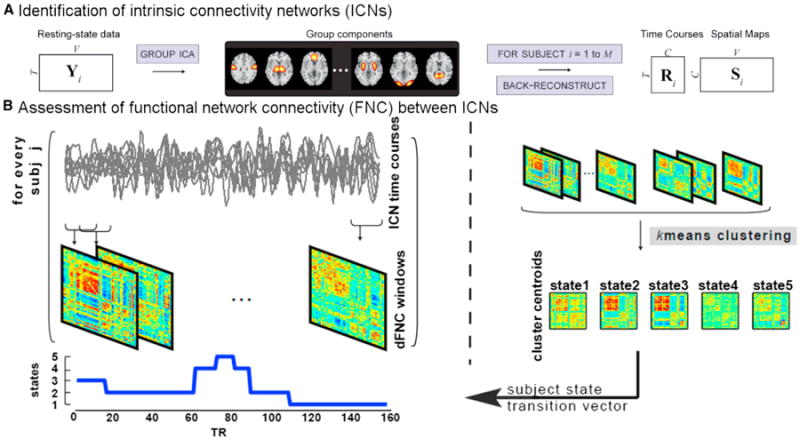
The dynamic FNC approach to estimate temporal dynamics starts with group independent component analysis (ICA) to decompose fMRI data into intrinsic connectivity networks. The group ICA approach (Erhardt et al., 2011b) provides a measure of the component time courses (above left) and spatial maps for each subject. Dynamic functional network connectivity is estimated as a cross-correlation (more specifically covariance) from windowed portions of the time courses. Finally, k-means clustering is used to identify states and determine which state a given subject is occupying at a given time. Figure modified and reprinted with permission from Erhardt et al. (2011b).

2.2. Time-Varying Spatial Maps via Independent Vector Analysis

Another very interesting direction is the focus on variation over time in spatial coupling. Because fMRI data are spatiotemporal, one can conceive of chronnectomic changes as the spatial patterns of correlated networks themselves instead of a focus on the connectivity among fixed spatial networks. In an early example of this an ICA was run on subsets of data over time to evaluate changes in the default mode network (Kiviniemi et al., 2011). A newer approach using independent vector analysis (IVA), which generalizes ICA to multiple data sets and performs a joint source separation such that the statistical dependence across them is fully taken into account (Anderson et al., 2014; Kim et al., 2006). A key advantage of this for studying dynamics is the ability to analyze short records of data, as joint processing enables better performance in the estimation without imposing additional constraints. IVA maximizes independence among temporal subsets of the data (called source component values or SCVs) rather than among the full data set, which is the case for ICA. The IVA approach also captures the dependence across time windows within a network so that changes over time in a given network can be tracked. We can capture chronnectomic changes in spatial coupling by again using overlapping windows of data and organizing the window from each subject as shown in Figure 2A. The SCVs that are highly dependent across the data sets will be those that are approximately static and those with more variability (less dependence among the source components within the source vector) will report on the dynamic spatial components. Because neither the temporal nor the spatial domain is constrained, the resulting decomposition successfully identifies the spatiotemporal dynamics in a data-driven manner.

Figure 2. An Approach to Estimate Time-Varying Connectivity Spatial Patterns from fMRI Data using Independent Vector Analysis and Example Showing Coupling between these Spatial Connectivity Patterns Varies in Schizophrenia.

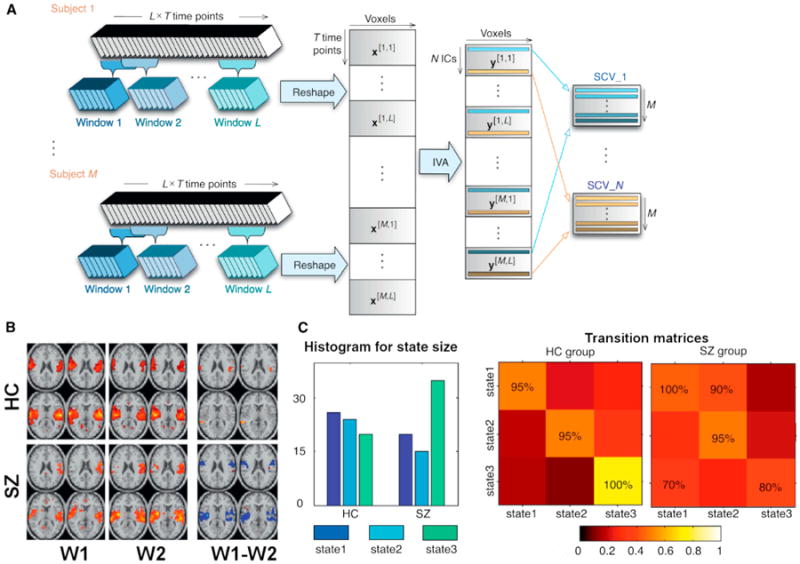
(A) Independent vector analysis approach to characterize spatially dynamic and static components. Here, spatial maps of a component vector are related over the time windows but should be distinct from the spatial maps of all other components (whether within or outside the current window w_i).

(B) Patients show more variability in their spatial patterns overall. (Left) One-sample t test results for two time windows. (Right) Two-sample t test results showing significant bilateral changes in schizophrenia patients versus controls.

(C) Estimation of spatial dynamic temporal lobe coupling (mutual information) to other networks confirms increased dependence between state 3 relative to other states in schizophrenia patients (left). Schizophrenia patients also show significantly more cross-state transitions in temporal lobe with increased likelihood of transitioning from state 3 to state 1 (80% versus 100%, right). Color represents the transition probability. Figure modified and reprinted with permission from Ma et al. (2014).

We analyzed healthy controls and patients with schizophrenia using the windowed IVA approach shown in Figure 2A with seven windows, each of which overlapped by 50% to cover a 200 time point resting fMRI data set (Ma et al., 2014). Thirty components were estimated, of which 12 were determined to be BOLD related. Networks revealed very different spatial variation in patients versus controls (Figure 2B). We next computed probabilities to capture the spatial coupling by characterizing the transition probabilities for each state, which tells us whether a subject with a certain spatial pattern at a certain time is more or less likely to transition to another spatial pattern at a future time. Results indicated that controls show significantly less probability of transition between states (see example showing that patient temporal lobe state [state 3] is more likely to transition to another state [state 1] in Figure 2C). This provides a nice way to summarize changes in spatial patterns over time and to track differences in disease. One can also evaluate changes in the dependencies between pairs of spatial networks over time. To estimate spatial dependencies we can compute a mutual information matrix for each subject and each window (this is a matrix that indicates how similar each spatial pattern is to another spatial pattern over time). The schizophrenia patients show considerably more dependence among state 3 to other states than do the controls. This is a simple summary measure of only seven windows but it indicates that spatial dynamics can be sensitive measures of disease state. A full assessment of the spatial dynamics for each TR hence promises to more fully characterize the changes.

2.3. Time-Varying Graph Metrics

Graph theory has become an important and widely used approach to summarize brain function (Sporns, 2011).In addition, concepts such as “small-worldness” and “rich club networks” have already been studied extensively in the context of schizophrenia (Bullmore and Sporns, 2009; Zalesky et al., 2012). Extensions to time-varying graphs can be accomplished by incorporating multilayer network approaches, which attempt to quantify temporal variation in graph structure by constricting adjacency tensors to estimate multilayer graph statistics. This has been applied to examine brain network changes (over the span of days to hours to several minutes) in learning (Bassett et al., 2011) and interhemispheric coordination (Doron et al., 2012).

The dependency among ICA-based models (i.e., among network dependency) has also been quantified using static graph metrics on fMRI data (Yu et al., 2013, 2011). Changes in networks can also be directly assessed in the context of chronnectomics via the calculation of time-varying graph metrics. Such an approach is quite sensible as the nodes are then based on strongly coherent regions/networks (Erhardt et al., 2011a) as opposed to being derived by univariate correlations or region of interests that may not map well to the underlying functional architecture and capture the rich multivariate nature of fMRI data. This can easily be extended to time-varying graph metrics by computing graph metrics on the windowed FNC matrices.

Figure 3 shows an example of changes in connectivity strength over time. Group spatial ICA was used to derive dynamically changing connectivity matrices as in section 2.1 (Allen et al., 2014) followed by calculation of connectivity strength as a function of time and modularity analysis to identify consistent states. A weighted brain network was built for each time window and calculation of time-varying measures of various graph measures (Sporns, 2011) including connectivity strength, clustering coefficient, and global efficiency for each connectivity state. Results show changes over time in graph measures between groups that are robust and meaningful. The ability to utilize graph measures provides an intuitive way to assess various questions such as whether patients spend more or less time in a “rich club” configuration (van den Heuvel et al., 2012).

Figure 3. Time-Varying Aspects of Graph Metrics and Summary of Resulting Module for Patients and Controls.

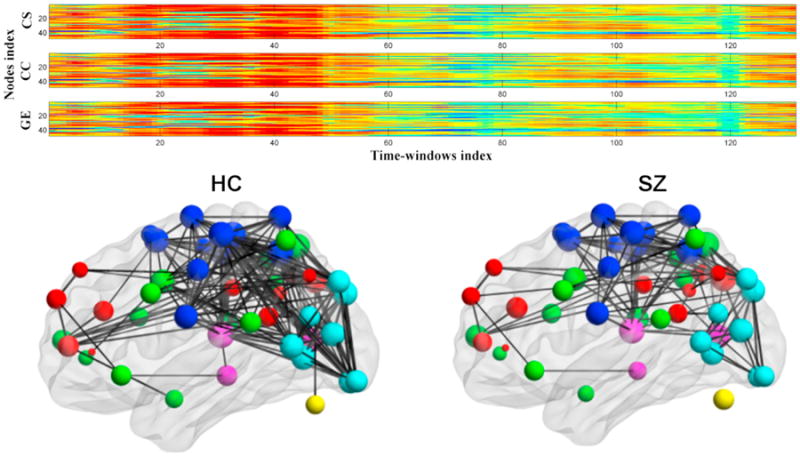
(Top) Example of time-varying output from dynamic graph approach; patients generally tend to have lower values. Time-varying network metrics for schizophrenia patients and healthy controls.

(Bottom) Graph built from a single dynamic state (Yu et al., 2013).

Figure modified and reprinted with permission from Yu et al. (2013).

3. Validation

It is clear that there is highly interesting information contained within the dynamic connectivity patterns. However, since the chronnectomic field is quite young, there is a need to validate the results and characterize the replicability and utility of the observed time-varying patterns. A few useful approaches to validation include the use of simulations, incorporation of information from concurrent EEG/fMRI studies, and correlation of resting results with task-based results and measurable behavioral information.

Simulations

Simulations can be used to help validate methods used to estimate and characterize dynamic connectivity. We can quite easily generate data under a model of dynamic neural connectivity with variations in time, space, and both time and space, distinct changes in one or more sources, different noise properties/contrast-to-noise-ratio, etc. This enables us to evaluate the robustness of the algorithms and test some simple scenarios (of course fully realistic models are much harder as we are still learning about the properties of brain connectivity). Previous simulations carried out via the simulation toolbox simTB (Erhardt et al., 2012) (http://mialab.mrn.org/software/simbtb) can be seen for groupICA (Allen et al., 2012) as well as for a dynamic FNC approach (Allen et al., 2014). As an example, we show one proposed simulation in Figure 4A. We used the SimTB framework to simulate fMRI timeseries under a model of dynamic neural connectivity, then applied k-means clustering to estimate FC states from windowed covariance matrices as done with the real data. As shown in Figure 4A, the clustering provided excellent estimates of both the discrete neural states and the transitions between states, suggesting that the clusters derived from real data faithfully reflect the structure and temporal properties of dynamic connectivity. Further work utilizing both real and simulated data (Smith et al., 2011) should explore the suitability of different connectivity metrics as applied to studies of dynamics in large-scale networks as well as to evaluate the impact of various noise levels and other factors on the results.

Figure 4. Example of Simulation Approach to Help Validate and Assess Robustness of Time-Varying Connectivity Results.

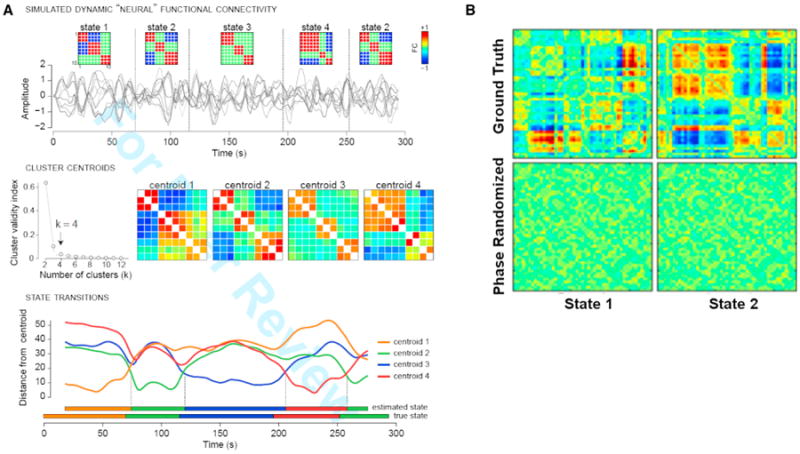
(A) Validation of clustering approach with simulated data. (Top row) Simulated fMRI time series for ten nodes are generated under a model of dynamic neural connectivity where 4 states are possible (state 2 repeats). Simulation parameters (TR = 2 s, 148 volumes) are matched to experimental data; connectivity states are modeled after clusters observed in real data. (Middle row) Windowed covariance matrices are estimated from the simulated time series and are subjected to k-means clustering with the L1 distance metric. The elbow criterion correctly identifies k = 4 clusters, and cluster centroids show high similarity to the true states. (Bottom row) The distance of each window to each cluster centroid. The assignment of individual windows to states is very accurate. Distances and state assignments are plotted at the time point corresponding to the window center.

(B) Original dynamic functional network connectivity states (top) and results after phase randomization (bottom) as in Handwerker et al. (2012) look random (not at all like the top row) and thus show no evidence of spurious structure (Damaraju et al., 2014). Figure modified and reprinted with permission from Allen et al. (2014) and Damaraju et al. (2014).

As a lesson in the important of such simulations, in a recent paper (Handwerker et al., 2012) seed-based approaches identified effects from spurious correlations generated via phase randomization (e.g., randomly permuting the relative delay of the time courses) (Prichard and Theiler 1994). Figure 4B shows two states from a dynamic FNC analysis performed on identical data with and without phase randomization (Damaraju et al., 2014). Results for phase randomized data did not capture patterns resembling a real effect and look quite random. Hence, the results confirm that the timing of the events is critical to the observed structure found for the multivariate dFNC approach. In this case the multivariate approach worked quite well; however, there are probably other scenarios that will impact a multivariate approach, and it is essential to understand the limitations of each analytic approach.

Task-rest correlations

An additional way to validate includes correlation of time-varying connectivity patterns that have known task-related patterns. For example, in recent work (Shirer et al., 2011) a classifier was trained to identify specific patterns of whole-brain connectivity as subjects rested quietly, remembered the events of their day, subtracting numbers, or (silently) singing lyrics; in other work (Gonzalez-Castillo et al., 2012), subjects were continuously alternating between a variety of simple tasks; we have also gathered multitask data to assess the predictive power of dynamic states compared to static connectivity. Such an approach can provide additional confidence in connectivity states by integrating rest and task data and enabling us to associate particular static patterns with specific task behavior. Some initial work on dynamic connectivity in the context of task and rest data has been performed (Sakoğlu et al., 2010), but additional work in this area is needed.

Concurrent EEG/fMRI

The use of imaging modalities such as EEG, which can capture millisecond timing changes, in conjunction with fMRI is a powerful way to help validate chronnectomics patterns. In one recent example, work has shown that sleep state can be predicted using time-varying fMRI connectivity trained using a concurrent EEG/fMRI data set (Tagliazucchi and Laufs, 2014). In this case the authors used a small data set that included both EEG and fMRI data to train a classifier on the fMRI patterns associated with indicators of deep sleep assessed via the EEG data. They then applied this classifier to fMRI data from 1,000 functional connectomes and found that much of the resting fMRI data included periods of time when the patterns of connectivity were consistent with the sleep patterns observed in the training data set. This is a striking result, and certainly changes the interpretation of any results based on such data. It is also highly relevant for patient studies, considering the possibility that patients are dozing off. This could lead to a conclusion that such patterns are characteristic of brain illness, when in fact they are simply a by-product of the patients being drowsier, perhaps due to the illness or to a certain medication. Though EEG cannot fully validate the fMRI results as they are measuring different but related physiologic measures, the integration of the two can provide additional validity by relating rapid EEG measures with relatively slower fMRI measures. The examples we have discussed use EEG data windowed over a multisecond period of time; of course it is also possible to more directly capitalize on the timing information of the EEG data using direct data fusion approaches.

4. From States to Knowledge: A Case for Metastates

The previous section summarizes approaches for estimating and characterizing states (i.e., time-varying patterns of spatial and/or temporal coupling); however, in these initial approaches, subjects were allowed to be in only a single “state” at a given point in time. A more flexible approach is to consider the possibility that multiple states might be represented to varying degrees at the same point in time. One of the more promising approaches is to consider the fMRI data to be comprised of a smaller number of connectivity “states” (possibly overlapping) that recur at varying times in the data and that reflect underlying brain function in a meaningful way. Recent work suggests that a model that considers overlapping states is a better way to model dynamic connectivity (Leonardi et al., 2014).

This leads back to the issue discussed in Section 2, which is how a state should be defined. For example, should the connectivity patterns for each state be maximally different (or independent) from one another? Or instead should the changes in time be different (e.g., one rapidly changes and another slowly changes)? Or is some other criteria needed? This is currently an open question, and in fact, each method for defining a state has its own advantages; however, it does lead to challenges in terms of defining a canonical chronnectome. Along these lines, we discuss one promising approach that, instead of summarizing states individually, provides a higher dimensional summary of the states (called a metastate) (Miller et al., 2014a, 2014b). Such an approach enables us to ask some intuitive questions about the dynamics and complexity of brain connectivity. It also enables us to summarize the state information (which includes a time-varying pattern of connectivity for each state) into a much more condensed summary measure (e.g., how many states did a given individual enter during a 5 min experiment). The metastate approach appears useful not only because it summarizes information across the different states, but also because it appears to provide largely consistent information even if the states are defined using different criteria. In the next sections we first briefly discuss various ways to define connectivity states followed by approaches to summarize the state information statistically both within a given state and among states.

4.1. Criteria for Defining States

As mentioned in Section 2, different metrics can be used to define a given metastable state, and it is not yet clear what the “optimal” approach is. For example, most approaches rely on a windowed correlation to capture time-varying connectivity, followed by some method to identify consistent patterns in the data. It is the last step that we will focus on in this section. Various analytic approaches appear to identify consistent and replicable states. Previous work has used k-means clustering (Allen et al., 2014) or principal component analysis (PCA) (Leonardi et al., 2013). Other possible measures include spatial or temporal ICA, or more general statistical measures such as sparsity or measures of temporal variation (Eavani et al., 2013). The specific criteria used can produce quite different results (see Figure 5A for a comparison of spatial ICA or k-means) with each criterion having particular advantages and disadvantages. In the case of spatial ICA versus k-means, the spatial ICA solution tended to provide smaller sets of regions, which is not surprising as the ICA algorithm used emphasizes both independence and sparsity, a topic that has led to interesting discussions by themselves (Calhoun et al., 2013a; Daubechies et al., 2009). The k-means approach is instead maximizing a criteria based on the distance between the states. Interestingly, the spatial ICA solution in this case appears to highlight meaningful sets of network pairs including the default mode network and the cerebellum. There are many other criteria that could be used as this is simply an analytic choice. It remains to be seen whether a specific criterion will always provide a more meaningful identification of state patterns or whether the criteria used should depend on the question being asked.

Figure 5. Differences in Resulting State Patterns Depend on the Approach Used and Summary of Metastate Occupancy Level.

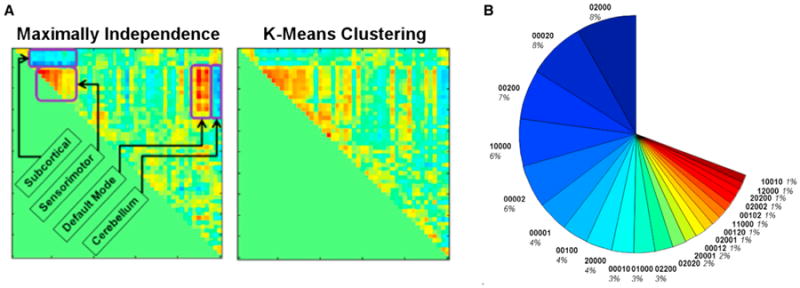
(A) Maximizing independence among temporal states provides what looks like a plausible result but is quite different from a k-means solution.

(B) Occupancy of metastates for rest fMRI of healthy individuals (n = 400) coded as 5-vector (5 states estimated). Most subjects occupy only 1 or 2 states at once. Figure modified and reprinted with permission from Miller et al. (2014a).

4.2. Within-State Summary Measures

To date most work has focused on within-state summary measures, including things like dwell time (how long an individual spends in a given state) (Allen et al., 2014), cell-by-cell comparison of connectivity (Allen et al., 2014; Leonardi et al., 2013), phase differences, change-points (Cribben et al., 2012), bivariate correlations (Lindquist et al., 2014), and number of transitions (Damaraju et al., 2014). There is a lot of useful information that we can learn from characterizing the properties of each state individually; however, we are left with properties across multiple states. While this is useful in achieving our goal of capturing information that may map onto the fMRI data for only a limited period of time, there may be some benefit to developing a metric that captures dynamic connectivity information at a more global level. As we will show, the metastate approach does this and has the additional advantage that it may be somewhat robust to the specific criteria used to generate the state matrix. Specifically, we show an example where this approach provides consistent results across four different state defining criteria.

4.3. Cross-State (Global) Summary Measures (e.g., Metastates)

As with much brain imaging research, a core challenge for a chronnectomics analysis is to summarize the data in ways that simultaneously reduce their dimensionality and expose features that are strongly predictive of important population characteristics. The native dimension of time-varying network correlation space and windowed connectivity can easily exceed 1,000. We have found strong evidence for the power of higher-dimensional (in our case, 5D) but still tractable characterization of windowed connectivity in terms of the additive contributions of a set of overlapping states obtained according to some specified optimization criterion (using, for example, temporal ICA, spatial ICA, PCA, or k-means clustering) (Miller et al., 2014a, 2014b). The contribution of each of the (five) overlapping states for a specific time is characterized by a five element vector that is called a metastate. There can be a large number of possible metastates occupied in theory; however, Figure 5B shows a summary of metastate occupancy in 400 healthy subjects, which indicates (1) only 22 of these metastates are occupied more than 1% of the time, (2) these states include mostly single-or double-state occupancy, and (3) females show more single-state occupancy than males, who show more double-state occupancy (Miller et al., 2014a, 2014b).

Using a large, balanced multisite data set, we have also investigated the effect of a diagnosis of schizophrenia on four interrelated measures of metastate dynamism, separately evaluated with respect to states defined using four common algorithms (Miller et al., 2014a, 2014b). Four interrelated measures of metastate dynamic fluidity and range were assessed, including: (1) the number of distinct metastates a subject passes through; (2) the number of switches from one metastate to another; (3) the span (maximal distance) of the realized metastates; (4) the total distance traveled in the state space. These analyses yielded consistent and significant evidence for reduced connectivity dynamism in schizophrenia patients (see Table 1) and provide strong evidence in support of such summary measures. Note, this reduced metastate dynamism is not inconsistent with our earlier mention of greater spatial variability (and among state transition probability) in patients. Just as graph theory includes hundreds of possible summary measures (Sporns 2011), there are also many possible ways to compute cross-state summary measures. More complex measures can also be calculated— for example, the concept of a k-level hub (e.g., metastates that are returned to k or more times), and related concepts such as absorbing metastates (subjects stay for extended periods of time) and transient metastates (subjects come in and out multiple short periods of time). It remains to be seen which measures will ultimately be the most useful.

Table 1. Schizophrenia Effects on Connectivity Dynamism Measures Persist with Various State Estimation Methods.

Dynamism Measure	Comparisons of Several Metastate Metrics (Schizophrenia – Controls)
Metastate metrics	tICA	sICA	PCA	K-means
Number of distinct metastates	−5.65 (p = 4.11e-006)	−2.63 (p = 0.007)	−5.78 (p = 6.03e-008)	−6.52 (p = 1.52e-007)
Number of metastate changes	−2.20 (p = 6.62e-008)	−1.29 (p = 2.71e-006)	−2.22 (p = 2.09e-010)	−5.57 (p = 8.23e-007)
L2 span of realized metastates	−5.37 (p = 1.41e-006)	−2.59 (p = 0.003)	−4.80 (p = 5.88e-007)	−2.71 (p = 1.52e-009)
Total distance traveled in state space	−9.19 (p = 1.89e-006)	−4.29 (p = 0.0008)	−6.78 (p = 1.76e-006)	−10.04 (p = 5.31e-007)

Data from Miller et al. (2014a, 2014b).

5. Dynamic States Appear to Be Sensitive and Specific Markers of Mental Illness

We showed a few examples of patient/control differences already, but in this section we highlight additional work that shows the important promise of chronnectomic analyses in the context of complex mental illness. We also discuss the use of both static and dynamic measures of connectivity.

5.1. Schizophrenia and Bipolar Disorder

One key goal for the field is to evaluate the utility of dynamic connectivity information in a clinical population. For example, the ability to differentiate between schizophrenia and bipolar disorder using a biological marker would have an important impact in the clinic (especially for early presentation). These disorders are at times hard to differentiate since they both often present with psychotic symptoms. Research shows that some bipolar disorder patients can go years misdiagnosed as much as 45% of the time (Meyer and Meyer, 2009). The consequence of miscategorization is costly both economically and in terms of human suffering (DiLuca and Olesen, 2014), as patients respond optimally to different treatments and getting them on the correct treatment earlier impacts their long-term prognosis.

Schizophrenia and bipolar disorder are complex conditions with diverse and heterogeneous clinical presentations, and though previous studies indicate altered metabolism in cingulate gyrus, temporal gyrus, and insula (Hosokawa et al., 2009), to date there has been little success in identifying biomarkers (fMRI or otherwise) that are specific to each of these groups. Part of the difficulty is the use of symptom-based categories that are imperfect (Cuthbert and Insel, 2010; Insel et al., 2010).

The use of static connectivity measures is providing some promise of yielding biomarkers of illness (Arbabshirani et al., 2013), but despite this success, it is still unclear whether such approaches will provide enough sensitivity to be of use in the clinic. But there is yet hope that we can improve on static measures. As we have shown, the use of static connectivity measures on fMRI data probably includes “blurring” of brain connectivity patterns, especially for rest fMRI data, which works with data that is collected during an unknown behavioral condition without even a control task. The use of dynamic connectivity measures will probably provide a more accurate assessment of brain connectivity, hence enabling us to more accurately define chronnectomic-based biomarkers as well as more cleanly capture other information that is changing over time but is not directly related to disease (such as drowsiness) (Larson-Prior et al., 2011; Tagliazucchi and Laufs, 2014).

Figure 6A shows several dynamic states in a large (n > 300) data set of schizophrenia patients and controls in which the patients are spending significantly more time in the relatively less connected state 4 (also showing less negative correlation among default mode to other networks) (Damaraju et al., 2014). The fact that a single state is well represented in the patients strongly suggests the need to model dynamic states in order to capture such information. Note, also, that part of the diagnosis challenge may be due to the use of symptom-based categories. Because such symptoms are often unreliable and downstream of the biological effects of the illness, various studies are challenging these boundaries and proposing a dimensional approach to mental illness (Keshavan et al., 2011). Dynamic connectivity provides a promising way to help evaluate the merits of a categorical or continuous diagnosis as well as the relative merits of the categories themselves (Du et al., 2014; Narayanan et al., 2014).

Figure 6. Summary of State Patterns and Significant Differences in Patients versus Controls.

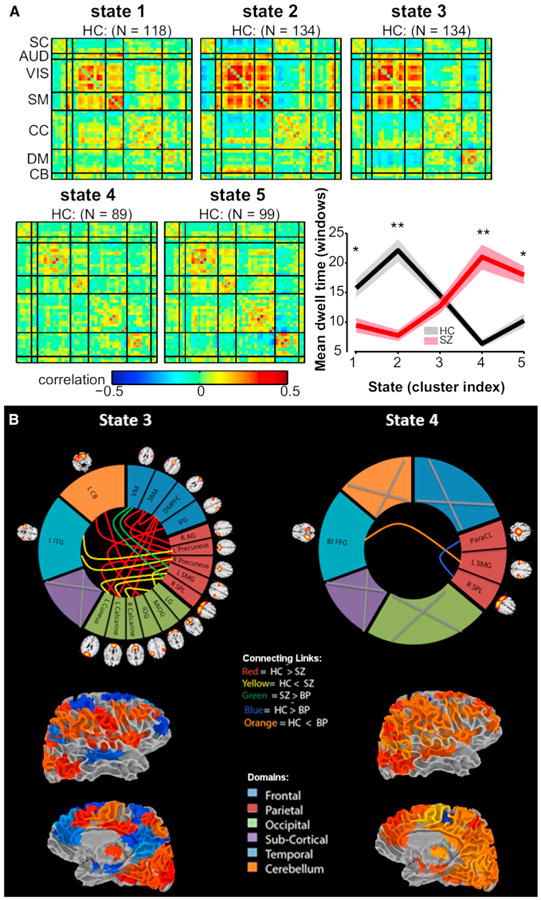
(A) Five transient state connectivity patterns estimated from schizophrenia data. Patients spend significantly more time in the relatively less connected state 4 (red line in graph on right) whereas controls spend more time in states 1–3 (Damaraju et al., 2014).

(B) Dynamic functional network connectivity results suggesting specific states differentiate schizophrenia, bipolar, and healthy controls, and that most of these are tied to a single state in this case. (Top) Significant patient versus control differences within each state indicated by colored links. (Bottom) Surface view of the state in brain space for lateral and medial views of the brain. Figure modified reprinted with permission from Damaraju et al. (2014).

Data clearly show that incorporation of dynamics may provide a more sensitive and specific marker of disease than static connectivity. Figure 6B shows evidence that a dynamic approach reveals differences in patients with bipolar disorder that are again unique to a specific state (state 4) (right) whereas most of the schizophrenia and some shared bipolar-related differences occur in state 3 (left) (Rashid et al., 2014). Results also show that one state in the schizophrenia data appears much more frequently than in the healthy controls, and patients show less overall dynamism (e.g., they spent longer time in a single state [versus multiple states] and also visited fewer possible states than controls) (Miller et al., 2014a, 2014b). Neither of these interesting results is observable from the static data. The importance of these results, if this holds up, is that the ability of methods that focus on dynamics to separate out information about symptoms and patient unique information may well help us to better differentiate patients and eventually to improve diagnosis during a time when they are difficult to differentiate clinically. Of note, an important limitation for the results presented here is the fact that the patients are medicated; additional work is needed to decouple the medication effects from the true disease effects.

5.2. Predictive Value of Static and Dynamic Information

There are multiple examples of the predictive power of certain time-varying connectivity patterns, including deep sleep (Tagliazucchi and Laufs, 2014; Tagliazucchi et al., 2013), day dreaming (Kucyi and Davis, 2014), psychedelic states (Tagliazucchi et al., 2014), and consciousness (Hudson et al., 2014), which suggest a canonical utility to the chronnectome. We and others have previously identified multiple replicable connectivity differences in schizophrenia patients (Calhoun et al., 2008; Garrity et al., 2007) and in our recent work certain findings were more apparent in a static analysis and others more apparent in a dynamic connectivity analysis (Damaraju et al., 2014). Other less direct aspects of connectivity also appear to be more preserved in the static or dynamic world; for example, we have observed certain aspects of connectivity that appear to be better characterized by a static model, such as that of decreased low-frequency power in schizophrenia and bipolar patients (Calhoun et al., 2012; Garrity et al., 2007). In addition, the approach we discuss in Section 2.2 provides an elegant way to capture both static and dynamic changes in spatial maps. The fact that static and dynamic models capture information in different ways motivates models that can appropriately capture both types of information. In order to provide a direct evaluation of the utility of static and dynamic connectivity we performed a classification using either (1) static FNC, (2) dynamic FNC, or (3) both static FNC and dynamic FNC. Using a set of 61 healthy controls, 60 patients with schizophrenia, and 38 with bipolar (Rashid et al., 2014), we used a k-nearest neighbor classifier with k-fold cross-validation and found that static FNC = 70%, dynamic FNC = 80.5%, and static + dynamic = 90% in overall accuracy, providing strong evidence that combining dynamic and static connectivity improves sensitivity. This suggests (1) that dynamic FNC is more useful than static FNC and (2) that combining static and dynamic FNC is more useful than either approach alone in the context of identifying bio-markers of mental illness. This strongly suggests that we should be incorporating both static and dynamic information as we move forward.

6. Additional Approaches

The field of chronnectomics is rapidly growing, and there are still many more aspects of time-varying brain connectivity that need to be studied. This includes (1) models that can capture both spatial and temporal coupling, (2) ways to better capture both static and dynamic connectivity, and (3) application of existing approaches to large data sets to evaluate the canonical utility of the chronnectome, i.e., how reproducible are the identified states and how useful are they at predicting various measures such as brain disease or sleep state. Undoubtedly, many other new approaches will emerge as well. One alternative approach to fMRI data that starts to move in the direction of capturing both spatial and temporal dynamics is the use of a four-dimensional spectral decomposition approach (called a 4D Fourier transform). In this approach, rather than identifying specific correlation patterns that change in time, the goal is to identify specific spatial and temporal frequency patterns that change in time (for example, a recurring low-frequency time course produced by a smooth circular region in the brain). These spectral patterns can then be characterized using a metastate approach as described in Section 4.3. Using data previously analyzed with a windowed FNC approach (Damaraju et al., 2014), five maximally spatially independent spectral patterns were then obtained using spatial ICA (see Figure 7) and converted to metastates. Corrected for age, gender, and motion, the effect of schizophrenia on all four measures of spatiotemporal spectral dynamism was negative and significant. This tells us that there is considerable spatiotemporal dynamic connectivity ongoing in the fMRI data and motivates additional approaches to evaluate such information.

Figure 7. Spatiotemporal Spectra Patterns Identified from Resting fMRI Data.

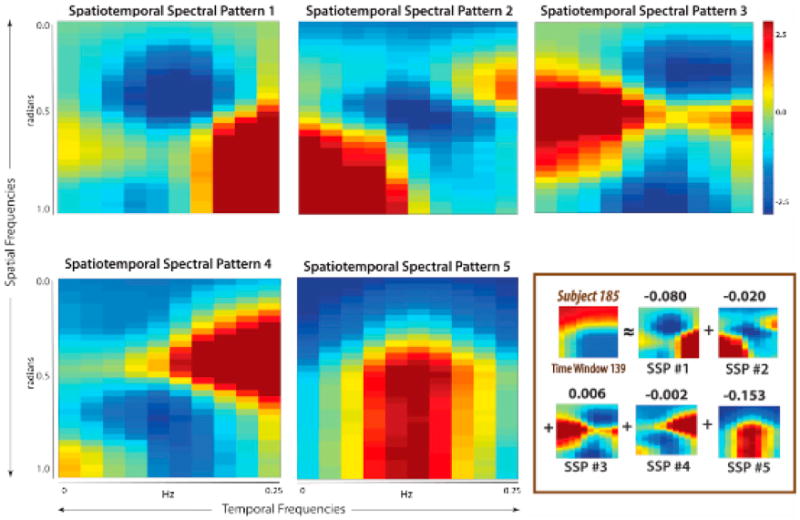
(Nonboxed) The five basis spatiotemporal spectral patterns obtained from sICA of all windowed spatiotemporal spectral profile (wSTSP). (Boxed) Specific wSTSP expressed as weighted sum of the spatiotemporal spectral profiles. Figure modified and reprinted with permission from Miller and Calhoun (2014).

7. Conclusions

The fMRI community has rapidly become aware of the need to move beyond functional connectivity approaches that calculate only average maps over the entire experiment. We define the chronnectome as a set of metrics that summarize connectivity over a range of time-scales, primarily focusing on shorter time-frames, but also relevant for slower state-related connectivity changes (e.g., task versus rest [Calhoun et al., 2008]). We have reviewed a number of promising multivariate approaches to this complex but important problem. Initial work suggests that it is possible to estimate canonical time-varying connectivity patterns that can predict various behaviors and distinguish disease states. These methods open up the possibility of better characterizing mental illness in the spirit of the NIMH defined research domain criteria (RDoC), representing an important advance in our approach to mental illness (Cuthbert and Insel, 2010; Insel et al., 2010). These data suggest that chronnectomics will enable improved characterization of pathophysiology and improved classification for diagnosis or subgrouping. Dynamic connectivity also has broad applicability to many other domains including substance use, other brain disorders, and classification of normal states of consciousness. However, we have only scratched the surface thus far. A great deal of additional work is still needed to validate existing models, build improved models, and develop high-level summary statistics.