Automated 3D Segmentation of Multiple Surfaces with a Shared Hole: Segmentation of the Neural Canal Opening in SD-OCT Volumes

Abstract

The need to segment multiple interacting surfaces is a common problem in medical imaging and it is often assumed that such surfaces are continuous within the confines of the region of interest. However, in some application areas, the surfaces of interest may contain a shared hole in which the surfaces no longer exist and the exact location of the hole boundary is not known a priori. The boundary of the neural canal opening seen in spectral-domain optical coherence tomography volumes is an example of a “hole” embedded with multiple surrounding surfaces. Segmentation approaches that rely on finding the surfaces alone are prone to failures as deeper structures within the hole can “attract” the surfaces and pull them away from their correct location at the hole boundary. With this application area in mind, we present a graph-theoretic approach for segmenting multiple surfaces with a shared hole. The overall cost function that is optimized consists of both the costs of the surfaces outside the hole and the cost of boundary of the hole itself. The constraints utilized were appropriately adapted in order to ensure the smoothness of the hole boundary in addition to ensuring the smoothness of the non-overlapping surfaces. By using this approach, a significant improvement was observed over a more traditional two-pass approach in which the surfaces are segmented first (assuming the presence of no hole) followed by segmenting the neural canal opening.

1 Introduction

Many medical imaging applications exist for which it is desirable to segment multiple interacting three-dimensional surfaces. Example approaches for enabling the optimal segmentation of multiple surfaces include a graph-theoretic approach [1], which transforms the multiple surface segmentation problem into that of obtaining a minimum-closure in a constructed graph, and the graph-cut approach [2] which transforms a multi-object labeling problem (with geometric constraints) directly into that of obtaining a minimum-cost s-t cut in a constructed graph. However, in some applications, a set of interacting surfaces have a shared “hole” in which the surfaces do not exist. An example of such an application is that of segmenting the neural canal opening (NCO, the boundary of a “hole”) and the surrounding surfaces within spectral-domain optical coherence tomography (SD-OCT) volumes (Figs. 1(a)-(c)). The NCO is an important structure relevant to glaucoma [3,4] as it can provide a stable reference by which to monitor structural changes of the optic nerve head [3].

Fig. 1.

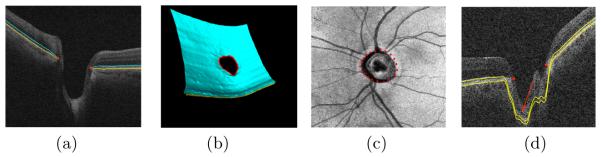
The surfaces and the NCO depicted on (a) a central xz-slice from a human OCT image and (b) a 3D rendering of the segmented surfaces. (c) The xy-location of the NCO depicted on a projection image. (d) An example where the segmented surfaces are “pulled” away from the NCO by deeper structures (indicated by the arrow).

Previously, a Markov model based approach [5] was proposed for the segmentation of the optic disc and cup margins in time-domain OCT images. More recently, a two-step graph-theoretic approach [4] was proposed for the same in SD-OCT images. The method began by segmenting the surrounding surfaces while ignoring the fact that the surfaces do no exist inside the NCO, and subsequently segmenting the projected location of the NCO (i.e., projected boundary of the hole) in a projection image. The fact that the initial multiple-surface segmentation ignored the existence of the hole makes the segmentation more prone to errors in this region due to a deeper structure (indicated by the red arrow in Fig. 1(d)) inside of the NCO “pulling” the surfaces away from their actual locations near the boundary of the hole. Furthermore, they were only able to quantitatively evaluate their algorithm in the x-y plane using projected manual tracings of the optic disc, and thus, it is difficult to assess the accuracy of the neural canal opening points in the z-direction (i.e., depth direction).

In this work, we present an approach for simultaneously segmenting multiple surfaces with a hole and apply the approach for the segmentation of the NCO in 3D and the surrounding surfaces from the SD-OCT volumes of glaucoma patients. This contrasts with prior 3D work which has focused on using a single two-step approach. In particular, the general framework of our approach reflects an extension of the graph-theoretic approach [1] proposed for simultaneous segmentation of multiple surfaces (without a hole). The overall cost function was extended to incorporate the hole boundary and new boundary constraints were included to ensure the feasibility of the set of surfaces. The proposed method was also compared to the previously proposed [4] two-step approach, where it showed a significant improvement (p < 0.001) in the accuracy of the segmentation of the NCO boundary location. We also demonstrated the ability to measure important parameters such as the minimum rim width (MRW) using these segmentations, where the measurements obtained did not significantly differ from those obtained using the manual delineations.

2 Method

Formulation of the Surfaces with a Shared Hole Problem

Assume we have a volume of dimensions X × Y × Z and wish to find n layered surfaces with a shared hole as illustrated in Fig. 1. The presence of the hole, divides the volume into three regions (see Fig. 2) namely the outside $\mathcal{O}$, the boundary $\mathcal{B}$ and the inside of the hole $\mathcal{H}$. Intuitively, we will consider a surface set with a shared hole feasible if 1) individual surface smoothness constraints are satisfied outside the hole, 2) the surfaces obey minimum and maximum surface distance constraints outside the hole, 3) the surfaces come together at the hole boundary, and 4) the hole boundary satisfies its own set of smoothness constraints.

Fig. 2.

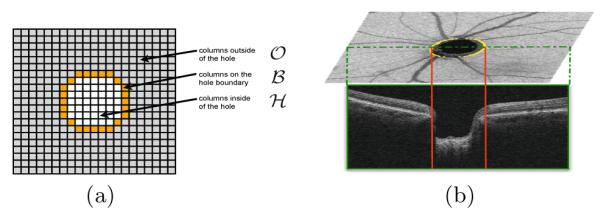
(a) The 2D overview of the division of columns into the three sets: the hole boundary, the hole itself and the region outside the hole. (b) An example of the 2D segmentation of the NCO boundary that is used to define set $\mathcal{B}$.

Each of the n surfaces {f₁(x, y), … , f_n(x, y)} are defined over the columns in $\mathcal{O}\cup \mathcal{B}$, where the smoothness constraint for each surface i is defined by:

$$\mid f_i(x+1,y)-f_i(x,y)\mid \le {\Delta }_{x_i}\text{and}\mid f_i(x,y+1)-f_i(x,y)\mid \le {\Delta }_{y_i},$$ (1)

where Δ_xi (Δ_yi) is the x-smoothness (y-smoothness) parameter for surface i (see Figs. 3(a) and (b)). For each of the columns in $\mathcal{O}$, each i−(i + 1) pair of surfaces (where surface i + 1 is directly “above” surface i) is also constrained by the surface distance constraints, where ${\delta }_{i,i+1}^l\le f_{i+1}(x,y)-f_i(x,y)\le {\delta }_{i,i+1}^u,$, where ${\delta }_{i,i+1}^l$ and ${\delta }_{i,i+1}^u$ are the minimum and maximum allowed distance between the surfaces, respectively. Note that these two feasibility constraints are defined similarly as in the standard multiple surface segmentation problem (without a hole) [1].

Fig. 3.

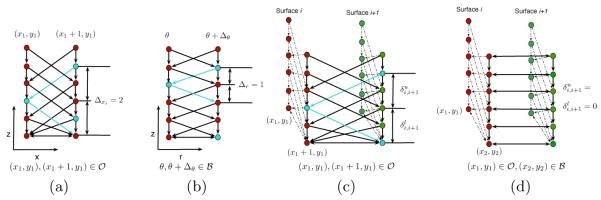
Illustration of the smoothness constraints within regions (a) $\mathcal{O}$ and (b) $\mathcal{B}$, and the surface-interaction constraints within regions (c) $\mathcal{O}$ and (d) $\mathcal{B}$

We also require that the x-y projection of the hole boundary be representable using a function defined in polar coordinates f_b(θ) (i.e., having one intersection per sampled angular ray) and that this projected boundary be sufficiently smooth: ∣f_b(θ)−f_b(θ+Δ_θ)∣ ≤ Δ_r where Δ_θ is the angular distance between sampled rays and Δ_r is the smoothness parameter specifying the maximum change in radial position between angular rays. Furthermore, for columns in $\mathcal{B}$, we require that the minimum and maximum distance between all surfaces be equal to 0 (i.e., the surfaces come together at any column on the shared hole boundary), as depicted in Figs. 3(c) and (d).

Cost of a feasible surface set with a shared hole

For the segmentation of the surfaces and the shared hole, every voxel in the volume will be assigned n+1 costs: one cost, C_surfi (x, y, z) (i = 1, … , n), associated with the unlikeliness of belonging to each of the n surfaces and one cost, C_b(x, y, z), associated with belonging to the boundary of the shared hole. Then, the cost of a feasible surface set with a shared hole (given $\mathcal{O},\mathcal{B}$) is defined as follows:

$$C_T=\sum _{i=1}^n\sum _{(x,y)\in \mathcal{O}}{c}_{{\text{surf}}_i}(x,y,f_i(x,y\left)\right)+\lambda \sum _{(x,y)\in \mathcal{B}}{c}_{\mathrm{b}}(x,y,f_1(x,y\left)\right),$$ (2)

where the first term is associated with the “on-surface” costs in region $\mathcal{O}$ and the second term is associated with the cost of the shared hole boundary points.

Segmentation of Multiple Surfaces with a Shared Hole

The iterative approach proposed for the segmentation of surfaces and the NCO is illustrated in Fig. 4. As an initialization step, the original formulation of the graph-theoretic approach [1,6] (where the existence of the hole is ignored) is used to segment the junction of the inner and outer segments (IS/OS line) (marked in blue in Fig. 1(a)) of the photoreceptors and the Bruch’s membrane (BM) (marked in yellow in Fig. 1(a)) in the volumetric image. Next, the following two steps (labeled Iteration A and Iteration B) are repeated until achieving convergence of the segmented boundary column-set $\mathcal{B}$. In the first step (Iteration A), we create a projection image and update our estimate of the projected boundary columns $\mathcal{B}$ of the NCO by finding a minimum-closure in a graph. In the second step (Iteration B), given this estimate of $\mathcal{B}$, we find the corresponding optimal (see Eq. 2) set of feasible surfaces that meet at the hole boundary in the volumetric image by solving another single minimum-closure problem in a constructed graph. Further details of each step are provided below.

Fig. 4.

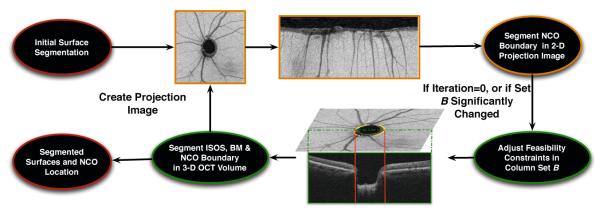
Schematic showing the segmentation process

Iteration A: Segmentation of projected hole boundary columns

The projection image was created by averaging 20 pixels above and below the BM surface. This projection image was then polar transformed and the NCO was segmented using a graph-theoretic approach that incorporated shape priors [7].

Iteration B: Simultaneous segmentation of the surfaces and the NCO shared hole

Before computing the cost functions for the regions $\mathcal{O},\mathcal{B}$ and $\mathcal{H}$, the volumetric image was also polar-transformed with an angular spacing of 1°. In the volumetric images, the NCO can be difficult to identify at the upper and lower regions of the NCO where the end points get closer together and the large blood vessels that characterize these regions of the retina also cast large vessels shadows. However, in the polar-transformed scans, the NCO’s continuity is maintained, making it easier to visualize and delineate.

The cost function for the regions $\mathcal{O}$ and $\mathcal{H}$ consisted of on-surface cost terms derived from Gaussian-derivative filters, while the cost function for $\mathcal{B}$ incorporated textural features learned from a training set. As the NCO boundary can be modeled as a “corner”, the textural features used to learn the properties of the NCO boundary points included corner detectors such as Harris and SUSAN [8] as well as first order steerable Gaussian derivatives at scales σ = {1, 2, 3, 4, 5} and orientations θ = {0°,±30°,±60°,±90°}, computed in 2D and 3D.

The training set (described further in Section 3) utilized here consisted of 25 radial volumes that each contained 180 slices, where the NCO was identified in all of the slices. The background samples were limited to a random selection of five samples near the NCO per slice. A random forest, an ensemble classifier [9], was then trained to identify the NCO boundary points in the volumetric image. The individual feature significances were used to select a smaller set of features, where the final set of 20 features only contained those that contributed at least 2% to the overall feature significance.

Finally, two surfaces, the IS/OS line and Bruch’s membrane, and their shared hole were segmented simultaneously in the polar coordinate space using the above defined feasibility constraints and cost functions. The value of λ was set to 8 to emphasize the hole boundary cost.

3 Experimental Methods

The data used in this experiment consisted of 44 optic nerve head SD-OCT scans obtained from 44 patients that presented with varying stages of glaucoma. The scans were obtained on a Cirrus (Carl Zeiss Meditec, Inc., Dublin, CA) SD-OCT scanner and were acquired from a region 2mm × 2mm × 6mm and contained 200 × 200 × 1024 voxels. The volumetric scans were converted into the polar coordinate space where the slices were 1° apart. Manual delineations were obtained from an independent expert (trained to detect the NCO boundary in SD-OCT images) on 10 randomly selected radial slices from each of the 44 scans. These tracings were then verified by a second independent expert, with a third and final verification being performed by a glaucoma specialist to give us our consensus manual tracings. The 25 independent datasets used to train the NCO classifier were also obtained from human patients on a Cirrus SD-OCT scanner, using the same imaging protocol described above.

The segmentation accuracy obtained using the proposed method (Approach III) was statistically compared (using a paired t-test) to results obtained when using a two-step approach, where the projected location of the NCO was computed using 1) a pixel classification approach (Approach I) [6] and, 2) a graph-theoretic approach (Approach II) [4]. These two boundary column-set estimates were then projected down onto the initial segmentation of the Bruch’s membrane to give us the 3D location of the NCO.

The metrics used to gauge the accuracy of the segmentation consisted of the unsigned difference between 1) the 2D segmentation in the projection image and the manual delineations, 2) the z locations of the automated segmentation and the manual delineations, and 3) the 3D Euclidean distance between the automated segmentation and the manual delineations.

Additionally, the minimum rim width (MRW) [10], a metric associated with the progression of glaucoma and defined as the minimum distance from the NCO to the internal limiting membrane (ILM), was also computed using the proposed method and statistically compared to values obtained using the manual tracings.

4 Results

Table 1 shows the complete summary of the accuracy assessment conducted using the three metrics described above. The 3D Euclidean distance (in microns) between the manual delineations and the segmented NCO for Approaches I, II and III were found to be 139.67 ± 61.68 μm, 136.77 ± 38.24 μm and 55.29 ± 33.97 μm, respectively. The errors noted in Approaches I and II for all 3 metrics were found to be significantly larger (p < 0.001) than those obtained using the proposed method.

Table 1.

Summary of accuracy assessment of the NCO segmentation. The errors are expressed in microns (and voxels).

	2D	z	3D
Pixel Classification	128.36 ± 61.23	46.85 ± 30.21	139.67 ± 61.68
(Approach I)	(4.28 ± 2.04)	(23.99 ± 15.47)
Two-step Graph Method	62.28 ± 26.74	117.21 ± 43.14	136.77 ± 38.24
(Approach II)	(2.08 ± 0.89)	(60.01 ± 22.09)
Proposed Iterative Method	46.05 ± 28.40	29.58 ± 20.24	55.29 ± 33.97
(Approach III)	(1.54 ± 0.95)	(15.15 ± 10.36)

Fig. 5 show the iterative results obtained on a dataset. As shown, the error in the location of the NCO substantially reduces from iteration to iteration, until the final result coincides with the manually delineated point. The mean MRW computed using the manually delineated points was found to be 179 ± 81.46 μm. The MRW computed using Approaches I, II and III were 247.23 ± 74.95 μm, 241.50 ± 103.94 μm and 184.09 ± 84.06 μm, respectively. The MRW measurements obtained using Approaches I and II were found to significantly (p < 0.0001) differ from those obtained using the manual tracings, while the MRW measurements obtained using Approach III was not significantly different (p > 0.05) from those obtained using the manual tracings.

Fig. 5.

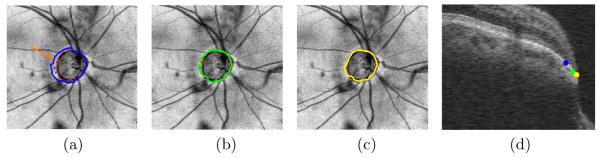
An example of the segmentation result obtained after the (a) first (blue), (b) second (green) and (c) third (yellow) iteration. The manual tracings are marked in red. (d) The 3D location of the segmented NCO and the manual tracings for the location indicated on (a).

5 Conclusion and Discussion

We have presented an iterative graph-based method for the automated simultaneous segmentation of surfaces with a shared hole. A graph-theoretic approach [1] was reformulated to meet the new requirements of surfaces that meet at a shared hole boundary, thereby allowing for the boundary of the hole to be detected in 3D. The proposed method was applied to the segmentation of the NCO in SD-OCT images obtained from patients that presented with varying stages of glaucoma, where it showed good accuracy in the 2D plane as well as in 3D, as well as a significant improvement over existing approaches.

Furthermore, this method allows for the computation of the minimum rim width in 3D. This provides an objective measure that could be used to augment the subjective planimetry assessments that are currently used to assess the progression of the disease.