Abstract
The small molecule universe (SMU) is defined as a set of over 1060 synthetically feasible organic molecules with molecular weight less than ∼500 Da. Exhaustive enumerations and evaluation of all SMU molecules for the purpose of discovering favorable structures is impossible. We take a stochastic approach and extend the ACSESS framework (Virshup et al. J. Am. Chem. Soc. 2013, 135, 7296–7303) to develop diversity oriented molecular libraries that can generate a set of compounds that is representative of the small molecule universe and that also biases the library toward favorable physical property values. We show that the approach is efficient compared to exhaustive enumeration and to existing evolutionary algorithms for generating such libraries by testing in the NKp fitness landscape model and in the fully enumerated GDB-9 chemical universe containing 3 × 105 molecules.
Introduction
The small molecule universe of organic molecules with molecular weight < ∼500 Da is estimated to contain ∼1060 stable compounds.2 This vast number of structures makes the prospect of mining the SMU a daunting but an enticing task. Synthetic chemistry over the last century has produced ∼60 million compounds.3 Diversity oriented synthesis (DOS) and natural product motifs provide a means to create libraries with diverse structures of potential value.4 However, the rate of molecular discovery has not kept pace with the demand for molecular species that address compelling challenges,5 and one hopes to develop theoretical approaches to accelerate the pace of progress.
Computational efforts are underway to develop strategies that map and mine molecular space. Reymond’s group has enumerated organic libraries that contain hundreds of billions of novel compounds.6 However, computational considerations limit exhaustive enumeration to molecules up to ∼20 heavy atoms - enumeration of GDB-17 required over 11 CPU-years.6 The size of the small molecule universe makes its exploration and mining very challenging indeed. We have devised a chemical space exploration method called Algorithm for Chemical Space Exploration with Stochastic Search (ACSESS)1 that allows computationally feasible surveying of unexplored regions of the small molecule universe without exhaustive enumeration.
While chemical space mapping and exploration is itself a novel undertaking, it does not guarantee the discovery of useful structures. Some success in identifying valuable structures was accomplished using the enumerated GDB-11 and GDB-137 libraries, but screening of every member of a large enumerated library is very demanding. Hence, there is a pressing need for computational approaches that bias molecular searches to produce useful libraries of compounds drawn from the vastness of molecular space. Here, we describe a method within the ACSESS framework to mine chemical space for collections of diverse compounds possessing favorable values (defined within a threshold from the global optimum) of a targeted physical property. The performance of this approach is tested on a GDB-9 enumerated space. As an example, we show that the property-optimizing ACSESS procedure can be used to construct libraries of diverse, large dipole moment molecules (within GDB-9) without enumerating all molecules within the GDB-9 space. We also evaluate the performance of the property-optimizing ACSESS method using the NKp fitness landscape. The NKp model landscape has been used to test the performance of various evolutionary algorithms.8,9 This model tunes the “ruggedness” of the property landscape by changing the length of a bit string (specified by the parameter N) and the numbers of local hills and valleys (specified by the parameters K and p).8,9 To our knowledge, this is the first time that the NKp landscape model was used to compare strategies for chemical space search. These studies demonstrate that property-optimizing ACSESS maximizes the diversity of useful molecules more efficiently than popular simple genetic algorithms. The approach presented here can likely be extended to other molecular design challenges in drug discovery and materials design.
Method
We begin with a definition of terms and a review of ACSESS.
Chemical space is defined as an N-dimensional Cartesian space in which compounds can be mapped using cheminformatics descriptors. Descriptors describe physical, chemical, and topological properties of the compounds. In our analysis, each compound is mapped using a set of 40 autocorrelation descriptors (which defines our molecular space).10 For each molecule, we computed the Moreau-Broto autocorrelation descriptor.10 This descriptor encodes the correlations of atomic properties in a molecule as a function of the topological distance between atoms in the molecule. Both the molecular structure and the physicochemical properties of a molecule can be encoded in this way, which is used successfully to construct structure–activity relationships.11 The autocorrelation descriptor is
| 1 |
where
dij is the shortest bond distance between atoms i and j, and pi, pj are the descriptors of atoms i and j, respectively.
The properties p were atomic number, Gasteiger–Marsili partial charge, atomic polarizability, topological steric index, and unity (i.e., pi =1 for all i).10 Values of d that represent the topological distance (bond distance), ranges from 0 to 7.10 The choice of the range for d is based on a previous study.1 The use of the above five listed atomic properties and topological distance results in a 40 dimensional descriptor. Here, the molecular descriptors of the generated molecules are mean centered and normalized to have unit variance.
The chemical space distance between two compounds is defined as the Euclidean distance between compounds based on their descriptors
| 2 |
| 3 |
| 4 |
where dik and djk are the kth descriptor of molecules i and j, N is the length of the descriptor vector, Dij is the Euclidean distance between molecules i and j, Dijham is the Hamming distance between two bit strings i and j of length N, XOR(i,j) is the count of bit positions that differ in the two strings, Dmin is the distance of the nearest molecule j from molecule i, i.e., the nearest-neighbor distance of the molecule i, and M is the number of molecules in the library.
The molecular fitness of any structure is a real valued molecular property. The magnitude of the molecular dipole moment, or a value drawn from the NKp model, is used in our analysis.
Next we introduce the property-optimizing ACSESS strategy to find optimal structures. We then describe property calculations within the enumerated (GDB-9) chemical universe and the enumerated binary fitness model (NKp landscape). Finally, we describe searching for optimal structures within both fitness landscapes using the property-optimizing ACSESS strategy.
ACSESS Algorithm To Search Molecular Space
ACSESS samples from a chemical space by iteratively optimizing (maximizing) the nearest-neighbor distances (diversity) of a subset of compounds in the space of all possible compounds.1 There are four main steps in the property-optimizing ACSESS calculation described here: (1) initialize a library, (2) breed new compounds, (3) remove compounds that do not have a property value above a threshold, and (4) select a maximally diverse subset of property qualified structures.1 ACSESS can be seeded with a collection of compounds or with a single molecule. The initial library is modified by making mutations and crossovers. Among the generated compounds, a diverse subset is chosen by applying either maximin or cell-based partitioning algorithms.1 The maximin algorithm maximizes the nearest-neighbor distance between compounds. It does so by applying an iterative approach where, to start with, a compound from a library is randomly selected. It then selects the next compound that is furthest from the initial compound in chemical space distance (eq 2). The next compound from the library it selects will be the furthest from both of the initially selected compounds. This process is repeated until a desired diverse library size is obtained.12 On the other hand, a cell-based partitioning algorithm effectively partitions the chemical space into discrete multidimensional grids and picks a molecule that falls in each grid.13 The advantage of cell-based partitioning is that it scales linearly with large library size.
Earlier implementations of ACSESS did not include an approach to property optimization. As modified here, the modified ACSESS now iteratively selects a maximally diverse set of solutions with property values above a threshold value. In order to iteratively increase the property value, we increase the property value cutoff linearly with each iteration until a desired property value threshold is reached. Initially the threshold is set to a low value to ensure that the population does not collapse to zero size because of the fitness constraint. A schematic of this algorithm is shown in Figure 1.
Figure 1.
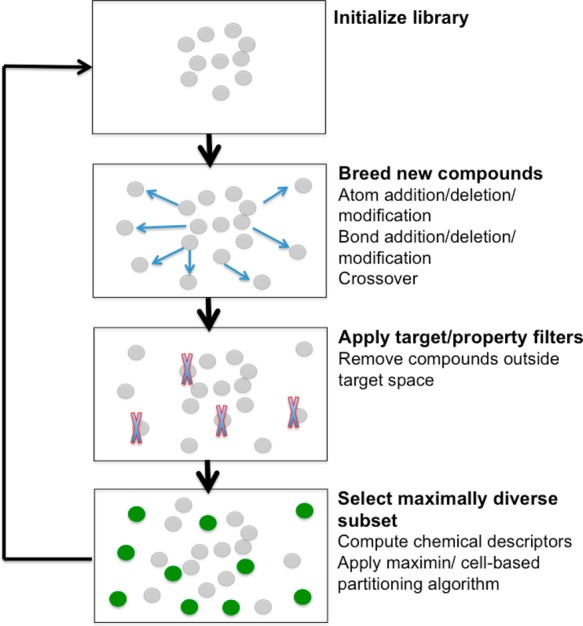
Property-optimizing ACSESS procedure uses property filter and diversity-biased sampling to construct a diverse library with properties above a cutoff value.
Software
Property-optimizing ACSESS made use of OpenEye OEChem TK14 for molecule generation, OpenEye MolProp TK14 for filtering, and OpenEye OMEGA TK100,15 for conformer generation.
Optimization within GBD9 Property Landscape
We computed the Boltzmann-averaged dipole moment of all molecules in GDB-9 and pursued strategies to identify molecules in this set with large dipole moments. Compounds among the 300,000 compounds of GDB-9 with nine of fewer heavy atoms (allowed atom types include C, N, O, S, and Cl) defined the search space.14 For each molecule, the dipole moment (D) was computed using
| 5 |
where μi is the dipole moment of a single conformation, β was computed using Boltzmann constant (kB) 3.1668 × 10–6 Hartree per Kelvin and temperature (T) 298 K, i belonging to a set of conformations C, and Ei is the internal energy of conformation i. Conformations for each molecule, including stereoisomers, were generated using OMEGA and flipper tools.100,15 Each conformation was energy minimized, and the total dipole moment was computed using AM1 calculations as implemented in the Gaussian 09 package.16 Dipole moments were stored in a database and retrieved during ACSESS exploration of the chemical space.17 ACSESS was used to create a maximally diverse set of compounds with dipole moments above a threshold value of 5.5 D (the 90th percentile of GDB-9 dipole moments).
Optimization in the NKp Fitness Landscape Model
In addition to the GDB-9 molecular space, we tested our approach on a known binary fitness landscape. We chose the NKp model since it has been widely used to test the performances of genetic algorithms.18,19 The NKp fitness landscape maps a binary string to a fitness value from 0 to 1.18,19 The fitness of a binary string is the summation of the fitness contribution of each cell scaled by the length of the string (eq 6). In this model, we model a binary string and its NKp fitness value as representing a molecule and the molecule’s property value, respectively (as in the case of GDB-9 molecules and their dipole moments). A binary string is associated with three parameters: (1) its length N, (2) the number K of associations each bit makes to other bits in a string (ranges from 0 to N-1), and (3) the fitness contribution or weight p (also ranges from 0 to 1) of each bit position. By varying the parameters K and p, we constructed a fitness landscape with multiple optima (to mimic the multiple optima case in the GDB-9 space; details presented in the Supporting Information).
The fitness (Φ) of a bit string (g) in the NKp fitness landscape model is18
| 6 |
where
We computed the fitness of all possible bit strings of 19 bits using the NKp model (eq 6). We then applied property-optimizing ACSESS runs to create a maximally diverse set of bit strings with an NKp value equal to a threshold value of ∼0.3 (the global maximum within our enumerated NKp model). In this case, the property-optimizing ACSESS library was modified to work with the binary strings. The mutations were defined as the bit flips, and crossovers were defined as combinations of two fragments of binary strings by cutting them both at a randomly chosen position. The maximin algorithm used the Hamming distance (eq 3) measure to compute the nearest-neighbor distances (eq 4).
Results
We enumerated all possible 19-bit patterns and computed their fitness with N = 19, K = 9, and p = 0.9 (total of 524,288 bit strings, which is similar to the number of molecules in the GDB-9 space). We also computed the averaged dipole moments of all molecules in GDB-9. The distributions are shown in Figure 2.
Figure 2.
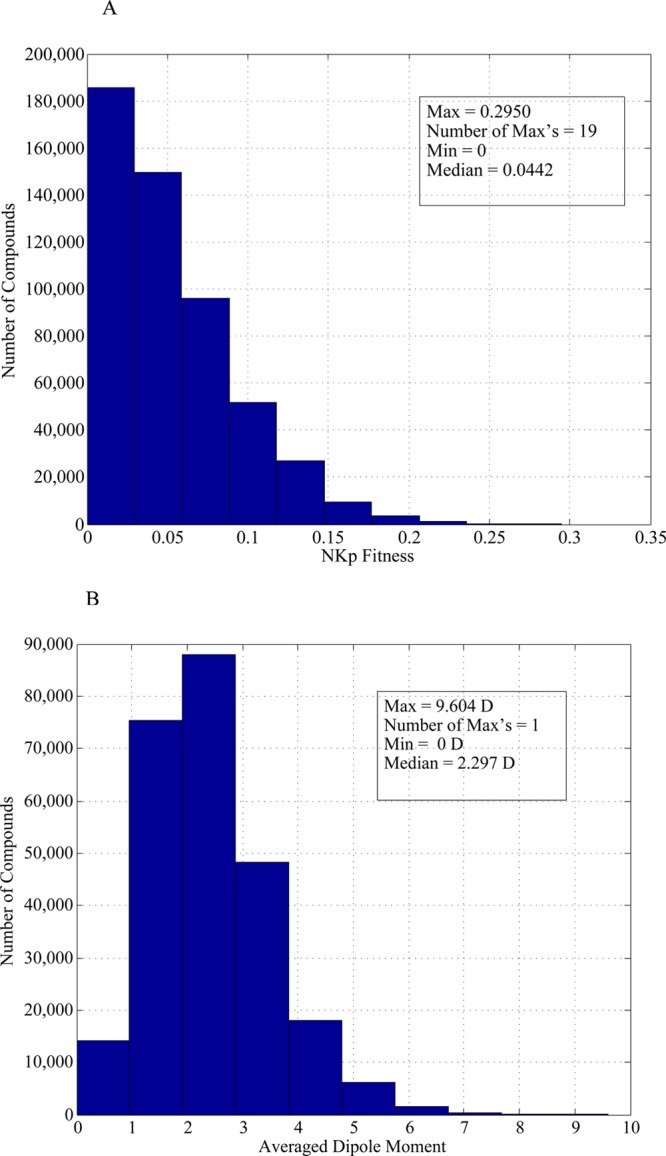
Distribution of molecular property values for (A) the enumerated NKp landscape with N = 19, K = 9, p = 0.9 and (B) the dipole moments of all molecules in GDB-9.
ACSESS Exploration of a NKp Model Space
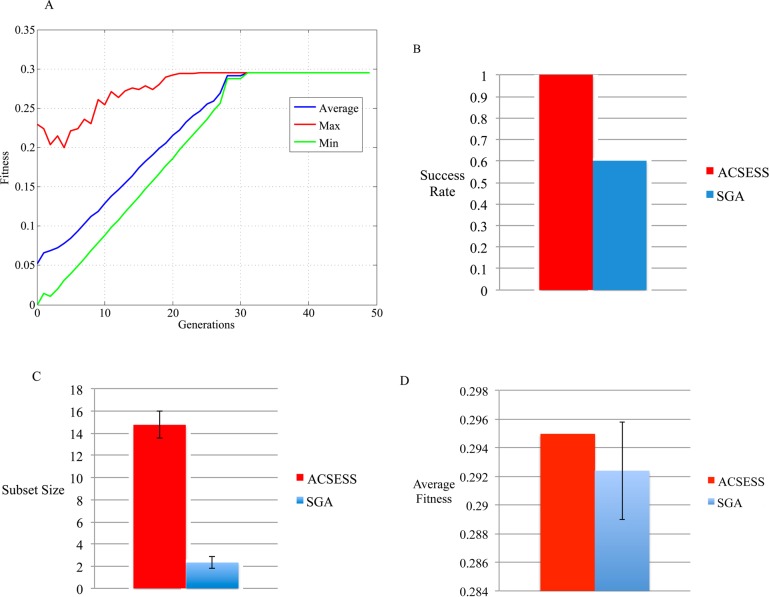
We used the property-optimizing ACSESS method to construct a diverse set of strings in the N = 19, K = 9, and p = 0.9 fitness landscape. First, a maximally diverse set of binary strings was generated without using fitness-based selection (Figure 3A). The maximally diverse set was used to seed the property-optimizing ACSESS method that maximizes fitness (Figure 3B). As shown in Figure 3B, the property-optimizing ACSESS method finds the fittest solutions after 30 iterations without exhaustively enumerating and evaluating all possible bit strings.
Figure 3.
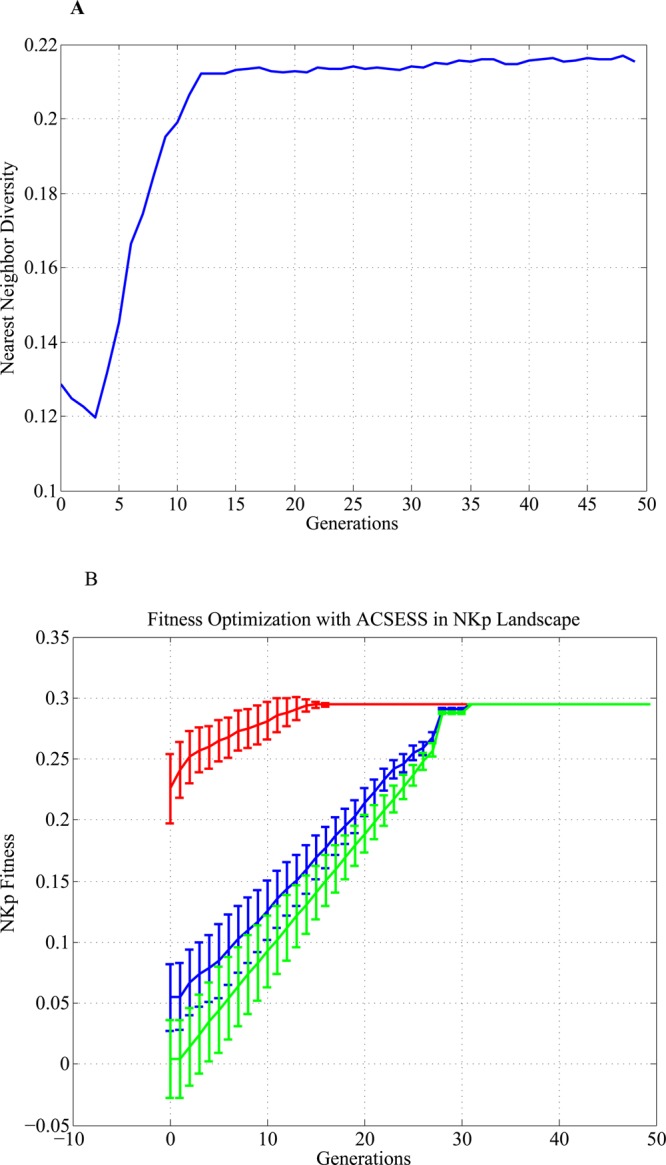
(A) Diversity biased sampling and (B) fitness-biased sampling. Diversity is first maximized to generate solutions that span a given chemical space. Here, the nearest-neighbor diversity (eq 4) is defined as the average hamming distance (eq 3) to the nearest neighbor. The diverse solutions seed the property-optimizing ACSESS method, and the fitness of the diverse set is improved iteratively. The global optimum in our enumerated NKp model space was found within 30 iterations of our optimization (data shown are averaged over ten different runs).
Comparing Property-Optimizing ACSESS with Simple Genetic Algorithm Searches
To judge the performance of the property-optimizing ACSESS method relative to a simple genetic algorithm (SGA) that uses elitism (selecting the fittest molecules at each iteration),20 we implemented a SGA as an extension of ACSESS for molecular library design. We ensured fair comparison by 1) applying NKp based fitness filters to SGA and ACSESS in every generation and 2) initializing both algorithms with the same diverse subset sampled using ACSESS (Figure 3A). With the parameters and simulation steps exactly the same as in ACSESS, the only difference between ACSESS and SGA is that, at each iteration, SGA selects an equal number of the fittest solutions without considering the diversity among the solutions. Figure 4A indicates that the SGA finds the best solution (with the largest NKp fitness value). However, SGA tends to be trapped in local extrema more often than ACSESS (Figure 4B, 40% of SGA runs failed to find the optimum structures as opposed to 0% for ACSESS). On average, the solutions that SGA finds are suboptimal compared to those found using ACSESS (Figure 4D). Also, among the fittest solutions (solutions having the largest NKp fitness function value, 19 total possibilities binary strings), the number of fittest solutions found by SGA is smaller (on average ∼3 fittest solutions) compared to the number of fittest solutions found by ACSESS (on average ∼15 fittest solutions) (Figure 4C).
Figure 4.
Comparison of property-optimizing ACSESS outcomes to the simple genetic algorithm (SGA) optimization for generating multiple solutions with the largest NKp fitness value. SGA iteratively samples the fittest solutions and improves upon them. (A) indicates that SGA finds the fittest solutions (global maximum in the constructed NKp model) after 30 iterations. (B) indicates that property-optimizing ACSESS runs escapes local optima more effectively than do the SGA runs, i.e. the success rate of finding largest fitness solution of property-optimizing ACSESS is 100% compared to 60% for SGA (from 10 runs of each method). (C) indicates that the property-optimizing ACSESS runs also performs better than SGA to sample diverse fittest solutions as it samples a larger number of fittest solutions compared to SGA. (D) indicates that, on average, the fitness of solutions generated by property-optimizing ACSESS is larger than that of SGA.
ACSESS Explorations in GDB-9
Property-optimizing ACSESS was used to sample diverse molecules in GDB-9 with average dipole moments ≥5.5D (the top 10% of molecules). As in the NKp model space exploration, ACSESS first generated a maximally diverse set of compounds, without fitness optimization, spanning the GDB-9 universe (Figure 5A). The maximally diverse set was used to seed the next step, where the fitness of the diverse set was improved iteratively. Figure 5B indicates that ACSESS finds diverse molecular structures with dipole moments above the 90th percentile of compounds in the GDB-9 universe without exhaustively enumerating and evaluating each molecule.
Figure 5.
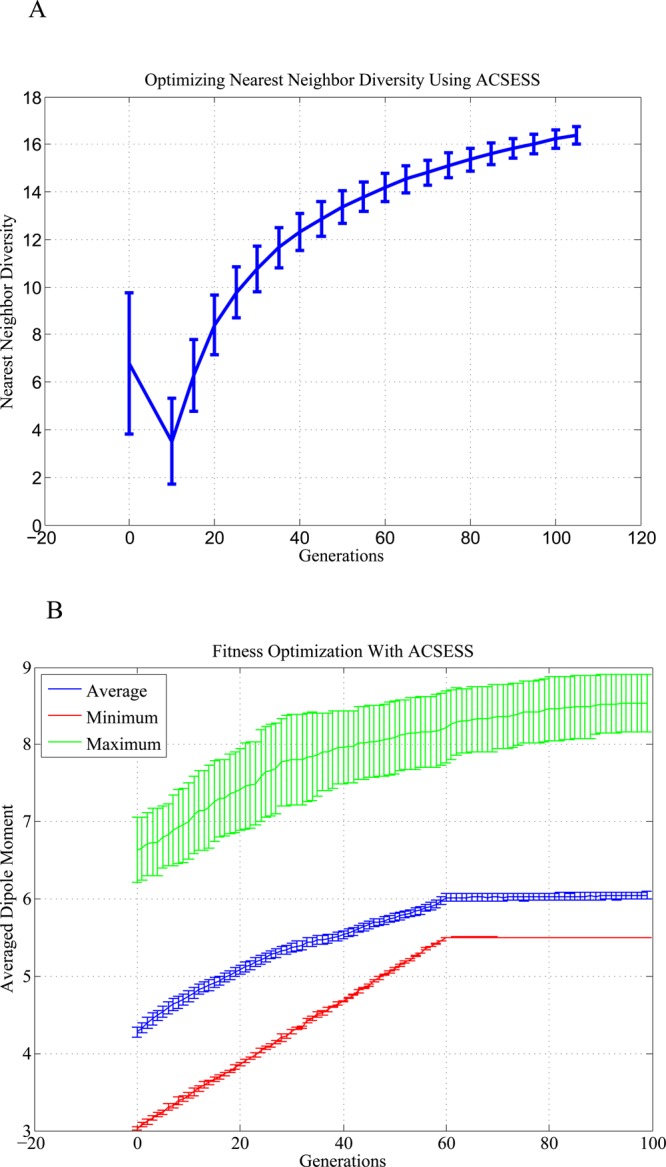
Progress of ACSESS runs that sample GDB-9. The plots show the mean of the dipole moments from multiple runs, and the error bars represent one standard deviation from the mean of either nearest-neighbor distance or dipole moment. (A) Initially, a maximally diverse set (measured by nearest-neighbor distance) is generated. (B) The maximally diverse set is used to maximize their dipole moments. The minimum dipole moment found after 60 iterations is the desired dipole moment threshold (i.e., the top 10% fittest molecules).
Comparisons of Property-Optimizing ACSESS and Genetic Algorithm Methods for Property Optimization
We compared the performance of ACSESS to standard genetic algorithms (SGAs) to judge the relative performance for property biased library design. We ensured fair comparison by 1) applying dipole moment filtering in every generation for SGAs and property-optimizing ACSESS and 2) initializing all algorithms with the same diverse subset of GDB-9 structures generated using ACSESS (Figure 5A). SGAs are used mainly for fitness optimization, but they can also maintain the diversity of solutions using techniques such as roulette wheel selection and tournament selection.20,21 We now explore how well ACSESS optimizes the fitness and diversity of the library by comparing to these standard approaches. We compare the performance of ACSESS with SGAs where each method starts with the same diverse set constructed using ACSESS (Figure 5A).
As summarized in Table 1, we found, on average, that ACSESS generate molecules with similar or more favorable dipole moments (fitness) compared to SGAs, but ACSESS generates a more diverse set of fit molecules (dipole moment ≥5.5D) compared to SGAs. More specifically, ACSESS generates molecules with higher dipole moments (fitness) than SGA with roulette wheel selection, but ACSESS generates solutions of similar fitness to SGA with tournament selection (Figure 6A). SGA with elitism (selecting the fittest solutions in every generation) performs marginally better than ACSESS. However, Figure 6B indicates that the diversity (measured using the nearest-neighbor Euclidean distance defined in eq 4) of the molecular library for ACSESS is much larger than is found with the SGAs. In fact, the nearest-neighbor Euclidean distance (Euclidean distance of ∼10) of the library generated by ACSESS is similar to the nearest-neighbor Euclidean distance (Euclidean distance of ∼12) that is found for the enumerated GDB-9 molecules with dipole moments ≥5.5D. These results indicate that the diversity of the ACSESS generated library is similar to the diversity of the enumerated GBD-9 universe that contains only the compounds above a fitness cutoff. These findings are similar to those from the model NKp landscape, where ACSESS generated multiple global optima without becoming trapped in local optima. In contrast, the SGAs became trapped in local optima in 40% of the runs (Figure 4B) and produced far fewer fittest solutions (Figure 4C). These calculations indicate that the diversity enforcement in ACSESS yields sampling of different high fitness regions of the GDB-9 space favorably compared to SGAs. It is important to note that, while ACSESS generates large diversity solutions, the fitness is still comparable to and better, in some cases, compared to that found with popular simple genetic algorithms (Figures 4D and 6A).
Table 1. Performance of Methods Based on the Computed Fitness and Diversity: Comparison of ACSESS with Simple Genetic Algorithms (SGAs).
| methods | dipole moment | diversity (eq 4) |
|---|---|---|
| GA-Roulette | 5.8 ± 0.03 | 6.5 ± 0.7 |
| GA-Tournament | 6.4 ± 0.08 | 3.5 ± 0.7 |
| GA-Elitism | 6.74 ± 0.08 | 5.4 ± 0.4 |
| ACSESS | 6.05 ± 0.05 | 9.7 ± 0.6 |
Figure 6.
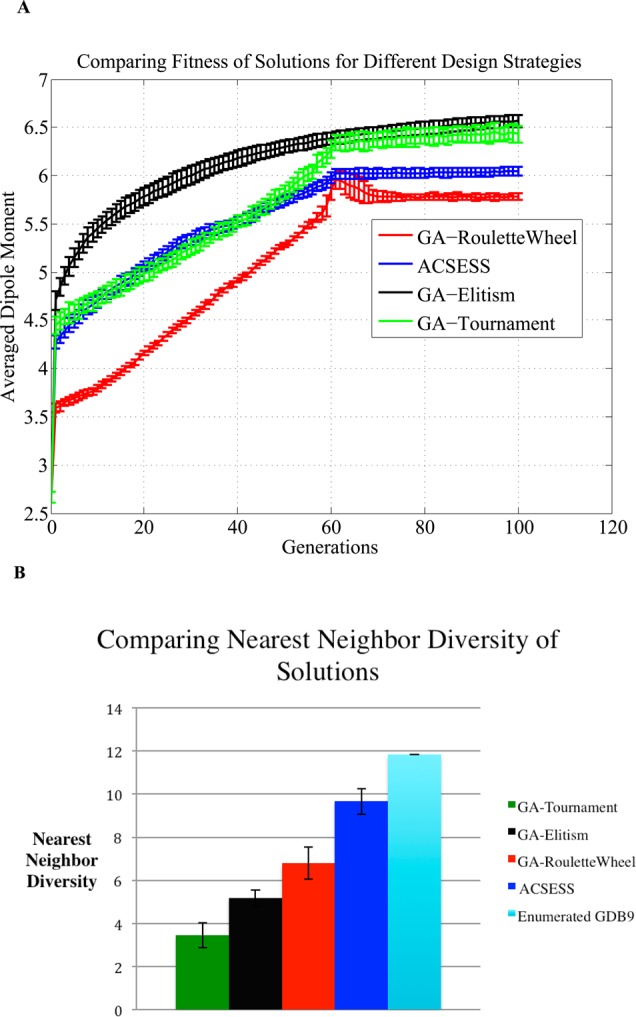
ACSESS and SGAs runs that maximize the dipole moments (fitness) of diverse molecules. The two plots track the average fitness of libraries generated by each design algorithm (color coded differently), and the error bars represent one standard deviation from the mean for multiple runs. (A) compares the fitness of the library optimized using ACSESS with three other genetic algorithms (colored coded differently). (B) compares the diversity of the fit libraries generated by ACSESS and SGAs.
Self-Organizing Maps of GDB-9 and of Sampled Solutions
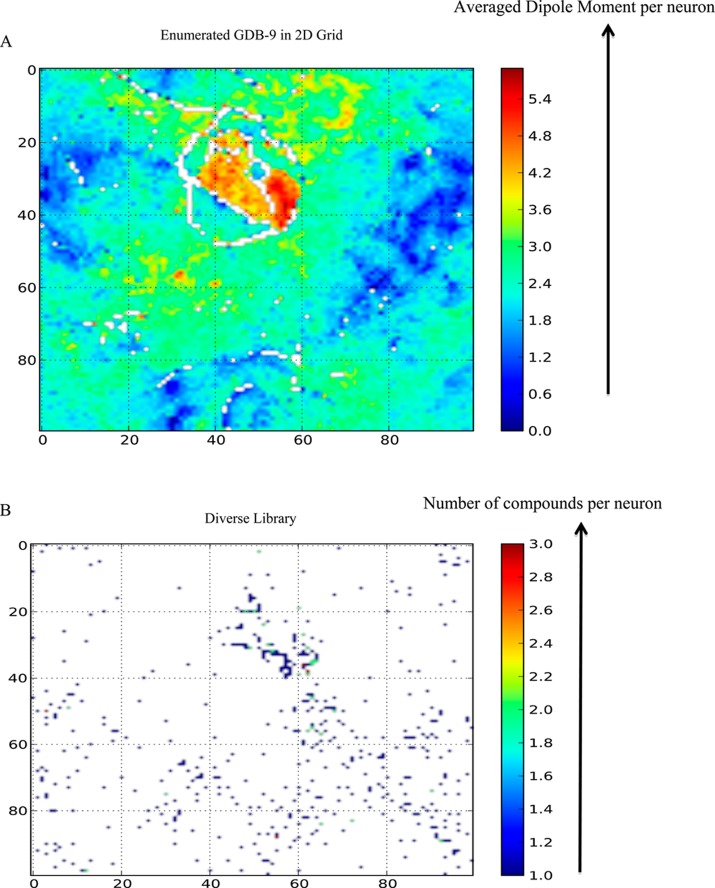
Additional insight into performance of property-optimizing ACSESS and SGAs is obtained by visualizing the sampled molecules with respect to the enumerated molecular space. For this purpose, we projected the 40 dimension chemical space into two dimensions using a self-organizing map (SOM). SOMs are widely used in cheminformatics.22 They have the useful property of representing high-dimensional neighborhood relationships.22 A 100 × 100 torroidal grid was used where each grid point is a neuron.23,24 The SOM in this case was trained using the enumerated GDB-9. During the training, each neuron is randomly assigned a chemical space coordinate, and the neurons are trained by presenting a descriptor vector for each molecule.23,24 Neurons compete with each other for the presented descriptor vector and adjust their coordinates based on the descriptor vector closest to them.22 In the resulting two-dimensional representation after training the structurally similar molecules clumped together in the same neuron or nearby neurons, and the structurally is similar molecules are assigned to the more distant neurons.
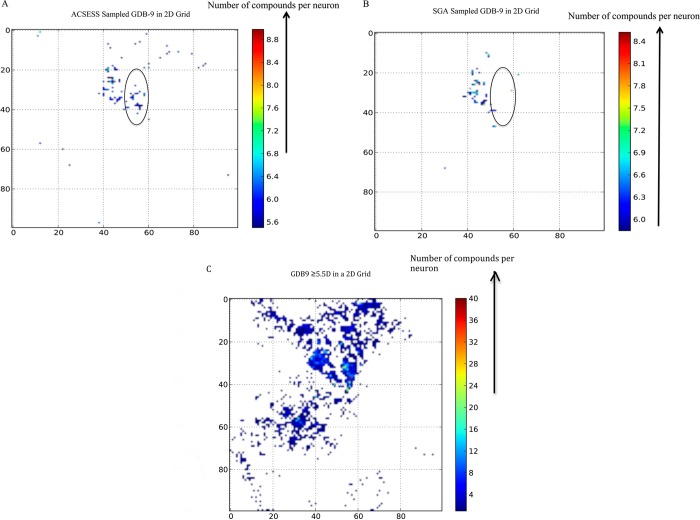
We projected the enumerated GDB-9 on the SOM and also the maximally diverse subset of GDB-9 sampled using ACSESS without maximizing the dipole moments (Figures 7A and 7B). Comparing Figures 7A and 7B we see that by maximizing the diversity of GDB-9 molecules, we are able to sample various regions of the enumerated GDB-9. We also projected, on the trained SOM, the libraries designed using property-optimizing ACSESS (Figure 8A) and SGA (using the elitist selection scheme, Figure 8B) and compared those with the high-activity regions (dipole moment ≥5.5 D) within GDB-9 (Figure 8C).
Figure 7.
SOM for the enumerated and sampled GDB-9. (A) shows the full GDB-9 with color-bar representing average dipole moment per neuron from blue (low) to red (high). (B) shows the ACSESS designed diverse library (without maximizing the dipole moment). The filling of the plot in B indicates that the diverse library from ACSESS spans the GDB-9 space. The color bar in B indicates the number of molecules assigned to each neuron. The white space in both maps indicates regions where no compounds are assigned.
Figure 8.
Comparison of the diversity found in an ACSESS library and in an SGA-elitist library to the fully enumerated GDB-9 library. The color bars in A and B indicate the number of compounds per neuron. (A) shows the more fit molecules (molecules above the fitness cutoff) generated by ACSESS, (B) shows the more fit molecules (molecules above the fitness cutoff) generated by SGA (elitist), and (C) shows the fittest regions of GDB-9 (≥5.5D dipole moment) where the color bar represents the number of compounds per neuron. The oval indicates molecules in GDB-9 that are discovered using ACSESS but missed by SGAs.
Figure 8 indicates that the high activity regions of GDB-9 are identified in ACSESS analysis (Figure 8A in oval) but overlooked by SGA-elitist analysis (Figure 8B oval). The medium activity regions (yellow colored regions in Figure 7A) populated by the ACSESS library that lie above the black oval (Figure 8A) are absent in SGA library (Figure 8B). The underperformance of SGA explains why libraries generated by SGAs have lower diversity compared to the ACSESS generated libraries. While ACSESS is able to explore different activity islands of GDB-9, the SGAs fail to do so.
Conclusions
In this study, we showed that property-optimizing ACSESS explorations navigate large chemical spaces to find compounds with favorable targeted property values. ACSESS not only samples diverse regions of chemical space but also samples useful regions without having to enumerate and test every single molecule. In fact, only ∼30,000 fitness evaluations were carried out to locate the different optimal regions of GDB-9 (which contains ∼300,000 molecules). We explored ACSESS performance in an NKp landscape and in the GDB-9 for molecular dipole moment. In these studies, ACSESS performs favorably in terms of discovering diverse fit solutions compared to standard genetic algorithms, and ACSESS performs much more efficiently than exhaustive enumeration.
ACSESS can also be used to sample astronomically large chemical spaces, and this represents a research direction. Since property-optimized ACSESS libraries contains multiple favorable molecules, one can choose from among the diverse available alternatives. This approach may assist in reducing attrition in molecular design challenges. Studies presented here on known landscapes demonstrate that property-optimized ACSESS can indeed help to discover diverse useful molecules from the vastness of libraries chemical space and may assist in successful molecular discovery.
Acknowledgments
We thank Professor Peter Wipf for helpful discussions. Support for this project was provided by NIH UPCMLD (P50-GM067082) and by the Samsung Advanced Institute of Technology (SAIT) Global Research Outreach (GRO) program. We thank OpenEye Scientific Software (Santa Fe, NM) for the use of Omega, OEChem, MolProp, and other tools.
Supporting Information Available
Qualitative comparisons between the NKp landscape and the GDB-9 dipole property landscape is shown using autocorrelation plots. We also include the CPU times for different steps in the ACSESS calculation. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Virshup A. M.; Contreras-García J.; Wipf P.; Yang W.; Beratan D. N. Stochastic Voyages into Uncharted Chemical Space Produce a Representative Library of All Possible Drug-like Compounds. J. Am. Chem. Soc. 2013, 135, 7296–7303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bohacek R. S.; McMartin C.; Guida W. C. The Art and Practice of Structure-Based Drug Design: A Molecular Modeling Perspective. Med. Res. Rev. 1996, 16, 3–50. [DOI] [PubMed] [Google Scholar]
- Lipkus A. H.; Yuan Q.; Lucas K. A.; Funk S. A.; Bartelt W. F.; Schenck R. J.; Trippe A. J. Structural Diversity of Organic Chemistry. A Scaffold Analysis of the CAS Registry. J. Org. Chem. 2008, 73, 4443–4451. [DOI] [PubMed] [Google Scholar]
- Isidro-Llobet A.; Murillo T.; Bello P.; Cilibrizzi A.; Hodgkinson J. T.; Galloway W. R. J. D.; Bender A.; Welch M.; Spring D. R. Diversity-Oriented Synthesis of Macrocyclic Peptidomimetics. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 6793–6798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dandapani S.; Marcaurelle L. A. Grand Challenge Commentary: Accessing New Chemical Space for “Undruggable” Targets. Nat. Chem. Biol. 2010, 6, 861–863. [DOI] [PubMed] [Google Scholar]
- Ruddigkeit L.; van Deursen R.; Blum L. C.; Reymond J.-L. Enumeration of 166 Billion Organic Small Molecules in the Chemical Universe Database GDB-17. J. Chem. Inf. Model. 2012, 52, 2864–2875. [DOI] [PubMed] [Google Scholar]
- Blum L. C.; van Deursen R.; Bertrand S.; Mayer M.; Bürgi J. J.; Bertrand D.; Reymond J.-L. Discovery of α7-Nicotinic Receptor Ligands by Virtual Screening of the Chemical Universe Database GDB-13. J. Chem. Inf. Model. 2011, 51, 3105–3112. [DOI] [PubMed] [Google Scholar]
- Kauffman S. A.; Weinberger E. D. The NK Model of Rugged Fitness Landscapes and Its Application to Maturation of the Immune Response. J. Theor. Biol. 1989, 141, 211–245. [DOI] [PubMed] [Google Scholar]
- Stadler P. F. Landscapes and Their Correlation Functions. J. Math. Chem. 1996, 20, 1–45. [Google Scholar]
- Moreau J. L.; Broto P. Autocorrelation of Molecular Structures: Application to SAR Studies. Nouv. J. Chim 1980, 4, 764. [Google Scholar]
- Bauknecht H.; Zell A.; Bayer H.; Levi P.; Wagener M.; Sadowski J.; Gasteiger J. Locating Biologically Active Compounds in Medium-Sized Heterogeneous Datasets by Topological Autocorrelation Vectors: Dopamine and Benzodiazepine Agonists. J. Chem. Inf. Comput. Sci. 1996, 36, 1205–1213. [DOI] [PubMed] [Google Scholar]
- Schmuker M.; Givehchi A.; Schneider G. Impact of Different Software Implementations on the Performance of the Maxmin Method for Diverse Subset Selection. Mol. Divers. 2004, 8, 421–425. [DOI] [PubMed] [Google Scholar]
- Xue L.; Stahura F. L.; Bajorath J. Cell-Based Partitioning. Methods Mol. Biol. 2004, 275, 279–290. [DOI] [PubMed] [Google Scholar]
- Blum L. C.; Reymond J.-L. 970 Million Druglike Small Molecules for Virtual Screening in the Chemical Universe Database GDB-13. J. Am. Chem. Soc. 2009, 131, 8732–8733. [DOI] [PubMed] [Google Scholar]
- OEChem 1.7.5; OMEGA 2.4.4; MolProp 2.1.2. OpenEye Scientific Software. www.eyesopen.com, 2014. [Google Scholar]
- Hawkins P. C. D.; Skillman A. G.; Warren G. L.; Ellingson B. A.; Stahl M. T. Conformer Generation with OMEGA: Algorithm and Validation Using High Quality Structures from the Protein Databank and Cambridge Structural Database. J. Chem. Inf. Model. 2010, 50, 572–584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09, Revision A.02; 2009.
- Computing D.Definitive Guide to MongoDB: The NoSQL Database for Cloud and Desktop Computing; 2010; Vol. 44, p 328. [Google Scholar]
- Barnett L.Ruggedness and Neutrality - The NKp Family of Fitness Landscapes. In Proceedings of the 6th International Conference on Artificial Life; Adami C., Belew R., Kitano H., Taylor E., Eds.; Cambridge, MA, 1998; pp 18–27. [Google Scholar]
- Geard N.; Wiles J.; Hallinan J.; Tonkes B.; Skellett B.. A Comparison of Neutral Landscapes - NK, NKp and NKq. Proc. 2002 Congr. Evol. Comput. CEC′02 (Cat. No. 02TH8600) 1; pp 205–210.
- Eiben A. E.; Smith J. E.. Introduction to Evolutionary Computing: With 28 Tables; Rozenberg G., Bäck Th., Eiben A. E., Kok J. N., Spaink H. P., Eds.; Springer: Heidelberg, Berlin, 2003; pp 59–65. [Google Scholar]
- Mitchell M.An Introduction to Genetic Algorithms (Complex Adaptive Systems); The MIT Press: Cambridge, 1998; p 124–128. [Google Scholar]
- Sadowski J.; Wagener M.; Gasteiger J. Assessing Similarity and Diversity of Combinatorial Libraries by Spatial Autocorrelation Functions and Neural Networks. Angew. Chem., Int. Ed. Engl. 1995, 34, 2674–2677. [Google Scholar]
- Brown N.; McKay B.; Gasteiger J. The de Novo Design of Median Molecules within a Property Range of Interest. J. Comput.-Aided. Mol. Des. 2004, 18, 761–771. [DOI] [PubMed] [Google Scholar]
- Van Deursen R.; Reymond J.-L. Chemical Space Travel. ChemMedChem 2007, 2, 636–640. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.