Detecting Significant Changes in Protein Abundance

Abstract

We review and demonstrate how an empirical Bayes method, shrinking a protein's sample variance towards a pooled estimate, leads to far more powerful and stable inference to detect significant changes in protein abundance compared to ordinary t-tests. Using examples from isobaric mass labeled proteomic experiments we show how to analyze data from multiple experiments simultaneously, and discuss the effects of missing data on the inference. We also present easy to use open source software for normalization of mass spectrometry data and inference based on moderated test statistics.

Introduction

Detecting significant changes in protein abundance is a fundamental task in mass-spectrometry based experiments when trying to compare treated to untreated cells, wildtypes to mutants, or samples from diseased to non-diseased subjects. The statistical inference for proteomic data in these settings is usually based on standard 2-sample t-tests, comparing the measured relative or absolute abundances for each peptide or protein across the conditions of interest. However, sample sizes are often small, sometimes as small as 4 or 8 samples total, which results in great uncertainty in the sample variability estimates. Since these estimates are used in the test statistics to assess the statistical significance of the observed fold change, proteins exhibiting a large fold change are often declared non-significant because of a large sample variance, while at the same time small observed fold changes might be declared statistically significant, because of a small sample variance.

Additional methods to assess biological and technical sources of variability have been proposed^1–6, including methods to analyze data from multiple experiments simultaneously. For case-control iTRAQ experiments, Oberg et al.⁷ and Hill et al.⁸ extended a linear mixed effects approach originally proposed by Kerr and Churchill^9,10 as analysis of variance for gene expression studies. This mixed model adjusts for potential differences due to channel e ects, loading, mixing, and sample handling. The parameter of interest in the model is the interaction between protein and group status, with a statistically significant result indicating differential expression (abundances) between cases and controls. One of the noteworthy features of this approach is that it simultaneously estimates protein relative abundance and assesses differential expression, albeit with substantial computational cost due to the numerical complexity of optimizing the likelihood and estimating a rather large number of parameters. Herbrich et al.¹¹ demonstrated that estimating protein abundances using median sweeps reduces computational cost substantially, and is as efficient yet more robust than protein abundance estimation procedures based on linear mixed effects models.

An implicit assumption in the approach of Oberg et al.⁷ and Hill et al.⁸ is that the biological variability is the same for all proteins identified and quantified. Though “all models are wrong, but some are useful”¹², incorrect model assumptions can lead to a loss in power even if no bias is incurred. This was for example observed in gene expression studies when LIMMA (“Linear Models for Microarray Data”)¹³ was introduced as an empirical Bayes approach that specifically allowed for a realistic distribution of biological variances, compared to the models of Kerr and Churchill^9,10, which assumed constant variability. The statistical trick in LIMMA is to use the full data to shrink the observed sample variances towards a pooled estimate. This results in far more stable and powerful inference compared to ordinary t-tests particularly when the number of samples is small¹³, yet still allows for a distribution of variances. LIMMA arguably is the contemporary analytical standard for gene expression experiments, as evidenced by over 6,000 citations in the last ten years (http://scholar.google.com). LIMMA has also been sporadically used in the context of proteomic experiments^14–19, but is far from being regarded as the analytical standard. This is surprising since proteomic experiments often have somewhat small sample sizes, and for those the potential gains of an empirical Bayes procedure are highest. One possible explanation for this phenomenon (besides being originally developed for a different genomic application) might be that LIMMA has been implemented as a Bioconductor package in the language R, a statistical environment the proteomics community only recently started to embrace^20–26.

In this manuscript we use examples from isobaric mass labeled proteomics to demonstrate how better results in case-control studies can be achieved by using the LIMMA moderated test statistics. We show how to analyze data from multiple experiments simultaneously, and discuss the effects of missing data on the inference. We give sufficient detail for the statistically inclined reader to understand what happens “under the hood” of this empirical Bayes approach, and also present easy to use open source software for the practitioner to carry out the normalization of these mass spectrometry data, and to readily obtain the inference from moderated test statistics.

Materials and Methods

Sample Description

The data stem from two Trypanosoma brucei transgenic cell lines overexpressing either TbHslV-wild type or TbHslV-mutant protease. The T.brucei mitochondrion contains a proteasome-like ATP-dependent protease named TbHslVU that plays a critical role in regulating the timing of mitochondrial DNA replication²⁷. Previous experiments suggested that TbHslVU controls the timing of kDNA synthesis by degrading “positive regulator of replication”^27,28. To search for TbHslVU substrates its catalytically active subunit (denoted as TbHslV-wt) and its catalytically dead mutant (denoted as TbHslV-mt) were fused to the tandem a nity purification (TAP) tag. TAP-tagged TbHslV-wt or TbHslV-mt overexpressing cell lines were generated and the overexpressed proteins were purified using a TAP protocol adapted from Ringpis Ringpis et al.²⁹. TbHslV-wt and TbHslV-mt were performed in four independent biological replicates.

Quantitative mass spectrometry was used to identify proteins that are associated with overexpressed and purified TbHslV-mt but not with TbHslV-wt treated similarly; since the latter binds and degrades its substrates. Proteins were digested with trypsin, labeled using the eight-plex iTRAQ isobaric mass tags (ABSciex) and analyzed using tandem mass spectrometry on an LTQ Velos Orbitrap interfaced with an Eksigent 2D NanoLC as previously described^11,30,31, except mass tagged peptides were fractionated by basic reverse phase chromatography³². Peptides were identified using Proteome Discoverer v1.4 (Thermo Scientific, San Jose, CA) and Mascot v2.2 (Matrix Sciences). Software defaults were used to control the false discovery rate (FDR) and only peptides spectra with less than 1% FDR and less than 30% isolation interference were included in analysis.

Protein log₂ relative abundances were estimated using the method of Herbrich et al.¹¹ In this procedure, a logarithmic transformation of the reporter ion intensities is employed since systematic effects and variance components are usually assumed to be additive on this scale^7,8. The log₂ reporter ion intensities for each spectrum are “median-polished” by subtracting the spectrum median log₂ intensity from the observed log₂ intensities. The relative abundance estimate for a particular protein is calculated as the median of these residuals, from all reporter ion intensity spectra belonging to this protein. Corrections for differences in amounts of material loaded in the channels and sample processing are carried out by subtracting the channel median from the relative abundance estimate, normalizing all channels to have median zero.

Statistical Inference

Two group comparisons

To detect differentially expressed proteins in a balanced proteomic experiment with n cases (log₂ relative abundances X_1p, . . . , X_np for protein p) and n controls (log₂ relative abundances Y_1p, . . . , Y_np), inference is typically based on a 2-sample t-test for each protein p, with test statistic

$$t_p=\frac{\text{estimated log fold change}}{\text{estimated standard error}}=\frac{{\stackrel{‒}{X}}_p-{\stackrel{‒}{Y}}_p}{s_p\sqrt{2∕n}},$$ (1)

where X̄_p and Ȳ_p are the group mean log₂ relative abundances, and

$$s_p=\sqrt{\frac{{\sum }_i{(X_{ip}-{\stackrel{‒}{X}}_p)}^2+{\sum }_i{(Y_{ip}-{\stackrel{‒}{Y}}_p)}^2}{n-2}}$$ (2)

is the within-group sample standard deviation. For each protein, a p-value is then calculated referring the test statistic t_p to a t-distribution with d_p = 2 × n − 2 degrees of freedom as null distribution. For the above the log₂ relative abundances are assumed to be normally distributed with equal variance in each group, although t-tests are robust to departures from the normality assumption unless outliers are present and sample sizes are small³³. Similar test statistics can be calculated for non-equal group variances and unbalanced experiments.

Moderated statistics

The above approach estimates the variance $s_p^2$ and standard error $s_p\sqrt{2∕n}$ for each protein separately (equations 1 and 2), and does not use information (such as experimental precision) shared across all proteins. An alternative approach “Linear Models for Microarray Data” (LIMMA)¹³, also applicable for mass-spectrometry based high throughput experiments, uses the fact that under a normality assumption for the log₂ relative abundances the sample variance follows a scaled χ² distribution

$$s_p^2\mid {\sigma }_p^2\sim \frac{{\sigma }_p^2}{d_p}\times {\chi }_{d_p}^2,$$ (2)

where ${\sigma }_p^2$ is the true (unknown) variance, and d_p are the degrees of freedom associated with the experiment. In contrast to the ordinary 2-sample t-test where ${\sigma }_p^2$ is regarded as a fixed (but unknown) parameter, LIMMA is an Empirical Bayes procedure where the protein variances are assumed to follow a scaled inverse χ² distribution

$$\frac{1}{{\sigma }_p^2}\sim \frac{1}{d_0\times s_0^2}\times {\chi }_{d_0}^2.$$ (4)

The parameters d₀ and $s_0^2$ are estimated from the observed data via maximum likelihood. Using such as a scaled inverse χ² distribution for the protein variances implies that the set of protein sample variances s² follows a scaled F distribution¹³, e.g.

$$s^2\sim s_0^2\times F_{d_p,d_0}.$$ (5)

Under the above hierarchical model, the posterior for a protein's sample variance is moderated: the observed protein sample variance $s_p^2$ is shrunk towards the common prior value $s_0^2$, with the magnitude of shrinkage depending on the relative sizes of the observed and prior degrees of freedom d_p and d₀:

$$s_{p_{\left[\text{moderated}\right]}}^2=\frac{d_p\times s_p^2+d_0\times s_0^2}{d_p+d_0}=\lambda \times s_p^2+(1-\lambda )\times s_0^2\text{with}\lambda =\frac{d_p}{d_p+d_0}\in (9,1).$$ (6)

Thus, the shrinkage of the sample variance $s_p^2$ towards a common mean $s_0^2$ will be most pronounced when few data are available, as d_p and therefore λ will be small. The p-values are then derived referring the moderated t-statistic

$$t_{p\left[\text{moderated}\right]}=\frac{\text{estimated log fold change}}{\text{moderated standarad error}}=\frac{\stackrel{‒}{X}-\stackrel{‒}{Y}}{s_{p\left[\text{moderated}\right]}\sqrt{2∕n}}$$ (7)

to a t distribution with d_p + d₀ degrees of freedom. Note that only the estimates of the standard errors change, and the estimated log fold changes in the numerator remain the same.

Multiple experiments

To achieve a desired sample size it is often necessary to carry out multiple experiments. These data can be analyzed by expanding the two-sample t-test into a more general linear model framework. For example, the regression for two 8-plex iTRAQ experiments can be written as

$$\mathsf{E}\left[Z_{pijk}\right]={\alpha }_p+{\tau }_p\times 1_{\{i=1\}}+{\gamma }_p\times 1_{\{k=2\}}$$ (8)

where Z_pijk denotes the measured log₂ relative abundances of protein p in sample j ∈ {1, . . . , 4} under condition i ∈ {0, 1} in experiment k ∈ {1, 2}, i.e. 4 mutants and 4 wildtypes in each of two experiments (the 1 in equation 8 denotes the standard indicator function). For more than two experiments, the above equation can simply be expanded by allowing more parameters to indicate the extra experiments, or a mixed effects model can be used with a random effect for the experiment^7,8,11. The inference to assess differential expression is on the parameter τ_p, the expected difference in log₂ relative abundances of protein p when comparing a mutant and a wildtype from the same experiment. Statistical significance is based on the observed fold change, and an estimate of its standard error. The latter can be derived by estimating the variability separately for each protein. Alternatively, LIMMA also allows for pooling information across all proteins within the above linear model framework, generating moderated t-statistics and p-values¹³.

Multiple comparisons

Since hundreds or even thousands of proteins can be identified and quantified in a typical mass spectrometry experiment, multiple comparisons corrections are imperative. The most popular procedure is the Bonferroni correction which controls the family wise error rate (FWER), that is, the probability of at least one type I error (i.e. false positive). Only proteins with nominal p-value less than α/N are declared differentially expressed, where α is the desired FWER (typically, 5%), and N is the number of proteins assessed. The consequence of such a strong protection against any false positives is usually a large number of false negatives, that is truly differentially expressed proteins not declared significant. Thus, in high-throughput experiments with potentially many differentially expressed proteins, a more desirable parameter arguably is the false discovery rate (FDR), designed to control the proportion of false positives among a set of proteins declared differentially expressed. The original FDR approach by Benjamini and Hochberg³⁴ was extended by Storey^35–37 to so-called “q-values”, which have a similar interpretation for the FDR as p-values have for type-I error control: the q-value for a protein is defined as the minimum FDR that can be attained (i.e., the expected proportion of false positives incurred) when calling that protein differentially expressed. In other words: when testing for differential expression, if a protein has a q-value of 0.10, we expect 10% among the proteins that show smaller p-values to be false positives. The q-values are calculated from the observed p-values after estimating the proportion of differentially expressed proteins in the experiment (see Storey and Tibshirani³⁷ for details).

Simulations

To compare the performances of the ordinary 2-sample t-tests and the empirical Bayes moderated t-tests with regards to power and type I error (true and false positives), we simulated data mimicking the above described T.brucei 8-plex iTRAQ experiment with 4 mutants and 4 wildtypes. The log₂ relative abundances of mutants and wildtypes for 1,394 proteins were generated from a normal distribution with variances according to the scaled inverse χ² distribution (equation 4) with estimated parameters d₀ = 4.43 prior degrees of freedom and a scaling factor of $s_0^2=0.032$ (Supplementary Figure 1). The means of the normal distributions were chosen to reflect the desired fold changes in the respective simulations. A 50% fold change was used in all simulations when only a single experiment was considered, and both 25% and 50% fold changes were used in separate simulations when multiple experiments were analyzed.

Software

A software vignette to carry out the analyses described in this manuscript and to reproduce the simulations is available at www.biostat.jhsph.edu/~kkammers/software/eupa/. The software is freely available as Free Software under the terms of the Free Software Foundation's GNU General Public License in source code form.

Results

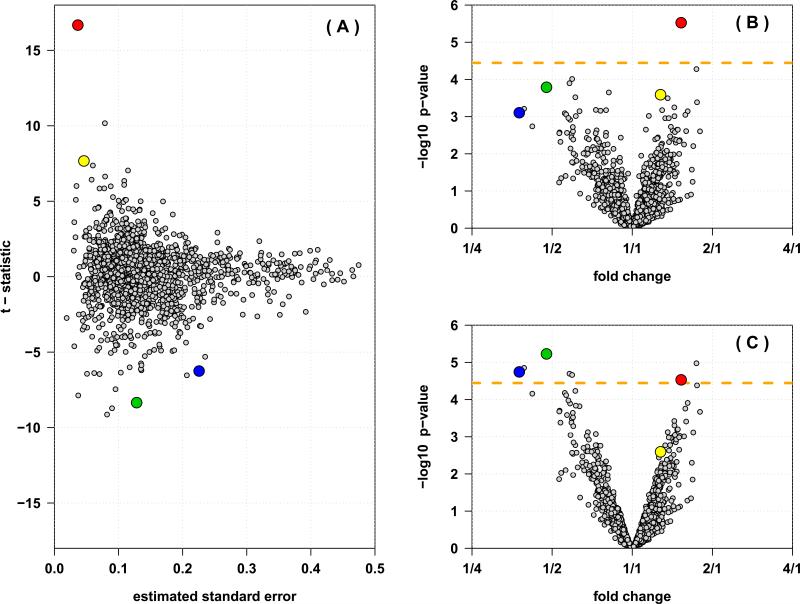
A total of 2,047 proteins were identified and quantified in the T.brucei 8-plex iTRAQ experiment. To reduce the impact of possible false positive identifications, we only retained the 1,394 proteins with 2 or more peptides quantified. With an ordinary 2-sample t-test to assess differential expression we find that most of the statistically significant differences were from proteins with little sample variability (Figure 1A). Among the 1,394 proteins, 258 (18.5%) achieved nominal significance at a 5% level, but only one protein was declared differentially expressed after multiple comparisons correction using the Bonferroni method (Figure 1B). Noteably, this protein had very small sample variability (8th smallest among the 1,394 proteins). While only few more proteins were nominally significant at a 5% level when using moderated t-statistics (277, 19.9%), seven proteins achieved statistical significance after Bonferroni correction (p < 3.6 × 10⁻⁵, Figure 1C). Moreover, at a FDR of 1% (i.e. q < 0.01) only 1 protein is declared differentially expressed when using ordinary test statistics, compared to 23 proteins declared differentially expressed when moderated test statistics are employed (FDR of 5%: 30 and 98 proteins, respectively; FDR of 10%: 120 and 184 proteins). Thus, at the same error level many more proteins can be declared differentially expressed when using the moderated compared to the ordinary t-statistics. This improvement is achieved by shrinking particularly the extreme variances towards a common mean (Supplementary Figure 2). As a consequence, compared to their ordinary test statistics, proteins with low sample variability have less significant moderated test statistics, proteins with large sample variability have more significant moderated test statistics, and test statistics from proteins with moderate sample variability remain largely unchanged (Supplementary Figure 3).

Figure 1.

Inference from an 8-plex iTRAQ experiment with four cases and four controls, with 1,394 proteins identified and quantified. (A) The estimated standard error (x-axis) versus the t-statistic (y-axis) for each protein. The largest t-statistics (and thus, most significant p-values) tend to be from those proteins that show the smallest sample variability. (B) The volcano plot showing the estimated fold changes (x-axis) versus the − log₁₀ p-values (y-axis) for each protein. (C) The volcano plot from the inference based on the moderated t-statistics. Four proteins are highlighted in each panel, illustrating how proteins with small sample variability can show very low p-values despite small fold changes (red and yellow), while proteins with larger fold changes do not necessarily show significant differential expression (green and blue). The Bonferroni corrected significance level is indicated by the orange line. Pooling information from the entire distribution of all proteins improves power to detect differentially expressed proteins, and reduces statistical significance of proteins with small sample variability.

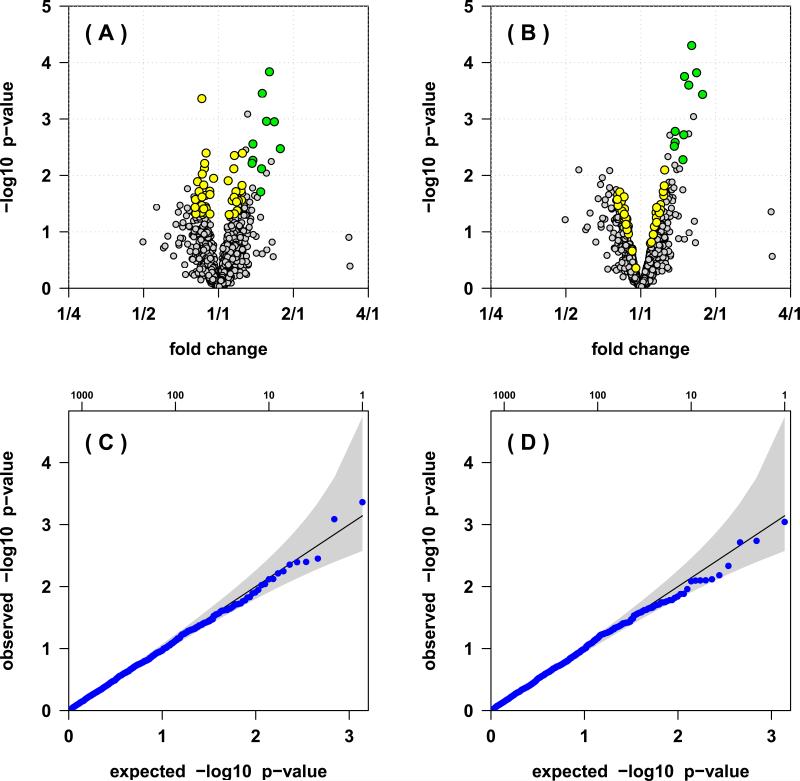
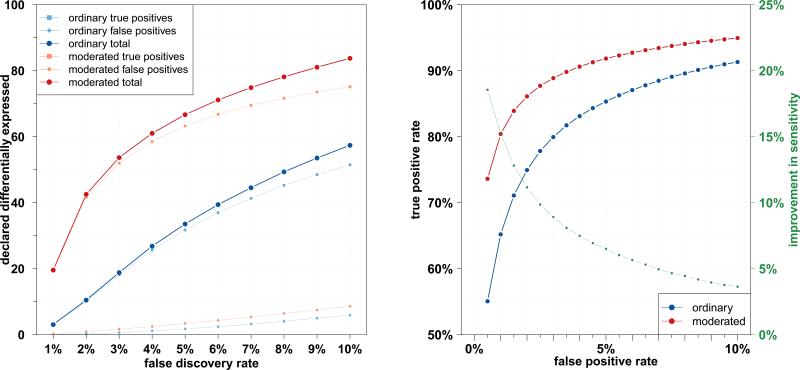
In a simulation study with ten differentially expressed proteins (50% fold change) we visualize how the differentially expressed proteins become more significant when moderated test statistics are used (Figure 2A and 2B, green dots), while spurious associations with small observed fold changes tend to become less significant (Figure 2A and 2B, yellow dots). This improvement in detecting differentially expressed proteins through moderated test statistics is not owed to an overall increase in false positives, as both the ordinary 2-sample t-test and the moderated t-test properly control the type I error (Figure 2C and 2D). To quantify the potential gains in true discovery while maintaining error control via the FDR, we increased the number of differentially expressed proteins to 100 and averaged the results over 1,000 iterations. For all levels of FDR control between 1% and 10%, the empircal Bayes approach using moderated test statistic produces substantially larger lists of proteins declared differentially expressed, detecting more truly differentially expressed proteins while maintaining proper error control (Figure 3, left). Displaying the results on a receiver operating characteristic (ROC) curve, we find that at equal false positive rates the true positive rate is substantially higher when using moderated test statistics (Figure 3, right).

Figure 2.

Inference for a simulated 8-plex iTRAQ experiment with four cases and four controls, and 1,394 proteins. (A) The volcano plot showing the estimated fold changes (x-axis) versus the log₁₀ p-values (y-axis) for each protein. (B) The volcano plot from the inference based on the moderated – t-statistics. The ten proteins simulated with a 50% fold change are highlighted in green. Pooling information from the entire distribution of all proteins improves power to detect these differentially expressed proteins. In addition, non-differentially expressed proteins with nominally significant p-values (less than 0.05) and small estimated fold changes (less than 25%) are highlighted in yellow, which highlights how pooling information from the entire distribution of all proteins reduces the false positive identification rate. The quantile-qunatile (QQ) plots for the p-values of the non-differentially expressed proteins based on the ordinary 2-sample t-test (C) and the moderated t-test (D) show that both approaches properly control the type I error.

Figure 3.

Results from the simulation study. Left: for all levels of false discovery rate control targeted (1% – 10%, x-axis), the empircal Bayes approach using moderated test statistic produces larger lists of proteins declared differentially expressed (y-axis), thus detecting more truly differentially expressed proteins while maintaining proper error control. Right: the same results presented in a ROC curve. For all false positive rates (0.5% – 10%, x-axis), the true positive rate (y-axis, black) is substantially higher when using moderated test statistics, yielding a large difference in sensitivity (y-axis, green).

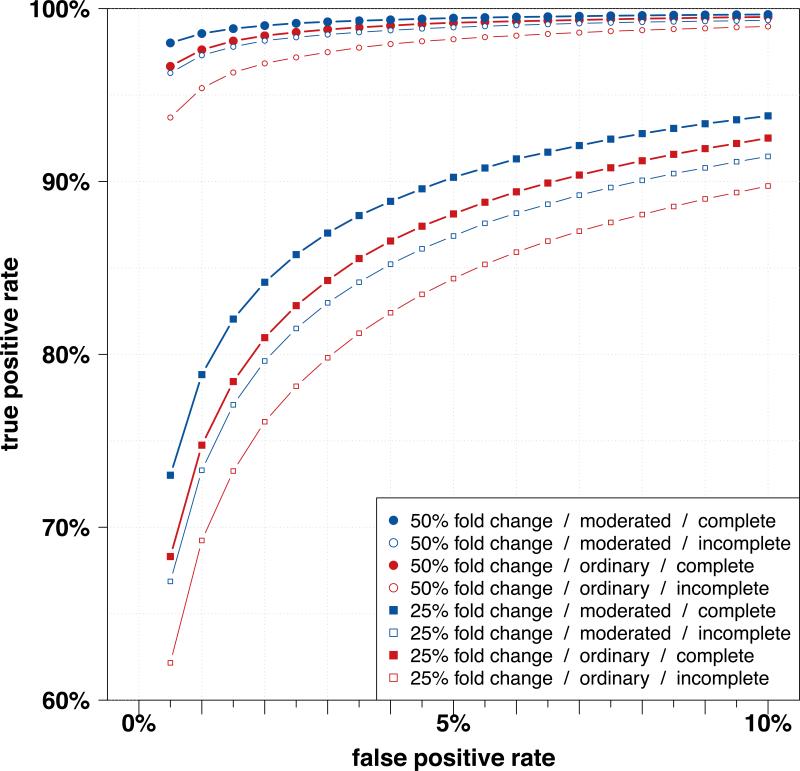
Equivalent results were obtained when multiple experiments were analyzed simultaneously. We simulated three replicate 8-plex iTRAQ experiments with 100 differentially expressed proteins using the same parameters for the variability as above, and analyzed the data using the linear model displayed in equation (8). We used both ordinary test statistics (analyzing each protein separately) and the moderated test statistics using LIMMA. We recorded false positives and false negatives for a variety of significance thresholds, and averaged the results over 1,000 iterations. Since the power to detect differentially expressed proteins increases with the number of experiments, we also show the findings for lower fold changes. For all false positive rates between 0.5% and 10% considered and fold changes of 25% and 50%, the true positive rate (sensitivity) was again higher when using the the empircal Bayes approach with moderated test statistics (Figure 4). In addition, we simulated experiments with three replicates and randomly selected 10% of proteins as missing in each experiment. While the presence of missing data generally results in a loss of power to detect differentially expressed proteins, these data can still be analyzed using linear models with moderated test statistics and proper type I error control. The findings for this setting were the same, supporting the variance shrinking approach as more powerful (Figure 4). In particular, in the presence of missing data, the amount of shrinkage of the variance depends on the actual observed experimental degrees of freedom (Supplementary Figure 4).

Figure 4.

Results from the simultaneous analysis of three simulated iTRAQ experiments using the linear model in equation (8). For all false positive rates (0.5% – 10%, x-axis) considered, the true positive rate (y-axis) is substantially higher when using the moderated test statistics (blue) instead of the ordinary test statistics (red). Compared were fold changes of 50% (circles) and 25% (squares), with complete data (solid symbol) or 10% missing in each experiment (open symbol).

Discussion

Identifying differentially expressed proteins is a task in proteomic studies commonly carried out simply using t-tests. In this manuscript we demonstrated how better results can be achieved by using moderated t-statistics from the empirical Bayes procedure LIMMA¹³. This approach shrinks the sample variances used in the estimation of the standard error of the observed fold changes towards a common mean. Thus, proteins with low sample variability have less significant moderated than ordinary t-statistics, and proteins with large sample variability have more significant moderated than ordinary t-statistics. Consequently, statistical significance increases for proteins with large fold change and relatively large sample variances (affecting the false negative rate) and statistical significance decreases for proteins with small fold change and relatively small sample variances (affecting the false positive rate). The observation that proteins with larger fold changes tend to become more significant (Supplementary Figure 5) can be even more pronounced when proteins with larger fold changes also tend to have higher variability even after the logarithmic transformation of the relative abundances, i.e. when there is a mean-variance relationship (Supplementary Figure 6). In the manuscript we have presented methods and results using isobaric mass labeled proteomic experiments, but note that these empirical Bayes methods are directly applicable in other settings as well. In fact, they can be used for any technology that yields measures of peptide or protein abundance, including label-free experiments.

We also showed how to jointly analyze data from multiple experiments, a necessity for example in iTRAQ experiments which limit the number of labels and thus the number samples that can be run simultaneously. Accounting for possible between experiment variability is important to maximize the power to detect differentially expressed proteins, and LIMMA provides a convenient and powerful framework to do so simply by specifying the design matrix (which also allows for experiments with multiple groups, beyond case-control studies¹³). An alternative approach to analyze data from multiple experiments, commonly used for example in meta analyses of genomic data from different studies, is based on inverse variance weighting (IVW): the observed effect sizes (fold changes) from different experiments are weighted by their respective inverse variances, and combined into a single test statistic. When sample sizes are such that the individual test statistics approximately follow a normal distribution, the IVW based test statistic also follows a normal distribution, and a p-value can readily be calculated. In proteomic experiments with data from few samples such as 8-plex iTRAQ, the test statistics follow t-distributions with only very few degrees of freedom, and thus are far from normality. In these settings the p-values have to be based on permutation tests (such as the one proposed in Storey and Tibshirani³⁷) as the null distribution is unknown. In addition to the computational expense incurred, the procedure is also not very powerful in this setting as the weights themselves are subject to large variability due to the small sample size. We found that by first using empirical Bayes methods to moderate the variances in each experiment, and thus stabilizing the weights in the IVW procedure, the power to detect differentially expressed proteins can be greatly improved, although not up to the same level as the LIMMA model for the simultaneous analysis of multiple experiments (data not shown). This was even true for simulations where the prior scaling factor $s_0^2$ was doubled in one experiment compared to the other two. Additional complications using IVW can occur in the presence of missing data, and when sample sizes are extremely small, as the actual number of possible permutations will be very low as well. Thus, LIMMA provides a more convenient and powerful framework to analyze such data than IVW.

The existence of missing data is largely owed to the nature of the methods used in proteomic studies, as peptide and protein identification between experiments can vary, sometimes substantially^38–41. Although missing values for peptides and proteins due to biological differences are of scientific interests, these missing values can also be a nuisance arising from technical issues. Low or missing peptide intensities observed by the mass spectrometer can occur due to low peptide abundance, low peptide-dependent ionization efficiency, or the peptide signal distributed across multiple peptide charge states or different modified forms of the peptide. Peptide interactions with columns or other peptides in complex peptide mixtures or small differences instrument ion sampling contribute to inconsistent peptide detection and missing values when comparing repeat MS analyses of the same sample. In multiplex analyses, such as isobaric mass tagging, missing values can also occur from signal dilution due to a low abundance peptide being present in one sample but a much lower abundance or absence in the other samples.

In this manuscript we also explained the effects of such missing data on the statistical inference with LIMMA, which performs a complete case analysis contrasting the cases to the controls within experiment. The amount of variance shrinkage depends on the actual observed experimental degrees of freedom - the more data (samples) are observed for a protein, the less the shrinkage towards the common mean variance. Missing data generally results in a loss of power to detect differentially expressed proteins, and depending on the nature of the missingness, can also introduce bias and affect the type I error^42,43. In proteomic studies the missingness rate is commonly related to abundance^38,39. However, in data from multiple isobaric mass labeled proteomic experiments such as 8-plex iTRAQ we observe that the reporter ion intensity is usually observed in all channels within an experiment, or in none. That is, when a peptide is identified and quantified, the data are usually complete for all samples within an experiment¹¹. Thus, the rate of missingness is much stronger related to the sampling method used by the instrument (i.e., experiment ID) than absolute abundance, let alone relative abundance (fold change). For other types of experiments such as label-free quantification it might be necessary however to address the missing data explicitly for example using imputation methods^44–46 before employing empirical Bayes methods, since the missingness pattern might be strongly related to protein abundance. This would violate the notion of “missingness completely at random”, an implicit assumption in complete case analyses^42,43.

Highlights.

• We review empirical Bayes methods for genomics and proteomics.

• We show these methods have more power to detect changes in protein abundance.

• We show examples from isobaric mass labeled proteomic experiments.

• We present easy to use open source software for normalization and analysis.