Single molecule study of heterotypic interactions between mucins possessing the Tn cancer antigen

Abstract

Mucins are linear, heavily O-glycosylated proteins with physiological roles that include cell signaling, cell adhesion, inflammation, immune response and tumorgenesis. Cancer-associated mucins often differ from normal mucins by presenting truncated carbohydrate chains. Characterization of the binding properties of mucins with truncated carbohydrate side chains could thus prove relevant for understanding their role in cancer mechanisms such as metastasis and recognition by the immune system. In this work, heterotypic interactions of model mucins that possess the Tn (GalNAcαThr/Ser) and T (Galβ1–3GalNAcαThr/Ser) cancer antigens derived from porcine submaxillary mucin (PSM) were studied using atomic force microscopy. PSM possessing only the Tn antigen (Tn-PSM) was found to bind to PSM analogs possessing a combination of T, Tn and STn antigens as well as biosynthetic analogs of the core 1 blood group A tetrasaccharide (GalNAcα1–3[Fucα1–2] Galβ1–3GalNAcαSer/Thr). The rupture forces for the heterotypic interactions ranged from 18– to 31 pN at a force-loading rate of ∼0.5 nN/s. The thermally averaged distance from the bound complex to the transition state (x_β) was estimated to be in the range 0.37–0.87 nm for the first barrier of the Bell Evans analysis and within 0.34–0.64 nm based on a lifetime analysis. These findings reveal that the binding strength and energy landscape for heterotypic interactions of Tn-PSM with the above mucins, resemble homotypic interactions of Tn-PSM. This suggests common carbohydrate epitope interactions for the Tn cancer antigen with the above mucin analogs, a finding that may be important to the role of the Tn antigen in cancer cells.

Introduction

Mucins are large, heavily O-glycosylated proteins (Hollingsworth and Swanson 2004). Secreted mucins are essential in providing the structural framework of the mucous barrier and in protecting the cell surface against external hazards (Thornton et al. 2008). Membrane bound mucins play important roles in cell signaling, cell adhesion, inflammation, immune response and tumorgenesis (Hollingsworth and Swanson 2004). Mucin functionality is controlled, in part, through its O-glycosylation, which is one of the most prevalent posttranslational modifications of proteins. Despite the vast knowledge of glycosylation mechanisms and the functions of glycosylated proteins in general, the biological roles of mucin glycosylation are still poorly understood (Barchi 2013).

The O-glycans on mucins are predominately found in tandem repeated peptide domains rich in serine, threonine and proline, with over 50% of the Ser or Thr residues containing O-linked glycans (Hollingsworth and Swanson 2004). These heavily O-glycosylated peptide domains have an extended unfolded conformation (Brockhausen 2006). Mucin type O-glycosylation begins with the addition of α-GalNAc transferred to Ser and Thr residues by a family of polypeptide GalNAc transferases (Burchell et al. 2001; Bennett et al. 2012), which are further extended into longer diverse glycan structures through the action of additional glycosyltransferases residing in the Golgi complex (Barchi 2013).

The carbohydrate structures of mucins associated with cancer cells are often abnormal (Burchell et al. 2001; Brockhausen 2006). In particular, truncated glycans are often present, which can be highly sialylated and less sulphated (Brockhausen 2006; Freire and Osinaga 2012; Radhakrishnan et al. 2014). Truncated cancer mucin glycans include the Tn (GalNAcαThr/Ser) and T (Galβ1–3GalNAcαThr/Ser) antigens as well as sialylated versions of these (Brockhausen 2006). The unusual expression of the Tn antigen was among the first to be associated with the human Tn syndrome (Ju et al. 2011) first described in 1957 by Moreau et al. (1957). The Tn epitope is a cancer-specific target for immunotherapy and is also recognized as a candidate for the development of diagnostic monoclonal antibodies for use in human cancer vaccine studies (Beatson et al. 2010; Heimburg-Molinaro et al. 2011). Interest in the Tn epitope is partly due to the fact that it is recognized by immune cells and elicits antitumor antibodies (Wandall et al. 2010; Lakshminarayanan et al. 2012; Madsen et al. 2013). On the other hand, further glycosylation beyond the GalNAc group of the Tn-epitope has been shown to protect cancer cells from NK cell-mediated antibody-dependent cellular toxicity (Lakshminarayanan et al. 2012) and to mediate protection from immune-mediated killing of cancer cells (Suzuki et al. 2012). Since most cancer cells show increased expression of the short glycan epitopes, a growth or survival advantage associated with the expression of these glycans is believed to exist. The observation that expression of sialylated Tn (sialyl-Tn, STn) increases proliferation and metastatic potential of cancer cells (Brockhausen 2006; Chiricolo et al. 2006; Julien et al. 2006) led to the hypothesis that mucin upregulation in adenocarcinomas protects cells from immune-mediated killing while the STn glycophenotype promotes proliferation and metastasis (Madsen et al. 2013). The mechanisms underlying such facilitated proliferation and metastasis induced by the Tn and STn epitopes are still unknown, and specific interactions between these glycan epitopes and molecular-binding partners such as other proteins or carbohydrate receptors may play key roles.

Hakomori introduced the term “glycosynapse” to describe a cell surface microdomain responsible for carbohydrate-dependent cell adhesion coupled with signaling (Hakomori 2002). This concept is analogous to the “immunological synapse” that controls adhesion and signaling between immunocytes (Bromley et al. 2001). Over the last decade, the body of experimental data revealing the role of carbohydrate–carbohydrate interactions (CCIs) in cellular systems has increased (Bucior and Burger 2004; Handa and Hakomori 2012). Despite the growing number of studies documenting the capability of carbohydrate-medicated cell aggregation, the adhesion mechanisms remain poorly understood. This may be due to the experimental challenges created by the low strength of the individual CCIs, combined with the inherent structural variation in the carbohydrate decorations on biological surfaces. Furthermore, carbohydrate-mediated interactions rely on multivalency in order to form intra- and intermolecular bond strengths assuring stable attachments. Even though such a strategy has the beneficial consequence of enabling rapid modulation of attachment strengths through regulations of the number of the low-affinity interactions, it further adds to the experimental challenges when aiming at determining bond strengths (Lundquist and Toone 2002).

Force probes such as atomic force microscopy (AFM) allow quantification of binding strength with pico Newton sensitivity and are well suited to address questions related to CCI. Examples of successful applications of force probes to CCI studies include incorporation of lipids modified with the Lewis^X (Le^X) trisaccharide (Galβ1–4[Fucα1–3]GlcNAc-) into giant vesicles followed by quantification of the adhesion energy using micropipette aspiration (Gourier et al. 2004), and quantification of adhesion forces between Le^x determinants by AFM (Tromas et al. 2001). In addition, homotypic interactions between mucins with different well-defined carbohydrate decorations including the Tn-antigen have been quantified using AFM (Haugstad et al. 2012). Although homotypic interactions of mucins possessing the Tn-antigen may be important for understanding their role in cancer cells, knowledge about the interactions of mucins possessing the Tn-antigen with other mucins or glycoproteins with different carbohydrate structures may also provide similar insights. In the present study, heterotypic interactions between Tn-PSM and other PSM analogs possessing different glycan structures (Table I) are investigated by AFM.

Table I.

Schematic illustration of mucins studied and the fraction of different carbohydrate structures

Sample	Relative amount of different carbohydrate side chains
	Mono	Di	Tri	Tetra	NeuNGla
	100	0	0	0	0
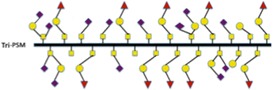	28	26	46	0	54
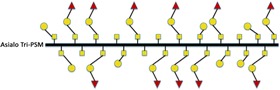	24	28	48	0	0
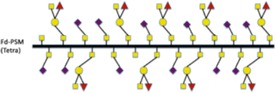	58	0	2	40	45

^aThe amount of NeuNGl is the total fraction of NeuNGl on the mono, di, tri and tetra saccharide side chains.

Results

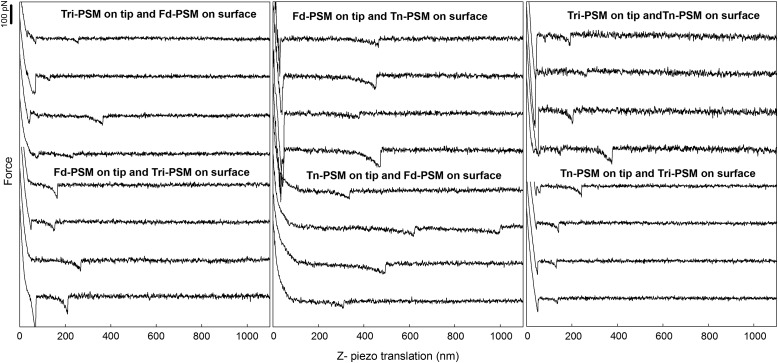
The study of mucin heterotypic interactions was conducted employing AFM-based force spectroscopy (Figure 1). The mucins in Table I possess glycan side chains ranging from the 100% monosaccharide Tn structure (Tn-PSM) to an unmodified mucin containing a range of structures including the Tn an STn antigens, and core 1 blood group A tetrasaccharide (Fd-PSM) (structures in Table I are based, in part, on the biosynthetic summary by Cummings and coworkers; Ju et al. 2014). In addition, the sialic acid residue (NeuNGl) was removed in some mucins to examine its effects on binding. The observed force jumps in the force distance curves (Figure 2) were interpreted as the rupture of intermolecular bonds formed between the mucin molecules immobilized on the tip and on the sample surface. The force jumps occurred at tip-surface separations up to ∼1800 nm. This is in line with previous observations of mucin homotypic interactions (Haugstad et al. 2012). Rupture forces in the range 5–50 pN were identified (Figures 2 and 3) for force-loading rates up to 1 nN/s. Unbinding forces up to several hundred pN were observed at higher loading rates.

Fig. 1.

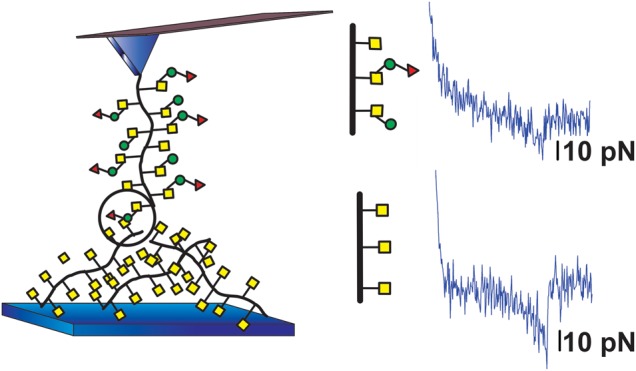
Schematic illustration of measurement setup for mucin interaction studies. Mucin interactions are studied using AFM-based force spectroscopy employing AFM tips and sample surfaces onto which mucins are covalently linked. When studying heterotypic mucin interactions the mucins immobilized on the AFM tip and the sample surface have differing glycan compositions.

Fig. 2.

Selected examples of force retraction curves obtained in experiments using mucin functionalized AFM tips and mica surfaces from Table II. The glycan decoration of the mucin molecules immobilized on the tip and on the surface are specified in each panel as the sample names. In each gallery of force curves displayed, the four lower force curves are obtained using the inverted immobilization configuration relative to the four upper curves. The experiments were performed at room temperature using liquid cells filled with aqueous 100mM HEPES buffer, pH 7.2, containing 1mM CaCl₂ and MnCl₂.

Fig. 3.

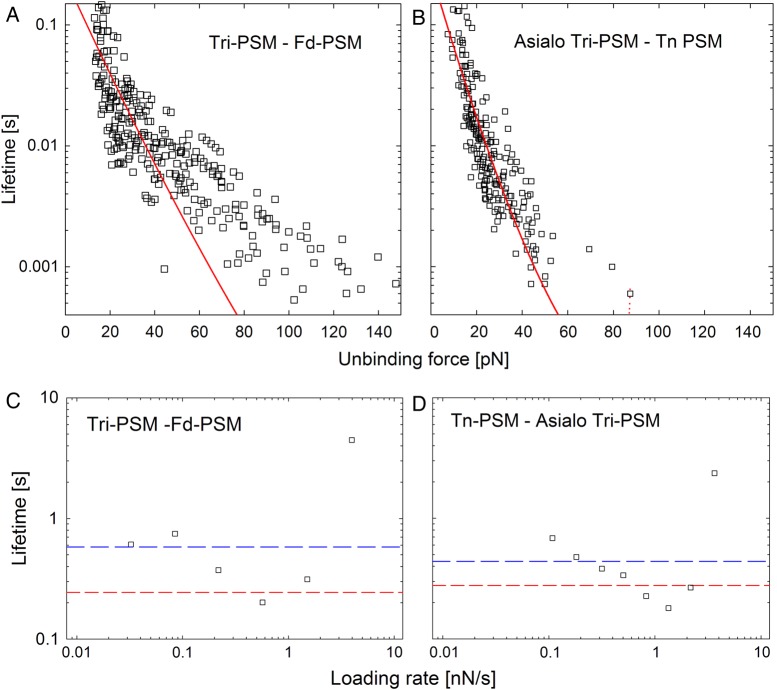
Unbinding force as a function of loading rate (squares) visualized for selected sample series. The data in the different loading rate intervals are displayed in different colors and the most likely rupture force determined for each of them is indicated (blue circles). (A) Tn-PSM_Tip and Tri-PSM_Mica, (B) Tri-PSM_Tip and Tn-PSM_Mica, (C) combined dataset including observations obtained using both immobilization configurations obtained for Tri-PSM interacting with Tn-PSM, (D) Tn-PSM_Tip and Asialo Tri-PSM_Mica, (E) Asialo Tri-PSM_Tip and Tn-PSM_Mica and (F) combined dataset including observations obtained using both immobilization configurations obtained for Asialo Tri-PSM interacting with Tn-PSM.

The fraction of force curves containing unbinding data

For three of the five mucin pairs, it was observed that the fraction of AFM force–distance curves containing signatures of intermolecular interaction (i.e., between molecules immobilized to the AFM tip and the sample surface, respectively (P_int)), depend on the immobilization configuration (Table II). Due to the potential influence of the relative positioning of the molecules, that is, on the AFM tip or the sample surface, each pair of mucin samples was investigated in two separate experimental series.

Table II.

Fraction of force curves containing force rupture events for the different mucin combinations

Tipa	Sample surfaceb	Pintc (%)	Totald	Pcontrole (%)	Totald
Tri- PSM	Tn- PSM	34.8	4714	0.8	2253
Tn-PSM	Tri-PSM	9.4	5409	0.7	1065
Tn-PSM	Fd-PSM	33	2240	0.3	1045
Fd-PSM	Tn-PSM	5.5	2416	–	–
Tri-PSM	Fd-PSM	24.9	2168	0	1200
Fd-PSM	Tri-PSM	4.7	2740	–	–
Asialo Tri-PSM	Tn-PSM	7.4	2312	0.4	2384
Tn-PSM	Asialo Tri-PSM	6.5	2400	0.7	1065
Tri-PSM	Asialo Tri-PSM	3.7	2400	0.8	2253
Asialo-Tri-PSM	Tri-PSM	2.8	2400	0.4	2384

^aMucin sample covalently linked to the AFM tip through amino groups on the mucins.

^bMucin sample covalently linked to the mica surfaces through amino groups on the mucin.

^cFraction of force curves containing force rupture events observed when using the AFM tip and sample surface described in Columns 1 and 2.

^dTotal number of force curves obtained for each measurement series.

^eFraction of force curves containing rupture events observed when the mucin functionalized AFM tip was probed against silanized mica.

For Tri-PSM_Tip interacting with Fd-PSM_Mica, P_int was 24.9%, and decreased to 4.7% for the inverted immobilization configuration. The highest P_int was obtained for the Tri-PSM_Tip and Tn-PSM_Mica (P_int = 34.8%), while the smallest P_int was obtained for Asialo Tri-PSM_Tip interacting with Tri-PSM_Mica (P_int = 2.8%).

Control measurements probing the interactions of the mucin_Tip against silanized surfaces were performed to assess the specificity of the observed interaction and to ensure that the molecules were attached to the AFM tip and sample surfaces. The fraction of curves containing rupture events, P_int, remained <1% for all samples investigated within this control (Table II). The finding that these fractions are significantly smaller than for the experimental series within the mucin–mucin interactions, also demonstrate the success of the immobilization protocol.

Energy landscape of the interactions

The interaction forces and loading rates were determined separately for each unbinding event observed in the force curves. The measured forces showed an overall tendency to increase with increasing loading rate. This is also reflected in the values determined for the most likely rupture force (f*) (Figure 3). The parameters extracted for the energy landscape of the interactions (Tables III and IV) based on the distribution of the observed forces did not depend on the immobilization configuration (Figures 3 and 4). Separate determination of the parameters in the energy landscapes performed based on data obtained for each of the two immobilization configurations showed similar ranges of f* at corresponding loading rates (Figures 3 and 4). For example, for the Tri-PSM_Tip−Tn-PSM_Mica interaction, f* was determined to be 32 pN at a force-loading rate close to 1.5 pN/s and 33 pN for the inverted immobilization configuration. At a force-loading rate close to 0.45 nN/s f* was 25 pN for the Tri-PSM_Tip−Tn-PSM_Mica interaction and 28 pN for the inverted immobilization configuration. Combined datasets containing data obtained for both immobilization configurations were additionally analyzed to evaluate the robustness of the parameters obtained (Figure 3C and F). At a force-loading rate close to 0.5 nN/s, f* was in the range 18–31 pN for all sample series.

Table III.

Estimated parameters for the energy landscape obtained by curve fitting using the Bell–Evans formalism

Immobilization configuration		rf (nN/s)	f* (pN)	xβ# (nm)	τ# (s)	τ (s)
Tri-PSM	Tn-PSM	0.08	21			5.04
		0.19	23			3.84
		0.40	25	0.87	3.75	2.39
		0.89	28			2.12
		2.06	37			5.92
		4.76	89	0.17		0.20
		10.61	110			0.21
Tn-PSM	Fd-PSM	0.43	31			6.94
		0.72	30			3.61
		1.24	32	0.84	5.55	3.10
		2.06	34			2.74
		3.69	36			2.42
Tri-PSM	Fd-PSM	0.08	16			0.75
		0.22	18	0.54	0.58	0.37
		0.57	20			0.20
		3.97	58			4.47
Tn-PSM	Asialo Tri-PSM	0.11	16			0.69
		0.18	17			0.48
		0.32	19			0.38
		0.50	21	0.64	0.44	0.34
		0.83	22			0.23
		1.34	23			0.18
		2.17	29			0.27
		3.63	46			2.37
Tri-PSM	Asialo Tri-PSM	0.23	14			0.17
		0.45	18			0.13
		0.96	22	0.37	0.14	0.08
		1.83	33			0.12
		3.55	46			0.22

Fig. 4.

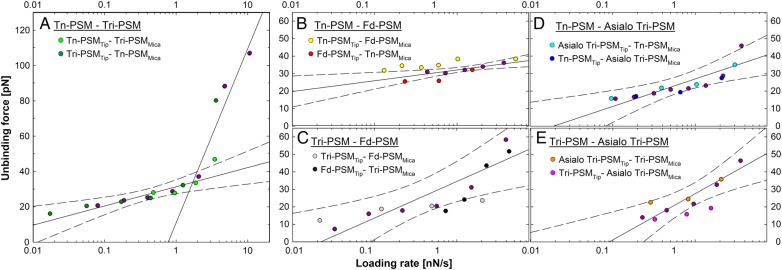
Dynamic force spectra obtained for different mucin pairs. The data obtained for the two immobilization configurations are displayed separately as well as combined (C and F). Linear regression lines (solid lines) for determination of x_β^# and τ^# were included together with the 95% confidence interval (dashed lines) for the combined data of the two immobilization configurations for each sample series (purple circles). The figure shows how f* increases with increasing loading rate. The f* values obtained from the two immobilization configurations were for most sample series in the range of the 95% confidence interval of the linear regression of the combined data. (A) Tn-PSM interacting with Tri-PSM, (B) Tn-PSM interacting with Fd-PSM, (C) Tri-PSM interacting with Fd-PSM, (D) Tn-PSM interacting with Asialo Tri-PSM and (E) Tri-PSM interacting with Asialo Tri-PSM.

The dynamic force spectra show the most likely unbinding force plotted against loading rate (Figure 4). The linear part of f* versus ln(r_f), where r_f is the force-loading rate, indicates a forced dissociation governed by one limiting barrier (Eq. (5)). For Tn-PSM interacting with Tri-PSM a rapid increase in rupture forces was observed at loading rates >2 nN/s. Two regression lines could be fit to the dynamic force spectra (Figure 4A), indicating that the energy landscape of this interaction contains two energy barriers. In the further analysis, f* and the lifetime of the interactions (τ) (Table III) were obtained from a fit constrained by the distance to the activation barrier (x_β^#). An example of intermediate results and a consistency check in the parameter estimation procedure are illustrated in the Supplementary data. In most cases, the variation of f* by the described consistency check was <10%. The values of x_β^# and τ^# (Table III) were obtained from a linear regression of f* versus ln(r_f) (Eq. (5)). The obtained parameter values of τ^# were found to be in accord with the prior determined values of τ. For the mucin interactions, the distance from the energy minimum to the first energy barrier in the energy landscape, x_β^#, ranged from 0.37 to 0.87 nm.

Lifetime analysis

The lifetime of the interactions (τ(f)) decreased with increasing unbinding force (Figure 5A and B). The distance to the activation barrier (x_β), the lifetime of interaction (τ) and Gibbs free energy (ΔG^#) was determined for the heterotypic interactions based on the observed force dependence of the lifetimes (Eq. (2)) obtained using both immobilization configurations. The analysis was performed both with the assumption the scaling factor of Eq. (2) was ν = 2/3, which represents a potential with linear and cubic terms (Figure 5A and B) and with ν = 1 which represents the Bell–Evans formalism. The values for the parameters determined by this method (Table IV) were in accordance with the estimated values based on the Bell–Evans formalism (Table III). More precisely, the determined x_β values were in the range 0.21–0.74 nm, whereas τ was in the range 0.04–2.34 s. The lifetimes estimated when assuming ν = 1 were in four of five cases slightly lower than the lifetimes estimated when assuming ν = 2/3. Parameter τ₀ determined from the force-dependent lifetime (Figure 5C and D and Table IV) was for all sample series lower than the τ^# determined from the linear regression of the dynamic force spectra (Table III). However, for each sample series, both values are within the range of τ values determined for the different loading rate intervals (Table III), and the relative value of the parameter values when comparing different sample series also follow the same trend (the lifetime of the complex Tri-PSM/Tn-PSM is the longest, Tri-PSM/Fd-PSM is intermediate, whereas the complexes Tri-PSM/Asialo Tri-PSM and Tn-PSM/Fd-PSM shows the shortest lifetime). The parameter ΔG^# was for the investigated interactions determined to be in the range 5.8–13.4k_BT (Table IV). As for the parameters extracted based on analyses of the lifetime values, the ΔG^# was found to be lowest for the complexes Tri-PSM/Asialo Tri-PSM and Tn-PSM/Fd-PSM with values of 5.8 and 6.4k_BT, respectively.

Fig. 5.

Top panels: lifetime τ(f) as a function of unbinding force. The red line is the fit of Eq. (2) to the experimental data. Bottom panels: lifetime τ(f) determined using the Bell–Evans formalism as a function of loading rate (squares), obtained from the linear regression of the dynamic force spectra (blue line) and the lifetime analysis (red line) for (A and C) Tri-PSM interacting with Fd-PSM and (B and D) Tn-PSM interacting with Asialo Tri-PSM.

Table IV.

Estimated parameters of heterotypic mucin interactions based on the force dependence of lifetime for each sample series

Sample series/parameter	ν = 1		ν = 2/3
	xβ (nm)	τ (s)	xβ (nm)	τ (s)	ΔG# (kBT)
Tri-PSM and Tn-PSM	0.74	2.34	0.64	1.28	9.0
Tn-PSM and Fd-PSM	0.21	0.05	0.34	0.18	6.4
Tri-PSM and Fd-PSM	0.39	0.13	0.39	0.24	13.4
Tn-PSM and Asialo Tri-PSM	0.45	0.12	0.62	0.28	8.9
Tri-PSM and Asialo Tri-PSM	0.31	0.04	0.44	0.09	5.8

Estimated with ν = 1 and 2/3.

Discussion

Characteristics of mucin heterotypic interactions

Data in the present study were obtained employing covalent anchoring of the mucin molecules. Due to the much higher strength of covalent bonds when compared with physical bonds (i.e., hydrogen and ionic bonds), with the former being in the order of 1.4–2.0 nN (Grandbois et al. 1999), anchoring through covalent bonds permits repeated determination of non-covalent intermolecular interactions occurring between the immobilized molecules. Anchoring of macromolecules by divalent ionic bridges commonly used for AFM imaging, as employed, for example, for DNA and mucins (Hansma and Laney 1996; Rivetti et al. 1996; Round et al. 2002), may not be equally applicable for force spectroscopy.

For all mucin interactions in the present study the most likely rupture force, f*, was independent of the immobilization configurations (Figures 3 and 4), and the values obtained were, irrespective of the immobilization configurations, within or close to the 95% confidence interval for the linear regression of the combined dataset. This consistency adds credibility to the determined parameters. The values of f* determined for the heterotypic mucin interaction are comparable with the CCI forces reported by other research groups. The self-interaction forces between the cancer-associated glycan Le^X, quantified using AFM, was found to be equal 20 ± 4 pN (loading rate not stated) (Tromas et al. 2001). This interaction force is in the same range as the homotypic (Haugstad et al. 2012) and heterotypic (present study) interaction forces determined for the PSM samples using AFM. Interaction forces between disaccharides anchored to membrane coated surfaces have been probed by colloidal force microscopy (Lorenz et al. 2012). The reported rupture forces were in the range 25–50 pN, which is in the same force range as the f* values determined in the current study. The analogous unbinding forces observed for disaccharides immobilized on colloidal particles and mucins immobilized on surfaces points towards the interpretation that the rupture events observed for both systems are dominated by CCI (Lorenz et al. 2012). The similarity of the force spectra obtained for the self-interactions of GalNAc decorated polyacrylamide or GalNAc-PEG with Tn-PSM determined by optical tweezers (Sletmoen et al. unpublished) also combined with the indication that such carbohydrate-mediated interactions are weaker than amino acid-mediated interactions in most cases (Bizzarri and Cannistraro 2010) indicate the importance of the oligosaccharides in the observed mucin interactions. A direct investigation of self-interactions with deglycosylated apo-mucins was not performed as they would be difficult to conduct and interpret due to apo-mucin's significantly reduced polymer stiffness and reduced chain dimensions (Shogren et al. 1989).

Parameter values of x_β from 0.21 to 0.74 nm were obtained for the different mucin interactions based on the analysis of the lifetime using for υ = 1 (Table IV). These values are within the range reported for other biomolecular interactions where carbohydrates are involved, including GAG self-interactions of cartilage aggrecan (Harder et al. 2010) and monoclonal antibody against linear tetramannonse (Martines et al. 2012). They are smaller than the x_β values determined for the interaction between mucin and antibodies, being equal to 2.0–2.8 nm (Sulchek et al. 2005). A comparison of this distance with the expected range of different non-covalent bonds indicates that more than one atomic group is involved in the molecular interaction. The parameters x_β and τ were also determined by the Bell–Evans formalism (Table III). These two methods are different in the sense that the lifetime analysis only determines one value for each parameter whereas the Bell–Evans formalism also provides a separate value for each loading rate interval. The parameters determined by the different approaches were in the same range, indicating consistency between the analysis methods.

The apparent free-energy of activation, ΔG^#, was in the range 5.8–13.4k_BT (Table IV). The free energy of carbohydrate–carbohydrate or carbohydrate–protein interactions has to our knowledge not previously been determined using this approach. However, ΔG^# determined based on AFM data related to protein unfolding was found to be 14.7k_BT using ν = 2/3 (Dudko et al. 2008). Furthermore, molecular dynamics simulations of disaccharide binding to galectin-1, in which the ligand was pulled away from the binding site using a mechanical probe, gave ΔG^# values ranging from 5 to 6k_BT (Echeverria and Amzel 2011). These data were found to be in good agreement with data obtained for the same system using ITC measurements (Schwarz et al. 1998). When applying a related approach on Galectin-8 interacting with different oligosaccharides, values ranging from 12 to 25k_BT were also obtained (Kumar et al. 2013). The data obtained in the present paper for heterotypic mucin interactions are thus in the same range as previously obtained for similar systems.

Heterotypic versus homotypic interactions

The parameter P_int was observed to depend on the immobilization configurations (Table II). This indicates that when comparing P_int obtained for heterotypic interactions, that is, in any study where different molecule are immobilized on each of the two probe surfaces, care has to be taken to check if the value could be dependent of the experimental procedure. Such dependence was observed for Tri-PSM interacting with Tn-PSM, Tn-PSM interacting with Fd-PSM and Tri-PSM interacting with Fd-PSM. In the present study, P_int decreased compared with its value obtained for the inverted immobilization configuration when a mucin showing a high tendency of homotypic interaction (i.e., Tn-PSM and Tri-PSM; Haugstad et al. 2012) was immobilized onto the sample surface (Table II). The observation that P_int for Tn-PSM_Tip interacting with Tri-PSM_surface is 9.4% and increased to 34.8% for the inverted immobilization configuration illustrates this point. A possible reason for this result is that the geometries of the mica surface (flat) and AFM tip (rounded) mediate different cis (i.e., homotypic) interactions among the grafted mucins on the respective surfaces, which, in turn, affects their trans (i.e., heterotypic in the present case) interactions. Cis interactions may be greater or less among the different mucins grafted on the mica sample surface, when compared with the cis interactions for the mucins grafted on the ATM tip. Thus, cis interactions are viewed to compete with the trans interactions between the mucins, and the more extensive cis interactions among the mica surface anchored mucins could make them less available for trans interactions with the mucin immobilized to the AFM tip.

The arguments presented above may also explain the relatively high probability for trans interactions observed for Fd-PSM_Surface interacting with Tn-PSM_Tip (Table II). More precisely, since Fd-PSM has a low probability for homotypic interactions (Haugstad et al. 2012) and thus only to a small extent engages in cis interactions, its glycan groups remain available for trans interactions. Interestingly, Asialo Tri-PSM show a low probability for both homotypic and heterotypic interactions (Table II; Haugstad et al. 2012). This indicates that not only the presence but also the availability of the potentially interacting groups determine the interaction probabilities.

Biological implications of the increased activity of the Tn antigen in mucins

The ability of glycoproteins to interact via CCI is not a well-studied topic. However, functionalized fluorescent silica nanoparticles have been used to study the interaction of monosaccharides with galactolipids (Zhao et al. 2012). Specific interactions were observed between galactose and 3-sulfogalactose, and no interaction (hetero- or homotypic) was observed for galactose or glucose. The ability for self-interaction of carbohydrate sidechains on mucins indicated by the present data is thus not a general property of monosaccharides. High specificity is also previously observed for the self-interactions of more complex oligosaccharide structures. For example, high-mannose type N-linked glycans with six mannosyl residues have been shown to display self-interaction properties, but did not interact with N-linked glycans with various structures having multiple GlcNAc termini (Yoon et al. 2013).

The PSM samples investigated in the present AFM study all contain the Tn-epitope, containing the peptide-linked GalNAc group. It is tempting to suggest that the interactions of the various PSM molecules may be based on the Tn-epitope alone, with little or no influence from the remaining carbohydrate groups. This is based on our ongoing studies quantifying the self-interactions of GalNAc groups immobilized onto two opposing surfaces using dual beam optical tweezers (Sletmoen et al. in preparation). This ongoing study also quantifies the interaction between synthetic polymers with GalNAc side chains. High similarity was observed between the force–loading rate plots obtained for the synthetic polymers conjugated with GalNAc groups and Tn-PSM, a finding suggests that the mucin homotypic interactions are independent of the protein backbone. However, clear conclusions related to the contributions of the different carbohydrate groups to the observed interactions require additional experiments involving separate surfaces functionalized with the different glycans found in the mucins.

Finally, because of their large size and extended linear conformation, fully glycosylated mucins have been suggested to have an anti-adhesive function (Carraway et al. 2009). In this context, the present observation that mucins possessing the Tn antigen, as found in cancer patients, show increased tendencies for heterotypic interaction is noteworthy. Invasiveness is known to underlie cancer aggressiveness and to be a hallmark of malignancy. It is also well known that most malignant tumors have elevated levels of the Tn-epitope, but its effects remain unclear. The increased level of Tn-epitopes was recently shown to stimulate cell adhesion to the extracellular matrix, as well as migration and invasiveness (Gill et al. 2013). Furthermore, truncation of O-glycans by epigenetic silencing of the COSMC chaperone gene was recently found to induce increased proliferation, compromised adhesion and invasiveness. (Radhakrishnan et al. 2014). In these respects, the self-interaction abilities of mucins containing elevated levels of the Tn-epitope, as quantified in this study, suggest a mechanistic role of this epitope in cancer cells. Indeed, regulating the density of Tn-epitopes in mucins may be part of a larger cellular system of regulating the density of N- and O-linked glycans and ganglioside receptors in cellular homeostasis in metazoans (Dam and Brewer 2010; Dennis and Brewer 2013).

Conclusions

The experimental data presented in this paper reveal the existence of heterotypic interactions between mucins with different glycan decoration patterns. The probability for interaction, P_int depends on the immobilization configuration, whereas the strength and lifetime of the interaction as well as the parameters characterizing its energy landscape do not. The most likely rupture forces of heterotypic interactions were found to be in the range 12–80 pN. This force range is equal to the force range observed for the homotypic interactions determined earlier for the same samples (Haugstad et al. 2012). The results show that mucins displaying high levels of Tn-epitopes interact with mucins bearing glycans with a different composition including the “fully decorated” Fd-PSM, which possesses the core 1 blood group A tetrasaccharide as well as STn and Tn antigens. We conclude that the observed heterotypic interactions of mucins containing elevated levels of Tn-epitope contribute to the possible mechanistic understanding of the biological importance of the Tn-epitope in cancer cells.

Materials and methods

Preparation of mucin samples

The O-glycosylated tandem repeated domains from pig submaxillary gland mucin Fd-PSM and Tri-PSM (Table I) were isolated and purified from frozen porcine submaxillary glands as previously reported (Gerken et al. 1997). The complete peptide sequence of PSM has been determined and its biochemical and physical properties are well known (Eckhardt et al. 1997). Mucin samples with modified carbohydrate compositions were prepared from the native PSM tandem repeat domains by chemical and enzymatic treatments as described (Gerken et al. 2002). Tn-PSM containing only α-GalNAc residues (Table I) was obtained by treatment of native PSM with mild trifluormethane sulfonic acid (Gerken et al. 1992). Asialo Tri-PSM (Table I) was prepared from Tri-PSM by neuraminidase catalyzed removal of N-glycolylneuraminic acid (NeuNGl) (Gerken and Dearborn 1984). All samples were purified by gel filtration on Sephacryl S200, lyophilized and stored at −18°C. The oligosaccharide composition of each mucin sample was determined by carbon-13 NMR spectroscopy (Table I) (Gerken and Jentoft 1987).

Immobilization of mucins onto mica slides and AFM tips

The immobilization procedure (Figure 1A) is a modified version of a previously reported procedure (Sletmoen et al. 2004, 2009) also used for determination of the homotypic mucin interactions (Haugstad et al. 2012). All AFM tips (Veeco OTR4 silicon nitride cantilevers, nominal spring constant 0.02 N/m) and all freshly cleaved mica slides (SPI Supplies) were first cleaned in a 1 : 1 (v/v) solution of MeOH and HCl and rinsed in Mq-water (deionized water, resistivity 18 MΩ cm, obtained using a MilliQ unit, Millipore). The tips and slides used for most of the sample series were silanized in a 3% solution of carboxyl silane (N-(trimethoxysilylpropyl) ethylenediamine triacetic acid, ABCR GmbH & Co) in 1 mM acetic acid for 20 min and rinsed in Mq-water. Lyophilized mucin samples were dissolved in 50 mM boric acid (pH 5.8) (concentration of 50 or 100 µg/mL) to which 1-(3-dimethylaminopropyl)-3-ethylcarbodiimide hydrochloride (EDAC, Sigma-Aldrich) was added (to a final concentration 1 mg/mL) to catalyze the covalent coupling of the N-terminal amine of the mucin peptide to the silanized carboxylic acid mica surface (or AFM tip). When functionalizing AFM tips, the concentration of mucin was 50 µg/mL and the incubation time 1 h, while functionalizing the mica surfaces, the mucin concentration used was 100 µg/mL and the incubation time 2 h. After incubation, AFM tips and mica slides with mucins were rinsed in Mq-water. The samples were used for the interaction studies within a few hours. Storing the functionalized AFM tips and mica surfaces for up to 1 day at 4°C in MilliQ water did not adversely affect the results.

Fd-PSM was immobilized to the mica or the AFM tip via its carboxyl groups. This process was conducted by first incubating mica slides and AFM tips with a 1% (v/v) freshly prepared solution of aminosilane (trimethoxysilylpropyl–diethylenetriamine, Sigma-Aldrich) in 1 mM acetic acid. Fd-PSM (50 and 100 µg/mL for the AFM tips and mica, respectively) was subsequently covalently attached to the aminosilane coating using EDAC (1 mg/mL, in aqueous 50 mM boric acid, pH 5.8, incubated overnight, room temperature). We have previously shown that linking the mucin to the sample surface by its carboxyl groups instead of its amino groups did not lead to any difference in the net interaction data (Haugstad et al. 2012). Increasing the incubation time from 2 h to overnight did not significantly change the data recordings.

Determination of single molecular pair interactions

The interactions between mucin immobilized on mica and AFM tips were studied employing a ForceRobot 300 (JPK instruments, Berlin) equipped with a high-precision mapping stage. The measurements were conducted in buffered aqueous solutions (100 mM HEPES buffer, pH 7.2, with 1 mM MnCl₂ and 1 mM CaCl₂) at room temperature. Force unbinding studies were carried out with one type of mucin attached to the tip and another attached to the mica sample surface (Figure 1B). In addition, the mucins attached to the two surfaces were swapped to assess the effect of reversing the immobilized surfaces.

The interactions between each mucin pair were determined from force–distance curves probed at several locations on the mica surface using the precision mapping stage of the force robot. Each force distance curve was obtained using a contact time with the surface of 0.5 s to allow interactions before the tip was retracted. The z-piezo retraction speed was varied from 1 to 4 μm/s to probe different ranges of loading rates. A contact set-point of 400 pN was typically used, trials in the range 200–600 pN indicated no significant differences in the observed unbinding properties.

The deflection sensitivity was determined for each tip by analyzing a force retraction curve on a solid surface (unfunctionalized glass). The spring constant was determined for each tip by measuring thermal fluctuations of the cantilever in a position well separated from the surface (Hutter and Bechhoefer 1993; te Riet et al. 2011). Control measurements consisted of testing of the mucin_Tip against a silanized mica surface. More extensive control measurements have previously been reported (i.e., silanized tip tested against mucin-coated mica surfaces) (Haugstad et al. 2012).

Analysis of mucin unbinding data

The force unbinding data were extracted from >3500 force–distance curves for each immobilization configuration and analyzed as previously outlined (Haugstad et al. 2012). A force jump in a force–distance curve was interpreted as evidence of interaction between the mucins on the sample surface and on the tip. The number of force curves with and without force jumps were counted and used to determine P_int. Parameter P_int was determined based on the data recorded at z-piezo retraction speeds of 1 and 2 µm/s. In addition to the unbinding force, the loading rate and distance from the contact point were determined for each force jump. The loading rate not only depends on the the z-piezo retraction speed but also on the elasticity and length of the molecules linking the tip to the sample surface. The loading rate was therefore determined for each force jump from the slope Δf/Δt prior to each observed dissociation event.

Force jumps containing only one peak were accepted and transferred to the ensemble of force jumps that formed the basis for further analysis provided that the cantilever had returned to the resting position before and after the force jump. Rupture events occurring at or close to the contact point between the AFM tip and the mica surface can be caused by unspecific interactions with the mica surface and were therefore not included in the ensemble. Dissociation events occurring close to the contact point of the curves were accepted and transferred to the ensemble of unbinding events provided that the cantilever had returned to its resting position before the force jump. Note that for the determination of P_int, force jumps containing more than one peak were also included.

In AFM force measurements, the retraction of the cantilever applies an external force to molecular bonds formed between the mucins on the tip and sample surface. This external force aids the thermal activation in the unbinding process and thereby decreases the activation barrier(s) separating bound from free states. As a consequence, the dissociation rate (k_off(f)) at an applied constant loading force f increases as

$$k_{\mathrm{off}}(f)=k^0\exp \left[\frac{f{x}_{\beta }}{k_{\mathrm{B}}T}\right],$$ (1)

where k⁰ is the dissociation rate at zero applied force, k_BT is the thermal energy and x_β is the thermally averaged distance from the bound complex to the transition state along the direction of the pulling force.

In this study, two approaches were used to determine parameters of the various mucin energy landscapes. The first approach is proposed by Dudko and co-workers involves determination of the force-dependent lifetime of the system (Dudko et al. 2008) based on the application of Kramers theory to a set of different free-energy profiles. The theory results in an analytic expression of the force-dependent lifetime according to

$$\tau (f)={\tau }_0{\left(1-\frac{vf{x}_{\beta }}{\mathrm{\Delta }{G}^{\mathrm{\#}}}\right)}^{1-(1/v)}\exp \left[-\frac{\mathrm{\Delta }{G}^{\mathrm{\#}}}{k_{\mathrm{B}}T}(1-{(1-vf{x}_{\beta }/\mathrm{\Delta }{G}^{\mathrm{\#}})}^{1/v})\right],$$ (2)

where τ₀ is the lifetime of the interaction and ΔG^# is the free energy of activation in absence of pulling force. Parameter ν is a scaling factor which reflects the geometry of the underlying free-energy potential adopting the value ν = 0.5 for a harmonic well with a cusp-like barrier, and ν = 2/3 for a potential containing linear and cubic terms. For ν = 1, the formula reflects the Bell and Evans model, which represents a special case within the formalism (Evans and Ritchie 1997; Evans 1998,  2001).

The second approach used in this study to determine parameters describing the energy landscape of interactions is based on the Bell and Evans model (Evans 1998; Evans 2001; Evans and Calderwood 2007). At constant force-loading rate, r_f, the theory predicts a distribution of rupture forces P(f):

$$P(f)=k^0\exp \left(\frac{x_{\beta }f}{k_{\mathrm{B}}T}\right)\exp \left[\frac{k^0{k}_{\mathrm{B}}T}{x_{\beta }{r}_{\mathrm{f}}}\left(1-\exp \left(\frac{x_{\beta }f}{k_{\mathrm{B}}T}\right)\right)\right].$$ (3)

The most likely rupture force, f*, is determined from the maximum of the probability density distribution:

$$\frac{\mathrm{\partial }P(f)}{\mathrm{\partial }f}=0{|}_{f=f^{\ast }},$$ (4)

yielding a relation between f* and the natural logarithm of the force-loading rate in a force ramping experiment:

$$f^{\ast }=\frac{k_{\mathrm{B}}T}{x_{\beta }}\ln \left(\frac{x_{\beta }}{k_{\mathrm{B}}T}{r}_{\mathrm{f}}{\tau }_0\right).$$ (5)

Equation (5) suggests that observations where f* increases linearly with ln(r_f) indicate an unbinding pathway with one rate-limiting barrier (Bell 1978; Evans 1998; Evans 2001).

These expressions were used as a basis to extract parameters of the energy landscape applying the following procedure. Individual unbinding forces versus the loading rate where grouped into intervals of r_f. The ensemble of unbinding forces within each of these intervals were used as a basis for the fit of P(f) (Eq. (3)). The average of the force-loading rate within each ensemble allows determining an estimate of f*. This user guided process is taking into account the balance between having a smallest possible range of r_f, needed in order to assure that the average r_f within the interval a good approximation, and the need to have a reasonable number of observed unbinding forces in the fitting of P(f). Averaged x_β and τ₀ parameters were for each barrier within the energy landscapes of the mucin pairs obtained by fitting f* versus ln(r_f) (Eq. (5)). The averaged parameters of x_β, referred to as x_β^#, were subsequently used for a consistency check, performed through a constraint fit of P(f) keeping x_β constant equal to x_β^#. The obtained fitting parameter τ₀^# within each interval and the x_β^#, where then used to obtain a second estimate of f*.

Supplementary data

Supplementary data for this article are available online at http://glycob.oxfordjournals.org/.

Conflict of interest statement

None declared.

Funding

Funding to T.A.G. by the National Institutes of Health National Cancer Institute grant R01 CA 078834 is acknowledged.

Abbreviations

AFM, atomic force microscopy; CCI, carbohydrate–carbohydrate interaction; EDAC, 1-(3-dimethylaminopropyl)-3-ethylcarbodiimide hydrochloride; PSM, porcine submaxillary mucin.