Coarse Grained Normal Mode Analysis vs. Refined Gaussian Network Model for Protein Residue-Level Structural Fluctuations

Abstract

We investigate several approaches to coarse grained normal mode analysis on protein residual-level structural fluctuations by choosing different ways of representing the residues and the forces among them. Single-atom representations using the backbone atoms C_α, C, N, and C_β are considered. Combinations of some of these atoms are also tested. The force constants between the representative atoms are extracted from the Hessian matrix of the energy function and served as the force constants between the corresponding residues. The residue mean-square-fluctuations and their correlations with the experimental B-factors are calculated for a large set of proteins. The results are compared with all-atom normal mode analysis and the residue-level Gaussian Network Model. The coarse-grained methods perform more efficiently than all-atom normal mode analysis, while their B-factor correlations are also higher. Their B-factor correlations are comparable with those estimated by the Gaussian Network Model and in many cases better. The extracted force constants are surveyed for different pairs of residues with different numbers of separation residues in sequence. The statistical averages are used to build a refined Gaussian Network Model, which is able to predict residue-level structural fluctuations significantly better than the conventional Gaussian Network Model in many test cases.

1 Introduction

Proteins are biomolecules, each formed by a chain of small molecules called amino acids. There are total 20 different amino acids. They can make many different chains of amino acids, and hence different proteins. There are hundreds of thousands of different proteins, with distinct biological functions supporting diverse biological forms and processes. They are key molecular elements of life and are fundamental research subjects of life sciences (Berg et al. 2006).

The biological function of a protein is determined by the protein’s 3D structure. The 3D structure is determined by the protein’s amino acid sequence. In other words, a given protein, with a given amino acid sequence, always assumes a certain 3D structure, which then helps to perform certain functions. Therefore, the 3D structure carries important information for the understanding of the protein and in particular, its sequence-structure-function relations (Berg et al. 2006).

While a protein folds to an unique structure, it also fluctuates and makes thermodynamic movements. The movements can be different for different atoms or residues or fragments of the protein, and may correspond to certain functional differences. Therefore, the determination of the structural fluctuation is an equally important issue as the determination of the structure itself in protein modeling. In X-ray crystallography, the structural fluctuation is measured by the so-called atomic B-factors, which are proportional to the atomic mean-square-fluctuations (Drenth 2006).

In contrast to structural determination, which is mainly through physical experiments, such as X-ray crystallography and NMR, the structural fluctuation can be analyzed theoretically for a given structure. For example, it can be traced by molecular dynamics simulation in the force field of the protein. It can in particular be determined in an analytical form using the so-called normal mode analysis (NMA) (Brooks et al. 1989; Schlick 2002).

The normal mode analysis usually requires a singular-value-decomposition of the Hessian matrix of the energy function, which is costly for an all-atom model, yet the estimation on the fluctuation may not necessarily always accurate, because of the errors in the force field approximation. A simplified residue-level model called the Gaussian Network Model (GNM) has been proposed in recent years and proved to be more efficient as well as accurate than NMA (Micheletti et al. 2004; Cui and Bahar 2006).

In this paper, we investigate several new approaches to residue-level normal mode analysis. Similar to GNM, we take the residues as the basic units in a protein and use a single backbone atom (or a combination of several backbone atoms) to represent each residue. Different from GNM, the force constants for pairs of representative atoms are not the same and are instead extracted from the Hessian matrix of the energy function. Therefore, the models can be considered as coarse-grained NMA.

Using the new models, we calculate the mean-square-fluctuations of the residues and their correlations with the experimental B-factors (called the B-factor correlations) for a large set of proteins. We compare them with the all-atom normal mode analysis and the residue-level Gaussian Network Model. We show that our models perform more efficiently than the all-atom normal mode analysis, and the B-factor correlations are also higher. The B-factor correlations are comparable with those estimated by the Gaussian Network Model and in some cases better.

Following the development of the coarse-grained NMA, we conduct a statistical survey on the extracted force constants, for different pairs of residues with different numbers of separation residues in sequence. We then base on their statistical averages to build a refined Gaussian Network Model. We show that the force constants for the neighboring residue pairs are always about one-magnitude larger than other pairs in contact. Therefore, in the refined GNM, the entries of the contact matrix can be defined in the same way as the conventional GNM except that the bi-diagonal entries have large magnitudes. We show that such a simply refined GNM can predict residue-level structural fluctuations significantly better than the conventional GNM in many test cases.

The paper is organized as follows. In Section 2, we provide a general background on normal mode analysis. We describe the system of equations of motion and its linear approximation, and derive the solution to the linear system for normal mode analysis. In Section 3, we introduce the Gaussian Network Model, and discuss its relationship with normal mode analysis. In Section 4, we describe the coarse-grained NMA and present the test results. In Section 5, we discuss the statistics of the force constants. We then describe the refined GNM and show the test results. We make concluding remarks in Sect. 6. Sections 2 and 3 are expository sections. They do not contain new insights into NMA or GNM. However, they do provide a more rigorous mathematical description on these topics than most in current literature, and show mathematically the relationship between the two approaches. Sections 4 and 5 describe the methods of coarse-grained NMA and refined GNM and the test results, and are the sections with new contributions.

2 Normal Mode Analysis

A normal mode is a pattern of motion of an oscillating system in which all parts of system move sinusoidally with the same frequency and a fixed phase relation. An oscillating system may have multiple normal modes. The motion of the system is then a collecting result of all its normal mode motions (Morin 2008). For example, a mass-spring system, i.e., a set of objects connected with springs, would vibrate with different modes corresponding to different amplitudes and frequencies, even when the masses of the objects and the force constants of the springs are all the same.

A protein structure fluctuates around its native state. In other words, the atoms in the protein vibrate around their equilibrium positions, as if they all are connected by some sort of springs. Therefore, protein structural fluctuations can be estimated approximately via normal mode analysis as well. Brooks and Karplus (1983) and Go et al. (1983) are among the first who applied the normal mode analysis to study the structural fluctuations of a small protein bovine pancreatic trypsin inhibitor (BPTI). Levitt et al. (1985) later performed a detailed analysis on larger proteins including BPTI, Crambin, Ribonuclease, Lysozyme. Ever since, the method has been used widely for routine structural analysis in protein modeling (Micheletti et al. 2004; Cui and Bahar 2006).

NMA assumes the protein in a stable state, where the potential energy has reached an energy minimum. Therefore, around this state, the potential energy can be approximated by a quadratic function. The system of equations of motion for the protein can then be solved in an analytical form, and the normal modes of the motion can be extracted from the solution for analysis of atomic vibrations as well as overall structural fluctuations. We provide a brief description on the system of equations of motion used in classical molecular dynamics simulation, the closed form solution to the approximated system, and the formulas for computing the atomic vibrations.

Lemma 2.1

Suppose that a biological molecule has n atoms. Let r(t) be the collection of the coordinates of the atoms in the given molecule at time t such that r(t) = {r_i(t) : i = 1,…, 3n}, where r_3j−2(t), r_3j−1(t), r_3j(t) are the x, y, z coordinates of atom j at time t, j = 1,…, n. Let E_p(r) be the potential energy function. Then the molecular motion can be described as a collection of movements of the atoms in the molecule, as given in the following system of equations of motion:

$${\mathit{Mr}}^{″}=-\nabla E_p\left(r\right)$$ (1)

where M is a diagonal matrix with the diagonal element m_ii being the mass of atom i. Proof Let the Lagrangian of the physical system for the molecule be defined as the following:

$$L(r,r^{\prime },t)=\frac{1}{2}{\left(r^{\prime }\right)}^{T}M\left(r^{\prime }\right)-E_p\left(r\right).$$

Then

$$\frac{\partial L}{\partial r}=-\nabla E_p\left(r\right),\frac{\partial L}{\partial r^{\prime }}={\mathit{Mr}}^{\prime },$$

and

$$\frac{d}{\mathit{dt}}\left(\frac{\partial L}{\partial r^{\prime }}\right)={\mathit{Mr}}^{″}.$$

Based on the Euler–Lagrange equation,

$$\frac{d}{\mathit{dt}}\left(\frac{\partial L}{\partial r^{\prime }}\right)=\frac{\partial L}{\partial r},$$

we then have

$${\mathit{Mr}}^{″}=-\nabla E_p\left(r\right).$$

The potential energy function E_p(r) is usually given in a complicated nonlinear form. Therefore, the system of (1) can only be solved numerically. While many methods have been developed for the solution of the system, they all are computationally costly even for the calculation of very short period trajectories (say in nanoseconds), because they have to use very small time steps (in femtoseconds) to match the fast atomic motions so they can keep the accuracy of the calculations (Brooks et al. 1989; Schlick 2002).

For normal mode analysis, the potential energy function is approximated by a quadratic function at its energy minimum. Let r⁰ be the minimum energy state, and assume without loss of generality that E(r⁰) = 0. Then

$$E_p\left(r\right)\approx \frac{1}{2}\sum _{\mathit{ij}}{\phantom{\mid }\frac{{\partial }^2{E}_p}{\partial r_i\partial r_j}\mid }_{r=r^0}(r_i-r_i^0)(r_j-r_j^0).$$

Let Δr = r − r⁰. The function can also be written as

$$E_p\left(r\right)\approx \frac{1}{2}{\left(\Delta r\right)}^T\left[{\nabla }^2{E}_p\right(r^0\left)\right]\left(\Delta r\right).$$ (2)

By using this approximation, the system of (1) becomes

$$M\Delta r^{″}={\mathit{Mr}}^{″}=-\nabla E_p\left(r\right)=-\nabla \left[\frac{1}{2}{\left(\Delta r\right)}^T\left[{\nabla }^2{E}_p\right(r^0\left)\right]\left(\Delta r\right)\right]=-{\nabla }^2{E}_p\left(r^0\right)\Delta r.$$

That is,

$$M\Delta r^{″}=-{\nabla }^2{E}_p\left(r^0\right)\Delta r.$$ (3)

The above equation can be solved analytically via the singular-value-decomposition of the Hessian matrix ▿²E_p(r₀). Suppose that the molecule has n atoms. Then the dimension of the Hessian matrix is 3n by 3n and has 3n singular-value and singular-vector pairs. Among them, the first 6 values corresponding to 3 translational and 3 rotational motions are equal to zeros, while the remaining 3n − 6 defines 3n − 6 normal modes. The detailed formulas for obtaining the normal modes are given in the following lemma.

Lemma 2.2

Suppose that the singular-value-decomposition of the mass-weighted Hessian matrix, H = M^−1▿2E_p(r⁰), is given by UʌU^T . Then the solution of the system of (3) is given by the following functions:

$$\Delta r_i\left(t\right)=\sum _{j=1}^{3n}{U}_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j),{\omega }_j=\sqrt{{\Lambda }_{\mathit{jj}}},i=1,\dots ,3n,$$ (4)

where α_j and β_j can be determined by the given conditions of the system. Proof Let H = M^−1▿2E_p(r⁰). Then

$$M\Delta r^{″}=-{\nabla }^2{E}_p\left(r^0\right)\Delta r=-\mathit{MH}\Delta r,$$

and

$$\Delta r_i^{″}=-\sum _{j=1}^{3n}{H}_{\mathit{ij}}\Delta r_j,$$

Let $\Delta r_i\left(t\right)={\sum }_{j=1}^{3n}{U}_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j)$. Then

$$\Delta r_i^{″}=-\sum _{j=1}^{3n}{U}_{\mathit{ij}}{\alpha }_j{\omega }_j^2\cos ({\omega }_{j}t+{\beta }_j),$$

and

$$\begin{array}{cc}\hfill -\sum _{j=1}^{3n}{H}_{\mathit{ij}}\Delta r_j=& -\sum _{j=1}^{3n}{H}_{\mathit{ij}}\sum _{k=1}^{3n}{U}_{\mathit{jk}}{\alpha }_k\cos ({\omega }_{k}t+{\beta }_k)\hfill \\ \hfill =& -\sum _{k=1}^{3n}\left[\sum _{j=1}^{3n}{H}_{\mathit{ij}}{U}_{\mathit{jk}}\right]{\alpha }_k\cos ({\omega }_{k}t+{\beta }_k)\hfill \\ \hfill =& -\sum _{k=1}^{3n}{U}_{\mathit{ik}}{\Lambda }_{\mathit{kk}}{\alpha }_k\cos ({\omega }_{k}t+{\beta }_k),\hfill \end{array}$$

proving that

$$\Delta r_i\left(t\right)=\sum _{j=1}^{3n}{U}_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j),w_j=\sqrt{{\Lambda }_{\mathit{jj}}},i=1,\dots ,3n$$

is a solution to the system of (3), where αj is called the amplitude, ωj the angular frequency, and βj the phase of the jth normal-mode of motion.

Now let q_j = α_j cos(ω_jt + β_j). Then

$$\Delta r_i\left(t\right)=\sum _{j=1}^{3n}{U}_{\mathit{ij}}{q}_j,\Delta r=\mathit{Uq}.$$

Also,

$$\begin{array}{cc}\hfill E_p\left(r\right)& =\frac{1}{2}{\left(\Delta r\right)}^T\left[{\nabla }^2{E}_p\right(r^0\left)\right]\left(\Delta r\right)=\frac{1}{2}{\left(\Delta r\right)}^{T}H\left(\Delta r\right)\hfill \\ \hfill & =\frac{1}{2}{\left(\mathit{Uq}\right)}^{T}U\Lambda U^T\left(\mathit{Uq}\right)=\frac{1}{2}{q}^T{\Lambda }_q\hfill \\ \hfill \Rightarrow & E_p\left(r\right)=\frac{1}{2}\sum _{j=1}^{3n}{\Lambda }_{\mathit{jj}}{q}_j^2=\frac{1}{2}\sum _{j=1}^{3n}{\omega }_j^2{q}_j^2.\hfill \end{array}$$

Then the time-averaged potential energy for each mode is

$$\frac{1}{2}{\omega }_j^2{\langle }_j,q_j\rangle =\frac{1}{2}{\omega }_j^2{\alpha }_j^2\langle \cos ({\omega }_{j}t+{\beta }_j),\cos ({\omega }_{j}t+{\beta }_j)\rangle =\frac{1}{4}{\omega }_j^2{\alpha }_j^2.$$

Since at the thermal equilibrium, the averaged potential energy should be equal to the kinetic energy k_BT/2 for each mode, we then have

$${\alpha }_j^2=\frac{2k_{B}T}{{\omega }_j^2}=2k_{\mathit{B}}T{\Lambda }_{\mathit{jj}}^{-1}.$$ (5)

Once the solution f’:r(t) for the system of (3) is obtained, the average fluctuation of r(t) from its equilibrium position r⁰(t) can be calculated using a simple formula, as given in the following theorem.

Theorem 2.3

Let the solution to the system of (3) be given by $\Delta r_i\left(t\right)={\sum }_{j=1}^{3n}{U}_{\mathit{ij}}{\alpha }_j\times \cos ({\omega }_{j}t+{\beta }_j),{\omega }_j^2={\Lambda }_{\mathit{jj}},{\alpha }_j^2=2k_{B}T{\Lambda }_{\mathit{jj}}^{-1},i=1,\dots ,3n$. Let UʌU^T be the singular-value-decomposition of the mass-weighted Hessian matrix H = M^−1▿2E_p(r⁰). Then the mean-square-fluctuation of the ith mode motion of the molecule is

$$\langle \Delta r_i,\Delta r_i\rangle =k_{B}T\sum _{j=1}^{3n}{U}_{\mathit{ij}}{\Lambda }_{\mathit{jj}}^{-1}{U}_{\mathit{ij}},i=1,\dots ,3n.$$ (6)

Proof

$$\begin{array}{cc}\hfill \langle \Delta r_i,\Delta r_i\rangle =& \langle \sum _{j=1}^{3n}{U}_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j),\sum _{j=1}^{3n}{U}_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j)\rangle \hfill \\ \hfill =& \sum _{j=1}^{3n}\langle U_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j),U_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j)\rangle \hfill \\ \hfill =& \sum _{j=1}^{3n}{U}_{\mathit{ij}}{\alpha }_j^2{U}_{\mathit{ij}}\langle \cos ({\omega }_{j}t+{\beta }_j),\cos ({\omega }_{j}t+{\beta }_j)\rangle \hfill \\ \hfill =& \frac{1}{2}\sum _{j=1}^{3n}{U}_{\mathit{ij}}{\alpha }_j^2{U}_{\mathit{ij}}=\frac{1}{2}\sum _{j=1}^{3n}{U}_{\mathit{ij}}2k_{B}T{\Lambda }_{\mathit{jj}}^{-1}{U}_{\mathit{ij}}=k_{B}T\sum _{j=1}^{3n}{U}_{\mathit{ij}}{\Lambda }_{\mathit{jj}}^{-1}{U}_{\mathit{ij}}.\hfill \end{array}$$

If we use ν_j(t) to represent the position vector of atom j at time t, then ν_j(t) = (r_3j−2(t), r_3j−1(t), r_3j(t))^T, and the mean-square-fluctuation of atom j can be calculated as

$$\langle \Delta v_j,\Delta v_j\rangle =\langle \Delta r_{3j-2},\Delta r_{3j-2}\rangle +\langle \Delta r_{3j-1},\Delta r_{3j-1}\rangle +\langle \Delta r_{3j},\Delta r_{3j}\rangle .$$ (7)

Note that if the singular value ʌ_jj is small, then the frequency ω_j is small and, therefore the corresponding mode is slow. Thus, the smaller the singular value, the slower the corresponding mode; and the slower a mode is, the larger mean-square-fluctuation it makes. Also, the atomic mean-square-fluctuation is usually related to the experimentally detected average atomic fluctuation, which, in X-ray crystallography, is represented by the so-called temperature factor or B-factor. Let the B-factor for atomj be denoted by B_j. Then

$$B_j=\frac{8{\pi }^2}{3}\langle \Delta v_j,\Delta v_j\rangle .$$ (8)

From equations (6), (7), and (8) above, we see that the B-factors are proportional to the atomic mean-square-fluctuations, and thus inversely proportional to all the singular values ʌ_jj (or square frequency _ωj²). Therefore, the largest contributions to the atomic displacements come from the lowest frequency normal modes (small ʌ_jj or _ωj²). In addition, the singular vectors corresponding to the lowest frequency normal modes represent the most globally distributed or collective motions. For these reasons, studies on NMA usually focus on only a few low frequency normal modes, and in real applications, only several terms in (6) corresponding to the smallest singular values are used for the evaluation of the atomic mean-square-fluctuations.

3 Gaussian Network Model

NMA requires the availability of the potential energy function and the computation of the Hessian matrix of the function. Tirion (1996) demonstrated that an approximation to the Hessian can be obtained by using a single parameter for all the atomic pairs in a close distance. The analysis with such an approximation can be as accurate as using the exact Hessian. Along this line, Bahar et al. (1997, 1998), Haliloglu et al. (1997) later made further simplification on conventional normal mode analysis using the Gaussian Network Model (GNM). In this model, a protein structure is described at a coarse level with the amino acid residues as the basic units and is considered as an elastic network with the residues as nodes and the contact connections among them as springs. Each residue can be represented by one of its backbone atoms, say C_α, or a selected point in the residue, say the geometric center of the side-chain. Two residues are said to be in contact if they are close in distance (usually, in a 7 Å cutoff distance). All the springs are assumed to be the same, i.e., have the same force constant. Figure 1 shows an example elastic network model for a protein structure 1HEL.

Fig. 1.

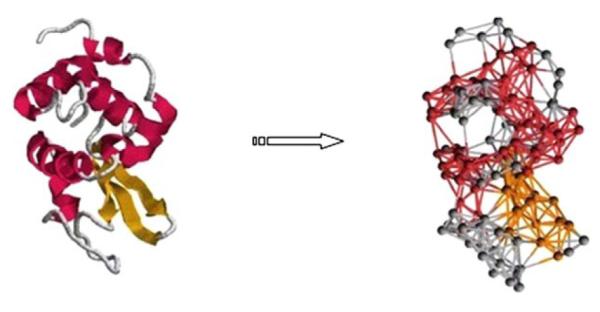
The picture on the left shows the C_α trace of 1HEL. The one on the right shows all connections between C_α nodes for 1HEL to indicate the nature of the elastic network analyzed by GNM (Cui and Bahar 2006).

Once an elastic network is constructed, the energy function for the protein can be defined without referring to the protein’s atomic level potentials: Assume that the protein has m residues. Let r be the collection of the coordinates of the residues in the protein such that r = {r_i : i = 1,…, 3m}, where r_3i−2, r_3i−1, r_3i are the x, y, z coordinates of residue i. Correspondingly, let ν be the collection of the coordinate vectors of the residues such that ν = {ν_i = (ν_i1, ν_i2, ν_i3)^T = (r_3i−2, r_3i−1, r_3i)^T : i = 1,…, m}. Let Δν_i = ν_i - ν⁰ be the displacement of residue i from its equilibrium position ν⁰ and k_ij be the force constant for the spring between residues i and j. Then the total force on residue i would be

$$\sum _{j=1}^m{k}_{\mathit{ij}}\Delta v_j\text{with}{k}_{\mathit{ii}}=-\sum _{j=1,j\ne i}^m{k}_{\mathit{ij}},$$

and the potential energy contributed from residue i would be

$$\sum _{j=1}^m\Delta v_i^T{k}_{\mathit{ij}}\Delta v_j∕2=\sum _{j=1}^m(\Delta v_{i1}{k}_{\mathit{ij}}\Delta v_{j1}+\Delta v_{i2}{k}_{\mathit{ij}}\Delta v_{j2}+\Delta v_{i3}{k}_{\mathit{ij}}\Delta v_{j3})∕2.$$

we then have the total potential energy of the protein to be

$$\begin{array}{cc}\hfill E_p\left(r\right)=& \sum _{i,j=1}^m\Delta v_i^T{k}_{\mathit{ij}}\Delta v_j∕2\hfill \\ \hfill =& \sum _{i,j=1}^m(\Delta v_{i1}{k}_{\mathit{ij}}\Delta v_{j1}+\Delta v_{i2}{k}_{\mathit{ij}}\Delta v_{j2}+\Delta v_{i3}{k}_{ij}\Delta v_{j}3)∕2.\hfill \end{array}$$ (9)

Since in GNM, the spring forces are kept constant and are zeros if the distances between any pairs of residues are larger than 7 Å, we can define k_ij = kΓ_ij for some constant k and

$${\Gamma }_{\mathit{ij}}=\{\begin{array}{cc}-1\hfill & \text{if}i\ne j\text{and}{d}_{\mathit{ij}}\le 7\mathrm{Å}\hfill \\ 0\hfill & \text{if}i\ne j\text{and}{d}_{\mathit{ij}}>7\mathrm{Å},\hfill \\ -{\sum }_{j=1,j\ne i}^m{\Gamma }_{\mathit{ij}}\hfill & \text{if}i=j.\hfill \end{array}\phantom{\}}$$ (10)

Here, Γ = {Γ_ij : i,j = 1,…, m} form a matrix called the contact matrix. Let Δν_j = {Δν_ij : i = 1,…, m}, j = 1, 2, 3. Then the energy function in (9) can be written as

$$E_p\left(r\right)=\frac{k}{2}(\Delta v_{\cdot 1}^T\Gamma \Delta v_{\cdot 1}+\Delta v_{\cdot 2}^T\Gamma \Delta v_{\cdot 2}+\Delta v_{\cdot 3}^T\Gamma \Delta v_{\cdot 3}).$$ (11)

An example contact matrix can be found in Fig. 2.

Fig. 2.

This is an example of a contact matrix.

Based on the theory of statistical physics, at a given temperature, the probability of a physical state r to occur is subject to the Gibbs–Boltzmann distribution

$$p\left(r\right)=\frac{1}{Z}\exp (-E_p(r)∕k_{B}T),$$ (12)

where k_B is the Boltzmann constant, T the temperature, and Z the partition function.

Given the energy function in (11) and the fact that ∫_R^3m p(r)dr = ∫_R^3m p(r)dΔr = 1, it follows that

$$\begin{array}{cc}\hfill Z=& {\int }_{R^{3m}}\exp (-E_p(r)∕k_{B}T)d\Delta r\hfill \\ \hfill =& {\int }_{R^{3m}}\exp [-k(\Delta v_{\cdot 1}^T\Gamma \Delta v_{\cdot 1}+\Delta v_{\cdot 2}^T\Gamma \Delta v_{\cdot 2}+\Delta v_{\cdot 3}^T\Gamma \Delta v_{\cdot 3})∕2k_{B}T]d\Delta v\hfill \\ \hfill =& \prod _{i=1}^3{\int }_{R^m}\exp [-k(\Delta v_{\cdot 1}^T\Gamma \Delta v_{\cdot 1})∕2k_{B}T]d\Delta v_{\cdot 1}\hfill \end{array}$$

By changing all the variables Δνl to Δu, we then have

$$Z=Z^{\prime 3},Z^{\prime }={\int }_{R^m}\exp (-k\Delta u^T\Gamma \Delta u∕2k_{B}T)d\Delta u.$$

Let Γ = UʌU^T be the singular-value-decomposition of Γ. Then

$$Z^{\prime }={\int }_{R^m}\exp (-k\Delta w^T\Lambda \Delta w∕2k_{B}T)d\Delta w$$ (13)

where Δω = U^T Δu. Then $Z=Z^{\prime 3},Z^{\prime }={\prod }_{j=1}^m{Z}_j$, with

$$Z_j={\int }_R\exp (-k{\Lambda }_{\mathit{jj}}\Delta w_j^2∕2k_{B}T)d\Delta w_j,$$ (14)

Note that given the probability distribution of a physical state, p(r), we can evaluate the expectation value of any property related to this physical state, f(r), using the integral ∫_R^3m f(r)p(r)dr It follows that if we consider the fluctuation of residue $i,\Delta v_i^T\Delta \mathit{vi}$, as a function f(r) of state r, we can calculate the mean-square-fluctuation using the integral ${\int }_{R^{3m}}\Delta v_i^T\Delta v_{i}p\left(r\right)\mathit{dr}$. We give a formula for the calculation of this integral in the following theorem.

Theorem 3.1

Let the potential energy function E_p(r) for a given protein be defined as (11). Let the singular-value-decomposition of Γ be given by UʌU^T . Then the mean-square-fluctuation (Δν_i, Δν_i) can be calculated by the formula:

$$\langle \Delta v_i,\Delta v_i\rangle =\frac{3k_{B}T}{k}\sum _{j=1}^m{U}_{\mathit{ij}}{\Lambda }_{\mathit{jj}}^{-1}{U}_{\mathit{ij}},i=1,\dots ,m,$$ (15)

where k is a force constant, k_B the Boltzmann constant, and T the absolute temperature. Proof Note that for any i = 1,…, m,

$$\begin{array}{cc}\hfill \langle \Delta v_i,\Delta v_i\rangle =& {\int }_{R^{3m}}\Delta v_i^T\Delta v_{i}p\left(r\right)\mathit{dr}\hfill \\ \hfill =& {\int }_{R^{3m}}\Delta v_i^T\Delta v_i\frac{1}{Z}\exp (-E_p(r)∕k_{B}T)\mathit{dr}\hfill \\ \hfill =& \frac{1}{Z}{\int }_{R^{3m}}\Delta v_i^T\Delta v_i\prod _{l=1}^3\exp (-k\Delta v_{\cdot l}^{T}U\Lambda U^T\Delta v_{\cdot l}∕2k_{B}T)d\Delta v_{\cdot l}.\hfill \end{array}$$

Since $\Delta v_i^T\Delta v_i=\Delta v_{i1}^2+\Delta v_{i2}^2+\Delta v_{i3}^2$ and Z = Z’³ by (13),

$$\langle \Delta v_i,\Delta v_i\rangle =\frac{1}{Z^{\prime }}\sum _{l-1}^3{\int }_{R^m}\Delta v_{il}^2\exp (-k\Delta v_{\cdot l}^{T}U\Lambda U^T\Delta v_{\cdot l}∕2k_{B}T)d\Delta v_{\cdot l}.$$

By changing all the variables Δν_l to Δu, we then have

$$\langle \Delta v_i,\Delta v_i\rangle =\frac{3}{Z^{\prime }}{\int }_{R^m}\Delta u_i^2\exp (-k\Delta u^{T}U\Lambda U^T\Delta u∕2k_{B}T)d\Delta u.$$

Let Δu = UΔω. Then

$$\begin{array}{cc}\hfill \langle \Delta v_i,\Delta v_i\rangle =& \frac{3}{Z^{\prime }}{\int }_{R^m}\left(\sum _{j,k=1}^m{U}_{\mathit{ij}}{U}_{\mathit{ik}}\Delta w_j\Delta w_k\right)\exp (-k\Delta w^T\Lambda \Delta w∕2k_{B}T)d\Delta w\hfill \\ \hfill =& \frac{3}{Z^{\prime }}{\int }_{R^m}\left(\sum _{j,k=1}^m{U}_{\mathit{ij}}{U}_{\mathit{ik}}\Delta w_j\Delta w_k\right)\prod _j^m\exp (-k{\Lambda }_{\mathit{jj}}\Delta w_j^2∕2k_{B}T)d\Delta w_j.\hfill \end{array}$$

Note that if j ≠ k for Δω_jΔω_k,

$${\int }_{R^m}\Delta w_j\Delta w_k\prod _j^m\exp (-k{\Lambda }_{\mathit{jj}}\Delta w_j^2∕2k_{B}T)d\Delta w_j=0.$$

But if j = k for Δω_jΔω_k,

$$\begin{array}{cc}\hfill {\int }_{R^m}& \Delta w_j\Delta w_k\prod _j^m\exp (-k{\Lambda }_{\mathit{jj}}\Delta w_j^2∕2k_{B}T)d\Delta w_j\hfill \\ \hfill & =Z_j^{m-1}{\int }_{R^m}\Delta w_j^2\exp (-k{\Lambda }_{\mathit{jj}}\Delta w_j^2∕2k_{B}T)d\Delta w_j.\hfill \end{array}$$

It follows that for any i = 1,…, m

$$\begin{array}{cc}\hfill & \langle \Delta v_i,\Delta v_i\rangle =\sum _{j=1}^m\frac{3}{Z_j}{\int }_R{U}_{\mathit{ij}}{U}_{\mathit{ij}}\Delta w_j^2\exp (-k{\Lambda }_{\mathit{jj}}\Delta w_j^2∕2k_{B}T)d\Delta w_j\hfill \\ \hfill & =\frac{3k_{B}T}{k}\sum _{j=1}^m{U}_{\mathit{ij}}{\Lambda }_{\mathit{jj}}^{-1}{U}_{\mathit{ij}}\frac{1}{Z_j}{\int }_R\exp (-k{\Lambda }_{\mathit{jj}}\Delta w_j^2∕2k_{B}T)d\Delta w_j\hfill \\ \hfill & =\frac{3k_{B}T}{k}\sum _{j=1}^m{U}_{\mathit{ij}}{\Lambda }_{\mathit{jj}}^{-1}{U}_{\mathit{ij}}.\hfill \end{array}$$

Note that the formula for calculating the mean-square-fluctuations of the residues in (15) is very similar to that for calculating the mean-square-fluctuations of the atoms in (6). It is not a coincident because GNM can indeed be considered as residue level NMA with the energy function approximated by using the contact matrix as the Hessian matrix. In other words, if we consider the function E_p(r) in (11) to be a harmonic approximation to the potential energy function for the protein at the residue level, we can perform NMA for the protein at its residue level in the same way as that at the atomic level. We provide some further justifications in the following.

Note that the energy function E_p(r) in (11) is symmetric with respect to Δν_l, l = 1, 2, 3. Therefore, the system of equations of motion for the residues can be reduced to three independent and identical subsystems:

$$M\Delta v_{\cdot l}^{″}=-k\Gamma \Delta v_{\cdot l},l=1,2,3.$$ (16)

Theorem 3.2

Consider E_p(r) in (11) to be a harmonic approximation to the potential energy function of the protein at an equilibrium state r⁰. Let M be the mass matrix of the residues and H = M⁻¹Γ. Then, the solution to the system of equations of motion for the residues in (16) is given by

$$\Delta v_{\mathit{il}}\left(t\right)=\sum _{j=1}^m{U}_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j),{\omega }_j=\sqrt{k{\Lambda }_{\mathit{jj}}},i=1,\dots ,m,l=1,2,3.$$ (17)

where α_j and β_j can be determined by the given conditions of the system.

Proof Since the system of equations of motion can be reduced to three independent and identical subsystems, we only need to solve any of them, which can be put into the following general form:

$$M\Delta u^{″}=-k\Gamma \Delta u.$$

Let H = M⁻¹Γ. Let UʌU^T be the singular value decomposition of H. Then, by using a similar argument for Lemma 2.2, we can have

$$\Delta u_i\left(t\right)=\sum _{j=1}^m{U}_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j),{\omega }_j=\sqrt{k{\Lambda }_{\mathit{jj}}},i=1,\dots ,m,$$

meaning that

$$\Delta v_{il}\left(t\right)-\sum _{j=1}^m{U}_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j),{\omega }_j=\sqrt{k{\Lambda }_{\mathit{jj}}},i=1,\dots ,m,l=1,2,3.$$

Based on the argument that at the thermal equilibrium, the averaged potential energy should be equal to the kinetic energy k_BT/2 for each mode, we then have

$${\alpha }_j^2=\frac{2k_{B}T}{{\omega }_j^2}=\frac{2k_{B}T}{k{\Lambda }_{\mathit{jj}}}.$$ (18)

Therefore, we can have the following theorem for the calculation of the residue mean-square-fluctuations.

Theorem 3.3

Let the solution to the system of (16) be given by $\Delta {\mathit{vi}}_l\left(t\right)={\Sigma }_{j=1}^m{U}_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j),i=1,\dots ,m,l=1,2,3,{\omega }_j^2=k{\Lambda }_{\mathit{jj}},{\alpha }_j^2=2k_{B}T∕k{\Lambda }_{\mathit{jj}}$. Let UʌU^T be the singular-value-decomposition of the matrix H = M⁻¹Γ. Then the mean-square-fluctuations of the residues can be calculated by the formula,

$$\langle \Delta v_i,\Delta v_i\rangle =\frac{3k_{B}T}{k}\sum _{j=1}^m{U}_{\mathit{ij}}{\Lambda }_{\mathit{jj}}^{-1}{U}_{\mathit{ij}},i=1,\dots ,m.$$ (19)

Proof Based on the discussion in Theorem 3.2,

$$\langle \Delta v_i,\Delta v_i\rangle =\sum _{l=1}^3\langle \Delta v_{il},\Delta v_{il}\rangle =3\langle \Delta u_i,\Delta u_i\rangle ,$$

with $\Delta u_i={\sum }_{j=1}^m{U}_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j),i=1,\dots ,m,{\omega }_j^2=k{\Lambda }_{\mathit{jj}},{\alpha }_j^2=2k_{B}T∕k{\Lambda }_{\mathit{jj}}$. Then

$$\begin{array}{cc}\hfill \langle \Delta u_i,\Delta u_i,\rangle =& \langle \sum _{j=1}^m{U}_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j),\sum _{j=1}^m{U}_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j)\rangle \hfill \\ \hfill =& \sum _{j=1}^m\langle U_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j),U_{\mathit{ij}}{\alpha }_j\cos ({\omega }_{j}t+{\beta }_j)\rangle \hfill \\ \hfill =& \sum _{j=1}^m{U}_{\mathit{ij}}{\alpha }_j^2{U}_{\mathit{ij}}\langle \cos ({\omega }_{j}t+{\beta }_j),\cos ({\omega }_{j}t+{\beta }_j)\rangle \hfill \\ \hfill =& \frac{1}{2}\sum _{j=1}^m{U}_{\mathit{ij}}{\alpha }_j^2{U}_{\mathit{ij}}=\frac{k_{B}T}{k}\sum _{j=1}^m{U}_{\mathit{ij}}{\Lambda }_{\mathit{jj}}^{-1}{U}_{\mathit{ij}},\hfill \end{array}$$

proving that

$$\langle \Delta v_i,\Delta v_i\rangle =\frac{3k_{B}T}{k}\sum _{j=1}^m{U}_{\mathit{ij}}{\Lambda }_{\mathit{jj}}^{-1}{U}_{\mathit{ij}}.$$

Note that if M is an identity matrix, then H = Γ and the formula in (19) for calculating the mean-square-fluctuations of the residues using NMA will be the same as that in (15) using GNM. In other words, GNM for calculating the residue mean-square-fluctuations is equivalent to NMA with the contact matrix used as the Hessian approximation and with all the residues assumed to have a unit mass.

4 Coarse-Grained Normal Mode Analysis

As described in Sect. 2, in classical NMA, the system of equations of motion is solved with a quadratic approximation to the potential energy function. This approximation is accurate enough only in a small neighborhood of the energy minimum state (or structure). It also depends on the original potential energy function, which itself is an approximation obtained semi-empirically (Brooks et al. 1989; Schlick 2002). In addition, the classical NMA is usually conducted at the atomic level, which is subject to all the atomic level errors induced in energy calculations. As a result, the structural fluctuations predicted by NMA are often even worse than those by GNM, which is in fact a coarser model than NMA (Micheletti et al. 2004; Cui and Bahar 2006).

As analyzed in Sect. 3, the GNM method can be considered as a type of residue level NMA. In GNM, a residue contact matrix is defined using the distances between the residues (the distances between the representative atoms C_α, N, C, or C_β). If the distance between two different residues is less or greater than the given cutoff value, say 7 Å, then a constant, −1 or 0 (or more accurately, −k or 0), is allocated for the entry in the matrix, respectively. In other words, constants are assigned to the entries throughout the matrix according to the contact distances. The advantage of using GNM is that the model is simple and easy to construct, the dimension of the model is much smaller (proportional to the number of residues) than atomic level NMA, and the computation is efficient. In addition, GNM does not require the exact potential energy and the Hessian, reducing not only computational cost but also possible errors in atomic energy calculations.

Physically speaking, in GNM, the protein is viewed as an elastic network with the residues as nodes and the contact distances as the links. The links are approximated by springs and assigned with some spring constants. In other words, the forces between the residues in contact are approximated by some harmonic forces. Mathematically speaking, this is equivalent to saying that a quadratic approximation is used to represent the potential energy for the residue interactions of the protein. As a first approximation, in GNM, a single spring constant is assigned to all the residue pairs in contact. However, different pairs of residues may interact differently with different force constants. A more accurate model may be built if these differences can be considered.

Here, we investigate an alternative approach to coarse-grained normal mode analysis. Instead of using a homogeneous force constant for all the interactions among the residues in contact, we assign different force constants for different types of interactions in terms of related residue types and distances. In a certain sense, it can also be considered as a refined, nonhomogeneous Gaussian Network Model. There have been several efforts made in the past to refine GNM: For example, Taner and Jernigan (2006) defined the force constants in terms of the residue contact distances, and Kondrashov et al. (2006) assigned different force constants for residue pairs of different sequence distances. We derive the force constants from the atomic level Hessian matrix of the potential energy function. Therefore, our approach can be considered to be more physics-based.

Much work has been done in the past on coarse-grained normal mode analysis at different coarse levels and with different calculation schemes. Early work includes using graph theoretical methods to estimate protein shapes and structural flexibility by Mitchell et al. (2001) and by Jacobs et al. (2001). Tama et al. (2000), and Li and Cui (2002) proposed an approach to use residue fragments as building blocks for computing low frequency normal modes. Approaches have been studied using rigid components of proteins as basic units for normal mode analysis (Schuyler and Chirikjian 2004; Ahmed and Gohlke 2006; Demerdash and Mitchell 2012). Work has also been done in Lu and Ma (2008, 2011) with the Hessian elements derived from all-atom normal mode analysis and some universal force constants. Our method differs from these approaches in using the Hessian matrix of the energy function to extract the force constants for residue interactions and further determine them based on their probability distributions in a large set of know protein structures.

For a given structure, we first perform sufficient steps of energy minimization in an atomic-level force field. Once an energy minimum is reached, we save the Hessian matrix of the energy function and use it to derive the force constants for residue interactions. Let R_i and R_j be two residues represented by two atoms A_i and A_j, where A_i and A_j must have two position vectors (ν_i1, ν_i2, ν_i3)^T and (ν_j1, ν_j2, ν_j3)^T and correspond to a 3 by 3 submatrix S^(ij) of the Hessian H. We then define the force constant for residues R_i and R_j to be the average value of the entries in S^(ij). In other words, if k_ij is the force constant for residues R_i and R_j, then k_ij = − ∥ S^{(ij) ∥} _F, where ∥ · ∥ _F is the matrix Frobenius norm. More precisely,

$$k_{\mathit{ij}}=\{\begin{array}{cc}-{\Vert S^{\left(\mathit{ij}\right)}\Vert }_F\hfill & \text{if}i\ne j,\hfill \\ -{\Sigma }_{j,j\ne i}^m{k}_{\mathit{ij}}\hfill & \text{if}i=j,\hfill \end{array}\phantom{\}}$$

where m is the number of residues in the protein. Then, the matrix Γ = {k_ij : i,j = 1,…, m} can serve as a reduced Hessian matrix for coarse-grained NMA.

We have applied this new model to a set of protein structures downloaded from the PDB (Berman et al. 2010). The resolutions of the structures are 1.5 Å or higher and the sequence similarity is 30 % or lower. The sizes of the structures are from small to large, with the numbers of atoms ranging from 35 to 2387. We have employed the CHARMM version 27b2 (Brooks et al. 2009) for energy minimization and implemented a Matlab NMA code for residue normal mode calculations. For each structure, we have used different representative atoms C_α, N, C, or C_β for residues, to obtain the reduced Hessian. We have computed the residue mean-square-fluctuations and their correlations with the B-factors of the corresponding representative atoms of the residues (B-factor correlations). We call our model the coarse-grained NMA or cgNMA for short. A cgNMA with C_α, N, C, or C_β as the representative atoms for the residues is denoted as cgNMA(C_α), cgNMA(N), cgNMA(C), cgNMA(C_β), respectively.

For comparison, we have also computed the residue mean-square-fluctuations and their B-factor correlations for each structure, using GNM with C_α, N, C, C_β as the representative atoms for the residues. A GNM with C_α, N, C, or C_β as the representative atoms for the residues is denoted as GNM(C_α), GNM(N), GNM(C), GNM(C_β), respectively. An atomic level NMA has also been performed for each structure with the CHARMM NMA routine. The mean-square-fluctuations of C_α atoms are recorded and compared with their experimental B-factors as well.

A more sophisticated cgNMA is to use a set of atoms to represent each residue. Let two residues R_i and R_j be represented by the same types of N atoms, A_i1,…, A_iN and A_j1 …, A_jN, respectively. Let S^(ij) be the 3N by 3N submatrix of the Hessian matrix H corresponding to the representative atoms of R_i and R_j. Wereduce S^(ij) to a 3 by 3 matrix T^(ij), with

$$T_{\mathit{xy}}^{\left(\mathit{ij}\right)}=\mathbf{sqrt}\left(\sum _{k=1}^N\sum _{l=1}^N{\left[S_{3(k-1)+x,3(l-1)+y}^{\left(\mathit{ij}\right)}\right]}^2\right),x,y=1,2,3.$$

We then define the force constant k_ij for residues R_i and R_j to be the average value of the entries in T^(ij), i.e.,

$$k_{\mathit{ij}}=\{\begin{array}{cc}-{\Vert T^{\left(\mathit{ij}\right)}\Vert }_F\hfill & \text{if}i\ne j,\hfill \\ -{\Sigma }_{j,j\ne i}^m{k}_{\mathit{ij}}\hfill & \text{if}i=j,\hfill \end{array}\phantom{\}}$$

where m is the number of residues in the protein. We denote this model by cgNMA(M), meaning the coarse-grained NMA with multiple representative atoms. In particular, we have used C_α, N, C for cgNMA(M) in our test.

We have divided the test structures into three groups of relatively small-,medium-, and large-sized structures. We then summarize the test results for each of them separately. Tables 1, 2, and 3 show the test results on small, medium, and large structures, respectively. In these tables, we have listed the names of the proteins (ID), the numbers of the atoms and residues in the proteins (TA and TR), and the B-factor correlations of the computed residue mean-square-fluctuations for the structures using different methods. The methods include GNM with different representative atoms, GNM(C_α), GNM(N), GNM(C), GNM(C_β), the coarse-grained NMA with different representative atoms, cgNMA(C_α), cgNMA(N), cgNMA(C), cgNMA(C_β), cgNMA(M), and classical NMA using CHARMM. The B-factor correlations are calculated against the B-factors of the representative atoms except for NMA for which the B-factors of C_α atoms are compared with. For cgNMA(M), the averages of fluctuations of representative atoms of residues are compared with the averages of B-factors of representative atoms of residues.

Table 1.

B-factor correlations for small-sized structures^a

ID	TA	TR	GNM(Cα)	GNM(N)	GNM(C)	GNM(Cβ)	cgNMA(Cα)	cgNMA(N)	cgNMA(C)	cgNMA(Cβ)	cgNMA(M)	NMA
2OLX	35	4	0.885	0.857	0.410	0.925	0.776	0.867	0.664	0.859	0.738	−0.933
2OL9	51	6	0.689	0.970	0.831	0.741	0.886	0.989	0.898	0.722	0.965	0.881
1YJO	55	6	0.434	0.568	0.543	−0.054	0.445	0.238	0.524	0.549	0.423	−0.149
1XY2	69	8	0.562	0.474	0.354	0.596	0.458	−0.104	0.722	0.507	0.771	0.081
1NOT	96	13	0.523	0.508	0.305	−0.005	0.567	0.971	0.405	0.010	0.814	0.056
1PEN	109	16	0.270	0.406	−0.099	0.149	0.056	0.707	−0.164	−0.033	0.193	0.699
1OB4	110	5	−0.744	−0.721	−0.402	NaN	0.930	0.956	−0.091	0.845	0.543	0.463
1OB7	111	5	−0.463	−0.371	−0.711	NaN	0.952	0.843	0.947	0.381	0.926	−0.001
1AKG	112	16	0.185	0.483	0.225	0.593	−0.229	0.621	0.025	0.141	0.071	−0.027
1KYC	138	15	0.754	0.863	0.625	0.586	0.784	0.538	0.725	0.664	0.706	0.600
1ETN	147	12	−0.274	−0.107	−0.377	0.288	−0.537	0.019	−0.298	−0.358	−0.490	0.463
1ETL	147	12	0.628	0.658	0.214	0.655	0.355	0.540	0.583	−0.258	0.606	0.847
1PEF	153	18	0.808	0.810	0.828	0.710	0.888	0.897	0.701	0.761	0.790	0.609
1ETM	160	12	0.432	0.365	−0.135	0.287	0.027	0.496	0.400	0.081	0.462	0.896
1O06	172	20	0.844	0.881	0.782	0.812	0.900	0.779	0.873	0.488	0.923	0.750
1HJE	214	13	0.616	0.526	0.701	0.057	0.562	0.741	0.686	0.652	0.838	0.209
1P9I	225	29	0.625	0.678	0.606	0.524	0.603	0.805	0.885	0.092	0.813	0.405
2JKU	255	35	0.656	0.689	0.487	0.515	0.850	0.480	0.647	0.396	0.654	0.698
1RJU	257	36	0.431	0.425	0.367	0.285	0.235	−0.070	0.358	0.168	0.274	−0.041
2NLS	273	36	0.530	0.658	0.507	0.384	0.088	0.653	0.618	0.233	0.701	0.430
1VRZ	277	13	0.327	0.420	−0.193	0.313	−0.203	0.511	0.398	−0.157	0.271	0.807
1AIE	295	31	0.155	0.250	0.178	0.365	0.712	0.447	0.566	0.322	0.584	0.670
1GK7	335	39	0.821	0.790	0.872	0.748	0.822	0.763	0.806	0.670	0.808	0.690
1Q9B	345	43	0.656	0.699	0.864	0.509	0.646	0.614	0.830	0.291	0.789	0.570
1YZM	361	46	0.901	0.853	0.900	0.789	0.939	0.938	0.849	0.549	0.925	0.472
6RXN	367	45	0.594	0.497	0.593	0.487	0.304	0.369	0.332	0.216	0.415	0.254
1USE	382	40	−0.142	0.006	−0.174	−0.230	−0.399	−0.003	−0.132	0.075	−0.236	0.384
1BX7	387	51	0.706	0.639	0.717	0.478	0.868	0.417	0.653	0.221	0.637	0.507
2DSX	399	52	0.127	−0.010	−0.046	0.272	0.433	0.407	0.536	0.107	0.487	−0.079
1UOY	452	64	0.671	0.674	0.630	0.053	0.628	0.654	0.719	0.760	0.746	0.609
1U06	470	55	0.434	0.422	0.544	0.492	0.377	0.285	0.374	0.111	0.322	0.553
1GVD	491	52	0.591	0.316	0.555	0.772	0.570	0.658	0.808	0.579	0.747	0.421
1FF4	503	65	0.674	0.651	0.624	0.578	0.555	0.314	0.509	0.700	0.512	0.564

^aID-protein ID, TA-total number of atoms, TR-total number of residues, GNM(C_α, N, C, C_β)—residue B-factor correlations using GNM with different choices of representative atoms, cgNMA(C_α, N, C, C_β)—residue B-factor correlations using cgNMA with different choices of representative atoms, cgNMA(M)—residue B-factor correlations using cgNMA with a combination of C_α, N, C atoms as the representative atom, NMA—correlations using NMA

Table 2.

Factor correlations for medium-sized structures^a

ID	TA	TR	GNM(Cα)	GNM(N)	GNM(C)	GNM(Cβ)	cgNMA(Cα)	cgNMA(N)	cgNMA(C)	cgNMA(Cβ)	cgNMA(M)	NMA
1LR7	522	73	0.620	0.667	0.751	0.624	0.795	0.704	0.628	0.449	0.712	0.629
1ZVA	551	75	0.690	−0.078	0.510	0.775	0.579	0.736	0.845	0.312	0.812	0.714
2BF9	562	35	0.419	0.249	−0.021	0.147	0.521	0.556	0.840	0.197	0.762	0.367
2EHS	598	75	0.747	0.269	0.302	0.570	0.565	0.717	0.720	0.386	0.761	0.330
1UHA	623	82	0.583	0.491	0.463	0.540	0.308	0.568	0.387	0.216	0.498	0.749
1FK5	626	93	0.485	0.414	0.378	0.441	0.362	0.554	0.516	0.489	0.539	0.351
1OPD	642	85	0.398	0.559	0.382	0.317	0.796	0.298	0.255	0.072	0.355	0.372
1X3O	642	80	0.654	0.606	0.694	0.550	0.453	0.409	0.514	0.339	0.542	0.177
2E3H	651	81	0.605	0.775	0.652	0.540	0.632	0.654	0.665	0.488	0.741	0.680
1USM	661	77	0.798	0.669	0.738	0.719	0.780	0.761	0.840	0.350	0.865	0.613
1ULR	677	87	0.495	0.387	0.354	0.548	0.223	0.421	0.648	0.482	0.695	0.561
1I71	683	83	0.549	0.608	0.466	0.334	0.380	0.355	0.325	0.283	0.334	0.353
2PKT	688	91	−0.286	−0.209	−0.288	−0.042	−0.165	−0.220	−0.279	−0.257	−0.247	−0.245
1N7E	700	95	0.497	0.511	0.454	0.431	0.385	0.583	0.409	0.074	0.534	0.301
2IP6	702	87	0.572	0.404	0.549	0.493	0.826	0.644	0.772	0.473	0.733	0.322
2EAQ	705	89	0.695	0.631	0.659	0.483	0.688	0.622	0.743	0.336	0.775	0.707
2FQ3	721	85	0.348	0.270	0.190	0.549	0.508	0.659	0.697	0.290	0.679	0.609
2RB8	723	93	0.517	0.432	0.530	0.653	0.485	0.314	0.530	0.269	0.515	0.292
1GXU	726	88	0.421	0.388	0.288	0.557	0.581	0.825	0.643	0.530	0.762	0.756
2PLT	727	98	0.481	0.360	0.410	0.161	0.187	0.450	0.493	0.058	0.543	0.248
1ABA	728	87	0.613	0.556	0.547	0.554	0.057	0.602	0.636	0.438	0.649	0.648
1R7J	729	90	0.368	0.377	0.405	0.489	0.078	0.277	0.344	0.325	0.244	0.4
1V05	731	96	0.632	0.670	0.662	0.511	0.389	0.382	0.506	0.166	0.482	0.5
1CYO	731	88	0.741	0.800	0.807	0.682	0.774	0.683	0.803	0.618	0.763	0.694
3BZQ	742	99	0.466	0.344	0.356	0.562	0.351	0.176	0.110	0.057	0.167	0.492
1W2L	746	97	0.397	0.421	0.284	0.432	0.432	0.611	0.582	0.117	0.647	0.130
2MCM	769	112	0.820	0.770	0.787	0.778	0.643	0.673	0.757	0.509	0.821	0.789
1Z21	771	96	0.433	0.214	0.253	0.626	0.289	0.403	0.484	0.352	0.490	0.540
2BRF	775	100	0.710	0.764	0.770	0.693	0.535	0.561	0.711	0.400	0.742	0.612
1NOA	778	113	0.615	0.578	0.651	0.406	0.485	0.485	0.589	0.213	0.615	0.531
1NNX	780	93	0.631	0.711	0.661	0.314	0.517	0.584	0.550	0.515	0.581	0.665
5CYT	800	103	0.331	0.333	0.266	0.435	0.102	0.402	0.458	0.327	0.431	0.248
1QAU	812	112	0.620	0.580	0.617	0.563	0.533	0.526	0.546	0.286	0.587	0.758
2QJL	816	99	0.594	0.407	0.546	0.327	0.497	0.403	0.620	0.048	0.610	0.297
2NUH	818	104	0.771	0.756	0.696	0.738	0.685	0.834	0.871	0.508	0.878	0.734
2CE0	828	99	0.529	0.710	0.629	0.326	0.628	0.626	0.651	0.479	0.726	0.307

^aSee descriptions in Table 1

Table 3.

B-factor correlations for large-sized structures^a

ID	TA	TR	GNM(Cα)	GNM(N)	GNM(C)	GNM(Cβ)	cgNMA(Cα)	cgNMA(N)	cgNMA(C)	cgNMA(Cβ)	cgNMA(M)	NMA
1V70	832	105	0.162	0.166	0.190	0.424	0.285	0.279	0.281	0.395	0.282	0.265
1RRO	846	108	0.418	0.616	0.257	0.277	0.546	0.305	0.216	0.272	0.200	0.115
3VUB	855	101	0.607	0.512	0.618	0.273	0.365	0.278	0.338	0.295	0.324	0.300
1CCR	855	111	0.351	0.322	0.331	0.323	0.530	0.288	0.541	0.343	0.509	0.379
1EW4	863	106	0.547	0.314	0.357	0.625	0.447	0.645	0.671	0.200	0.693	0.542
2VIM	864	104	0.212	0.094	0.160	0.347	0.221	0.312	0.282	0.104	0.357	0.243
2I24	872	113	0.494	0.443	0.515	0.288	0.441	0.334	0.436	0.119	0.417	0.296
1UKU	873	102	0.742	0.721	0.773	0.710	0.720	0.335	0.486	0.255	0.462	0.519
1IFR	878	113	0.637	0.689	0.590	0.652	0.330	0.413	0.524	0.405	0.534	0.462
2CG7	879	90	0.379	0.455	0.436	0.286	0.308	0.349	0.315	0.256	0.364	0.355
1PZ4	890	113	0.843	0.838	0.809	0.766	0.844	0.801	0.861	0.731	0.873	0.702
1WPA	906	107	0.417	0.254	0.214	0.385	0.380	0.476	0.638	0.261	0.568	0.459
1AHO	925	64	0.562	0.393	0.413	0.504	0.339	0.349	0.474	0.217	0.496	0.552
1QTO	934	122	0.334	0.374	0.293	0.422	0.725	0.599	0.622	0.462	0.670	0.672
1WHI	937	122	0.270	0.307	0.224	0.382	0.414	0.348	0.222	0.068	0.290	0.492
1PMY	937	123	0.685	0.575	0.660	0.478	0.702	0.530	0.699	0.282	0.715	0.262
2PPN	963	107	0.668	0.590	0.579	0.476	0.468	0.281	0.535	0.287	0.492	0.542
1NKO	991	122	0.368	0.409	0.437	0.411	0.322	0.525	0.476	0.383	0.539	0.583
1E5K	1423	188	0.859	0.662	0.727	0.716	0.620	0.620	0.625	0.380	0.684	0.741
2R16	1476	175	0.616	0.625	0.580	0.355	0.411	0.545	0.444	0.136	0.487	0.579
2VYO	1609	206	0.761	0.768	0.773	0.621	0.739	0.642	0.732	0.308	0.760	0.645
2IMF	1700	203	0.514	0.503	0.513	0.565	0.401	0.514	0.552	0.020	0.541	0.491
1O08	1722	221	0.309	0.308	0.410	0.452	0.616	0.408	0.562	0.296	0.521	0.281
2C71	1736	205	0.560	0.506	0.600	0.614	0.584	0.547	0.769	0.351	0.742	0.491
1ATG	1749	231	0.497	0.553	0.543	0.409	0.154	0.288	0.233	0.188	0.323	0.465
2VPA	1750	204	0.576	0.609	0.443	0.613	0.594	0.593	0.644	0.440	0.669	0.591
1WBE	1774	204	0.549	0.559	0.539	0.495	0.574	0.522	0.485	0.411	0.538	0.575
2HQK	1810	213	0.365	0.553	0.272	0.677	0.743	0.733	0.588	0.333	0.716	0.715
2CWS	1847	227	0.696	0.690	0.640	0.566	0.524	0.644	0.596	0.346	0.642	0.618
1BYI	1848	224	0.552	0.365	0.411	0.489	0.133	0.290	0.369	0.184	0.372	0.223
1NLS	1872	237	0.515	0.580	0.486	0.502	0.385	0.568	0.554	0.484	0.628	0.813
2AGK	1885	233	0.512	0.524	0.564	0.587	0.514	0.727	0.781	0.392	0.820	0.687
2HYK	1893	237	0.515	0.550	0.483	0.556	0.593	0.396	0.491	0.351	0.523	0.392
3SEB	1948	238	0.826	0.844	0.859	0.709	0.720	0.666	0.699	0.538	0.745	0.709
2V9V	2387	135	0.528	0.578	0.424	0.514	0.594	0.663	0.471	0.216	0.572	0.663

^aSee description in Table 1

In Tables 1, 2, and 3, we see consistently that the results from cgNMA methods are comparable with GNM except when C_β atoms are used as the representative atoms. Both types of methods performed much better than NMA. Among all these methods, it seems that cgNMA(M) performed the best for all three categories of structures. Tables 4, 5, and 6 compare the test results for different pairs of methods for small, medium, and large structures, respectively. In these tables, we compare the B-factor correlations of the residue mean-square-fluctuations of the structures produced by each pair of methods, method A vs. method B, denoted as A-B. We list the numbers of B-factor correlations of method A that are significantly higher (or lower (−) than that of method B. If the difference of two B-factor correlations is within 1.0e–02, we consider them to be comparable (=). From these tables, we see more clearly how different methods performed and compared to each other. It seems that GNM using C_α as the representative atom performed the best among all GNM methods; cgNMA using N or C as the representative atom performed better than using C_α or C_β; cgNMA(M) performed better than GNM(C_α) and NMA consistently.

Table 4.

Comparison of B-factor correlations for small structures^a

	cgNMA(Cα)-GNM(Cα)	cgNMA(N)-GNM(N)	cgNMA(C)-GNM(C)	cgNMA(M)-GNM(Cα)
+	13	17	17	16
−	17	13	12	14
=	3	3	4	3
	cgNMA(Cα)-NMA	cgNMA(N)-NMA	cgNMA(C)-NMA	cgNMA(M)-NMA
+	22	19	22	23
−	9	12	11	10
=	2	2	0	0

^a+: number of structures whose B-factor correlations for the two different models are positive; −: number of structures whose B-factor correlations for the two different models are negative; =: number of structures whose B-factor correlations for the two different models are comparable

Table 5.

Comparison of B-factor correlations for medium-sized structures^a

	cgNMA(Cα)-GNM(Cα)	cgNMA(N)-GNM(N)	cgNMA(C)-GNM(C)	cgNMA(M)-GNM(Cα)
+	10	19	19	23
−	24	16	13	9
=	2	1	4	4
	cgNMA(Cα)-NMA	cgNMA(N)-NMA	cgNMA(C)-NMA	cgNMA(M)-NMA
+	15	18	21	25
−	20	16	13	9
=	1	2	2	2

^aSee descriptions in Table 4

Table 6.

Comparison of B-factor correlations for large-sized structures^a

	cgNMA(Cα) - GNM(Cα)	cgNMA(N) - GNM(N)	cgNMA(C) - GNM(C)	cgNMA(M) - GNM(Cα)
+	13	13	19	18
−	19	22	15	15
=	3	0	1	2
	cgNMA(Cα)-NMA	cgNMA(N)-NMA	cgNMA(C)-NMA	cgNMA(M)-NMA
+	15	15	19	22
−	18	15	16	11
=	2	5	0	2

^aSee descriptions in Table 4

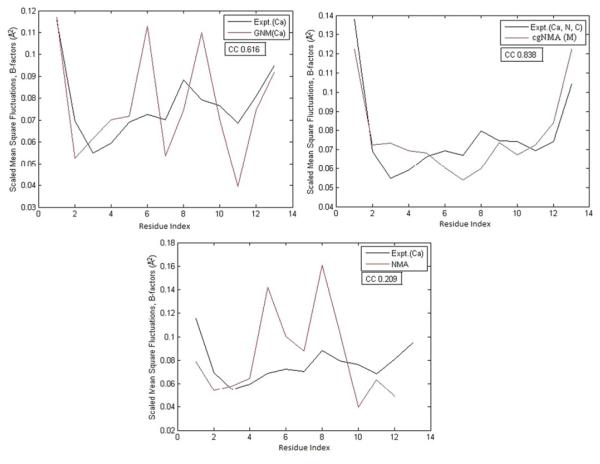
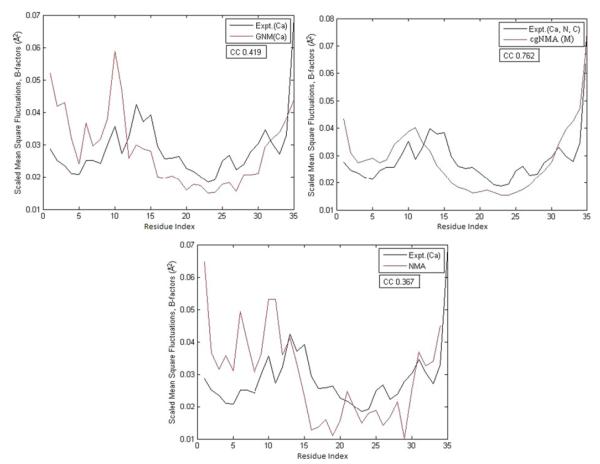
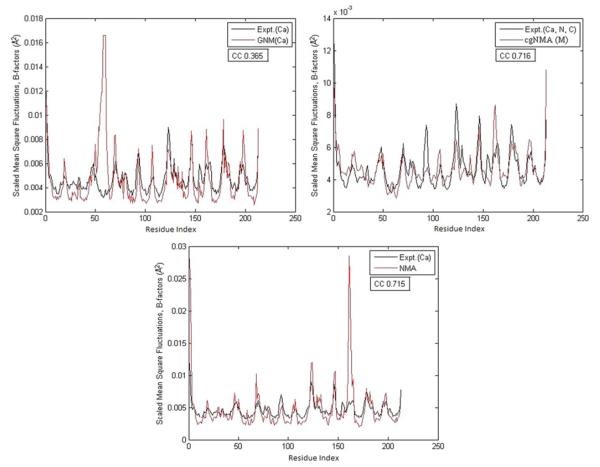
Figures 3, 4, and 5 demonstrate the test results on three example structures, 1HJE, 2BF9, and 2HQK, each representing a small, medium, and large structure. For each structure, the residue mean-square-fluctuations calculated by GNM(C_α), cgNMA(M), and NMA are shown in red curves. The experimental B-factors of the representative atoms are shown in black curves. In Fig. 3, the B-factor correlations of the residue mean-square-fluctuations of the structure calculated by GNM(C_α), cgNMA(M), and NMA are 0.616, 0.838, and 0.209, respectively. In Fig. 4, the B- factor correlations of the residue mean-square-fluctuations of the structure calculated by GNM(C_α), cgNMA(M), and NMA are 0.419, 0.762, and 0.367, respectively. In Fig. 5, the B-factor correlations of the residue mean-square-fluctuations of the structure calculated by GNM(C_α), cgNMA(M), and NMA are 0.365, 0.716, and 0.715, respectively.

Fig. 3.

(a) The residue mean-square-fluctuations calculated by GNM(C_α) for 1HJE are compared with the experimental B-factors of C_α. (b) The residue mean-square-fluctuations calculated by cgNMA(M) for 1HJE are compared with the experimental B-factors of C_α. (c) The residue mean-square-fluctuations calculated by NMA for 1HJE are compared with the experimental B-factors of C_α

Fig. 4.

(a) The residue mean-square-fluctuations calculated by GNM(C_α) for 2BF9 are compared with the experimental B-factors of C_α. (b) The residue mean-square-fluctuations calculated by cgNMA(M) for 2BF9 are compared with the experimental B-factors of C_α. (c) The residue mean-square-fluctuations calculated by NMA for 2BF9 are compared with the experimental B-factors of C_α

Fig. 5.

(a) The residue mean-square-fluctuations calculated by GNM(C_α) for 2HQK are compared with the experimental B-factors of C_α. (b) The residue mean-square-fluctuations calculated by cgNMA(M) for 2HQK are compared with the experimental B-factors of C_α. (c) The residue mean-square-fluctuations calculated by NMA for 2HQK are compared with the experimental B-factors of C_α

5 Refined Gaussian Network Model

In this section, we present a new Gaussian Network Model based on our study on coarse-grained NMA as described in Sect. 4. We consider the requirement on an energy function as a key distinction between GNM and NMA. Indeed, the coarse-grained NMA in Sect. 4 still requires the availability of an energy function to obtain the Hessian matrix, although it conducts the same analysis as GNM at the residue level. However, we do see that with nonhomogeneous force constants extracted from the Hessian matrix, the coarse-grained NMA such as cgNMA(M) performs better than GNM. The question then is whether or not GNM can be improved by introducing some nonhomogeneous force constants, yet without requiring the Hessian matrix from an energy function.

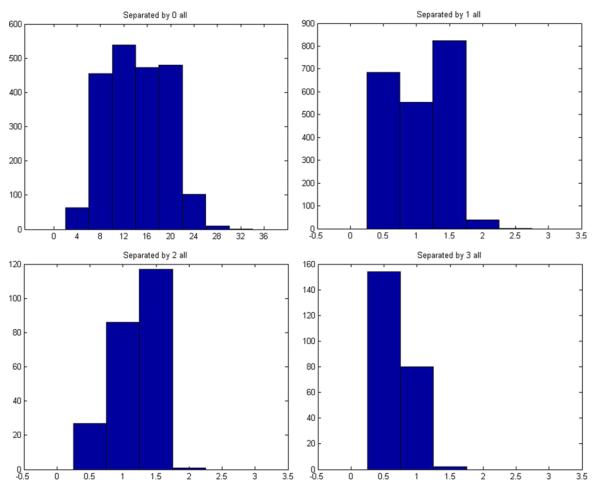
In order to answer this question, we have examined the Hessian matrices of our downloaded structures. We collected all the force constants (the entries in the Hessian matrices) defined in cgNMA(M). For each structure, we have a matrix of force constants {k_ij : i,j = 1,…, m} where m is the number of residues in the structures. We then grouped the constants for all the residue pairs in contact but separated by s residues in sequence, where s = 0, 1, 2, 3, etc. For a fixed s, different residue pairs do not have significantly different force constants. However, for different s, the force constants are different, especially between the directly connected pairs (s = 0) and other types of pairs (s > 0). Figure 6 shows the distributions of the force constants for residue pairs in contact but separated by 0, 1, 2, 3 residues in sequence. Clearly, the constants are around 12 units when s = 0, and are all around 1 unit when s > 0. Based on the above survey, we have a reason to suggest that the forces between the residue pairs in contact should not be treated as the same. At the very least, the forces between directly connected residue pairs should be stronger than others in a magnitude. In other words, the force constants for directly connected residue pairs should be at least one magnitude larger than others. These constants correspond exactly to the bidiagonal elements of the contact matrices. Therefore, a simple way to build a new Gaussian Network Model that incorporates this nonhomogeneity of the force constants is to define all the entries of the contact matrix in the same way as the conventional GNM except for the bidiagonal entries set to a number of larger mag nitude, say −10. Such a model may reflect more accurately the real residue interactions in proteins. We call it a GNM model with nonhomogeneous force constants or nhGNM for short. An example nhGNM contact matrix can be found in Fig. 7. We have tested the nhGNM model on a large set of protein structures, each time with the force constants for directly connected residue pairs set to −8, −9, −10, −11, −12, −13, −14, or −15, to see if the results vary with varying these constants. Again, we divide the structures into three groups corresponding to relatively small-, medium-, and large-sized structures. The test results on each group are shown in Tables 7, 8, and 9 separately. In each table, we show the B-factor correlations of the residue mean-square-fluctuations of the proteins calculated by nhGNM. For comparison, we have also listed the B-factor correlations obtained using GNM. For both types of models, C_α atoms were used as the representative atoms for the residues. We use “+” to mean that nhGNM with one of the selected force constants has a higher B-factor correlation than GNM,“−” to mean the opposite. We use “=” to mean that the difference in the B-factor correlations computed by GNM and nhGNM is small within 1.0e–02.

Fig. 6.

The distributions of the force constants for pairs of residues separated by 0,1,2,3 residues in sequence.

Fig. 7.

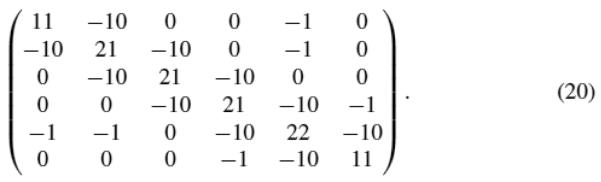
An example of an nhGNM contact matrix.

Table 7.

B-factor correlations of nhGNM for small-sized structures^a

ID	TA	TR	GNM	nhGNM-8	nhGNM-9	nhGNM-10	nhGNM-11	nhGNM-12	nhGNM-13	nhGNM-14	nhGNM-15	nhGNM-GNM
2OLX	35	4	0.885	0.885	0.885	0.885	0.885	0.885	0.885	0.885	0.885	=
2OL9	51	6	0.689	0.891	0.894	0.897	0.898	0.9	0.901	0.902	0.903	+
1YJO	55	6	0.434	0.43	0.43	0.43	0.43	0.43	0.43	0.43	0.43	=
1XY2	69	8	0.562	0.557	0.548	0.54	0.532	0.525	0.518	0.512	0.506	=
1NOT	96	13	0.523	0.72	0.724	0.726	0.728	0.729	0.729	0.728	0.727	+
1PEN	109	16	0.270	0.236	0.228	0.22	0.213	0.207	0.201	0.196	0.191	−
1OB4	110	5	−0.744	−0.744	−0.744	−0.744	−0.744	−0.744	−0.744	−0.744	−0.744	=
1OB7	111	5	−0.463	−0.463	−0.463	−0.463	−0.463	−0.463	−0.463	−0.463	−0.463	=
1AKG	112	16	0.185	−0.038	−0.054	−0.068	−0.079	−0.09	−0.099	−0.107	−0.115	−
1KYC	138	15	0.754	0.744	0.745	0.746	0.747	0.748	0.748	0.749	0.75	=
1ETN	147	12	−0.274	−0.503	−0.51	−0.515	−0.518	−0.521	−0.523	−0.524	−0.526	=
1ETL	147	12	0.628	0.5	0.483	0.468	0.455	0.444	0.435	0.426	0.419	−
1PEF	153	18	0.808	0.853	0.856	0.859	0.862	0.864	0.866	0.868	0.869	+
1ETM	160	12	0.432	0.159	0.138	0.121	0.106	0.094	0.084	0.075	0.067	−
1O06	172	20	0.844	0.907	0.91	0.912	0.914	0.916	0.917	0.918	0.919	+
1HJE	214	13	0.616	0.856	0.86	0.862	0.864	0.864	0.863	0.862	0.86	+
1P9I	225	29	0.625	0.61	0.608	0.607	0.605	0.604	0.603	0.602	0.601	−
2JKU	255	35	0.656	0.621	0.621	0.621	0.622	0.622	0.623	0.624	0.624	−
1RJU	257	36	0.431	0.42	0.416	0.413	0.409	0.406	0.402	0.398	0.395	=
2NLS	273	36	0.530	0.55	0.545	0.539	0.532	0.525	0.517	0.508	0.499	+
1VRZ	277	13	0.327	0.134	0.105	0.079	0.055	0.032	0.012	−0.006	−0.023	−
1AIE	295	31	0.155	0.287	0.3	0.312	0.323	0.333	0.343	0.351	0.36	+
1GK7	335	39	0.821	0.821	0.82	0.82	0.82	0.82	0.82	0.82	0.819	=
1Q9B	345	43	0.656	0.814	0.818	0.821	0.823	0.824	0.824	0.824	0.823	+
1YZM	361	46	0.901	0.94	0.941	0.943	0.944	0.944	0.945	0.946	0.946	+
6RXN	367	45	0.594	0.534	0.529	0.524	0.52	0.516	0.512	0.509	0.505	−
1USE	382	40	−0.142	−0.303	−0.311	−0.318	−0.323	−0.328	−0.333	−0.337	−0.34	=
1BX7	387	51	0.706	0.801	0.806	0.811	0.815	0.818	0.821	0.823	0.825	+
2DSX	399	52	0.127	0.057	0.059	0.061	0.064	0.067	0.071	0.075	0.079	−
1UOY	452	64	0.671	0.691	0.691	0.691	0.691	0.691	0.691	0.69	0.689	+
1U06	470	55	0.434	0.43	0.428	0.427	0.426	0.425	0.424	0.424	0.423	=
1GVD	491	52	0.591	0.361	0.35	0.341	0.334	0.328	0.322	0.318	0.314	−
1FF4	503	65	0.674	0.755	0.76	0.765	0.769	0.773	0.777	0.78	0.783	+

^aID-protein ID, TA-total number of atoms, TR-total number of residues, GNM—residue B-factor correlations using GNM, nhGNM-k—residue B-factor correlations using nhGNMwith -k as the value for the bidiagonal elements in the contact matrix, nhGNM-GNM—comparison between nhGNM and GNM: “+”—nhGNM has a higher B-factor correlation than GNM, “−”—nhGNM has a lower B-factor correlation than GNM, “=”—nhGNM has a comparable B-factor correlation with GNM

Table 8.

B-factor correlations of nhGNM for medium-sized structures^a

ID	TA	TR	GNM	nhGNM -8	nhGNM-9	nhGNM- 10	nhGNM- 11	nhGNM- 12	nhGNM- 13	nhGNM- 14	nhGNM- 15	nhGNM- GNM
1LR7	522	73	0.620	0.693	0.7	0.706	0.712	0.717	0.722	0.727	0.731	+
1ZVA	551	75	0.690	0.626	0.616	0.606	0.597	0.588	0.579	0.571	0.563	−
2BF9	562	35	0.419	0.596	0.601	0.605	0.607	0.608	0.609	0.609	0.608	+
2EHS	598	75	0.747	0.648	0.637	0.627	0.618	0.609	0.601	0.593	0.586	−
1UHA	623	82	0.583	0.578	0.573	0.568	0.563	0.558	0.554	0.549	0.544	=
1FK5	626	93	0.485	0.44	0.434	0.427	0.421	0.415	0.409	0.403	0.398	−
1OPD	642	85	0.398	0.583	0.598	0.611	0.623	0.634	0.644	0.653	0.661	+
1X3O	642	80	0.654	0.589	0.58	0.572	0.564	0.557	0.55	0.543	0.537	−
2E3H	651	81	0.605	0.663	0.665	0.666	0.666	0.665	0.665	0.663	0.661	+
1USM	661	77	0.798	0.727	0.719	0.712	0.705	0.699	0.693	0.688	0.683	−
1ULR	677	87	0.495	0.433	0.42	0.407	0.395	0.383	0.371	0.359	0.349	−
1I71	683	83	0.549	0.508	0.51	0.512	0.515	0.517	0.519	0.522	0.524	−
2PKT	688	91	−0.286	−0.246	−0.242	−0.237	−0.234	−0.23	−0.226	−0.223	−0.22	=
1N7E	700	95	0.497	0.473	0.474	0.474	0.474	0.475	0.475	0.475	0.476	−
2IP6	702	87	0.572	0.654	0.661	0.667	0.673	0.679	0.684	0.689	0.694	−
2EAQ	705	89	0.695	0.797	0.797	0.796	0.794	0.792	0.79	0.788	0.786	+
2FQ3	721	85	0.348	0.259	0.252	0.246	0.24	0.235	0.23	0.225	0.221	−
2RB8	723	93	0.517	0.564	0.564	0.565	0.564	0.564	0.564	0.563	0.562	+
1GXU	726	88	0.421	0.352	0.347	0.341	0.337	0.332	0.328	0.325	0.322	−
2PLT	727	98	0.481	0.479	0.476	0.472	0.469	0.466	0.462	0.459	0.456	=
1ABA	728	87	0.613	0.412	0.392	0.372	0.354	0.337	0.321	0.306	0.291	−
1R7J	729	90	0.368	0.219	0.231	0.208	0.204	0.2	0.197	0.194	0.191	−
1V05	731	96	0.632	0.641	0.636	0.632	0.627	0.622	0.618	0.613	0.608	+
1CYO	731	88	0.741	0.733	0.731	0.729	0.727	0.725	0.724	0.722	0.721	=
3BZQ	742	99	0.466	0.495	0.497	0.499	0.501	0.502	0.503	0.504	0.505	+
1W2L	746	97	0.397	0.388	0.384	0.38	0.377	0.374	0.372	0.369	0.367	=
2MCM	769	112	0.820	0.875	0.876	0.877	0.878	0.878	0.878	0.878	0.878	+
1Z21	771	96	0.433	0.305	0.297	0.29	0.283	0.277	0.272	0.267	0.262	−
2BRF	775	100	0.710	0.716	0.713	0.711	0.708	0.706	0.703	0.701	0.699	+
1NOA	778	113	0.615	0.661	0.662	0.663	0.663	0.663	0.663	0.663	0.662	+
1NNX	780	93	0.631	0.566	0.556	0.546	0.537	0.528	0.519	0.511	0.504	−
5CYT	800	103	0.331	0.235	0.223	0.212	0.202	0.192	0.183	0.173	0.165	−
1QAU	812	112	0.620	0.615	0.613	0.611	0.609	0.607	0.605	0.604	0.602	=
2QJL	816	99	0.594	0.569	0.56	0.552	0.544	0.537	0.53	0.523	0.517	−
2NUH	818	104	0.771	0.791	0.788	0.784	0.78	0.777	0.773	0.769	0.765	+
2CE0	828	99	0.529	0.606	0.612	0.616	0.621	0.625	0.628	0.631	0.634	+

^aSee descriptions in Table 7.

Table 9.

B-factor correlations of nhGNM for large-sized structures^a

ID	TA	TR	GNM	nhGNM-8	nhGNM-9	nhGNM-10	nhGNM-11	nhGNM-12	nhGNM-13	nhGNM-14	nhGNM-15	nhGNM-GNM
1V70	832	105	0.162	0.171	0.17	0.17	0.17	0.17	0.17	0.169	0.169	=
1RRO	846	108	0.418	0.626	0.641	0.654	0.665	0.676	0.685	0.693	0.701	+
3VUB	855	101	0.607	0.622	0.614	0.605	0.597	0.589	0.581	0.573	0.566	+
1CCR	855	111	0.351	0.398	0.402	0.407	0.411	0.414	0.418	0.421	0.425	+
1EW4	863	106	0.547	0.369	0.355	0.343	0.333	0.323	0.314	0.306	0.299	−
2VIM	864	104	0.212	0.252	0.253	0.254	0.254	0.254	0.253	0.253	0.252	+
2I24	872	113	0.494	0.476	0.474	0.472	0.47	0.469	0.468	0.467	0.466	−
1UKU	873	102	0.742	0.77	0.771	0.772	0.772	0.773	0.773	0.773	0.773	+
1IFR	878	113	0.637	0.561	0.551	0.541	0.532	0.524	0.516	0.508	0.501	−
2CG7	879	90	0.379	0.366	0.367	0.368	0.368	0.369	0.37	0.371	0.371	=
1PZ4	890	113	0.843	0.858	0.857	0.855	0.853	0.852	0.85	0.848	0.846	+
1WPA	906	107	0.417	0.446	0.446	0.446	0.446	0.445	0.445	0.444	0.444	+
1AHO	925	64	0.562	0.521	0.516	0.511	0.506	0.502	0.497	0.493	0.489	−
1QTO	934	122	0.334	0.362	0.366	0.369	0.372	0.375	0.378	0.381	0.384	+
1WHI	937	122	0.270	0.3	0.305	0.31	0.314	0.319	0.323	0.326	0.33	+
1PMY	937	123	0.685	0.667	0.661	0.656	0.651	0.647	0.643	0.639	0.636	−
2PPN	963	107	0.668	0.638	0.635	0.633	0.631	0.629	0.627	0.625	0.624	−
1NKO	991	122	0.368	0.347	0.344	0.341	0.338	0.335	0.332	0.329	0.326	−
1E5K	1423	188	0.859	0.827	0.821	0.815	0.809	0.804	0.798	0.793	0.789	−
2R16	1476	175	0.616	0.608	0.601	0.594	0.588	0.582	0.576	0.57	0.564	−
2VYO	1609	206	0.761	0.787	0.784	0.78	0.777	0.773	0.77	0.767	0.763	+
2IMF	1700	203	0.514	0.492	0.49	0.488	0.486	0.484	0.483	0.482	0.48	−
1O08	1722	221	0.309	0.362	0.368	0.373	0.378	0.383	0.388	0.392	0.397	+
2C71	1736	205	0.560	0.607	0.606	0.604	0.602	0.6	0.598	0.596	0.595	+
1ATG	1749	231	0.497	0.52	0.518	0.515	0.513	0.51	0.507	0.504	0.501	+
2VPA	1750	204	0.576	0.593	0.594	0.594	0.594	0.593	0.592	0.591	0.59	+
1WBE	1774	204	0.549	0.557	0.555	0.553	0.551	0.55	0.548	0.546	0.545	+
2HQK	1810	213	0.365	0.244	0.237	0.231	0.225	0.221	0.216	0.212	0.208	−
2CWS	1847	227	0.696	0.699	0.697	0.696	0.694	0.692	0.69	0.688	0.686	=
1BYI	1848	224	0.552	0.454	0.444	0.435	0.426	0.418	0.411	0.404	0.397	−
1NLS	1872	237	0.515	0.579	0.578	0.577	0.575	0.574	0.572	0.57	0.568	+
2AGK	1885	233	0.512	0.579	0.573	0.567	0.561	0.554	0.549	0.543	0.538	+
2HYK	1893	237	0.515	0.569	0.569	0.568	0.567	0.566	0.565	0.563	0.562	+
3SEB	1948	238	0.826	0.853	0.851	0.848	0.845	0.842	0.838	0.835	0.832	+
2V9V	2387	135	0.528	0.555	0.556	0.556	0.557	0.558	0.559	0.56	0.561	+

^aSee descriptions in Table 7

We see from Tables 7, 8, and 9 that in many test cases, the nhGNM performed significantly better than GNM. Out of total 33 relatively small-sized structures, nhGNM predicted the residue mean-square-fluctuations no worse than GNM for 23 cases (Table 7). nhGNM outperformed GNM significantly for 12 cases. Out of total 36 relatively medium-sized structures, nhGNM predicted the residue mean-square-fluctuations no worse than GNM for 19 cases. nhGNM outperformed significantly GNM for 13 cases. Out of total 35 relatively large-sized structures, nhGNM predicted the residue mean-square-fluctuations no worse than GNM for 23 cases. nhGNM out-performed GNM significantly for 20 cases.

Note that in general, nhGNM performed similarly for the tested force constants for directly connected residue pairs {−8, −9, −10, −11, −12, −13, −14, −15}. We were not able to identify an optimal value, but we would suggest just using −12 for such contact pairs while −1 for all other types. It is also possible to run nhGNM multiple times for this whole set of force constants, remove obvious outliers, and take the average results.

6 Concluding Remarks

In this paper, we have investigated several possible approaches to coarse-grained normal mode analysis. Similar to GNM, we take the residues as the basic units in a protein and use a single backbone atom (or a combination of several backbone atoms) to represent each residue. Different from GNM, the force constants for pairs of representative atoms are not the same and are instead extracted from the Hessian matrix of the energy function.

Using the new models, we have calculated the mean-square-fluctuations of the residues and their correlations with the experimental B-factors (called the B-factor correlations) for a large set of proteins. We have compared them with the all-atom normal mode analysis and the residue-level Gaussian Network Model. We have shown that our models performed more efficiently than the all-atom normal mode analysis, and the B-factor correlations are also higher. The B-factor correlations are comparable with those estimated by the Gaussian Network Model and in some cases better.

Following the development of the coarse-grained NMA, we have conducted a statistical survey on the extracted force constants, for different pairs of residues with different numbers of separation residues in sequence. We then based on their statistical averages to build a refined Gaussian Network Model. We have shown that the force constants for the neighboring residue pairs are always about one-magnitude larger than other pairs in contact. Therefore, in the refined GNM, the entries of the contact matrix could be defined in the same way as the conventional GNM except that the bidiagonal entries have large magnitudes. We have shown that such a simply refined GNM could predict residue-level structural fluctuations significantly better than the conventional GNM in many test cases.

The coarse-grained NMA and refined GNM do not always outperform conventional methods such GNM. In our future efforts, we would like to examine each of our test cases more carefully and find the causes for the disagreements between the predicted structural fluctuations and the experimental B-factors, and to further improve our predictions. We would also like to apply our methods to a few biologically interesting proteins such as the HIV-1 protease and the human telomerase and analyze the results in great details. The structures of these proteins have just been modeled in recent studies (Yang et al. 2008; Steczkiewicz et al. 2011). Accurate predictions on their structural fluctuations may provide great insights into how the dynamics of the structures relate to their functions.

Another direction to explore is to develop a relatively accurate residue-level energy function so that the residue-level NMA can be carried out exactly as the atomic-level NMA. This could be difficult but challenging because of the lack of complete physical understanding of the residue interactions. Much work has been done for developing residue-level potentials using statistical approaches such as residue-residue contact potentials (Miyazawa and Jernigan 1985; Sippl 1990), residue distance or angle potentials (Kuszewski et al. 1996; Wu et al. 2007a, 2007b; Huang et al. 2011), and residue C_α only potentials (Wu et al. 2007a, 2007b). These residue-level potentials may provide a basis for defining a complete residue-level energy function, with which a residue-level NMA can be performed.

Note that the B-factor is a consequence of the dynamic disorder in the crystal caused by the temperature-dependent vibration of the atoms in the structure (Drenth 2006). This is the reason that we can compare the computed atomic or residue mean-square fluctuations with the B-factors detected by X-ray crystallography. However, protein crystals have also static disorder: molecules, or parts of molecules, in different unit cells do not occupy exactly the same position or have exactly the same orientation (Drenth 2006). With this static disorder also included, the B-factor may not always reflect the atomic fluctuations correctly. In future work, we will consider to compare the computed atomic or residue mean-square fluctuations with the atomic or residue fluctuations in NMR structural ensembles, for which a better correlation between theoretically computed and experimentally estimated structural fluctuations may be obtained.

Finally, we would like to point out that the phrase “coarse-grained NMA” can be confusing. In general, by “coarse-grained NMA” we mean the normal mode analysis beyond the atomic level. More specifically, we mean the residue-level normal mode analysis requiring the Hessian or partial Hessian of the energy function, which is different from the analysis via other nonenergy-based methods such as GNM. In this sense, the residue-level normal mode analysis we have conducted using the force constants extracted from the Hessian of the energy function is still called the coarse-grained NMA. So is the residue-level NMA to be explored using a residue-level energy function.