Principles of Chemical Bonding and Band Gap Engineering in Hybrid Organic–Inorganic Halide Perovskites

Abstract

The performance of solar cells based on hybrid halide perovskites has seen an unparalleled rate of progress, while our understanding of the underlying physical chemistry of these materials trails behind. Superficially, CH₃NH₃PbI₃ is similar to other thin-film photovoltaic materials: a semiconductor with an optical band gap in the optimal region of the electromagnetic spectrum. Microscopically, the material is more unconventional. Progress in our understanding of the local and long-range chemical bonding of hybrid perovskites is discussed here, drawing from a series of computational studies involving electronic structure, molecular dynamics, and Monte Carlo simulation techniques. The orientational freedom of the dipolar methylammonium ion gives rise to temperature-dependent dielectric screening and the possibility for the formation of polar (ferroelectric) domains. The ability to independently substitute on the A, B, and X lattice sites provides the means to tune the optoelectronic properties. Finally, ten critical challenges and opportunities for physical chemists are highlighted.

Introduction

Hybrid organic–inorganic halides have been of interest since the start of the 20th century;¹ however, the first report of a perovskite-structured hybrid halide appears to have been by D. Weber in 1978.^2,3 In the same journal volume, he reported both CH₃NH₃PbX₃ (X = Cl, Br, I) and the CH₃NH₃SnBr_1–xI_x solid solution. In the subsequent decades, these materials were studied in the context of their solid-state chemistry and physics,⁴⁻⁶ with the first solar cell reported in 2009.⁷ The resulting explosion of research effort and success in the photovoltaic applications of these materials has been the subject of many review papers and commentaries.⁸⁻¹⁴

Hundreds of materials have been tried and tested for use as light absorbing layers in solar cells, so one question has been frequently posed: what makes hybrid halide perovskites special? The question is difficult to answer with certainty as our understanding of the physical properties of these materials, including how the solar cells operate, continues to evolve. One of the unique features of this class of material is their large dielectric constants (ϵ₀ > 20), compared to conventional semiconductors (ϵ₀ < 20), which include a rotational component associated with molecular dipole relaxation.

The aim of this Feature Article is to step back and recount the fundamental physical chemistry underpinning the performance—and potential limitations—of hybrid perovskite materials. The work discussed here is primarily from our research group;^13,15−21 however, many others have contributed to the computational studies in the area. Simulations on the electronic structure, alloy formation, and lattice defects have been the subject of recent review papers.²²⁻²⁵

We previously produced a gentle introduction to the fundamental chemistry of hybrid perovskites,¹⁷ which is not duplicated here. Instead, we first discuss the principles of chemical bonding in these systems, followed by approaches to tune the electronic structure, and finally outline ten outstanding challenges in the field.

Chemical Bonding

The chemical bonding in hybrid perovskites with ABX₃ stoichiometry (shown in Figure 1) can be separated into three distinct components. It should be noted that these materials are organic–inorganic but not organometallic—following the IUPAC definition—as there is no direct bond between a metal and carbon atom. In the context of metal–organic frameworks, they are considered to be I³O⁰ materials²⁹ due to the combination of a three-dimensional inorganic network with a zero-dimensional (molecular) organic component.

Figure 1.

Schematic of the perovskite crystal structure with respect to the A, B, and X lattice sites. The redox chemistry of the component ions can be used to influence the valence and conduction band energies and orbital composition, and hence the stability of electrons and holes in the material.²⁶ Note that for larger molecular A sites layered perovskites are formed.^27,28 Beyond halide perovskites, a wider range of stoichiometries and superstructures are known, e.g., the Ruddlesden–Popper, Aurivillius, and Dion–Jacobson phases.

a. Metal Halide Framework

The bonding within the BX₃^– anionic framework is unambiguously heteropolar (mixed ionic/covalent interactions). The formal oxidation states of Pb(+2) and I(−1), resulting from the chemical composition, are a good approximation of the chemical species here. Electrostatic interactions dominate between ions with net charge. As usual, the quantification of partial charges remains ill-defined due to the collective nature of the periodic electronic wave function.^30,31 The Born effective charges in halide perovskites are large (the value for Pb can exceed 4),³² consistent with high ionicity.

The lattice energy (defined with respect to the ions held infinitely far apart) and electrostatic site potentials are listed for a range of perovskite stoichiometries in Table 1. In comparison to the three types of oxide (group VI anion) perovskite, for the halide (group VII anion) perovskite the electrostatic stabilization is notably reduced. The lattice energy is just −29.71 eV per ABX₃ cell, with an electrostatic potential on the anion site ca. 50% of the group VI anions. Due to this weaker potential alone, lower ionization potentials (workfunctions) are expected for halide perovskites compared to, for example, metal oxides.^33,34 A second consequence is that lattice vacancies are facile to form²¹ and do not result in deep ionization levels. In contrast, for rocksalt-structured metal halides, the halide is in an octahedral coordination environment with a large confining electrostatic potential. In such cases, a halide vacancy will trap electrons with ionization levels deep in the band gap: an F-center.

Table 1. Lattice Energy (eV/cell) and Site Madelung Potentials (in units of V) for a Range of ABX₃ Perovskite Compositions (Cubic Lattice, a = 6 Å) Assuming the Formal Oxidation State of Each Species^a.

stoichiometry	Elattice	VA (V)	VB (V)	VX (V)
I–V–VI3	–140.48	–8.04	–34.59	16.66
II–IV–VI3	–118.82	–12.93	–29.71	15.49
III–III–VI3	–106.92	–17.81	–24.82	14.33
I–II–VII3	–29.71	–6.46	–14.85	7.75

^aThe potentials are aligned to a common vacuum level at 0 V. The hybrid halide perovskites are of type I–II–VII₃. Reprinted with permission from ref (17). Copyright 2014 American Chemical Society.

For CH₃NH₃PbI₃, the formal electronic configurations of Pb 6s²6p⁰ and I 5p⁶ are apparent from the electronic band structure, where the upper valence band is formed from the I p orbitals and the lower conduction band is formed from the unoccupied Pb p orbitals. There is an admixture of Pb s in the valence band, but here the cationic lone pair electrons are stereochemically inactive,³⁵ at least in the equilibrium structural configuration. Polar instabilities of the Pb(II) ion are common in ferroelectric and multiferroic oxide perovskites.³⁶

Strong hybridization (orbital overlap) along the octahedral framework results in light electron (0.15 m_e) and hole (0.12 m_e) effective masses a fraction of the free electron mass.¹⁹ These light carrier masses provide the means for high-mobility band transport in high-quality materials. The high atomic numbers of lead and iodine suggest that relativistic effects are important for an accurate determination of the electronic structure.¹⁹ Many-body electron–electron interactions have been shown to be important. These factors combine to make high-quality electronic structure studies, such as relativistic GW theory, computationally and methodologically challenging. While density functional theory calculations can now be performed routinely on system sizes of up to 100 s of atoms, for relativistic quasi-particle self-consistent GW theory CH₃NH₃PbI₃ represents the most complex system studied to date. Note that this approach is superior to non-self-consistent G₀W₀ methods but still neglects electron–phonon coupling, which may be important for these structurally soft materials.

b. Intermolecular Interaction

Methylammonium is a closed-shell 18-electron cation. (In contrast to several erroneous statements in the published literature, CH₃NH₃⁺ is not a free radical.) The CH₃NH₃⁺ molecules in neighboring cages are ∼6 Å apart. The large permanent electric dipole (2.29 D with respect to the center of charge of the ion) results in an estimated electrostatic point dipole–dipole interaction energy of 25 meV.¹⁶ For two static dipoles, the interaction tails off as (1/r³); however, the screening effect of two freely rotating dipoles shortens this Keesom force (one component of the van der Waals interaction) to (1/r⁶).

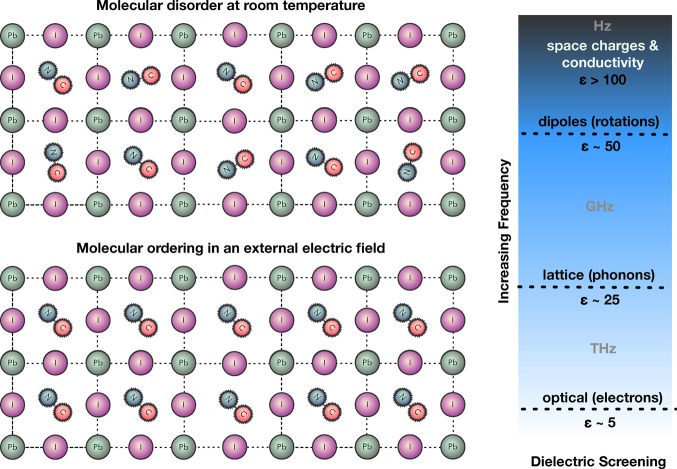
As the dipole–dipole interaction energy is comparable to available thermal energy at room temperature, we expect a complex ferroelectric behavior. Monte Carlo simulations have shown that for a fixed lattice a striped antiferroelectric alignment of dipoles is favored at low temperatures, which become increasingly disordered and finally paraelectric at high temperatures.¹⁷ At room temperature, there is significant local structure which can be linked with regions of high and low electrostatic potential. Even for a single-crystal film the topology of the electrostatic potential resembles a bulk heterojunction more familiar to organic photovoltaics. Larger polar domain structures have recently been observed from piezoelectric force microscopy, which may be associated with effects from local chemical and lattice strain.³⁷ Tunable ferroelectric polarization has also been predicted to occur in the Sn analogues.³⁸

The orientation of molecular dipoles is involved in the unusual dielectric response of CH₃NH₃PbI₃. At high (optical) frequencies, there exists the standard electronic response of the system to an applied electric field. At lower (THz) frequencies, an additional vibrational response from lattice phonons gives rise to the static dielectric constant of 25 (previously computed from density functional perturbation theory).¹⁹ The molecular response occurs at even lower frequencies (GHz regime), which can be associated with rotational order. Toward audio frequencies a “colossal” permittivity emerges, which can be linked to ionic and/or electronic conductivity: the Maxwell–Wagner effect. These contributing factors are summarized in Figure 2.

Figure 2.

Schematic of the ordering of molecular dipoles in the presence of an external electric field, as well as the four regimes in the dielectric response from lowest frequency (electronic excitations) to highest frequency (space charges and electronic or ionic conductivity). Each process will have a characteristic relaxation time and can combine to give a complex temporal response to an external perturbation.

c. Molecule–Framework Interaction

The dominant bonding between the molecule (A site) and framework is electrostatic in nature. CH₃NH₃⁺ is a positively charged ion inside a negatively charged cage, so there is a strong electrostatic potential (∼8 V; Table 1) holding the molecule at its lattice site.

An additional electrostatic contribution to the chemical bonding between the molecular dipole and the PbI₆ octahedra is the charge–dipole interaction, which is dependent on the dipole orientation. There is also the effect of primary polarization. Given the appreciable polarizability of the I^– ions (ca. 7 × 10^–24 cm³), an induced dipole interaction is expected (the so-called Debye force). Due to these interactions, a correlation is expected between molecular orientation and octahedral deformation in molecular dynamic simulations;¹⁷ more in-depth studies are ongoing. The molecular dipole–framework interaction has also been discussed in terms of hydrogen bonds; however, both interactions are electrostatic in nature and are difficult to distinguish between. The significant mobility of the cations (including hydrogen atoms) at room temperature¹⁶ does suggest that a dipole interaction is a more appropriate and general description.

The van der Waals interaction collectively describes the intermolecular (Keesom force) and molecule–framework (Debye force) interactions discussed above. It should be noted, however, that the term “van der Waals” is sometimes used synonymously with “London dispersion”. Within density functional theory, there are now many flavors of dispersion-corrected exchange-correlation functional, which aim to recover a description of the London force (secondary polarization) associated with dynamic correlation. By taking a first-generation generalized-gradient functional (e.g., PBE³⁹) which overestimates equilibrium bond lengths by 1–2%, the addition of a weakly attractive r^–6 potential will result in better agreement with experimental structures. It does not require that these interactions are “London dispersion” in nature. Our approach has been to employ a functional optimized for solids (e.g., PBEsol⁴⁰ or HSE06⁴¹), which quantitatively describes structural parameters of dense materials without system-specific parametrization. In addition to improved lattice parameters, PBEsol also describes the vibrational properties of solid-state systems more accurately.⁴²

From this discussion, it is clear that a variety of interactions give rise to the properties of the hybrid perovskites important to their photovoltaic performance. In particular, the combination of the light carrier effective masses provided by the metal halide framework and the strong dielectric screening—including the molecule–framework and intermolecular interactions—favors free carrier generation over excitons (bound electron–hole pairs) upon illumination.

Band Gap Engineering

It is possible to chemically substitute on all of the perovskite lattice sites, and appropriate examples of each can be found in the literature. It is important to recognize the chemical distinction between the three approaches.

In the limit of a small perturbation, the physical response to a hydrostatic volume change can be described by the band gap deformation potential⁴³

1

which for CH₃NH₃PbI₃ is positive (α_V^R = 2.45 eV).¹⁷ As the fundamental band gap is determined at the boundary of the Brillouin zone (R for the pseudocubic structure), the out-of-phase band-edge states are stabilized as the lattice expands. Temperature-dependent photoluminescence indicates a decrease in band gap with decreasing temperature (lattice contraction) from 1.61 eV at 300 K to 1.55 eV at 150 K, which is at the onset of a phase change.⁴⁴ The chemical effects of substitution will generally exceed this physical volume effect, as discussed below.

A-Site Substitution

The A site of CH₃NH₃PbI₃ does not directly contribute to the frontier electronic structure, but it can have an indirect influence by changing the crystal structure (Figure 3).

Figure 3.

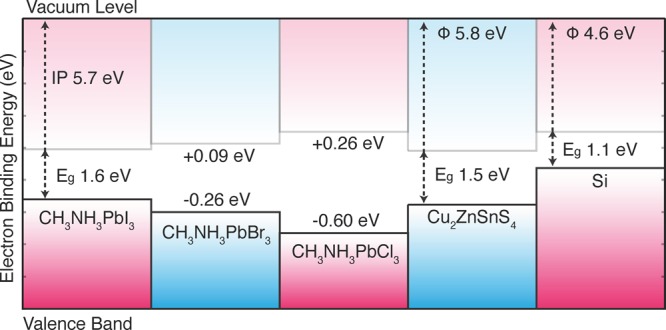
Calculated natural band offsets of CH₃NH₃PbI₃ and related materials based on density functional calculations (with quasi-particle corrections). Interfacial or surface electric dipoles (or quadrupoles) are not considered here. Adapted with permission from ref (17). Copyright 2014 American Chemical Society.

Following eq 1, lower band gap values should be observed for smaller molecular cations. The replacement of CH₃NH₃⁺ by NH₄⁺ in the perovskite lattice reduces the band gap by 0.3 eV.¹⁹ The smallest possible counterion is a proton (H⁺); HPbI₃ has a theoretical cubic perovskite lattice parameter of 6.05 Å and an associated band gap of less than 0.3 eV.¹⁷

The limitation of this logic (hydrostatic deformation) is the relationship between the size of the ion and the local structure. For example, in reality both NH₄PbI₃ and HPbI₃ adopt alternative chain or layer structures due to a mismatch in ionic radius.^45,46 The geometric constraints for the formation of a stable perovskite lattice are summed up in the radius ratio rules, which have been recently extended to hybrid perovskites.⁴⁷ An A-site ion too small for the BX₃ framework results in an instability of the octahedral networks with respect to tilting, which can change the electronic properties (e.g., a transition from an antiferroelectric to ferroelectric phase).

CH₃NH₃PbI₃ has a Goldschmidt tolerance factor of 0.91 (unstable with respect to tilting). NH₄PbI₃ has a tolerance factor of 0.76, and an alternative nonperovskite structure is favored. More asymmetric molecular ions (e.g., formamidinium, NH₂CHNH₂⁺ or FA) can also result in “built-in” structural distortions due to their deviation from spherical symmetry. The chemical and physical strains associated with the molecular substitution cannot be neglected when considering band gap engineering.⁴⁸

The choice of A-site ions that are too large for the BX₃ framework can result in layered perovskite structures (e.g., Ruddlesden–Popper type A_n–1A₂^′B_nX_3n+1 phases). The quantum confinement associated with these layered structures has itself attracted significant interest.^27,28

B-Site Substitution

Substitution on the B site can be used to directly alter the conduction band. Isovalent substitution of Pb for Sn has been successfully reported;⁴⁹ however, Sn(II) is less chemically stable in an octahedral environment.⁵⁰ Oxidation to Sn(IV) results in the low performance and high carrier concentrations found for the Sn halide perovskites. The stability of Ge(II) is further reduced, owing to its lower binding energy 4s² electrons and is unlikely to result in a candidate photovoltaic material.

The so-called “double” perovskites are well-known for metal oxides. Here the B site is substituted by two aliovalent ions (one higher and one lower oxidation state)

2

An example here would be the substitution of Pb(II) by Bi(III) and Tl(I), which is likely to reduce the electronic band gap due to the lower binding energy of the Bi 6p orbitals and the fluctuations in electrostatic potential caused by the combination of monovalent and trivalent ions. An advantage of this approach is that controlled substitutions beyond the 1:1 stoichiometry could be used to influence the n-type (excess Bi) or p-type (excess Tl) carrier concentrations.

X-Site Substitution

For CH₃NH₃PbI₃, the anion (X site) dictates the valence band energy.¹⁵ The observed band gap changes upon halide substitution are influenced by the electronic states of the anion; i.e., from Cl to Br to I the valence band composition changes from 3p to 4p to 5p with a monotonic decrease in electron binding energy (lower ionization potential). The valence band energy varies by as much as 0.6 eV between the methylammonium chloride and iodide perovskites. This holds true for other choices of the molecular ion: the substitution of Br by I in FAPbX₃ decreases the optical band gap from 2.23 to 1.48 eV.⁵¹

The successful incorporation of the tetrafluoroborate polyanion into the perovskite structure has been recently reported.⁵² We have shown, however, that both BF₄^– and PF₆^– do not hybridize significantly with Pb, which results in an increase in the band gaps and a decrease in the band widths.²⁰ Such substations, if stable structures were formed, could be exploited to produce a novel high-k dielectric with potential applications in transistors or memristors.

Conclusion and Challenges

In addition to their application in photovoltaics, hybrid halide perovskites display a rich physical chemistry. We have discussed the salient features of their chemical bonding and routes to tuning the properties beyond the widely studied methylammonium lead iodide.

Hybrid halide perovskites still pose many fundamental challenges relating to their physical chemistry and chemical physics. Ten issues of current interest include:

• 1.Local structure — the average crystal structure inferred from standard X-ray diffraction experiments is likely to be far from the local structure of the perovskite framework.
• 2.Dynamic disorder — knowledge is required of the time scales associated with molecular motion and how this changes from single crystals to thin films and with the method of preparation.
• 3.Lattice point defects — there have been reports of n-type, p-type, and intrinsic semiconducting samples of CH₃NH₃PbI₃. What causes this behavior, and how can the semiconductivity be controlled?
• 4.Ionic conductivity — many perovskite materials support vacancy-mediated ion diffusion. Is iodine, methylammonium, or hydrogen mass transport contributing to low-frequency impedance spectra?
• 5.Surface and interfaces — the chemical nature of extended defects is poorly understood, in particular the interface between the perovskite and the hole transport layer.
• 6.Ferroelectricity — simulations demonstrate short-range ferroelectric order at room temperature; however, external electric fields and internal strains will change this behavior.
• 7.Grain boundaries and domain walls — the perovskite microstructure may provide alternative pathways for conductivity and electron–hole separation or recombination. What is their form and abundance?
• 8.Increased stability — the long-term air instability of these materials is in part associated with the volatility of the molecular components. The development of alternative ions without labile protons would be advantageous.
• 9.Pb-free compositions — a major goal remains to identify a (stable) Pb-free material that maintains the same exceptional performance as CH₃NH₃PbI₃ in solar cells. The difficulty is in maintaining a small band gap with lighter metals.
• 10.Device models — there are standard electron transport models for p–n junction devices and extensions to bulk heterojunctions; however, there is no band transport model that encompasses the complex behavior of the hybrid perovskites including current–voltage hysteresis.

Biography

Prof. Aron Walsh holds the Chair of Materials Theory in the Centre for Sustainable Chemical Technologies at the University of Bath. He was awarded his BA and Ph.D from Trinity College Dublin (Ireland), completed a postdoctoral position at the National Renewable Energy Laboratory (USA), and held a Marie Curie fellowship at University College London (UK). His research combines computational technique development and applications at the interface of solid-state chemistry and physics.

The authors declare no competing financial interest.