Abstract
Background/Objectives
Older adults with chronic kidney disease (CKD) and their healthcare providers face difficult decisions about treatments that may be sensitive to prognosis. We developed mortality risk prediction models for older adults with CKD which included comorbidities and measures of health status/utilization not associated with particular co-morbid conditions (non-disease-specific measures).
Design
Retrospective cohort study
Setting
Kaiser Permanente Northwest (KPNW) Health Maintenance Organization
Participants
4,054 patients with severe CKD (estimated glomerular filtration rate <30 ml/min/1.73m2), including 1,915patients aged 65-79 and 2,139 aged ≥80 years who received care at KPNW between 2000-2008.
Measurements
We used Cox proportional hazards analysis to examine the association between selected patient characteristics and all-cause mortality and to generate age-group specific risk prediction models. Predicted and observed risks were evaluated by quintile.Predictors from our Cox models were translated into a points-based system. We used internal validation to provide best estimates of how these models might perform in an external population.
Results
Our risk prediction models used 16 characteristics to identify patients with the highest risk of mortality at 2 years for adults ages 65-79 and ≥80. Predicted and observed risks agreed within 5% for each quintile; a 4-5 fold increase in 2-year predicted mortality risk was observed between highest and lowest quintiles. The c-statistics for each model (0.68-0.69) indicated effective discrimination without evidence of significant overfit (slope shrinkage 0.06-0.09). Models for each age group performed similarly for mortality prediction at 6 months and 2 years in terms of discrimination and calibration.
Conclusion
When validated, these risk prediction models may be helpful in supporting discussions about prognosis and treatment decisions sensitive to prognosis in older adults with CKD in real-world clinical settings.
Keywords: elderly, chronic kidney disease, risk, mortality
INTRODUCTION
Chronic kidney disease (CKD) is increasingly common in older adults, affecting 30% of adults over age of 70 and 50% of adults over 80.1;2 Older adults with CKD often have limited life expectancy and high burden of comorbidity, and must often choose between a large number of recommended treatments.3-6An improved ability to predict mortality for older adults with CKD might help patients and their providers to develop treatment priorities and to set realistic expectations about the future.
Accurate prediction of mortality poses some unique challenges in older adults. Prior studies have demonstrated that the traditional risk factors likely to predict mortality among younger adults (comorbidities and anthropomorphic measures), may be less predictive in older patients for who measures of functional status and frailty may play a more significant role.7-9 Adults of all ages with CKD may be more likely to experience decline in functional status than their counterparts with normal kidney function.6
While mortality risk scores have been developed for older adults and for patients with CKD, to our knowledge there are no prediction models designed to examine risk of mortality among older CKD patients. Most risk prediction models for mortality in older adults have incorporated both traditional risk factors (comorbidities, patient demographics) and risk factors more common among the elderly, such as decreased functional status and increased healthcare utilization.10-16 In many of these models, the contribution of variables related to functional status was second only to age and was frequently equivalent to or greater than traditional comorbidities.10-12;15;16Measures of functional status may better encapsulate the severity and cumulative interactive effects of multiple comorbidities than would be afforded by considering the presence or absence of a single disease process. Conversely, available risk prediction models for mortality among adults with CKD have been age-neutral and have focused on traditional risk factors for mortality prediction without incorporating functional measures.17-20
We have utilized a retrospective cohort created from data collected as part of routine clinical care to develop risk prediction models for older adults ages 65-79 and ages ≥80 with moderate to severe CKD (estimated glomerular filtration rate, eGFR, <30 ml/min/1.73m2) to predict mortality at six months and at two years. We developed models which include both traditional risk factors for death as well as those with specific relevance to older patients, such as characteristics reflective of overall health status. Because the risk of mortality varies with age and the relative contribution of many predictors depends on age, we developed age-specific models for two age groups (65-79 and ≥80 year olds). To support the frequent need to set treatment goals over different time frames particularly given different prioritization of treatment decisions for the individual patient, we developed models for two distinct time-frames (6 months and 2 years). Our pragmatic approach to model development, using readily available clinic data selected based on clinical relevance, may improve generalizability and ease of integration of a mortality risk prediction model into the management strategy for older adults with CKD.
METHODS
Setting
We conducted a retrospective cohort study within a group-model health maintenance organization, Kaiser Permanente Northwest (KPNW), which serves approximately 450,000 individuals in the Portland, Oregon and Vancouver, Washington area; similar to the broader U.S. population, approximately 12% of this patient population is age 65 or older. A single medical record system (Epicare) has been utilized at KPNW since 1997. The institutional review boards of both KPNW and Oregon Health and Science University approved this study.
Cohort identification and follow-up
We identified a cohort of older adults (ages 65 and older) within KPNW with severe chronic kidney disease (defined as twoeGFR values of <30 ml/min/1.73m2, at least 90 and no more than 730 days apart) between the years of 2000-2008 who had not been treated with chronic dialysis. Patients with an intervening normal eGFR (>60 ml/min/1.73m2) between their two qualifying eGFR values of <30 ml/min/1.73m2 were excluded (n=1,837), to eliminate patients who did not appear to have a sustained eGFR in the target range. The second qualifying eGFR served as the index date for cohort entry and follow-up.We used the CKD-EPI equation to estimate GFR in accordance with international CKD guidelines; some data also suggest potential for improved accuracy of GFR estimation using this formula.21-23 Patients with any history of renal replacement therapy (dialysis or transplantation) were identified via linkage to an internal dialysis registry within KPNW and were excluded from cohort entry. Patients must have had at least 1 year of KPNW membership with pharmacy benefits for inclusion in the cohort. Patients were subdivided into two age groups:adults aged 65-79 years and adults ages 80 and older.
Measurement of baseline characteristics
Baseline characteristics collected during the one year period before cohort entry included comorbidities, age at cohort entry, race, gender, laboratory data, healthcare utilization, and pharmacy data.Comorbidities were identified via International Classification of Diseases, Ninth Revision (ICD-9) codes obtained from the outpatient electronic medical record. Vital statistics and laboratory data were obtained from the medical record. Creatinine was the sole laboratory value incorporated into the models; pharmacy data utilized consisted of a composite variable for number of antihypertensive medications.Pharmacy information was obtained through the KPNW pharmacy database. Age, gender, and duration of follow-up were obtained through the enrollment database. Healthcare utilization information (frequency of hospitalizations and emergency room visits), was obtained through the linked databases. We evaluated both traditional measures andmeasure of health status and utilization that are not tied to particular comorbid conditions (we refer to these as non-disease specific measures) intended to capture functional and overall health status (e.g., frailty, increased healthcare utilization).24Traditional measures included demographics, laboratory data, vital statistics, pharmacy data, and comorbidities. Non-disease specific measures included markers of healthcare utilization (≥2 hospitalizations or emergency room visits in the 2 years prior to cohort entry) and health conditions likely to be reflective of frailty or poor functional status (weight loss of ≥10 lbs. within 12 months, a fall or hip fracture during the 2 years prior to cohort entry, or a diagnosis of dementia or orthostatic hypotension).
Identification of primary endpoint: all-cause mortality
The study outcome was all-cause mortality within 2 years of cohort entry. Deaths were ascertained using the KPNW enrollment database which records the date of death for patients who died while members of KPNW.
Sample size considerations and candidate predictor characteristics
Adequacy of sample size in the development of prediction models hinges on the number of events in relation to the number of predictor characteristics under consideration, and the subsequent degrees of freedom required. We considered 20 events per degree of freedom to be adequate, following current practice.18;25;26For adults, ages 65-79, there were 195 deaths within 6 months, and 519 within two years of cohort entry, allowing 10 and 26 degrees of freedom respectively. Ten degrees of freedom was insufficient to develop a separate and comparable multivariable model; in lieu of this,we developed a mortality prediction model for 2 years and evaluated the ability of that model to also predict mortality at 6 months. We applied the same approach to model development for adults ages 80 and older. We included both qualifying eGFR values in the model; given the correlation between these two variables, they should be interpreted as a single predictor. We examined the rate of change of eGFR for each cohort participant via a linear model using the two qualifying eGFR values. We incorporated health-status characteristics as part of a 3-tiered composite variable which designated patients has having 0, 1-2, or ≥3 of these characteristics. In developing our model, we included only those predictors for which there was <10% missing data; this specifically resulted in the exclusions of measures of proteinuria (missing in approximately 30% of cohort members). Variable selection was completed a priori before evaluating exposure-outcome associations in our data.
Statistical analysis
We used Cox Proportional Hazards Regression to evaluate the relationship of each predictor variable with mortality over two years. Continuous variables were modeled using restricted cubic splines; decisions about the number and locations of the knots were made using methods proposed by Harrell.27 Categorical variables were modeled using indicator variables.
We translated coefficients from our Cox regression model into a points-based system; higher numbers of points mean a greater risk of death. The linear predictor in the Cox model (sum of the products of coefficient by covariate) was converted to an arbitrary new “points” scale ranging from zero upward, in which the lowest-risk category for each predictor had zero points. The points scale increases linearly with the linear predictor. An increase of 50 points was equivalent to an increase in the linear predictor of 0.691, corresponding to a hazard ratio of 2.0. Patients had to score at least 235 points to place in the highest risk quintile (80th percentile or higher). These methods for conversion of regression coefficients into risk score points was well-described by the Framingham Heart Study investigators.28
We evaluated the discrimination of our models (the ability of our models to accurately assign a higher probability of mortality to patients who died), using the concordance statistic (c-statistic). A c-statistic value of 1.0 indicates perfect prediction, while a c-statistic of 0.5 indicates prediction no better than chance. Similar c-statistics and Hosmer-Lemeshow statistics for our model when applied to 2-year and 6-month follow-up allowed us to use the same model to examine mortality risk for both time periods. We used bootstrapping (re-sampling within our cohort)29to validate our model, and we used a slope shrinkage statistic to measure the degree of overfit. We examined model calibration - a measure of how well the predicted risk generated by our models agreed with actual risks- using the Hosmer-Lemeshow statistic and graphical tools. The Hosmer-Lemeshow statistic generates a chi-squared test comparing the actual risk of the outcome (mortality) to the predicted risk for each quintile of predicted risk; a non-significant value indicates good calibration, while a significant p-value indicates disagreement between the predicted and observed risks. We calculated an R2 statistic for our 2-year prediction tool to examine how much variance in mortality risk was explained by our models.30 We used R version 2.14.2 statistical software for all analyses.
RESULTS
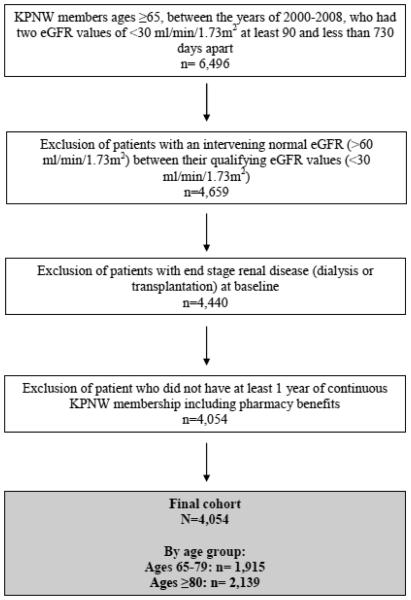
We identified 4,054 patients for inclusion in this cohort:1,915patients aged65-79 and 2,139 aged ≥80 years. (Figure 1)Women made up a slightly greater proportion of adults over 80 compared with those adults ages 65-79. (Table 1) The prevalence of comorbidities was generally similar for both age groups, although diabetes and smoking were more common in adults ages 65-79. The overall burden of non-disease specific measures (zero, 1-2, or ≥3) was comparable across age groups. All of the characteristics described in Table 1 were included in the prediction models.
Figure 1.
Flowchart for cohort development. KPNW = Kaiser Permanente Northwest Health Maintenance Organization. eGFR = estimated glomerular filtration rate.
Table 1.
Baseline characteristics of cohort; these characteristics were retained in the prediction models. The“number of antihypertensive agents” variable was incorporated into the risk score for adults age 80+, but not into the risk score for adults ages 65-79.Values provided are percentages of total cohort. eGFR = estimated glomerular filtration rate. BMI = Body mass index.
| Total cohort n= 4,054 | ||
|---|---|---|
| Baseline characteristics |
Ages 65-79
(n = 1,915) |
Ages ≥80
(n = 2,139 ) |
| Gender (% female) | 27.4 | 34.9 |
| eGFR (ml/min/1.73m2) | ||
| ≤15 | 2.7 | 2.4 |
| 16-29 | 44.6 | 50.4 |
| Coronary artery disease | 19.4 | 22.0 |
| Heart failure | 18.3 | 24.7 |
| Hypertension | 38.0 | 40.7 |
| Peripheral vascular disease | 9.9 | 9.4 |
| Diabetes | 25.0 | 14.8 |
| Stroke | 5.4 | 6.0 |
| * Tobacco abuse | 10.5 | 4.9 |
| Statin use | 26.9 | 18.3 |
| ** Number of antihypertensive medications | ||
| 0 | 2.5 | 3.8 |
| 1-2 | 1.8 | 1.8 |
| 3+ | 43.0 | 47.1 |
| BMI (kg/m2) | ||
| ≤18.5 | 0.5 | 1.4 |
| 18.6-30 | 22.8 | 32.3 |
| >30 | 20.9 | 11.3 |
| Non-disease specific measures*** | (n=1688) | (n=1640) |
| Weight loss of≥10 lbs. during a 12 month period**** | 20.5 | 17.0 |
| ≥ 2 ER or Inpatient admissions in 2 years prior to cohort entry | 29.2 | 31.2 |
| Orthostatic hypotension | 1.9 | 1.7 |
| Hip fracture during the 2 years prior to cohort entry | 0.8 | 1.7 |
| Dementia diagnosis in the 3 months prior to cohort entry | 0.8 | 1.6 |
| Fall during the 2 years prior to cohort entry | 1.8 | 3.4 |
| Number of non-disease specific measures | ||
| Zero | 15.6 | 12.4 |
| 1-2 | 32.6 | 33.0 |
| ≥3 | 2.5 | 3.9 |
Tobacco abuse refers to documentation of smoking history during the 2 year period prior to cohort entry.
Number of antihypertensive medications refers to the number of medications prescribed during the 3 months prior to index (0, 1-2, or 3+ medications)
Percent of patients with non-disease specific measures was based number of patients with two weight values during 2 year period prior to cohort entry, which was necessary for estimation of weight loss.
Two documented weights no more than 12 months apart during the 2-year baseline period prior to cohort entry were used to assess this characteristic.
Mortality rates for our cohort varied by age and length of follow-up. Six month mortality rates ranged from 10.2 (95% Confidence Interval [CI] 9.0; 11.7) for those aged 65-79 to 17.5 (95% CI 16.0; 19.2) for those aged ≥80. Two year mortality rates ranged from 27.7 (95% CI 25.8; 29.8) for those aged 65-79 to 44.2 (95% CI 42.1; 46.3) for those aged ≥80.
The relative contribution of each variable to the model is in Table 2, and the absolute risk associated with a total number of points is in Table 3.The predicted risks are adjusted for all variables in the Cox models. The relative value of a given characteristic is not comparable across age-specific models as points are assigned on an arbitrary scale within the model. The interplay of variables is what results in a patient’s overall risk; the value of an individual variable should not be considered at the expense of the complete model. The intent of Table 2 is to highlight patterns in the relationship between a given variable and mortality; the exact point total assigned to any given value of each continuous variable is not provided. We considered inclusion of a variable for rate of change of eGFR, but found this predictor did not affect net reclassification of risk and, as such, did not include that variable in the final models.
Table 2.
Points associated with patient characteristics. Data presented here provide information on general trends, range of points associated with a given characteristic, and age-specific differences in points associated with a given characteristic; all possible data points for continuous variables are not provided. The variable for antihypertensive medication use was not included in the risk score for adults age 65-79. BMI = Body Mass Index, kg/m2 GFR = glomerular filtrate rate, ml/min/1.73m2. SBP = systolic blood pressure, mmHg
| Risk score for ages 65-79
years |
Risk score for ages ≥80
years |
|||
|---|---|---|---|---|
| Characteristics | Points | |||
| Index GFR | ||||
| 30 | 0 | 0 | ||
| 20 | 41 | 32 | ||
| 10 | 74 | 63 | ||
| 2 | 100 | 89 | ||
| Second GFR | ||||
| 30 | 30 | 2 | ||
| 20 | 12 | 2 | ||
| 10 | 6 | 1 | ||
| 5 | 3 | 0 | ||
| Baseline SBP | ||||
| 240 | 0 | 0 | ||
| 180 | 19 | 1 | ||
| 140 | 30 | 2 | ||
| 120 | 33 | 12 | ||
| 80 | 35 | 45 | ||
| Age | ||||
| Age 65 | 0 | Age 80 | 0 | |
| Age 70 | 17 | Age 86 | 14 | |
| Age 75 | 18 | Age 92 | 52 | |
| Age 79 | 22 | Age 98 | 60 | |
| BMI | ||||
| 60 | 2 | 0 | ||
| 40 | 0 | 14 | ||
| 30 | 7 | 21 | ||
| 25 | 26 | 32 | ||
| 15 | 73 | 54 | ||
| 10 | 96 | 100 | ||
| Gender | ||||
| Male | 24 | 30 | ||
| Female | 0 | 0 | ||
| History of heart failure | ||||
| Present | 46 | 24 | ||
| Absent | 0 | 0 | ||
| History of cardiovascular disease | ||||
| Present | 25 | 11 | ||
| Absent | 0 | 0 | ||
| Tobacco use | ||||
| Present | 14 | 11 | ||
| Absent | 0 | 0 | ||
| History of hypertension | ||||
| Present | 0 | 0 | ||
| Absent | 12 | 7 | ||
| Statin use | ||||
| Yes | 0 | 0 | ||
| No | 23 | 15 | ||
| Antihypertensive medication use | ||||
| 0 medications | n/a | 0 | ||
| 1-2 medications | n/a | 5 | ||
| 3+ medications | n/a | 9 | ||
|
Number of non-disease specific
measures |
||||
| 0 characteristics | 0 | 0 | ||
| 1-2 characteristics | 44 | 46 | ||
| 3+ characteristics | 51 | 62 | ||
Table 3.
Points associated with percent risk of mortality at 2 years
| Risk score for ages 65-79 years | Risk score for ages ≥80 years | ||
|---|---|---|---|
| Points | Percent mortality risk | Points | Percent mortality risk |
| 66 | 5 | 45 | 10 |
| 118 | 10 | 75 | 15 |
| 149 | 15 | 97 | 20 |
| 173 | 20 | 115 | 25 |
| 191 | 25 | 129 | 30 |
| 207 | 30 | 143 | 35 |
| 220 | 35 | 155 | 40 |
| 233 | 40 | 165 | 45 |
| 244 | 45 | 176 | 50 |
| 255 | 50 | 186 | 55 |
| 265 | 55 | 195 | 60 |
| 275 | 60 | 205 | 65 |
| 285 | 65 | 214 | 70 |
| 295 | 70 | 224 | 75 |
| 305 | 75 | 234 | 80 |
| 316 | 80 | 246 | 85 |
| 328 | 85 | 259 | 90 |
| 342 | 90 | 278 | 95 |
| 361 | 95 | ||
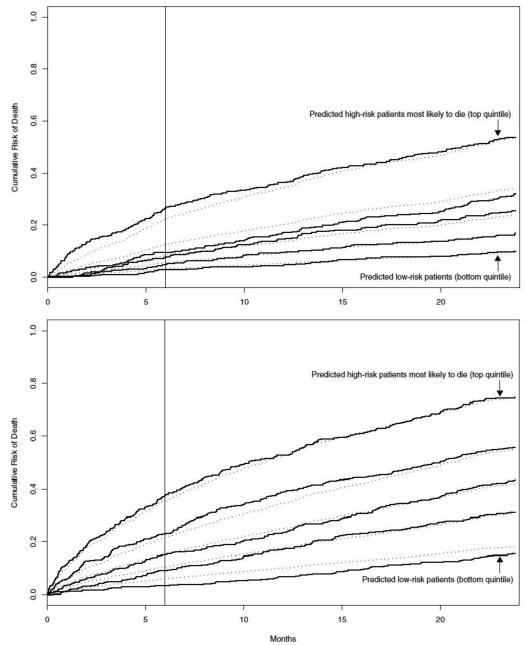
Data were examined in quintiles defined by predicted risk of mortality; predicted and observed risks agreed within 5% for each quintile. The agreement between observed and predicted risk for each model is represented in the Kaplan-Meier (Figure 2). The Hosmer-Lemeshow statistics for calibration were non-significant for ages 65-79 (13.5, p value 0.140 and 12.2, p value 0.141 on 9 degrees of freedom), and for ages ≥80 (15.6, p value 0.075 and 5.2, p value 0.74) at 6 months and 2 years respectively, suggesting adequate calibration of fit for all models.
Figure 2.
Kaplan-Meier failure plots of prediction models for ages 65-79 (top) and >80 (bottom). This Kaplan-Meier failure curve shows the observed risk (solid lines) and predicted risk (dotted lines) of mortality according to quintiles of predicted risk based on the risk score.The vertical line demarcates 6 months, whereas the overall plot ends at 24 months (2 years).
We observed a 4.6-fold difference in 2-year mortality risk across quintiles among the oldest old (age ≥80), and a 5.6-fold difference in 2-year mortality risk across quintiles among adults ages 65-79. The bootstrapped c-statistics were similar for ages 65-79 and ≥80 at two years (0.683 and 0.684, respectively) and at 6 months (0.683 and 0.685, respectively), suggesting effective and similar discrimination regardless of age and length of follow-up. The slope shrinkage values were also similar across age groups and time periods (0.09 for ages 65-79 at both time periods, 0.07 and 0.06 for ages ≥80 at 2 years and 6 months respectively), suggesting no evidence of meaningful over-fit in both populations.The R2 statistic was calculated for the 2-year mortality model, with all variables included in that model, and showed that a similar percentage of the variation in mortality was explained by the 2-year prediction models for each age group; R2 was 24.1% for ages 65-79 (95% CI 19.6%; 28.6%) and 23.0% for ages ≥80 (95% CI 19.7%; 26.4%). Calculation of an R-squared statistic for a model which excluded the composite variable for non-disease specific measures and for a model which excluded eGFR suggested that the contribution of these two predictor variables was similar.
We examined the characteristics of our 2-year model at the 6 month time period and found reasonable calibration (as evidenced by non-significant and similar Hosmer-Lemeshow statistics for both time periods) and simultaneously no overt evidence of over-fit (based on the similar and low slope-shrinkage). Similar patterns of observed versus predicted risk for both time periods are also reinforced by our Kaplan-Meier failure plots. (Figure 2)
DISCUSSION
Our risk prediction models effectively predicted mortality for adults age 65-79 and ≥80 at 6 months and 2 years, as illustrated by our c-statistics in the range of 0.68-0.69. The effective calibration of our models, supported by the calculated Hosmer-Lemeshow statistics, is critical given the potential for providers to use these models to evaluate predicted probability of death in the milieu of shared decision-making. Perhaps of greater import, the 4-7 times greater risk of 2-year mortality experienced by patients in the highest versus lowest risk quintiles is profound and likely to alter clinical management for those patients with the greatest risk of death.
Our c-statistics were consistent with those described by previous studies to predict mortality in community-dwelling older adults.11-16;18 Although the bootstrapping method we utilized provides a c-statistic which may be slightly lower than a value not based on internal re-sampling, the resultant c–statistic is more likely to reflect the discrimination these risk scores would provide in future, external, populations.
We incorporated similar predictors for the prognostic models for each age group. The only difference in models by age group was the exclusion of the “number of antihypertensive medications” variable for adults ages 65-79, due to limitations in degrees of freedom. This variable was felt to be less predictive of mortality than the other included characteristics, based on clinical expertise. The ability of our models to reasonably predict mortality across both age groups using the same predictors, despite quite different observed mortality risk by age, highlights the relevance of these characteristics to mortality risk among older adults with CKD.
The same patient characteristics predicted mortality at 6 months and 2 years with reasonable agreement between observed and predicted risk and acceptable calibration. We were not able to develop an independent risk score for 6 months due to an insufficient number of deaths. Future studies in larger cohorts could potentially utilize a greater number of deaths to evaluate other predictor variables for shorter term mortality in older adults with CKD.
The increasing prevalence of CKD in older adults, and in particular moderate to severe decrements in renal function among the oldest old, highlights the importance of age-specific risk assessment.28The development of models for age-subsets among older adults (ages 65-79 and ≥80) is a particular strength because this approach takes into account different baseline hazard for mortality which accompanies increasing age. Novelty of our prediction models was further enhanced by incorporation of both traditional risk factors and less-traditional non-disease specific measures reflective of functionality and healthcare utilization. Because those characteristics most reflective of mortality risk can differ for older versus younger adults, less traditional characteristics such as measures of functional status and healthcare utilization may play a critical role in enhancing mortality prediction for older adults with CKD.10-12;15-16 In addition, we are hopeful that the use of readily available data collected as part of routine clinical care will support greater generalizability and ease of integration of these risk prediction models into varied clinical settings, after external validation. For similar reasons, we have translated our prediction models into a point-based scoring system to provide a more user-friendly interface for future users.
Estimated GFR and the composite variable for non-disease specific measures were important contributors to the percent of mortality risk explained by our model for each age group. This is best illustrated via clinical scenarios. Hypothetical patient A, a 70 year old gentleman with a history of cardiovascular disease and hypertension whose baseline eGFR value is 20 would receive 83 points from our risk prediction model, translating to a 5-10% risk of mortality within two years (see Tables 2 and 3, ages 65-79). Hypothetical patient B, might havethe same health conditions and gender, as well as an eGFR of 10 and three or more non-disease specific measures (such as dementia, falls, and two emergency room visits in the past year) resulting in a point total of 167and a two-year mortality risk of 20-25%. A similar exercise can be performed among adults ages 80 and older; as expected, a lower burden of comorbidities is needed to achieve a similar risk of death in this oldest age group versus a comparable but younger peer.
Incorporation of change in eGFR into our models did not improve mortality prediction based on net reclassification (meaning, patients were not re-classified into a risk group more reflective of their actual risk based on inclusion of this variable in our models). This is counter to popular wisdom that rapidly declining renal function may be a surrogate for overall decline in health. We used a linear model incorporating only two eGFR values to estimate renal function decline, and it may be that a mixed-model approach which could incorporate all available eGFR data might present a more accurate picture of eGFR trajectory and could influence mortality prediction differently. We chose a linear model to optimize the accuracy of our model when generalized to broader populations, using the minimum number of eGFR values required to meet the definition of CKD. While a future study might incorporate a more complex approach to develop a variable for change in eGFR, that approach would likely come at the expense of pragmatism and generalizability.
The use of data collected as part of usual clinical care has both positive and negative implications. Our goal was to develop models that relied on data that are commonly available for older adults with CKD as part of their routine clinical care with the intention to facilitate use of this risk score across many different outpatient provider practices and health systems. Because these data are retrospective, however, we cannot assess and take into account the severity of comorbidities, which could significantly impact an individual’s mortality risk. We were also limited in collection of characteristics potentially relevant to older adults; for example, we have identified weight loss via retrospective chart review but cannot truly ascertain if weight loss was intentional or unintentional in this setting. Although we did incorporate re-sampling to internally validate our mortality prediction models, external validation in a separate cohort is necessary before consideration of incorporation of these risk scores into clinical practice.
Efforts to improve the accuracy of mortality prediction have the potential to improve care among older adults with CKD. Assuming reasonable accuracy is maintained after external validation, we are hopeful these pragmatic mortality prediction models may be valuable to older adults with CKD and their care providers to support important clinical decisions related to prognosis and prioritization of therapies including primary care decisions such as value of nephrology referral as well nephrology-specific decisions surrounding preventive and preparatory interventions such as dialysis access placement. In this way, incorporation of an age-specific, externally validated risk prediction model into CKD management for older patients may help optimize healthcare utilization, and provide a more patient-centered overall approach to care for this unique patient population.
ACKNOWLEDGMENT
Funding source: Funding for this project was provided by a National Institutes of Health, National Institute on Aging (NIA) Grants for early Medical/Surgical Specialists’ Transition to Aging Research (GEMSSTAR) R03 award.
Sponsor’s role: The funding source played no role in study design, study execution, analysis of results, or study conclusions.
Footnotes
Conflict of Interest: The editor in chief has reviewed the conflict of interest checklist provided by the authors and has determined that the authors have no financial or any other kind of personal conflicts with this paper.
REFERENCES
- (1).U.S. Renal Data System . USRDS 2013 Annual Data Report: Atlas of Chronic Kidney Disease and End-Stage Renal Disease in the United States. National Institutes of Health, National Institute of Diabetes and Digestive and Kidney Disease; Bethesda, MD: [Google Scholar]
- (2).O'Hare AM, Bertenthal D, Covinsky KE, et al. 2006;17:846–853. doi: 10.1681/ASN.2005090986. [DOI] [PubMed] [Google Scholar]
- (3).O'Hare AM, Choi AI, Bertenthal D, et al. Age affects outcomes in chronic kidney disease. J Am Soc Nephrol. 2007;18:2758–2765. doi: 10.1681/ASN.2007040422. [DOI] [PubMed] [Google Scholar]
- (4).Stevens LA, Li S, Wang C, et al. Prevalence of CKD and comorbid illness in elderly patients in the United States: Results from the Kidney Early Evaluation Program (KEEP) Am J Kidney Dis. 2010;55:S23–S33. doi: 10.1053/j.ajkd.2009.09.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Jassal SV, Chiu E, Hladunewich M. Loss of independence in patients starting dialysis at 80 years of age or older. N Engl J Med. 2009;361:1612–1613. doi: 10.1056/NEJMc0905289. [DOI] [PubMed] [Google Scholar]
- (6).Shlipak MG, Stehman-Breen C, Fried LF, et al. The presence of frailty in elderly persons with chronic renal insufficiency. Am J Kidney Dis. 2004;43:861–867. doi: 10.1053/j.ajkd.2003.12.049. [DOI] [PubMed] [Google Scholar]
- (7).Lee SJ, Go AS, Lindquist K, et al. Chronic conditions and mortality among the oldest old. Am J Public Health. 2008;98:1209–1214. doi: 10.2105/AJPH.2007.130955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Goodwin JS. Embracing complexity: A consideration of hypertension in the very old. J Gerontol A Biol Sci Med Sci. 2003;58:653–658. doi: 10.1093/gerona/58.7.m653. [DOI] [PubMed] [Google Scholar]
- (9).Fried LP, Tangen CM, Walston J, et al. Frailty in older adults: Evidence for a phenotype. J Gerontol A Biol Sci Med Sci. 2001;56:M146–M156. doi: 10.1093/gerona/56.3.m146. [DOI] [PubMed] [Google Scholar]
- (10).Lee SJ, Lindquist K, Segal MR, et al. Development and validation of a prognostic index for 4-year mortality in older adults. JAMA. 2006;295:801–808. doi: 10.1001/jama.295.7.801. [DOI] [PubMed] [Google Scholar]
- (11).Mazzaglia G, Roti L, Corsini G, et al. Screening of older community-dwelling people at risk for death and hospitalization: The Assistenza Socio-Sanitaria in Italia project. J Am Geriatr Soc. 2007;55:1955–1960. doi: 10.1111/j.1532-5415.2007.01446.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Schonberg MA, Davis RB, McCarthy EP, et al. Index to predict 5-year mortality of community-dwelling adults aged 65 and older using data from the National Health Interview Survey. J Gen Intern Med. 2009;24:1115–1122. doi: 10.1007/s11606-009-1073-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Desai MM, Bogardus ST, Jr., Williams CS, et al. Development and validation of a risk-adjustment index for older patients: The high-risk diagnoses for the elderly scale. J Am Geriatr Soc. 2002;50:474–481. doi: 10.1046/j.1532-5415.2002.50113.x. [DOI] [PubMed] [Google Scholar]
- (14).Inouye SK, Bogardus ST, Jr, Vitagliano G, et al. Burden of illness score for elderly persons: Risk adjustment incorporating the cumulative impact of diseases, physiologic abnormalities, and functional impairments. Med Care. 2003;41:70–83. doi: 10.1097/01.MLR.0000039829.60382.12. [DOI] [PubMed] [Google Scholar]
- (15).Carey EC, Covinsky KE, Lui LY, et al. Prediction of mortality in community-living frail elderly people with long-term care needs. J Am Geriatr Soc. 2008;56:68–75. doi: 10.1111/j.1532-5415.2007.01496.x. [DOI] [PubMed] [Google Scholar]
- (16).Carey EC, Walter LC, Lindquist K, et al. Development and validation of a functional morbidity index to predict mortality in community-dwelling elders. J Gen Intern Med. 2004;19:1027–1033. doi: 10.1111/j.1525-1497.2004.40016.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Keane WF, Zhang Z, Lyle PA, et al. Risk scores for predicting outcomes in patients with type 2 diabetes and nephropathy: the RENAAL study. Clin J Am Soc Nephrol. 2006;1:761–767. doi: 10.2215/CJN.01381005. [DOI] [PubMed] [Google Scholar]
- (18).Johnson ES, Thorp ML, Yang X, et al. Predicting renal replacement therapy and mortality in CKD. Am J Kidney Dis. 2007;50:559–565. doi: 10.1053/j.ajkd.2007.07.006. [DOI] [PubMed] [Google Scholar]
- (19).Landray MJ, Emberson JR, Blackwell L, et al. Prediction of ESRD and death among people with CKD: The Chronic Renal Impairment in Birmingham (CRIB) prospective cohort study. Am J Kidney Dis. 2010;56:1082–1094. doi: 10.1053/j.ajkd.2010.07.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Berthoux F, Mohey H, Laurent B, et al. Predicting the risk for dialysis or death in IgA nephropathy. J Am Soc Nephrol. 2011;22:752–761. doi: 10.1681/ASN.2010040355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Levey AS, Stevens LA, Schmid CH, et al. A new equation to estimate glomerular filtration rate. Ann Intern Med. 2009;150:604–612. doi: 10.7326/0003-4819-150-9-200905050-00006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Kidney Disease Improving Global Outcomes (KDIGO) CKD Work Group KDIGO 2012 Clinical Practice Guideline for the Evaluation and Management of Chronic Kidney Disease. Kid Dis Kid Int Suppl. 2013;3:1–150. [Google Scholar]
- (23).Matsushita K. Comparison of risk prediction using the ckd-epi equation and the mdrd study equation for estimated glomerular filtration rate. JAMA. 2012;307:1941–1951. doi: 10.1001/jama.2012.3954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Bowling CB, Booth JN, III, Safford MM, et al. Nondisease-specific problems and all-cause mortality in the Reasons for Geographic and Racial Differences in Stroke study. J Am Geriatr Soc. 2013;61:739–746. doi: 10.1111/jgs.12214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Smith LR, Harrell FE, Muhlbaier LH, Schwartz HA. Grady ML, editor. Problems and potentials in modeling survival. Medical effectiveness research data methods (summary report) 2013:151–159. AHCPR1992 92-0056. [Google Scholar]
- (26).Harrell FE. Cox proportional hazards regression model (Ch 19) In: Harrell FE, editor. Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis. Springer Science+Business Media, Inc.; New York, NY: 2001. pp. 465–507. [Google Scholar]
- (27).Harrell FE. Regression Modeling Strategies. Springer; New York: 2001. General Aspects of Fitting Regression Models; pp. 11–37. [Google Scholar]
- (28).Sullivan LM, Massaro JM, D'Agostino RB., Sr Presentation of multivariate data for clinical use: The Framingham Study risk score functions. Stat Med. 2004;23:1631–1660. doi: 10.1002/sim.1742. [DOI] [PubMed] [Google Scholar]
- (29).Efron B, Tibshirani R. An Introduction to the Bootstrap. Chapman and Hall; New York: 1993. [Google Scholar]
- (30).Nagelkerke NJ. A note on a general definition of the coefficient of determination. Biometrika. 1991;78:691–692. [Google Scholar]
- (31).Bowling C, Sharma P, Fox CS, et al. Prevalence of reduced estimated glomerular filtration rate among the oldest old from 1988-1994 through 2005-2010. JAMA. 2013;310:1284–1286. doi: 10.1001/jama.2013.252441. [DOI] [PMC free article] [PubMed] [Google Scholar]