Hydraulic fracture during epithelial stretching

Abstract

The origin of fracture in epithelial cell sheets subject to stretch is commonly attributed to excess tension in the cells’ cytoskeleton, in the plasma membrane, or in cell-cell contacts. Here we demonstrate that for a variety of synthetic and physiological hydrogel substrates the formation of epithelial cracks is caused by tissue stretching independently of epithelial tension. We show that the origin of the cracks is hydraulic; they result from a transient pressure build-up in the substrate during stretch and compression maneuvers. After pressure equilibration cracks heal readily through actomyosin-dependent mechanisms. The observed phenomenology is captured by the theory of poroelasticity, which predicts the size and healing dynamics of epithelial cracks as a function of the stiffness, geometry and composition of the hydrogel substrate. Our findings demonstrate that epithelial integrity is determined in a tension-independent manner by the coupling between tissue stretching and matrix hydraulics.

Epithelial cell sheets are two-dimensional active materials capable of performing a broad diversity of functions including morphogenesis, wound healing, tissue compartmentalization, and protection against environmental pathogens¹. Epithelial sheets carry out these functions in a dynamic mechanical environment characterized by elevated levels of cell and tissue stretching^2,3. During epithelial morphogenesis, for example, cells experience several-fold changes in their surface area to enable the formation of complex three-dimensional shapes^4,5. During adult life, the epithelium of diverse organs functions routinely in the presence of significant levels of stretch such as those arising from breathing maneuvers, cardiac pulses, or peristaltic contractions². Under physiological conditions, stretch is a potent stimulus for growth, differentiation, secretion, remodeling, and gene expression^6-9. Failure to withstand stretch, however, causes epithelial fracture, which may lead to developmental defects and severe clinical conditions^10,11,12.

Mechanisms underlying epithelial fracture during stretch are poorly understood, but they are commonly associated with excessive tension in key stress bearing elements of the cell monolayer. Indeed, excessive tension due to monolayer overstretching or cytoskeletal contraction has been shown to cause the disruption of cell-cell and cell-matrix adhesions^12-15. Excessive tension has also been shown to rupture the cell membrane^16,17, which may lead to cell death and formation of cracks within the epithelium¹⁸. Here we developed a new experimental approach to study fracture dynamics of micropatterned epithelial monolayers adhered to soft hydrogel substrates. Using this approach we demonstrate that tissue stretching causes epithelial cracks whose origin is not tensile, but rather hydraulic.

A device to study epithelial mechanics during stretch

The principle of the technique is as follows. A thin layer of soft hydrogel is polymerized and chemically attached on a stretchable polydimethylsiloxane (PDMS) membrane (Fig. 1a,b). The resulting double-layered substrate is mounted on a custom-made stretching device compatible with inverted and upright optical microscopy (Fig. 1a). The substrate is stretched over a lubricated O-ring by applying negative pressure underneath its outer annular area (Supplementary Fig. 1a). The device produces homogeneous and equibiaxial strain with user-controlled amplitude and time-course (Supplementary Fig. 1b,c).

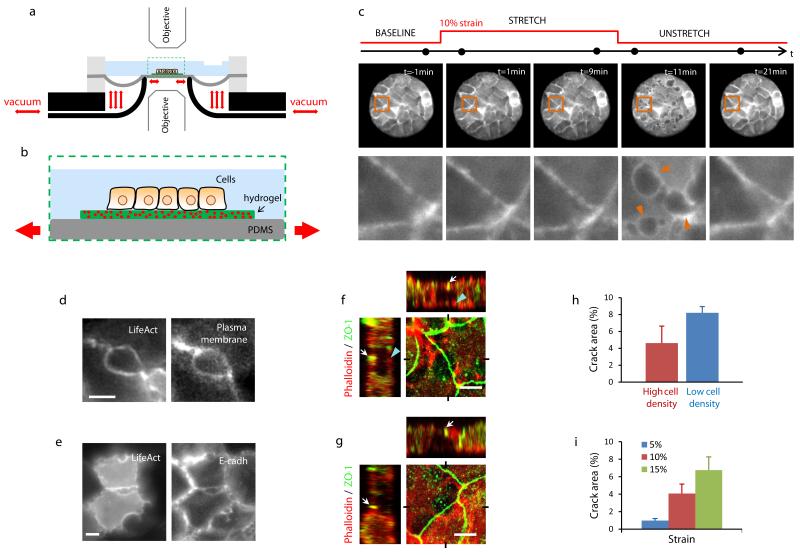
Figure 1. Epithelial fracture during stretch/unstretch maneuvers.

a, Scheme of the stretching device (see Methods and Supplementary Fig. 1). b, Zoomed view of the region enclosed by a dashed rectangle in (a). c, LifeAct-GFP MDCK cluster before, during and after a 10 min pulse of 10% biaxial strain. The bottom row is a zoom of the region highlighted in the upper row. Arrowheads point at cracks after stretch cessation. The acquisition time of each snap shot is marked by a black dot on the time axis (top). d, Live fluorescence images of MDCK cells expressing LifeAct-Ruby (left) and a fluorescently-labeled plasma membrane green marker (right). Images were obtained 30 s after stretch cessation. Scale bar, 5μm. e, Live fluorescence images of MDCK cells expressing LifeAct-GFP (left) and E-cad-RFP (right). Images were obtained 30 s after stretch cessation. Scale bar, 5μm. f-g, Confocal x-y, x-z and y-z sections of cracks. Cells were fixed immediately after stretch cessation and stained for F-actin (phalloidin, red) and ZO-1 (green) (Supplementary methods). Sections show that ZO-1 remained intact at the apical surface (white arrows). In (f), a discontinuous actin layer was present at the basal surface of the cluster (blue arrowheads) and the largest crack diameter was located in the medial plane. In (g), no basal actin layer was present and the largest crack diameter was located in the basal plane. See Supplementary Fig. 6 for confocal sections of additional cracks (Scale bar, 5 μm). h, Crack area in epithelial clusters at high density (37±3 cells/pattern, mean±SEM, n=5) and low density (19±1 cells/pattern, mean±SEM, n=5). Representative images of the clusters before and after stretch are shown in Supplementary Fig. 9. i, Dependence of crack area with strain (n=6). In (h) and (i), crack area was expressed as a percentage of the total pattern area. Epithelial clusters are 80 μm in diameter.

As an experimental model system we used Madin-Darby Canine Kidney (MDCK) epithelial cells adhered on soft polyacrylamide (PAA) hydrogel substrates. To enhance experimental reproducibly and to improve mechanical characterization of the system, we used micropatterning technology to restrict the cells to circular islands pre-coated with collagen-I^14,19 (Supplementary methods). When cells were seeded on these islands they readily formed cohesive clusters comprising ~15-20 cells. In the absence of stretch, the clusters displayed characteristic features of epithelial layers, including tight junctions, adherens junctions, and F-actin accumulation at the lateral cell membranes (Supplementary Fig. 2).

Epithelial clusters fracture upon stretch release

We first subjected the hydrogels and the overlying cells to a pulse of stretch of 10 min duration and 10% biaxial strain (Fig. 1c). Upon stretching, no changes were apparent in cell morphology, actin distribution, and cluster cohesiveness. Promptly after stretch cessation, however, cracks of diverse size and shape appeared between the cortexes of adjacent cells and healed within minutes (Fig. 1c, Supplementary Videos 1 and 2). These interfacial cracks did not originate from a transient detachment of the cortex from the membrane, as is commonly seen in blebbing-like phenomena^20,21 or during the dissociation of cell doublets under tension²². Instead, the cell cortex, the cell membrane, and E-cadherin remained localized at the crack periphery, indicating the dissociation of adherens junctions at the cadherin-cadherin level (Fig. 1d,e, Supplementary Fig. 3, Supplementary Video 3).

Importantly, the observed responses were not specific to cells seeded on synthetic PAA hydrogels; epithelial clusters seeded on matrigel, a physiological mixture of growth factors and structural proteins such as laminin, entactin, and collagen, showed similar cracks and healing dynamics (Supplementary Fig. 4). To further assess whether epithelial fracture occurred in physiological matrices, we decellularized porcine trachea and used it as substrate. Similarly to the case of PAA and matrigel, cell clusters seeded on these substrates showed interfacial cracks upon unstretching (Supplementary Fig. 5). In light of the generality of the phenomenology, we focus our attention hereafter on PAA hydrogels, which show higher reproducibility, accessibility, and versatility than matrigel or decellularized animal tissue.

Morphological and structural characterization of the cracks

To characterize the morphology of the cracks we analyzed the localization of F-actin and the tight junction protein ZO-1 at different z-planes immediately after stretch cessation (Fig. 1f,g). This analysis showed that despite the rupture of adherens junctions (Fig 1e, Supplementary Fig. 3) most tight junctions remained intact (Fig. 1f,g, Supplementary Fig. 6). However, in rare occasions tight junctions also failed, thus fully compromising epithelial permeability (Supplementary Fig. 7). In some cracks, the largest diameter was located in medial cell planes and a discontinuous actin layer was present at their basal side (Fig. 1f). In other cracks, this discontinuous actin layer was absent and the largest crack diameter was located at the cell base (Fig. 1g, Supplementary Fig. 6).

We next studied whether epithelial fracture involved not only failure of cell-cell adhesions but also failure of cell-substrate adhesions. To do so, we subjected cells labeled with LifeAct-Ruby and Talin-GFP to a pulse of 10% stretch and 10 min duration (Supplementary Fig. 8). Before stretch, talin accumulated at discrete focal adhesions throughout the monolayer. This spatial distribution did not vary during the application of the stretch pulse. Upon stretch cessation, however, talin localized at the crack contour and some focal adhesions under the cracks experienced shape changes. These data indicate that crack formation involves the disruption and remodeling of focal adhesions within epithelial clusters.

The polarity, mechanics, and cytoskeletal organization of epithelial layers depends on cell density²³. To study the role of cell density in epithelial fracture we subjected micropatterned islands grown at different densities to a pulse of 10% strain and 10 min duration. Cells at higher densities exhibited significantly lower crack area, indicating that maturity of cell-cell junctions or the cortical organization of the actin cytoskeleton play a significant role in determining the formation and growth of epithelial cracks (Fig. 1h, Supplementary Fig. 9).

To study the dependence of crack formation on stretch magnitude, we subjected the clusters to a series of stretch pulses of same duration (10 min) but different magnitude (5%, 10%, 15%, strain). These pulses were applied in random order and spaced by 30 min intervals to enable healing. These experiments revealed that total crack area increased with strain magnitude and that any potential threshold for crack formation must fall below 5% strain (Fig 1i).

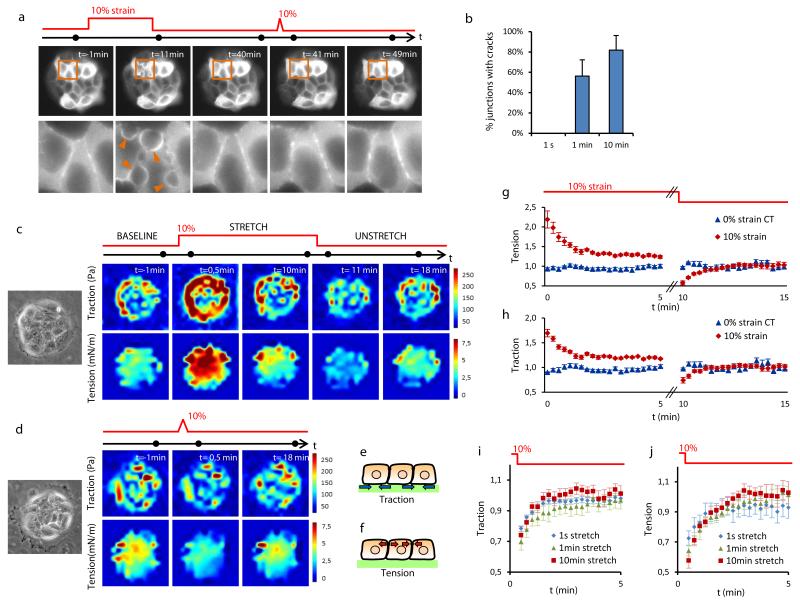
To further characterize the cracks we subjected the clusters to a series of three stretch pulses of the same magnitude (10% strain) but different duration (1 s, 1 min, 10 min), applied in random order and spaced by 30 min intervals (Fig. 2a). These experiments showed that the number and size of the cracks increased with the duration of stretch; in response to 10 min pulses, most cell-cell junctions exhibited cracks, whereas in response to 1 s pulses cracks were largely absent (Fig. 2b).

Figure 2. Cracks are independent of epithelial tension.

a, Time-lapse imaging of patterned clusters (top) and zoomed regions (bottom) of MDCK cells expressing LifeAct-GFP before and after application of successive pulses of 10 min and 1s duration. Arrowheads point at cracks. The acquisition time of each snap shot is marked by a black dot on the time axis. b, Percentage of junctions with cracks after stretch pulses of 1 s, 1 min or 10 min duration. Stretch pulses were applied consecutively to each pattern, in a random order and spaced by >15 min (n=6 different patterns). c,d, Colour maps showing traction forces (top) and epithelial tension (bottom) before, during and after a 10 min (c) or 1 s (d) stretch pulses. Phase contrast images on the left show the measured MDCK cell cluster. e,f, Schemes illustrating the physical meaning of traction and tension in the epithelial clusters. g,h, Traction forces and tension during and after a 10 min duration and 10% strain pulse versus a 0% strain (both normalized to baseline levels). i,j, Traction forces and tension after stretch pulses of different duration normalized to baseline levels. Error bars in g-j show SEM of n=6 clusters per condition. Epithelial clusters are 80 μm in diameter.

Epithelial cracks are independent of epithelial tension

The fracture of epithelial monolayers subjected to stretch is commonly attributed to the mechanical failure of cell-cell junctions due to large tensile stresses^12-15. However, tension levels within cell monolayers have never been measured during stretching. To do so, we mapped traction forces at the cell-substrate interface using Monolayer Traction Force Microscopy²⁴ and we mapped monolayer tension within and between cells using Monolayer Stress Microscopy²⁵ (Fig. 2c-f).

Before stretch application, traction forces localized predominantly but not exclusively at the margin of the clusters (Fig. 2c, Supplementary Fig. 10). These marginal tractions were not balanced locally at the subcellular level, however. Instead, they were transmitted through cell-cell junctions, giving rise to an average monolayer tension of 4.2 mN/m. Upon application of a stretch pulse of 10 min duration, cell tractions at the cluster periphery and monolayer tension throughout the cluster experienced a rapid increase followed by a slow relaxation toward values that were slightly higher than baseline levels (Fig. 2c,g,h, Supplementary Fig. 10). Immediately after stretch cessation, tractions and tensions dropped below baseline levels and recovered within minutes (Fig. 2c,g,h).

This type of mechanical responses to stretch has been previously found in single isolated cells^26-28. The increase in tension upon stretching, which is generically termed reinforcement, is commonly attributed to rapid mechanotransduction responses as well as to passive strain hardening of the acto-myosin cytoskeleton^29-31. Conversely, the drop of tension after stretch cessation, which is commonly termed fluidization, is attributed to unspecific inelastic rearrangements in the cytoskeleton^26,28,32. Our findings show that the paradigms of reinforcement and fluidization scale up to the supracellular level. More intriguingly, they show that contrary to common wisdom, cracks do not form when tension is highest but rather when it is lowest.

Stretch pulses of shorter duration led to similar mechanical responses both in quality and quantity (Fig. 2d,i,j, Supplementary Fig. 11); tractions and tensions increased during stretch application but dropped below baseline levels promptly after stretch cessation. Thus, stretching maneuvers of different duration led to sharply different responses in terms of crack formation but nearly identical responses in terms of traction and tension patterns. This lack of correlation implies an unanticipated fracture mechanism that is independent of epithelial tension.

The origin of epithelial cracks is hydraulic

We hypothesized that such mechanism might involve hydraulics of the hydrogel substrate. An elastomeric hydrogel is a material formed by a three-dimensional polymer network and an aqueous solvent. Hydrogels are poroelastic materials; deformation is coupled to long-range flow of the solvent into, away from, and within the network³³. Since solvent migration is dragged by friction between the solvent and the network, hydrogels behave as incompressible materials at short time-scales, while they exhibit local and global volumetric changes at longer time-scales.

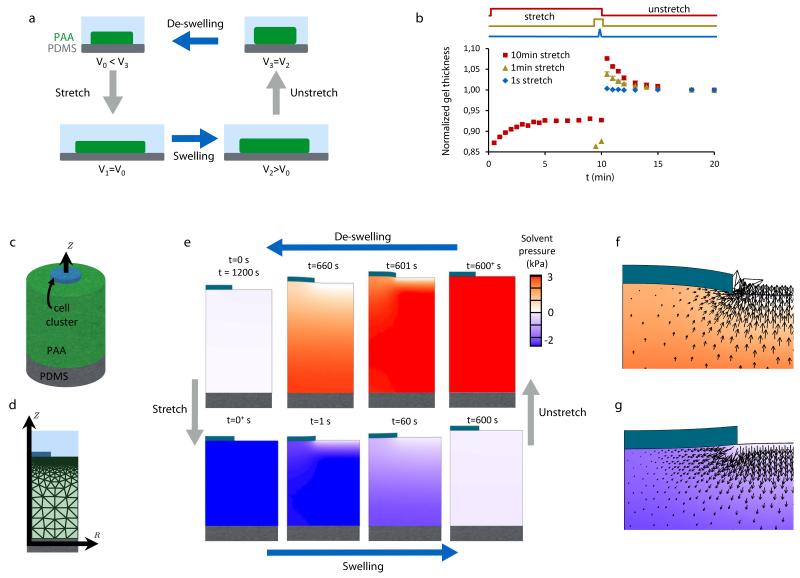
The theory of poroelasticity has been successful at predicting the coupling between mechanics and solvent migration in a broad diversity of synthetic and physiological hydrogels³⁴ including the cell cytoplasm^20,35. The behavior of elastomeric hydrogels composed of flexible polymers undergoing large deformations, such as our PAA hydrogels, can be understood and quantified by recent theoretical advances^36,37. The swelling state of the hydrogel is set by a balance between the mixing entropy of the system, which tends to attract solvent into the network, and the entropy of the polymer chains, which tends to expel solvent. Deformation affects the chemical potential of the solvent, thereby driving its diffusive flow. This theory predicts that an ideal hydrogel stretched laterally as in our experiments will initially thin down to preserve volume, and over a longer time-scale, will swell as a result of solvent influx (Fig. 3a). Conversely, when the hydrogel is unstretched or compressed, it will experience an increase in thickness followed by a gradual efflux of solvent (de-swelling). If the hydrogel is partially covered by an impermeable barrier, such as the tight epithelial islands in our experiments, solvent efflux will be blocked, leading to a local pressure increase across the barrier.

Figure 3. Stretch induces poroelastic flows and pressure beneath the cell cluster.

a, Illustration of the coupling between hydrogel stretching and swelling. Immediately after a rapid stretch or unstretch maneuver, the hydrogel volume is conserved. With time, the free energy balance in the hydrogel causes poroelastic flows that lead to progressive swelling or de-swelling of the hydrogel. b, Time evolution of PAA hydrogel thickness during and after stretch pulses of 1 s, 1 min, and 10 min (normalized to baseline levels). Stretch pulses were applied successively to each pattern, in a random order and spaced by >15 min (n=4 different patterns, error bars are SEM). c, Idealization of the gel underneath an epithelial cluster as a cylindrical region covered by a disc-like impermeable barrier (modeled epithelial clusters are 80 μm in diameter and the gel is 156 μm in thickness). This gel domain is modeled with the large deformation poroelastic theory (Supplementary Note 1). d, Axisymmetric finite element discretization of the system shown in (c). e, Solvent pressure and deformation of the gel during the stretch-unstretch maneuver in the presence of an impermeable disc-like barrier as predicted by the model. f, Solvent flow pattern near the edge of the epithelial cluster 6 s after stretch cessation. g, Solvent flow pattern near the edge of the epithelial cluster 6 s after stretch application.

Based on this theoretical framework, we hypothesized that if the time scale of stretching pulses is comparable with the characteristic time of solvent exchange, significant pressures might buildup across the epithelium upon unstretching, potentially challenging its mechanical integrity. If this hypothesis were true, cell clusters adhered on a non-hydrogel elastomer should not exhibit cracks. We tested this idea by stretching clusters of MDCK cells adhered on soft silicone gels. Consistent with our hypothesis and contrary to the case of PAA hydrogels, no cracks were observed on such soft gels (Supplementary Fig. 12). We also hypothesized that if the monolayer was made leakier, the solvent should be readily expelled through permeable cell-cell junctions and no cracks should form. We tested this hypothesis by applying stretch/unstretch maneuvers during the formation of cell-cell junctions after a short exposure to trypsin (Supplementary Fig. 13). These experiments showed that, consistent with our hypothesis, confluent cell clusters with leaky tight junctions do not display cracks.

These results prompted us to study deeper the applicability of the theory of poroelasticity to our data. To study whether the theory captured PAA hydrogel hydraulics in our experiments, we used optical microscopy to measure hydrogel thickness during stretch pulses of different duration (Fig. 3b). In the case of long pulses (10 min duration), the hydrogels shrunk immediately after stretching but, over a time scale of minutes, they progressively swelled up to an equilibrium thickness. Conversely, upon unstretching, the hydrogels suddenly increased their thickness but shrunk slowly towards baseline levels. In the case of fast pulses (1s duration), the hydrogels behaved as purely elastic materials with negligible poroelastic flows. Overall, these observations are well captured by the theory, both in magnitude and quality, and support the notion that the origin of epithelial fracture is hydraulic (Fig. 3c-g, Supplementary Video 4, Supplementary Notes 1,2). After cessation of a stretch of 10 min duration, we estimate an over-pressure at the interface between the hydrogel and the cells of ~3 kPa; interfacial pressures within this order of magnitude are common in physiology and pathophysiology^38,39. By contrast, after a short pulse of 1s duration we estimate negligible flow rates and pressures, consistent with the absence of epithelial cracks.

Poroelastic theory predicts crack size and sealing dynamics

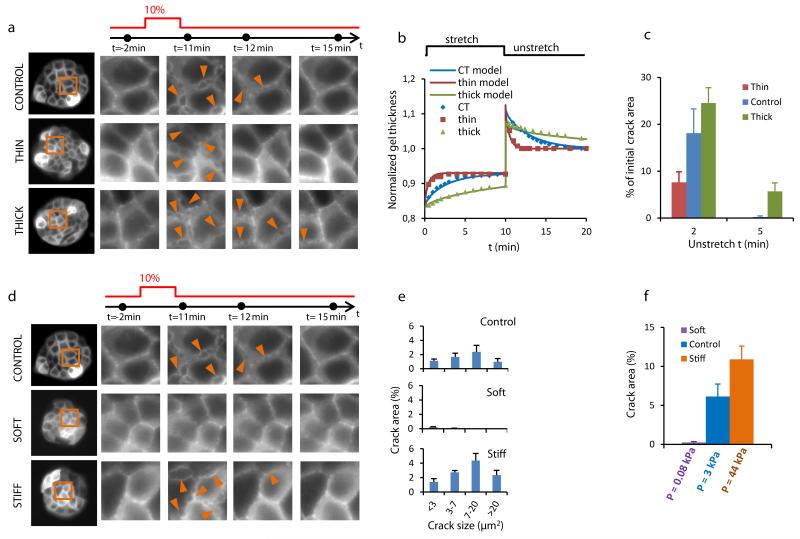
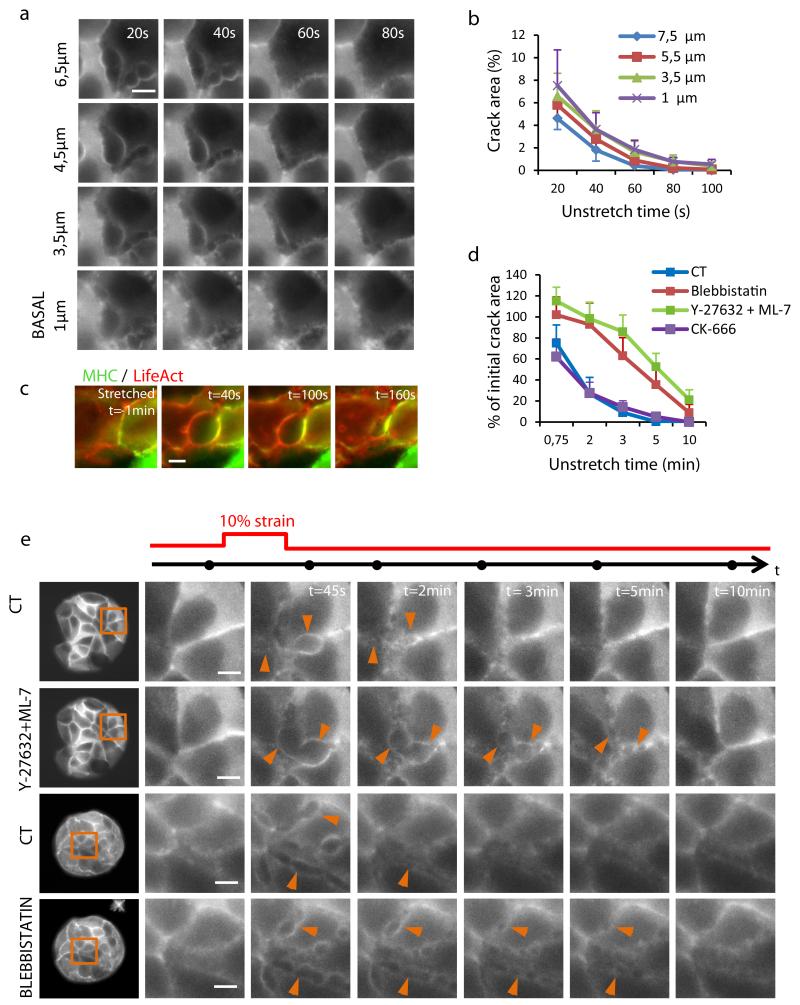
We next used the theory to produce additional testable predictions. A first set of predictions concerns hydrogel geometry. The theory predicts that the pressure that builds up immediately after stretch cessation is independent of the initial hydrogel thickness, but that the characteristic time for pressure relaxation is proportional to the square of the thickness. We confirmed these predictions in hydrogels of different initial thickness (68 μm to 358 μm) (Fig. 4a, Supplementary Notes 1,2). When we applied stretch pulses of 10 min duration and 10% strain, cracks appeared in all cell clusters regardless of the hydrogel thickness. However, the healing dynamics were much faster in thinner hydrogels, consistent with the fact that the relaxation of transepithelial pressure was faster (Fig. 4b,c).

Figure 4. The origin of cracks is hydraulic.

a, (left) Clusters of MDCK cells expressing LifeAct-GFP on PAA hydrogels of different thickness. (right) Time-lapse evolution of the regions highlighted in orange on left panels before and after a 10 min pulse of 10% biaxial stretch. The acquisition time of each snap shot is marked by a black dot on the time axis (top). Arrowheads point to a subset of cracks. b, Time evolution of the thickness of three PAA hydrogels of same stiffness (12 kPa) but different initial thickness (CT=168 μm, thin=54 μm, thick=358 μm) during and after application of a 10 min stretch pulse. Solid lines are fits of the poroelastic model described in Supplementary Note 1. c, Percentage of the initial crack area that remains open 2 and 5 min after unstretching hydrogels of different thickness (n=4 per condition, CT=156.3± 9.8 μm, thin=59.3±3.8 μm, thick=345.0±15.3 μm, mean±SEM). d, (left) Clusters of MDCK expressing LifeAct-GFP on PAA hydrogels of same initial thickness but different stiffness (0.2, 12, 200kPa). (right) Time-lapse evolution of the regions highlighted on left panels before and after a 10 min 10% biaxial stretch. e, Distribution of crack size 45 s after unstretch in clusters attached to hydrogels of different stiffness (0.2kPa, 12kPa and 200kPa). f, Percentage of crack area 45s after stretch cessation in clusters attached to substrates of different stiffness. Values on the x-axis are hydraulic pressures at the cell-gel interface estimated from the poroelastic theory (Supplementary Note 1). Error bars show SEM. Epithelial clusters are 80 μm in diameter.

A second set of predictions concerns hydrogel stiffness; stiff hydrogels should buildup higher pressures and thereby increase the crack area. To test this prediction we produced hydrogels with nominal Young’s moduli of 200Pa, 12kPa and 200kPa, for which we estimated over-pressures upon unstretching of ~0.08 kPa, 3 kPa and 44 kPa, respectively (Supplementary Notes 1,2). As predicted, when we stretched cell clusters on these hydrogels we observed that the total crack area was much larger in clusters seeded on stiff hydrogels than on soft ones (Fig. 4d-f).

A final set of predictions concerns the size of the epithelial cluster. Our Finite Element simulations of the epithelium/gel geometry predict that immediately after stretch cessation, when cracks form, the pressure distribution under the gel is nearly constant except for a 2 μm rim at the cluster edge (Supplementary Note 1). Moreover, for a fully swollen gel, the magnitude of this pressure is independent of the cluster size. Consistent with this prediction we observed that crack area was uniform throughout the gel and independent of the cluster size (Supplementary Fig. 14, Supplementary Video 5). Taking together all the evidence reported above, we conclude that epithelial cracks during stretch cessation are caused by the buildup of solvent pressure in the hydrogel.

A striking feature of our experiments is that cracks appeared after stretch cessation but not after stretch application, yet the pressure difference across the epithelium during stretch cessation and stretch application has nearly the same magnitude but opposite sign. This observation highlights the asymmetry of polarized epithelial layers and indicates that tight junctions are able to withstand higher normal pressure differences than adherens junctions. To further support this observation, we subjected a cohesive monolayer spanning the entire gel (> 3 mm diameter) to a stretch pulse of 10% strain and 10 min duration. Contrary to the case of micropatterned clusters, cell-cell junctions within large cohesive monolayers exhibited no fractures during stretch/unstretch maneuvers and the underlying gels did not experience volume changes (Supplementary Fig. 15). This finding shows that apical tight junctions are able to withstand the applied pressure differences and prevent transepithelial flows during stretching.

Crack sealing is driven by myosin

We finally turned to the dynamics of crack healing. Immediately after stretch cessation, the cracks begun to seal and the monolayer quickly regained its original integrity (Fig. 5a,b). Quantification of z-stacks during this process revealed that crack area was initially larger on the basal plane of the clusters than on the apical plane. With time, crack area decreased at a similar rate in all planes, thus implying that sealing proceeded from the apical to the basal planes (Fig. 5a,b). The time evolution of crack area was remarkably similar to that of hydrogel thickness (Fig. 3b, Fig. 5), strongly suggesting that the equilibration of the pressure difference between the cell interior and the crack is a main determinant of the healing rate.

Figure 5. Cracks seal from apical to basal plane in a myosin dependent fashion.

a, Live fluorescence images of MDCK cells expressing LifeAct-GFP showing the time evolution of cracks after stretch at different z-planes. Arrowheads point at one representative crack. b, Crack area expressed as a percentage of pattern area at different z-planes and times after stretch cessation (height increases from basal to apical). c, Live imaging of cells expressing LifeAct-Ruby and MHC-GFP during stretch and at different times during crack sealing. d, Time evolution of crack area expressed as a percentage of crack area in untreated controls immediately after stretch cessation. Error bars show SEM of n=4 clusters per condition. e, (left) Clusters of MDCK cells expressing LifeAct-GFP or LifeAct-Ruby before (CT) and after 30 min incubation with 30 μM Y-27632 and 60 μM ML-7 or 80 μM Blebbistatin. (right) Magnified views of regions highlighted on left panels before and after a 10 min 10% biaxial stretch. Note that the same cluster was used successively for control and treatment. Arrowheads point at representative cracks. The acquisition time of each snap shot is marked by a black dot on the time axis (top). Scale bar, 5μm. Epithelial clusters are 80 μm in diameter.

Wound healing at the subcellular scale has been the subject of much recent attention and two main sealing mechanisms are commonly invoked. The first one involves the formation of an actomyosin ring around the wound, whose contraction drives the wound edges together like a purse string^40,41. The second mechanism involves the protrusion of basal lamellipodia into the wounded area⁴². Z-stacks in LifeAct-GFP cells revealed an accumulation of actin and myosin at the surface of the crack (Fig. 5a,c). To test whether contraction of this acto-myosin structure contributes to crack sealing we treated cells with the myosin II inhibitor blebbistatin or with a mixture of the Rho Kinase inhibitor Y-27632 and the myosin light chain kinase inhibitor ML7. To minimize experimental variability, we first subjected the cell clusters to a stretch/unstretch maneuver of 10% strain and 10 min duration, we next incubated the cells for 30 min with the inhibitors, and we finally subjected the cell clusters to a second stretch/unstretch maneuver (again 10% strain, 10 min duration). By using this protocol we were able to compute in the same cluster the ratio between the crack area after treatment and before treatment and its time evolution (Fig. 5d,e). Cell clusters treated with blebbistatin or with the combination of ML7 and Y-27632 showed a slower closure rate than controls, indicating an involvement of myosin in crack sealing (Fig. 5d,e, Supplementary Videos 6,7). To study the role of lamellipodial protrusion we inhibited the complex ARP2/3 using CK-666. This inhibitor did not alter wound closure kinetics (Fig. 5d). Therefore, unlike the case of cracks generated by transmigrating neutrophils or blunt tips⁴², lamellipodial protrusion was not involved in healing of hydraulic cracks. Inhibition of stretch activated channels using Gd(3+) or inhibition of aquaporins using Hg(2+)⁴³ did not alter crack formation or sealing rate, indicating that solvent accumulated in cracks was not expelled through the cell body (Supplementary Figs. 16,17). Taken together, these findings put forward an unconventional wound healing strategy in which the wound healing rate is set by the balance between cortical tension and the pressure difference between the cell interior and the crack.

Implications for epithelial toughness and physiology

Our findings portray epithelia as material interfaces remarkably robust to sudden hydraulic stress. In contrast to suspended epithelial monolayers under tension¹², our epithelia did not exhibit catastrophic brittle failure with localized cell-cell separation at a few large cracks. Instead, we observed distributed hydraulic cracks of sub-cellular size (Fig. 4e) throughout nearly all cell-cell junctions, rarely leading to significant trans cracks. Since cell-cell separation requires significant work per unit area (Γ ~6 mN/m, Supplementary Note 3), this distributed deformation mechanism maximizes the material toughness. Interestingly, other biological materials such as protein materials⁴⁴ or nacre^45,46 also enhance toughness by distributed cracking, using however seemingly unrelated mechanisms and architectures⁴⁷.

Our findings establish a new mechanism for monolayer fracture. Rather than depending on the ability of cell-cell junctions to withstand tension in the epithelial plane, the mechanism reported here relies on poroelastic flows and pressures normal to that plane. Because this mechanism applies to both synthetic and physiological hydrogel matrices, our results raise the question of how it might be exploited or avoided in vivo. In a general physiological context, the extra-cellular matrix is architecturally and compositionally heterogeneous, and hydraulically connected to other tissues, possibly with buffered solvent pressure. Mechanical stretch will thus affect differently the solvent chemical potential in different regions of the extra-cellular matrix, and therefore drive solvent flows. If properly regulated, these flows into and away from the epithelium might contribute to control the permeability in leaky epithelia or to sculpt tissue shape during morphogenesis. By contrast, in tight epithelia in which sealing is a strict requirement, the phenomena described here would seem unfavorable to proper physiological function. In this regard, particularly interesting physiological scenarios are aging, inflammatory disorders, and fibrosis, all of which characterized by a patchy epithelium and a thicker and stiffer extracellular matrix^48-50. Because these physical and geometric properties favor hydraulic fracture during tissue stretching, they might also contribute to drive further epithelial disruption and to prevent proper wound healing.

Outlook

Our study establishes the physical rules by which poroelastic flows and pressures can be tuned by the magnitude of tissue stretching, as well as by the stiffness and geometry of the extracellular matrix. Because these rules are general and inescapable, they must have played a central role in defining the shape, architecture, and composition of the extracellular matrix during evolution. For this very same reason, these rules provide new limits and opportunities in engineering of biomimetic systems.

METHODS

Fabrication of stretchable PDMS membranes

PDMS was mixed 10:1 (base:crosslinker) and degassed for 1 h. Uncured PDMS was spin-coated on methacrylate plates to a thickness of 80-100 μm, and cured at 65 °C overnight. The resulting PDMS membranes were then peeled off the plates and clamped between the rings of the stretching device (Supplementary Fig. 1).

PDMS membrane treatment for hydrogel binding

Stretchable PDMS membranes were UV irradiated in a plasma cleaner for 1 min, in order to render the PDMS surface hydrophilic. Instead of using benzophenone to bind hydrogels to PDMS, as previously reported⁵¹, we added 3-Aminopropyl triethoxysilane (APTES) 10% in ethanol at the center of the membrane for 1 h at 65 °C. After thorough cleaning with PBS, Glutaraldehyde (1.5% in PBS) was poured at the center of the dish and incubated for 25 min at room temperature. After cleaning with PBS, treated PDMS membranes were allowed to air dry prior to use.

Polyacrylamide hydrogels

PAA hydrogel preparation was adapted from previous protocols^23,52,53. PAA hydrogels were polymerized between two coverslips treated with Repel-Silane (2% dimethyldichlorosilane). For 12 kPa hydrogels (Young modulus), a stock solution containing a concentration of 7.5% acrylamide, 0.16% bisacrylamide, 0.5% ammonium persulphate, 0.05% tetramethylethylenediamine and 1% 200-nm-diameter red fluorescence carboxylate-modified beads (Fluospheres, Invitrogen) was prepared in a 10 mM Hepes solution. For 0.2 and 200 kPa hydrogels, acrylamide and bisacrylamide concentrations were 3% acrylamide 0.05% bisacrylamide, and 12% acrylamide 0.55% bisacrylamide, respectively. After polymerization, one coverslip was removed and the PAA hydrogel was pressed against the coated stretchable PDMS membrane and left overnight at 37 °C in a humid chamber for covalent binding. Then the remaining coverslip was removed and the PAA hydrogel was incubated with Sulfo-SANPAH under UV light (254 nm wavelength at a distance of 5-8 cm for 5 min). After thoroughly washing with MiliQ water and PBS, hydrogels were ready for coating with extracellular matrix.

Cell patterning on soft PAA hydrogels

Cells were patterned on extracellular matrix protein (Collagen-I). One hour before seeding the cells, the PDMS patterning membranes were air dried and incubated in a solution of 2% Pluronic F-127 (Sigma-Aldrich) in PBS to avoid damage of the hydrogels when removing the PDMS patterning membrane. The membranes were then washed with PBS, air dried for 20 min, and deposited on the surface of the PAA hydrogels. A drop of 0.1 mg/ml collagen-I was placed in the gaps of the PDMS patterning membranes and left overnight at 4 °C. The PDMS patterning membranes were removed afterwards and the hydrogels were washed with PBS and incubated with cell culture media for 3 h. For cell seeding, the culture medium was removed and a 50 μl drop containing ~50,000 cells was placed on the PAA hydrogels. 30 min after seeding, the unattached cells were washed away and more medium was added. Cells were allowed to spread and proliferate in the patterns for at least 16 h before the beginning of the experiments.

Matrigel gel on stretchable PDMS membranes

BD Matrigel (BD BioSciences) aliquots were stored at −80 °C, transferred to refrigerator (4 °C) overnight prior to use and prepared on ice. Matrigel was mixed with 1% 200-nm-diameter red fluorescent carboxylate-modified beads (Fluospheres, Invitrogen). A 30-50 μl drop of this mixture was placed on the treated stretchable PDMS membrane, covered with a 12 mm diameter coverslip (previously treated with Repel-Silane) and allowed to polymerize at 37 °C overnight in a humid chamber. Once polymerized, the coverslip was carefully removed and the matrigel hydrogel was then ready for cell seeding.

Decellularized tissue from porcine trachea on stretchable PDMS membranes

Porcine tracheas obtained from a local provider were decellularized adapting a protocol described previously^54,55. Briefly, tracheas were cleaned to remove any attached connective tissue. Then, they were subjected to several freezing and thawing cycles, and washed extensively with PBS (1×). Subsequently, tracheas were immersed in deionized water for two days and then in 1% sodium dodecyl sulfate (SDS) detergent for 7 days. Finally, they were rinsed with PBS (1×) to eliminate SDS from the matrix. The inner part of the tracheas, corresponding to mucosa and submucosa tissue layers, was separated and stored in PBS (1×) at 4 °C until use. All solutions contained 1% Penicillin-Streptomycin and 1% Amphotericin-B to avoid contaminations during cell culture. For stretch experiments, a 1 cm² piece of tissue was cut, nitrogen dried and pressed against a treated stretchable PDMS membrane overnight at 37 °C in a humid chamber. Once adhered, it was incubated with 0.1 mg/ml collagen-I overnight at 4 °C, washed and incubated with complete media before cell seeding.

Stretch device and experiments

Experiments were performed with a custom-built stretching device that produced uniform biaxial deformations of stretchable PDMS membranes and of the overlying hydrogels and cells (Supplementary Fig. 1a). The stretchable PDMS membrane was placed on a lubricated O-ring positioned over the objective of an inverted optical microscope or under the objective of an upright optical microscope. A transient vacuum pressure applied to the outer annular area of O-ring stretched the membrane, and consequently, stretched the attached hydrogel and cells. The strain waveform was computer-controlled using a PID vacuum controller and a pressure sensor. Stretch experiments were performed >16 h after seeding the cells. Strain rate was ~0.05 s⁻¹. Strain calibration was performed by measuring distances between 9 fluorescent beads on the top and bottom surfaces of PAA hydrogels adhered to stretchable PDMS membranes.

Traction microscopy

Traction forces were computed using Fourier-transform traction microscopy with finite gel thickness as described previously²⁴. Gel displacements between any experimental time point and its relative reference image obtained after cell trypsinization (both for relaxed and strained states) were computed using home-made particle imaging velocimetry software.

Monolayer stress microscopy (MSM)

Monolayer stresses were computed using monolayer stress microscopy^25,23. MSM uses traction forces and force balance demanded by Newton’s laws to map the two-dimensional stress tensor σ in the monolayer:

$$\sigma =\left(\begin{array}{cc}\hfill {\sigma }_{xx}\hfill & \hfill {\sigma }_{xy}\hfill \\ \hfill {\sigma }_{yx}\hfill & \hfill {\sigma }_{yy}\hfill \end{array}\right)$$

For each point in the monolayer, we then computed the average normal stress within and between cells defined as $\overline{\sigma }=({\sigma }_{xx}+{\sigma }_{yy})∕2$ and refer to it as monolayer tension. In the 2D approximation $\overline{\sigma }$ has units of surface tension.