Replication of a Gene-Environment Interaction via Multimodel Inference: Additive-Genetic Variance in Adolescents’ General Cognitive Ability Increases with Family-of-Origin Socioeconomic Status

Abstract

The present study of general cognitive ability attempts to replicate and extend previous investigations of a biometric moderator, family-of-origin socioeconomic status (SES), in a sample of 2,494 pairs of adolescent twins, non-twin biological siblings, and adoptive siblings assessed with individually administered IQ tests. We hypothesized that SES would covary positively with additive-genetic variance and negatively with shared-environmental variance. Important potential confounds unaddressed in some past studies, such as twin-specific effects, assortative mating, and differential heritability by trait level, were found to be negligible. In our main analysis, we compared models by their sample-size corrected AIC, and base our statistical inference on model-averaged point estimates and standard errors. Additive-genetic variance increased with SES—an effect that was statistically significant and robust to model specification. We found no evidence that SES moderated shared-environmental influence. We attempt to explain the inconsistent replication record of these effects, and provide suggestions for future research.

Background

Biometric Modeling of General Cognitive Ability

Gene-environment interaction (G × E) occurs when the phenotypic effect of genetic factors varies as a function of one or more environmental variables. The present work is concerned with an extension of the G × E concept: estimating how much the magnitudes of all biometric variance components depend upon one or more observable variables. We will use “biometric moderation” to refer to the phenomenon that the biometric decomposition of a phenotype varies as a function of some observable variable, the “biometric moderator.” We will specifically be concerned with biometric moderation in general cognitive ability (GCA, the phenotype) by family-of-origin socioeconomic status (SES, the moderator). We will attempt to replicate the result of Turkheimer et al. (2003): increasing additive-genetic variance and decreasing shared-environmental variance with increasing SES.

GCA is that ability which is tapped by all cognitively demanding tasks. Often identified with Spearman’s (1904) g, it can be operationalized as a composite score from a battery of tests that adequately samples the domain of cognitive tasks and specific abilities—for example, Full-Scale IQ (FSIQ) from an individually administered IQ test. Decades of research (to say the least—see Galton, 1869) have made clear that general cognitive ability is a substantially heritable trait. Estimates of its heritability typically range from 0.50 to 0.70 (Bouchard & McGue, 1981, 2003; Deary, Spinath, & Bates, 2006), and are sometimes as high as ~0.80 (Rijsdijk, Vernon, & Boomsma, 2002).

As we described above, an important principle in contemporary behavior-genetic research is that the magnitude of a biometric variance component may depend upon other variables (moderators). The heterogeneity of heritability estimates for GCA across studies may reflect the influence of such moderators. The role of one of them, age, has been well replicated: the general trend is that, from early childhood through late adolescence or early adulthood, IQ’s heritability increases while its shared-environmentality decreases (Bouchard & McGue, 2003; Deary et al., 2006). A more tentative biometric moderator is family-of-origin SES. Two theoretical perspectives—those of Sandra Scarr (1992) and of Bronfenbrenner & Ceci (1994)—predict that cognitive abilities will be more heritable among children from higher-SES families. The two theories make that prediction for somewhat different reasons: Scarr’s theory emphasizes active gene-environment correlation (r_GE; Plomin, DeFries, & Loehlin, 1977), whereas Bronfenbrenner & Ceci emphasize parental facilitation of “proximal processes” in development. Scarr (Scarr-Salapatek, 1971) was the first to investigate whether the heritability of children’s GCA might vary as a function of their family SES. This and other earlier studies (Fischbein, 1980; van den Oord & Rowe, 1998; Rowe, Jacobson, & van den Oord, 1999) are reviewed in Supplementary Note #1 (Online Resource).

Turkheimer et al. (2003): A × SES and C × SES effects

In an important study that has generated much interest, Turkheimer et al. (2003) applied the continuous-moderator model of Purcell (2002) in a small sample of 319 pairs of 7-year-old twins. They found that the biometric decomposition of FSIQ (from the Wechsler Intelligence Scale for Children) varied as a function of parental SES They operationalized SES as a composite of parental education, income, and occupational status. At the upper extreme of the SES variable, IQ variance decomposed into ~80% additive-genetic variance and near-zero shared-environmental variance, whereas at the lower extreme of the SES variable, it decomposed into near-zero additive-genetic variance and ~60% shared-environmental variance. Further, unshared-environmental variance decreased with SES. However, judging by what is mentioned in the title and abstract of Turkheimer et al.’s article, it is the moderation of genetic variance (a specific form of G × E, which we will designate as A × SES) that is of primary interest, with the moderation of shared-environmental variance (shorthand, C × SES) of secondary interest.

It is important to recognize that, since family SES is the same for both twins in a pair, irrespective of zygosity, it is effectively part of the shared environment as far as twin models are concerned. However, the association between family SES and children’s GCA is surely at least partly genetically mediated, as evident from the larger associations between family characteristics and offspring ability in biological families vis-à-vis adoptive families (e.g., Scarr & Weinberg, 1978; Kirkpatrick, McGue, & Iacono, 2009). This is an example of passive r_GE (Plomin et al., 1977): parental cognitive ability and SES are positively correlated, and higher-ability parents pass on their trait-relevant genes to their children as well as provide them with an enriched rearing environment. Because r_GE can result in spurious detection of G × E, it is advisable to incorporate SES into the moderation model as a fixed regressor, which will partial out any phenotypic variance due to correlation between SES and A (Purcell, 2002; van der Sluis, Posthuma, & Dolan, 2012).

We are aware of five studies of GCA interpretable as attempts at replicating Turkheimer et al.’s (2003) A × SES and C × SES effects (Harden, Turkheimer, & Loehlin, 2007; van der Sluis, Willemsen, de Geus, Boomsma, & Posthuma, 2008; Grant, Kremen, Jacobson, Franz, Xian, et al., 2010; Hanscombe et al., 2012; Bates, Lewis, & Weiss, 2013). The effects’ replication record among these studies is mixed, possibly due to heterogeneity among the studies with respect to participant age (child, adolescent, adult) and country (USA, UK, Netherlands). The studies also vary with regard to how SES was operationalized. SES is not completely temporally stable¹; parental income and occupational status, in particular, can change with the vicissitudes of the labor economy. Only Hanscombe et al. had the advantage of repeated measures of SES (although the adult participants in Grant et al.’s (2010) study were asked for the highest education level their parents ever achieved). Details concerning the five replication studies are available in Supplementary Note #2 (Online Resource).

Of course, the A × SES and C × SES effects could be spurious. The A × SES element seems less plausible from sample-size considerations alone, since it is only supported in samples of fewer than 1000 twin pairs (Turkheimer et al., 2003; Harden et al., 2007; Bates et al., 2013). Several phenomena can lead to detection of spurious G × E. One of these is differential heritability (or shared-environmentality) by phenotype level. If the influence of A increases, or the influence of C decreases, with increasing GCA, then this heterogeneity may appear to be a biometric moderation effect of SES, simply because SES and GCA are positively correlated². Another complication is if there is greater assortative mating for GCA at lower SES levels (Loehlin, Harden, & Turkheimer, 2009). Because assortative mating deflates twin-based estimates of additive-genetic variance and commensurately inflates estimates of shared-environmental variance, it would then appear that additive-genetic variance increases with SES.

Finally, there is the issue of the specificity of biometric-moderation effects. Under the continuous-moderator model, biometric moderation may be thought of simply as heteroskedasticity in the regression of the phenotype onto the putative moderator. The specificity issue concerns how well an analysis can resolve which and how many biometric-moderation effects are nonzero—that is, which biometric variance components are heteroskedastic. Purcell (2002) remarked on this issue when discussing a substantial estimate of a C × SES effect in simulated data when the true generating model only had an A × SES effect. Both Turkheimer et al. (2003) and Hanscombe et al. (2012) refer to the issue as well. It is also evident in Harden et al.’s Table 5: the estimate of the A × SES effect when the C × SES effect was fixed to zero was very similar to the estimate of the C × SES effect when the A × SES effect was fixed to zero. This calls to mind an essential fact: inference about a parameter from a given model is ipso facto model-dependent; specifically, it depends upon which other parameters are free to be estimated in the model at hand. We wish to bring attention to one specific questionable practice that is widespread in behavior genetics: that of selecting one single model that is best (by some criterion), and then basing inference only on that model, as though no others had ever been considered. Breiman (1992, p. 738) has called this practice “a quiet scandal.” We instead provide an alternative approach: inference about parameters can be based on multiple models; in fact, one can (in a sense) select many or even all models under consideration, each only to the extent that it is supported by the data. Much of the present study is conducted using methods of multimodel inference. Awareness of these methods is not as widespread as we believe it should be, which is why we describe them in the Appendix. Our description mostly follows that of Burnham & Anderson (2001, 2002, 2004), whose work we recommend for further details.

Study Overview

Our study, which attempts to replicate the A × SES and C × SES effects of Turkheimer et al. (2003), improves upon previous replication attempts in several ways. First, our large sample is composed of twins, non-twin biological siblings, and adoptive siblings, assessed at a range of ages spanning the teenage years. A prior study of IQ in a substantially identical sample has been reported (Kirkpatrick, McGue, & Iacono, 2009). The presence of adoptees provides us with a “backstop” against artifacts stemming from passive r_GE and assortative mating, and allows us to directly estimate shared-environmental variance (and, in principle, variance due to covariance between the A and C factors). Second, we also have parental phenotype—IQ scores for the parents of the twins and siblings—and therefore can estimate assortative mating, both SES-independent and SES-dependent. Third, we have data on the same three SES indices used in the original Turkheimer et al. (2003) report.

Our primary analysis attempts to replicate the A × SES and C × SES moderation effects. We will compare performance of SES-moderation models when the age-moderation effects established in the literature, A × Age and C × Age, are included versus when they are not. In addition, we conduct three preliminary analyses prior to the primary analysis, and one exploratory analysis subsequently to it. The first preliminary analysis serves to test for a source of spurious moderation effects, SES-dependent assortative mating among parents (i.e., IQ correlation between mothers and fathers being dependent upon their SES). In our second preliminary analysis, we identify the sources of variance that should be represented in our model. The ACE model is quite plausible a priori from existing literature (reviewed above), especially for an adolescent (rather than adult) sample, and in light of the dearth of evidence for non-additive genetic variance in the domain of cognitive abilities (Bouchard, 2004). However, we can estimate more than two sources of familial variance in our sample. One possibility would be twin-specific environmental effects (“twin effects”), which would contribute to between-family variance among twins but not among non-twin siblings. Another possible source of variance is assortative mating. We need not assume that the additive-genetic correlation between full siblings is 0.5—we can estimate it from the data, because an ACE model would be identified by MZ twins and adoptees alone. Once the sources of variance are identified, our third preliminary analysis will determine whether the biometric decomposition of IQ varies as a function of trait level (that is, whether the influence of heredity and shared environment differs across the IQ distribution). This constitutes another test for a source of spurious moderation effects. Finally, after the main analysis, we will explore the possibility that the SES-moderation effects are age-dependent; we hypothesize that they will weaken through adolescence.

Methods

Sample

The primary sample (N = 4,973 from 2,494 sibling pairs) consisted of twins from the Minnesota Twin Family Study (“MTFS”; Iacono, Carlson, Taylor, Elkins, & McGue, 1999; Iacono & McGue, 2002; Keyes et al., 2009), and non-twin sibling pairs from the Sibling Interaction and Behavior Study (“SIBS”; McGue et al. 2007). In addition to this primary sample, one of our secondary analyses used a sample of 3,916 parents from MTFS and SIBS. Written informed assent or consent was obtained from all participants, with parents providing written consent for their minor children. The primary sample is substantially identical to that of Kirkpatrick et al. (2009), and MTFS and SIBS, their cognitive ability testing, and their zygosity determination and inclusion criteria have been described there and elsewhere (e.g., Kirkpatrick et al., 2014). We have therefore relegated many details concerning the sample and measurements to a Supplementary Methods section (Online Resource).

For the present study, we used parental data only from parents who were the “original rearing” parents in the family. Usually, the original rearing parents would be the biological parents of the family’s offspring, unless it was known that one of them had limited contact with the children while they were growing up (due to divorce, etc.). In the case of families with only adopted offspring, the original rearing parents would be those with whom the offspring were originally placed for adoption, unless again it was known that one of them had limited contact with the children.

SES

Our analysis used three family-level SES variables: (1) the higher of the parents’ occupational statuses, (2) midparental educational attainment, and (3) annual household income. We only used the occupational and educational data of the original rearing parents. If data were available only for one of the parents, we took that parent’s occupation and education as the higher occupational status and the average education level of the couple, respectively. After exclusions, at least one family-level SES variable was observed for 2,501 families.

Mothers’ and fathers’ occupational status was assessed during the recruitment phone interview with families’ mothers. Occupational status was coded on the Hollingshead scale (Hollingshead, 1957). We reverse-scored the Hollingshead scale so that higher values, on a scale of 1 to 7, represent higher status. We coded as missing the occupational status of those who did not work full-time in their reported occupation, those who reported their occupation as “homemaker,” and those reported to be retired, disabled, or institutionalized.

Mothers’ and fathers’ educational attainment was also assessed during the phone interview. We harmonized educational attainment from the slightly different phone interviews given to different subsamples into a five-point scale (1 = less than high school, 2 = high school, 3 = some post-secondary education, 4 = four-year college degree, 5 = graduate/professional degree).

Annual household income was collected by parental report at the intake assessment of MTFS, and at the first follow-up visit of SIBS. Income was measured on an ordinal scale representing income brackets: 0 = “less than $10,000,” 1 = “$10,001 to $15,000,” and so forth, up to a maximum of 12 = “Over $80,000.”

Of the 2,501 families, the percentages missing data on each family-level SES variable were 7.4% for occupational status, 0.6% for educational attainment, and 8.4% for household income. Around 85% of families had no missing observations, 14% had one missing observation, and 1% had two missing observations. As did Turkheimer et al. (2003) and Myrianthopoulos & French (1968), we converted each family’s score on the three SES variables into a cumulative proportion (from that variable’s empirical CDF), and then averaged the available proportions, producing an SES score for each family (if only one proportion was available, it was taken as the family’s SES score). There were 2,494 families having both an SES score and FSIQ for at least one of the offspring. There were 2,382 families in which SES and at least one parent’s FSIQ score were available.

Analyses

Unless stated otherwise, all analyses were conducted in OpenMx (Boker et al., 2011), via full-information maximum-likelihood (FIML) estimation from raw data. In most of our analyses, the endogenous variable was offspring IQ, which is assumed to follow a bivariate normal distribution (conditional on age, sex, and SES).

For model comparison and multimodel inference (see Appendix), we used Hurvich & Tsai’s (1989) sample-size-corrected version of Akaike’s Information Criterion, AICc:

$$\mathit{AICc}=-2\mathit{logL}(\widehat{\mathbf{\theta }}\mid M,x)+2k+\frac{2k(k+1)}{N-k-1}$$ (1)

In large samples, AICc differs little from AIC. However, some (e.g., Burnham & Anderson, 2004) argue that AICc should always be used in practice, and that AIC’s reputation for overfitting has resulted partly from failure to use AICc in simulation studies.

We proceeded by fitting models, assessing model performance via AICc, and using the performance of previously fitted models to guide specification of subsequent ones. We refrain from reporting parametric inference until all models informative about a particular parameter have been fitted, and—so that Akaike weights can be used—until all AIC-comparable models have been fitted as well. At that point, if more than one model informative about the parameter had been fitted, we computed model-averaged point estimates, with confidence intervals and p-values³ from the model-averaged standard error, under the assumption of normal sampling distribution. We also obtained a 95% confidence set for the best-approximating model. Details concerning Akaike weights, model-averaging, and the confidence set are provided in the Appendix. Very briefly, Akaike weights are AICcs transformed to proportions so that smaller AICcs have larger weights. These weights are used to compute averages of parameter estimates and their standard errors across models. The confidence set is expected to contain the “best” model with probability 0.95 over repeated sampling, and helps to quantify model-selection uncertainty due to sampling error.

Results

We first estimated IQ standard deviations and sibling correlations, separately by family type, while correcting for age and sex (McGue & Bouchard, 1984), which is especially important in the present case since members of a sibling pair from SIBS were not necessarily the same age and sex, whereas MTFS twins were. From these estimates (Table I), we can see that the DZ-twin correlation and SD were greater than those of the non-twin full sibs, suggesting the possibility of twin effects. The presence of adoptees also enables us to estimate r_GE. However, it is evident that the phenotypic variance among adoptees was greater, not less than, the variance among biological offspring (which includes the twins), in which case the estimated correlation between A and C (r_AC) would be negative—in other words, that a typical person’s genes and shared environment affect IQ in opposite directions. On its face, this is a difficult conclusion to accept. We therefore decided not to fit any models including an r_AC estimate. In any event, the four standard-deviation parameters in Table I were not significantly different from one another (LRT χ²(3) = 4.25, p = 0.2353), which is not suggestive of significant r_AC.

Table I.

Age- and Sex-corrected FSIQ correlations and standard deviations, by type of sibling relationship.

	MZ twins	DZ twins	Ado Sibs	Bio Sibs	Mixed Sibs
SD (SE)	13.69 (0.25)	13.72 (0.30)	14.09 (0.38)	12.92 (0.42)	a
r (SE)	0.77 (0.01)	0.50 (0.03)	0.11 (0.06)	0.36 (0.06)	0.24 (0.07)

notes: “Ado” = both siblings adopted, “Bio” = both siblings are biological offspring of parents, “Mixed” = one sibling is adopted and one is biological offspring.

^aIn mixed families, the standard deviation of biological offspring was constrained equal to that of bio sibs, and the standard deviation of adoptees was constrained equal to that of ado sibs.

Preliminary analyses

To test for SES-dependent assortative mating, we modeled parental IQ with a bivariate normal distribution, having a different mean (which was conditioned on SES via regression) and standard deviation for mothers and fathers. We fit two models, one in which the spousal correlation was allowed to vary linearly with SES, and one in which it was constant with respect to SES. The former model estimated that the spousal correlation would be 0.41 at the bottom of the SES distribution, and 0.30 at the top—a change of −0.11 (95% CI: −0.29, 0.06), which was not statistically distinguishable from zero (LRT χ²(1) = 1.56, p = 0.2114). The estimate of the spousal correlation from the latter model (constant across SES) was moderate, and very close to the meta-analytic average reported over 30 years ago (Bouchard & McGue, 1981): r = 0.35 (95% CI: 0.30, 0.39). Obviously, it differed significantly from zero (LRT χ²(1) = 186.43, p = 1.908×10⁻⁴²).

This analysis indicated that parental assortative mating is moderate in magnitude, and is not SES-dependent, which rules out one possible source of spurious G × E. As explained by Kirkpatrick et al. (2009, footnote 1), if we assume a high heritability for adult IQ, that spouses select mates for psychometric IQ per se, and that the phenotypic spousal correlation perfectly reflects a genetic spousal correlation, then the classical twin model would underestimate heritability by about 28%, and commensurately overestimate shared-environmentality. However, these are “worst-case scenario” assumptions, and are generally not true. Further, in our dataset, the ACE variance components are identified by the adoptees and MZ twins alone, whose covariances are not affected by the true genetic correlation between full siblings. As described in the next section, we actually estimated this genetic correlation.

To decide which sources of variance to include in our biometric models, we fit Models #1through #4 (collectively, “Block #1”). These four models represented the four combinations of the twin effects path γ_T0 fixed (to zero) versus free, and full-sib genetic correlation r_A fixed (to 0.5) versus free. All four included the main effects of sex and age. Additionally, we estimated a separate intercept (β₀) for twins, biological SIBS offspring, and adoptees, and a separate SES main effect (β_SES) for biological offspring (including twins) and adoptees. If we were to apply the ACE model to our dataset without SES main effects, variance due to SES per se would otherwise be variance due to C, but this is not the case for variance due to A-SES correlation, as it does not contribute to variance among adoptees nor to covariance between unrelated siblings reared together. Hence, estimating separate SES main effects for biological children and adoptees is a prudent way to control for A-SES correlation (a form of passive r_GE). Since the association between parental SES and offspring IQ partly reflects this correlation in the case of biological children, but not for adoptees, we naturally anticipate a larger main effect of SES for biological offspring.

The four models’ AICcs are presented in Table II. Because Block #1 was the first part of a series of comparable models (the general form of which is depicted in Figure 1), Table II also includes their Akaike weights, which are calculated relative to the AICcs of all models in this comparable set. From Table II, it can be seen that the best-approximating model within this block is #4, which has both r_A and γ_T0 fixed to their null values. As anticipated, we conclude from Block #1 that the biometric ACE components are sufficient to describe our data, and that fixing both r_A and γ_T0 to their null values improves model efficiency. In the previous section, we conclude that the spousal correlation for IQ is not SES-dependent, and we report here that the genetic correlation for full sibs differs unimportantly from 0.5. On the basis of the foregoing, we resolved here to assume in further analyses that the effects of assortative mating are negligible.

Table II.

Model-fitting results from Block #1: AICcs (underline) and Akaike weights.

	Free γT0	Fix γT0 = 0
Free rA	38631.89 6.75 × 10−6 (Model #1)	38629.88 1.85 × 10−5 (Model #2)
Free rA = 0.5	38629.91 1.82 × 10−5 (Model #3)	38627.9 4.99 × 10−5 (Model #4)

Table notes: The models in this block differ by whether they have r_A and γ_T0 as fixed or free parameters. r_A is the correlation between latent factors A₁ and A₂ for full siblings (including DZ twins). γ_T0 is the path loading for twin-specific environmental effects. AICcs are underlined; Akaike weights are proportions. Smaller AICcs and greater Akaike weights both correspond to a more-preferable model. A model’s Akaike weight is interpretable as the posterior probability that the model is the best at approximating full reality in the population, given the size of the sample and the set of models under consideration (see Appendix).

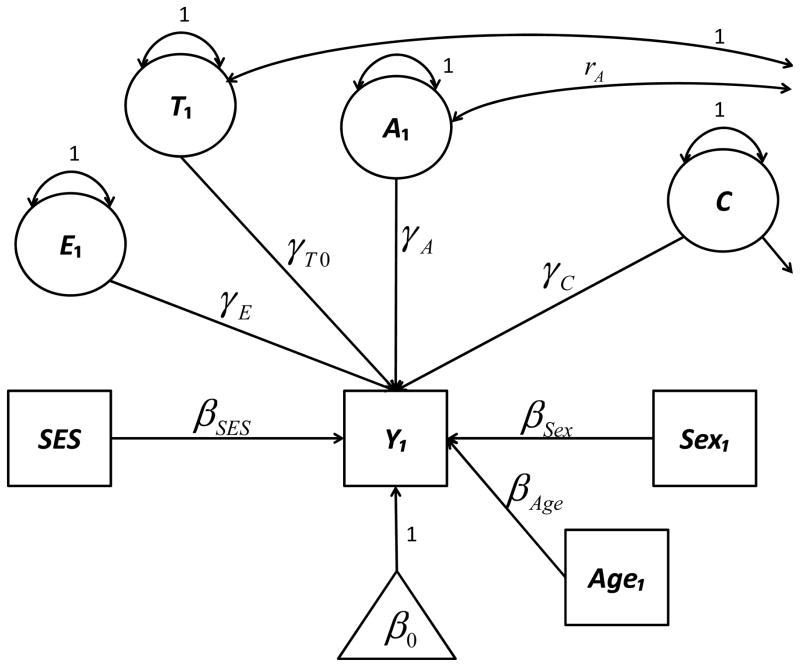
Figure 1. Biometric moderation model—general form for Blocks #1, #2, and #3.

For ease of presentation, only twin #1’s side of the diagram is shown. The path loadings onto the latent A, C, and E variables are allowed to depend upon moderators, and might be written thus: γ_A = γ_A0 + γ_A1(Age₁) + γ_A2(SES) + γ_A3(SES × Age₁), γ_C = γ_C0 + γ_C1(Age₁) + γ_C2(SES) + γ_C3(SES × Age₁), and γ_E = γ_E0 + γ_E1(Age₁) + γ_E2(SES). For example, γ_A0 is the main effect of A, γ_A1 is the A × Age effect, γ_A2 is the A × SES effect, and γ_A3 is the A × Age× SES effect. In Block #1, only main effects (γ_A0, γ_C0, γ_E0, γ_T0) were estimated. In Block #2, moderation effects of age (γ_A1, γ_C1, γ_E1) and SES (γ_A2, γ_C2, γ_E2) were introduced, and in Block #3, the interactions (γ_A3, γ_C3) were introduced. The twin-effects parameter γ_T0 was only ever estimated in Block #1, and the loading onto T was never conditioned on moderators. Separate values of β₀ were estimated for twins, biological SIBS offspring, and adoptees. Separate values of β_SES were estimated for biological offspring of parents (including twins) and for adoptees.

The models of Block #1 are the only ones that provide single estimates for the ACE variance components, since models with a biometric-moderation effect estimate, in a sense, different component values at different levels of the moderator. The model-averaged point estimates from Block #1 of additive-genetic variance, shared-environmental variance, and unshared-environmental variance are respectively 109.06, 23.25, and 43.19, which sum to total residual variance 175.50, and respectively yield standardized estimates of 0.62, 0.13, and 0.25.

To assess whether the influence of heredity and shared environment depend upon trait level, we used DeFries-Fulker regression (DeFries & Fulker, 1985, 1988) with double-entered data (Rodgers & McGue, 1994; Rodgers & Kohler, 2005) which has been used for similar purposes in other studies (e.g., Cherny, Cardon, Fulker, & DeFries, 1992). With double-entered data, phenotype scores are mean-centered within kinship groups, and then each sibling pair (twins being a special case of siblings) is entered into the dataset twice, with the labels “sibling #1” and “sibling #2” reversed for each entry. Since our data support the use of a model with the ACE biometric components, the DeFries-Fulker regression equation we used is

$$K_1=b_1{K}_2+b_2(K_{2}R)+b_3(K_2^2)+b_4(K_2^{2}R)+b_5({\mathit{Age}}_1)+b_6({\mathit{Sex}}_1)$$ (2)

where K₁ is the phenotype score of sibling #1, K₂ is the phenotype score of sibling #2, R is the coefficient of relationship (1 for MZ twins, 0.5 for full siblings, and 0 for adoptive siblings), Age₁ is the age of sibling #1, and Sex₁ is a dummy variable for whether or not sibling #1 is female. In this model, the interaction coefficients b₃ and b₄ represent how much the shared-environmentality and heritability, respectively, depend upon trait level.

This DeFries-Fulker regression requires complete data within sibling pairs. There were 2,479 pairs in which FSIQ was available for both members. We conducted the regression represented by Eq. (2) via an implementation of Kohler & Rodgers’ (2001) “efficient DF estimation” in the R statistical computing language. The interaction estimates were both small and statistically indistinguishable from zero: b̂₃ = −2.87×10⁻⁵ (95% CI: −2.36×10⁻³, 2.30×10⁻³; p = 0.9807) and b̂₄ = 7.40×10⁻⁴ (95% CI: −1.72×10⁻³, 3.21×10⁻³; p = 0.5560). Further, the joint test of the two interactions was not significant (Wald χ²(2) = 1.05, p = 0.5913). This DeFries-Fulker regression required exclusion of incomplete sibling pairs, and was only informative about the standardized, not raw, additive-genetic and shared-environmental variance components. Nonetheless, we regard it as reasonably good evidence that the additive-genetic and shared-environmental components do not linearly vary across the FSIQ continuum, ruling out another possible source of spurious G × E.

Primary Analysis: Can we replicate SES-moderation effects?

To address our research question, we fit Block #2, consisting of Models #5 through #19. These models comprise the eight combinations of A × SES, C × SES, and E × SES effects being included or excluded. Each such combination was fitted twice: once including A × Age and C × Age effects, and again with them dropped.

The AICcs and Akaike weights of this block are reported in Table III, from which we draw several conclusions. For one, the inclusion of any kind of SES-moderation effect improved model efficiency, indicating that the regression of IQ onto SES is heteroskedastic. More importantly, models that included an A × SES effect clearly fared better than those that did not, and those that included an E × SES effect fared slightly better than those that did not. But, the C × SES effect appeared quite extraneous. Further, the AICc rank-orders within each column of Table III are nearly identical, indicating that the SES-moderation effects’ contributions to relative model efficiency depended little on whether or not age-moderation effects were included. From these results, we concluded that our data support only an A × SES effect, but not a C × SES effect.

Table III.

Model-fitting results of Block #2: AICcs (underlined) and Akaike weights.

		Age-Moderation Effects
		AC	None
SES-Moderation Effects	ACE	38612.34 0.1188 (Model #5)b	38613.93 0.0538 (Model #13)b
	AC	38612.75 0.0972 (Model #6)b	38614.08 0.0498 (Model #14)b
	AE	38612.21 0.1268 (Model #7)b	38611.91 0.1478 (Model #15)b
	CE	38615.26 0.0277 (Model #8)b	38616.38 0.0158 (Model #16)
	A	38612.46 0.1120 (Model #9)b	38612.1 0.1339 (Model #17)b
	C	38619.31 0.0036 (Model #10)	38619.78 0.0029 (Model #18)
	E	38621.47 0.0012 (Model #11)	38620.83 0.0017 (Model #19)
	None	38628.91 3.00 × 10−5 (Model #12)	38627.9 4.99 × 10−5 (Model #4)a

^aModel #4 is part of Block #1 (see Table II).

^bModel is in the 95% confidence set for best-approximating model (see Appendix).

Table notes: AICcs are underlined; Akaike weights are proportions. Smaller AICcs and greater Akaike weights both correspond to a more-preferable model. The overall preferred model, #15, is bolded. A model’s Akaike weight is interpretable as the posterior probability that the model is the best at approximating full reality in the population, given the size of the sample and the set of models under consideration (see Appendix). “Age Moderation Effects” are those latent biometric factors the loadings of which were allowed to be moderated by age; ”none” indicates that no age-moderation effects were included, whereas “AC” indicates that both A × Age and C × Age effects were included. “SES Moderation Effects” are those latent biometric factors the loadings of which were allowed to be moderated by SES. For example, the models in the row marked “CE” included C × SES and E × SES effects.

Exploratory Analysis

Perhaps the A × SES effect apparent in our data weakens with age. Perhaps there is a small C × SES effect lurking in our data that is only operative among younger participants. Certainly, if these SES-moderation effects decline with age, it would help to explain why attempts to replicate them in adults (van der Sluis et al., 2008; Grant et al., 2010) failed. To investigate these possibilities, we fit Block #3, composed of Models #20 through #22. Both age- and SES-moderation effects for A and C should be included, since we were considering the moderation effects of an age × SES interaction. We also included the SES-moderation effect on E, since it received limited support in Block #2. Model #20 included the A × Age × SES and C × Age × SES effects, Model #21 only the former, and Model #22 only the latter. Except where these three-way interactions are concerned, we do not utilize point estimates or standard errors from Models #20, #21, and #22 in model-averaging, partly because of these models’ exploratory nature, but primarily because the parameters of greatest interest in our study are age- and SES-moderation effects, which lose interpretability once the three-way interactions are included.

The three models’ AICcs and Akaike weights are reported in Table IV. None of the interaction effects contributed to model performance. On this basis alone, we conclude that there is no age-dependent SES-moderation. But, we are now ready to draw inferences about those interaction parameters, and a number of other parameters of interest as well.

Table IV.

Model-fitting results of Block #3.

Model Number (Free Interaction Parameters)	AICc	Akaike Weight
Model #20 (A × Age × SES, C × Age × SES)	38616.27	0.0167
Model #21b (A × Age × SES only)	38614.25	0.0457
Model #22b (C × Age × SES only)	38614.31	0.0444
Model #5a (none)	38612.34	0.1188

^aModel #5 is part of Block #2 (see Table III).

^bModel is in the 95% confidence set for best-approximating model (see Appendix).

A model’s Akaike weight is interpretable as the posterior probability that the model is the best at approximating full reality in the population, given the size of the sample and the set of models under consideration (see Appendix). Smaller AICcs and greater Akaike weights both correspond to a more-preferable model.

Overall Results

Table V lists model-averaged parameter estimates, plus corresponding confidence intervals and p-values based on the assumption of normal sampling distribution. The estimates of neither three-way interaction from Block #3 differed significantly from zero. Consistent with existing literature, we did observe a significant increase in additive-genetic variance, and a significant decline in shared-environmental variance, with increasing age. Most interestingly, we replicated only the A × SES effect of Turkheimer et al. (2003): additive-genetic variance varied positively with family SES. The C × SES effect was not in the hypothesized direction and was estimated with little statistical precision. Finally, although the AICcs provided some support for an E × SES effect, the model-averaged results show that we do not have sufficient evidence to conclude that it differs from zero.

Table V.

Multimodel inference from Blocks #1 through #3.

Parameter	Point Estimate (CI)	P-value
Full-Sib Genetic Correlation (rA)	0.489 (0.380, 0.599)	0.8483a
Twin Effects (γT0)	1.27×10−5 (−3.593, 3.593)b	1.000
A × SES Effect	2.969 (1.095, 4.843)	0.0019
C × SES Effect	1.299 (−2.762, 5.360)	0.5307
E × SES Effect	0.891 (−0.244, 2.027)	0.1264
A × Age Effect	0.318 (0.024, 0.611)	0.0339
C × Age Effect	−1.437 (−2.254, −0.621)	0.0006
A × SES × Age Effect	0.160 (−0.383, 0.703)	0.5635
C × SES × Age Effect	−0.272 (−1.794, 1.250)	0.7260
SES Main Effect, adoptees (βSES,A)	6.961 (1.617, 12.305)	0.0107
SES Main Effect, bio offspring (βSES,B)	16.047 (13.892, 18.202)	3.073×10−48

Table notes: Models #20, #21, and #22 (Block #3) are only included in calculating model-averaged inference for the three-way interactions (A × SES × Age and C × SES × Age; explanation in text). Otherwise, point estimates and standard errors for each parameter were calculated from all models among Models #1 through #19 in which the parameter was freely estimated. Confidence intervals and p-values were calculated from point estimates and standard errors, assuming a normal sampling distribution. Signs on moderation effects are reported so that a negative value indicates that the loading on the latent biometric factor becomes more negative as the moderator becomes more positive.

^aNull parameter value for r_A is 0.5.

^bThe sign of the twin-effects parameter (γ_T0) is arbitrary, since the actual corresponding variance component is ${\gamma }_{T0}^2$. The 95% profile-likelihood confidence interval for ${\gamma }_{T0}^2$, from Model #3 (γ_T0 free, r_A fixed), is (0, 12.27).

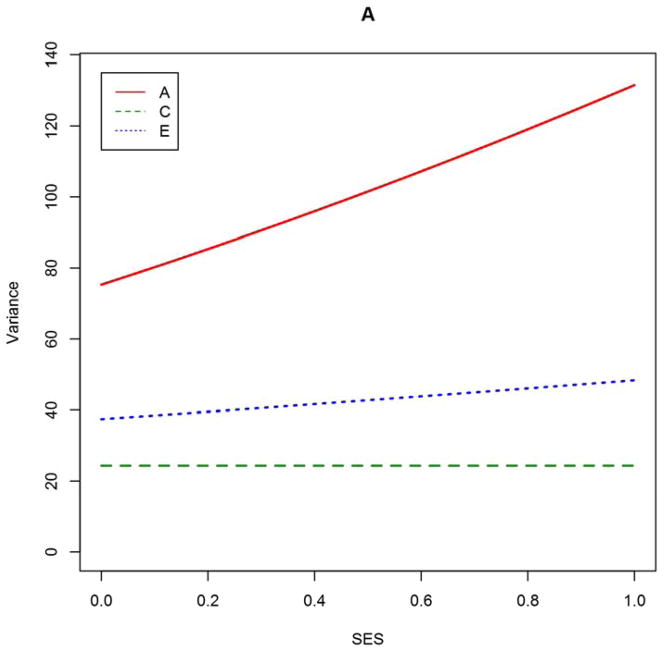
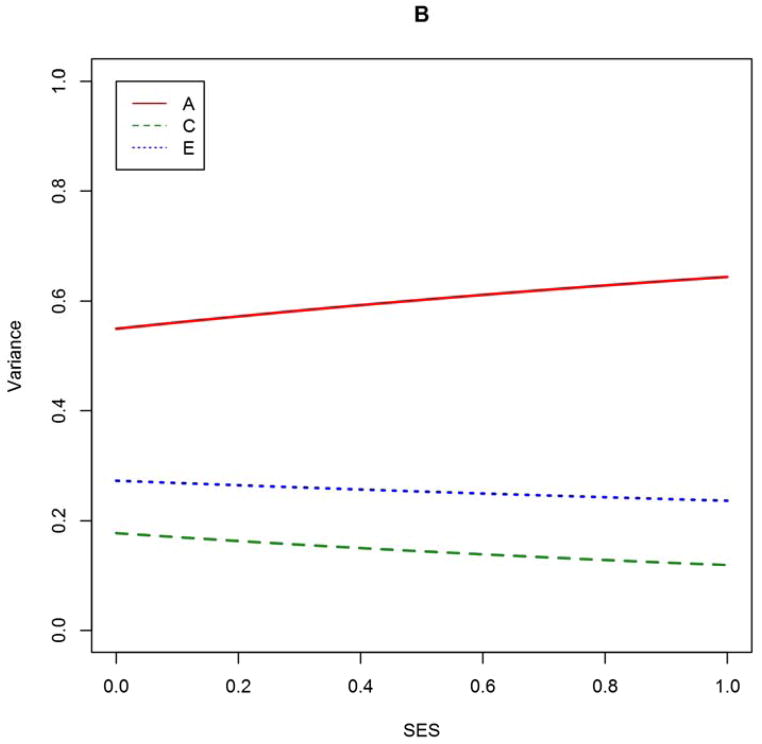
Although model-averaging is well-suited for inference about one parameter at time, it does not necessarily make for easy interpretation. Consider the model-averaged estimate of the A × SES effect, 2.969. Because the SES variables were scaled to the interval [0,1], this value means that for the highest-SES families, the loading onto A is greater than that for the lowest-SES families by 2.969. But to really interpret this value, one would need a value for the main-effect of A, which is not a parameter of interest. Sometimes, a meritorious model can tell a complete story in a way that model-averaging cannot easily do. For this reason, we also report point estimates and standard errors from the two most AICc-favored models, Model #15 (A × SES, E × SES, no age-moderation) and Model #17 (A × SES only), respectively (Table S2 in Online Resource). It can be seen that the model-conditional estimates of free parameters do not differ drastically from the corresponding model-averaged estimates. In Figure 2, we graph how the biometric decomposition would vary by SES according to the estimates from Model #15, expressed in raw variance components and in normalized variance proportions.

Figure 2. Biometric variance components (A) and variance proportions (B) as function of SES, based on estimates from best-approximating Model #15.

At a given point on the abscissa in panel B, the ordinate positions of each curve sum to unity. SES is a composite of parental educational attainment, parental occupational status, and household income, transformed to cumulative proportions (mean = 0.58, SD = 0.24). Model #15 included A × SES and E × SES effects.

Discussion

Guided by existing data and theory, we fit a number of biometric models to a relatively large dataset collected from twins, non-twin biological siblings, and adoptive siblings. We compared models by a sample-size corrected version of AIC, the AICc (Hurvich & Tsai, 1989). We compared models’ AICcs to first resolve basic questions of specification, then to attempt to replicate the SES effects of primary interest, and finally to explore the possibility of age-dependent SES effects. We first resolved that an a priori plausible ACE model would suffice for our purposes, and that the effects of assortative mating and of differential heritability/shared-environmentality by trait level were negligible. We fit models with various SES-moderation effects, both including and excluding two age-moderation effects identified in the literature. We observed support for the hypothesized A × SES effect, weakly suggestive evidence of an E × SES effect, but none for the hypothesized C × SES effect. Our exploratory analysis did not provide any evidence for age-dependent SES-moderation effects. Thus, our study shows that additive-genetic variance in GCA increases with family-of-origin SES. This replication of the A × SES effect is robust to model specification: what all models belonging to the 95% confidence set (marked with superscript “b” in Tables III and IV), save one, have in common is a free A × SES parameter. The effect is also statistically significant (Table V): it would survive (overly conservative) Bonferroni correction for the 17 p-values we report.

The A × SES and C × SES interactions from Turkheimer et al. (2003) are the biometric-moderation effects of primary interest in this study, and although they have generated much interest, they have not been replicated together in any study of general cognitive ability applying Purcell’s continuous-moderation model. They have failed replication twice (Grant et al., 2010; van der Sluis et al., 2008), and the C × SES component has been replicated once (Hanscombe et al., 2012). Our study constitutes the third replication of the A × SES element, after Harden et al. (2007) and Bates et al. (2013). Interestingly, the A × SES effect has only been observed in U.S. samples in which parental income was available as an SES variable. It has not replicated in European samples nor in an American sample in which only parental education was available. In public health, it has been shown that income and education each provide different information about health-relevant aspects of an individual’s SES, and are usually not so highly correlated that entering both into a regression analysis produces multicollinearity problems (Braveman et al., 2005). Further, a given SES variable’s relations with other variables can differ by country, and by demographic strata and regions within countries (Uher, Dragomirecka, & Papezova, 2006; Braveman et al., 2005). Possibly, the A × SES effect is a distinct moderation effect of family income in the United States. More research is needed to evaluate this tentative proposition. In the present study, we could have conducted analyses to gauge how much each of the three SES variables contributed to the A × SES effect. However, this would be a greater undertaking than it might seem, since rigorously gauging variables’ relative importance can be rather involved in multiple regression (Azen & Budescu, 2003), let alone in a structural equation model involving interactions with latent variables.

Our study, Bates et al. (2013), Harden et al. (2007), and Turkheimer et al. (2003) were all conducted in samples of American youth in which parental income was available, but the C × SES effect only occurs alongside the A × SES effect in the original 2003 study. We offer a speculative explanation for why this is so. Our sample, Harden et al.’s, Bates et al.’s, and Grant et al.’s (2010) are predominantly Caucasian, but Turkheimer et al.’s is mostly (54%) African-American. Perhaps low SES is not enough to produce the extreme deprivation that, according to Scarr (1992), is necessary to amplify the differential effect of the rearing environment; perhaps low SES must be combined with membership in a disadvantaged minority group whose place in and experience of American society is unique due to the historical legacy of slavery.

The fact that the A × SES effect has failed replication in adults suggests that it could be age-dependent. But, Hanscombe et al.’s (2012) graphs and point estimates show no clear age-related trend; further, we tested this hypothesis directly, and it was not supported. The availability of IQ data at different ages, which allowed us to directly estimate the age-dependence of SES-moderation effects, is one of several advantages our study has over some existing ones. Another advantage is that we were able to empirically check for possible sources of spurious results, including assortative mating, and differential heritability/shared-environmentality by trait level. Still another advantage was the availability of adoptees, whose data are informative about shared-environmental variance, without bias due to assortative mating, passive r_GE, or violations of the “equal environments assumption” for twins. We were also able to calculate different SES main effects for adoptees and biological children. The one for adoptees shows that family SES has a moderate, environmental effect on children’s cognitive functioning, equal to a 7-point IQ advantage for children from the highest-SES families versus the lowest-SES families. Finally, we consider our use of multimodel inference to be a major advantage of our study, because it enables us to produce point estimates and confidence intervals based on all fitted models informative about a parameter, each to the extent that AICc favors it over others. This avoids the bias resulting from conditioning one’s parametric inference only upon a single model (Lukacs et al., 2009).

We wish to temper our endorsement of multimodel inference with a few caveats. First, we must emphasize that Model #15 (A × SES, E × SES, no age-moderation) is not necessarily most likely to be the true model because it has the smallest AICc. Likewise, a model’s Akaike weight is not the posterior probability that the model is the true model. AIC is not intended to discover the “true” model in the first place. Instead, as stated by Browne (2000, p. 129), AIC is “not appropriate for selecting the best-fitting model in some general sense independent of sampling error, but…for indicating models whose calibrations can be trusted given a specified sample size.”

Second, our conclusions depend upon the candidate set of models under consideration⁴. We wanted to obtain estimates of each SES-moderation effect from models in which other moderation effects were variously present or absent. We had to balance that objective with the needs to preserve interpretability and a manageable scope, to avoid blindly empirical “data fishing,” and keep our analyses relevant to our research objectives. It slightly complicates matters that our candidate model set evolved as our analyses proceeded, in that we used the results from previously fitted models to guide specification of subsequent ones. Also, for the sake of interpretability and maintaining a manageable scope, we proceeded from simpler to more-complicated models. In these respects, our approach bears some resemblance to stepwise forward-selection. However, we deliberately avoided some of the most objectionable aspects of stepwise analyses. We did not conduct a purely data-driven, blindly empirical analysis. Our analysis was guided by subject-matter knowledge, each block of models was intended to address a specific question, and we saved the most exploratory analyses for last. Further, we did not use significance testing for model selection, nor did we base our conclusions solely upon the final model.

One restriction we imposed upon the candidate set is that all the biometric-moderation models we considered are of the form of Purcell’s (2002) continuous-moderator model. There are other model formulations arguably more appropriate for estimating G × E in the presence of r_GE, such as others described by Purcell (2002), and those of Rathouz, Van Hulle, Rodgers, Waldman, and Lahey (2008) or of Price and Jaffee (2008)—all of which involve biometrically decomposing the putative moderator in some way. We decided to retain the Purcell formulation because existing studies of SES-moderation have used it, and our study is intended as a replication study of Turkheimer et al. (2003). Nonetheless, inclusion of SES main effects in our models is a rather vexing problem. If one thinks of the path diagram in, say, Figure 1 as a simultaneous regression of IQ onto both observable and latent variables, then clearly the main effect of SES must be included if any interactions of SES with latent variables are to be included as well. With data from twins only, SES will necessarily account for variance otherwise attributable to C (or to r_AC, which would appear as variance due to C). Our data enabled us to separately estimate the β_SES path coefficient for adoptees and biological offspring; both effect sizes are nontrivial, and possibly, enough shared-environmental variance was partialled out that the C × SES effect was rendered impossible. On the other hand, including the two SES main effects allows us to be reasonably certain that our A × SES result is not an artifact of correlation between SES and latent variable A. Because we conditioned our models upon SES (as a fixed regressor in the definition of the model-expected phenotypic mean), any phenotypic variance due to SES or to covariance between SES and latent variable A would be partialled out (Purcell, 2002; van der Sluis, Posthuma, & Dolan, 2012).

Our study raises several other questions that can guide future research. We have already suggested three: to what extent are SES-moderation effects dependent upon country, SES measure, or ethnic minority status? Future studies could attempt to test specific hypotheses made by the Scarr (1992) and Bronfenbrenner & Ceci (1994) theories about SES-moderation. For instance, Scarr’s theory predicts that C × SES effects are only likely to be observed when the lowest echelons of SES are represented in the sample. Similarly, Bronfenbrenner and Ceci emphasize the importance of environmental stability for effective development. Since family SES is correlated with stability of the rearing environment (Evans, 2004), perhaps stability is what really drives SES-moderation effects. It would also be interesting to investigate another correlate of SES—parental phenotype, that is, parental cognitive ability—as a biometric moderator. Finally, behavior geneticists could attempt to replicate the A × SES effect when genetic factors are not latent, but measured as molecular-genetic data. Exciting avenues of G × E research remain to be explored.

Appendix: The Information-Theoretic Approach and Multimodel Inference

Kullback & Leibler’s important 1951 paper concerns, inter alia, derivation of a metric representing how well one probability distribution is approximated by another. Specifically, it is the expected amount of information (in Kullback & Leibler’s generalized Shannon-Wiener sense) lost when one probability distribution is approximated by another. This metric has become known as Kullback-Leibler (KL) divergence. A sensible objective of model selection, then, is to choose the model that has the smallest KL divergence from full reality. Full reality, of course, is not known, and may not even be knowable in principle; possibly, any complete description of full reality would be infinitely long. If we accept the possibility that no statistical model can completely describe full reality, then the premise of a “true model” that generated the data becomes rather dubious. These issues pose no problem, however, if one is only interested in the relative divergence of different models, since the unknown constants depending upon full reality cancel out from subtraction.

In a series of important contributions in the 1970s, Hirotugu Akaike⁵ showed that the maximized joint loglikelihood of a model’s parameters estimates how relatively “close” (in a KL-divergence sense) the model is to full reality, except that this estimator is biased upward, because it represents the fit of the model in the same data from which its parameters were estimated. Akaike further showed that, in large samples, the magnitude of this bias is in fact approximately equal to k, the number of free parameters. Subtracting k from the loglikelihood thus serves to estimate the expected loglikelihood of the model when “plugging in” parameter estimates previously obtained from a separate, independent sample of the same size. Akaike multiplied this bias-adjusted loglikelihood by -2 (to turn it into a bias-adjusted deviance), obtaining what has become known as Akaike’s Information Criterion,

$$\mathit{AIC}=-2\mathit{logL}(\widehat{\mathbf{\theta }}\mid M,x)+2k$$ (4)

where θ̂ is the vector of maximum-likelihood estimates of model M’s k parameters, as estimated from dataset x. In theory, the candidate model with the smallest AIC is expected to be the model that best approximates full reality, conditional on sample size N and the set of candidate models considered. The expected relative KL divergence of two candidate models may be estimated simply by subtracting their AICs.

As is evident from the previous paragraph, AIC is a penalized fit index. The unpenalized model deviance, −2logL(θ̂|M, x), by itself is a poor measure of a model’s merit, as it may be made arbitrarily small by adding parameters and increasing model complexity. AIC’s penalty is the approximate amount by which model deviance is underestimated when assessing the model in the same sample in which its parameters are being estimated. In other words, AIC has deep theoretical connections to cross-validation (discussed further by Stone, 1977; Shao, 1997; and Browne, 2000). Specifically, in large samples, it is expected to select that model in the candidate set which minimizes error of prediction in new samples of the same size from the population, where error is based on a loglikelihood function (Hastie, Tibshirani, & Friedman, 2009). Since maximizing normal likelihood is equivalent to minimizing quadratic loss, and since many analyses assume (at least implicitly) a normal distribution, in many contexts AIC is expected to select that model in the candidate set which minimizes mean squared error of prediction. We therefore phrase our interpretations of AIC in terms of “efficiency” or “performance”—shorthand for expected relative efficiency or performance—rather than “fit,” because, again, one can just add more parameters to improve model fit to the data at hand.

However, one of AIC’s appealing qualities is that it allows the expected relative efficiency of all the models in the candidate set to be compared to one another. Unlike the likelihood ratio test (LRT), AIC can be used to compare multiple models to one another and rank them in terms of their merit; they need not be a sequence of nested models. In fact, different models’ AICs will be comparable to one another provided that the models all: (1) are fitted to the same dataset (and in particular, have the same N); (2) have the same endogenous variable(s) (which are no longer considered “the same” if they have been transformed); and (3) either have likelihood functions from the same family of distributions or use fully normalized densities as likelihoods (Burnham & Anderson, 2002).

We now describe how AIC can be used to weight the results of multiple models under consideration, and obtain model-averaged point estimates and sampling variances. Let AIC_min denote the smallest AIC in a set of m comparable models. Then, those models’ AICs can be re-expressed relative to AIC_min. For some model l, let Δ_l = AIC_l − AIC_min. Then, model l’s Akaike weight can be calculated as

$$w_l=\frac{exp(-{\mathrm{\Delta }}_l/2)}{{\sum }_{i=1}^{m}exp(-{\mathrm{\Delta }}_i/2)}$$ (5)

Do this for all models l = 1, …, m. The resulting Akaike weights are normalized (sum to 1); each is interpretable as the posterior probability that its model is the one that minimizes KL divergence from full reality in the population (again conditional on N and the candidate set of comparable models; Burnham & Anderson, 2002). The implicit prior probability on each model in the set calculated is not equal for all models. Instead, it is a “savvy prior” that takes into consideration the number of free parameters relative to sample size (see Burnham & Anderson, 2004).

Once Akaike weights are computed for all comparable models in the candidate set, a pragmatic way to proceed is to average each parameter’s estimates, and their corresponding sampling variances, across those models in which the parameter is free to be estimated⁶ (Burnham & Anderson, 2002). For purposes of model-averaged estimates, the Akaike weights need to be re-normalized so that they sum to 1 within the subset of models in which the parameter of interest is free. If some parameter θ is a free parameter in some subset of the comparable set of models, then for some model l within that subset, the re-normalized Akaike weight $w_l^{\ast }$ equals

$$w_l^{\ast }=\frac{w_l}{{\sum }_{i\in \mathcal{S}}{w}_i}$$ (6)

Do this for all models l, l ∈ . With the re-normalized weights, the model-averaged point estimate of θ can be calculated:

$$\widehat{\theta }.=\sum _{i\in \mathcal{S}}{w}_i^{\ast }{\widehat{\theta }}_i$$ (7)

where θ̂_i is the maximum-likelihood estimate of θ, conditional on model i. In a sense, when computing θ̂, one is “integrating out” the model-dependence of the point estimates by averaging across models informative about the parameter, each contributing to the average in proportion to its relative weight-of-evidence. The model-averaged point estimate θ̂ has estimated sampling variance equal to (Burnham & Anderson, 2004):

$$\widehat{\mathit{var}}(\widehat{\theta }.)=\sum _{i\in \mathcal{S}}{w}_i^{\ast }\left[{\widehat{\mathit{var}}}_i({\widehat{\theta }}_i)+{({\widehat{\theta }}_i-\widehat{\theta }.)}^2\right]$$ (8)

where ${\widehat{\mathit{var}}}_i({\widehat{\theta }}_i)$ is the estimated sampling variance of the MLE of θ, conditional on model i. Thus, the model-averaged sampling variance represents a weighted average of within-model variance estimates and between-model variance estimates. In the simplest application, one uses the square root of $\widehat{\mathit{var}}(\widehat{\theta }.)$ as the standard error to form confidence intervals and test null hypotheses, assuming asymptotic normality of θ̂., which is what we do herein.

The chief advantage of multimodel inference is that it enables the researcher to base inference about parameters on all models under consideration, allowing each model to contribute in proportion to how well it is supported by the data (Burnham & Anderson, 2002). Even if, say, the best-approximating model has the shared-environmental effect fixed to zero, it does not necessarily follow that the best estimate of the effect is zero, especially if other models under consideration had AICs close to that of the best model. The multimodel approach attempts to avoid the biased estimation and inference that result from conditioning one’s conclusions on a single best model (Lukacs, Burnham, & Anderson, 2009). In applied contexts, information-theoretic model-averaging can also improve predictive accuracy (e.g., Kapetanios, Labhard, & Price, 2008).

We acknowledge, though, that model-averaged estimates are not always easily interpretable, whereas a set of parameter estimates, taken together from the single “best” model, can tell a coherent “story,” and help the investigator form a gestalt whose whole may be greater than the sum of its parts. But, whatever criteria were used to select the “best” model are prone to sampling error. With this in mind, some way of quantifying model-selection uncertainty is desirable. Akaike weights can be applied to form a confidence set for the best-approximating model, expected to contain, with a given probability over repeated sampling, the model in the candidate set that minimizes KL divergence in the population. For this purpose, we adopt a simple but easily understood method: sum Akaike weights from greatest to least until the cumulative sum first equals or exceeds the desired coverage probability; the confidence set is composed of those models whose Akaike weights contributed to the cumulative sum at that stopping point (Burnham & Anderson, 2002).