Quantifying the impact of decay in bed-net efficacy on malaria transmission

Abstract

Insecticide-treated nets (ITNs) are at the forefront of malaria control programs and even though the percentage of households in sub-Saharan Africa that owned nets increased from 3% in 2000 to 53% in 2012, many children continue to die from malaria. The potential impact of ITNs on reducing malaria transmission is limited due to inconsistent or improper use, as well as physical decay in effectiveness. Most mathematical models for malaria transmission have assumed a fixed effectiveness rate for bed-nets, which can overestimate the impact of nets on malaria control. We develop a model for malaria spread that captures the decrease in ITN effectiveness due to physical and chemical decay, as well as human behavior as a function of time. We perform uncertainty and sensitivity analyses to identify and rank parameters that play a critical role in malaria transmission. These analyses show that the basic reproduction number R₀, and the infectious human population are most sensitive to bed-net coverage and the biting rate of mosquitoes. Our results show the existence of a backward bifurcation for the case in which ITN efficacy is constant over time, which occurs for some range of parameters and is characterized by high malaria mortality in humans. This result implies that bringing R₀ to less than one is not enough for malaria elimination but rather additional efforts will be necessary to control the disease. For the case in which ITN efficacy decays over time, we determine coverage levels required to control malaria for different ITN efficacies and demonstrate that ITNs with longer useful lifespans perform better in malaria control. We conclude that malaria control programs should focus on increasing bed-net coverage, which can be achieved by enhancing malaria education and increasing bed-net distribution in malaria endemic regions.

1. Introduction

Malaria is a mosquito-borne disease that currently affects over 100 countries worldwide but the highest incidence and mortality rates are reported in sub-Saharan Africa. The World Health Organization (WHO) estimates that 660,000–971,000 people die every year from malaria and approximately 90% of the deaths occur in children under five years of age World Health Organization (WHO) (2012). During the past decade, several interventions have been used to reduce malaria transmission. These include insecticide-treated nets (ITNs), indoor residual spraying (IRS), intermittent preventive treatment in pregnant women and infants, larval control, and other vector control interventions. ITNs are bed-nets treated with pyrethroid, an insecticide that kills and repels mosquitoes, and thus provide a barrier around people sleeping under them. Since malaria typically affects rural and poor populations, ITNs have proven to be one of the most effective interventions in reducing morbidity and mortality due to their low cost and ease in implementation (Lengeler and et al., 2004). In this paper, ITNs refer to long-lasting insecticidal nets (LLINs) and conventional nets. Due to the logistical challenges of using conventional nets, which required being impregnated with insecticide every six months, LLINs were introduced. LLINs are designed to retain their effectiveness for up to three years even after repeated washing (WHO, 2011; Pulkki-Brännström et al., 2012).

Although the percentage of households in sub-Saharan Africa that owned bed-nets increased from 3% in 2000 to 53% in 2012 World Health Organization (WHO) (2012), many children continue to die from malaria due to inconsistent and improper use; e.g., using bed-nets for fishing or drying fish (Minakawa et al., 2008). Even though 53% of households reported owning at least one bed-net, less than 35% sub-Saharan Africans sleep under bed-nets (World Health Organization (WHO), 2012). Studies have shown that lack of education on malaria transmission and control, limited access to ITNs, and the weather (e.g., people tend to sleep outside when it is hot) play a role in ITN effectiveness (De La Cruz et al., 2006). Additionally, the effectiveness of ITNs wanes due to wear, tear, long exposure to direct sunlight, frequent washing, and human behavior (Kayedi et al., 2008; Atieli et al., 2010; WHO, 2011). Understanding the impact of these limitations can help us assess the effectiveness of ITNs, devise optimal control strategies, and guide public health policy.

Mathematical and computational models for infectious disease transmission have been used to understand infectious disease dynamics and the impact of intervention strategies. Several studies have assessed the impact of ITNs on malaria control (Killeen et al., 2007; Killeen and Smith, 2007; Gu et al., 2009; Govella et al., 2010; Chitnis et al., 2010; Okumu et al., 2013; Okell et al., 2012; Briët et al., 2012; Agusto et al., 2013; Stevens et al., 2013); however, most of these studies have assumed a constant bed-net effectiveness rate for the net’s lifespan and do not account for physical deterioration and behavioral factors. Killeen et al. (2007) used field-parametrized models to demonstrate that protecting about 35–65% of a population through ITNs can lead to an equitable community-wide protection against malaria. Chitnis et al. (2010) used difference equations to assess the impact of ITNs and IRS on malaria control; their results showed that ITNs are more effective than IRS. Assuming a constant rate for net effectiveness, Okumu et al. (2013) investigated the impact of three kinds of LLINs, untreated nets, and indoor residual spraying; they concluded that untreated nets provided similar protection as all three LLINs. Also, assuming a constant rate for net effectiveness, Okell et al. (2012) used the Lives Saved Tool model, a computer-based simulation model, to assess the impact of LLINs among children and household members; they showed that net priority should be given to children to reduce mortality from malaria. Briët et al. (2012) used the OpenMalaria modeling platform–a stochastic simulation, to assess several factors associated with LLIN effectiveness including coverage, net attrition, and both physical and chemical decay. They concluded that LLIN attrition rate and the insecticide decay rate were important factors for determining malaria transmission. Finally, Agusto et al. (2013) used a system of ordinary differential equations and a linearly decreasing function of bed-net usage to model the relationship between bed-net coverage and malaria transmission; they concluded that bed-net usage has a positive impact in reducing malaria transmission. The model in Agusto et al. (2013) omits the fact that ITN efficacy declines over time, as well as immune humans and incubating individuals; these assumptions weaken the biology and predictive power of the model since these aspects are important in designing and implementing interventions.

In the present work, we propose a model that describes malaria transmission dynamics between humans and mosquitoes, as well as accounts for ITN usage to reduce infection. The model uses a non-linear function to describe the decay of ITN efficacy over time, which is consistent with empirical data (Tami et al., 2004). We assume that all bed-nets are distributed or replaced at the same time, which is reasonable as an approximation. To the best of our knowledge, this is the first mathematical model for malaria transmission, which explores the impact of replacing ITNs after their useful life on malaria control. As in Ngwa and Shu (2000); Chitnis et al. (2008) and Ngonghala et al. (2014b), we include a class of asymptomatic immune humans who can transmit malaria, although to a lesser extent compared to infectious humans. Our model allows us to derive analytical results and prove the existence of a backward bifurcation when ITN efficacy is constant. Using constant and variable ITN efficacies, we estimate threshold values of ITN coverage required to reduce malaria transmission. Also, we explore the impact of the length of the useful life of ITNs on malaria control. Finally, we perform uncertainty and sensitivity analyses to identify and rank parameters that play a critical role in malaria transmission and control.

2. Model derivation

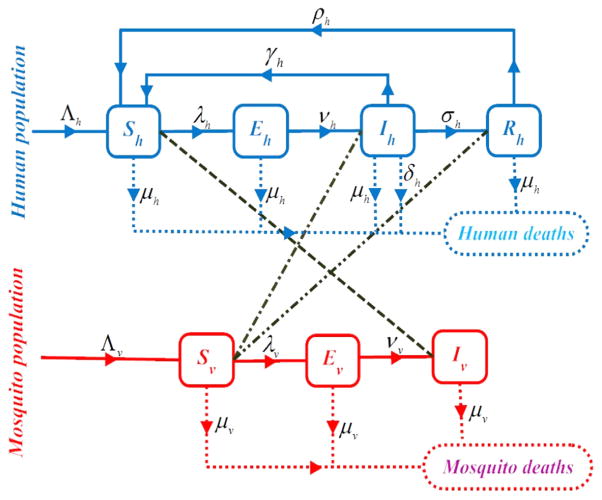
The human population is described by four classes such that at time t ≥0, there are S_h(t) susceptible, E_h(t) exposed, I_h(t) infectious, and R_h(t) immune humans. Malaria does not confer permanent immunity, thus, immunity in this work refers to partial immunity. Note that immunity to malaria is sustained by continuous exposure to infection (Aron, 1983). The mosquito population is divided into three classes such that at time t ≥0, there are S_v(t) susceptible, E_v(t) exposed and I_v(t) infectious mosquitoes. With these divisions, the total human and mosquito populations at time t, are N_h(t) = S_h(t)+E_h(t)+I_h(t)+R_h(t) and N_v(t) = S_v (t)+E_v(t)+I_v(t), respectively. Note that the subscripts h and v refer to humans and mosquitoes, respectively. See Table 1 for brief descriptions, baseline values and ranges of values of the parameters used in the model and Fig. 1 for schematics of the model.

Table 1.

Descriptions, baseline values and ranges of values of parameters for the malaria model (2.4). Human recruitments consist of new human births and immigrants. Using estimated birth rates from Central Intelligence Agency (CIA) (2014a) for the 10 sub-Saharan African countries that accounted for about 87% of residents in hyperendemic or holoendemic malaria regions in 2010 Noor et al. (2014), we obtain a birth rate of approximately 38 births per thousand per year. We assume an approximate human immigration rate of 18 humans per year, which is within the range in Chitnis et al. (2008). Also, we assume that 40% of infectious humans recover without acquiring immunity and that the minimum biting rate is 1/10² bites on humans per mosquito per day. Assuming a non-zero minimum mosquito-biting rate is reasonable, since, due to inefficient usage, decay in ITN-efficacy, possible human activities out of ITNs at night, etc., ITN protection against mosquito-bites might not be 100% efficient.

Parameter	Description and dimension	Baseline value	Range	Reference
Λh	Human recruitment rate (Humans × day−1)	103/(55 × 365)	[103/72, 103/35] × 1/365	Chitnis et al. (2008), Central Intelligence Agency (CIA) (2014a)
Λv	Mosquito recruitment rate (Mosquitoes × day−1)	104/14	[104/21, 104/14]	Teboh-Ewungkem (2009)
μh	Human natural death rate (Day−1)	1/(55 × 365)	[1/72, 1/35] × 1/365	Central Intelligence Agency (CIA) (2014b)
μv0	Mosquito natural death rate (Day−1)	1/14	[1/21, 1/14]	Davidson and Draper (1953), Giles and Warrel (2002)
μ̃v	ITN-induced mosquito death rate(Day−1)	1/14	[1/21, 5/10]	Lines et al. (1987)
δh	Human disease-induced death rate (Day−1)	32.9/(365 × 103)	[0, 41/105]	Chitnis et al. (2008)
νh	Rate at which exposed humans become infectious (Day−1)	1/14	[67/103, 2/10]	Molineaux and Gramiccia (1980), Mehlhorn and Armstrong (2001), Chitnis et al. (2008)
νv	Rate at which exposed mosquitoes become infectious (Day−1)	1/10	[29/103, 33/102]	Macdonald et al. (1957), Chitnis et al. (2008)
σ̃h	Rate at which infectious humans acquire immunity (Day−1)	1/285	[14/104, 17/103]	Molineaux and Gramiccia (1980), Chitnis et al. (2008)
α	Proportion of infectious humans who recover without acquiring immunity (Dimensionless)	4/10	[0, 1]
γ̃h	Rate at which infectious humans recover without acquiring immunity (Day−1)	1/4	[1/180, 1/4]	Filipe et al. (2007)
ρh	Rate at which immune humans lose immunity (Day−1)	1/(5 × 365)	[55/106, 11/103]	Chitnis et al. (2008)
βmin	Minimum mosquito biting rate (Day−1)	1/102	[0, 1/10]
βmax	Maximum mosquito biting rate (Day−1)	5/10, 1	[1/10, 1]	Molineaux et al. (1979), Gupta et al. (1994), Chitnis et al. (2008)
b0	Initial personal protection or ITN coverage (Dimensionless)	53/100	[0, 1]	World Health Organization (WHO) (2012), Malaria Communities Program (2014)
T	Useful life of insecticide-treated nets (ITNs) (Day)	3 × 365	[180, 3 × 365]	WHO (2007), WHO (2011), Pulkki-Brännström et al. (2012)
pvh	Disease transmission probability from infectious mosquitoes to susceptible humans (Dimensionless)	22/103	[1/102, 27/102]	Davidson and Draper (1953), Krafsur and Armstrong (1978), Nedelman (1985)
phv	Disease transmission probability from infectious humans to susceptible mosquitoes (Dimensionless)	48/102	[72/103, 64/102]	Boyd (1949), Smalley and Sinden (1977), Nedelman (1984)
θphv	Disease transmission probability from immune humans to susceptible mosquitoes (Dimensionless)	48/103	[72/104, 64/102]	Boyd (1949), Smalley and Sinden (1977), Nedelman (1984)

Fig. 1.

Schematics depicting transitions of humans and mosquitoes between different compartments (solid lines), transmission of malaria from infectious mosquitoes to susceptible humans (dashed line), and transmission of malaria from infectious and immune humans to susceptible mosquitoes (dash-dotted lines). Mortalities are denoted by dotted lines. The transition and mortality rates are described in Table 1 and the total human and mosquito populations are, respectively, N_h = S_h + E_h + I_h + R_h and N_v = S_v + E_v + I_v.

In our model derivation, it is assumed that malaria cannot be transmitted vertically or horizontally. That is, all new human and mosquito births are susceptible and there is no direct human-to-human or mosquito-to-mosquito transmission. We assume that the average life span of humans in malaria endemic regions is 1/μ_h; i.e., μ_h is the natural mortality rate of humans. Similarly, the average life span of mosquitoes is 1/μ_v0; i.e., μ_v0 is the natural mortality rate of mosquitoes. Additionally, mosquitoes die at rate μ̃_v due to the use of ITN’s. The size of the susceptible human and mosquito populations increase as a result of recruitments that occur at rates Λ_i for i ∈ {h, v} and decline as a result of infection, with forces of infection given by Eq. (2.1), and mortality. Human recruitments consist of new births and immigrations. The susceptible human population also increases due to natural recovery of infectious humans at rate γ̃_h; i.e., 1/γ̃_h is the average duration of infection. Similarly, immune humans move to the susceptible class after they lose their immunity at rate ρ_h; i.e., 1/ρ_h is the average duration of immunity. The exposed populations grow as a result of new human and mosquito infections and decline as a result of mortality and when humans and mosquitoes move to the infectious class at a rate ν_i for i ∈{h, v}, respectively; 1/ν_i is the average incubation period. As in Ngwa and Shu (2000); Chitnis et al. (2006) and Ngonghala et al. (2014b), we assume that new mosquito infections can also arise as a result of contact with immune humans. Although immune humans might not present any clinical symptoms of malaria, some of them (mostly adults in hyper-endemic regions) might harbor gametocytes within their blood stream, which can be picked-up by mosquitoes during blood meals. The infectious classes are populated by individuals moving in from the exposed classes and decrease as a result of death. The infectious human population is further reduced by disease-related mortality at rate δ_h, when humans recover at rate γ̃_h, or acquire immunity at rate σ̃_h. We assume that a proportion α, where 0≤α≤1 of the infectious humans recover from infection without acquiring immunity, while the rest acquires immunity. The immune human class grows when humans acquire immunity and decreases when they die naturally or lose their immunity.

We follow the approach in Ngwa and Shu (2000) and Agusto et al. (2013) to model the forces of infection λ_h and λ_v:

$${\lambda }_h(b_{\beta })=\frac{p_{vh}\beta (b_{\beta }(t))I_v}{N_h},{\lambda }_v(b_{\beta })=\frac{p_{hv}\beta (b_{\beta }(t))(I_h+\theta R_h)}{N_h},$$ (2.1)

where p_vh is the probability that a bite from an infectious mosquito will infect a susceptible human, p_hv is the probability that an infectious human will infect a susceptible mosquito, θp_hv, is the probability that an immune human will infect a susceptible mosquito. The parameter θ, 0 ≤ θ ≤ 1, captures the fact that the immune humans are less infectious. β is the average number of mosquito-bites that a human receives per day, which depends on a number of factors including mosquito-based malaria control measures such as bed-net use. Finally, b_β is a parameter to capture the implementation and efficacy of personal protection through the use of ITNs.

Bed-nets protect humans from mosquito bites and hence reduce the probability of malaria transmission. In addition to protecting humans who sleep under ITNs, they also offer some level of community-wide protection against malaria by killing adult mosquitoes, thereby reducing the available number of mosquitoes, which can bite humans (Killeen and Smith, 2007; Maxwell et al., 2002). Generally, the efficacy of LLINs is high when they are acquired and after being impregnated with insecticides, but decays over time. However, the protection level does not completely diminish since even without insecticide, nets act as physical barriers between mosquitoes and humans. Some studies have shown that untreated bed-nets offer about half the level of protection offered by ITNs against malaria (Clarke et al., 2001; WHO, 2007) and others have shown that they provide similar protection (Okumu et al., 2013). We assume that after ITNs have lost their insecticidal properties, they offer about half the same level of protection as new ITNs and the same level of protection as regular untreated nets. Also, we assume that all bed-nets are distributed and/or replaced at the same time. Although this is a simplifying assumption, it is a reasonable approximation towards quantifying the impact of replacing ITNs on malaria control. An appropriate functional form for the biting or contact rate of mosquitoes β(b_β(t)), must capture these important aspects. Thus, we model β(b_β(t)) through the following functional form:

$$\begin{array}{l}\beta (b_{\beta }(t))={\beta }_{\mathit{max}}-({\beta }_{\mathit{max}}-{\beta }_{\mathit{min}})b_{\beta }(t),\\ b_{\beta }(t)=\frac{2^n+1}{2^{n+1}}\left(\frac{2^n-1}{2^n+1}+\frac{1}{1+{\left(\frac{\mathit{t}modT}{T/2}\right)}^n}\right)b_0,\end{array}$$ (2.2)

where n>1 is a dimensionless shape constant and T >0 is the useful life or duration of ITN efficacy. Observe that T can also represent the replacement or distribution period of ITNs. The parameter b₀, for 0 ≤ b₀ ≤ 1, captures the initial ITN coverage, where b₀ = 0 represents no coverage and b₀ = 1 depicts full coverage. This functional form for β captures the fact that regular untreated nets are half as efficient as ITNs; thus, lim_t→0⁺ b_β(t) = b₀ is the proportion of ITN usage in Agusto et al. (2013) and lim_t→T⁻ b_β(t) = b₀/2. See Fig. 2(a) and (b) for a graphical illustration of the dynamics of the time-dependent functions b_β and β.

Fig. 2.

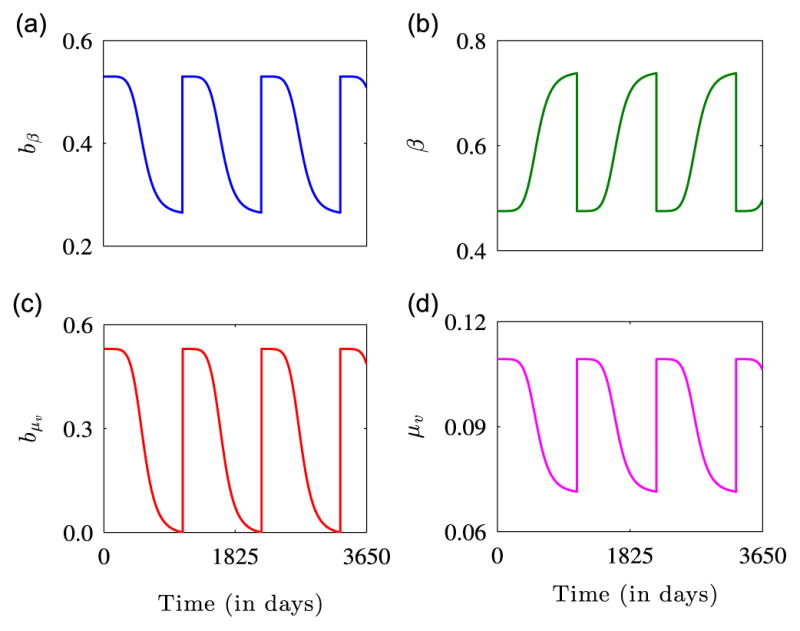
Graphical illustration of the dynamics of (a) bed-net efficacy, (b) mosquito biting rate, (c) bed-net efficacy due to mosquito mortality, and (d) mosquito mortality rate for the parameters: β_min = 0.01, β_max = 1.0, b₀ = 0.53 (World Health Organization (WHO), 2012), T = 3 × 365, n = 6, μ_v0 = 1/14, and μ_v1 = 1/14. Figure (a) shows the protective power of ITNs. The effectiveness of the ITNs is high initially, but declines with time until the net is replaced or retreated. Figure (b) shows how the biting rate of mosquitoes is low soon after adoption of an ITN, but as the insecticide diminishes, the biting rate increases. Figures (c) and (d) show that as the effectiveness of mosquito nets declines with time, mosquito mortality due to ITN use also declines. For each of the figures, it is assumed that the useful life of ITNs is 3 years (WHO, 2011) and the dynamics are presented for 3650 days or 10 years.

As the efficacy of insecticides on ITNs depletes over time, the ITN-induced mortality rate of mosquitoes μ̃_v, also declines. Therefore, we model the mortality rate of mosquitoes μ_v(b_μv (t)) with the functional form:

$$\begin{array}{l}{\mu }_v(b_{{\mu }_v}(t))={\mu }_{v0}+{\stackrel{\sim }{\mu }}_v(t)={\mu }_{v0}+{\mu }_{v1}{b}_{{\mu }_v}(t),\\ b_{{\mu }_v}(t)=\frac{2^n+1}{2^n}\left(-\frac{1}{2^n+1}+\frac{1}{1+{\left(\frac{\mathit{t}modT}{T/2}\right)}^n}\right)b_0,\end{array}$$ (2.3)

where μ_v1 is a positive constant and b_μv measures the efficacy of ITNs in killing mosquitoes that land on them. Observe that lim_t→0⁺ b_μv (t) = b₀ and lim_t→T⁻ b_μv (t) = 0. Thus, the functional form for μ_v captures the fact that the only source of death for mosquitoes, when there is no insecticide on bed-nets, is natural mortality. See Fig. 2(c) and (d) for a graphical illustration of the functions b_μv and μ_v.

We note here that b_β and b_μv can also be modeled through other functional forms. These include slightly modified versions of Hill functions of the form b₀/(1+(t/T)ⁿ), Weibull or general exponential functional forms such as: b₀e^{−(ln 2)(t/T)n}, smooth-compact functions of the form, b₀e^{n −n/(1− (t/T)2)}, if t <T and 0, otherwise, etc., where b₀ represents the initial ITN coverage or efficacy before decline in efficacy kicks in and n is a dimensionless shape constant. Note that the first two functional forms attain half their initial efficacies when t=T and approach zero asymptotically in the long-term limit, while the third functional form attains a value of zero at t=T.

From the above description, the model that governs the transmission of the malaria disease is

$$\begin{array}{l}{\stackrel{.}{S}}_h={\mathit{\Lambda }}_h+\alpha {\stackrel{\sim }{\gamma }}_h{I}_h+{\rho }_h{R}_h-{\lambda }_h(b_{\beta }(t))S_h-{\mu }_h{S}_h,\\ {\stackrel{.}{E}}_h={\lambda }_h(b_{\beta }(t))S_h-({\nu }_h+{\mu }_h)E_h,\\ {\stackrel{.}{I}}_h={\nu }_h{E}_h-({\delta }_h\alpha {\stackrel{\sim }{\gamma }}_h+(1-\alpha ){\stackrel{\sim }{\sigma }}_h+{\mu }_h)I_h,\\ {\stackrel{.}{R}}_h=(1-\alpha ){\stackrel{\sim }{\sigma }}_h{I}_h-({\rho }_h+{\mu }_h)R_h,\\ {\stackrel{.}{S}}_v={\mathit{\Lambda }}_v-{\lambda }_v(b_{\beta }(t))S_v-{\mu }_v(b_{{\mu }_v}(t))S_v,\\ {\stackrel{.}{E}}_v={\lambda }_v(b_{\beta }(t))S_v-({\nu }_v+{\mu }_v(b_{{\mu }_v}(t)))E_v,\\ {\stackrel{.}{I}}_v={\nu }_v{E}_v-{\mu }_v(b_{{\mu }_v}(t))I_v,\end{array}$$ (2.4)

where the respective total human and mosquito populations are governed by the equations

$${\stackrel{.}{N}}_h={\mathit{\Lambda }}_h-{\mu }_h{N}_h-{\delta }_h{I}_h,{\stackrel{.}{N}}_v={\mathit{\Lambda }}_v-{\mu }_v(b_{{\mu }_v})N_v,$$ (2.5)

and α is the proportion of infectious humans who recover without acquiring any immunity. For notational convenience, we set γ_h = αγ̃_h and σ_h = (1−α)σ̃_h.

3. Model analysis and results when b_β = b_μv =b₀ = b, where b is a constant

When the ITN efficacy rates b_β and b_μv are constant and equal, the functional forms of the mosquito biting and mortality rates reduce to those in Agusto et al. (2013). This section explores the dynamics of system (2.4) for b_β = b_μv = b.

3.1. Positivity and boundedness of solutions

All the variables of the malaria model (2.4) are non-negative since they represent different human and mosquito disease statuses. It can be shown that for non-negative initial conditions, model (2.4) has non-negative solutions. It can also be verified that when b_β = b_μv = b = constant, the biologically feasible region $\mathit{\Omega }\subset {ℝ}_{+}^7$ defined by

$$\mathit{\Omega }=\left\{(S_h(t),E_h(t),I_h(t),R_h(t),S_v(t),E_v(t),I_v(t))\in {ℝ}_{+}^7:0\le N_h(t)\le \frac{{\mathit{\Lambda }}_h}{{\mu }_h},0\le N_v(t)\le \frac{{\mathit{\Lambda }}_v}{{\mu }_v(b_{{\mu }_v})}\right\},$$ (3.1)

is positively invariant and attracting for system (2.4). That is, solutions that originate from, or enter Ω remain trapped in Ω. See, for example, Ngonghala et al. (2012) for details of a similar proof. Therefore, the malaria model (2.4) is mathematically well-posed. This basic property of the model system is formalized in the following theorem:

Theorem 3.1

The biologically feasible region $\mathit{\Omega }\subset {ℝ}_{+}^7$ defined by Eq. (3.1) is positively invariant and attracting for system (2.4) with prescribed non-negative initial conditions in ${ℝ}_{+}^7$.

3.2. Basic reproduction number and disease-free equilibrium

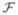
The disease-free equilibrium of system (2.4) is E_df = (Λ_h/μ_h, 0, 0, 0, Λ_v/μ_v(b_μv), 0, 0) and the basic reproduction number R₀, of the model computed using the next generation matrix approach (Van den Driessche and Watmough, 2002; Ngonghala et al., 2012) is the dominant eigenvalue or spectral radius of the next generation matrix , where

$$\begin{array}{l}\mathcal{F}=\left(\begin{array}{ccccc}0& 0& 0& 0& \beta p_{vh}\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& \frac{\beta p_{hv}{\mathit{\Lambda }}_v{\mu }_h}{{\mu }_v{\mathit{\Lambda }}_h}& \frac{\theta \beta p_{hv}{\mathit{\Lambda }}_v{\mu }_h}{{\mu }_v{\mathit{\Lambda }}_h}& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right),\\ \mathcal{V}=\left(\begin{array}{ccccc}{A}_{11}& 0& 0& 0& 0\\ -{\nu }_h& A_{22}& 0& 0& 0\\ 0& -{\sigma }_h& A_{33}& 0& 0\\ 0& 0& 0& A_{44}& 0\\ 0& 0& 0& -{\nu }_v& {\mu }_v\end{array}\right),\end{array}$$ (3.2)

$$A_{11}={\nu }_h+{\mu }_h,A_{22}={\gamma }_h+{\sigma }_h+{\delta }_h+{\mu }_h,A_{33}={\rho }_h+{\mu }_h,A_{44}={\nu }_v+{\mu }_v.$$ (3.3)

That is,

$$R_0=\sqrt{\frac{{\beta }^2{\rho }_{vh}{p}_{hv}{\mathit{\Lambda }}_v{\mu }_h{\nu }_h{\nu }_v({\rho }_h+{\mu }_h+\theta {\sigma }_h)}{{\mathit{\Lambda }}_h{\mu }_v^2({\rho }_h+{\mu }_h)({\nu }_h+{\mu }_h)({\nu }_v+{\mu }_v)({\gamma }_h+{\sigma }_h+{\delta }_h+{\mu }_h)}}.$$ (3.4)

In order to determine the long-term dynamics of the disease-free equilibrium E_df, we compute the following Jacobian matrix of System (2.4) at the disease-free equilibrium E_df:

$$J=\left(\begin{array}{ccccccc}-{\mu }_h& 0& {\gamma }_h& {\rho }_h& 0& 0& -\beta p_{vh}\\ 0& -A_{11}& 0& 0& 0& 0& \beta p_{vh}\\ 0& {\nu }_h& -A_{22}& 0& 0& 0& 0\\ 0& 0& {\sigma }_h& -A_{33}& 0& 0& 0\\ 0& 0& -\frac{\beta p_{hv}{\mathit{\Lambda }}_v{\mu }_h}{{\mu }_v{\mathit{\Lambda }}_h}& -\frac{\theta \beta p_{hv}{\mathit{\Lambda }}_v{\mu }_h}{{\mu }_v{\mathit{\Lambda }}_h}& -{\mu }_v& 0& 0\\ 0& 0& \frac{\beta p_{hv}{\mathit{\Lambda }}_v{\mu }_h}{{\mu }_v{\mathit{\Lambda }}_h}& \frac{\theta \beta p_{hv}{\mathit{\Lambda }}_v{\mu }_h}{{\mu }_v{\mathit{\Lambda }}_h}& 0& -A_{44}& 0\\ 0& 0& 0& 0& 0& {\nu }_v& -{\mu }_v\end{array}\right).$$ (3.5)

Let λ be an eigenvalue of J, then since the first column of J has only one non-zero entry, λ = −μ_h is an eigenvalue of J. By a similar argument, we conclude that λ = −μ_v is also an eigenvalue of J. Observe that each of the first and the fifth columns of J contains only one entry. By deleting these columns and the corresponding rows, we can reduce the Jacobian matrix to a 5 × 5 matrix. The characteristic equation of the reduced 5 × 5 Jacobian matrix is

$${\lambda }^5+B_4{\lambda }^4+B_3{\lambda }^3+B_2{\lambda }^2+B_1\lambda +B_0=0,$$ (3.6)

where

$$\begin{array}{l}{B}_4={\mu }_v+A_{11}+A_{22}+A_{33}+A_{44},\\ B_3={\mu }_v(A_{11}+A_{22}+A_{33}+A_{44})+A_{11}(A_{22}+A_{33}+A_{44})+A_{22}(A_{33}+A_{44})+A_{22}{A}_{33},\\ B_2={\mu }_v(A_{11}(A_{33}+A_{44})+A_{22}(A_{11}+A_{44})+A_{33}(A_{22}+A_{44}))+A_{22}{A}_{44}(A_{11}+A_{33})+A_{11}{A}_{33}(A_{22}+A_{44}),\\ B_1={\mu }_v(A_{22}{A}_{44}(A_{11}+A_{33})+A_{11}{A}_{33}(A_{22}+A_{44}))+A_{11}{A}_{22}{A}_{33}{A}_{44}(1-K),\\ B_0={\mu }_v{A}_{11}{A}_{22}{A}_{33}{A}_{44}(1-R_0^2),\\ K=\frac{{\beta }^2{\nu }_v{p}_{hv}{p}_{vh}{\mathit{\Lambda }}_v{\mu }_h{\nu }_h}{{\mathit{\Lambda }}_h{\mu }_v{A}_{11}{A}_{22}{A}_{33}{A}_{44}}<\frac{{\beta }^2{\mathit{\Lambda }}_v{\mu }_h{\nu }_h{p}_{vh}{p}_{hv}{\nu }_v(({\rho }_h+{\mu }_h)+\theta {\sigma }_h)}{{\mathit{\Lambda }}_h{\mu }_v^2({\rho }_h+{\mu }_h)({\nu }_h+{\mu }_h)({\nu }_v+{\mu }_v)({\gamma }_h+{\sigma }_h+{\delta }_h+{\mu }_h)}=R_0^2.\end{array}$$

Since all coefficients of Eq. (3.6) are positive when R₀ <1, Descartes rule of signs assures us that Eq. (3.6) does not have any positive real solution. It can be verified with the Routh–Hurwitz conditions that all solutions of Eq. (3.6) are negative or have negative real parts. Therefore, E_df is locally and asymptotically stable when R₀ <1. On the other hand, when R₀ >1, B₀ <0, which indicates that Eq. (3.6) has at least one positive real solution and E_df is unstable. This result is summarized in the following theorem:

Theorem 3.2

The disease-free equilibrium E_df, of system (2.4) with β and μ_v given by Eqs. (2.2) and (2.3), where b_β = b_μv = b is constant is locally asymptotically stable when R₀ <1 and unstable when R₀ >1.

3.3. Endemic equilibria and backward bifurcation

In this section, we explore the possibility of endemic equilibria and a backward bifurcation. In simple epidemic models, typically, the bifurcation will be forward or supercritical, which means that there are no endemic states when R₀ <1. However, the phenomenon of backward or subcritical bifurcation occurs when a stable disease-free equilibrium co-exists with two endemic equilibria, one of which is stable in a region where the basic reproduction number is less than one (Ngonghala et al., 2012; Castillo-Chavez and Song, 2004; Dushoff et al., 1998). Backward bifurcations have been found in many epidemiological models for certain ranges of parameter values and several biological mechanisms (Hadeler and VandenDriessche, 1997; Dushoff et al., 1998; Castillo-Chavez and Song, 2004). See Gumel (2012) and the references therein for sources of backward bifurcation and some epidemiological models that have been shown to exhibit the phenomenon of backward bifurcation. From these studies, it appears that the backward bifurcation is connected to complex biological and social interactions of the infectious class. This phenomenon has important disease-control implications as it asserts that reducing the basic reproduction number to less than one is not enough for disease eradication. Furthermore, a backward bifurcation implies that additional control measures will be needed to bring an epidemic under control; i.e., the basic reproduction number will need to fall below another threshold value, $R_0^{bb}$.

The endemic equilibria of system (2.4) are given by $E_e=(S_h^{\ast },E_h^{\ast },I_h^{\ast },R_h^{\ast },S_v^{\ast },E_v^{\ast },I_v^{\ast })$, where

$$\begin{array}{ll}\hfill S_h^{\ast }& =\frac{{\mathit{\Lambda }}_h{A}_{11}{A}_{22}{A}_{33}}{A_{11}{A}_{22}{A}_{33}({\lambda }_h^{\ast }+{\mu }_h)-{\lambda }_h^{\ast }{\nu }_h({\rho }_h{\sigma }_h+{\gamma }_h{A}_{33})},\\ \hfill E_h^{\ast }& =\frac{{\lambda }_h^{\ast }{\mathit{\Lambda }}_h{A}_{22}{A}_{33}}{A_{11}{A}_{22}{A}_{33}({\lambda }_h^{\ast }+{\mu }_h)-{\lambda }_h^{\ast }{\nu }_h({\rho }_h{\sigma }_h+{\gamma }_h{A}_{33})},\\ \hfill I_h^{\ast }& =\frac{{\lambda }_h^{\ast }{\nu }_h{\mathit{\Lambda }}_h{A}_{33}}{A_{11}{A}_{22}{A}_{33}({\lambda }_h^{\ast }+{\mu }_h)-{\lambda }_h^{\ast }{\nu }_h({\rho }_h{\sigma }_h+{\gamma }_h{A}_{33})},\\ \hfill R_h^{\ast }& =\frac{{\lambda }_h^{\ast }{\nu }_h{\sigma }_h{\mathit{\Lambda }}_h}{A_{11}{A}_{22}{A}_{33}({\lambda }_h^{\ast }+{\mu }_h)-{\lambda }_h^{\ast }{\nu }_h({\rho }_h{\sigma }_h+{\gamma }_h{A}_{33})},\\ \hfill S_V^{\ast }& =\frac{{\mathit{\Lambda }}_v}{{\lambda }_v^{\ast }+{\mu }_v},E_v^{\ast }=\frac{{\lambda }_v^{\ast }{\mathit{\Lambda }}_v}{A_{44}({\lambda }_v^{\ast }+{\mu }_v)},I_v^{\ast }=\frac{{\lambda }_v^{\ast }{\nu }_v{\mathit{\Lambda }}_v}{{\mu }_v{A}_{44}({\lambda }_v^{\ast }+{\mu }_v)},\end{array}$$

with

$$\begin{array}{l}{\lambda }_h^{\ast }=\frac{p_{vh}\beta (b_{\beta })I_v^{\ast }}{N_h^{\ast }}\\ =\frac{p_{vh}\beta (b_{\beta }){\nu }_v{\mathit{\Lambda }}_v}{{\mu }_v{A}_{44}}\frac{A_{11}{A}_{22}{A}_{33}({\lambda }_h^{\ast }+{\mu }_h)-{\lambda }_h^{\ast }{\nu }_h({\rho }_h{\sigma }_h+{\gamma }_h{A}_{33})}{{\mathit{\Lambda }}_h(A_{11}{A}_{22}{A}_{33}+{\lambda }_h^{\ast }(A_{33}(A_{22}+{\nu }_h)+{\nu }_h{\sigma }_h))}\frac{{\lambda }_v^{\ast }}{{\lambda }_v^{\ast }+{\mu }_v},\end{array}$$ (3.7)

$${\lambda }_v^{\ast }=\frac{p_{hv}\beta (b_{\beta })(I_h^{\ast }+\theta R_h^{\ast })}{N_h^{\ast }}=\frac{{\lambda }_h^{\ast }{p}_{hv}\beta (b_{\beta }){\nu }_h(A_{33}+\theta {\sigma }_h)}{A_{11}{A}_{22}{A}_{33}+{\lambda }_h^{\ast }(A_{33}(A_{22}+{\nu }_h)+{\nu }_h{\sigma }_h)}.$$ (3.8)

It can be verified that the common denominator of $S_h^{\ast },E_h^{\ast },I_h^{\ast }$ and $R_h^{\ast }$ is positive. That is, $A_{11}{A}_{22}{A}_{33}({\lambda }_h^{\ast }+{\mu }_h)-{\lambda }_h^{\ast }{\nu }_h({\rho }_h{\sigma }_h+{\gamma }_h{A}_{33})={\lambda }_h^{\ast }{\nu }_h({\mu }_h{\sigma }_h+{\delta }_h{A}_{33})+{\mu }_h{A}_{22}{A}_{33}({\lambda }_h^{\ast }+A_{11})>0$. Substituting the value of ${\lambda }_v^{\ast }$ from Eq. (3.8) in Eq. (3.7) and expanding in ${\lambda }_h^{\ast }$ yields the following polynomial equation:

$$A_2{\lambda }_h^{\ast 2}+A_1{\lambda }_h^{\ast }+A_0=0,$$ (3.9)

where

$$\begin{array}{l}{A}_2={\mu }_v{\mathit{\Lambda }}_h{A}_{44}((A_{22}+{\nu }_h)A_{33}+{\nu }_h{\sigma }_h)(\beta p_{hv}{\nu }_h(A_{33}+\theta {\sigma }_h)+{\mu }_v((A_{22}+{\nu }_h)A_{33}+v_h{\sigma }_h)),\\ A_1={\mu }_v{\mathit{\Lambda }}_h{A}_{11}{A}_{22}{A}_{33}{A}_{44}(\beta p_{hv}{\nu }_h(A_{33}+\theta {\sigma }_h)+2{\mu }_v((A_{22}+{\nu }_h)A_{33}+{\nu }_h{\sigma }_h))\\ -{\beta }^2{p}_{vh}{p}_{hv}{\nu }_h{\nu }_v{\mathit{\Lambda }}_v(A_{33}+\theta {\sigma }_h)({\mu }_h(A_{22}{A}_{33}+{\nu }_h{\sigma }_h)+{\nu }_h({\delta }_h+{\mu }_h)A_{33}),\\ A_0={\mathit{\Lambda }}_h{({\mu }_v{A}_{11}{A}_{22}{A}_{33})}^2{A}_{44}(1-R_0^2).\end{array}$$

The solution of Eq. (3.9) is given by ${\lambda }_h^{\ast }=(-A_1\pm \sqrt{A_1^2-4A_0{A}_2})/(2A_2)$. By setting the discriminant $A_1^2=4A_0{A}_2$, to zero and solving the resulting equation in R₀, we obtain the following threshold value of R₀:

$$R_0^{bb}=\sqrt{1-\frac{A_1^2}{4{\mathit{\Lambda }}_h{({\mu }_v{A}_{11}{A}_{22}{A}_{33})}^2{A}_{44}{A}_2}},$$ (3.10)

such that Eq. (3.9) has no real solution when $R_0<R_0^{bb}$ and two real solutions when $R_0^{bb}<R_0<1$. This establishes the possibility of a backward bifurcation and therefore proves the following theorem:

Theorem 3.3

The malaria transmission model (2.4) with β(b_β) = β_max −(β_max − β_min)b_β and μ_v(b_μv) = μ_v0 + μ_v1b_μv, where b_β = b_μv= b is constant has

1. a single endemic equilibrium solution if any of the following three conditions is satisfied:

   1. A₀ <0 or R₀ >1,

   2. A₁ <0 and A₀ = 0, or

   3. A₁ <0 and $A_1^2-4A_0{A}_2=0$,

2. two endemic equilibrium solutions and hence the possibility of a backward bifurcation if A₀ >0, A₁ <0 and $A_1^2=4A_0{A}_2>0$,

3. no endemic equilibrium solution if the conditions in (a) and (b) are not satisfied.

We establish a parameter window within which a backward bifurcation is possible. To this effect, it suffices to demonstrate that there is a positive endemic equilibrium when the basic reproduction number R₀, is unity. Clearly, when R₀ = 1, A₀ = 0 and A₂ >0. Thus, it is enough to show that A₁ <0. When R₀ = 1, A₁ can be re-written as

$$A_1={\mu }_v{\mathit{\Lambda }}_h{A}_{11}{A}_{22}{A}_{33}{A}_{44}\left(\beta p_{hv}{\nu }_h(A_{33}+\theta {\sigma }_h)+{\mu }_v(A_{22}{A}_{33}+{\nu }_h)-\frac{{\mu }_v{\nu }_h{A}_{33}}{{\mu }_h}({\delta }_h-{\mu }_h)\right).$$

Therefore, A₁ <0

$$\begin{array}{l}\iff {\mu }_h(\beta p_{hv}{\nu }_h(A_{33}+\theta {\sigma }_h)+{\mu }_v(A_{22}{A}_{33}+{\nu }_h))<{\mu }_v{\nu }_h{A}_{33}({\delta }_h-{\mu }_h)\\ \iff {\delta }_h>\frac{{\mu }_h(\beta p_{hv}{\nu }_h(A_{33}+\theta {\sigma }_h)+{\mu }_v(({\gamma }_h+{\sigma }_h+{\mu }_h+{\nu }_h)A_{33}+{\nu }_h{\sigma }_h))}{{\mu }_h({\nu }_h-{\mu }_h)A_{33}}\mathit{and}{\nu }_h>{\mu }_h.\end{array}$$

This indicates that a backward bifurcation does not occur at R₀ = 1, if δ_h <μ_h or ν_h <μ_h, and provides a necessary condition for the existence of a backward bifurcation (stated in Theorem 3.4):

Theorem 3.4

The malaria model (2.4) with β and μ_v given by Eqs. (2.2) and (2.3), where b_β = b_μv =b = constant exhibits a backward bifurcation if δ_h >μ_h(β p_hvν_h(A₃₃ +θσ_h)+ μ_v((γ_h + σ_h + μ_h + ν_h) A₃₃ + ν_hσ_h)) /μ_v(ν_h − μ_h)A₃₃ and ν_h >μ_h.

Although, we have established conditions on the human disease-related mortality rate δ_h, and the rate at which exposed humans become infectious ν_h, for which our model can exhibit a backward bifurcation, other parameters such as the recovery rates γ_h and σ_h, can also be used for the investigation. See Section 3.4 for a sensitivity analysis of $R_0^{bb}$ to the individual parameters of system (2.4) and the positive parameter groupings A₁₁, A₂₂, A₃₃,and A₄₄.

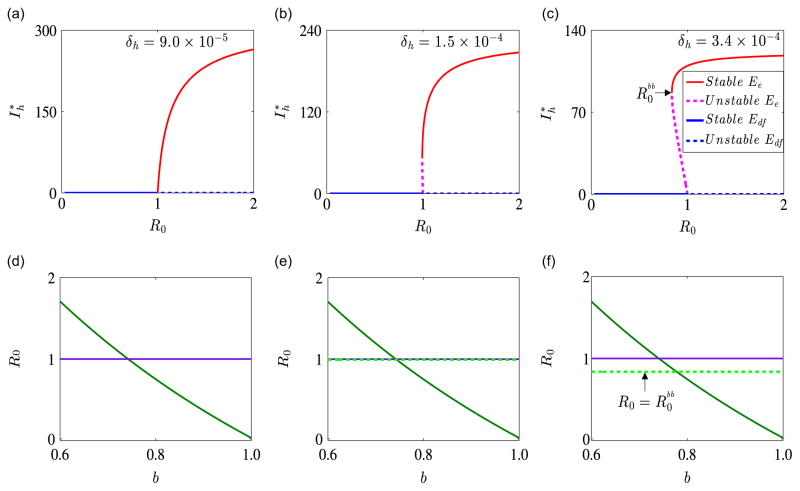
We now illustrate numerically the existence and stability of endemic equilibria and the occurrence of a backward bifurcation for system (2.4). Unless otherwise stated here and in subsequent sections, the parameters used in our simulations are the baseline parameters provided in Table 1. Fig. 3 illustrates the dynamics of system (2.4) for γ̃_h = 1/30, ρ_h = 9 × 10⁻³ and within parameter regimes determined by the human disease-induced mortality rate δ_h, where a forward or a backward bifurcation occurs. Apart from the fact that a higher value of δ_h might be required for a backward bifurcation, the same qualitative results are obtained with the baseline values of γ̃_h and ρ_h. Fig. 3(a) shows a forward bifurcation, wherein a stable disease-free equilibrium solution exists when R₀ <1 and a stable endemic equilibrium solution exists when R₀ >1. Fig. 3(b) shows a barely noticeable backward bifurcation when $R_0^{bb}=0.99<1$. Figure 3(c) indicates that for $R_0<R_0^{bb}=0.84$, there is an asymptotically stable disease-free equilibrium solution E_df and for $R_0^{bb}<R_0<1$, there is a backward bifurcation. This result implies that a locally stable disease-free equilibrium solution coexists with a locally stable endemic equilibrium and an unstable endemic equilibrium. These results confirm Theorems 3.2 and 3.3.

Fig. 3.

Bifurcation diagrams for γ̃_h = 1/30, ρ_h = 9 × 10⁻³ and different values of the human disease-induced death rate δ_h. On the graphs, solid red lines represent stable interior or endemic equilibrium solutions E_e, dashed red lines represent unstable endemic equilibrium solutions, solid blue lines represent stable disease-free equilibrium solutions E_df, and dashed blue lines represent unstable disease-free equilibrium solutions. Graphs (a)–(c) show the infectious human population I_h as a function of the basic reproduction number R₀. Graph (a) shows a forward bifurcation for δ_h = 9.0 × 10⁻⁵, which might represent a mild version of malaria, Graph (b) is the bifurcation diagram for the case δ_h = 1.5 × 10⁻⁴, and Graph (c) shows a backward bifurcation for δ_h = 3.4 × 10⁻⁴, which might represent a severe version of malaria. On the second row, the basic reproduction number R₀ is plotted against ITN coverage, b. The minimum level of ITN coverage required contain the malaria disease is given by the point of intersection of the solid green curve and (i) the dashed green line when there is backward bifurcation (Graphs (e) and (f)) and (ii) the solid purple line when there is no backward bifurcation (Graph (d)). (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this article.)

The existence and stability of an endemic equilibrium solution represent the case in which malaria persists in a community. Our results show that a backward bifurcation is connected to the disease-induced human mortality rate, that is, the backward bifurcation might be characterized by severe and deadly malaria strain since it requires a higher number of human deaths compared to the forward bifurcation. The critical value $R_0^{bb}=0.84$, at which the backward bifurcation in Fig. 3(c) occurs corresponds to an ITN coverage of about b=0.78. Hence, our results indicate that around 78% ITN coverage might be required to control malaria effectively when a backward bifurcation occurs and about 74% coverage when there is no backward bifurcation. This confirms the fact that more control effort is required in a backward bifurcation situation than in a forward bifurcation situation.

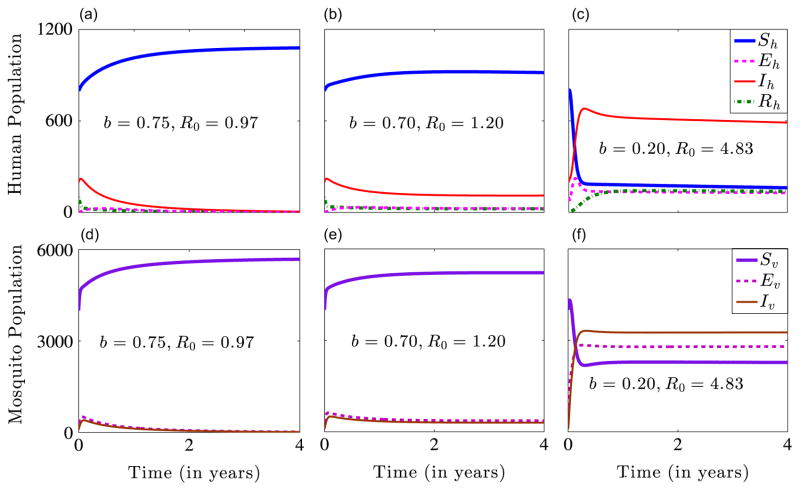
Fig. 4 shows the dynamics of system (2.4) for γ̃_h = 1/30, ρ_h = 9 × 10⁻³, the other parameters in Table 1 and b∈{0.20, 0.70, 0.75}. For b = 0.75, R₀ = 0.97<1, and the system approaches the disease-free equilibrium solution over time (Fig. 4(a) and (d)). This represents the situation in which 75% ITN coverage is successful in containing the malaria disease. For b = 0.70, R₀ = 1.20>1 and the system approaches the endemic equilibrium solution over time (Fig. 4(b) and (e)). This depicts the situation in which 70% ITN coverage is unsuccessful in containing the malaria disease. For b = 0.2, R₀ = 4.83>1 and the system converges to the endemic equilibrium solution (Fig. 4(c) and (f)). In this case, the disease persists due to inadequate ITN coverage. This numerical solution agrees with the analytical result presented in Theorem 3.2.

Fig. 4.

Numerical solutions of system (2.4) for b∈{20, 0.70, 0.75} and the other parameters in Table 1. The initial conditions used are $(S_h^0,E_h^0,I_h^0,R_h^0,S_v^0,E_v^0,I_v^0)=(800,100,200,0,4000,300,100)$. Graphs (a) and (d) show stable disease-free human and mosquito equilibrium solutions. Graphs (b) and (c) show stable endemic human equilibrium solutions, while graphs (e) and (f) show stable endemic mosquito equilibrium solutions.

3.4. The impact of bed-nets and parameters on the basic reproduction number and backward bifurcation

We assess the impact of the parameters of the malaria model (2.4) on the basic reproduction number R₀, and the backward bifurcation threshold parameter $R_0^{bb}$, by computing the elasticity indices of R₀ and $R_0^{bb}$ to the model parameters at the parameter values given in Table 1. According to the approach in Chitnis et al., 2008; Moore et al., 2012 and Ngonghala et al. (2014b), the elasticity index of R₀ (respectively, $R_0^{bb}$) to a parameter x, where x is any of the parameters in Table 1, is given by ${\mathit{\Gamma }}_x^{R_0}=\frac{\partial R_0}{\partial x}\times \frac{x}{R_0}$ (respectively, ${\mathit{\Gamma }}_x^{R_0^{bb}}=\frac{\partial R_0^{bb}}{\partial x}\times \frac{x}{R_0^{bb}}$). Since these indices quantify the ratio of relative changes on R₀ and $R_0^{bb}$ in response to corresponding changes in the parameters, they can identify critical parameters for disease control. This approach states that the basic reproduction number or the backward bifurcation threshold is most sensitive to the parameter with the largest elasticity index value and least sensitive to the parameter with the smallest elasticity index value. Table 2(a) provides the elasticity indices of R₀ to the 18 parameters, arranged in order of decreasing magnitude and hence decreasing sensitivity. As expected, the basic reproduction number is most sensitive to the bed-net coverage parameter b, with an elasticity index of −1.5408. This implies that a 1% increase in the proportion of humans who acquire protection through bed-net use will lead to an approximately 1.54% decrease on the basic reproduction number and vice versa. The basic reproduction number is also highly sensitive to the maximum biting rate of mosquitoes, β_max, and the natural mosquito mortality rate, μ_v0. The public health implication of these results is that increasing ITN coverage and decreasing the mosquito biting rate are important for malaria control. The basic reproduction number is least sensitive to the rate at which exposed humans become infectious, ν_h.

Table 2.

Elasticity indices of (a) the basic reproduction number R₀ and (b) the backward bifurcation threshold value $R_0^{bb}$, computed at the parameter values in Table 1 with γ̃_h = 1/30 and ρ_h = 9 ×10⁻³. These indices quantify relative changes in R₀ and $R_0^{bb}$ in response to corresponding changes in the parameters. The magnitude of an index provides an indication of how sensitive R₀ (respectively, $R_0^{bb}$) is to a parameter, while the sign indicates the direction of change; i.e., whether R₀ or $R_0^{bb}$ increases as the parameter increases (+) or R₀ (respectively, $R_0^{bb}$) decreases as the parameter increases (−). The elasticity indices are presented in order of decreasing magnitude.

Parameter	Elasticity index	Parameter	Elasticity index
(a) Elasticity indices of the basic reproduction number R0.
b	−1.5408	γ̃h	−0.4279
βmax	+0.9888	α	−0.3905
μv0	−0.8242	νv	+0.2611
Λh	−0.5000	σ̃h	−0.0562
Λv	+0.5000	θ	+0.0114
phv	+0.5000	ρh	−0.0113
pvh	+0.5000	βmin	+0.0112
μh	+0.4980	δh	−0.0009
μv1	−0.4368	νh	+0.0003
(b) Elasticity indices of the threshold value of the basic reproduction number, $R_0^{bb}$.
b	+7.6150	phv	−0.8608
βmax	−1.8939	α	+0.8478
μv0	+1.2403	νv	−0.6158
Λh	+1.1002	σ̃h	+0.2471
pvh	−1.1002	μh	−0.1892
Λv	−1.1002	νh	−0.1025
γ̃h	+1.0125	ρh	−0.0867
μv1	+0.9674	βmin	−0.0671
δh	−0.8812	θ	−0.0196

Although the elasticity indices presented in Table 2(a) are computed for the parameter values in Table 1, we can also find analytical expressions for the indices. For example, if we consider the most sensitive parameter b, then differentiating R₀ with respect to b gives $\frac{{dR}_0}{db}=-\left(\frac{{\beta }_{\mathit{max}}-{\beta }_{\mathit{min}}}{\beta }+\frac{{\mu }_{v1}}{{\mu }_v}+\frac{{\mu }_{v1}}{2({\mu }_v+{\mu }_v)}\right)R_0$. Note that dR₀/db <0, which implies that an increase in the number of people who benefit from bed-net protection, will trigger a decrease in the basic reproduction number and vice versa. The closed form analytical expressions of the elasticity indices of the seven parameters to which R₀ is most sensitive are:

$$\begin{array}{l}{\mathit{\Gamma }}_b^{R_0}=-\left(\frac{{\beta }_{\mathit{max}}-{\beta }_{\mathit{min}}}{\beta }+\frac{{\mu }_{v1}}{{\mu }_v}+\frac{{\mu }_{v1}}{2({\mu }_v+{\nu }_v)}\right)b,{\mathit{\Gamma }}_{{\beta }_{\mathit{max}}}^{R_0}=\frac{(1-b){\beta }_{\mathit{max}}}{\beta },\\ {\mathit{\Gamma }}_{{\mu }_{v0}}^{R_0}=-\left(\frac{{\mu }_{\nu 0}}{{\mu }_v}+\frac{{\mu }_{v0}}{2({\mu }_v+{\nu }_v)}\right),\\ {\mathit{\Gamma }}_a^{R_0}=-\frac{1}{2}\left(\frac{\theta {\stackrel{\sim }{\sigma }}_h}{{\rho }_h+{\mu }_h+\theta (1-\alpha ){\stackrel{\sim }{\sigma }}_h}+\frac{{\stackrel{\sim }{\gamma }}_h-{\stackrel{\sim }{\sigma }}_h}{\alpha {\stackrel{\sim }{\gamma }}_h+(1-\alpha ){\stackrel{\sim }{\sigma }}_h+{\delta }_h+{\mu }_h}\right),\\ {\mathit{\Gamma }}_{{\mathit{\Lambda }}_h}^{R_0}=-\frac{1}{2},{\mathit{\Gamma }}_{{\mathit{\Lambda }}_v}^{R_0}={\mathit{\Gamma }}_{p_{hv}}^{R_0}={\mathit{\Gamma }}_{p_{vh}}^{R_0}=\frac{1}{2}.\end{array}$$

In order to better explore the effects of the parameters of system (2.4) on the (backward bifurcation)threshold parameter grouping $R_0^{bb}$, we computed the elasticity indices of $R_0^{bb}$ to both the positive parameter groupings A₁₁, A₂₂, A₃₃ and A₄₄, and the individual model parameters. Our indices reveal that $R_0^{bb}$ is highly sensitive to A₂₂ with an index of + 1.2020, followed by A₁₁ and A₄₄ with the same index (+1.1002) and least sensitive to A₃₃ with an index of −0.0872. Since A₂₂ is the sum of the natural and disease-induced mortality rates, and the recovery rates from infectiousness, increasing any of these parameters, (e.g., increasing recovery from infectiousness by treating more infectious humans) will increase A₂₂ and hence $R_0^{bb}$. Decreasing any of these parameters will decrease A₂₂ and hence $R_0^{bb}$. Table 2(b) provides the elasticity indices of $R_0^{bb}$ to the individual parameters of the model system, (2.4). As was the case with R₀, the threshold $R_0^{bb}$, is most sensitive to the bed-net coverage b, with an elasticity index of about +7.6, indicating that a 1% increase (or decrease) in ITN coverage will generate a 7.6% increase (or decrease) in $R_0^{bb}$. This, again, highlights the importance of ITNs in the fight against malaria. Additionally, $R_0^{bb}$ is highly sensitive to the maximum mosquito-biting rate β_max, the natural mosquito mortality rate μ_v0, the human and mosquito birth rates Λ_h and Λ_v, respectively, and the transmission probability from infectious mosquitoes to susceptible humans. Note that the higher the value of $R_0^{bb}$, the less the extra effort required to eradicate the disease when R₀<1. On the other hand, $R_0^{bb}$ is least sensitive to ρ_h, β_min and θ.

4. Model analysis and results for time-dependent b_β and b_μv

In this section, we explore the dynamics of the non-autonomous malaria model (2.4), with the time-dependent periodic forces of infection, λ_h and λ_v, and the mosquito mortality rate, μ_v, defined by Eqs. (2.1)–(2.3). With this modification, the equation describing the total mosquito population becomes Ṅ_v = Λ_v − (μ_v0+μ̃_v (t))N_v.

4.1. Positivity and boundedness of solutions

We demonstrate that the biologically feasible region $\mathit{\Omega }\subset {ℝ}_{+}^7$, defined by

$$\mathit{\Omega }=\left\{(S_h,E_h,I_h,R_h,S_v,E_v,I_v)\in {ℝ}_{+}^7:S_h+E_h+I_h+R_h=N_h\le \frac{{\mathit{\Lambda }}_h}{{\mu }_h},S_v+E_v+I_v=N_v\le \frac{{\mathit{\Lambda }}_v}{{\mu }_v^m}\right\},$$

where ${\mu }_v^m={inf}_{t\in [0,T]}({\mu }_{v0}+{\stackrel{\sim }{\mu }}_v(t))$, is a positively invariant and compact attracting set with respect to system (2.4).

To this effect, if N_h(0) is the initial condition of the first equation of (2.5), i.e., the equation describing the rate of change of the total human population, then the solution of this equation is $N_h(t)=e^{-{\mu }_{h}t}{N}_h(0)+{\int }_0^t({\mathit{\Lambda }}_h-{\delta }_h{I}_h)e^{{\mu }_h(s-t)}ds\le e^{-{\mu }_{h}t}{N}_h(0)+{\int }_0^t{\mathit{\Lambda }}_h{e}^{{\mu }_h(s-t)}ds$, since I_h(t)≥0. Thus, N_h(t)≤N_h(0)e^−μ_h^t+Λ_h/μ_h (1−e^−μ_ht)≤ Λ_h/μ_h, if N_h(0)≤Λ_h/μ_h. Observe that N_h(t)→Λ_h/μ_h as t→∞. Similarly, if N_v(0) is the initial condition of the equation: ${\stackrel{.}{N}}_v={\mathit{\Lambda }}_v-({\mu }_{v0}+{\stackrel{\sim }{\mu }}_v(t))N_v$, which governs the rate of change of the total mosquito population, then ${\stackrel{.}{N}}_v\le {\mathit{\Lambda }}_v-{\mu }_v^m{N}_v$ and $N_v(t)\le N_v(0)e^{-{\mu }_{v}t}+{\mathit{\Lambda }}_v/{\mu }_v^m(1-e^{-{\mu }_v^{m}t})$. Thus, N_v(t)≤Λ_v/μ_v, if $N_v(0)\le {\mathit{\Lambda }}_v/{\mu }_v^m$. Therefore, Ω is positively invariant. Furthermore, if N_h(0)>Λ_h/μ_h or $N_v(0)>{\mathit{\Lambda }}_v/{\mu }_v^m$, then either the solutions enter Ω in finite time, or N_h(t)→Λ_h/μ_h as t→∞ and $N_v(t)\to {\mathit{\Lambda }}_v/{\mu }_v^m$ as t→∞.

Next, consider the set $\mathit{\Omega }\subseteq {ℝ}_{+}^7$, equipped with the 1-norm (L₁-norm): ||(S_h, E_h, I_h, R_h, S_v, E_v, I_v)||₁ = |S_h|+|E_h|+|I_h|+|R_h|+|S_v|+|E_v|+|I_v|. Then the set $\mathit{\Omega }=[0,{\mathit{\Lambda }}_h/{\mu }_h]\times [0,{\mathit{\Lambda }}_h/{\mu }_h]\times [0,{\mathit{\Lambda }}_h/{\mu }_h]\times [0,{\mathit{\Lambda }}_h/{\mu }_h]\times [0,{\mathit{\Lambda }}_v/{\mu }_v^m]\times [0,{\mathit{\Lambda }}_v/{\mu }_v^m]\times [0,{\mathit{\Lambda }}_v/{\mu }_v^m]$ is clearly a closed and bounded subset of ${ℝ}_{+}^7$. Thus, Ω is a compact subset of ${ℝ}_{+}^7$.

Hence, Ω is positively invariant, compact and attracting with respect to the model (2.4), i.e., all solutions in ${ℝ}_{+}^7$ eventually enter Ω. This result can be formalized into the following theorem:

Theorem 4.1

Let λ_h, λ_v and μ_v be given by Eqs. (2.1) and (2.3). Then the closed set

$$\mathit{\Omega }\left\{(S_h,E_h,I_h,R_h,S_v,E_v,I_v)\in {ℝ}_{+}^7;E_h+I_h+R_h+S_h\le \frac{{\mathit{\Lambda }}_h}{{\mu }_h},E_v+I_v+S_v\le \frac{{\mathit{\Lambda }}_v}{{\mu }_v^m}\right\},$$

where ${\mu }_v^m={inf}_{t\in [0,T)}({\mu }_{v0}+{\stackrel{\sim }{\mu }}_v(t))$ is positively invariant and attracting with respect to the model (2.4).

We now establish the disease-free equilibrium of Eq. (2.4) with time-dependent b_β and b_μv. Since the only dynamic coupling between the human and mosquito populations in our model is through the malaria infection, in the absence of the disease, the full model reduces to a decoupled system that is equivalent to Eq. (2.5) with I_h=0. In this case, S_h=N_h and S_v=N_v, and the equations reduce to:

$${\stackrel{.}{S}}_h={\mathit{\Lambda }}_h-{\mu }_h{S}_h,{\stackrel{.}{S}}_v={\mathit{\Lambda }}_v-({\mu }_{v0}+{\stackrel{\sim }{\mu }}_v(t))S_v,$$ (4.1)

The first equation of (4.1) has a unique positive solution S_h(t) = S_h(0)e^−μ_ht+(Λ_h/μ_h)(1−e^−μ_ht). Since S_h(t)→Λ_h/μ_h as t→∞, the equilibrium solution $S_h^{\ast }={\mathit{\Lambda }}_h/{\mu }_h$, of the first equation of (4.1) is globally and asymptotically stable. The second equation of (4.1) has a unique T-periodic positive solution, $S_v^{\ast }(t)$, Nakata and Kuniya (2010). Let S_v(t) be any other solution of the second equation of (4.1) and suppose $y(t)=S_v^{\ast }(t)-S_v(t)$ for t≥0. Then ẏ(t) = −(μ_v0 + μ̃_v(t))y(t). The solution, y(t), of this equation satisfies $\mid y(t)\mid =\mid y_0\mid e^{-{\int }_0^t({\mu }_{v0}+{\stackrel{\sim }{\mu }}_v(s))ds}\le \mid y_0\mid e^{-{\mu }_{v0}t}$, where $y_0=S_v^{\ast }(0)-S_v(0)\ne 0$. This implies that $\underset{t\to \infty }{lim}\mid y(t)\mid =\underset{t\to \infty }{lim}\mid S_v^{\ast }(t)-S_v(t)\mid =0$. Thus, the unique T-periodic positive solution, $S_v^{\ast }(t)$, of the second equation of (4.1) is globally attractive in ℝ₊, indicating that the disease-free equilibrium of the full system (2.4) is E_df (t) = (Λ_h/μ_h, 0, 0, 0, $S_v^{\ast }(t)$, 0, 0), and we have the following theorem:

Theorem 4.2

The equation describing the susceptible mosquito population, i.e., the second equation of (4.1), with b_μv given by Eq. (2.3) has a unique T-periodic globally attractive positive solution, $S_v^{\ast }(t)$.

4.2. Basic reproduction number and stability of the disease-free periodic solution

Let 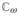be the ordered Banach space of all T-periodic functions from ℝ to ℝ⁷, which is equipped with maximum norm ||.|| and a positive cone ${ℂ}_{\omega }^{+}=\{\varphi \in {ℂ}^{\omega }\mid \varphi (t)\ge 0,\text{for}\text{all}t\in ℝ\}$. Following the approach in Wang and Zhao (2008), the basic reproduction number is defined as the spectral radius of the linear operator L:

$$(L\varphi )(t)={\int }_0^{\infty }Y(t,t-a)\mathcal{F}(t-a)\varphi (t-a)da\text{for}\text{any}t\in ℝ,\varphi \in {ℂ}_{\omega }$$

where Y(t, s) is a 5×5 matrix solution of the system dY(t, s)/dt= 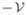(t)Y(t, s) for any t≥s, Y(s, s) = I₅, I₅ is the 5×5 identity matrix, ϕ(s) denotes the initial distribution of infectious individuals, 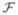(s)ϕ(s) represents the rate at which new infections are produced by infectious individuals who are introduced into the population at time s and Y(t, s)ϕ(s) denotes the distribution of those infected individuals who were newly infected at time s, and who remain infected at time t≥s. The matrix 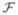(t) is populated by new human and mosquito infections and the matrix and 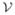(t) is populated by the difference between transition rates that reduce the population of the destination compartments and transitions which increase the population of the destination compartment. Here, the matrices 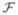and 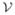have the same form as the corresponding matrices in (3.2), with β replaced by β(b_β(t)), μ_v replaced by μ_v(b_μv (t)) and Λ_v/μ_v replaced by $S_v^{\ast }(t)$, where $S_v^{\ast }(t)$ is the susceptible mosquito component of the disease-free equilibrium solution and β(b_β(t)) and μ_v(b_μv (t)) are given by Eqs. (2.2) and (2.3).

This approach provides the basic reproduction number, as well as proves that the disease-free equilibrium E_df(t), is locally and asymptotically stable when the basic reproduction number is less than unity and unstable when the basic reproduction number is greater than unity (Wang and Zhao, 2008). Since our system is so complex that we cannot obtain a closed-form expression for the basic reproduction number, we use numerical techniques to explore the dynamics of the basic reproduction number. Since system (2.4) satisfies the conditions in Wang and Zhao (2008), we follow the following algorithm outlined in the paper to compute the basic reproduction number:

Let W(t, λ) for t≥0 be the standard fundamental matrix of

$$\frac{dW}{dt}=\left(-\mathcal{V}(t)+\frac{1}{\lambda }\mathcal{F}(t)\right)W,W\in {ℝ}^n,\lambda \in (0,\infty )\text{with}W(0,\lambda )=I.$$

Then by Theorem 2.1 in Wang and Zhao (2008), the basic reproduction number is the unique solution of ρ(W(T, λ)) = 1, where ρ is the spectral radius of W(T, λ). The basic reproduction number is then computed using the following steps:

Step 1: For a given value of λ, the matrix W(T, λ) is computed numerically using the built-in MATLAB ordinary differential equations solver, ode45. Other standard numerical integrators such as forward-Euler, Runge–Kutta methods, or linear multistep methods can also be used.

Step 2: Then the spectral radius ρ(W(T, λ)) is calculated using the built-in MATLAB eigenvalue function, max(abs(eig(W(T, λ)))).

Step 3: Let g(λ) = ρ(W(T, λ))−1. Then a numerical root finding bisection method is used to find the zero of g.

4.3. Investigation of threshold ITN coverage required for malaria containment

We investigate the relationship between the basic reproduction number of the periodic malaria transmission model (2.4) and the initial ITN coverage b₀ for different values of the maximum biting rate, β_max and the lifespan of ITNs, T. We consider the dynamics of three basic reproduction numbers, R₀, $R_0^{[b]}$ and $R_0^T$ corresponding to b_β = b_μv = b₀, a time-averaged b_j, i.e., $b_j=[b_j]=1/T{\int }_0^T{b}_j(t)dt$, and time-dependent periodic b_j, respectively, where j∈{β, μ_v}. R₀ and $R_0^{[b]}$ can be computed using the next generation matrix approach, while $R_0^T$ can be computed using the algorithm outlined in Section 4.2. In order to determine which of these thresholds estimates disease transmission risk better, we plot the dynamics of each of them as a function of the initial ITN coverage b₀ for β_max∈{0.5, 1.0} and n=6, while keeping all the other parameters as presented in Table 1. Fig. 5 illustrates the dynamics of the basic reproduction number of our model as a function of b₀ for the three case-scenarios. Fig. 5(a) shows the dynamics of the three basic reproduction numbers for β_max = 0.5. We can infer from the figure that R₀ and $R_0^{[b]}$ underestimate the disease transmission risk for 0.24≤b₀≤0.6 and 0.5≤b₀≤0.6, respectively. This shows that for b_β = b_μv = b₀, about 24% ITN coverage might be required to contain malaria; for b_j = [b_j], j∈{β, μ_v}, about 50% coverage might be required to bring malaria under control; while for the time-dependent periodic case, about 60% ITN cover-age might be required to contain malaria. The first case might be reasonable in areas of extremely low malaria prevalence, however, it is probably not applicable in malaria endemic regions. The cases for $R_0^{[b]}$ and $R_0^T$ seem to be realistic for malaria endemic areas. Based on the conclusions in Killeen et al. (2007), a 60% personal coverage will result in an equitable community-wide protection. This result confirms the importance of capturing the fact that ITN efficacy declines over time when developing models for malaria transmission. Fig. 5(b) shows that about 51% ITN coverage might be required to control malaria when β_max = 1. In this case, R₀<1 for 0.51≤b₀≤1. However, $R_0^{[b]}$ and $R_0^T$ are always greater than one, illustrating that in areas of hyper-endemic malaria, where mosquitoes can easily bite humans, ITNs alone may not be sufficient to control malaria. In such a situation, ITNs must be combined with other malaria control measures to reduce disease spread.

Fig. 5.

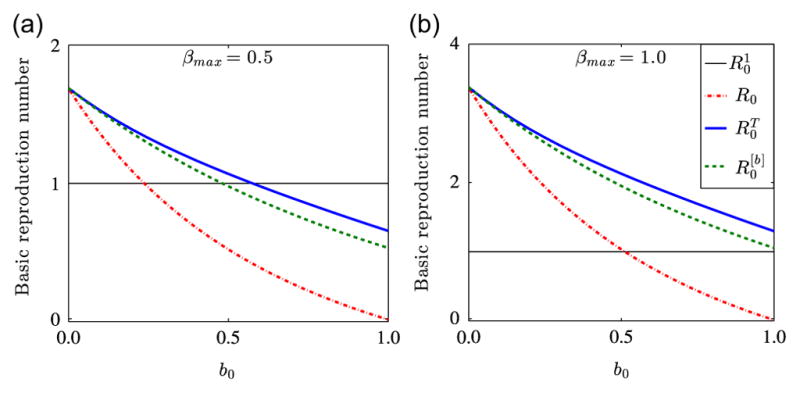
The basic reproduction number of model (2.4) for β_max∈{0.5, 1.0} as a function of ITN coverage, b₀. Solid blue lines show the basic reproduction number ${\mathrm{R}}_0^T$, for time-dependent periodic b_j, dashed green lines denote the basic reproduction number $R_0^{[b]}$, for time-averaged b_j, where j∈{β, μ_v}, and dash-dotted red lines denote the basic reproduction number R₀, for b_β = b_μv = b₀. Figure (a) indicates that ITN alone may be enough to control malaria, while figure (b) indicates that ITN alone might not be enough to control malaria, if ITN efficacy declines over time. The horizontal line denoted by $R_0^1$ represents a basic reproduction number of value unity. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this article.)

The World Health Organization recommends LLINs as a mosquito control measure against malaria because of their 3-year lifespan as opposed to regular nets, which require insecticide treatment every 6–12 months (WHO, 2007; Pulkki-Brännström et al., 2012). We consider two scenarios that explore different levels of LLIN usage and effectiveness on malaria control–the impact of proper use and replacement of LLINs at the end of their lifespan and the impact of human behavior leading to reduced LLIN efficacy. Also, we explore the impact of introducing ITNs with longer lifespans on malaria control.

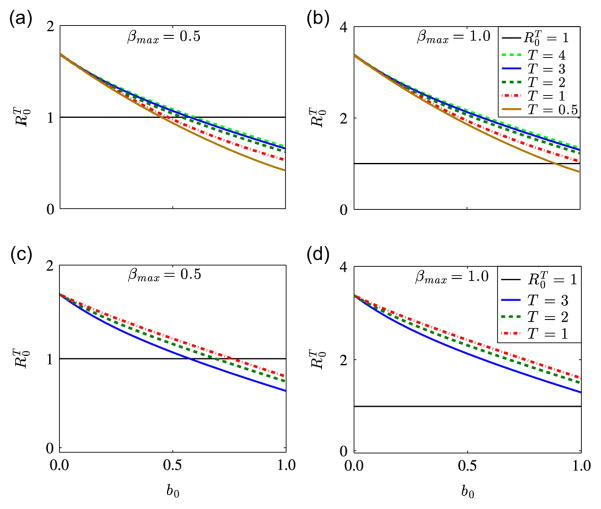
The top panels of Fig. 6 show the basic reproduction number $R_0^T$ for different ITN lifespans. In this case, we assume that the lifespan of the bed-net, T, coincides with the replacement period. Fig. 6(a) shows the results when β_max = 0.5, which represents a low mosquito biting rate. The solid brown line shows that if nets are replaced every six months, approximately 45% ITN coverage is required to control malaria. The dash-dotted red line shows that if nets are replaced on a yearly basis, about 48% coverage will be required. The dashed dark green line shows that if nets are replaced every two years, about 54% coverage will be required. The solid blue line shows that if nets are replaced every three years, 58% ITN coverage will be required. The dashed light green line shows that if nets are replaced every four years, 60% ITN protection may be required to control the disease. The biological implication of these results is that for areas where malaria prevalence is low (or mosquito-biting rates are low), the sooner ITNs are replaced, the lower the coverage that will be required to control malaria. However, there will be a cost associated with the replacement of ITNs. Thus, continuous replacement may not be possible in many malaria endemic areas. Fig. 6(b) shows the results when β_max = 1.0. The results suggest that in areas where malaria prevalence is high (or mosquito-biting rates are high), controlling malaria transmission will require a higher ITN coverage. For example, even if ITNs were replaced every six months, more than 89% coverage will be required to bring malaria under control. In other words, control becomes more difficult when the replacement period is longer.

Fig. 6.

Simulation results for three ITN efficacy levels and two mosquito biting rates. The top panels show the scenario when the ITNs’ lifespan coincides with the replacement period. The bottom panels show the case when the ITNs’ lifespan is shorter than or equal to the replacement period. Figures (a) and (b) suggest that in both, moderately and highly endemic malaria regions, rapid replacement of ITNs can play an important role in malaria control, while graphs (c) and (d) indicate that when the ITNs’ lifespan is shorter than the replacement period, it will be harder to control malaria.

In the bottom panels, it is assumed that the lifespan of ITNs is shorter than or the same as the replacement period. Fig. 6(c) (bottom left panel) shows the results when β_max = 0.5, which represents a low mosquito biting rate. The dash-dotted red line shows that if the useful life of ITNs is one year, about 76% ITN coverage would be required for malaria containment, whereas if the lifespan is 3 years, about 58% ITN coverage would be required. This suggests that ITNs with a longer lifespan will perform better for malaria control than those with shorter lifespans. Fig. 6 (d) shows the results when β_max = 1.0, which represents a high mosquito biting rate. This indicates that in areas with high malaria prevalence, ITNs alone might not be sufficient to control malaria.

4.4. Dynamics of the full non-autonomous model system

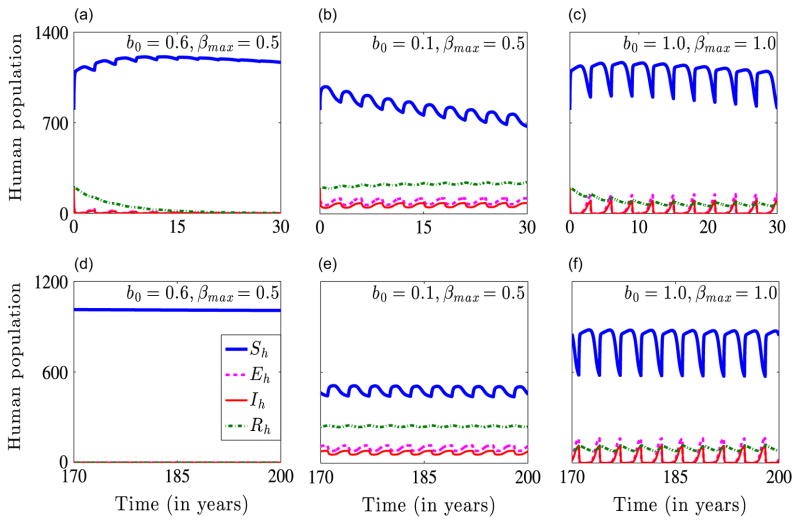
We now illustrate the dynamics of the full non-autonomous model system when R₀<1 and for two cases in which R₀>1. The case in which R₀<1 is attained with an initial ITN coverage of b₀ = 0.6 and a maximum mosquito-biting rate of β_max = 0.5, while the cases for which R₀>1 are obtained by with the respective bed-net coverage and maximum biting rate pairs (b₀ = 0.1, β_max = 0.5) and (b₀ = 1.0, β_max = 1.0). Figs. 7 and 8 show numerical simulations of system (2.4) for the baseline parameters in Table 1, different values of the initial ITN coverage b₀, and the maximum mosquito-biting rate β_max. The top row of Fig. 7, i.e., Fig. 7(a)–(c) show transient dynamics of the human population, while the bottom row of Fig. 7, i.e., Fig. 7(d)–(f) show the long-term asymptotic dynamics of the human population. Fig. 7(a) and (d) indicate that the disease dies out when b₀ = 0.6 and β_max = 0.5, since this parameter regime generates a basic reproduction number that is less than one. Fig. 7(b) and (e) show that the disease establishes itself in the population for a low initial ITN coverage of b₀ = 0.1 and β_max = 0.5, since this parameter set gives a basic reproduction number that is bigger than one. Fig. 7(c) and (f) depict the dynamics when both b₀, and β_max, are high. For example, when b₀ = 1.0 and β_max = 1.0, the disease persists in the population. That is, in areas in which mosquitoes bite humans frequently, the disease persist irrespective of the level of ITN coverage. This implies that in highly endemic areas, ITNs might not be enough to control malaria transmission. Thus, areas with high malaria prevalence might need other interventions such as indoor residual spraying, intermittent preventive treatment, and artemisinin-based combination therapies to control the infection. The corresponding long-term dynamics of the mosquito population are illustrated in Fig. 8. The long-term dynamics illustrated in Figs. 7–8 depict bounded periodic oscillations, which are due to the forcing introduced by the time-periodic parameters b_β and b_μv.

Fig. 7.

Simulation results showing the dynamics of the non-autonomous model (2.4) for 3 values of b₀ and β_max and initial conditions $(S_h^0,E_h^0,I_h^0,R_h^0,S_v^0,E_v^0,I_v^0)=(800,100,200,0,4000,1000,1000)$. Graphs (a) and (d) show a scenario where the disease dies out: b₀ = 0.6 and β_max = 0.5. Graphs (b) and (e) show a scenario where the disease persists: b₀ = 0.1 and β_max = 0.5. Graphs (c) and (f) show that when the biting rate of mosquitoes is very high, the disease persists even when ITN coverage in the community is at its maximum: b₀ =1.0 and β_max = 1.0.

Fig. 8.

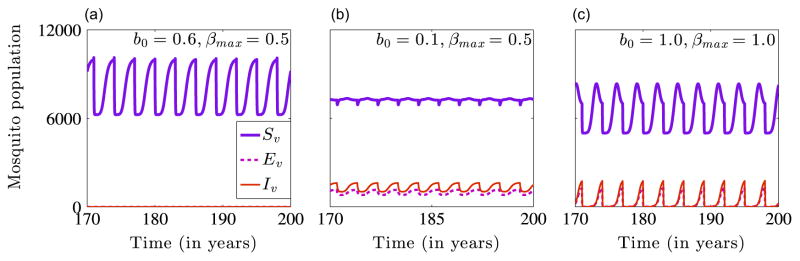
Simulation results showing the long-term dynamics of the mosquito population in the non-autonomous model (2.4) for different values of b₀ and β_max. The initial conditions used are $(S_h^0,E_h^0,I_h^0,R_h^0,S_v^0,E_v^0,I_v^0)=(800,100,200,0,4000,1000,1000)$. The disease dies out for b₀ = 0.6 and β_max = 0.5 (Graph (a)) and persists when b₀ = 0.1 and β_max =0.5 (Graph (b)) and when b₀ = 1.0 and β_max = 1.0 (Graph (c)).

Fig. 9 compares the dynamics of system (2.4) for periodic time-dependent and averaged b_β and b_μv. Fig. 9(a) shows a rapid decline in infection prevalence due to the high effectiveness of ITNs at the beginning of the policy implementation. However, as the effectiveness of the ITNs decreases, damped waves of infection are observed before the system relaxes to the disease-free equilibrium. Fig. 9(b) depicts a monotonic decline in disease prevalence. This implies that a strategy consisting of low ITN coverage and frequent replacement will not be as effective as one that involves high coverage initially and maintaining this level until the ITNs lose their effectiveness.

Fig. 9.

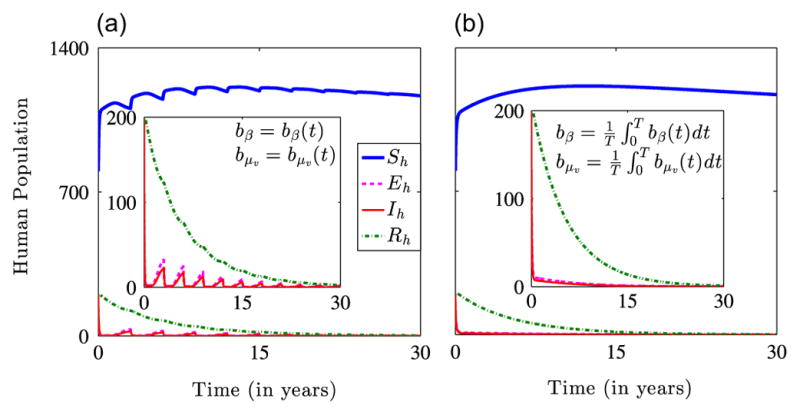
Simulation results illustrating the dynamics of the non-autonomous model (2.4) for the initial conditions $(S_h^0,E_h^0,I_h^0,R_h^0,S_v^0,E_v^0,I_v^0)=(800,100,200,0,4000,1000,1000)$ and the parameters in Table 1 with b₀ = 0.6 and β_max = 0.5. (a) Dynamics for periodic time-dependent b_β and b_μv showing a fast initial decline and damped secondary waves of infection over time. (b) Dynamics of system (2.4) for time-averaged b_β and b_μv. The smaller plots highlight the decline in the exposed, infectious and immune populations.

5. Global uncertainty and sensitivity analyses

Parameter estimation constitutes a critical component of epidemic modeling. Inputs vary considerably due to, among other factors, errors in parameter estimation and uncertainty in parameter values. Hence, it is important to identify parameters that have significant influence on the results. This can be achieved through sensitivity and uncertainty quantification. The infectious human population, I_h, is subject to malaria-related mortality. This population also depends on other malaria-related epidemiological parameters; therefore, it is necessary to investigate the impact of uncertainty and variability in these parameters to accurately predict malaria transmission and control.

We use the Latin Hyper-cube Sampling (LHS) and Partial Rank Correlation Coefficient (PRCC) techniques (Marino et al., 2008) to perform a global uncertainty and sensitivity analyses of our non-autonomous model. Specifically, we sample the twenty parameters of the non-autonomous model system and measure their statistical influence on I_h. As in Moore et al. (2012), we assign the baseline parameters in Table 1 to the mean values of the corresponding parameter ranges and set the respective lower and upper bounds of each parameter range to 67% and 133% of the baseline (or mean) value. We then assume that each parameter follows a uniform distribution and partition each parameter range into 1000 equiprobable subintervals. This gives a 1000×20 matrix whose rows consist of unique collections of parameters randomly drawn from the uniform pdf without replacement and each row of the matrix is used to integrate system (2.4). Fig. 10 shows the PRCCs for all the parameters of system (2.4). Our analyses indicate that variability or uncertainty in bed-net coverage b₀, the maximum mosquito biting rate β_max, and the rate at which exposed humans become infectious ν_h, have the most significant impact on the infectious human population I_h. The public health interpretation of this result is that reducing contacts between humans and mosquitoes is important in controlling the size of the infectious human population. The PRCC for b₀ is the largest and negative, which indicates that shielding humans from mosquito bites, through the use of ITNs, can reduce human infections. The positive and large value of β_max indicates that implementing control measures such as ITNs, which protect mosquitoes from biting humans, will cause a decrease in malaria prevalence. The human recovery rate γ̃_h, the proportion of infectious humans who recover without acquiring immunity α, the infectivity of infectious mosquitoes p_vh, the natural mosquito mortality rate μ_{v 0}, and the infectivity of infectious humans p_hv, also impact I_h significantly.

Fig. 10.

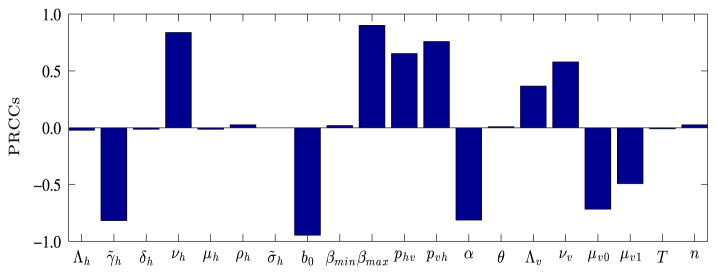
PRCCs depicting how sensitive the infectious human population, I_h is to the parameters of system (2.4) on day 365. The larger the magnitude of the PRCC, the more significant the parameter is in generating uncertainty or variability in I_h. The sign of the PRCC indicates whether an increase in a parameter will lead to more infections (+) or less infections (−). Clearly, uncertainty or variability in b, β_max, ν_h, γ̃_h, α, and p_vh influence the magnitude of the infectious class, I_h the most.

The PRCCs presented in Fig. 10 correspond to day 365; however, the dynamics of the PRCCs may vary over time. Hence, to fully characterize how sensitive the infectious human population is to the parameters of system (2.4), we investigate the evolution of the PRCCs over time. Fig. 11 shows the dynamics of the PRCCs for 0<t≤3000 days. Observe that only the parameters α, γ̃_h, and ν_h have significant influence on the infectious class, I_h, initially. However, as time progresses, there is a clear demarcation between statistically significant PRCCs (shown in Fig. 11) and non-statistically significant PRCCs (not shown in Fig. 11), with non-statistically significant PRCCs clustered around the horizontal axis. Note that in this study, a PRCC is considered to be statistically significant if the p-value is less than 10⁻⁵. The dashed-dotted vertical line in Fig. 11 highlights the PRCCs on day 365, which are illustrated in Fig. 10.

Fig. 11.

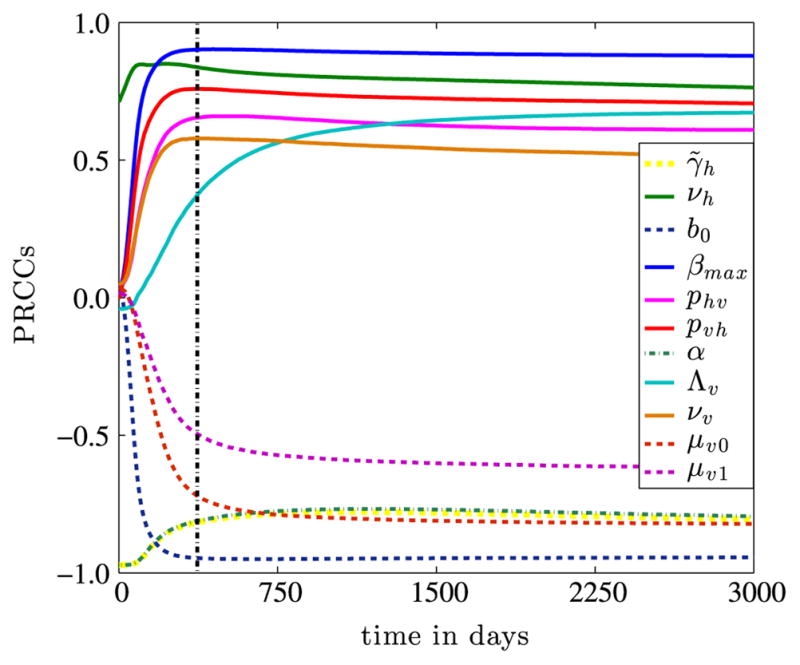
Dynamics of statistically significant PRCCs of parameter values of model (2.4) with respect to I_h for 3000 days. Although non-statistically significant PRCCs are omitted, they are clustered around the horizontal axis within the interval (−0.1, 0.1). The dashed-dotted vertical line denotes day 365.

Finally, we use the LHS/PRCC technique to investigate the effect of uncertainty and variability in the input parameters of the corresponding autonomous system obtained by setting b_β = b_μv = b (where b is a constant), on I_h. Table 3 lists the statistically significant (p-value <10⁻⁵) PRCCs. The results are consistent with those obtained for the non-autonomous system, that is, bed-net coverage b₀ and the maximum mosquito biting rate β_max are the most influential in affecting the magnitude of the infectious human population.

Table 3.

PRCCs of parameters that affect I_h significantly. The level of significance is set at p-value <10⁻⁵

Parameter	PRCC	Parameter	PRCC	Parameter	PRCC	Parameter	PRCC
b	−0.9308	γ̃h	−0.7774	μv0	−0.6569	μv1	−0.3779
βmax	+0.8747	α	−0.7650	phv	+0.6071	Λv	+0.3293
νh	+0.8031	pvh	+0.7155	νv	+0.5150

6. Discussion and conclusion

Malaria continues to spread around the world, therefore, understanding the impact of mitigation strategies such as ITNs can help us inform public health policy. We developed a model that describes malaria dynamics between humans and mosquitoes, and investigated the impact of ITNs on malaria infection and control. The function used to model personal protection through ITN captures the decrease in effectiveness due to physical decay and human behavior, as well as mosquito biting behavior as a function of time.

We computed the basic reproduction number R₀, and showed the existence of a backward bifurcation when R₀<1 and bed-net efficacy is constant over time. We showed that the backward bifurcation occurs for the case of severe malaria. The policy implication of the backward bifurcation is that reducing R₀ to less than one is not enough to eradicate malaria. Therefore, a combination of mitigation strategies may be used to control the spread of malaria. The numerical simulations for the backward bifurcation show that in order to control the epidemic, R₀ must be less than 0.84, which corresponds to a bed-net coverage of 78%. Thus, a 78% coverage will be required to control the epidemic. Based on the algorithm presented in Wang and Zhao (2008), we computed numerically the basic reproduction number for the case in which ITN efficacy is non-constant.

We calculated and used elasticity indices to determine the local sensitivity of R₀ and $R_0^{bb}$ to the parameters. This analysis indicates that bed-net coverage has the most impact on both the reproductive number R₀ and the backward bifurcation threshold $R_0^{bb}$, followed by the biting rate of mosquitoes, and the natural mosquito mortality rate. We infer from the local sensitivity analysis that increasing ITN coverage, reducing the maximum biting rate of mosquitoes, destroying mosquito breeding grounds near human domiciles, and reducing the probability of a mosquito infecting a human or treating more infectious humans will raise $R_0^{bb}$ towards unity, while driving down R₀ at the same time – a favorable step towards disease eradication. Global uncertainty and sensitivity analyses to investigate the impact of parameter variation on the infectious human class were performed using the LHS and PRCC techniques. The analysis reveals that bed-net coverage, the mosquito biting rate, and the rate at which exposed humans become infectious, have the most significant influence on the infectious human population. Overall, our uncertainty and sensitivity analysis results show that bed-net coverage and mosquito biting rate contribute the most to the severity of malaria or are the most important parameters in reducing disease spread, therefore, educational programs must emphasize the importance of using bed-nets consistently to reduce malaria spread.

Our numerical simulations show that for a low mosquito biting rate, if nets are replaced every six, twelve, twenty-four, or thirty-six months, approximately 45%, 48%, 58%, and 60% coverage will be required to control the disease, respectively. This asserts that replacing the nets regularly will require lower coverage levels; however, there will be cost associated with the replacement of bed-nets, which may not be possible in many malaria endemic regions. However, for high mosquito biting rates, even if nets are replaced or re-impregnated with insecticides every six months, approximately 89% coverage will be needed to bring malaria under control. Additionally, for longer replacement periods, ITNs might need to be complemented with other control measures in order to achieve a successful control campaign. For the scenario when the ITNs have a shorter lifespan than the replacement period, a higher coverage rate will be needed. This suggests that ITNs with a longer lifespan will perform better for malaria control than those with a shorter lifespan. Although we fixed the shape constant n, to 6 in our analysis, similar qualitative results are obtained for values of n that are smaller or bigger than 6. This is obvious from our global sensitivity analysis, since n is one of the parameters with the least influence on the infectious human population.

We conclude that understanding the time dependent dynamics of epidemiological parameters for malaria transmission is crucial for developing realistic estimates of their impact and providing decision support. Our model provided a more realistic representation of the complex dynamics involving malaria transmission and ITNs dynamics, which can be used to develop policies for malaria control. Our analysis also suggests that designing nets with a longer useful life will be more effective in the fight against malaria, which aligns well with previous studies. This framework can be extended, with slight modifications, to other vector-borne diseases and to explore the socio-economic impact of malaria (see Ngonghala et al. (2014a) for a sample methodology).

HIGHLIGHTS.

• Insecticide-treated nets (ITNs) with long lifespans perform better in malaria control.

• Malaria dynamics is most sensitive to ITN coverage and the biting rate of mosquitoes.

• When ITN efficacy is constant, 78% net coverage could result in malaria elimination.

• When ITN efficacy decays over time, 45–60% coverage could lead to malaria elimination.

• Some parameter regimes result in periodic oscillations implying disease persistence.