A random forest classifier for the prediction of energy expenditure and type of physical activity from wrist and hip accelerometers

Abstract

Wrist accelerometers are being used in population level surveillance of physical activity (PA) but more research is needed to evaluate their validity for correctly classifying types of PA behavior and predicting energy expenditure (EE). In this study we compare accelerometers worn on the wrist and hip, and the added value of heart rate (HR) data, for predicting PA type and EE using machine learning. Forty adults performed locomotion and household activities in a lab setting while wearing three ActiGraph GT3X+ accelerometers (left hip, right hip, non-dominant wrist) and a HR monitor (Polar RS400). Participants also wore a portable indirect calorimeter (COSMED K4b2), from which EE and metabolic equivalents (METs) were computed for each minute. We developed two predictive models: a random forest classifier to predict activity type and a random forest of regression trees to estimate METs. Predictions were evaluated using leave-one-user-out cross-validation. The hip accelerometer obtained an average accuracy of 92.3% in predicting four activity types (household, stairs, walking, running), while the wrist accelerometer obtained an average accuracy of 87.5%. Across all 8 activities combined (laundry, window washing, dusting, dishes, sweeping, stairs, walking, running), the hip and wrist accelerometers obtained average accuracies of 70.2% and 80.2% respectively. Predicting METs using the hip or wrist devices alone obtained root mean square errors (rMSE) of 1.09 and 1.00 METs per 6-minute bout, respectively. Including HR data improved MET estimation, but did not significantly improve activity type classification. These results demonstrate the validity of random forest classification and regression forests for PA type and MET prediction using accelerometers. The wrist accelerometer proved more useful in predicting activities with significant arm movement, while the hip accelerometer was superior for predicting locomotion and estimating EE.

1. Introduction

Physical activity (PA) is defined as any bodily movement, produced by skeletal muscles, that results in energy expenditure (Caspersen et al 1985). There are a variety of methods to measure PA in a population, ranging from direct observation to self-report. Accelerometers are a popular measurement tool because they are objective and are relatively inexpensive and easy to deploy in large-scale studies (Mathie et al 2004). Accelerometers are most often placed on the hip of the participant to be closer to the center of mass thereby capturing gross muscle movements such as walking or running. They are mostly used in this context to assess PA intensity using laboratory calibrated cut points. Machine learning (ML) methods for measuring PA types from accelerometers have been gaining research attention because they can handle the massive data yield from the newer devices. Compared to more traditional methods of analysis, which utilize a discretized proxy of total hip acceleration (i.e. “counts per minute”) on only one or two axes, ML approaches analyse the raw acceleration signal on all three axes. In conventional methods, levels of PA are grouped into coarse categories of PA intensity based on thresholds (“cut-points”) of accelerometer counts - sedentary, light, moderate, or vigorous intensity (Freedson et al 1998). This provides a general summary of PA intensity but is prone to measurement error. For example, bicycling is often under-represented in intensity due to the relatively small amount of hip movement that occurs, while riding in a vehicle can register high values of acceleration and over-represent the amount of physical activity occurring (Kerr et al 2013). Moreover, the sensitivity and specificity of the cut-points used to classify PA intensity is often poor and no information is available about the underlying behavior. Moving beyond intensity and identifying specific behaviours has value for PA research. For example, determining how a participant accumulated 30 minutes of PA has important implications for PA surveillance and the design of tailored interventions to increase PA. Further, several studies have shown important relations between disease and resistance exercise which is poorly measured by hip worn accelerometers (Braith & Stewart 2006). However, to classify specific behaviours, which not be characterized by simple linear relationships with acceleration, more sophisticated machine learning methods are needed that can model patterns of acceleration specific to certain types of activity .Machine learning algorithms that have been applied to activity recognition include decision trees (Bonomi et al 2009a), random forests (Ellis et al 2014), support vector machines (SVM) (Liu et al 2011) and artificial neural networks (ANN) (Staudenmayer et al 2009),

Metabolic equivalents (METs) are an index of the intensity of physical activity and are often used as a measure of EE that is comparable across people of different weights. A gold standard measure of EE is indirect calorimetry, but this is expensive and requires bulky devices that prohibit measurement in free-living. Due to these restraints, researchers often use accelerometers as a proxy. Researchers have estimated METs from accelerometer counts using a single linear regression equation (Freedson et al 1998) or two-stage linear regression approach (Crouter et al 2010). Some studies have found that first estimating PA type and then learning specific regression equations for each activity type improves MET estimation (Albinali 2010, Bonomi et al 2009b, Ruch et al 2013).

Accelerometer studies of EE prediction have relied almost exclusively on hip devices worn during the waking day. However, wrist placement is now used in population level surveillance of PA (e.g., the National Health and Nutrition Examination Survey [NHANES] because compliance is better and devices can be used to monitor the entire 24 hour period (Troiano & Mc Clain 2012). Wearing a wrist accelerometer overnight also enables an assessment of sleep, which has is now recognized as an independent risk factor for cardiovascular disease and cancer (Cappucio et al 2011). However, wrist-worn devices may over-estimate EE because they capture any arm movement rather than movement of the center of mass. Wrist data may, however, play an important role in distinguishing different behaviours that involve more than central mass movement, e.g. household chores, that may contribute to overall EE. Moreover, measurement error may be magnified when simple algorithms are used that assume a linear relationship between PA intensity and the magnitude of acceleration of the wrist. Wrist-worn accelerometers have been found to be effective for measurement of PA (Esliger et al 2011, Kinnunen et al 2012), but previous studies have found a wrist-worn accelerometer to be less accurate than a hip-worn accelerometer for predicting PA (Atallah et al 2011, Bao & Intille 2004, Mannini et al 2013). However, more sophisticated classification models may overcome the difficulties introduced by a wrist accelerometer. More research is needed to evaluate the validity of a wrist-worn device for measuring PA. In addition, it is unknown the extent to which heart rate (HR) data can be used to improve PA prediction from wrist accelerometers, although it seems to improve predictions from hip-based devices (Brage et al 2004).

In this work we evaluated the use of a random forest algorithm for predicting both PA type and METs from accelerometer and HR data. We compared the random forest to established methods for predicting METs from accelerometer data. We investigated the performance with three accelerometer positions—each hip and the wrist—and combinations of those positions. We also investigated the added value of including HR data in making predictions.

2. Methods

2.1. Data Collection

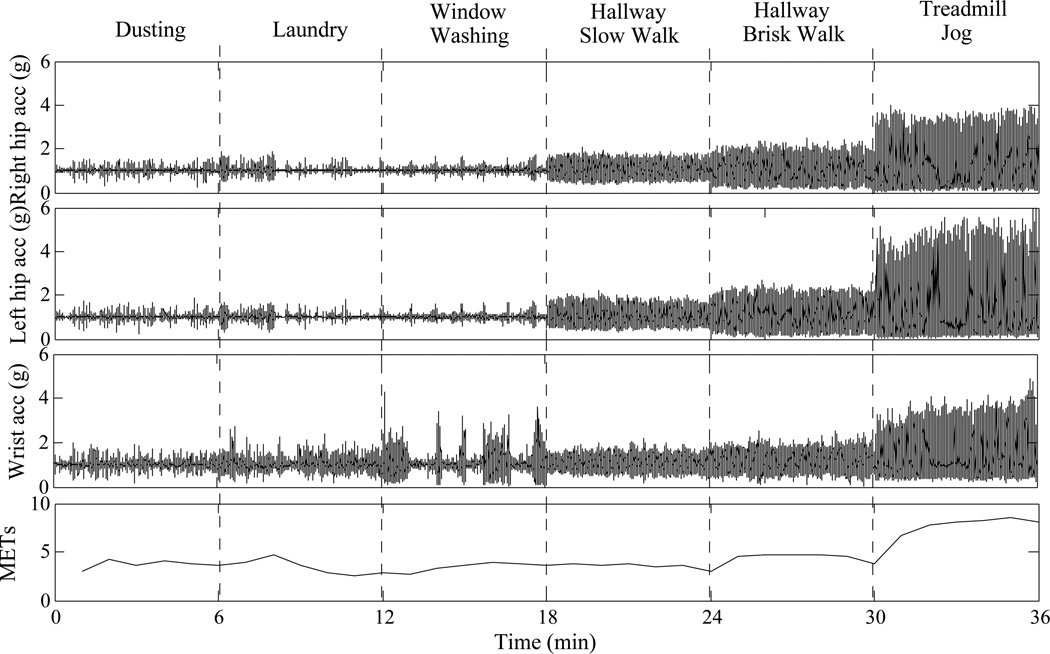
Forty adults (21 women, 19 men; mean age = 35.8 ± 12.1 yrs; BMI = 24.8 ± 2.9) performed a prescribed routine in a lab setting. Activities were selected from a set of eight locomotion and household activities, listed in table 1. Researchers deigned four routines consisting of six minutes each of three household and three locomotion activities. In each routine, locomotion activities included both walking in a hallway and walking or jogging on a treadmill. Walking pace was instructed to be either slow or brisk, at a self-selected pace, and jogging was instructed to be at a self-selected pace. Each participant was randomly assigned to one of these routines. Between each activity in the routine the participants had a few minutes to relax while the researchers prepared the next activity. Participants wore three ActiGraph GT3X+ accelerometers—one on the left hip, one on the right hip and one on the non-dominant wrist. The accelerometers measured raw acceleration along three axes at a sample rate of 30Hz (range ± 6g, g = 9.81m/s). Participants also wore a Polar RS400 HR monitor, from which HR in beats per minute was recorded. Participants also wore a COSMED K4b2 portable indirect calorimeter, which collected breath-by-breath data on ventilatory parameters (i.e., oxygen consumption [VO₂]). A computer clock synchronized devices’ clocks. VO₂ data were used to infer EE and normalized to metabolic equivalents (METs) for each minute. A MET is defined as the ratio of the metabolic rate (O₂·kg⁻¹·min⁻¹) during a specific PA to the metabolic rate at rest. 1 MET represents the energy cost of sitting quietly at rest. Table 1 reports statistics about the measured METs for each activity type, and Figure 1 shows an example trace of accelerometer and MET measurements for an individual.

Table 1.

Physical activity types measured in the study, with corresponding average and standard deviations of measured METs

	Minutes	METs
Household activities
Laundry	90	2.95 (0.81)
Window Washing	90	3.23 (0.87)
Dusting	90	3.52 (0.77)
Dishes	144	2.64 (0.63)
Sweeping	144	4.02 (0.92)
Locomotion activities
Stairs	144	6.38 (1.50)
Slow Walk	228	2.98 (0.67)
Brisk Walk	228	4.35 (1.06)
Jog	198	7.96 (1.89)

Figure 1.

An example of accelerometer and MET measurements for one participant performing an activity routine. Data was not captured between activities. Time (min)

2.2. Data Processing

We chose to analyse data in 1-minute epochs, as this is an appropriate unit for physical activity behaviours that has been used in previous studies (Ellis et al 2014, Staudenmayer et al 2009). The accelerometer data were aggregated into non-overlapping 1-minute windows, and a 45-dimensional feature vector was computed from each window. The feature vector contained a variety of time- and frequency-domain statistics that are commonly used in analysis of raw accelerometer signals (Bao & Intille 2004, Mannini et al 2013, Staudenmayer & Pober 2009, Zhang et al 2012). The majority of features were computed from the vector magnitude of acceleration, ${\mathrm{a}}_{\nu }=\sqrt{{\mathrm{a}}_x^2+{\mathrm{a}}_y^2+{\mathrm{a}}_z^2}$. The vector magnitude captures the magnitude of acceleration independent of the orientation of the device. Features computed from the magnitude include standard time-domain features such as the mean and standard deviation. We also computed angular features that captured information about the orientation of the accelerometer. These included the mean and standard deviations of the roll, pitch and yaw angles, as well as the principal direction of motion computed via eigen-decomposition of the acceleration covariance matrix.

A complete list of features can be found in table 2.

Table 2.

Features computed from each minute of accelerometer data. Single-axis features were computed from each axis of measurement, as well as from the vector magnitude of acceleration. Each resulting feature vector is 148-dimensional.

Vector magnitude features	Multi-axis features
Average	Correlations between axes
Standard deviation	Average roll, pitch and yaw
Coefficient of variation	Standard deviations of roll, pitch and yaw
Minimum and maximum	Principal direction of motion
25th and 75th percentiles
Lag 1-second autocorrelation
Third and fourth moments
Skewness and kurtosis
Dominant frequency and power at dominant frequency
Total energy and entropy
15 FFT coefficients

The features were normalized in order to stabilize the algorithm to differences in scale across features. Features were normalized to have mean zero and standard deviation one with respect to the training set. When including HR data, the feature vector was appended with one additional dimension consisting of the HR as a percentage of the participant’s maximum HR. Maximum HR was estimated for each participant by maxHR = 220 – age.

2.3. Predictive models

We developed two predictive models: a random forest classifier to predict PA type and a random forest of regression trees to estimate EE. Preliminary experiments showed that random forests achieved the highest accuracy compared to several other popular machine learning algorithms (e.g., support vector machines, k nearest neighbour, neural networks) (Ellis et al 2014). Random forests are combinations of classification or regression trees, models that can represent nonlinear and multimodal functions and are relatively efficient to learn. Each random forest model takes as input a feature vector computed from one minute of acceleration (and HR) data. The output of the first model is a predicted PA type for the minute. The output of the second model is a numeric MET value of predicted EE during the minute.

2.3.1. Classification tree

A classification tree is a predictive model that consists of leaves, that represent activity types, and branches that represent conjunctions of signal features. For a test data point, the activity type is predicted by traversing the tree according to the results of the branch conjunctions on the test data point's features. When a leaf node is reached, the plurality activity type contained in that leaf is predicted for the data point. The training phase of the algorithm consists of constructing the decision tree, i.e. learning the branches that lead to a tree that correctly classifies as many examples in the training data set as possible. At the beginning of the learning process, one leaf contains all training examples. In each iteration, the algorithm selects one leaf to split into two by selecting a conjunction over one feature that minimizes the impurity of each of the resulting leaves. Leaf impurity is measured according to Gini's diversity index. The Gini index of a leaf node is 1 − ∑_i p² (i), where the sum is over the activity types i in the leaf, and p(i) is the observed fraction of examples of activity i in the leaf. A pure node (with all examples of the same activity type) has Gini index 0; otherwise the Gini index is positive. The process of splitting leaf nodes continues until a minimum number of examples in each leaf node are reached. Requiring a minimum number of examples in each leaf node greater prevents over-fitting on the training dataset.

2.3.2. Regression tree

A regression tree is the counterpart to a classification tree for continuous outputs. Training and testing of regression trees works in much the same way as classification trees, with the exception that the criterion for choosing a split is the mean squared error in each leaf node. We use regression forests to predict energy expenditure directly from accelerometer features. Another approach that has been successful in previous studies (Albinali 2010) is to use a two-stage prediction process that first detects specific activity types and then applies a type-specific model to estimate EE. We performed preliminary experiments similar to this approach, using our random forest classifier to predict activity types, then learning a type-specific linear regression to estimate EE, but found that the direct regression forest outperformed that method.

2.3.3. Random forest

A random forest is a collection of randomized decision trees (Breiman 2001). Shotton et al. (2011) used random forests to recognize human posture from data collected by the Xbox Kinect. Each decision tree in the forest is learned from a random subset of training examples and a random subset of features. To classify a test example, the outputs from each decision tree are averaged to determine the overall output. Specifically, each tree is traversed until reaching a leaf node. A probability score is assigned according to the ratio of training examples of each activity type that belong to the leaf node. These probability scores are averaged over each tree in the forest to obtain an overall probability score for the example. Finally, the activity type with highest probability is predicted for that example.

2.3.4. Comparison with published methods

We compared our approach against two published methods to estimate METs. Staudenmayer et al computed six features (10^th, 25^th, 50^th, 75^th and 90^th percentiles plus lag one autocorrelation) from the second-level accelerometer counts in each minute, and trained a neural network to predict METs. We compared two variations of the neural network: one we trained on our dataset, by replicating the methodology used by Staudenmayer et al, and one was a pre-trained neural network that was trained on a dataset collected by Staudenmayer et al. Crouter et al (2010) trained a multiple regression model from 10-s accelerometer counts. We used a pre-trained implementation of Crouter et al’s model provided by the ActiLife software.

2.3.5 Prediction settings

In our random forest experiments, we learned random forests consisting of 500 classification or regression trees. To learn each regression tree, 1300 training examples and 30% of features were randomly sampled, and a regression tree was learned with a minimum leaf size of 5. To learn each classification tree, 1300 training examples and 30% of features were randomly sampled, and a regression tree was learned with a minimum leaf size of 1.

Predictions were evaluated on the minute level, using leave-one-subject-out (LOSO) cross validation. In LOSO cross validation, models are trained on data from all subjects except one that is used for the test set. LOSO validation prevents training and testing the model on temporally adjacent data points, which can cause overfitting and artificially high results. LOSO validation is also the closest simulation of how the model might be used in practice, as an “off the shelf” algorithm for processing the data from a previously unseen participant.

The performance of each classifier was evaluated based on overall accuracy, precision, recall, and F-score. Precision measures the proportion of predicted examples of an activity type that are correct. Precision (P) is calculated as P = TP / (TP + FP), where TP is the number of true positives, and FP is the number of false positives. Recall measures the proportion of true examples of an activity type that are correctly identified (also called sensitivity). Recall (R) is calculated as R = TP / (TP + FN), where TP is the number of true positives, and FN is the number of false negatives. F-score is a measure of accuracy, and is computed as the harmonic mean of precision and recall, F-score = 2PR / (P + R). These metrics provide detailed information about how the algorithm performs on each activity type. MET estimation was evaluated using bias, standard error, and root mean squared error.

3. Results

3.1. Estimating physical activity energy expenditure

In order to demonstrate the effectiveness of the random forest classifier, we first compared the performance of our EE estimator from the right hip accelerometer to the two previously published algorithms described in section 2.3.4. Staudenmayer et al (2009) used a neural network to estimate EE from 1-second accelerometer counts. Crouter et al (2010) used a two-regression model to estimate EE from 10-second accelerometer counts. To be comparable with these published methods, we evaluated the performance averaged over an entire six-minute activity bout. For the pre-trained algorithms, we performed a naïve calibration to account for the fact that the algorithms were developed on different datasets, and differing lab environments may affect measurement slightly. This was done by calculating the average bias of the predictions made by the pre-trained algorithm on our training dataset, and subsequently subtracting this bias from each prediction made on the test set. The resulting predictions had no significant bias. Table 3 presents the results of these experiments. Both our random forest EE estimation is comparable to, or outperforms in some instances, the previously published algorithms.

Table 3.

Root mean square error (rMSE) for prediction of EE from an accelerometer on the right hip—a comparison to published methods. Metrics are reported per activity bout, including non steady-state data.

	rMSE
Random forest	1.00
Staudenmayer et al. neural network	1.12
Staudenmayer et al. neural network (pre-trained)	1.47
Crouter at al. two regressions (pre-trained)	1.35

^*Bias is not significantly different from zero (p < 0.05).

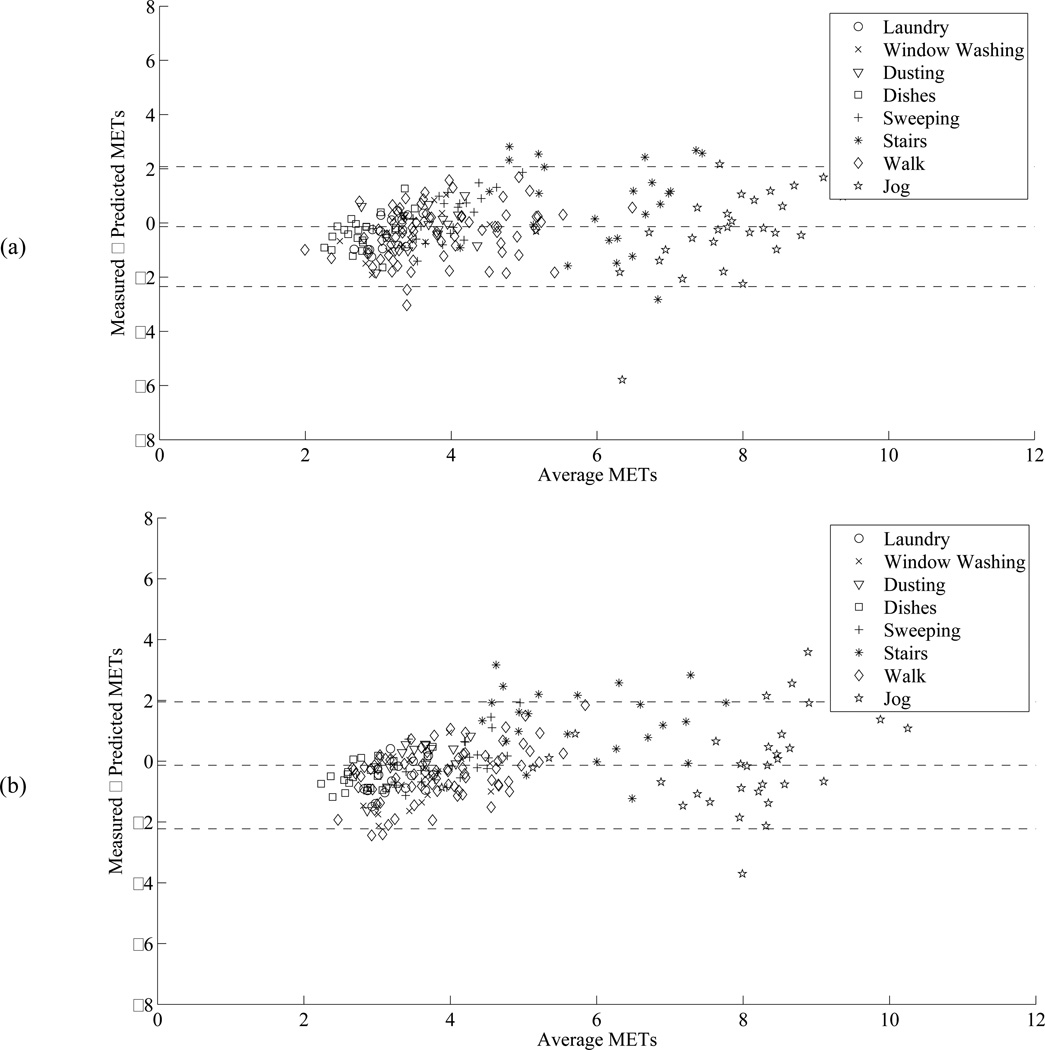
Evaluating the performance over an activity bout averages out some of the over- and underestimations in subsequent minutes, and so tends to produce lower error values than a per-minute evaluation. In table 4 we evaluate predictions by each minute and averaged over an activity bout. For the per-minute predictions, we included only steady-state VO₂ data, i.e., the middle four minutes of the six minutes of performed activity when oxygen uptake was at a plateau, thereby minimizing variability associated the initial metabolic response to an activity. Table 4 also presents results for estimating EE from each accelerometer position. Predicting EE using the right hip and wrist devices alone obtained per-minute rMSEs of 1.09 and 1.00 METs, respectively. The improvement in performance between the wrist and hip accelerometer was significant (paired t-test, t(1319) = −4.47, p < 0.01). Including HR data significantly improved MET prediction (Wrist: t(1319) = 43.01, p < 0.01; Right hip: t(1319 = 44.30, p < 0.01). Using a second accelerometer improved performance significantly (wrist added to right hip: t(1319) = 43.94, p < 0.01), and using HR along with two accelerometers further improved performance (HR added to wrist and right hip: t(1319) = 24.75, p < 0.01). There was no significant bias observed with any device position. Figure 2 shows Bland-Altman plots for bout-level MET prediction from the right hip and wrist accelerometers.

Table 4.

Root mean square error (rMSE) for prediction of energy expenditure for each device position (and combination of devices). Metrics reported by minute are over only steady-state data, metrics reported by bout include non steady-state data. Bias was not significantly different from zero (p < 0.05).

	By minute	By bout
Wrist	1.29	1.09
Right hip	1.18	1.00
Left hip	1.16	1.00
Wrist and right hip	0.30	0.24
Wrist and HR	0.29	0.23
Right hip and HR	0.30	0.25
Wrist, right hip and HR	0.12	0.09

Figure 2.

Bland–Altman plot showing the differences between measured and predicted METs per activity bout for the (a) right hip accelerometer and (b) wrist accelerometer.

3.2. Classifying activity types

We evaluated the performance of a classifier that predicted all eight activities individually. Because the household activities proved difficult to distinguish and have similar relevance for health, we also evaluated a classifier that grouped all five household activities into a single category. Grouping the household activities in this way results in four activity types: household activity, stairs, walking, and jogging. Table 5 presents the overall accuracy for each accelerometer position and various combinations of positions, in predicting the two sets of activities. In predicting all eight activities, the single highest performing accelerometer position was on the wrist, with an overall accuracy of 80.2%. However, when the household activities were combined into a single category, the hip accelerometer achieved a higher average overall accuracy (92.3%) than the wrist accelerometer (87.5%). Combining data from both the hip and wrist accelerometers improved performance for both activity sets. However, including HR data provided no improvement in either prediction setting.

Table 5.

Overall accuracy for prediction of all eight activity types and four combined activity types, for each device position and combination.

	All eight activities	Combined household activities
Wrist	80.2%	87.5%
Right hip	70.2%	92.3%
Left hip	72.5%	92.3%
Wrist and right hip	83.6%	93.1%
Wrist and HR	79.3%	86.8%
Right hip and HR	69.6%	92.3%
Wrist, right hip and HR	82.9%	92.4%

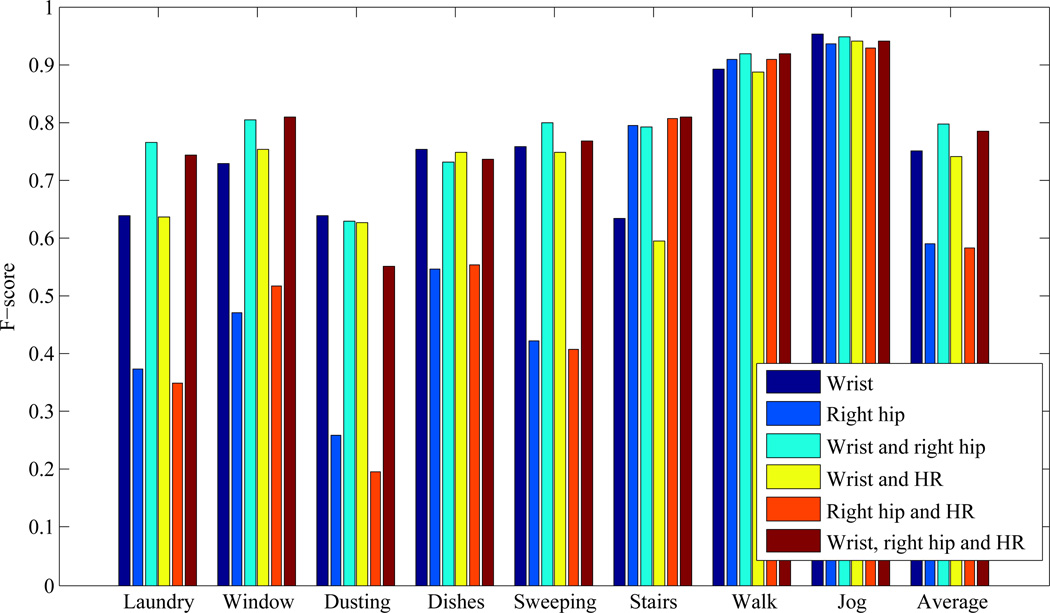
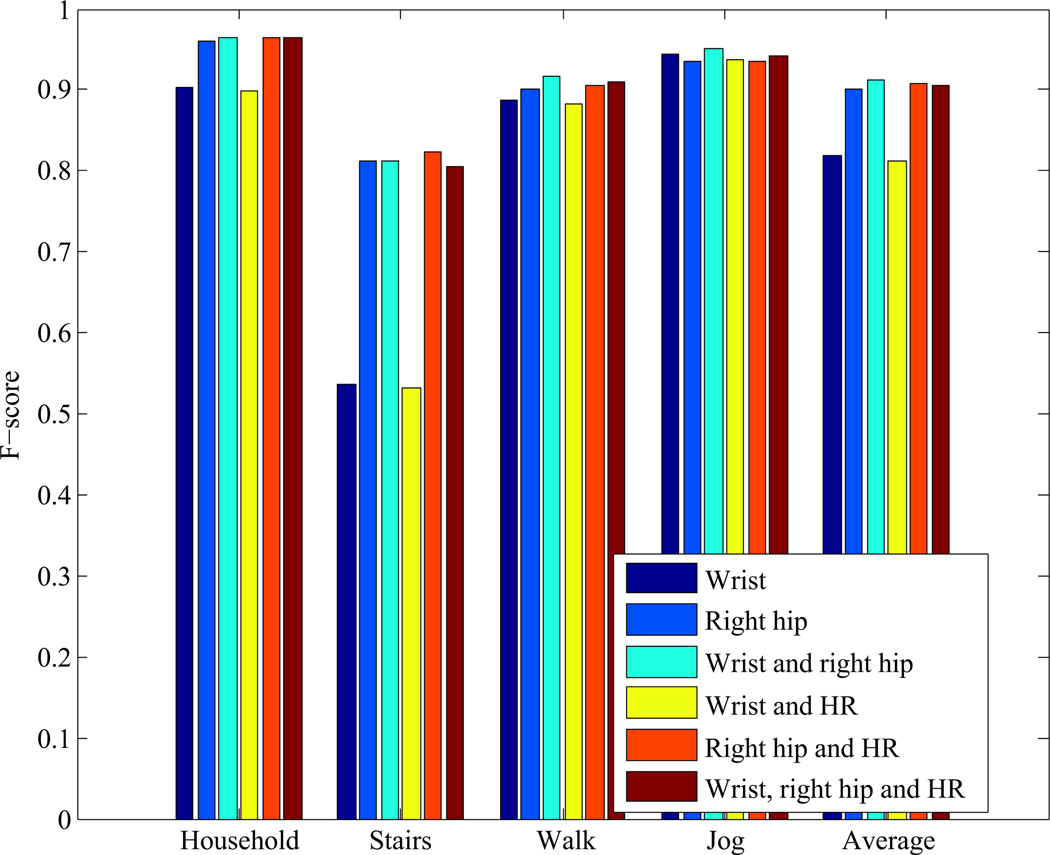
Figures 3 and 4 display the F-score for each activity type, and tables 3 and 4 break down the performance by precision and recall. As expected, the wrist accelerometer outperforms the hip accelerometers on activities with significant arm movement—i.e., the household chores. For the locomotion activities, where the dominant motion is in the torso, the hip accelerometers perform better. The only activity where the wrist accelerometer severely underperforms the hip accelerometer is stairs—in this case we might speculate that the arm movement during climbing stairs is very similar to the arms movements during walking, leading to misclassifications between the two. The confusion matrices in tables 5 and 6 confirm that there are fewer misclassifications between stairs and walking using the hip accelerometer than the wrist. Additionally, the confusion matrix for the hip accelerometer demonstrates that many more misclassifications are made between the household activities than between household and locomotion activities.

Figure 3.

F-scores for prediction of all eight activity types (laundry, window washing, dusting, dishes, sweeping, stairs, walking and jogging) for each device location (and combinations of devices).

Figure 4.

F-scores for prediction of the four grouped activity types (household activity, stairs, walking and jogging) for each device position (and combinations of devices).

Table 6.

Confusion matrix for prediction of all eight activities types from the wrist accelerometer. Rows represent number of examples of true activities; columns represent number of examples of predicted activities. Entries along the diagonal indicate correct predictions.

	Laundry	Window	Dust	Dish	Sweep	Stairs	Walk	Jog
Laundry	58	5	2	11	6	0	8	0
Window	2	55	7	3	4	1	18	0
Dusting	1	4	41	11	8	1	24	0
Dishes	3	1	4	104	14	2	10	0
Sweeping	3	0	4	7	101	10	13	0
Stairs	1	1	0	9	10	46	65	6
Walk	2	1	4	11	5	7	426	0
Jog	0	4	0	4	7	3	18	165

4. Discussion and Conclusions

One goal of this study was to demonstrate the effectiveness of machine learning techniques for predicting PA type and EE using accelerometers. As PA measurement goals become more aggressive (i.e., measuring specific behaviours rather than intensity levels, or using devices on the wrist that may capture extraneous movement) the techniques we use to process and analyse data will need to become more sophisticated as well. Our random forest algorithm outperformed published methods for EE estimation, and achieved relatively high accuracy predicting activity types. Although some studies present classification results with higher accuracy (e.g., Zhang et al 2012), every dataset is different and comparisons are only equivalent on the same dataset with identical evaluation methods (i.e., LOSO).

The second goal was to compare the performance of wrist and hip positions for accelerometers, in light of the recent trend toward wrist devices. We found that the wrist accelerometer was more successful in predicting activities with significant arm movement (e.g., household activities), while the hip accelerometer was superior for predicting locomotion. In estimating EE, both device positions produced comparable results. This is a novel result with respect to previous studies that found the wrist position sub-optimal for EE estimation (e.g., Mannini et al 2013), and we believe is due to the random forest’s ability to model highly nonlinear patterns in the data. More research is needed to validate these results on a larger sample size with a more diverse set of activities.

Limitations of this study include the small sample size of only 40 participants and the restriction of PA routines to a laboratory setting. Physical activity in free-living is more variable than when measured in the lab and hence more difficult to predict, as Gyllensten & Bonomi demonstrated (2011). Collecting minute-level energy expenditure data in free-living scenarios is prohibitively difficult, but future studies can collect free-living data for activity prediction by using devices such as wearable cameras to capture ground truth (Ellis et al 2013). Additionally, one activity that researchers found to be very difficult to predict, particularly from a wrist accelerometer, was stationary cycling (Rosenberger et al 2013, Mannini et al 2013). This activity was not included in our dataset, although the random forest classifier has shown to be successful predicting outdoor cycling in another study (Ellis et al 2013). This study also did not attempt complex modelling of HR data or individual calibration of heart rate beyond a simple calculation from the participant’s age. A more sophisticated approach to including HR in prediction models might have increased its predictive power, as other studies have leveraged HR to improve prediction performance (Brage et al 2004, Strath et al 2001). However, these methods also require individual calibration, which is an added burden for study participants and researchers.

Table 7.

Confusion matrix for prediction of all eight activities types from the right hip accelerometer. Rows represent number of examples of true activities; columns represent number of examples of predicted activities. Entries along the diagonal indicate correct predictions.

	Laundry	Window	Dust	Dish	Sweep	Stairs	Walk	Jog
Laundry	29	8	4	45	7	0	3	0
Window	4	43	9	24	15	0	1	0
Dusting	4	11	23	12	45	0	1	0
Dishes	14	7	7	99	17	0	0	0
Sweeping	5	15	38	21	61	1	3	0
Stairs	0	2	0	4	0	110	22	6
Walk	3	1	1	12	0	21	435	7
Jog	0	0	0	1	0	1	12	196