Fast inference in generalized linear models via expected log-likelihoods

Abstract

Generalized linear models play an essential role in a wide variety of statistical applications. This paper discusses an approximation of the likelihood in these models that can greatly facilitate computation. The basic idea is to replace a sum that appears in the exact log-likelihood by an expectation over the model covariates; the resulting “expected log-likelihood” can in many cases be computed significantly faster than the exact log-likelihood. In many neuroscience experiments the distribution over model covariates is controlled by the experimenter and the expected log-likelihood approximation becomes particularly useful; for example, estimators based on maximizing this expected log-likelihood (or a penalized version thereof) can often be obtained with orders of magnitude computational savings compared to the exact maximum likelihood estimators. A risk analysis establishes that these maximum EL estimators often come with little cost in accuracy (and in some cases even improved accuracy) compared to standard maximum likelihood estimates. Finally, we find that these methods can significantly decrease the computation time of marginal likelihood calculations for model selection and of Markov chain Monte Carlo methods for sampling from the posterior parameter distribution. We illustrate our results by applying these methods to a computationally-challenging dataset of neural spike trains obtained via large-scale multi-electrode recordings in the primate retina.

1 Introduction

Systems neuroscience has experienced impressive technological development over the last decade. For example, ongoing improvements in multi-electrode recording (Brown et al. 2004; Field et al. 2010; Stevenson and Kording 2011) and imaging techniques (Cossart et al. 2003; Ohki et al. 2005; Lütcke et al. 2010) have made it possible to observe the activity of hundreds or even thousands of neurons simultaneously. To fully realize the potential of these new high-throughput recording techniques, it will be necessary to develop analytical methods that scale well to large neural population sizes. The need for efficient computational methods is especially pressing in the context of on-line, closed-loop experiments (Donoghue 2002; Santhanam et al. 2006; Lewi et al. 2009).

Our goal in this paper is to develop scalable methods for neural spike train analysis based on a generalized linear model (GLM) framework (McCullagh and Nelder 1989). This model class has proven useful for quantifying the relationship between neural responses and external stimuli or behavior (Brillinger 1988; Paninski 2004; Truccolo et al. 2005; Pillow et al. 2008; Truccolo et al. 2010), and has been applied successfully in a wide variety of brain areas; see, e.g., (Vidne et al. 2012) for a recent review (Of course, GLMs are well-established as a fundamental tool in applied statistics more generally). GLMs offer a convenient likelihood-based approach for predicting responses to novel stimuli and for neuronal decoding (Paninski et al. 2007), but computations involving the likelihood can become challenging if the stimulus is very high-dimensional or if many neurons are observed.

The key idea presented here is that the GLM log-likelihood can be approximated cheaply in many cases by exploiting the law of large numbers: we replace an expensive sum that appears in the exact log-likelihood (involving functions of the parameters and observed covariates) by its expectation to obtain an approximate “expected log-likelihood” (EL) (a phrase coined by Park and Pillow in (2011). Computing this expectation requires knowledge, or at least an approximation, of the covariate distribution. In many neuroscience experiments the covariates correspond to stimuli which are under the control of the experimenter, and therefore the stimulus distribution (or least some moments of this distribution) may be considered known a priori, making the required expectations analytically or numerically tractable. The resulting EL approximation can often be computed significantly more quickly than the exact log-likelihood. This approximation has been exploited previously in some special cases (e.g., Gaussian process regression (Sollich and Williams 2005; Rasmussen and Williams 2005) and maximum likelihood estimation of a Poisson regression model (Paninski 2004; Field et al. 2010; Park and Pillow 2011; Sadeghi et al. 2013)). We generalize the basic idea behind the EL from the specific models where it has been applied previously to all GLMs in canonical form and discuss the associated computational savings. We then examine a number of novel applications of the EL towards parameter estimation, marginal likelihood calculations, and Monte Carlo sampling from the posterior parameter distribution.

2 Results

2.1 Generalized linear models

Consider a vector of observed responses, r = (r₁, ..., r_N), resulting from N presentations of a p dimensional stimulus vector, x_i (for i = 1, ..., N). Under a GLM, with model parameters θ, the likelihood for r is chosen from an exponential family of distributions (Lehmann and Casella 1998). If we model the observations as conditionally independent given x (an assumption we will later relax), we can write the log-likelihood for r as

$$L\left(\theta \right)\equiv \log \rho (r\mid \theta ,\left\{x_i\right\})=\sum _{n=1}^N\frac{1}{c\left(\varphi \right)}\left(a\left(x_n^T\theta )\right)r_n-G\left(x_n^T\theta \right)\right)+\mathrm{const}\left(\theta \right),$$ (1)

for some functions a(), G(), and c(), with φ an auxiliary parameter (McCullagh and Nelder 1989), and where we have written terms that are constant with respect to θ as const(θ). For the rest of the paper we will consider the scale factor c(φ) to be known and for convenience we will set it to one. In addition, we will specialize to the “canonical” case that $a\left(x_n^T\theta \right)=x_n^T\theta$ is the identity function. With these choices, we see that the GLM log-likelihood is the sum of a linear and non-linear function of θ,

$$L\left(\theta \right)=\sum _{n=1}^N\left(x_n^T\theta \right)r_n-G\left(x_n^T\theta \right)+\mathrm{const}\left(\theta \right).$$ (2)

This expression will be the jumping-off point for the EL approximation. However, first it is useful to review a few familiar examples of this GLM form.

First consider the standard linear regression model, in which the observations r are normally distributed with mean given by the inner product of the parameter vector θ and stimulus vector x. The log-likelihood for r is then

$$L\left(\theta \right)=\sum _{n=1}^N-\frac{{\left(r_n-x_n^T\theta \right)}^2}{2{\sigma }^2}+\mathrm{const}\left(\theta \right)$$ (3)

$$\propto \sum _{n=1}^N\left(x_n^T\theta \right)r_n-\frac{1}{2}{\left(x_n^T\theta \right)}^2+\mathrm{const}\left(\theta \right),$$ (4)

where for clarity in the second line we have suppressed the scale factor set by the noise variance σ². The non-linear function G(.) in this case is seen to be proportional to $\frac{1}{2}{\left(x_n^T\theta \right)}^2$.

As another example, in the standard Poisson regression model, responses are distributed by an inhomogeneous Poisson process whose rate is given by the exponential of the inner product of θ and x. (In the neuroscience literature this model is often referred to as a linear-nonlinear-Poisson (LNP) model (Simoncelli et al. 2004)). If we discretize time so that r_n denotes the number of events (e.g., in the neuro-science setting the number of emitted spikes) in time bin n, the log-likelihood is

$$L\left(\theta \right)=\sum _{n=1}^N\log \left(\exp \left(-\exp \left(x_n^T\theta \right)\right)\frac{{\left(\exp \left(x_n^T\theta \right)\right)}^{r_n}}{r_n!}\right)$$ (5)

$$=\sum _{n=1}^N\left(x_n^T\theta \right)r_n-\exp \left(x_n^T\theta \right)+\mathrm{const}\left(\theta \right).$$ (6)

In this case we see that G(.) = exp(.).

As a final example, consider the case where responses are distributed according to a binary logistic regression model, so that r_n only takes two values, say 0 or 1, with $p_n\equiv p(r_n=1\mid x_n^T,\theta )$ defined according to the canonical “logit” link function

$$\log \left(\frac{p_n}{1-p_n}\right)=x_n^T\theta .$$ (7)

Here the log-likelihood is

$$L\left(\theta \right)=\sum _{n=1}^N\log \left(p_n^{r_n}{(1-p_n)}^{1-r_n}\right)$$ (8)

$$=\sum _{n=1}^N\left(x_n^T\theta \right)r_n-\log (1-p_n)$$ (9)

$$=\sum _{n=1}^N\left(x_n^T\theta \right)r_n-\log \left(1+\exp \left(x_n^T\theta \right)\right),$$ (10)

so G(.) = log (1 + exp(.)).

2.2 The computational advantage of using expected log-likelihoods over log-likelihoods in a GLM

Now let's examine Eq. (2) more closely. For large values of N and p there is a significant difference in the computational cost between the linear and non-linear terms in this expression. Because we can trivially rearrange the linear term as ${\sum }_{n=1}^N{\left(x_n^T\theta \right)}^2{r}_n=\left({\sum }_{n=1}^N{x}_n^T{r}_n\right)\theta$, its computa a single evaluation of the weighted sum over vectors $x{\sum }_{n=1}^N\left(x_n^T{r}_n\right)$, no matter how many times the log-likelihood is evaluated. (Remember that the simple linear structure of the first term is a special feature of the canonical link function; our results below depend on this canonical assumption.) More precisely, if we evaluate the log-likelihood K times, the number of operations to compute the linear term is O(Np + Kp); computing the non-linear sum, in contrast, requires O(KNp) operations in general. Therefore, the main burden in evaluating the log-likelihood is in the computation of the non-linear term. The EL, denoted by $\tilde{L}\left(\theta \right)$, is an approximation to the log-likelihood that can alleviate the computational cost of the non-linear term. We invoke the law of large numbers to approximate the sum over the non-linearity in Eq. (2) by its expectation (Paninski 2004; Field et al. 2010; Park and Pillow 2011; Sadeghi et al. 2013):

$$L\left(\theta \right)=\sum _{n=1}^N\left(\left(x_n^T\theta \right)r_n-G\left(x_n^T\theta \right)\right)+\mathrm{const}\left(\theta \right)$$ (11)

$$\approx \left(\sum _{n=1}^N{x}_n^T{r}_n\right)\theta -N\mathbf{E}\left[G\left(x^T\theta \right)\right]\equiv \tilde{L}\left(\theta \right),$$ (12)

where the expectation is with respect to the distribution of x. The EL trades in the O(KNp) cost of computing the nonlinear sum for the cost of computing E [G(x^T θ)] at K different values of θ, resulting in order O(Kz) cost, where z denotes the cost of computing the expectation E [G(x^T θ)]. Thus the nonlinear term of the EL can be be computed about $\frac{Np}{z}$ times faster than the dominant term in the exact GLM log-likelihood. Similar gains are available in computing the gradient and Hessian of these terms with respect to θ.

How hard is the integral E [G(x^T θ)] in practice? I.e., how large is z? First, note that because G only depends on the projection of x onto θ, calculating this expectation only requires the computation of a one-dimensional integral:

$$\mathbf{E}\left[G\left(x^T\theta \right)\right]=\int G\left(x^T\theta \right)p\left(x\right)dx=\int G\left(q\right){\zeta }_{\theta }\left(q\right)dq,$$ (13)

where ζ_θ is the (θ-dependent) distribution of the one-dimensional variable q = x^T θ. If ζ_θ is available analytically, then we can simply apply standard unidimensional numerical integration methods to evaluate the expectation.

In certain cases this integral can be performed analytically. Assume (wlog) that E [x] = 0, for simplicity. Consider the standard regression case: recall that in this example

$$G\left(x^T\theta \right)\propto \frac{{\theta }^{T}x{x}^T\theta }{2},$$ (14)

implying that

$$\mathbf{E}\left[G\left(x^T\theta \right)\right]=\frac{{\theta }^{T}C\theta }{2},$$ (15)

where we have abbreviated E [xx^T] = C. It should be noted that for this Gaussian example one only needs to compute the non-linear sum in the exact likelihood once, since ${\sum }_{n}G\left(x_n^T\theta \right)={\theta }^T\left({\sum }_n{x}_n{x}_n^T\right)\theta$ and ${\sum }_n{x}_n{x}_n^T$ can be precomputed. However, as discussed in Section 2.3, if C is chosen to have some special structure, e.g., banded, circulant, Toeplitz, etc., estimates of θ can still be computed orders of magnitude faster using the EL instead of the exact likelihood.

The LNP model provides another example. If p(x) is Gaussian with mean zero and covariance C, then

$$\mathbf{E}\left[G\left(x^T\theta \right)\right]=\int \exp \left(x^T\theta \right)\frac{1}{{\left(2\pi \right)}^{\frac{p}{2}}{\mid C\mid }^{\frac{1}{2}}}\exp \left(-x^T{C}^{-1}x∕2\right)dx$$ (16)

$$=\exp \left(\frac{{\theta }^{T}C\theta }{2}\right),$$ (17)

where we have recognized the moment-generating function of the multivariate Gaussian distribution.

Note that in each of the above cases, E [G(x^T θ)] depends only on θ^T Cθ. This will always be the case (for any nonlinearity G(.)) if p(x) is elliptically symmetric, i.e.,

$$p\left(x\right)=h\left(x^T{C}^{-1}x\right),$$ (18)

for some nonnegative function h(.)¹. In this case we have

$$\mathbf{E}\left[G\left(x^T\theta \right)\right]=\int G\left(x^T\theta \right)h\left(x^T{C}^{-1}x\right)dx$$ (19)

$$=\int G\left(y^T{\theta }^{\prime }\right)h\left({\Vert y\Vert }_2^2\right){\mid C\mid }^{1∕2}dy,$$ (20)

= where we have made the change of variables y = C^−1/2x, α’ = C^1/2α. Note that the last integral depends on θ’ only through its norm; the integral is invariant with respect to transformations of the form θ’ → Oθ’, for any orthogonal matrix O (as can be seen by the change of variables z = O^T y). Thus we only need to compute this integral once for all values of ${\Vert {\theta }^{\prime }\Vert }_2^2={\theta }^{T}C\theta$, up to some desired accuracy. This can be precomputed off-line and stored in a one-d lookup table before any EL computations are required, making the amortized cost z very small.

What if p(x) is non-elliptical and we cannot compute ζ_θ easily? We can still compute E [_G(xT θ)] approximately in most cases with an appeal to the central limit theorem (Sadeghi et al. 2013): we approximate q= x^Tθ in Eq. (13) as Gaussian, with mean E [θ^T x] = θ^T[x] = 0 and variance var(θ^T x) θ^T Cθ. This approximation can be justified by the classic results of Diaconis and Freedman (1984), which imply that under certain conditions, if d is sufficiently large, then ζ_θ is approximately Gaussian for most projections θ. (Of course in practice this approximation is most accurate when the vector x consists of many weakly-dependent, light-tailed random variables and θ has large support, so that q is a weighted sum of many weakly-dependent, light-tailed random variables). Thus, again, we can precompute a lookup function for E [G(x^T θ)], this time over the two-d table of all desired values of the mean and variance of q. Numerically, we find that this approximation often works quite well; Fig. 1 illustrates the approximation for simulated stimuli drawn from two non-elliptic distributions (binary white noise stimuli in A and Weibull-distributed stimuli in B).

Fig. 1.

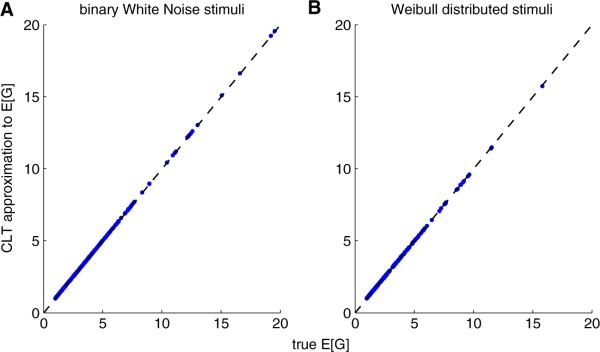
The normal approximation for ζ_θ is often quite accurate for the computation of E [G] (Eq. (13) in the text). Vertical axis corresponds to central limit theorem approximation of E [G], and horizontal axis corresponds to the true E [G], computed numerically via brute-force Monte Carlo. We used a standard Poisson regression model here, corresponding to an exponential G function. The stimulus vector x is composed of 600 i.i.d. binary (a) or Weibull (b) variables; x has mean 0.36 in panel A, and the Weibull distribution in panel B has scale and shape parameters 0.15 and 0.5, respectively. Each dot corresponds to a different value of the stimulus filter θ. These were zero-mean, Gaussian functions with randomly-chosen norm (uniformly distributed on the interval 0 to 0.5) and scale (found by taking the absolute value of a normally distributed variable with variance equal to 2)

2.3 Computational efficiency of maximum expected log-likelihood estimation for the LNP and Gaussian model

As a first application of the EL approximation, let us examine estimators that maximize the likelihood or penalized likelihood. We begin with the standard maximum likelihood estimator,

$${\widehat{\theta }}_{MLE}=\arg \underset{\theta }{\max }L\left(\theta \right).$$ (21)

Given the discussion above, it is natural to maximize the expected likelihood instead:

$${\widehat{\theta }}_{MELE}=\arg \underset{\theta }{\max }\tilde{L}\left(\theta \right),$$ (22)

where “MELE” abbreviates “maximum EL estimator.” We expect that the MELE should be computationally cheaper than the MLE by a factor of approximately Np/z, since computing the EL is approximately a factor of Np/z faster than computing the exact likelihood. In fact, in many cases the MELE can be computed analytically while the MLE requires a numerical optimization, making the MELE even faster.

Let's start by looking at the standard regression (Gaussian noise) case. The EL here is proportional to

$$\tilde{L}\left(\theta \right)\propto {\theta }^T{X}^{T}r-N\frac{{\theta }^{T}C\theta }{2},$$ (23)

where we have used Eq. (15) and defined X = (x₁, ..., x_N)^T . This is a quadratic function of θ; optimizing directly, we find that the MELE is given by

$${\widehat{\theta }}_{\mathrm{MELE}}={\left(NC\right)}^{-1}{X}^{T}r.$$ (24)

Meanwhile, the MLE here is of the standard least-squares form

$${\widehat{\theta }}_{MLE}={\left(X^{T}X\right)}^{-1}{X}^{T}r,$$ (25)

assuming X^T X is invertible (the solution is non-unique otherwise).

The computational cost of determining both estimators is determined by the cost of solving a p-dimensional linear system of equations; in general, this requires O(p³) time. However, if C has some special structure, e.g., banded, circulant, Toeplitz, etc. (as is often the case in real neuroscience experiments), this cost can be reduced to O(p) (in the banded case) or O(p log(p)) (in the circulant case) (Golub and van Van Loan 1996). The MLE will typically not enjoy this decrease in computational cost, since in general X^T X will be unstructured even when C is highly structured. (Though counterexamples do exist; for example, if X is highly sparse, then X^T X may be sparse even if C is not, for sufficiently small N).

As another example, consider the LNP model. Somewhat surprisingly, the MELE can be computed analytically for this model (Park and Pillow 2011) if p(x) is Gaussian and we modify the model slightly to include an offset term so that the Poisson rate in the n-th time bin is given by

$${\lambda }_n=\exp ({\theta }_0+x_n^T\theta ),$$ (26)

with the likelihood and EL modified appropriately. The details are provided in Park and Pillow (2011) and also, for completeness, the methods section of this paper; the key result is that if one first optimizes the EL Eq. (12) with respect to the offset θ₀ and then substitutes the optimal θ₀ back into the EL, the resulting “profile” expected log-likelihood max_θ0 $\tilde{L}(\theta ,{\theta }_0)$, is a quadratic function of θ, which can be optimized easily to obtain the MELE:

$${\widehat{\theta }}_{\mathrm{MELE}}=\arg \underset{\theta }{\max }\underset{{\theta }_0}{\max }\tilde{L}(\theta ,{\theta }_0)$$ (27)

$$=\arg \underset{\theta }{\max }{\theta }^T{X}^{T}r-\sum _{n=1}^N{r}_n\frac{{\theta }^{T}C\theta }{2}$$ (28)

$$={\left(\left(\sum _n{r}_n\right)C\right)}^{-1}{X}^{T}r.$$ (29)

Note that this is essentially the same quadratic problem as in the Gaussian case Eq. (23) with the total number of spikes ${\sum }_n{r}_n$ replacing the number of samples N in Eq. (23). In the neuroscience literature, the function $\frac{X^{T}r}{{\sum }_n{r}_n}$ is referred to as the spike-triggered average, since if time is discretized finely enough so that the entries of r are either 0 or 1, the product $X^T\frac{r}{{\sum }_n{r}_n}$ is simply an average of the stimulus conditioned on the occurrence of a ‘spike’ (r = 1). The computational cost for computing ${\widehat{\theta }}_{\mathrm{MELE}}$ here is clearly identical to that in the Gaussian model (only a simple linear equation solve is required), while to compute the MLE we need to resort to numerical optimization methods, costing O(KNp), with K typically depending superlinearly on p. The MELE can therefore be orders of magnitude faster than the MLE here if Np is large, particularly if C has some structure that can be exploited. See Park and Pillow (2011), Sadeghi et al. (2013) for further discussion.

What about estimators that maximize a penalized likelihood? Define the maximum penalized expected log-likelihood estimator (MPELE)

$${\widehat{\theta }}_{\mathrm{MPELE}}=\arg \underset{\theta }{\max }\tilde{L}\left(\theta \right)+\log \left(f\left(\theta \right)\right),$$ (30)

where log(f (θ)) represents a penalty on θ; in many cases f (θ) has a natural interpretation as the prior distribution of θ. We can exploit special structure in C when solving for the MPELE as well. For example, if we use a mean-zero (potentially improper) Gaussian prior, so that $\log \left(f\left(\theta \right)\right)=-\frac{1}{2}{\theta }^{T}R\theta$ for some positive semidefinite matrix R, the MPELE for the LNP model is again a regularized spike-triggered average (see Park and Pillow (2011) and methods)

$${\widehat{\theta }}_{\mathrm{MPELE}}={\left(C+\frac{R}{{\sum }_n{r}_n}\right)}^{-1}\frac{X^{T}r}{{\sum }_n{r}_n}.$$ (31)

For general matrices R and C, the dominant cost of computing ${\widehat{\theta }}_{\mathrm{MPELE}}$ will be O(Np + p³). (The exact maximum a posteriori (MAP) estimator has cost comparable to the MLE here, O(KNp)). Again, when C and R share some special structure, e.g. C and R are both circulant or banded, the cost of ${\widehat{\theta }}_{\mathrm{MPELE}}$ drops further.

If we use a sparsening L₁ penalty instead (David et al. 2007; Calabrese et al. 2011), i.e., log(f (α)) = −λ||θ||₁, with λ a scalar, ${\widehat{\theta }}_{\mathrm{MPELE}}$ under a Gaussian model is defined as

$${\widehat{\theta }}_{\mathrm{MPELE}}=\arg \underset{\theta }{\max }{\theta }^T{X}^{T}r-N\frac{{\theta }^{T}C\theta }{2}-\lambda {\Vert \theta \Vert }_1;$$ (32)

the MPELE under an LNP model is of nearly identical form. If C is a diagonal matrix, classic results from subdifferential calculus (Nesterov 2004) show that ${\widehat{\theta }}_{\mathrm{MPELE}}$ is a solution to Eq. (32) if and only if ${\widehat{\theta }}_{\mathrm{MPELE}}$ satisfies the subgradient optimality conditions

$$-N{C}_{jj}{\left({\widehat{\theta }}_{\mathrm{MPELE}}\right)}_j+{\left(X^{T}r\right)}_j=\lambda \mathrm{sign}{\left({\widehat{\theta }}_{\mathrm{MPELE}}\right)}_j\text{if}{\left({\widehat{\theta }}_{\mathrm{MPELE}}\right)}_j\ne 0$$ (33)

$$\mid -N{C}_{jj}{\left({\widehat{\theta }}_{\mathrm{MPELE}}\right)}_j+{\left(X^{T}r\right)}_j\mid \le \lambda \text{otherwise},$$ (34)

for j = 1, ..., p. The above equations imply that ${\widehat{\theta }}_{\mathrm{MPELE}}$ is a soft-thresholded function of $X^{T}r:{\left({\widehat{\theta }}_{\mathrm{MPELE}}\right)}_j=0$ if |(X^T r)j| ≤λ, and otherwise

$${\left({\widehat{\theta }}_{\mathrm{MPELE}}\right)}_j=\frac{1}{N{C}_{jj}}\left({\left(X^{T}r\right)}_j-\lambda \mathrm{sign}{\left({\widehat{\theta }}_{\mathrm{MPELE}}\right)}_j\right),$$ (35)

for j = 1, ..., p. Note that Eq. (35) implies that we can independently solve for each element of ${\widehat{\theta }}_{\mathrm{MPELE}}$ along all values of λ (the so-called regularization path). Since only a single matrix-vector multiply (X^T r) is required, the total complexity in this case is just O(Np). Once again, because X^T X is typically unstructured, computation of the exact MAP is generally much more expensive.

When C is not diagonal we can typically no longer solve Eq. (32) analytically. However, we can still solve this equation numerically, e.g., using interior-point methods (Boyd and Vandenberghe 2004). Briefly, these methods solve a sequence of auxiliary, convex problems whose solutions converge to the desired vector. Unlike problems with an L₁ penalty, these auxiliary problems are constructed to be smooth, and can therefore be solved in a small number of iterations using standard methods (e.g., Newton-Raphson (NR) or conjugate gradient (CG)). Computing the Newton direction requires a linear matrix solve of the form (C + D)θ = b, where D is a diagonal matrix and b is a vector. Again, structure in C can often be exploited here; for example, if C is banded, or diagonal plus low-rank, each Newton step requires O(p) time, leading to significant computational gains over the exact MAP.

To summarize, because the population covariance C is typically more structured than the sample covariance X^T X, the MELE and MPELE can often be computed much more quickly than the MLE or the MAP estimator. We have examined penalized estimators based on L₂ and L₁ penalization as illustrative examples here; similar conclusions hold for more exotic examples, including group penalties, rank-penalizing penalties, and various combinations of L₂ and L₁ penalties.

2.4 Analytic comparison of the accuracy of EL estimators with the accuracy of maximum-likelihood estimators

We have seen that EL-based estimators can be fast. How accurate are they, compared to the corresponding MLE or MAP estimators? First, note that the MELE inherits the classical consistency properties of the MLE; i.e., if the model parameters are held fixed and the amount of data N tends to infinity, then both of these estimators will recover the correct parameter θ, under suitable conditions. This result follows from the classical proof of the consistency of the MLE (van der Vaart 1998) if we note that both (1/N)L(θ) and $(1∕N)\tilde{L}\left(\theta \right)$ converge to the same limiting function of θ.

To obtain a more detailed view, it is useful to take a close look at the linear regression model, where we can analytically calculate the mean-squared error (MSE) of these estimators. Recall that we assume

$$r\mid x\sim \mathcal{N}(x^T\theta ,I),$$ (36)

$$x\sim \mathcal{N}(0,I).$$ (37)

(For convenience we have set σ² 1). We derive the following MSE formulas in the methods:

$$\mathbf{E}\left[{\Vert {\widehat{\theta }}_{\mathrm{MELE}}-\theta \Vert }_2^2\right]=\frac{{\theta }^T\theta +p({\theta }^T\theta +1)}{N},$$ (38)

$$\mathbf{E}\left[{\Vert {\widehat{\theta }}_{MLE}-\theta \Vert }_2^2\right]=\frac{p}{N-p-1};$$ (39)

see Shaffer (1991) for some related results. In the classical limit, for which p is fixed and N → ∞ (and the MSE of both estimators approaches zero), we see that, unless θ = 0, the MLE outperforms the MELE:

$$\underset{N\to \infty }{\lim }N\mathbf{E}\left[{\Vert {\widehat{\theta }}_{\mathrm{MELE}}-\theta \Vert }_2^2\right]>\underset{N\to \infty }{\lim }N\mathbf{E}\left[{\Vert {\widehat{\theta }}_{MLE}-\theta \Vert }_2^2\right]=p.$$ (40)

However, for many applications (particularly the neuro-science applications we will focus on below), it is more appropriate to consider the limit where the number of samples and parameters are large, both N → ∞ and p → ∞, but their ratio $\frac{p}{N}=\rho$ is bounded from zero and In this limit we see that

$$\mathbf{E}\left[{\Vert {\widehat{\theta }}_{\mathrm{MELE}}-\theta \Vert }_2^2\right]\to \rho ({\theta }^T\theta +1)$$ (41)

$$\mathbf{E}\left[{\Vert {\widehat{\theta }}_{MLE}-\theta \Vert }_2^2\right]\to \frac{\rho }{1-\rho }.$$ (42)

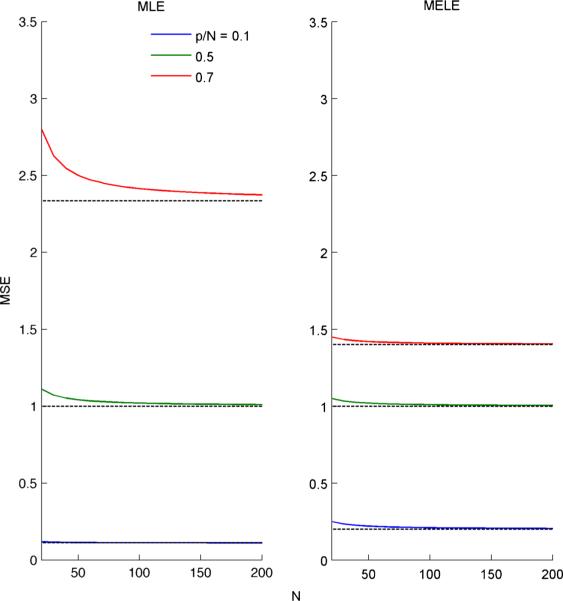
See Fig. 7 for an illustration of the accuracy of this approximation for finite N and p.

Fig. 7.

Finite sample comparisons to the limiting values of the MLE and MELE MSE as p, N → ∞, $\frac{p}{N}\to \rho$. We plot the true mean-squared error (MSE) (colored lines) as a function of finite sample size for different values of $\frac{p}{N}$ for both the MLE (left column) and MELE (right column). Black dashed lines show limiting MSE when p, N → ∞, $\frac{p}{N}\to \rho$. The quality of the approximation does not seem to depend on $\frac{p}{N}$ for the MELE and is within 1% accuracy after about 100 samples. For the MLE, this approximation depends on $\frac{p}{N}$. However, while the quality of the approximation depends on the estimator used, for data regimes common in neuroscience applications $(\frac{p}{N}\sim 0.01,N\sim 10000)$ the limiting approximation is acceptable

Figure 2a (left panel) plots these limiting MSE curves as a function of ρ. Note that we do not plot the MSE for values of ρ > 1 because the MLE is non-unique when p is greater than N; also note that Eq. (42) diverges as ρ ↗ 1, though the MELE MSE remains finite in this regime. We examine these curves for a few different values of θ^T θ; note that since σ² = 1, θ^T θ can be interpreted as the signal variance divided by the noise variance, i.e., the signal-to-noise ratio (SNR):

$$SNR=\frac{\mathbf{E}\left[{\theta }^T{x}^{T}x\theta \right]}{{\sigma }^2}$$ (43)

$$=\frac{{\theta }^T\theta }{1}.$$ (44)

The second line follows from the fact that we choose stimuli with identity covariance. The key conclusion is that the MELE outperforms the MLE for all $\rho >\frac{SNR}{1+SNR}$. (This may seem surprising, since for a given X, a classic result in linear regression is that the MLE has the lowest MSE amongst all unbiased estimators of θ (Bickel and Doksum 2007). However, the MELE is biased given X, and can therefore have a lower MSE than the MLE by having a smaller variance).

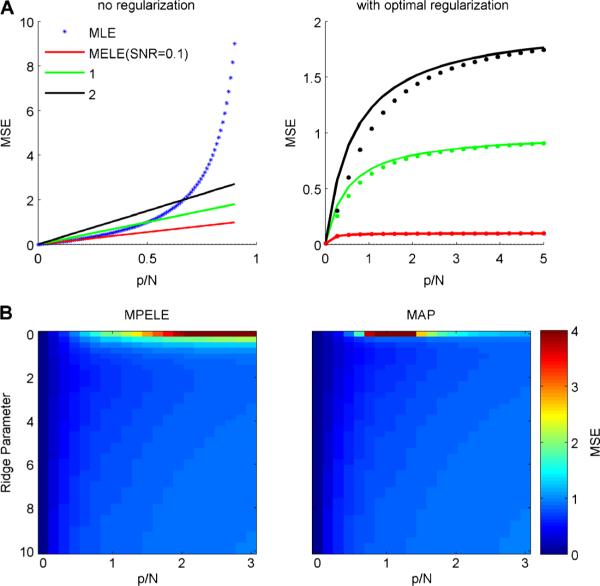
Fig. 2.

Comparing the accuracy of the MAP and MPELE in the standard linear regression model with Gaussian noise. a (left) The mean squared error (MSE) for the MELE (solid lines) and the MLE (dotted line) is shown as a function of p/N the ratio of the number of parameters to number of samples. We plot results for the asymptotic case where the number of samples and dimensions goes to infinity but the ratio p/N remains finite. Different colors denote different values for the true filter norm; recall that the MSE of the MLE is independent of the true value of θ, since the MLE is an unbiased estimator of θ in this model. The MLE mean squared error is larger than that of the MELE when p/N is large. b MSE for both estimators when L2 regularization is added. The MSE is similar for both estimators for a large range of ridge parameters and values of p/N. a (right) For each value of p/N, separate ridge parameters are chosen for the MPELE and MAP estimators to minimize their respective mean squared errors. Solid curves correspond to MPELE (as in left panel); dotted curves to MAP estimates. The difference in performance between the two optimally-regularized estimators remains small for a wide range of values of SNR and p/N. Similar results are observed numerically in the Poisson regression (LNP) case (data not shown)

What if we examine the penalized versions of these estimators? In the methods we calculate the MSE of the MAP and MPELE given a simple ridge penalty of the form $\log \left(f\left(\theta \right)\right)=-\frac{R}{2}{\Vert \theta \Vert }_2^2$, for scalar R. Figure 2b (top panel) plots the MSE for both estimators (see Eqs. (85, 101) in the methods for the equations being plotted) as a function of R and ρ for an SNR value of 1. Note that we now plot MSE values for ρ > 1 since regularization makes the MAP solution unique. We see that the two estimators have similar accuracy over a large region of parameter space. For each value of ρ we also compute each estimator's optimal MSE—i.e., the MSE corresponding to the the value of R that minimizes each estimator's MSE. This is plotted in Fig. 2a (right panel). Again, the two estimators perform similarly.

In conclusion, in the limit of large but comparable N and p, the MELE outperforms the MLE in low-SNR or high-(p/N) regimes. The ridge-regularized estimates (the MPELE and MAP) perform similarly across a broad range of (p/N) and regularization values (Fig. 2b). These analytic results motivate the applications (using non-Gaussian GLMs) on real data treated in the next section.

2.5 Fast methods for refining maximum expected log-likelhood estimators to obtain MAP accuracy

In settings where the MAP provides a more accurate estimator than the MPELE, a reasonable approach is to use ${\widehat{\theta }}_{\mathrm{MPELE}}$ as a quickly-computable initializer for optimization algorithms used to compute ${\widehat{\theta }}_{MAP}$. An even faster approach would be to initialize our search at ${\widehat{\theta }}_{\mathrm{MPELE}}$, then take just enough steps towards ${\widehat{\theta }}_{MAP}$ to achieve an estimation accuracy which is indistinguishable from that of the exact MAP estimator. (Related ideas based on stochastic gradient ascent methods have seen increasing attention in the machine learning literature (Bottou 1998; Boyles et al. 2011)). We tested this idea on real data, by fitting an LNP model to a population of ON and OFF parasol ganglion cells (RGCs) recorded in vitro, using methods similar to those described in Shlens et al. (2006), Pillow et al. (2008); see these earlier papers for full experimental details. The observed cells responded to either binary white-noise stimuli or naturalistic stimuli (spatiotemporally correlated Gaussian noise with spatial correlations having a 1/F power spectrum and temporal correlations defined by a first-order autoregressive process; see Appendix for details). As described in the methods, each receptive field was specified by 810 parameters, with $\frac{p}{N}=0.021$. For the MAP, we use a simple ridge penalty of the form $\log \left(f\left(\theta \right)\right)=-\frac{R}{2}{\Vert \theta \Vert }_2^2$.

Many iterative algorithms are available for ascending the posterior to approximate the MAP. Preconditioned conjugate gradient ascent (PCG) (Shewchuk 1994) is particularly attractive here, for two reasons. First, each iteration is fairly fast: the gradient requires O(Np) time, and multiplication by the preconditioner turns out to be fast, as discussed below. Second, only a few iterations are necessary, because the MPELE is typically fairly close to the exact MAP in this setting (recall that ${\widehat{\theta }}_{\mathrm{MPELE}}\to {\widehat{\theta }}_{MAP}$ as N/p ∞), and we have access to a good preconditioner, ensuring that the PCG iterates converge quickly. We chose the inverse Hessian of the EL evaluated at the MELE or MPELE as a pre-conditioner. In this case, using the same notation as in Eqs. (27) and (31), the preconditioner is simply given by ${\left(C{\sum }_n{r}_n\right)}^{-1}$ or ${(C{\sum }_n{r}_n+RI)}^{-1}$. Since the EL Hessian provides a good approximation for the log-likelihood Hessian, the preconditioner is quite accurate; since the stimulus covariance C is either proportional to the identity (in the white-noise case) or of block-Toeplitz form (in the spatiotemporally-correlated case), computation with the preconditioner is fast (O(p) or O(p log p), respectively).

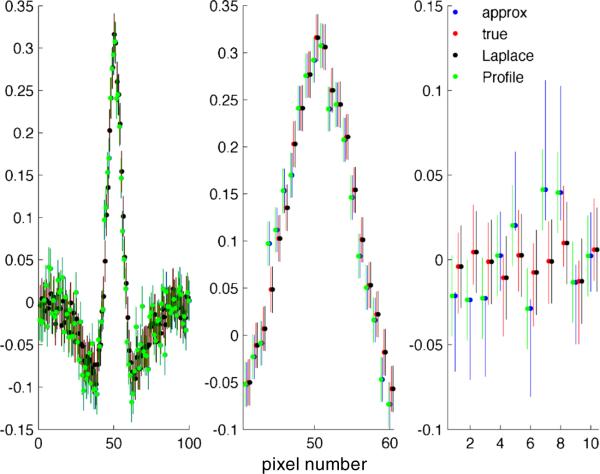
For binary white-noise stimuli we find that the MELE (given by Eq. (27) with C = I) and MLE yield similar filters and accuracy, with the MLE slightly outperforming the MELE (see Fig. 3a). Note that in this case, ${\widehat{\theta }}_{\mathrm{MELE}}$ can be computed quickly, O(pN), since we only need to compute the matrix-vector multiplication X^T r. On average across a population of 126 cells, we find that terminating the PCG algorithm, initialized at the MELE, after just two iterations yielded an estimator with the same accuracy as the MAP. To measure accuracy we use the cross-validated log-likelihood (see Appendix). It took about 15× longer to compute the MLE to default precision than the PCG-based approximate MLE (88±2 vs 6±0.1 seconds on an Intel Core 2.8 GHz processor running Matlab; all timings quoted in this paper use the same computer). In the case of spatiotemporally correlated stimuli (with ${\widehat{\theta }}_{\mathrm{MPELE}}$ given by Eq. (31)), we find that 9 PCG iterations are required to reach MAP accuracy (see Fig. 3b); the MAP estimator was still slower to compute by a significant factor (107±8 vs 33±1 seconds).

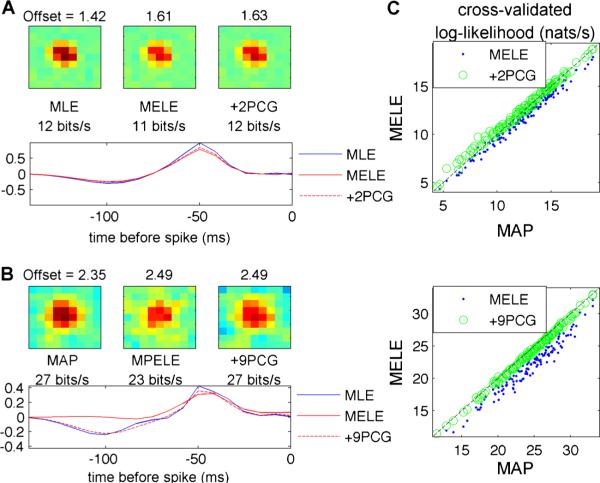
Fig. 3.

The MPELE provides a good initializer for finding approximate MAP estimators using fast gradient-based optimization methods in the LNP model. a The spatiotemporal receptive field of a typical retinal ganglion cell (RGC) in our database responding to binary white-noise stimuli and fit with a linear-nonlinear Poisson (LNP) model with exponential non-linearity, via the MLE. The receptive field of the same cell fit using the MELE is also plotted. The goodness-offit of the MLE (measured in terms of cross-validated log-likelihood; see Appendix) is slightly higher than that of the MELE (12 versus 11 bits/s). However, this difference disappears after a couple pre-conditioned conjugate gradient (PCG) iterations using the true likelihood initialized at the MELE (see label +2PCG). Note that we are only showing representative spatial and temporal slices of the 9×9×10 dimensional receptive field, for clarity. b Similar results hold when the same cell responds to 1/f correlated Gaussian noise stimuli (for correlated Gaussian responses, the MAP and MPELE are both fit with a ridge penalty). In this case 9 PCG iterations sufficed to compute an estimator with a goodness-of-fit equal to that of the MAP. c These results are consistent over the observed population. (top) Scatterplot of cross-validated log-likelihood across a population of 91 cells, responding to binary white-noise stimuli, each fit independently using the MLE, MELE or a couple PCG iterations using the true likelihood and initialized at the MELE. (bottom) Log-likelihood for the same population, responding to 1/f Gaussian noise, fit independently using an L2 regularized MAP, MPELE or 9 PCG iterations using the true regularized likelihood initialized at the MPELE

2.5.1 Scalable modeling of interneuronal dependencies

So far we have only discussed models which assume conditional independence of responses given an external stimulus. However, it is known the predictive performance of the GLM can be improved in a variety of brain areas by allowing some conditional dependence between neurons (e.g., (Truccolo et al. 2005; Pillow et al. 2008); see Vidne et al. (2012) for a recent review of related approaches). One convenient way to incorporate these dependencies is to include additional covariates in the GLM. Specifically, assume we have recordings from M neurons and let r_i be the vector of responses across time of the ith neuron. Each neuron is modeled with a GLM where the weighted covariates, $x_n^T{\theta }_i$, can be broken into an offset term, an external stimulus component x^s, and a spike history-dependent component

$$x_n^T{\theta }_i={\theta }_{i0}+{\left(x^s\right)}^T{\theta }_i^s+\sum _{j=1}^M\sum _{k=1}^{\tau }{r}_{j,n-k}{\theta }_{ijk}^H,$$ (45)

for n = 1, ..., N, where τ denotes the maximal number of lags used to predict the firing rate of neuron i given the activity of the the observed neurons indexed by j. Note that this is the same model as before when ${\theta }_{ijk}^H=0$ for j = 1, 2, ...., M; in this special case, we recover an inhomogeneous Poisson model, but in general, the outputs of the coupled GLM will be non-Poisson. A key challenge for this model is developing estimation methods that scale well with the number of observed neurons; this is critical since, as discussed above, experimental methods continue to improve, resulting in rapid growth of the number of simultaneously observable neurons during a given experiment (Stevenson and Kording 2011).

One such scalable approach uses the MELE of an LNP model to fit a fully-coupled GLM with history terms. The idea is that estimates of θ^s fit with ${\theta }_{ijk}^H=0$ will often be similar to estimates of θ^s without this hard constraint. Thus we can again use the MELE (or MPELE) as an initializer for θ^s, and then use fast iterative methods to refine our estimate, if necessary. More precisely, to infer θ_i for i = 1, 2, ...., M, we first estimate ${\theta }_i^s$, assuming no coupling or self-history terms (${\theta }_{ijk}^H=0$ for j = 1, 2, ...., M) using the MELE (Eq. (27) or a regularized version). We then update the history components and offset by optimizing the GLM likelihood with the stimulus filter held fixed up to a gain factor, α_i, and the interneuronal terms ${\theta }_{ijk}^H=0$ for i ≠ j:

$$\left({\theta }_{i0},{\alpha }_i,{\theta }_i^H\right)=\arg \underset{\left({\theta }_0,\alpha ,{\theta }_{ijk}^H=0\forall i\ne j\right)}{\max }L\left(\left({\theta }_0,\alpha {\widehat{\theta }}_{\mathrm{MPELE}},{\theta }^H\right)\right)+\log \left(f\left({\theta }_0,\alpha {\widehat{\theta }}_{\mathrm{MPELE}},{\theta }^H\right)\right).$$ (46)

Holding the shape of the stimulus filter fixed greatly reduces the number of free parameters, and hence the computational cost, of finding the history components. Note that all steps so far scale linearly in the number of observed neurons M. Finally, perform a few iterative ascent steps on the full posterior, incorporating a sparse prior on the interneuronal terms (exploiting the fact that neural populations can often be modeled as weakly conditionally dependent given the stimulus; see Pillow et al. (2008) and Mishchenko and Paninski 2011 for further discussion). If such a sparse solution is available, this step once again often requires just O(M) time, if we exploit efficient methods for optimizing posteriors based on sparsity-promoting priors (Friedman et al. 2010; Zhang 2011).

We investigated this approach by fitting the GLM specified by Eq. (45) to a population of 101 RGC cells responding to binary white-noise using 250 stimulus parameters and 105 parameters related to neuronal history (see Appendix for full details; $\frac{p}{N}=0.01$). We regularize the coupling history components using a sparsity-promoting L₁ penalty of the form $\lambda {\sum }_j\mid {\theta }_{ij}^H\mid$; for simplicity, we parametrize each coupling filter ${\theta }_{ij}^H$ with a single basis function, so that it is not necessary to sum over many k indices. (However, note that group-sparsity-promoting approaches are also straightforward here Pillow et al. (2008)). We compute our estimates over a large range of the sparsity parameter λ using the “glmnet” coordinate ascent algorithm discussed by Friedman et al. (2010).

Figure 4b compares filter estimates for two example cells using the fast approximate method and the MAP. The filter estimates are similar (though not identical); both methods find the same coupled, nearest neighbor cells. Both methods achieve the same cross-validated prediction accuracy (Fig. 4b). The fast approximate method took an average of 1 minute to find the entire regularization path; computing the full MAP path took 16 minutes on average.

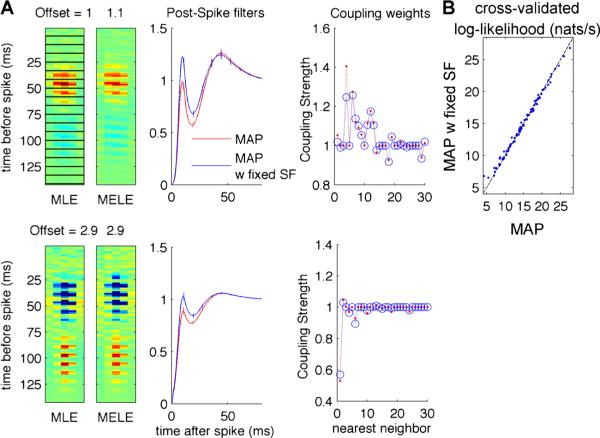
Fig. 4.

Initialization with the MPELE using an LNP model, then coordinate descent using a sparsity-promoting prior, efficiently estimates a full, coupled, non-Poisson neural population GLM. a Example stimulus, self-history, and coupling filters for two different RGC cells (top and bottom rows). The stimulus filters are laid out in a rasterized fashion to map the three-dimensional filters (two spatial dimensions and one temporal dimension) onto the two-dimensional representation shown here. Each filter is shown as a stack (corresponding to the temporal dimension) of two dimensional spatial filters, which we outline in black in the top left to aid the visualization. MAP parameters are found using coordinate descent to optimize the exact GLM log-likelihood with L₁-penalized coupling filters (labeled MAP). Fast estimates of the self-history (see Appendix for details of errorbar computations) and coupling filters are found by running the same coordinate descent algorithm with the stimulus filter (SF) fixed, up to a gain, to the MELE of an LNP model (labeled ‘w fixed SF’; see text for details). Note that estimates obtained using these two approaches are qualitatively similar. In particular, note that both estimates find coupling terms that are largest for neighboring cells, as in Pillow et al. (2008), Vidne et al. (2012). We do not plot the coupling weights for cells 31–100 since most of these are zero or small. b Scatter-plot comparing the cross-validated log-likelihood over 101 different RGC cells show that the two approaches lead to comparable predictive accuracy

2.6 Marginal likelihood calculations

In the previous examples we have focused on applications that require us to maximize the (penalized) EL. In many applications we are more interested in integrating over the likelihood, or sampling from a posterior, rather than simply optimization. The EL approximation can play an important role in these applications as well. For example, in Bayesian applications one is often interested in computing the marginal likelihood: the probability of the data, p(r), with the dependence on the parameter θ integrated out (Gelman et al. 2003; Kass and Raftery 1995). This is done by assigning a prior distribution f (θ|R), with its own “hyper-parameters” R, over θ and calculating

$$\begin{array}{cc}\hfill F\left(R\right)\equiv p(r\mid x_1,\dots ,x_N,R)=& \int p(r,\theta \mid x_1,\dots ,x_N,R)d\theta \hfill \\ \hfill =& \int p(r\mid \theta ,x_1,\dots ,x_N)f(\theta \mid R)d\theta .\hfill \end{array}$$ (47)

Hierarchical models in which R sets the prior over θ_i for many neurons i simultaneously are also useful (Behseta et al. 2005); the methods discussed below extend easily to this setting.

We first consider a case for which this integral is analytically tractable. We let the prior on θ be Gaussian, and use the standard regression model for r|θ:

$$p(r,\theta \mid X,R)=p(r\mid X,\theta )f(\theta \mid R)$$ (48)

$$=\mathcal{N}(X\theta ,{\sigma }^2\mathbf{I})\mathcal{N}(0,R^{-1}),$$ (49)

where I is the identity matrix. Computing the resulting Gaussian integral, we have

$$\log F\left(R\right)=\frac{1}{2}\log \left(\det \left(\Sigma R\right)\right)+\frac{r^{T}X\Sigma X^{T}r}{2{\sigma }^4}+\mathrm{const}\left(R\right),$$ (50)

$$\Sigma ={(X^{T}X{\sigma }^2+R)}^{-1}.$$ (51)

If R and X^T X do not share any special structure, each evaluation of F (R) requires O(p³) time.

On the other hand, if we approximate p(r|X, θ) by the the expected likelihood, the integral is still tractable and has the same form as Eq. (50), but with $\Sigma ={(NC{\sigma }^2+R)}^{-1}$ assuming are faster for example, if C and R can be diagonalized (or made banded) in a convenient shared basis, then F (R) can often be computed in just O(p) time.

When the likelihood or prior is not Gaussian we can approximate the marginal likelihood using the Laplace approximation (Kass and Raftery 1995)

$$\begin{array}{cc}\hfill \log F\left(R\right)\approx & \log p({\theta }_{MAP}\mid R)-\frac{1}{2}\log \left(\det (-H\left({\theta }_{MAP}\right))\right)\hfill \\ \hfill =& {\theta }_{MAP}^T{X}^{T}r-\sum _{n}G\left(x_n^T{\theta }_{MAP}\right)+\log \left(f({\theta }_{MAP}\mid R)\right)-\frac{1}{2}\log \left(\det (-H\left({\theta }_{MAP}\right))\right),\hfill \end{array}$$ (52)

again neglecting factors that are constant with respect to R. H (θ_MAP) is the posterior Hessian

$$H_{ij}=\frac{{\partial }^2}{\partial {\theta }_i\partial {\theta }_j}\left(-\sum _{n}G\left(x_n^T\theta \right)+\log \left(f(\theta \mid R)\right)\right).$$ (53)

evaluated at θ = θ_MAP. We note that there are other methods for approximating the integral in Eq. (47), such as Evidence Propagation (Minka 2001; Bishop 2006); we leave an exploration of EL-based approximations of these alternative methods for future work.

We can clearly apply the EL approximation in Eqs. (52–53). For example, consider the LNP model, where we can approximate E [G(θ₀ + x^T θ)] as in Eq. (16); if we use a normal prior of the form f (θ^s|R) = N (0, R⁻¹), then the resulting EL approximation to the marginal likelihood looks very much like the Gaussian case, with the attending gains in efficiency if C and R share an exploitable structure, as in our derivation of the MPELE in this model (recall Section 2.3).

This EL-approximate marginal likelihood has several potential applications. For example, marginal likelihoods are often used in the context of model selection: if we need to choose between many possible models indexed by the hyperparameter R, then a common approach is to maximize the marginal likelihood as a function of R (Gelman et al. 2003). Denote R̂ = arg max_R F (R). Computing R̂ directly is often expensive, but computing the maximizer of the EL-approximate marginal likelihood instead is often much cheaper. In our LNP example, for instance, the EL-approximate R̂ can be computed analytically if we can choose a basis such that C = I and R ∝ I:

$$\widehat{R}=\{\begin{array}{cc}\frac{p}{\frac{q}{N_s^2}-\frac{p}{N_s}}\mathbf{I}\hfill & \text{if}p<\frac{q}{N_s}\hfill \\ \infty \hfill & \text{if}p\ge \frac{q}{N_s},\hfill \end{array}\phantom{\}}$$ (54)

with $q\equiv {\Vert X^{T}r\Vert }_2^2$ and $N_s={\sum }_{n=1}^N{r}_n$; see Appendix for the derivation. Since ${\widehat{\theta }}_{\mathrm{MPELE}}={(C+\frac{R}{{\sum }_n{r}_n})}^{-1}\frac{X^{T}r}{{\sum }_n{r}_n}$, an infinite value of R corresponds to ${\widehat{\theta }}_{\mathrm{MPELE}}$ equal to zero: infinite penalization. The intuitive interpretation of Eq. (54) is that the MPELE should be shrunk entirely to zero when there isn't enough data, quantified by $\frac{q}{N_s}$, compared to the dimensionality of the problem p. Similar results hold when there are correlations in the stimulus, C ≠ I, as discussed in more detail in the methods.

Figure 5 presents a numerical illustration of the resulting penalized estimators. We simulated Poisson responses to white-noise Gaussian stimuli using stimulus filters with p = 250 parameters. We use a standard iterative method for computing the exact R̂: it is known that the optimal R̂ obeys the equation

$$\widehat{R}=\frac{p-\widehat{R}{\sum }_i{H}^{-1}{\left({\widehat{\theta }}_{MAP}\right)}_{ii}}{{\widehat{\theta }}_{MAP}{\left(\widehat{R}\right)}^T{\widehat{\theta }}_{MAP}\left(\widehat{R}\right)},$$ (55)

under the Laplace approximation (Bishop 2006). Note that this equation only implicitly solves for R̂, since R̂ is present on both sides of the equation. However, this leads to the following common fixed-point iteration:

$${\widehat{R}}_{i+1}=\frac{p-{\widehat{R}}_i{\sum }_i{H}^{-1}{\left({\widehat{\theta }}_{MAP}\right)}_{ii}}{{\widehat{\theta }}_{MAP}{\left({\widehat{R}}_i\right)}^T{\widehat{\theta }}_{MAP}\left({\widehat{R}}_i\right)},$$ (56)

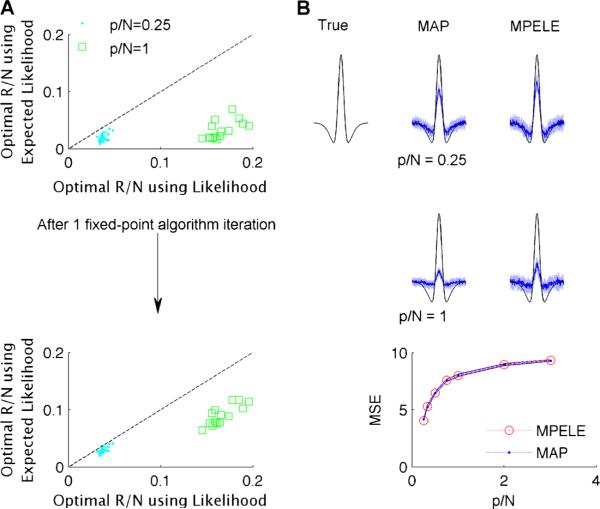
with R̂ estimated as lim_i→∞ R̂_i, when this limit exists. We find that the distance between the exact and approximate R̂ values increases with $\frac{p}{N}$, with the EL systematically choosing lower values of R̂ (Fig. 5a top). This difference shrinks after a single iteration of Eq. (56) initialized using Eq. (54) (Fig. 5a bottom). The remaining differences in R̂ between the two methods did not lead to differences in the corresponding estimated filters ${\widehat{\theta }}_{MAP}\left(\widehat{R}\right)$ (Fig. 5b). In these simulations the exact MAP typically took about 20 times longer to compute than a single iteration of Eq. (56) initialized using Eq. (54) (10 versus 0.5 sec).

Fig. 5.

The EL can be used for fast model selection via approximate maximum marginal likelihood. Thirty simulated neural responses were drawn from a linear-nonlinear Poisson (LNP) model, with stimuli drawn from an independent white-noise Gaussian distribution. The true filter (shown in black in B) has p = 250 parameters and norm 10. a Optimal hyper-parameters R (the precision of the Gaussian prior distribution) which maximize the marginal likelihood using the EL (top left column, vertical axis) scale similarly to those which maximize the full Laplace-approximated marginal likelihood (top left column, horizontal axis), but with a systematic downward bias. After a single iteration of the fixed point algorithm used to maximize the full marginal likelihood (see text), the two sets of hyper-parameters (bottom left column) match to what turns out to be sufficient accuracy, as shown in (b): the median filter estimates (blue lines) (± absolute median deviation (light blue), based on 30 replications) computed using the exact and one-step approximate approach match for a wide range of $\frac{p}{N}$. The MSE of the two approaches also matches for a wide range of $\frac{p}{N}$

We close by noting that many alternative methods for model selection in penalized GLMs have been studied; it seems likely that the EL approximation could be useful in the context of other approaches based on cross-validation or generalized cross-validation (Golub et al. 1979), for example. We leave this possibility for future work. See Conroy and Sajda (2012) for a related recent discussion.

2.7 Decreasing the computation time of Markov chain Monte Carlo methods

As a final example, in this section we investigate the utility of the EL approximation in the context of Markov chain Monte Carlo (MCMC) methods (Robert and Casella 2005) for sampling from the posterior distribution of θ given GLM observations. Two approaches suggest themselves. First, we could simply replace the likelihood with the exponentiated EL, and sample from the resulting approximation to the true posterior using our MCMC algorithm of choice (Sadeghi et al. 2013). This approach is fast but only provides samples from an approximation to the posterior. Alternatively, we could use the EL-approximate posterior as a proposal density within an MCMC algorithm, and then use the standard Metropolis-Hastings correction to obtain samples from the exact posterior. This approach, however, is slower, because we need to compute the true log-likelihood with each Metropolis-Hastings iteration.

Figure 6 illustrates an application of the first approach to simulated data. We use a standard Hamiltonian Monte Carlo (Neal 2012) method to sample from both the true and EL-approximate posterior given N = 4000 responses from a 100-dimensional LNP model, with a uniform (flat) prior. We compare the marginal median and 95 % credible interval computed by both methods, for each element of θ. For most elements of the θ vector, the EL-approximate posterior matches the true posterior well. However, in a few cases the true and approximate credible intervals differ significantly; thus, it makes sense to use this method as a fast exploratory tool, but perhaps not for conclusive analyses when N/p is of moderate size. (Of course, as N/p → ∞, the EL approximation becomes exact, while the true likelihood becomes relatively more expensive, and so the EL approximation will become the preferred approach in this limit).

Fig. 6.

The EL approximation leads to fast and (usually) accurate MCMC sampling from GLM posteriors. 4000 responses were simulated from a 100-dimensional LNP model using i.i.d. white-noise Gaussian stimuli. 10⁶ Markov Chain Monte Carlo samples, computed using Hybrid Monte Carlo, were then drawn from the posterior assuming a flat prior, using either the exact Poisson likelihood or the EL approximation to the likelihood. The left column displays the median vector along with 95 % credible regions for each marginal distribution (one marginal for each of the 100 elements of θ); approximate intervals are shown in blue, and exact intervals in red. In the middle and right column we have zoomed in around different elements for visual clarity. Statistics from both distributions are in close agreement for most, but not all, elements of θ. Replacing the EL-approximate likelihood with the EL-approximate profile likelihood yielded similar results (green). The Laplace approximation to the exact posterior also provided a good approximation to the exact posterior (black)

For comparison, we also compute the median and credible intervals using two other approaches: (1) the standard Laplace approximation (computed using the true likelihood), and (2), the profile EL-posterior, which is exactly Gaussian in this case (recall Section 2.3). The intervals computed via (1) closely match the MCMC output on the exact posterior, while the intervals computed via (2) closely match the EL-approximate MCMC output; thus the respective Gaussian approximations of the posterior appear to be quite accurate for this example.

Experiments using the second approach described above (using Metropolis-Hastings to obtain samples from the exact posterior) were less successful. The Hamiltonian Monte Carlo method is attractive here, since we can in principle evaluate the EL-approximate posterior cheaply many times along the Hamiltonian trajectory before having to compute the (expensive) Metropolis-Hastings probability of accepting the proposed trajectory. However, we find (based on simulations similar to those described above) that proposals based on the fast EL-approximate approach are rejected at a much higher rate than proposals generated using the exact posterior. This lower acceptance probability in turn implies that more iterations are required to generate a sufficient number of accepted steps, sharply reducing the computational advantage of the EL-based approach. Again, as N/p → ∞, the EL approximation becomes exact, and the EL approach will be preferred over exact MCMC methods—but in this limit the Laplace approximation will also be exact, obviating the need for expensive MCMC approaches in the first place.

3 Conclusion

We have demonstrated the computational advantages of using the expected log-likelihood (EL) to approximate the log-likelihood of a generalized linear model with canonical link. When making multiple calls to the GLM likelihood (or its gradient and Hessian), the EL can be computed approximately O(Np/z) times faster, where N is the number of data samples collected, p is the dimensionality of the parameters and z is the cost of a one-dimensional integral; in many cases this integral can be evaluated analytically or semi-analytically, making z trivial. In addition, in some cases the EL can be analytically optimized or integrated out, making EL-based approximations even more powerful. We discussed applications to maximum penalized likelihood-based estimators, model selection, and MCMC sampling, but this list of applications is certainly far from exhaustive.

Ideas related to the EL approximation have appeared previously in a wide variety of contexts. We have already discussed previous work in neuroscience (Paninski 2004; Park and Pillow 2011; Field et al. 2010; Sadeghi et al. 2013) that exploits the EL approximation in the LNP model. Similar approximations have also been used to simplify the likelihood of GLM models in the context of neural decoding (Rahnama Rad and Paninski 2011). In the Gaussian process regression literature, the well-known “equivalent kernel” approximation can be seen as a version of the EL approximation (Rasmussen and Williams 2005; Sollich and Williams 2005); similar approaches have a long history in the spline literature (Silverman 1984). Finally, the EL approximation is somewhat reminiscent of the classical Fisher scoring algorithm, in which the observed information matrix (the Hessian of the negative log-likelihood) is replaced by the expected information matrix (i.e., the expectation of the observed information matrix, taken over the responses r) in the context of approximate maximum likelihood estimation. The major difference is that the EL takes the expectation over the covariates x instead of the responses r. A potential direction for future work would be to further explore the relationships between these two expectation-based approximations.

Appendix: methods

A.1 Computing the mean-squared error for the MPELE and MAP in the linear-Gaussian model

In this section we provide derivations for the results discussed in Section 2.4. We consider the standard linear regression model with Gaussian noise and a ridge (Gaussian) prior of the form $f\left(\theta \right)\propto \exp (-cp\frac{{\theta }^T\theta }{2})$, with c a scalar. We further assume that the stimuli x are i.i.d. standard Gaussian vectors. We derive the MSE of the MPELE and MAP, then recover the non-regularized cases (i.e., the MLE and MELE) by setting c to zero. Note that we allow the regularizer to scale with the dimensionality of the problem, p, for reasons that will become clear below. The resulting MAP and MPELE are then found by

$${\widehat{\theta }}_{MAP}=\arg \underset{\theta }{\max }{\theta }^T{X}^{T}r-\frac{1}{2}{\theta }^T(X^{T}X+cpI)\theta$$ (57)

$$={(X^{T}X+cpI)}^{-1}{X}^{T}r$$ (58)

$${\widehat{\theta }}_{\mathrm{MPELE}}=\arg \underset{\theta }{\max }{\theta }^T{X}^{T}r-\frac{1}{2}(N+cp){\theta }^T\theta$$ (59)

$$=\frac{X^{T}r}{N+cp},$$ (60)

j where we consider X_ij ~ N (0, 1) ᗊi, j . For convenience notation we defione the quantity S̃ = X^T X + cpI and therefore write the MAP as${\widehat{\theta }}_{MAP}={\tilde{S}}^{-1}{X}^{T}r$.

As usual the MSE can be written as the sum of a squared bias term and a variance term

$$\mathbf{E}\left[{\Vert \widehat{\theta }-\theta \Vert }_2^2\right]={\Vert \mathbf{E}\left[(\widehat{\theta }-\theta )\right]\Vert }_2^2+\mathbf{E}\left[{\Vert \widehat{\theta }-\mathbf{E}\left[\widehat{\theta }\right]\Vert }_2^2\right].$$ (61)

The bias of the MAP equals

$$\mathbf{E}\left[({\widehat{\theta }}_{MAP}-\theta )\right]=\mathbf{E}\left[{\widehat{\theta }}_{MAP}\right]-\theta$$ (62)

$$=\mathbf{E}\left[\mathbf{E}\left[{\widehat{\theta }}_{MAP}\mid X\right]\right]-\theta$$ (63)

$$=\mathbf{E}\left[{\tilde{S}}^{-1}{X}^T\mathbf{E}\left[r\mid X\right]\right]-\theta$$ (64)

$$=\mathbf{E}\left[{\tilde{S}}^{-1}{X}^{T}X\theta \right]-\theta .$$ (65)

The second line follows from the law of total expectation (Johnson and Wichern 2007) and the fourth follows from the fact E[r|X] = xθ.

From the law of total covariance, the variance can be written as

$$\mathbf{E}\left[{\Vert {\widehat{\theta }}_{MAP}-\mathbf{E}\left[{\widehat{\theta }}_{MAP}\right]\Vert }_2^2\right]=\mathbf{tr}\left(\mathrm{Cov}\left({\widehat{\theta }}_{MAP}\right)\right)$$ (66)

$$=\mathbf{tr}\left(\mathbf{E}\left[\mathrm{Cov}({\theta }_{MAP}\mid X)\right]+\mathrm{Cov}\left(\mathbf{E}[{\widehat{\theta }}_{MAP}\mid X]\right)\right).$$ (67)

The term $\mathrm{Cov}({\widehat{\theta }}_{MAP}\mid X)$ equals

$$\mathrm{Cov}({\widehat{\theta }}_{MAP}\mid X)={\tilde{S}}^{-1}{X}^T\mathrm{Cov}(r\mid X)X{\tilde{S}}^{-1}$$ (68)

$$={\tilde{S}}^{-1}{X}^{T}X{\tilde{S}}^{-1}.$$ (69)

In the second line we use the fact that Cov(r|X) = I. The term $\mathbf{E}[{\widehat{\theta }}_{MAP}\mid X]$ was used to derive Eq. (65 and equals S̃^–1 X^T Xθ.

Substituting the relevant quantities into Eq. (61), we find that the mean squared error of the MAP is

$$\mathbf{E}\left[{\Vert {\widehat{\theta }}_{MAP}-\theta \Vert }_2^2\right]={\Vert (\mathbf{E}\left[{\tilde{S}}^{-1}{X}^{T}X\right]-I)\theta \Vert }_2^2+\mathbf{tr}\left(\mathbf{E}\left[{\tilde{S}}^{-1}{X}^{T}X{\tilde{S}}^{-1}\right]+\mathrm{Cov}\left({\tilde{S}}^{-1}{X}^{T}X\theta \right)\right).$$ (70)

The MSE of the MPELE can be computed in a similar fashion. The bias of the MPELE equals

$$\mathbf{E}\left[({\widehat{\theta }}_{\mathrm{MPELE}}-\theta )\right]=\mathbf{E}\left[{\widehat{\theta }}_{\mathrm{MPELE}}\right]-\theta$$ (71)

$$=\mathbf{E}\left[\mathbf{E}\left[{\widehat{\theta }}_{\mathrm{MPELE}}\mid X\right]\right]-\theta$$ (72)

$$=\mathbf{E}\left[{(N+cp)}^{-1}{X}^T\mathbf{E}\left[r\mid X\right]\right]-\theta$$ (73)

$$={(N+cp)}^{-1}\mathbf{E}\left[X^{T}X\theta \right]-\theta$$ (74)

$$={(N+cp)}^{-1}N\theta -\theta .$$ (75)

To derive the fourth line we have again used the fact E[r|X] Xθ = Xθ to show that $\mathbf{E}[{\widehat{\theta }}_{\mathrm{MPELE}}\mid X]={(N+cp)}^{-1}{X}^{T}X\theta$. The fifth line follows E [X^T X] = NI. To compute the variance we again use the law of total covariance which requires the computation of a term $\mathbf{E}\left[\mathrm{Cov}({\widehat{\theta }}_{\mathrm{MPELE}}\mid X)\right]$,

$$\mathbf{E}\left[\mathrm{Cov}({\widehat{\theta }}_{\mathrm{MPELE}}\mid X)\right]=\mathbf{E}\left[{(N+cp)}^{-1}{X}^T\mathrm{Cov}(r\mid X)X{(N+cp)}^{-1}\right]$$ (76)

$$=\mathbf{E}\left[{(N+cp)}^{-1}{X}^{T}X{(N+cp)}^{-1}\right]$$ (77)

$$={(N+cp)}^{-2}N\mathbf{I}.$$ (78)

We use the fact that Cov(r|X) = I to derive the second line and the definition E [X^T X] = NI to derive the third.

Using the bias-variance decomposition of the MSE, Eq. (61), we find that the mean squared error of the MPELE estimator is

$$\mathbf{E}\left[{\Vert {\widehat{\theta }}_{\mathrm{MPELE}}-\theta \Vert }_2^2\right]={\Vert \left(\frac{N}{N+cp}-1\right)\theta \Vert }_2^2+\frac{1}{{(N+cp)}^2}\left(Np+\mathbf{tr}\left(\mathrm{Cov}\left(X^{T}X\theta \right)\right)\right).$$ (79)

The term tr (Cov(X^T Xθ) can be simplified by taking advantage of the fact that rows of X are i.i.d normally distributed with mean zero, so their fourth central moment can be written as the sum of outer products of the second central moments (Johnson and Wichern 2007).

$$\mathbf{E}\left[{\left(X^{T}X\right)}_{ij}{\left(X^{T}X\right)}_{kl}\right]=N\mathbf{E}\left[X_{1i}{X}_{1j}{X}_{1k}{X}_{1l}\right]+N(N-1){\delta }_{ij}{\delta }_{kl}$$ (80)

$$=N({\delta }_{ij}{\delta }_{kl}+{\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk})+N(N-1){\delta }_{ij}{\delta }_{kl}.$$ (81)

We then have

$$\mathbf{E}\left[{\Vert {\widehat{\theta }}_{\mathrm{MPELE}}-\theta \Vert }_2^2\right]={\Vert \left(\frac{N}{N+cp}-1\right)\theta \Vert }_2^2+\frac{1}{{(N+cp)}^2}\left(Np\left(1+{\Vert \theta \Vert }_2^2\right)+N{\Vert \theta \Vert }_2^2\right).$$ (82)

Without regularization (c = 0) the MSE expressions simplify significantly:

$$\mathbf{E}\left[{\Vert {\widehat{\theta }}_{MLE}-\theta \Vert }_2^2\right]=\mathbf{tr}\left(\mathbf{E}\left[{\left(X^{T}X\right)}^{-1}\right]\right)$$ (83)

$$\mathbf{E}\left[{\Vert {\widehat{\theta }}_{MELE}-\theta \Vert }_2^2\right]=\frac{{\theta }^T\theta +p({\theta }^T\theta +1)}{N}.$$ (84)

(The expression for the MSE of the MLE is of course quite well-known.) Noting that (X^T X)⁻¹ is distributed according to an inverse Wishart distribution with mean $\frac{1}{N-p-1}\mathbf{I}$ (Johnson and Wichern 2007), we recover Eqs. (38) and (39).

For c ≠ 0 we calculate the MSE for both estimators in the limit N, p → ∞ , with $0<\frac{p}{N}=\rho <\infty$. In this limit Eq. (82) reduces to

$$\mathbf{E}\left[{\Vert {\widehat{\theta }}_{\mathrm{MPELE}}-\theta \Vert }_2^2\right]\to \frac{\rho +{\theta }^T\theta (c^2{\rho }^2+\rho )}{{(1+cp)}^2}.$$ (85)

To calculate the limiting MSE value for the MAP we work in the eigenbasis of X^T X. This allows us to take advantage of the Marchenko-Pastur law (Marchenko and Pastur 1967) which states that in the limit N, p → ∞ but $\frac{p}{N}$ remains finite, the eigenvalues of $\frac{X^{T}X}{N}$ converge to a continuous random variable with known distribution. We denote the matrix of eigenvectors of X^T X by O:

$$X^{T}X=OL{O}^T,$$ (86)

with the diagonal matrix L containing the eigenvalues of X^T X.

Evaluating the first and last term in the MAP MSE Eq. (70) leads to the result

$${\Vert \left(\mathbf{E}\left[{\tilde{S}}^{-1}{X}^{T}X\right]-I\right)\theta \Vert }_2^2+\mathbf{tr}\left(\mathrm{Cov}\left({\tilde{S}}^{-1}{X}^{T}X\theta \right)\right)$$ (87)

To evaluate the last term in the above equation, first note that

$${\tilde{S}}^{-1}{X}^{T}X\theta =O{(L+cpI)}^{-1}L{O}^T\theta .$$ (88)

Abbreviate D = (L + cpI)⁻¹L, for convenience. Now we have

$$\mathbf{E}\left[{\Vert {\tilde{S}}^{-1}{X}^{T}X\theta \Vert }_2^2\right]={\theta }^T\mathbf{E}\left[O{D}^2{O}^T\right]\theta$$ (89)

$$=\mathbf{E}\left[{\theta }^{T}O{D}^2{O}^T\theta \right]$$ (90)

$$=\mathbf{E}\left[\mathbf{tr}\left(D^2{O}^T\theta {\theta }^{T}O\right)\right]$$ (91)

$$=\mathbf{tr}\mathbf{E}\left[D^2{O}^T\theta {\theta }^{T}O\right]$$ (92)

$$=\mathbf{tr}\mathbf{E}\left[D^2\mathbf{E}\left[O^T\theta {\theta }^{T}O\mid D\right]\right]$$ (93)

In the last line we have used the law of total expectation. Since the vector O^T θ is uniformly distributed on the sphere ${\Vert \theta \Vert }_2^2$. given L, $\mathbf{E}[O^T\theta {\theta }^{T}O\mid D]=\frac{{\Vert \theta \Vert }_2^2}{p}\mathbf{I}$. Thus

$$\mathbf{E}\left[{\Vert {\tilde{S}}^{-1}{X}^{T}X\theta \Vert }_2^2\right]=\frac{{\Vert \theta \Vert }_2^2}{p}\mathbf{tr}\left(\mathbf{E}\left[{\left({(L+cpI)}^{-1}L\right)}^2\right]\right).$$ (94)

We can use similar arguments to calculate the second term in Eq. (87).

$$\mathbf{E}\left[{\theta }^T{\tilde{S}}^{-1}{X}^{T}X\theta \right]=\mathbf{E}\left[{\theta }^{T}OD{O}^T\theta \right]$$ (95)

$$=\mathbf{tr}\mathbf{E}\left[D\right]\frac{{\Vert \theta \Vert }_2^2}{p}$$ (96)

Substituting this result and Eq. (94) into Eq. (87) we find

$${\Vert \left(\mathbf{E}\left[{\tilde{S}}^{-1}{X}^{T}X\right]-I\right)\theta \Vert }_2^2+\mathbf{tr}\left(\mathrm{Cov}\left({\tilde{S}}^{-1}{X}^{T}X\theta \right)\right)={\Vert \theta \Vert }_2^2-2\mathbf{tr}\mathbf{E}\left[D\right]\frac{{\Vert \theta \Vert }_2^2}{p}+\frac{{\Vert \theta \Vert }_2^2}{p}\mathbf{trE}\left[D^2\right]$$ (97)

$$=\frac{{\Vert \theta \Vert }_2^2}{p}\mathbf{E}\left[\mathbf{tr}{(D-\mathbf{I})}^2\right]$$ (98)

$$=\frac{{\Vert \theta \Vert }_2^2}{p}\mathbf{E}\left[\mathbf{tr}\left({(L+cpI)}^{-1}{L-\mathbf{I})}^2\right)\right].$$ (99)

Using the result given above and noting that $\mathbf{tr}\left(\mathbf{E}\left[{\tilde{S}}^{-1}{X}^{T}X{\tilde{S}}^{-1}\right]\right)=\mathbf{tr}\left(\mathbf{E}\left[{(L+cp\mathbf{I})}^{-2}L\right]\right)$, the MAP MSE can be written as

$$\mathbf{E}\left[{\Vert {\widehat{\theta }}_{MAP}-\theta \Vert }_2^2\right]=\mathbf{tr}\left(\mathbf{E}\left[{(L+cp\mathbf{I})}^{-2}L\right]\right)+\frac{{\Vert \theta \Vert }_2^2}{p}\mathbf{E}\left[\mathbf{tr}\left({(L+cpI)}^{-1}{L-\mathbf{I})}^2\right)\right].$$ (100)

Taking the limit N, p → ∞ with $\frac{p}{N}$ finite,

$$\mathbf{E}\left[{\Vert {\widehat{\theta }}_{MAP}-\theta \Vert }_2^2\right]\to \rho \mathbf{E}\left[\frac{l}{{(l+cp)}^2}\right]+{\Vert \theta \Vert }_2^2\mathbf{E}\left[{\left(\frac{l}{(l+cp)}-1\right)}^2\right].$$ (101)

where l is a continuous random variable with probability density function $\frac{d\mu }{dl}$ found by the Marchecko-Pastur law

$$\frac{d\mu }{dl}=\frac{1}{2\pi l\rho }\sqrt{(b-l)(l-a)}{\mathcal{I}}_{[a,b]}\left(l\right)$$ (102)

$$a\left(\rho \right)={(1-\sqrt{\rho })}^2$$ (103)

$$b\left(\rho \right)={(1+\sqrt{\rho })}^2.$$ (104)

Using Eq. (102) we can numerically evaluate the limiting MAP MSE. The results are plotted in Fig. 2.

Figure 7 evaluates the accuracy of these limiting approximations for finite N and p. For the range of N and p. For the range of N and p used in our real data analysis $(\frac{p}{N}\sim 0.01,N\sim 10000)$, the approximation is valid.

A.2 Computing the MPELE for an LNP model with Gaussian stimuli

The MPELE is given by the solution of Eq. (30), which in this case is

$${\widehat{\theta }}_{\mathrm{MPELE}}=\arg \underset{\theta ,{\theta }_0}{\max }{\theta }_0\sum _{n=1}^N{r}_n+{\left(X\theta \right)}^{T}r-N\mathbf{E}\left[\exp \left({\theta }_0\right)\exp \left(x^T\theta \right)\right]-\log f\left(\theta \right).$$ (105)

Since xθ is Normally distributed, xθ ~ N (0, θ^T Cθ), we can analytically calculate the expectation, yielding

$${\widehat{\theta }}_{\mathrm{MPELE}}=\arg \underset{\theta ,{\theta }_0}{\max }{\theta }_0\sum _{n=1}^N{r}_n+{\left(X\theta \right)}^{T}r-N\exp \left({\theta }_0\right)\exp \left(\frac{{\theta }^{T}C\theta }{2}\right)-\log f\left(\theta \right).$$ (106)

Optimizing with respect to θ₀ we find

$$\exp \left({\theta }_0^{\ast }\right)=\frac{{\sum }_{n=1}^N{r}_n}{N}\exp \left(-\frac{{\theta }^{T}C\theta }{2}\right).$$ (107)

Inserting ${\theta }_0^{\ast }$ into Eq. (106) leaves the following quadratic optimization problem

$${\widehat{\theta }}_{\mathrm{MPELE}}=\arg \underset{\theta }{\max }-\frac{{\theta }^T\left(C{\sum }_{n=1}^N{r}_n\right)\theta }{2}+{\theta }^T{X}^{T}r-\log f\left(\theta \right).$$ (108)

Note that the first two terms here are quadratic; i.e., the EL-approximate profile likelihood is Gaussian in this case. If we use a Gaussian prior, f (θ) ∝ exp(θ^T Rθ/2), we can optimize for ${\widehat{\theta }}_{\mathrm{MPELE}}$ analytically to obtain Eq. (31).

A.3 Calculating R̂ for the LNP model

For the LNP model with E [G(x^T θ) approximated as in Eq. (16) and f (θ|R) = N (0, R⁻¹), the Laplace approximation (52) to the marginal likelihood yields

$$\log F\left(R\right)\approx \sum _{n=1}^N{\widehat{\theta }}_0^{\ast }{r}_n+{\left(X{\widehat{\theta }}_{\mathrm{MPELE}}\right)}^{T}r-N\Delta t\exp \left({\widehat{\theta }}_0^{\ast }\right)\exp \left(\frac{{\left({\widehat{\theta }}_{\mathrm{MPELE}}\right)}^{T}C{\widehat{\theta }}_{\mathrm{MPELE}}}{2}\right)+\log \left(f({\widehat{\theta }}_{\mathrm{MPELE}}\mid R)\right)-\frac{1}{2}\log \left(\det (-H\left({\widehat{\theta }}_{\mathrm{MPELE}}\right))\right)$$ (109)

$$=-\frac{{\left({\widehat{\theta }}_{\mathrm{MPELE}}\right)}^{T}C{\widehat{\theta }}_{\mathrm{MPELE}}}{2}\sum _{n=1}^N{r}_n+{\left(X{\widehat{\theta }}_{\mathrm{MPELE}}\right)}^{T}r-\frac{{\left({\widehat{\theta }}_{\mathrm{MPELE}}\right)}^{T}R{\widehat{\theta }}_{\mathrm{MPELE}}}{2}+\frac{1}{2}\log \left(\det \left(R\right)\right)-\frac{1}{2}\log \left(\det (-H\left({\widehat{\theta }}_{\mathrm{MPELE}}\right))\right)$$ (110)

$$=-\frac{{\left({\widehat{\theta }}_{\mathrm{MPELE}}\right)}^T(C{N}_s+R){\widehat{\theta }}_{\mathrm{MPELE}}}{2}+{\left(X{\widehat{\theta }}_{\mathrm{MPELE}}\right)}^{T}r+\frac{1}{2}\log \left(\det \left(R\right)\right)-\frac{1}{2}\log \left(\det (-H\left({\widehat{\theta }}_{\mathrm{MPELE}}\right))\right),$$ (111)

where the second line follows from substituting in Eq. (107) and we have denoted ${\sum }_{n=1}^N{r}_n$ as N_s in the third line. Note that from the definition of the L2 regularized MPELE Eq. (31) we can write

$$X^{T}r=(C{N}_s+R){\widehat{\theta }}_{\mathrm{MPELE}},$$ (112)

and simplify the first two terms

$$-\frac{{\left({\widehat{\theta }}_{\mathrm{MPELE}}\right)}^T(C{N}_s+R){\widehat{\theta }}_{\mathrm{MPELE}}}{2}+{\left(X{\widehat{\theta }}_{\mathrm{MPELE}}\right)}^{T}r=\frac{{\left({\widehat{\theta }}_{\mathrm{MPELE}}\right)}^T(C{N}_s+R){\widehat{\theta }}_{\mathrm{MPELE}}}{2}=\frac{{\left(X^{T}r\right)}^T{(C{N}_s+R)}^{-1}{X}^{T}r}{2}.$$ (113)

Noting that C I, R = βI Eq. (113) simplifies further to $\frac{1}{2}$ (N + β)⁻¹ q with q ≡ ${\Vert X^{T}r\Vert }_2^2$. Using the fact that the profile Hessian is $-H\left({\widehat{\theta }}_{\mathrm{MPELE}}\right)=C{N}_s+R$ and the assumptions C I, R = βI the last two terms in Eq. (111) reduce to

$$\frac{1}{2}\log \left(\det \left(R\right)\right)-\frac{1}{2}\log \left(\det (-H\left({\widehat{\theta }}_{\mathrm{MPELE}}\right))\right)=\frac{p}{2}\log \left(\beta \right)-\frac{p}{2}\log (N_s+\beta ).$$ (114)

Combining these results we find

$$\log F\left(R\right)\approx \frac{1}{2}{(N_s+\beta )}^{-1}q+\frac{p}{2}\log \left(\beta \right)-\frac{p}{2}\log (N_s+\beta ).$$ (115)

Taking the derivative of Eq. (115) with respect to β we find that the critical points, ${\widehat{\beta }}_c$ obey

$$0=-\frac{q}{{(N_s+{\widehat{\beta }}_c)}^2}+p\frac{N_s}{(N_s+{\widehat{\beta }}_c){\widehat{\beta }}_c},$$ (116)

$${\widehat{\beta }}_c=\left(\frac{N_s^{2}p}{q-p{N}_s},\infty \right).$$ (117)

If $p\ge \frac{q}{N_s}$, the only critical points is ∞ β is constrained to be positive. When $p<\frac{q}{N_s}$, the critical point ${\widehat{\beta }}_c=\frac{p}{\frac{q}{N_s^2}-\frac{p}{N_s}}$ is the maximum since log F Eq. (115) evaluated at this point is greater than log F evaluated at ∞:

$$\begin{array}{cc}\hfill \log F\left(\frac{N_s^{2}p}{q-p{N}_s}\right)=& \frac{1}{2}\left(\frac{q}{N_s}-p+p\log \left(\frac{p}{q}{N}_s\right)\right)\ge 0\hfill \\ \hfill =& \underset{\beta \to \infty }{\lim }\log F.\hfill \end{array}$$ (118)

Therefore R̂ satisfies Eq. (54) in the text.

We can derive similar results for a more general case if C and R are diagonalized by the same basis. If we denote this basis by M, we then have the property that the profile Hessian CN_s + R = M(D^cN_s + D^r)M^T where D^c and D^r are diagonal matrices containing the eigenvalues of C and R. In this case the last two terms of Eq. (111) reduce to

$$\frac{1}{2}\log \left(\det \left(R\right)\right)-\frac{1}{2}\log \left(\det (-H\left({\widehat{\theta }}_{\mathrm{MPELE}}\right))\right)=\frac{1}{2}\sum _{i=1}^p\log \left(\frac{D_{il}^r}{D_{ii}^c{N}_s+D_{ii}^r}\right).$$ (119)

Defining X^T r rotated in the coordinate system specified by M as $\tilde{q}=M^T{X}^{T}r$, Eq. (113) simplifies to

$$\frac{{\left(X^{T}r\right)}^T{(C{N}_s+R)}^{-1}{X}^{T}r}{2}=\frac{1}{2}\sum _{i=1}^p{\tilde{q}}_i^2{(D_{ii}^c{N}_s+D_{ii}^r)}^{-1}.$$ (120)

Combining terms we find

$$\log F\left(R\right)\approx \frac{1}{2}\left(\sum _{i=1}^p{\tilde{q}}_i^2{(D_{ii}^c{N}_s+D_{ii}^c)}^{-1}+\log \left(\frac{D_{ii}^r}{D_{ii}^c{N}_s+D_{ii}^r}\right)\right).$$ (121)

Taking the gradient of the above equation with respect to the eigenvalues of R, $D_{jj}^{r\ast }$, we find that the critical points obey

$$0=-\frac{{\tilde{q}}_j^2}{{\left(D_{jj}^c{N}_s+D_{jj}^{r^{\ast }}\right)}^2}+\frac{D_{jj}^c{N}_s}{D_{jj}^{r\ast }\left(D_{jj}^c{N}_s+D_{jj}^{r\ast }\right)}$$ (122)

$$D_{jj}^{r\ast }=\left(\frac{{\left(D_{jj}^c{N}^s\right)}^2}{{\tilde{q}}_j^2-D_{jj}^c{N}_s},\infty \right).$$ (123)

If $D_{jj}^c{N}_s\ge {\tilde{q}}_j^2$, the only critical point is ∞ since $D_{jj}^{r\ast }$ is constrained to be positive (R is constrained to be positive definite).

A.4 Real neuronal data details

Stimuli are refreshed at a rate of 120 Hz and responses are binned at this rate (Fig. 3) or at 10 times (Fig. 4) this rate. Stimulus receptive fields are fit with 81 (Fig. 3) or 25 (Fig. 4) spatial components and ten temporal basis functions, giving a total of 81×10 = 810 or 25 × 10=250 stimulus filter parameters. Five basis functions×are=delta functions with peaks centered at the first 5 temporal lags while the remaining 5 are raised cosine ‘bump’ functions (Pillow et al. 2008). The self-history filter shown in Fig. 4 is parameterized by 4 cosine ‘bump’ functions and a refractory function that is negative for the first stimulus time bin and zero otherwise. The coupling coefficient temporal components are modeled with a decaying exponential of the form, exp (−bτ), with b set to a value which captures the time-scale of cross-correlations seen in the data. The errorbars of the spike-history functions in Fig. 4a show an estimate of the variance of spike-history function estimates. These are found by first estimating the covariance of the spike-history basis coefficients. Since the L1 penalty is non-differentiable we estimate this covariance matrix using the inverse log-likelihood Hessian of a model without coupling terms, say $H_0^{-1}$, evaluated at the MAP and MPELE solutions, which are found using the full model that assumes non-zero coupling weights. The covariance matrix of the spike-history functions are then computed using the standard formula for the covariance matrix of a linearly transformed variable. Denoting the transformation matrix from spike-history coefficients to spike-history functions as B, the covariance of spike-history function estimates is $B^T{H}_0^{-1}$. Figure 4 plots elements off the diagonal of this matrix. We use the activity of 100 neighboring cells yielding a total of 100 coupling coefficient parameters, 5 self-history parameters, 250 stimulus parameters, and 1 offset parameter (356 parameters in total). The regularization coefficients used in Fig. 3b and 4 are found via cross-validation on a novel two minute (14,418 samples) data set. Model performance is evaluated using 2 minutes of data not used for determining model parameters or regularization coefficients. To report the log-likelihood in bits per second, we take the difference of the log-likelihood under the model and log-likelihood under a homogeneous Poisson process, divided by the total time.

The covariance of the correlated stimuli was spatiotemporally separable, leading to a Kronecker form for C. The temporal covariance was given by a stationary AR(1) process; therefore this component has a tridiagonal inverse (Paninski et al. 2009). The spatial covariance was diagonal in the two-dimensional Fourier basis. We were therefore able to expoit fast Fourier and banded matrix techniques in our computations involving C.