Abstract
Förster resonance energy transfer (FRET) techniques have proven invaluable for probing the complex nature of protein–protein interactions, protein folding, and intracellular signaling events. These techniques have traditionally been implemented with the use of one or more fluorescence band-pass filters, either as fluorescence microscopy filter cubes, or as dichroic mirrors and band-pass filters in flow cytometry. In addition, new approaches for measuring FRET, such as fluorescence lifetime and acceptor photobleaching, have been developed. Hyperspectral techniques for imaging and flow cytometry have also shown to be promising for performing FRET measurements. In this study, we have compared traditional (filter-based) FRET approaches to three spectral-based approaches: the ratio of acceptor-to-donor peak emission, linear spectral unmixing, and linear spectral unmixing with a correction for direct acceptor excitation. All methods are estimates of FRET efficiency, except for one-filter set and three-filter set FRET indices, which are included for consistency with prior literature. In the first part of this study, spectrofluorimetric data were collected from a CFP–Epac–YFP FRET probe that has been used for intracellular cAMP measurements. All comparisons were performed using the same spectrofluorimetric datasets as input data, to provide a relevant comparison. Linear spectral unmixing resulted in measurements with the lowest coefficient of variation (0.10) as well as accurate fits using the Hill equation. FRET efficiency methods produced coefficients of variation of less than 0.20, while FRET indices produced coefficients of variation greater than 8.00. These results demonstrate that spectral FRET measurements provide improved response over standard, filter-based measurements. Using spectral approaches, single-cell measurements were conducted through hyperspectral confocal microscopy, linear unmixing, and cell segmentation with quantitative image analysis. Results from these studies confirmed that spectral imaging is effective for measuring subcellular, time-dependent FRET dynamics and that additional fluorescent signals can be readily separated from FRET signals, enabling multilabel studies of molecular interactions.
Key terms: CFP, YFP, Epac, cAMP, spectroscopy, hyperspectral, microscopy, imaging, flow cytometry
Over the past century, fluorescence labeling has emerged as a standard technique for the study of proteins in the intracellular environment. Förster resonance energy transfer (FRET), a specialized fluorescence labeling technique utilizing two fluorophores, has been especially advantageous in the study of intracellular protein–protein interactions. The advent of fluorescent protein mutants has greatly increased the utility of FRET assays in live-cell and even whole tissue studies.
FRET assays are currently widely used in the biosciences, as evidenced by the many methodological and review articles describing the implementation of FRET assays. Despite this, FRET assays remain sophisticated techniques, both from biological experimentation and equipment instrumentation perspectives (1,2). While traditional techniques for measuring FRET involved two- or three-color microscopy or flow cytometry experiments, newer techniques have focused on other attributes of FRET, such as fluorescence lifetime (3), acceptor photobleaching (4), and two-photon excitation FRET (5). Some of these methods have been shown to be effective at circumventing the detector cross-talk, fluorophore concentration sensitivity, and photobleaching sensitivity present in multicolor FRET assays. However, these more sophisticated techniques also have limitations. For example, the fluorescence lifetime of fluorescent proteins is sensitive to the local refractive index (6) and can become difficult to implement in multifluor scenarios or tissues with high auto-fluorescence contributions. In addition, acceptor photobleaching can be prohibitive in time-lapse live-cell assays (2). For these reasons, traditional multicolor FRET techniques remain common, and are sometimes the only possible technique that can be implemented, especially for live-cell dynamic studies.
A viable alternative for improving the accuracy of two-and three-color FRET assays is to increase the number of bands sampled through spectral techniques. Commercial instruments are now available for performing spectral fluorescence microscopy (7,8) or spectral flow cytometry (9). With appropriate analytical techniques, spectral instruments inherently account for the spectral cross-talk present in two- or three-color FRET techniques, and should allow FRET measurements to be performed within the context of complex mixtures of fluorophores or autofluorescent tissues. Although spectral measurement techniques for FRET have been proposed (9,10) and initially tested (11), the effectiveness of spectral FRET measurements, in comparison to traditional two-and three-color FRET measurements, has not been quantitatively assessed.
The purpose of this study is to compare the effectiveness of traditional fluorescence filter set methods to spectroscopic and spectral imaging methods for estimating FRET response. We used a CFP–Epac–YFP fusion protein for the FRET probe, in which Epac is a cAMP-binding protein, and CFP–YFP FRET decreases with cAMP binding (12). This and similar probes have been characterized in several other studies (12–16), and should be representative of a range of common fluorescent protein-based FRET probes. The sensitivity of each FRET method to subtle changes in FRET efficiency was measured using cAMP concentration-response in lysed cells. Donor-only and acceptor-only trials were used as photobleaching controls. This study presents the FRET response under actual experimental (nonidealized) conditions for a range of FRET levels (not simply on–off). High wavelength-resolution spectrofluorimetry scans were performed, and data were subsequently resampled to model measurements conducted using traditional fluorescence microscope filter set measurements. This approach allows realistic comparisons between very different FRET analysis methods, as the starting point for each method is the same dataset. This approach was then used with hyperspectral confocal microscopy and quantitative image analysis to demonstrate the effectiveness of spectral unmixing for quantitatively identifying multiple fluorophores in FRET studies. With appropriate labeling techniques and spectral detection hardware, this approach is extendable to many fluorophores, on either microscopy or flow cytometry platforms.
Materials and Methods
Cell Culture and Fluorescent Protein Expression
Culture of HEK-293 cells was performed as described previously (17). Briefly, HEK-293 cells were maintained in 10 mL of Minimal Essential Medium (MEM, Life Technologies Inc., Grand Island, NY) containing 10% v/v fetal bovine serum (Gemini Bio-Products, West Sacramento, CA), and grown in 100-mm culture dishes at 37°C in a humidified atmosphere of 95% air, 5% CO2.
For spectrofluorimetric experiments, cells were plated at ∼60% confluence in 100-mm dishes for transfection with fluorescent protein-encoding constructs. Cells were transfected with constructs encoding either CFP, YFP, or the CFP–Epac– YFP probe (12) using the Fugene6 reagent (Promega, Madison, WI) as described in the manufacturer's instructions with 10 μg cDNA and 18 μL Fugene6 reagent per 100 mm dish. Forty-eight hours posttransfection, cells were detached with phosphate-buffered saline containing 0.03% EDTA, resuspended in a standard extracellular buffer containing (mM): 145 NaCl, 4 KCl, 10 HEPES, 10 d-glucose, 1 MgCl2, 1 CaCl2, pH 7.4. Cells were maintained at room temperature, 20–22° C, and assayed within 4 h. All reagents were purchased from Sigma-Aldrich (St. Louis, MO), unless otherwise stated.
For microscopy experiments, cells were plated at ∼60% confluence onto 30-mm round coverslips in six-well plates. Cells were transfected as described above, except that 1 μg cDNA and 3 μL Fugene6 reagent were used per well. Fortyeight hours posttransfection, coverslips were placed in an imaging chamber, bathed with 2.8 mL of extracellular buffer (as described above) and imaged. Selected coverslips were allowed to incubate with 2.4 μg/mL Hoechst 33342 (Invitrogen Life Sciences) for 20 min prior to imaging to visualize nuclei.
Spectrofluorimetry
All spectrofluorimetric experiments were conducted using a Quanta Master 40 (Photon Technology International, Birmingham, NJ) spectrofluorimeter. Immediately prior to spectrofluorimetry, cells were lysed using 20 strokes of a dounce. Cell lysate was placed in 1-cm square plastic cuvettes. Spectra were acquired using a dwell time of 0.05 ms per wavelength, 1 nm wavelength spacing, and averaging 20 scans for the final spectrum. A cAMP dose-response was assessed by adding cAMP to achieve the following concentrations: 0, 0.2, 0.5, 1, 2, 5, 10, 20, and 50 μM. For each trial, the fluorescence emission spectrum was acquired first at 415 nm excitation (450–650 nm emission) and then at 505 nm excitation (520–650 nm emission). At 415 nm, the CFP (donor) excitation efficiency is 63% of its peak value, while the YFP (acceptor) excitation efficiency is 0.5% of its peak value. Hence, the fluorescence emission spectrum at 415 nm excitation corresponds to the sum of CFP emission from direct CFP excitation and YFP emission from FRET, with negligible direct excitation of YFP (note that the three-filter set and the corrected spectral FRET indices still attempt to account for direct acceptor excitation, as shown below). At 505 nm excitation, the CFP excitation efficiency is 4% of its peak value, while the YFP excitation efficiency is 75% of its peak value. Hence, the fluorescence emission spectrum at 505 nm excitation primarily represents YFP emission from direct YFP excitation. The spectra of CFP-only and YFP-only were also measured. Additional controls were also conducted to measure CFP and YFP photobleaching. At least three trials were conducted for each experimental condition.
Confocal Microscopy
All microscopy experiments were performed using an inverted spectral confocal microscope (A1R, Nikon Instruments, Inc.) equipped with a 40× oil immersion objective with a numerical aperture of 1.3 (40× Oil DIC H N2, Nikon Instruments, Inc.). Images were acquired using 405 nm excitation and hyperspectral emission from 432 to 606 nm, in 6 nm increments (30 wavelength bands). All FRET images and experimental controls were acquired using a laser power of 12.0 (A.U.), a constant photomultiplier voltage, a confocal pinhole of 4.9 Airy disc units, a scan size of 512 × 512, a scan speed of 1/2 (A.U.), and four frames averaged per image. Due to the very weak excitation of YFP at 405 nm, the image of YFP-transfected cells used for the pure spectrum of YFP was acquired using a laser power of 100, a pixel dwell time of 4.8 μs, and an averaging of 16 frames per image.
Time course experiments were conducted for 10 min, with images acquired at 10-s intervals. For FRET experiments, cells were treated with 10 μM forskolin and 10 μM rolipram or vehicle control (buffer) after 30 s. For CFP and YFP photobleaching controls, cells were treated with 10 μM forskolin and 10 μM rolipram after 30 s.
Spectrofluorimetry Analysis
Fluorescence emission spectra were processed using a custom script written in MATLAB (The MathWorks, Natick, MA). Six FRET analysis techniques were simulated: one fluorescence filter set, two fluorescence filter sets, three fluorescence filter sets, three fluorescence filter sets corrected for donor concentration, acceptor–donor peak intensity ratio, and linear spectral ummixing. To simulate traditional fluorescence microscopy results (one, two, and three filter sets), the fluorescence emission spectrum was multiplied by the corresponding dichroic beamsplitter and emission filter transmission spectra, as described below. Calculations for one, two, and three filter set methods were performed using approaches similar to those presented in Gordon, et al. (1998) (1). The nomenclature for variables is redefined for clarity. A common spectroscopy approach, the acceptor-to-donor peak emission ratio was also calculated. Finally, a linear unmixing approach was implemented to simulate hyperspectral microscopy techniques. The FRET efficiency (18) was calculated for each approach except for the one-filter set approach. Each method is described in detail below.
One filter set
For evaluation of the one-filter set approach, a standard CFP–YFP FRET filter set (49052 ET–ECFP/EYFP FRET, Chroma Technology Corp., Bellows Falls, VT) was convolved with the emission spectrum using 415-nm excitation. The integrated area of the convolved spectrum, Ff, was calculated. Ff represents the measured signal due to sensitized acceptor emission, but also may include nonnegligible cross-talk from emission of the donor or nonsensitized emission of the acceptor (due to direct excitation). In addition, this measure does not account for changes in donor or acceptor concentration, photobleaching, or stoichiometry. As others have shown that one-filter set estimates of the FRET efficiency can be highly inaccurate (1,2), the integrated area was used only as a FRET index. The average emission spectrum for CFP and YFP was also convolved with the FRET beamsplitter and emission filter and the integrated areas were calculated as Fd and Fa, respectively. No further correction was made.
Two filter set
For evaluation of the two-filter set approach, a CFP filter set (49001 ET–ECFP, Chroma Technology Corp.) was convolved with the emission spectrum using 415-nm excitation. The integrated area was used as the total signal measured from the donor filter set, Df. The average CFP and YFP emission spectra were also convolved with the donor filter set to yield Dd and Da, respectively. The FRET filter set was also used, as described in the one-filter set method. The FRET efficiency was calculated, using the method similar to Gordon, et al. (1998) (1), which is summarized below.
A general coefficient describing the ratio of donor-to-acceptor quantum yield and optical transmission was calculated as:
| (1) |
where QYa and QYd are the quantum yield of the acceptor and donor, respectively; ϕaand ϕd are the percent of the acceptor or donor signal transmitted by the acceptor or donor emission filter, respectively; and TF and TD represent neutral density filters and were assumed to be 1.
Cross-talk terms for the two-filter set approach were calculated as:
| (2) |
| (3) |
| (4) |
| (5) |
The third cross-talk coefficient, , is not a true cross-talk term, but instead attempts to quantify the amount of donor and direct (nonstimulated) acceptor emission that is present in measurements made with the FRET filter set as a function of donor and acceptor emission using the donor filter set. Similarly, the fourth cross-talk coefficient, , is not a true measure of cross-talk but instead tries to account for the amount of direct (nonstimulated) acceptor emission in the donor filter set as a function of donor emission. It is only valid to use these terms when donor and acceptor stoichiometry is fixed.
Using the two-filter set approach, the FRET efficiency was calculated as:
| (6) |
where SEcorr is the acceptor sensitized emission and UNQUEcorr is the unquenched donor emission. SEcorr was calculated as:
| (7) |
where SE represents the sensitized acceptor emission (that may also include acceptor emission from direct acceptor excitation) and is defined as Ff for the two-filter set approach; and DE represents the acceptor emission from direct (nonstimulated) excitation. In the case of the two-filter set approach, it is not possible to make a direct measurement of the nonstimulated acceptor emission, hence DE is estimated using a cross-talk term that attempts to quantify the sum of donor and nonstimulated acceptor emission measured using the FRET filter set as a function of donor and acceptor emission measured using the donor filter set:
| (8) |
where QUE is the quenched donor emission (also known as Df).
UNQUEcorr is defined by adding back a portion of the sensitized acceptor emission to the quenched donor signal (QUE):
| (9) |
Three filter set
For evaluation of the three-filter set approach we made use of the FRET and donor filter sets, as described above, as well as the acceptor filter set. For the acceptor filter set, a YFP filter set (49003 ET–EYFP, Chroma Technology Corp.) was convolved with the FRET emission spectrum and the resultant spectrum was integrated to yield Af. The average CFP and YFP emission spectra were also multiplied by the acceptor filter set to yield Ad and Aa, respectively.
Cross-talk terms for the three-filter set approach were calculated as:
| (10) |
| (11) |
| (12) |
A partially corrected three-filter set FRET index was calculated, as described in Berney et al. (2003) (2):
| (13) |
where SE is the sensitized acceptor emission (measured as Ff, as described in the one-filter set section, QUE represents the quenched emission of the donor detected using the FRET filter set, and DE represents the acceptor emission from direct (nonstimulated) excitation. These can be written as:
| (14) |
| (15) |
An alternative to Eq. (13), is to further correct for changes in donor concentration (due to photobleaching, diffusion, and other kinetic phenomena). In this case, the FRET level was normalized to donor concentration, as the donor and acceptor have a one-to-one stoichiometry:
| (16) |
where SEcorr represents the sensitized emission of the acceptor, corrected for direct donor and acceptor emission and for filter cross-talk terms and UNQUEcorr represents the unquenched emission of the donor (emission that would occur if no quenching from FRET were present).
SEcorr can be defined as:
| (17) |
where QUE represents the quenched donor emission and DEcorr represents the acceptor emission from direct (nonstimulated) excitation. These can be written as:
| (18) |
| (19) |
UNQUEcorr can be defined as:
| (20) |
Peak intensities
The ratio of donor and acceptor peak emission intensities was also used to calculate the FRET efficiency. The peak fluorescence emission intensity of the acceptor (YFP, at 525 nm, represented by ) and the peak fluorescence emission intensity of the donor (CFP, at 473 nm, represented by ) were taken as single points from the spectrofluorimeter data. This was performed using the FRET emission spectra acquired at 415 nm excitation. By assuming that the peak intensities represented relative contributions of donor and acceptor, the FRET efficiency was calculated as:
| (21) |
where SE was defined as the acceptor (YFP) peak intensity measured using spectra acquired from the FRET sample, , and UNQUE was calculated as the sum of donor and acceptor peak intensities:
| (22) |
where QUE was defined as the donor (CFP) peak intensity measured using spectra from the FRET sample, , and SE was defined as above. It should be noted that this calculation assumes that the loss in donor emission due to quenching can be recovered by adding back the gain in sensitized emission of the acceptor, at the peak intensity wavelengths.
Spectral (linear) unmixing
Spectral analysis was performed by using nonnegatively constrained linear unmixing of the FRET emission spectra (415 nm excitation). The unmixing library contained the average CFP and YFP emission spectra, normalized to unity (Fig. 1A). Linear least-squares regression was performed using the lsqnonneg algorithm in MATLAB software (MathWorks, Natick, MA). The spectral FRET efficiency was then calculated as the sensitized acceptor emission, normalized to the unquenched donor:
Figure 1.
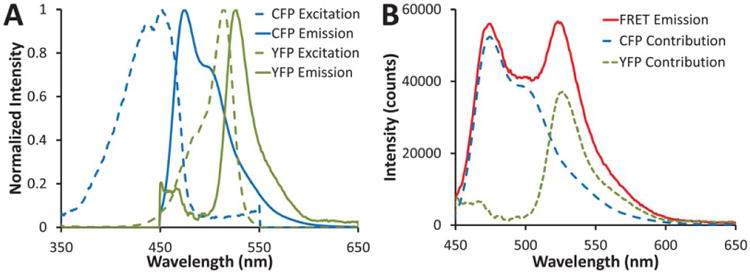
A: Excitation (dashed lines) and emission (solid lines) spectra of CFP (blue) and YFP (green), normalized to the peak intensity value. B: A typical FRET emission spectrum (red solid line) with the estimated CFP (blue long-dash line) and YFP (green short-dash line) contributions indicated. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com]
| (23) |
where SE was defined as the abundance of the acceptor (YFP) calculated from linear unmixing of the emission spectrum measured from the FRET sample, . UNQUE was calculated as the sum of donor and acceptor abundances:
| (24) |
where QUE was defined as the abundance of the donor (CFP) calculated from the FRET sample, , and SE was defined as above. It should be noted that this calculation assumes that the loss in donor emission due to quenching can be recovered by adding back the gain in sensitized emission of the acceptor.
Corrected spectral (linear) unmixing
The spectral FRET efficiency above, ESpectral, was also corrected for acceptor emission that results from direct (nonstimulated) excitation. A method similar to that used by Chen et al. (11) was applied, but modified to include an averaged ratio for acceptor emission that is insensitive of overall signal (expression) level. A cross-talk term was defined to account for acceptor emission using the donor peak excitation wavelength (415 nm) to acceptor emission using the acceptor excitation wavelength (505 nm) using linearly unmixed abundances calculated from hyperspectral images of the acceptor (YFP) only:
| (25) |
Hence, represents the fraction of the unmixed acceptor emission in a FRET study that would be due to direct acceptor excitation at the donor excitation wavelength. A corrected acceptor sensitized emission was then calculated by multiplying this ratio by the measured sensitized emission and then subtracting this product from the measured sensitized emission:
| (26) |
A corrected spectral FRET efficiency was then calculated:
| (27) |
where UNQUE was calculated as:
| (28) |
As in the case of ESpectral, it should be noted that this calculation assumes that the loss in donor emission due to quenching can be recovered by adding back the gain in sensitized emission of the acceptor. Because this calculation is similar to efficiency calculations above, we have retained the nomenclature, ESpectral Corrected.
Spectrofluorimetry Postprocessing
The mean FRET cAMP concentration-response for all trials was calculated using each of the techniques discussed above. However, each of the FRET analysis techniques yields slightly different FRET efficiencies. In addition, it is desirable to relate FRET efficiencies to specific substrate concentrations. In order to effectively compare these techniques, the mean FRET efficiency at each substrate concentration (n = 3 trials) for each technique was scaled to the minimum and maximum FRET efficiency values. After scaling, the resultant value was subtracted from one (forcing the FRET cAMP concentration-response to vary between 0 and 1 and to increase with increasing cAMP concentration). The mean dose-response was fit to a modified Hill equation:
| (29) |
where FRET is the predicted FRET response, FRET0 is the measured FRET response at 0 μM cAMP (basal), FRETN is the measured FRET response at 50 μM cAMP, A is the Hill coefficient, and EC50 is the cAMP concentration producing half of the maximum change in FRET. The mean of the absolute error was calculated as a measure of the goodness-of-fit of the Hill equation.
Confocal Microscopy Image Analysis
Confocal microscopy images were exported as 16-bit unscaled TIFF files. A spectral library was constructed by sampling spectra from CFP-transfected, YFP-transfected, or non-transfected Hoechst-labeled HEK-293 cells. Each end-member of the spectral library was normalized to a peak value of unity. Images were analyzed using a custom script incorporating a nonnegative linear least-squares unmixing algorithm (lsqnonneg, MATLAB). The root-mean-square (RMS) percent error image was calculated as the RMS residual divided by the RMS signal and was used for visual confirmation of unmixing accuracy. The unmixed CFP and YFP images were used to calculate a FRET image, as described in Eqs. (23) and (24). The unmixed CFP and YFP images were also summed to produce a total fluorescent protein (CFP+YFP) emission image used for locating positively expressing cells.
Unmixed images were quantitatively analyzed using Cell Profiler software(19). Nuclei between 8 and 30 μm diameter were identified in the unmixed Hoechst image using MoG global thresholding with an approximate area covered by nuclei of 10% and a threshold correction factor of 1.5. Positively expressing regions between 10 and 50 mm diameter were identified in the CFP+YFP image using Otsu Adaptive thresholding with a threshold correction factor of 1. Nuclei within expressing cells were then masked and subsequently propagated to estimate the borders of expressing cells using Otsu Global thresholding with a correction factor of 1 and a regularization factor of 0.5. Expressing cell cytoplasm was then identified by subtracting nuclear areas from expressing cell areas. Cytoplasm areas with a solidity ≥ 0.4 were selected for analysis. The mean cytoplasmic intensity of Hoechst, CFP, YFP, RMS percent error, CFP+YFP, and FRET efficiency was calculated for each cell and then averaged for each image in the time course. Multiple time courses were averaged for each experiment (n = 8 for FRET experiments and n = 5 for photobleaching controls) and the standard error-of-the-mean calculated.
Results
Spectrofluorimetry scans of CFP (donor) and YFP (acceptor) resulted in the expected spectra (Fig. 1A). For the spectral FRET approaches it was necessary to construct a spectral library in which each pure spectrum was measured over the same wavelength range as the experimental FRET spectra. Hence, the YFP scan in Figure 1 extends to a much lower range (450 nm) than is typically used to measure YFP emission. By measuring the fluorescence emission identically for each species, from 450 to 650 nm, it can be seen that the pure spectra for CFP and YFP can be used to very accurately account for a given FRET emission spectrum (Fig. 1B). CFP photobleaching controls displayed a decrease of 30–40% intensity in CFP emission over the time course of the experiment; whereas YFP photobleaching controls displayed negligible changes in YFP emission (Supporting Information Fig. 1).
Increasing levels of cAMP resulted in a decrease in FRET (Figs. 2 and 3). This can be confirmed by careful inspection of the emission spectra at different cAMP concentrations, verifying that when the acceptor emission decreases, the donor emission increases (Figs. 2A and 2B). There was some instrument-dependent fluctuation in total signal intensity, as evidenced by the variations in the magnitude of the spectra (Fig. 2A). We have previously observed these fluctuations to be due to mixing in the cuvette (a stir-bar and stirrer used). However, the ratio of the YFP emission to CFP emission clearly decreased with increasing cAMP (Fig. 2B). Because of this fluctuation in total signal intensity, corrected or ratiometric FRET approaches are not affected and performed substantially better than the one-filter set approach (as described below).
Figure 2.
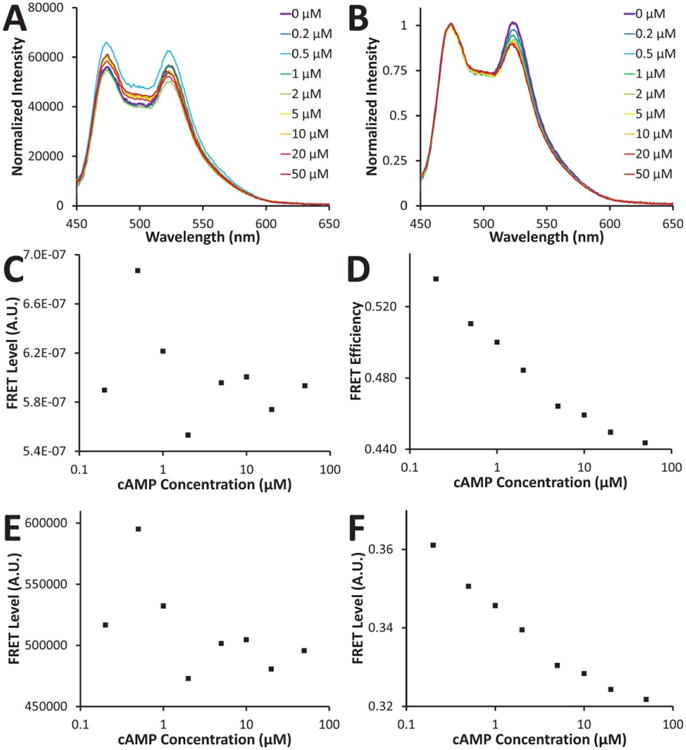
A: cAMP dose-dependence of FRET emission; B: the same data normalized to the CFP emission peak (473 nm); C: FRET response calculated using a one filter set method; D: FRET response calculated using a two filter set method; E: FRET response calculated using a three filter set method; F: FRET response calculated using a three filter set method and corrected for changes in CFP concentration. Note that panels C and E represent FRET indices, whereas panels D and F represent FRET efficiencies. Normalized FRET responses are shown in Figure 4. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com]
Figure 3.
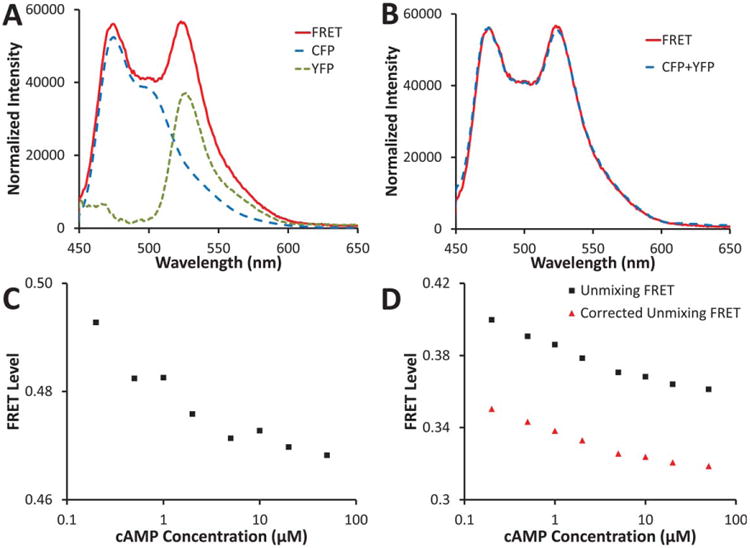
A: FRET spectrum (red solid line) for basal (0 μM) cAMP from Figure 2 showing estimated contributions of CFP (long-dash blue line) and YFP (short-dash green line) calculated using linear unmixing; B: the sum of the estimated CFP and YFP contributions (dashed blue line) very closely matches the FRET spectrum from A (solid red line); C: FRET efficiency calculated using the CFP peak intensity (473 nm) and the YFP peak intensity (525 nm); D: FRET efficiency calculated by linear unmixing, as shown in A, and dividing the CFP abundance by the CFP+YFP abundance (black squares); the linear unmixing FRET has been further corrected by estimating the percent of the acceptor signal that is due to direct excitation and then subtracting this percent from the total acceptor signal before dividing by the donor signal (red triangles), as shown in Eq. (13). Normalized FRET responses are shown in Figure 4. [Color figure can be viewed in the online issue which is available at wileyonlinelibrary.com]
One Filter Set
FRET measurements made with a single filter set produced the expected decrease in FRET with increasing cAMP concentration (Fig. 2C). However, significant fluctuations in FRET level were associated with the one-filter set method, resulting in a trend that was difficult to characterize.
Two Filter Set
The two-filter set method attempts to compensate for changes in donor concentration by normalizing to the donor emission that would be expected if no FRET were occurring [unquenched donor emission, Eq. (6)]. This compensation resulted in a dose-response curve that is significantly improved over the one-filter set method (Fig. 2D).
Three filter Set
The three-filter set analysis was performed in two ways [Eqs. (13) and (16)]. The first is a commonly used approach (1,20) that does not normalize to donor or acceptor concentration. The second approach attempts to normalize the FRET level to fluctuations in donor concentration (or photobleaching) (1). The first approach resulted in a decrease in FRET with increasing cAMP, but demonstrated significant deviations from a trend (Fig. 2E). The second approach resulted in a response that was much more consistent with the expected cAMP concentration dependence (Fig. 2F).
Peak Intensities
The effectiveness of three spectral approaches was also assessed for measuring FRET. The ratio of YFP/CFP peak intensity was measured by first measuring the CFP and YFP spectra (Fig. 3A, dotted and dashed lines), and then dividing the YFP emission peak intensity (at 525 nm) by the CFP emission peak intensity (at 473 nm). The cAMP concentration response displayed the expected decrease in FRET with increasing cAMP concentration (Fig. 3C). Some deviation from a smooth trend could be seen in the single trial.
Spectral (Linear) Unmixing
Linear unmixing was performed using mean CFP and YFP spectra (average of three trials from different days) as end-members (Fig. 3A). Due to the spectral simplicity of this two-fluorophore system, a basic least-squares linear unmixing analysis resulted in an accurate fit to the measured FRET spectra, when excited at 415 nm (Fig. 3B). The FRET efficiency was estimated as a function of CFP and YFP abundances (Fig. 3D). A single trial showed minimal deviation from a smooth trend.
Corrected Spectral (Linear) Unmixing
The corrected linear unmixing analysis was performed using the same data as the linear unmixing analysis, with the addition of an acceptor emission scan (using the acceptor excitation wavelength, 505 nm for YFP). In theory, this correction should remove the portion of the YFP emission that is due to direct excitation of YFP. In practice—for the CFP–Epac–YFP probe, which maintains a 1:1 donor-to-acceptor stoichiometry—the correction procedure simply results in lowering the FRET efficiency by a relatively constant amount (Fig. 3D). Hence, this correction may not always be necessary to perform when making spectral FRET measurements.
Comparison of FRET Measurement Techniques
To compare the sensitivity of each FRET analysis approach to experimental variations, three cAMP concentration response trials were performed. The estimated FRET level at each cAMP concentration was averaged across all trials for each FRET analysis approach. As discussed in the Materials and Methods section, results from each approach were normalized to range from between 0 and 1 and were subtracted from unity to yield a response that increases with increasing cAMP concentration (Fig. 4). The trendline indicates a fit using the Hill equation.
Figure 4.
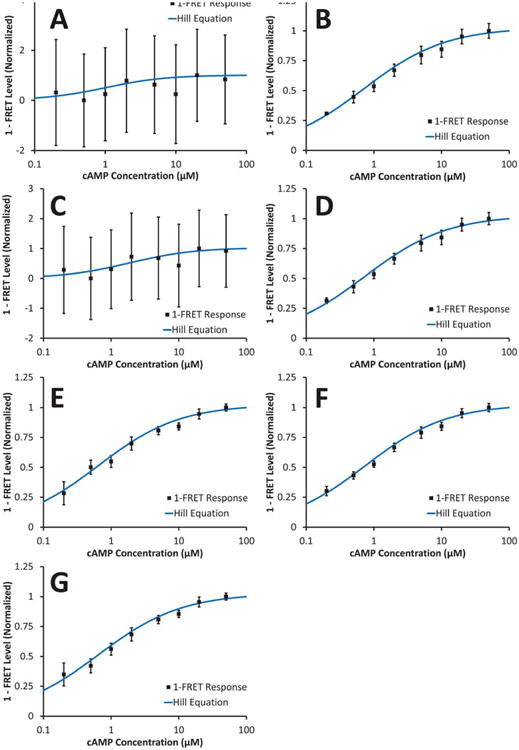
1-FRET response normalized to minimum and maximum FRET levels. Error bars indicate the standard error-of-the-mean (n = 3) for each cAMP concentration. A: one-filter set method; B: two-filter set method; C: three-filter set method; D: three-filter set method and corrected for changes in CFP concentration; E: YFP-CFP peak intensity ratio; F: linear unmixing YFP-CFP ratio; G: linear unmixing YFP-CFP ratio, corrected for direct excitation of YFP. Note that panels A and C represent FRET indices, whereas panels B, D, E, F, and G represent FRET efficiencies. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com]
The one-filter set approach demonstrated the highest variance (evidenced by the error bars indicating ± 1 standard error-of-the-mean, Fig. 4A), while the linear unmixing approach demonstrated the lowest variance (Fig. 4F). The two-filter set, three-filter set (donor concentration corrected), peak intensity, and linear unmixing approaches provided consistent fits with the Hill equation.
To assess the accuracy of each approach, fit statistics for the Hill equation were calculated, as well as the coefficient of variation (CV) of the data, averaged across all cAMP concentrations (Table 1). The linear unmixing approach provided the lowest average CV, followed by the three-filter set (corrected) approach. The three-filter set approach provided the best fit for the Hill equation, although the fit error was essentially the same as that of the linear unmixing approach. As would be expected, the poorest results were obtained with the one-filter set approach, with an average CV that was more than three-fold higher than the observed reduction in FRET at saturating (50 μM) cAMP concentration. Hence, one-filter set measurements were insufficient for identifying even saturating changes in cAMP concentration.
Table 1.
Comparison of different FRET measurement methods.
| EC50 (μM) | Hill Coefficient | Mean CV | Mean Error from Hill Equation | |
|---|---|---|---|---|
| One filter set | 0.98 | 1 | 8.43 | 0.198 |
| Two filter set | 0.65 | 0.72 | 0.13 | 0.019 |
| Three filter set uncorrected* | 1.73 | 0.89 | 18.89 | 0.140 |
| Three filter set corrected | 0.67 | 0.71 | 0.13 | 0.019 |
| Peak radio | 0.60 | 0.72 | 0.17 | 0.023 |
| Linear unmixing | 0.69 | 0.72 | 0.10 | 0.019 |
| Linear unmixing corrected | 0.60 | 0.71 | 0.16 | 0.022 |
All methods are measures of FRET efficiency except for those indicated by *, which are FRET indices that have been included as they have been used in prior literature. Linear unmixing produced the lowest coefficient of variation and second lowest error from fitting the Hill equation, while the three-filter set uncorrected method produced the highest coefficient of variation and the one-filter set method produced the highest error from fitting the Hill equation. EC50 represents the cAMP concentration required to achieve 50% of the full FRET response, CV is the coefficient of variation. n = 3 trials.
The EC50 and Hill coefficient were consistent among the two-filter set, three-filter set (corrected), peak ratio, and linear unmixing approaches. The range of values for the EC50 was 0.60–0.69 μM, while the range of values for the Hill coefficient was 0.71–0.72. These correspond with literature values for the EC50 of Epac2-camps of 0.92 μM from Nikolaev et al (12), and 1.2 μM from Blackman et al. (16). Analysis of data obtained using the one-filter set approach yielded a Hill coefficient of 1. However, this can be attributed to the overall poor fit of the data to the Hill equation. In each case initial estimate for the Hill coefficient and EC50 were 1 and 1 μM, respectively.
Confocal Microscopy Spectral Unmixing and Quantitative Image Analysis
Raw spectral image data contained contributions from Hoechst, CFP, and YFP. Images were summed to visualize total fluorescence emission (Fig. 5A). A spectral library was then constructed by measuring the average spectrum from a region of interest in single-label images: Hoechst alone, CFP alone, and YFP alone (Fig. 5B). Nonnegative linear least-squares unmixing using the spectral library resulted in effective identification of each of the end-members (Figs. 5C– 5E). The sum of the CFP and YFP images (CFP+YFP, Fig. 5F) and the FRET efficiency image (Fig. 5G) were then calculated. The RMS percent error image (Fig. 5H) was used to visually inspect the accuracy of unmixing results. Bright regions indicate a low percent of the signal is accounted for, while dark regions indicate a high percent of the signal is accounted for. As can be seen in Figure 5, H the dark regions (most signal accounted for) correspond to nuclei and highly expressing cells while the bright regions (low signal accounted for) correspond to blank regions or nonexpressing cells. Hence, high emission intensities are well accounted for using hyperspectral imaging and linear unmixing, while background noises from nonexpressing cells or blank regions are not well accounted for. Only these highly expressing cells were selected for further quantitative analysis using Cell Profiler, as described below and in the Materials and Methods section.
Figure 5.
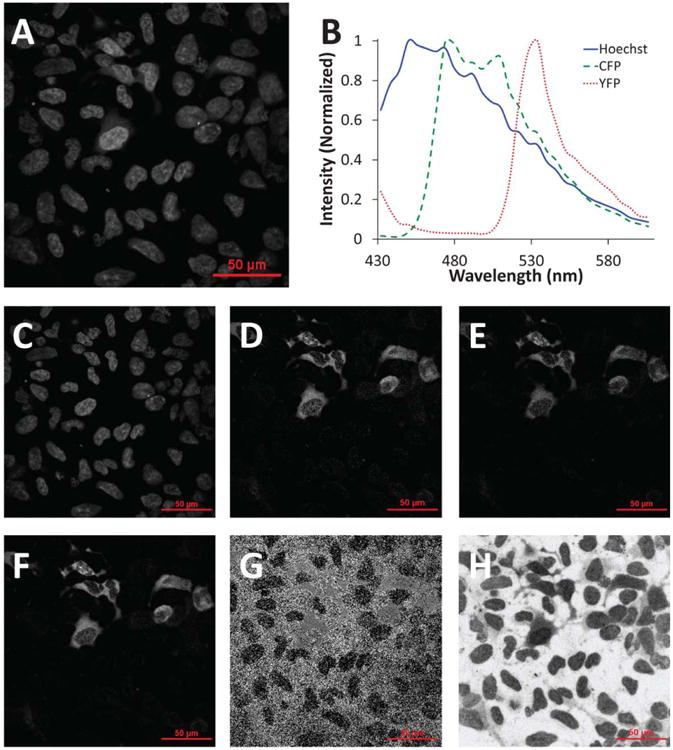
Hyperspectral confocal microscope images were unmixed to calculate fluorophore intensities and the FRET efficiency. A: Raw hyperspectral confocal microscope image (all wavelength bands summed) of HEK-293 cells expressing the CFP-Epac-YFP probe; B: the spectral library used for linear unmixing; nonnegatively constrained linear unmixing was used to calculate images for C: Hoechst, D: CFP, and E: YFP; F: the unmixed CFP and YFP images were summed to locate expressing (transfected) cells; G: the FRET efficiency was calculated using equation 23 (note that this image was later masked so that only regions with sufficient signal were used for single-cell FRET calculations, as shown in Figure 6); H: the root-mean-square (RMS) percent error associated with linear unmixing was calculated as the RMS residual from unmixing divided by the RMS signal of the original spectral image. [Color figure can be viewed in the online issue which is available at wileyonlinelibrary.com]
Linearly unmixed images were used for quantitative analysis of single-cell FRET. For each image, the nuclei were first identified (Fig. 6A). Expressing cells were then identified using propagation from the nuclei and the CFP+YFP image (Fig. 6B). The cytoplasm of expressing cells was then defined as the space between nuclei and cell borders. The FRET efficiency within the cytoplasm (Fig. 6C) was averaged for each cell and a per-image average was then calculated for each increment in the time course. The per-image average was then averaged for multiple time-courses (Fig. 6D). Cells treated with forskolin and rolipram displayed the expected decrease in FRET efficiency (due to an increase in intracellular cAMP) while cells treated with buffer displayed little or no change in FRET efficiency. CFP-alone and YFP-alone photobleaching controls were also conducted and the average CFP and YFP intensities were calculated to confirm that there was negligible photobleaching during the course of the experiment (Fig. 6E).
Figure 6.
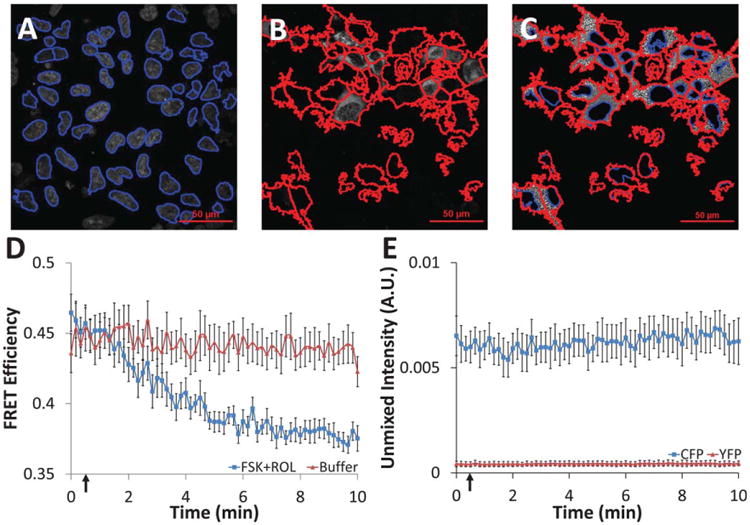
Single-cell time course data were extracted from unmixed hyperspectral confocal images using feature identification and quantification in Cell Profiler software. A: All nuclei were first identified from the unmixed Hoechst image (nuclei outlines shown in blue); B: nuclei within expressing cells were expanded to identify expressing cell borders (cell outlines shown in red); C: the area between nuclei and cell borders was labeled as expressing cell cytoplasm (nuclei shown in blue, cell borders in red, grayscale values represent FRET efficiency); mean intensity values were measured on a per-cell basis for cytoplasm regions with a solidity ≥0.4; D: administration of 10 μM forskolin (adenylyl cyclase activator) and 10 μM rolipram (phosphodiesterase inhibitor) at 30 seconds (indicated by arrow) resulted in the expected increase in cytosolic cAMP and a subsequent decrease in cytosolic FRET efficiency for cells expressing the CFP-Epac-YFP probe, while cells treated with buffer had displayed no change (average of all cells in each field of view, n = 8 fields of view, error bars are the standard error of the mean); E: CFP and YFP controls showed nonsignificant photobleaching over the time course of the experiment (average of all cells in each field of view, n = 5 fields of view, error bars are the standard error of the mean).
Discussion
There is a wide range of documented approaches for estimating energy transfer in FRET (1,2,18,21–25). Some are relatively simple (13,14,25,26), while others are complex and attempt to correct for many variables such as cross-talk and changes in concentration or photobleaching (1,2). For many investigators, the selection of a FRET analysis approach is often based on the availability of instrumentation, rather than a quantitative assessment of which method is best for a given assay. Having said this, some instrument modifications are relatively easy and inexpensive—such as the addition of a fluorescence filter cube—and if they result in improved performance, are worth pursuing. While FRET estimation is possible through imaging modes other than wavelength-dependent analysis—such as fluorescence lifetime (3,27) and acceptor photobleaching (4)—we have focused on wavelength-dependent techniques, as they correspond to the vast majority of microscopy (and flow cytometry) equipment, and as this approach enables imaging and analysis of additional fluorophores. In this article, we have acquired a representative experimental dataset based on the cAMP concentration-response of a CFP–Epac–YFP fusion protein. We have used this dataset to assess the effectiveness of several common FRET approaches—single-filter set and three-filter set FRET indices, as well as two-filter set and three-filter set FRET efficiencies—for measuring a range of energy transfer efficiencies (instead of just high and low FRET, as has been commonly reported for many studies). Assessing FRET response over a continuum of values is especially important for evaluating the dynamic range of a FRET assay and for testing the sensitivity of the FRET measurement technique, for either microscopy or flow cytometry studies. We then applied the linear unmixing approach followed by feature identification to calculate single-cell and time course averages for live-cell FRET experiments. The combination of spectral unmixing, feature identification, and quantitative image analysis allows sensitive, highly specific, quantitative, and unbiased analysis of single-cell FRET data.
To facilitate the comparison of all of the FRET approaches, each method has been normalized to vary between 0 and 1, and to increase with increasing cAMP response (corresponding to 1-normalized FRET level). The standard error for each approach has also been correspondingly normalized, allowing for effective comparisons of the dose-response and associated error for each FRET approach. It has been shown that this approach of characterizing the CFP– Epac–YFP FRET system using cell lysate and minimum and maximum FRET responses can be used to estimate the absolute cAMP concentration (13).
In this study, we have compared multiple FRET measurement approaches, starting from common experimental and control datasets. From visual comparison of all approaches (Fig. 4), it is clear that the one-filter set and three-filter set uncorrected approaches yield much higher standard errors (and poorer fits to the Hill equation) than two-filter set, three-filter set corrected, peak ratio, and linear unmixing approaches. Interestingly, one-filter set and three-filter set uncorrected approaches do not normalize to CFP emission, while the remaining approaches do. This is supported by CFP (donor) and YFP (acceptor) photobleaching controls (Supporting Information Fig. 1), which revealed a 30–40% decrease in CFP intensity over the time-course of the experiment, but negligible changes in YFP. Prior studies also indicate that normalizing to at least one of the fluorophores results in increased accuracy of FRET measurements (1,2,21). Without normalization, changes in expression level, photobleaching, or detector noise may all result in perceived changes in the FRET level, although in reality are measurement artifact. In general, measures of FRET that provide higher levels of self-correction without requiring additional measurements (such as the spectral FRET efficiency) produce accurate results while maintaining lower levels of error. In theory, the linear spectral unmixing approaches provide the highest level of self-correction, as they incorporate many wavelengths of information from a single acquisition step. For a more complete discussion of FRET error propagation, see Berney et al. (2003) (2). In support of this, there is some measure of error in the photobleaching measurements themselves (Supporting Information Fig. 1). For the CFP–Epac–YFP construct, the donor:-acceptor stoichiometry is fixed at 1:1. In this case, it should only be necessary to correct for changes in donor concentration or photobleaching (21). In summary, correcting for donor and acceptor concentrations or photobleaching is probably only advantageous in cases where there are appreciable changes in stoichiometry or differential photobleaching; in other cases, these corrections may actually increase the total error of the measurement.
In addition to commonly used fluorescence filter set approaches, we have evaluated three spectral analysis approaches: the ratio of acceptor-to-donor peak emission intensities, linear spectral unmixing, and linear spectral unmixing corrected for direct excitation of the acceptor. Each of these methods resulted in a FRET response that changed over the range of cAMP concentrations (Fig. 4). Of the FRET approaches tested, the uncorrected linear unmixing approach resulted in the lowest standard error (averaged over all cAMP concentrations) and second lowest error in fitting the Hill equation (Table 1). The corrected linear unmixing approach resulted in a higher error, likely due to the additional measurement required for correction and the error propagation during calculations (see discussion above). Because of the lower sensitivity to detector noise in any single wavelength channel, and because linear unmixing (where there are more wavelengths than fluorophores) circumvents errors from detector cross-talk, linear unmixing likely represents a robust FRET analysis approach.
Hyperspectral imaging, linear unmixing, and segmentation with quantitative image analysis present an effective approach for extracting quantitative data from multilabel FRET studies. We have used this approach to assess cytosolic cAMP kinetics. However, this approach could easily be extended to include additional fluorescent labels and/or more sophisticated image analysis routines. For example, the addition of organellar labels and colocalization algorithms could be implemented to assess the subcellular distribution of FRET signals. In addition, it should be possible to extend the two-filter set, three-filter set, and spectral imaging approaches for measuring other FRET probes or nonprobe FRET methods (such as homo- or hetero-dimerization). For assays with fixed dimerization stoichiometry, it may be possible to utilize a single fluorescence emission spectral scan to calculate FRET efficiencies. However, for cases where the donor–acceptor stoichiometry is widely variable, it will likely be necessary to sample the emission spectrum at more than one excitation wavelength. For highly labeled samples (five or more fluorophores), it may be necessary to adequately sample the excitation–emission matrix and to consider more sophisticated spectral analysis algorithms, as described below.
There are many algorithms available for analyzing spectral data. Chang (2003) provides an in-depth discussion of spectral imaging analysis techniques (28), while Keshava and Mustard present a good introduction to spectral mixing models (29). We have used linear unmixing, as it is one of the most widely used approaches for analyzing spectral microscopy (30,31)—and more recently, spectral flow cytometry (9)—data. Linear unmixing has been previously utilized for quantitative analysis of spectral two-photon microscopy of CFP and YFP mixtures (10). Here, we have demonstrated that linear unmixing can also be used to calculate FRET efficiency with a lower mean standard-error-of-the-mean than most currently used FRET measurement approaches. For systems with poor signal-to-noise characteristics, more complex mixtures of fluorophores, or unknown fluorescence contributions, it may be desirable to apply alternative unmixing or spectral analysis techniques (28,29,32,33). For example, constrained energy minimization has been shown to be a potential analysis algorithm for cases where the spectral library cannot be fully characterized but the spectra of interest are known (34). Another alternative may be to employ spectral phasor analysis, which could significantly speed up the spectral analysis process, albeit at a loss of some spectral and/or intensity information (35). Furthermore, in limited signal-to-noise systems, an unmixing algorithm that accounts for the noise characteristics of the detector may be preferable (36). Despite this, linear unmixing will likely provide satisfactory results for a range of FRET applications that are not prohibitively noise-limited or complex, as is the case in many fluorescence microscopy and flow cytometry assays. Testing of further unmixing algorithms, and their specific impact on FRET sensitivity and reproducibility, is a potential area for study that could result in improvements in FRET measurements with little or no changes in equipment configuration.
Supplementary Material
Acknowledgments
The authors would like to thank Drs. János Szöllősi, Srinivas Palanki, and Kevin West for helpful discussions on the work, and Dr. M. Conti for providing plasmids encoding CFP, YFP, and CFP-Epac-YFP, and to acknowledge support from NIH grants P01 HL066299, R01 HL094455, and S10 RR027535, NSF grant DBI-1156596, the University of South Alabama Center for Lung Biology Summer Undergraduate Research Fellowship, and the ISAC Scholar's Program.
Calculation Nomenclature
Symbol Description
- d
Donor
- A
Acceptor
- G
Correction term accounting for differences in donor and acceptor quantum yield and filter transmission efficiencies
- QYi
Quantum yield of species i
- ϕi
Percent of the signal from species i (donor or acceptor) that is transmitted by the corresponding fluorescence filter cube
- TF
Fractional transmission of any neutral density filters used in conjunction with the FRET filter cube
- TD
Fractional transmission of any neutral density filters used in conjunction with the donor filter cube
- QUE
Quenched donor emission (donor emission in the presence of quenching by energy transfer)
- UNQUE
Unquenched donor emission (donor emission that would occur with no quenching by energy transfer)
- UNQUEcorr
Unquenched donor emission, corrected for cross-talk
- SE
Sensitized acceptor emission (acceptor emission due to energy transfer from the donor)
- SEcorr
Sensitized acceptor emission, corrected for cross-talk
- DE
Direct acceptor emission (acceptor emission due to direct excitation)
- Ei
FRET efficiency, calculated using method i
- FRETi
FRET index or FRET response, calculated using method i
- Da
Emission of the acceptor only, measured using the donor filter set
- Dd
Emission of the donor only, measured using the donor filter set
- Df
Emission of the FRET pair, measured using the donor filter set
- Aa
Emission of the acceptor only, measured using the acceptor filter set
- Ad
Emission of the donor only, measured using the acceptor filter set
- Af
Emission of the FRET pair, measured using the acceptor filter set
- Fa
Emission of the acceptor only, measured using the FRET filter set
- Fd
Emission of the donor only, measured using the FRET filter set
- Ff
Emission of the FRET pair, measured using the FRET filter set
The peak fluorescence emission intensity of species i (donor or acceptor) in sample j (donor, acceptor, or FRET)
The unmixed abundance of species i (donor or acceptor) in sample j (donor, acceptor, or FRET)
Cross-talk: Ratio of donor emission measured using acceptor filter set to donor emission measured using FRET filter set
Cross-talk: Ratio of acceptor emission measured using FRET filter set to acceptor emission measured using acceptor filter set
Cross-talk: Ratio of donor emission measured using FRET filter set to donor emission measured using donor filter set
Cross-talk: Ratio of acceptor emission measured using donor filter set to acceptor emission measured using FRET filter set
Cross-talk: Ratio of acceptor emission measured using donor filter set to acceptor emission measured using acceptor filter set
Cross-talk: Ratio of donor and acceptor emission measured using FRET filter set to donor and acceptor emission measured using donor filter set
Cross-talk: Ratio of acceptor to donor emission measured using donor filter set
Cross-talk: Ratio of unmixed acceptor abundance measured using FRET excitation wavelength band to unmixed acceptor abundance measured using FRET excitation wavelength band (bands are assumed monochromatic for laser lines)
- EC50
The effective concentration at which a half-maximal response is obtained
- A
The Hill coefficient
Footnotes
Additional Supporting Information may be found in the online version of this article.
The authors have no conflict of interest to declare.
Literature Cited
- 1.Gordon GW, Berry G, Liang XH, Levine B, Herman B. Quantitative fluorescence resonance energy transfer measurements using fluorescence microscopy. Biophys J. 1998;74:2702–2713. doi: 10.1016/S0006-3495(98)77976-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Berney C, Danuser G. FRETor no FRET: A quantitative comparison. Biophys J. 2003;84:3992–4010. doi: 10.1016/S0006-3495(03)75126-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sun Y, Hays NM, Periasamy A, Davidson MW, Day RN. Monitoring protein interactions in living cells with fluorescence lifetime imaging microscopy. Imaging and Spectroscopic Analysis of Living Cells: Optical and Spectroscopic Techniques. 2012:371. doi: 10.1016/B978-0-12-391857-4.00019-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gu Y, Di W, Kelsell D, Zicha D. Quantitative fluorescence resonance energy transfer (FRET) measurement with acceptor photobleaching and spectral unmixing. J Microsc. 2004;215:162–173. doi: 10.1111/j.0022-2720.2004.01365.x. [DOI] [PubMed] [Google Scholar]
- 5.Elangovan M, Wallrabe H, Chen Y, Day RN, Barroso M, Periasamy A. Characterization of one-and two-photon excitation fluorescence resonance energy transfer microscopy. Methods. 2003;29:58–73. doi: 10.1016/s1046-2023(02)00283-9. [DOI] [PubMed] [Google Scholar]
- 6.Suhling K, Siegel J, Phillips D, French PMW, Lévêque-Fort S, Webb SED, Davis DM. Imaging the environment of green fluorescent protein. Biophys J. 2002;83:3589–3595. doi: 10.1016/S0006-3495(02)75359-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zimmermann T, Rietdorf J, Pepperkok R. Spectral imaging and its applications in live cell microscopy. FEBS Lett. 2003;546:87–92. doi: 10.1016/s0014-5793(03)00521-0. [DOI] [PubMed] [Google Scholar]
- 8.Garini Y, Young I, McNamara G. Spectral imaging: principles and applications. Cytometry A. 2006;69A:735–747. doi: 10.1002/cyto.a.20311. [DOI] [PubMed] [Google Scholar]
- 9.Goddard G, Martin JC, Naivar M, Goodwin PM, Graves SW, Habbersett R, Nolan JP, Jett JH. Single particle high resolution spectral analysis flow cytometry. Cytometry A. 2006;69A:842–851. doi: 10.1002/cyto.a.20320. [DOI] [PubMed] [Google Scholar]
- 10.Thaler C, Vogel S. Quantitative linear unmixing of CFP and YFP from spectral images acquired with two-photon excitation. Cytometry A. 2006;69A:904–911. doi: 10.1002/cyto.a.20267. [DOI] [PubMed] [Google Scholar]
- 11.Chen Y, Mauldin JP, Day RN, Periasamy A. Characterization of spectral FRET imaging microscopy for monitoring nuclear protein interactions. J Microsc. 2007;228:139–152. doi: 10.1111/j.1365-2818.2007.01838.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nikolaev VO, Büunemann M, Hein L, Hannawacker A, Lohse MJ. Novel single chain cAMP sensors for receptor-induced signal propagation. J Biol Chem. 2004;279:37215–37218. doi: 10.1074/jbc.C400302200. [DOI] [PubMed] [Google Scholar]
- 13.Börner S, Schwede F, Schlipp A, Berisha F, Calebiro D, Lohse MJ, Nikolaev VO. FRET measurements of intracellular cAMP concentrations and cAMP analog permeability in intact cells. Nat Prot. 2011;6:427–438. doi: 10.1038/nprot.2010.198. [DOI] [PubMed] [Google Scholar]
- 14.Ponsioen B, Zhao J, Riedl J, Zwartkruis F, Van Der Krogt G, Zaccolo M, Moolenaar WH, Bos JL, Jalink K. Detecting cAMP-induced Epac activation by fluorescence resonance energy transfer: Epac as a novel cAMP indicator. EMBO Rep. 2004;5:1176–1180. doi: 10.1038/sj.embor.7400290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lissandron V, Terrin A, Collini M, D'alfonso L, Chirico G, Pantano S, Zaccolo M. Improvement of a FRET-based indicator for cAMP by linker design and stabilization of donor–acceptor interaction. J Mol Biol. 2005;354:546–555. doi: 10.1016/j.jmb.2005.09.089. [DOI] [PubMed] [Google Scholar]
- 16.Blackman BE, Horner K, Heidmann J, Wang D, Richter W, Rich TC, Conti M. PDE4D and PDE4B function in distinct subcellular compartments in mouse embryonic fibroblasts. J Biol Chem. 2011;286:12590–12601. doi: 10.1074/jbc.M110.203604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rich TC, Fagan KA, Nakata H, Schaack J, Cooper DMF, Karpen JW. Cyclic nucleotide–gated channels colocalize with adenylyl cyclase in regions of restricted cAMP diffusion. J Gen Physiol. 2000;116:147–162. doi: 10.1085/jgp.116.2.147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Clegg RM. Fluorescence resonance energy transfer. Curr Opin Biotechnol. 1995;6:103–110. doi: 10.1016/0958-1669(95)80016-6. [DOI] [PubMed] [Google Scholar]
- 19.Carpenter A, Jones T, Lamprecht M, Clarke C, Kang I, Friman O, Guertin D, Chang J, Lindquist R, Moffat J. CellProfiler: image analysis software for identifying and quantifying cell phenotypes. Genome Biol. 2006;7:R100. doi: 10.1186/gb-2006-7-10-r100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Galperin E, Verkhusha VV, Sorkin A. Three-chromophore FRET microscopy to analyze multiprotein interactions in living cells. Nat Meth. 2004;1:209–217. doi: 10.1038/nmeth720. [DOI] [PubMed] [Google Scholar]
- 21.Xia Z, Liu Y. Reliable and global measurement of fluorescence resonance energy transfer using fluorescence microscopes. Biophys J. 2001;81:2395–2402. doi: 10.1016/S0006-3495(01)75886-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ishikawa-Ankerhold HC, Ankerhold R, Drummen GPC. Advanced fluorescence microscopy techniques—FRAP, FLIP, FLAP, FRET and FLIM. Molecules. 2012;17:4047–4132. doi: 10.3390/molecules17044047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lohse MJ, Nuber S, Hoffmann C. Fluorescence/bioluminescence resonance energy transfer techniques to study G-protein-coupled receptor activation and signaling. Pharmacol Rev. 2012;64:299–336. doi: 10.1124/pr.110.004309. [DOI] [PubMed] [Google Scholar]
- 24.Padilla-Parra S, Tramier M. FRET microscopy in the living cell: Different approaches, strengths and weaknesses. BioEssays. 2012;34:369–376. doi: 10.1002/bies.201100086. [DOI] [PubMed] [Google Scholar]
- 25.Zhou X, Herbst-Robinson KJ, Zhang J. Visualizing dynamic activities of signaling enzymes using genetically encodable FRET-based biosensors: From designs to applications. Imaging and Spectroscopic Analysis of Living Cells: Optical and Spectroscopic Techniques. 2012;317 doi: 10.1016/B978-0-12-391857-4.00016-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zaccolo M. Use of chimeric fluorescent proteins and fluorescence resonance energy transfer to monitor cellular responses. Circ Res. 2004;94:866–873. doi: 10.1161/01.RES.0000123825.83803.CD. [DOI] [PubMed] [Google Scholar]
- 27.Steinkamp JA. Fluorescence lifetime flow cytometry. Emerging Tools for Single-Cell Analysis. 2002:175–196. [Google Scholar]
- 28.Chang CI. Hyperspectral imaging: Techniques for Spectral Detection and Classification. Kluwer Academy, Plenum Publishers; 2003. [Google Scholar]
- 29.Keshava N, Mustard JF. Spectral unmixing. IEEE Signal Process Mag. 2002;19:44–57. [Google Scholar]
- 30.Leavesley SJ, Annamdevula N, Boni J, Stocker S, Grant K, Troyanovsky B, Rich TC, Alvarez DF. Hyperspectral imaging microscopy for identification and quantitative analysis of fluorescently-labeled cells in highly autofluorescent tissue. J Biophotonics. 2012;5:67–84. doi: 10.1002/jbio.201100066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lerner JM, Gat N, Wachman E. Approaches to spectral imaging hardware. Curr Protoc Cyto. 2010;53:1–12. doi: 10.1002/0471142956.cy1220s53. [DOI] [PubMed] [Google Scholar]
- 32.Williams P, Hunt A., Jr ER Estimation of leafy spurge cover from hyperspectral imagery using mixture tuned matched filtering. Remote Sens Environ. 2002;82:446–456. [Google Scholar]
- 33.Harris AT. Spectral mapping tools from the earth sciences applied to spectral microscopy data. Cytometry A. 2006;69A:872–879. doi: 10.1002/cyto.a.20309. [DOI] [PubMed] [Google Scholar]
- 34.Farrand WH, Harsanyi JC. Mapping the distribution of mine tailings in the Coeur d'Alene River Valley, Idaho, through the use of a constrained energy minimization technique. Remote Sens Environ. 1997;59:64–76. [Google Scholar]
- 35.Fereidouni F, Bader AN, Gerritsen HC. Spectral phasor analysis allows rapid and reliable unmixing of fluorescence microscopy spectral images. Optics Express. 2012;20:12729–12741. doi: 10.1364/OE.20.012729. [DOI] [PubMed] [Google Scholar]
- 36.Novo D, Grégori G, Rajwa B. Generalized unmixing model for multispectral flow cytometry utilizing nonsquare compensation matrices. Cytometry A. 2013;83A:508–520. doi: 10.1002/cyto.a.22272. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


