Abstract
Biodiversity offsetting, which means compensation for ecological and environmental damage caused by development activity, has recently been gaining strong political support around the world. One common criticism levelled at offsets is that they exchange certain and almost immediate losses for uncertain future gains. In the case of restoration offsets, gains may be realized after a time delay of decades, and with considerable uncertainty.
Here we focus on offset multipliers, which are ratios between damaged and compensated amounts (areas) of biodiversity. Multipliers have the attraction of being an easily understandable way of deciding the amount of offsetting needed. On the other hand, exact values of multipliers are very difficult to compute in practice if at all possible.
We introduce a mathematical method for deriving minimum levels for offset multipliers under the assumption that offsetting gains must compensate for the losses (no net loss offsetting). We calculate absolute minimum multipliers that arise from time discounting and delayed emergence of offsetting gains for a one-dimensional measure of biodiversity. Despite the highly simplified model, we show that even the absolute minimum multipliers may easily be quite large, in the order of dozens, and theoretically arbitrarily large, contradicting the relatively low multipliers found in literature and in practice.
While our results inform policy makers about realistic minimal offsetting requirements, they also challenge many current policies and show the importance of rigorous models for computing (minimum) offset multipliers. The strength of the presented method is that it requires minimal underlying information. We include a supplementary spreadsheet tool for calculating multipliers to facilitate application.
Keywords: compensation ratio, decision support tool, mitigation ratio, no net loss, offset ratio, offsetability, replacement ratio, time discounting
Introduction
Biodiversity offsetting is compensation for ecological and environmental damage caused by development activities (ten Kate, Bishop & Bayon 2004; Bekessy et al. 2010; BBOP 2013; Bull et al. 2013). Recently, offsetting has been gaining political acceptance and support all around the world (Kiesecker et al. 2009; Palmer & Filoso 2009; Madsen, Carroll & Moore Brands 2010). In this work, we concentrate on the ratio between the amounts of area (negatively) impacted and the area compensated. This ratio has been called a multiplier (Dunford, Ginn & Desvousges 2004; Bruggeman et al. 2005; Moilanen et al. 2009), mitigation ratio (Bendor 2009), offset ratio (Moilanen et al. 2009), compensation ratio (McKenney & Kiesecker 2010; Vaissiere et al. 2013) and replacement ratio (Dalang & Hersperger 2010; McKenney & Kiesecker 2010). We adopt the term multiplier for the present work. Multipliers are a superficially easily understandable way forward with offsetting, answering the question ‘how much biodiversity needs to be managed, protected or restored so as to compensate for the environmental damage that development activities have caused’. Nevertheless, it is generally unknown how large multipliers should be to achieve the key requirement of no net loss (Dunford, Ginn & Desvousges 2004; Harper & Quigley 2005; Gibbons & Lindenmayer 2007).
Several studies have analysed offsets empirically, often finding relatively low multipliers (of size <10). Some examples from the literature are summarized in Table1. In many such cases, no net loss offsetting is unlikely. For example, Quigley & Harper (2006a, b) found that while official requirements resulted in offset ratios that should be on average 6·8:1 (area gained: area lost), the mean realized offset ratio was only 1·5:1, thereby failing legal requirements for no net loss. There are also some examples of relatively large offset ratios in the empirical literature (see Table1). For example, Pickett et al. (2013) investigate offsetting for frogs in ponds that were lost due to the construction of the Sydney Olympic Park. In this rare example of confirmed successful offsetting, they found that losses of natural habitat for frogs could be robustly offset by a 19-fold increase in pond area via the construction of compensating artificial ponds.
Table 1.
Examples of offset multipliers (offset ratios, compensation ratios or replacement ratios) from the literature
| Multiplier | Reference | Application |
|---|---|---|
| Between 2 and 6 | Cameron, Cohen & Morrison (2012) | Solar energy development in Mojave Desert, USA |
| 4 | Vaissiere et al. (2013) | Compensation of damaged ecosystem services, Bay of Brest, France |
| Between 1·5 and 8 | Dalang & Hersperger (2010) | Replacement ratio estimates for Swiss dry grassland biotopes |
| 1·5 (average realized multiplier); 6·8 (average multiplier that would meet the official requirements) | Quigley & Harper (2006a,b) | Habitat compensation projects in Canada, where the NNL requirement was not achieved for all projects. |
| Between 1 and 10 | Environmental Law Institute (2002) | Legal requirements for wetland compensation in the USA |
| 1 or less | Zedler (1996) | Minimum replacement ratio allowed by regulatory agencies for certain areas in the USA |
| 19 | Pickett et al. (2013) | Habitat offsetting of a threatened frog in Sydney Olympic Park |
| 30 | DEADP (2007) | South Africa's Western Cape policy for critically endangered habitats |
In this work, we investigate multipliers in the context of time. One of the most common criticisms levelled at biodiversity offsets is that they exchange certain losses for uncertain gains: if offsets are implemented via habitat restoration, the compensation may only become realized after a long time delay (up to many decades or even centuries in the case of forests), and often only with partial success (Stokstad 2008; Suding 2011). In some cases, it is implausible that losses truly can be recovered (Moilanen et al. 2009; Maron et al. 2010). Another relevant temporal component included in the present work is permanence (offset duration): how long are the offsets guaranteed to remain (Dargusch et al. 2010; McKenney & Kiesecker 2010; van Oosterzee, Blignaut & Bradshaw 2012)?
We develop a mathematical model to understand how large the multipliers should at least be under time discounting. Time discounting is widely used in economics to model the expected return on interest: future gains are given less value than immediate gains (Philibert 2003; Green & Myerson 2004). It can also be used in conservation to fairly balance immediate losses (due to development) with hypothetical future gains that follow habitat restoration, management or protection (Laibson 1997; Moilanen et al. 2009). Time discounting leads to the concept of net present value: what is the value of future income, or gained environmental value in this case, when discounted into the present day (Di Minin et al. 2013; Overton, Stephens & Ferrier 2013).
Specifically, we analytically derive minimum multipliers for offsetting conditional on the method of time discounting, linear additionality and permanence of gains. By additionality, it is meant that gains must be obtained by offset actions and not by other factors. We present numerical values for minimum multipliers for a wide range of parameter combinations and include a ‘recipe’ for easy reading of these results. As a supplement, we also include a simple spreadsheet application which allows straightforward application of the proposed methods in specific planning situations. While the present treatment is purposefully simplified and mathematical, we emphasize that our results have direct operational relevance for empirical offsetting cases and discussion about adequate offset multipliers in them.
Materials and methods
We present a method for deriving minimum levels for offsetting, given time delay in and duration of the offsetting action. We analyse the case in which effectively immediate losses are to be compensated by delayed future gains. The conceptual components included are the produced environmental value (biodiversity value or condition) and its response to damage and offsetting, time discounting, which accounts for delayed and uncertain offsetting responses, additionality, which requires that gains must be obtained by offset actions and not by other factors (in the business-as-usual scenario), and permanence, which measures how long the offsetting benefits are guaranteed to persist in the landscape (IUCN 2013). We refer to Table2 for the definition of the above concepts and to Table3 for mathematical notation.
Table 2.
Definitions of some central terms
| Term | Explanation |
|---|---|
| Additionality | A requirement that offsetting gains must be higher than those in the expected business-as-usual scenario (IUCN 2013) |
| Minimum multiplier | A minimum bound for no net loss multipliers (typically calculated using simplified methods) |
| Multiplier (offset multiplier, offset ratio, compensation ratio, replacement ratio) | The ratio of the area offset and the area damaged when the principle of no net loss is required (e.g. Dunford, Ginn & Desvousges 2004; Bruggeman et al. 2005; Moilanen et al. 2009) |
| No net loss | A requirement that offsetting gains must be at least as large as losses, when compared to the expected business-as-usual scenario (Dunford, Ginn & Desvousges 2004; Harper & Quigley 2005; Gibbons & Lindenmayer 2007; BBOP 2013; IUCN 2013) |
| Permanence | A requirement that offsetting gains must last at least as long as the impacts are expected to persist (IUCN 2013) |
| Time discounting (time preference) | Relative valuation of future value. Typically gains or losses in the far future are valued less than those in the near future (e.g. Philibert 2003; Green & Myerson 2004). |
| Present value | Future value which has been time discounted to reflect its current value (Di Minin et al. 2013; Overton, Stephens & Ferrier 2013) |
Table 3.
Mathematical symbols
| Symbol | Explanation |
|---|---|
| M | Offset multiplier |
| A0, A1 | Damaged area, offset area |
| q | Condition of an area |
| V (A, t) | Environmental value produced in area A at time t. In the examples this is specified as V (A, t) = q (t) A |
| t1 | Start of the offsetting period |
| T0, T1 | End of the period when damage has effect, end of the offsetting period |
| Loss (A, t), Gain (A, t) | Loss of value in area A at time t, gain of value in area A at time t |
| D, r | Discount factor, discount rate |
| δloss, δgain | Relative loss of condition q in area A0, relative gain in condition q in area A1 |
We define the (offset) multiplier as the ratio of the area offset A1 and the area damaged A0 when no net loss is required (Dunford, Ginn & Desvousges 2004; Bruggeman et al. 2005; Moilanen et al. 2009):
| eqn 1 |
When the size of the damaged area is assumed to be known, the size of the offset area A1 can be calculated from Eqn 1 based on biodiversity lost from damage and gained from offsetting relative to the estimated business-as-usual (counterfactual) scenarios. The business-as-usual scenarios can include factors other than offsetting actions, such as active and passive management. For example, if compensation increases the condition of area as much as the impact decreases it, and both actions take place simultaneously, then the compensated area should be as large as the damaged area, yielding an offset multiplier equal to one; M = 1. In reality, the gain of condition from offsetting can be smaller than the initial damage: it is easy to completely destroy habitat but the converse action, restoration from a destroyed to a fully natural state, is practically impossible for most environments (Maron et al. 2012). Moreover, the offsetting action can take place after a time delay. In such situations, the area compensated should be (much) larger, yielding an offset multiplier (much) larger than one; M > 1.
Before presenting a general method for computing a minimum M, we illustrate the process by a simple example (see Fig.1). Assume that every year t any area A yields a proportional environmental value V (A, t) = q (t) A, where q (t) describes the condition of area A and takes its values between zero and one [a type of proportional environmental value is considered, for example, in the habitat hectares approach (Parkes, Newell & Cheal 2003)]. We assume that an area A0 of pristine quality (q = 1) is damaged by development activity in the present year (t = 0), lowering its condition from 1 to 0. The drop of condition is permanent, and it is estimated that without development activity, the condition would have stayed at the level q = 1. Hence, at each year, the environmental value loss in A0 is (1 × A0) – (0 × A0) = A0 (Fig.1a). Next, an offsetting action starts in area A1 at time t = t1, increasing its condition from 0 to 1. Assuming that without offsetting q would stay zero, the yearly environmental value gain in A1 is (0 × A1) + (1 × A1) = A1 (Fig.1b). The offsetting action ends at time t = T1 at which point permanence is no longer guaranteed and, in this example, q falls back to zero. Future losses and gains are made comparable with present losses and gains by discounting methods (which bear relation to the computation of compound interest), so that future losses and gains are typically given less weight than those close to the present time. A basic discounting model is the exponential model which corresponds to a constant rate of discounting, that is having a fixed discount rate for loss and gain for each year (Fig.1c,d). Assuming, for example, a discount rate of 5%, the present value of the biodiversity loss in A0 amounts to the sum of discounted losses for every year in the future, which equals 21·0 × A0 (sum of the bars in panel Fig1c, when extended over the infinite time interval, is 21). Similarly, if the offsetting action starts at the year t1 = 5 and ends at T1 = 20, the present value of the biodiversity gain in A1 is 8·9 × A1 (sum of the bars in panel Fig.1d is 8·9). Hence, in order for A1 to be large enough for no net loss offsetting, A1 must be at least M = 21·0/8·9 = 2·4 times as large as A0.
Figure 1.
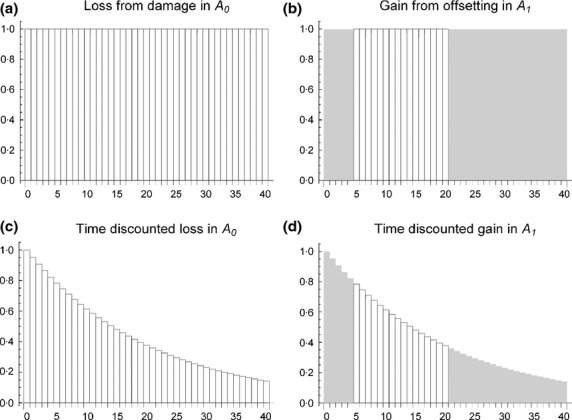
An example of biodiversity loss and gain in a damaged area A0 and the offset area A1 where damage is permanent and the temporary offsetting action takes place between the years t = 5 and t = 20: The actual loss of biodiversity value in area A0 (panel a) and gain of biodiversity value in the offset area A1 (panel b) are higher than the discounted loss (panel c) and discounted gain (panel d). The grey areas in panels b and d indicate differences between loss and gain. The present value of loss is the sum of bars in panel c, and the present value of gain is the sum of bars in panel d. Although the graphs end at t = 40, positive loss exists indefinitely, because the damage was assumed to be permanent. Offset multiplier is the ratio A1/A0 where A1 is large enough so that the present values of gain and loss are equal. A constant discount rate of r = 5% is applied.
We next derive a general formula for computing minimum multipliers. Consider points in time (years) t = 0, 1, 2,…, where t = 0 corresponds to the present time. Suppose that any area A produces value, measured by a function V (A, t). This value may be interpreted, for example in terms of the change in intrinsic biodiversity value or the value of ecosystem services generated by the area. The loss from damage at time t is then given by the differences of the produced value in the damaged area, Vdmg (A0, t), and the value in the estimated business-as-usual scenario (where no damage occurred), Vbau (A0, t), and similarly in the case of gain in the offset area A1:
To capture temporal preferences and uncertainty about the future, losses and gains are discounted to present time (Moilanen et al. 2009; Pouzols, Burgman & Moilanen 2012; Overton, Stephens & Ferrier 2013);
 |
where D (t) is a discount factor (see Table4 for the exponential and quasi-hyperbolic models of time discounting). The most common form is discounting at constant rate r, in which D (t) = 1/(1 + r)t. The numbers T0 and T1 denote the ends of the time intervals during which the damage has effect or offsetting actions are completed, respectively. (Both of these time intervals may also be infinite). It follows from the no net loss principle that gains must compensate losses, Gain (A1) ≥ Loss (A0), implying a minimum requirement that
| eqn 2 |
Table 4.
Minimum multipliers for commonly used discount factors. The most common model for discrete time discounting is the exponential model, which corresponds to a constant discount rate r. Quasi-hyperbolic discounting is another commonly used model: it prefers immediate payment to delayed payments and its rate depends on two parameters β and γ between zero and one (Frederick, Loewenstein & O'Donoghue 2002). Some studies have proposed discount rates which prefer future payments instead (Gollier 2010; Kula & Evans 2011). We have abbreviated R = 1/(1 + r)
| Time discounting model | Discount factor D (t) | Minimum multiplier; immediate loss of δloss units, delayed permanent gain of δgain units (t1 > 0) | Minimum multiplier; immediate loss of δloss units, delayed temporary gain of δgain units (t1 > 0) |
|---|---|---|---|
| Exponential | D (t) = Rt |  |
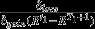 |
| Quasi-hyperbolic | D (0) = 1; D (t) = βγt for t > 0 | 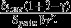 |
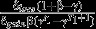 |
As the damaged area A0 is assumed to be known, Eqn 2 implicitly defines the size of the required offset area A1, and the offset multiplier can be solved from Eqns 1 and 2.
In the case where the environmental value is proportional to the area, the multiplier is easy to solve, as was seen in the example above. For example, let us assume that the destruction is immediate (occurring at t = 0) and permanent (T0 = ∞) and that it results in a relative loss of condition δloss, so that Loss (A0, t) = δloss A0 for all t. Assume further that an offsetting action increases the condition of area A1 by the fraction δgain between t1 and T1 (0 ≤ t1 < T1 ≤ ∞), where Gain (A1, t) = δgain A1. Then from the requirement of no net loss (Eqn 2), we get
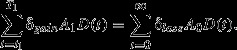 |
Using Eqn 1, we solve
In case exponential discounting is applied with rate r, this simplifies to
| eqn 3 |
where R = 1/(1 + r). If T1 = ∞, then the term 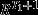 should be replaced by zero; see Table4 for variants of this formula.
should be replaced by zero; see Table4 for variants of this formula.
Note that while we have above formulated all values in discrete time (often years), these quantities could just as well be derived in continuous time, as is often performed in theoretical analyses. Calculations described here have also been implemented in a simple Excel application to facilitate easy application by practitioners (Supporting Information).
Results
Using the method presented above, we have analysed minimum multipliers for different parameter combinations to cover a large range of cases which show that realistic multipliers may be much larger than many multipliers reported in the literature. Here we have made the following additional technical assumptions, which generalize the simple example from the previous section (Fig.1): (i) the produced environmental value is proportional to area; V (A, t) = q (t)A, (ii) damage in area A0 is immediate (occurring at t = 0) and permanent (T0 = ∞), (iii) loss is complete; Loss (A0, t) = A0 for all t, (iv) offsetting action takes place between years t1 and T1 (t1 ≤ T1), (v) offsetting action fully compensates for the local environmental losses; Gain (A1, t) = A1 for all t between t1 and T1, (vi) in the business-as-usual scenarios, loss and gain are both zero and (vii) exponential discounting with rate r is applied (We below explain how to calculate the correct multiplier when per area unit gains are smaller than per area unit losses).
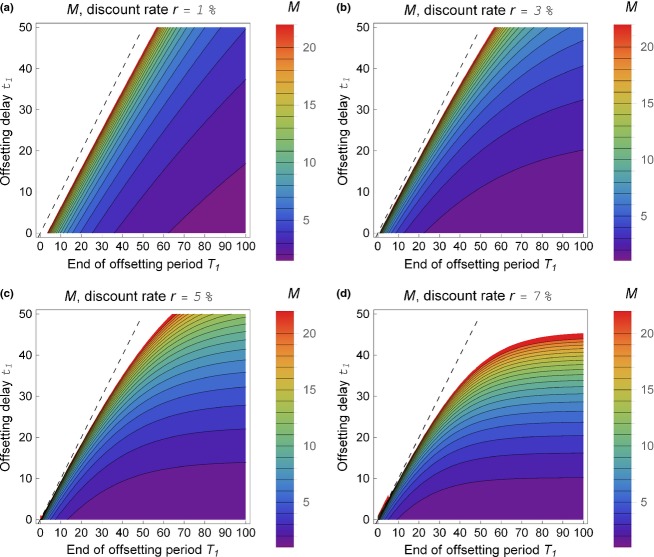
Figures2 and 3 show such minimum multipliers for a wide range of parameters. In the plot range of Fig.2, the multipliers vary between zero and over 100, but can well be even higher than that. A zero multiplier represents the theoretical special case where no damage has occurred. In Fig.2, it is assumed that the offsets will be permanent (T1 = ∞) and multipliers are plotted for a range of offsetting delays t1 and discount rates r. As Eqn 3 shows, the multipliers increase with both of these parameters; in fact, a multiplier with delayed offsetting is 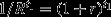 times higher than a multiplier with immediate offsetting. As Fig.3 shows, if a finite offsetting period is assumed, the multiplier increases the shorter the offsetting period (T1−t1) gets, eventually approaching infinity as T1 approaches t1. On the other hand, due to exponential discounting model, if the offsetting period is sufficiently long, multipliers from non-permanent offsetting approach those from permanent offsetting.
times higher than a multiplier with immediate offsetting. As Fig.3 shows, if a finite offsetting period is assumed, the multiplier increases the shorter the offsetting period (T1−t1) gets, eventually approaching infinity as T1 approaches t1. On the other hand, due to exponential discounting model, if the offsetting period is sufficiently long, multipliers from non-permanent offsetting approach those from permanent offsetting.
Figure 2.

Minimum multiplier M as a function of exponential time discount rate r and offsetting delay t1. The figure has been computed assuming a relative decrease of 1 in condition of site A0 at t = 0 and a relative improvement of 1 in condition at site A1 at time t1. Biodiversity value is proportional to the area, as in Fig.1 and Table4. In the white area, the multipliers quickly increase with r and t1, having a value of 117 in the upper right-hand corner. The minimum multiplier in the lower left-hand corner is 1.
Figure 3.
Minimum multiplier M as a function of the offsetting delay t1 and the end of offsetting period T1 ≥ t1. The assumptions are same as in Fig.2, and additionally, a relative increase of 1 in condition of area A1 is assumed at time T1. The four panels include minimum multipliers for exponential time discounting of rate (a) r = 1%, (b) r = 2·0%, (c) r = 5·0% and (d) r = 7·0%. The values are only shown for the cases where T1 ≥ t1, leaving empty the part of the graph where T1 < t1 (left-hand side of the dashed line). On the right-hand side of the dashed line, the values increase and can be much higher than 20, the closer they are to the dashed line and the higher they are in the y-axis.
All the presented multipliers assume that δloss = 1 and δgain = 1. In general, these parameters can be anything between zero and one. For general δloss and δgain, a minimum multiplier can be computed simply with further multiplication by the relative loss ratio δloss/δgain (by Eqn 3). We illustrate these observations by an example: if δloss/δgain = 1, then with an offsetting delay of 10 years and a discount rate of 5%, the multiplier is 1·6. If, in addition, offsetting is expected to last only 10 years, the multiplier is 3·9. If, in addition, offsetting is estimated to be less efficient, so that δgain = 0·2, the multiplier is 1/0·2 = 5 times 3·9, that is, 19·6.
For readers' convenience, we include a recipe for calculating a minimum multiplier M using only the plots in Figs2 and 3 when the necessary parameters are known. Note that this recipe is only meant as an easy first step in estimating the size of a minimum multiplier – the estimation of exact no net loss multipliers is instead a demanding task.
Assume that the parameters t1, T1, δloss, δgain and r are known. If offsetting is not permanent (T1 is finite), assume also that r takes one of the values 1%, 3%, 5% or 7%.
If offsetting is permanent (T1 is infinite), then Fig.2 gives a multiplier M0 which corresponds to r and t1. If offsetting is not permanent, then depending on r, a multiplier M0 which corresponds to t1 and T1 can be picked from one of the panels in Fig.3. We call M0 a reference multiplier.
The reference multiplier M0 has been computed under the (optimistic) assumption that the ratio of relative loss and gain equals one. Hence, by Eqn 3, the sought minimum multiplier M is given by M = M0 δloss/δgain.
Discussion
We have developed policy-relevant theory for biodiversity offsetting, focusing on multipliers while considering time discounting and delayed compensation – which is commonly the case when habitat restoration is involved (Maron et al. 2012). Main components included in the present analysis are additionality, permanence and time discounting. Here, we modelled additionality via a simple linear effect: the higher the gain achieved by offsetting action the lower the area multiplier needed for no net loss offsetting. When offset duration shortens (lower permanence), the minimum multiplier increases but not linearly, as the effects of permanence interact with time discounting. The multiplier is strongly influenced by time discounting and the delay in achieving offsetting gains, leading to high, exponentially increasing multipliers when development of compensation is much delayed. These computations could be considered, for example, together with other considerations at the initial offsetability determination stage of the hierarchy of impact avoidance, mitigation and offsetting (Pilgrim et al. 2013). Although the values of individual minimum multipliers vary depending on the model parameters, our results show that minimum multipliers can be large compared to those previously presented in the literature. Thus, the analysis demonstrates the importance of rigorous models for computing (minimum or exact) offset multipliers.
Time discounting is a critical component of the present analysis. We use time discounting in the sense of equitability: first, a yearly return on investment is expected from economic investment (implying time discounting for future gains). If this investment is enabled via ecological damage, it is fair that the same or higher time discounting should be applied to ecological compensation – it is not fair if immediate losses are only compensated by far future hypothetical gains. The discount rate can also model the offsetting risk, as an immediate certain gain may be preferable to a risky delayed gain. Some studies have proposed that the future could be valued equally or even higher than present (Gollier 2010; Kula & Evans 2011); we nevertheless adopt the equitability perspective in the present analysis. While we have explicitly discussed two discounting models, the exponential and the quasi-hyperbolic model, the methods presented in this paper can be formulated for any preferred model of time discounting and it is easy to see that the loss and gain functions can be defined using different discount factors to allow more detailed analysis of time discounting.
We have calculated minimum bounds for offset multipliers: this is a key concept that is not defined explicitly in otherwise exhaustive and robust frameworks for offsetting (Pilgrim et al. 2013). The analysis was based on a simple one-dimensional response of habitat to habitat management or restoration, implying that the multipliers we calculate are almost certainly an underestimation of what is truly needed for no net loss offsetting. In reality, biodiversity is a highly multidimensional entity. Therefore, while we find high multipliers in the one-dimensional case (Figs2 and 3), even higher multipliers would be needed if several different components of loss needed to be compensated with different actions in different areas. On the other hand, multidimensional measures of environmental value should be preferred in applications as one-dimensional measures may lead to different sizes of multipliers depending on the measure selected (cf. Table1). Due to its simplicity, our method can nevertheless be operationally useful, and quick to apply starting point, compared to a possibly very difficult task of exact estimation of exact no net loss multipliers.
Other limitations and simplifications applied in the present work include that the work is non-spatial, environmental value on the left axis may be difficult to define, and costs are not included. We have further assumed a constant counterfactual (business-as-usual) scenario, although other scenarios would obviously affect the sizes of multipliers (Bull et al. 2014). In fact, the model is intentionally simple and aims to derive minimum multipliers under minimal conditions. Even with (optimistic) minimal assumptions, we find that large multipliers may be needed. Including spatiality would not decrease these multipliers. Costs are not relevant for the analysis of the multiplier for a specific offsetting action. Further accounting for uncertainty would increase, not decrease, multipliers: if responses are uncertain, robustly guaranteeing no net loss needs a large multiplier instead of a smaller one (Moilanen et al. 2009; Pouzols, Burgman & Moilanen 2012; Pilgrim et al. 2013). In the present case, uncertainty could be partially included by making a conservative estimate of the response function, the amount of gain in the function and delay in the development of compensation. Using more sophisticated frameworks, such as RobOff (Pouzols, Burgman & Moilanen 2012; Pouzols & Moilanen 2013), it is possible to explore the implications of many interacting factors such as multiple biodiversity components, different uncertainty models, alternative models of sustainability and varying planning horizons. As a final consideration, the present analysis applies to the two major classes of offsets that can be distinguished depending on the type of offset or compensation action: restoration and averted loss offsets (BBOP 2013; IUCN 2013). There is no need to make such distinction in the analysis above.
In conclusion, if multipliers smaller than suggested by the present analysis are used, it is unlikely that no net loss will be achieved in biodiversity offsetting.
Acknowledgments
All authors were supported by the ERC-StG grant 260393 to A.M. (project GEDA). A.M. was also supported by the Academy of Finland Centre of Excellence programme 2012–2017, grant 250444 and the Finnish Natural Heritage Services (Metsähallitus). We thank Aija Kukkala for technical assistance.
Data accessibility
Excel spreadsheet tool: uploaded as online supporting information.
Supporting Information
Additional Supporting Information may be found in the online version of this article.
Excel spreadsheet tool for calculating minimum offset multipliers.
References
- Bekessy SA, Wintle BA, Lindenmayer DB, Mccarthy MA, Colyvan M, Burgman MA. Possingham HP. The biodiversity bank cannot be a lending bank. Conservation Letters. 2010;3:151–158. [Google Scholar]
- Bendor T. A dynamic analysis of the wetland mitigation process and its effects on no net loss policy. Landscape and Urban Planning. 2009;89:17–27. [Google Scholar]
- Bruggeman DJ, Jones ML, Lupi F. Scribner KT. Landscape equivalency analysis: methodology for estimating spatially explicit biodiversity credits. Environmental Management. 2005;36:518–534. doi: 10.1007/s00267-004-0239-y. [DOI] [PubMed] [Google Scholar]
- Bull JW, Suttle KB, Gordon A, Singh NJ. Milner-Gulland EJ. Biodiversity offsets in theory and practice. Oryx. 2013;3:269–380. [Google Scholar]
- Bull JW, Gordon A, Law EA, Suttle KB. Milner-Gulland EJ. Importance of baseline specification in conservation intervention and achieving no net loss of biodiversity. Conservation Biology. 2014;28:799–809. doi: 10.1111/cobi.12243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Business and Biodiversity Offsets Programme (BBOP) To No Net Loss and Beyond: An Overview of the Business and Biodiversity Offsets Programme (BBOP) Washington, D.C.: 2013. URL http://www.foresttrends.org/biodiversityoffsetprogram/guidelines/Overview_II.pdf [accessed 28 April 2014] [Google Scholar]
- Cameron DR, Cohen BS. Morrison SA. An approach to enhance the conservation-compatibility of solar energy development. PLoS ONE. 2012;7:e38437. doi: 10.1371/journal.pone.0038437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dalang T. Hersperger AM. How much compensation do we need? Replacement ratio estimates for Swiss dry grassland biotopes. Biological Conservation. 2010;143:1876–1884. [Google Scholar]
- Dargusch P, Lawrence K, Herbohn J. Medrilzam A small-scale forestry perspective on constraints to including REDD in international carbon markets. Small-Scale Forestry. 2010;9:485–499. [Google Scholar]
- DEADP (Department of Environmental Affairs and Development Planning) Provincial Guideline on Biodiversity Offsets. Cape Town, South Africa. 2007. URL http://www.westerncape.gov.za/text/2007/3/pgwcoffsetsguidelinedraft_5march_07.pdf [accessed 28 April 2014]
- Di Minin E, MacMillan DC, Goodman PS, Escott B, Slotow R. Moilanen A. Conservation businesses and conservation planning in a biological diversity hotspot. Conservation Biology. 2013;27:808–820. doi: 10.1111/cobi.12048. [DOI] [PubMed] [Google Scholar]
- Dunford RW, Ginn TC. Desvousges WH. The use of habitat equivalency analysis in natural resource damage assessments. Ecological Economics. 2004;48:49–70. [Google Scholar]
- Environmental Law Institute. Banks and fees: the status of offsite wetland mitigation in the United States. Washington, DC: 2002. URL http://www.eli.org/research-report/banks-and-fees-status-site-wetland-mitigation-united-states [accessed 28 April 2014] [Google Scholar]
- Frederick S, Loewenstein G. O'Donoghue T. Time discounting and time preference: a critical review. Journal of Economic Literature. 2002;40:351–401. [Google Scholar]
- Gibbons P. Lindenmayer DB. Offsets for land clearing: no net loss or the tail wagging the dog? Ecological Management & Restoration. 2007;8:26–31. [Google Scholar]
- Gollier C. Ecological discounting. Journal of Economic Theory. 2010;145:812–829. [Google Scholar]
- Green L. Myerson J. A discounting framework for choice with delayed and probabilistic rewards. Psychological Bulletin. 2004;130:769–792. doi: 10.1037/0033-2909.130.5.769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harper DJ. Quigley JT. No net loss of fish habitat: a review and analysis of habitat compensation in Canada. Environmental Management. 2005;36:343–355. doi: 10.1007/s00267-004-0114-x. [DOI] [PubMed] [Google Scholar]
- IUCN. Independent report on biodiversity offsets. IUCN, International Council on Mining & Metals; 2013. URL http://www.icmm.com/biodiversity-offsets [accessed 28 April 2014] [Google Scholar]
- ten Kate K, Bishop J. Bayon R. Biodiversity Offsets: Views, Experience, and the Business Case. Gland, Switzerland and Cambridge, UK: IUCN; 2004. Insight Investment, London, UK. [Google Scholar]
- Kiesecker JM, Copeland H, Pocewicz A, Nibbelink N, McKenney B, Dahlke J, Holloran M. Stroud D. A framework for implementing biodiversity offsets: selecting sites and determining scale. BioScience. 2009;59:77–84. [Google Scholar]
- Kula E. Evans D. Dual discounting in cost-benefit analysis for environmental impacts. Environmental Impact Assessment Review. 2011;31:180–186. [Google Scholar]
- Laibson D. Golden eggs and hyperbolic discounting. Quarterly Journal of Economics. 1997;112:443–477. [Google Scholar]
- Madsen B, Carroll N. Moore Brands K. State of biodiversity markets report: offset and compensation programs worldwide. 2010. URL http://www.ecosystemmarketplace.com/documents/acrobat/sbdmr.pdf [accessed 28 April 2014]
- Maron M, Dunn PK, McAlpine CA. Apan A. Can offsets really compensate for habitat removal? The case of the endangered red-tailed black-cockatoo. Journal of Applied Ecology. 2010;47:348–355. [Google Scholar]
- Maron M, Hobbs RJ, Moilanen A, Matthews JW, Christie K, Gardner TA, Keith D, Lindenmayer DB. McAlpine CA. Faustian bargains? Restoration realities in the context of biodiversity offset policies. Biological Conservation. 2012;155:141–148. [Google Scholar]
- McKenney BA. Kiesecker JM. Policy development for biodiversity offsets: a review of offset frameworks. Environmental Management. 2010;45:165–176. doi: 10.1007/s00267-009-9396-3. [DOI] [PubMed] [Google Scholar]
- Moilanen A, van Teeffelen AJA, Ben-Haim Y. Ferrier S. How much compensation is enough? A framework for incorporating uncertainty and time discounting when calculating offset ratios for impacted habitat. Restoration Ecology. 2009;17:470–478. [Google Scholar]
- van Oosterzee P, Blignaut J. Bradshaw CJA. iREDD hedges against avoided deforestation's unholy trinity of leakage, permanence and additionality. Conservation Letters. 2012;5:266–273. [Google Scholar]
- Overton JM, Stephens RTT. Ferrier S. Net present biodiversity value and the design of biodiversity offsets. Ambio. 2013;42:100–110. doi: 10.1007/s13280-012-0342-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer MA. Filoso S. Restoration of ecosystem services for environmental markets. Science. 2009;325:575–576. doi: 10.1126/science.1172976. [DOI] [PubMed] [Google Scholar]
- Parkes D, Newell G. Cheal D. Assessing the quality of native vegetation: the ‘habitat hectares’ approach. Ecological Management & Restoration. 2003;4:S29–S38. [Google Scholar]
- Philibert C. Discounting the future. Internet Encyclopaedia of Ecological Economics. International Society for Ecological Economics; 2003. URL http://isecoeco.org/pdf/philibert.pdf [accessed 28 April 2014] [Google Scholar]
- Pickett EJ, Stockwell MP, Bower DS, Garnham JI, Pollard CJ, Clulow J. Mahony MJ. Achieving no net loss in habitat offset of a threatened frog required high offset ratio and intensive monitoring. Biological Conservation. 2013;157:156–162. [Google Scholar]
- Pilgrim JD, Brownlie S, Ekstrom JMM, Gardner TA, von Hase A, ten Kate K, et al. A process for assessing the offsetability of biodiversity impacts. Conservation Letters. 2013;6:376–384. [Google Scholar]
- Pouzols FM, Burgman MA. Moilanen A. Methods for allocation of habitat management, maintenance, restoration and offsetting, when conservation actions have uncertain consequences. Biological Conservation. 2012;153:41–50. [Google Scholar]
- Pouzols FM. Moilanen A. RobOff: software for analysis of alternative land-use options and conservation actions. Methods in Ecology and Evolution. 2013;4:426–432. [Google Scholar]
- Quigley JT. Harper DJ. Effectiveness of fish habitat compensation in Canada in achieving no net loss. Environmental Management. 2006a;37:351–366. doi: 10.1007/s00267-004-0263-y. [DOI] [PubMed] [Google Scholar]
- Quigley JT. Harper DJ. Compliance with Canada's Fisheries Act: a field audit of habitat compensation projects. Environmental Management. 2006b;37:336–350. doi: 10.1007/s00267-004-0262-z. [DOI] [PubMed] [Google Scholar]
- Stokstad E. Environmental regulation: new rules on saving wetlands push the limits of the science. Science. 2008;320:162–163. doi: 10.1126/science.320.5873.162. [DOI] [PubMed] [Google Scholar]
- Suding KN. Toward an era of restoration in ecology: successes, failures and opportunities ahead. Annual Review of Ecology, Evolution, and Systematics. 2011;42:465–487. [Google Scholar]
- Vaissiere AC, Levrel H, Hily C. Le Guyader D. Selecting ecological indicators to compare maintenance costs related to the compensation of damaged ecosystem services. Ecological Indicators. 2013;29:255–269. [Google Scholar]
- Zedler JB. Coastal mitigation in Southern California: the need for a regional restoration strategy. Ecological Applications. 1996;6:84–93. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Excel spreadsheet tool for calculating minimum offset multipliers.
Data Availability Statement
Excel spreadsheet tool: uploaded as online supporting information.