Framing air pollution epidemiology in terms of population interventions, with applications to multi-pollutant modeling

Abstract

Air pollution epidemiology continues moving toward the study of mixtures and multi-pollutant modeling. Simultaneously, there is a movement in epidemiology to estimate policy-relevant health effects that can be understood in reference to specific interventions. Scaling regression coefficients from a regression model by an interquartile range (IQR) is one common approach to presenting multi-pollutant health effect estimates. We are unaware of guidance on how to interpret these effect estimates as an intervention. To illustrate the issues of interpretability of IQR-scaled air pollution health effects, we analyzed how daily concentration changes in two air pollutants (NO₂ and PM_2.5; nitrogen dioxide and particulate matter with aerodynamic diameter ≤ 2.5μm) related to one another within two seasons (summer and winter), within three cities with distinct air pollution profiles (Burbank, California; Houston, Texas; and Pittsburgh, Pennsylvania). In each city-season, we examined how realistically IQR-scaling in multipollutant lag-1 time-series studies reflects a hypothetical intervention that is possible given the observed data. We proposed 2 causal conditions to explicitly link IQR-scaled effects to a clearly defined hypothetical intervention. Condition 1 specified that the index pollutant had to experience a daily concentration change of greater than one IQR, reflecting the notion that the IQR is an appropriate measure of variability between consecutive days. Condition 2 specified that the co-pollutant had to remain relatively constant. We found that in some city-seasons, there were very few instances in which these conditions were satisfied (e.g., 1 day in Pittsburgh during summer). We discuss the practical implications of IQR scaling and suggest alternative approaches to presenting multi-pollutant effects that are supported by empirical data.

Air pollution epidemiology is increasingly moving toward analysis of mixtures and multi-pollutant modeling,^1,2 which has motivated a robust discussion of the analytical methods and regulatory frameworks that are best-suited for this complex undertaking.^3–5 Including multiple co-pollutants as independent variables in a regression model remains a common technique in time-series studies of acute effects.^6–14 In this approach, the investigator often multiplies the regression coefficient by some large concentration change (e.g., an interquartile range [IQR]) to express the health effect of one pollutant, controlling for the co-pollutant(s).^12,13,15 This scaling technique is a form of regression coefficient standardization.

Although the statistical challenges associated with highly correlated exposure variables are well-known in air pollution epidemiology,^3,16 there has been less attention paid to the causal interpretation of health effects under this IQR scaling framework. Although there is a movement in epidemiology to estimate policy-relevant effects that can be defined in reference to specific interventions,^17–19 investigators rarely explicitly state the intervention that IQR-scaled health effects correspond to. As researchers continue to improve communication between the fields of epidemiology and risk assessment, more explicit dialogue about the chosen modeling and scaling approach behind effect estimate calculation will enable more evidence-based regulatory policies.²⁰ Regression coefficient standardization is argued to permit comparison of health effects of multiple exposures on one outcome, or one association across various populations.^21,22 However, the technique has come under criticism for conflating specific characteristics of a given study (e.g., sampling design) and causal effects.²³ For example, two hypothetical studies with identical populations and identical health effect estimates of a single pollutant but very different exposure distributions (say, due to sampling) will result in greatly different scaled effects. Thus, the scaling of the health effect estimate is very sensitive to the exposure profile of the sample(s), as well as to the effect of exposure.²⁴ It has been argued that such scaling results in effect estimates without causal interpretation.²⁵

In recent years, other sub-fields of epidemiology have grappled with how to explicitly define the intervention that a given effect estimate corresponds to. Social epidemiology, in particular, has articulated the challenges of defining interventions in the presence of immutable exposure variables, highly correlated independent variables, and social selection.^26–28 In some cases, effect estimates have been demonstrated to rely on covariate strata with no variability in the exposure (non-positivity or “off-support” estimation),^27,29,30 which prevents defining a counterfactual intervention, and may introduce bias.³¹ While post-model regression coefficient scaling does not threaten validity in the same manner as off-support estimation, it may present an analogous situation from a causal perspective: health effect estimates that represent hypothetical interventions that are poorly defined, unobserved in the empirical data, and perhaps impossible. While unfeasible/impossible interventions do not necessarily threaten the identifiability of a causal parameter,³² in epidemiology we often care about the practical applications of our findings, and the feasibility of effect estimates is central to this assessment.^33,34

To illustrate the concerns related to unclearly defined or impossible health effect estimates in air pollution epidemiology, we analyze a simple exposure regimen of two ambient air pollutants, assessing how daily concentration changes in two pollutants relate to one another. Specifically, we analyze nitrogen dioxide (NO₂) and particulate matter with aerodynamic diameter ≤ 2.5μm (PM_2.5), co-pollutants that are frequently studied in multi-pollutant models.^35–37 We analyze these co-pollutants in three US cities with different air pollution profiles, to illustrate how several factors (e.g., emission sources, local meteorology) may affect the extent to which an IQR-scaled effect estimate may be appropriate in a given dataset. Having described the conventional IQR-scaling approach for multi-pollutant models (hereafter called “the IQR approach”), we first identify one set of causal conditions that may link the IQR approach to an underlying real-world intervention. We then map the IQR approach onto several distinct air pollution profiles, to examine whether the intervention ostensibly represented by the IQR-scaled effect is empirically observed in various geographic regions and seasons. Our goal is to assess the extent to which the parameter estimate scaling commonly presented in the epidemiologic literature reflects real-world exposure scenarios for acute air pollution health effects. We also aim to provide examples of how researchers can assess the appropriateness of the air pollution effect estimates they present in acute health-effects studies. Our ultimate goal is to stimulate a discussion on best practices for air pollution health effect scaling, enabling calculation and presentation of more realistic health effect estimates for scientific and regulatory purposes.

Causal conditions underlying the IQR approach

Although IQR scaling is standard practice, we are unaware of a detailed explication of how to interpret and apply the effects it produces, in terms of real-world health effects. Linking a health effect estimate to an underlying causal parameter requires causal assumptions, which are separate from the statistical assumptions required for unbiased estimation from a regression model (e.g., linearity given the link function, correct specification of main terms and interaction terms, independent observations).³² We define one set of causal assumptions below, in the form of two separate but related causal conditions. We recognize that these causal conditions are unlikely to capture the causal meaning that each researcher attributes to her/his IQR-scaled air pollution effects; these are our attempt to express a potential intervention represented by IQR-scaled effects.

The first condition relates to using the IQR over the study period as a scaling interval. Here we focus on acute air pollution effects estimated in time-series studies, specifically lag 1 (consecutive days) effects. We use “lag-1 effect” to refer to the effect of the air pollution concentration on the previous day (day X-1) on a health outcome on the index day (day X). We use “daily difference” to refer to air pollution concentration changes between the day before the index day (day X-1) and the index day (day X). The daily difference and the lag-1 effect are distinct phenomena, and we posit that they are connected. Because the lag-1 health effects of one or more air pollutants are estimated between consecutive days, a hypothetical experiment corresponding to this lag would intervene on exposure to increase/decrease pollutant concentration(s) over a similar, temporally short time-frame. This implies that for intervention-relevant scaling of lag-1 health effects, the scaling interval applied to the regression coefficient should reflect an amount of variability that is possible in the exposure of interest, in this case an air pollutant, on consecutive days. Normally the IQR that is used for regression scaling is calculated from the full distribution of that air pollutant for the whole study period or across a season, thus including the extremes of exposure across the study period, regardless of how temporally close these extreme concentrations are. We hypothesized that the IQR across a season, which is often used to present results in this field, would often be larger than the IQR of daily differences within a season. This gives rise to the first causal condition, formalized below: that an IQR-sized concentration change should be observed on some consecutive days in the study period.

Second, when multiplying one pollutant’s coefficient by an IQR, controlling for co-pollutant(s), there is a tacit assumption that the concentration in one pollutant can change by a large interval while holding the co-pollutant(s) relatively constant (in cases where co-pollutants are modeled as main terms only, without interaction terms). This particular condition is seldom empirically examined, and so it is not known if days with a large concentration change in one pollutant and relatively small changes in the co-pollutant(s) actually exist. Given the strong correlation among many ambient air pollutants, assessing the feasibility of a hypothetical intervention defined by an IQR-scaled multi-pollutant regression coefficient requires examining this condition. The hypothetical intervention defined by these conditions (which the IQR approach estimates, in our opinion) is as follows: If we were to change the index pollutant by a large (IQR-sized) interval between day X-1 and day X, holding the co-pollutant constant between these consecutive days, what would be the effect on the health outcome on day X? We now test how frequently these conditions hold, using real-world data for two pollutants in three locations in the U.S.

Data source

We obtained ambient air pollution data from the U.S. Environmental Protection Agency’s Air Quality System for the years 2010 through 2012. We analyzed daily concentrations (24-hour averages) of NO₂ in parts per billion (ppb) and PM_2.5 in micrograms per cubic meter (μg/m³) from a central monitoring station in each of the following cities: Burbank, California; Houston, Texas; and Pittsburgh, Pennsylvania. These locations were chosen because they represent diverse air pollution profiles, emissions sources, and climatic conditions, enabling analysis of the joint NO₂/PM_2.5 exposure regimen across a variety of real-world settings of interest. NO₂ and PM_2.5 were chosen because both are associated with a host of acute adverse health outcomes,^35,38 and because they are frequently analyzed together in multi-pollutant models.^9,36,37 When there was more than one monitoring station in a city, we chose the monitoring station that had data for all of the EPA’s criteria air pollutants in the years we studied.

Methodological approach

We analyzed how daily concentration changes in one pollutant (the index pollutant) varied with daily concentration changes in the co-pollutant. We chose to focus on the daily differences between consecutive days in our analyses, corresponding to lag-1 health effects. In the literature, both PM_2.5 and NO₂ have been demonstrated to cause adverse health outcomes at lag 1.^35,38 We calculated consecutive daily concentration differences by subtracting the previous day’s pollutant concentration from each daily concentration. Because the strength and direction of pollutant correlations may change between seasons, we analyzed concentration changes separately by season.¹⁶ We analyzed daily multi-pollutant concentration changes in summer (defined as June – August) and winter (defined as December – February) across the study years. We chose to use a consistent, simplified approach for defining seasons across cities to enable comparison of results. Multiple lag structures and combinations of lags may be of real-world interest; here we present only one combination, in order to focus the discussion and to enable comparison between cities and seasons.

Sources of variability

We analyzed two related sources of variability for each pollutant in each of the six city-seasons (3 cities × 2 seasons). First, we examined the distribution of daily pollutant concentrations across the study years, within each city-season. This distribution and its parameters are referred to as “study period” (e.g., study period IQR). Studies that employ IQR scaling typically use this study period IQR to scale effect estimates.

Separately, we analyzed daily concentration differences to represent a lag-1 effect. We refer to this distribution and its parameters as “daily difference,” e.g., the daily-difference IQR is the IQR of daily concentration changes in the air pollutant. This terminology distinguishes the daily-difference IQR from the study-period IQR, which is conventionally (though not exclusively³⁹) analyzed in air pollution epidemiology.

Assessing whether causal conditions are met

We operationalized the two conditions discussed above, in order to quantify how many days within a city-season met each condition for scaling of lag 1 health effects. The first condition, that a study period IQR adequately reflects concentration differences between consecutive days, we refer to as Condition 1. This condition involves only one pollutant, and it is satisfied for a given day if the absolute value of the daily difference equals or exceeds the study period IQR for that pollutant in the given city-season. We opted to consider the absolute value of the daily difference between consecutive days because days with large concentration changes reflect the first condition regardless of the direction of the concentration change.

Condition 2 includes the rule defined in Condition 1 as well as a second condition, that the concentration of the co-pollutant remains relatively constant while the index pollutant of interest changes by a large interval (i.e., the IQR). Therefore, Condition 2 is a compound condition that involves both co-pollutants. We operationalized “remains relatively constant” as days with a low absolute value-daily difference (specifically, days whose absolute value-daily differences were in the lowest tertile). We chose the 33^rd percentile as the cutoff for “low absolute daily difference” because it excludes days with high and moderately large concentration changes, while still capturing a reasonable proportion of days. In defining Condition 2, we imposed a dichotomous cutoff on what is a continuous phenomenon (variability in the co-pollutant); therefore we ran sensitivity analyses of Condition 2, fluctuating the “low daily difference” cutoff. We considered the 40^th and 20^th percentiles as alternative cutoffs and examined how results changed.

In a given pair of co-pollutants, one must consider changes in each individual pollutant and its co-pollutant as separate questions. If a day satisfies Condition 2 with NO₂ as the main pollutant and PM_2.5 as the co-pollutant, that day will by definition not satisfy Condition 2 when considering PM_2.5 as the main pollutant and NO₂ as the co-pollutant. Therefore, we ran all analyses twice, once considering NO₂ as the index pollutant and PM_2.5 as the co-pollutant, and the second time switching the two.

To provide a concrete example, in Pittsburgh during winter, the study period IQR for NO₂ was 9.7 ppb. The 33^rd percentile of absolute value-daily differences for PM_2.5 was 2.0 μg/m³. Considering NO₂ as the index pollutant and PM_2.5 as the co-pollutant, days where the NO₂ daily difference was more extreme than 9.7 ppb satisfy Condition 1 (large change in index pollutant). Among these days of large NO₂ concentration change, the subset that had PM_2.5 daily differences with absolute value less than 2.0 μg/m³ satisfy criterion 2.

Analysis

We compared the study-period distribution and the daily-difference distribution for both NO₂ and PM_2.5 in each city-season. We present median values, quartile values, and the IQR. We compared the study period IQR to the daily difference IQR by calculating a ratio of the two values. This enabled direct comparison of the two metrics of variability, and of how study period parameters map onto the distribution of daily differences. For both daily concentrations over the study period and daily differences, we calculated Pearson correlation coefficients for NO₂ and PM_2.5 for each city-season. We compared the study-period correlation to the daily-difference correlation using the method of Steiger for dependent correlations (specifically, Steiger’s modification of Dunn and Clark’s z; equation 15^{40 p.247}).

To determine the extent to which the Conditions of the IQR method were met in each city-season, we present the number and percent of days that satisfied each, separately for NO₂ and PM_2.5 as the index pollutant. We represent these findings graphically, in daily difference scatterplots between NO₂ and PM_2.5 for each city-season. We use lines and shading to represent the two conditions. All analyses were conducted using R (version 2.13.1, R Foundation for Statistical Computing; Vienna, Austria).

Results

In all cities and seasons, greater NO₂ variability occurred in the winter than summer, as indicated by IQRs (Table 1). Burbank had the largest IQRs for NO₂, with values between 6.9 ppb (summer daily difference IQR) and 12.2 ppb (winter study period IQR). Interquartile ranges for PM_2.5 were lowest in Houston, between 4.5 μg/m³ (summer daily difference IQR) and 6.1 μg/m³ (summer study period IQR). PM_2.5 variability was higher during winter in Burbank (10.6 μg/m³, study period IQR), as compared with summer months.

Table 1.

Season-stratified study-period distribution daily difference distribution for ambient NO₂ and PM_2.5 in three US cities, 2010 – 2012

		NO2 (ppb)						PM2.5 (μg/m3)
Summer		Burbank (n=218 days)		Houston (n=265 days)		Pittsburgh (n=250 days)		Burbank (n=218 days)		Houston (n=265 days)		Pittsburgh (n=250 days)
		SP	Diff.	SP	Diff.	SP	Diff.	SP	Diff.	SP	Diff.	SP	Diff.
	25th percentile	14.4	−3.5	8.4	−1.9	6.2	−1.8	16.3	−2.3	9.6	−2.2	9.5	−3.5
	Median	19.8	−0.6	10.5	−0.4	8.9	0.3	19.1	0.5	11.7	0.0	12.9	−0.1
	75th percentile	25.3	3.4	13.1	2.3	11.9	2.5	22.8	2.9	15.6	2.3	17.3	3.0
	IQR	11.0	6.9	4.7	4.2	5.7	4.3	6.5	5.2	6.1	4.5	7.8	6.5
	SP IQR: diff. IQR ratioa	1.60		1.11		1.32		1.25		1.34		1.20
Winter		Burbank (n=198 days)		Houston (n=265 days)		Pittsburgh (n=241 days)		Burbank (n=198 days)		Houston (n=265 days)		Pittsburgh (n=241 days)
		SP	Diff.	SP	Diff.	SP	Diff.	SP	Diff.	SP	Diff.	SP	Diff.
	25th percentile	20.5	−5.3	12.0	−5.1	9.2	−4.2	11.5	−4.5	8.4	−2.8	7.0	−3.8
	Median	26.9	0.6	16.5	−0.1	13.8	−0.3	15.8	0.6	10.9	0.1	10.7	0.2
	75th percentile	32.7	4.6	20.5	4.8	19.0	4.0	22.0	4.5	13.4	2.8	15.0	3.6
	IQR	12.2	9.9	8.5	9.9	9.7	8.2	10.6	9.0	5.1	5.6	8.0	7.4
	SP IQR: diff. IQR ratioa	1.23		0.86		1.19		1.17		0.90		1.08

^aSP IQR: diff. IQR ratio expresses the ratio of the study period IQR to the daily difference IQR within each city-season

Abbreviations:

SP, Study period distribution; Diff., Daily difference distribution; IQR, interquartile range; NO₂, nitrogen dioxide; PM_2.5, particulate matter with aerodynamic diameter ≤2.5μm; ppb, parts per billion; μg/m³, micrograms per cubic meter

Generally, the study period IQR was greater than the daily difference IQR (10 of 12 city-seasons, Table 1), reflecting greater variability across the season than between consecutive days. In summer, study period IQRs were consistently larger than the daily difference IQRs. For example, in Burbank the study-period IQR of NO₂ (11.0 ppb) was 60% larger than the daily difference IQR (6.9 ppb). Other differences were in the 20% – 35% range (except for Houston, 11%). In winter, no study-period IQR was more than 25% greater than its corresponding daily difference IQR.

The study-period correlations between NO₂ and PM_2.5 were similar to the daily- difference correlations between pollutants in all city-seasons (Table 2). For all cities, ambient NO₂ and PM_2.5 were more strongly correlated during winter months as compared with summer months. Pittsburgh exhibited the strongest correlations between NO₂ and PM_2.5 – approximately 0.45 during summer and 0.70 during winter. The study-period correlations between pollutants and daily-difference correlations between pollutants did not differ meaningfully within any city-season (P>0.05 for all comparisons).

Table 2.

Season-stratified correlations between ambient NO₂ and PM_2.5 for daily concentrations over the study period and daily differences

	Burbank		Houston		Pittsburgh
	Study period distribution	Daily difference distribution	Study period distribution	Daily difference distribution	Study period distribution	Daily difference distribution
Summer	0.054	0.163	0.206	0.164	0.447	0.436
Winter	0.392	0.439	0.411	0.444	0.766	0.697

In examining the number of days that met Condition 1, generally 10% to 25% of days per city-season had a daily difference exceeding the study-period IQR (Table 3). Considering NO₂ as the index pollutant, summer days in Burbank and Pittsburgh had a smaller proportion: 10 days in Burbank (4.6%) and 17 in Pittsburgh (6.8%). Among these days of high concentration change in the index pollutant, the proportion that met the additional requirement of Condition 2 was always below 50%, in many cases much lower (less than 25% in 6 of 12 city-seasons). This demonstrates that a minority of high-difference days in the index pollutant exhibited small differences in the co-pollutant. The overall proportion of days that met Condition 2 never exceeded 7%, and in some cases was below 1%. During summertime, considering NO₂ as the index pollutant, there were only 2 such days (0.9%) in Burbank, and 1 such day in Pittsburgh (0.4%).

Table 3.

Number and percent of days fulfilling Condition 1 and Condition 2 ^a across each city-season, with the index pollutant as NO₂ and PM_2.5 separately

		Index pollutant: NO2			Index pollutant: PM2.5
		Burbank No. (%)	Houston No. (%)	Pittsburgh No. (%)	Burbank No. (%)	Houston No. (%)	Pittsburgh No. (%)
Summer	Condition 1	10 (4.6)	47 (17.7)	17 (6.8)	26 (11.9)	46 (17.4)	39 (15.6)
	Condition 2	2 (0.9)	17 (6.4)	1 (0.4)	8 (3.7)	17 (6.4)	14 (5.6)
Winter	Condition 1	21 (10.6)	63 (23.8)	37 (15.4)	32 (16.2)	68 (25.7)	30 (12.4)
	Condition 2	5 (2.5)	16 (6.0)	4 (1.7)	9 (4.5)	13 (4.9)	2 (0.8)

^aCondition 1 stipulates that the absolute value-daily differences of the index pollutant exceed the study period-IQR; Condition 2 requires Condition 1 as well as stipulating that the absolute value of the co-pollutant’s daily difference is in the lower tertile of daily difference absolute values (when NO₂ is the index pollutant, PM_2.5 is the co-pollutant and vice versa).

Abbreviations:

NO₂, nitrogen dioxide; PM_2.5, particulate matter with aerodynamic diameter ≤2.5μm

A region may fail to meet the joint stipulations of Condition 2 because of failure to satisfy either component of this condition. There may be inadequate variability in daily differences for the index pollutant (i.e., not meeting Condition 1). Or, on such days of high variability, the co-pollutant may also generally exhibit high daily differences (i.e., not meeting Condition 2). Figures 1 and 2 graphically demonstrate two such instances in which few days met Condition 2. In Burbank during summer, there were relatively few days meeting Condition 1 for either index pollutant. Such days are represented by dots that fall outside of the dashed lines. In particular when NO₂ was the index pollutant (Figure 1A), the large majority of days clustered near the x-axis origin. The shaded regions in the graph represent further restriction to days that satisfy Condition 2, i.e., days of low concentration change. Application of this Condition further restricts the number of days that are on-support for the IQR method, leaving only two days that satisfy both conditions.

Figure 1.

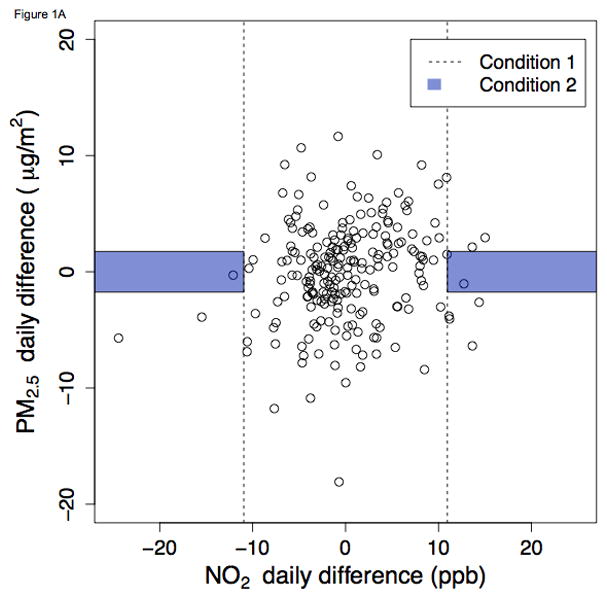
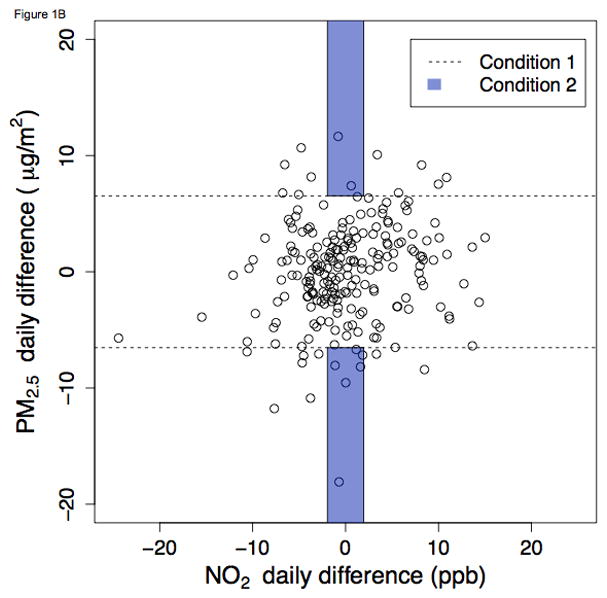
Ambient NO₂ and PM_2.5 daily differences during summer in Burbank, California, 2010 – 2012. Figures 1 and 2 graphically demonstrate which days met Conditions 1 and 2 for selected city-seasons (summer in Burbank and winter in Pittsburgh). The points in scatterplots are the same for A and B, with the index pollutant toggled (NO₂ for A, PM_2.5 for B). Days that satisfy Condition 1 (i.e., days with absolute value-daily differences exceeding the study period IQR) are represented by the points that fall outside of the dashed lines. Within this region beyond the dashed lines, days that satisfy Condition 2 are represented by the dots within the shaded region of “low daily difference in the co-pollutant” (i.e., the 33^rd percentile of absolute value-daily differences). A. NO₂ as index pollutant B. PM_2.5 as index pollutant

Figure 2.

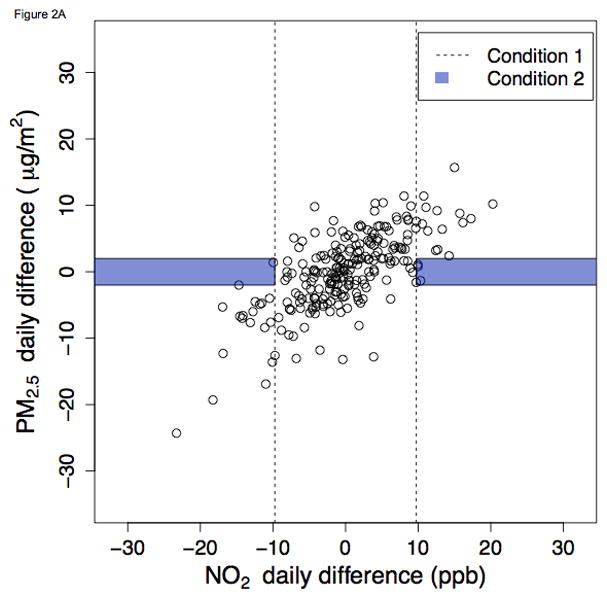
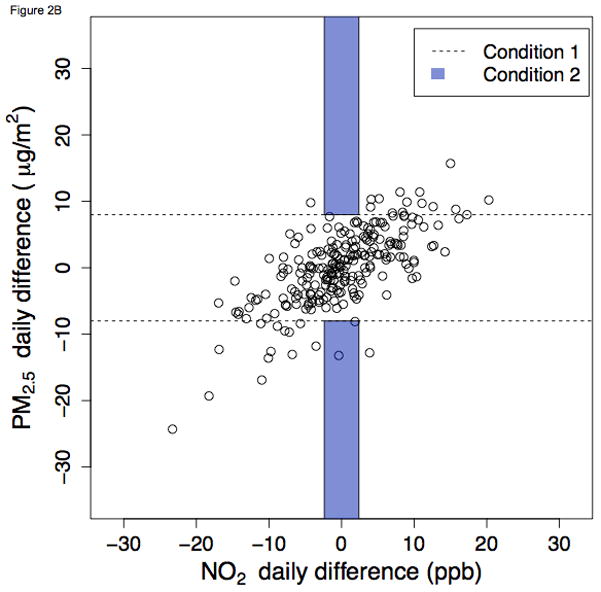
Ambient NO₂ and PM_2.5 daily differences during winter in Pittsburgh, Pennsylvania, 2010 – 2012 A. NO₂ as index pollutant B. PM_2.5 as index pollutant

Figure 2 shows daily differences during winter in Pittsburgh. In this instance, a moderate proportion of days met Condition 1 (dots outside of the dashed lines). However, due to the high correlation between PM_2.5 and NO_2, very few days satisfy Condition 2 (e.g., the two dots within the shaded region in Figure 2B). Complete graphics for all city-seasons and both index pollutants are presented in the web appendix. In sensitivity analyses examining alternative definitions of Condition 2, results were not greatly changed (eTable 1, eFigures 5 and 6). When the “low-concentration-change” cutoff was increased to the 40^th percentile, the proportion of days satisfying Condition 2 still never exceeded 10%. When decreased to the 20^th percentile, it was more frequently below 1%.

Discussion

We analyzed changes in daily concentrations in ambient PM_2.5 and NO₂ across three cities and two seasons to demonstrate how researchers may assess whether IQR scaling realistically reflects hypothetical interventions that are possible given the observed data. We attempted to demonstrate that the issues of time-scale of exposure variability, regression coefficient scaling, and correlation between co-pollutants have implications for the causal interpretation of multi-pollutant health effects. Ultimately, our goal was to determine whether IQR-scaling of multi-pollutant health effects reflects actual daily changes in multi-pollutant exposure regimens.

We believe that scaling air pollution effects to an interquartile interval implies that this is a reasonable concentration change in the time-window in which health effects are being estimated. In considering whether the study period IQR is an appropriate scaling interval for lag-1 health effects in time-series studies (i.e., Condition 1), we found that such variability was infrequently represented in season-stratified analyses. We also analyzed whether there were days in which a second co-pollutant’s concentration remained relatively constant, alongside the large daily difference in the index pollutant (i.e., Condition 2). We found that such daily concentration changes were adequately represented in very few real-data scenarios. For example, at least 5% of days in Houston exhibited this type of variability in the co-exposures of NO₂ and PM_2.5, making the IQR-scaled health effect estimate readily understandable as a hypothetical intervention. However, we also observed that such days are almost never observed in some city-seasons, for example Burbank during summer and Pittsburgh in both seasons. At least two factors contributed to this: (1) daily differences in pollutants rarely exceeded the study period IQR, and (2) days of high concentration changes in one pollutant also generally exhibited high concentration changes of the co-pollutant. In such scenarios, the hypothetical intervention, that of changing one pollutant a large amount while holding the other constant, is not supported by our data.

The approach that we used to characterize changes in multi-pollutant exposure regimens required several simplifications. First, air pollution health effects occur at various time lags in addition to lag 1.^41,42 Second, although we used ambient pollutant concentrations from central site monitors, the true exposures of individuals are not necessarily represented by these central monitors. Exposure science continues to improve estimation of ambient air pollution for individual persons, where they spend their time.⁴³ Third, our definition of “high change in concentration of the index pollutant” was based on the literature (i.e., a study period IQR), but our definition of “small change in the co-pollutant” was arbitrary; however, we examined alternative definitions. Fourth, precise definitions of season depend on local meteorology, and our simplified definitions may not optimally capture the full winter and summer air pollution profiles in our chosen cities. Finally, the three cities we selected represent distinct ambient air pollution profiles but do not represent the full range of ambient air pollution profiles. In light of this, it is worth noting that several of the correlations between NO₂ and PM_2.5 that we observed in this study were lower (i.e., <0.20 during summer in Burbank and Houston) than correlations commonly observed in many multi-pollutant studies (i.e., >0.50 during winter in Pittsburgh, and in other regions^6,10). Higher co-pollutant correlations would decrease the probably that Condition 2 would be satisfied.

Nevertheless, our goal was to examine the practical interpretation of IQR-scaled health effects in multiple-pollutant modeling. Conducting this analysis across regions and seasons required uniform methods across the city-seasons; hence, our simplifying assumptions. We found evidence of ill-defined/unfeasible causal effects in some cases (given our particular definition of a hypothetical intervention). It is worth noting that (as in our examples), a single modeling or scaling approach may have a stronger empirical data basis in one region or season than others. It is our intent that this example should catalyze discussion of causal interpretation of health effects in environmental epidemiology, including how such effect estimates map onto interventions.^18,19 Our general approach may also be applied using different pollutants, lag structures, time-scales, and exposure measurement methods. Although we addressed IQR scaling for single pollutants at temporally short lags (i.e., condition 1) and IQR scaling for multiple pollutants (i.e., condition 2) in one discussion, it is not a necessary feature of our approach to consider these issues in tandem.

Our approach of connecting IQR scaling to a hypothetical intervention is only one possible approach. With our causal conditions, we attempted to link commonly presented health effect estimates to a causal parameter of interest; however, these specific rules and this general approach are not broadly accepted by researchers presenting these health effects. Defining a hypothetical intervention is investigator-dependent; for example one could choose to hypothetically intervene on other variables in the multivariable model (e.g., temperature), while another investigator may consider them nuisance variables. Similarly, the failure to empirically observe an exposure-change scenario does not mean that such a scenario/intervention is not possible, and the health effects of such unobserved scenarios may well be of interest. However, investigators must be cautious in assigning causal interpretation to such interventions. In some cases, IQR scaling may violate the consistency assumption, which requires that “one needs to be able to explain how a certain level of exposure could be hypothetically assigned to a person exposed to a different level.”⁴⁴ Although less broadly appreciated than the causal assumptions of positivity and exchangeability,^31,45,46 consistency is nonetheless an important assumption for sharply defining causal contrasts.

Conclusions

The continued move toward mixtures and multi-pollutant research promises to more realistically reflect the ambient air pollution profile that humans are exposed to. This shift holds scientific promise as well as hurdles. We have aimed to elucidate one of these challenges, the importance of defining a hypothetical intervention that reflects actual air pollution scenarios that are contained in the dataset. The most immediate implication of our work is the suggestion that investigators should consider scaling air pollution health effects using distributions that reflect the temporal association between exposure and outcome (e.g., daily differences for lag-1 research; maximal concentration change over a 4-day window for lag-4 health effects; concentration changes within a day for lag-0 health effects), rather than the distribution over the entire study period. Different air pollution exposure periods (e.g., long-term health effects), modeling approaches (e.g., non-linearity or flexibly modeled exposure variables), and study designs (e.g., case-crossover) will likely require different approaches to defining a hypothetical intervention. We also believe that scaling co-pollutants simultaneously to reflect joint air pollution exposure changes is a promising future direction^47,48 (e.g., through the use of the g-computation plug-in estimator).^49,50 By more clearly defining a hypothetical intervention in reference to empirical data, we can aid in the interpretation of our presented health effect estimates, making them more readily applicable for scientific and regulatory purposes.