Abstract
Models of information transmission in the brain largely rely on firing rate codes. The abundance of oscillatory activity in the brain suggests that information may be also encoded using the phases of ongoing oscillations. Sensory perception, working memory and spatial navigation have been hypothesized to use phase codes, and cross-frequency coordination and phase synchronization between brain areas have been proposed to gate the flow of information. Phase codes generally require the phase of the oscillations to be reset at specific reference points for consistent coding, and coordination between oscillators requires favorable phase resetting characteristics. Recent evidence supports a role for neural oscillations in providing temporal reference windows that allow for correct parsing of phase-coded information.
Introduction
Phase-resetting [1-7] is defined in terms of ongoing self-sustained oscillatory (rhythmic) activity, which is abundant in the brain [8]. Brain rhythms reflect synchronized fluctuations in excitability across a population of neurons and are grouped by frequency: delta (0.5-4 Hz), theta (4-10 Hz), alpha (8-12 Hz), beta (10-30 Hz) and gamma (30-100 Hz) [9]. Neural oscillations may provide timing windows that chunk information, and the phase within a cycle may serve as a frame of reference for both internal and external events. Phase-resetting performs three main functions: 1) align the phase of an oscillation to a specific reference point for a given event or stimulus so that the phasic information can be decoded consistently, 2) allow a periodic stimulus to control the frequency and phase of a neural oscillator to provide the appropriate time frame for encoding and decoding and 3) allow mutually coupled oscillators to coordinate their frequencies and phases. Here, we summarize recent progress on identifying putative information coding and transmission schemes in the mammalian brain that employ phase-resetting of ongoing neural oscillations. The scope of this review is how the theory of phase-resetting of nonlinear oscillators constrains the implementation of these schemes. Alternate approaches to describe the dynamics of rhythm generators, such as those based on many-body physics [10], are beyond the scope of this review.
Phase-Resetting
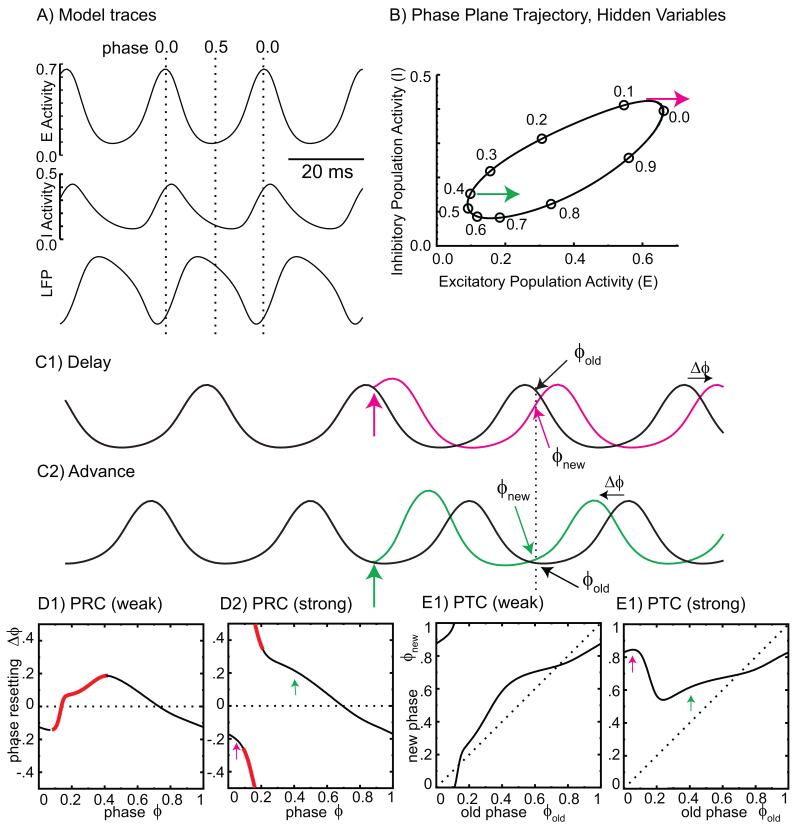
Phase-resetting characteristics can be measured for a single oscillating neuron [11,12] or for network oscillators [13,14]. Figure 1 defines the phase of an oscillator and shows how it can be reset, using a simple network oscillator model [15] that consists of the average firing rates of two neural populations, one excitatory (E) and one inhibitory (I). The phase φ evolves from 0 to 1 (some choose modulo 2π or Pi instead) in proportion to elapsed time (φ=t/Pi) for an undisturbed oscillator, but can be permanently reset by an external stimulus. The advance or delay is tabulated as the phase resetting Δφ in a phase response curve (PRC), or alternatively as the phase transition curve (PTC) with the new phase as a function of the old phase φnew = φold + Δφ. In Figure 1C, the new phase is established within a single cycle, but in practice more cycles may be required. A continuous PRC is shown for a relatively weak stimulus (Figure 1D1), and a discontinuous one is shown for a stronger stimulus (Figure 1D2). The discontinuity results from the abrupt transition between delays due to prolonging an existing peak (Figure 1C1) and advances due to initiating a new peak (Figure 1C2). The distinction between the two types of PRCs is much clearer in the PTC. Both PTCs depict partial resetting, although that in E2 is more complete than in E1. Many coding schemes require complete resetting, meaning that the PTC is flat and the new phase is independent of the old phase. Complete resetting is not guaranteed for arbitrary stimuli to a given oscillator.
Figure 1. Phase-resetting explained using the Wilson-Cowan model.
A. Excitatory (E) and inhibitory (I) activity and the simulated local field potential (LFP). Phase 0 is the peak of the E activity. B. Phase is marked on the cycle in the plane of the firing rates of the two populations. Magenta and green arrows indicate the direction of an external excitation (applied to the excitatory population). C. An external perturbation (vertical colored arrows) phase shifts the perturbed (colored) traces for the excitatory poplation compared to unperturbed (black) traces by the amount shown by horizontal arrows. (C1) An input at phase 0.05 causes a delay. (C2). An input at phase 0.4 causes an advance. The old phase just prior to the stimulus is repeated on the unperturbed (black) waveform at multiples of the cycle period (vertical dashed line) after the input, but the new phase on the colored traces at that point differs from the old phase by the phase shift. D. The PRC plots the phase shift as a function of the phase of the input perturbation. Slopes outside the stabilizing range (−2 to 0) are indicated in red. (D1) Weak input. (D2) Strong input. The arrows correspond to the perturbations in B and C. E. The phase transition curve plots the new phase (modulo one) versus the old phase. E1. For a weak input, the range of new phases is equal to that of old phases. E2. For a strong input, the range of new phases can be much smaller than the range of old phases.
The LFP and EEG measure synchronization of collective neural activity. A robust debate is ongoing regarding the role of phase resetting in event-related potentials detected in the EEG in response to a single sensory stimulus [16,17], and in the stimulus-synchronized response to a periodic train of such inputs [18,19]. A recent study [20] listed several mechanisms for generating a stimulus-synchronized response: 1) additional stimulus-locked activity that is recruited by the stimulus, 2) resetting of a single oscillator with no change in power, or 3) a complete reset by a common input that synchronizes a population of uncoupled oscillators with the same frequency but random initial phases, producing an increase in measured power. A phase-resetting mechanism as in (2) does not require the power to be unchanged. For example, the amplitude of the forced oscillation in the center trace of Figure 2B is larger than that of the unforced oscillation, which would result in a change in power as well as phase. Changes in the amplitude of an oscillation caused by a phase resetting stimulus are ignored, but not precluded, by phase resetting theory. The statistical test commonly used to detect phase coherence is more sensitive than that used to detect response power [20], so simple power and phase analyses may be insufficient to distinguish between mechanisms 1 and 2, for example.
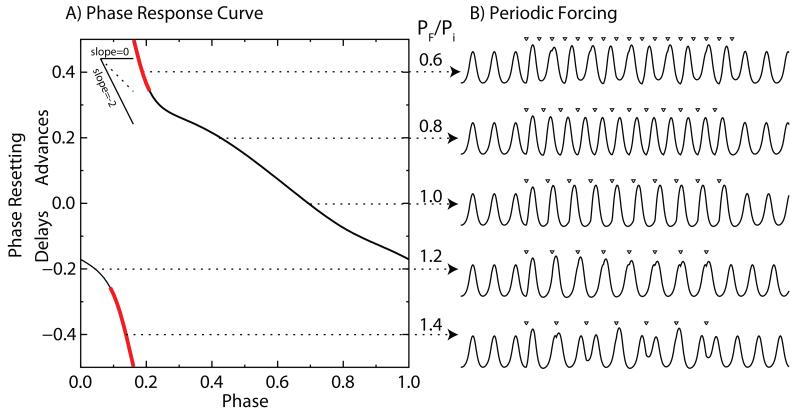
Figure 2. Phase-locking explained using the Wilson-Cowan model.
A. Phase response curve for strong input as in Figure 1D2. B. Forcing with a periodic train of stimuli (open triangles) at different PF/Pi ratios produces phase-locking only in the middle three traces, in which the corresponding point on the PRC exists and a slope within the stable range (see inset). Red indicates an unstable slope. Note that the position of the triangles within the forced cycle shifts as the forcing frequency changes.
For electrophysiological signals with variable cycle shape and amplitude, signal processing methods such as the Hilbert transform or convolution with a Morlet wavelet can be used instead of picking reference points to determine the phase, but caution should be exercised to determine that there is indeed an underlying nonlinear oscillation with a well-defined phase. Moreover, the frequency may also fluctuate due to external input [21,22] or intrinsic noise [23], and the PRC may be frequency dependent [24]. Nevertheless, this conceptual framework for phase resetting is quite generally applicable to nonlinear oscillators.
Phase-locking
A single input can reset the phase of an oscillator, and a train of inputs may phase-lock an oscillator such that the phase of the oscillator has a consistent relationship to each input. For an oscillator with intrinsic period Pi to be phase-locked by a stimulus with period PF, the change in period (PiΔφ(φ) ) due to the forcing must equal the difference between the intrinsic and forced periods (Pi-PF). The phasic relationships therefore change as the forcing period changes (Figure 2). The PRC limits the range of frequencies that allow a stable one-to-one locking because a point on the PRC must exist that has both the required amount of resetting and the correct slope for stability. Unfortunately, the theory of phase-locking is incomplete, and the theory presented here strictly applies only if the phase resetting can be assumed to be either pulsatile or weak or both. For pulsatile coupling [2,3,25,26], the effect of an arbitrary input is assumed to be complete before the next one arrives (but see [27,28]). For weak coupling [3,13,29], the response to an arbitrary input can be predicted using the infinitesimal PRC (iPRC), defined as the phase resetting curve obtained in the limit as the perturbation becomes very small. In order for a unidirectional forcing to be stable, the slope of the PRC at the locking point must be between −2 and 0 [2,25].
For mutual coupled oscillators, the phase-resetting can be measured for the input from the partner oscillator, and must allow a common frequency to be reached. An approximate stability criterion [26] is that the sum of the slopes at the locking point φi for each oscillator Δφ’(φ1)+Δφ’(φ2) must be negative but again, not too steep. Perhaps surprisingly, delays may facilitate synchrony between two oscillators with mutual coupling [26,30] by allowing the inputs to fall in PRC regions with stabilizing slope. Reciprocally coupled oscillators embedded in larger circuits also facilitate zero-lag synchronization in these larger circuits [30]. The stabilizing effects of negative PRC slopes generalize to all-to-all networks [31] and cross-frequency synchronization [32], resulting in wide implications of this theory. Recent modeling studies generalize these results to include the interaction of synaptic plasticity with phase-resetting properties [33,34].
Theta-Gamma Hypothesis
The theta-gamma hypothesis [35] of phase coding suggests that sequences in working memory are replayed with each item represented by cell assemblies active during sequential gamma cycles at different phases within a theta cycle, so theta phase codes for sequence order. Cross-frequency coupling of theta and gamma and phase synchronization between brains areas are thought to be critical mechanisms [36] in the formation of the cell assemblies that are activated on a particular gamma cycle. Partitioning neural responses recorded in monkey visual and auditory cortex using theta cycles permits the extraction of significantly more information that can be obtained otherwise [37], and robust increases in theta (and delta) band synchronization between brain areas are observed when patients correctly retrieve information from memory [38], support the role of the theta cycle as a temporal windowing mechanism. Phase-resetting theory can provide insight into cross-frequency phase-locking of gamma within a theta cycle [32,39,40] by establishing constraints on the existence and stability of N:1 locking modes, and by establishing constraints on the type of phase resetting required in different coding schemes described below, for example complete versus partial resetting.
Rhythmic Motor Activity for Active Sensing
Whisking and sniffing in rats at theta frequency [41] are rhythmic motor processes that are hypothesized to underlie active sensing. A proposed encoding scheme for active sensing postulates that internally generated oscillations, together with feedback from an element that detects the phase between external inputs and the internal rhythm, comprise a phase-locked loop [42]. This loop adjusts its frequency to stably phase-lock to the rhythmic inputs, in a manner constrained by phase-resetting theory. The phase detector, hypothesized to be implemented in thalamocortical neurons, smoothly encodes the phase of a novel input within the cycle of the rhythmic input. The angle of contact within the whisking cycle [42] is hypothesized to encode the boundaries of a perceived shape using the phase within the active sensing rhythm. Saccades may also mediate active sensing, as they can entrain delta and theta oscillations in primary visual cortex [43]. The effects of active sensing extend beyond the primary sensory cortices; hippocampal theta phase in monkeys is also reset by saccades [44], which may be important for the coding schemes described in the section on Hippocampal Phase Codes.
Rhythmic Sensory Coding and Decoding
Rhythmic auditory stimuli can phase-lock delta oscillations in primary auditory cortex [18], suggesting that the brain has specific mechanisms for processing rhythmic inputs [19]. Rhythmic stimulation produces no increase in delta power [18], and the alignment of the delta oscillation with expected stimulus times persists for a few cycles after the stimuli stopped, providing evidence for a phase-resetting mechanism. Moreover, attention controls delta phase-resetting so that for an attended stream of rhythmic stimuli, the time of the next expected stimulus occurs at the maximum excitability phase in regions tuned to the frequency of the stimulus, but at the minimum in those regions tuned to a different frequency. Periodic auditory stimuli can also entrain alpha oscillations that control excitability levels in visual cortex [45], suggesting that this cross-modal resetting by non-preferred stimuli contributes temporal information to multisensory integration [46].
The ability of auditory cortex to entrain to periodic inputs has motivated a theory of speech perception in which delta entrains to the rhythms of speech phrases and theta to syllables. A recent model [47,48] uses a phase-locked loop to allow the frequency of the intrinsic theta oscillator to vary within the theta range and remain locked to the slowly-varying input syllabic rhythm. Beta and gamma model oscillators are phase-locked at multiples of the theta frequency in a cascade, and the phase of the nested oscillators must be reset to a constant value at the beginning of each theta cycle for consistent coding. Information in the model is encoded by cell firing binned within each gamma cycle. The cascaded oscillator theory is supported by the ability of delta band entrainment to predict speech recognition scores [49], as well as a recent study showing that envelope tracking information improves the intelligibility of speech [50].
Communication Through Coherence
The communication through coherence (CTC) hypothesis [21] posits that groups of neurons in lower cortical areas (for example V1) compete to drive the gamma oscillation in higher areas (like V2). Attended stimuli compete more successfully, and phase-lock the higher area so that their inputs alone arrive consistently during the maximal excitability phase of the gamma oscillation in the higher area. Gamma oscillations in vivo are thought to result from the interaction between excitatory pyramidal cells and inhibitory interneurons, likely via multiple mechanisms [51]. However, the phase-resetting characteristics of network gamma oscillators have only recently begun to be examined, and there is no guarantee that their phase resetting characteristics are favorable for unidirectional or bidirectional phase locking. The PRC has recently been measured for gamma oscillations induced in hippocampal area CA3 in slices by carbachol or optogenetic stimulation [14]. The resultant biphasic PRCS were simulated using the same two-population firing rate model [15] used in Figures 1 and 2.
Two-population models comprised of several hundred conductance-based excitatory and inhibitory spiking neurons, in which individual neurons fire sparsely and randomly, have also been used to gain insight into the PRC for network oscillators. In this model [52], the PRC for simulated pulses of optogenetic stimulation was monophasic, with phase advances during the latter part of the rising phase of the simulated LFP, and little effect at other phases. Furthermore, two similar model gamma generators coupled via mutual excitation phase-locked, but only approximately, and in a bistable manner because either generator could lead the other. A recent review suggests that the faster (more strongly excited) gamma generator of this type would most effectively drive its mutually coupled partner in the manner required by CTC [51]. Another study [21] used a similar model comprised of populations of spiking neurons to respond to a recent challenge to the CTC hypothesis, namely that gamma frequency in areas V1 and V2 varies from moment to moment as a result of changing stimulus contrast. The experimental part of the study found that variation in gamma frequency between the two areas is correlated [21]. The computational part of the study showed that a model V2 network driven by excitatory input from a similar model V1 network oscillator [21] was able to follow fluctuations in frequency that were induced in V1, so that the oscillations remained coherent. More work is required to determine if and how population oscillators can coordinate their activity with the correct phasic relationship for coherence [51].
Hippocampal Phase Codes
The oscillatory interference model [53] posits that spatial locations are encoded using the relative phases between a reference theta oscillator and additional oscillators whose frequencies are increased by velocity in their respective preferred directions. The phases of the velocity controlled oscillators (VCOs) will slip with respect to the reference oscillator. Phase resetting theory imposes the constraint that distinct oscillators must be functionally uncoupled to prevent locking [54] or sticking [23]. As they slip, the peak of each VCO will coincide with the reference oscillator each time a characteristic distance has been traversed in its preferred direction. The exact spatial location of the place fields depends on how the phase of the oscillators is initialized: the phase difference between the velocity modulated oscillators and the reference oscillator is the integral of the velocity modulation plus the initial phase difference. Therefore, in this model, phase resetting of the oscillators plays a critical role in establishing place fields and changing the firing fields based on context [55], as well as correcting for noise in path integration. Reward locations, turning points, and other environmental boundaries have been suggested to provide resetting signals, usually complete resetting signals that reset the phases of all oscillators to zero. This theory is not universally accepted: a competing theory of hippocampal encoding of spatial information uses firing rate coding rather than phases, and is implemented in continuous attractor models [56] with moving bumps of activity that code for an animal’s location by exploiting the spatial tuning (place fields) of the component neurons. However, an oscillatory interference model can also be implemented as a continuous attractor model [57].
A different proposed phase code suggests that the biphasic ability of excitatory synaptic inputs to jitter the spike timing of CA1 and CA3 hippocampal pyramidal neurons phase-locked by a sinusoidal theta oscillation is useful for encoding memories [58]. The biphasic response is due to the unconventional protocol; when CA1 neurons are biased in a pacemaker regime they exhibit a monophasic PRC [11].
Cerebellar Timing Mechanisms
As evidenced above, neural oscillations are often hypothesized to serve as clocks, providing a reference phase to use for information coding; moreover, complete phase-resetting of the clock is often required for encoding. Mechanisms for complete resetting are varied. One example is provided by pacemaking cerebellar Golgi cells, which pause for one cycle period before resuming pacing after a burst evoked by depolarization, so the burst completely resets their phase. A recent review suggested that such resetting may allow specific Golgi neurons to escape entrainment with the local theta rhythm in order to emit a signal coded with respect to theta phase [59]. Subtheshold theta frequency oscillations in inferior olivary neurons may serve as a master clock for cerebellar generation of temporal patterns. In order to achieve precision greater than a theta period, it was recently suggested that the coupling between olivary neurons allows them to break into phase-locked clusters able to keep time at a higher resolution [60]. Phase-resetting theory constrains the tendency of networks to break up into clusters [31].
Spike timing in oscillatory neurons is determined by the iPRC
The spike-triggered average (STA) and covariance (STC) of the input preceding a spike can provide insight into the feature space encoded by a neuron. Both the STA [61] and the STC have been derived from the iPRC [62]. The relationship of the STA and STC to phase codes, if any, has not been determined. The serial cross-correlation coefficients for a series of interspike intervals in a noisy pacemaker have also been recently derived from the iPRC [63]. Moreover, the iPRC has also been used to predict spike timing in the presence of strong noise [29]. STN neurons are regular pacemakers in vitro, but fire irregularly in healthy intact animals. The biophysical basis of their phase resetting curve has been explained [12,64]. The deterministic interaction of the measured iPRC [29] with the known noise stimulus pattern was sufficient to predict spike times under weak coupling assumptions [24]. This is remarkable because the neurons appeared to be firing in a fluctuation-driven rather than pacemaking regime. Heterogeneity in the PRCs across the population may serve to actively decorrelate STN neurons [65]. Surprisingly, another study [66] showed that for low input correlations, heterogeneous oscillators exhibited more noise-induced stochastic synchronization than homogeneous oscillators.
Conclusions
Phase-locking and phase-resetting are two related and important concepts that contribute to and constrain schemes for encoding of information by phasic relationships. Rhythmic sensing (including speech decoding) and active sensing seem to be the most promising areas in which to firmly establish the use of phase codes. Although phase and frequency are hypothesized to act as direct carriers of information in some cases, this review also highlights how controlling the relative phase and frequency of neural oscillations is critical in order for various coding strategies to work. The role of neural oscillations to bin, or chunk, information, and the cross-frequency synchronization implicit in the gamma-theta hypothesis are emerging as universal organizational principles. Areas requiring more investigation include complete resetting mechanisms required to initialize phase codes, the phase-resetting properties of network oscillators, and the mechanisms by which network oscillators coordinate their activity, as well as the effects of noise on this coordination, and better statistical tools to determine the degree to which phase resetting mechanisms contribute to observed EEG and LFP activity.
*Highlights (for review).
The phase of population oscillators underlying brain rhythms can be reset.
Phase-resetting theory can help explain how brain rhythms phase-lock.
Phase-locking between brain rhythms may facilitate information transfer.
Oscillator phases, or relative phases, may encode information.
Coding schemes based on relative phases generally rely on complete phase-resetting.
Acknowledgements
This work was supported in part by the National Institutes of Health grant R01NS054281 to CCC as well as the computational core of P30GM103340, and the Mathematical Biosciences Institute and the National Science Foundation under grant DMS 0931642.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interest statement
Nothing declared.
References and recommended reading
Papers of particular interest, published within the period of review, have been highlighted as:
• of special interest
•• of outstanding interest
- 1.Winfree AT. The Geometry of Biological Time. Springer London, Limited; 1990. [Google Scholar]
- 2.Ermentrout B, Terman DH. Foundations of mathematical neuroscience. Springer; 2010. [Google Scholar]
- 3.Schultheiss NW, Prinz AA, Butera RJ. Phase Response Curves in Neuroscience: Theory, Experiment, and Analysis. Springer; 2011. [Google Scholar]
- 4.Glass L, Mackey MC. From Clocks to Chaos: The Rhythms of Life. Princeton University Press; 1988. [Google Scholar]
- 5.Tass PA. Phase Resetting in Medicine and Biology: Stochastic Modelling and Data Analysis. Springer; 2007. [Google Scholar]
- 6.Pikovsky A, Kurths J. Synchronization: A Universal Concept in Nonlinear Sciences. Cambridge University Press; 2003. [Google Scholar]
- 7.Canavier C. Phase response curve. Scholarpedia. 2006;1:1332. [Google Scholar]
- 8.Buzsaki G. Rhythms of the Brain. Oxford University Press; 2011. [Google Scholar]
- 9.International federation of societies for electroencephalography and clinical neurophysiology. Electroencephalogr. Clin. Neurophysiol. 1974;37:521. doi: 10.1016/0013-4694(74)90096-0. [DOI] [PubMed] [Google Scholar]
- 10.Vitiello G. The use of many-body physics and thermodynamics to describe the dynamics of rhythmic generators in sensory cortices engaged in memory and learning. Curr. Opin. Neurobiol. 2015;31:7–12. doi: 10.1016/j.conb.2014.07.017. [DOI] [PubMed] [Google Scholar]
- 11.Wang S, Musharoff MM, Canavier CC, Gasparini S. Hippocampal CA1 pyramidal neurons exhibit type 1 phase-response curves and type 1 excitability. J. Neurophysiol. 2013;109:2757–2766. doi: 10.1152/jn.00721.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Farries MA, Wilson CJ. Phase response curves of subthalamic neurons measured with synaptic input and current injection. J. Neurophysiol. 2012;108:1822–1837. doi: 10.1152/jn.00053.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhang C, Lewis TJ. Phase response properties of half-center oscillators. J. Comput. Neurosci. 2013;35:55–74. doi: 10.1007/s10827-013-0440-1. [DOI] [PubMed] [Google Scholar]
- 14.Akam T, Oren I, Mantoan L, Ferenczi E, Kullmann DM. Oscillatory dynamics in the hippocampus support dentate gyrus-CA3 coupling. Nat. Neurosci. 2012;15:763–768. doi: 10.1038/nn.3081. •• This study induced an in vitro analog of the gamma oscillation pharmacologically, and found that the PRCs for the response of the LFP to stimulation of the dentate gyrus or the alveus contained regions of advance and delay. Weak stimulation produced partial resetting, and strong stimulation produced complete resetting. The PRCs for the two different stimuli were shifted relative to each other. In order to match the patterns of advances and delays using the Wilson-Cowan model, in both cases the inhibitory population had to be perturbed more strongly than the excitatory population, and this effect was more pronounced for alveus stimulation. Optogenetic stimulation was also used to both to induce gamma oscillations and to measure a PRC to brief kicks in the level of stimulation. The PRCs were again biphasic with partial and complete resetting produced by weak and strong stimulation. Furthermore, a sinusoidally modulated stimulation could entrain the oscillation with a phase lag that was strongly dependent on the forcing frequency.
- 15.Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 1972;12:1–24. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Shah AS, Bressler SL, Knuth KH, Ding M, Mehta AD, Ulbert I, Schroeder CE. Neural dynamics and the fundamental mechanisms of event-related brain potentials. Cereb. Cortex N. Y. N 1991. 2004;14:476–483. doi: 10.1093/cercor/bhh009. [DOI] [PubMed] [Google Scholar]
- 17.Sauseng P, Klimesch W, Gruber WR, Hanslmayr S, Freunberger R, Doppelmayr M. Are event-related potential components generated by phase resetting of brain oscillations? A critical discussion. Neuroscience. 2007;146:1435–1444. doi: 10.1016/j.neuroscience.2007.03.014. [DOI] [PubMed] [Google Scholar]
- 18.Lakatos P, Musacchia G, O’Connel MN, Falchier AY, Javitt DC, Schroeder CE. The spectrotemporal filter mechanism of auditory selective attention. Neuron. 2013;77:750–761. doi: 10.1016/j.neuron.2012.11.034. •• This study examined the entrainment of the current source density in primary auditory cortex in monkeys presented with two simultaneous input streams. Each stream had different pure tones and different intervals between tones. Only one stream was attended, and only the attended stream entrained the CSD. The phase of the CSD oscillation encodes the expected time until the next rhythmic stimulus in the attended stream. Since the excitability was maximized in the area tuned to the attended frequency and minimized in others, the probability of attended stimulus detection was maximized while minimizing detection of distractors. The CSD was averaged over multiple trials, thus delta phase was random prior to stimulation but coherent during and for some time after stimulation. Although phase resetting is theoretically permanent, in the absence of the periodic stimulus the delta frequency is likely to wander so that averages over multiple trials no longer line up some time after the forcing stimulus stops. The mechanism of differential phase resetting of preferred and non-preferred frequencies, and its modulation by attention, is an important direction for future research.
- 19.Calderone DJ, Lakatos P, Butler PD, Castellanos FX. Entrainment of neural oscillations as a modifiable substrate of attention. Trends Cogn. Sci. 2014;18:300–309. doi: 10.1016/j.tics.2014.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ding N, Simon JZ. Power and phase properties of oscillatory neural responses in the presence of background activity. J. Comput. Neurosci. 2013;34:337–343. doi: 10.1007/s10827-012-0424-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Roberts MJ, Lowet E, Brunet NM, Ter Wal M, Tiesinga P, Fries P, De Weerd P. Robust Gamma Coherence between Macaque V1 and V2 by Dynamic Frequency Matching. Neuron. 2013;78:523–536. doi: 10.1016/j.neuron.2013.03.003. • This study presents novel experimental data on the coherence between V1 and V2 during the presentation of gratings with different contrast; varying the level of contrast modulated the frequency of ongoing gamma oscillation coherently in V1 and V2. Pyramidal-interneuron network gamma models were constructed to represent the superficial layers of V1 and layer 4 of V2. Both interneurons and pyramidal cells were driven in the V2 model in a feedforward manner by pyramidal neurons in V1. The dynamic frequency matching suggests that V2 is operating as a phase-locked loop that follows the forcing frequency in V1. Frequency matching was achieved in the model within a limited range of frequencies and below a maximal rate of frequency change.
- 22.Cohen MX. Fluctuations in Oscillation Frequency Control Spike Timing and Coordinate Neural Networks. J. Neurosci. 2014;34:8988–8998. doi: 10.1523/JNEUROSCI.0261-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Thounaojam US, Cui J, Norman SE, Butera RJ, Canavier CC. Slow noise in the period of a biological oscillator underlies gradual trends and abrupt transitions in phasic relationships in hybrid neural networks. PLoS Comput. Biol. 2014;10:e1003622. doi: 10.1371/journal.pcbi.1003622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Miranda-Domínguez Ó , Netoff TI. Parameterized phase response curves for characterizing neuronal behaviors under transient conditions. J. Neurophysiol. 2013;109:2306–2316. doi: 10.1152/jn.00942.2012. [DOI] [PubMed] [Google Scholar]
- 25.Canavier CC. Encyclopedia of Computational Neuroscience: SpringerReference. Springer; 2014. Pulse Coupled Oscillators. DOI 10.1007/978-1-4614-7320-6_774-1. [Google Scholar]
- 26.Canavier CC, Wang S, Chandrasekaran L. Effect of phase response curve skew on synchronization with and without conduction delays. Front. Neural Circuits. 2013;7:194. doi: 10.3389/fncir.2013.00194. • This study provides a comprehensive description of the effect of conduction delays and skew in the PRC on the phase-locking of two reciprocally pulse-coupled oscillators. Conditions are established for the stability of zero-lag synchrony, and for bistability of nonzero lag synchrony in which either oscillator can lead. The results can be applied to network oscillators if the net resetting effect that one oscillator exerts on the other over an oscillatory cycle can be quantified as a PRC, in other words, as a function of phase. Moreover, the synchronizing motif of two reciprocally pulse-coupled oscillators embedded within larger circuits can be understood using this framework.
- 27.Castejón O, Guillamon A, Huguet G. Phase-amplitude response functions for transient-state stimuli. J. Math. Neurosci. 2013;3:13. doi: 10.1186/2190-8567-3-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Krishnan GP, Bazhenov M, Pikovsky A. Multipulse phase resetting curves. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2013;88:042902. doi: 10.1103/PhysRevE.88.042902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wilson CJ, Barraza D, Troyer T, Farries MA. Predicting the responses of repetitively firing neurons to current noise. PLoS Comput. Biol. 2014;10:e1003612. doi: 10.1371/journal.pcbi.1003612. • This paper blurs the distinction between the “mean-driven” regime that characterizes pacemaking neurons, and the fluctuation-driven regime in which excitable neurons are randomly driven to spike threshold as a result of their noisy inputs. The iPRC was estimated for pacemaking subthalamic neurons using a noise regression method. Pacemakers were forced with a train of brief current pulses of random amplitude, and the resultant firing times were accurately estimated using a phase model based on the iPRC, even when the noise was strong enough to eliminate any apparent periodicity in the spike times. This demonstrates that oscillatory dynamics governed by the PRC cannot be ruled out simply because spike times appear random. In addition, a systematic change in the shape (skewness) of the iPRC was noted when the basal firing rate was increased using applied current and incorporated into their phase model of noisy pacemaking.
- 30.Gollo LL, Mirasso C, Sporns O, Breakspear M. Mechanisms of zero-lag synchronization in cortical motifs. PLoS Comput. Biol. 2014;10:e1003548. doi: 10.1371/journal.pcbi.1003548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Achuthan S, Canavier CC. Phase-resetting curves determine synchronization, phase locking, and clustering in networks of neural oscillators. J. Neurosci. Off. J. Soc. Neurosci. 2009;29:5218–5233. doi: 10.1523/JNEUROSCI.0426-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Malerba P, Kopell N. Phase resetting reduces theta-gamma rhythmic interaction to a one-dimensional map. J. Math. Biol. 2013;66:1361–1386. doi: 10.1007/s00285-012-0534-9. [DOI] [PubMed] [Google Scholar]
- 33.Akcay Z, Bose A, Nadim F. Effects of synaptic plasticity on phase and period locking in a network of two oscillatory neurons. J. Math. Neurosci. 2014;4:8. doi: 10.1186/2190-8567-4-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fink CG, Murphy GG, Zochowski M, Booth V. A dynamical role for acetylcholine in synaptic renormalization. PLoS Comput. Biol. 2013;9:e1002939. doi: 10.1371/journal.pcbi.1002939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lisman JE, Jensen O. The θ-γ neural code. Neuron. 2013;77:1002–1016. doi: 10.1016/j.neuron.2013.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Watrous AJ, Ekstrom AD. The spectro-contextual encoding and retrieval theory of episodic memory. Front. Hum. Neurosci. 2014;8:75. doi: 10.3389/fnhum.2014.00075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kayser C, Ince RAA, Panzeri S. Analysis of slow (theta) oscillations as a potential temporal reference frame for information coding in sensory cortices. PLoS Comput. Biol. 2012;8:e1002717. doi: 10.1371/journal.pcbi.1002717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Watrous AJ, Tandon N, Conner CR, Pieters T, Ekstrom AD. Frequency-specific network connectivity increases underlie accurate spatiotemporal memory retrieval. Nat. Neurosci. 2013;16:349–356. doi: 10.1038/nn.3315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tikidji-Hamburyan R, Lin EC, Gasparini S, Canavier CC. Effect of heterogeneity and noise on cross frequency phase-phase and phase-amplitude coupling. Netw. Bristol Engl. 2014;25:38–62. doi: 10.3109/0954898X.2014.886781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Fontolan L, Krupa M, Hyafil A, Gutkin B. Analytical Insights on Theta-Gamma Coupled Neural Oscillators. J. Math. Neurosci. 2013;3:16. doi: 10.1186/2190-8567-3-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ranade S, Hangya B, Kepecs A. Multiple modes of phase locking between sniffing and whisking during active exploration. J. Neurosci. Off. J. Soc. Neurosci. 2013;33:8250–8256. doi: 10.1523/JNEUROSCI.3874-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zacksenhouse M, Ahissar E. Temporal decoding by phase-locked loops: unique features of circuit-level implementations and their significance for vibrissal information processing. Neural Comput. 2006;18:1611–1636. doi: 10.1162/neco.2006.18.7.1611. [DOI] [PubMed] [Google Scholar]
- 43.Ito J, Maldonado PE, Gruen S. Cross-frequency interaction of the eye-movement related LFP signals in V1 of freely viewing monkeys. Front. Syst. Neurosci. 2013;7:1. doi: 10.3389/fnsys.2013.00001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Jutras MJ, Fries P, Buffalo EA. Oscillatory activity in the monkey hippocampus during visual exploration and memory formation. Proc. Natl. Acad. Sci. U. S. A. 2013;110:13144–13149. doi: 10.1073/pnas.1302351110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Romei V, Gross J, Thut G. Sounds reset rhythms of visual cortex and corresponding human visual perception. Curr. Biol. CB. 2012;22:807–813. doi: 10.1016/j.cub.2012.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Thorne JD, Debener S. Look now and hear what’s coming: On the functional role of cross-modal phase reset. Hear. Res. 2014;307:144–152. doi: 10.1016/j.heares.2013.07.002. [DOI] [PubMed] [Google Scholar]
- 47.Ghitza O. Linking speech perception and neurophysiology: speech decoding guided by cascaded oscillators locked to the input rhythm. Front. Psychol. 2011;2:130. doi: 10.3389/fpsyg.2011.00130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ghitza O, Giraud A-L, Poeppel D. Neuronal oscillations and speech perception: critical-band temporal envelopes are the essence. Front. Hum. Neurosci. 2013;6:340. doi: 10.3389/fnhum.2012.00340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ding N, Chatterjee M, Simon JZ. Robust cortical entrainment to the speech envelope relies on the spectro-temporal fine structure. NeuroImage. 2013;88C:41–46. doi: 10.1016/j.neuroimage.2013.10.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Doelling KB, Arnal LH, Ghitza O, Poeppel D. Acoustic landmarks drive delta-theta oscillations to enable speech comprehension by facilitating perceptual parsing. NeuroImage. 2014;85(Pt 2):761–768. doi: 10.1016/j.neuroimage.2013.06.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Cannon J, McCarthy MM, Lee S, Lee J, Börgers C, Whittington MA, Kopell N. Neurosystems: brain rhythms and cognitive processing. Eur. J. Neurosci. 2014;39:705–719. doi: 10.1111/ejn.12453. • This review points out that there is nothing in the general theory of phase resetting to guarantee that the phasic relationship of a forcing oscillator to a forced oscillator, or that of two mutual coupled oscillators, will satisfy the optimal phase relationships required by CTC. They also state that the PING (pyramidal-interneuronal network gamma) network oscillator models have optimal phase resetting properties for CTC. A frequency matched periodic excitation, regardless of any conduction delay, will trigger, directly or indirectly, a volley of local inhibition that wears off exactly when the next periodic input is expected. For mutually coupled oscillators, the (slightly) faster oscillator recovers from inhibition first, and therefore phase-locks the other oscillator via a similar mechanism.
- 52.Witt A, Palmigiano A, Neef A, El Hady A, Wolf F, Battaglia D. Controlling the oscillation phase through precisely timed closed-loop optogenetic stimulation: a computational study. Front. Neural Circuits. 2013;7:49. doi: 10.3389/fncir.2013.00049. • The goal of this study is develop methods that can precisely test the role of oscillations and oscillation phase in neural function. To this end, a model of the effect of optogenetic stimulation of Channelrhodopsin-induced photocurrents was carefully calibrated using experimental data, and incorporated into model networks of conductance-based inhibitory and excitatory neurons. The induction of gamma oscillations by sustained optogenetic stimulation as well as the phase-resetting properties of pulsatile optogenetic stimulation were simulated as a step towards the development of closed-loop protocols to perturb the phase of ongoing oscillations in vivo. They suggest that the direction of information flow between coupled oscillators can potentially be reversed by appropriately timed perturbations that cause a lagging oscillator to become the leading oscillator.
- 53.Burgess N, Barry C, O’Keefe J. An oscillatory interference model of grid cell firing. Hippocampus. 2007;17:801–812. doi: 10.1002/hipo.20327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Remme MWH, Lengyel M, Gutkin BS. Democracy-independence trade-off in oscillating dendrites and its implications for grid cells. Neuron. 2010;66:429–437. doi: 10.1016/j.neuron.2010.04.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hasselmo ME. How We Remember: Brain Mechanisms of Episodic Memory. The MIT Press; 2011. [Google Scholar]
- 56.Yoon K, Buice MA, Barry C, Hayman R, Burgess N, Fiete IR. Specific evidence of low-dimensional continuous attractor dynamics in grid cells. Nat. Neurosci. 2013;16:1077–1084. doi: 10.1038/nn.3450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Blair HT, Wu A, Cong J. Oscillatory neurocomputing with ring attractors: a network architecture for mapping locations in space onto patterns of neural synchrony. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 2014;369:20120526. doi: 10.1098/rstb.2012.0526. • This study shows how spatial information can be encoded using a phase code in a continuous attractor network. Multiple ring attractors are comprised of theta bursters. Each ring attractor has a different preferred direction, and activity bumps rotate around the ring at theta fre-quency modulated by velocity in the preferred direction. The theta neurons do not have spatial tuning. Nonetheless, spatial position information can be encoded in the space of relative phases between the rings. The advantage of using the relative phases of the velocity controlled oscillators rather than their phases with respect to a reference oscillator is that it confers robustness to shared noise. Resetting mechanisms are still required to coordinate the phases between rings in response to specific environmental stimuli.
- 58.Borel M, Guadagna S, Jang HJ, Kwag J, Paulsen O. Frequency dependence of CA3 spike phase response arising from h-current properties. Front. Cell. Neurosci. 2013;7:263. doi: 10.3389/fncel.2013.00263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.D’Angelo E, Solinas S, Mapelli J, Gandolfi D, Mapelli L, Prestori F. The cerebellar Golgi cell and spatiotemporal organization of granular layer activity. Front. Neural Circuits. 2013;7:93. doi: 10.3389/fncir.2013.00093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Lefler Y, Torben-Nielsen B, Yarom Y. Oscillatory activity, phase differences, and phase resetting in the inferior olivary nucleus. Front. Syst. Neurosci. 2013;7:22. doi: 10.3389/fnsys.2013.00022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ermentrout GB, Galán RF, Urban NN. Relating neural dynamics to neural coding. Phys. Rev. Lett. 2007;99:248103. doi: 10.1103/PhysRevLett.99.248103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Arthur JG, Burton SD, Ermentrout GB. Stimulus features, resetting curves, and the dependence on adaptation. J. Comput. Neurosci. 2013;34:505–520. doi: 10.1007/s10827-012-0433-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Schwalger T, Lindner B. Patterns of interval correlations in neural oscillators with adaptation. Front. Comput. Neurosci. 2013;7:164. doi: 10.3389/fncom.2013.00164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Farries MA, Wilson CJ. Biophysical basis of the phase response curve of subthalamic neurons with generalization to other cell types. J. Neurophysiol. 2012;108:1838–1855. doi: 10.1152/jn.00054.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Wilson CJ. Active decorrelation in the basal ganglia. Neuroscience. 2013;250:467–482. doi: 10.1016/j.neuroscience.2013.07.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Zhou P, Burton SD, Urban NN, Ermentrout GB. Impact of neuronal heterogeneity on correlated colored noise-induced synchronization. Front. Comput. Neurosci. 2013;7:113. doi: 10.3389/fncom.2013.00113. [DOI] [PMC free article] [PubMed] [Google Scholar]