Thin-layer modeling of convective and microwave-convective drying of oyster mushroom (Pleurotus ostreatus)

Abstract

Oyster mushroom samples were dried under selected convective, microwave-convective drying conditions in a recirculatory hot-air dryer and microwave assisted hot-air dryer (2.45 GHz, 1.5 kW) respectively. Only falling rate period and no constant rate period, was exhibited in both the drying technique. The experimental moisture loss data were fitted to selected semi-theoretical thin-layer drying equations. The mathematical models were compared according to three statistical parameters, i.e. correlation coefficient, reduced chi-square and residual mean sum of squares. Among all the models, Midilli et al. model was found to have the best fit as suggested by 0.99 of square correlation coefficient, 0.000043 of reduced-chi square and 0.0023 of residual sum of square. The highest effective moisture diffusivity varying from 10.16 × 10⁻⁸ to 16.18 × 10⁻⁸ m²/s over the temperature range was observed in microwave-convective drying at an air velocity of 1.5 m/s and the activation energy was calculated to be 16.95 kJ/mol. The above findings can aid to select the most suitable operating conditions, so as to design drying equipment accordingly.

Introduction

Edible mushrooms are one of the most sustainable sources of proteins. Nowadays, mycoproteins are considered as a substitute to meat protein. More than 2000 described species exist in nature but only 35 species are cultivated commercially, and of those, about 20 species are intensively cultivated on an industrial scale (Chang 1999). Study shows that edible mushrooms have essential amino acid index, nutritional index and protein score values range between that of vegetables and meats (Garcha et al. 1993). Among edible mushrooms, Pleurotus ostreatus (oyster mushrooms) has pleasant flavor, several proteins, minerals (Ca, P, Fe and Mg), and low in carbohydrate quantities and fat, constituting excellent dietary food (Silva et al. 2002). Oyster mushrooms are considered as highly perishable commodities because they have a high moisture content of 75–90 % (wb), thus, limiting the shelf life up to 2 days or less under ambient conditions of temperature and humidity and this has proved to be one of the major constraints in commercialization. In order to increase the shelf life several processing methods have been explored. Canning of oyster mushrooms is done commonly on a commercial scale, but it is a bit expensive. In case of large scale freezing, cost and electric power supply involved in running cold chains become major constraints (Kulshreshtha et al. 2009). However, drying seems to be the most economically feasible processing method to enhance the shelf life of mushrooms. Among drying, commonly used convective hot-air dryers are simple, economical means of extending the shelf life but microwave-convective heating can prove to be a better alternative over hot-air drying as it combines the effect of both microwave and hot-air drying. The idea to combine fast heating of microwave and low temperature convective drying has been investigated by a number of researchers. Zhang et al. (2006) reported a review on trends in microwave-related drying of fruits and vegetables indicating the advantages of combining conventional drying methods with microwave heating. The review also clearly indicates that combination of drying methods leads to better drying processes than using microwave or conventional drying methods alone. In case of microwave drying only, heat losses are considerably reduced as the electromagnetic energy is dissipated directly in the drying material, but the capital and operating costs are higher. Thus, to overcome the economical constraints, microwave drying is combined with convective drying, where the air stream carries away the moisture evaporated during the microwave irradiation.

The convective mode of heat transfer is used in conventional heating which is followed by conduction where heat must diffuse in from the surface of the material deep into fruits and vegetables. In microwave processing, heat is generated throughout the material, leading to faster heating rates, compared to conventional heating where heat is usually transferred from the surface to the interior (Poonnoy et al. 2007).

The drying kinetics is often used to describe the combined macroscopic and microscopic mechanisms of heat and mass transfer during drying, and it is affected by drying conditions, types of dryer and characteristics of materials to be dried (Giri and Prasad 2007). Thin-layer drying of mushrooms involves drying of slices of mushrooms in a single layer. Currently, there are three types of thin-layer drying models used to describe the drying phenomenon of farm product, namely, theoretical model, which considers only the internal resistance to moisture transfer between product and heating air; semi-theoretical and empirical models which consider only the external resistance (Midilli et al. 2002; Panchariya et al. 2002). Emperical model gives a relation between average moisture and drying time, whereas theoretical model takes into the geometry of the product, its mass diffusivity and conductivity. Semi-theoretical models are derived from Fick’s second law of diffusion, such as Page model, Henderson and Pabis model, Two-term model, Logarithmic model and Midilli et al. (2002) model (Table 1).

Table 1.

Mathematical models given by various authors for drying curves

No.	Model name	Model	References
1	Lewis	MR = exp(−kt)	Bruce (1985)
2	Page	MR = exp(−kt n)	Page (1949)
3	Henderson and Pabis	MR = a exp(−kt)	Henderson and Pabis (1961)
4	Logarithmic	MR = a exp(−kt) + c	Togrul and Pehlivan (2002)
5	Two-term	MR = a exp(−k 0 t) + b exp(−k 1 t)	Henderson (1974)
6	Midilli et al. (2002)	MR = aexp(−kt n) + bt	Midilli et al. (2002)

The aim of this work was to model the drying kinetics of the mushroom in a recirculatory hot-air dryer and a microwave-convective dryer over a wide range of temperature. In addition, the effective diffusivities and activation energies of the mushroom samples were also calculated and presented.

Material and methods

Experimental apparatus

Recirculatory hot-air drying system

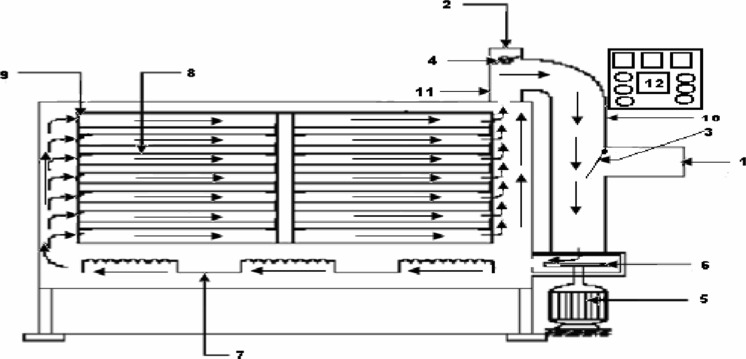
The recirculatory hot-air dryer (S.D. Instruments Pvt. Ltd, Kolkata, West Bengal, India) was used for drying of mushrooms. As shown in Fig. 1, dryer consists of broadly heaters and heating control unit, drying chamber, air flow ducts, blower, measurement sensors, and control panel. All interior parts of the tray dryer including trays were made of Stainless steel-304 and 5 cm thick insulation was provided on all sides of the dryer. Two booster heaters and one control heater of 4000 kW was provided to heat the air. The air was re-circulated in such a way that exhausted air was diverted towards the inlet duct. The energy required for heating the mixed air (fresh and exhausted air) was less as compared to heating fresh air, as it recovers the part of energy escaping out by entrapping exhausted air. The temperature of heated air was displayed on the control panel, which was measured by Pt-100 sensor (Platinum resistance thermometers, Simplicon Pvt. Ltd., Mumbai, India). The air velocity in the drying chamber was measured with an anemometer (Vane Anemometer-ABH-4225, Hyderabad, Andhra Pradesh, India) with an accuracy ± 2 %. An analytical balance (Sartorius TE 153S, Sartorius Weighing India Pvt. Ltd., Bangalore, Karnataka, India) was used for measuring mass with a measurement precision of ± 0.001 g.

Fig. 1.

Schematic diagram of recirculatory hot-air dryer. (1) Fresh air inlet port (2) Exhaust air outlet port (3) Inlet air flow control flap (4) Exhaust air flow control flap (5) Blower motor (6) Blower (7) Heaters (8) Drying chamber fitted with 12 trays (9) Louvers (10) Exhaust air passage (11) Exhaust air outlet duct (12) Control panel. (Courtesy: Bag SK 2009)

Microwave-convective drying system

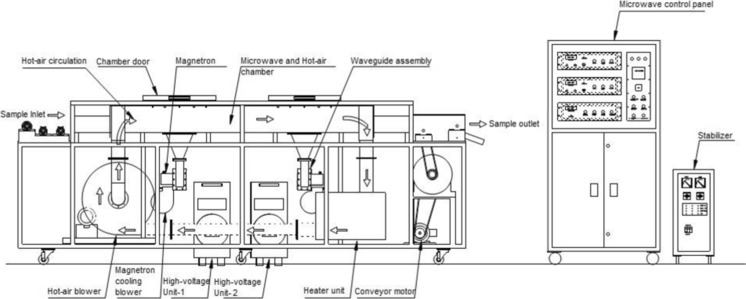
The microwave assisted hot-air drying system (Enerzi Microwave Systems Pvt. Ltd., Bangalore, Karnataka, India) was used to dry mushroom slices. As shown in Fig. 2, the instrument comprises of two microwave sources of 1.5 kW capacity each, with a microwave power range of 250–3000 W and a working frequency of 2450 MHz. For hot-air circulation, heater of 6 kW power was fitted, air temperature could vary from 25 to 200 °C, and air velocity could vary from 50 to 150 lpm. The drying chamber was made up of 2 mm thick Stainless steel-304 having an overall length of 2 m, and dimension of 300 mm (width) * 200 mm (height), outside body was made up of mild steel, coated with anti-corrosive epoxy powder coating. Equipment had a drying capacity of 20–100 kg/h depending on type of food and microwave power applied for heating and drying of food materials. Perplex trays were used for holding food material inside the dryer.

Fig. 2.

Schematic diagram of microwave-convective dryer. (Courtesy: Enerzi Microwave Systems Pvt. Ltd., Bangalore, India)

Experimental material

Fresh oyster mushrooms (Pleurotus ostreatus) were obtained from Rural Development Centre, Indian Institute of Technology Kharagpur, India. The growth conditions of the analyzed mushrooms were similar to those normally available to the consumers. Mushrooms were disinfected by dipping in solution of 0.25 % potassium metabisulphite and 0.1 % citric acid for 5 min. After disinfection, stalks (stipe) of the mushrooms were removed by cutting. The pileus (cap) 50 mm in width and 5 mm in thickness were selected to be subjected to drying experiments. Initial moisture content of mushroom was 90.5 ± 1 %, obtained using hot-air oven (Relco-DTC96S1, Kolkata, West Bengal, India) at 105 °C until it reached a fixed weight. Each run in the experiment was performed in triplicate.

Experimental procedure

The dryers were started 1 h prior to the actual experiment, so as to achieve steady-state temperature conditions during each experimental run. The weighed mushroom samples were spread uniformly in a single layer over the tray. Drying experiments were performed at 50, 60 and 70 °C in the recirculatory hot-air dryer and microwave-convective dryer. The air velocity was 1 ± 0.05 m/s for recirculatory hot-air dryer and in microwave-convective dryer the air velocity was set at 0.5, 1 and 1.5 m/s, power density was adjusted to 1 W/g (Funebo and Ohlsson 1998). The input power (W) was displayed on the control panel, which was measured by potentiometer dial control. For measuring output power, 1 L cool tap water was poured into a microwave-safe container and the initial temperature of water was recorded. The container was then placed on the centre of dryer shelf. Water was heated for exactly 62 s at full power, followed by measurement of final temperature. The difference between the final and initial temperature was calculated and the difference was multiplied by factor 70, which was expressed as output power (W). Samples were removed, weighed and replaced; this entire process took less than a minute. Relative humidity of the ambient air changed between 21 % and 23 %. The weight loss of samples was measured using analytical balance (Sartorius TE 153S, Sartorius Weighing India Pvt. Ltd., Bangalore, Karnataka, India) in a range of 0–300 g (±0.001 g) during drying at 5 min interval for first half an hour, then at 10 min for next hour, followed by the 15 min interval till next 1.5 h and finally at every half an hour interval till it reached 5 % moisture content (wb). Dry matter present in the mushroom sample was calculated by using moisture content (wet basis) and amount of the sample subjected to drying. Moisture contents of the dried mushroom samples were also expressed on the dry basis. Each experiment was performed in triplicate.

Theoretical considerations

Modeling of the thin-layer drying curves

For studying the drying characteristics of Pleurotus mushrooms, it is very important to model the drying behavior effectively. The data obtained at different temperatures of drying were fitted into 6 commonly used thin-layer drying models, listed in Table 1. In single layer drying experiments, the moisture ratio of oyster mushrooms was calculated using the following Eq. (1).

$$\mathrm{MR}=\frac{{\mathrm{M}}_{\mathrm{t}}-{\mathrm{M}}_{\mathrm{e}}}{{\mathrm{M}}_0-{\mathrm{M}}_{\mathrm{e}}}$$ 1

The drying rates of oyster mushrooms were calculated using Eq. (2).

$$\mathrm{Drying}\mathrm{Rate}=\frac{M_{t+\mathrm{d}t}-{\mathrm{M}}_t}{\mathrm{d}t}$$ 2

where, M is the moisture content of the product at any time, in g water/g dry matter; M₀ is the initial moisture content of the product, M_e is the equilibrium moisture content, M_t+dt and M_t, are the moisture contents at t + dt and t, respectively, and t is drying time. Over a long period of time the values of M_e becomes insignificant and relatively small as compared to M_t and M₀. Over long period of time, in case of convective drying values for M_e stands negligible (Tulek 2011; Giri and Prasad 2007; Diamente and Munro 1991; Ertekin and Yaldiz 2004 and Thakor et al. 1999). Thus the Eq. 1 can be simplified as

$$\mathrm{MR}=\frac{{\mathrm{M}}_{\mathrm{t}}}{{\mathrm{M}}_{\mathrm{o}}}$$ 3

Correlation coefficient and error analysis

Correlation coefficient (R²), the reduced chi-square (ϰ²) and the root mean square error (RMSE) were calculated so as to evaluate the goodness of fit of the tested mathematical models to the experimental data. The best model describing the thin layer drying characteristics of oyster mushroom was chosen as the one with the lowest reduced chi-square (ϰ²) and RMSE and the highest R². The reduced chi-square (ϰ²) and the root mean square error (RMSE) can be calculated as follows:

$${\mathrm{\chi }}^2=\frac{{\displaystyle {\sum }_{i=1}^N{\left(\mathrm{M}{\mathrm{R}}_{\mathit{exp},\mathrm{i}}-\mathrm{M}{\mathrm{R}}_{\mathrm{pre}\mathit{.}i}\right)}^2}}{N-z}$$ 4

$$\mathrm{RMSE}=\sqrt{\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{\left(\mathrm{M}{\mathrm{R}}_{\mathrm{pre},\mathrm{i}}-\mathrm{M}{\mathrm{R}}_{\mathit{exp}\mathit{.}i}\right)}^2}}$$ 5

where, MR_exp,i is the ith experimental moisture ratio, MR_pre,i is the ith predicted moisture ratio, N is the number of observation and z is the number of constants. In this study, the nonlinear or linear regression analysis was performed using OriginPro 8.5.0 SR1 (OriginLab Corporation, Northampton, Massachusetts, USA).

Calculation of effective diffusivities

Fick’s diffusion equation is generally used to describe the drying characteristics of the biological products in the falling rate period. If we assume that the moisture distribution in the food sample is uniform then Eq. (6) is used to predict the moisture diffusion in food particles with slab geometry.

$$\mathrm{MR}=\frac{8}{{\mathrm{\pi }}^2}{\displaystyle {\sum }_{n=0}^{\infty }\frac{1}{{\left(2\mathrm{n}+1\right)}^2}\exp \left(-\frac{{\left(2\mathrm{n}+1\right)}^2{\mathrm{\pi }}^2{\mathrm{D}}_{\mathrm{eff}}\mathrm{t}}{4{{\mathrm{L}}_0}^2}\right)}$$ 6

where, D_eff is the effective diffusivity (m²/s); L₀ is the half thickness of slab (m) and n is a positive integer. For long drying period, Eq. (6) can be further simplified to only the first term of series (Tutuncu and Labuza 1996). Thus, Eq. (6) can be expressed in logarithmic form as follows:

$$\ln \mathrm{MR}=\ln \frac{8}{{\mathrm{\pi }}^2}-\frac{{\mathrm{\pi }}^2{\mathrm{D}}_{\mathrm{eff}}\mathrm{t}}{4{{\mathrm{L}}_0}^2}$$ 7

Diffusivities are typically determined by plotting experimental drying data in terms of ln MR versus drying time t in Eq. (7), because the plot gives a straight line with a slope as follows (Zhengfu et al. 2007):

$$\mathrm{Slope}=\frac{{\mathrm{\pi }}^2{\mathrm{D}}_{\mathrm{eff}}}{4{{\mathrm{L}}_0}^2}$$ 8

Calculation of activation energy

The temperature dependence of the effective diffusivity has been shown to follow an Arrhenius relationship (Saravacos and Maroulis 2001; Simal et al. 1996).

$${\mathrm{D}}_{\mathrm{eff}}={\mathrm{D}}_0\exp \left(-\frac{{\mathrm{E}}_{\mathrm{a}}}{\mathrm{RT}}\right)$$ 9

where, D₀ is the pre-exponential factor of the Arrhenius equation (m²s⁻¹), E_a is the activation energy (kJ mol⁻¹), R is the universal gas constant (8.314 × 10⁻³ kJ mol⁻¹ K⁻¹), and T is the absolute air temperature (K). The activation energy is determined from the slope of the Arrhenius plot, ln(D_eff) vs. 1/T.

Results and discussion

Analysis of drying characteristics of oyster mushroom

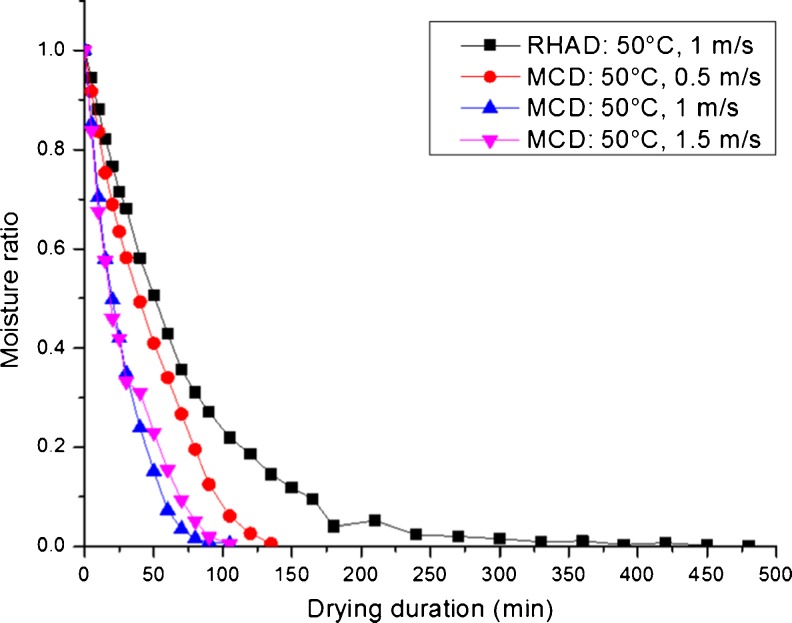
The mushrooms were dried at 50, 60 and 70 °C in the recirculatory hot-air dryer as thin layer with sample thickness of 5 mm, which were spread uniformly in a single layer over the tray. The initial moisture content of mushrooms was about 90.5 ± 1 % (wb). The moisture ratio versus drying duration at different air-velocities for recirculatory hot-air dried and microwave-convective dried oyster mushrooms is shown in Fig. 3 for 50 °C, where moisture ratio of mushroom in first 30 min of drying at 1 m/s in recirculatory hot-air dryer and 0.5, 1 and 1.5 m/s in microwave-convective dryer were 0.682, 0.582, 0.349 and 0.333. Similar results were obtained at 60 and 70 °C in first 30 min of drying.

Fig. 3.

Effect of drying air velocity on moisture ratio of mushrooms in RHAD and MCD at 50 °C

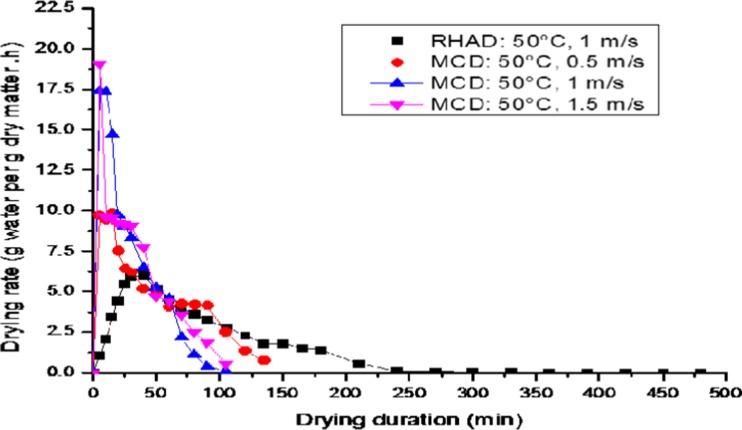
The drying rate versus drying duration at different air-velocities for recirculatory hot-air dried and microwave-convective dried oyster mushrooms is shown in Fig. 4 for 50 °C, the drying rate of mushroom in first 30 min of drying, at 1 m/s in recirculatory hot-air dryer and 0.5, 1 and 1.5 m/s in microwave-convective dryer were 5.913, 6.234, 8.323 and 9.03 g water/g dry matter/h. Similar results were obtained at 60 and 70 °C in first 30 min of drying.

Fig. 4.

Effect of drying air velocity on drying rate of mushrooms in RHAD and MCD at 50 °C

Drying resulted in lowering of moisture content of mushrooms from an initial value of 90.5 ± 1 % (wb) to a final value of 5 % (wb), pronounced moisture loss was observed in the initial stage of drying. To attain a final moisture content of 5 % (wb), it took approximately 480, 420 and 360 min in recirculatory hot-air dryer at 1 m/s at drying temperatures of 50, 60 and 70 °C respectively, whereas it took 135, 105 and 100 min at 0.5 m/s, 105, 90, and 70 min at 1 m/s and 105, 80, and 70 min at 1.5 m/s respectively at drying temperatures of 50, 60 and 70 °C in microwave-convective dryer. Thus, drying time required was lower for microwave-convective drying (MCD) as compared to recirculatory hot-air drying (RHAD).

After first half an hour of drying in both dryers, the moisture content and drying rate decreased gradually. As depicted by drying curves at different temperatures, drying takes place in falling rate period as there is no such constant rate period in the drying of mushrooms (Tulek 2011; Arora et al. 2003; Giri and Prasad 2007). Thus, this shows that diffusion is the governing factor behind the movement of moisture in mushrooms. It was observed that the drying process hastened up as the drying temperature was increased, thus shortening the drying time. The results obtained were in harmony with the drying characteristic studies of Oyster mushrooms performed on a laboratory cabinet type tray dryer (Tulek 2011).

It was observed that with every 10 °C increase in drying temperature from 50 to 70 °C in recirculatory hot-air dryer, the drying time decreased by 12.5 and 14.29 % at 1 m/s of drying air velocity, and for microwave-convective dryer, drying time decreased by 22.22 and 4.76 % at 0.5 m/s of drying air velocity, 14.29 and 22.22 % at 1 m/s of drying air velocity and 23.83 and 12.5 % at 1.5 m/s of drying air velocity. It was observed that with equal increase in drying temperature, drying time did not decrease uniformly. Thus, the drying time reduced by 71.87, 75 and 72 % at 50, 60 and 70 °C respectively by using microwave-convective drying over recirculatory hot-air dryer at 1 m/s of drying air velocity. It was also observed that the drying rate at same air velocity is higher in case of microwave-convective drying as compared to that of recirculatory hot-air dryer.

Fitting of the drying curves

Data obtained from drying experiment, basically the moisture content was converted to moisture ratio (MR) and was fitted to the six models listed in Table 1. As RMSE and ϰ² approach zero, the closer the prediction is to experimental data. Different drying models were compared on the basis of their R², ϰ² and RMSE so as to evaluate their respective goodness of fit. The statistical results of different model including their model coefficients are listed in Tables 2 and 3. In all cases, R² values were higher than 0.9530, ϰ² and RMSE values were lower than 0.00294 and 0.0366, respectively. R² values of Two-term and Midilli et al. (2002) model at all temperatures were higher than 0.98, and corresponding ϰ² and RMSE values were lower than 0.000294 and 0.0141.

Table 2.

Estimated values of the coefficients for selected thin-layer drying models

Drying method	Parameters		Thin layer drying models
	AV* (m/s)	Ta (°C)	Lewis	Page		Henderson & Pabis		Logarithmic			Two-term				Midilli et al. (2002)
			K	k	N	k	a	k	a	c	k0	k1	a	b	k	n	a	b
RHAD	1	50	0.0141	0.0092	1.1006	0.0143	1.0127	0.0142	1.0151	−0.0033	0.0143	0.0474	1.0165	−0.0038	0.0088	1.1107	0.9999	0.00001
		60	0.0141	0.0226	0.8908	0.0138	0.9823	0.0142	0.9750	0.0109	0.0138	0.1409	0.9810	0.0012	0.0236	0.8796	0.9991	0.00001
		70	0.0138	0.0420	0.7469	0.0129	0.9524	0.0150	0.9281	0.0419	0.0129	−0.4864	0.1082	0.8442	0.0586	0.6563	1.0003	−0.0002
MCD	0.5	50	0.0196	0.0112	1.1420	0.0202	1.0269	0.0140	1.1818	−0.1910	0.0202	0.0520	0.3070	0.7200	0.0176	0.9749	0.9983	−0.0010
		60	0.0297	0.0137	1.2201	0.0314	1.0510	0.0263	1.1091	−0.0792	0.0314	0.0520	0.9830	0.0681	0.0136	1.2185	0.9955	−0.0001
		70	0.0314	0.0166	1.1827	0.0329	1.0423	0.0276	1.0972	−0.0763	0.0329	0.0520	0.9850	0.0574	0.0185	1.1412	0.9986	−0.0002
	1	50	0.0367	0.0259	1.1042	0.0376	1.0213	0.0332	1.0551	−0.0497	0.0376	0.0520	0.9830	0.0382	0.0289	1.0580	0.9968	−0.0003
		60	0.0337	0.0207	1.1425	0.0346	1.0241	0.0279	1.0957	−0.0961	0.0346	0.0538	0.9939	0.0302	0.0243	0.0243	0.9905	−0.0006
		70	0.0363	0.0220	1.1504	0.0375	1.0282	0.0303	1.1026	−0.0977	0.0375	0.0520	0.9830	0.0451	0.0265	1.0708	0.9963	−0.0006
	1.5	50	0.0292	0.0182	1.1328	0.0298	1.0171	0.0232	1.1032	−0.1139	0.0298	0.0520	0.9830	0.0341	0.0206	1.0636	0.9810	−0.0006
		60	0.0489	0.0255	1.2124	0.0510	1.0404	0.0443	1.0872	−0.0622	0.0510	0.0520	0.9830	0.0574	0.0264	1.1960	0.9987	−0.0001
		70	0.0471	0.0274	1.1737	0.0488	1.0330	0.0415	1.0865	−0.0711	0.0488	0.0520	0.9830	0.0499	0.0305	1.1274	0.9989	−0.0004

AV* air velocity, T ^a Drying temperature, RHAD Recirculatory hot-air drying, MCD Microwave convective drying

Table 3.

Statistical analysis of different thin layer drying models

Drying method	Parameters		Thin-layer drying models
	AV* (m/s)	Ta (°C)	Lewis			Page			Henderson and Pabis			Logarithmic			Two-term			Midilli et al. (2002)
			R2	ϰ2	RMSE	R2	ϰ2	RMSE	R2	ϰ2	RMSE	R2	ϰ2	RMSE	R2	ϰ2	RMSE	R2	ϰ2	RMSE
RHAD	1	50	0.9785	0.0003	0.0091	0.9530	0.0001	0.0062	0.9778	0.0003	0.0087	0.9775	0.0003	0.0087	0.9875	0.0003	0.0087	0.9876	0.0002	0.0056
		60	0.9664	0.0004	0.0112	0.9848	0.0002	0.0069	0.9764	0.0004	0.0107	0.9696	0.0004	0.0100	0.9896	0.0005	0.0107	0.9980	0.0002	0.0067
		70	0.9788	0.0025	0.0263	0.9561	0.0005	0.0104	0.9789	0.0025	0.0242	0.9806	0.0023	0.0213	0.9847	0.0029	0.0242	0.9976	0.0003	0.0066
MCD	0.5	50	0.9768	0.0014	0.0366	0.9720	0.0009	0.0275	0.9872	0.0014	0.0348	0.9798	0.0002	0.0127	0.9862	0.0015	0.0348	0.9979	0.0002	0.0130
		60	0.9790	0.0013	0.0345	0.9795	0.0001	0.0071	0.9720	0.0009	0.0283	0.9797	0.0004	0.0177	0.9813	0.0010	0.0283	0.9995	0.0001	0.0065
		70	0.9716	0.0010	0.0300	0.9816	0.0001	0.0093	0.9794	0.0008	0.0254	0.9798	0.0002	0.0116	0.9829	0.0008	0.0254	0.9997	0.00004	0.0053
	1	50	0.9750	0.0006	0.0228	0.9741	0.0003	0.0158	0.9695	0.0005	0.0215	0.9798	0.0002	0.0120	0.9948	0.0006	0.0215	0.9982	0.0002	0.0120
		60	0.9723	0.0009	0.0281	0.9709	0.0003	0.0164	0.9693	0.0008	0.0265	0.9799	0.0001	0.0092	0.9918	0.0009	0.0265	0.9990	0.0001	0.0088
		70	0.9723	0.0009	0.0280	0.9726	0.0003	0.0147	0.9793	0.0008	0.0257	0.9890	0.0001	0.0091	0.9920	0.0009	0.0257	0.9991	0.0001	0.0082
	1.5	50	0.9703	0.0011	0.0314	0.9745	0.0006	0.0227	0.9690	0.0011	0.0306	0.9779	0.0002	0.0136	0.9891	0.0012	0.0306	0.9975	0.00003	0.0141
		60	0.9708	0.0011	0.0313	0.9792	0.0001	0.0090	0.9792	0.0009	0.0275	0.9862	0.0005	0.0181	0.9912	0.0010	0.0275	0.9991	0.0001	0.0085
		70	0.9729	0.0008	0.0271	0.9899	0.0001	0.0090	0.9638	0.0007	0.0241	0.9872	0.0001	0.0104	0.9930	0.0008	0.0241	0.9998	0.00002	0.0043

AV* air velocity, T ^a Drying temperature, RHAD Recirculatory hot-air drying, MCD Microwave convective drying

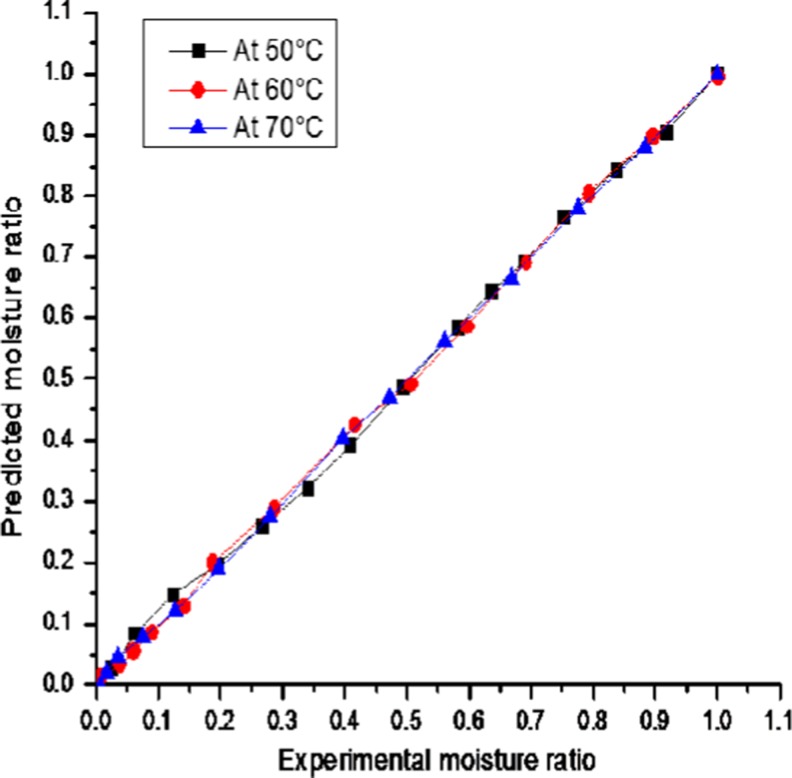
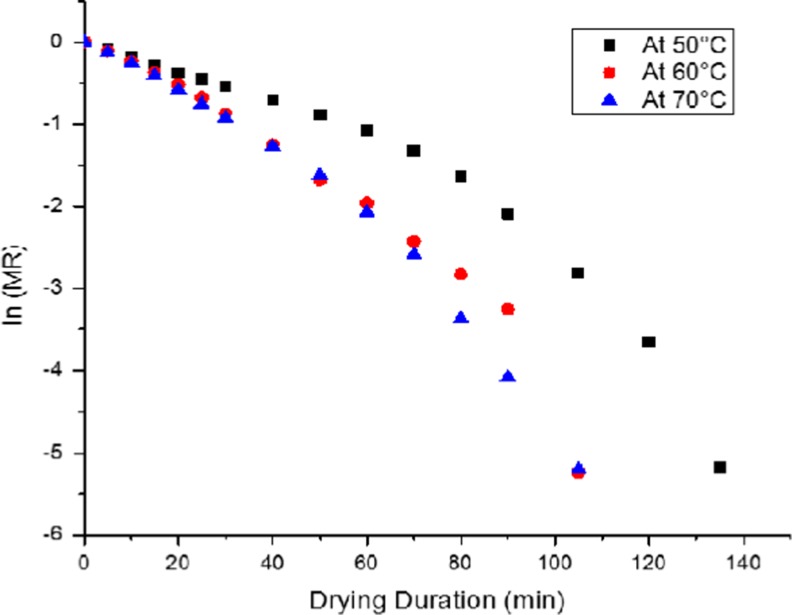
Figure 5 shows the comparative analysis of different drying models at the drying temperature of 50 °C in recirculatory hot-air dryer at air velocity of 1 m/s, similar results can also be obtained at in microwave convective dryer at different air velocity and drying temperatures. It was observed that at certain levels under and over estimation occurred while comparing with the experimental data. During the first 60 min Lewis model developed by Bruce (1985), Page model developed by Page (1949), Henderson and Pabis model developed by Henderson and Pabis (1961), Logarithmic model developed by Togrul and Pehlivan (2002) and Two-term model developed by Henderson (1974) presented underestimation in moisture ratio (above experimental value). Till 120 min Henderson and Pabis model, Lewis model and Logarithmic model presented overestimation in moisture ratio (below experimental value). Henderson and Pabis model and Two-term model present underestimation during time period of 180 to 300 min and then 300 min onwards present overestimation in moisture ratio. Lewis model present underestimation in moisture ratio during period of 180 to 360 min, whereas present overestimation in moisture ratio during period of 360 to 480 min. On the contrary, Midilli et al. (2002) fits the experimental data perfectly during entire drying process (Fig. 6). Thus among all six drying models, Midilli et al. (2002) model yielded a highest R² value which varied from 0.988 to 0.999 in both the dryers for all drying temperature, ϰ² and RMSE values were also comparatively lower and varied from 0.00027 to 0.000023 and 0.0141 to 0.0043. The goodness of fit calculated for fitting the experimental data was satisfactory, so this model was finally chosen to predict the drying characteristics of mushroom in both recirculatory hot-air and microwave-convective dryer.

Fig. 5.

Midilli et al. (2002) model fitted to the drying data for MCD at 0.5 m/s

Fig. 6.

ln MR vs drying duration at 0.5 m/s at different drying temperatures in MCD

Determination of effective diffusivities and activation energy

The average values of effective diffusivities of oyster mushrooms in drying process at 50 to 70 °C, at an air velocity of 1 m/s in recirculatory hot-air dryer varied from 2.87 × 10⁻⁸ to 3.17 × 10⁻⁸ m²/s, whereas in case of microwave-convective dryer at 1 m/s the effective diffusivity varied from 11.09 × 10⁻⁸ to 12.39 × 10⁻⁸ m²/s. As, expected effective diffusivity increased with increase in drying temperature and air velocity, it was also observed that the effective diffusivity values were higher for microwave-convective dryer as compared to recirculatory hot-air dryer (Table 4).

Table 4.

Effective diffusivity and activation energy of RHAD and MCD

Dryer	Air velocity (m/s)	Deff (m2/s)	Ea (kJ/mol)
RHAD	1	2.87*10−8 to 3.17*10−8	21.998
MCD	0.5	7.04*10−8to 10.62*10−8	18.558
	1	11.09*10−8 to 12.39*10−8	17.126
	1.5	10.16*10−8 to 16.1798*10−8	16.945

The logarithm of effective diffusivity as a function of reciprocal of absolute temperature was plotted, and the activation energy was calculated. Unlike conventional warming systems, microwaves penetrate food and expand heat throughout the material (Schiffman 1992). As microwave penetrates food, a gradient is created wherein the moisture migrates towards the superficial layers of food and is simultaneously carried away by the hot-air. As the result, in microwave-convective drying less energy is required to facilitate diffusion of moisture from food, resulting in lowering of activation energy. Thus, the activation energy required in microwave-convective dryer was found to be lower than recirculatory hot-air dryer. Even for same air velocity of 1 m/s, the activation energy was 21.998 kJ/mol for recirculatory hot-air dryer, whereas for microwave-convective dryer it was 17.126 kJ/mol. These results were in agreement with the previous investigations done on calculation of activation energy of Oyster mushrooms (Tulek 2011). The lower activation energy in case of microwave-convective drying indicates that drying of mushroom requires less energy and is hence a cost and energy-saving method.

Conclusion

The characteristics of oyster mushrooms with 5 mm of the thickness in microwave convective dryer and recirculatory hot-air dryer were studied, the thin layer drying kinetics was analyzed, and six commonly used models were used to fit the experimental data. The results indicate that the Midilli et al. (2002) model fits the drying experimental data better than the others; the drying time of oyster mushroom decreases and the effective diffusivity increases as the drying air velocity increases; the whole drying process of oyster mushrooms took place in a falling rate period, the heating temperature was in range between 50 and 70 °C. In case of temperature above 70 °C, a charred phenomenon was observed in dried samples. The most important aspect of drying technology is the mathematical modelling of the drying processes and equipment. Its purpose is to allow design engineers to choose the most suitable operating conditions and then size the drying equipment and drying chamber accordingly to meet desired operating conditions. The principle of modelling is based on having a set of mathematical equations that can adequately characterize the system. In particular, the solution of these equations must allow prediction of the process parameters as a function of time at any point in the dryer based only on the initial conditions (Günhan et al. 2005). The study showed that the convective-microwave drying of mushroom was much faster than conventional hot-air drying, particularly towards the end of the drying process. At the same air velocity of 1 m/s the drying time reduction in microwave-convective dryer was up to 75 %. The moisture transfer can be described by diffusion, where the effective diffusivities were within ranges as predicted by the previous experiments on drying of Oyster mushroom, and the temperature dependence of the effective moisture diffusivities was shown to follow an Arrhenius relationship. The effective diffusivity was observed to vary with the type of drying and the drying conditions. Lowest activation energy was required to facilitate diffusion in a microwave-convective dryer at 1.5 m/s. Thus, microwave-convective drying proved to be an effective drying method over recirculatory hot-air drying for drying of oyster mushroom, as the microwave drying offers opportunities as less drying time, uniform energy and high thermal conductivity to the inner sides of the material, space utilization, sanitation, energy saving, precise process control, fast start-up and shut down conditions with high quality finished products (Decareau 1992; Zhang et al. 2006).