Combining multidimensional genomic measurements for predicting cancer prognosis: observations from TCGA

Abstract

With accumulating research on the interconnections among different types of genomic regulations, researchers have found that multidimensional genomic studies outperform one-dimensional studies in multiple aspects. Among many sources of multidimensional genomic data, The Cancer Genome Atlas (TCGA) provides the public with comprehensive profiling data on >30 cancer types, making it an ideal test bed for conducting and comparing different analyses. In this article, the analysis goal is to apply several existing methods and associate multidimensional genomic measurements with cancer outcomes in particular prognosis, with special focus on the predictive power of genomic signatures. We exploit clinical data and four types of genomic measurement including mRNA gene expression, DNA methylation, microRNA and copy number alterations for breast invasive carcinoma, glioblastoma multiforme, acute myeloid leukemia and lung squamous cell carcinoma collected by TCGA. To accommodate the high dimensionality, we extract important features using Principal Component Analysis, Partial Least Squares and Least Absolute Shrinkage and Selection Operator (Lasso), which are representative of dimension reduction and variable selection techniques and have been extensively adopted, and fit Cox survival models with combined important features. We calibrate the predictive power of each type of genomic measurement for the prognosis of four cancer types and find that the results vary across cancers. Our analysis also suggests that for most of the cancers in our study and the adopted methods, there is no substantial improvement in prediction when adding other genomic measurement after gene expression and clinical covariates have been included in the model. This is consistent with the findings that molecular features measured at the transcription level affect clinical outcomes more directly than those measured at the DNA/epigenetic level.

INTRODUCTION

In the past decade, cancer research has entered the era of personalized medicine, where a person’s individual molecular and genetic profiles are used to drive therapeutic, diagnostic and prognostic advances [1]. In order to realize it, we are facing a number of critical challenges. Among them, the complexity of molecular architecture of cancer, which manifests itself at the genetic, genomic, epigenetic, transcriptomic and proteomic levels, is the first and most fundamental one that we need to gain more insights into. With the fast development in genome technologies, we are now equipped with data profiled on multiple layers of genomic activities, such as mRNA-gene expression, DNA methylation, microRNA, copy number alterations (CNA) and so on. A limitation of many early cancer-genomic studies is that the ‘one-dimensional’ analysis of a single type of genomic measurement was conducted, most frequently on mRNA-gene expression. They can be insufficient to fully exploit the knowledge of cancer genome, underline the etiology of cancer development and inform prognosis. Recent studies have noted that it is necessary to collectively analyze multidimensional genomic measurements. One of the most significant contributions to accelerating the integrative analysis of cancer-genomic data have been made by The Cancer Genome Atlas (TCGA, https://tcga-data.nci.nih.gov/tcga/), which is a combined effort of multiple research institutes organized by NCI. In TCGA, the tumor and normal samples from over 6000 patients have been profiled, covering 37 types of genomic and clinical data for 33 cancer types. Comprehensive profiling data have been published on cancers of breast, ovary, bladder, head/neck, prostate, kidney, lung and other organs, and will soon be available for many other cancer types.

Multidimensional genomic data carry a wealth of information and can be analyzed in many different ways [2–15]. A large number of published studies have focused on the interconnections among different types of genomic regulations [2, 5–8, 12–14]. For example, studies such as [5, 6, 14] have correlated mRNA-gene expression with DNA methylation, CNA and microRNA. Multiple genetic markers and regulating pathways have been identified, and these studies have thrown light upon the etiology of cancer development. In this article, we conduct a different type of analysis, where the goal is to associate multidimensional genomic measurements with cancer outcomes and phenotypes. Such analysis can help bridge the gap between genomic discovery and clinical medicine and be of practical importance. Several published studies [4, 9–11, 15] have pursued this kind of analysis. In the study of the association between cancer outcomes/phenotypes and multidimensional genomic measurements, there are also multiple possible analysis objectives. Many studies have been interested in identifying cancer markers, which has been a key scheme in cancer research. We acknowledge the importance of such analyses. In this article, we take a different perspective and focus on predicting cancer outcomes, especially prognosis, using multidimensional genomic measurements and several existing methods.

Consider mRNA-gene expression, methylation, CNA and microRNA measurements, which are commonly available in the TCGA data. We note that the analysis we conduct is also applicable to other datasets and other types of genomic measurement. We choose TCGA data not only because TCGA is one of the largest publicly available and high-quality data sources for cancer-genomic studies, but also because they are being analyzed by multiple research groups, making them an ideal test bed. Literature review suggests that for each individual type of measurement, there are studies that have shown good predictive power for cancer outcomes. For instance, patients with glioblastoma multiforme (GBM) who were grouped on the basis of expressions of 42 probe sets had significantly different overall survival with a P-value of 0.0006 for the log-rank test. In parallel, patients grouped on the basis of two different CNA signatures had prediction log-rank P-values of 0.0036 and 0.0034, respectively [16]. DNA-methylation data in TCGA GBM were used to validate CpG island hypermethylation phenotype [17]. The results showed a log-rank P-value of 0.0001 when comparing the survival of subgroups. And in the original EORTC study, the signature had a prediction c-index 0.71. Goswami and Nakshatri [18] studied the prognostic properties of microRNAs identified before in cancers including GBM, acute myeloid leukemia (AML) and lung squamous cell carcinoma (LUSC) and showed that the sum of expressions of different hsa-mir-181 isoforms in TCGA AML data had a Cox-PH model P-value < 0.001. Similar performance was found for miR-374a in LUSC and a 10-miRNA expression signature in GBM. A context-specific microRNA-regulation network was constructed to predict GBM prognosis and resulted in a prediction AUC [area under receiver operating characteristic (ROC) curve] of 0.69 in an independent testing set [19]. However, it has also been observed in many studies that the prediction performance of omic signatures vary significantly across studies, and for most cancer types and outcomes, there is still a lack of a consistent set of omic signatures with satisfactory predictive power. Thus, our first goal is to analyze TCGA data and calibrate the predictive power of each type of genomic measurement for the prognosis of several cancer types. In multiple studies, it has been shown that collectively analyzing multiple types of genomic measurement can be more informative than analyzing a single type of measurement. There is convincing evidence showing that this is true for understanding cancer biology. However, it is less clear whether combining multiple types of measurements can lead to better prediction. Thus, ‘our second goal is to quantify whether improved prediction can be achieved by combining multiple types of genomic measurements in TCGA data’.

METHODS

We analyze prognosis data on four cancer types, namely “breast invasive carcinoma (BRCA), glioblastoma multiforme (GBM), acute myeloid leukemia (AML), and lung squamous cell carcinoma (LUSC)”. Breast cancer is the most frequently diagnosed cancer and the second cause of cancer deaths in women. Invasive breast cancer involves both ductal carcinoma (more common) and lobular carcinoma that have spread to the surrounding normal tissues. GBM is the first cancer studied by TCGA. It is the most common and deadliest malignant primary brain tumors in adults. Patients with GBM usually have a poor prognosis, and the median survival time is ∼15 months. The 5-year survival rate is as low as 4%. Compared with some other diseases, the genomic landscape of AML is less defined, especially in cases without recognizable karyotype abnormalities, which consist of ∼40% of all adult patients. The outcome is usually grim for them since the cytogenetic risk can no longer help guide the decision for their treatment [20]. Lung cancer accounts for ∼28% of all cancer deaths, more than any other cancers in both men and women. The prognosis for lung cancer is poor. Most lung-cancer patients are diagnosed with advanced cancer, and only 16% of the patients will survive for 5 years after diagnosis. LUSC is a subtype of the most common type of lung cancer—non-small cell lung carcinoma.

Data collection

The data information flowed through TCGA pipeline and was collected, reviewed, processed and analyzed in a combined effort of six different cores: Tissue Source Sites (TSS), Biospecimen Core Resources (BCRs), Data Coordinating Center (DCC), Genome Characterization Centers (GCCs), Sequencing Centers (GSCs) and Genome Data Analysis Centers (GDACs) [21]. The retrospective biospecimen banks of TSS were screened for newly diagnosed cases, and tissues were reviewed by BCRs to ensure that they satisfied the general and cancer-specific guidelines such as no <80% tumor nuclei were required in the viable portion of the tumor. Then RNA and DNA extracted from qualified specimens were distributed to GCCs and GSCs to generate molecular data. For example, in the case of BRCA [22], mRNA-expression profiles were generated using custom Agilent 244 K array platforms. MicroRNA expression levels were assayed via Illumina sequencing using 1222 miRBase v16 mature and star strands as the reference database of microRNA transcripts/genes. Methylation at CpG dinucleotides were measured using the Illumina DNA Methylation assay. DNA copy-number analyses were performed using Affymetrix SNP6.0. For the other three cancers, the genomic features might be assayed by a different platform because of the changing assay technologies over the course of the project. Some platforms were replaced with upgraded versions, and some array-based assays were replaced with sequencing. All submitted data including clinical metadata and omics data were deposited, standardized and validated by DCC. Finally, DCC made the data accessible to the public research community while protecting patient privacy.

All data are downloaded from TCGA Provisional as of September 2013 using the CGDS-R package. The obtained data include clinical information, mRNA gene expression, CNAs, methylation and microRNA. Brief data information is provided in Tables 1 and 2. We refer to the TCGA website for more detailed information. The outcome of the most interest is overall survival. The observed death rates for the four cancer types are 10.3% (BRCA), 76.1% (GBM), 66.5% (AML) and 33.7% (LUSC), respectively. For GBM, disease-free survival is also studied (for more information, see Supplementary Appendix).

Table 1:

Clinical information on the four datasets

	BRCA	GBM	AML	LUSC
Number of patients	403	299	136	90
Clinical outcomes
Overall survival (month)	(0.07, 115.4)	(0.1, 129.3)	(0.9, 95.4)	(0.8, 176.5)
Event rate	8.93%	72.24%	61.80%	37.78%
Clinical covariates
Age at initial pathology diagnosis	(27, 89)	(10, 89)	(18, 88)	(40, 84)
Race (white versus non-white)	299/104	273/26	126/10	49/41
Gender (male versus female)		174/125	73/63	67/23
WBC (>16 versus ≤16)			105/21
ER status (positive versus negative)	314/89
PR status (positive versus negative)	266/137
HER2 final status
Positive	76
Equivocal	71
Negative	256
Cytogenetic risk
Favorable			28
Normal/intermediate			82
Poor			26
Tumor stage code (T1 versus T_other)	113/290
Lymph node stage (positive versus negative)	200/203
Metastasis stage code (positive versus negative)	10/393
Recurrence status		6
Primary/secondary cancer		281/18
Smoking status
Current smoker				16
Current reformed smoker >15				18
Current reformed smoker ≤15				56
Tumor stage code (positive versus negative)				34/56
Lymph node stage (positive versus negative)				13/77

Table 2:

Genomic information on the four datasets

Number of patients	BRCA	GBM	AML	LUSC
	403	299	136	90
Omics data
Gene expression
Platform	Agilent 244 K custom gene expression G4502A_07	Agilent 244 K custom gene expression G4502A_07	Affymetrix human genome HG-U133_Plus_2	Agilent 244 K custom gene expression G4502A_07
Number of patients	526	500	173	154
Features before clean	15 639	16 407	18 131	15 521
Features after clean	Top 2500	Top 2500	Top 2500	Top 2500
DNA methylation
Platform	Illumina DNA methylation 27/450 (combined)	Illumina DNA methylation 27/450 (combined)	Illumina DNA methylation 450	Illumina DNA methylation 27/450 (combined)
Number of patients	929	398	194	385
Features before clean	1662	1622	14 959	1578
Features after clean	1662	1622	Top 2500	1578
miRNA
Platform	IlluminaGA/HiSeq_miRNASeq (combined)	Agilent 8*15 k human miRNA-specific microarray		IlluminaGA/HiSeq_miRNASeq (combined)
Number of patients	983	496		512
Features before clean	1046	534		1046
Features after clean	415	534		430
CAN
Platform	Affymetrix genome-wide human SNP array 6.0	Affymetrix genome-wide human SNP array 6.0	Affymetrix genome-wide human SNP array 6.0	Affymetrix genome-wide human SNP array 6.0
Number of patients	934	563	191	178
Features before clean	20 500	20 501	20 501	17 869
Features after clean	Top 2500	Top 2500	Top 2500	Top 2500

For clinical covariates, we collect those suggested by the notable papers [22–25] that the TCGA research network has published on each of the four cancers. For BRCA, we include age, race, clinical calls for estrogen receptor (ER), progesterone (PR) and human epidermal growth factor receptor 2 (HER2), and pathologic stage fields of T, N, M. In terms of HER2 Final Status, Florescence in situ hybridization (FISH) is used to supplement the information on immunohistochemistry (IHC) value. Fields of pathologic stages T and N are made binary, where T is coded as T1 and T_other, corresponding to a smaller tumor size (≤2 cm) and a larger (>2 cm) tumor size, respectively. N is coded as negative corresponding to N0 and Positive corresponding to N1–N3, respectively. M is coded as Positive for M1 and negative for others. For GBM, age, gender, race, and whether the tumor was primary and previously untreated, or secondary, or recurrent are considered. For AML, in addition to age, gender and race, we have white cell counts (WBC), which is coded as binary, and cytogenetic classification (favorable, normal/intermediate, poor). For LUSC, we have in particular smoking status for each individual in clinical information.

For genomic measurements, we download and analyze the processed level 3 data, as in many published studies. Elaborated details are provided in the published papers [22–25]. In brief, for gene expression, we download the robust Z-scores, which is a form of lowess-normalized, log-transformed and median-centered version of gene-expression data that takes into account all of the gene-expression arrays under consideration. It determines whether a gene is up- or down-regulated relative to the reference population. For methylation, we extract the beta values, which are scores calculated from methylated (M) and unmethylated (U) bead types and measure the percentages of methylation. They range from zero to one. For CNA, the loss and gain levels of copy-number changes have been identified using segmentation analysis and GISTIC algorithm and expressed in the form of log₂ ratio of a sample versus the reference intensity. For microRNA, for GBM, we use the available expression-array-based microRNA data, which have been normalized in the same way as the expression-array-based gene-expression data. For BRCA and LUSC, expression-array data are not available, and RNA-sequencing data normalized to reads per million reads (RPM) are used, that is, the reads corresponding to particular microRNAs are summed and normalized to a million microRNA-aligned reads. For AML, microRNA data are not available.

Data processing

The four datasets are processed in a similar manner. In Figure 1, we provide the flowchart of data processing for BRCA. The total number of samples is 983. Among them, 971 have clinical data (survival outcome and clinical covariates) available. We remove 60 samples with overall survival time missing or equal to 0. Male breast cancer is relatively rare, and in our situation, it accounts for only 1% of the total sample. Thus we remove those male cases, resulting in 901 samples. For mRNA-gene expression, 526 samples have 15 639 features profiled. There are a total of 2464 missing observations. As the missing rate is relatively low, we adopt the simple imputation using median values across samples. In principle, we can analyze the 15 639 gene-expression features directly. However, considering that the number of genes related to cancer survival is not expected to be large, and that including a large number of genes may create computational instability, we conduct a supervised screening. Here we fit a Cox regression model to each gene-expression feature, and then select the top 2500 for downstream analysis. For a very small number of genes with extremely low variations, the Cox model fitting does not converge. Such genes can either be directly removed or fitted under a small ridge penalization (which is adopted in this study). For methylation, 929 samples have 1662 features profiled. There are a total of 850 missing observations, which are imputed using medians across samples. No further processing is conducted. For microRNA, 1108 samples have 1046 features profiled. There is no missing measurement. We add 1 and then conduct log₂ transformation, which is frequently adopted for RNA-sequencing data normalization and applied in the DESeq2 package [26]. Out of the 1046 features, 190 have constant values and are screened out. In addition, 441 features have median absolute deviations exactly equal to 0 and are also removed. Four hundred and fifteen features pass this unsupervised screening and are used for downstream analysis. For CNA, 934 samples have 20 500 features profiled. There is no missing measurement. And no unsupervised screening is conducted. With concerns on the high dimensionality, we conduct supervised screening in the same manner as for gene expression. In our analysis, we are interested in the prediction performance by combining multiple types of genomic measurements. Thus we merge the clinical data with four sets of genomic data. A total of 466 samples have all the measurements available for downstream analysis. Because of our specific analysis goal, the number of samples used for analysis is considerably smaller than the starting number.

Figure 1:

Flowchart of data processing for the BRCA dataset.

For all four datasets, more information on the processed samples is provided in Table 1. The sample sizes used for analysis are 403 (BRCA), 299 (GBM), 136 (AML) and 90 (LUSC) with event (death) rates 8.93%, 72.24%, 61.80% and 37.78%, respectively. Multiple platforms have been used. For example for methylation, both Illumina DNA Methylation 27 and 450 were used.

Feature extraction

For cancer prognosis, our goal is to build models with predictive power. With low-dimensional clinical covariates, it is a ‘standard’ survival model fitting problem. However, with genomic measurements, we face a high-dimensionality problem, and direct model fitting is not applicable.

Denote as the survival time and as the random censoring time. Under right censoring, one observes For simplicity of notation, consider a single type of genomic measurement, say gene expression. Denote as the gene-expression features. Assume iid observations. We note that D ≫ n, which poses a high-dimensionality problem here. For the working survival model, assume the Cox proportional hazards model. Other survival models may be studied in a similar manner. Consider the following ways of extracting a small number of important features and building prediction models.

Principal component analysis

Principal component analysis (PCA) is perhaps the most extensively used ‘dimension reduction’ technique, which searches for a few important linear combinations of the original measurements. The method can effectively overcome collinearity among the original measurements and, more importantly, significantly reduce the number of covariates included in the model. For discussions on the applications of PCA in genomic data analysis, we refer to [27] and others. PCA can be easily conducted using singular value decomposition (SVD) and is achieved using R function prcomp() in this article. Denote as the PCs. Following [28], we take the first few (say P) PCs and use them in survival model fitting. are uncorrelated, and the variation explained by decreases as increases.

The standard PCA technique defines a single linear projection, and possible extensions involve more complex projection methods. One extension is to obtain a probabilistic formulation of PCA from a Gaussian latent variable model, which has been proposed in [29]. Others include the sparse PCA and PCA that is constrained to certain subsets. We adopt the standard PCA because of its simplicity, representativeness, extensive applications and satisfactory empirical performance.

Partial least squares

Partial least squares (PLS) is also a dimension-reduction technique. Unlike PCA, when constructing linear combinations of the original measurements, it utilizes information from the survival outcome for the weight as well. The standard PLS method can be carried out by constructing orthogonal directions Z_m’s using X’s weighted by the strength of their effects on the outcome and then orthogonalized with respect to the former directions. More detailed discussions and the algorithm are provided in [28]. In the context of high-dimensional genomic data, Nguyen and Rocke [30] proposed to apply PLS in a two-stage manner. They used linear regression for survival data to determine the PLS components and then applied Cox regression on the resulted components. Bastien [31] later replaced the linear regression step by Cox regression. The comparison of different methods can be found in Lambert-Lacroix S and Letue F, unpublished data.

Considering the computational burden, we choose the method that replaces the survival times by the deviance residuals in extracting the PLS directions, which has been shown to have a good approximation performance [32]. We implement it using R package plsRcox.

Least absolute shrinkage and selection operator

Least absolute shrinkage and selection operator (Lasso) is a penalized ‘variable selection’ method. As described in [33], Lasso applies model selection to choose a small number of ‘important’ covariates and achieves parsimony by generating coefficients that are exactly zero. The penalized estimate under the Cox proportional hazard model [34, 35] can be written as

where 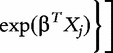denotes the log-partial-likelihood and is a tuning parameter. The method is implemented using R package glmnet in this article. The tuning parameter is chosen by cross validation. We take a few (say P) important covariates with non-zero effects and use them in survival model fitting.

There are a large number of variable selection methods. We choose penalization, since it has been attracting a lot of attention in the statistics and bioinformatics literature. Comprehensive reviews can be found in [36, 37]. Among all the available penalization methods, Lasso is perhaps the most extensively studied and adopted. We note that other penalties such as adaptive Lasso, bridge, SCAD, MCP and others are potentially applicable here. It is not our intention to apply and compare multiple penalization methods.

Under the Cox model, the hazard function with the selected features is of the form where is an unspecified baseline-hazard function, and is the unknown vector of regression coefficients. The selected features can be the first few PCs from PCA, the first few directions from PLS, or the few covariates with nonzero effects from Lasso.

Model evaluation

In the area of clinical medicine, it is of great interest to evaluate the predictive power of an individual or composite marker. We focus on evaluating the prediction accuracy in the concept of discrimination, which is commonly referred to as the ‘C-statistic’. For binary outcome, popular measures such as the ROC curve and AUC belong to this category. Simply put, the C-statistic is an estimate of the conditional probability that for a randomly chosen pair (a case and control), the prognostic score calculated using the extracted features is higher for the case. When the C-statistic is ∼0.5, the prognostic score is no better than a coin-flip in determining the survival outcome of a patient. On the other hand, when it is close to 1 (0, usually transforming values <0.5 to those >0.5), the prognostic score always accurately determines the prognosis of a patient. For more relevant discussions and new developments, we refer to [38, 39] and others. For a censored survival outcome, the C-statistic is essentially a rank-correlation measure, to be specific, some linear function of the modified Kendall’s τ [40]. Several summary indexes have been pursued employing different techniques to cope with censored survival data [41–43]. We choose the censoring-adjusted C-statistic which is described in details in Uno et al. [42] and implement it using R package survAUC. The C-statistic with respect to a pre-specified time point τ can be written as

where is the indicator function and is the Kaplan–Meier estimator for the survival function of the censoring time Finally, the summary C-statistic is the weighted integration of time-dependent . , where is proportional to is the Kaplan–Meier estimator, and a discrete approximation to is based on increments in the Kaplan–Meier estimator [41]. It has been shown that the nonparametric estimator of C-statistic based on the inverse-probability-of-censoring weights is consistent for a population concordance measure that is free of censoring [42].

ANALYSES

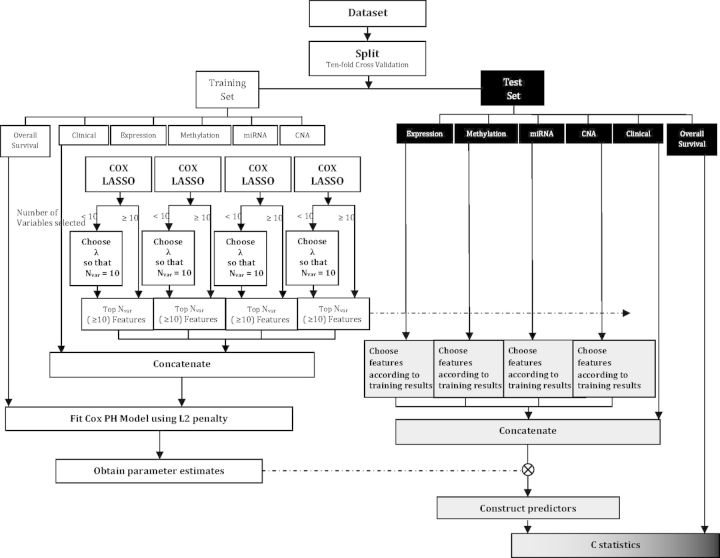
Ideally, prediction evaluation involves clearly defined independent training and testing data. In TCGA, there is no clear-cut training set versus testing set. In addition, considering the moderate sample sizes, we resort to cross-validation-based evaluation, which consists of the following steps.

1. Randomly split data into ten parts with equal sizes.

2. Fit different models using nine parts of the data (training). The model construction procedure has been described in Section 2.3.

3. Apply the training data model, and make prediction for subjects in the remaining one part (testing). Compute the prediction C-statistic.

4. Repeat (b) and (c) over all ten parts of the data, and compute the average C-statistic.

5. Randomness may be introduced in the split step (a). To be more objective, repeat Steps (a)–(d) 500 times. Compute the average C-statistic. In addition, the 500 C-statistics can also generate the ‘distribution’, as opposed to a single statistic.

The LUSC dataset have a relatively small sample size. We have experimented with splitting into 10 parts and found that it leads to a very small sample size for the testing data and generates unreliable results. Thus, we split into five parts for this specific dataset. To establish the ‘baseline’ of prediction performance and gain more insights, we also randomly permute the observed time and event indicators and then apply the above procedures. Here there is no association between prognosis and clinical or genomic measurements. Thus a fair evaluation procedure should lead to the average C-statistic ∼0.5. In addition, the distribution of C-statistic under permutation may inform us of the variation of prediction. A flowchart of the above procedure is provided in Figure 2.

Figure 2:

Flowchart of data analysis.

PCA–Cox model

For PCA–Cox, we select the top 10 PCs with their corresponding variable loadings for each genomic data in the training data separately. After that, we extract the same 10 components from the testing data using the loadings of the training data. Then they are concatenated with clinical covariates. With the small number of extracted features, it is possible to directly fit a Cox model. We add a very small ridge penalty to obtain a more stable estimate without seriously modifying the model structure. After building the vector of predictors, we are able to evaluate the prediction accuracy. Here we acknowledge the subjectiveness in the choice of the number of top features selected. The consideration is that too few selected features may lead to insufficient information, and too many selected features may create problems for the Cox model fitting. We have experimented with a few other numbers of features and reached similar conclusions.

PLS–Cox model

For PLS–Cox, we select the top 10 directions with the corresponding variable loadings as well as weights and orthogonalization information for each genomic data in the training data separately. After that, we form the 10 directions for the testing data using the extracted information. Then they are concatenated with clinical covariates. The other steps are the same as the PCA–Cox.

Lasso–Cox model

For Lasso–Cox, if the cross-validated tuning parameter leads to more than 10 selected variables, then those variables are used in downstream analysis. If fewer than 10 variables are selected, we modify the tuning parameter value until 10 variables are selected. For simplicity in calculation, in one equation, we apply the same amount of penalization to all variables. In principle, we can apply the approach in [43] and allow for different degrees of penalization to different variables. The steps left are the same as the PCA–Cox.

RESULTS

Individual model predictions

The analysis results for clinical covariates and each type of genomic measurement for the four cancers are shown in Table 3. The prediction performance of clinical covariates varies across cancers, with C-statistic from as high as 0.65 for GBM and AML to as low as 0.54 for BRCA. For BRCA under PCA–Cox, CNA has the best prediction performance (C-statistic 0.76), closely followed by mRNA gene expression (C-statistic 0.74). For GBM, all four types of genomic measurement have similar low C-statistics, ranging from 0.53 to 0.58. For AML, gene expression and methylation have similar C-statistics, which are considerably larger than that of CNA. For LUSC, gene expression has the highest C-statistic, which is considerably larger than that for methylation and microRNA. For BRCA under PLS–Cox, gene expression has a very large C-statistic (0.92), while others have low values. For GBM, again gene expression has the largest C-statistic (0.65), followed by methylation (0.59). For AML, methylation has the largest C-statistic (0.82), followed by gene expression (0.75). For LUSC, the gene-expression C-statistic (0.86) is considerably larger than that for methylation (0.56), microRNA (0.43) and CNA (0.65). In general, Lasso–Cox leads to smaller C-statistics. For example for BRCA, the C-statistic of gene expression is 0.55, compared to 0.74 under PCA-Cox and 0.92 under PLS-Cox. Similar observations are made for AML and LUSC. For GBM, all three methods have low C-statistics. With the distribution computed across multiple splits, we are able to obtain the variation of C-statistic. The standard deviations are also shown in Table 3. For BRCA and LUSC, the variations are relatively high, while the variation is very low for GBM. The high variations are caused by the small sample size (LUSC) and/or low event rate (BRCA). The significance of difference between two types of measurements and two methods can be inferred using the variances and is omitted here. Comparing the obtained C-statistics against those obtained under permutation using the Wilcoxon test suggests that the differences are significant, although the magnitudes of C-statistic improvement are not necessarily dramatic.

Table 3:

Prediction performance of a single type of genomic measurement

Method	Data type	Estimate of C-statistic (standard error)
		BRCA	GBM	AML	LUSC
	Clinical	0.54 (0.07)	0.65 (0.01)	0.65 (0.03)	0.56 (0.07)
PCA	Expression	0.74 (0.05)	0.57 (0.01)	0.70 (0.03)	0.76 (0.06)
	Methylation	0.60 (0.07)	0.53 (0.01)	0.74 (0.03)	0.48 (0.07)
	miRNA	0.62 (0.06)	0.56 (0.01)		0.54 (0.07)
	CNA	0.76 (0.06)	0.58 (0.01)	0.54 (0.04)	0.72 (0.07)
PLS	Expression	0.92 (0.04)	0.65 (0.01)	0.75 (0.03)	0.86 (0.04)
	Methylation	0.59 (0.07)	0.59 (0.01)	0.82 (0.03)	0.56 (0.07)
	miRNA	0.51 (0.07)	0.56 (0.01)		0.43 (0.07)
	CNA	0.54 (0.08)	0.55 (0.01)	0.48 (0.04)	0.65 (0.07)
LASSO	Expression	0.55 (0.08)	0.58 (0.02)	0.63 (0.03)	0.55 (0.08)
	Methylation	0.53 (0.08)	0.52 (0.01)	0.62 (0.04)	0.50 (0.08)
	miRNA	0.70 (0.07)	0.55 (0.01)		0.50 (0.08)
	CNA	0.54 (0.08)	0.59 (0.02)	0.51 (0.04)	0.58 (0.08)

Integrated model predictions

The analysis results for combining multiple types of measurement are provided in Table 4. In combining, we start with the clinical covariates, which are of low dimension and usually have important implications. Based on the clinical covariates, we incorporate mRNA-gene expressions. The consideration is that molecular features measured at the transcription level affect cancer clinical outcomes more directly than those measured at the DNA/epigenetic level (CNA, mutation status and methylation). Molecular features at the DNA level affect clinical outcomes by influencing mRNA expressions. Similarly, microRNAs influence mRNA expressions through translational repression or target degradation, which then affect clinical outcomes. Then based on the clinical covariates and gene expressions, we add one more type of genomic measurement. With microRNA, methylation and CNA, their biological interconnections are not thoroughly understood, and there is no commonly accepted ‘order’ for combining them. Thus, we only consider a grand model including all types of measurement. For AML, microRNA measurement is not available. Thus the grand model includes clinical covariates, gene expression, methylation and CNA. In addition, in Figures 1–4 in Supplementary Appendix, we show the distributions of the C-statistics (training model predicting testing data, without permutation; training model predicting testing data, with permutation). The Wilcoxon signed-rank tests are used to evaluate the significance of difference in prediction performance between the C-statistics, and the P-values are shown in the plots as well.

Table 4:

Prediction performance of combining multiple types of genomic measurements

Method	Data type	Estimate of C-statistic (standard error)
		BRCA	GBM	AML	LUSC
PCA	Clinical	0.54 (0.07)	0.65 (0.01)	0.65 (0.03)	0.56 (0.07)
	Clc + expression	0.73 (0.06)	0.64 (0.01)	0.68 (0.03)	0.74 (0.06)
	Clc + expr + methylation	0.72 (0.06)	0.64 (0.01)	0.76 (0.03)	0.70 (0.07)
	Clc + expr + miRNA	0.71 (0.06)	0.63 (0.01)		0.70 (0.07)
	Clc + expr + CNA	0.70 (0.07)	0.65 (0.01)	0.65 (0.03)	0.71 (0.07)
	Clc + expr + methyl + CNA			0.75 (0.03)
	Clc + expr + methyl + miRNA + CNA	0.73 (0.07)	0.63 (0.01)		0.68 (0.07)
PLS	Clinical	0.54 (0.07)	0.65 (0.01)	0.65 (0.03)	0.56 (0.07)
	Clc + expression	0.92 (0.04)	0.66 (0.01)	0.75 (0.03)	0.86 (0.04)
	Clc + expr + methylation	0.83 (0.05)	0.64 (0.01)	0.83 (0.02)	0.76 (0.05)
	Clc + expr + miRNA	0.82 (0.06)	0.65 (0.01)		0.69 (0.07)
	Clc + expr + CNA	0.91 (0.04)	0.66 (0.01)	0.74 (0.03)	0.82 (0.04)
	Clc + expr + methyl + CNA			0.83 (0.03)
	Clc + expr + methyl + miRNA + CNA	0.72 (0.06)	0.64 (0.01)		0.69 (0.07)
LASSO	Clinical	0.54 (0.07)	0.65 (0.01)	0.65 (0.03)	0.56 (0.07)
	Clc + expression	0.57 (0.08)	0.64 (0.01)	0.64 (0.03)	0.53 (0.08)
	Clc + expr + methylation	0.57 (0.08)	0.62 (0.02)	0.65 (0.04)	0.52 (0.08)
	Clc + expr + miRNA	0.65 (0.07)	0.61 (0.02)	-	0.55 (0.08)
	Clc + expr + CNA	0.52 (0.08)	0.65 (0.01)	0.63 (0.03)	0.57 (0.08)
	Clc + expr + methyl + CNA			0.65 (0.04)
	Clc + expr + methyl + miRNA + CNA	0.60 (0.08)	0.61 (0.02)		0.56 (0.08)

We again observe significant differences across cancers. Under PCA–Cox, for BRCA, combining mRNA-gene expression with clinical covariates can significantly improve prediction compared to using clinical covariates only. However, we do not see further benefit when adding other types of genomic measurement. For GBM, clinical covariates alone have an average C-statistic of 0.65. Adding mRNA-gene expression and other types of genomic measurement does not lead to improvement in prediction. For AML, adding mRNA-gene expression to clinical covariates leads to the C-statistic to increase from 0.65 to 0.68. Adding methylation may further lead to an improvement to 0.76. However, CNA does not seem to bring any additional predictive power. For LUSC, combining mRNA-gene expression with clinical covariates leads to an improvement from 0.56 to 0.74. Other models have smaller C-statistics. Under PLS–Cox, for BRCA, gene expression brings significant predictive power beyond clinical covariates. There is no additional predictive power by methylation, microRNA and CNA. For GBM, genomic measurements do not bring any predictive power beyond clinical covariates. For AML, gene expression leads the C-statistic to increase from 0.65 to 0.75. Methylation brings additional predictive power and increases the C-statistic to 0.83. For LUSC, gene expression leads the C-statistic to increase from 0.56 to 0.86. There is no further improvement afterward. Under Lasso–Cox, for BRCA, gene expression and microRNA bring additional predictive power, but not CNA. For GBM, we again observe that genomic measurements do not bring any additional predictive power beyond clinical covariates. Similar observations are made for AML and LUSC.

Discussions

It should be first noted that the results are method-dependent. As can be seen from Tables 3 and 4, the three methods can generate significantly different results. This observation is not surprising. PCA and PLS are dimension reduction methods, while Lasso is a variable selection method. They make different assumptions. Variable selection methods assume that the ‘signals’ are sparse, while dimension reduction methods assume that all covariates carry some signals. The difference between PCA and PLS is that PLS is a supervised approach when extracting the important features. In this study, PCA, PLS and Lasso are adopted because of their representativeness and popularity. With real data, it is practically impossible to know the true generating models and which method is the most appropriate. It is possible that a different analysis method will lead to analysis results different from ours. Our analysis may suggest that in practical data analysis, it may be necessary to experiment with multiple methods in order to better comprehend the prediction power of clinical and genomic measurements.

Also, different cancer types are significantly different. It is thus not surprising to observe one type of measurement has different predictive power for different cancers. For most of the analyses, we observe that mRNA gene expression has higher C-statistic than the other genomic measurements. This observation is reasonable. As discussed above, mRNA-gene expression has the most direct effect on cancer clinical outcomes, and other genomic measurements affect outcomes through gene expression. Thus gene expression may carry the richest information on prognosis. Analysis results presented in Table 4 suggest that gene expression may have additional predictive power beyond clinical covariates. However, in general, methylation, microRNA and CNA do not bring much additional predictive power. Published studies show that they can be important for understanding cancer biology, but, as suggested by our analysis, not necessarily for prediction. The grand model does not necessarily have better prediction. One interpretation is that it has much more variables, leading to less reliable model estimation and hence inferior prediction.

CONCLUSION

Multidimensional genomic studies are becoming popular in cancer research. Most published studies have been focusing on linking different types of genomic measurements. In this article, we analyze the TCGA data and focus on predicting cancer prognosis using multiple types of measurements. The general observation is that mRNA-gene expression may have the best predictive power, and there is no significant gain by further combining other types of genomic measurements. Our brief literature review suggests that such a result has not been reported in the published studies and can be informative in multiple ways. We do note that with differences between analysis methods and cancer types, our observations do not necessarily hold for other analysis methods and cancers. This study inevitably suffers a few limitations. Although the TCGA is one of the largest multidimensional studies, the effective sample size may still be small, and cross validation may further reduce sample size. Multiple types of genomic measurements are combined in a ‘brutal’ manner. We incorporate the interconnection between for example microRNA on mRNA-gene expression by introducing gene expression first. However, more sophisticated modeling is not considered. PCA, PLS and Lasso are the most commonly adopted dimension reduction and penalized variable selection methods. Statistically speaking, there exist methods that can outperform them. It is not our intention to identify the optimal analysis methods for the four datasets. Despite these limitations, this study is among the first to carefully study prediction using multidimensional data and can be informative.

SUPPLEMENTARY DATA

Supplementary data are available online at http://bib.oxfordjournals.org/.

Key Points.

• Multidimensional studies are becoming popular in cancer research. However, most of the existing studies have focused on linking different types of measurements.

• We study predicting cancer prognosis using multiple types of genomic measurements. We adopt three methods for extracting important features, and use a cross-validation based approach with C-statistic to measure prediction.

• The analysis results are method-dependent. In general, the Lasso method leads to smaller C-statistics than PCA and PLS.

• mRNA-gene expression in general have more predictive power than the other types of genomic measurements. Introducing more genomic measurements does not lead to significantly improved prediction over gene expression.

• Studying prediction has important implications. There is a need for more sophisticated methods and extensive studies.

Biographies

Qing Zhao is a doctoral student in Department of Biostatistics, Yale University.

Xingjie Shi is a doctoral student in biostatistics currently under a joint training program by the Shanghai University of Finance and Economics and Yale University.

Yang Xie is Associate Professor at Department of Clinical Science, UT Southwestern.

Jian Huang is Professor at Department of Statistics and Actuarial Science, University of Iowa.

BenChang Shia is Professor in Department of Statistics and Information Science at FuJen Catholic University. His research interests include data mining, big data, and health and economic studies.

Shuangge Ma is Associate Professor at Department of Biostatistics, Yale University.

FUNDING

National Institute of Health (grant numbers CA142774, CA165923, CA182984 and CA152301); Yale Cancer Center; National Social Science Foundation of China (grant number 13CTJ001); National Bureau of Statistics Funds of China (2012LD001).