Comparison and integration of deleteriousness prediction methods for nonsynonymous SNVs in whole exome sequencing studies

Abstract

Accurate deleteriousness prediction for nonsynonymous variants is crucial for distinguishing pathogenic mutations from background polymorphisms in whole exome sequencing (WES) studies. Although many deleteriousness prediction methods have been developed, their prediction results are sometimes inconsistent with each other and their relative merits are still unclear in practical applications. To address these issues, we comprehensively evaluated the predictive performance of 18 current deleteriousness-scoring methods, including 11 function prediction scores (PolyPhen-2, SIFT, MutationTaster, Mutation Assessor, FATHMM, LRT, PANTHER, PhD-SNP, SNAP, SNPs&GO and MutPred), 3 conservation scores (GERP++, SiPhy and PhyloP) and 4 ensemble scores (CADD, PON-P, KGGSeq and CONDEL). We found that FATHMM and KGGSeq had the highest discriminative power among independent scores and ensemble scores, respectively. Moreover, to ensure unbiased performance evaluation of these prediction scores, we manually collected three distinct testing datasets, on which no current prediction scores were tuned. In addition, we developed two new ensemble scores that integrate nine independent scores and allele frequency. Our scores achieved the highest discriminative power compared with all the deleteriousness prediction scores tested and showed low false-positive prediction rate for benign yet rare nonsynonymous variants, which demonstrated the value of combining information from multiple orthologous approaches. Finally, to facilitate variant prioritization in WES studies, we have pre-computed our ensemble scores for 87 347 044 possible variants in the whole-exome and made them publicly available through the ANNOVAR software and the dbNSFP database.

Introduction

One of the greatest challenges in whole exome sequencing (WES) studies is the ability to distinguish pathogenic mutations from a large number of background variations. A common strategy is to filter for novel nonsynonymous single nucleotide variants (nsSNVs) that are found in patients and computationally predicted to be deleterious, which relies on the accuracy of the prediction methods (1). Multiple algorithms were developed for predicting such deleteriousness based on different information of the variant, such as its sequence homology (2), protein structure (3,4) and evolutionary conservation (5). These methods demonstrated themselves to be useful, however, they are not directly comparable with each other due to the difference in information and algorithms they used for predicting deleteriousness. Therefore, it is still unclear which one(s) to use for prioritizing nsSNVs in WES-based studies of human diseases to minimize both false-positive and false-negative prediction rates. While a few comparison studies have been done (6–10), the range of methods under comparison and/or the size of benchmark dataset often limited their scope and generalizability for WES studies.

One of the keys to a fair comparison lies in unbiased testing datasets. To ensure such fair comparison, we manually curated three distinct testing datasets, on which no prediction methods compared were tuned (Table 1). On these three testing datasets, we performed a comprehensive comparative study of 18 deleteriousness prediction scoring methods, including 11 function prediction scores [PolyPhen-2 (v2.2.2, released in Feb, 2013) (15), SIFT (Human_db_37_ensembl_63, released in August, 2011) (16), MutationTaster (data retrieved in 2013) (8), Mutation Assessor (release 2) (2), FATHMM (v2.3) (17), LRT (November, 2009) (6), PANTHER (version 6.1) (18), PhD-SNP (version 2.0.6) (19), SNAP (version 1.0.8) (20), SNPs&GO (21) and MutPred (version 1.0) (22)], 4 ensemble scores [CADD (23), PON-P (24), KGGSeq (version 0.2) (25) and CONDEL (26)] and 3 conservation scores [GERP++ (27), SiPhy (28) (http://www.broadinstitute.org/mammals/2x/siphy_hg19/) and PhyloP (phyloP46way_placental) (29) (http://hgdownload.soe.ucsc.edu/goldenPath/hg19/phyloP46way/placentalMammals/)] (Table 2) on their performance to prioritize nsSNVs in WES studies. Here function prediction scores refer to scores that predict the likelihood of a given nsSNV causing deleterious functional change of the protein; conservation scores refer to scores that measure the conservativeness of a given nucleotide site across multiple species and ensemble scores refer to scores that combine information of multiple component scores. To facilitate more accurate variant prediction, we also developed and evaluated two ensemble-based approaches, support vector machine (SVM) (30) and logistic regression (LR) (31), that integrate multiple scoring methods for which whole-exome data are available.

Table 1.

Description of the four datasets used in our study

Dataset	Training dataset	Testing dataset I	Testing dataset II	Testing dataset III
TP	14 191	120	6279	0
TN	22 001	124	13 240	10 164
Total	36 192	244	19 519	10 164
Source	Uniprot database (11,12)	Recent Nature Genetics publications for TP variants	VariBench dataset II (10,13) without mutations in training dataset	CHARGE database (14)
		CHARGE database (14) for TN variants

TP: true positive, number of deleterious mutations that were treated as TP observations in modeling. TN: true negative, number of non-deleterious mutations that were treated as true negative observations in modeling. Total: total number of mutations for each dataset (Total = TP + TN).

Table 2:

Summary of deleteriousness prediction methods analyzed in our study

Name	Category	Score used for analysis	Deleterious threshold	Information used
SIFT	Function prediction	1 − Score	>0.95	Protein sequence conservation among homologs
PolyPhen-2	Function prediction	Score	>0.5	Eight protein sequence features, three protein structure features
LRT	Function prediction	Score * 0.5 (if Omega ≥1) or 1 − Score * 0.5 (if Omega <1)	P	DNA sequence evolutionary model
MutationTaster	Function prediction	Score (if A or D) or 1 − Score (if N or P)	>0.5	DNA sequence conservation, splice site prediction, mRNA stability prediction and protein feature annotations
Mutation Assessor	Function prediction	(Score-Min)/(Max − Min)	>0.65	Sequence homology of protein families and sub-families within and between species
FATHMM	Function prediction	1 − (Score-Min)/(Max − Min)	≥0.45	Sequence homology
GERP++ RS	Conservation score	Score	>4.4	DNA sequence conservation
PhyloP	Conservation score	Score	>1.6	DNA sequence conservation
SiPhy	Conservation score	Score	>12.17	Inferred nucleotide substitution pattern per site
PON-P	Ensemble score	Score	P	Random forest methodology-based pipeline integrating five predictors
PANTHER	Function prediction	Score	P	Phylogenetic trees based on protein sequences
PhD-SNP	Function prediction	Score	P	SVM-based method using protein sequence and profile information
SNAP	Function prediction	Score	P	Neural network-based method using DNA sequence information as well as functional and structural annotations
SNPs&GO	Function prediction	Score	P	SVM-based method using information from protein sequence, protein sequence profile and protein function
MutPred	Function prediction	Score	>0.5	Protein sequence-based model using SIFT and a gain/loss of 14 different structural and functional properties
KGGSeq	Ensemble score	Score	P	Filtration and prioritization framework using information from three levels: genetic level, variant-gene level and knowledge level
CONDEL	Ensemble score	Score	>0.49	Weighted average of the normalized scores of five methods
CADD	Ensemble score	Score	>15	63 distinct variant annotation retrieved from Ensembl Variant Effect Predictor (VEP), data from the ENCODE project and information from UCSC genome browser tracks

Score indicates raw score for the corresponding function prediction/conservation score output. Max/Min indicates the max/min prediction score. Classification outcome for deleterious threshold was used for qualitative prediction score analysis. P means that categorical prediction outcome given by the prediction method was used for dichotomizing prediction outcomes.

Results

Curation of training and testing datasets

To compare the performance of the prediction methods, we constructed four datasets; one for training our SVM and LR model and three for testing their performance against all the deleteriousness prediction methods. Quality of machine learning models, such as SVM and LR, can be influenced by selection of component scores as well as the selection of parameters. To optimize the selection of component scores and parameters for our SVM and LR model, we collected training dataset, on which we performed feature selection and parameter tuning for our models. Training dataset is composed of 14 191 deleterious mutations as true positive (TP) observations and 22 001 neutral mutations as true negative (TN) observations, all based on the Uniprot database (11,12). Note that the TN observations contain both common [maximum minor allele frequency (MMAF) >1% in diverse populations of the 1000 Genomes project (32)] and rare (MMAF ≤1%) variants to ensure the generalizability of our model. To reduce potential bias in our comparison, we manually collected testing datasets from three distinct contexts. Testing dataset I consists of 120 TP observations that are deleterious variants recently reported to cause Mendelian diseases, diseases caused by single-gene defects, with experimental support in 57 recent publications (after 1 January 2011) from the journal Nature Genetics and 124 TN observations that are common neutral variants (MMAF >1%) newly discovered from participants free of Mendelian disease from the Atherosclerosis Risk in Communities (ARIC) study (32) via the Cohorts for Heart and Aging Research in Genomic Epidemiology (CHARGE) sequencing project (14,33). Testing dataset II is derived from the VariBench (13) dataset II, a benchmark dataset used for performance evaluation of nsSNV scoring methods. Because VariBench dataset II contains mutations that overlap our training dataset, we removed these mutations and curated 6279 deleterious variants as our TP observations and 13 240 common neutral variants (MMAF >1%) as our TN observations. As rare variants may have different features compared with common variants in the populations (34), a prediction method that puts too much weight on those features may not perform well in separating rare deleterious variants from rare neutral variants. In order to evaluate the performance of prediction methods on rare variants, we also prepared testing dataset III that contains 10 164 rare neutral mutations (singletons) from 824 European Americans from the cohort random samples of the ARIC study (32) via the CHARGE sequencing project (14,33). Note that as testing dataset I and III were collected from recently available projects and publications and that testing dataset II was used solely for benchmark in performance comparison studies, they are unlikely to be used for tuning current prediction methods evaluated in our study. Even though prediction methods, such as FATHMM, applied Varibench datasets (from which our testing dataset II was derived), they only used the data for performance evaluation purpose, not for model tuning (10). Therefore, to our knowledge, our testing datasets are unbiased benchmark datasets to ensure a fair comparison between different prediction methods. A summary of the datasets is presented in Table 1, and the complete datasets are available in Supplementary Material, Table S8.

Prediction scores

We obtained nine deleteriousness prediction scores, including six function prediction scores (PolyPhen-2, SIFT, MutationTaster, Mutation Assessor, FATHMM and LRT) and three conservation scores (GERP++, SiPhy and PhyloP), for all variants in all datasets. Additionally, we obtained nine more deleteriousness prediction scores (PANTHER, PhD-SNP, SNAP, SNPs&GO, MutPred, PON-P, KGGSeq, CONDEL and CADD) for testing dataset I and three more scores for testing datasets II and III (KGGSeq, CONDEL and CADD) (Table 2). Note that we were not able to harvest all 18 deleteriousness prediction scores for all four datasets, mostly due to the accessibility of most of scores from web interface and the speed of obtaining these scores for relatively large datasets. Nevertheless, we still successfully obtained nine deleteriousness prediction scores for all datasets that we used, which is already the largest in scale for similar comparison studies.

To construct our own ensemble scores, we used these nine scores (SIFT, PolyPhen-2, GERP++, MutationTaster, Mutation Assessor, FATHMM, LRT, SiPhy and PhyloP) for all potential human nsSNVs collected in the dbNSFP database, along with the MMAF observed in diverse populations of the 1000 Genomes project (32), as our component scores. After imputing missing values for observations in training dataset, we employed SVM and LR algorithms for computing these two ensemble scores and evaluated three kernel functions (linear, radial and polynomial kernel) for the SVM approach, all based on default parameters (Table 3).

Table 3.

Missing values for four datasets (%)

Dataset	Training dataset (%)	Testing dataset I (%)	Testing dataset II (%)	Testing dataset III (%)
SIFT	6.91	2.87	3.83	3.96
PolyPhen-2	3.79	2.87	0.55	0.02
LRT	10.49	13.93	7.97	11.33
MutationTaster	0.04	0.41	0.10	0.11
Mutation Assessor	1.51	3.69	2.23	2.67
FATHMM	4.05	5.73	3.48	6.69
GERP++	0	0	0	0.01
PhyloP	0	0	0	0
SiPhy	0	0	0	0.285
PON-P	NA	13.93	NA	NA
PANTHER	NA	47.95	NA	NA
PhD-SNP	NA	6.56	NA	NA
SNAP	NA	9.02	NA	NA
SNPs&GO	NA	15.98	NA	NA
MutPred	NA	7.37	NA	NA
KGGSeq	NA	0.82	0.05	0.82
CONDEL	NA	0.41	0.0003	0.32
CADD	0	0	0	0

(%), The percentage of missing values for each prediction scores for the corresponding dataset. NA, not available.

From univariate analysis of nine deleteriousness prediction scores and MMAF of training dataset, we found that all of the 10 predictors showed significant difference in median scores between TP and TN groups, suggesting that all 10 predictors work well in separating TP observation from TN observations (P < 0.01, Wilcox rank sum test with Bonferroni adjustment) (Supplementary Material, Table S1 and Fig. S1). Moreover, all deleteriousness prediction scores showed positive association with deleteriousness while MMAF showed negative association with deleteriousness (Supplementary Material, Table S1). This is consistent with previous findings. Higher prediction score from deleteriousness prediction tools indicates higher risk of deleteriousness, while higher MMAF means that the mutation is common and therefore is oftentimes less likely to be deleterious.

We next evaluated the extent of collinearity in the training data, because high levels of collinearity may affect the stability of prediction models and inflate variance of parameter estimation. From the results, only PolyPhen-2 HVAR and PolyPhen-2 HDIV, two scores from PolyPhen-2 trained on different datasets, raised our concern, because they have the highest collinearity and therefore may affect the stability of our prediction models (Pearson correlation coefficient = 0.946). To further examine their effect on model stability, we applied stepwise model selection. Results suggested that we include both PolyPhen-2 HVAR and HDIV into final prediction models. As for LR model, reduced model generated from the model selection procedure included both scores (Supplementary Material, Table S6). As for SVM model, to increase stability of our final models, we applied regularization on linear, radial and polynomial SVM models. From 5-fold cross-validation results, we chose parameter cost = 1 to penalize L2 norm of weights of all predictors to ensure robustness of our final models (Supplementary Material, Fig. S5).

Comparison of quantitative predictions

We compared the quantitative predictions of the deleteriousness prediction methods from five different aspects. First, to estimate the relative contribution of each prediction score in our SVM and LR models, we applied multiple LR on these nine prediction scores and MMAF. The results showed that when evaluated by the estimated coefficients in our LR model, all deleteriousness prediction scores (except for SIFT and MutationTaster), conservation scores and MMAF were statistically significant predictors for estimating deleteriousness of the mutation in our training dataset at α = 0.05 significance level, after adjusting for remaining scores in the multiple LR model. This suggests that although most of the function prediction scores have already taken certain conservation measures into account, independent conservation scores can still bring additional information to the ensemble score. Among all significant deleteriousness prediction scores, FATHMM contributed the most to estimating deleteriousness. The adjusted odds of a mutation being deleterious is 4.6 times higher than being neutral for 0.1 increase of FATHMM score when remaining scores in the multiple LR model remain constant (P < 0.001, Wald-test) (Supplementary Material, Table S2).

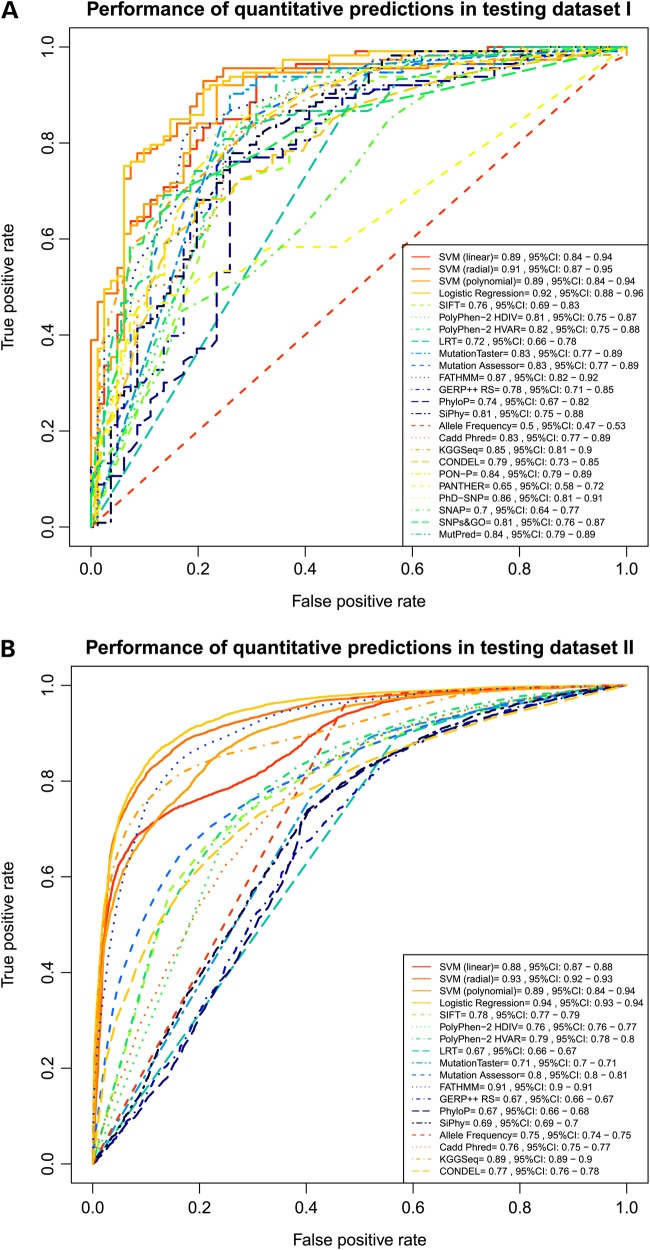
Second, we compared the predictive performance of individual deleteriousness prediction scores altogether, including function prediction scores and conservation scores, using area under the curve (AUC) score from receiver operating characteristic (ROC) plots and true negative rate (TNR, or specificity) as measurements. We found that FATHMM performed the best in all three testing datasets, as expected. The probability of a TP observation having a higher predicted deleterious score than a TN observation is the highest for FATHMM. In testing dataset I, the probability of a TP observation having a higher predicted FATHMM score than a TN observation is 0.87 [AUC = 0.87, 95% confidence interval (CI): 0.82–0.92], which was statistically significantly better than the worst performing prediction score, PANTHER (AUC = 0.65, 95% CI: 0.58–0.72). FATHMM also achieved the highest performance in testing dataset II (AUC = 0.91 for FATHMM, 95% CI: 0.9–0.91) (Fig. 1). In testing dataset III that contains only rare neutral variants, normalized FATHMM median score is the second lowest, indicating a relatively high tendency of correctly classifying TN variants. Note that even though PolyPhen-2 HVAR has a lower normalized median score, it did not achieve as high specificity as FATHMM (shown below). Therefore, FATHMM demonstrated itself to be consistently the best performing individual deleteriousness prediction method for separating deleterious variants from neutral variants in its quantitative predictions.

Figure 1.

ROC curves for existing prediction scores and our ensemble scores. These two plots illustrated performance of quantitative prediction outcomes for existing prediction scores and our ensemble prediction scores evaluated by the ROC curve and AUC score for the ROC curve. Higher AUC score indicates better performance. Top plot used testing dataset I as benchmark dataset and bottom plot used testing dataset II as benchmark dataset (see Table 1). 95% CI indicates 95% confidence interval computed with 2000 stratified bootstrap replicates.

Third, within all individual deleteriousness prediction methods, we compared function prediction methods with conservation methods. We found that function prediction methods tend to perform better than conservation scores, especially in separating common neutral mutations from deleterious mutations. From ROC plots that grouped function prediction scores and conservation scores, we found that the average probability of a TP variant having a higher predicted deleterious score than a TN variant is statistically significantly higher for function prediction scores than for conservation scores. Indeed, the average probability of a TP variant having a higher predicted deleterious score than a TN variant is 0.73 for function prediction scores (AUC = 0.73, 95% CI: 0.72–0.75) in testing dataset I and is 0.71 (AUC = 0.71, 95% CI: 0.7–0.71) in testing dataset II, while for conservation prediction scores the probabilities are only 0.66 (AUC = 0.66, 95% CI: 0.62–0.71) and 0.6 (AUC = 0.6, 95% CI: 0.6–0.61) in these two datasets (Supplementary Material, Fig. S3).

Fourth, we compared existing ensemble methods, both with themselves and with their individual component scores. We found that KGGSeq performed the best and it was the only existing ensemble scores that outperformed all of its component scores. The probability of a TP variant having a higher KGGSeq score than a TN variant is 0.85 in testing dataset I (AUC = 0.85, 95% CI: 0.81–0.90) and is 0.89 in testing dataset II (AUC = 0.89, 95% CI: 0.89–0.90). Not only did it achieve the highest performance among all existing ensemble scores, it also outperformed all its component scores (SIFT, PolyPhen-2, LRT, MutationTaster and PhyloP) for separating deleterious variants from common neutral variants. For example, in testing dataset II, the probability of a TP variant having a higher predicted deleterious score than a TN variant is 0.89 (AUC = 0.89, 95% CI: 0.89–0.90) for KGGSeq, which is statistically significantly higher than all its component scores (AUC = 0.78, 95% CI: 0.77–0.79 for SIFT; AUC = 0.76, 95% CI: 0.76–0.77 for PolyPhen-2 HDIV; AUC = 0.77, 95% CI: 0.78–0.8 for PolyPhen-2 HVAR; AUC = 0.67, 95% CI: 0.66–0.67 for LRT; AUC = 0.71, 95% CI: 0.7–0.71 for MutationTaster and AUC = 0.67, 95% CI: 0.66–0.68 for PhyloP). In testing dataset I, KGGSeq also performed better than all its component scores (AUC = 0.85, 95% CI: 0.81–0.9), but some of the difference was not statistically significant. On the other hand, other existing ensemble scores achieved only intermediate performance compared with its component scores. For example, the probability of a TP variant having a higher predicted deleterious score than a TN variant is 0.77 for CONDEL (AUC = 0.77, 95% CI: 0.76–0.78) in testing dataset II, which was statistically lower than its component score Mutation Assessor (AUC = 0.8, 95% CI: 0.8–0.81). In testing dataset I, CONDEL also achieved intermediate performance (AUC = 0.79, 95% CI: 0.73–0.85), which is worse than two of its component scores but the difference was not statistically significant (Fig. 1).

Moreover, we have found that ensemble scores that integrate component scores that are specific to protein features may perform better than ensemble scores that integrate a large amount of unfocused component scores. For example, KGGSeq, which integrated five component scores (SIFT, PolyPhen-2, LRT, MutationTaster and PhyloP), performed better than CADD, which integrated more than 40 component scores (including deleteriousness prediction scores such as SIFT, PolyPhen-2, GERP++ and many more whole genome annotation information such as reference allele, GC content and methylation level, which are beyond the scope of our comparison) in both testing datasets. Nevertheless, our results show that integration of several deleteriousness prediction tools may be helpful in identifying deleterious mutations from common neutral mutations. Therefore, we developed our own ensemble scores LR and SVM that integrated 10 component scores to test this hypothesis and the results are discussed below.

Fifth, we compared our two ensemble methods, both with each other and with all other existing deleteriousness prediction methods. Our two ensemble scores both integrated nine deleteriousness prediction scores including SIFT, PolyPhen-2, GERP++, MutationTaster, Mutation Assessor, FATHMM, LRT, SiPhy and PhyloP as well as the MMAF (to allow for the contribution of allele frequency to deleterious mutation discovery), but they used slightly different algorithms (LR for LR score and SVM with three different kernel functions for three SVM scores) to integrate their component scores. From our results, our ensemble scores not only outperformed all its components, but also outperformed all other deleteriousness prediction methods evaluated. Indeed, the probability of a TP variant having a higher predicted LR score than a TN variant is 0.92 in testing dataset I (AUC = 0.92, 95% CI: 0.88–0.96) and in testing dataset II (AUC = 0.94, 95% CI: 0.93–0.94), both followed by radial SVM (AUC = 0.91 with 95% CI: 0.87–0.95 for testing dataset I and AUC = 0.93 with 95% CI: 0.92–0.93 for testing dataset II), indicating excellent separation of TP and TN variants. Both LR score and radial SVM score have significantly larger AUCs compared with FATHMM (the best individual deleteriousness prediction score tested) and KGGSeq (the best existing ensemble score tested) in testing dataset I (P-values < 0.02, one-sided test with 2000 bootstrap) and testing dataset II (P-values of $2.20\times {10}^{-16}$, one-sided test with 2000 bootstrap). In testing dataset III with only neutral variants, LR achieved the lowest median score (0.195) among all normalized deleteriousness scores, indicating the highest tendency of correctly classifying TN observations (Supplementary Material, Figs S2 and S4).

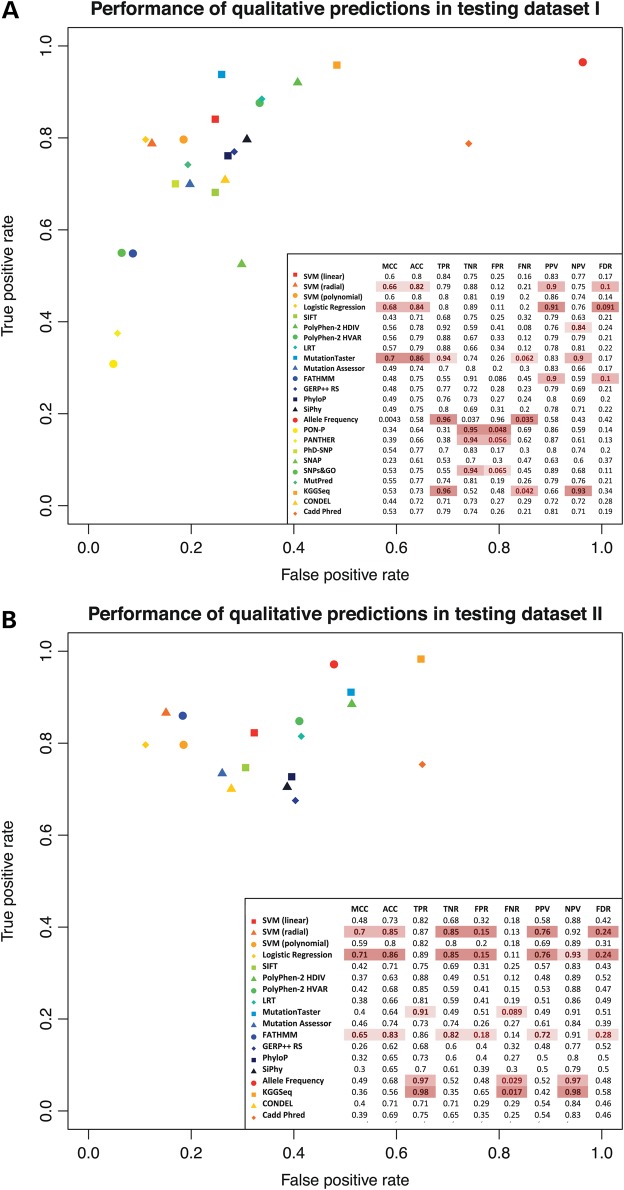
Comparison of qualitative predictions

For many function prediction tools, such as SIFT, MutationTaster and PolyPhen-2, categorical predictions are available in addition to quantitative function scores. For conservation scores, we determined their optimal cutoffs for their qualitative predictions based on their ROC curves for the training data (see Materials and Methods section). Therefore, we dichotomized such categorical prediction outcomes and compared their performance using a series of different measurements, such as Matthews correlation coefficient (MCC), true positive rate (TPR, or sensitivity) and TNR, for testing datasets I and II, which contained both TP and TN observations. As testing dataset III contained only TN observations, we applied TNR as the sole measurement for qualitative prediction performance. Our results showed that existing deleteriousness prediction methods tend to have unstable performance in different testing datasets and on different measurements of qualitative outcomes. For example, the best agreement between binary prediction from deleteriousness prediction tools and the actual observation was achieved by MutationTaster in testing dataset I (MCC = 0.7), which did not retain in testing dataset II (MCC = 0.4 for MutationTaster, which is the 10th among the 17 scores compared). Similar results were also observed when using TPR and TNR as measurement. For example, while KGGSeq correctly classified the most TP variants in testing datasets I (TPR = 0.96) and II (TPR = 0.98), it failed to maintain its predictive power in correctly classifying TN variants (TNR = 0.52 and 0.35 for these two datasets, respectively) (Fig. 2). Indeed, its TNR became even lower when evaluated on testing dataset III (0.22) (Supplementary Material, Fig. S4).

Figure 2.

Sensitivity and specificity plots for existing prediction scores and our ensemble scores. These two plots illustrated the performance of qualitative prediction outcomes of existing prediction scores and our ensemble prediction scores, evaluated by sensitivity and specificity. Higher sensitivity/specificity score indicates better performance. Top plot used testing dataset I as benchmark dataset and bottom plot used testing dataset II as benchmark dataset (see Table 1). The tegend table showed various qualitative prediction performance measurements for each prediction tool. MCC is a correlation coefficient between the observed and predicted binary classification, ranging from −1 to 1, where 1 indicates perfect prediction, −1 indicates total disagreement between prediction and observation. $\text{MCC}=\left((\text{TP}\times \text{TN}-\text{FP}\times \text{FN})/\left(\sqrt{(\text{TP + FP})(\text{TP + FN})(\text{TN + FP})(\text{TN + FN})}\right)\right),$ where TP, TN, FP and FN denotes true positive, true negative, false positive and false negative, respectively. ACC denotes accuracy; $\text{ACC}=((\mathrm{TP}+\text{TN)}/(\mathrm{TP}+\text{FP}+\text{TN}+\text{FN))}$. TPR denotes true positive rate, or sensitivity; $\text{TPR}=(\mathrm{TP}/(\text{TP}+\text{FN}))$. TNR denotes true negative rate, or specificity; $\text{TNR}=(\mathrm{TN}/(\text{TN}+\text{FP}))$. FPR denotes false-positive rate; $\text{FPR}=(\text{FP}/(\text{TN}+\text{FP}))$. FNR denotes false-negative rate; $\text{FNR}=(\text{FN}/(\text{TP}+\text{FN}))$. PPV denotes positive predictive value; $\text{PPV}=(\text{TP}/(\text{TP}+\text{FP}))$. NPV denotes negative predictive value; $\text{NPV}=(\text{TN}/(\text{TN}+\text{FN}))$. FDR denotes false discovery rate; $\text{FDR}=(\text{FP}/(\text{FP}+\text{TP}))$. For each qualitative prediction performance measurement, top three performance scores were highlighted. The brighter the highlight color, the better the performance.

On the other hand, our ensemble scores remained to be high performing methods by various performance measurements in all three testing datasets. For example, LR achieved the second best agreement between binary prediction from deleteriousness prediction tools and the actual observation in testing dataset I (MCC = 0.68) and the best agreement in testing dataset II (MCC = 0.71), all followed by radial SVM (MCC = 0.66 for testing dataset I, MCC = 0.7 for testing dataset II). Similar results were also observed when using TPR and TNR as measurements. For example, in testing datasets I and II, LR correctly classified >80% of TP variants (TPR = 0.8, 95% CI: 0.76–0.84 for testing dataset I, TPR = 0.86, 95% CI: 0.855–0.865) and >85% of TN variants (TNR = 0.89, 95% CI: 0.86–0.92 for testing dataset I, TNR = 0.85, 95% CI: 0.845–0.855 for testing dataset II) (Fig. 2). In classifying rare neutral variants, LR and SVM with radial kernel also achieved excellent performance. They correctly classified the most TN variants in testing dataset III (TNR = 0.84 for LR, 95% CI: 0.83–0.85, TNR = 0.85 for SVM, 95% CI: 0.84–0.86), statistically significantly higher than the third best tool, FATHMM (TNR = 0.79, 95% CI: 0.78–0.80) (Supplementary Material, Fig. S4). This implies that large-scale ensemble methods may be able to take advantage of different deleteriousness prediction tools and achieve a more balanced qualitative prediction performance than individual tools.

Parameter tuning and feature selection for ensemble approaches

All the analyses described above on ensemble approaches (LR and SVM) used default parameters. To assess whether these parameters can be optimized to achieve substantially better performance, we performed 5-fold cross validation on training dataset. Based on the AUC values of ROC curves for different parameter cocktails (Supplementary Material, Fig. S5), we found that the performance of default parameter for SVM with linear, radial and polynomial kernel was rather similar to that of other parameter settings, indicating that LR and SVM have already reached optimal performance using default settings so that the uses of default settings for these two models were justified. To examine whether our model can be further enhanced using different combinations of prediction scores, we applied stepwise feature selection and generated a reduced model, which lacks MutationTaster score. From step-wise feature selection, all prediction scores except for MutationTaster (SIFT score, PolyPhen-2 HDIV, PolyPhen-2, LRT, Mutation Assessor, FATHMM, GERP++, PhyloP, SiPhy and MMAF) were chosen to be the optimal feature combination with Akaike information criterion (AIC) of 16483.91 (Supplementary Material, Table S6). To compare the performance of this reduced model with our final model, which contains all prediction scores, we calculated the accuracy and AUC value of the ROC curve of both models. Results showed that these two models share the same accuracy (accuracy = 0.91 for both reduced model and our final model) and that there is no statistical significant difference between the reduced model and our final model (AUC = 0.97, 95% CI: 0.968–0.971 for both models) (Supplementary Material, Table S7). Thus, the only difference in predictive performance between our final model and the reduced model with the optimal feature combination lies in the inclusion of MutationTaster. MutationTaster comprises unique features, such as splice site analysis, protein length analysis and direct or indirect protein feature analysis, which could potentially enhance our model in the future when more training data are available. Therefore, to allow for information of unique feature analysis from MutationTaster, we included it into our final model, which achieved the optimal performance as with the reduced model with the optimal combination of prediction scores.

Discussion

In this study, we evaluated the predictive performance of 18 existing prediction methods and 2 new ensemble prediction methods on 3 manually curated testing datasets. Among the existing methods, FATHMM achieved the highest discriminative power as evaluated by AUC values of ROC curve. However, our two ensemble methods that incorporated nine deleteriousness prediction scores and MMAF, achieved the highest discriminative power and outperformed popular tools such as SIFT, GERP++ and PolyPhen-2. Our results demonstrated the value of combining information from multiple deleteriousness prediction methods. To facilitate variant prioritization in exome sequencing studies, we also merged mutations all but testing dataset III, generated our whole-exome ensemble-based prediction scores using LR and SVM algorithms and made the prediction scores for 87 347 044 possible variants in the whole-exome publicly available in ANNOVAR (35) software and dbNSFP database (36,37).

Collinearity is an indicator of redundancy of prediction method pairs. To estimate such redundancy and avoid numerical instability of our model, we performed collinearity analysis on current 18 scoring methods and MMAF. Results show that PolyPhen-2 HDIV and PolyPhen-2 HVAR scores have the highest linear correlation. PolyPhen-2 HDIV and PolyPhen-2 HVAR are positive correlated with each other; every 1 increase of PolyPhen-2 HDIV score is associated with 0.946 increase of PolyPhen-2 HVAR score (Pearson correlation coefficient = 0.946 evaluated on testing dataset I, Supplementary Material, Fig. S10). Such strong association potentially owes to the fact that they share the same algorithm. Indeed, the only difference between these two scores lies in their training datasets. While PolyPhen-2 HDIV uses alleles encoding human proteins and their closely related mammalian homologs as TN observations, PolyPhen-2 HVAR applies common human nsSNVs as TN observations. Therefore, algorithm redundancy exists between these two prediction scores and was captured by Pearson Correlation Coefficient statistic. On the other hand, the least linear correlation was observed between MMAF and SIFT. SIFT score and MMAF are negative correlated with each other; every 1 increase of SIFT is associated with 0.030 decrease of MMAF, indicating little redundancy within this pair of scoring methods (Pearson correlation coefficient = −0.030 evaluated on testing dataset I, Supplementary Material, Fig. S10).

Besides predictive performance, ease of use and speed are also important aspects for application of a function prediction method. For large-scale WES on Mendelian diseases, it is necessary to perform queries on tens of thousands of variants in a relatively short period of time. Some authors of deleteriousness prediction methods provide software tools or web servers, on which batch queries are performed. Based on our experience, currently SIFT, PolyPhen-2, MutationTaster, Mutation Assessor and KGGSeq have the highest ease of use and speed among all methods tested, which allows for direct batch queries using genome coordinates. To facilitate querying multiple predictions for large number of nsSNVs, Liu et al. developed a database compiling prediction scores from six prediction algorithms (SIFT, PolyPhen-2, LRT, MutationTaster, Mutation Assessor and FATHMM) and three conservation scores (PhyloP, GERP++ and SiPhy) for all possible nsSNVs in human genome. With the dbNSFP tool, users no longer need to use individual software tools or web servers; instead they can obtain all scores easily from dbNSFP. We have also made all dbNSFP scores available directly in the ANNOVAR software, so that users can perform automated queries on all function prediction scores rapidly (<1 min for a typical exome). We have now incorporated the SVM and LR scores into the ANNOVAR tool and dbNSFP, and we believe that these data sources will benefit researchers working on exome sequencing studies.

Missing values is another concern when applying a prediction method to large-scale WES data. Some methods tend to restrict their predictions to well-annotated proteins or transcripts, which may improve the prediction accuracy for non-missing scores, but they suffer from higher rate of missing values. For example, PON-P has a higher missing rate than their component scores because it depends on the availability of all component scores. Based on the datasets we used for training and testing, we observed some scores (PANTHER, SNPs&GO, PON-P and LRT) with relatively high (>10%) rate of missing values (Table 3). To reduce such bias caused by missing values, we used imputed scores for computing our SVM and LR scores if some component scores are missing.

Our study also suggested that we increase the predictive power of the prediction tools by integrating them through machine learning algorithms, such as LR and SVM. Both LR and SVM scores have enhanced performance than all existing prediction tools, indicating that current prediction tools may provide orthogonal information that can be integrated using such ensemble-based approaches for better performance. Such performance may be further enhanced if we could update our SVM and LR models dynamically, with more component scores and more accurate TP/TN observations, as other machine learning applications. However, due to the computation cost and the technical challenge of dynamically implementing many of the existing deleteriousness prediction methods online or locally for large numbers of mutations, we were not able to realize this function. Nevertheless, we were still optimistic that in the future, when most of the existing deleteriousness prediction tools come up with whole exome prediction scores, like the CADD team, or when they come up with an interface/software package that can handle large dataset easily, there may be possibilities of realizing such dynamic update of our ensemble scores. Moreover, even though LR performed better than SVM in our study, we caution that this does not necessarily suggest that LR is superior for this type of tasks. LR is relatively a simpler algorithm and therefore may be better when the data are simpler and do not require kernel transformation. More complex machine learning algorithms, such as SVM, Random Forest and Neural Network, can better handle data in large-scale and with multi-collinearity, which already appeared to some extend in our intermediate level training data (Supplementary Material, Fig. S6). In the future when the input scores are more complex and more correlated, more complex machine learning algorithms may be preferred over LR. For example, if we would like to integrate information such as phenotypic information (38,39), pathway information (40) and protein interaction (41), we may consider those more complex machine learning algorithms.

A problem associated with every comparison study is the quality of the datasets. We used various ways to make sure that our four datasets are of high quality. For training dataset, we separated the deleterious mutations in Uniprot database according to the genetic model of the underlying disease (dominant, recessive or unspecified) and conducted independent analysis, with the initial hypothesis that the mutations identified from recessive disease have higher reliability. With no significant difference observed among the three groups, we combined them as a single deleterious mutation set to increase estimation accuracy. We also limited the neutral mutations in testing dataset I to the nsSNVs that were observed more than ten times (as reported in dbSNP) with 1% or higher MMAF in the population. As for neutral mutation set for testing dataset II, we require mutations to have MMAF >1% or being observed >22 times in dbSNP. This MMAF cutoff may help to eliminate variants that were due to sequencing error or potentially deleterious variants with low MMAF (34). However, as rare and common variants may have different features, a method that performs well with relatively common (MMAF >1%) neutral mutations may not perform well with rare neural mutations. Therefore, we collected singleton nsSNVs from 824 exomes with strict control of the mapping quality and individual phenotypes as a test set for rare neural variants. Our results showed that our ensemble scores outperformed all other scores evaluated with higher TNR (i.e. lower false-positive rate). Another issue associated with dataset is the overlap between our testing datasets and the original training datasets of the prediction scoring methods compared. If a prediction method is tested using a dataset, which overlaps its training dataset, then it is likely that its performance evaluation will be biased. In order to avoid this issue, we manually collected all three testing datasets, on which no current prediction scoring method is likely to be trained. For example, testing dataset I has TP observations manually collected from recent publications of Nature Genetics and TN observations from recently available data from CHARGE project. Applying these testing datasets helps us provide a relatively unbiased evaluation of performance of current prediction scoring methods.

Thusberg et al. previously published a nice comparison of nine deleteriousness prediction methods. Although seven out of nine of their compared methods (PolyPhen-2, SIFT, PANTHER, PhD-SNP, SNAP, SNPs&GO and MutPred) overlap our study, there are major differences between their study and ours. First, we included many more up-to-date methods into comparison. For example, we included recently published methods such as Mutation Assessor, FATHMM and CADD. Second, our comparison has a larger diversity. While they focused exclusively on the function prediction methods that use information of amino acid substitutions, we not only included methods based on such amino acid substitutions and but also methods that are based on DNA sequence information (such as conservation scores) and ensemble scores. Third, while Thusberg et al. only compared binary predictions, we compared both the continuous prediction scores and the binary predictions. Finally, we constructed new ensemble-based methods (i.e. LR and SVM) that take advantage of the characteristics of multiple algorithms in a single application. Nevertheless, we also evaluated the same datasets provided by Thusberg and present the results in Supplementary Material, Figure S7.

In summary, we have performed a comparative study of several popular prediction algorithms for nsSNVs in response to the demand of developing a practical guideline for their use in WES-based human disease studies. Using 3 independent testing datasets, we evaluated 18 existing deleteriousness prediction methods on their quantitative and qualitative prediction performance and demonstrated the potential of ensemble approaches (LR and SVM). We recommended the regular use of such ensemble methods in prioritizing disease-causing nsSNVs to boost the predictive power.

Materials and Methods

Training and testing datasets

We manually collected four datasets of nsSNVs based on the Uniprot database, previous publication in Nature Genetics, CHARGE sequencing project and VariBench dataset (Table 1). Training dataset included 14 191 deleterious mutations, which were annotated as causing Mendelian disease and 22 001 neutral mutations, which were annotated as not known to be associated with any phenotypes, all based on Uniprot annotation. Considering that some algorithms may have used a part of the nsSNVs in the Uniprot set as training data, we constructed our first independent testing dataset, testing dataset I, to reduce potential bias associated with the Uniprot data. It included 120 deleterious mutations recently reported in the journal Nature Genetics that belong to 54 different genes and cause 49 diverse diseases, and 124 neutral mutations newly discovered from the CHARGE sequencing project. To ensure the quality of these deleterious mutations, we used mutations that were reported to cause Mendelian diseases with experimental supports and were published after 1 January 2011. To ensure the quality of the neutral mutations, we applied the following criteria when selecting them: (i) with a MMAF >1% in 2269 exomes from the ARIC study via the CHARGE sequencing project (14); (ii) not reported in the 1000 Genomes Project or Uniprot and (iii) with Hardy–Weinberg exact test, P-value > 0.01. The 1% threshold for MMAF was chosen to minimize the contamination of potential Mendelian disease-causing mutations in the neutral control set. To provide high quality benchmark datasets, on which novel variant scoring methods can be evaluated, Thusberg et al. curated VariBench datasets, seven different datasets of high quality variants, whose effects were experimentally verified. These seven datasets cover variants with different properties, such as variants affecting protein tolerance, variants affecting transcription factor binding sites and variants affecting mRNA splice site. Because our study is mostly related to variants affecting protein tolerance, we chose this dataset as benchmark dataset. Original TN observations from this dataset contain 17 393 nsSNV extracted from dbSNP database build 131. Original TP observations from this dataset contain 14 610 missense variations obtained by manual curation from the PhenCode database downloaded in June, 2009, IDBases and from 16 individual LSDBs. Because 57.02% of TP observations and 23.87% of TN observations overlap our training dataset, we removed these variants from VariBench dataset and constructed our second independent testing dataset, testing dataset II, and curated 6279 deleterious variants as our TP observations and 13 240 common neutral variants (MMAF >1%) as our TN observations. In addition to the first two testing datasets that contain only common variants as TN observations, we also prepared testing dataset III that contains only 10 164 singleton neutral mutations (MMAF <0.1%). We collected the rare neutral nsSNVs from 824 European Americans from cohort random samples of the ARIC study(30) via the CHARGE sequencing project (14). We retained only nsSNVs that have only one alternative allele observed in the sample (i.e. singletons). We further removed nsSNVs that have been reported in the 1000 Genomes Project or the NHLBI's Exome Sequencing Project, to make sure those nsSNVs are truly rare and novel. To reduce the artifacts that are due to mapping errors, we further filtered out any nsSNVs that reside outside the strict mask of the 1000 Genome Project and that with an ENCODE (42) mappability score smaller than 1. To reduce interpretation complication, we removed nsSNVs that correspond to multiple transcripts as to RefSeq, Ensembl and Uniprot. After the above filtering steps, we retained 10 164 rare nsSNVs. As this number is too large to interrogate all the prediction methods, we only compared the methods that are relatively easy to scale up for large number of queries, which include SIFT, PolyPhen-2, LRT, MutationTaster, Mutation Assessor, FATHMM, CONDEL, KGGSeq and our two ensemble scores.

Training dataset was used for modeling LR and SVM and testing datasets I and II were used for evaluating the performance of all deleteriousness prediction methods on separating deleterious mutations from common neutral mutations and testing dataset III was used for evaluating the performance on distinguishing rare neutral mutations.

Additionally, to compare the performance of all deleteriousness prediction tools with the result from Thusberg et al., we derived two additional testing dataset, additional testing dataset I and additional testing dataset II, from benchmark dataset from his team (Supplementary Material, Table S4). The results are shown in Supplementary Material, Figures S7 and S8.

Deleteriousness prediction methods

We compared the predictive performance of all prediction methods (Table 2). Despite their differences in the use of prediction features, training data and statistical models, the premise of most algorithms was that nsSNVs, which are evolutionarily conserved and/or lead to critical protein structure changes, are likely to be deleterious. Each method assigns a quantitative prediction score measuring the likelihood of an nsSNV being deleterious as well as qualitative prediction such as ‘benign’ or ‘damaging’ based on some algorithm-specific threshold for the prediction score, except for SiPhy, GERP++ and PhyloP, which only provide a prediction score.

In order to compare the performance of the quantitative scores of these prediction methods, we obtained all the prediction scores (Supplementary Material, Table S5). Among them, PolyPhen-2, SIFT, MutationTaster, Mutation Assessor, FATHMM, LRT, SiPhy, GERP++ and PhyloP were obtained from the dbNSFP database version 2.1; PON-P, PANTHER, PhD-SNP, SNAP and SNPs&GO were obtained via the PON-P webserver; MutPred, Condel (ensemble score of SIFT, PolyPhen-2 and Mutation Assessor) and KGGSeq were obtained manually through their own webservers or software package. Due to the limitation of the PON-P webserver that each batch query can only submit up to 10 variants, we only obtained PON-P, PANTHER, PhD-SNP, SNAP and SNPs&GO scores for testing dataset I. It is noted that the prediction scores obtained from dbNFSP database underwent transformation from original prediction scores (Table 2). We plotted the ROC curve for each of these prediction scores, together with MMAF and ensemble scores, and computed their AUC value of the ROC curve as cumulative statistics to evaluate their performances. As for testing dataset III that contains only TN observation, we were not able to plot the ROC curve. Therefore, we rescaled all the transformed prediction scores with suggested binary cutoff from their continuous prediction score into 0–1 scale with 0.5 being the binary cutoff of deleteriousness. We calculated the median of all prediction scores and demonstrate our results in Supplementary Material, Figure S2.

We also compared the performance of qualitative categorization of these prediction methods. We dichotomized prediction scores according to their current dichotomizing threshold recommended in the literature (36,37) for those providing dichotomizing thresholds. Note that there are three categorical outcomes for LRT, D (Deleterious), N (Neutral) and U (Unknown). In order to rule out the influence of unknown prediction outcomes and more accurately assess its performance, we discarded the mutations with U prediction outcome and calculated its qualitative prediction performance measurements such as MCC, TPR and TNR. Note that MCC is a balanced measurement of qualitative prediction outcome and it ranges from −1 to 1 (43). For the remaining prediction methods with no available dichotomizing thresholds, such as SiPhy, GERP++ and PhyloP, we calculated the thresholds as the points that were closest to the left-upper corner in their ROC curves with training dataset and used these thresholds for dichotomization with all testing datasets. We compared their sensitivity and specificity at the dichotomous thresholds for testing datasets I and II and demonstrate the results in Figure 2. As for testing dataset III that contains only TN observations, we calculated TNR for all deleteriousness prediction scores and demonstrate the results in Supplementary Material, Figure S4. We also dichotomized our ensemble-based scores according to their standard dichotomizing threshold (0 for SVM and 0.5 for LR) and incorporated them into qualitative comparison with other prediction methods.

Missing scores

As for mutations whose prediction scores contained certain missing values (Table 3), we used BPCA fill program, a tool designed to impute large dataset with correlated columns or rows with good performance in previous studies, to impute these missing values for each of such mutation, by borrowing information from its available scores. The imputation was conducted for PolyPhen-2, SIFT, MutationTaster, Mutation Assessor, FATHMM, LRT, SiPhy, GERP++ and PhyloP using all non-missing scores for all potential nsSNVs in human exome collected in the dbNSFP database v2.1. We reported the overall missing value percentage before and after imputation in Supplementary Material, Table S3. Because there was <3% missing rate for all the prediction tools after imputation, the small percentage of mutations with missing values was discarded in our comparison analysis without risking selection bias. These imputed scores were used to compute two ensemble-based scores using SVM and LR algorithms. Note that to avoid the effect of imputed score on performance evaluation in testing phase, mutations with any missing values were excluded to ensure that comparison of all deleteriousness prediction scores was done using only output scores from the prediction methods.

SVM and LR

In order to analyze the advantage of incorporating various prediction scores, we used two models, SVM and LR, to compute the ensemble-based scores. We harvested output scores from all of the prediction methods for all mutations in all of our datasets, combined them with MMAF from various populations and integrated them into input files for constructing LR and SVM, with linear kernel, radial kernel and polynomial kernel using R package e1071 (44). Performance for each model under each specific setting was tested on testing datasets I and II and was evaluated using R package ROCR (45). Because testing dataset III contains only TN observations, we applied manually calculated TNR for evaluating its performance.

To assess whether the parameters of our SVM model can be optimized to generate substantially better performance, we performed 5-fold cross validation on training set for different parameter cocktails. For linear SVM, cost of 0.01, 0.1, 1 (default), 10 and 100 were evaluated for performance. For polynomial SVM, degree of 2, 3 (default), 4, 5 and 6 with default parameter for cost were analyzed. For radial SVM, different combinations of gamma of 0.01, 0.1, 1, 10, 100 and 1/11 (default) and cost of 0.01, 0.1, 1 (default), 10 and 100 were evaluated. Default parameters for all SVMs were chosen as a result. Moreover, in order to assess the relative contribution of each prediction score to the performance of LR and SVM, we tested several modified SVM and LR models with one prediction score deleted from the original models and plotted average ROC curve and AUC value, as shown in Supplementary Material, Figure S9. In addition, in order to test whether our model can be further improved by using different combinations of prediction scores, we applied step-wise model selection using Akaike Information Criterion (AIC) statistic as a criterion. The resulting model from step-wise model selection is shown in Supplementary Material, Table S6 and is compared with our final model in Supplementary Material, Table S7.

To assess the model assumption and evaluate pair-wise redundancy of prediction scores, we checked the multi-collinearity between all pairs of predictors using R and demonstrate the results in Supplementary Material, Figure S6.

ROC curves

We used ROC curves and their AUC values to compare the performance of the quantitative individual prediction scores and the ensemble-based scores. For each prediction/ensemble score we evaluated, we varied the threshold for calling deleterious nsSNVs from the minimum value to the maximum value of this score. And for each threshold, we computed corresponding sensitivity (TP/(TP + FN)), and specificity (1 – FP/(FP + TN)) for this score, with respect to its proportions of true positive and true negative nsSNVs at this threshold, where TP, FP, FN and TN corresponds to true positive, false positive, false negative and true negative predictions, respectively. Having values for each point value for each score, the corresponding ROC curve was therefore obtained by plotting sensitivity against 1 – specificity at each threshold for this score. On the other hand, for qualitative prediction evaluation, we computed the point estimates of sensitivity and specificity instead, using dichotomized prediction/ensemble score. The ROC plot and sensitivity against specificity plot were generated using R package ROCR and the 95% CI using 2000 bootstrap was generated using R package pROC (46).

Supplementary Material

Supplementary Material is available at HMG online.

Author Contributions

X.L., K.W. and P.W. designed the study. X.J. and X.L. compiled the data. C.D. and P.W. conducted the analysis. E.B. provided critical comments. R.G. and E.B. provided ARIC sequence data. C.D., P.W., K.W. and X.L. wrote the manuscript. X.L. and K.W. coordinated all steps of the study.

Funding

This work was supported by National Institute of Health (R01-HL116720, R01-CA169122 and R01-HL106034 to P.W.; RC2-HL02419 and U54HG003273 to X.J., E.B., R.G. and X.L. and R01-HG006465 to C.D. and K.W).