Incorporating Chromatin Accessibility Data into Sequence-to-Expression Modeling

Abstract

Prediction of gene expression levels from regulatory sequences is one of the major challenges of genomic biology today. A particularly promising approach to this problem is that taken by thermodynamics-based models that interpret an enhancer sequence in a given cellular context specified by transcription factor concentration levels and predict precise expression levels driven by that enhancer. Such models have so far not accounted for the effect of chromatin accessibility on interactions between transcription factor and DNA and consequently on gene-expression levels. Here, we extend a thermodynamics-based model of gene expression, called GEMSTAT (Gene Expression Modeling Based on Statistical Thermodynamics), to incorporate chromatin accessibility data and quantify its effect on accuracy of expression prediction. In the new model, called GEMSTAT-A, accessibility at a binding site is assumed to affect the transcription factor’s binding strength at the site, whereas all other aspects are identical to the GEMSTAT model. We show that this modification results in significantly better fits in a data set of over 30 enhancers regulating spatial expression patterns in the blastoderm-stage Drosophila embryo. It is important to note that the improved fits result not from an overall elevated accessibility in active enhancers but from the variation of accessibility levels within an enhancer. With whole-genome DNA accessibility measurements becoming increasingly popular, our work demonstrates how such data may be useful for sequence-to-expression models. It also calls for future advances in modeling accessibility levels from sequence and the transregulatory context, so as to predict accurately the effect of cis and trans perturbations on gene expression.

Introduction

A central challenge in quantitative biology today is to understand the precise relationship between gene expression and regulatory sequences, especially enhancers. Enhancers (1,2), also called cis-regulatory modules in some contexts, are sequences ∼1 kbp long that harbor DNA binding sites for one or more transcription factors (TFs) that act together to regulate a gene's expression pattern (3–6). Recent technological breakthroughs such as genome-wide chromatin-state profiling (7,8) and massively parallel reporter assays (9,10) are leading the way in rapid and effective discovery of enhancers. The next frontier (1) is to learn to interpret an enhancer’s sequence and predict the expression level driven by the enhancer in a given trans-regulatory context, e.g., a particular tissue or cell type (11–13). Various studies have attempted to meet this challenge, and a line of attack that has met with considerable initial success is that of thermodynamics-based models (14–21).

Thermodynamics-based sequence-to-expression models have proven capable of producing highly accurate fits to complex gene-expression patterns. The hallmark of these models is that they are built around molecular interactions involving TF proteins, DNA, and the basal transcriptional machinery, and they use the language of statistical thermodynamics to map combinations of interactions, both strong and weak, to gene expression levels. Fits of these models to sequence and expression data capture underlying mechanistic details of gene regulation at a convenient level of abstraction. For instance, DNA-binding strengths of TFs and the potency of activation or repression by a DNA-bound TF appear as free parameters of these models, and their optimal values learned from data provide quantitative insights into underlying regulatory mechanisms. One key aspect missing from the mechanistic view adopted in today’s thermodynamics-based models is that of chromatin state.

A significant advance in recent years in the field of regulatory genomics is the realization that the chromatin state, e.g., specific histone modifications and general accessibility patterns, of cis-regulatory regions strongly correlates with expression and with regulatory events leading to expression (22–24). Genome-wide profiling of DNaseI hypersensitive (DHS) sites, representing regions of relatively accessible chromatin, or of specific histone modifications such as H3K27ac, has proven to be a powerful strategy to map regulatory DNA and pinpoint active enhancers (25–28). For instance, genome-wide, high-resolution, in vivo mapping of DHS sites has helped chart the regulatory DNA landscape of Drosophila early embryo development (29), showing how chromatin accessibility may influence genome-wide overlapping patterns of TF binding during embryogenesis (22,23,30). In addition, we now know that chromatin state (e.g., accessibility) of a genomic segment is an effective predictor of its regulatory activity (26,31,32) and an important feature in predicting TF occupancy therein (33). In particular, incorporation of accessibility data has significantly improved the accuracy of predicting in vivo TF occupancy over baseline models that used sequence-specific motifs alone (34,35). These findings naturally raise the question: does chromatin-state information also improve our ability to quantitatively predict expression levels driven by an enhancer? To our knowledge, this question has not yet been systematically and empirically answered, and it is the subject of this study.

Based on our knowledge today, we might expect an affirmative answer to the above question. Since chromatin accessibility data improves our ability to predict TF-DNA binding (23,30,35), and since it is generally accepted that better prediction of TF-DNA binding should lead to better expression prediction, it follows that accessibility data ought to improve sequence-to-expression prediction. However, testing this hypothesis requires coupling the two computational aspects mentioned above, i.e., using accessibility data for TF-DNA binding prediction and using binding prediction for expression prediction, and evaluating the integrated approach using an appropriate data set. This was the methodological challenge we faced in this work.

Moreover, it was not clear to us going into this study whether the resolution of available data and the expressivity of today’s sequence-to-expression models are adequate to demonstrate the advantage of incorporating accessibility data, even if such an advantage exists. Note that our goal was not to use accessibility data to identify enhancers and then predict expression from their sequence; rather, we wanted to test whether variations of accessibility within known enhancers, at the ∼20- to 25-bp resolution (22,29), can inform sequence-to-expression models in useful ways. This required that the models be sensitive enough to register quantitative variations of DNA accessibility at individual binding sites and that the accessibility data pertain to the same cell types for which we do have accurate sequence-to-expression models.

In this work, we build and evaluate a quantitative model that maps regulatory DNA sequence to the expression of the regulated gene while integrating DNA accessibility data. Several studies (18–21,36,37) have proposed quantitative models of the sequence-to-expression relationship. One such quantitative model is GEMSTAT (Gene Expression Modeling Based on Statistical Thermodynamics), a statistical thermodynamics-based model of sequence readout that we previously showed to successfully model dozens of enhancers involved in specification of the anterior-posterior (A/P) axis in early Drosophila embryos (21). GEMSTAT is the only available general purpose tool that can be trained to model the regulatory activities of a set of enhancers with a common assignment of free parameters. Moreover, its thermodynamics-based formulation lends itself to incorporation of accessibility data in an intuitive and semimechanistic manner, to an extent that one may study how accessibility of individual binding sites may impact expression. These considerations, along with our extensive experience with GEMSTAT, made it a natural choice for the modeling framework adopted here. The regulatory system we chose comprises the above-mentioned A/P patterning enhancers from Drosophila, in part because this system has been the subject of several modeling studies by us (21,38,39) and others (16,19,40,41), and also because chromatin accessibility data are available for the developmental stage represented by this data set. We find strong evidence that incorporating accessibility data into GEMSTAT improves fits, confirming the central hypothesis of this work.

Materials and Methods

Data collection

We modeled here the same data set used in the original work presenting the GEMSTAT model (21). The data set comprises 1) 37 experimentally characterized enhancers involved in the regulation of A/P patterning genes in stage 4–6 Drosophila embryos; 2) quantitative profiles of the gene-expression pattern driven by each enhancer; 3) DNA-binding motifs (expressed as position weight matrices (PWMs)) of six TFs, namely bicoid (BCD), caudal (CAD), hunchback (HB), giant (GT), knirps (KNI), and Kruppel (KR); and 4) a quantitative profile of the concentration of each TF (see Fig. S1 in the Supporting Material). He et al. (21) collected the sequences from Gallo et al. (42), TF concentration profiles from Poustelnikova and colleagues (43,44), gene-expression profiles from Segal and co-workers (19), the PWM of BCD from Bergman et al. (45), and the PWMs of the other TFs from Noyes et al. (46). Following He et al., we chose to model gene expression within 20–80% of the A/P axis.

Chromatin accessibility data from DNaseI hypersensitivity (DHS) assays in embryonic stage 5 were gathered from Berkeley Drosophila Transcription Network Project (BDTNP) Release 5 (22,29). We ranked the genome-wide DHS scores (at 20 bp resolution), with rank 1 representing the smallest DHS score. The rank-ordered DHS scores were then divided by the total number of windows in the genome. These normalized scores were on the scale of 0 (least accessible) to 1 (most accessible). Rank-based normalized DHS scores within the 37 enhancers were extracted and used to compute the accessibility score, Acc(S), of each annotated binding site, S. (The scheme for annotating binding sites is described below.) Acc(S) was simply the rank-normalized score of the 20 bp segment that includes the site, S, or the average of multiple segments if the site overlaps with multiple segments.

The GEMSTAT model

GEMSTAT (21) is a sequence-to-expression model of transcriptional regulation founded on the statistical thermodynamic framework proposed by Shea and Ackers (47). In this framework, transcriptional regulation occurs through the interactions of three major components: 1) enhancer (DNA), 2) TF molecules, and 3) the basal transcriptional machinery (BTM), i.e., the molecular complex that assembles at the promoter and initiates transcription (Fig. 1 A). All of these interactions (TF-DNA, BTM-DNA, and TF-BTM) are assumed to happen in thermodynamic equilibrium, and the equilibrium mRNA level is assumed to be proportional to the fractional occupancy of the BTM at the promoter. Under standard assumptions of statistical mechanics, GEMSTAT computes this fractional occupancy by considering all possible configurations of DNA-bound TFs and BTM (Fig. 1 A) and taking the total equilibrium probability of BTM-bound configurations. The equilibrium probability, P(σ), of a configuration σ is assumed to follow the Boltzmann distribution. Thus, P(σ) = exp(− βE(σ))/Z, where β = 1/k_BT (with k_B the Boltzmann constant and T the temperature), E(σ) denotes the energy associated with configuration σ, and Z denotes the partition function. The energy, E(σ), is modeled in GEMSTAT using free parameters that represent energies associated with interactions in σ. Of particular interest are two TF-specific free parameters that model TF-BTM and TF-DNA interactions, as described below.

• 1.The parameter txpEffect(f), corresponding to a TF f (Fig. 1 A) represents the quantity exp(− βE(f · BTM)), where E(f · BTM) is the interaction energy between a molecule of the TF f and the BTM.
• 2.To model the binding energy E(f · S) of a molecule of TF f at a cognate site S, GEMSTAT uses a second TF-specific free parameter, bindingWt(f) (Fig. 1 A), and also makes use of a theory proposed by Berg and von Hippel (48) as follows. The energy E(f · S) is modeled in GEMSTAT as

$$E\left(f·S\right)=E\left(f·S_{\text{opt}}\right)+\Delta E\left(S,S_{\text{opt}}\right),$$ (1)

where S_opt denotes the optimal binding site for f and ΔE(S,S_opt) denotes the mismatch energy of site S with respect to S_opt (49). The free parameter, bindingWt(f) represents the quantity exp(− βE(f · S_opt)) at unit concentration of the TF f. Berg and von Hippel (48) linked ΔE(S,S_opt) to the log-likelihood ratio (LLR) scores of sites S and S_opt as

$$\beta \Delta E\left(S,S_{\text{opt}}\right)=\mathrm{LLR}\left(S_{\text{opt}}\right)-\mathrm{LLR}\left(S\right),$$

where the log-likelihood ratio score LLR(S) for a site S is computed from the PWM of f and the genomic background distribution. When it is not important to mention the identity of the TF f, we write Eq. 1 as

$$E\left(S\right)=E\left(S_{\text{opt}}\right)+\Delta E\left(S,S_{\text{opt}}\right).$$ (2)

Figure 1.

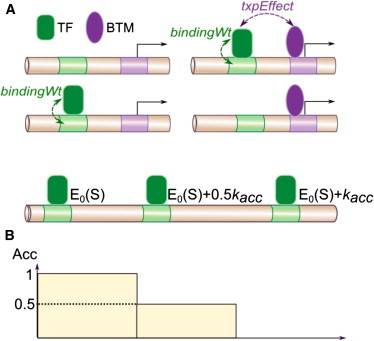
(A) GEMSTAT models the major components of transcriptional regulation and their interactions in thermodynamic equilibrium. Shown are all possible molecular configurations of a transcriptional system where the enhancer contains a single binding site for a TF, with the TF (green) bound or not bound at its site and the BTM (purple) bound or not bound at the promoter. Arrows indicate TF-DNA and TF-BTM interactions, represented by the parameters bindingWt and txpEffect, respectively. GEMSTAT uses the energies associated with these interactions to predict the level of gene expression in the system. (B) GEMSTAT-A assumes that the TF-DNA binding energy at a site S changes according to the accessibility of S. Shown is an example with three identical binding sites where GEMSTAT estimates the same TF-DNA binding energy E₀(S). GEMSTAT-A assigns a local accessibility score, Acc(S), to each site S (bottom, y axis), and models the TF-DNA binding energy as E₀(S) + k_acc(1 − Acc(S)). To see this figure in color, go online.

The GEMSTAT-A model

The new quantitative model for predicting gene expression by taking chromatin accessibility data into account, called GEMSTAT with Accessibility (GEMSTAT-A), is an extension of GEMSTAT. GEMSTAT-A integrates chromatin accessibility data to explore the interplay between accessibility, TF-DNA binding strength, and gene expression (Fig. 1 B). We first assigned a local accessibility score, Acc(S), on a scale of 0–1 (where 0 = inaccessible), to each TF binding site S. To model how accessibility of S affects the energy E(S), GEMSTAT-A redefines E(S) in Eq. 2 by incorporating Acc(S) as

$$E\left(S\right)=E\left(S_{\text{opt}}\right)+\Delta E\left(S,S_{\text{opt}}\right)+k_{\text{acc}}\left(1-\mathrm{Acc}\left(S\right)\right),$$ (3)

where k_acc > 0 is a free parameter optimized in the course of fitting the data and is a phenomenological parameter reflecting the effect of accessibility. Thus, instead of setting a threshold to define accessible and inaccessible TF binding sites, GEMSTAT-A uses quantitative accessibility scores in calculating the binding energy. For brevity, we use the notation E₀(S) to represent the term E(S_opt) + ΔE(S,S_opt) of Eq. 2, i.e., the energy that GEMSTAT estimates to be associated with TF binding at S, and rewrite Eq. 3 as

$$E\left(S\right)=E_0\left(S\right)+k_{\text{acc}}\left(1-\mathrm{Acc}\left(S\right)\right).$$ (4)

Model training

The GEMSTAT-A model was trained using the same strategy that was used for GEMSTAT (21). The inputs for training were the 37 enhancer sequences with their A/P expression profiles, as well as PWMs and concentration profiles of six TFs. For each TF, all PWM matches in an enhancer with LLR score (defined above) at least 0.4 times the LLR score of the optimal site were annotated as binding sites. In addition, in GEMSTAT-A, each annotated site S was assigned a local accessibility score, Acc(S), as described above, in estimating the TF-DNA binding energy at S. Both models considered self-cooperative DNA binding of BCD as well as KNI and were used in Direct Interaction mode (see He et al. (21)). The number of free parameters in GEMSTAT was 15 (the txpEffect and bindingWt parameters for each TF, one parameter to model the basal level of gene expression, and one parameter for each TF that we assumed to have self-cooperative DNA binding; see Table S5 for details.), whereas GEMSTAT-A had one additional free parameter (the accessibility-effect parameter k_acc). Model parameters were fit to maximize the average wPGP score (explained below) between model predictions and real expression profiles (see Text S1 in the Supporting Material for details).

Evaluation of model predictions using weighted pattern-generating potentials

State of the art quantitative models of gene expression adopt two common approaches to evaluate their predictions, namely the average correlation coefficient and the root mean-square error. However, these do not always capture the salient features of a one-dimensional expression pattern, as shown in Kazemian et al. (36). To address these issues, a new scoring function, called weighted pattern-generating potential (wPGP) was presented by Samee and Sinha (38). This scoring function was designed for two purposes: 1) to be sensitive to both the shape and magnitude of the predicted expression profiles, and 2) to avoid biases toward or against overly broad or overly narrow domains of expression (see Text S1 in the Supporting Material for details).

Results

A thermodynamics-based model that integrates chromatin accessibility data

The new model, to our knowledge, proposed here, called GEMSTAT-A (A for accessibility), is an extension of GEMSTAT (see brief overview of GEMSTAT in Materials and Methods and Fig. 1 A). To incorporate the effects of varying local accessibility within an enhancer, we modified the GEMSTAT model as follows. First, a local accessibility score, Acc(S), is assigned to each annotated TF binding site S, based on given accessibility data (e.g., DHS data). The score is on a scale of 0 to 1 (where 0 = inaccessible). Next, the TF-DNA binding energy at site S is modulated by this accessibility score and defined to be

$$E\left(S\right)=E_0\left(S\right)+k_{\text{acc}}\left(1-\mathrm{Acc}\left(S\right)\right),$$

where E₀(S) is the TF-DNA binding energy at S as estimated by GEMSTAT (cf. Eq. 2) using the TF’s motif, and k_acc > 0 is a free parameter.

In GEMSTAT (i.e., the original model), every TF binding site is considered to be completely accessible, which is equivalent to setting the local accessibility score to 1. (Note that setting Acc(S) = 1 implies E(S) = E₀(S) in the above formula.) In reality, if the local accessibility is low (Acc(S) < 1), GEMSTAT may overestimate the contribution of the site by ignoring its accessibility score. GEMSTAT-A increases the binding energy (decreases the strength) of less accessible sites while maintaining the original estimates for sites in highly accessible regions. Other than this modification of how the binding energy is estimated, GEMSTAT-A is identical to GEMSTAT in how enhancer sequence and trans context are mapped to the expression level driven by the enhancer. Note that GEMSTAT-A has one additional free parameter to be optimized, viz., the accessibility-effect parameter, k_acc.

Chromatin accessibility data improve expression predictions

We asked whether GEMSTAT-A could fit expression profiles of real enhancers better than GEMSTAT by making use of experimentally measured accessibility variations within the enhancer. To test this, we resorted to a data set used in the original GEMSTAT study (21) (see Data collection for details). Both GEMSTAT and GEMSTAT-A were fit to this data set, using identical parameter optimization procedures. In addition, GEMSTAT-A was made to utilize rank-normalized chromatin accessibility data in embryonic development stage 5 (see Materials and Methods). We also note that although the modeling setup was kept mostly identical to that of He et al. (21), we made one change, common to both GEMSTAT and GEMSTAT-A modeling: the wPGP score was used to measure the goodness of fit between experimentally observed and model-predicted enhancer readouts (see Materials and Methods).

Expression predictions from GEMSTAT and GEMSTAT-A for each enhancer were evaluated using the wPGP score. These are shown in Fig. 2 and Table S1. Overall, GEMSTAT-A was evaluated at a wPGP score of 0.773 (averaged over 37 enhancers), whereas GEMSTAT showed an average wPGP of 0.745 (average cross-validation wPGP is 0.741 for GEMSTAT-A and 0.679 for GEMSTAT (see Table 1 for details). GEMSTAT-A produced better fits than GEMSTAT (wPGP score improved by ≥0.05) on 15 of 37 enhancers (Fig. S2 A), whereas it produced worse fits than GEMSTAT on 6 of 37 enhancers (Fig. S2 C). (Within the former group of 15 better-predicted enhancers, the average wPGP score improved by 0.18.) These 21 cases included enhancers where one of the models had a wPGP score ≤0.5, which in our experience (also see Fig. S2) is a sign that the model failed completely on that enhancer; the differences in fits on these enhancers are likely not due to consideration of accessibility data directly but to the different parameter settings utilized by the two models. Ignoring these cases, we can identify 11 cases where GEMSTAT-A fits the data better and four enhancers where it fits worse than GEMSTAT (Table S1, last column). We interpret this as strong evidence that incorporating chromatin accessibility data improves gene-expression predictions. To better appreciate the nature of the differences between the two models in their fits and to qualitatively assess the improvement due to accessibility information, we plotted the model predictions along with real expression patterns for a selection of enhancers (Figs. 3 and S2).

Figure 2.

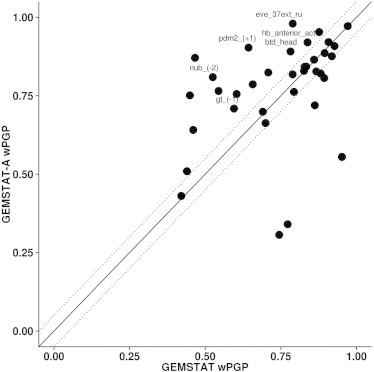
Evaluations of expression predictions from GEMSTAT and GEMSTAT-A. The goodness of fit between predicted and real expression for each enhancer was assessed by wPGP score, shown here for all 37 enhancers. Dotted lines delineate regions where the difference in wPGP between the two models is ≥0.05. A selection of enhancers where GEMSTAT-A improves fits are labeled and their expression patterns are shown in Fig. 3.

Table 1.

10-fold cross-validation assessment of GEMSTAT and GEMSTAT-A

Model	No. of parameters	Training wPGP	CV wPGP (SD)
GEMSTAT-A	16	0.773	0.741 (0.005)
GEMSTAT	15	0.745	0.679 (0.008)

Each model was tested with 10-fold cross-validation, repeated five times with different (random) definitions of the 10 folds. Shown for each model are the number of free parameters used, the wPGP score from parameter optimization over all 37 enhancers (Training wPGP), and the wPGP score from cross-validation (CV wPGP) averaged (with standard deviation (SD) in parentheses) over the five repeats.

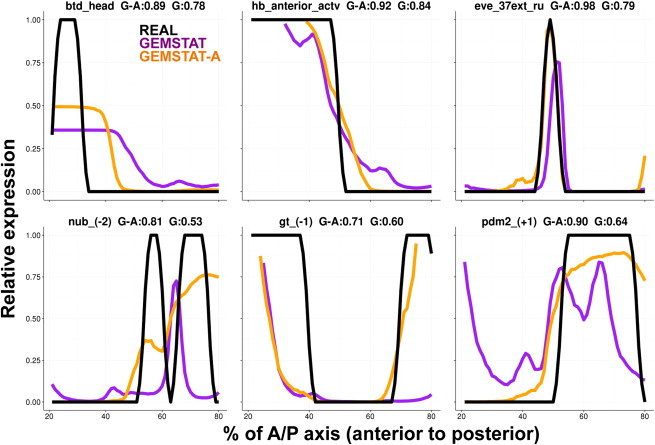
Figure 3.

Expression predictions from GEMSTAT and GEMSTAT-A. The predicted expression profiles of GEMSTAT-A (orange lines) and GEMSTAT (purple lines) are compared to experimentally determined readouts (black lines) for six selected enhancers. Each expression profile is on a relative scale of 0 to 1 (y axis) and shown for the region between 20% and 80% of the A/P axis of the embryo. The label of each panel is in the format enhancer name, wPGP by GEMSTAT-A (G-A), wPGP by GEMSTAT (G). To see this figure in color, go online.

We noted that on some enhancers (e.g., those in Fig. 3, upper row), GEMSTAT-A fits showed refinements of GEMSTAT predictions, resulting in more accurately defined boundaries of expression domains. On other enhancers, there were more qualitative improvements, e.g., GEMSTAT-A correctly models the posterior domain of gt_(−1), correctly removes a spurious anterior domain prediction made by GEMSTAT on the enhancer pdm2_(+1), and dramatically improves upon the boundaries of the predicted expression domain of the enhancer nub_(−2). Interestingly, the change in GEMSTAT-A’s prediction from the GEMSTAT prediction is more accurate biologically for some cases, although the prediction does not match the data. For example, the posterior expression in our predicted readout for eve_37ext_ru is indeed in those locations along the A/P axis where the seventh stripe of the eve gene is formed. A detailed comparison of relative successes and failures as well as examples where one model completely failed to capture the spatial pattern driven by an enhancer whereas the other model was successful are shown in Fig. S2.

Thus, our initial observations on model fits over all enhancers indicated, both quantitatively and qualitatively, a conspicuous improvement due to chromatin accessibility data. Rigorously speaking, GEMSTAT-A fits are expected to be at least as good as GEMSTAT, since the former has one extra parameter, the accessibility effect k_acc. A common method of comparing models of varying complexity is to evaluate their cross-validation accuracy (21). We therefore performed 10-fold cross-validation with either model, where each fold uses 33–34 of the 37 enhancers as training data and the remaining three to four enhancers as the testing data. Since partitioning of the 37 enhancers into 10 folds is done at random, we repeated the entire 10-fold cross validation exercise five times (with different random partitioning in each repeat) for each model. The average cross-validation wPGP across all five runs of 10-fold cross-validation was 0.679 and 0.741 for GEMSTAT and GEMSTAT-A, respectively (Table 1). (Detailed results from cross-validation are shown in Table S3.) This analysis clearly shows the improved ability of GEMSTAT-A, compared to GEMSTAT, to predict expression readouts, even after accounting for the additional free parameter.

To verify the above effect further, we next repeated the modeling exercise by 1) using accessibility data from embryonic stage 14 instead of from the earlier embryonic stage 5 to which the expression data correspond, 2), using a randomly shuffled version of the normalized accessibility scores across the whole genome and extracting local accessibility profiles in the 37 enhancers, or 3) shuffling the accessibility scores across the 37 enhancers. (The last exercise was motivated by the fact that enhancers are known to have higher accessibility in general, and genome-wide permutation of accessibility scores is likely to assign low accessibility values within enhancers, thus presenting an unrealistic random control.)

GEMSTAT-A was trained on these three different incorrect settings of chromatin accessibility data and then evaluated by the wPGP score (Tables 2 and S4). In all three cases, the advantage of GEMSTAT-A over GEMSTAT was entirely lost, and the optimal value of the k_acc parameter reported was weak or close to 0, suggesting that the model found no advantage to using the incorrect accessibility data. These negative controls thus confirmed that the improved fits found by GEMSTAT-A are mainly due to using chromatin accessibility data from the appropriate developmental stage.

Table 2.

Effect of chromatin accessibility data used in GEMSTAT-A

Model	DNA accessibility data	wPGP	Kacc
GEMSTAT	No accessibility data	0.745	N/A
GEMSTAT-A	Embryonic stage 5	0.773	17.6
GEMSTAT-A	Embryonic stage 14	0.742	4.62
GEMSTAT-A	Shuffling across whole genome	0.734	0.91
GEMSTAT-A	Shuffling across all enhancers	0.735	0.97

Results from GEMSTAT-A trained with different variations on input chromatin accessibility data: data from embryonic developmental stage 5 (stage matching the modeled expression patterns), embryonic stage 14 (mismatched stage), or two different randomly shuffled versions of the stage 5 data (see text). Also shown, in the first row, is the result from GEMSTAT, which does not use accessibility data. For each variation of input accessibility data, shown are the wPGP score (averaged over 37 enhancers) and the optimized value of the accessibility effect parameter (k_acc). Results in the last two rows (shuffled versions of stage 5 accessibility data) are averaged over three different repeats of the assessment (using different random shuffling).

GEMSTAT-A learns much stronger thermodynamic parameters

In the process of training sequence-to-expression models, information about inputs (enhancer sequences and trans-regulatory context) and output (expression pattern driven by enhancers) of a regulatory function is used to automatically learn values for the free parameters of the model. Both GEMSTAT and GEMSTAT-A utilize two free parameters for each TF. One of these TF-specific parameters is called the DNA binding weight parameter (bindingWt), which helps estimate the occupancy of the TF at a binding site. The other is called the transcription effect parameter (txpEffect), which represents the strength of activation or repression due to a DNA-bound TF molecule. These parameters have intuitive semantics, so their optimal values reported by a trained model are of interest; for example, these values indicate whether TFs bind their respective consensus site strongly or weakly, whether one activator is more effective than another, etc. In other words, the trained model parameters paint a quantitative picture of the underlying regulatory mechanisms. It is natural to ask whether two models trained on the same data, identical in all respects except that one is aware of accessibility data and one is not, suggest similar quantitative views of the underlying mechanistic reality. We examined the optimal values of the bindingWt and txpEffect parameters for each of the six TFs used in the model, as learned by GEMSTAT and GEMSTAT-A separately. We were surprised to see that the same parameters were often trained to very different values: GEMSTAT-A was found to learn much stronger parameters (in some cases one to two orders of magnitude stronger) than GEMSTAT. The bindingWt parameter of both activators and repressors was assigned a greater value (stronger binding strengths) by GEMSTAT-A compared to GEMSTAT (Fig. 4 A and Table S2). The bindingWt parameter of HB was around 50-fold greater in GEMSTAT-A, whereas that of KNI was ∼13-fold greater. The txpEffect parameter describes the regulatory effect of a TF and takes values >1 for activators and <1 for repressors. We observed that GEMSTAT-A assigned values to the activator TFs BCD and CAD that were about twofold greater than values learned by GEMSTAT (Fig. 4 B and Table S2). Likewise, for three of the four repressor TFs (GT, KNI, and KR), GEMSTAT-A assigned lower txpEffect values, reflecting stronger repression ability, especially in the case of KR, whose txpEffect was ∼20-fold stronger in GEMSTAT-A.

Figure 4.

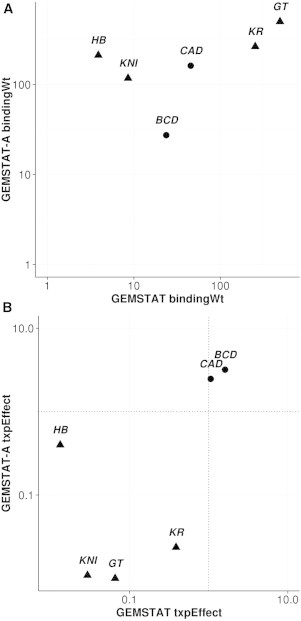
GEMSTAT-A learns stronger parameter values. Shown are the bindingWt (A) and txpEffect (B) parameters of each TF learned from GEMSTAT (x axis) and GEMSTAT-A (y axis). In both A and B, both axes are on a logarithmic scale. Repressors are represented by triangles and activators by circles. The txpEffect parameter for an activator is >1, and higher values indicate stronger activation. This parameter for a repressor is <1, and lower values indicate stronger repression.

The apparent discrepancy between the optimal parameter settings found by GEMSTAT and those found by GEMSTAT-A may be an artifact of the optimization procedure, with the two models finding two distant local optima in the search space. To address this, we repeated the optimization procedure for GEMSTAT by initializing the search at the optimal parameter values found by GEMSTAT-A. If GEMSTAT can explain the data well with parameter settings in the neighborhood of this initial point, then the discrepancy between optimal models noted above is not real. However, this new optimization produced a wPGP score of 0.72, which is inferior to that reported by the original GEMSTAT optimization, thus suggesting that the two models do indeed reach their best fits with dramatically different parameter values. We speculate on the implications of this observation in the Discussion section.

GEMSTAT-A improves expression prediction by reducing the contribution of inaccessible binding sites

We showed above that GEMSTAT-A is able to achieve better predictions of enhancer readouts with a simple modification of the estimated binding energy of a TF at its sites. This suggests the existence of TF binding sites in relatively inaccessible segments within the enhancer, which GEMSTAT was forced to incorporate in its predictions but which GEMSTAT-A could ignore by exploiting accessibility information. We investigated this potential explanation of why GEMSTAT-A produces better fits. For each annotated binding site within the enhancer (recall that these are identical between the two models), we removed the accessibility information for that site only, designating it as completely accessible (Acc(S) = 1), and recomputed the expression profile predicted by GEMSTAT-A. The new goodness of fit (wPGP) was calculated and compared to the original wPGP score of GEMSTAT-A for that enhancer. The difference in wPGP values, for the same model with or without use of accessibility information on that site, was plotted for each site (ΔwPGP in Fig. 5 A). We also plotted the change in estimated binding energy of each site due to incorporation of local accessibility values (ΔΔE in Fig. 5 B). (Parameters were not retrained in this analysis. See Table S6 for details.)

Figure 5.

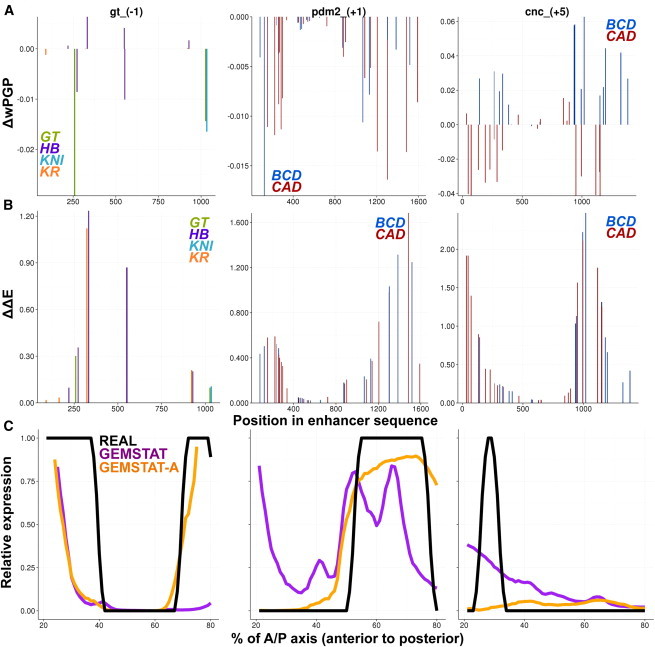
Accessibility of individual sites is utilized by GEMSTAT-A to improve predictions. Details of GEMSTAT-A modeling on enhancers gt_(−1), pdm2_(+1), and cnc_(+5) are shown in the left, middle, and right columns, respectively. (A) Change in goodness of fit (ΔwPGP) of GEMSTAT-A predictions when a binding site’s accessibility score is forced to a value of 1 (maximum accessibility), shown for each site as a function of its location in the enhancer. (B) Reduction in estimated binding energy (ΔΔE) due to local accessibility is shown for each annotated binding site as a function of the site’s location in the enhancer sequence. Only sites for a subset of TFs (repressors at left and activators at middle and right) are shown. (C) Predicted expression profiles of GEMSTAT-A (orange lines) compared to GEMSTAT predictions (purple lines) and experimentally determined readouts (black lines).

Fig. 5 shows examples of the above-mentioned explanation of how GEMSTAT-A improves fits by weakening the estimated binding energy of sites in less accessible regions. One such example is that of the enhancer gt_(−1), where both GEMSTAT and GEMSTAT-A correctly predict the anterior domain, but the posterior domain (∼70–80% of the A/P axis) is not predicted by GEMSTAT and is correctly predicted by GEMSTAT-A (Fig. 5 C, left). A natural explanation for this difference is that binding sites capable of repressing expression in the posterior domain are present in less accessible regions of the enhancer, and although GEMSTAT-A ignores their potential contribution, GEMSTAT includes this contribution, leading to the absence of a posterior domain in its prediction. Indeed, Fig. 5 A (left) shows that a binding site of the repressor GT, located at position ∼250 in the enhancer, is one such site: if GEMSTAT-A were to designate this site as accessible, its goodness of fit (wPGP) would diminish by ∼0.03. Fig. 5 B shows that the estimated binding energy of this GT site was indeed lower due to local accessibility values. The same figure also shows a KR site (at position ∼300) that is inaccessible, but whose accessibility score is not relevant to the fits of GEMSTAT-A for this enhancer.

A similar explanation applies to the enhancer pdm2_(+1), for which GEMSTAT incorrectly predicted an anterior domain of expression, whereas GEMSTAT-A correctly predicted lack of expression in the anterior (Fig. 5 C, middle). The natural explanation for this difference is the existence of an activator site capable of driving anterior expression, whose local inaccessibility leads GEMSTAT-A to ignore the site but whose inclusion leads GEMSTAT to predict the spurious anterior expression. Fig. 5 B (middle) shows that there are several BCD sites in the enhancer that satisfy this property; BCD is expressed anteriorly (Fig. S1) and its sites are therefore capable of causing GEMSTAT to predict anterior expression unless their effect is ignored based on local chromatin inaccessibility. Thus, these two examples provide deeper insights into how GEMSTAT-A can use local accessibility to suppress the activating or repressive effects of binding sites, leading to more accurate predictions of enhancer readout.

The above analysis also explains why GEMSTAT-A performed poorly on a few enhancers. One such example is the enhancer cnc_(+5), where GEMSTAT-A failed to predict the anterior expression domain (Fig. 5 C, right). This enhancer has several BCD sites in relatively inaccessible locations (Fig. 5 B, right), and by ignoring or diminishing their potential activating influence, GEMSTAT-A loses its ability to predict the anterior domain. Indeed, if it were to ignore the accessibility scores of these sites (i.e., if it assumed that they are accessible), its wPGP value would improve, as revealed by Fig. 5 A (right). Such aberrant cases were rare in our evaluations, and may be attributed to the spatial resolution of accessibility data (see Discussion), among other possibilities.

Discussion

Quantitative models such as GEMSTAT have been shown to have the expressive power to capture the complex relationship between regulatory sequence and precise gene-expression patterns, i.e., the so-called cis-regulatory code (6,13). Their appeal lies in achieving this expressiveness within a biophysically motivated framework (so that fit models can be interpreted more easily) while making simplifications that hide mechanistic details on which little information is available. One such simplification heretofore has been to model TF-DNA binding as entirely determined by the binding site and the PWM, by adopting Berg and von Hippel's theory (48,50). The role of local chromatin structure and epigenetic modifications has been ignored in these models, understandably so, since appropriate data for learning this role have been lacking. (Also, the few existing models for predicting nucleosome occupancy profiles (51–53) have not reached the level of accuracy necessary for coupling them to enhancer models (data not shown).) However, the recent wave of studies profiling the chromatin landscape, especially DNA accessibility, in specific cell types (54) or developmental stages (23) has changed this situation. Our work responds to this exciting new development in regulatory genomics by incorporating DNA accessibility data into sequence-to-expression models and asking whether this may at least partly address the limitations introduced by the simplification mentioned above. We find the answer to be in the affirmative, at least in the context of our modeling framework and the data set analyzed here.

We note that the role of chromatin accessibility in sequence-based models of gene expression has not been previously studied. There have been several interesting computational analyses of accessibility data that have shown the prodigious impact of accessibility on TF-DNA binding profiles (23,30,35), as well as the correlation between changing accessibility and changing expression (29,54,55), but these studies do not quantify the impact of accessibility data on sequence-based prediction of precise spatiotemporal expression patterns. We also note that our answer to the above-mentioned question did not have to be affirmative. Even though accessibility clearly shapes expression (24), its influence might have been simply in making the entire enhancer available for function; in this case, a modeling study that already begins the assumption of an open enhancer will not gain any significant advantage from accessibility data. Our affirmative answer suggests a more nuanced role, where variation of accessibility within the enhancer carries information useful for the functional interpretation of the binding sites present in the enhancer.

It is worth noting that GEMSTAT-A is a phenomenological extension that adds accessibility information to GEMSTAT. In reality, chromatin accessibility is likely the result of complex processes involving the nucleosome, TFs, chromatin remodeling factors, and DNA (sequence) (56). Future sequence-to-expression models may strive to incorporate these processes directly at suitable levels of parameterization, with accessibility being an intermediate dependent variable predicted from sequence and the cellular context rather than an independent variable, as is the case in GEMSTAT-A. One example of such future work is to model the influence of pioneer factors (57), which exhibit sequence-specific binding and seem to remodel the accessibility profile locally. The transcription factor ZELDA is a strong candidate for this special treatment in the context of our data set, with recent studies recording its widespread and significant regulatory influence (58,59) on many of the gene-expression patterns we have modeled here. Computational (30) and experimental (58) work have strongly suggested that this influence is mediated via accessibility, and it has been noted that the ZELDA binding motif is highly enriched in hot spots of multi-TF binding (60). It is expected that a part of the advantage of using accessibility data will be observed if GEMSTAT is modified to use ZELDA as a DNA-binding protein that makes local chromatin more accessible. We chose not to use ZELDA as one of the regulatory inputs in this work, so that we would get a more accurate view of the role of accessibility variations in shaping expression readouts of enhancers.

In principle, the data used as input to GEMSTAT-A should correspond to a cell type—in our case, position along the A/P axis of the embryo. This is the case for the TF concentration profiles used here, with GEMSTAT-A making separate predictions for each bin along the A/P axis, using relative TF concentration values for that bin. However, this is not the case for the accessibility data used, which correspond to whole embryo measurements. We thus believe that the advantage observed by us is an underestimate of what cell-type-specific accessibility data, already available in other contexts (24,54), can confer upon sequence-to-expression models. For instance, the coarseness of accessibility data might negatively impact the accuracy of GEMSTAT-A on an enhancer that functions for a short period of time (compared to the longer period over which the accessibility data is aggregated), or an enhancer driving expression in relatively few cells of the embryo. This may explain some failures of GEMSTAT-A modeling. For the enhancer oc_(+7), for example, we found that sites for HB (a repressor which presumably limits the gene’s expression in a narrow anterior domain) are mostly in the inaccessible regions (data not shown). This might have caused GEMSTAT-A to predict a broad ectopic expression pattern for this enhancer (Fig. S2 C). It is also worthwhile to note that we used the wPGP score to measure the goodness of fit. In some cases, wPGP scores do not reflect our visually perceived quality of fit. The wPGP score has been found to be a superior choice in comparison to the two commonly used goodness-of-fit scores, namely, the sum of squared errors and the correlation coefficient (36,38). Our experiences from these published studies were convincing enough for us to choose wPGP as the goodness-of-fit score here. Future work will continue improving the design of goodness-of-fit scores for such models.

An interesting observation made during our model comparisons (with and without accessibility data) was that the parameter values learned in GEMSTAT-A fits were stronger than those learned in GEMSTAT fits. Stronger parameter values for a TF imply that each binding site of that TF is regarded as having a greater contribution to the enhancer’s function. To see why this might be the case, suppose that an enhancer has two TF binding sites for the same TF, and that each of these sites has the same binding affinity and concentration, but one site is accessible and the other is not. In GEMSTAT, each TF binding site is supposed to be completely accessible, so the two sites make equal contributions to the gene expression. However, GEMSTAT-A is aware that one of the binding sites is inaccessible and will therefore attribute greater contribution to the accessible site to achieve the same level of gene expression. This will result in GEMSTAT-A using stronger parameter values.

Conclusions

In conclusion, we have shown here for the first time, to our knowledge, how thermodynamic models of enhancer readouts may leverage accessibility information to explain the data with higher accuracy. We have commented above on the limits of the accessibility data used here, and we expect that the potential shortcomings of using embryo-wide data may be alleviated by refined, cell-type-specific data in the future. This study also makes it more interesting to assess additional mechanisms of accessibility and the role of histone modifications. These will be subjects of our future studies. Finally, although we demonstrate the utility of our modeling for a model organism, the impact of this modeling framework will be much higher if data on mammalian gene-expression levels under a large number of different conditions are available, along with experimentally derived knowledge of the major regulators under those conditions. Extending this framework to mammalian systems will be a major direction for future research.

Supporting Material

Table S6. Effect of accessibility data on each TF binding site

For each annotated binding site within the enhancer, the accessibility information was removed for the site only to test its contribution to the predicted expression pattern. Columns are TF binding sites with their individual relative position in the enhancer, local accessibility score, change in estimated binding energy (ΔΔE), and the difference in wPGP values (ΔwPGP).