Switching of Bacterial Flagellar Motors Is Triggered by Mutant FliG

Abstract

Binding of the chemotaxis response regulator CheY-P promotes switching between rotational states in flagellar motors of the bacterium Escherichia coli. Here, we induced switching in the absence of CheY-P by introducing copies of a mutant FliG locked in the clockwise (CW) conformation (FliG^CW). The composition of the mixed FliG ring was estimated via fluorescence imaging, and the probability of CW rotation (CW_bias) was determined from the rotation of tethered cells. The results were interpreted in the framework of a 1D Ising model. The data could be fit by assuming that mutant subunits are more stable in the CW conformation than in the counterclockwise conformation. We found that CW_bias varies depending on the spatial arrangement of the assembled subunits in the FliG ring. This offers a possible explanation for a previous observation of hysteresis in the switch function in analogous mixed FliM motors—in motors containing identical fractions of mutant FliM^CW in otherwise wild-type motors, the CW_bias differed depending on whether mutant subunits were expressed in strains with native motors or native subunits were expressed in strains with mutant motors.

Introduction

The bacterial flagellar motor contains a switch that is responsible for changes in the direction of rotation, and consists of rings of three types of proteins: FliG, FliM, and FliN. The FliG ring, with 26 subunits, interfaces with the stator. Each FliG subunit, and hence the FliG ring, prefers to be in the lower-energy counterclockwise (CCW) conformation, causing the motor to rotate in a default CCW direction. The FliM ring acts as a receptor for the ligand CheY-P, and CheY-P binding stabilizes thermally driven transitions of the switch to the CW state (1). The switch responds ultrasensitively to chemotactic signals, causing the probability of CW rotation (CW_bias) to increase in a sigmoidal fashion over a narrow range of CheY-P concentrations (2–4).

In strains lacking the cheY gene, motors rotate exclusively CCW, and cells swim smoothly. Switching can be induced in such strains either via changes in temperature (5) or by creating motors that contain mixtures of wild-type (WT) and mutant subunits predisposed to be in the CW conformation. Minamino et al. (6) studied WT strains containing various amounts of FliG^CW, a CW-locked mutant of Salmonella (ΔPAA) found by Togashi et al. (7), and concluded that only a small fraction of FliG has to be in the ΔPAA form to affect CW-CCW switching. In cheY-deleted strains, as more FliG^CW was expressed, tethered cells went from exclusively CCW to partially CW with pauses, and then to exclusively CW. Bren and Eisenbach (8) studied strains containing various amounts of a CW-biased mutant of FliM, and found hysteresis. For the same numbers of mutant versus WT subunits in the motor, the CW_bias differed depending on whether mutant subunits were expressed in strains with native motors or native subunits were expressed in strains with mutant motors.

Here, we generated switching in Escherichia coli strains lacking the cheY gene by expressing mixtures of FliG^CW (9) and FliG^WT. We employed total internal reflection fluorescence microscopy (TIRFM) to determine the makeup of the mixed motors. We developed a 1D Ising model to quantitatively describe the induction of switching as a function of the switch composition. We assumed that the FliG^CW subunits were more stable in the CW conformation than in the CCW conformation, in contrast to the FliG^WT subunits, which were more stable in the CCW conformation. We obtained the best fits to experimental data when the free-energy difference between the two conformations of the mutant (E_m) was approximately twice that of the free-energy difference (E) between the two conformations of the WT subunit. Further theoretical analysis showed that for a fixed number of mutant switch subunits in otherwise WT rings, the CW_bias varied depending on the arrangement of the mutants in the rings. Based on this, we quantitatively explained the observed hysteresis in switch function in mixed FliM motors by assuming that nearest-neighbor interactions between individual FliM subunits influence FliM assembly. Hysteresis in switch function was not observed for mixed FliG rings. Therefore, it is unlikely that nearest-neighbor FliG-FliG interactions (which depend on the conformations of neighboring FliG subunits) contribute significantly to FliG assembly.

Materials and Methods

Strains and plasmids

Strains (all derivatives of the WT strain RP437 (10)) were constructed to allow variable expression of FliG^CW or FliG^WT in a WT (genomic fliG^WT) or mutant (genomic fliG^CW) background, respectively. We refer to these strains as forward and reverse strains, respectively. The forward strain (PL14) was constructed by transforming strain PL4 (ΔcheY, sticky fliC (11)) with pTrc99A- fliG^CW. The reverse strain (PL99) was constructed by transforming strain PL34 (ΔcheY, sticky fliC, fliG^CW (11)) with ptrc99A-fliG^WT. The fliG^CW mutation was generated in E. coli by introducing a ΔPAA deletion (7) in the WT fliG^WT allele. Strain PL34 was transformed with pHL31 (eYFP-fliG^WT, ptrc99A (12)) to create strain PL86. Strains were grown in tryptone broth at 33°C to OD₆₀₀ = 0.5 in the presence of ampicillin (100 μg/l). Isopropyl β-D-1-thiogalactopyranoside (IPTG; 0–15 μM) was added at the start of the growth culture to control the level of expression of the pTrc99A constructs. To create motors with eYFP-FliG^WT subunits, strain DFB225 (a fliG null strain (13)) was transformed with pHL31 and pKAF131 (sticky fliC, pACYC184-fliC^sticky (1)). An IPTG concentration of 10 μM resulted in tethered motor speeds similar to those of WT tethered motors, and these motors were imaged via TIRFM to estimate $I_o$, the average intensity of motors whose FliG content was entirely eYFP-FliG^WT. Cells were washed twice with motility buffer (0.01 M potassium phosphate (pH 7.0), 10⁻⁴ M EDTA, 0.067 M NaCl) and sheared before tethering.

Image analysis and cell selection

Tethered cell rotation was recorded using a digital camera (DCC1240M; Thorlabs) at 67 fps. Rotational speeds and switching statistics were determined using custom-written codes in MATLAB (The MathWorks, Natick, MA) (11). Ellipsoidal fitting to contrast-enhanced or binary images of the cells yielded the change in cell orientation with time. A fraction of tethered cells (<10%) continuously jiggled back and forth without completing full rotations, which were interpreted as indefinite pausing. These cells were not analyzed. Among the cells that rotated and switched, only those with absolute motor speeds >1 Hz were retained for further analysis (9). This selection criterion was applied uniformly to all of the data collected for TIRF-based estimation of the fraction of FliG in the FliG^CW form, or the phase-contrast-based estimation of CW_bias. To calculate CW_bias, motor switching traces were converted to binary traces by assigning all positive (negative) speeds a value of 1 (−1). CW_bias was then calculated as the fraction of the time motors spent rotating CW over a 20 s running window.

TIRF background correction

Tethered motor intensities were determined from raw TIRF images as previously described (9). These intensities were then corrected for background contributions due to eYFP-FliG subunits that were present in the cell but not associated with motors. To calculate the contributions of nonmotor eYFP-FliG, we expressed eYFP-only subunits in the cytoplasm and measured the average background contributions from TIRF images of tethered motors. The intensities of motors containing eYFP-FliG were corrected for this background at the relevant induction levels. It is reasonable to assume that the cytoplasmic eYFP contribution correctly reflects the contribution of nonmotor FliG-eYFP, since that latter is known to be present in the cytoplasm, e.g., in cells with a FliF null background (12). The same protocol was applied in the determination of $I_o$.

Results and Discussion

CW_bias as a function of FliG^CW expression

We constructed the forward strain (PL14) by introducing a vector (ptrc99A) encoding the fliG^CW allele into a strain carrying genomic fliG^WT but lacking the cheY gene. Expression was controlled via the concentration of the inducer (IPTG). We also carried out the experiment in reverse: the reverse strain (PL99) was constructed by introducing the same vector encoding the fliG^WT allele into a strain carrying genomic fliG^CW, also lacking the cheY gene. Motors were observed to switch in either strain. The switching traces were converted to binary traces, as discussed in the Materials and Methods. A sample binary version is shown in Fig. 1 A. The CW_bias was estimated as a function of the inducer levels for both strains, as shown in Fig. 1 B. The squares represent experiments conducted using the forward strain. The circles represent experiments conducted using the reverse strain. As expected, increasing cellular concentrations of FliG^CW in the forward strain led to an increase in the CW_bias (squares), and increasing cellular concentrations of FliG^WT in the reverse strain led to a decreasing CW_bias (circles).

Figure 1.

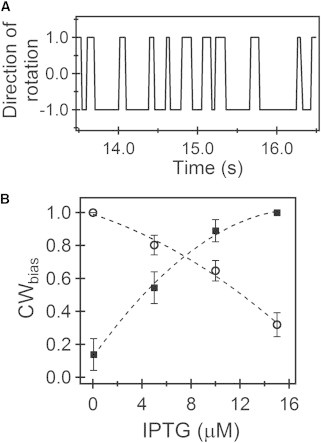
Mixed-motor switching. (A) Sample binary switching trace of a tethered motor consisting of a mix of CW-only and WT FliG subunits. Positive (negative) values indicate CCW (CW) rotation. (B) Measurements of average CW_bias calculated from switching traces as a function of inducer (IPTG) concentrations. Sample sizes ranged from n = 18 motors to n = 42 motors. Error bars are standard errors and the dotted curves are a guide to the eye. Squares indicate experiments in the forward strain (fliG^WT background with a vector expressing fliG^CW) and circles indicate experiments in the reverse strain (fliG^CW background with a vector expressing fliG^WT).

To estimate the makeup of the FliG ring in these mixed motors, we expressed an eYFP-FliG^WT construct from the same ptrc99A expression system (pHL31 (12)) in strains carrying genomic fliG^CW (PL86), and imaged tethered motors via TIRFM. The intensities of eYFP-FliG^WT were calculated as described in Lele et al. (9) and further detailed in Materials and Methods. Such measurements were repeated for different induction levels. A representative population measurement at 5 μM IPTG is shown in Fig. 2 A. To determine the fraction of eYFP-FliG^WT in the FliG rings, we normalized the average intensity values (obtained from population measurements at each induction level) by the average intensity ($I_o$) of motors whose FliG was entirely eYFP-FliG^WT. To estimate $I_o$, we expressed eYFP-FliG^WT in a fliG null strain (DFB225) and measured intensities in functional tethered motors. The variation of the fraction of eYFP-FliG^WT as a function of inducer concentration is shown in Fig. 2 B. These measurements were limited to inducer concentrations of 0–10 μM because at higher inducer concentrations (15 μM or more), the cellular eYFP-FliG^WT signals were strong enough to make motor intensity profiles difficult to separate from the background. Hence, we estimated the value of the eYFP-FliG^WT fraction at 15 μM IPTG by extrapolating the curve in Fig. 2 B using a simple fit $A\left(1-e^{-k\ast IPTG}\right)+y_o$. It is possible that the incorporation of eYFP-FliG^WT subunits is different from FliG subunits, which would be a limitation of our study. However, the speeds of eYFP-FliG^WT motors were essentially the same as those of FliG^WT motors (data not shown), indicating that motor assembly was not adversely affected by the fusion product.

Figure 2.

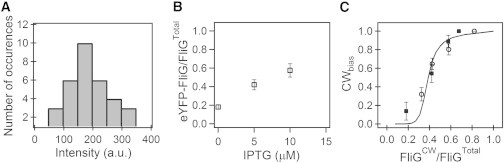
(A) TIRFM measurements of the intensities of YFP-FliG^WT subunits in otherwise CW-only tethered motors (in strains with fliG^CW on the genome and an IPTG-inducible vector carrying eyfp-fliG^WT). This particular measurement (n = 33 motors) was obtained at an IPTG concentration of 5 μM. (B) Mean YFP-FliG/FliG^Total fractions (from distributions of the sort shown in A) of YFP-FliG subunits incorporated in motors, shown as a function of inducer concentration. (C) CW_bias as a function of the fraction of FliG^CW in otherwise WT motors. Squares (circles) indicate experiments in which strains carried fliG^WT (fliG^CW) on the genome and a vector expressing fliG^CW (fliG^WT). No hysteresis in switch function is seen. The black curve is the model prediction for N = 26, E = 0.25, E_m = 0.45, and J = 1.9.

As noted above, hysteresis in the switch function was observed in motors made from mixtures of FliM^CW and FliM^WT subunits (8). Specifically, for the same ratio of FliM^CW and FliM^WT subunits, a higher CW_bias was observed in strains in which FliM^WT was expressed from a plasmid compared with strains in which FliM^WT was expressed genomically. A comparison of whole-cell extracts with basal-body extracts showed that whole-cell FliM^CW/FliM^WT ratios were a good approximation for motor FliM^CW/FliM^WT ratios. The reasons for the hysteresis were not clear.

To test whether a similar hysteresis is observable in our data, we plotted CW_bias, shown in Fig. 1 B, as a function of the fraction of FliG^Total that is FliG^CW, inferred from Fig. 2 B. The results are shown in Fig. 2 C. The squares represent data over varying FliG^CW expression levels in the forward strain, and the circles represent data over varying FliG^WT expression levels in the reverse strain. In the former case, we calculated the fractions of FliG^CW from the data in Fig. 2 B by making two assumptions. First, the expression levels of either kind of FliG subunit from ptrc99A (or from the genome) are similar given their comparable sizes (fliG^WT allele = 996 bp; fliG^CW allele = 987 bp). This is a reasonable assumption considering that the promoters are the same, and the cloning sites/plasmid copy numbers/induction levels (for expression from the vector) remain the same. Second, as found for FliM mixed motors, the intracellular FliG^CW/FliG^WT ratios are a good approximation of the motor FliG^CW/FliG^WT ratios. This assumption is valid for the following reasons: Consider the ratio of the expression level of the mutant at two different induction levels ($C_{IPTG1}^{FliGCW}/C_{IPTG2}^{FliGCW}$). It is straightforward to show that if the latter assumption is correct, then

$$C_{IPTG1}^{FliGCW}/C_{IPTG2}^{FliGCW}={\left[Fli{G}^{CW}/\left(Fli{G}^{Total}-Fli{G}^{CW}\right)\right]}_{IPTG1}/{\left[Fli{G}^{CW}/\left(Fli{G}^{Total}-Fli{G}^{CW}\right)\right]}_{IPTG2}.$$

We estimated the ratios in the right-hand side from the data in Fig. 2 B and independently determined the ratio in the left-hand side by directly measuring the average whole-cell brightness via TIRFM. The right-hand ratios were 0.3 (IPTG1 = 0 μM, IPTG2 = 5 μM) and 0.52 (IPTG1 = 5 μM, IPTG2 = 10 μM). These compared favorably with the left-hand ratios, 0.38 (IPTG1 = 0 μM, IPTG2 = 5 μM) and 0.54 (IPTG1 = 5 μM, IPTG2 = 10 μM), lending support to the assumption. The data in Fig. 2 C suggest that mixed FliG motors do not exhibit the same kind of hysteresis in switching that was observed in mixed FliM motors.

1D Ising model

To explain the sigmoidal nature of CW_bias versus the fraction of FliG^CW molecules shown in Fig. 2 C, we analyzed switching in the framework of a simple 1D Ising model (14–16) with periodic boundary conditions. We described the Hamiltonian for the system as

$$H=-J\sum _1^N{\sigma }_i{\sigma }_{i+1}-E\sum _1^{N-m}{\sigma }_i+E_m\sum _1^m{\sigma }_i,$$ (1)

where E_m (E) is a measure of the free-energy difference between the CW and CCW conformations of an individual FliG^CW (FliG^WT) subunit, and J is the interaction energy between neighboring subunits, which we assume is the same irrespective of the type of subunits. This is a reasonable assumption considering that biochemical data have shown that FliG^CW has a conformation similar to that of FliG^WT in the CW state (6). It is this interaction through which the mutant subunits influence the propensity of neighboring WT subunits to adopt the CW conformation (CW propensity). N is the total number of subunits, and m is the number of mutant subunits. The first term on the right in Eq. 1 sums up the interactions between neighboring subunits. The second (third) term represents the free-energy contributions of N-m (m) WT (mutant) FliG subunits. All values are in units of k_BT, where k_B is Boltzmann’s constant and T is the absolute temperature. Each of the N (=26) FliG subunits can adopt one of two conformations: CCW (${\sigma }_i=+1$) or CW (${\sigma }_i=-1$). For a single mutant subunit (m = 1), the partition function can be determined via the transfer matrix approach (17):

$$Z=tr\left(\alpha W^N\right),\text{where}W=\left[\begin{array}{cc}{e}^{J+E}& e^{-J}\\ e^{-J}& e^{J-E}\end{array}\right]\text{and}\alpha =\left[\begin{array}{cc}{e}^{-E-Em}& 0\\ 0& e^{E+Em}\end{array}\right].$$ (2)

We assume typical values of J (∼4/2) and E (= 0.5/2) reported in the literature for the flagellar switch (18,19). For increasing numbers of m, the partition function can be suitably modified to include the configuration or arrangement of the ring. For example, if two mutant subunits (m = 2) are separated by two FliG^WT subunits, $Z=tr\left(\left(\alpha W\right)W^2\left(\alpha W\right)W^{22}\right)$, whereas if the two mutant subunits are separated by eight FliG^WT subunits, then $Z=tr\left(\left(\alpha W\right)W^8\left(\alpha W\right)W^{16}\right)$. The CW_bias can then be calculated as

$$C{W}_{bias}=e^{JN-EN}/Z_m.$$ (3)

The extreme conformations (CW and CCW) are not the only ones adopted by the ring. Entropic factors cause intermediate configurations to have finite probabilities, consistent with the notion of mixed states (18). However, we do not discuss those here, since the CW_bias is a very good indicator of the physiologically relevant activity of the complex. To determine the effect of increasing fractions of FliG^CW on the CW_bias, we first randomly generated all possible arrangements of m FliG^CW subunits in a ring consisting of (N – m) FliG^WT subunits (5000 samples). Next, for each configuration, the partition function Z was determined and the CW_bias was calculated from Eq. 3. The CW_bias was then averaged over all 5000 values. In this fashion, the CW_bias versus FliG^CW fractions (= m/N) was calculated. The predictions (black curve) are shown in Fig. 2 C. The curve, which is a reasonable fit to the experimental data, was calculated by assuming E_m ∼2 E.

Effect of assembly on CW_bias

Cooperativity plays an important role in the assembly of large complexes in biological systems (20). In the context of the assembly of the FliG ring, cooperativity refers to the preferential association of WT subunits together, minimizing contact with FliG^CW subunits to reduce the energy penalty (J) incurred at the boundaries between the two kinds of subunits. A second possibility is that the FliG ring is assembled noncooperatively, such that individual FliG^CW subunits are incorporated at random in a ring of otherwise FliG^WT subunits. As the number of mutant molecules (m) increases, the number of ways to arrange them in the ring increases as well. Certain ring configurations are entropically favored, and on an average many more motors would have those particular ring configurations. We examined how such FliG^CW sequestration, or lack thereof, affected the CW_bias.

Since individual FliG^CW subunits prefer to be in the CW conformation, the energetic penalty incurred by introducing a single FliG^CW in an otherwise WT ring is 4J. Adding more FliG^CW subunits adjacent to the single subunit does not result in additional penalties since no new boundaries (interfaces between a mutant and neighboring WT subunits) are created, as shown in the upper schematic in Fig. 3 A. However, for m nonsequestered subunits (bottom), there are 2m boundaries, resulting in an energetic penalty of m × 4J that increases the overall propensity of the ring to adopt the CW conformation. The increase in propensity also occurs in part due to entropic factors that ultimately reduce the partition function with increasing R-1. The effect of assembly on the CW_bias as a function of the number of FliG^WT subunits between pairs of mutants is shown on the right in Fig. 3 A. For simplicity, we calculated the plots by assuming that R-1 is the same between distinct pairs. The ordinate is CW_bias normalized by the expected value for two adjacent mutant subunits (R-1 = 0), CW^§_bias. As can be observed in the figure, CW_bias/CW^§_bias is the lowest for the adjacent pair and progressively increases to a final value as the number of FliG^WT subunits separating the pair increases. As noted before, this effect is amplified by an increasing number of mutants. This dependence of CW_bias on the configuration is present at finite coupling energies between subunits (18,19). Such a dependence would vanish under the limiting and unrealistic case of infinite coupling between subunits (J→ ∞), as specified by the concerted model of allostery (i.e., the Monod-Wyman-Changeux model (21)).

Figure 3.

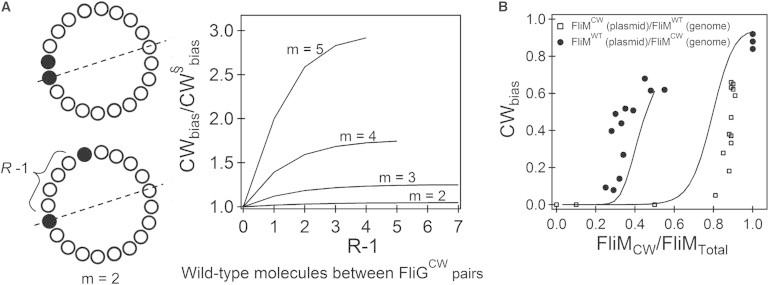
(A) The schematic on the left illustrates the differences in the configuration for sequestered (top) and nonsequestered (bottom) mutants. Black circles indicate FliG^CW subunits. The dotted line indicates the line of symmetry (for m = 2), which limits the number of unique ways to arrange the mutants. On the right is CW_bias plotted as a function of the gap (R-1) for varying m (FliG^CW subunits). The ordinate is a ratio of the CW_bias (calculated for increasing R-1 WT subunits between m-1 pairs) to the CW^§_bias expected when all m mutants are sequestered during ring assembly (R-1 = 0). E = 0.25, E_m = 0.45, J = 1.45. (B) Role of assembly in generating hysteresis in switch function (symbols indicate experimental data from Bren and Eisenbach (8)). Squares (circles) indicate experiments in which strains carried fliM^WT (fliM^CW) on the genome and a vector expressing fliM^CW (fliM^WT). The black curve on the left was calculated for rings assembled by maximizing the possible separations between all m-1 mutants. The black curve on the right was calculated by sequestering all mutant FliM subunits during ring assembly. N = 34, E = 0.25, E_m = 0.45, J = 1.45.

Possible origin of hysteresis in switch function

Fig. 3 B shows the previously observed hysteresis in switch function (8). The squares represent experiments in a strain in which a FliM^CW mutant was expressed via an inducible plasmid in cells (strain A) carrying fliM^WT on the genome. The circles represent experiments in cells (strain B) in which FliM^WT was expressed via an inducible plasmid in a strain carrying the mutant fliM^CW on the genome. As can be seen, the switch function (CW_bias) exhibits a hysteresis depending on the type of genomic fliM. One explanation for the hysteresis effect could be the dependence of CW_bias on the arrangement of mutant subunits in an otherwise WT ring. If there are differences in the way the ring assembles in the two types of strains, then it is possible to use the mixed-ring model to explain the observed hysteresis. We assumed that FliM^CW subunits are sequestered in strain A (R-1 = 0), but are not sequestered in strain B. The two curves in Fig. 3 B represent model predictions based on this simple assumption and explain the observed data reasonably well. As expected, sequestration leads to reduced CW_bias until the numbers of FliM^CW subunits in motors exceed a particular value.

Three-dimensional reconstructions from electron cryomicrographs of the C-ring in strains carrying the fliG^CW gene used in this work have revealed that the most recurring symmetry is 34-fold, indicating that there are likely to be 34 FliM/FliN complexes in CW-only motors (22). However, a recent hypothesis suggests that the FliM assembly in such FliG^CW motors carries as few as 26 FliM/FliN complexes, and the ring assembly remains incomplete (23). In presenting the explanation for hysteresis in the FliM ring, we made the assumption that FliM subunits assemble into a complete ring of 34 subunits. However, this is not a necessary assumption for explaining the data, since ultimately the CW_bias is determined by the FliG ring conformation. Irrespective of whether or not FliM forms a ring, FliM subunits must interact with FliG subunits (possibly mediated by FliN subunits) to effect a conformational change. Thus, it is possible to reproduce the analysis shown in Fig. 3 B by assuming that the FliG^WT subunits in contact with the mutant FliM subunits incorporated in the C-ring have a higher propensity to adopt the CW conformation.

Hysteresis in assembly/disassembly of biological macromolecules is known to occur (24,25). If our explanation of hysteresis in the switch function due to FliM assembly differences is correct, it points to differences in the assembly mechanism of the FliM and FliG rings. FliG assembles before the FliM ring and interacts strongly with the FliF ring (26). It is possible that during the assembly, an energetic penalty is incurred when a FliG^CW subunit is positioned next to a FliG^WT subunit, influenced by the coupling interactions between the pair. However, these interactions are rendered unimportant by the strong FliF-FliG interactions that likely drive the assembly. As a result, hysteresis is not observed. On the other hand, a significant part of the motor FliM binds through weak interactions in the C-ring, and it is possible that the energetic penalties incurred (influenced by the interactions between a WT and a mutant FliM subunit) make a significant contribution to the assembly. Sequestration is likely achieved through FliM exchange. How such sequestration depends on the FliM properties (e.g., native FliM versus mutant FliM) and how it can be experimentally determined will be a subject of future work.

Author Contributions

P.P.L. and H.C.B. designed the work and wrote the article. P.P.L. performed the research and analyzed the data.