A Well-Balanced Preexisting Equilibrium Governs Electron Flux Efficiency of a Multidomain Diflavin Reductase

Abstract

Diflavin reductases are bidomain electron transfer proteins in which structural reorientation is necessary to account for the various intramolecular and intermolecular electron transfer steps. Using small-angle x-ray scattering and nuclear magnetic resonance data, we describe the conformational free-energy landscape of the NADPH-cytochrome P450 reductase (CPR), a typical bidomain redox enzyme composed of two covalently-bound flavin domains, under various experimental conditions. The CPR enzyme exists in a salt- and pH-dependent rapid equilibrium between a previously described rigid, locked state and a newly characterized, highly flexible, unlocked state. We further establish that maximal electron flux through CPR is conditioned by adjustable stability of the locked-state domain interface under resting conditions. This is rationalized by a kinetic scheme coupling rapid conformational sampling and slow chemical reaction rates. Regulated domain interface stability associated with fast stochastic domain contacts during the catalytic cycle thus provides, to our knowledge, a new paradigm for improving our understanding of multidomain enzyme function.

Introduction

Many redox systems are composed of separate protein modules whose functions are conserved through evolution and can be divided into a reductase component capable of oxidizing reduced nucleotides, a transporter that shuttles electrons between the reductase module and the final electron acceptor that constitutes the third partner. Such multicomponent organization is well illustrated by the mixed-function oxidases system based on cytochrome P450 (CYP) monooxygenases. Many modular combinations of the components exist, depending on the type of transporter and reductase, leading to an important diversity of electron delivery systems (1). Diflavin reductases are key enzymes within these systems. They assemble a transporter module containing the flavin mononucleotide (FMN) cofactor, located at the N-terminus with a reductase module containing the flavin adenine dinucleotide (FAD) cofactor, located at the C-terminus on the same polypeptide joined by a connecting domain (2). This typical order (FMN-connecting-FAD) is exemplified in protein families of different physiological functions such as NADPH cytochrome P450 reductases (CPRs), nitric oxide synthases (NOS), methionine synthase reductases, the flavoprotein component of sulfite reductases, and novel diflavin oxidoreductases (1). CPR is the obligatory electron supplier for the various eukaryotic microsomal CYPs and possesses, on top of the abovementioned domains, an N-terminal trans-membrane segment. CPR transfers electrons from NADPH to CYP in a precise way: NADPH → FAD → FMN → acceptor. Beyond CYP, CPR also provides electrons to other artificial acceptors such as cytochrome c or natural acceptors such as cytochrome b₅, heme oxygenase, and to the fatty acid elongation system.

The arrangement of the domains in CPR was first determined from the crystal structure of the oxidized, soluble form of rat CPR (3) and was then later confirmed for oxidized CPR originating from different species (Fig. 1 a for human CPR), in the presence or absence of bound nucleotides (4–6). In this structure, also named closed or compact form, the two cofactors are ideally positioned for an electron transfer (ET) from FAD to FMN. However, in this structural arrangement, the FMN is well buried and far from the surface of the molecule, hence preventing ET to the various protein acceptors. Similarly, for CPR a clear demonstration of the rearrangements was obtained in 2009 with crystallographic structures of CPR mutants (7,8) evidencing large domain movements leading to open conformations compatible with external ET from FMN to acceptors (Fig. 1, b and c). Multiple groups have also evidenced small-to-large domain rearrangements by various techniques (9), ranging from small-angle x-ray scattering (SAXS) (10,11), small-angle neutron scattering (11), neutron reflectometry (12), fluorescence resonance energy transfer (13), nuclear magnetic resonance (NMR) (10), and electron double resonance (14) to mass spectrometry (15), linked either to catalytic events (flavin reduction, ligand binding) or to the chemical environment of CPR (ionic strength of the solvent). Very recently, the crystal structure of a complex between heme oxygenase and a mutated CPR revealed a new open conformation for the CPR, providing a picture of how electrons may be transported from FMN to heme acceptors (16).

Figure 1.

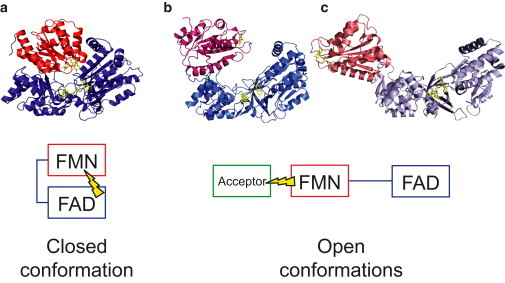
Closed and open conformations of CPR. (a) Human CPR (Protein Data Bank (PDB) PDB 3QE2, chain A); (b) ΔTGEE mutant of rat CPR (PDB 3ES9, chain A); (c) yeast-human chimeric CPR (PDB 3FJO). Crystallographic structures were aligned on the FAD/connecting domain (residues 248–680 in human sequence). (Red) FMN domain; (blue) FAD/connecting and linker region. (Yellow sticks) FMN and FAD moieties. (Boxes) Closed and open conformations (same color-code as structures). (Yellow flash) Symbolic representation of the ET in the two states. To see this figure in color, go online.

From these different studies, authors have concluded that reduction of CPR under anaerobic conditions (chemically, by either NADH or NADPH) promotes domain rearrangements leading to an equilibrium between compact and extended conformations that depends on the type of reductants. On the contrary, nucleotide binding (NADP⁺ or 2′-5′ ADP) tends to form more compact structures, with either oxidized or reduced CPR. The commonly accepted hypothesis of the domain movements occurring during catalysis is as follows (17). Upon binding of NADPH to CPR, immediately followed by FAD reduction, CPR adopts a compact form favoring ET between FAD and FMN. Release of NADP⁺ while CPR is still reduced shifts the conformational equilibrium toward extended forms capable of ET from FMN to external acceptors. This concerted model favors a schematic view of CPR at steady state in which ET steps (FAD → FMN or FMN → acceptors) are tightly coupled with domain movements (compact or extended forms, respectively).

Ionic strength has long been recognized as an important factor influencing ET from CPR to acceptors (18–20). More recently, the dramatic effect of ionic strength on CPR domain organization was also highlighted (11,15,21). Interestingly, Huang et al. (11) demonstrated that the extent of structural changes associated with high ionic strength conditions (transition from compact to extended forms) is far more important than those detected for reduction only. This result clearly questions the level of accuracy of the actual descriptions of the extended forms, mostly being viewed as a finite ensemble of defined structures in which the FMN domain has moved away from the FAD domain but still contains some contacts with it.

In this work, we provide a thorough structural, dynamic, and thermodynamic characterization of the soluble form of human microsomal CPR using SAXS and NMR spectroscopy under various conditions. We provide a comprehensive structural analysis of the extended (open) conformations and also describe the dynamic nature of the equilibrium between the compact and extended conformations. We demonstrate that the structural transitions seen in CPR are not rate-limiting and establish the correlation between the landscape of domain conformation and enzyme catalysis. We finally present, to our knowledge, a new picture of CPR functioning, where a rapid equilibrium between two distinct catalytically competent states controls the efficiency of electron flux from reduced nucleotides to electron acceptors.

Materials and Methods

Expression and purification of CPR

For SAXS and enzymatic analysis, CPR protein was overexpressed as detailed in Aigrain et al. (7). For NMR analysis, ²H-¹⁵N labeled CPR was obtained using the same protocol as described in Vincent et al. (5). Unlabeled and isotopically enriched CPRs were purified using the following protocol: His-tagged proteins were bound on a TALON Polyhistidine-Tag Purification Resin (Clontech, Mountain View, CA) equilibrated with buffer A (20 mM Tris-HCl (pH 8)) containing 0.5 M NaCl and designated as buffer B. Two washing steps were made with buffer B containing 0.01 M imidazole. A thrombin cleavage step removed the N-terminal His-tag, avoiding potential His-tag effects and facilitating the interpretation of hydrodynamic properties of the CPR. A quantity of 200 units of thrombin (>2800 NIH units/mg protein, Sigma-Aldrich, St. Louis, MO) was incubated during 2 h with the protein solution at room temperature under rotation. After cleavage, the protein was eluted with Buffer B from the TALON resin. The fractions were collected and 1 mM PMSF (phenylmethylsulfonyl fluoride) was added to stop the thrombin cleavage reaction and 1 mM DTT (dithiothreitol) to avoid the formation of disulfide bridges. CPR was fully oxidized using 1 mM ferricyanide and purified through gel filtration chromatography using a Superdex-200 (GE Healthcare, Pittsburgh, PA), equilibrated with Buffer A, containing 1 μM FMN, 1 μM FAD, 1 mM DTT, and 1 mM EDTA. Purity of the sample was determined by sodium dodecyl-sulfate polyacrylamide gel electrophoresis and examination of the 280/455-nm absorbance ratio measured by optical spectroscopy. CPR samples were concentrated to 40 mg/mL (∼570 μM) and stored at 4°C before usage.

SAXS experiments

SAXS experiments were conducted at the Synchrotron SOLEIL facility (Saint-Aubin, France), on the SWING Beamline. All experiments were performed at 20°C. Measurements were made in Buffer A (pH 7.4 or 6.7), 1 μM FAD and FMN and various NaCl concentrations (0, 200, 300, 400, 500, and 700 mM for pH 7.4 and 0, 400, 600, and 800 mM for pH 6.7). A series of experiments were also collected in presence of 100 μM NADP⁺ in buffer A (pH 7.4) 1 μM FAD and FMN and various NaCl concentrations (0, 300, or 700 mM). Solutions were filtered and degassed before use. To obtain the highest possible quality for SAXS data, 500 μg of CPR was injected on a Biosec3-300 column (Agilent Technologies, Santa Clara, CA) at 0.2 mL/min preequilibrated with the relevant buffer and data were collected using the combined SEC-SAXS setup for each experimental condition. Selected frames from the main elution peak were averaged and background-subtracted following the procedure reported in Pérez and Nishino (22).

Global analysis of the SAXS curve series

The SAXS intensity curve resulting from a multipopulated solution is the weighted average of the curves from each of the individual species (23). In the case of a series of samples made of a single type of protein displaying two specific conformational states L and U, any protein-concentration normalized curve I_i(Q) from that series (where the index, i, spans the various measurements resulting in different L/U proportions) can be expressed as the linear combination of the two theoretical curves I_L(Q) and I_U(Q) corresponding to each of the two conformational states,

$$I_i\left(Q\right)={\alpha }_i{I}_L\left(Q\right)+\left(1-{\alpha }_i\right)I_U\left(Q\right),$$ (1)

where α_i is comprised between 0 and 1 and represents the fraction of the population in the state L. In this case, the index i denotes increasing ion concentrations and α_i monotonically decreases with i. Note that if the two curves I_L(Q) and I_U(Q) cross at a given Q_cross value (i.e., I_U(Q_cross) = I_L(Q_cross)), then it immediately results from Eq. 1 that all I_i(Q) curves cross each other at the same Q_cross value, giving rise to an isoscattering point.

Alternatively, the experimental I_i(Q) curve can also be expressed as the linear combination of any two other available experimental curves I_j(Q) and I_k(Q), such that

$$I_i\left(Q\right)={\alpha }_i^{jk}{I}_j\left(Q\right)+\left(1-{\alpha }_i^{jk}\right)I_k\left(Q\right),$$ (2)

where α_i^jk represents the projection of the scattering curve I_i(Q) onto the scattering curve I_j(Q) and (1−α_i^jk) is then the projection of the scattering curve I_i(Q) onto the scattering curve I_k(Q). Hence, two given experimental curves {I_j, I_k} may form a basis to decompose all other curves using the parameters ${\alpha }_{\mathit{i}}^{\mathit{jk}}$, and different pairs of curves can be used as bases.

The equilibrium evolution is described by the coefficients α_i in Eq. 1, but only the parameters ${\alpha }_{\mathit{i}}^{\mathit{jk}}$ in Eq. 2 can be directly retrieved from the experimental data. However, provided that the order j < k is respected and because α_i varies monotonically with i, the evolution of the ${\alpha }_{\mathit{i}}^{\mathit{jk}}$ parameters as a function of i is an affine function of the evolution of the α_i parameters, which can then be derived as follows: The coefficients α_i^jk were retrieved using the singular value decomposition procedure applied to overdetermined systems using the data analysis software IDL (Excelis, Boulder, CO). This was done for i spanning the increasing NaCl concentrations in each of the two series of experimental curves at pH = 6.7 and pH = 7.4 independently, and {j,k} standing for the following pairs of NaCl concentrations at pH = 7.4: {0 mM, 400 mM}, {0 mM, 500 mM}, {0 mM, 700 mM}, {200 mM, 500 mM}, and {200 mM, 700 mM}. For a better estimation of the parameters α_i^jk, the curves were weighted by Q², to enhance the contribution of the intensity at intermediate Q values where the difference between the extreme curves is the highest. Each decomposed experimental curve I_i(Q) was checked to be conveniently reproduced by the corresponding combination of I_j(Q) and I_k(Q) curves.

For each {j,k} considered, 1−α_i^jk displays a sigmoidal evolution as a function of NaCl concentration. The two series of coefficients (pH 6.7 and 7.4) were fitted independently, using an equation of the type

$${\alpha }_i^{jk}=B^{jk}+T^{jk}\times \frac{e^{a^{jk}-b^{jk}\times {\left[\text{NaCl}\right]}_i}}{1+e^{a^{jk}-b^{jk}\times {\left[\text{NaCl}\right]}_i}},$$ (3)

where B^jk and T^jk represent the lower and upper values used for fitting each of the sigmoids, and a^jk and b^jk refer to the thermodynamic model used below to describe the salt-dependent L/U equilibrium. The parameters α_i^jk were subsequently renormalized between 0 and 1 by replacing B^jk and T^jk by 0 and 1, respectively, and averaged over the different bases {j,k}, thus providing average values for the coefficients α_i with the best possible precision. The error bars correspond to the standard deviation derived for the various ${\alpha }_{\mathit{i}}^{\mathit{jk}}$, obtained using the different {j,k} bases. The averaged coefficients α_i were then fitted to the classical chemical denaturation law at pH = 6.7 and pH = 7.4 independently:

$${\overline{\alpha }}_i=\frac{e^{\frac{\Delta G^w-m\times \left[\text{NaCl}\right]}{RT}}}{1+e^{\frac{\Delta G^w-m\times \left[\text{NaCl}\right]}{RT}}}.$$ (4)

These averaged coefficients are related to the fraction of the U state by the relation $p_U=1-\overline{\alpha }$ at each salt concentration. The SAXS curve of the U state was extrapolated for the high salt limit from the experimental curves at [NaCl] = 0 mM and [NaCl] = 500 mM, and from Eq. 2, resulting in

$$I_U=\frac{\left(1-{\overline{\alpha }}_{500\text{mM}}\right)I_{0\text{mM}}-\left(1-{\overline{\alpha }}_{0\text{mM}}\right)I_{500\text{mM}}}{{\overline{\alpha }}_{0\text{mM}}-{\overline{\alpha }}_{500\text{mM}}}.$$ (5)

Upon unfolding of the native state, the change in Gibbs free energy is classically described by the relation ΔG = ΔG^w − m × [NaCl] (24), where ΔG^w and m values are parameters describing the stability of the native state in absence of denaturant and the steepness of the transition, respectively. The midpoint transition defined as the denaturant concentration for which the unfolded and native states are equally populated is calculated as ΔG^w/m. In this case, the equilibrium constant describing the L/U equilibrium can be expressed as

$$K_e=e^{-\frac{\left(\Delta G^w-m\left[\text{NaCl}\right]\right)}{RT}}.$$ (6)

Ensemble optimization method (EOM) analysis

The ensemble optimization method (EOM) is a set of programs that provide a selection of a subset of multidomain protein conformations from a randomly generated ensemble, under the constraint of a SAXS experimental curve (25). The curve resulting from the average of the selected subset curves then matches the experimental data. Ten thousand conformations of the two-domain protein CPR were first generated using the routine RANCH90 program by randomly representing the linker between the two domains, while keeping the two domains rigid. The selection of the subsets was then performed using the program GAJOE13 with 100 cycles under the constraint of the extrapolated curve of the U-state.

NMR experiments

Samples used for NMR spectroscopy contained 500 μM ¹⁵N-²H labeled CPR in Buffer A (pH 7.4) and 95%/5% H₂O/D₂O. All experiments were conducted at 37°C using a 950-MHz ¹H frequency Avance III spectrometer (Bruker, BioSpin, France) equipped with a cryoprobe. The backbone resonance assignment obtained at low ionic strength (5) could be easily transferred to higher ionic strengths and the ¹⁵N relaxation analysis was carried out as previously described in Vincent et al. (5). The NMR ¹H chemical shifts were corrected from the salt-dependent HDO chemical shift variations (26).

Kinetic experiments

Cytochrome c reductase activity of the CPR was measured spectrophotometrically as previously described in Aigrain et al. (21) at 20°C in Buffer A pH 7.4 or 6.7 with various concentrations of NaCl.

Results and Discussion

SAXS experiments

Analysis of our SAXS scattering curves shows that human CPR in solution exists, as a first approximation, in a two-state equilibrium which is conditioned not only by ionic strength as shown in Huang et al. (11), Hay et al. (14), and Jenner et al. (15), but also by pH. At low ionic strength and pH 7.4, the scattering curve (Fig. 2 a) is well explained by a structural model derived from the closed CPR conformation (6) (Fig. 2 a, inset), thus confirming our previous NMR study (5) and the recent SAXS study (11).

Figure 2.

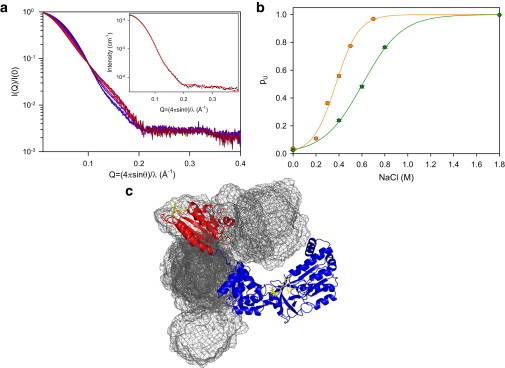
SAXS analysis of the ionic strength-mediated conformational transition of CPR. (a) Scattering curves from 0 M (blue) to 0.7 M (red) NaCl concentration at pH 7.4, normalized to protein concentration. (Dark red) Extrapolated curve at high ionic strength. (Inset) Fit of the 0 M scattering curve to the crystal structure of the closed conformation (6) with loop conformation optimization using DADIMODO software (28). (b) Fractions of the U state (p_U) at pH 7.4 (orange) and pH 6.7 (green), with their respective fits to the denaturation law. (c) One of the 11 EOM-derived structures used to reproduce the scattering curve extrapolated for the U state is represented as ribbons (blue, FAD/connecting domain; red, FMN domain). The mesh (calculated with the MESH feature of the PYMOL software (42)) represents the van der Waals surface of the reunion of the 11 FMN domains determined by EOM. All conformations were superimposed on the FAD/connecting domain. To see this figure in color, go online.

When NaCl concentration is increased, the scattering curves gradually change (Fig. 2 a), presenting a steeper initial slope that indicates an increase in the population of states having larger radii of gyration (R_g). The existence of an isoscattering point suggests a transition between two states ((27) and Materials and Methods) that we further define as an equilibrium K_e,

$$\begin{array}{c}L\underset{k_L}{\overset{k_U}{\rightleftharpoons }}U,\\ K_e=\frac{k_U}{k_L}=\frac{p_U}{p_L},\\ p_U+p_L=1,\end{array}$$ (7)

between the closed conformations, thereafter referred to as the locked state (L) and a new state U (unlocked, see below), with k_U and k_L being the forward and backward rates and p_U and p_L being the populations of the U and L states, respectively.

A further analysis of the SAXS curves using a method based on global analysis of all experimental curves in the framework of chemically induced denaturation theory (24) (see Materials and Methods) allowed evaluation of p_U and p_L at each ionic strength and for both pH values. The fact that the uncertainties on the extracted populations are small in Fig. 2 b confirms a posteriori the two-state character of the conformational transition. In addition, the experimental curves at pH = 6.7 could be efficiently decomposed by pairs of curves obtained at pH = 7.4. This strongly suggests that the states L and U are very similar at the two pH values. ΔG^w represents the free energy of the L to U transition in the absence of salt and m represents the dependence of free energy on denaturant concentration. The midpoint transition for which the L and U states are equally populated (p_L = p_U = 0.5) can be estimated by ΔG^w/m and is obtained at pH 7.4 for NaCl concentration of 372 ± 59 mM. Lowering the pH to 6.7 leads to a significant perturbation of the equilibrium, as demonstrated by the shift of the SAXS-derived midpoint transition to 605 ± 35 mM (Fig. 2 b). The ΔG^w values are equal to 9.12 ± 0.73 kJ⋅mol⁻¹ and 8.66 ± 0.25 kJ⋅mol⁻¹ and the m values to 24.46 ± 1.91 kJ⋅mol⁻¹⋅M⁻¹ and 14.30 ± 0.41 kJ⋅mol⁻¹⋅M⁻¹ for pH 7.4 and 6.7, respectively. The difference between the two ΔG^w values most likely corresponds to changes in the degree of protonation of some residues at the interface of the FMN and FAD/connecting domains. The presence of NADP⁺ (100 μM) added to the equilibration buffer did not change any of these SAXS scattering curves when performed at pH 7.4 and at 0, 300, or 700 mM NaCl concentration (data not shown). This demonstrates that the binding of the oxidized pyridine nucleotide does not favor the L state at near-physiological pH and over a large range of ionic strength. In summary, ionic strength and pH are efficient and independent parameters controlling the L/U equilibrium.

SAXS scattering data extrapolated to high salt concentration reveal that the U state has a larger R_g value (35 Å) than the L state (26 Å) and a multimodal distance distribution, consistent with the two domains being relatively separated from each other (see Fig. S1 in the Supporting Material). Attempts to reproduce the extrapolated scattering curve (see Fig. S2 A) with a single conformation using the DADIMODO (28) algorithm were unsuccessful. Instead, using the EOM algorithm (25), the best fit was obtained with 11 structures having different relative positions and orientations for the two CPR domains (Fig. 2 c; and see Fig. S2 B). That a SAXS curve can be fitted by a small number of structures is a typical situation for systems with a continuous set of different conformations. This is due to the strong degeneracy of SAXS information and should not be assigned to the actual existence of a small number of exclusive populated states without further information (25). Besides, a large number of different subensembles returned by EOM results in virtually the same agreement with the experimental curve and those ensembles range from 6 to 19 individuals each. Our result just underlines that large variations of the relative orientations and positions of the two CPR domains are necessary to account for the state U, but does not provide any indication on the number of such conformations. Therefore, the SAXS data strongly suggest that the U state should be described as a large ensemble of conformations, including a large proportion of extended conformations.

NMR experiments

To further characterize the L/U equilibrium, we collected a series of ¹⁵N-TROSY NMR spectra of ²H-¹⁵N labeled CPR at various NaCl concentrations at pH 7.4. The ¹⁵N-TROSY spectra collected at 0 and 0.8 M NaCl concentrations, where the L and U states are respectively predominant, had similar patterns (Fig. 3 a), indicating that at high ionic strength the protein is still folded and that the folds of individual domains are well conserved in the L and U states. This observation confirmed the SAXS study in that the L and U states differ by domain organization. A single ¹H/¹⁵N cross-peak was observed for each amide group at each salt concentration (Fig. 3 b), suggesting fast exchange between the different species populated during the titration. For a subset of residues, ¹H and ¹⁵N chemical shift variations were linear when plotted against salt concentration (e.g., V158 and R293; see Fig. 3 b). However, most cross-peaks had more complex behavior, as visible in Fig. 3 b.

Figure 3.

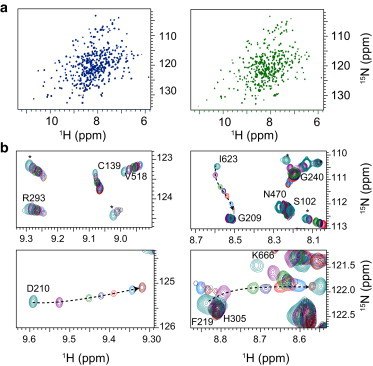
Salt-mediated conformational changes monitored by NMR. (a) ¹⁵N TROSY NMR spectra collected at 0 M (blue) and at 0.8 M (green) NaCl concentrations. (b) Closeup views of selected cross-peaks from ¹⁵N TROSY experiments collected from 0 M (green) to 1 M (brown) NaCl concentrations on a ¹⁵N-²H labeled CPR sample. (Dotted line) Trajectories for residues D210, F219, and I623 that show large chemical shift variation in ¹H or ¹⁵N dimension. To see this figure in color, go online.

The vast majority of cross-peaks showed detectable peak shifts between 0 and 1 M ionic strengths and the chemical shift differences between the two salt concentrations were, on average, −0.031 ± 0.053 and 0.08 ± 0.28 ppm for ¹H and ¹⁵N nuclei, respectively, with maximal peak deviation of 0.27 ppm and 1.76 ppm, respectively (see Fig. S3 A). The relatively small chemical shift changes during titration greatly facilitated the transfer of peak assignment from low to high ionic strength conditions. This allowed us to map the chemical shift perturbation onto the CPR closed conformation (see Fig. S3 B) for 237 amino acids (110 and 119 in the FMN and FAD domains, respectively and 8 in the interdomain linker). The largest deviations were found for residues T79, G112, D210, F219, I220, and Q225 in the FMN domain, residues S243, R246, and Q247 in the interdomain linker, and residues K270, A281, D355, C366, S421, W422, E581, I623, and G672 in the FAD/connecting domain. All these residues are present at domain surfaces or in the interdomain linker. Of interest, most of these residues are found near the interdomain interface. Chemical shifts are exquisitely sensitive to the local chemical environment, and the salt-induced domain reorganization in CPR is prone to lead to chemical shift variations, in particular for residues near the interdomain interface. However, chemical shifts also report on protein-ion interactions, which can span a wide range of affinity and may lead to chemical shift variations of similar magnitude to those observed in this experiment (29,30). Therefore, the estimations of the relative contribution of nonspecific and site-specific protein-ion interactions and conformational changes to chemical shift were rendered difficult. Nevertheless, the observation of a single cross-peak for each amino acid during the titration strongly indicated that all chemical states of the enzyme, including those characterized by distinct conformational states L and U, are rapidly interconverting in solution. As a consequence, the L/U exchange rate k_ex (= k_L + k_U) must be at least ∼10 times larger than the largest difference in chemical shifts Δν between the two states, i.e., k_ex >> 2πΔν with Δν = |ν_L−ν_U|. To provide a low estimation of k_ex, we considered a maximal Δν value of 100 Hz (∼0.1 ppm for the ¹H nucleus at 950 MHz), which is in the high range of Δν observed on CPR, but still smaller than the largest shifts. This value is also commonly observed in the case of diamagnetic protein-protein interactions. We then calculated that the L/U exchange rate is faster than ∼600 s⁻¹. Because there was no evidence of line-broadening during the titration, the actual exchange rate is most likely much faster than this extreme low estimation, thus pointing to the highly dynamic nature of the L/U equilibrium.

Because chemical shift analysis did not provide any structural clue, we used ¹⁵N relaxation data to characterize the domain organization in the U state. Interdomain mobility can be efficiently probed by ¹⁵N R₁ and R₂ relaxation rates that report on hydrodynamic properties of protein domains. For example, a rigid bidomain protein is characterized by a single rotational diffusion tensor (i.e., a single averaged correlation time τ_c). This was the case for CPR at 0 M ionic strength (5), in agreement with the predominant locked conformation. In contrast, when significant domain dynamics exist, each domain may experience distinct apparent correlation times, in particular when their sizes and/or shapes are different. For matter of comparison, we predicted the hydrodynamic and relaxation properties of full-length CPR and isolated FMN and FAD domains using HYDRONMR (31). For the full-length enzyme, we found averaged R₁ and R₂ values of 0.26 ± 0.01 s⁻¹ and 56.7 ± 2 s⁻¹, respectively, which corresponded to an averaged R₂/R₁ of 221 ± 16 and correlation time of 30 ns. As already noted (5), a good correlation was found between these predictions and experimental data obtained at 0 mM NaCl concentration, in agreement with the predominantly closed conformation at low ionic strength. For the isolated FMN domain, we found averaged R₁ and R₂ values of 1.2 ± 0.02 s⁻¹ and 11.8 ± 0.3 s⁻¹, respectively, which corresponded to averaged R₂/R₁ of 9.8 ± 0.5 and correlation time of 6 ns. For the isolated FAD domain, we found averaged R₁ and R₂ values of 0.31 ± 0.02 s⁻¹ and 46.7 ± 2.8 s⁻¹, respectively, which corresponded to an averaged R₂/R₁ of 149 ± 18 and a correlation time of 24.2 ns.

We then collected ¹⁵N relaxation parameters at 800 mM salt concentrations where the U state is predominantly populated (Fig. 4 and see Table S1 in the Supporting Material). The ¹⁵N R₂/R₁ values were significantly lower for the FMN domain (59.8 ± 20.0) than for the FAD/connecting domain (181 ± 71) and corresponded to apparent correlation times of 15.2 ± 2.6 and 26.6 ± 5.4 ns, respectively. It is therefore apparent that the relaxation parameters obtained at 800 mM NaCl concentration are intermediate between those observed on the locked state and predicted for isolated domains. All these observations firmly suggest that in the U state, the FMN and FAD/connecting domains most likely freely tumble within a range restricted by the short linker and explore at the sub-τ_c timescale (10–30 ns) a large and most likely continuous ensemble of relative orientations and positions, in full agreement with SAXS analysis. Of note, increasing the ionic strength to 1 M (Fig. 4 and see Table S1) resulted in a small reduction in correlation times values for both domains in agreement with an increased population of the U state at higher ionic strength. We concluded that high ionic strength disrupts the interdomain interface, leading to an unlocked (U) and highly flexible state that populates conformers having the FMN moiety exposed to solvent, and is therefore compatible with interaction with other solutes.

Figure 4.

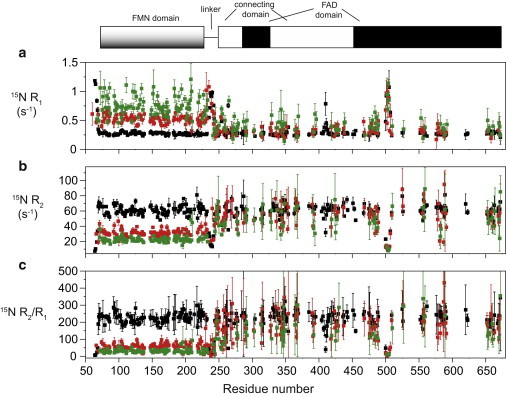
NMR ¹⁵N relaxation data collected at 950 MHz ¹H frequency at T = 310 K and at various ionic strengths. (a–c) ¹⁵N R₁, R₂, and R₂/R₁ values, respectively. (Red squares) Relaxation data collected at 0.8 M and (green squares) 1 M NaCl concentrations. To facilitate the comparison with relaxation obtained at low ionic strength, we also represented the data measured previously at 0 M ionic strength (black) (5). (Top) The domain organization illustrates the linear localization of the FMN-domain, the linker region, and the intertwined FAD and connecting domains. To see this figure in color, go online.

Kinetic experiments

The influence of the L/U equilibrium on electron flux was also assessed by measuring spectrophotometrically the cytochrome c reduction, in the same buffer conditions as those used for the SAXS experiments (Fig. 5 a). At pH 7.4 and 6.7, the initial rates (k_obs) of cytochrome c reduction display a bell-shaped curve when plotted against ionic strength, as previously observed in Sem and Kasper (19).

Figure 5.

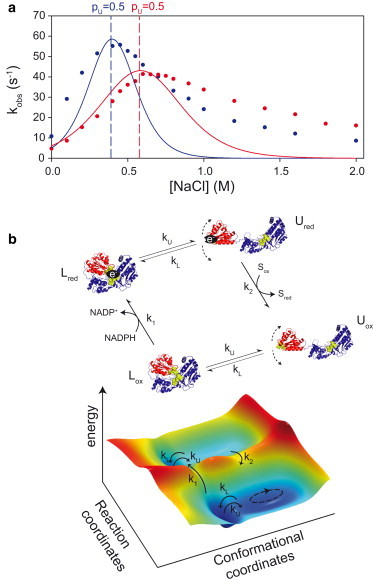
Linking conformational equilibrium and catalytic efficiency. (a) Cytochrome c reduction initial rate k_obs versus NaCl concentration measured at pH 7.4 (blue) and 6.7 (red). (Lines) The k_obs values fitted from the equation derived from the kinetic scheme in (b). (b) Kinetic scheme coupling conformational transitions and reaction rates k₁ and k₂. (ox) Oxidized; (red) reduced; (S) final electron acceptor. (Blue) FAD/connecting domain; (red) FMN domain. The corresponding multidimensional energy landscape is shown below. To see this figure in color, go online.

The striking correlation between maximal CPR activity (Fig. 5 a, red and blue dots) and SAXS-derived midpoint conformational transitions (Fig. 5 a, dashed lines indicating p_U = 0.5) at both pH values unambiguously demonstrates that, under steady-state conditions, electron flux is controlled by the L/U equilibrium observed for the oxidized enzyme at the resting state. More particularly, maximal electron flux occurs when K_e is close to 1, i.e., when the two conformational states are almost equally populated. The link between the proportion of the U state and cytochrome c reduction rate has already been reported in Huang et al. (11) using a SAXS-derived D_max value as a rough estimate of the population of the extended forms and for a limited salt concentration range (0–0.54 M). Here we also observed the similar linear relationship between reduction rate and p_U at low salt concentration (<400 mM), but the increase of salt concentration to higher concentration (1.8 M in our case) allowed us to detect the full transition. Therefore, our data demonstrate that maximal electron flux to external acceptors occurs when the conformational equilibrium of CPR is adequately balanced.

To rationalize these observations, we adapted and evaluated a kinetic scheme initially set up for NOS (Fig. 5 b, and see Section S1 in the Supporting Material (32,33),). In this model, the L state supports the NADPH-based FAD-mediated FMN reduction (k₁) whereas the U state supports the cytochrome c reduction (k₂). Although this model aggregates the different chemical steps occurring in the L state (hydride transfer from NADPH to FAD, ET from FAD to FMN, and the association and dissociation steps of the nucleotides) in a single rate constant (k₁), this simplification can serve as a first approximation of the real CPR mechanism. Here we further consider K_e independent of the CPR oxidation state. This hypothesis is supported by the limited impact of CPR reduction on SAXS-derived pairwise distance distribution (11). In addition, the NADPH-based reduction has a relatively weak effect on the R_g values of CPR (<3 Å) (11) compared to the R_g difference between the L and U states described in our work (9 Å). We provide in the Supporting Material an in-depth computational analysis of the kinetic model. Notably we found that the shape of the enzymatic turnover k_obs versus L/U relative populations depends on whether conformational changes are faster or slower than chemical rates, i.e., k_U, k_L >> k₁, k₂ or k_U, k_L << k₁, k₂. If one assumes fast conformational changes, the model predicts a bell-shape curve when plotting k_obs versus p_U or p_L. Our NMR study demonstrated that the L/U exchange rate k_ex = k_U + k_L is much faster than ∼600 s⁻¹, a value that is higher than k₁ and k₂ rates previously measured (2). This further supports the idea that conformational changes may not be rate-limiting. This result sharply contrasts with previous assumptions for NOS (32–34). Under these conditions, catalysis proceeds through the exploration of a multidimensional free-energy landscape (35) (Fig. 5 b) in which fast domain dynamics and slow reaction rates are coupled. The model predicts that maximal activity is achieved for

$$K_e=\frac{k_U}{k_L}=\sqrt{\frac{k_1}{k_2}}$$ (8)

(see also the Supporting Material). Here, the optimal CPR electron flux is effectively observed when K_e is close to unity (Fig. 5 a), in good agreement with the fact that reported values for k₁ and k₂ are in a similar range (2). Even though the model combines multiple elementary steps into single k₁ and k₂ rate constants, the global shape of the experimental k_obs curve (Fig. 5 a, plain blue and red lines) is satisfactorily reproduced using the SAXS-derived p_L/p_U values calculated with the denaturation-type equation parameters and k₁/k₂ simulated values of 250/220 s⁻¹ and 180/165 s⁻¹ at pH 7.4 and 6.7, respectively (Fig. 5 a, and see Section S1 and Eq. S9 in the Supporting Material). These predicted reduction rates are of the order of magnitude classically described for CPR (2). Additional salt-dependent factors might reflect the deviation of the simulated curve at high ionic strength, or alternative kinetic mechanisms may be predominant at high ionic strength. Taken together, these results suggest that the L and U states characterized in the absence of ET are fully relevant to describe the conformational equilibrium adopted by CPR during catalysis and that the relative populations of the two fast-exchanging conformational states directly control the efficiency of electron flux. Of note, this mechanism does not exclude possible additional conformational changes that may occur during the chemical steps k₁ and k₂.

Conclusions

In this article, we describe the free energy landscape of CPR in solution as a conformational equilibrium between a locked state (L), characterized by a closed rigid conformation, and a novel unlocked state (U), characterized by a large set of conformations. The structural transitions allowing the L/U switch have a relatively low energy barrier revealing the highly dynamic nature of domain conformational sampling in CPR. We further show that the free energy landscape is not modified upon NADP⁺ binding, contrarily to previously published results (10,13). In contrast, it can be efficiently reshaped not only by ionic strength, as already described in Huang et al. (11), Jenner et al. (15), Aigrain et al. (21), and Haque et al. (32), but also by pH. The largely nonphysiological conditions investigated here were used to accurately estimate the relative proportions of the L and U states under various ionic strength and pH conditions. The observation and analysis of a conformational equilibrium under multiple conditions allowed here the direct estimation of substate populations, including at near physiological conditions (pH 7.4 and 150 mM [NaCl]). This approach can therefore advantageously complement other attempts based on combined analysis of computation-based simulations and SAXS or NMR measurements obtained under a single condition (36–39).

The influence of electrostatics in controlling ET from CPR to acceptors has been extensively studied (reviewed in Pudney et al. (13)). In previous reports, electrostatic effects on acceptors’ reduction rates were interpreted as direct consequences of the changes in the interactions between CPR and acceptors (20,40,41). Here, the salt-dependency of electron flux to acceptors is proposed to predominantly stem from the ionic strength-dependent preexisting L/U equilibrium. We also provide a kinetic mechanism stipulating that the conformational state of CPR may not be significantly altered by the oxidation/reduction cycle. Such a mechanism sharply contrasts with the commonly accepted model for CPR (11), which assumes that the progress along the reaction coordinates is associated with stepwise conformational changes, starting the cycle with the L state (nucleotide binding, FAD reduction, and interflavin ET) and pursuing the reaction with discrete extended conformations (ET to acceptors). In the mechanism we propose here, CPR populates the L and U states several times before productive chemical steps (k₁ and k₂). Indeed, the global catalytic rate k_obs depends on conformational equilibrium parameters (p_U, p_L, k_U, and k_L) and on chemical rate constants (k₁ and k₂) that aggregate all kinetic parameters related to intrinsic properties of the enzyme (redox potentials, intradomain electron/proton transfer rates) or thermodynamic parameters (on- and off-rates for substrate/product binding or intermolecular ET).

The existence of multiple conformations exposing the FMN cofactor to the solvent in the U state provides, to our knowledge, a new template to apprehend CPR functioning. In the U state, domains movements are only restricted by natural obstacles (membrane, other domains, acceptors, etc.). The various discrete and extended conformations reported by other groups (10,11,13,15) may not be compatible with CPR-acceptor complexes due to steric hindrance of the endoplasmic reticulum surface with the N-terminal membrane spanning domain and the following FMN domain. In contrast, if we apply the ensemble of conformations from the U state to full-length CPR, the FAD domain can explore the many structural conformations leading to complexes compatible with ET to acceptors. A putative ET-to-acceptor state has recently been described with the x-ray structure of a complex between a mutated CPR and heme oxygenase (16). The intrinsic domain flexibility in reduced CPR may therefore facilitate the search for optimal interaction with the acceptor before the external ET. Our description of the CPR mechanism may be generalizable to other bidomain diflavin reductases for which the electron flux could be optimal when the populations of the L and U states match the k₁/k₂ value (see Eq. 8), or, written differently, when the state corresponding to the slowest reaction is favored. Hence, ionic strength or pH and more generally physicochemical parameters can directly tune overall electron flux not only through modulating chemical rates but also by controlling the stability of the interface of the two domains and the conformational equilibrium. Genetic or posttranslational changes of the residues at the interface are other potential mechanisms that may impact the overall activity without necessarily affecting other kinetic parameters (6,11,21,32). The kinetic mechanism we provide here can also possibly apply to other multidomain enzymes: an ultrafast conformational exchange at each catalytic step between competent states characterized by rapid stochastic interdomain interactions and the short lifetime of domain interfaces can control the global enzymatic output. In such a situation, maximal efficiency of the enzyme would be obtained when the relative populations of productive conformations adequately match individual catalytic rates. By rapidly sampling active conformations, extensive enzyme dynamics may therefore provide an elegant solution to the requirement of enzymes to adopt distinct conformations during catalysis.

Author Contributions

O.F. and F.F. purified proteins and collected SAXS and enzymatic data. J.P., E.L., and G.T. designed SAXS and enzymatic experiments. O.F., F.F., and J.P. collected SAXS data. J.P. and G.T. analyzed SAXS data. E.L. designed NMR experiments and analyzed kinetic schemes. O.F. and E.L. performed and analyzed NMR experiments. E.G., C.S., and D.P. participated in early stages of the project and commented on the manuscript. G.T., E.L., and J.P. wrote the manuscript.