Selection and Reduced Population Size Cannot Explain Higher Amounts of Neandertal Ancestry in East Asian than in European Human Populations

Abstract

It has been hypothesized that the greater proportion of Neandertal ancestry in East Asians than in Europeans is due to the fact that purifying selection is less effective at removing weakly deleterious Neandertal alleles from East Asian populations. Using simulations of a broad range of models of selection and demography, we have shown that this hypothesis cannot account for the higher proportion of Neandertal ancestry in East Asians than in Europeans. Instead, more complex demographic scenarios, most likely involving multiple pulses of Neandertal admixture, are required to explain the data.

Main Text

Initial genomic studies found Neandertal ancestry in non-African populations, suggesting that some ancestral admixture occurred between Neandertals and the ancestors of modern Eurasian populations.^1,2 One proposed explanation for this observation is that there was one pulse of Neandertal admixture in the Levant before humans migrated further into Europe and Asia.^2–4 However, more recent genomic studies^2–5 show that there are higher levels of Neandertal ancestry in East Asian populations than in Europeans. Initially, such a finding would appear to contradict the one-pulse admixture model. Additional pulses of Neandertal admixture into East Asian populations would be required to explain the increased Neandertal ancestry in East Asian populations.^5–8

Recently, Sankararaman et al.⁹ proposed a provocative hypothesis that could potentially rescue the one-pulse admixture model. They hypothesized that Neandertal alleles were weakly deleterious in humans. Because current evidence suggests that East Asian populations experienced stronger historical bottlenecks and had smaller effective population sizes,^10–14 the ability of purifying selection to remove weakly deleterious alleles from the population might have been less effective in East Asians than in Europeans.¹⁵ The reason for this is that in the smaller East Asian population, weakly deleterious alleles might have drifted to higher frequencies. In the larger European population, however, the effect of drift would be smaller. Thus, there could have been a single pulse of Neandertal admixture in the ancestral Eurasian population, but because Europeans were better able than East Asians to remove weakly deleterious Neandertal alleles, Neandertal ancestry appears to have increased in East Asians.

Here, we used forward-in-time Wright-Fisher simulations to explicitly test this hypothesis (Figure S1). To do this, we wrote our own custom Python simulations, called “Forward_Neanderthal” (see Web Resources). We simulated 1,000,000 ancestry-informative sites as independent loci, all of which received a single pulse of Neandertal admixture at t_admix generations ago. However, each of these ancestry-informative sites could biologically correspond to a larger segment of Neandertal ancestry.

We assumed that a single admixture event between humans and Neandertals occurred t_admix = 1,900 generations ago. This time corresponds to 47,500 years ago if we assume 25 years/generation. We chose this time to reflect a plausible time at which admixture could have occurred between Neandertals and humans.^9,16 At each locus, at the start of the simulation (at time t_admix), we assumed that a proportion (f) of the chromosomes contained Neandertal ancestry. In practice, each of the 1,000,000 loci began the simulation with the Neandertal ancestry at frequency f. We examined f = {0.02, 0.04}, corresponding to plausible amounts of Neandertal admixture in human populations.^2,5,9 Although we note that there might have been a distribution of values of initial Neandertal ancestry across the genome, this variability should not affect our results unless the initial starting frequency of Neandertal ancestry were to differ between European and East Asian populations. Given that our models assume a single pulse of Neandertal admixture in the ancestral Eurasian population, which itself is randomly mating, there is little reason to conclude that f should vary between the populations under the models we are testing.

We then allowed the populations to evolve to the present day under demographic models with parameters estimated from data (see below). We did this by adjusting the frequencies of the alleles deterministically according to the standard selection equations (see below) and by binomial sampling to model genetic drift. The total number of chromosomes drawn to form the next generation varied over time to reflect the changes in population size over time. At the end of the simulation, we examined the remaining amount of Neandertal ancestry in each population. In order to have a fair basis of comparison to Sankararaman et al.,⁹ for each site we sampled the same number of chromosomes from our simulated populations as in the 1000 Genomes Project¹⁷ CEU (Utah residents with ancestry from northern and western Europe from the CEPH collection; 174 chromosomes) and CHB (Han Chinese in Beijing, China; 190 chromosomes) populations. Under the assumption of independence and exchangeability among sites, a single haplotype can be modeled as a series of Bernoulli draws with success p₁...p_k over the k sites in the genome (p_i is the frequency in the sample of the Neandertal allele at the i^th site). Therefore, the expected Neandertal ancestry per haplotype is equivalent to the mean frequency of Neandertal alleles (p₁...p_k) in the sample. In other words, $E\left[\text{Neandertal}\right]=(1/k){\sum }_{i=1}^k{p}_i$. Thus, we computed the average Neandertal ancestry per genome (p_all) by averaging the per-site frequencies of Neandertal alleles in the sample over all 1,000,000 sites. Our approach is also analogous to that used in Sankararaman et al.,⁹ except that we assume that Neandertal ancestry is known rather than inferred (see below for further discussion) and that all sites are independent. We calculated the ratio of Neandertal ancestry in the East Asian population to that in the European population (R) by dividing the average ancestry in the East Asian population by the average in the European population (R = p_{all_ASN} / p_{all_EUR}). We also recorded the proportion of sites still polymorphic for Neandertal ancestry in the sample (p_var), as well as the frequency of Neandertal alleles only at those sites where the Neandertal alleles were still segregating (p_seg). We assessed simulation variance by replicating the entire simulation process for a given model 20 times. 95% confidence intervals (CIs) were calculated as $\text{CI}={\overline{p}}_{\text{all}}\pm 1.96\sigma$, where ${\overline{p}}_{\text{all}}$ and σ denote the mean and SD, respectively, of Neandertal ancestry per individual over the 20 simulation replicates.

Because the effects that Neandertal alleles have on human fitness are unclear, we allowed Neandertal alleles to have a range of effects from neutral to strongly deleterious. We defined the relative fitness of individuals heterozygous for Neandertal and human ancestry as 1 + hs and the fitness of individuals homozygous for Neandertal ancestry as 1 + s (s is the selection coefficient, and h is the dominance coefficient). First, we used scalar values of s = {0, −10⁻⁵, −10⁻⁴, −10⁻³, −10⁻²}. Additionally, we assumed that the selection coefficients (s) of the Neandertal alleles were drawn from a negative gamma distribution with parameters inferred from nonsynonymous SNPs by Boyko et al.¹⁸ In particular, for the population-scaled selection coefficient, we used a gamma distribution that had a shape parameter (α = 0.184) and a scale parameter (β = 8,200). Because this gamma distribution describes the distribution of 2Ns, we divided the value of 2Ns by 2 × 25,636 (the value of N used in Boyko et al.) to obtain the distribution of the selection coefficient, s. The parameters of this gamma distribution were estimated for new nonsynonymous mutations and might not necessarily reflect the distribution of fitness effects for Neandertal alleles in humans. However, given the extremely limited information regarding the distribution of fitness effects of Neandertal alleles in humans, this gamma distribution is a reasonable first approximation because it includes a mixture of nearly neutral, weakly deleterious, and strongly deleterious alleles.

We investigated multiple models of dominance (h). We considered the standard models of codominance (h = 0.5) and recessive effects (h = 0). We also examined models of underdominance (h = 2) and overdominance, where individuals who are heterozygous for Neandertal ancestry have the lowest and highest fitnesses, respectively. Some special care was needed when we used the gamma distribution of selective effects. The value of s from the Boyko et al.¹⁸ gamma distribution refers to the fitness effect of the heterozygous genotype, and 2s refers to the fitness of the homozygous genotype. In our simulations, s refers to the fitness effect of the homozygous genotype. Consequently, for simulations where h = 0.5 and h = 0, we multiplied the value of s obtained from the gamma distribution by 2.

We examined several different demographic models that have been fit to the East Asian and European populations (Tables S1 and S2). We first used the bottleneck models fit by Keinan et al.¹¹ (Table S1). The Keinan et al. bottleneck model assumes an ancestral human population size of N that then experienced two different bottlenecks, one of which was at approximately the same time in the European and East Asian populations (about 4,000 generations ago). However, this first bottleneck was older than the pulse of Neandertal admixture (t_admix = 1,900 generations ago). Because this earlier bottleneck was completed prior to the start of the simulations, we did not include it in the model. Rather, we assumed that the population remained at a constant size (N) until t_B generations ago, when a bottleneck occurred. The duration of the bottleneck is described by t_Blen, and the population size during the bottleneck is N_B individuals. After the bottleneck, the population recovered to N individuals and remained that size until the simulation finished. Note that the Keinan et al.¹¹ model considers the European and East Asian populations separately from each other. As such, we also simulated the two populations separately (Figure S1).

The degree to which the different models matched the observed proportion of Neandertal ancestry in either population was quite variable (Figure 1A). In models where the observed present-day Neandertal ancestry was approximately compatible with the amounts observed in empirical data (between 0.5% and 5%), the ratio of Neandertal ancestry in East Asians to Neandertal ancestry in Europeans (R) was close to 1 (Figure 1B). It never matched the R values estimated from empirical data⁹ (R = 1.14–1.31). This same result held regardless of the dominance coefficient, strength of selection, or initial proportion of Neandertal ancestry in the ancestral population (f = 4%; Figures S2 and S3).

Figure 1.

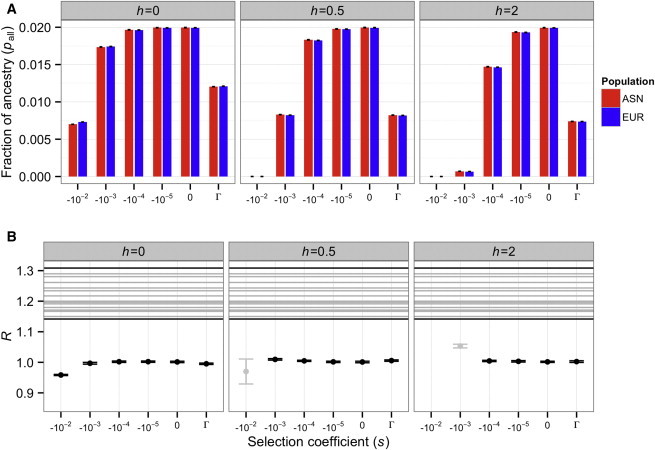
Predicted Neandertal Ancestry in East Asian and European Populations under the Keinan et al. Demographic Model when f = 2%

Each column depicts results for a different dominance coefficient (h). Γ denotes a gamma distribution of fitness effects. Error bars denote approximate 95% confidence intervals on our simulations.

(A) The fraction of Neandertal ancestry in East Asian (ASN) and European (EUR) populations.

(B) Ratio of Neandertal ancestry in East Asians to Neandertal ancestry in Europeans (R). Horizontal lines indicate the ratios of mean Neandertal ancestry observed in empirical comparisons of an East Asian and a European population.⁹ Models where the final proportion of Neandertal ancestry is concordant with the empirical data (between 0.5% and 5% in A) are colored black. Otherwise, they are colored gray. Note that across these models, the maximum value of R is only slightly higher than 1.0. However, the lowest observed value of R in the empirical data⁹ (in a comparison of IBS [Iberian population in Spain] and CHS [Southern Han Chinese]) is 1.14. Thus, demography differences combined with purifying selection cannot generate an excess amount of Neandertal ancestry in East Asians relative to Europeans as large as that seen in the empirical data.

In order to investigate the sensitivity of our results to the precise demographic model assumed, we performed additional simulations where we varied some of the bottleneck parameters. First, we investigated whether changing the duration of the bottleneck (t_Blen) would affect our results. In the initial model, we assumed that t_Blen = 100 generations. We conducted additional simulations with t_Blen = 50 generations and t_Blen = 200 generations. Importantly, in both cases, we kept the overall severity of the bottleneck (F = t_Blen / 2N_B) the same as in the original Keinan et al. study.¹¹ In order to do this, we changed the number of individuals in the bottleneck (Table S1). We found that the length of the bottleneck had little impact on our results (Figures S4 and S5). For the models where the observed present-day Neandertal ancestry was approximately similar to the amount observed in empirical data (between 0.5% and 5%), the ratio of Neandertal ancestry in East Asians to Neandertal ancestry in Europeans (R) remained close to 1 and did not match the R values estimated from empirical data,⁹ regardless of the dominance coefficient or strength of selection (Figures S4 and S5).

Second, we wanted to determine whether our results would be qualitatively different if the bottleneck in East Asia was actually more severe than estimated by Keinan et al.¹¹ We investigated models with bottlenecks 2- and 5-fold more severe than that estimated by Keinan et al.¹¹ Here, we kept the length of the bottleneck fixed at 100 generations (Table S1). Importantly, we did not change the severity of the bottleneck in the European population; we kept it at the original severity as estimated by Keinan et al. When Neandertal sites were weakly deleterious, nearly neutral, or recessive, increasing the severity of the bottleneck had little effect on our results (Figures S6 and S7). These models predicted R values close to 1, which is too low to be compatible with the observed ratio of East Asian to European Neandertal ancestry.⁹ When h ≥ 0.5 and s ≤ −0.001, some R values were in the range of, or even greater than, those seen in the empirical data (Figures S6 and S7). However, the predicted proportion of Neandertal ancestry in modern humans was too low in these models (<0.5%; Figures S6A and S7A) to be compatible with the observed data (>1%).⁹ Thus, although the more severe bottleneck might allow for some strongly selected Neandertal sites to drift to higher frequency in East Asians than in Europeans, such a model does not fit all aspects of the data. In summary, even if the East Asian bottleneck was 2- to 5-fold more severe than estimated, if we assume that the severity of the bottleneck in Europe was accurately estimated, purifying selection combined with the greater effect of genetic drift in the East Asian population cannot explain the higher proportion of Neandertal ancestry in East Asians than in Europeans.

Our findings suggest that reduced efficacy of purifying selection, due to greater genetic drift, in East Asians relative to Europeans cannot explain the observed increase in the proportion of Neandertal ancestry in East Asians. The reason for this is that greater drift in East Asians had two competing effects on Neandertal ancestry (Figure 2). For sites where both the Neandertal and human alleles were segregating at the end of the simulation, the Neandertal alleles tended to be at higher frequency in East Asians than in Europeans (Figure 2; Table S3). However, greater drift in East Asians also means that Neandertal alleles are lost from the population at a faster rate. Our simulations predicted that East Asian populations should have fewer sites with segregating Neandertal alleles than European populations (Figure 2; Table S3). These two competing effects of drift canceled each other out, yielding R values close to 1. For neutral alleles, this cancellation followed exactly from the mathematical formulation of the Wright-Fisher model. The expected value of the frequency of an allele at initial frequency f does not change after a generation of genetic drift, regardless of the population size.^19,20

Figure 2.

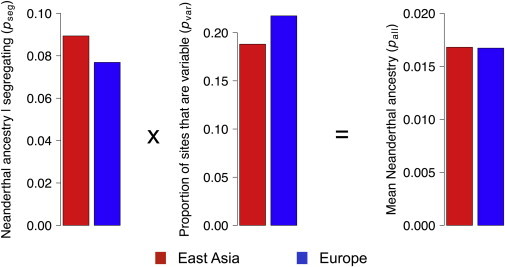
The Smaller Effective Population Size in East Asians Than in Europeans Has Two Competing Effects on Patterns of Neandertal Ancestry

(Left) The average Neandertal allele frequency at the end of the simulation given that the site segregates for the Neandertal and human allele (p_seg). Note that here, the average allele frequency in East Asia is higher than that seen in Europe as a result of the greater effects of genetic drift in East Asia than in Europe.

(Center) The percentage of sites (out of a total of 1,000,000 sites) where a Neandertal allele and a human allele are both still segregating at the end of the simulation (p_var). Note that fewer sites are segregating in the East Asian population because more were lost by genetic drift in this population.

(Right) The mean Neandertal ancestry per individual (p_all) is the product of both the mean frequency of alleles given that they are segregating and the percentage of sites that are segregating. Note that these two effects cancel each other out. These results suggest that East Asian and European individuals will have similar amounts of Neandertal ancestry under this model of demography and selection.

To examine the mechanism of allele-frequency change with selection, we conducted additional simulations in which the population was set to the size of the bottlenecks estimated in Keinan et al.¹¹ We ran these simulations for 100 generations and recorded the average frequency of the Neandertal alleles at the end of the simulation (which would correspond to the end of the population bottlenecks in the full demographic model). For the bottlenecks estimated by Keinan et al.,¹¹ the average Neandertal allele frequencies were essentially the same in both populations (Figure 3A; Figure S8). The nearly neutral theory predicts that mutations where −1 < Ns < 0 (according to our scaling of the relative fitnesses) are nearly neutral and are primarily affected by drift rather than selection.^15,21,22 Thus, Neandertal alleles where s > −0.0018 are predicted to be nearly neutral and primarily affected by drift in both populations, suggesting that the analytical predictions for neutral alleles approximately hold here as well. More strongly deleterious alleles also showed similar frequencies between the two populations, indicating that the subtle difference in the population size during the East Asian and European bottlenecks is too small to show a change in the effect of selection between the two populations in such a short time period. Because the bottleneck was estimated to be only slightly more severe in East Asia, the threshold at which alleles were nearly neutral was fairly similar between the populations (bottom panel of Figure 3A).

Figure 3.

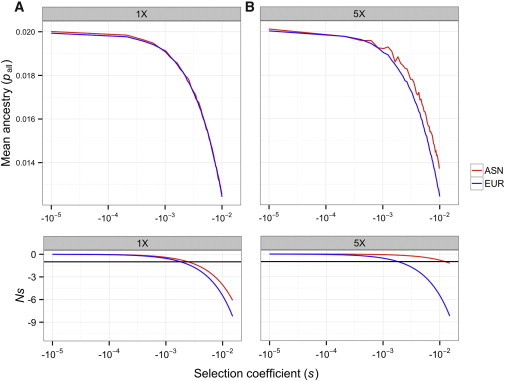
Predicted Mean Neandertal Allele Frequency at the End of the Population Bottlenecks in East Asian and European Populations for the Additive Case

(A) Population sizes were set to those inferred in Keinan et al.¹¹

(B) The ASN population size was assumed to be 5-fold smaller than that estimated in Keinan et al.¹¹ In all cases, constant-sized populations were simulated for 100 generations. The bottom plots show how Ns changes as a function of s.

In (A), both populations have a similar value of Ns across the range of s. Alleles with s > −0.0018 are nearly neutral (Ns > −1) in both populations. In (B), when s < −0.0018, alleles in the ASN population remain nearly neutral, whereas those in the EUR population are more strongly selected. Here, f = 2%.

To examine whether the pattern seen in Figure 3A would hold with a stronger bottleneck in East Asia, we made the East Asian population size 5-fold smaller than that estimated by Keinan et al.¹¹ while keeping the European population size the same as originally estimated (Table S1). Again, nearly neutral alleles (s > −0.0018) were primarily affected by drift. As such, the Neandertal frequencies in East Asian and Europeans were predicted to be the same for the reasons discussed above (Figure 3B; Figure S8). Only when the selection coefficients for Neandertal alleles became more deleterious did we see a difference in allele frequency. When s < −0.0018, we saw that East Asians had a slightly higher frequency of Neandertal alleles than did Europeans (Figure 3B). Here, Neandertal alleles were predicted to be nearly neutral in East Asians but more affected by selection in Europeans (bottom panel of Figure 3B). This is the effect that Sankararaman et al.⁹ hypothesized could explain the higher Neandertal ancestry in East Asians. But, our simulations suggest that this effect is unlikely to occur in practice because it requires a stronger bottleneck than that estimated for East Asia and a selection too strong to be compatible with observed amounts of Neandertal ancestry (see below).

Next, we wanted to assess whether other demographic features not included in the Keinan et al.¹¹ bottleneck model would influence our conclusions. Specifically, the Keinan et al.¹¹ model does not consider shared ancestry between the East Asian and European populations, migration between populations, or recent population growth. Thus, we performed additional simulations under a different human demographic model fit to the site-frequency spectrum of East Asian, European, and African populations.²³ This model jointly considers both the European and East Asian populations with migration between them and includes recent exponential population growth in both populations. This model also includes an unsampled African population that exchanges migrants with the European and East Asian populations. We included the African population because we wanted to investigate whether a higher migration rate between Africa and Europe than between Africa and East Asia could increase the values of R. Because the African population does not start with any Neandertal ancestry, migrants from Africa would be unlikely to carry Neandertal ancestry and would thus decrease the overall proportion of Neandertal ancestry in the population into which they migrate.

As before, we assumed that the Neandertal admixture occurred at time t_admix = 1,900 generations ago. In the Gravel et al.²³ model, this time occurred during the Eurasian population bottleneck, after the ancestral African population split from the ancestral Eurasian population. Thus, we started our simulation by introducing Neandertal ancestry at f = {0.02, 0.04} into the ancestral Eurasian population, which had size N_b. After t₁ generations, this population split into European and East Asian populations with initial population sizes N_EUR0 and N_ASN0, respectively, and growth rates r_EUR and r_ASN, respectively. The probabilities of migration, m, were assumed to be symmetric and were set to the previously estimated values.²³ Migration was assumed to be conservative, meaning that it does not change the populations sizes.²⁴ The frequency of the Neandertal allele in the European population after migration (f′_EUR) was f′_EUR = f_EUR(1 − m_{EUR_ASN} − m_{EUR_AFR}) + f_ASN(m_{EUR_ASN}) + f_AFR(m_{EUR_AFR}), where f_EUR is the frequency in the European population before migration. These populations continued to grow exponentially for t₂ generations, at which time the simulation was concluded. Table S2 shows the parameter values used for these simulations.

This more complex demographic model²³ showed results similar to those from the Keinan et al.¹¹ model. The ratio of Neandertal ancestry in East Asians to Neandertal ancestry in Europeans (R) remained close to 1 (Figure 4; Figure S9) for the models where the observed present-day Neandertal ancestry was approximately similar to that observed in empirical data (between 0.5% and 5%). Again, the observed R values estimated from the empirical data fell outside the range predicted by our models. Importantly, our implementation of the multi-population demographic model²³ included a higher migration rate between Africa and Europe than between Africa and East Asia. Thus, the fact that this model did not yield R values consistent with the observed data (Figure 4B) suggests that the previously estimated²³ rates of differential migration between African and non-African populations are insufficient to dilute the Neandertal ancestry in Europeans in relation to the Neandertal ancestry East Asians.

Figure 4.

Predicted Neandertal Ancestry in East Asian and European Populations under the Gravel et al. Complex Demographic Model when f = 2%

Each column depicts results for a different dominance coefficient (h). Γ denotes a gamma distribution of fitness effects. Error bars denote approximate 95% confidence intervals on our simulations.

(A) The fraction of Neandertal ancestry in East Asian (ASN) and European (EUR) populations.

(B) Ratio of Neandertal ancestry in East Asians to Neandertal ancestry in Europeans (R). Horizontal lines indicate the ratios of mean Neandertal ancestry observed in empirical comparisons of an East Asian and a European population.⁹ Models where the final proportion of Neandertal ancestry is concordant with the empirical data (between 0.5% and 5% in A) are colored black. Otherwise, they are colored gray. Note that across these models, the maximum value of R is only slightly higher than 1.0. However, the lowest observed value of R in the empirical data⁹ (in a comparison of IBS and CHS) is 1.14. Thus, demography differences combined with purifying selection cannot generate an excess amount of Neandertal ancestry in East Asians relative to Europeans as large as that seen in the empirical data.

Our analyses are predicated on the assumption that the amount of Neandertal ancestry in present-day East Asia is truly higher than that in Europe. Our study did not assess whether there is differential performance of the statistical approaches to identifying Neandertal ancestry across different human populations. Multiple statistical approaches—including D statistics,^5,7 a conditional-random-field approach based on multiple summary statistics,⁹ and methods based on linkage disequilibrium^5,6,25—all suggest that East Asians have 15%–30% more Neandertal ancestry than European populations. These statistical methods measure different features of the data and have distinct underlying assumptions. Thus, the fact that they provide concordant results suggests that differential power is unlikely to explain the higher amount of Neandertal ancestry in East Asia. However, to better address whether the increased Neandertal ancestry in East Asia as inferred by the D statistic could be an artifact of complex demography, we conducted neutral coalescent simulations²⁶ under the Gravel et al.²³ demographic model, in which we included zero, one, or two pulses of Neandertal admixture⁶ (Tables S4 and S5). Importantly, unlike our previous results that assumed that Neandertal ancestry could be unambiguously identified, the D statistics were applied to simulated genetic-variation data as done in practice. We found that higher migration rates between Europe and Africa than between East Asia and Africa in a model with one pulse of Neandertal admixture are not sufficient to generate the observed increase in Neandertal ancestry in East Asian populations (Table S4).

However, there are two possible ways a simple demographic model with one pulse of Neandertal admixture could still explain the patterns seen in the data. First, Neandertal alleles could have differential fitness effects in European and East Asian populations (i.e., s is different between Europeans and East Asians). Second, if all Neandertal sites are co-dominant or under-dominant and tend to be moderately to strongly deleterious (s ≤ −0.001), R becomes larger (Figures 1 and 4; Figures S2 and S9 and Table S3). Yet, as discussed previously, R only matched the empirical data when the bottleneck in East Asia was 2- to 5-fold more severe than estimated (Figures S6 and S7). However, for such a model to be compatible with the amount of Neandertal ancestry observed in human populations,⁹ the initial admixture proportion (f) would have to be substantially greater than 10% (Figure S10). Without additional support, both of these models seem biologically less plausible than alternative demographic models.

In sum, our simulations suggest that across a wide range of biologically realistic models, a single pulse of Neandertal admixture, combined with the reduced efficacy of purifying selection against weakly deleterious alleles in East Asians, cannot explain the R values observed in empirical data. Instead, more complex demographic scenarios, possibly including an additional pulse or wave of Neandertal admixture into East Asian populations, must be invoked. Such two-pulse models have been shown to fit the observed data^5,6,8 better than the single-pulse-with-migration model,⁶ even when only the genomic regions most likely to be neutrally evolving are considered.²⁵ In our simulations, across a range of different values for the strength of selection acting on Neandertal ancestry, a two-pulse model with realistic admixture proportions^6,25 could generate the R values observed in the actual data (Figures S11 and S12 and Table S3), suggesting that such a model is one viable explanation for differential patterns of Neandertal ancestry between East Asian and European populations.

Web Resources

The URL for data presented herein is as follows:

• Forward_Neanderthal, https://github.com/LohmuellerLab/Forward_Neanderthal