Abstract
A kinetic model of the effect of agonist and anesthetics on ligand-gated ion channels, developed in earlier work, is further refined and used to predict traces observed in fast-perfusion electrophysiological studies on recombinant GABAA receptors under a wide range of agonist and/or anesthetic concentrations. The model incorporates only three conformational states (resting, open, and desensitized) but allows for the modulation of the conformational free energy landscape connecting these states resulting from adsorption of agonist and/or anesthetic to the bilayer in which the protein is embedded. The model is shown to reproduce the diverse and complex features of experimental traces remarkably well, including both anesthetic-induced and agonist-induced traces, as well as the modulation of agonist-induced traces by anesthetic, either coapplied or continuously present. The solutions to the kinetic equations, which give the time-dependence of each of the nine protein states (three ligation states for each of the three conformations), describe the flow of probability among these states and thus reveal the kinetic underpinnings of the traces. Many of the parameters in the model, such as the desorption rate constants of anesthetic and agonist, are directly related to model-independent experimental measurements and thus can serve as a definitive test of its validity.
Introduction
There is a broad consensus that inhalation anesthetics act by inhibiting the development of an action potential in postsynaptic membranes, and that they do so by modulating the activity of the membrane proteins that mediate synaptic neurotransmission. Although there is less agreement on specific protein targets, the most likely candidates are thought to be postsynaptic receptors, most of which are members of the cys-loop family of pentameric ligand-gated ion channels (pLGICs). However, the mechanism(s) by which small molecules with anesthetic potency influence receptor activity remain unknown. Indeed, it is not even known whether the anesthetic effect of many of these molecules occurs through direct binding to localized sites on receptors, or indirectly through adsorption to (and modulation of the physical properties of) the bilayer in which the receptors are embedded, or perhaps some combination of the two.
The difficulty in determining the molecular mechanism arises in large part because receptor activity is complex and incompletely understood. Fast-perfusion electrophysiological studies have explored the response of receptors to a pulse of their neurotransmitter agonist, which induces a conformational change that opens transmembrane channels through which selected ions can flow. (Rapid solution exchange provides a good experimental approximation of a “pulse” (boxcar) function, in which agonist concentration changes instantaneously from zero to some constant positive value at the beginning of the pulse, and returns instantaneously to zero at the end of the pulse.) For most receptors, single-channel measurements have revealed that the ion conductance in its open state(s) appears to be constant. For a patch containing a large number of receptors, the measured ion current is thus proportional to the fraction of channels in conducting states. The resulting current traces therefore provide, to within a multiplicative constant, the fraction of proteins in a conducting (open channel) conformation as a function of time. These traces can exhibit a remarkably complex time-dependence, the features of which may vary sensitively with agonist concentration. The degree of complexity increases in the presence of anesthetics, which modulate characteristic features of these traces in a manner that depends sensitively on anesthetic concentration.
The general class of mechanism by which anesthetics influence receptor activity can be categorized as either direct (binding to localized sites) or indirect (bilayer-mediated). However, neither the discovery of protein sites to which an anesthetic binds at clinical concentrations, nor (alternatively) an unambiguous determination that clinical concentrations of anesthetics modulate physical properties of lipid bilayers, would in itself provide a mechanistic understanding of anesthesia. Either way, a fundamental understanding additionally requires development of a detailed kinetic model that explicitly incorporates anesthetic effects (whether binding or bilayer-mediated), and that reproduces the complex kinetics of agonist-induced current traces and the modulation of these traces by anesthetics over a wide range of both agonist and anesthetic concentrations. To be of any predictive value, such an approach must also be susceptible to model-independent experimental verification or falsification, which can thus serve to distinguish unambiguously between direct binding and bilayer-mediated models of anesthetic mechanisms. Although this may seem an obvious goal, a comprehensive kinetic model has not yet been suggested for a direct binding mechanism of action of inhalation anesthetics. This is perhaps surprising, given the current enthusiasm for a binding mechanism, the sophistication of fast-perfusion electrophysiological methods, and the availability of software through which numerical solutions can be obtained for classical kinetic schemes involving standard (Markovian) binding and conformational transitions.
For various members of the pLGIC family of receptors (predominantly GABAA and acetylcholine receptors), kinetic models have certainly been proposed to rationalize the experimentally observed response of the receptor to its agonist. The simplest models of GABAAR kinetics presume that the protein can exist in one of three conformational states: resting, open, and desensitized, in which only the open state conducts ions (1). The agonist interacts with the protein solely by binding to its pair of equivalent extracellular sites, which destabilizes the resting state relative to both the (kinetically favored) open state and the (thermodynamically favored) desensitized state. Such models can capture some of the general features of current traces, such as rapid activation followed by a gradual decrease in current (desensitization) in the continued presence of saturating concentrations of agonist. However, it is well known that they fail to reproduce the temporal complexity of experimental traces, particularly at high agonist concentrations (e.g., multiple timescales of desensitization) unless additional conformational states are added to the kinetic scheme. With the inclusion of such states and the appropriate adjustment of kinetic parameters, these kinetic models can indeed reproduce observed traces, albeit over limited ranges of concentration (2–7). However, aside from the improbability that a protein requires so many distinct conformational states for proper function, the value of such a model is limited, since the existence of those states cannot be confirmed experimentally. Furthermore, even with additional conformational states, such models are not able to reproduce traces over the broadest range of agonist concentration.
We have previously developed a general kinetic model (8) in which aqueous solutes (agonist and/or anesthetic) can adsorb to the bilayer, and thereby modulate the conformational free energy landscape of the protein. Although the model includes only the minimal set of three protein conformational states, this study shows that it can nonetheless reproduce the full range of complex features of electrophysiological traces. In brief, the complexity results from the time-dependence of solute adsorption to the bilayer, which modulates the rate constants of conformational transitions. As a first test, the model was shown (8) to provide excellent fits to data obtained for the special case in which currents were induced by volatile anesthetics alone (i.e., in the absence of agonist, which thus greatly simplifies the kinetic mechanism) in recombinant α1β2γ2L GABAA receptors (9). Although this is a simpler special case, these fits provided values of parameters, such as bilayer adsorption and desorption rate constants of these anesthetics, which, in principle, could be directly compared with independent experimental measurements, and could thus serve as an unambiguous test of the model.
The next step is clearly to apply the full kinetic model developed in (8)—which includes binding of agonist to its canonical sites as well as adsorption of both agonist and anesthetics to the bilayer—to a set of experimental results for one (or preferably more) receptors. A conclusive test would require an extensive set of very accurate electrophysiological traces, in which concentrations of agonist and anesthetic(s) are independently and systematically varied over a wide range, up to concentrations far in excess of binding saturation of agonist and clinical values of anesthetics. Given its importance to the elucidation of anesthetic mechanisms, and more fundamentally to the mechanism of the complex agonist-induced behavior of receptors, it is surprising that such a comprehensive set of electrophysiological results simply does not exist in the literature for any one receptor. Validation of any kinetic model—whether based on direct binding of anesthetic or bilayer-mediated effects of both anesthetic and agonist—is extremely difficult in the absence of such data. Fortunately, however, many of the defining features of current traces are shared (at least qualitatively) by related receptor isoforms studied in different labs; these consistent features thus provide a sufficiently challenging test for any kinetic model. Of course, the model must not only be capable of reproducing observed traces, but its assumptions and architecture must be physically reasonable, and the values of any fitted parameters must also be susceptible to model-independent experimental confirmation.
We consider in this study the detailed characteristics of current traces through GABAA receptors, as these receptors have been extensively studied by fast-perfusion electrophysiological methods, and they have the advantage—common among inhibitory (anion-selective) receptors—that currents can be induced not only by agonists, but by supraclinical concentrations of anesthetics. To provide the most comprehensive test of the model, we examine predictions for three general classes of current traces, each over an extremely wide range of concentrations: anesthetic-induced (without agonist), agonist-induced (without anesthetic), and modification of agonist-induced traces by varying concentrations of anesthetic, either coapplied or continuously present.
Materials and Methods
The general kinetic model was developed in Cantor et al. (8), hereafter labeled “I” to which the reader is referred for details; it is summarized in the next section, as well as in a recent review (10). All references to numbered equations and figures in Cantor et al. (8) are notated “I.xx,” where xx is the equation or figure number. The subsequent section describes the further development of the approach, in which we have incorporated a set of additional approximations, which reduce significantly the number of independent kinetic parameters. This is followed by descriptions of the parameter set and methodology.
Kinetic model
The protein is assumed to exist in one of three conformational states: X = R (resting), D (desensitized), and O (open); only the open state is conducting. Conformational transitions among all three pairs of states are allowed; the desensitized state can thus be accessed from either the resting state (branched desensitization) or open state (linear desensitization). The two agonist binding sites are assumed to be equivalent, so that a protein in conformation X can exist in one of three ligation states {A0X, A1X, A2X}, with appropriate statistical factors in the rate equations of binding and unbinding to account for the degeneracy of the monoliganded state. The kinetic scheme is shown in Fig. I.1 (i.e., Fig. 1 in (8)); for convenience, it has been provided as well in Fig. S1 in the Supporting Materials. The fraction of protein in state X with i bound agonist molecules is denoted ; because the fractions add to 1, the protein distribution is defined by any eight of these nine fractions. The kinetics of conformational transitions and the binding of agonist to protein sites are modeled using standard forms for the rate equations, expressed in terms of , as detailed in Eqs. I.2 and I.3 (i.e., Eqs. 2 and 3 in (8)).
Each conformational state can be interpreted as a local minimum along a generalized conformational coordinate that describes the protein free energy landscape, as illustrated in Fig. I.2, and in Fig. 3 in (10). The landscape changes significantly upon binding of agonist. For example, with no agonist bound, the lowest free energy minimum is that of the resting state (A0R), whereas for the diliganded protein, the free energy minima corresponding to the open and desensitized states (A2O and A2D) are both lower than that of the resting state (A2R). Of course, the landscape describes not just the minima, but all points along the trajectories of conformational transitions, including the maxima associated with the barrier (activated complex) between each pair of conformational states. Free energy landscapes based on the parameter set used in this work are shown in Fig. S2 for both the unliganded and diliganded protein.
Adsorption of solutes (agonist or anesthetic) onto the lipid bilayer of the postsynaptic membrane alters the physical properties of the bilayer. The bilayer constitutes an important part of the fluid environment of the protein, so changes in bilayer physical properties can change the protein free energy, to a degree that may vary with position on the free energy landscape. The entire landscape, including the local minima (conformational states) and the maxima separating them, will thus be modulated nonuniformly by changes in bilayer properties, i.e., the free energy will change to a degree that varies with position along the conformational coordinate. Let x represent a generalized conformational coordinate and G°(x) the standard free energy landscape of the protein, where the standard state (°) refers to the absence of any adsorbed solutes. In a Langmuir approximation, let θs represent the fractional bilayer adsorption of solute s (agonist or anesthetic), i.e., the fraction of its surface density at saturation. The free energy will vary with a sensitivity λs(x) that depends both on location on the conformational landscape (x) and the identity of the solute. At low adsorption, the change will be proportional to θs, i.e.,
| (1) |
Consider the effect of adsorption on the kinetics of a conformational transition AiX → AiY (i.e., from state X to state Y, with i ligands bound). Let AiXY‡ represent the activated complex, at which the free energy reaches a maximum along the trajectory AiX → AiY. To reasonable approximation, the transition rate constant depends exponentially on ΔG‡, the molar free energy barrier between the initial state (x = AiX) and the activated complex (x = AiXY‡), with
| (2) |
and
| (3) |
where = represents the difference in sensitivities (to solute s) of the protein in the activated complex and in its initial state. If ≠ 0, then membrane adsorption/desorption of solute will cause k to vary with θs as in the following:
| (4) |
where k° represents the standard rate constant (i.e., at θs = 0), and we define a dimensionless sensitivity of the rate constant: . Because adsorption/desorption of solutes does not occur instantaneously (i.e., θs varies with time), and because the exponential function can be such a sensitive function of its argument, the rate constants of conformational transitions are thus strongly time-dependent.
The time-dependence of adsorption, θs(t), is determined in a simple Langmuir approximation of adsorption/desorption kinetics, given in Eq. I.7. The equilibrium adsorption of solute at aqueous concentration cs is thus (Eq. I.9):
where Kads,s = kon,s/koff,s.
Additional approximations
The general model contains kinetic parameters that involve binding and unbinding of agonist to receptor, standard rate constants of transitions among conformational states for different degrees of ligation, the rate constants of adsorption/desorption to the bilayer for both agonist and anesthetic, and the sensitivities (described above) of rate constants of conformational transitions. Thermodynamic constraints reduce the number of independent parameters somewhat, as described by Eqs. I.12 to I.20. The physical principles inherent in the approximations of the model lead to additional relationships among both 1) the sensitivities and 2) the standard rate constants that further reduce the number of independent parameters, as follows.
Sensitivity parameters
Eq. I.18 indicates that the difference in sensitivities of the rate constants of opposing conformational changes is independent of ligation state:
| (5) |
where {X,Y} = {R,O}, {O,D}, or {R,D}. These relations are exact, since they arise from thermodynamic constraints. As noted in Eq. I.19, each of these differences in the sensitivities of opposing rate constants is proportional to the difference in sensitivities of the free energies of the two states:
| (6) |
The sensitivity of the free energy of the state X to bilayer adsorption of a solute s presumably depends on the structural properties of the conformational state (shape, etc.) in the membrane domain. Since the binding of agonist A to conformational state X is presumed not to affect the structural properties of state X, it is thus reasonable to assume that the sensitivity of that state is independent of ligation, i.e.,
| (7) |
This will presumably remain a good approximation at any point on the protein free energy landscape; not just at a local minimum (conformational state), but also at a maximum (activated complex), or anywhere else. The notation for the minima and maxima can thus be simplified to λs,X and , respectively. If so, then the difference in sensitivities of two different points on the protein free energy landscape will also be independent of ligation state. If the two points correspond to a pair of conformational states {X, Y}, then Eq. 7 simply regenerates the constraints given in Eq. 5 that arise from thermodynamic considerations. But if the two points on the free energy landscape correspond instead to a conformational state X and an adjacent transition state XY‡, then since
| (8) |
it follows that the sensitivities of the rate constants are also independent of ligation state, i.e.,
| (9) |
For each solute s, this provides a set of 12 constraints, rather than just the six constraints given by Eqs. I.18 and I.19. There is one additional constraint relating opening, linear, and branched desensitization given by Eq. I.20, so that altogether only 18 – 13 = 5 independent sensitivity parameters remain for each solute.
Standard rate constants
The rate constants are standard state values, in that they describe the kinetics of conformational transitions in the absence of solute adsorption to the bilayer. The thermodynamic constraints given by Eq. I.17 (one for each ligation state) reduce this number from 18 to 15. Unlike the sensitivities, these standard rate constants are strongly affected by ligation state (increased ligation shifts the equilibrium from the resting to the open and desensitized states). The equivalence of the two binding sites results in the two constraints given by Eq. I.15, which is expressed in terms of the rate constants in Eq. I.16. For example, for the opening/closing standard rate constants:
| (10) |
Since the two ligand binding sites are equivalent, it is reasonable to assume further that the binding of a ligand alters the rate constant for a particular conformational transition by a constant multiplicative factor, i.e., independent of the number of ligands already bound. In other words, for each transition X→Y, a coefficient vX→Y is defined such that
| (11) |
and thus . This leaves 10 independent parameters for the standard rate constants: for any five of the six X→Y transitions. Note finally that the original constraints in Eq. I.16 are the ratio of the individual constraints for the opposing conformational transitions X→Y and Y→X. These two constraints can now be reexpressed to relate the agonist dissociation constants Kd,X and Kd,Y for a pair of states {X, Y}, where Kd,X = ku,X/kb,X, and thus
| (12) |
| (13) |
Parameter set
As described above, there are 10 independent parameters for the standard rate constants, and five independent sensitivity parameters for each solute. The six agonist binding/unbinding rate constants (kb,X, ku,X; X = {R, O, D}) are constrained by the two thermodynamic relations given in Eqs. 12 and 13, leaving four independent parameters. The adsorption (on-) and desorption (off-) rate constants for each solute (kon,ag, koff,ag; kon,an, koff,an) are unconstrained. The total number of independent parameters thus depends on which solutes are present. With both agonist and anesthetic, a total of 28 parameters need be specified; the number is reduced to 21 if only agonist is present. On the other hand, if only anesthetic is present, then since only the unligated state of the protein can exist, the diliganded standard rate constants and binding/unbinding parameters are eliminated, leaving only 12 independent parameters.
Fortunately, some of these parameters are directly related to specific characteristics of experimental traces. For example, the rate constants of binding/unbinding to the resting state {kb,R, ku,R}, the standard rate constant of opening from the diliganded resting state , and the associated equilibrium constant K°open,2 = are determined from the dependence on agonist concentration of the shape of the current rise to its peak at the beginning of the pulse. Also, the fraction of protein in the open state at equilibrium in the absence of agonist has been estimated for various GABAA receptors (typically of order 0.01% to 0.1%), which thus constrains K°open,0 = , and the extent of desensitization at sufficiently high concentrations of agonist (high enough to ensure that the protein is essentially entirely diliganded, but not so high as to adsorb significantly to the bilayer) determines K°deslin,2 = . The equilibrium constant Kads = kon/koff of bilayer partitioning (adsorption/desorption) has been measured for various solutes, including anesthetics. As discussed elsewhere (10), the limited information available for transport-limited desorption rate constants of small solutes indicates that the range of values of koff is fairly narrow—within an order of magnitude of 100 s−1—for a surprisingly broad range of compounds.
Table 1 lists the parameter values used in the calculations reported in this article. They were chosen largely to reproduce the features of the current traces published in a series of papers (9,11–14) on the effects of inhalation anesthetics such as isoflurane on recombinant α1β2γ2L GABAA receptors, over a broad range of agonist and isoflurane concentrations. Of the 28 parameters, the 14 constants of agonist binding and standard conformational transitions (columns 1 to 4 in Table 1) depend only on the protein and agonist; they are independent of any effects of bilayer adsorption and would thus need to specified for any model of agonist activation of receptors that includes both linear and branched desensitization. By contrast, the four constants involving bilayer adsorption {koff,ag, Kads,ag, koff,an, Kads,an} depend only on the solute (agonist or anesthetic) and the bilayer, i.e., they are independent of the protein. Only the 10 sensitivities (αs,X→Y) depend both on the protein and on bilayer-mediated effects. Note that only three of the independent parameters {Kd,R, Kads,ag, and Kads,an} involve concentrations; the rest are either first-order rate constants or dimensionless.
Table 1.
Values of independent parameters
| Kd,R | ku,R | ku,O | ku,D | koff,ag | Kads,ag−1 | koff,an | Kads,an−1 |
| 167 μM | 100 s−1 | 0.40 s−1 | 4.0 s−1 | 40 s−1 | 10 mM | 320 s−1 | 2 mM |
| K°open,0 | K°open,2 | αag,R→O | αag,O→R | αan,R→O | αan,O→R | ||
| 2.9 × 10−4 | 30 | 8.1 × 10−4 s−1 | 800 s−1 | 6.0 | −1.0 | −9.1 | −2.5 |
| K°deslin,0 | K°deslin,2 | αag,O→D | αag,D→O | αan,O→D | αan,D→O | ||
| 0.22 | 1.5 | 0.84 s−1 | 1.1 s−1 | 0.0 | 0.5 | −0.4 | 10.7 |
| αag,R→D | αan,R→D | ||||||
| 5.4 × 10−3 s−1 | 1.0 s−1 | 6.4 | −14.4 | ||||
An extended version of Table 1, containing additional (derived) parameters is given in Table S1. The effects of various representative levels of solute adsorption on the transition rate constants are shown in Table S2. Fig. S2 provides corresponding diagrams of the free energy landscapes for the unliganded and diliganded protein, with and without adsorbed solutes.
Solution of kinetic equations
The time-dependent distribution of protein states is described by the fractions . For a given parameter set, these are obtained from numerical solutions of the coupled differential equations given by Eq. I.2. In earlier work on anesthetic-induced traces (8), fits of the model to the experimental traces of Haseneder et al. (9) for long pulses of the anesthetics isoflurane and sevoflurane determined the parameters of the kinetic equations. For that (zero agonist) case, only three (A0R, A0O, and A0D) of the nine protein states are populated, so the model simplifies considerably. It was found that the data could be fit by the model in the absence of any contribution from branched desensitization, i.e., if the desensitized state is only accessed by linear desensitization from the open state (A0O A0D). On the other hand, if access to the desensitized state were restricted to occur only from the resting state (A0R A0D), then it was found that some of the basic qualitative features of the traces could not be reproduced. In the work presented here, an analogous result was found for the case of agonist-induced traces (without anesthetic); they could also be fit very well with no contribution from the branched desensitization pathway (regardless of ligation), using identical values of the subset of parameters shared by the two cases. Additionally, for both cases, incorporation of both branched and linear desensitization resulted in equally good fits, but with different parameter sets. However, to reproduce the features of all three cases considered here (anesthetic modulation of agonist-induced traces as well as anesthetic- and agonist-induced traces) over the broadest possible range of solute concentrations, it was necessary to include both the branched and linear desensitization pathways; it could not be achieved with linear desensitization alone.
The measured current is proportional to the fraction of protein in an open conformation, irrespective of ligation, i.e., to . Because the numerical solution of the kinetic equations (Eq. I.2) provides the complete protein state distribution and its time derivatives, it gives a complete snapshot of the probability distribution and of the rate of flow of probability among these states at any moment, and thus elucidates the predominant kinetic pathways followed under various agonist/anesthetic conditions, and the origins of many of the characteristics of the traces. For example, as will be discussed below, it indicates under which conditions the desensitized state is accessed through the branched or linear paths, and the pathway followed from the diliganded desensitized state A2D back to the unliganded resting state A0R upon washout at the end of a pulse of agonist.
Results
Three general types of current traces are considered: 1) anesthetic-induced (without agonist), 2) agonist-induced (without anesthetic), and 3) modification of agonist-induced traces by varying concentrations of anesthetic, either coapplied or continuously present. Because different researchers have studied GABAA receptors with a range of different subunit compositions, and using different electrophysiological methods, it is not surprising that published results differ substantially. We rely principally on a series of papers (9,11–15) that explored a broad range of concentrations both of agonist and of various inhalation anesthetics, including the very important case of anesthetic-induced traces. For a short pulse of agonist, they (and other groups) have also examined the effect of different modes of application of anesthetic: either coapplied with agonist or continuously present (13,16,17). Since predictions of bilayer-mediated and binding models of agonist effects differ substantially at extremely high agonist concentrations cag, we consider particularly the results of Mercik et al. (18), who explored this range of concentrations. A set of parameter values (Table 1) was determined that reproduces the features of all of these data. The predicted traces for each of the three general cases are considered sequentially. For each, the results are described for different ranges of concentrations, and for each concentration range, an overview of the kinetic underpinnings (the flow of protein probability) is described. This is complemented by animation software, provided in the Supporting Material, that dynamically illustrates the time-dependent flow of probability among all protein states in the kinetic scheme. It is run interactively, allowing the user to vary agonist concentration, anesthetic concentration, and pulse duration.
Anesthetic-induced currents
Fig. 1 a provides the response to a long (1.5 s) pulse of isoflurane for different values of anesthetic concentration can as predicted by the model using the parameters listed in Table 1. These traces can be compared with the results of Haseneder et al. (9), who studied the activation of recombinant α2β2γ2L GABAA receptors in response to a 1.5 s pulse of the volatile anesthetics isoflurane and sevoflurane, each over a wide range of can. The features of the experimental traces are well reproduced by the model: specifically 1) the onset of the pulse and approach to equilibrium, and 2) the deactivation following the end of the pulse (i.e., upon washout of anesthetic).
Figure 1.
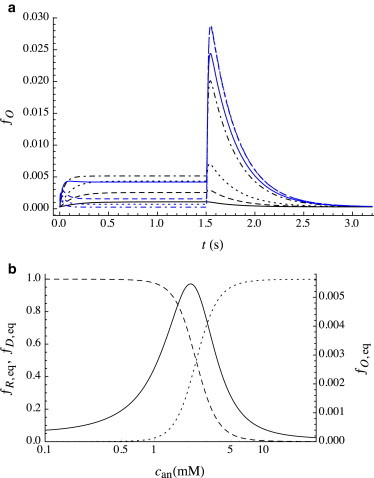
(a) Predicted open fraction ƒO(t) for a 1.5 s pulse of anesthetic for a wide range of concentrations: can = 0.5 mM (black solid line), 1.0 mM (black dashed line), 1.5 mM (black dotted line), 2.5 mM (black dot-dashed line), 3.0 mM (blue solid line), 5.0 mM (blue dashed line), 7.5 mM (blue dotted line), and 15.0 mM (blue dot-dashed line). (b) Equilibrium conformational distribution as a function of anesthetic concentration can: ƒO,eq (solid line), ƒR,eq (dashed line), and ƒD,eq (dotted line). Note the different scales for ƒO,eq (right ordinate) and for ƒR,eq and ƒD,eq (left ordinate). The shape of the distribution results from the increase in G(R) and the decrease in G(D) relative to G(O) upon bilayer adsorption of anesthetic. A key feature is the prediction of a very steep decrease in ƒO,eq after its maximum (i.e., for can > can,max ≈ 2 mM) as observed experimentally (9), which is inconsistent with a mechanism based on anesthetic binding to a channel-blocking site. To see this figure in color, go online.
Onset of pulse
As discussed in detail by Cantor et al. (8), at low can the open fraction rises monotonically and slowly to its equilibrium value ƒO,eq(can). With increasing can, both the rate of the initial rise and the value of ƒO,eq increase, with ƒO,eq reaching a maximal value at concentration can,max that is roughly an order of magnitude larger than the clinical concentration of isoflurane. For can > can,max, the initial rise in current continues to accelerate but the approach to the equilibrium value is no longer monotonic, with the value of ƒO,eq decreasing rapidly with increasing can; nearly to zero at roughly 5can,max, as shown in Fig. 1 b.
This latter observation is very important, as this precipitous drop in over only a fivefold increase in concentration is completely inconsistent with a “blocking” mechanism, i.e., the binding of the anesthetic to a putative site that blocks the flow of ions through the channel. In addition, the rate of acceleration of the initial rise with increasing can is also far greater than would be predicted by a simple binding model. Haseneder et al. (9) and Hapfelmeier et al. (13) modeled these current traces by including a kinetic step of binding to a site that blocks ion flow through the channel, but a comparison of predicted and experimental equilibrium currents at can = 15 mM in Figs. 4a and 6b in Haseneder et al. (9) shows that the agreement is poor at the highest concentrations.
Even for this relatively simple case (no agonist), the flow of protein probability is complex. Initially, almost all of the protein is in the resting state, with extremely low rate constants (and thus negligibly slow kinetics) of the conformational transitions to either the open or desensitized state; both are of order 10−3 s−1. Upon introduction of anesthetic in the aqueous phase (assuming rapid solution exchange), equilibration with the bilayer occurs on a timescale of order (koff,an + cankon,an)−1. The predicted desorption rate constant for isoflurane is high enough (koff,an = 320 s−1) that the approach to adsorption equilibrium is essentially complete in less than 10 ms. Because the values of αan,R→O = −9.1 and αan,R→D = −14.4 are negative, anesthetic adsorption significantly accelerates both opening (A0R → A0O) and branched desensitization (A0R → A0D), but to a far greater extent for the latter than the former. Except at high can, which is considered below, the increase in these transition rate constants from their values in the absence of anesthetic to their equilibrium values at can is essentially complete before the resulting flow of protein probability has begun, so the two conformational transitions occur essentially under the influence of the rate constants at equilibrium adsorption. For the reverse processes (A0D → A0R and A0O → A0R), since the magnitudes of both αan,O→R (= −2.5) and αan,D→R (= +3.3) are relatively small, the rate constants of both of these reverse processes change far less upon adsorption of anesthetic than do the rate constants for A0R → A0D and A0R → A0O. The equilibrium thus shifts from the resting state toward both the open and desensitized states, but unequally, increasingly favoring the desensitized state at higher can. With increasing can, the increase in results in the development of a small current, but the concomitant, and far larger increase in causes an increasing fraction of protein to go directly to the desensitized state.
As can reaches and exceeds can,max, branched desensitization becomes so rapid that it competes with adsorption, and thus the flow of protein probability begins before has reached its equilibrium value. The result is that the initial flow into the open state over the first few milliseconds generates an open fraction the exceeds its equilibrium value: the ultimate rise of to its equilibrium value reduces ƒR nearly to zero, inducing a net flow from A0O to A0D via the A0R state, i.e., A0O → A0R → A0D. The timescale of flow through these two sequential steps is determined by the slower rate constant (). Because αan,O→R < 0, increases with can, and the decrease of current (after it passes through its maximum near the beginning of the pulse) to its equilibrium value occurs more rapidly with increasing can.
Deactivation
As observed experimentally, a “rebound” current is predicted to occur within a few tenths of a second upon washout, the magnitude of which (unlike the equilibrium reached during the pulse) increases monotonically with increasing can; it approaches a maximum at concentrations not much higher than can,max. The rapid washout of anesthetic (on the submillisecond timescale) causes desorption of anesthetic from the bilayer, which occurs on the timescale of a few milliseconds (koff,an = 320 s−1) as discussed above. At lower levels of bilayer adsorption, the conformational transition rate constants are sufficiently low that they occur on a much slower timescale than anesthetic desorption, and thus the relaxation back to the zero-absorption equilibrium is well described as occurring under the influence of the standard (zero-absorption) rate constants . For low can, ƒD,eq is small, so the dominant process upon washout is A0O → A0R, and there is thus no rebound peak. At higher can, an increasing fraction of protein is in the A0D state at the end of the pulse, and it is the return from A0D to A0R via A0O, i.e., A0D → A0O → A0R, that is responsible for the rebound current. Because (≈85 s−1) >> (≈3.8 s−1), the dominant path out of the A0D state is directly to A0R, so even if all the protein is in the A0D state at the beginning of washout, the rebound peak remains small (ƒO ≈ 0.03). The height of the rebound peak thus varies with ƒD,eq, which in turn is a very strong function of can, as shown in Fig. 1 b. The peak in the rebound is reached in a time determined by the rate of depletion of A0D: as ƒD drops and ƒO rises, the rate of the A0D → A0O step decreases compared with A0O → A0R, and the subsequent decay of the rebound peak occurs on a timescale determined by ≈ 2.8 s−1.
Agonist-induced currents
Current traces evoked by a long pulse of agonist have been obtained experimentally for GABAA receptors, although generally only for a limited range of agonist concentrations. Although the details vary among experimental groups, the dependence of the qualitative features of these traces on cag are reasonably consistent and are reproduced by the predicted traces as shown in Fig. 2. Since Kd,R (the agonist dissociation constant for the resting state) varies widely among GABAA receptor isoforms, values of cag are expressed in terms of Kd,R. These features are described below, for progressively higher cag; they are readily interpreted in the context of our kinetic model.
Figure 2.
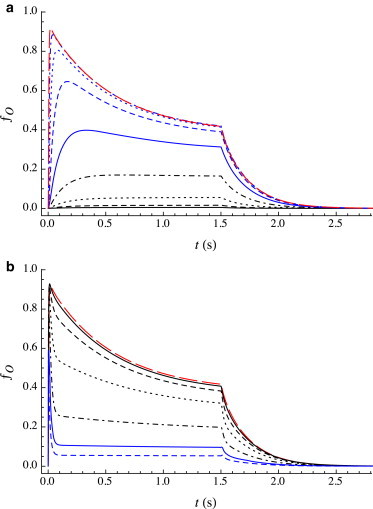
Predicted open fraction ƒO(t) for a 1.5 s pulse of agonist over a wide range of concentrations (expressed relative to Kd,R = 167 μM) in equal multiplicative increments of 101/3 = 2.154. (a) cag/Kd,R = 0.01 (black line), 0.02154 (black dashed line), 0.04642 (black dotted line), 0.1 (black dot-dashed line), 0.2154 (blue line), 0.4642 (blue dashed line), 1 (blue dotted line), 2.154 (blue dot-dashed line), and 4.642 (red long dashed line). (b) cag/Kd,R = 4.642 (red long dashed line), 10 (black line), 21.54 (black dashed line), 46.42 (black dotted line), 100 (black dot-dashed line), 215.4 (blue line), 464.2 (blue dashed line), and 1000 (blue dotted line). To see this figure in color, go online.
Very low cag
Note first that the binding affinity is predicted to be more than two orders of magnitude weaker for the R state than for either the O or D states. Upon agonist binding, the O state is kinetically favored ( or ), but the D state is thermodynamically favored (Kd,D < Kd,O ≪ Kd,R). Currents begin to be observed for cag ∼10Kd,O. For sufficiently low cag (∼50Kd,O) such that the current reaches no more than perhaps 20% of its maximum value, little functional desensitization is observed: ƒO rises monotonically and slowly to its steady-state value. This plateau arises from sequential kinetics: upon binding of the first agonist molecule to the R state (A0R + A → A1R), the subsequent shift in conformational distribution toward the desensitized state is essentially entirely a slow transfer in two parts: A1R → A2O → A2D. (The direct path from R to D, branched desensitization, is sufficiently slow that it makes no appreciable contribution.) The predominant path for the first part (A1R → A2O) depends on the details of the parameter values, and can favor either A1R + A → A1O + A → A2O or A1R + A → A2R → A2O.
Note that although ƒO reaches its steady-state value within ∼0.5 s, the system has not yet reached equilibrium. Because the rate constants of linear desensitization and resensitization are both small, the net transfer from A1R to A2D is slow. Thus, it takes far longer to attain the equilibrium values of the fractions of protein in all nine of the conformational/ligation states than it does to reach the steady-state current.
cag∼ Kd,R
Slow desensitization begins to be observed on a single timescale as cag is increased (but still sufficiently less than Kd,R such that the peak current is well below its maximum value). The extent of desensitization increases with cag, correlating with an increase in the fraction in the open state at its peak. With increasing cag, as the value of the peak current reaches its maximum, desensitization remains slow and well approximated by a single exponential. Over this range of concentrations, the observed desensitization is entirely a result of a transition from the O to the D state, predominantly in the diliganded form at higher cag. Also, with increasing cag the peak current is reached increasingly rapidly, indicating that binding of a pair of ligands to the R state (rather than the subsequent A2R → A2O step) remains rate-limiting.
Deactivation is complex. At the end of the pulse, almost all of the protein is in either the A2O or A2D states; we consider their fates separately. A2O is straightforward: the dominant path is A2O → A2R → 2A + R. A2D is more complex: unbinding of the first ligand (A2D → A + A1D) is predicted to dominate both of the conformational transitions (A2D → A2O or A2D → A2R), whereas A1D undergoes both further ligand unbinding and A1D → A1O (→ A1R) at competitive rates. As a result, although the decay of is approximately exponential, rises through a small maximum and then decays (more slowly), so that ƒO(t) is not well fit by a single exponential during deactivation.
cag> Kd,R
An initial fast component of functional desensitization is observed, the extent of which increases with cag at values well in excess of Kd,R. The subsequent slow desensitization has time constant similar to that observed at lower cag. In the context of our model, the decrease in ƒO associated with the fast component of desensitization is not caused by an increase in ƒD, but rather by a shift in the A2R A2O equilibrium back from the open to the resting state, i.e., an increase in ƒR. This reequilibration results from bilayer adsorption of agonist, which alters the rate constants of opening and closing unequally: opening is slowed (αag,R→O ≈ 6) with little effect on closing (αag,O→R ≈ −1). At these saturating concentrations of agonist, the adsorption-induced changes in rate constants occur on a timescale that is significantly slower than the rapid initial rise to the peak current, which follows the sequential mechanism 2A + R → A + AR → A2R A2O. The timescale of binding is of order (cagkb,R)−1, whereas the timescale of equilibration of the final pair of reversible opening/closing steps is of order . Thus, for cag < , binding is rate-limiting, whereas for cag > , channel opening is rate-limiting. So, in this concentration range (particularly at higher cag) the formation of the peak occurs in a few milliseconds, which is an order of magnitude faster than the predicted timescale of equilibration of agonist adsorption: (koff,ag + cagkon,ag)−1 ≈ koff,ag−1 = 0.025 s. The peak current is thus reached before effects of adsorption become significant.
For many GABAA receptors, the timescale of the slow component of functional desensitization has been observed to remain fairly independent of cag (4,5,15) even as cag is raised to values at which significant fast desensitization occurs (resulting, in the context of our kinetic model, from bilayer adsorption of agonist). The rate of slow desensitization is determined by kslowdes = . Because both of these rate constants are little changed from their standard values, the corresponding sensitivities, αag,O→D and αag,D→O, must be zero, or nearly so. In other words, the part of the free energy landscape connecting the O and D states is unaffected by agonist adsorption.
Deactivation is more complex than at the somewhat lower concentrations described in the previous section (binding saturation, but without adsorption) because of the modulation of rate constants during the first few hundredths of a second of washout, as agonist desorbs from the bilayer: this is the origin of the steep initial decay.
cag >> Kd,R
Adsorption of agonist to the bilayer occurs on a timescale (cagkon,ag)−1. At extremely high values of cag, significant adsorption thus occurs before equilibration of A2R and A2O. Since adsorption of agonist slows the A2R → A2O transition (while slightly accelerating the A2O → A2R transition) the equilibrium shifts toward the closed state, and the peak open fraction thus decreases with increasing cag. The onset of this effect has been observed by various groups that have explored current traces at high cag (4,15), but most strikingly by Mercik et al. (18) who obtained traces in response to agonist concentration in the 10 to 100 mM range. This mechanism also predicts the observed reduction in the equilibrium open fraction ƒO,eq (i.e., after slow desensitization is complete).
Anesthetic modulation of agonist-induced currents
The effect of anesthetics on the response to a pulse of agonist of duration τ has most commonly been explored in one of two general protocols: coapplication of the two solutes (i.e., can = 0 for t < 0 and t > τ) or in the continuous presence of anesthetic at concentration can, i.e., before, during and after the agonist pulse. Predicted traces of both types are considered next.
Coapplied anesthetic
Various concentration ranges of agonist and the anesthetic isoflurane (as well as sevoflurane, xenon and nitrous oxide) have been explored (11–14,19).
For the very low agonist concentrations discussed in the section “Very low cag” above (i.e., for which the peak current is no more than 20% or so of the maximum, and the current rises monotonically to its steady-state value), coapplication of the anesthetic isoflurane has multiple effects, as shown in Fig. 3 a for cag = Kd,R/10 = 16.7 μM. As can is increased, the peak current increases and is reached more rapidly, and slow desensitization begins to be observed. At this low agonist concentration, the maximum in the peak current occurs at can ∼ 0.75 mM. With further increase in can, the peak current drops but continues to be reached more rapidly; the extent and rate of desensitization are predicted to increase as well. By can ≈ 5 mM, the desensitization has become extremely fast. As was the case for the anesthetic-only traces described earlier, a rebound current upon washout is predicted. This overall behavior agrees with observations for isoflurane (11) and sevoflurane (14).
Figure 3.
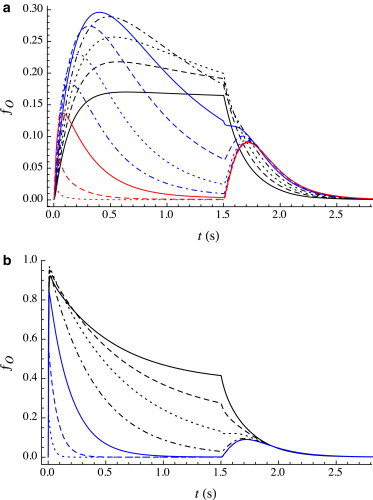
Predicted open fraction ƒO(t) for a 1.5 s pulse of coapplied agonist and isoflurane. (a) cag = 0.1Kd,R = 16.7 μM; can = 0 mM (black line), 0.15 mM (black dashed line), 0.3 mM (black dotted line), 0.5 mM (black dot-dashed line), 0.75 mM (blue line), 1.0 mM (blue dashed line), 1.25 mM (blue dotted line), 1.6 mM (blue dot-dashed line), 2.2 mM (red line), 3 mM (red dashed line), and 5 mM (red dotted line). (b) cag = 6Kd,R = 1.0 mM; can = 0 mM (black line), 0.2 mM (black dashed line), 0.7 mM (black dotted line), 1.6 mM (black dot-dashed line), 3 mM (blue line), 6 mM (blue dashed line), and 15 mM (blue dotted line). To see this figure in color, go online.
The acceleration to the peak and initial increase in its magnitude arise largely from the rapid increase in with increasing can. At higher can, the decrease in the peak is due largely to the enormous acceleration of branched desensitization (A2R → A2D), whereas the increase in extent of desensitization arises largely from the very positive value of αan,D→O, which shifts the A2O A2D equilibrium toward the D state.
At higher cag corresponding to binding saturation (cag > Kd,R), an example of which is shown in Fig. 3 b, the effect of increasing can is predicted to differ somewhat from its effect at lower cag. The can-dependence of the rebound current is similar to what is predicted at subsaturating cag. Both the rate and the extent of desensitization increase with can; the peak open fraction, which is large at low can, decreases significantly at sufficiently high can. Although two of the effects of the increasing can—the increased extent of desensitization and decreased initial peak—agree with observations for isoflurane and sevoflurane (11,14), the shape of the predicted desensitization differs significantly from some of the experimental traces. For example, in the experimental traces in Fig. 1 in Neumahr et al. (11), and Fig. 3 in Hapfelmeier et al. (14), increasing can results in growth of a fast initial component to desensitization, but does not significantly alter the time constant of slow desensitization. In contrast, the model does not predict the appearance of a fast component but predicts a gradual acceleration in the overall rate of desensitization. We note that other experimental results are in closer agreement to the predictions of our model; for example, a study on isoflurane effects on GABA channels in crayfish (20) does exhibit a gradual increase in the rate of desensitization with increasing can, at cag = 10 mM, without the development of a fast component.
Given these differences, it is important to consider the origin of the predicted acceleration in desensitization, i.e., in the net flow of probability from A2O to A2D. It arises because anesthetic adsorption shifts the predominant pathway from direct (A2O → A2D) to indirect (A2O A2R → A2D.) Consider the indirect pathway: at low can, is small, and the prior quasi-equilibrium of the two opposing faster steps A2O A2R strongly favors A2O, so the overall rate constant for the indirect pathway is ≈ .03 s−1, i.e., it makes negligible contribution to desensitization. So, in the absence of anesthetic adsorption, desensitization is governed by the direct route, since . Adsorption of anesthetic results in acceleration of A2R → A2D (αR→D = −14.4) and A2R → A2O (although to a lesser degree; αR→O = −9.1), the net effect of which is an increase in that ultimately exceeds kdirect, the indirect route thus becoming the dominant pathway of desensitization.
Fig. 4 compares traces evoked by coapplied agonist and isoflurane at extremely high can (= 15 mM) as a function of cag. The size of the rebound peak increases from ∼0.03 at cag = 0 to ∼0.09 at cag = 5 μM and remains at this value with increasing can. This increase in peak height occurs over a narrow range of very low (submicromolar) concentrations. The peak shape, and the concentration at which its height increases (∼0.1 μM) is in agreement with experimental traces, as seen in Fig. 3B in Hapfelmeier et al. (12). However, the magnitude of the predicted increase in the rebound peak is significantly less than observed experimentally.
Figure 4.
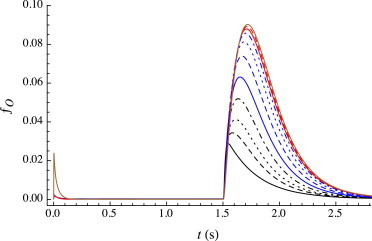
Predicted open fraction ƒO(t) for a 1.5 s pulse of coapplied agonist and isoflurane; all at the same extremely high anesthetic concentration (can = 15 mM) but with varying (extremely low) agonist concentrations: cag = 0 μM (black line), 0.02 μM (black dashed line), 0.04 μM (black dotted line), 0.08 μM (black dot-dashed line), 0.15 μM (blue line), 0.3 μM (blue dashed line), 0.6 μM (blue dotted line), 1.25 μM (blue dot-dashed line), 2.5 μM (red line), 5 μM (red dashed line), and 100 μM (brown line). The rebound peak reaches its maximum at ∼5 μM. As is evident in the predicted trace at cag = 100 μM, an initial peak current is predicted to develop (with no effect on the rebound) and continues to grow as cag is further increased (not shown), as observed experimentally (e.g., see Fig. 3B in 12). To see this figure in color, go online.
This growth of the rebound peak is readily understood in the context of the model. At the end of the pulse, virtually all of the protein is in the D conformation. For cag < Kd,R, it is predominantly unliganded, whereas for cag > Kd,R, it is diliganded. Regardless of ligation, anesthetic desorption occurs on a faster timescale (koff,an = 320 s−1) than either agonist dissociation or conformational transitions from the AiD state. The path back from AiD to A0R thus occurs largely under the influence of the standard rate constants. For the unliganded case (as discussed earlier for anesthetic-induced traces), upon washout, the path back from A0D to A0R is predominantly via the direct route, because , and thus the rebound peak is small (ƒO,peak ≈ 0.03). However, for the diliganded case the other processes dominate, because is so small. The higher value of ƒO,peak (≈0.09) arises largely from two routes to the open state: A2D → A2O and A2D → A1D + A → A1O. The peak remains small in absolute terms, however, because other paths from A2D to A0R that do not involve the open state still prevail overall, largely through A2D → A1D + A → A1R + A → A0R + 2A, or A2D → A0D + 2A → A0R + 2A. The timescale of the decay is determined largely from the closing transitions AiO → AiR; because there are significant contributions from all three ligation states (i = 0, 1, 2), with rate constants spread from 2.8 s−1 to 26.7 s−1, the decay is not well fit by a single exponential.
Continuous application of anesthetic
All the cases discussed above involve coapplication of anesthetic with agonist during the pulse. However, it is important to examine as well the effect of the continuous presence of an anesthetic (i.e., before, during and after the agonist pulse) on the response of GABAA receptors to a very short pulse of agonist at saturating concentrations. Aside from providing an additional test of the model, the latter protocol far more closely mimics the effect of anesthetics on inhibitory postsynaptic currents. Two general trends are typically observed for volatile anesthetics such as isoflurane (13,16,17; R. Haseneder, unpublished data) although the details vary significantly with GABAA subunit composition (17). With increasing isoflurane concentration 1) the initial peak current remains approximately constant up to clinical concentrations (MAC), beyond which it drops rapidly, and 2) the timescale of deactivation lengthens, even at very low can, reaching a maximum at ∼1 mM ≈ 3 MAC (17,21). These two trends have opposing effects on the total ion flow Q (integrated current), which thus rises from its value in the absence of anesthetic to a maximum at supraclinical concentrations and decreases thereafter (21). Traces predicted from the kinetic model are shown in Fig. 5 a for a short pulse at saturating cag, over a broad range of anesthetic concentrations. The total ion flow relative to its value in the absence of anesthetic, Q(can)/Q(0) is graphed in Fig. 5 b, along with the value of the peak open fraction relative to its value in the absence of anesthetic, ƒO,peak(can)/ƒO,peak(0). In good agreement with the experimental results cited above, the slowing of deactivation is already evident at clinical concentrations of anesthetic. The total ion flow thus rises with can, increasing by a factor of two at can ≈ 1 mM, although the peak current is beginning to decrease. With further increase in can, the peak current drops dramatically. In the context of the model, the reduction in peak current results from the anesthetic-induced shift in the equilibrium between the A0R and A0D states (prior to the agonist pulse) as evident in Fig. 1 b. In the range of roughly 1 to 2 mM, although the peak current is reduced, the total ion flow is still larger than in the absence of anesthetic.
Figure 5.
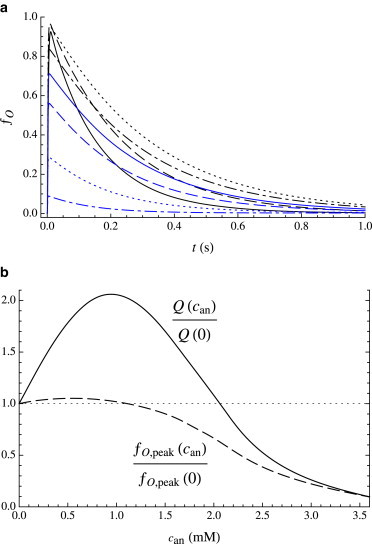
(a) Response to a short pulse (10 ms) of agonist (cag = 10Kd,R = 1.67 mM), for varying continuous concentration of anesthetic: can = 0 (black line), 0.3 mM (black dashed line), 0.9 mM (black dotted line), 1.5 mM (black dot-dashed line), 1.8 mM (blue line), 2.1 mM (blue dashed line), 2.7 mM (blue dotted line), and 3.6 mM (blue dot-dashed line). (b) Solid curve, Q(can)/Q(0): dependence of total ion flow (integrated current) on can, relative to total ion flow for can = 0. Dashed curve, ƒO,peak(can)/ƒO,peak(0): dependence of peak open fraction on can, relative to peak open fraction for can = 0. To see this figure in color, go online.
Discussion
Approximations
The effect of solute adsorption on the free energy landscape is modeled using two simplistic approximations. In the Langmuir approximation, the partitioning between the aqueous and bilayer phases is quantified by treating the bilayer essentially as a single (effectively two-dimensional) unstructured layer onto which solutes adsorb, with adsorbed molecules interacting only through excluded volume. The quality of this approximation is likely to worsen with increasing surface densities, both because solutes may adsorb over a range of depths in the bilayer, with different kinetic and thermodynamic characteristics, and because there may be strong interactions among adsorbed solutes. The second approximation is that the effect on the free energy landscape of an adsorbed solute is linear in its surface density (Eq. 1), which may be inaccurate if adsorption alters the physical properties of the bilayer itself. Although valid at low adsorption, both of these approximations are likely to become increasingly inaccurate at high levels of adsorption. Unfortunately, it is not yet possible to improve on these approximations, because relevant experimental data (such as the bilayer adsorption isotherm of each solute) are not presently available.
Parameter set
The parameters were chosen to reproduce reasonably well a broad range of electrophysiological traces. Although we found no evidence of any other set of parameters that could provide such broad qualitative agreement, a comprehensive search to eliminate such possibilities would be virtually impossible. However, the important conclusion is that it is indeed possible to reproduce the full range of features of these traces using this model, and that some of the key parameters, such as koff,ag and koff,an, are directly related to model-independent experimental measurements, and could thus serve as a definitive test of the model. Although the values of bilayer desorption rate constants for isoflurane and GABA have not been reported, the predicted values, koff,isoflurane ≈ 320 and koff,GABA ≈ 40, certainly fall in the range (10 to 1000 s−1) of the compounds for which transport-limited desorption rate constants have been obtained or estimated, as discussed elsewhere (10).
It is useful to examine patterns among the values of the predicted sensitivities, αs,X→Y. For three of the six transitions (O→D, O→R, and D→R) the magnitudes of the sensitivities are very small, both for agonist and anesthetic. On the other hand, the sensitivities are of large magnitude for both R→O and R→D, although of opposite signs for the two solutes: negative for isoflurane and positive for GABA. Only for αs,D→O, is there a significant difference in the magnitude for agonist and anesthetic. These correlations could perhaps be interpreted if it were known which bilayer property might be responsible for coupling of bilayer composition to changes in protein free energy, and how that property depends on the identity of the adsorbed solute. If agonist and anesthetic have closely related effects on this property (although perhaps to a different degree per mole fraction of solute in the bilayer), then the values of the sensitivities might be expected to scale by a single multiplicative constant. For example, it has been suggested (22,23) that it is the depth-dependent distribution of lateral pressures within the bilayer that couples to the protein free energy landscape. Anesthetics reside predominantly near the aqueous interfaces, where they increase lateral pressures, resulting largely from excluded volume effects, and thus decrease lateral pressures in the bilayer interior; this results in an increase in lipid area and a decrease in bilayer thickness. If, when adsorbed to the bilayer surface, agonists such as GABA or glycine interact principally through electrostatics and hydrogen bonds to lipid head groups, they may well reduce inter-head group repulsions, and thus reduce the lateral pressure in that region. If so, then the effects of anesthetics and agonist on the free energy landscape would be expected to have opposite signs, resulting in opposite signs of αag,X→Y and αan,X→Y, as predicted in the kinetic analysis.
In light of the relatively large number of parameters in our kinetic model, it is useful to consider the minimum number of parameters that would be required for the alternative approach, i.e., a direct binding kinetic scheme, in which both anesthetic and agonist interact with the receptor only by binding to specific sites. As noted earlier, 14 of the 28 parameters in our model—four ligand unbinding/binding and 10 standard rate constants of conformational transitions—depend only on the protein and the binding of its agonist, and would thus need to be specified for any three-state model of receptors that includes both linear and branched desensitization. Inclusion of additional conformational states in the scheme—necessary to reproduce key features of agonist-induced traces, such as multiple timescales of desensitization—would require a minimum of five more parameters per additional state, without yet having considered the effects of anesthetics. Even for the simplest case in which an anesthetic binds only to a single site on the receptor, specification of a minimum of 12 additional rate constants would be required for the three-state system (26 parameters, total) and 20 additional constants for the four-state system (34, total) as illustrated by the representative scheme in Fig. S3. However, even the latter would almost certainly be insufficiently robust to account either for agonist-only behavior, or for its modulation by anesthetics, for two reasons. First, as discussed in the introduction, kinetic models of agonist-induced currents (2–7) have typically required two additional desensitizated states (and often additional open states) to reproduce experimental traces. Second, anesthetics are known to affect current traces over a significantly larger range of concentrations than can be accounted for by a single binding site, so any truly comprehensive binding model would require multiple anesthetic binding site(s) of significantly different affinities; the same can be argued for agonist as well. The total number of parameters for a binding model that could account for the full range of features of agonist-induced, anesthetic-induced and anesthetic modulation of agonist-induced traces would thus be vastly in excess of the 28 required in our kinetic model.
What can be concluded from this study of the kinetic mechanism of volatile anesthetic modulation of ion channel activity? Recent studies (24) have indeed identified various locations in which an inhalation (desflurane) and an intravenous (propofol) anesthetic have co-crystallized with prokaryotic members of the pLGIC family, generally interpreted as providing strong support in favor of a direct binding mechanism of their anesthetic action. However, binding affinities (and thus their potential relevance to anesthesia) have not been measured for these sites. More generally, identification of such sites doesn’t rationalize the Meyer-Overton correlation over the remarkably broad range of molecular characteristics (size, polarity, shape, flexibility, etc.) of inhalation anesthetics or its well-known exceptions. With regard to these exceptions—most notably the lack of anesthetic potency of nonimmobilizers—it should be noted that results of the essential negative control experiment, co-crystallization of the receptor with a nonimmobilizer, have not been reported. Additionally, within the context of a binding model, it seems difficult to explain the remarkably narrow range of sensitivities to a given anesthetic within the human population: what is the essential process imitated by anesthetics with such minimal molecular specificity that generates such enormous selection pressure? One plausible idea that has been suggested (25) is that the small cavities ubiquitous to many membrane proteins may be essential to facilitate conformational changes that involve (for example) motions of adjacent alpha helices in transmembrane bundles; by occupying these sites, which could presumably accommodate a wide range of small molecules, anesthetics could impede these motions and thereby influence protein function. However, at least for GABAA receptors, the effect of anesthetics in electrophysiological studies, as modeled in this work, is to accelerate conformational transitions, as has been discussed elsewhere (8). Also, although this suggestion could certainly account for the breadth of molecular characteristics among anesthetics, it does not rationalize the Meyer-Overton correlation of anesthetic potency with bilayer partitioning, if the sizes and shapes of these cavities are not critical for endogenous function.
In any case, no kinetic model in which agonist and anesthetics interact with receptors entirely through binding to localized sites, has yet been proposed that can reproduce the full range of effects of anesthetics (over a broad range of anesthetic and agonist concentrations) on electrophysiological traces; this is not surprising in the context of the above discussion. By contrast, the kinetic model discussed in this article can not only reproduce the diverse features of electrophysiological traces (and does so with only three protein conformational states) but involves key parameters that can be determined through model-independent experimental measurements. And as discussed elsewhere (10), in the context of the bilayer lateral pressure profile it not only explains the Meyer-Overton correlation but it correctly predicts known exceptions, such as the cutoff in potency in long-chain n-alkanols (26), and predicted the anesthetic potency of long-chain polyhydric alkanols—unexpected in the context of a binding model, given the very large volume of those compounds—that was subsequently demonstrated experimentally (27). Finally, since details of temporal modulation of receptor activity—desensitization and deactivation—appear to be important (or perhaps even essential) for proper protein function, if these characteristics result from (nonspecific) adsorption of neurotransmitter to the bilayer, then the model provides a plausible explanation of the strong apparent selection pressure for correct anesthetic sensitivity (10,28), and predicted that noncognate neurotransmitters would significantly modulate receptor activity, as subsequently demonstrated experimentally (29).
Author Contributions
Both D.K.L. and D.J.A. developed software, contributed to model development, and performed extensive kinetic analysis. R.S.C. designed the model, developed software, performed kinetic modeling and analysis, and wrote this article.
Acknowledgments
We thank Jim Sonner for provocative discussions and many valuable suggestions.
Supporting Material
References
- 1.Jones M.V., Westbrook G.L. Desensitized states prolong GABAA channel responses to brief agonist pulses. Neuron. 1995;15:181–191. doi: 10.1016/0896-6273(95)90075-6. [DOI] [PubMed] [Google Scholar]
- 2.Burkat P.M., Yang J., Gingrich K.J. Dominant gating governing transient GABA(A) receptor activity: a first latency and Po/o analysis. J. Neurosci. 2001;21:7026–7036. doi: 10.1523/JNEUROSCI.21-18-07026.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Celentano J.J., Hawkes A.G. Use of the covariance matrix in directly fitting kinetic parameters: application to GABAA receptors. Biophys. J. 2004;87:276–294. doi: 10.1529/biophysj.103.036632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Celentano J.J., Wong R.K. Multiphasic desensitization of the GABAA receptor in outside-out patches. Biophys. J. 1994;66:1039–1050. doi: 10.1016/S0006-3495(94)80885-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Haas K.F., Macdonald R.L. GABAA receptor subunit gamma2 and delta subtypes confer unique kinetic properties on recombinant GABAA receptor currents in mouse fibroblasts. J. Physiol. 1999;514:27–45. doi: 10.1111/j.1469-7793.1999.027af.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lema G.M.C., Auerbach A. Modes and models of GABAA receptor gating. J. Physiol. 2006;572:183–200. doi: 10.1113/jphysiol.2005.099093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Milescu L.S., Akk G., Sachs F. Maximum likelihood estimation of ion channel kinetics from macroscopic currents. Biophys. J. 2005;88:2494–2515. doi: 10.1529/biophysj.104.053256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cantor R.S., Twyman K., Haseneder R. A kinetic model of ion channel electrophysiology: bilayer-mediated effects of agonists and anesthetics on protein conformational transitions. Soft Matter. 2009;5:3266–3278. [Google Scholar]
- 9.Haseneder R., Rammes G., Hapfelmeier G. GABAA receptor activation and open-channel block by volatile anaesthetics: a new principle of receptor modulation? Eur. J. Pharmacol. 2002;451:43–50. doi: 10.1016/s0014-2999(02)02194-5. [DOI] [PubMed] [Google Scholar]
- 10.Sonner J.M., Cantor R.S. Molecular mechanisms of drug action: an emerging view. Annu. Rev. Biophys. 2013;42:143–167. doi: 10.1146/annurev-biophys-083012-130341. [DOI] [PubMed] [Google Scholar]
- 11.Neumahr S., Hapfelmeier G., Kochs E. Dual action of isoflurane on the γ-aminobutyric acid (GABA)-mediated currents through recombinant α1β2γ2L-GABAA-receptor channels. Anesth. Analg. 2000;90:1184–1190. doi: 10.1097/00000539-200005000-00035. [DOI] [PubMed] [Google Scholar]
- 12.Hapfelmeier G., Haseneder R., Zieglgänsberger W. Coadministered nitrous oxide enhances the effect of isoflurane on GABAergic transmission by an increase in open-channel block. J. Pharmacol. Exp. Ther. 2001;298:201–208. [PubMed] [Google Scholar]
- 13.Hapfelmeier G., Haseneder R., Zieglgänsberger W. Isoflurane slows inactivation kinetics of rat recombinant α1β2γ2L GABAA receptors: enhancement of GABAergic transmission despite an open-channel block. Neurosci. Lett. 2001;307:97–100. doi: 10.1016/s0304-3940(01)01950-4. [DOI] [PubMed] [Google Scholar]
- 14.Hapfelmeier G., Schneck H., Kochs E. Sevoflurane potentiates and blocks GABA-induced currents through recombinant α1β2γ2 GABAA receptors: implications for an enhanced GABAergic transmission. Eur. J. Anaesthesiol. 2001;18:377–383. doi: 10.1046/j.0265-0215.2001.00848.x. [DOI] [PubMed] [Google Scholar]
- 15.Krampfl K., Bufler J., Adelsberger H. Desensitization characteristics of rat recombinant GABAA receptors consisting of α1β2γ2S and α1β2 subunits expressed in HEK293 cells. Neurosci. Lett. 2000;278:21–24. doi: 10.1016/s0304-3940(99)00888-5. [DOI] [PubMed] [Google Scholar]
- 16.Jones M.V., Harrison N.L. Effects of volatile anesthetics on the kinetics of inhibitory postsynaptic currents in cultured rat hippocampal neurons. J. Neurophysiol. 1993;70:1339–1349. doi: 10.1152/jn.1993.70.4.1339. [DOI] [PubMed] [Google Scholar]
- 17.Benkwitz C., Banks M.I., Pearce R.A. Influence of GABAA receptor γ2 splice variants on receptor kinetics and isoflurane modulation. Anesthesiology. 2004;101:924–936. doi: 10.1097/00000542-200410000-00018. [DOI] [PubMed] [Google Scholar]
- 18.Mercik K., Zarnowska E.D., Mozrzymas J.W. Saturation and self-inhibition of rat hippocampal GABAA receptors at high GABA concentrations. Eur. J. Neurosci. 2002;16:2253–2259. doi: 10.1046/j.1460-9568.2002.02307.x. [DOI] [PubMed] [Google Scholar]
- 19.Hapfelmeier G., Zieglgänsberger W., Kochs E. Nitrous oxide and xenon increase the efficacy of GABA at recombinant mammalian GABAA receptors. Anesth. Analg. 2000;91:1542–1549. doi: 10.1097/00000539-200012000-00045. [DOI] [PubMed] [Google Scholar]
- 20.Adelsberger H., Wilde J., Dudel J. Multiple mechanisms of block by the anesthetic isoflurane of a γ-aminobutyric acid activated chloride channel in crayfish. J. Comp. Physiol. A Neuroethol. Sens. Neural Behav. Physiol. 1998;182:51–58. doi: 10.1007/s003590050157. [DOI] [PubMed] [Google Scholar]
- 21.Banks M.I., Pearce R.A. Dual actions of volatile anesthetics on GABAA IPSCs. Anesthesiology. 1999;90:120–134. doi: 10.1097/00000542-199901000-00018. [DOI] [PubMed] [Google Scholar]
- 22.Cantor R.S. The lateral pressure profile in membranes: a physical mechanism of general anesthesia. Biochemistry. 1997;36:2339–2344. doi: 10.1021/bi9627323. [DOI] [PubMed] [Google Scholar]
- 23.Cantor R.S. The influence of membrane lateral pressures on simple geometric models of protein conformational equilibria. Chem. Phys. Lipids. 1999;101:45–56. doi: 10.1016/s0009-3084(99)00054-7. [DOI] [PubMed] [Google Scholar]
- 24.Nury H., Van Renterghem C., Corringer P.-J. X-ray structures of general anaesthetics bound to a pentameric ligand-gated ion channel. Nature. 2011;469:428–431. doi: 10.1038/nature09647. [DOI] [PubMed] [Google Scholar]
- 25.Eckenhoff R.G. Why can all of biology be anesthetized? Anesth. Analg. 2008;107:859–861. doi: 10.1213/ane.0b013e31817ee7ee. [DOI] [PubMed] [Google Scholar]
- 26.Cantor R.S. Breaking the Meyer-Overton rule: predicted effects of varying stiffness and interfacial activity on the intrinsic potency of anesthetics. Biophys. J. 2001;80:2284–2297. doi: 10.1016/S0006-3495(01)76200-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mohr J.T., Gribble G.W., Cantor R.S. Anesthetic potency of two novel synthetic polyhydric alkanols longer than the n-alkanol cutoff: evidence for a bilayer-mediated mechanism of anesthesia? J. Med. Chem. 2005;48:4172–4176. doi: 10.1021/jm049459k. [DOI] [PubMed] [Google Scholar]
- 28.Cantor R.S. Receptor desensitization by neurotransmitters in membranes: are neurotransmitters the endogenous anesthetics? Biochemistry. 2003;42:11891–11897. doi: 10.1021/bi034534z. [DOI] [PubMed] [Google Scholar]
- 29.Milutinovic P.S., Yang L., Sonner J.M. Anesthetic-like modulation of a γ-aminobutyric acid type A, strychnine-sensitive glycine, and N-methyl-d-aspartate receptors by coreleased neurotransmitters. Anesth. Analg. 2007;105:386–392. doi: 10.1213/01.ane.0000267258.17197.7d. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


