Measurement of Subcellular Force Generation in Neurons

Abstract

Forces are important for neuronal outgrowth during the initial wiring of the nervous system and after trauma, yet subcellular force generation over the microtubule-rich region at the rear of the growth cone and along the axon has never, to our knowledge, been directly measured. Because previous studies have indicated microtubule polymerization and the microtubule-associated proteins Kinesin-1 and dynein all generate forces that push microtubules forward, a major question is whether the net forces in these regions are contractile or expansive. A challenge in addressing this is that measuring local subcellular force generation is difficult. Here we develop an analytical mathematical model that describes the relationship between unequal subcellular forces arranged in series within the neuron and the net overall tension measured externally. Using force-calibrated towing needles to measure and apply forces, in combination with docked mitochondria to monitor subcellular strain, we then directly measure force generation over the rear of the growth cone and along the axon of chick sensory neurons. We find the rear of the growth cone generates 2.0 nN of contractile force, the axon generates 0.6 nN of contractile force, and that the net overall tension generated by the neuron is 1.3 nN. This work suggests that the forward bulk flow of the cytoskeletal framework that occurs during axonal elongation and growth-cone pauses arises because strong contractile forces in the rear of the growth cone pull material forward.

Introduction

Axonal elongation is the process by which neurons send out long cellular projections during embryonic development (1) and regeneration following trauma (2). Given the poor prognosis associated with spinal cord injury or nerve damage (3,4), there is a strong need to develop more effective therapeutics (5). Forces are among the most effective known stimuli for promoting axonal elongation. For example, axons can be stretched at a rate of up to 8 mm/day in response to applied forces, a rate that is ∼8× faster than typical elongation rates (6,7). Yet, to our knowledge, the quantitative profile of subcellular force generation in neurons in the microtubule-rich region at the rear of the growth cone and along the axon has never been directly measured. Our work is motivated by the shared idea that if we develop a better understanding of neuronal mechanics (8,9), then the methods to promote axonal regeneration will follow (10).

Growing neurons are composed of four main regions: a neuronal cell body where >95% of proteins are synthesized; a long axon that transmits information and material; shorter dendrites that later form synaptic contacts; and the growth cone at the tip. Inside neurons is a dense meshwork of cytoskeletal proteins and embedded organelles. The two most important cytoskeletal proteins involved in axonal elongation are actin filaments and microtubules (8). Actin is found along the length of the axon in a cortical meshwork that lies under the plasma membrane and is enriched in the peripheral domain (P-domain) of the growth cone. It is particularly important for modulating the rate of axonal elongation and controlling the direction that growth cones move. Microtubules are at a high density in the central domain (C-domain) of the growth cone and in the center of the axon. They are also involved in axonal guidance and their normal activity is critical for axonal elongation (1,11).

A major question has been whether long microtubules advance during elongation as the result of microtubule translocation or assembly (12). Our approach to answering this has been to track the motion of mitochondria stably docked to the cytoskeletal meshwork (13,14). Mitochondria are large organelles that can be easily visualized in low light conditions using the fluorescent dye MitoTracker (Life Technologies, Grand Island, NY). After kinesin and dynein motor-driven fast transport at a rate of ∼3600 μm/h (15), mitochondria stably dock for hours to microtubules, actin filaments, and intermediate/neuronal filaments (16–19). As a means to test whether docked mitochondria track the motion of the axonal cytoskeletal meshwork, we have conducted experiments where we measured the movement of docked mitochondria, large 1-μm polystyrene beads bound to the outside of axons and axonal branch points (20). Along the axon, docked mitochondria slowly move forward with a velocity profile that increases with distance from the cell body at a rate between 0 and 50 μm/h. Because this movement occurs at a rate ∼100 times slower than fast transport, it is straightforward to distinguish between this movement and fast axonal transport in kymographs (14). For both the beads and branch points, we found these markers advanced in the same pattern as docked mitochondria. Combined with other studies, this indicates that axons elongate by bulk advance of the cytoskeletal meshwork in vivo (21), in cultured neurons from chicken, rat, and Drosophila (14,21,22) and in response to forces generated in or applied to the growth cone (20,23).

The observation of bulk movement raises the question of how it arises. Classic studies (24–26) paired with more recent work (27,28) have demonstrated that growth cones pull and contractile forces are generated at the leading edge of the growth cone in the actin-rich peripheral domain. Nonetheless, a major question that has never been directly addressed is whether net pulling or pushing forces are generated at the rear of the growth cone over the microtubule-rich region and/or along the axon. We recently reported that the microtubule-associated protein dynein generates forces that push material in neurons forward in bulk (13). In addition, Kinesin-1 has been demonstrated to drive microtubule sliding from the neuronal cell body (29). Likewise, because microtubule assembly generates a pushing force (30), it seems very reasonable that the net forces generated in these regions are expansive. Nonetheless, the C-domain of the growth cone (31,32) and the axon (33) both contain an organized actin cytoskeleton. In light of this complexity, it is difficult to predict whether: 1) the net forces generated at the rear of the growth cone push or pull, or 2) the tension observed along the axon (34,35) arises because contractile forces are generated locally in the axon, or 3) strong contractile forces generated in growth-cone P-domain are transmitted to the axon along the cytoskeletal continuum.

Here we start with an analysis of the subcellular movement profile of material along the axon at steady-state force balance to address the fundamental question of whether neurons are inherently viscoelastic solids (9,34,36,37) or fluids (23). (For an excellent introduction to cell mechanics, see Janmey et al. (38) and Howard (39).) In our experiments, we find a continuous flow of material at a steady rate when the position of the growth cone and the tension generated by the neuron are constant. This suggests the axon is a fluid, and that strong contractile forces pulling material forward are generated in the microtubule-rich region at the rear of the growth cone. To test if forces are generated specifically along the axon, we disrupt the neuronal attachment to the substrate, using trypsin, while tracking subcellular movement. We find that contraction occurs along the axon, which suggests weaker net contractile forces are generated along the axon. This suggests that axons are not simply passive fluids; rather, they are active fluids that generate internal forces. Based on these experimental observations, we create a theoretical framework for discussing how unequal forces act in series in the context of active fluids. Led by the modeling, we develop an approach to measuring subcellular force generation we call “force balance rheology”. It is unique in that it does not require a priori knowledge of the cellular viscoelastic properties. With it, we make direct measurements of subcellular force generation in neurons, and find that strong contractile forces are generated in the rear of the growth cone and weaker contractile forces are generated along the axon.

Materials and Methods

Cell culture

Chick sensory neurons were isolated as previous described in Lamoureux et al. (20) from embryonic day 10–11 embryos obtained from the Michigan State University Poultry Farm. Dorsal root ganglia were removed from the spinal cord and placed in L-15 medium, pH 7.1, made from powder (Item No. 41300039; Life Technologies). After excess tissue was removed with forceps, the ganglia were placed in 0.25% trypsin for 8–10 min at 37°C and allowed to settle to the bottom of tube. The trypsin solution was then removed, replaced with supplemented L-15, and triturated slowly until the tissue had dispersed into a homogenous solution. This was then dripped into substrate-coated culture dishes containing supplemented L-15 media. L-15 is supplemented with 0.6% glucose, 1 mM glutamine, 100 U/mL penicillin, 136 μg/mL streptomycin sulfate, 10% fetal calf serum, 50 ng/mL 7S nerve growth factor (Harlan Bioproducts, Indianapolis, IN), and N9 growth supplement (20). Neurons were grown in plastic dishes (35-mm cell culture dishes, Model No. 430165; Corning, Tewksbury, MA) coated with 0.01% PO solution for 1 h at room temperature, rinsed 3× with sterile dH₂O, and incubated with 250 ng/mL laminin at 37°C for 1 h. Unless otherwise noted, reagents were purchased from Sigma (St. Louis, MO).

Force-calibrated towing needles are used to measure neuronal stress

For our experiments, towing needles were made on a P-97 Flaming/Brown micropipette puller (Sutter Instrument, Novato, CA) and manually calibrated as described in Lamoureux et al. (40). Before use, the towing needle was coated by dipping in a 0.01% poly-ornithine solution for a half-hour, then dipped in 1 mg/mL Concanavalin A solution for a half-hour. Once an appropriately oriented axonal candidate was located on the dish, a calibrated needle and a reference needle, held together in a double needle holder (Esselte Leitz, Stuttgart, Germany), were brought into the viewing field with a hydraulic micromanipulator (Narishige International, East Meadow, NY). After zero-distance images were captured, the coated needle was brought in contact with the active growth cone. A small push across the dish to displace the growth cone from its present attachments begins the process of attaching the growth cone to the calibrated needle. Once the growth cone has become attached to the coated needle, it is lifted off the substrate and given a little more time to firmly attach to the needle. Then it is brought down near the dish to achieve a better plane of focus and the time-lapse imaging is begun with 10-s intervals capturing both phase and florescent images at 40× magnification. At the end of the assay, after the growth cone is detached from the needle, a set of images is captured to verify the calibration of the towing needle.

Mitochondrial imaging

Mitochondria were labeled and imaged as described in Lamoureux et al. (20) with 0.1 μM MitoTracker Red CMXRos (Life Technologies), incubated for 2 min, and recovered in fresh L-15 for 2 h. Cultures were maintained in a ringcubator device to warm the dish to 37°C on the stage of a DM IRB inverted microscope and observed with an N Plan L 40×/0.55 corrPh2 with an adjustable collar infinity/0–2/c objective (Leica Microsystems, Buffalo Grove, IL). Cells were illuminated with a 100 W Xenon lamp attenuated 98% with neutral density filters through a Texas Red cube (Chroma Technology, Rockingham, VT) for visualization of MitoTracker. On the Leica DM IRB, transmitted light exposure was controlled with a VMM-D3 controller and CS25 shutter (Vincent Associates; Rochester, NY). Fluorescent light exposure was controlled with a Lambda 10-C (Sutter Instruments). The software MICRO-MANAGER (Vale Lab, University of California-San Francisco, San Francisco, CA) was used to control the shutters and camera (Orca-ER charge-coupled device camera, Model No. CA742-95; Hamamatsu, Hamamatsu City, Japan). Exposure times were set between 100 and 200 ms. Docked mitochondrial velocities were measured by changes in position over 10–30 min intervals on the kymographs and plotted against their initial position along the axon in relation to the growth cone using the software IMAGEJ (National Institutes of Health, Bethesda, MD).

Trypsin application experiments

After a 10-min baseline period, with image capture occurring in 5- or 10-s intervals, trypsin was added to the dish at a final concentration of 0.5%.

Results

Axons are viscous fluids, even at rest

A fundamental question, when considering how to measure and interpret the profile of subcellular force generation, is whether to treat the cell as a viscoelastic solid or as a fluid. This has a major impact on the underlying mathematics needed to model the problem, as well as the experimental design needed to assess forces. An important consideration is the timescale of the observation. For an ideal viscoelastic Maxwell fluid, when force is instantaneously applied it behaves as solid and the viscous properties (η) can be ignored. In contrast, when a constant force is applied, the elastic properties are negligible and the material behavior approaches that of a fluid. In considering solid models (e.g., the standard linear model or the Poynting-Thomson model (41,42)), at very short timescales materials act as pure solids, at intermediate times there is flow in response to force where both viscosity and elasticity must be considered, and over long timescales the material behaves again as a solid. For both viscoelastic fluid and solid models, the parameter that determines if the timescale of observation is short, intermediate, or long is the viscoelastic relaxation time constant (τ). This is defined as the ratio of the viscosity over the Young’s modulus (i.e., τ = η/E). (For a nuanced discussion of effects of timescale on various mechanical models, see Karato (42).) For cells, τ is typically estimated to be ∼10 s (27,43).

Neurons have been extensively modeled as a solid (9,34,36,37,44,45) based on the observation that, like a spring, they support a static rest-tension that does not dissipate over periods of minutes to hours. Here “rest tension” is defined as the level of tension that is generated internally by the neuron and is typically constant over time. Nonetheless, it is also well established that neurons elongate at a constant rate in response to a constant high force. Thus, neurons in some ways act like a solid and in other ways like a fluid. To directly test if axons are solids or fluids over long time periods, we asked the simple question of whether material along the axon is stationary or if there is a subcellular flow when axonal length and neuronal rest tension are constant over time. On the one hand, if points along the axon were stationary, it would indicate that neurons are inherently viscoelastic solids; on the other, the observation of flow under a constant force would suggest they are fluids.

To measure forces, we used micromanipulators to place force-calibrated towing needles in front of growth cones (40). We then allowed the growth cone to adhere to the tip of the needle and then lifted it up from the substrate (Fig. 1 A). After a period of 30–60 min to allow neurons to come to steady state, the endogenous forces were estimated by measuring the deflection of the needle (Fig. 1 B). From a total of 23 neurons, we found the mean externally measured steady-state rest tension F_SS to be 1.3 nN ± 0.3 (mean ± 95% confidence interval (CI)) (1 nN = 100 μdyne). In all cases, the neurons pulled the towing needle toward the cell body. Consistent with many prior studies, this indicates that the net forces generated in neurons are contractile, and relatively constant over time (9,23–25,34,46).

Figure 1.

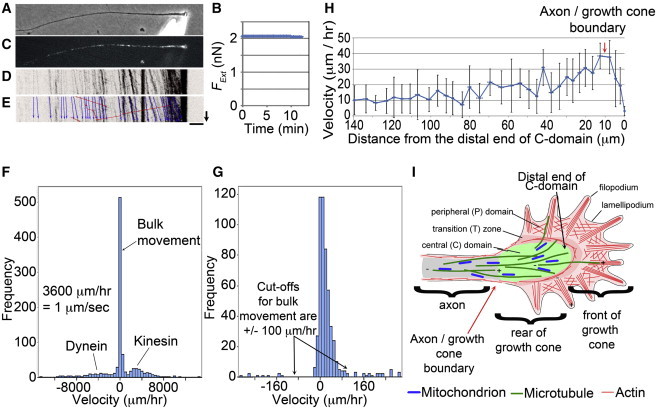
Neurons are fluids that generate strong contractile forces in the growth cone. (A) Phase image of a chick sensory neuron attached to a force-calibrated glass towing needle. (B) Plot of the external force over time. (C) The distribution of mitochondria labeled with MitoTracker (Life Technologies). (D) A color-inverted kymograph of mitochondrial position over 12 min. (E) The kymograph from (D) was duplicated, with docked mitochondria (blue arrows) and fast transported mitochondria (red arrows). (Black arrow, 5 min; bar, 10 μm.) (F) The velocity distribution for all of the mitochondria. This graph spans the range between 15,000 and −15,000 μm/h; each bin is 500 μm/h wide and the tall bin in the center spans the range from 250 to −250 μm/h. (G) The velocity distribution of docked mitochondria. This graph spans the range between 300 and −300 μm/h, with each bin covering a 10 μm/h velocity range and the central bin spanning 5 to −5 μm/h. (H) Docked mitochondria move forward with a velocity profile that increases along the axon. (Red arrow) Boundary between the axon and growth cone; error bars are 95% CI. (I) Cartoon of a neuron showing the boundary between the axon and growth cone; adapted with permission from Suter and Miller (8). To see this figure in color, go online.

To determine whether the cytoskeletal framework flows or is stationary at steady-state rest tension, we acquired time-lapse images of mitochondria labeled with MitoTracker (Fig. 1 C) and converted these to kymographs (Fig. 1 D). As previously described in Roossien et al. (13), we used the movement of docked mitochondria as fiduciary markers for the bulk movement of the cytoskeletal meshwork. Here we classified a mitochondrion as docked if it moved at a velocity between 100 and −100 μm/h. To illustrate this, the kymograph in Fig. 1 D was duplicated and blue lines were drawn over docked mitochondria and red lines over fast transported mitochondria (Fig. 1 E). In total, we measured the velocities of 934 mitochondria in 23 neurons. Of these, 278 mitochondria moved toward the growth cone at a velocity >100 μm/h and 165 moved toward the cell body at a velocity <−100 μm/h. We classified these respectively as being transported by kinesin via fast anterograde transport and by dynein via fast retrograde transport. In addition, there were 491 mitochondria that moved at a velocity between −100 and 100 μm/h. We classified these as moving by bulk transport. A summary of these data are shown binned in Fig. 1 F. The average velocities for fast anterograde, fast retrograde, and bulk transport were 2808 ± 168, −3875 ± 595, and 17 ± 1.5 μm/h (average ± 95% CI), respectively. In terms of the units commonly used for fast transport, these values are 0.8 ± 0.1, −1.1 ± 0.2, and 0.005 ± 0.0004 μm/s (average ± 95% CI).

These values are consistent with previous studies that characterized fast and bulk transport of mitochondria in neurons (14,47). To more closely examine the distribution of docked mitochondrial movement, we rebinned the data over the range of 300 to −300 μm/h (Fig. 1 G). From this graph, it is clear that there is bias in the movement toward the growth cone that corresponds with an average movement of 17 ± 1.5 μm/h for the docked mitochondria noted above. This is consistent with our previous studies that have indicated that in addition to fast transport, there is a bulk forward movement of docked mitochondria in neurons (13,14,20,21). Plotting the motion of the docked mitochondria as a function of distance from the growth cone, we found they moved forward in a velocity gradient that increased along the axon (Fig. 1 H). Because this movement occurred under conditions where axonal length and neuronal rest tension were constant over tens of minutes, the data suggest that the axon is a fluid.

The presence of flow implies underlying forces. Based on the pattern of flow, it is possible to make a few limited inferences with regard to the subcellular pattern of force generation. Examining the velocity profile closely, we found the velocity of docked mitochondria movement increases along the axon to a region ∼7–12 μm from the distal end of growth-cone C-domain and then decreases in velocity (red arrow, Fig. 1, H and I). Considering that mitochondria are excluded from the actin-rich region at the front of the growth cone, this pattern indicates that there is a constant contraction over the microtubule-rich region at the rear of the growth cone (where mitochondria are found) paired with stretching of the axon. Because neurons as a whole generate tension, these data qualitatively suggest that contractile forces are generated in the growth cone but leave open the question of what is occurring in terms of local force generation along the axon.

Axons generate weak contractile forces

The forward flow of the cytoskeletal meshwork along the axon, seen at steady-state force balance, could occur for one of three reasons: the axon could be stretched passively as the result of strong growth-cone contraction; expansive forces along the axon could assist the pull of the growth cone; or strong contractile forces in the growth cone could overcome weak contractile forces in the axon. The challenge in distinguishing among these is that because there is a mechanical continuum among the axon, the growth cone, and the substrate, contractile forces generated in the growth cone that pull the substrate rearwards also generate an equal and opposite force that pulls the axon forward. To remove the complication of this reaction force, we treated neurons with trypsin to disrupt adhesions between the neuron and the substrate (48). The underlying rationale here is that when attachments to the external environment are severed, local flow will arise from local forces. We then monitored subcellular strain along the axon. In total, we conducted 31 experiments and observed 43 axons.

Overall, we found 13 were minimally affected, while another 12 were caused to retract to approximately half their original length. The remaining 18 retracted completely or near completely back to their cell body over a 30–60 min period. In all cases where the growth cone retracted, either partially or completely, contraction occurred along the axon (Fig. 2). This seems to exclude the possibility that the dominant forces generated along the axon are expansive; if they were, the distances between points along the axon would increase over time. Instead, the data are consistent with previous studies that have suggested that contractile forces are generated in the axon (24,34).

Figure 2.

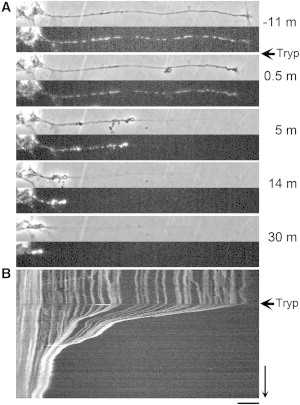
Contractile forces are generated along the axon. (A) Chick sensory neurons labeled with MitoTracker (Life Technologies) were observed in phase and fluorescence for ∼10 min and trypsin was bath-applied (denoted by ←Tryp). At 0.5 min after application, the growth cone starts to collapse. By 5 min, it is evident that the distances between axonal mitochondria decrease and buckling occurs along the entire axon. (B) The kymograph shows the pattern of mitochondrial movement. (Bar, 20 μm; arrow, 10 min.)

Forces in series

While the total force generated by neurons has been extensively characterized (23,25,28,46,49), mapping subcellular force generation, even in nonneuronal cells (50–52), is a very challenging problem. A major issue is that very little has been done in terms of considering how forces add together when they are in series. As a case in point, it is well understood that when two springs are combined in parallel, the equivalent spring constant is equal to the sum of the individual spring constants. In contrast, when springs are arranged in series, the reciprocal of the equivalent spring constant is equal to the sum of the reciprocals of the individual spring constants. Likewise, when forces work in parallel, the net force measured externally is equal to the sum of the component forces. Yet in the context of cell mechanics, to the best of our knowledge, the net force produced by two unequal forces acting in series within a viscous fluid has never been discussed. To better understand this problem, we link the axon and the growth cone, each represented by a motor and a dashpot arranged in parallel, together in series with a spring that represents a force-calibrated towing needle that is used to both measure and control forces (Fig. 3). The motors represent the activity of molecular motors/cytoskeletal assembly and the dashpots account for the resistance to flow due to the composition of the cytoskeleton. While both the growth cone and axon are understood to be viscoelastic structures, in this study we are interested in the response of these neuronal compartments to forces on timescales longer than the respective viscoelastic relaxation constants (hence the absence of spring components in the axon and growth cone in this model).

Figure 3.

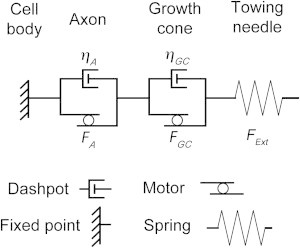
A motor-dashpot model of a neuron. The neuron is divided into three main sections: a stationary cell body, the axon, and the growth cone. The spring at the distal end represents the force-calibrated towing needle attached to the growth cone. Both the axon and growth-cone region are represented as a dashpot and motor in parallel, which represent viscosity and the net activity of molecular motors, respectively.

For the axon and growth cone together, the length is

$$L=L_A+L_{GC},$$ (1)

and the differential equation describing how this changes in time is

$$\frac{dL}{dt}=\frac{d{L}_A}{dt}+\frac{d{L}_{GC}}{dt}.$$ (2)

To determine the rate at which the axon changes in length, two forces are considered: the global tension in the system (F_Ext) as measured externally by the towing needle, and the local force generation in the axon (F_A). The rate of change in axonal length over time is

$$\frac{d{L}_A}{dt}=\frac{F_{\text{Ext}}-F_A}{{\eta }_A},$$ (3)

where η_A is the viscosity of the axon. The equation for the rate of expansion or contraction of the growth cone has the same form,

$$\frac{d{L}_{GC}}{dt}=\frac{F_{\text{Ext}}-F_{GC}}{{\eta }_{GC}},$$ (4)

where F_GC is the local force generation of the growth cone and η_GC is the viscosity of the growth cone. Linking Eqs. 2–4 gives the differential equation that describes the total length of the neuron:

$$\frac{dL}{dt}=\frac{F_{\text{Ext}}-F_A}{{\eta }_A}+\frac{F_{Ext}-F_{GC}}{{\eta }_{GC}}.$$ (5)

If the towing needle is unperturbed, over time both the total length of the neuron and the measured force approaches steady state. The value for the externally measured steady-state tension (F_SS) is called the “neuronal rest tension” in the literature, and it is experimentally defined as the force measured on a towing needle when the total length of the neuron is steady over time (53). To find the steady-state tension, we set dL/dt = 0 and F_Ext = F_SS and solve for F_SS,

$$F_{SS}=\frac{F_A{\eta }_{GC}+F_{GC}{\eta }_A}{{\eta }_A+{\eta }_{GC}},$$ (6)

which may be rewritten as

$$F_{SS}=F_A\frac{{\eta }_{GC}}{{\eta }_A+{\eta }_{GC}}+F_{GC}\frac{{\eta }_A}{{\eta }_A+{\eta }_{GC}}.$$ (7)

The final equation states that the externally measured force is a function of both the internally generated forces and the ratio of local viscosities. Under the simple case where viscosity is uniform, the external force is the mean of the local force generation. Likewise, when the local viscosity in a region approaches zero, the externally measured force approaches the local force generation of that region. This occurs because when the local viscosity in a region approaches zero, that dashpot no longer makes a contribution to the overall force balance. Thus the tension at that point in the series approaches the force generated at that point. Because the tension at all points in the system must be the same, F_SS approaches the local force in the softer region. To illustrate this, we have graphed out an example where we set the local force generation in the growth cone to be 2 nN and that of the axon to be 1 nN (Fig. 4). When viscosity of the axon is much less than the growth cone, the externally measured force approaches the force generated in the axon. In contrast, when the growth cone has a viscosity greatly lower than the axon, the reverse occurs. Thus, depending on the relative viscosities in the growth cone and axon, the force measured at the towing needle can be close to the force generated in the growth cone, the force generated along the axon, or the mean of the two forces. One aspect of this that is particularly interesting is that while the externally measured force is typically taken as a constant that reflects the inherent level of cellular force generation, this work suggests that externally measured force instead depends on the details of the subcellular profiles of viscosity and internal force generation.

Figure 4.

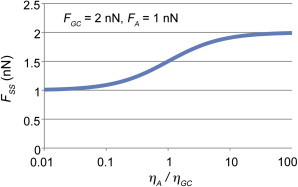
Externally measured overall tension depends on the relative levels of internal force generation and viscosity. When forces act in series, the measured external steady-state force is a function of relative local viscosity. Using Eq. 7, values of 2 and 1 nN were input as the levels of local force generation in the growth cone and axon. The ratio of viscosity in the axon and growth cone (η_A/η_GC) was then systematically varied and the externally measured steady-state net force (F_SS) was calculated. When η_A = η_GC, the measured force is equal to the mean of the local forces. In contrast, when η_A ≠ η_GC, the measured force approaches the local force in the less viscous region. To see this figure in color, go online.

A biophysical approach to measure force generation along the axon and in the growth cone

The development of this theoretical framework provided us with an important insight into how to measure force generation along the axon and in the rear of the growth cone. We noted that when the external force is balanced with the local force, a region neither expands nor contracts (Eqs. 2 and 3). This suggested local force may be estimated by systematically varying the applied external force while monitoring subcellular strain. When a local region is neither expanding nor contracting, it follows that the local force is equal to the external force. An advantage of this approach, which we call “force balance rheology” (because it examines rheological flow under conditions where external forces are balanced with local forces), is that it does not require knowledge of the cellular viscous or elastic properties; thus, concerns about the effects of prestress on viscoelastic parameters (54) can be addressed separately.

To put this into practice, growth cones were attached to force-calibrated towing needles (Fig. 5 A). The applied force was systematically varied and subcellular strain was monitored by tracking the movement of docked mitochondria (Fig. 5 B). Initially, a high tension was applied to the neuron by moving the towing needle forward rapidly for a couple of minutes. This created a large deflection of the needle and thus a large force. The neuron responded by stretching at a high rate along the axon and to a lesser degree over the most distal 10 μm (i.e., the region that we operationally defined as the rear of the growth cone in the previous section). As the growth cone moved forward, the deflection of the towing needle, and thus, the tension, decreased. In the kymograph (Fig. 5 C) we looked for the force range where the rate of docked mitochondrial advance at ∼10 μm from the towing needle (i.e., the axon/growth-cone boundary) matched the movement of the towing needle: note the parallel yellow arrows in the 30–40 min time range in Fig. 5 C. When the growth cone neither expanded nor contracted, we inferred that the local force generation was equal to the external force (i.e., F_GC = F_Ext, Fig. 5 D).

Figure 5.

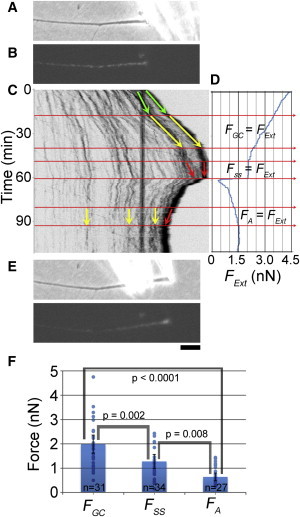
Direct measurement of subcellular force generation by force balance rheology. (A) Growth cones were attached to force-calibrated towing needles and the deflection of the needle was used to estimate force. (B) Docked mitochondria were tracked to monitor expansion and contraction along the axon and growth cone. (C) A kymograph used to track subcellular movement. (D) A graph of the externally measured force based on the bending of the towing needle. (E) A phase and fluorescent picture of the neuron at the end of the experiment (bar, 10 μm). (F) A graph of the measured forces. (Dots) Results from individual experiments. Error bars are 95% CI. To see this figure in color, go online.

As the growth cone continued to advance, the tension on the needle decreased further. When the net force generated in the neuron equaled the force on the towing needle, the growth cone stopped advancing. We note that while the growth cone was not advancing, mitochondria along the axon still moved forward as seen by the converging red lines between 50 and 60 min on the kymograph (Fig. 5 C). This indicates that the contractile force generation in the growth cone was greater than the contractile force generation along the axon. The point where the tension and the position of the growth cone are steady over time is defined as the externally measured steady-state rest tension F_SS (Fig. 5 D).

To measure the force generated along the axon, we decreased the tension on the needle by moving it back in a single step toward the neuronal cell body. This is observed as a large drop in tension at 60 min in Fig. 5 D. Because the tension on the needle was lower than the force generated by the neuron, the rear of the growth cone retracted and points along the axon contracted. As the growth cone moved back, the needle deflected and the force increased. As tension rose, there was a point at which the docked mitochondria along the length of the axon were stationary relative to the substrate. At this point the force generated along the axon is balanced by the force measured by the towing needle (i.e., F_A = F_Ext). During this time, we also note that the tip of the axon retracted and contraction occurred in the growth cone (red and yellow arrows at 90 min). This is consistent with the generation of strong contractile forces in the growth cone (F_GC > F_Ext). The tension level where docked mitochondria are stationary along the axon, we define as the value for axonal force generation F_A (Fig. 5 D).

Using this approach, we evaluated the force parameters for 34 neurons. In this data set, we found axonal force generation to be F_A = 0.6 ± 0.2 nN (mean ± 95% CI, n = 27); growth-cone force generation was F_GC = 2.0 ± 0.4 nN (mean ± 95% CI, n = 31); and the steady-state rest tension was F_SS = 1.3 ± 0.3 nN (mean ± 95% CI, n = 34) (Fig. 5 F). One-way ANOVA was conducted in MINITAB (Minitab Inc., State College, PA) to determine whether there were differences in the level of force generation among the axon, growth cone, and rest tension. We found a statistically significant difference between groups F(2, 89) = 20.12, p < 0.0001. Using post-hoc Tukey simultaneous tests for differences of means, we found significant differences between F_GC and F_SS (p = 0.002), F_A and F_SS (p = 0.008), and F_A and F_GC (p < 0.0001).

Because we are now able to measure the three forces (i.e., F_A, F_GC, and F_SS) directly, force balance rheology allows us to approximate the relationship between growth cone and axonal viscosity. We rewrite Eq. 7 so that the ratio of the viscosities r = η_A/η_GC is expressed as a function of these forces:

$$r=\frac{{\eta }_A}{{\eta }_{GC}}=\frac{F_A-F_{SS}}{F_{SS}-F_{GC}}.$$ (8)

Using our average measured values of these forces, we find r = 1, which implies the axon is as viscous as the rear of the growth cone in these neurons. This relationship is displayed in Fig. 6.

Figure 6.

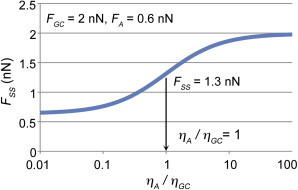
Force measurements can be used to determine the relative viscosities of subcellular regions. Inputting our measured values of F_GC and F_A into Eq. 7, the predicted steady-state force balance was plotted as a function of the relative viscosity of the axon and the growth cone. Our measured value for the steady-state force of 1.3 nN indicates that the ratio η_A/η_GC is 1. Within the bounds of experimental error, this suggests the axon has a viscosity similar to the rear of the growth cone. To see this figure in color, go online.

Discussion

It is well accepted that growth cones pull (24–27,55) and axons are under tension (9,24,34,46), and it is likewise clear that pushing forces are associated with microtubules (13,30,56,57). What has never been thoroughly analyzed or quantified is whether the net forces generated across the rear of the growth cone and along the axon are contractile or expansive. What makes this a particularly difficult question to answer, based on available information, is that both regions are rich in microtubules yet contain organized actin structures (i.e., rings, arcs, and the contractile node) (32,33). Here we develop equations and a method for analyzing and measuring subcellular force generation. The strength of our approach is that it gives a direct readout for local force generation without the requirement of inferring forces based on subcellular viscoelastic properties (27,50,51). Using it, we find that the net local forces generated in the rear of the growth cone and along the axon are contractile. Altogether, this suggests that the forward bulk flow of the cytoskeletal framework that occurs during axonal elongation occurs because strong contractile forces in the rear of the growth cone overcome weak contractile forces along the axon and thus pull the cytoskeletal framework forward.

A fundamental decision when modeling mechanics over time periods longer than the viscoelastic relaxation time coefficient (58) is whether to treat an object as a viscoelastic solid or fluid (39). For simple passive materials, it is easy to decide. If the material deforms at a constant rate in response to a force, it is a fluid; if it maintains its shape over time, it is a solid. Under low, moderate, or high forces, neurons respectively retract, maintain a constant length, or lengthen (36). Considering the axon as a passive material, the observation that neurons maintain a constant length under the influence of moderate forces over periods of minutes to hours suggests they are solids. Accordingly, axons have been extensively modeled as such (9,34,36,37,44). Our experiments are unique in that they are, to our knowledge, the first to directly monitor the subcellular strain gradient at steady-state rest tension. They reveal that when a neuron maintains a constant length under a constant force there is a constant expansion of the axon and constant contraction in the rear of the growth cone (Fig. 1). Based on our experimental observations here and prior studies that have visualized the movement of microtubules (59), docked mitochondria (14), and the morphology of growth cones in vivo (60), this provides an explanation for the increase in the size and complexity of growth cones during pauses at decision regions in the process of axonal path-finding. Thus, while neurons as a whole may at times appear to act like a solid (in the sense that total neuronal length is constant under an applied force), this behavior arises as the result of a complex pattern of subcellular flow (Figs. 1 and 2).

In the context of our data and prior studies that have proposed and demonstrated that forces are generated internally in the axon (9,24,34), we modeled both the growth cone and the axon as a motor and viscous dashpot in parallel (Fig. 3). Doing so led us to ask: when a weak force is generated along the axon and a strong force is generated at the growth cone, what is being measured in terms of total force at the towing needle? Starting from first principles we developed a one-dimensional set of differential equations to model this problem. We found that when the viscosity in two compartments is the same, the net force F_Ext is the mean of the two forces acting in series. Nonetheless, when the viscosity in two compartments is different the net force approaches the force generated in the less viscous of the two regions (Fig. 4). An important implication of this work is that measurement of total tension provides only a rough estimate of the mean forces in the cell. Furthermore, if one region of the cell is particularly compliant, the measurement will be biased toward the force generated in that region. This suggests that the externally measured level of cellular force generation should be interpreted with caution.

It is widely acknowledged that force generation and viscosity are heterogeneous in cells (50,51) and tissues (61). Yet mapping subcellular stress gradients and, in turn, patterns of subcellular force generation is an exceptionally challenging problem (62). The most sophisticated contemporary approaches (50,51) are to map external traction forces (63) and subcellular viscoelastic properties, then to model the cell as an isotropic homogenous solid (51) or fluid (27) and to use modeling to infer subcellular internal stress. A limitation is that this requires information about subcellular viscoelastic properties. And because prestress/force generation increases both viscosity and elasticity (64,65), this leads to the circular problem that accurate measurements of viscosity are needed to map forces, but accurate measurements of forces are needed to map viscosity. In considering the motor dashpot model (Fig. 3), a straightforward means to measure subcellular force generation that did not require knowledge of subcellular viscosity became apparent. That being when the externally measured force on the towing needle is equal and opposite to the local force generated in a region, that region will neither expand nor contract. We put this into practice by systematically varying the force applied to neurons using force-calibrated towing needles while monitoring subcellular strain using docked mitochondria (Fig. 5). When the local strain rate in a region is equal to zero, it follows that the local force generation is equal and opposite to the force measured by the towing needle. Using this, we found the mean levels of force generation to be 2.0 and 0.6 nN in the growth cone and axon, while the net steady-state tension was 1.3 nN. Because the net force was equivalent to the mean of the component forces, Eq. 7 suggests the viscosity of the growth cone and the axon are similar (Fig. 6). Given that unequal force generation in viscous fluids is a ubiquitous problem in cells and tissues, we see both a great need and potential for the application of these equations to diverse problems in cellular mechanics.

It is well accepted that growth cones pull and that axons are under tension (24–28,34,35). Likewise, it is equally clear that microtubule assembly and the microtubule-associated motors Kinesin-1 and dynein generate pushing forces (13,29,30). What has never been directly addressed is whether tension along the axon is generated as the result of local contractile forces or if it occurs as the result of the forward pull of the growth cone. Here, we find clear evidence indicating that contractile forces are generated in both the microtubule-rich region at the rear of the growth cone and along the axon. This in no way challenges the idea that pushing forces are associated with microtubules; instead, it indicates that there may be other microtubule-associated motors, such as Kinesin-12 and Kinesin-5 (66,67), that generate contractile forces on the microtubule array. Likewise, this raises the possibility that actin-based structures, such as arcs or the contractile node (31,32,68), could be generating high levels of tension in these subcellular regions. Because there are excellent pharmacological tools to disrupt non-muscle myosin II (69), dynein (70), and Kinesin-5 (71), we think it will be straightforward and interesting to utilize the approach we have developed here to directly test the subcellular contributions these proteins make to force generation and bulk transport in neurons.

At a biological level, this work provides a framework that explains why axons retract when they are detached from the substrate, why they elongate at a steady rate under high forces, and yet maintain a constant length in response to moderate forces. Likewise, it provides a biomechanical explanation for the observations that microtubules in Xenopus spinal cord neurons (59) and docked mitochondria in chick sensory neurons (14) move forward into the growth cone in bulk during growth-cone pauses; and for the enlargement of growth cones when they pause in vivo at decision points (60). More generally, the motor dashpot model provides a solution to the important problem in cell and tissue mechanics (72) of how to model cells or tissues that maintain their shape over time like a solid when unperturbed, yet deform and grow in response to high or low forces like a fluid.

Finally, we note that our findings that the rear of the growth cone and the axon are both fluids that generate internal force demonstrate that these regions behave like active matter (73). Because the actin-rich P-domain does as well (27), this indicates that the well-developed mathematics of active matter hydrodynamics can be applied to the neuron as a whole (73). We think this is exciting because it has the potential to lead to important insights into the mechanics of axonal elongation. Furthermore, our derivation of analytic equations that describe the behavior of unequal forces working in the context of a fluid could be integrated into active matter hydrodynamics. This would extend that theory in a way that would allow the modeling of more complex problems where the spatial distribution of force generation is heterogeneous.

Conclusions

Forces are critical for axonal elongation and growth-cone navigation, yet the global profile of subcellular force generation in neurons has never been described. In particular, it is unknown whether the microtubule-rich region at the rear of the growth cone and the axonal shaft generate the expansive forces that assist the forward pull of the P-domain of the growth cone or the contractile forces that oppose it. Here we first establish that neurons behave as viscous fluids under steady-state conditions. We then develop an analytic model that describes the relationship between the total force generated by a cell and unequal subcellular forces generated in series within active fluids. It indicates that overall tension measurements reflect the average level of subcellular force generation when the overall viscosity is relatively uniform. Using this model, we develop a technique for directly measuring subcellular force generation that does not require prior knowledge of viscosity. With it we find neurons generate weak contractile forces along the axon, strong contractile forces in the growth cone, and that the net force measured at the growth cone is close to the average of these two values. This provides definitive evidence that the net forces generated across the rear of the growth cone and along the axon are contractile. Together, the motor dashpot model of neurons we develop here paired with our experimental observations suggests that one reason growth cones enlarge when they pause at decision regions during growth-cone navigation in vivo is that strong contractile forces in the growth cone pull material from the axon forward. More generally, the theory and experimental techniques we develop have the potential to be important for understanding how the interaction between unequal forces shapes cells and tissues during development and in pathology.

Author Contributions

K.E.M. designed the research; P.L. performed the research; K.E.M., P.L., and M.O. analyzed the data; and K.E.M. and M.O. wrote the article.