Dominance Genetic Variation Contributes Little to the Missing Heritability for Human Complex Traits

Zhihong Zhu; Andrew Bakshi; Anna AE Vinkhuyzen; Gibran Hemani; Sang Hong Lee; Ilja M Nolte; Jana V van Vliet-Ostaptchouk; Harold Snieder; The LifeLines Cohort Study; Tonu Esko; Lili Milani; Reedik Mägi; Andres Metspalu; William G Hill; Bruce S Weir; Michael E Goddard; Peter M Visscher; Jian Yang

doi:10.1016/j.ajhg.2015.01.001

. 2015 Mar 5;96(3):377–385. doi: 10.1016/j.ajhg.2015.01.001

Dominance Genetic Variation Contributes Little to the Missing Heritability for Human Complex Traits

Zhihong Zhu ¹, Andrew Bakshi ¹, Anna AE Vinkhuyzen ¹, Gibran Hemani ^1,², Sang Hong Lee ¹, Ilja M Nolte ³, Jana V van Vliet-Ostaptchouk ^3,⁴, Harold Snieder ³; The LifeLines Cohort Study⁵, Tonu Esko ^6,^7,^8,⁹, Lili Milani ⁶, Reedik Mägi ⁶, Andres Metspalu ^6,¹⁰, William G Hill ¹¹, Bruce S Weir ¹², Michael E Goddard ^13,¹⁴, Peter M Visscher ^1,¹⁵, Jian Yang ^1,^15,^∗

PMCID: PMC4375616 PMID: 25683123

Abstract

For human complex traits, non-additive genetic variation has been invoked to explain “missing heritability,” but its discovery is often neglected in genome-wide association studies. Here we propose a method of using SNP data to partition and estimate the proportion of phenotypic variance attributed to additive and dominance genetic variation at all SNPs ( $h_{S N P}^{2}$ and $δ_{S N P}^{2}$ ) in unrelated individuals based on an orthogonal model where the estimate of $h_{S N P}^{2}$ is independent of that of $δ_{S N P}^{2}$ . With this method, we analyzed 79 quantitative traits in 6,715 unrelated European Americans. The estimate of $δ_{S N P}^{2}$ averaged across all the 79 quantitative traits was 0.03, approximately a fifth of that for additive variation (average $h_{S N P}^{2}$ = 0.15). There were a few traits that showed substantial estimates of $δ_{S N P}^{2}$ , none of which were replicated in a larger sample of 11,965 individuals. We further performed genome-wide association analyses of the 79 quantitative traits and detected SNPs with genome-wide significant dominance effects only at the ABO locus for factor VIII and von Willebrand factor. All these results suggest that dominance variation at common SNPs explains only a small fraction of phenotypic variation for human complex traits and contributes little to the missing narrow-sense heritability problem.

Introduction

Phenotypic variation of most traits related to human health (e.g., obesity and blood pressure) is due to many genes and their interplay with environmental factors.¹ These traits are called “complex traits” to differentiate them from Mendelian traits. In 1918, Fisher reconciled biometrical and Mendelian modeling of complex traits and partitioned total genetic variance into sources of variation due to additive, dominance (allelic interaction within locus), and epistatic (allelic interaction between loci) effects.² Fisher’s subsequent work predicted that for fitness and fitness-related traits, the amount of additive genetic variation in the population should be small because of natural selection.³ Yet despite nearly a century of theoretical and empirical work since 1918, the quantification and relative importance of non-additive genetic variation remains controversial. In humans, additive and non-additive variance components are usually estimated by comparing resemblance between close relatives, for example in twin studies, and there have been many efforts to estimate non-additive genetic variance in twin studies.^4–8 Such estimates, however, can be biased due to confounding with common environmental effects within families.

In theory, the total genetic variance can be partitioned into the variance components due to additive, dominance, additive-by-additive, additive-by-dominance, and dominance-by-dominance epistatic variation as well as many higher-order terms.^9,10 In practice, however, even with data from large pedigrees, it is difficult to estimate all these genetic variance components, not only because of the partial confounding in coefficients of relatedness for these genetic components but also because the coefficients for the higher-order epistatic variance are small and therefore the sampling errors of their estimates are large.¹¹ Further, theory shows that rather small proportions of non-additive variance due to dominance and multi-locus epistatic are expected to be found in outbred populations.^11,12

On the other hand, genome-wide association studies (GWASs) facilitated by high-throughput genotyping technologies have been enormously successful in identifying SNPs that are associated with complex traits.¹³ For most complex traits, however, a large portion of trait narrow-sense heritability (h²) remains unexplained, the so-called “missing heritability” problem.^14,15 SNP-trait associations are most often identified by fitting additive models so that phenotypic variation explained by the top associated SNPs in GWASs is per definition additive, and per definition h² does not include non-additive genetic variance. Hence, missing narrow-sense heritability appears not relevant to non-additive variation. However, it has been suggested that estimates of h² could be inflated in the presence of non-additive variation such as epistatic variation,^16,17 and highly non-additive models of biology appear consistent with the resemblance of relatives.¹⁷ Therefore, to place the findings from SNP discoveries in context, precise and unbiased partitioning of total genetic variance is required. In this study, we proposed a method of estimating dominance genetic variance by using genome-wide SNP data and applied the method in the analyses of 79 quantitative traits in humans.

Material and Methods

Statistical Models

In quantitative genetics theory,^2,9,10 additive (A) variance at a single locus is defined as the genetic variance explained by the regression of genotypic value (expected value of phenotypic mean in each genotypic class) on genotype, and dominance (D) variance is defined as the residual genetic variance that is not explained by the regression. Let a = (μ_BB – μ_AA) / 2 and d = μ_AB − (μ_AA + μ_BB) / 2 with μ_AA, μ_AB, and μ_BB being the phenotypic means in the three genotypic classes AA, AB, and BB, respectively. Under the assumption of Hardy-Weinberg equilibrium (HWE), additive variance ( $σ_{a}^{2}$ ) is 2p(1 – p)[a + (1 – 2p)d]², dominance variance ( $σ_{d}^{2}$ ) is [2p(1 – p)d]², and genotypic variance ( $σ_{g}^{2}$ ) is $σ_{a}^{2} + σ_{d}^{2}$ , with p being the frequency of allele B. Additive variance is the variance for the average effect of allele substitution,¹⁰ i.e., β = a + (1 – 2p)d, which contains a term due to dominance interaction between two alleles. Such difference between interaction and variance resulting from the interaction is a source of great confusion, not least in the discussion of the importance of epistatic interaction and epistatic variance.¹² Dominance variance is the variation in the deviations of the genotypic values from the regression. These definitions are consistent with the question we seek to ask, i.e., how much extra genetic variance can be explained by dominance variation on top of the A-only model. In GWASs, however, the analysis is often performed based on the model¹⁸

y = μ + x_{A} b_{A} + x_{D} b_{d} + e,

(Equation 1)

where y is the phenotypic value; μ is the mean term; x_A is coded as 0, 1, or 2 and x_D is coded as 0, 1, or 0 for the three genotypic classes AA, AB, and BB; and e is the residual, $e \sim N (0, σ_{e}^{2})$ . However, this model is not orthogonal because x_A and x_D are correlated, i.e., cov(x_A,x_D) = 2p(1 − p)(1 − 2p) under HWE. We cannot simply partition additive and dominance variance as var(x_Ab_A) and var(x_Db_D) because they do not add up to the total genetic variance, i.e., $var (x_{A} b_{A}) + var (x_{D} b_{D})$ $\neq var (x_{A} b_{A} + x_{D} b_{D})$ . In a multiple regression analysis of the A+D model, the true parameters of the regression coefficients are b_A = a and b_D = d, whereas in a simple regression analysis of the A-only model, b_A = a + (1 − 2p)d. We therefore re-parameterize Equation 1 as

y = μ + x_{A} β + x_{D}^{'} d + e

(Equation 2)

where β = a + (1 – 2p)d, which is the same as the regression coefficient of y on x_A in a GWAS based on the A-only model, and $x_{D}^{'}$ = 0, 2p, or (4p – 2) for genotypes AA, AB, or BB. This model is orthogonal because cov(x_A, x’_D) = 0, meaning that the estimate of β is independent of whether d is fitted in the model or not and vice versa, and the definitions of additive and dominance variances are exactly consistent with those defined in classical quantitative genetics, i.e., $σ_{a}^{2} = var (x_{A} β) = 2 p (1 - p) {[a + (1 - 2 p) d]}^{2}$ and $σ_{d}^{2} = var (x_{D}^{'} d) = {[2 p (1 - p) d]}^{2}$ with $σ_{a}^{2} + σ_{d}^{2} = σ_{g}^{2}$ .

Following the GREML approach¹⁹ we developed previously, we can fit dominance effects of all SNPs together as random effects in a mixed linear model, i.e.,

y = μ + \sum_{i} w_{A (i)} u_{A (i)} + \sum_{i} w_{D (i)} u_{D (i)} + e .

(Equation 3)

For a SNP i, $w_{A (i)} = (x_{A (i)} - 2 p_{i}) / \sqrt{2 p_{i} (1 - p_{i})}$ and $w_{D (i)} = (x_{D (i)}^{'} - 2 p_{i}^{2}) / [2 p_{i} (1 - p_{i})]$ , which are essentially the standardized forms of x_A and x_D because $E (x_{A})$ = 2p, $E (x_{D}^{'})$ = 2p², $var (x_{A})$ = 2p(1 – p), and $var (x_{D}^{'})$ = 4p²(1 – p)². u_A and u_D are additive and dominance effects (random effects) corresponding to the standardized genotype variables w_A and w_D, respectively. The SNP-based model can be transformed to an individual-based model as

y = μ + g_{A} + g_{D} + e,

(Equation 4)

where $g_{A} = \sum_{i} w_{A (i)} u_{A (i)}$ and $g_{D} = \sum_{i} w_{D (i)} u_{D (i)}$ , which can be defined as the genome-wide additive and dominance genetic values of an individual, respectively. Then, the phenotypic covariance between individuals j and k is $cov (y_{j}, y_{k}) = π_{A (j k)} σ_{A}^{2} + π_{D (j k)} σ_{D}^{2} + σ_{e}^{2}$ , where $σ_{A}^{2} = var (g_{A})$ , $σ_{D}^{2} = var (g_{D})$ , π_A(jk) and π_D(jk) are the additive and dominance genetic relationships between individuals j and k, respectively, and $σ_{e}^{2}$ is the residual variance. Using the method of equating the SNP-based model (Equation 3) to the individual-based model (Equation 4),¹⁹ we get

π_{A (j k)} = \frac{1}{m} \sum_{i} (w_{A (i j)} w_{A (i k)}) = \frac{1}{m} \sum_{i} \frac{(x_{A (i j)} - 2 p_{i}) (x_{A (i k)} - 2 p_{i})}{2 p_{i} (1 - p_{i})}

π_{D (j k)} = \frac{1}{m} \sum_{i} (w_{D (i j)} w_{D (i k)}) = \frac{1}{m} \sum_{i} \frac{(x_{D (i j)}^{'} - 2 p_{i}^{2}) (x_{D (i k)}^{'} - 2 p_{i}^{2})}{4 p_{i}^{2} {(1 - p_{i})}^{2}},

where m is the number of SNPs. Because $cov (x_{A}, x_{D}^{'}) = 0$ , the correlation between π_A and π_D is also expected to be zero, and therefore the estimates of $σ_{A}^{2}$ and $σ_{D}^{2}$ are independent in a sample of unrelated individuals. More generally, if there are fixed covariates such as principal components, we can re-write Equation 4 in matrix form as

y = Cb + g_{A} + g_{D} + e,

(Equation 5)

where y is a n × 1 vector of phenotypes of all the individuals, C is a n × c matrix of c covariates, b is a c × 1 vector of the effects of the covariates, g_A and g_D are n × 1 vectors of genome-wide additive and dominance values of all individuals, respectively, and e is an n × 1 vector of residuals. If there are no covariates, C will be a n × 1 vector of ones and b = μ. The (co)variance matrix of phenotypes is

var (y) = var (g_{A}) + var (g_{D}) + var (e) = Θ_{A} σ_{A}^{2} + Θ_{D} σ_{D}^{2} + I σ_{e}^{2}

where Θ_A and Θ_D are the additive and dominance genetic relationship matrices (GRM), respectively. This is a typical mixed linear model, and the variance components can be estimated by the REML approach.²⁰ The variance explained by additive and dominance variation at all SNPs are defined as $h_{S N P}^{2} = σ_{A}^{2} / (σ_{A}^{2} + σ_{D}^{2} + σ_{e}^{2})$ and $δ_{S N P}^{2} = σ_{D}^{2} / (σ_{A}^{2} + σ_{D}^{2} + σ_{e}^{2})$ , respectively, where $h_{S N P}^{2}$ is interpreted as the narrow-sense heritability (h²) captured by SNPs and $H_{S N P}^{2} = h_{S N P}^{2} + δ_{S N P}^{2}$ is the broad-sense heritability (H²) captured by SNPs. We can assess the significance of $h_{S N P}^{2}$ or $δ_{S N P}^{2}$ by likelihood ratio test (LRT) and calculate the standard errors (SEs) of the estimates of $h_{S N P}^{2}$ or $δ_{S N P}^{2}$ via the delta method.¹⁰

We named this method GREMLd following the previous nomenclature²¹ and have implemented it in the GCTA software tool (see Web Resources).

Analysis of GWAS Data

We used SNP genotype data from three published GWASs, i.e., the Atherosclerosis Risk in Communities (ARIC) study (n = 8,682 European Americans),²² the population-based biobank of the Estonian Genome Center at the University of Tartu (EGCUT) study (n = 10,652),²³ and the LifeLines (LL) study (n = 13,386).²⁴ Informed consent was obtained from all subjects. To partition and estimate the proportions of variance explained by additive and dominance variation at all common SNPs ( $h_{S N P}^{2}$ and $δ_{S N P}^{2}$ ) for quantitative traits, we first performed analyses in the ARIC cohort for a number of quantitative traits and used the EGCUT and LL data as a replication dataset for a few traits that showed a substantial component of dominance variance from the analysis of the ARIC data.

Information on genotyping and quality controls (QC) in the three data sets are summarized in Table S1. To be able to merge multiple datasets, genotype data from different genotyping platforms were imputed separately to 1000 Genomes (1000G) reference panels²⁵ via IMPUTE v.2.²⁶ After imputation, we excluded SNPs with MAF < 0.01, HWE test p value < 10⁻⁶, or imputation R² < 0.6. We then extracted SNPs on HapMap phase 3 (HM3) for two reasons. First, the HM3 SNP set was optimized to capture common genetic variation in the human genome.²⁷ Second, there has been a debate on applying the SNP-based heritability estimation approach in dense coverage SNP data (e.g., 1000G imputed data), which has not led to a clear conclusion^28,29 and needs further investigation. We finally retained 1,174,402, 1,177,501, and 1,158,700 SNPs in the ARIC, EGCUT, and LL cohorts, respectively, for analysis. To remove cryptic relatedness, we used all the HM3 SNPs to estimate the additive genetic relationships between all the individuals in each cohort and removed one of each pair of individuals with estimated genetic relatedness >0.025. We retained 6,715, 6,420, and 7,850 unrelated individuals in the ARIC, EGCUT, and LL cohorts, respectively. In the combined dataset of the EGCUT and LL cohorts, there were 1,140,901 HM3 SNPs in common across the two cohorts and 11,965 unrelated individuals (pairwise genetic relatedness < 0.025).

There are hundreds of phenotypes (including those measuring the same trait at multiple visits) in the ARIC data, which are related to height, obesity, lipoproteins, diabetes, blood phenotypes, carotid artery, heart function, smoking, etc. We used data at the first visit because the sample size was smaller in the follow-up visits. We did not use the mean phenotype averaged across multiple visits because (strictly speaking) mean phenotype is a different trait. We excluded traits with missing rate >40% and excluded those categorical traits with the number of classes <10. There were 79 quantitative traits included in the analysis. A summary description of the phenotypes is presented in Table S2. We replicated the estimates of $h_{S N P}^{2}$ and $δ_{S N P}^{2}$ in the EGCUT and LL cohorts for four traits (see Results), i.e., systolic blood pressure (SBP), BMI, weight (WT), and waist circumference (WC). Each of the phenotypes was corrected for age, standardized to z-score, and inverse normal transformed, in males and females separately, in each cohort. Pairwise correlations between the 79 traits in ARIC are shown in Figure S1. The first 20 principal components (PCs) estimated from the SNP data³⁰ were included as fixed covariates in the GREMLd analyses.

Genome-wide Association Tests for Dominance Variance at Individual SNPs

We used the method described in Equation 3 to perform genome-wide association tests for dominance variance at individual SNPs for all the 79 traits in the ARIC data, and further for 4 traits that showed a substantial estimate of $δ_{S N P}^{2}$ in the ARIC data, in the combined data of the LL and EGCUT cohorts. The first 20 PCs were also fitted as covariates in the association analyses.

Results

We estimated $h_{S N P}^{2}$ and $δ_{S N P}^{2}$ via the GREMLd method for the 79 traits using ∼1.17M SNPs and 6,715 unrelated individuals in the ARIC cohort (Materials and Methods). The method uses genome-wide SNP data to estimate the additive and dominance GRMs and fits both GRMs in a mixed linear model to estimate $h_{S N P}^{2}$ and $δ_{S N P}^{2}$ simultaneously. The additive and dominance genotype variables at single SNPs are parameterized such that genome-wide additive and dominance GRMs are uncorrelated. Therefore, the estimate of $h_{S N P}^{2}$ is independent of whether $δ_{S N P}^{2}$ is fitted in the model or not, and vice versa. This is demonstrated empirically by the tiny correlation (r = 0.0003) of the off-diagonal elements between the additive and dominance GRMs in the ARIC data (Figure 1).

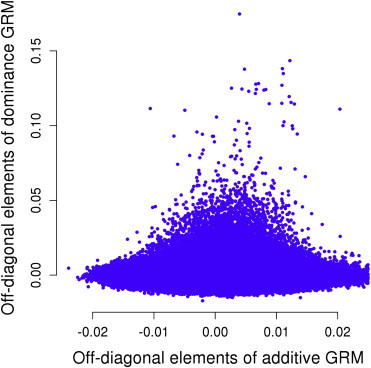
Off-Diagonal Elements of the Additive GRM against Those of the Dominance GRM

The correlation is 3.40 × 10⁻⁴, which is not significantly different from zero (p = 0.11).

The estimates of $h_{S N P}^{2}$ and $δ_{S N P}^{2}$ for the 79 traits are shown in Table S3, with their distribution being presented in Figure 2. The estimate of $h_{S N P}^{2}$ averaged across all the 79 traits was 0.15 (ranging from −0.07 to 0.48), consistent with that from a previous study in Asians.³¹ The estimate of $δ_{S N P}^{2}$ averaged across traits was 0.03 (ranging from −0.13 to 0.19). These results suggest that on average dominance variance is approximately a fifth of additive variance, consistent with $σ_{D}^{2}$ being much smaller than $σ_{A}^{2}$ as predicted from classical quantitative genetics theories¹¹ and observed in pedigree-based analyses of thousands of gene expression traits.³² We plotted the estimate of $δ_{S N P}^{2}$ against that of $h_{S N P}^{2}$ for each of these traits and did not observe a significant correlation between the estimates of $h_{S N P}^{2}$ and $δ_{S N P}^{2}$ (Figure S2), suggesting that traits that have a large component of $h_{S N P}^{2}$ do not necessarily have a substantial component of $δ_{S N P}^{2}$ . We further performed analyses with the genotyped data (593,521 SNPs genotyped on Affymetrix 6.0 array after QC, Table S1), and the results were similar to those using the imputed data (Figure S3).

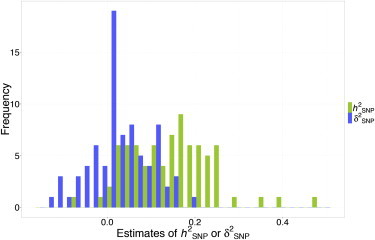
Distribution of the Estimates of $h_{S N P}^{2}$ and $δ_{S N P}^{2}$ for 79 Traits in the ARIC Cohort

To get an unbiased estimate of the mean of $h_{S N P}^{2}$ or $δ_{S N P}^{2}$ across all the traits, the estimates of $h_{S N P}^{2}$ and $δ_{S N P}^{2}$ for each trait were not constrained to be positive in the REML analysis. The mean estimates of $h_{S N P}^{2}$ and $δ_{S N P}^{2}$ are 0.15 and 0.03, respectively.

There were eight traits, related to obesity, blood pressure, and heart rate, which had nominally significant estimates of $δ_{S N P}^{2}$ (p < 0.05) (Table S3), e.g., systolic blood pressure (SBP, $δ_{S N P}^{2}$ = 0.16, SE = 0.07) and BMI ( $δ_{S N P}^{2}$ = 0.15, SE = 0.07). We then replicated the results for four of the eight traits (SBP, BMI, WT, and WC) having data available in the EGCUT (n = 6,420) and LL (n = 7,850) studies (Materials and Methods) and performed analyses in a combined set of EGCUT and LL samples (n = up to 11,965) (Figure 3). To avoid bias due to winner’s curse (the estimates of $δ_{S N P}^{2}$ for these four traits were selected by p values in the ARIC data), we did not include the ARIC cohort in the analysis of combined data. All the four traits appeared to have a strong component of additive variance, consistently across all the datasets. For dominance variance, however, none of estimates were replicated in the combined dataset of EGCUT and LL.

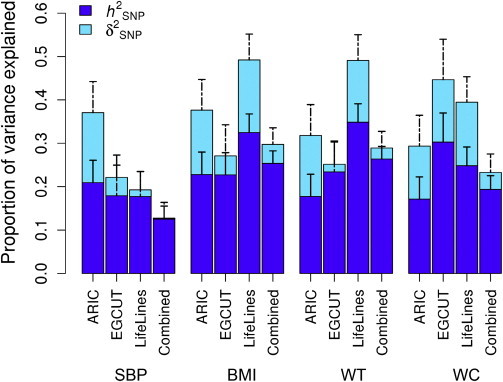
Estimates of $h_{S N P}^{2}$ and $δ_{S N P}^{2}$ in Three Independent Cohorts of ARIC, EGCUT, and LL and in the Combined Dataset of EGCUT and LL for Four Traits

Error bar represents the standard error.

Having not found any evidence of dominance variance for all the traits using all genome-wide SNPs, we asked whether there are any specific SNPs that have strong dominance effects. Using the orthogonal model as described above (Equation 2), we then performed genome-wide association analyses to test for dominance effect of each SNP for the 79 traits in the ARIC data using ∼1.17M HM3 SNPs (Materials and Methods). We identified the ABO blood group gene locus on chromosome 9 that had a genome-wide significant (p < 5 × 10⁻⁸) dominance effect on two traits: factor VIII (FVIII, p value for dominance effect P_D = 5.0 × 10⁻²⁷) and von Willebrand factor (vWF, P_D = 1.1 × 10⁻²⁵) (Figure 4). These are two correlated traits with a phenotypic correlation of 0.72. The top associated SNPs at the ABO gene locus are rs505922 for FVIII (MAF = 0.35) and rs612169 for vWF (MAF = 0.35), which are in high linkage disequilibrium (LD) with r = 0.96. The additive variation at this locus is known to explain more than 10% of the phenotypic variance for vWF.³³ In our study, the additive variation at the top associated SNP explained 11.4% of variance for FVIII (13.6% for vWF), and the dominance variation at the SNP explained 1.4% of variance for FVIII (1.3% for vWF), also consistent with additive genetic variance being several-fold larger than dominance genetic variance, even at a single SNP level. The estimates of a and d were 0.44 (SE = 0.02) and 0.26 (SE = 0.02) at rs505922 for FVIII, 0.47 (SE = 0.02) and 0.25 (SE = 0.02) at rs612169 for vWF, respectively, suggesting a partial dominance model of gene action. Even under a full dominance model, e.g., assuming a = d = 0.44 at rs505922 for FVIII, the additive variance (0.147) is still ∼3.8 times larger than dominance variance (0.039). In addition, we did not find SNPs that were associated with any other traits at genome-wide significance level (P_D < 5 × 10⁻⁸). We further performed GWAS analyses for the four traits (SBP, BMI, WT, and WC) in the combined EGCUT and LL sample of up to 11,965 unrelated individuals and did not find any SNP with dominance effect at genome-wide significance level (Figure S4).

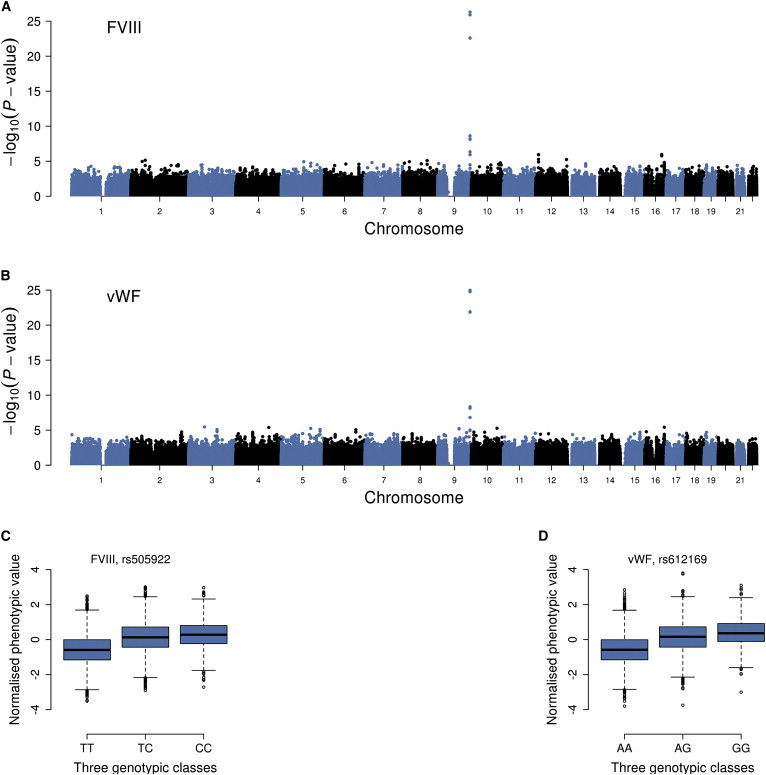
Genome-wide Association Tests for Dominance Effects for Factor VIII and von Willebrand Factor

(A and B) Manhattan plots of p values for dominance effects from the model of fitting both additive and dominance effects for factor VIII (FVIII) (A) and von Willebrand factor (vWF) (B). SNPs with genome-wide significant dominance effects are located at the *ABO* gene locus.

(C and D) Genotype-phenotype maps at the top SNP rs505922 for FVIII (C) and the top SNP rs612169 for vWF (D). The normalized phenotypic means in the three genotypic classes are −0.57, 0.12, and 0.30 at the SNP rs505922 for FVIII (C), and −0.57, 0.15, and 0.37 at the SNP rs612169 for vWF (D). Bars represent 2.5% and 97.5% quartiles of the phenotype distribution at each of the three genotypic classes.

Discussion

Results from GREMLd analyses show that on average across all the 79 quantitative traits, dominance genetic variance is about a fifth of additive genetic variance and that none of the traits show significant estimates of dominance variance. There are two possible explanations for these results: either dominance variance at causal variants is small or dominance variance at the underlying causal variants is not small but the observed dominance variance at the SNPs is small due to imperfect LD between SNPs and causal variants. In theory³⁴ and simulations (Figure S5), the proportion of genetic variance at a causal variant captured by a SNP is r² for additive variance, with r being the LD correlation between the SNP and the causal variant, and r⁴ for dominance variance, suggesting that if LD between SNPs and causal variants are weak to moderate, the observed dominance variance at SNPs will tend to be smaller than the observed additive variance even if the actual additive and dominance variance components at causal variants are equal. However, in a variance estimation analysis using genome-wide SNPs, an unobserved causal variant can be tagged by multiple SNPs. Therefore, variance explained by SNPs should be proportional to the multi-correlation between the causal variants and the SNPs in LD with the causal variants.

To calibrate the extent to which dominance variance decreases due to the imperfect LD between SNPs and causal variants, we performed two additional analyses. We calculated the multi-correlation R² between a SNP and all other SNPs within 1 Mb distance. Multi-correlation R² for additive variance (multi- $R_{x (A)}^{2}$ ) is defined as the multiple regression R² of x_A of the target SNP on x_A of other SNPs in the region, and that for dominance variance (multi- $R_{x^{'} (D)}^{2}$ ) is defined as the multiple regression R² of $x_{D}^{'}$ of the target SNP on $x_{D}^{'}$ of other SNPs. Both multi- $R_{x (A)}^{2}$ and multi- $R_{x^{'} (D)}^{2}$ were adjusted for chance correlation due to the use of multiple variables, analogs to the adjusted R² in a multiple regression analysis. In the ARIC dataset, the average multi- $R_{x (A)}^{2}$ and multi- $R_{x^{'} (D)}^{2}$ over all SNPs were 0.96 and 0.84, respectively, suggesting that if any one of the SNPs is missing, on average 96% of its additive variance and 84% of its dominance variance can be captured by the other SNPs, and that even if all causal variants are not present in the HapMap3 SNP panel, only 16% of dominance variance at common causal variants is missing, which is small given the mean $δ_{S N P}^{2}$ of 3.0%.

Further, we preformed simulation studies based on real SNP data in the ARIC cohort (Appendix A). We randomly sampled 10% of SNPs as a pool of “causal variants.” In each simulation, we randomly sampled 1,000 causal variants from the pool and simulated phenotypes with h² = δ² = 0.3. The analyses of the simulated data were performed in two scenarios: (1) using all the SNPs (including the pool of causal variants) and (2) using only 90% of the SNPs (excluding the pool of causal variants). In scenario 1 where the causal variants were a random subset of all SNPs and were included in the analysis, the estimates of h² and δ² were unbiased (Table S4). In scenario 2 where the causal variants were not included in the analysis, the estimate of $h_{S N P}^{2}$ was biased downward, more so for $δ_{S N P}^{2}$ . We further performed analyses reducing the number of SNPs used from 90% to 10% (Figure S6). Because the pool of causal variants (10% of the SNPs) was always left out of the analysis, reducing the number of SNPs used in the analysis (randomly sampled from the remaining 90% SNPs) decreased the LD between SNPs and causal variants. We observed a slightly faster decline of the estimate of $δ_{S N P}^{2}$ due to imperfect LD than that of $h_{S N P}^{2}$ , consistent with that predicted from theory. Even in a very extreme scenario, where only 10% SNPs were included in the estimation analysis, the ratio of ${\hat{h}}_{SNP}^{2}$ (0.20) to ${\hat{δ}}_{SNP}^{2}$ (0.13) was 1.48, not inconsistent with a ratio of average multi- $R_{x (A)}^{2}$ (0.67) to average multi- $R_{x^{'} (D)}^{2}$ (0.40) of 1.68 calculated in a random subset of 10% SNPs (see above for the method of calculating multi-R²), but much smaller than that observed in the analysis of the 79 real phenotypes ( ${\hat{h}}_{SNP}^{2} / {\hat{δ}}_{SNP}^{2}$ = ∼5). As suggested by Yang et al.,¹⁹ if causal variants tend to be in lower MAF than SNPs, the estimate of $h_{S N P}^{2}$ will be biased downward, more so if the causal variants are not included in estimation analysis. We then sought to test whether the observed ${\hat{h}}_{SNP}^{2} / {\hat{δ}}_{SNP}^{2}$ at SNPs would become larger if the unobserved causal variants tend to be in lower MAF than the SNPs by sampling causal variants from SNPs with MAF ≤ 0.1 (h² = 0.3 and δ² = 0.3). We found that both h² and δ² were underestimated ( ${\hat{h}}_{SNP}^{2}$ = 0.18 and ${\hat{δ}}_{SNP}^{2}$ = 0.18); however, the biases in ${\hat{h}}_{SNP}^{2}$ and ${\hat{δ}}_{SNP}^{2}$ were roughly equal so that ${\hat{h}}_{SNP}^{2} / {\hat{δ}}_{SNP}^{2}$ is still approximately equal to 1. All these results suggest that the observed large difference between ${\hat{h}}_{SNP}^{2}$ and ${\hat{δ}}_{SNP}^{2}$ in the analysis of real phenotypes is unlikely to be driven by imperfect tagging.

Taking all results together, the most plausible reason why we did not find a significant component of dominance variance for all the traits is that $δ_{S N P}^{2}$ is small so that we do not have sufficient power to detect it with statistical significance given the sample size used in this study. The power to detect $δ_{S N P}^{2}$ is determined by the non-centrality parameter (NCP) of the chi-square statistic, i.e., NCP = $δ_{S N P}^{4} / var ({\hat{δ}}_{S N P}^{2})$ . For additive genetic variance, we have derived in a previous study²¹ that $var ({\hat{h}}_{S N P}^{2})$ is approximately equal to 2 / [N² × var(GRM_A)], where N is the sample size and var(GRM_A) is the variance of the off-diagonal elements of the additive GRM, which is approximately 2 × 10⁻⁵ using all common SNPs. We show by empirical data that var(GRM_A) is approximately twice that of var(GRM_D), i.e., var(GRM_D) = 1 × 10⁻⁵, meaning that $var ({\hat{δ}}_{S N P}^{2})$ ≈2 / [N² × var(GRM_D)] ≈2 / (1 × 10⁻⁵ N²) (Figure S7). Given a simple size of 7,000, we will have only ∼12% and ∼35% of power to detect $δ_{S N P}^{2}$ of 0.05 and 0.1, respectively, at the significance level of 0.05.

Very little dominance variance is attributable to rare causal variants because that at a single variant is proportional to [2p(1 – p)]². For a rare variant with MAF < 0.01, even if the dominance effect is large (e.g., 1 standard deviation), the proportion of variance explained by dominance variation at it is tiny (<0.04%). If variants are deleterious there is reason to expect that degree of dominance is associated with the size of effect, i.e., those of largest effect are likely to be at lowest frequency, contributing to inbreeding depression but not generating much dominance variance.³⁵

We observed a significant estimate of dominance variance at the ABO gene locus for von Willebrand factor (1.28% of variance explained) and for factor VIII (1.36% of variance explained), which were also several-fold smaller than those for additive variation (>10% of variance explained). We then used simulations to test whether or not the observed dominance variation at the SNP was caused by the unexplained additive variation at the unobserved causal variant due to imperfect LD between the SNP and the causal variant. As shown in Figure S8, if the genetic effect at an unobserved causal variant is purely additive, there is no inflation in the test statistic for dominance effect at the linked SNP, suggesting that dominance variation at the ABO SNP is not driven by additive variation at the underlying causal variant.

We have shown by theory, simulations, and data analyses the use of SNP data to partition and estimate additive and dominance variance in unrelated individuals based on an orthogonal model. We found that, on average, dominance variation at all the common SNPs explain only 3% of variance for the traits analyzed in this study, 5-fold smaller than that for additive variation. Because rare variants contribute little to the dominance variance and a very large proportion (multi- $R_{x^{'} (D)}^{2}$ = 0.84) of dominance variation at common variants can be captured by common SNPs, the variance explained by dominance variation at all causal variants is also likely to be small (3% / 0.84 < 4%). Hence, even if the missing heritability problem is partly due to the over-estimation of h² in family/twin studies, it is highly unlikely to be caused by dominance variation. Therefore, dominance variation contributes little to the missing heritability.

Consortia

The members of the LifeLines Cohort Study are Behrooz Z. Alizadeh, Rudolf A. de Boer, H. Marike Boezen, Marcel Bruinenberg, Lude Franke, Pim van der Harst, Hans L. Hillege, Melanie M. van der Klauw, Gerjan Navis, Johan Ormel, Dirkje S. Postma, Judith G.M. Rosmalen, Joris P. Slaets, Harold Snieder, Ronald P. Stolk, Bruce H.R. Wolffenbuttel, and Cisca Wijmenga.

Acknowledgments

This research was supported by the Australian Research Council (130102666), the Australian National Health and Medical Research Council (1052684, 613601, 1048853), the USA NIH (GM057091, GM099568, MH100141), the Sylvia & Charles Viertel Charitable Foundation, and the UQ Foundation. This study makes use of data from the database of Genotypes and Phenotypes (dbGaP) under accession phs000090, the Lifelines study, and the EGCUT study (see the Supplemental Acknowledgments for the full set of acknowledgments for these data).

Appendix A

Simulations

We performed a series of simulations based on the real genotypes of ∼1.17M HapMap3 SNPs and 6,715 unrelated individuals in the ARIC cohort. To mimic the incomplete LD between the unobserved causal variants and the observed SNPs, we randomly sampled 10% of SNPs (∼117K SNPs) as a pool of causal variants, and used the other 90% as the observed SNPs. In each simulation replicate, we randomly sampled 1,000 causal variants from this pool and generated the phenotype of each individual based on Equation 3, where the additive and dominance effects were generated from the standard normal distribution and the residuals were generated from a normal distribution with mean 0 and variance var(g_A + g_D)[1 / (h² + δ²) – 1] (see Equation 4 for the definitions of g_A + g_D). We chose h² = 0.3 and δ² = 0.3. We then estimated $h_{S N P}^{2}$ and $δ_{S N P}^{2}$ based on Equation 5 in two scenarios: (1) all the SNPs (including the pool of causal variants) were included in the GREMLd estimation analysis, and (2) only the observed SNPs (excluding the pool of causal variants) were included in the GREMLd analysis. We repeated the simulation 100 times. In each scenario, we calculated the mean estimates of $h_{S N P}^{2}$ and $δ_{S N P}^{2}$ and their standard errors across all replicates.

We extended the simulations by reducing the number of observed SNPs included in the GREMLd analysis from 90% to 10% by steps of 10%. With the decreasing number of observed SNPs used in analysis, on average the LD between causal variants used for generating phenotype and the SNP used in analysis decreased. This simulation was to test whether or not the reduction in the estimate due to incomplete LD for $δ_{S N P}^{2}$ is faster than that for $h_{S N P}^{2}$ .

We further performed simulations to mimic causal variants tending to have lower minor allele frequency (MAF) than SNPs by randomly sampling causal variants from SNPs with MAF < 0.1. We randomly sampled 10% of SNPs as a pool of causal variants, simulated phenotype with the same parameter setting as above (1,000 causal variants, h² = 0.3, δ² = 0.3, and 100 simulation replicates), and estimated $h_{S N P}^{2}$ and $δ_{S N P}^{2}$ using the other 90% of SNPs (excluding the pool of causal variants).

Supplemental Data

Document S1. Figures S1–S8, Tables S1–S4, and Supplemental Acknowledgments

mmc1.pdf^{(1.5MB, pdf)}

Document S2. Article plus Supplemental Data

mmc2.pdf^{(2.4MB, pdf)}

Web Resources

The URLs for data presented herein are as follows:

1000 Genomes, http://browser.1000genomes.org
dbGaP, http://www.ncbi.nlm.nih.gov/gap
GCTA-GREMLd, http://ctgg.qbi.uq.edu.au/software/gcta/GREMLd.html
International HapMap Project, http://hapmap.ncbi.nlm.nih.gov/

References

1.Mackay T.F. The genetic architecture of quantitative traits. Annu. Rev. Genet. 2001;35:303–339. doi: 10.1146/annurev.genet.35.102401.090633. [DOI] [PubMed] [Google Scholar]
2.Fisher R.A. The correlation between relatives on the supposition of Mendelian inheritance. Trans. R. Soc. Edinb. 1918;52:399–433. [Google Scholar]
3.Fisher R.A. Clarendon press; Oxford: 1930. The Genetical Theory of Natural Selection. [Google Scholar]
4.Jinks J.L., Fulker D.W. Comparison of the biometrical genetical, MAVA, and classical approaches to the analysis of human behavior. Psychol. Bull. 1970;73:311–349. doi: 10.1037/h0029135. [DOI] [PubMed] [Google Scholar]
5.Treloar S.A., Martin N.G. Age at menarche as a fitness trait: nonadditive genetic variance detected in a large twin sample. Am. J. Hum. Genet. 1990;47:137–148. [PMC free article] [PubMed] [Google Scholar]
6.Herskind A.M., McGue M., Holm N.V., Sørensen T.I., Harvald B., Vaupel J.W. The heritability of human longevity: a population-based study of 2872 Danish twin pairs born 1870-1900. Hum. Genet. 1996;97:319–323. doi: 10.1007/BF02185763. [DOI] [PubMed] [Google Scholar]
7.Abney M., McPeek M.S., Ober C. Broad and narrow heritabilities of quantitative traits in a founder population. Am. J. Hum. Genet. 2001;68:1302–1307. doi: 10.1086/320112. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Ober C., Abney M., McPeek M.S. The genetic dissection of complex traits in a founder population. Am. J. Hum. Genet. 2001;69:1068–1079. doi: 10.1086/324025. [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Falconer D.S., Mackay T.F.C. Longman; England: 1996. Introduction to Quantitative Genetics. [Google Scholar]
10.Lynch M., Walsh B. Sinauer Associates; Sunderland: 1998. Genetics and Analysis of Quantitative Traits. [Google Scholar]
11.Hill W.G., Goddard M.E., Visscher P.M. Data and theory point to mainly additive genetic variance for complex traits. PLoS Genet. 2008;4:e1000008. doi: 10.1371/journal.pgen.1000008. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Mäki-Tanila A., Hill W.G. Influence of gene interaction on complex trait variation with multilocus models. Genetics. 2014;198:355–367. doi: 10.1534/genetics.114.165282. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Welter D., MacArthur J., Morales J., Burdett T., Hall P., Junkins H., Klemm A., Flicek P., Manolio T., Hindorff L., Parkinson H. The NHGRI GWAS Catalog, a curated resource of SNP-trait associations. Nucleic Acids Res. 2014;42:D1001–D1006. doi: 10.1093/nar/gkt1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Maher B. Personal genomes: The case of the missing heritability. Nature. 2008;456:18–21. doi: 10.1038/456018a. [DOI] [PubMed] [Google Scholar]
15.Manolio T.A., Collins F.S., Cox N.J., Goldstein D.B., Hindorff L.A., Hunter D.J., McCarthy M.I., Ramos E.M., Cardon L.R., Chakravarti A. Finding the missing heritability of complex diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Eichler E.E., Flint J., Gibson G., Kong A., Leal S.M., Moore J.H., Nadeau J.H. Missing heritability and strategies for finding the underlying causes of complex disease. Nat. Rev. Genet. 2010;11:446–450. doi: 10.1038/nrg2809. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Zuk O., Hechter E., Sunyaev S.R., Lander E.S. The mystery of missing heritability: Genetic interactions create phantom heritability. Proc. Natl. Acad. Sci. USA. 2012;109:1193–1198. doi: 10.1073/pnas.1119675109. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Purcell S., Neale B., Todd-Brown K., Thomas L., Ferreira M.A., Bender D., Maller J., Sklar P., de Bakker P.I., Daly M.J., Sham P.C. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Yang J., Benyamin B., McEvoy B.P., Gordon S., Henders A.K., Nyholt D.R., Madden P.A., Heath A.C., Martin N.G., Montgomery G.W. Common SNPs explain a large proportion of the heritability for human height. Nat. Genet. 2010;42:565–569. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Yang J., Lee S.H., Goddard M.E., Visscher P.M. GCTA: a tool for genome-wide complex trait analysis. Am. J. Hum. Genet. 2011;88:76–82. doi: 10.1016/j.ajhg.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Visscher P.M., Hemani G., Vinkhuyzen A.A., Chen G.B., Lee S.H., Wray N.R., Goddard M.E., Yang J. Statistical power to detect genetic (co)variance of complex traits using SNP data in unrelated samples. PLoS Genet. 2014;10:e1004269. doi: 10.1371/journal.pgen.1004269. [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Heard-Costa N.L., Zillikens M.C., Monda K.L., Johansson A., Harris T.B., Fu M., Haritunians T., Feitosa M.F., Aspelund T., Eiriksdottir G. NRXN3 is a novel locus for waist circumference: a genome-wide association study from the CHARGE Consortium. PLoS Genet. 2009;5:e1000539. doi: 10.1371/journal.pgen.1000539. [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Leitsalu L., Haller T., Esko T., Tammesoo M.L., Alavere H., Snieder H., Perola M., Ng P.C., Mägi R., Milani L. Cohort Profile: Estonian Biobank of the Estonian Genome Center, University of Tartu. Int. J. Epidemiol. 2014 doi: 10.1093/ije/dyt268. in press. Published online February 11, 2014. [DOI] [PubMed] [Google Scholar]
24.Stolk R.P., Rosmalen J.G., Postma D.S., de Boer R.A., Navis G., Slaets J.P., Ormel J., Wolffenbuttel B.H. Universal risk factors for multifactorial diseases: LifeLines: a three-generation population-based study. Eur. J. Epidemiol. 2008;23:67–74. doi: 10.1007/s10654-007-9204-4. [DOI] [PubMed] [Google Scholar]
25.Abecasis G.R., Altshuler D., Auton A., Brooks L.D., Durbin R.M., Gibbs R.A., Hurles M.E., McVean G.A., 1000 Genomes Project Consortium A map of human genome variation from population-scale sequencing. Nature. 2010;467:1061–1073. doi: 10.1038/nature09534. [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Howie B.N., Donnelly P., Marchini J. A flexible and accurate genotype imputation method for the next generation of genome-wide association studies. PLoS Genet. 2009;5:e1000529. doi: 10.1371/journal.pgen.1000529. [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Altshuler D.M., Gibbs R.A., Peltonen L., Altshuler D.M., Gibbs R.A., Peltonen L., Dermitzakis E., Schaffner S.F., Yu F., Peltonen L., International HapMap 3 Consortium Integrating common and rare genetic variation in diverse human populations. Nature. 2010;467:52–58. doi: 10.1038/nature09298. [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Lee S.H., Yang J., Chen G.B., Ripke S., Stahl E.A., Hultman C.M., Sklar P., Visscher P.M., Sullivan P.F., Goddard M.E., Wray N.R. Estimation of SNP heritability from dense genotype data. Am. J. Hum. Genet. 2013;93:1151–1155. doi: 10.1016/j.ajhg.2013.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Speed D., Hemani G., Johnson M.R., Balding D.J. Response to Lee et al.: SNP-based heritability analysis with dense data. Am. J. Hum. Genet. 2013;93:1155–1157. doi: 10.1016/j.ajhg.2013.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Price A.L., Patterson N.J., Plenge R.M., Weinblatt M.E., Shadick N.A., Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat. Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
31.Yang J., Lee T., Kim J., Cho M.C., Han B.G., Lee J.Y., Lee H.J., Cho S., Kim H. Ubiquitous polygenicity of human complex traits: genome-wide analysis of 49 traits in Koreans. PLoS Genet. 2013;9:e1003355. doi: 10.1371/journal.pgen.1003355. [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Powell J.E., Henders A.K., McRae A.F., Kim J., Hemani G., Martin N.G., Dermitzakis E.T., Gibson G., Montgomery G.W., Visscher P.M. Congruence of additive and non-additive effects on gene expression estimated from pedigree and SNP data. PLoS Genet. 2013;9:e1003502. doi: 10.1371/journal.pgen.1003502. [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Smith N.L., Chen M.H., Dehghan A., Strachan D.P., Basu S., Soranzo N., Hayward C., Rudan I., Sabater-Lleal M., Bis J.C., Wellcome Trust Case Control Consortium Novel associations of multiple genetic loci with plasma levels of factor VII, factor VIII, and von Willebrand factor: The CHARGE (Cohorts for Heart and Aging Research in Genome Epidemiology) Consortium. Circulation. 2010;121:1382–1392. doi: 10.1161/CIRCULATIONAHA.109.869156. [DOI] [PMC free article] [PubMed] [Google Scholar]
34.Weir B.S. Linkage disequilibrium and association mapping. Annu. Rev. Genomics Hum. Genet. 2008;9:129–142. doi: 10.1146/annurev.genom.9.081307.164347. [DOI] [PubMed] [Google Scholar]
35.Kacser H., Burns J.A. The molecular basis of dominance. Genetics. 1981;97:639–666. doi: 10.1093/genetics/97.3-4.639. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Figures S1–S8, Tables S1–S4, and Supplemental Acknowledgments

mmc1.pdf^{(1.5MB, pdf)}

Document S2. Article plus Supplemental Data

mmc2.pdf^{(2.4MB, pdf)}

[bib1] 1.Mackay T.F. The genetic architecture of quantitative traits. Annu. Rev. Genet. 2001;35:303–339. doi: 10.1146/annurev.genet.35.102401.090633. [DOI] [PubMed] [Google Scholar]

[bib2] 2.Fisher R.A. The correlation between relatives on the supposition of Mendelian inheritance. Trans. R. Soc. Edinb. 1918;52:399–433. [Google Scholar]

[bib3] 3.Fisher R.A. Clarendon press; Oxford: 1930. The Genetical Theory of Natural Selection. [Google Scholar]

[bib4] 4.Jinks J.L., Fulker D.W. Comparison of the biometrical genetical, MAVA, and classical approaches to the analysis of human behavior. Psychol. Bull. 1970;73:311–349. doi: 10.1037/h0029135. [DOI] [PubMed] [Google Scholar]

[bib5] 5.Treloar S.A., Martin N.G. Age at menarche as a fitness trait: nonadditive genetic variance detected in a large twin sample. Am. J. Hum. Genet. 1990;47:137–148. [PMC free article] [PubMed] [Google Scholar]

[bib6] 6.Herskind A.M., McGue M., Holm N.V., Sørensen T.I., Harvald B., Vaupel J.W. The heritability of human longevity: a population-based study of 2872 Danish twin pairs born 1870-1900. Hum. Genet. 1996;97:319–323. doi: 10.1007/BF02185763. [DOI] [PubMed] [Google Scholar]

[bib7] 7.Abney M., McPeek M.S., Ober C. Broad and narrow heritabilities of quantitative traits in a founder population. Am. J. Hum. Genet. 2001;68:1302–1307. doi: 10.1086/320112. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib8] 8.Ober C., Abney M., McPeek M.S. The genetic dissection of complex traits in a founder population. Am. J. Hum. Genet. 2001;69:1068–1079. doi: 10.1086/324025. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib9] 9.Falconer D.S., Mackay T.F.C. Longman; England: 1996. Introduction to Quantitative Genetics. [Google Scholar]

[bib10] 10.Lynch M., Walsh B. Sinauer Associates; Sunderland: 1998. Genetics and Analysis of Quantitative Traits. [Google Scholar]

[bib11] 11.Hill W.G., Goddard M.E., Visscher P.M. Data and theory point to mainly additive genetic variance for complex traits. PLoS Genet. 2008;4:e1000008. doi: 10.1371/journal.pgen.1000008. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib12] 12.Mäki-Tanila A., Hill W.G. Influence of gene interaction on complex trait variation with multilocus models. Genetics. 2014;198:355–367. doi: 10.1534/genetics.114.165282. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib13] 13.Welter D., MacArthur J., Morales J., Burdett T., Hall P., Junkins H., Klemm A., Flicek P., Manolio T., Hindorff L., Parkinson H. The NHGRI GWAS Catalog, a curated resource of SNP-trait associations. Nucleic Acids Res. 2014;42:D1001–D1006. doi: 10.1093/nar/gkt1229. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib14] 14.Maher B. Personal genomes: The case of the missing heritability. Nature. 2008;456:18–21. doi: 10.1038/456018a. [DOI] [PubMed] [Google Scholar]

[bib15] 15.Manolio T.A., Collins F.S., Cox N.J., Goldstein D.B., Hindorff L.A., Hunter D.J., McCarthy M.I., Ramos E.M., Cardon L.R., Chakravarti A. Finding the missing heritability of complex diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib16] 16.Eichler E.E., Flint J., Gibson G., Kong A., Leal S.M., Moore J.H., Nadeau J.H. Missing heritability and strategies for finding the underlying causes of complex disease. Nat. Rev. Genet. 2010;11:446–450. doi: 10.1038/nrg2809. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib17] 17.Zuk O., Hechter E., Sunyaev S.R., Lander E.S. The mystery of missing heritability: Genetic interactions create phantom heritability. Proc. Natl. Acad. Sci. USA. 2012;109:1193–1198. doi: 10.1073/pnas.1119675109. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib18] 18.Purcell S., Neale B., Todd-Brown K., Thomas L., Ferreira M.A., Bender D., Maller J., Sklar P., de Bakker P.I., Daly M.J., Sham P.C. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib19] 19.Yang J., Benyamin B., McEvoy B.P., Gordon S., Henders A.K., Nyholt D.R., Madden P.A., Heath A.C., Martin N.G., Montgomery G.W. Common SNPs explain a large proportion of the heritability for human height. Nat. Genet. 2010;42:565–569. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib20] 20.Yang J., Lee S.H., Goddard M.E., Visscher P.M. GCTA: a tool for genome-wide complex trait analysis. Am. J. Hum. Genet. 2011;88:76–82. doi: 10.1016/j.ajhg.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib21] 21.Visscher P.M., Hemani G., Vinkhuyzen A.A., Chen G.B., Lee S.H., Wray N.R., Goddard M.E., Yang J. Statistical power to detect genetic (co)variance of complex traits using SNP data in unrelated samples. PLoS Genet. 2014;10:e1004269. doi: 10.1371/journal.pgen.1004269. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib22] 22.Heard-Costa N.L., Zillikens M.C., Monda K.L., Johansson A., Harris T.B., Fu M., Haritunians T., Feitosa M.F., Aspelund T., Eiriksdottir G. NRXN3 is a novel locus for waist circumference: a genome-wide association study from the CHARGE Consortium. PLoS Genet. 2009;5:e1000539. doi: 10.1371/journal.pgen.1000539. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib23] 23.Leitsalu L., Haller T., Esko T., Tammesoo M.L., Alavere H., Snieder H., Perola M., Ng P.C., Mägi R., Milani L. Cohort Profile: Estonian Biobank of the Estonian Genome Center, University of Tartu. Int. J. Epidemiol. 2014 doi: 10.1093/ije/dyt268. in press. Published online February 11, 2014. [DOI] [PubMed] [Google Scholar]

[bib24] 24.Stolk R.P., Rosmalen J.G., Postma D.S., de Boer R.A., Navis G., Slaets J.P., Ormel J., Wolffenbuttel B.H. Universal risk factors for multifactorial diseases: LifeLines: a three-generation population-based study. Eur. J. Epidemiol. 2008;23:67–74. doi: 10.1007/s10654-007-9204-4. [DOI] [PubMed] [Google Scholar]

[bib25] 25.Abecasis G.R., Altshuler D., Auton A., Brooks L.D., Durbin R.M., Gibbs R.A., Hurles M.E., McVean G.A., 1000 Genomes Project Consortium A map of human genome variation from population-scale sequencing. Nature. 2010;467:1061–1073. doi: 10.1038/nature09534. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib26] 26.Howie B.N., Donnelly P., Marchini J. A flexible and accurate genotype imputation method for the next generation of genome-wide association studies. PLoS Genet. 2009;5:e1000529. doi: 10.1371/journal.pgen.1000529. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib27] 27.Altshuler D.M., Gibbs R.A., Peltonen L., Altshuler D.M., Gibbs R.A., Peltonen L., Dermitzakis E., Schaffner S.F., Yu F., Peltonen L., International HapMap 3 Consortium Integrating common and rare genetic variation in diverse human populations. Nature. 2010;467:52–58. doi: 10.1038/nature09298. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib28] 28.Lee S.H., Yang J., Chen G.B., Ripke S., Stahl E.A., Hultman C.M., Sklar P., Visscher P.M., Sullivan P.F., Goddard M.E., Wray N.R. Estimation of SNP heritability from dense genotype data. Am. J. Hum. Genet. 2013;93:1151–1155. doi: 10.1016/j.ajhg.2013.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib29] 29.Speed D., Hemani G., Johnson M.R., Balding D.J. Response to Lee et al.: SNP-based heritability analysis with dense data. Am. J. Hum. Genet. 2013;93:1155–1157. doi: 10.1016/j.ajhg.2013.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib30] 30.Price A.L., Patterson N.J., Plenge R.M., Weinblatt M.E., Shadick N.A., Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat. Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]

[bib31] 31.Yang J., Lee T., Kim J., Cho M.C., Han B.G., Lee J.Y., Lee H.J., Cho S., Kim H. Ubiquitous polygenicity of human complex traits: genome-wide analysis of 49 traits in Koreans. PLoS Genet. 2013;9:e1003355. doi: 10.1371/journal.pgen.1003355. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib32] 32.Powell J.E., Henders A.K., McRae A.F., Kim J., Hemani G., Martin N.G., Dermitzakis E.T., Gibson G., Montgomery G.W., Visscher P.M. Congruence of additive and non-additive effects on gene expression estimated from pedigree and SNP data. PLoS Genet. 2013;9:e1003502. doi: 10.1371/journal.pgen.1003502. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib33] 33.Smith N.L., Chen M.H., Dehghan A., Strachan D.P., Basu S., Soranzo N., Hayward C., Rudan I., Sabater-Lleal M., Bis J.C., Wellcome Trust Case Control Consortium Novel associations of multiple genetic loci with plasma levels of factor VII, factor VIII, and von Willebrand factor: The CHARGE (Cohorts for Heart and Aging Research in Genome Epidemiology) Consortium. Circulation. 2010;121:1382–1392. doi: 10.1161/CIRCULATIONAHA.109.869156. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib34] 34.Weir B.S. Linkage disequilibrium and association mapping. Annu. Rev. Genomics Hum. Genet. 2008;9:129–142. doi: 10.1146/annurev.genom.9.081307.164347. [DOI] [PubMed] [Google Scholar]

[bib35] 35.Kacser H., Burns J.A. The molecular basis of dominance. Genetics. 1981;97:639–666. doi: 10.1093/genetics/97.3-4.639. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Dominance Genetic Variation Contributes Little to the Missing Heritability for Human Complex Traits

Zhihong Zhu

Andrew Bakshi

Anna AE Vinkhuyzen

Gibran Hemani

Sang Hong Lee

Ilja M Nolte

Jana V van Vliet-Ostaptchouk

Harold Snieder

Tonu Esko

Lili Milani

Reedik Mägi

Andres Metspalu

William G Hill

Bruce S Weir

Michael E Goddard

Peter M Visscher

Jian Yang

Abstract

Introduction

Material and Methods

Statistical Models

Analysis of GWAS Data

Genome-wide Association Tests for Dominance Variance at Individual SNPs

Results

Figure 1.

Figure 2.

Figure 3.

Figure 4.

Discussion

Consortia

Acknowledgments

Appendix A

Simulations

Supplemental Data

Web Resources

References

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases