Stochastic Model of Endothelial TRPV4 Calcium Sparklets: Effect of Bursting and Cooperativity on EDH

Abstract

We examined the endothelial transient receptor vanilloid 4 (TRPV4) channel’s vasodilatory signaling using mathematical modeling. The model analyzes experimental data by Sonkusare and coworkers on TRPV4-induced endothelial Ca²⁺ events (sparklets). A previously developed continuum model of an endothelial and a smooth muscle cell coupled through microprojections was extended to account for the activity of a TRPV4 channel cluster. Different stochastic descriptions for the TRPV4 channel flux were examined using finite-state Markov chains. The model also took into consideration recent evidence for the colocalization of intermediate-conductance calcium-activated potassium channels (IK_Ca) and TRPV4 channels near the microprojections. A single TRPV4 channel opening resulted in a stochastic localized Ca²⁺ increase in a small region (i.e., few μm² area) close to the channel. We predict micromolar Ca²⁺ increases lasting for the open duration of the channel sufficient for the activation of low-affinity endothelial K_Ca channels. Simulations of a cluster of four TRPV4 channels incorporating burst and cooperative gating kinetics provided quantal Ca²⁺ increases (i.e., steps of fixed amplitude), similar to the experimentally observed Ca²⁺ sparklets. These localized Ca²⁺ events result in endothelium-derived hyperpolarization (and SMC relaxation), with magnitude that depends on event frequency. The gating characteristics (bursting, cooperativity) of the TRPV4 cluster enhance Ca²⁺ spread and the distance of K_Ca channel activation. This may amplify the EDH response by the additional recruitment of distant K_Ca channels.

Introduction

A complex bidirectional communication between endothelial (EC) and smooth muscle (SMC) cells regulates SMC constriction and vessel tone. Cytosolic calcium (Ca²⁺) regulates the ability of ECs to induce the release of vasoactive signals including the discharge of hyperpolarizing current to the SMC. In small resistance vessels, this NO-independent endothelium-derived hyperpolarizing (EDH) signaling is typically mediated by the activation of intermediate- (IK_Ca) and small- (SK_Ca) conductance Ca²⁺-activated potassium channels in response to an increase in Ca²⁺ concentration (1,2). Global EC Ca²⁺ mobilization results from transmembrane Ca²⁺ influx and/or Ca²⁺ release from the intracellular stores. Evidence suggests that localized Ca²⁺ influx from spontaneous or agonist-induced opening of the transient receptor vanilloid 4 (TRPV4) channel can also induce SMC hyperpolarization and vessel dilation through the EDH mechanism in resistance vessels (3–5).

TRPV4 channels are sensitive to a wide array of stimuli including epoxyeicosatrienoic acids, diacylglycerol and phorbol esters via PKC-dependent and independent pathways, osmotic changes, mechanical stimuli, Ca²⁺ levels, and temperature (6–8). In the vasculature, EC agonists like acetylcholine (4,5,9), shear stress (10), and sustained low pressures (3), in addition to exogenous agonists like GSK1016790A, 4-α phorbol 12,13-didecanoate (4αPDD), or 11-12 epoxyeicosatrienoic acids, may activate TRPV4 channels to produce a transient stationary Ca²⁺ burst (sparklet) within the EC that may ultimately result in vasodilation. Single-channel patch-clamp data reveals stochastic TRPV4 opening with pA current amplitude at resting membrane potential (−50 mv) (11). Activation of as few as three channels per EC may be sufficient to induce maximal vessel dilation (4). The role of individual activators and pathways resulting in TRPV4 channel openings is under investigation, as of this writing. Recent evidence suggests bursting activity and cooperative opening of TRPV4 channels in a cluster (4). The physiological relevance of such gating mechanisms has not been elucidated.

EC extensions over the internal elastic lamina toward SMCs, termed myoendothelial projections (MPs), have been observed in small-diameter vessels (12,13), and can play a role in the modulation of vascular tone (14). Recent studies provide evidence for the localization of TRPV4 channels with IK_Ca, inositol 1,4,5-triphosphate receptors (IP₃Rs), and connexins in/near MPs (3,15–18). Myoendothelial gap junctions (MEGJs) are often found at the tip of the MP, and allow for electrochemical communication between ECs and SMCs (12,13). Spontaneous and agonist-induced localized Ca²⁺ events mediated by transmembrane Ca²⁺ influx (TRPV4 sparklets (3–5)) or intracellular store Ca²⁺ release (pulsars (16) and wavelets (19)) have been observed in ECs near the MP sites.

Mathematical modeling offers a systematic approach for the analysis of complex signaling mechanisms, and it can serve as a tool for data interpretation and for guiding new experimental studies. Few theoretical studies have been carried out to investigate the role of ECs and MPs in the modulation of SMC Ca²⁺ and membrane potential (V_m) dynamics. We have previously examined SMC Ca²⁺ and V_m changes during EC stimulation through the development of an EC-SMC compartmental model (20). This model integrates detailed single EC (21) and SMC (22) models with electrical, chemical, and NO coupling pathways. Acetylcholine stimulation of ECs in the model increased global EC Ca²⁺ levels, activated EDH and NO pathways to hyperpolarize the SMC, and ultimately reduced global Ca²⁺ concentration in the SMC. We have also extended the compartmental model into a two-dimensional continuum model that incorporates accurate MP geometry from electron microscopy images and spatial localization of IK_Ca and IP₃Rs in the MP. This formulation was utilized to investigate the role of feedback in EC-SMC communication (23). Similarly, Brasen et al. (24) have developed a two-dimensional axisymmetric model incorporating the anatomical structure of MPs into a two-cell system. Their results show that MPs may rectify the signal between the EC and SMC. Previous models did not examine the role of TRPV4 channels. Moreover, they considered deterministic whole-cell current descriptions for membrane channels and pumps, and did not account for localized and stochastic channel openings.

In this study, we present the development of a computational model to examine the localized Ca²⁺ mobilization, in the vicinity of the MP, arising from a single or a cluster of TRPV4 channels. The TRPV4s were incorporated into a previously developed continuum EC-SMC model with MPs. The model accounts for preferential presence of the TRPV4s near the MPs as suggested in experimental studies. Stochastic opening of a TRPV4 channel was captured using a finite-state Markov chain. We utilize this model to examine the contribution of these channels to the regulation of vessel tone.

Materials and Methods

Continuum model

We have presented a general computational framework for modeling spatiotemporal Ca²⁺ events integrated with plasma membrane electrophysiology in single or coupled vascular cells in Nagaraja et al. (23) and Kapela et al. (25). The model assumes EC and SMC to be simplified rectangular domains with dimensions as shown in Fig. 1 A and implements only half of the EC and SMC by assuming symmetry for the other half. Moreover, the model incorporates an accurate MP geometry from experimental images and assumed high density of IK_Ca (25% of total, under control conditions) and IP₃Rs (10% of total) within the MP. The continuum model takes into account concentration gradients of Ca²⁺ and other ions within the EC and MP. The transport for individual ionic species is influenced by both electrical and concentration gradients, and was described using the Nernst-Planck electrodiffusion equation,

$${\delta }_{\text{buff}}\frac{\partial \left[S\right]}{\partial t}=\nabla \cdot \left(D_S\nabla \left[S\right]+z_{s}F{u}_{\text{ms}}\left[S\right]\nabla V\right)-R_s,$$ (1)

where S = Na⁺, K⁺, Cl⁻, and Ca²⁺; D_s is the diffusion coefficient of ionic species S; z_s is the valence of ionic species S; ∇V is the electrical gradient; F is the Faraday constant; and u_mS is the ionic mobility given by D_s/RT (where R is the ideal gas constant (8341 mJ∙mol⁻¹∙K⁻¹), and T is the absolute temperature). R_s is the source/sink term, which includes the expressions for cytosolic Ca²⁺ exchange with the ER/SR, and Ca²⁺ buffering in the EC and MP. The value δ_buff accounts for the Ca²⁺ buffering in the SMC using a fast buffering approximation. Transport of cytosolic IP₃ and Ca²⁺ within a uniformly distributed ER/SR store was described using

$${\delta }_{\text{buff}}\frac{\partial \left[S\right]}{\partial t}=\nabla \cdot \left(D_S\nabla \left[S\right]\right)-R_s,$$ (2)

where [S] is the concentration of any of the species (IP₃, Ca²⁺ ER, and SR) in the store. R_s is the source/sink term and includes Ca²⁺ exchange between stores and the cellular domains, and IP₃ production and degradation. A uniform distribution of transmembrane channels and pumps was considered along the boundary of the cellular domains. The membrane currents were defined as boundary fluxes across the top and bottom boundaries of the EC, SMC, and the MP boundaries, as

$$-n{N}_S=\frac{1}{z_{S}F}\sum _K{I}_{S,K},$$ (3)

where n is the normal to the surface and N_s is the membrane flux given by summation of all the transmembrane currents for species S (I_S,K). The membrane currents were distributed between the MP and bulk cell according to their respective volumes. The membrane current definitions and parameters are identical to the original models (20–22,25).

Figure 1.

Schematic of the continuum EC-SMC model. (A) Two-dimensional axisymmetric model geometry with SMC and EC as rectangular domains coupled with EC MP and MEGJs. (B) Cartoon illustration describing all the channels and pumps incorporated in the EC-MP-SMC continuum model in (A).

To estimate the characteristics of the TRPV4-mediated Ca²⁺ event in the EC and resulting vessel tone modulation, the model in Nagaraja et al. (23) was modified through the introduction of the single or a cluster of four TRPV4 channels in a localized region on the EC boundary 0.5 μm away from the MP (Fig. 1 B). The current carried by each cation S (I_TRPV4,S) through a single TRPV4 channel is described as

$$I_{\text{TRPV}4,S}\left(t,V_m,S_i\right)=P_{\text{TRPV}4,\text{S}}\frac{z_s^2{F}^2}{RT}{V}_m\frac{S_i-S_0{e}^{\frac{-z_s{V}_{m}F}{RT}}}{1-e^{\frac{-z_s{V}_{m}F}{RT}}},$$ (4)

where S_i is the concentration of Ca²⁺, K⁺, and Na⁺ inside the EC; S_o is the extracellular concentration; F is the Faraday constant; P_TRPV4,S is the ionic permeability; and V_m is the membrane potential. The net current (I_TRPV4,total) through the channel modulates the membrane potential (V_m) described using standard Hodgkin Huxley formalism (21), as follows:

$$I_{\text{TRPV}4,\text{total}}=\sum I_{\text{TRPV}4,\text{S}}.$$ (5)

A single TRPV4 channel-conductance of 45 pS for inward currents (at −100 to 0 mV) was reported using inside-out patch-clamp under symmetric intra- and extracellular ionic concentrations (26), and a single channel-conductance of 56–66 pS for inward currents (at −100 to 0 mV) was observed under near-physiological ionic concentrations using a cell-attached patch-clamp technique (11). We estimated the permeability for each ion (P_TRPV4,S) to match these conductances using the I_{TRPV4, total} description (Eqs. 4 and 5) and reported the permeability ratios (P_TRPV4,Ca:P_TRPV4,K:P_TRPV4,Na = 7.1:1.42:1 (27)). The calculated Ca²⁺ permeability for a single TRPV4 channel P_TRPV4,Ca was 6.8 × 10⁻¹³ – 8.5 × 10⁻¹³ cm³/s (which corresponds to 4 × 10⁻⁸–5 × 10⁻⁸ cm/s assuming 1 μF/cm² standard membrane capacitance and total EC membrane capacitance of 17 pF). In the model we use P_TRPV4,Ca control value of 4.5 × 10⁻⁸ cm/s. This corresponds to control values for P_TRPV4,Na and P_TRPV4,K of 6.5 × 10⁻⁹ cm/s and 8.77 × 10⁻⁹ cm/s, respectively.

Stochastic opening of TRPV4 channel

Two-state model

Individual channels are not constantly open and the ionic currents fluctuate stochastically. A single channel can be represented using a continuous-time homogenous finite-state Markov chain, which describes reversible transitions between a finite number of distinct states in which the ion channel can reside (28,29). The probability of transitions from one state to another is assumed to be independent of the current state. As a simplest case, we considered the TRPV4 channel to be either in a conducting (open) or nonconducting (close) state, presented here as Mechanism 1,

$$O\underset{\beta }{\overset{\alpha }{\rightleftarrows }}C,$$

where O is the open state, C is the close state, and α and β define the rate of transition from one state to another.

The probability density function for the closed-channel lifetime (f_c) and the open-channel lifetime (f_o) are distributed exponentially, as follows:

$$\begin{array}{c}{f}_c=\beta e^{-\beta t},\\ f_o=\alpha e^{-\alpha t}.\end{array}$$ (6)

The mean lifetime in any state is given by the reciprocal of sum of the transition rates that lead away from the state (30). This provides a mean open lifetime and mean closed lifetime of 1/α and 1/β, respectively, for the two-state model in Mechanism 1, given above. The transition rates α, β were calculated based on the reported mean open time (37 ms; 1/α) in Sonkusare et al. (4) and an assumed mean closed time of 780 ms (1/β). This estimate for the mean closed time provides an open probability (P_o; β/(α + β)) for an individual two-state TRPV4 channel of 0.045 as observed in Sonkusare et al. (4).

Three-state model

Ca²⁺ data obtained from a cluster of TRPV4 channels (3,4) reveals a Ca²⁺ burst of few seconds followed by longer inactivity periods, suggesting burst kinetics (i.e., openings are separated by short closed periods, before a long closed period). The two-state model cannot capture the experimentally observed Ca²⁺ burst. We simulated stochastic opening of a single TRPV4 channel using a simple three-state model (28) given here as Mechanism 2,

$$B\underset{k_1}{\overset{k_2}{\rightleftarrows }}O\underset{k_4}{\overset{k_3}{\rightleftarrows }}S,$$

where B is the blocked state (intraburst short closed state), O is the open state, and S is the shut state (interburst long closed state). The values k₁, k₂, k₃, and k₄ define the rates of transition from one state to another. The TRPV4 channel can reside in either of these three states. The model in Mechanism 2, given above, results in mean open time, mean blocked time, mean shut time, and burst length given by 1/(k₃ + k₁), 1/k₂, 1/k₄, and (1 + k₁/k₂)/k₃, respectively. The transition rates k_1–k₄ were calculated based on the reported mean open time (37 ms) of the TRPV4 channel, and observed long inactivity (shut time) of ∼1 min and burst duration of ∼5 s from the Ca²⁺ data in Sonkusare et al. (4). We assumed a mean channel blocked time (∼33 ms) to obtain an overall channel P_o of 0.045 as in the two-state model. The overall probability P₀ was calculated as described in Colquhoun and Hawkes (28). The three-state model provides a significantly higher open probability during the burst (P_o^burst) of ∼0.5.

Cluster of independent or cooperative TRPV4 channels

Stochastic openings of a cluster of four independent TRPV4 channels, with each individual channel represented by the Markov two- and three-state chain described in Mechanisms 1 and 2, respectively, were simulated using a reduced transition rate matrix (see the Supporting Material). Given a group of N independent and identical TRPV4 channels, the probability that k of these channels are open, p(k), is described by the binomial distribution as follows:

$$p\left(k\right)=\left(\begin{array}{l}N\\ k\end{array}\right)P_o^k{\left(1-P_o\right)}^{N-k}.$$ (7)

A 2-min-long simulation of a cluster of four independent channels followed the binomial distribution (see Results). The P_o of each individual channel in a cluster of four independent channels was observed as before to be 0.045, using both the two- and three-state models. The average number of open (active) TRPV4 channels (NP_o) in this simulation was 0.17 (close to the theoretical value of 4^∗P_o of 0.18).

Data in Sonkusare et al. (4) suggest that simultaneous opening of two, three, or four TRPV4 channels are significantly more frequent than expected based on the binomial distribution, indicating an interaction between the channels within a cluster. The cooperative two- and three-state models account for these channel interactions in a cluster through modulation of the transition rate from closed to open state (β), and shut state to open state (k₄), respectively, when at least one other channel in the cluster is in the open state (see the Supporting Material). For example, as shown in Fig. 2 for a cluster of four channels described using the three-state model, if channel 3 is in open state, the transition rate k₄ for channels 1, 2, and 4 was increased to k₄^′ to allow for cooperativity between the channels. Cooperativity increased the average number of open (active) TRPV4 channels (NP_o) to 0.27 in both the two- and three-state models.

Figure 2.

Cooperativity implementation of four TRPV4 channels. (A) Four TRPV4 channels in a cluster described using a simple two-state (open and close) Markov chain model. The rate parameter β, for transition of a channel from the closed state to the open state, was increased in the presence of at least one other channel in the open state. (B) TRPV4 channels implemented using a three-state (shut, block, and open) Markov chain to capture burst opening of the channel. The rate parameter k₄ describing the transition of a channel from the shut state to the open state was increased in the presence of at least one other channel in the open state.

Results

Continuous TRPV4 opening

A single TRPV4 channel opening was simulated through the introduction of TRPV4 current (Eq. 5). Ca²⁺ levels arising from continuous opening of the TRPV4 channel for 10, 100, 200, and 4000 ms are depicted as color-coded in Fig. 3 A. A micromolar increase in Ca²⁺ levels was observed within few milliseconds in a small area (0.25 μm²) around the TRPV4 channel location. Channel opening for longer durations increases the spread area of the Ca²⁺ event. The resulting Ca²⁺ spread can activate Ca²⁺-activated potassium channels (K_Ca) in the vicinity of the TRPV4 location. The contour lines in Fig. 3 B (black, yellow, red, and brown) represent the region of Ca²⁺ spread for 10, 100, 200, and 4000 ms TRPV4 open durations, respectively. The region was defined by Ca²⁺ concentrations higher than the half-activation of the IK_Ca channel ((EC₅₀) 740 nM (31)). Simulations predict Ca²⁺ activity spreading up to 0.3–6 μm radial distances for 10–4000 ms open time durations. The increase in the Ca²⁺ spread area did not increase linearly with channel open time.

Figure 3.

Spatial Ca²⁺ profiles resulting from a single TRPV4 channel opening. (A) Continuous opening of the TRPV4 channel for open times of 10, 100, 200, and 4000 ms resulted in micromolar Ca²⁺ concentrations progressively spreading over a larger area. (B) Contour lines (Ca²⁺ concentration equal to EC₅₀ of IK_Ca) indicate increasing Ca²⁺ spatial spread for 10, 100, 200, and 4000 ms of continuous opening of a TRPV4 channel and highlight the time evolution of the cell regions with at least 50% IK_Ca activity. To see this figure in color, go online.

Stochastic TRPV4 opening

Stochastic opening of a TRPV4 channel represented by a simple two-state Markov model (Mechanism 1) was simulated using a transition rate matrix (Eq. S3 in the Supporting Material) with α = 2.7 × 10⁻² ms⁻¹ and β = 1.3 × 10⁻³ ms⁻¹. A representative single channel record of 120-s duration is shown in Fig. S2 A in the Supporting Material, displaying random opening and closing of the TRPV4 channel with an overall P_o value of 0.045. Simulations with a two-state model could not capture the long quiescent period of TRPV4 channel inactivity observed in the experiment (4).

Three-state model

A three-state Markov chain model (Mechanism 2) was used to describe a single TRPV4 channel exhibiting bursting activity. Simulations were performed using a transition rate matrix obtained from the three-state model with k₁ = 2.35 × 10⁻² ms⁻¹, k₂ = 4.35 × 10⁻² ms⁻¹, k₃ = 3.23 × 10⁻⁴ ms⁻¹, and k₄ = 1.69 × 10⁻⁵ ms⁻¹ (Eq. S4 in the Supporting Material). These values were derived from the observed open time, open probability, interburst interval, and burst duration in Sonkusare et al. (4), as described in Materials and Methods. A representative single channel record with burst openings is shown in Fig. 4 A. TRPV4 superposition records for a cluster of four independent channels were simulated (data not shown) using the reduced transition rate matrix of the three-state model (Eq. S7 in the Supporting Material). Comparison between a single TRPV4 channel and a cluster of TRPV4 channels enable us to examine the physiological relevance of channel clustering in mediating Ca²⁺ signaling and EDH.

Figure 4.

Stochastic opening of a cluster of four TRPV4 channels implemented using a three-state Markov chain to simulate burst opening of the channel. (A) Illustrative example of a temporal profile of a single TRPV4 channel transition between the conducting (open) and nonconducting states (shut, block). (B) Example of a superposition temporal profile of the TRPV4 cluster, with the level number describing the number of open channels at a given time. (Inset) Zoomed-in view of a segment of the total simulation time for better visualization. (C) Experiment (4) (solid bar) and cooperative channel gating in the Markov model (solid checkered) demonstrated increased open probabilities of second, third, and fourth channel openings, respectively, relative to the binomial distribution (shaded) and a Markov model (shaded checkered) considering independent channels.

Cooperativity was implemented by increasing the transition rate k₄ to k₄′ when at least one other channel is in the open state. An eightfold increase in k₄′ was considered to match the experimentally observed NP_o value (Fig. S1). An illustrative superposition record of a cooperative TRPV4 cluster is displayed in Fig. 4 B. A significant number of second-, third-, and fourth-level openings is observed during the burst period followed by a long period of channel idleness (compare with Fig. S2 B). Similar to the two-state model, a cluster of independent channels resulted in an open probability distribution (Fig. 4 C, shaded checkered bar), which follows a binomial distribution (Fig. 4 C, shaded bar). An increase in the probabilities for second-, third-, and fourth-level openings was observed for simulations with cooperativity (Fig. 4 C, solid checkered bar), in agreement with the experimental observation (Fig. 4 C, solid bar). Statistical χ-squared test described in Draber et al. (32) was carried out to confirm for cooperativity in the simulations. The three-state model with cooperativity is able to closely capture the salient features of the TRPV4 cluster from the experiments. The different model implementations for the TRPV4 cluster allow us to examine the role of bursting and cooperativity in the modulation of vessel tone.

Ca²⁺ and V_m dynamics: stochastic continuum model

In the absence of agonist stimulation (i.e., no Ca²⁺ release from the stores), we examined the Ca²⁺ and V_m changes induced from the opening of a cluster of EC TRPV4s in the continuum model. Stochastic current (I_{stochastic,TRPV4,S}) from the TRPV4 channel cluster is provided by

$$I_{\text{stochastic,TRPV}4,\text{S}}\left(t\right)=I_{\text{TRPV}4,\text{S}}\left(t\right)\ast N\left(t\right),$$ (8)

where I_TRPV4,S(t) is the TRPV4 flux as described by the GHK equation (Eq. 5) and N(t) is the number of open TRPV4 channels at time t given by superposition records such as the records in Figs. 4 B and 5 B.

Figure 5.

Representative example of observed temporal EC Ca²⁺ and EC V_m profiles from the stochastic opening of the TRPV4 cluster in the continuum model. (A) Superposition temporal profile of TRPV4 cluster with cooperative gating kinetics implemented using the three-state model. (Right inset) Zoomed-in view for better visualization. (B) EC Ca²⁺ concentration around the TRPV4 cluster (0.25 μm² area) arising from the TRPV4 openings in (A). (C) EC V_m transients follow the EC Ca²⁺ events. (D) Local EC Ca²⁺ concentration around the TRPV4 cluster (0.25 μm² area) observed in different stochastic simulations.

A 2-min-long representative simulation using the three-state cooperative model is displayed in Fig. 5. The stochastic TRPV4 openings (Fig. 5 A) and the average Ca²⁺ concentration in a small area (0.25 μm²) around the cluster’s location (Fig. 5 B) are depicted. The TRPV4 current resulted in quantal Ca²⁺ increases with fixed amplitude of ∼4 μM. (Note: Average Ca²⁺ levels depend on the sampled region around the cluster; for an area of 2 μm², the amplitude was 1.8 μM.) Long inactivity periods following these stochastic Ca²⁺ transient bursts. Ca²⁺ events in different simulations are shown in Fig. 5 D. The Ca²⁺ transients closely resemble, in duration and spread area, the fluorescence recording of Ca²⁺ sparklets in the experiments (4,5).

The simulated Ca²⁺ sparklets activated the localized IK_Ca channels (25% of total in the vicinity of the TRPV4s) to produce EC (and SMC) hyperpolarization. The EC V_m profile shows hyperpolarizations corresponding to each Ca²⁺ sparklet (Fig. 5 C). An average EC hyperpolarization of ∼2.3 mV was estimated in the 2-min-long simulation.

Simulations were carried out using the alternative model implementations for the TRPV4 cluster openings. Spatial Ca²⁺ profiles obtained at the time of maximum Ca²⁺ spread, using: 1) the two-state model with independent channels (top, no bursting activity); 2) the three-state model with independent channels (middle, bursting activity); and 3) the three-state model with interacting channels (bottom, bursting activity with cooperativity) are depicted as color-coded in Fig. 6 A. The contour lines represent the region of the EC where the Ca²⁺ concentration is above the value of IK_Ca EC₅₀. Model simulations with no bursting activity or cooperativity (two-state independent channel model) resulted in ∼2 μm maximum radial distance for half-activation of the IK_Ca channels (Fig. 6 B). Bursting activity (three-state independent channel model) and bursting activity with cooperativity (three-state cooperative model) increased this radial distance by ∼3.2- and 4.5-fold, respectively (Fig. 6 B).

Figure 6.

Increase in distance of IK_Ca channel activation arising from burst and cooperative gating kinetics in the TRPV4 cluster. (A) Ca²⁺ concentration profile in the EC and the SMC at the time of maximum Ca²⁺ spread. TRPV4 channel cluster implemented with a two-state model (top, no bursting or cooperative gating kinetics), three-state model (middle, bursting activity), and three-state model with channel interactions (bottom, bursting and cooperativity). (Contour lines) Ca²⁺ concentration equivalent to EC₅₀ of IK_Ca channels. (B) Radial distance for half-maximum K_Ca channel activation in the simulations in (A). To see this figure in color, go online.

In the model we simulate a single EC coupled to a single SMC. We also assumed that under control conditions, 25% of the total IK_Ca channels are localized in close proximity to the TRPV4 cluster (i.e., within 1 μm). This corresponds to 36 IK_Ca channels, based on whole-cell IK_Ca conductance ($G_{{\text{IK}}_{\text{Ca}}}$) of 1.7 nS, single IK_Ca channel conductance of 17pS, and open probability of 0.7 (21,33). Fig. 7 A shows temporal changes in the EC V_m induced by the TRPV4 Ca²⁺ sparklet in a representative simulation. (Note: Similar levels of SMC hyperpolarization were obtained for a MEGJ resistance of 0.9 GΩ (20,34).) Mean EC V_m hyperpolarization of ∼6 mV is predicted during sparklet activity. Under the assumed arrangement of the TRPV4 and IK_Ca channels in the model, the second-, third-, and fourth-level TRPV4 opening resulted in ∼1.5–4.5 mV depolarization, attenuating the Ca²⁺-induced hyperpolarization.

Figure 7.

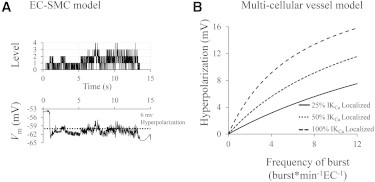
Predicted V_m hyperpolarization induced by a localized Ca²⁺ increase through TRPV4 channels (Ca²⁺ sparklet). (A) Temporal EC V_m profile (bottom) indicates an average EC hyperpolarization of ∼6 mV during the bursting activity of the TRPV4 cluster (top) in the single EC/single SMC model. (B) Hyperpolarization of the endothelium as a function of sparklet frequency and IK_Ca localization, predicted for an intact vessel with EC and SMC layers coupled by MEGJ.

In vivo, the hyperpolarization induced by TRPV4 sparklet in individual ECs will spread through homocellular gap junctions to neighboring ECs and through MEGJs to SMCs, causing vessel hyperpolarization and dilation. The bursting response in an individual cell from the IK_Ca channel activation seen in the model (Figs. 5 C and 7 A) will be smoothed, giving rise to a steady change in vessel’s membrane potential. The mean hyperpolarization of the endothelium will be determined by the frequency and duration of the sparklet events. Assuming TRPV4 sparklets with a mean duration, τ_burst; an average frequency of occurrence per EC site, f_burst; and an average number of active sites per EC, n_sites yields an average number of ECs, N = 1/(τ_burst × f_burst × n_sites), having an active event and open IK_Ca channels at any given time. Thus, hyperpolarizing current from each sparklet will spread, on average, in N cells. The resulting hyperpolarization of the endothelium can be approximated from a simplified electrical equivalent of an intact vessel segment (Fig. S3 and see Eq. S9 in the Supporting Material). For a representative scenario of τ_burst = 5 s, f_burst = 2 bursts per min per active site, and one active site per cell n_sites =1 (i.e., N = 6), IK_Ca conductance

$$g_{{\text{IK}}_{\text{Ca}}}={\gamma }_{{\text{IK}}_{\text{Ca}}}\cdot G_{{\text{IK}}_{\text{Ca}}}=0.25\times 1.72\text{nS}$$

(representing 25% of IK_Ca channels or 36 channels activated by a single TRPV4 sparklet), and net EC-SMC membrane resistance

$$R_m=\frac{1}{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$R_m^{\text{EC}}$}\right.+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\left(R_m^{\text{SMC}}+R_m^{\text{ME}}\right)$}\right.}$$

of ∼1.2–2.2 GΩ (for R_m^EC = 2–10GΩ, R_m^SMC = 2GΩ, and R_m^ME = 0.9GΩ (34–38)), the estimated vessel hyperpolarization is ΔV_m ≈ 2–3.4 mV (Eq. S9 in the Supporting Material). Fig. 7 B shows how this hyperpolarization can increase as a function of the sparklet frequency per EC (f_burst × n_sites) and the fraction of IK_Ca (${\gamma }_{{\text{IK}}_{\text{Ca}}}$) localized around the TRPV4 cluster. In the presence of 36 (25% of total), 72 (50%), and 144 (100%) localized IK_Ca channels around the TRPV4 cluster, the TRPV4-mediated Ca²⁺ sparklet (with assumed mean duration of 5 s) results in a vessel hyperpolarization of 0.3–15 mV for sparklet frequency between 0.1 and 12 bursts/min per EC (Fig. 7 B). Similar results were obtained with a multicellular computational model of an intact vessel segment (39). The vessel model predicted a similar ΔV_m value of 2.3 mV in the endothelium (simulating opening of 25% of IK_Ca channels in one EC out of 6 ECs (i.e., N = 6)). According to Eq. S9 in the Supporting Material, hyperpolarization also depends on the membrane resistance, and in microvessels with higher input resistance, achieved levels of hyperpolarization may be greater relative to larger vessels.

Discussion

The primary aim of the study was to examine the regulatory mechanism of EC TRPV4 channels in inducing vessel relaxation. Using the two-dimensional EC-SMC continuum model coupled with MP, we examined the localized Ca²⁺ events arising from activation of a single TRPV4 channel and a cluster of TRPV4 channels in the EC and the resulting vasodilatory response. Simulations showed the effect of TRPV4 and IK_Ca channel distribution, and burst and cooperative gating kinetics of TRPV4 channels in defining the localized Ca²⁺ event (sparklet), and the resulting SMC hyperpolarization.

Endothelial control of vascular tone is attributed to EC Ca²⁺ mobilization that may manifest as events with different spatiotemporal characteristics. Agonist or mechanical stimulation, for example, may increase global Ca²⁺ levels, the frequency of Ca²⁺ waves/oscillations, the presence and frequency of Ca²⁺ pulsars (events mediated by IP₃Rs in the vicinity of MP (16,35)), or of Ca²⁺ sparklets (events mediated by EC TRPV4 channels (3–5)). Evidence suggests a central role of TRPV4 channels in agonist- and mechanical-induced vasoactive signaling in the microcirculation (3–5).

TRPV4 Ca²⁺ sparklet

The model predicts local micromolar Ca²⁺ increases from a single TRPV4 channel opening for the duration of the channel’s open time (Fig. 3). The obtained Ca²⁺ levels in a small region around the TRPV4 channel are significantly higher than the nanomolar global Ca²⁺ increases usually observed experimentally (16,35) or predicted theoretically (21) in response to agonist or mechanical stimuli. These high local Ca²⁺ concentrations may be required to fully activate cellular components with low Ca²⁺ affinity, including IK_Ca channels whose affinity may be in the high nanomolar range (reported EC₅₀ values as high as 300–740 nM (31,40)).

Multiple TRPV4 channel opening in a cluster resulted in localized quantal Ca²⁺ increases (Fig. 5, B and D). Second-, third-, and fourth-level openings in the TRPV4 cluster lead to essentially constant amplitude increases in Ca²⁺ concentrations that return quickly to the previous baseline after channel closure, consistent with the experimental data (3–5). This allows examining channel gating characteristics based on the changes in Ca²⁺ levels, as was done in the experimental studies (4,5). The model corroborates the methodology utilized in these earlier analyses and shows that Ca²⁺ diffusion, extrusion, and buffering have minimal effect on the interpretation of the data.

In the experiments, TRPV4 channels with an average open time of milliseconds (4) generate a Ca²⁺ burst event (i.e., sparklet) of 1–10 s duration, followed by a long inactivity period before the occurrence of the next event. The significant increase in duration of the Ca²⁺ event, compared to channel open times, can be a result of bursting activity of the TRPV4 channel. Bursting kinetics of TRPV4s have been observed in single channel patch-clamp data (11,26). Model implementation of bursting in a cluster of four TRPV4 channels (Figs. 4 and 5) resulted in Ca²⁺ events lasting for seconds followed by longer inactivity periods (Fig. 5, B and D), as observed in the experiments. Burst activity in a cluster of independent TRPV4 channels enhanced the Ca²⁺ spread and activated IK_Ca channels at longer distances (Ca²⁺ concentrations >50% activation within 5 μm) (Fig. 6, A and B).

Cooperative activation of TRPV4 channels in a cluster has been suggested in experiments because multilevel openings appear much more frequently than suggested by the binomial distribution for random events (4). We have accounted for cooperativity in channel kinetics, capturing the increased probability of multilevel openings seen in the experiments. Cooperativity further enhances the Ca²⁺ spread. The combined effect of bursting and cooperativity is a Ca²⁺ spread of ∼7 μm (defined as the radial distance with Ca²⁺ levels greater than IK_Ca EC₅₀). Thus simulations suggest that the gating characteristics of TRPV4 cluster increase the sparklet’s area and presumably the resulting hyperpolarization by the recruitment of additional IK_Ca channels. It will be interesting to examine the effect of clustering of other TRP channels such as of TRPA1 and TRPV3, which have been shown to facilitate endothelium-dependent dilation in cerebral arteries (41,42). The coupled stochastic-continuum model presented here could be extended toward the analysis of experimental data from stimulation of such channels.

TRPV4-mediated hyperpolarization

EC hyperpolarization through the activation of IK_Ca and SK_Ca channels is a major contributor in NO-independent endothelium-derived vasodilation in microvessels (2). TRPV4 Ca²⁺ sparklets may activate nearby IK_Ca channels (3,4) to induce hyperpolarization and dilation. We tested the potential of TRPV4 sparklets to mediate EDH responses. The presence of high-density cellular components, including the K_Ca channels near microdomain structures like MPs, has been reported in small-resistance vessels (3,12,13,16,19). Micromolar localized Ca²⁺ increases around the MPs can potentially fully activate the nearby K_Ca channels (assuming an EC₅₀ as high as 740 nM). In the model of a single EC coupled to a single SMC, a TRPV4 sparklet activated colocalized IK_Ca channels in the vicinity of the cluster to generate ∼6 mV of hyperpolarization in the EC (Fig. 7 A).

Although cooperative gating in the cluster increased the Ca²⁺ spread (Fig. 6 A), it showed no significant amplification of hyperpolarization (data not shown). This was attributed to the positioning of a high density of IK_Ca channels within a very close proximity to the cluster (<1 μm). Within this area even a single TRPV4 channel produces saturating Ca²⁺ concentrations so multilevel opening in a cluster does not offer any additional advantage. On the contrary, at physiological ionic concentrations and around resting V_m, significant sodium influx currents (pA) are predicted from each TRPV4 opening. This can result in a few millivolts depolarization, which in the absence of additional K_Ca channel recruitment will have an attenuating effect on EDH signaling. Thus, the high Na⁺ influx and the micromolar Ca²⁺ levels in the vicinity of the TRPV4 cluster arising from a single channel opening suggest that bursting and cooperatively may benefit EDH signaling only if K_Ca channels are positioned at intermediate distances (3–10 μm) away from the cluster. Under the assumed arrangement of TRPV4 and IK_Ca channels in the model, we observed that second, third, and fourth TRPV4 channel opening from cooperative gating kinetics, result in a ∼1.5–4.5 mV depolarization (Fig. 7 A).

Sustained vessel hyperpolarization results from the spread of transient hyperpolarization generated in a single EC cell to its neighbors. The achieved vessel hyperpolarization will depend on many parameters including membrane resistances of the EC and SMC layers, the MEGJ resistance, the transient hyperpolarizing current, and the frequency and duration of the events. Simulations suggest a significant EC hyperpolarization through activation of TRPV4 channels, which increases with increasing the frequency and duration of the event and the amount of the K_Ca channels in proximity to the TRPV4 cluster (Fig. 7 A). Our calculations suggest that experimentally observed TRPV4 Ca²⁺ sparklets that typically have an average duration of ∼5 s and frequency of occurrence of two bursts/min per EC should induce ∼2.0 mV hyperpolarization, assuming that 36 channels (25% of total) are located near the cluster (Fig. 7 B). This is lower than what has been observed in experiments (∼10 mV) (4). This discrepancy may be attributed to a higher number of sparklet events/sites than observed experimentally, a very high number of K_Ca activated by each sparklet (i.e., the majority of IK_Ca), or to mechanisms amplifying TRPV4/IK_Ca-mediated hyperpolarization. Moreover, the predicted level of hyperpolarization depends on parameters such as membrane resistances (Eq. S9 in the Supporting Material) that have not been accurately characterized and which may change with stimulation or could vary between vessels. Furthermore, as the size of a vessel decreases, input resistance typically increases and this may result in significantly higher hyperpolarization for a given transmembrane current.

Local versus global Ca²⁺ activity

It is well established that a variety of stimuli can elicit global Ca²⁺ increases in ECs. A typical Ca²⁺ response has an initial transient that is mediated by store Ca²⁺ release (with peak concentrations of ∼0.4–1.5 μM (35,43)) followed by a lower plateau phase that is sustained by Ca²⁺ influx through Ca²⁺ permeable channels in the plasma membrane. This global Ca²⁺ mobilization is thought to mediate vasoactive signaling, including EDH responses. However, studies showed activation of IK_Ca channels by localized Ca²⁺ events such as pulsars and sparklets (3–5,16), and that a moderate global Ca²⁺ increase (∼30% above resting) by CPA (cyclopiazonic acid) did not lead to a significant activation of K_Ca channels in Ledoux et al. (16). Thus, evidence points toward a preferential activation of IK_Ca channels and EDH response to local rather than global Ca²⁺ increases.

Is there a mechanism that would allow for a portion of K_Ca channels to be relatively immune to global Ca²⁺ mobilization so that their activity can be regulated preferentially/exclusively by localized Ca²⁺ signaling? One possibility is that compartmentalization of TRPV4 and K_Ca channels may provide a locally confined, regulatory unit relatively inaccessible to global Ca²⁺ changes. Restriction of Ca²⁺ signals to subplasmalemma regions has been reported, suggesting the presence of cytosolic compartments (16,24,35,44,45).

Simulation results provide an alternative possibility. The preferential activation of the K_Ca channels to local rather than global Ca²⁺ increases may be a result of significantly higher Ca²⁺ concentrations in localized events (micromolar levels are predicted in the model (Fig. 6, B and D)) relative to nanomolar global Ca²⁺ increases during EC stimulation (21,35). Provided that the K_Ca EC₅₀ is in the high nanomolar range, global Ca²⁺ levels may not be sufficient to fully activate K_Ca and thus a significant portion of the channels is activated only by the high concentration local Ca²⁺ event. However, reported values for IK_Ca affinity for Ca²⁺ range from ∼100 nM to 740 nM (31,35,40,46). The predicted high local Ca²⁺ concentrations will be beneficial only if the EC₅₀ is in the high end of this range. (Note: A high EC₅₀ (740 nM, i.e., low affinity) for IK_Ca channels was assumed in the simulations.)

Interestingly, a high Ca²⁺ affinity for IK_Ca channels can make these channels significantly (if not fully) activated by global Ca²⁺ events. In this case, subsequent TRPV4 activation may result in EC depolarization that will attenuate rather than promote EDH. (Note: Recruitment of saturated K_Ca channels will not compensate for the depolarizing TRPV4 current.) An intermediate scenario where an IK_Ca channel is activated by both local events and global transients might also be possible. Further experimentation is required to determine the relative contribution of global and local Ca²⁺ events on IK_Ca channel activation.

Limitations

Many of the parameter values used here have not been previously quantified or may vary between different vessels. In this study, we try to remain consistent with our previous EC-SMC models with respect to parameter values and whole cell currents and examine responses over a range of values for parameters with significant uncertainty. The model is limited by the absence of quantitative data for the spatial distribution of important cellular components. Such data may significantly improve the predictive ability of the proposed models. The TRPV4 channel current was modeled using a GHK equation and ignores the effects of temperature, shear, and modulatory pathways on the channel. Moreover, simple Markov chain models were considered that can capture the observed channel behavior, but the actual gating mechanism could be more complex.

Conclusions

The developed model describes TRPV4-mediated signaling for the regulation of vessel dilation. Model simulations are in good agreement with experiments in isolated vessels, corroborating data for the role of TRPV4 signaling in vascular control. The model predicts a micromolar-localized Ca²⁺ increase through activation of cluster of four TRPV4 channels. This is significantly higher than the nanomolar global Ca²⁺ levels typically observed during EC stimulation. The model shows an enhanced Ca²⁺ spread as a result of burst opening and cooperative channel gating in the TRPV4 cluster. Ca²⁺ mobilization over several micron radial distances can recruit K_Ca channels and produce millivolts of EDH. The model predicts that amplification of EDH signaling by cooperativity in the TRPV4 cluster is more likely if K_Ca channels are not immediately adjacent to the TRPV4 channels, but at distances that can reach 10 μm away. The magnitude of the resulting hyperpolarization depends on a variety of parameters, including the sparklet frequency and the effective membrane resistance of the vessel wall. Nevertheless, for a wide range of parameter values predicted, TRPV4-induced hyperpolarization underestimates what has been recorded in some experiments. This may suggest additional mechanisms contributing to the observed EDH response.

Author Contributions

J.P., A.K., and N.M.T. are responsible for conception and design of the research; J.P. developed the computational code and performed the simulations; J.P., A.K., and N.M.T. interpreted the results of simulations; J.P. drafted the manuscript; J.P., A.K., and N.M.T. edited and revised the manuscript; and J.P., A.K., and N.M.T. approved the final version of the manuscript.

Supporting Citations

Reference (47) appears in the Supporting Material.