Two Fundamental Mechanisms Govern the Stiffening of Cross-linked Networks

Abstract

Biopolymer networks, such as those constituting the cytoskeleton of a cell or biological tissue, exhibit a nonlinear strain-stiffening behavior when subjected to large deformations. Interestingly, rheological experiments on various in vitro biopolymer networks have shown similar strain-stiffening trends regardless of the differences in their microstructure or constituents, suggesting a universal stiffening mechanism. In this article, we use computer simulations of a random network comprised of cross-linked biopolymer-like fibers to substantiate the notion that this universality lies in the existence of two fundamental stiffening mechanisms. After showing that the large strain response is accompanied by the development of a stress path, i.e., a percolating path of axially stressed fibers and cross-links, we demonstrate that the strain stiffening can be caused by two distinctly different mechanisms: 1) the pulling out of stress-path undulations; and 2) reorientation of the stress path. The former mechanism is bending-dominated and can be recognized by a power-law dependence with exponent 3/2 of the shear modulus on stress, whereas the latter mechanism is stretching-dominated and characterized by a power-law exponent 1/2. We demonstrate how material properties of the constituents, as well as the network microstructure, can affect the transition between the two stiffening mechanisms and, as such, control the dominant power-law scaling behavior.

Introduction

A random fiber network is a ubiquitous microstructure in many materials, ranging from metallic open cell foams through felts, paper, and rubbers (1–3), to the scaffolds of biopolymer filaments in soft tissue and the cell cytoskeleton (4–7). Although the mechanical behavior of these materials evidently depends on their constituents, the underlying network microstructure is particularly important at large strains. Numerous rheological experiments have shown that random fiber networks of in vitro reconstituted biopolymer networks exhibit strong nonlinear elastic strain stiffening accompanied by an increase of the shear modulus up to three orders of magnitude (8–21). Several synthetic polymer network systems show a phenomenology similar to that of biopolymer networks, albeit with a much weaker increase of the modulus up to a factor of ∼2 (22).

The strain stiffening in biopolymer networks can, generally speaking, be attributed to 1) the properties of the fibers; 2) the cross-links that mediate the interfiber force transmission; and 3) the network microstructure. Insofar as the fiber constituent is concerned, the physics of individual biopolymer fibers, such as actin filaments (F-actin), has been extensively studied within the framework of a Kratky-Porod wormlike chain model (23,24) for semiflexible chains and under various constraints on the chain ends (25–30). The cross-links found in biopolymers (31–34), however, have a diverse mechanical behavior. In addition, the cross-linking macromolecules that commonly interconnect biopolymer filaments at higher concentrations often tend to bundle the filaments into thicker fibers, thereby changing the network microstructure (14,16,35).

Despite these differences in microstructure and/or properties of the constituents, the nonlinear stiffening of biopolymer networks shows quite similar trends, as shown in Fig. 1. The stiffening of F-actin networks cross-linked by scruin (8,9) and that of cross-linked neurofilaments (36) can be characterized by a power-law relation with exponent 3/2 between the network shear modulus, G, and macroscopic stress, $\text{T}$ (Fig. 1 A). Since the cross-links in both these networks are relatively stiff, it has been suggested that the stiffening mechanism is the same (37,38). However, F-actin networks cross-linked by heavy meromyosin in a rigor state (rigor-HMM) (13), which are also considered to be rigidly cross-linked, show a stiffening behavior with an exponent that is far less than 3/2 (Fig. 1 B). Moreover, the stiffening exponent in F-actin/rigor-HMM networks is found to decrease as the cross-link concentration increases, the reason for which is not well understood (13). A similar decrease of the stiffening exponent with increasing concentration of interfiber connections has been observed in purely bundled F-actin networks cross-linked by fascin (14), as well as in branched collagen-I-type networks (19,20). On the other hand, F-actin networks cross-linked by the long flexible protein filamin (12,15) (Fig. 1 C), as well as rigidly cross-linked networks of the intermediate filament vimentin (36,39) (Fig. 1 D), start to stiffen according to a 3/2 power law, but at higher stress change to weaker stiffening. The weaker stiffening exponents are remarkably similar to those found in F-actin/rigor-HMM networks.

Figure 1.

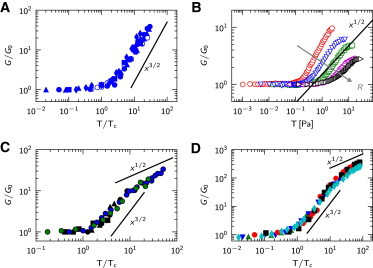
The nonlinear behavior of biopolymer networks plotted as the shear modulus, G, versus stress, T, or the shear modulus normalized by the initial shear modulus, G/G₀, versus stress normalized by the critical stress at the onset of nonlinearity, T/T_c, for (A) F-actin/scruin networks (8); (B) F-actin/rigor-HMM networks with actin concentration 19 μM, mean F-actin length 21 μm, and various increasing molar HMM/actin concentration ratios, $R=c_{\text{HMM}}/c_{\text{a}}$ (arrow) (13); (C) F-actin/filamin networks for lower F-actin concentrations (15); and (D) vimentin networks (39). To see this figure in color, go online.

The nonlinear response of all cross-linked networks mentioned above therefore exhibits qualitatively and quantitatively similar features.

It has been proposed that strain-stiffening of a rigidly cross-linked network characterized by a power-law dependence of the network shear modulus, G, on stress, $\text{T}$, with exponent 3/2 originates from the entropic nature of thermal filaments (8,26,37). To be more precise, a network in this view is seen as a collection of thermally undulating semiflexible chains whose number of possible conformations in the course of deformation reduces to one, namely the fully straight chain. When the filaments between cross-links are affinely coupled to the average deformation, the network response inherits the nonlinear features of the force-displacement relation of a single chain, which then leads to the prediction $G\propto {\text{T}}^{3/2}$. Note, however, that the filament deformation within the network might not be affine at all (40–42). Also, undulations of the filaments between the cross-links could be strongly suppressed due to short contour lengths relative to the filament persistence length (13) but also to constraints imposed by the cross-links (27,43). A physically more simple, athermal network model of rigidly cross-linked semiflexible-like fibers also predicts 3/2 power-law strain stiffening (38). In such a model, strain stiffening is the result of stretching out the undulations in the localized paths of high axial forces that develop as the network is deformed to large strain (38,44). Irrespective of whether the undulations are due to the stress paths that wiggle through the network microstructure and/or to effects of the thermal environment, the fact that they are being straightened out with continued network deformation is controlled by the filament bending energy.

In contrast to the network behavior characterized by an exponent 3/2, strain-stiffening behavior with a different exponent is not understood quite well. Deviation from 3/2 stiffening has been attributed to multiple possible mechanisms. For example, in the case of F-actin/HMM networks (13), it has been argued that time- or force-dependent cross-link unbinding/rupturing could alter strain-stiffening behavior, thereby explaining the lowering of the stiffening exponent. A three-dimensional dynamic finite-element model (45) indeed demonstrates that the dynamic behavior of cross-links (cross-links being allowed to unbind and rebind) could have a strong effect on the nonlinear response of enthalpic networks; while cross-link rupturing was shown to mainly give rise to a strong strain softening, cross-link rebinding is argued to lead to a strain-stiffening trend similar to that observed in the networks with static cross-links. Some deviation from the exponent 3/2 has been reported in theoretical studies to be a consequence of the cross-link properties (46,47). On the other hand, strain stiffening with exponents that are significantly smaller than 3/2 were also observed in discrete two-dimensional computational models of athermal stiff (48) or marginally stiff (49) filament networks, thereby suggesting that the stiffening with a low exponent can take place for a small ratio of the filament axial and bending stiffness, even with stiff (passive) cross-links. In addition to these two-dimensional network models, molecular dynamics simulations of cross-linked actin networks (50), which report stiffening exponents of ∼0.7, also indicate a trend where, all else being equal, the stiffening exponent increases with increasing extensional stiffness of the filaments. Despite the fact that stiffening with exponents below 3/2 has been clearly observed in various discrete network models, to our knowledge, an explanation in terms of the underlying physical mechanisms is still lacking.

In this article, we use computer simulations to study the strain stiffening of cross-linked biopolymer-like networks subjected to simple shear. Our basic three-dimensional network model consists of random athermal fibers interconnected by cross-links with tunable mechanical properties. In the model, the individual fibers are elastic rods that can stretch, bend, and twist, whereas cross-links are modeled as linear springs. By means of a parametric study of the dependence of the nonlinear network response on cross-link stiffness and network connectivity, we show that strain stiffening in our network model originates from two mechanisms. Both are associated with the development of a stress path, but in distinctly different ways. We demonstrate that the competition between these two mechanisms leads to a variety of possible stiffening behaviors, thus providing grounds for a unified interpretation of the nonlinear elasticity of biopolymer networks.

Materials and Methods

We use a numerical method proposed by Huisman et al. (51) to self-assemble a fully periodic representative volume element (RVE) of an athermal and random fiber network in three dimensions (Fig. 2 A).

Figure 2.

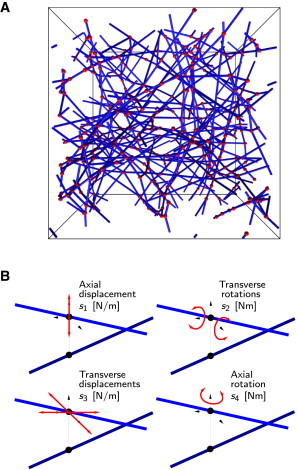
The cross-linked network model. (A) Example of a generated RVE with fibers shown in blue and cross-links in red. (B) A cross-link is a two-node element whose behavior is controlled by four independent spring constants. The cross-link is idealized by coupling the four spring constants to each other, $s=s_1=s_3=s_2/l_{\text{c}}^2=s_4/l_{\text{c}}^2$, where $l_{\text{c}}$ is the mean length of the fiber sections. The nondimensional system parameter $\tilde{s}=s{l}_{\text{c}}^3/\kappa$ used in our analysis, compares the cross-link stiffness to the fiber bending stiffness. To see this figure in color, go online.

The main idea behind the Huisman et al. network generation procedure (51) is to simulate the fiber dynamics subject to a weak 1/r² attractive force field between fibers such that a homogeneous and isotropic random network self-assembles (for more details, see the Supporting Material). The fibers are discretized by beam elements within a nonlinear finite-element code with axial, bending, and torsional properties that mimic semiflexible biopolymers. The microstructure of the generated networks is characterized by the triplet $\left(c_{\text{f}};l_0;l_{\text{c}}\right)$, where $c_{\text{f}}$ is the concentration of fiber material, $l_0$ the original length of the fibers, and $l_{\text{c}}$ the mean distance between cross-links on a fiber. In this article, all network realizations were generated in an RVE with size $W=2.5\mu \text{m}$ at a constant concentration $c_{\text{f}}=0.8\text{mg/mL}$, of fibers with initial length $l_0=5\mu \text{m}$ (51).

Due to the finite length of the fibers, the cross-link coordination is limited to 2-coordinated L cross-links, 3-coordinated T cross-links, and 4-coordinated X cross-links. A detailed investigation of quantitative measures for the connectivity of the networks (38) has revealed that it is uniquely determined by the ratio of the fiber length and the mean length of the fiber segment between two cross-links, $l_0/l_{\text{c}}$. Among several equivalent measures for connectivity, we have found it convenient to employ the relative number of X cross-links, which can be expressed as ${\tilde{n}}_{\text{X}}={[\left({\tilde{l}}_0-3\right)/\left({\tilde{l}}_0-1\right)]}^2$, where ${\tilde{l}}_0=l_0/l_{\text{c}}$ (38). Obviously, ${\tilde{n}}_{\text{X}}$ is 0 for the L-only network (${\tilde{l}}_0\to 3$) and 1 for the X-only network (${\tilde{l}}_0\to \infty$)

The stress-strain response of the networks is obtained by subjecting the RVE to simple shear in a quasistatic finite-element simulation, as described in (51) (see the Supporting Material and Žagar (52) for more details). Unless stated otherwise, the material parameters of the fiber beam elements are set to represent F-actin with stretching stiffness $\mu =4\times {10}^{-8}\text{N}$ (53), bending stiffness $\kappa =6.75\times {10}^{-26}{\text{Nm}}^2$ (54,55), and a torsional stiffness equal to the bending stiffness. Although we do account for torsional degrees of freedom, we know that they are irrelevant for the strain stiffening of rigidly crosslinked networks (38), but also for networks with compliant cross-links (Fig. S3). The mechanical behavior of the cross-links is represented by simple linear springs tuned by a single parameter, the spring constant, s (Fig. 2 B). For simplicity, we consider the cross-links to be permanent and do not account for any additional cross-linking that might occur during deformation, i.e., the connectivity of the network is constant. The mean macroscopic stress $\left(\text{T}\right)$ response to shear strain, $\text{Γ}$, is calculated as the ensemble average over 7–10 random RVE realizations at constant stress level. From this, the strain-dependent ensemble-averaged elastic shear modulus is obtained as $G=\partial \text{T}/\partial \text{Γ}$. We note that our network model is enthalpic.

Results

Small-strain behavior

The cross-link number, $\tilde{s}$, defined by $\tilde{s}=\left(s{l}_{\text{c}}^3\right)/\kappa$, is a measure of the cross-link stiffness relative to that of the fiber segment.

It is not surprising to see (Fig. 3 A) that the initial network response as a function of $\tilde{s}$ is reminiscent of the behavior of two springs connected in series, one spring representing the fibers and the other the cross-links. In the rigidly cross-linked limit (RCL), i.e., for $\tilde{s}\mathrm{\to \infty }$, the initial response is independent of $\tilde{s}$ and is fiber-dominated. Moreover, the RCL network at small strains is a bending-dominated structure, much like an open cell foam (1), with a linear dependence of the initial shear modulus, $G_0$, on the fiber bending stiffness, $G_0=G_0^{\infty }\propto \kappa$ (38). For $\tilde{s}$ below the transition marked by $\tilde{s}={\tilde{s}}_{\kappa }=\mathcal{O}\left(100\right)$, the initial response is cross-link-dominated, with $G_0/G_0^{\infty }\propto \tilde{s}$, whereas $G_0$ is expected to vanish in the limit $\tilde{s}\to 0$ when force can no longer be transmitted through the network. The value of the cross-link spring constant, $s_{\kappa }=\mathcal{O}\left({10}^{-5}\right)$ N/m, which marks the transition to a cross-link-dominated network response at small strains, is consistent with the spring constant of a highly compliant filamin cross-linking protein, estimated at small extension to be $\mathcal{O}\left({10}^{-6}\right)$ N/m (56). As a result, the small-strain response of an F-actin/filamin network is cross-link-dominated.

Figure 3.

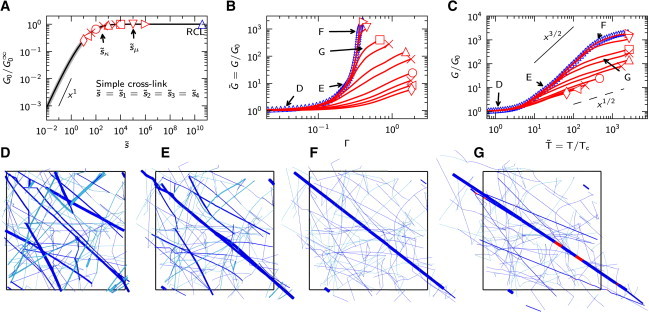
The effect of cross-link number $\tilde{s}$ of the networks with constant connectivity ${\tilde{n}}_{\text{X}}\approx 0.34$, $l_{\text{c}}\approx 0.86\mu \text{m}$. (A) The ensemble-averaged small strain response as a function of cross-link number $\tilde{s}$. The initial shear modulus, G₀, is normalized by the initial network shear modulus in the rigidly cross-linked limit $G_0^{\infty }$. The standard deviation is represented by the gray region. (B and C) The ensemble-averaged shear modulus, $\tilde{G}=G/G_0$, as a function of strain, Γ, and normalized stress, $\tilde{\text{T}}=\text{T}/{\text{T}}_{\text{c}}$, respectively, for selected $\tilde{s}$ values, as indicated by the symbols in (A). The response of the RCL networks is shown in blue. Standard deviations (up to about twice the symbol size) are not shown. (D–G) View of the deformed network at stress states indicated by the letters in (B) and (C) for the RCL case at $\tilde{\text{T}}\approx 1$ (D), $\tilde{\text{T}}\approx 20$ (E), and $\tilde{\text{T}}\approx 400$ (F) and for $\tilde{s}={10}^4$ at $\tilde{\text{T}}\approx 500$ (G). Filaments under tension/compression are shown in blue/light blue and cross-links in red. The thickness of a constituent is taken to be linearly proportional to its axial force normalized by the maximum axial force in the network, to help identify stress paths. To see this figure in color, go online.

Bending-dominated stiffening

Networks generally show a linear stress response at small strains, i.e., a constant stiffness, $G_0$, up to a critical strain, ${\text{Γ}}_{\text{c}}$, or critical stress, ${\text{T}}_{\text{c}}$, followed by nonlinear strain stiffening (see Fig. 3, B and C). RCL networks are found to stiffen rapidly with a 3/2 power-law dependence of the normalized shear modulus, $\tilde{G}$, on normalized stress, $\tilde{\text{T}}=\text{T}/{\text{T}}_{\text{c}}$ (Fig. 3 C, blue); the same phenomenology is observed in experiments on cross-linked F-actin/scruin (8,9) and neurofilament networks (36). The behavior of RCL networks, as well as the origin of their stiffening, has been studied extensively elsewhere (38); here, we briefly summarize the main findings.

Below the critical strain, ${\text{Γ}}_{\text{c}}$, RCL networks are bending-dominated structures that deform in a nonaffine manner, involving collective bending and reorientation of the fiber segments in the network (38,51). Inspection of the microstructure of an RCL network at small strain (Fig. 3 D) reveals a few fiber segments in the network that are highly stressed in their axial direction and separated from each other by low stress regions. As the strain is increased toward ${\text{Γ}}_{\text{c}}$, the number of these axially stressed segments grows while they gradually rotate toward a common direction. This eventually leads to the formation of a somewhat undulated bundle of highly axially stressed fiber segments that percolates through the network (Fig. 3 E, thick line). From the moment the undulated stress path emerges (i.e., at the critical strain ${\text{Γ}}_{\text{c}}$), continued shearing predominantly increases the axial stress in this bundle of segments so as to straighten the bundle out by bending the segments (Fig. 3 F) and localize the load transfer. For this reason, we refer to the bundle as the stress path. In contrast to the nonaffine behavior of the network at small strains, the 3/2 power-law strain stiffening in an RCL network is associated with and fully controlled by the affine stretching of a stress path. For that reason, this type of stiffening can be analyzed in terms of a single stress path in a box (38) (see below and the Supporting Material). When considered independent of the rest of the network, the stress path of an RCL network can be seen as a statically undulated filament under tension, which has been shown (28) to exhibit the same asymptotic behavior as a thermally undulated semiflexible chain in the MacKintosh model (26,37). It is due to this analogy that the 3/2 power-law stiffening can be explained by two points of view (38), even though the physical origin of the undulations is different.

At high stress, $\tilde{\text{T}}$, due to the finite axial stiffness of the fibers, the RCL network response becomes stretching-dominated and linear again, but now with a modulus $\tilde{G}={\tilde{G}}_{\mu }$ that scales with the axial stiffness, μ.

Finite strain effects

When the cross-link stiffness is decreased from the RCL limit, the network response starts to become affected significantly at the moment when stretching of the cross-links in the stress path at high $\tilde{\text{T}}$ becomes as favorable as stretching of the fiber sections; this occurs when $s\approx \mu /l_{\text{c}}$ or, equivalently, $\tilde{s}\approx {\tilde{s}}_{\mu }=\mu l_{\text{c}}^2/\kappa$ (Fig. 3, B and C, open inverted triangle). Below ${\tilde{s}}_{\mu }$, we observe that the network shear modulus at high $\tilde{\text{T}}$, instead of becoming constant ${\tilde{G}}_{\mu }$, transits to a novel power-law $\tilde{G}\propto {\tilde{\text{T}}}^{1/2}$ (Fig. 3 C, open triangle). Interestingly, power-law stiffening near an exponent of 1/2 has been observed in experiments for various biopolymer networks, as shown in Fig. 1 (12,13,15,19,20,39), as well as in two-dimensional computer simulations of stiff networks (48,49). However, a quantitative understanding of 1/2 power-law stiffening is lacking.

The 1/2 power-law region continues to be dominated by the mechanics of a stress path (Fig. 3 F), yet in this case, its stretching stiffness is controlled by the cross-links (Fig. 3 F, red). In addition, partitioning of the energy during deformation of a network with compliant cross-links clearly indicates that 1/2 stiffening behavior is dominated by stretching (axial), rather than bending, of the cross-links (Fig. S3). Thus, although the stress path stretching during 3/2 stiffening behavior could be accommodated only via bending out the undulations, a low cross-link compliance at large network strains allows for stretching of the stress path by stretching of the cross-links only. In addition, since the stiffness of the stress path composed of fiber sections and compliant cross-links is much smaller than that of the stress paths with only fiber sections, the shear strains can become larger (Fig. 3 B), giving rise to an enhanced reorientation of the stress path. In the next section, we show that a simple model of a stress path in a box can explain both the 1/2 and 3/2 scaling for strain-stiffening networks.

Stress path in a box

We idealize the nonlinear behavior of a network containing a stiffening stress path by that of a single fiber of filament sections and cross-links in a cubic box of size W (see Fig. 4). This nonlinear stress path is assumed to emerge under shear at a critical stress level, ${\text{T}}_{\text{c}}$, with corresponding strain ${\text{Γ}}_{\text{c}}$. Beyond this strain, the initially constant stiffness, $G_0$, changes abruptly into a stiffness that depends on the relative strain, $\gamma :=\text{Γ}-{\text{Γ}}_{\text{c}}$. As discussed in detail in the Supporting Material, $G\left(\gamma \right)$ can be shown to behave as $G\propto \left(\text{d}{f}_{\text{r}}/\text{d}r\right){\text{sin}}^2\beta$, where $f_{\text{r}}$ is the tensile force along this single fiber and $\beta =\text{arctanΓ}$.

Figure 4.

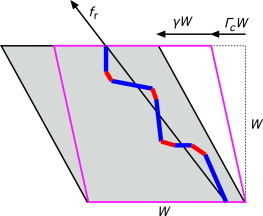
Simple shear of the box containing a percolating stress path comprised of fiber constituents (blue) and cross-links (red). The box at the critical strain, Γ_c, is shown in magenta. Subsequent shearing by γ is accomplished by extension of the stress path. To see this figure in color, go online.

The solution of $G\left(\gamma \right)$ has interesting scaling relations in two limiting situations. One limiting situation is the RCL network, for which it is found (38) that $G\propto {\text{T}}^{3/2}$. The exponent 3/2 is intimately related to the fact that an undulated (inextensible) filament stiffens rapidly as it is pulled taut. When the cross-link compliance is significant, this rapid stiffening of the filament does not take place and continued deformation can give rise to substantial reorientation of the stress path. Geometrically nonlinear effects associated with this give rise to the $G\propto {\text{T}}^{1/2}$ scaling for cross-link-dominated stiffening.

Effect of connectivity, ${\tilde{n}}_{\text{X}}$

In experiments where the concentration of cross-linking molecules is varied at a constant fiber concentration and a constant fiber length, it has been found that if the concentration of cross-linking molecules increases, the stiffening of the network decreases (cf. Fig. 1 B). However, the explanation for this is elusive. Since an increase in the concentration of the cross-linking molecule is expected to increase the network connectivity, we study how ${\tilde{n}}_{\text{X}}$, as a measure of connectivity, affects the nonlinearity of the network response. Moreover, we show that the results shown in Fig. 5 for three different values of ${\tilde{n}}_{\text{X}}$ can be rationalized in terms of the cross-link number, $\tilde{s}$.

Figure 5.

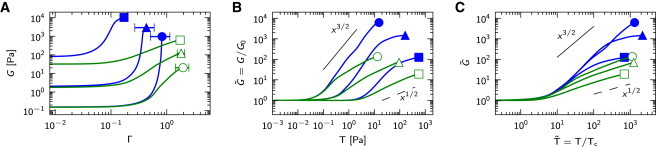
The effect of connectivity, ${\tilde{n}}_{\text{X}}$. The ensemble-averaged responses $G\left(\text{Γ}\right)$(A), $\tilde{G}\left(\text{T}\right)$(B), and $\tilde{G}\left(\tilde{\text{T}}\right)$ (C) of networks for cross-link spring constants $s\to \infty$ (blue) and $s\approx 4\times {10}^{-5}\text{N}/\text{m}$ (green) and connectivity ${\tilde{n}}_{\text{X}}\approx 0.12$, $l_{\text{c}}\approx 1.2\mu \text{m}$ (circles), ${\tilde{n}}_{\text{X}}\approx 0.34$, $l_{\text{c}}\approx 0.86\mu \text{m}$ (triangles), and ${\tilde{n}}_{\text{X}}\approx 0.72$, $l_{\text{c}}\approx 0.34\mu \text{m}$ (squares). Standard deviations (up to about twice the symbol size) are not shown. To see this figure in color, go online.

We first note that for constant $l_0$, ${\tilde{n}}_{\text{X}}$ is directly related to the mean cross-link spacing, $l_{\text{c}}$ (38), which in turn is key in the balance between cross-link and filament stiffness, as expressed by $\tilde{s}=s{l}_{\text{c}}^3/\kappa$.

As a consequence, by varying ${\tilde{n}}_{\text{X}}$ in Fig. 5 from 0.12 to 0.72, at fixed $l_0$ and at fixed cross-link spring constant $s\approx 4\times {10}^{-5}\text{N}/\text{m}$ (Fig. 5, green lines), we effectively change the value of $\tilde{s}$ by nearly two orders of magnitude. The cross-link spring constant, s, is chosen such that for moderate connectivity, ${\tilde{n}}_{\text{X}}\approx 0.34$ and $l_{\text{c}}\approx 0.86\mu \text{m}$ (Fig. 5, green triangle), ${\tilde{s}}_{0.34}$ is in the knee of the transition seen in Fig. 3 A (hence ≈${\tilde{s}}_{\kappa }$). At this connectivity, the small strain behavior is dominated by the bending of the fiber sections, since $G_0/G_0^{\infty }\approx 1$, whereas the nonlinear behavior is governed only by the finite strain effect (1/2 power-law stiffening), as seen in Fig. 3.

The network with low connectivity, ${\tilde{n}}_{\text{X}}\approx 0.12$ (Fig. 5, green circle), has longer fiber sections ($l_{\text{c}}=1.2\mu \text{m}$) than that with connectivity ${\tilde{n}}_{\text{X}}\approx 0.34$, and due to the decreased relative bending rigidity, the cross-link number, ${\tilde{s}}_{0.12}$, exceeds ${\tilde{s}}_{0.34}$. The response for ${\tilde{n}}_{\text{X}}\approx 0.12$ therefore starts as in the RCL limit and is followed by nonlinear behavior that is initially dominated by 3/2 stiffening. At increased stress, however, the response undergoes a bending-to-stretching transition, after which stiffening behavior is governed by the 1/2 mechanism, as is expected for $\tilde{s}>{\tilde{s}}_{\kappa }$. For networks with ${\tilde{n}}_{\text{X}}\approx 0.72$ (Fig. 5, green squares), on the other hand, this effect is reversed: a short section length ($l_{\text{c}}\approx 0.34\mu \text{m}$) increases the bending rigidity of fiber sections, so that ${\tilde{s}}_{0.72}<{\tilde{s}}_{0.34}$. Thus, such networks are initially softer than in the RCL limit (Fig. 5, blue squares) and exhibit $1/2$ stiffening.

The effect of connectivity on $\tilde{s}$ and the network response presented in Fig. 5 can explain the trends observed in experiments with F-actin/rigor-HMM networks (13) (Fig. 1 B) or branched collagen-I-type networks (19,20). The decreasing stiffening behavior observed for increasing HMM concentration at constant concentration of F-actin and constant F-actin length, for example, naturally emerge from a drop in $\tilde{s}$, which in turn shifts the network response from the 3/2 mechanism toward the 1/2 mechanism (Fig. 5, B and C). It is interesting to note that such an explanation suggests that F-actin/rigor-HMM network may behave as an RCL network only at small strains and for lower rigor-HMM concentrations. The low exponents observed specifically for F-actin/rigor-HMM networks, however, could also arise from the dynamic behavior of HMM molecules, as was originally argued by Tharmann et al. (13).

Characteristic ratio

As shown above, the stiffening behavior of the cross-linked networks can be understood in terms of the response of a single stress path. For RCL networks, the stress path comprises only fiber sections so that the dependence of the response on the fiber properties μ and κ can be conveniently related to the characteristic ratio $l_{\text{b}}/l_{\text{c}}$, where $l_{\text{b}}=\sqrt{\kappa /\mu }$ (57) (note that for a homogeneous beam with a circular cross section, $l_{\text{b}}$ is equal to half the beam radius).

In Fig. 6 we demonstrate how the response of an RCL network depends on the characteristic length, $l_{\text{b}}$.

Figure 6.

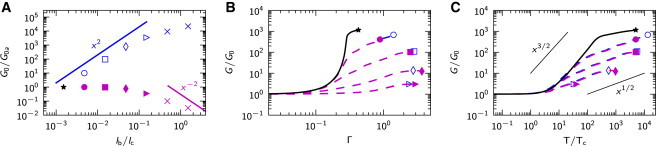
(A) Normalized initial shear modulus, $G_0/G_{0\text{a}}$, of the RCL network with $l_{\text{c}}=0.86\mu \text{m}$ versus characteristic ratio $l_{\text{b}}/l_{\text{c}}$, where $G_{0\text{a}}$ is the initial shear modulus calculated for the RCL F-actin network with $\mu ={\mu }_{\text{a}}=4\times {10}^{-8}$ N and $\kappa ={\kappa }_{\text{a}}=6.75\times {10}^{-26}$ N/m. The $l_{\text{b}}/l_{\text{c}}$ for the RCL F-actin network is indicated by the star. Larger values of $l_{\text{b}}/l_{\text{c}}$ are obtained either for $\mu <{\mu }_{\text{a}}$ and constant $\kappa ={\kappa }_{\text{a}}$ (magenta solid symbols) or for $\kappa >{\kappa }_{\text{a}}$ and constant $\mu ={\mu }_{\text{a}}$ (blue open symbols). The straight lines indicate the scaling laws of open-cell foams for the two extreme limits 1. (B and C) The large strain response of the RCL network for various $l_{\text{b}}/l_{\text{c}}$ ratios shown in (A), where $G/G_0$ is the network shear modulus scaled by the initial modulus, $G_0$, and $\text{T}/{\text{T}}_{\text{c}}$ is the stress scaled by the stress value at the onset of nonlinearity, ${\text{T}}_{\text{c}}$. To see this figure in color, go online.

For this, we use a single microstructure with fixed $l_{\text{c}}=0.86\mu \text{m}$, as shown in Fig. 3, D–F. The response for fiber properties set to represent F-actin, i.e., $\mu ={\mu }_{\text{a}}=4\times {10}^{-8}$ N and $\kappa ={\kappa }_{\text{a}}=6.75\times {10}^{-26}$ N/m, is indicated by the star in Fig. 6. Since in this case $l_{\text{b}}/l_{\text{c}}\approx 1/1000\ll 1$, networks with $l_{\text{b}}/l_{\text{c}}$ ratios larger than that of RCL F-actin are obtained for $\mu <{\mu }_{\text{a}}$ and constant $\kappa ={\kappa }_{\text{a}}$ (Fig. 6, magenta symbols) or for $\kappa >{\kappa }_{\text{a}}$ and constant $\mu ={\mu }_{\text{a}}$ (Fig. 6, blue symbols). As expected, the small strain response of the RCL network in Fig. 6 A is bending-dominated with $G_0\propto l_{\text{b}}^2$ or $G_0\propto \kappa$ for $l_{\text{b}}/l_{\text{c}}\ll 1$, as for open-cell foams (1), and stretching-dominated with $G_0\propto l_{\text{b}}^{-2}$ or $G_0\propto \mu$ for $l_{\text{b}}/l_{\text{c}}\to 1$. The response at large strains becomes increasingly less nonlinear for increasing $l_{\text{b}}/l_{\text{c}}$ (Fig. 6 B), with a clearly observable 3/2 to 1/2 stiffening transition (Fig. 6 C). In addition, the different responses corresponding to the same magnitude of $l_{\text{b}}/l_{\text{c}}$ (e.g., Fig. 6, B and C, open and solid symbols) are identical, indicating that the ratio $l_{\text{b}}/l_{\text{c}}$ is the key parameter in characterizing the response of an RCL network, like the spring number $\tilde{s}$ for the cross-linked networks in Figs. 3 and 5. Essentially, the same trends observed in Fig. 3 C for cross-linked networks in terms of the spring number $\tilde{s}$ are now confirmed in Fig. 6 C for RCL networks in terms of $l_{\text{b}}/l_{\text{c}}$.

In general, the stress path of cross-linked networks comprises fiber sections and cross-links in series so that its effective compliance can be estimated to be the sum of those of the fibers and the cross-links. Thus, we generalize the characteristic ratio of the composite stress path as ${\tilde{l}}_{\text{b}}/l_{\text{c}}=\sqrt{k_{\text{b}}/k_{\text{a}}}$, with effective bending spring constant $k_{\text{b}}\approx 1/\left(l_{\text{c}}^3/\kappa +1/s\right)$ and effective axial spring constant $k_{\text{a}}\approx 1/\left(l_{\text{c}}/\mu +1/s\right)$. The resulting effective ratio ${\tilde{l}}_{\text{b}}/l_{\text{c}}$ then takes the form

$$\frac{{\tilde{l}}_{\text{b}}}{l_{\text{c}}}\approx \sqrt{\frac{\tilde{s}{\left(l_{\text{b}}/l_{\text{c}}\right)}^2+1}{\tilde{s}+1}}.$$ (1)

In the RCL limit where $\tilde{s}\gg 1$, ${\tilde{l}}_{\text{b}}/l_{\text{c}}\to l_{\text{b}}/l_{\text{c}}$. On the other hand, for networks with constant filament constituents ($l_{\text{b}}/l_{\text{c}}=\text{const}.$), like the networks studied in Figs. 3 and 5, the characteristic ratio ${\tilde{l}}_{\text{b}}/l_{\text{c}}$ can be uniquely related to the cross-link number, $\tilde{s}$. For example, for networks with $l_{\text{b}}/l_{\text{c}}\ll 1$ and cross-link number $1\ll \tilde{s}\ll {\tilde{s}}_{\mu }$ (see Fig. 3), Eq. 1 suggests an inverse square-root dependence, i.e., ${\tilde{l}}_{\text{b}}/l_{\text{c}}\approx 1/\sqrt{\tilde{s}}$. In addition, note that a small characteristic ratio, ${\tilde{l}}_{\text{b}}/l_{\text{c}}\ll 1$, leads to the bending-dominated stiffening mechanism and network behavior characterized by the power law $\tilde{G}\propto {\tilde{\text{T}}}^{3/2}$. For higher characteristic ratios, the large strain behavior is showing a transition to stretching-dominated stiffening, characterized by the power-law exponent 1/2.

The precise determination of $k_{\text{a}}$ and $k_{\text{b}}$ of a composite stress path and the corresponding ${\tilde{l}}_{\text{b}}/l_{\text{c}}$ ratio requires detailed knowledge of the composition of the stress path, that is, the number of fiber sections and cross-links in the path, as well as their connectivity. Unfortunately, this information is generally difficult to obtain, since the stress path forms only after the network response passes its critical point and becomes nonlinear. Moreover, it can be expected that the stress-path composition is influenced by the concentration of the network constituents and the network microstructure, and this dependence is not yet known.

Additional complications in evaluating the effective spring constants $k_{\text{a}}$ and $k_{\text{b}}$ arise from the fact that the load-bearing network structure sometimes is more complex than a single stress path, as shown, for example, in Fig. 7. Commonly, these kinds of supportive frames are found in networks of larger connectivity (Fig. 7, A and B), but they can also be observed in networks of low to moderate connectivity when they have very compliant cross-links (Fig. 7 C). Similar supportive frames have also been observed by Kim et al. (44) in molecular dynamics simulations of F-actin networks.

Figure 7.

View through the deformed network realization showing load-bearing supportive frames ${\tilde{n}}_{\text{X}}\approx 0.72$ for the RCL limit in Fig. 5 (blue square) at $\text{T}\approx 30\text{Pa}$ (A), ${\tilde{n}}_{\text{X}}\approx 0.72$ for $s\approx 4e-5\text{N}/\text{m}$ in Fig. 5 (green square) at $\text{T}\approx 65\text{Pa}$ (B), ${\tilde{n}}_{\text{X}}\approx 0.34$ for $\tilde{s}=10$ in Fig. 3 (red diamond) at $\tilde{\text{T}}\approx 30$ (C). The axial stress map is obtained in the same way as in Fig. 3, D–F. To see this figure in color, go online.

Despite the difference in appearance, however, supportive frames are qualitatively not different from individual stress paths. For example, the RCL network with a high connectivity of ${\tilde{n}}_{\text{X}}\approx 0.72$, whose supportive frame is shown in Fig. 7 A, stiffens according to a 3/2 power law (Fig. 5 B, blue square), but if the cross-links are compliant, the stiffening of the same network follows a 1/2 power law (Fig. 5 B, green open square), despite the fact that the corresponding supportive frame is very different (see Fig. 7 B). These results suggest that a supportive frame consists of a set of several stress paths interconnected in series or in parallel, as directly suggested by Fig. 7. Hence, the specific architecture of a supportive frame is expected to affect only the magnitudes in the response, not those in the general scaling relations.

Discussion

In this computational study, we have performed a detailed investigation of the structure-property relations for a discrete random network of permanently cross-linked fibers, relating the stiffening behavior to the material properties of its constituents and the network microstructure.

The observation that the nonlinear network response is dominated by the behavior of a localized percolating path across axially stressed network constituents allows for a simple rationalization of the strain-stiffening behavior in terms of two fundamental mechanisms: 1) the pulling out of stress-path undulations; and 2) finite strain effects induced by reorientation of the stress path. Although the first of these is a bending-dominated mechanism that can be characterized by a power-law dependence with exponent 3/2 of the shear modulus, G, on stress, $\text{T}$, the second has been revealed here as a stretching-dominated finite strain effect that gives rise to a power-law relation between G and $\text{T}$ with exponent 1/2.

Which of the two stiffening mechanisms is active is determined by the characteristic ratio, ${\tilde{l}}_{\text{b}}/l_{\text{c}}$. Since ${\tilde{l}}_{\text{b}}/l_{\text{c}}$ relates material properties (bending and axial stiffnesses) of the network constituents to the key length scale of the microstructure ($l_{\text{c}}$), the same large strain network response can be obtained in various ways for different networks.

This unification of network behavior in terms of a single parameter can be demonstrated in the form of master plots of normalized shear modulus, $G/G_0$, against normalized stress, $\text{T}/{\text{T}}_{\text{c}}$, for different ${\tilde{l}}_{\text{b}}/l_{\text{c}}$, as shown in Fig. 8. This graph uniquely defines the bending-to-stretching transition at large strains over a wide range of material and topological parameters, spanning two decades of ${\tilde{l}}_{\text{b}}/l_{\text{c}}$.

Figure 8.

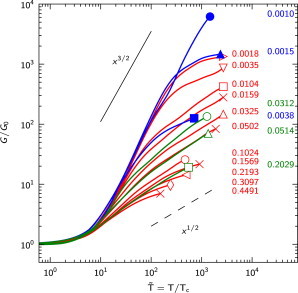
Compilation of all curves of $G/G_0$ versus normalized stress, $\text{T}/{\text{T}}_{\text{c}}$, along with the corresponding values of ${\tilde{l}}_{\text{b}}/l_{\text{c}}$, for the cases in Fig. 3C (where cross-link stiffness is varied at constant connectivity) and Fig. 5C (at constant cross-link stiffness but varying connectivity). To see this figure in color, go online.

There is a pronounced bending-dominated response at large strains leading to 3/2 power-law stiffening for ${\tilde{l}}_{\text{b}}/l_{\text{c}}\ll 1$. Such strain-stiffening behavior is found when the stress path developed in the network is much stiffer in tension than in bending. Examples of networks that stiffen in this way all the way up to fracture are F-actin/scruin networks (8,9) and cross-linked neurofilaments (36) (Fig. 1 A).

Networks associated with a somewhat higher characteristic ratio, e.g., ${\tilde{l}}_{\text{b}}/l_{\text{c}}\approx 0.01$, show a transition from 3/2 to 1/2 power-law stiffening. Fig. 1, C and D, suggests that F-actin/filamin networks and intermediate filament networks, respectively, can be classified in this way. In considering the transition between stiffening mechanisms experimentally, it should be noted that networks have a maximum stiffness (determined by the effective axial stiffness, $G\propto 1/\left(l_{\text{c}}/\mu +1/s\right)$). This may make it difficult to distinguish the transition between stiffening mechanisms from the approach to this maximum network stiffness.

For networks with ${\tilde{l}}_{\text{b}}/l_{\text{c}}\approx 0.1$, the large strain response is mainly dominated by the stretching mechanism, leading to stiffening with power-law exponent $1/2$. Increased characteristic ratios, ${\tilde{l}}_{\text{b}}/l_{\text{c}}$, can arise in networks from rather compliant filament interconnections, as could be the case for HMM molecules in F-actin/rigor-HMM networks (13) (Fig. 1 B) or perhaps collagen branching points in the case of branched collagen-I-type networks (19,20).

For networks with ${\tilde{l}}_{\text{b}}/l_{\text{c}}\to 1$, the stiffening ability is greatly diminished due to the 1/2 mechanism, whereas the onset of nonlinearity is pushed to larger strains. Trends of this kind can be observed in bundled F-actin/fascin networks at high fascin concentrations, which are unable to stiffen at all (14). In these networks, a higher fascin concentration can increase the bending resistance of the bundles in several simultaneous ways, e.g., by decreasing the length of the bundle segments (equivalent to $l_{\text{c}}$ in our model), increasing the bundle diameter (14), and/or increasing the coupling between the filaments within the bundle (58). Thus, a higher fascin concentration could increase ${\tilde{l}}_{\text{b}}/l_{\text{c}}$ to values of ∼1 and cause network rupture long before the finite strain effect can give rise to stiffening.

The characteristic ratio, ${\tilde{l}}_{\text{b}}/l_{\text{c}}$, also governs the initial network stiffness, $G_0$, and the critical strain, ${\text{Γ}}_{\text{c}}$, since it controls the bending-to-stretching transition at small strains as well. At smaller characteristic ratios, e.g., ${\tilde{l}}_{\text{b}}/l_{\text{c}}\le 0.1$, the small-strain network response is determined by the bending of the fibers, so that $G_0$ and ${\text{Γ}}_{\text{c}}$ in this regime follow the same scaling as developed in our previous work for RCL networks (38). In case of ${\tilde{l}}_{\text{b}}/l_{\text{c}}\to 1$ on the other hand, the initial network stiffness, $G_0$, becomes stretching-dominated, for which we generally expect $G_0\propto k_{\text{a}}$, the effective axial stiffness.

Conclusions

In conclusion, biopolymer-like networks of different constituents and different microstructures show strain-stiffening trends that can be understood in terms of the competition between two stiffening mechanisms. The relative importance of the two mechanisms for stiffening can be expressed through the effective characteristic ratio, ${\tilde{l}}_{\text{b}}/l_{\text{c}}$, of the network. The strain-stiffening trends observed experimentally in a wide variety of biopolymer networks can thus be characterized by this single parameter. In addition to the two fundamental mechanisms for stiffening presented here, it is important to note that the large strain response of some biopolymer networks may be much more complex due to the presence of additional mechanisms that can affect stiffening; examples of this include time- or force-dependent cross-link unbinding/rupturing and rebinding, which has been proposed as an explanation for the stiffening of F-actin/rigor-HMM networks (13). The extent to which these additional mechanisms affect the network response may be important and should be taken into account in future studies.