Abstract
Adequate sampling of conformation space remains challenging in atomistic simulations, especially if the solvent is treated explicitly. Implicit-solvent simulations can speed up conformational sampling significantly. We compare the speed of conformational sampling between two commonly used methods of each class: the explicit-solvent particle mesh Ewald (PME) with TIP3P water model and a popular generalized Born (GB) implicit-solvent model, as implemented in the AMBER package. We systematically investigate small (dihedral angle flips in a protein), large (nucleosome tail collapse and DNA unwrapping), and mixed (folding of a miniprotein) conformational changes, with nominal simulation times ranging from nanoseconds to microseconds depending on system size. The speedups in conformational sampling for GB relative to PME simulations, are highly system- and problem-dependent. Where the simulation temperatures for PME and GB are the same, the corresponding speedups are approximately onefold (small conformational changes), between ∼1- and ∼100-fold (large changes), and approximately sevenfold (mixed case). The effects of temperature on speedup and free-energy landscapes, which may differ substantially between the solvent models, are discussed in detail for the case of miniprotein folding. In addition to speeding up conformational sampling, due to algorithmic differences, the implicit solvent model can be computationally faster for small systems or slower for large systems, depending on the number of solute and solvent atoms. For the conformational changes considered here, the combined speedups are approximately twofold, ∼1- to 60-fold, and ∼50-fold, respectively, in the low solvent viscosity regime afforded by the implicit solvent. For all the systems studied, 1) conformational sampling speedup increases as Langevin collision frequency (effective viscosity) decreases; and 2) conformational sampling speedup is mainly due to reduction in solvent viscosity rather than possible differences in free-energy landscapes between the solvent models.
Introduction
Molecular dynamics (MD) simulations are routinely used to study the structure, function, and activity of biological molecules (1–4). Over 12,000 articles regarding MD were published in 2009 alone, with over 300 in the top scientific journals (5). However, without highly specialized supercomputers (6), simulation times accessible by the most commonly used atomistic methods—those that provide the highest level of detail—are still much shorter than the timescale of many important biomolecular processes, such as ligand binding, folding of most proteins, and enzyme turnover, which occur on timescales in the range of tens of microseconds to seconds and even longer (2,7–9). Without sufficiently long simulation times, these methods will most likely fail to sample some important conformations and structural transitions.
Atomistic MD simulation methods can be divided into two broad classes: those that treat solvent explicitly and those that treat solvent implicitly (10,11). The main objective of this study is to compare the speed of conformational sampling within these two very different approaches to treating solvent effects. We also investigate the purely computational speedup due to the algorithmic differences between two commonly used explicit and implicit solvent models—the particle mesh Ewald (PME) explicit solvent model and the generalized Born (GB) implicit solvent model.
Explicit-solvent methods, without further approximations, treat solvent molecules explicitly, i.e., interactions between all pairs of solute and solvent atoms are explicitly computed. The PME approximation, the most commonly used explicit-solvent method for biomolecular simulations, speeds up these computations by imposing an artificial periodicity on the entire system and treating the system as an infinite crystal with identical repeating cells (12–15). This assumption allows for a mathematical transformation that approximates the long-range interactions very efficiently, without significant loss in accuracy.
Implicit-solvent methods, on the other hand, speed up atomistic simulations by approximating the discrete solvent as a continuum, thus drastically reducing the number of particles to keep track of in the system. An additional effective speedup often comes from much faster sampling of the conformational space afforded by these methods. The GB approximation, the most commonly used implicit-solvent method in atomistic MD simulations, approximates long-range electrostatic interactions via an analytical formula (16–43):
| (1) |
| (2) |
| (3) |
| (4) |
where , and are the total, vacuum, and solvation energy contributions due to electrostatic interactions between atoms i and j. Here, and are the internal (solute) and external (solvent) dielectric constants, qi and qj are the charges of atoms i and j, rij is the distance between the atoms, and Bi and Bj are their effective Born radii. The effective Born radii account for the dielectric screening effect of the solvent, and their values reflect the atom’s degree of burial within the solvent. The term accounts for the screening effect of monovalent salt (44), with κ being the Debye-Hückel screening parameter.
Implicit treatment of solvent, although arguably less accurate than the explicit-solvent approach (45,46), is widely used in molecular simulations for two main reasons. First, the implicit-solvent method can be algorithmically/computationally faster, as measured by simulation time steps per processor (CPU) time, because the vast number of individual interactions between the atoms of individual solvent molecules do not need to be explicitly computed. Second, and now perhaps the main reason for the use of implicit- instead of explicit-solvent simulations, is that implicit-solvent simulations can sample conformational space faster (25,47–49). To some extent, the interest in implicit-solvent-based simulations is motivated by the need to sample very large conformational spaces for problems such as protein folding (50,51), binding-affinity calculations (48), or large-scale fluctuations of nucleosomal DNA fragments (52).
Two main factors are expected to contribute to the speedup of conformational sampling by implicit-solvent models such as the GB, compared to explicit-solvent models: 1) reduction of the effective solvent viscosity, which, ideally, has no effect on the energy landscape (thermodynamics) of the system; and 2) possible alterations of the energy landscape itself, some of which may have desirable speedup effects on kinetics but undesirable effects on thermodynamics (53,54). These issues will be discussed in the Results and Discussion section below, with the most detailed analysis presented for the case of miniprotein folding. This study does not investigate the accuracy of the implicit-solvent approximations, explicit water models, PME, force fields, etc. These very important issues have been extensively studied elsewhere (34,55–60). Comparing the accuracy of MD methods on realistic bimolecular structures is a complex, multidimensional problem; there is little hope of arriving at a full picture in a single study. However, the dimensionality of the problem is greatly reduced for efficiency (speedup) comparisons, so we are confident that careful tests on a few judiciously chosen molecular systems will give us a reasonably comprehensive picture, at least for the two commonly used solvent models we are going to analyze.
Several previous studies (25,47,48,51) have demonstrated that the speed of conformational sampling in implicit-solvent simulations can be ∼2–20 times faster than common explicit-solvent PME simulations. However, a number of important questions remain: 1) How does the speedup of conformational sampling depend on structure size and type of conformational change involved? The sampling speed is affected by an intricate balance between solute-solute and solute-solvent friction (61,62), and this balance is expected to be different for different types of systems and conformational transitions (47). 2) How do simulation parameter(s) that determine the effective solvent viscosity influence the speedup? The influence of solvent viscosity on kinetics has not been thoroughly investigated beyond small proteins (51,61,62) and peptides (47,63). 3) Is the speedup primarily due to reduced viscosity or to possible alterations of the free-energy landscapes by the implicit-solvent treatment? 4) What is the combined speedup—the rate of conformational sampling per day of real simulation time—when the algorithmic differences between realistic explicit- and implicit-model implementations are taken into account? After all, it is this effective speed that is of direct interest to practitioners. To address all of these questions, we have performed a systematic analysis across a range of structure sizes and types of conformational transitions.
The types of conformational changes considered here include dihedral angle flips in a protein, nucleosome tail collapse, unwrapping of DNA from the nucleosome core, and folding of a miniprotein. The solute structure sizes considered here range from 166 to 25,100 atoms.
The two speed-up methods we have chosen for comparison, the GB and the PME methods, are by no means unique. Many other approaches exist for increasing computational efficiency of atomistic MD simulations and for speeding up conformational sampling (for reviews, see, e.g., Onufriev (10) and Zuckerman (45)). Replica-exchange MD, for example (64–66), enhances conformational sampling by exchanging conformational samples across simulations at multiple temperatures. Accelerated MD simulations enhance conformational sampling by lowering the energy barrier between conformational states (46). The use of longer integration time steps for certain parts of the calculation can increase the simulation time per CPU time (67–69). However, these and many other speedup and enhanced-sampling methods can be applied to both the explicit- and implicit-solvent models. Since the focus of this work is comparing the effects of the two generic opposing solvent models on the efficiency of biomolecular simulations, we do not consider these additional speedup and enhanced-sampling methods here.
The remainder of this article is organized as follows. The structure preparation and simulation protocol used for the simulations are described in the Materials and Methods section. The results of the simulations are discussed in the Results and Discussion section. And our findings are summarized in the Conclusions.
Materials and Methods
We used five different molecular structures for this study: a 166-atom protein, CLN025 (70), a more stable version of chignolin (71), to study folding; a 4812-atom phospholipase C (Protein Data Bank (PDB) (72) ID 1GYM (73)) to study dihedral angle flips; a 25,100-atom nucleosome complex (PDB ID 1KX5 (74)) to study the collapse of histone tails onto the DNA and the unwrapping of the DNA from the histone core. The structure preparation and simulation protocols used for each of the above structures vary slightly from structure to structure. However, for the most part, the protocol described below was used, with variations from this protocol noted in the Methodological details section.
The protonation state for titratable groups were set using the H++ web server (75) for pK prediction and structure preparation, at pH 6.5. For explicit-solvent simulations, the structures were solvated in a truncated octahedral TIP3P (76) water box extending 10 Å from the solute. Counterions were added to the water box to neutralize the system while approximating a salt concentration of 0.145 M. The Amber ff10 (77) force field was used for both implicit- and explicit-solvent simulations.
To run the MD simulations, we used the GPU implementation of the Amber 12 MD software package with the SPFP model (78–80). The PME method (12) with constant-volume periodic boundary condition was used for explicit-solvent simulations and the OBC variant (igb5) of the GB method (16) for the implicit-solvent simulations. All references to PME in this article refer to the explicit-solvent PME method with a TIP3P water box. The simulation protocol consisted of five stages. First, the structure was relaxed with 2000 steps of conjugate-gradient energy minimization, with solute atoms restrained to the initial structure by a force constant of 5 kcal/mol/Å2. Next, the system was heated to 300 K over 600 ps, with a restraint force constant of 1 kcal/mol/Å2. The system was then equilibrated for 2 ns with a restraint force constant of 0.1 kcal/mol/Å2, followed by another 2 ns with a restraint force constant of 0.01 kcal/mol/Å2. All restraints were removed for the production stage. The simulation time step was 2 fs/iteration. A direct space cutoff of 8 Å was used for all stages of the PME simulations. No cutoff was used for the calculation of pairwise interactions, with rgbmax = 15 Å. Langevin dynamics (81) was used for temperature regulation with a collision frequency of γ = 0.01 ps−1. The Shake algorithm (82) was used to constrain covalently bound hydrogen atoms. For the analyses presented in the Results and Discussion section below, snapshots of the MD trajectory were taken every 10 ps. Default values were used for all other simulation parameters. See the Supporting Material for additional details.
Results and Discussion
Three different types of conformational transitions were considered here: small (dihedral angle flips), large (nucleosome histone tail collapse and DNA unwrapping from the nucleosome histone core), and mixed (folding of a miniprotein). Our choice of representative test structures was dictated by the need to run simulations of sufficient length to adequately sample the relevant conformation space in each representative case.
The total conformational sampling speedup offered by the implicit-solvent model, compared to the explicit-solvent alternative, may be due, at least in part, to the altering of the free-energy landscape, which may affect the underlying thermodynamics of the problem. Whether or not it is appropriate to use implicit solvent to benefit from the associated speedups depends on the problem at hand: for each of the conformational transitions considered here, we note the type of problem for which the model may still be useful despite the altered free-energy landscape.
In the following, we report standard error (SE) along with the mean value as mean ± SE. The computation of standard error is described in the Supporting Material.
Small conformational changes
Dihedral angle flips
Many biological processes, such as nonallosteric protein-ligand binding, involve small local conformational changes. To study such small conformational changes, we analyzed variations in χ1 and χ2 dihedral angles in explicit-solvent (TIP3P) PME and implicit-solvent GB simulations of an ∼300 residue protein, 1GYM.
For the 770 ns simulations considered here, the GB simulation does not explore exactly the same conformations as the explicit solvent (TIP3P) PME simulation. For example, the backbone root mean-square deviation (RMSD) relative to the starting structure is 1.6 Å for the explicit-solvent (TIP3P) PME simulation compared to 4.5 Å for the GB simulation (see Supporting Material). Therefore, to exclude, or at least reduce, the effect of larger global changes, we only considered groups where the distribution of the χ1 and χ2 angles were similar for the GB and explicit-solvent (TIP3P) PME simulations, i.e., the frequency at which the dihedral angle ranges were sampled differs by <10%. We identified 73 of 268 groups that met these criteria for χ1 angles, and 53 of 213 groups for χ2 angles.
To examine the sampling of χ1 and χ2 dihedral angles, we defined three ranges for all the dihedral angles (0–120°, 120–240°, and 240–360°) except the χ2 angles for ASN, ASP, HIS, PHE, and TYR. For those angles, we used two ranges, 180–0° and 0 to +180°. The frequency of χ1 (2.34 ± 0.002 flips/ns) and χ2 flips (7.55 ± 0.006 flips/ns) for the GB simulation is on average only slightly faster than the χ1 (1.58 ± 0.003 flips/ns) and χ2 flips (5.15 ± 0.005 flips/ns) for the explicit-solvent (TIP3P) PME simulation (Fig. 1).
Figure 1.
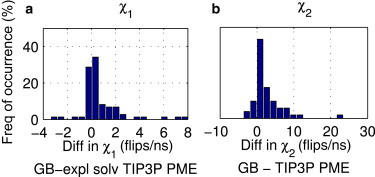
Difference in (a) χ1 and (b) χ2 dihedral angle flips (GB − explicit-solvent (TIP3P) PME) from 770 ns simulations of 1GYM protein. Flips are measured as changes in dihedral angles across distinct ranges of dihedral angles, as described in the text. To see this figure in color, go online.
Two conclusions can be made from examining Fig. 1: 1) on average, χ1 and χ2 flips occur only slightly (∼1.5 times) more frequently with the GB simulation than with the explicit-solvent (TIP3P) PME simulation; and 2) in some cases, the reverse is true.
We considered several different factors that may explain why one method samples these dihedral angles more frequently than the other. We analyzed the relationship between frequency of dihedral angle flips and 1) depth of burial within the protein, as measured by the effective Born radii of the Cβ and Cγ atoms for χ1 and χ2 angles, respectively (for an explanation, see the Supporting Material); 2) extent of hydrogen bonding between side chains and water, as measured by percentage of samples with such hydrogen bonds; 3) difference in side-chain conformation, as measured by residue RMSD; and 4) type of side chain. However, the correlations in each of these cases were not statistically significant (see Supporting Material), i.e., none of these factors could, separately, explain the differences in frequency of χ1 and χ2 dihedral angle flips. We speculate that some combination of these factors contributes to the differences in frequency of dihedral angle flips. For example, one would expect that the speedup for solvent-exposed surface groups would be higher than for buried groups. However, hydrogen bonds between side chains or steric constraints on large side chains, such as Tryptophan, can restrict the dihedral angles sampled, resulting in little or no difference in sampling speed between the implicit- and explicit-solvent models, even when the groups are on the surface.
Taking all of the above into account, we suggest that explicit solvent should be the primary choice for sampling dihedral transitions.
Large conformational changes
We considered two conformational changes to the 25,100 atom nucleosome, histone tail collapse and DNA unwrapping.
Nucleosome histone tail collapse
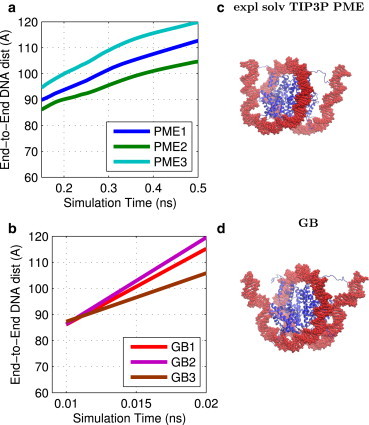
The nucleosome (PDB ID 1KX5) consists of an eight-protein histone core (H3, H3′, H4, H4′, H2A, H2A′, H2B, and H2B′) and a 147 bp DNA chain wrapped around the core (Fig. 2 a). In the PDB structure for 1KX5, the unstructured N-terminus tails for three of the histones (H3, H3′, and H2B′) extend well beyond the DNA surface. Experimentally, it has been shown that under physiological conditions, the unstructured positively charged histone tails collapse onto the negatively charged DNA (83). It has also been shown that histone tails regulate nucleosome mobility and stability (84), and MD simulations have been used to study this regulatory mechanism (85).
Figure 2.

Three sets of independent MD simulations of the nucleosome tail collapse. (a) PDB structure with three histone tails (H3, H3′, and H2B′) extended. (b) Structure with the positively charged histone tails collapsed onto the negatively charged DNA. DNA surface is shown in red and the histone backbone structure is shown in blue. Tail extension is measured as the distance from the N-terminus tail to the center of geometry of the DNA. (c–e) Results show moving average values, averaged over 0.5 ns, from three explicit-solvent (TIP3P) PME and GB simulations. Connecting lines are shown to guide the eye. Images were rendered using VMD (100). To see this figure in color, go online.
Both the explicit-solvent (TIP3P) PME and GB simulations reproduce the tail collapse (Fig. 2 b). The collapsed tail is highly unstructured and shows large conformational variation. For example, the number of histone H3 tail-DNA contacts fluctuates between 6 and 30 over the course of the simulation, even after the tail has collapsed. Since the question we are asking regards the general location of these highly unstructured tails, and not their specific conformations (which may also be highly dependent on the underlying gas-phase force field), the distance from the N-terminus of the histone to the geometric center of the DNA was used as the measure of histone tail extension. The collapsed state was defined as tail extension of <60 Å, representing the value below which all tails have clearly collapsed, both in explicit and implicit solvents (Fig. 2).
On average, the H3′ tail collapse is ∼100 times faster in the implicit-solvent GB simulation (0.10 ± 0.05 ns) than in the explicit-solvent (TIP3P) PME simulation (10 ± 4 ns); the H2B′ tail collapse is ∼7 times faster (0.05 ± 0.02 ns for GB compared to 0.34 ± 0.05 ns for PME), and the H3 tail collapse is almost no faster (0.71 ± 0.23 ns for GB compared to 0.82 ± 0.21 ns for PME). Clearly, there can be large variations from simulation to simulation.
Notice that in Fig. 2 a, the tails of H2B′ and H3 are not extended as far from the DNA as is the tail of H3′. Fig. 2 also shows that the H3′ N-terminus starts off ∼10 Å farther from the DNA than the N-termini for H3 and H2B′. This suggests that the H3 and H2B′ tails are already partially collapsed at the beginning of the simulation, which may explain why the speedup for the H3′ tail collapse is much larger than for the H2B′ and H3 tails.
Nucleosome DNA unwrapping
Accessibility to the DNA is critical for gene transcription, and therefore, the unwrapping of nucleosome DNA from the histone core has been extensively studied both experimentally (86) and computationally (87). Experiments have previously shown that at high pH, there is a loosening of the nucleosome structure (88). The implicit- and explicit-solvent TIP3P simulations show a similar effect, with the ends of the DNA unwrapping from the nucleosome core (Fig. 3). The ends of the DNA in an unwrapped state are extremely flexible, with fluctuations of >10 Å in end-to-end DNA distance after unwrapping. However, the DNA unwraps on average ∼30 times faster in the GB simulation (0.04 ± 0.02 ns) than in the explicit-solvent (TIP3P) PME simulation (1.3 ± 0.4 ns), averaged over three MD runs of equal length. Clearly, there can be large variations from simulation to simulation.
Figure 3.
Nucleosome DNA unwrapping at high pH. (a and b) DNA end-to-end distance for three explicit-solvent (TIP3P) PME (a) and GB (b) simulations. Moving average values, averaged over 0.5 ns, are shown, with connecting lines to guide the eye. (c) Ends of the DNA unwrapped from the histone core after 0.8 ns of an explicit-solvent (TIP3P) PME simulation. (d) Ends of the DNA unwrapped from the histone core after 0.03 ns of a GB simulation. DNA surface is shown in red and histone backbone structure in blue. Images were rendered using VMD (100). To see this figure in color, go online.
Note that even after 30 ns of explicit-solvent (TIP3P) PME simulation, the unwrapped DNA ends fail to fully extend out from the histone core, i.e., the end-to-end DNA distance in the explicit-solvent (TIP3P) PME simulation fails to exceed 150 Å. This is in contrast to the GB simulation, where the end-to-end DNA distance exceeds 200 Å after 2 ns of simulation. Most likely, the DNA in the explicit-solvent (TIP3P) PME simulation is unable to extend farther due to electrostatic repulsion between the ends of the DNA in the central cell and the DNA in neighboring cells, under the periodic boundary conditions. Therefore, to compare the GB and explicit-solvent (TIP3P) PME conformational sampling and effective speeds on an equal footing, we defined the unwrapped state as end-to-end DNA distance of 125 Å, a state that is sampled by both simulations (Fig. 3, a and b). Fig. 3, a and b, shows that the unwrapping process proceeds along similar reaction coordinates for both the PME and GB simulations, but over different timescales.
Methodological details
To study DNA unwrapping, we used the 1KX5 nucleosome with the histone tails removed (85), because the tails may hinder the unwrapping process. The condition of high pH was mimicked by setting all of the titratable sites to their deprotonated states. A larger box extending 36 Å beyond the solvent was used for the explicit-solvent (TIP3P) PME simulation to allow room for the DNA to unwrap.
Mixed case
Folding of a miniprotein
Generally, the protein folding problem can be broken down (89) into three subproblems: 1) predicting the folded structure; 2) identifying the folding pathway(s); and 3) quantifying the forces that determine the folded state. We focus here specifically on subproblem 1, predicting the folded structure, where success can be clearly quantified. For the exercise, we have chosen CLN025, which is arguably the smallest (only 10 residues) fast-folding miniprotein, previously used in atomistic studies of protein folding (70). The most straightforward approach would have been to compare the times it took for the protein to regain its known native conformation starting from a completely unfolded conformation at 300 K in explicit-solvent (TIP3P PME) versus implicit-solvent (GB) simulations. However, in contrast to implicit solvent, in which CLN025 readily folds on the timescale of several hundred nanoseconds, in explicit solvent at 300 K, not a single complete folding event occurred over 3 μs of the simulation time—a realistic maximum in this work. Fortunately, the problem of kinetic traps at 300 K can be circumvented by a folding protocol (90–92) commonly used in studies of protein folding in both explicit and implicit solvent. In this protocol, the protein is simulated at its melting temperature, at which the native and unfolded conformations are supposed to be equally represented, and the issue of kinetic traps is mitigated.
The problem of identifying the correct native state from the MD trajectory is solved most easily for the GB simulation (Fig. 4 d) by choosing the snapshot corresponding to the absolute minimum potential energy (molecular mechanics energy plus free energy of solvation), which yields a structure that deviates from the correct native one by 1.4 Å. In explicit solvent, the total potential energy is dominated by the noise from the solvent box, and so the entire folding landscape is needed (Fig. 4 c) to confirm that the free-energy minimum is indeed close (1.5 Å RMSD) to the known native state. To proceed, we define folding time as the transition time from an unfolded structure to the next folded structure, following the approach in Lindorff-Larsen et al. (93). Based on the work of those authors, we defined the folded and unfolded states as structures with backbone RMSD values of <1.5 Å and >4.5 Å, respectively, consistent with the location of the folded and unfolded basins of the miniprotein (Fig. 4 c). At the experimental melting temperature of ∼340 K, the GB simulation (Fig. 4 b) yields an average folding time of 10 ± 1 ns, compared to 70 ± 30 ns for the explicit-solvent (TIP3P) PME simulation (Fig. 4 a). The numbers of independent folding events are statistically significant in the two cases, 151 and 14, respectively.
Figure 4.
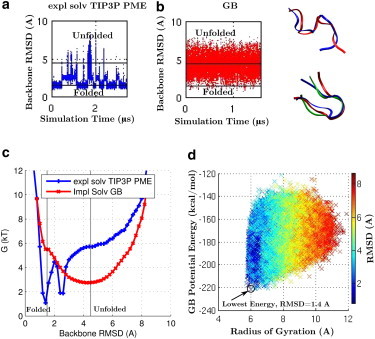
CLN025 miniprotein folding at its experimental melting temperature of 340 K. (a and b) RMSD of backbone heavy atoms relative to the starting structure for the explicit-solvent (TIP3P) PME simulation (a) and the GB simulation (b). The horizontal lines represent RMSD = 1.5 and 4.5 Å. Folded states are states with RMSD < 1.5 Å and unfolded states are states with RMSD > 4.5 Å. The trajectory is sampled every 100 ps for calculation of the RMSD values shown here. (c) Free-energy landscape for the explicit-solvent TIP3P PME and the GB simulations. (d) Potential energy, including solvation free energy, from the GB simulation, as a function of the distance (RMSD) from the experimental native structure. The lowest-energy structure approximates the correct folded state, as indicated by the low RMSD values. (Inset) Images of protein backbone conformations from representative snapshots for folded and unfolded states from the explicit-solvent (TIP3P) PME (blue) and GB (red) simulations. The starting structure (green) is shown for comparison. Images rendered using VMD (100). To see this figure in color, go online.
Let us now touch upon the more complex folding subproblems, 2 and 3. At the experimental melting temperature, the folded and unfolded states should be equally occupied. However, it is obvious from Fig. 4 that, qualitatively, neither method gives the 1:1 ratio of the native folded to the completely unfolded states. In fact, at 340 K in the GB solvent model, the native folded state is occupied only ∼1% of the time and the unfolded state ∼40% of the time. For the explicit-solvent TIP3P PME simulation, the qualitative trend is the opposite: at the melting temperature (340 K), the unfolded state is undersampled (∼3% of the time), whereas the native folded state is occupied ∼50% of the time. In both cases, a large percentage of the states (∼50% for both GB and PME) represent an intermediate state that is neither native folded nor completely unfolded. The Lindorff-Larsen et al. study (93) estimates that an explicit-solvent PME simulation at 370 K would be more representative of the melting temperature. The above suggests that the folded structure for CLN025 is under-stabilized in the GB model and over-stabilized in the explicit-solvent PME model, at least for the specific gas-phase force-field used (AMBER ff10). Another problem with the TIP3P PME simulation is that it yields a stable misfolded state at ∼2.5 Å RMSD (Fig. 4 c), in addition to the correct native state at ∼1.5 Å RMSD. The appearance of a nonnative compact intermediate is in contradiction to experiment, where CLN025 has been characterized as a two-state fast-folding protein with a unique native conformation (70). Given the obvious discrepancies between simulation and experiment, it is unclear how accurate the full free-energy profile of CLN025 produced by either of these simulations is, relative to experiment. Therefore, neither of the solvent models (with the underlying gas-phase force field used) may be suitable to address the more difficult and detailed subproblem 2, identifying the correct folding pathway. We can still ask, however, what would it take for the GB model to reproduce the TIP3P PME folding landscape as faithfully as possible? Obviously, the landscapes at 340 K (Fig. 4 c) are very different. We found, however, that by lowering the GB simulation temperature, one can improve the agreement between the GB and TIP3P landscapes (see the Supporting Material). Specifically, at 260 K, the GB landscape becomes a fair approximation to the explicit-solvent one at 340 K (Fig. 4 c), especially near its native basin. Given the similarity of the landscapes, it makes sense to estimate how much faster is the GB simulation, as compared to the explicit solvent, in its ability to generate the landscape (i.e., the potential of mean force). Assuming that two similar-shaped landscapes of equivalent resolution require the same number of folding events for their construction, we find that the GB model at 260 K is around three times faster per nanosecond of simulation than the TIP3P PME model at 340 K at generating the free-energy landscape of CLN025.
Subproblem 3, quantifying the forces that determine the folded state, is an interesting case. Energy landscapes are easier to obtain and are more intuitive in the implicit-solvent model, in which the solvent degrees of freedom are averaged out; each snapshot has a definite energy, including the free energy of solvation. In that sense, the model can help with physical reasoning, as long as one is aware of its limitations. For example, investigating folding forces near the energy minimum representing the correctly predicted native state of CLN025 is an appropriate task for the implicit-solvent model.
Effect of Langevin dynamics collision frequency, γ, on the speed of conformational sampling
Langevin dynamics was used for temperature regulation in our simulations, where the equation of motion for a particle i is given by (81)
| (5) |
where the particle has mass mi, position xi, and a force Fi acting on it at time t. A random force Ri represents the influence of the solvent or heat bath. Ri is assumed to be uncorrelated with the positions, velocities, and forces of the particle acting on it. In the regime , typically used in biomolecular simulations, where δt is the simulation time step, Ri is taken from a Gaussian distribution with mean zero and variance,
| (6) |
where kB is the Boltzmann constant and T is the absolute temperature. The preceding simulations used a collision frequency of γ = 0.01 ps−1. A value of γ ∼ 50 ps−1 would mimic a typical aqueous environment (94). However, lower values of γ are commonly used to increase the speed of conformational change in practical MD simulations. Fig. 5 shows the effect of different values of γ on the average speed of conformational sampling for GB simulations, for the conformational changes considered here: in general, conformational sampling speed decreases with increasing γ.
Figure 5.
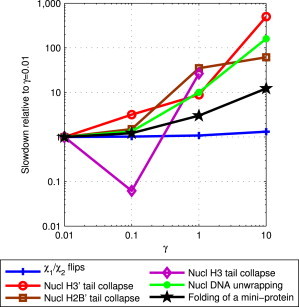
Effect of Langevin dynamics collision frequency, γ, on conformational sampling speed of GB simulations. Slowdown is computed relative to the average speed of conformational change at the baseline value of γ = 0.01 ps−1. The H3 histone tail did not collapse for γ = 10 ps−1, even after 22 ns of simulation (over 20 days of wall clock time), and therefore, this data point is not shown. Connecting lines shown to guide the eye. To see this figure in color, go online.
The collision frequency, γ, in the Langevin equation simultaneously controls two forces (62) expected to have opposing effects on conformational sampling speed: friction force (viscosity) and the random collision force—thermal kicks—due to Brownian motion (47,62,94). The latter may enhance conformational sampling by providing additional energy for crossing energy barriers (62). Thus, lowering γ reduces the beneficial effects of the thermal kicks on the sampling speed, but at the same time it helps speed up the sampling by increasing the diffusion rate. Which one of the two effects wins may depend on the type of the system and conformational change, as well as the value of γ. We find that for all the conformational changes considered here, lower values of γ always result in faster conformational sampling on average. That the speedups generally increase with decreasing collision frequency suggests that the speedup due to reduction in effective viscosity dominates any possible slowdown due to the decreased intensity of thermal kicks that help overcome small barriers in the energy landscape. We conjecture that the slowdown is relatively minor, because the free-energy landscapes in the GB model used here are relatively smooth, perhaps even artificially so compared to explicit solvent (53) and, possibly, reality (95).
The speedup in conformational sampling shown in Fig. 6 for GB with collision frequency γ = 0.01 ps−1 relative to TIP3P PME itself has two potential contributing factors, the associated reduction in solvent viscosity relative to the explicit solvent, and possible differences in the free-energy landscapes produced by the two solvent models (see, e.g., Fig. 4). To estimate the contribution to the entire conformational sampling speedup due to the decrease of the effective solvent viscosity alone, we note that alterations of the free-energy barriers, if they occur, are expected to be independent of the value of γ. With this in mind, the average viscosity-reduction speedup can be approximated from Fig. 5 as the increase of the sampling speed of γ = 0.01 ps−1 simulations relative to the γ = 10.0 ps−1 case, the latter being more representative of the collision frequency for liquid water (∼50 ps−1). The speedups are ∼1-fold, ∼60- to 500-fold, and ∼10-fold for small (χ1 and χ2 dihedral angle flips), large (nucleosome histone tail collapse and nucleosome DNA unwrapping), and mixed (folding of a miniprotein) conformational changes, respectively. Comparing these viscosity-reduction speedups to the total speedups for the GB relative to explicit-solvent PME simulations, ∼1-fold, ∼1- to 100-fold, and ∼7-fold for small, large, and mixed conformational changes, we see that the speedup due to lower collision frequency is, on average, not smaller than the entire conformational sampling speedup of GB compared to the explicit-solvent PME. Thus, relative to possible speedups due to alterations of the energy landscapes, for the systems studied here, the speedup due to the reduction in effective viscosity is dominant. The above analysis is necessarily very qualitative. For example, the collision frequency of 10.0 ps−1, or even 50.0 ps−1, only crudely approximates that of water. And TIP3P itself is ∼2.4 times faster than real water as measured by its self-diffusion rate (96).
Figure 6.
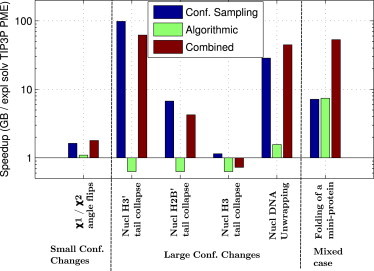
Average speedup for GB relative to explicit-solvent (TIP3P) PME simulations. The combined speedup includes the average speedup due to differences in the rate of conformational sampling, as well as due to algorithmic differences between the two methods. The Langevin dynamics collision frequency of γ = 0.01 ps−1 was used for these simulations. To see this figure in color, go online.
The combined speedup
Fig. 6 shows the combined speedup resulting from the use of implicit solvation (GB) relative to explicit treatment of the solvent (TIP3P + PME). The combined speedup comes from two distinct sources, 1) the increased rate of conformational sampling, and 2) algorithmic speedup.
The rate of conformational sampling is measured as the average simulation time required for a given conformational change. The effect of algorithmic speedup is measured by simulation time per unit of wall clock time (ns/day). The average combined speedup ranges from ∼0.7-fold to ∼60-fold for the structures and conformational changes studied here. Alternatively, one can think of this speedup in terms of an effective simulation time for GB MD. This effective time can be defined as the equivalent simulation time in explicit-solvent TIP3P PME MD (on the same resource) required to achieve comparable sampling of conformational space. For example, combining the ∼574 ns/day nominal computation speed for GB with the approximately sevenfold average speedup of conformational sampling, results in ∼4 μs/day effective speed for GB (see Table 1). The corresponding production simulation run of one month could probe effective timescales of >100 μs.
Table 1.
Speed of computation: explicit vs. implicit solvent
| Simulation method | Structure and conformational change |
|||
|---|---|---|---|---|
| Protein χ1, χ2 flips | Nucleosome tail collapse | Nucleosome DNA unwrap | Miniprotein folding | |
| Explicit solvent TIP3P PME | 20.55 ± 0.02 | 1.79 ± 0.02 | 0.92 ± 0.02 | 74 ± 1 |
| GB (nominal speed) | 21.86 ± 0.26 | 1.13 ± 0.00 | 1.39 ± 0.006 | 574 ± 2 |
| GB (effective speed) | 32.79 ± 0.40 | 1.4 ± 0.6/8 ± 3/113 ± 68 | 42 ± 28 | 4018 ± 1768 |
Nominal speed is the number of nanoseconds of simulation time per day of wall clock time (ns/day). Effective speed = (nominal speed) × (conformational sampling speedup). Qualitatively, the effective speed is the estimated simulation time required by the explicit-solvent TIP3P PME simulation to sample conformational space comparable to the corresponding GB simulation run for 1 day on the same resource. The three time values for the nucleosome tail collapse represent the results for the collapse of the H3, H2B′, and H3′ tails, respectively. Langevin collision frequency is γ = 0.01 ps−1; AMBER-12 on a single GTX680 GPU card with the SPFP precision model.
Without further approximations (97,98) aimed at improving the scaling (efficiency) of the model, the algorithmic complexity of GB scales as n2, whereas the scaling is NlogN for explicit-solvent (TIP3P) PME, where n is the number of solute atoms and N is the total number of atoms in the system, including the solvent. Therefore, generally, algorithmic speedup decreases with structure size for GB relative to explicit-solvent (TIP3P) PME, since n2 grows faster than NlogN, assuming that N itself does not grow faster than n2. This assumption is generally true for structures immersed in a solvent box of sufficient size to allow small conformational changes. However, in some cases, solvent boxes much larger than the solute are required to allow room for large conformational changes, such as for the unwrapping of DNA from the nucleosome core, or protein folding. In such cases, N becomes much larger than n, offsetting the PME advantage of scaling. Even for cases where explicit-solvent (TIP3P) PME is faster than GB (e.g., nucleosome tail collapse), when combined with the speedup due to conformational sampling, the overall speed of conformational sampling for GB can be faster.
Note that we did not use a cutoff for the calculation of long-range pairwise interactions for the GB simulations. Additional speedup of the GB simulation is possible using a cutoff. However, long-range electrostatic interactions decay slowly, and using a cutoff, which ignores such interactions beyond the cutoff distance, can significantly reduce the accuracy of the GB calculation. The loss of accuracy can be particularly significant for large, highly charged structures, such as the nucleosome. Fortunately, GB-specific alternatives to cutoffs have been developed (97,98).
Conclusions
Atomistic molecular dynamics simulations are routinely used to study structure, function, and activity of biological molecules. However, the utility of such studies is often limited by inadequate sampling of conformational space. Implicit-solvent-based simulations can speed up the sampling of conformational space relative to explicit-solvent simulations, but the speedup comes at the cost of making additional approximations to reality. In particular, implicit-solvent simulations can sample conformational space faster than can explicit-solvent simulations, but they may also alter the free-energy landscapes. These issues are discussed on a case-by-case basis for the types of problems considered here. In practice, the choice of solvent model is dictated by the accuracy/speed trade-offs, which are system-dependent: knowing what to expect is critical to making the right choice.
In this study, we compared the speeds of small, large, and mixed conformational changes simulated in implicit solvent using the GB approximation to those simulated in explicit solvent using the PME model to approximate the long-range forces. The conformational changes studied here consist of dihedral angle flips, nucleosome histone tail collapse, DNA unwrapping from the nucleosome histone core, and miniprotein folding.
Our results show that speedup of conformational change in implicit solvent can vary considerably, depending on the details of the transition, and can range from no speedup at all to almost a 100-fold speedup. In general, the larger the conformational change, the higher the speedup one may expect from the use of the implicit rather than the explicit solvent, but this tendency is not universal or uniform. Within each type of transition, a range of speedups were observed: for example, side-chain dihedral angle flips in a 300-residue protein are, on average, only ∼1.5-fold faster in implicit solvent, but for some groups the ratio can be 10:1 or <1. We expect these speedup values to be specific to current AMBER GB flavors that offer a reasonable compromise between accuracy and speed. The use of GB models available in other packages may result in different speedups (47). At the same time, more general conclusions, discussed below, are expected to be less sensitive to the specifics of the GB model.
The free-energy landscapes for the explicit-solvent PME and implicit-solvent GB simulations at a given temperature can also be quite different, as seen in the case of miniprotein folding. Where the goal of the GB simulation is to reproduce a specific free-energy landscape in explicit solvent, e.g., by lowering the simulation temperature, the speedups noted above may be different. For example, the speedup in folding rate is considerably lower (approximately threefold) when comparing simulations with similar free-energy landscapes than when comparing simulations at the same temperature (speedup is approximately sevenfold) at 340K, the experimental melting temperature of the miniprotein examined here.
We also examined the effect of the Langevin dynamics collision frequency, γ, on the speed of conformational change. Decreasing the value of γ may have opposing effects on conformational sampling by simultaneously reducing the solvent viscosity and at the same time reducing random collision force, which can speed up sampling by providing additional energy for crossing small energy barriers. We find that for all systems and types of conformational changes considered here, increasing the collision frequency reduces the speed of conformational change. Thus, using low values of γ seems always of benefit to implicit-solvent simulations where enhanced sampling is desired, at least when the possibility of altered dynamics (99) or kinetics (51) is irrelevant or can be ignored. By analyzing how the speedup changes with increasing γ, from near zero to values representative of true viscosity of water, we have concluded that conformational sampling speedup is mainly due to reduction in solvent viscosity rather than to possible differences in free-energy landscapes between the implicit GB and explicit PME treatment of solvation.
The nominal computational speed of an implicit-solvent simulation, that is the number of nanoseconds per day of simulation time, can be higher or lower than that of the corresponding explicit-solvent simulation due to differences in how the two approximations scale with system size. The most common explicit-solvent PME approximation for long-range forces scales as ∼NlogN, whereas the standard (without further approximations) GB implicit computation scales as ∼n2, where N is the total number of solvent and solute atoms combined and n is the number of solute atoms only. For example, a GB simulation of the 25,100-atom nucleosome is nominally 1.6 times slower than the explicit-solvent PME simulation with a small TIP3P solvent box extending 10 Å from the solute, whereas it is 1.6 times faster compared to a PME simulation in a larger 36 Å TIP3P solvent box. The choice of the box size is determined by the specifics of the problem, e.g., whether large conformational changes are expected. However, what matters in most cases is the effective speedup, which takes into account both computational speed and conformational sampling speed. For the types of conformational changes considered here, the effective speedup ranges from ∼0.7- to ∼60-fold for implicit-solvent GB simulations compared to explicit-solvent TIP3P PME simulations. For example, at 574 ns/day, the GB simulation for the 166-atom CLN025 miniprotein is approximately sevenfold faster than the explicit-solvent PME simulation (74 ns/day) on our computational platform. Combined with the additional approximately sevenfold conformational speedup, the 574 ns/day implicit-solvent MD simulation becomes equivalent to an explicit-solvent PME simulation at ∼4 μs/day for the CLN025 miniprotein folding simulation, making effective timescales of hundreds of microseconds accessible on conventional computing platforms. This example illustrates an important point: when it comes to sampling conformation space, simply considering computational speed, i.e., nanoseconds per day, may not be sufficient. Instead, one must also take into consideration the speed of conformational change when comparing implicit- and explicit-solvent methods. In this respect, the effective speedup, which takes into account both conformational search speed and computational speed, is more informative.
Acknowledgments
The authors acknowledge use of the HokieSpeed supercomputer at Virginia Tech.
This work was supported by National Institutes of Health grant GM076121 to A.O., Burroughs-Wellcome fund grant1011306 to R.A., National Science Foundation SI2-SSE grants NSF-1047875 and NSF-1148276 to R.C.W., a University of California UC Lab 09-LR-06-117793 grant to R.C.W., a fellowship from NVIDIA, and National Science Foundation grant CNS-0960081.
Supporting Material
References
- 1.Dodson G.G., Lane D.P., Verma C.S. Molecular simulations of protein dynamics: new windows on mechanisms in biology. EMBO Rep. 2008;9:144–150. doi: 10.1038/sj.embor.7401160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Karplus M., Kuriyan J. Molecular dynamics and protein function. Proc. Natl. Acad. Sci. USA. 2005;102:6679–6685. doi: 10.1073/pnas.0408930102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dror R.O., Dirks R.M., Shaw D.E. Biomolecular simulation: a computational microscope for molecular biology. Annu. Rev. Biophys. 2012;41:429–452. doi: 10.1146/annurev-biophys-042910-155245. [DOI] [PubMed] [Google Scholar]
- 4.Wang W., Donini O., Kollman P.A. Biomolecular simulations: recent developments in force fields, simulations of enzyme catalysis, protein-ligand, protein-protein, and protein-nucleic acid noncovalent interactions. Annu. Rev. Biophys. Biomol. Struct. 2001;30:211–243. doi: 10.1146/annurev.biophys.30.1.211. [DOI] [PubMed] [Google Scholar]
- 5.Schlick T., Collepardo-Guevara R., Xiao X. Biomolecular modeling and simulation: a field coming of age. Q. Rev. Biophys. 2011;44:191–228. doi: 10.1017/S0033583510000284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shaw D.E., Deneroff M.M., Wang S.C. Anton, a special-purpose machine for molecular dynamics simulation. Commun. ACM. 2008;51:91–97. [Google Scholar]
- 7.Sagui C., Darden T.A. Molecular dynamics simulations of biomolecules: long-range electrostatic effects. Annu. Rev. Biophys. Biomol. Struct. 1999;28:155–179. doi: 10.1146/annurev.biophys.28.1.155. [DOI] [PubMed] [Google Scholar]
- 8.Ratner M.A. Biomolecular processes in the fast lane. Proc. Natl. Acad. Sci. USA. 2001;98:387–389. doi: 10.1073/pnas.98.2.387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Grossfield A., Zuckerman D.M. Quantifying uncertainty and sampling quality in biomolecular simulations. Annu. Rep. Comput. Chem. 2009;5:23–48. doi: 10.1016/S1574-1400(09)00502-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Onufriev A. Continuum electrostatics solvent modeling with the generalized Born model. In: Feig M., editor. Modeling Solvent Environments. Wiley; New York: 2010. pp. 127–165. [Google Scholar]
- 11.Schlick T. Springer-Verlag; New York: 2002. Molecular Modeling and Simulation. An Interdisciplinary Guide. [Google Scholar]
- 12.Darden T., York D., Pedersen L. Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 13.Essmann U., Perera L., Pedersen L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995;103:8577–8593. [Google Scholar]
- 14.Toukmaji A.Y., Board J.A., Jr. Ewald summation techniques in perspective: a survey. Comput. Phys. Commun. 1996;95:73–92. [Google Scholar]
- 15.York D., Yang W. The fast Fourier Poisson method for calculating Ewald sums. J. Chem. Phys. 1994;101:3298–3300. [Google Scholar]
- 16.Onufriev A., Bashford D., Case D. Modification of the generalized Born model suitable for macromolecules. J. Phys. Chem. B. 2000;104:3712–3720. [Google Scholar]
- 17.Onufriev A., Bashford D., Case D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins. 2004;55:383–394. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- 18.Mongan J., Simmerling C., Onufriev A. Generalized Born model with a simple, robust molecular volume correction. J. Chem. Theory Comput. 2007;3:156–169. doi: 10.1021/ct600085e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Still W.C., Tempczyk A., Hendrickson T. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc. 1990;112:6127–6129. [Google Scholar]
- 20.Bashford D., Case D.A. Generalized born models of macromolecular solvation effects. Annu. Rev. Phys. Chem. 2000;51:129–152. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- 21.Hawkins G.D., Cramer C.J., Truhlar D.G. Pairwise solute descreening of solute charges from a dielectric medium. Chem. Phys. Lett. 1995;246:122–129. [Google Scholar]
- 22.Hawkins G.D., Cramer C.J., Truhlar D.G. Parametrized models of aqueous free energies of solvation based on pairwise descreening of solute atomic charges from a dielectric medium. J. Phys. Chem. 1996;100:19824–19839. [Google Scholar]
- 23.Ghosh A., Rapp C.S., Friesner R.A. Generalized Born model based on a surface integral formulation. J. Phys. Chem. B. 1998;102:10983–10990. [Google Scholar]
- 24.Lee M.S., Salsbury J.F.R., Brooks C.L., III Novel generalized Born methods. J. Chem. Phys. 2002;116:10606–10614. [Google Scholar]
- 25.Tsui V., Case D. Molecular dynamics simulations of nucleic acids with a generalized Born solvation model. J. Am. Chem. Soc. 2000;122:2489–2498. [Google Scholar]
- 26.Cramer C.J., Truhlar D.G. Implicit solvation models: equilibria, structure, spectra, and dynamics. Chem. Rev. 1999;99:2161–2200. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
- 27.David L., Luo R., Gilson M.K. Comparison of generalized Born and Poisson models: energetics and dynamics of HIV protease. J. Comput. Chem. 2000;21:295–309. [Google Scholar]
- 28.Im W., Lee M.S., Brooks C.L., 3rd Generalized Born model with a simple smoothing function. J. Comput. Chem. 2003;24:1691–1702. doi: 10.1002/jcc.10321. [DOI] [PubMed] [Google Scholar]
- 29.Schaefer M., Karplus M. A comprehensive analytical treatment of continuum electrostatics. J. Phys. Chem. 1996;100:1578–1599. [Google Scholar]
- 30.Calimet N., Schaefer M., Simonson T. Protein molecular dynamics with the generalized Born/ACE solvent model. Proteins. 2001;45:144–158. doi: 10.1002/prot.1134. [DOI] [PubMed] [Google Scholar]
- 31.Feig M., Im W., Brooks C.L., 3rd Implicit solvation based on generalized Born theory in different dielectric environments. J. Chem. Phys. 2004;120:903–911. doi: 10.1063/1.1631258. [DOI] [PubMed] [Google Scholar]
- 32.Archontis G., Simonson T. A residue-pairwise generalized born scheme suitable for protein design calculations. J. Phys. Chem. B. 2005;109:22667–22673. doi: 10.1021/jp055282+. [DOI] [PubMed] [Google Scholar]
- 33.Feig M., Onufriev A., Brooks C.L., 3rd Performance comparison of generalized born and Poisson methods in the calculation of electrostatic solvation energies for protein structures. J. Comput. Chem. 2004;25:265–284. doi: 10.1002/jcc.10378. [DOI] [PubMed] [Google Scholar]
- 34.Nymeyer H., García A.E. Simulation of the folding equilibrium of α-helical peptides: a comparison of the generalized Born approximation with explicit solvent. Proc. Natl. Acad. Sci. USA. 2003;100:13934–13939. doi: 10.1073/pnas.2232868100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Scarsi M., Apostolakis J., Caflisch A. Continuum electrostatic energies of macromolecules in aqueous solutions. J. Phys. Chem. A. 1997;101:8098–8106. [Google Scholar]
- 36.Dominy B.N., Brooks C.L. Development of a generalized Born model parametrization for proteins and nucleic acids. J. Phys. Chem. B. 1999;103:3765–3773. [Google Scholar]
- 37.Gallicchio E., Levy R.M. AGBNP: an analytic implicit solvent model suitable for molecular dynamics simulations and high-resolution modeling. J. Comput. Chem. 2004;25:479–499. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 38.Grant J.A., Pickup B.T., Nicholls A. The Gaussian generalized Born model: application to small molecules. Phys. Chem. Chem. Phys. 2007;9:4913–4922. doi: 10.1039/b707574j. [DOI] [PubMed] [Google Scholar]
- 39.Haberthür U., Caflisch A. FACTS: Fast analytical continuum treatment of solvation. J. Comput. Chem. 2008;29:701–715. doi: 10.1002/jcc.20832. [DOI] [PubMed] [Google Scholar]
- 40.Spassov V.Z., Yan L., Szalma S. Introducing an implicit membrane in generalized Born/solvent accessibility continuum solvent models. J. Phys. Chem. B. 2002;106:8726–8738. [Google Scholar]
- 41.Ulmschneider M.B., Ulmschneider J.P., Di Nola A. A generalized Born implicit-membrane representation compared to experimental insertion free energies. Biophys. J. 2007;92:2338–2349. doi: 10.1529/biophysj.106.081810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Tanizaki S., Feig M. A generalized Born formalism for heterogeneous dielectric environments: application to the implicit modeling of biological membranes. J. Chem. Phys. 2005;122:124706. doi: 10.1063/1.1865992. [DOI] [PubMed] [Google Scholar]
- 43.Zhang L.Y., Gallicchio E., Levy R.M. Solvent models for protein-ligand binding: comparison of implicit solvent Poisson and surface generalized Born models with explicit solvent simulations. J. Comput. Chem. 2001;22:591–607. [Google Scholar]
- 44.Srinivasan J., Trevathan M.W., Case D.A. Application of a pairwise generalized Born model to proteins and nucleic acids: inclusion of salt effects. Theor. Chem. Acc. 1999;101:426–434. [Google Scholar]
- 45.Zuckerman D.M. Equilibrium sampling in biomolecular simulations. Annu. Rev. Biophys. 2011;40:41–62. doi: 10.1146/annurev-biophys-042910-155255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pierce L.C., Salomon-Ferrer R., Walker R.C. Routine access to millisecond timescale events with accelerated molecular dynamics. J. Chem. Theory Comput. 2012;8:2997–3002. doi: 10.1021/ct300284c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Feig M. Kinetics from implicit solvent simulations of biomolecules as a function of viscosity. J. Chem. Theory Comput. 2007;3:1734–1748. doi: 10.1021/ct7000705. [DOI] [PubMed] [Google Scholar]
- 48.Amaro R.E., Cheng X., McCammon J.A. Characterizing loop dynamics and ligand recognition in human- and avian-type influenza neuraminidases via generalized Born molecular dynamics and end-point free energy calculations. J. Am. Chem. Soc. 2009;131:4702–4709. doi: 10.1021/ja8085643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Amaro R.E., Swift R.V., Bush R.M. Mechanism of 150-cavity formation in influenza neuraminidase. Nat. Commun. 2011;2:388. doi: 10.1038/ncomms1390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zagrovic B., Snow C.D., Pande V.S. Simulation of folding of a small α-helical protein in atomistic detail using worldwide-distributed computing. J. Mol. Biol. 2002;323:927–937. doi: 10.1016/s0022-2836(02)00997-x. [DOI] [PubMed] [Google Scholar]
- 51.Zagrovic B., Pande V. Solvent viscosity dependence of the folding rate of a small protein: distributed computing study. J. Comput. Chem. 2003;24:1432–1436. doi: 10.1002/jcc.10297. [DOI] [PubMed] [Google Scholar]
- 52.Ruscio J.Z., Onufriev A. A computational study of nucleosomal DNA flexibility. Biophys. J. 2006;91:4121–4132. doi: 10.1529/biophysj.106.082099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Johnson Q., Doshi U., Hamelberg D. Water’s contribution to the energetic roughness from peptide dynamics. J. Chem. Theory Comput. 2010;6:2591–2597. doi: 10.1021/ct100183s. [DOI] [PubMed] [Google Scholar]
- 54.Hamelberg D., Shen T., McCammon J.A. Insight into the role of hydration on protein dynamics. J. Chem. Phys. 2006;125:094905. doi: 10.1063/1.2232131. [DOI] [PubMed] [Google Scholar]
- 55.Tan C., Yang L., Luo R. How well does Poisson-Boltzmann implicit solvent agree with explicit solvent? A quantitative analysis. J. Phys. Chem. B. 2006;110:18680–18687. doi: 10.1021/jp063479b. [DOI] [PubMed] [Google Scholar]
- 56.Baker N.A. Improving implicit solvent simulations: a Poisson-centric view. Curr. Opin. Struct. Biol. 2005;15:137–143. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 57.Zhou R. Free energy landscape of protein folding in water: explicit vs. implicit solvent. Proteins. 2003;53:148–161. doi: 10.1002/prot.10483. [DOI] [PubMed] [Google Scholar]
- 58.Beauchamp K.A., Lin Y.-S., Pande V.S. Are protein force fields getting better? A systematic benchmark on 524 diverse NMR measurements. J. Chem. Theory Comput. 2012;8:1409–1414. doi: 10.1021/ct2007814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Hu Z., Jiang J. Assessment of biomolecular force fields for molecular dynamics simulations in a protein crystal. J. Comput. Chem. 2010;31:371–380. doi: 10.1002/jcc.21330. [DOI] [PubMed] [Google Scholar]
- 60.Shirts M.R., Pande V.S. Solvation free energies of amino acid side chain analogs for common molecular mechanics water models. J. Chem. Phys. 2005;122:134508. doi: 10.1063/1.1877132. [DOI] [PubMed] [Google Scholar]
- 61.Hagen S.J., Qiu L., Pabit S.A. Diffusional limits to the speed of protein folding: fact or friction? J. Phys. Condens. Matter. 2005;17:S1503–S1514. [Google Scholar]
- 62.Jagielska A., Scheraga H.A. Influence of temperature, friction, and random forces on folding of the B-domain of staphylococcal protein A: all-atom molecular dynamics in implicit solvent. J. Comput. Chem. 2007;28:1068–1082. doi: 10.1002/jcc.20631. [DOI] [PubMed] [Google Scholar]
- 63.Gee P.J., van Gunsteren W.F. Numerical simulation of the effect of solvent viscosity on the motions of a β-peptide heptamer. Chemistry. 2005;12:72–75. doi: 10.1002/chem.200500587. [DOI] [PubMed] [Google Scholar]
- 64.Sugita Y., Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999;314:141–151. [Google Scholar]
- 65.Okur A., Roe D.R., Simmerling C. Improving convergence of replica-exchange simulations through coupling to a high-temperature structure reservoir. J. Chem. Theory Comput. 2007;3:557–568. doi: 10.1021/ct600263e. [DOI] [PubMed] [Google Scholar]
- 66.Roitberg A.E., Okur A., Simmerling C. Coupling of replica exchange simulations to a non-Boltzmann structure reservoir. J. Phys. Chem. B. 2007;111:2415–2418. doi: 10.1021/jp068335b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Grubmüller H., Heller H., Schulten K. Generalized Verlet algorithm for efficient molecular dynamics simulations with long-range interactions. Mol. Simul. 1991;6:121–142. [Google Scholar]
- 68.Watanabe M., Karplus M. Dynamics of molecules with internal degrees of freedom by multiple timestep methods. J. Chem. Phys. 1993;99:8063–8074. [Google Scholar]
- 69.Tuckerman M.E., Martyna G.J., Berne B.J. Molecular dynamics algorithm for condensed systems with multiple time scales. J. Chem. Phys. 1990;93:1287–1291. [Google Scholar]
- 70.Honda S., Akiba T., Harata K. Crystal structure of a ten-amino acid protein. J. Am. Chem. Soc. 2008;130:15327–15331. doi: 10.1021/ja8030533. [DOI] [PubMed] [Google Scholar]
- 71.Honda S., Yamasaki K., Morii H. 10 residue folded peptide designed by segment statistics. Structure. 2004;12:1507–1518. doi: 10.1016/j.str.2004.05.022. [DOI] [PubMed] [Google Scholar]
- 72.Berman H.M., Westbrook J., Bourne P.E. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Heinz D.W., Ryan M., Griffith O.H. Crystal structure of phosphatidylinositol-specific phospholipase C from Bacillus cereus in complex with glucosaminylα1→6-D-myo-inositol, an essential fragment of GPI anchors. Biochemistry. 1996;35:9496–9504. doi: 10.1021/bi9606105. [DOI] [PubMed] [Google Scholar]
- 74.Davey C.A., Sargent D.F., Richmond T.J. Solvent mediated interactions in the structure of the nucleosome core particle at 1.9 Å resolution. J. Mol. Biol. 2002;319:1097–1113. doi: 10.1016/S0022-2836(02)00386-8. [DOI] [PubMed] [Google Scholar]
- 75.Anandakrishnan R., Aguilar B., Onufriev A.V. H++ 3.0: automating pK prediction and the preparation of biomolecular structures for atomistic molecular modeling and simulations. Nucleic Acids Res. 2012;40:W537–W541. doi: 10.1093/nar/gks375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Jorgensen W.L., Chandrasekhar J., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 77.Wickstrom L., Okur A., Simmerling C. Evaluating the performance of the ff99SB force field based on NMR scalar coupling data. Biophys. J. 2009;97:853–856. doi: 10.1016/j.bpj.2009.04.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Götz A.W., Williamson M.J., Walker R.C. Routine microsecond molecular dynamics simulations with AMBER on GPUs. 1. Generalized Born. J. Chem. Theory Comput. 2012;8:1542–1555. doi: 10.1021/ct200909j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Salomon-Ferrer R., Götz A.W., Walker R.C. Routine microsecond molecular dynamics simulations with AMBER on GPUs. 2. Explicit solvent particle mesh Ewald. J. Chem. Theory Comput. 2013;9:3878–3888. doi: 10.1021/ct400314y. [DOI] [PubMed] [Google Scholar]
- 80.Grand S., Goetz A., Walker R. SPFP: Speed without compromise—a mixed precision model for GPU accelerated molecular dynamics simulations. Comput. Phys. Commun. 2013;184:374–380. [Google Scholar]
- 81.Pastor R.W., Brooks B.R., Szabo A. An analysis of the accuracy of Langevin and molecular dynamics algorithms. Mol. Phys. 1988;65:1409–1419. [Google Scholar]
- 82.Ryckaert J.-P., Ciccotti G., Berendsen H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- 83.Bertin A., Leforestier A., Livolant F. Role of histone tails in the conformation and interactions of nucleosome core particles. Biochemistry. 2004;43:4773–4780. doi: 10.1021/bi036210g. [DOI] [PubMed] [Google Scholar]
- 84.Ferreira H., Somers J., Owen-Hughes T. Histone tails and the H3 αN helix regulate nucleosome mobility and stability. Mol. Cell. Biol. 2007;27:4037–4048. doi: 10.1128/MCB.02229-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Biswas M., Voltz K., Langowski J. Role of histone tails in structural stability of the nucleosome. PLOS Comput. Biol. 2011;7:e1002279. doi: 10.1371/journal.pcbi.1002279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Thåström A., Lowary P.T., Widom J. Measurement of histone-DNA interaction free energy in nucleosomes. Methods. 2004;33:33–44. doi: 10.1016/j.ymeth.2003.10.018. [DOI] [PubMed] [Google Scholar]
- 87.Voltz K., Trylska J., Langowski J. Unwrapping of nucleosomal DNA ends: a multiscale molecular dynamics study. Biophys. J. 2012;102:849–858. doi: 10.1016/j.bpj.2011.11.4028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Libertini L.J., Small E.W. Effects of pH on the stability of chromatin core particles. Nucleic Acids Res. 1984;12:4351–4359. doi: 10.1093/nar/12.10.4351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Dill K.A., Ozkan S.B., Weikl T.R. The protein folding problem. Annu. Rev. Biophys. 2008;37:289–316. doi: 10.1146/annurev.biophys.37.092707.153558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Simmerling C., Strockbine B., Roitberg A.E. All-atom structure prediction and folding simulations of a stable protein. J. Am. Chem. Soc. 2002;124:11258–11259. doi: 10.1021/ja0273851. [DOI] [PubMed] [Google Scholar]
- 91.Kannan S., Zacharias M. Simulated annealing coupled replica exchange molecular dynamics—an efficient conformational sampling method. J. Struct. Biol. 2009;166:288–294. doi: 10.1016/j.jsb.2009.02.015. [DOI] [PubMed] [Google Scholar]
- 92.Snow C.D., Sorin E.J., Pande V.S. How well can simulation predict protein folding kinetics and thermodynamics? Annu. Rev. Biophys. Biomol. Struct. 2005;34:43–69. doi: 10.1146/annurev.biophys.34.040204.144447. [DOI] [PubMed] [Google Scholar]
- 93.Lindorff-Larsen K., Piana S., Shaw D.E. How fast-folding proteins fold. Science. 2011;334:517–520. doi: 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- 94.Loncharich R.J., Brooks B.R., Pastor R.W. Langevin dynamics of peptides: the frictional dependence of isomerization rates of N-acetylalanyl-N′-methylamide. Biopolymers. 1992;32:523–535. doi: 10.1002/bip.360320508. [DOI] [PubMed] [Google Scholar]
- 95.Milanesi L., Waltho J.P., Volk M. Measurement of energy landscape roughness of folded and unfolded proteins. Proc. Natl. Acad. Sci. USA. 2012;109:19563–19568. doi: 10.1073/pnas.1211764109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Izadi S., Anandakrishnan R., Onufriev A.V. Building water models: a different approach. J Phys Chem Lett. 2014;5:3863–3871. doi: 10.1021/jz501780a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Anandakrishnan R., Daga M., Onufriev A.V. An n log n Generalized Born approximation. J. Chem. Theory Comput. 2011;7:544–559. doi: 10.1021/ct100390b. [DOI] [PubMed] [Google Scholar]
- 98.Anandakrishnan R., Onufriev A.V. An N log N approximation based on the natural organization of biomolecules for speeding up the computation of long range interactions. J. Comput. Chem. 2010;31:691–706. doi: 10.1002/jcc.21357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Rhee Y.M., Pande V.S. Solvent viscosity dependence of the protein folding dynamics. J. Phys. Chem. B. 2008;112:6221–6227. doi: 10.1021/jp076301d. [DOI] [PubMed] [Google Scholar]
- 100.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. 27–28. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


