Evolution of hosts paying manifold costs of defence

Abstract

Hosts are expected to incur several physiological costs in defending against parasites. These include constitutive energetic (or other resource) costs of a defence system, facultative resource costs of deploying defences when parasites strike, and immunopathological costs of collateral damage. Here, we investigate the evolution of host recovery rates, varying the source and magnitude of immune costs. In line with previous work, we find that hosts paying facultative resource costs evolve faster recovery rates than hosts paying constitutive costs. However, recovery rate is more sensitive to changes in facultative costs, potentially explaining why constitutive costs are hard to detect empirically. Moreover, we find that immunopathology costs which increase with recovery rate can erode the benefits of defence, promoting chronicity of infection. Immunopathology can also lead to hosts evolving low recovery rate in response to virulent parasites. Furthermore, when immunopathology reduces fecundity as recovery rate increases (e.g. as for T-cell responses to urogenital chlamydiosis), then recovery and reproductive rates do not covary as predicted in eco-immunology. These results suggest that immunopathological and resource costs have qualitatively different effects on host evolution and that embracing the complexity of immune costs may be essential for explaining variability in immune defence in nature.

1. Introduction

Hosts vary greatly in their response to infection, even when challenged by a common pathogen genotype. Some hosts mount a vigorous response, whereas others simply live with infection. Why is there such variability? One potential explanation is that there are varied costs associated with immune defence [1,2].

The cells and molecules that hosts deploy during infection can kill parasites (in a mode of defence called resistance) and reduce damage to host health/fitness without reducing parasite burden (in a mode of defence called tolerance) [3,4]. Resistance and tolerance confer benefits to hosts by mitigating the fitness impacts of parasitism, but these defences also incur physiological costs. For example, each activated human plasma cell secretes 50–100 million antibodies per hour for up to two weeks [5], draining amino acids that might otherwise contribute to growth or reproduction [6]. Experimental studies of rodents [7] and poultry [8] have confirmed the resource costs of immune defence. Furthermore, the powerful immune effector mechanisms that kill parasites (e.g. oxidative bursts; [9] or repair epithelial punctures (e.g. collagen deposition; [10]) often damage the host's own tissues (causing oxidative and fibrotic immunopathology, respectively, even to uninfected tissue).

Importantly, resistance-conferring, tolerance-conferring and pathological immune responses are all likely to demand host resources. Yet, to the best of our knowledge, few theoretical studies of host evolution have explicitly accounted for both resource-mediated and immunopathological costs of defence. Simultaneous accounting of these costs is necessary if we are to fully understand the evolution of host defences. For example, any host experiencing immunopathology must also be paying resource costs, but how do the joint costs affect the evolution of recovery rate? Furthermore, both parasites and immunopathology damage host tissue, but how do these contributions to virulence combine to shape host evolution? We have previously found that immunopathology qualitatively alters evolutionary trajectories of virulence when its cost increases with increasing recovery rate ([11], see also [12]). Here, we investigate effects of immunopathology, in combination with constitutive and inducible resource costs of defence, upon the evolution of host recovery rate.

We establish a general theoretical framework with constitutive and facultative resource costs of defence affecting host birth rate. We then incorporate immunopathology affecting either host survival or host reproduction. Indeed, while immunopathology kills many hosts [13,14], it can also have sublethal effects on reproduction (e.g. in urogenital infections). For example, fallopian tube scarring caused by immune responses to Chlamydia trachomatis infection often leads to infertility, but few other effects on host health [15]. This theoretical framework enables us to ask how we expect recovery rate to evolve, given the reality of both mortality and fecundity immunopathology combined with resource costs incurred in defence. We use this framework to address two interrelated questions. First, how does variability in the source and magnitude of physiological cost affect variability in host recovery rate and life history? Second, when, if ever, should a host mount a vigorous response that leads to rapid recovery from infection?

2. Theoretical framework

In the absence of genetic variation in the host and parasite, the epidemiological dynamics are modelled using the following set of differential equations:

1.1

and

1.2

Here, S and I are the numbers of susceptible (i.e. uninfected) and infected hosts, b_S and b_I are their per capita birth rates, μ is the natural per capita mortality rate, c is the rate of recovery from infection (in that case, the host is again susceptible), β is the transmission rate and α is the parasite-induced mortality rate.

Throughout, we will assume that b_T > μ and b_I < μ + α, because this is required for the stability of the epidemiological equilibrium. This simply means that the host has a positive per capita growth rate when uninfected and a negative per capita growth rate when infected. As a result, the population would grow without bound in the absence of the parasite, but the parasite keeps it in check. Allowing for density-dependent reproduction does not qualitatively alter the results whenever an evolutionarily stable strategy (ESS) exists, and therefore, we restrict attention to the density-independent case for analytical tractability (C.E. Cressler 2014, unpublished results).

As noted above, we will consider two distinct costs of defence: resource costs and immunopathological costs. Resource costs may result, for example, from energy allocation to the immune system reducing the energy available for other physiological processes [6]. We consider two types of resource cost: constitutive costs, which affect both susceptible and infected hosts, and facultative, or inducible, costs, which affect only infected hosts [16,17]. In either case, we will assume that costs are incurred as a reduction in birth rate.

To model constitutive resource costs of defence, we assume that the birth rate of infected hosts (b_I) is the same as that of susceptible hosts (b_S), but that both are decreasing functions of recovery rate c. Note that this implies infection does not impact fecundity, for example through the parasite targeting reproduction [18,19]. In particular, we assume that b_S = b_I = b − h(c), where h(c) is an increasing function of recovery rate. To model facultative resource costs, we assume that b_S = b and b_I = b – h(c).

Note that we assume resource costs are either entirely constitutive or entirely facultative. This allows us to evaluate how different types of cost affect host evolution; and while existing theory tends to include only constitutive costs, empirical work often fails to detect constitutive costs, whereas facultative costs are more frequently observed (reviewed in [20]). Thus, both theoretically and empirically, studying the influence of the two types of resource cost separately is worthwhile. Moreover, combining the results of an analysis of each cost separately with the results of previous theory investigating the optimal investment into constitutive versus facultative immune defences [16,17] can give insights into the more general case.

In addition to these resource costs of recovery, we consider immunopathology (IP) that operates in one of two ways: by increasing mortality rate when infected or by decreasing birth rate when infected. In the case of mortality IP, we assume that the parasite induces a rate of mortality given by α = γε, where ε > 0 is the parasite's exploitation strategy and γ > 0 is the exploitation rate per unit of ε. This parasite-induced mortality arises simply owing to the parasite exploiting the host. IP causes additional mortality over and above this value, and in a way that might depend on both c and ε. We denote the mortality owing to IP by f(ɛ, c), and assume α = γɛ + f(ɛ, c). In the case of fecundity IP, we suppose that the fecundity while infected is decreased by an amount g(ɛ, c) through IP, so that the birth rate of an infected animal is given by b_I = b − h(c) − g(ɛ, c) (including both the resource and IP costs). Table 1 presents the functional forms assumed for the birth rates and mortality rates under each of the possible combinations of costs explored here.

Table 1.

Functional forms for the per capita birth rates of susceptible (b_S) and infected (b_I) hosts and for the parasite-induced mortality rate (α) under each of the different combinations of resource and IP costs.

	constitutive cost	facultative cost
mortality IP	bS(c) = b − h(c)	bS(c) = b
	bI(c) = b−h(c)	bI(c) = b − h(c)
	α = γɛ + f(ɛ, c)	α = γɛ + f(ɛ, c)
fecundity IP	bS(c) = b − h(c)	bS(c) = b
	bI(c) = b − h(c) − g(ε, c)	bI(c) = b − h(c) − g(ε, c)
	α = γɛ	α = γɛ

Although the analytical results presented below are general and can therefore be used to understand how cost functions of any shape will affect host evolution, we assume particular forms for h(c), f(ε, c) and g(ε, c) to allow us to make quantitative predictions. In particular, we assume h(c) = λc², as accelerating resource costs guarantee the existence of an evolutionarily stable recovery rate in the absence of IP costs. For the IP cost functions, in the absence of mechanistic data suggesting appropriate functional forms, we follow Day et al. [11] and take a more phenomenological approach. In particular, we assume f(ε, c) = ϕ₀ + ϕ₁ε + ϕ₂c + ϕ₃εc and g(ε, c) = ψ₀ + ψ₁ε + ψ₂c + ψ₃εc. These forms can be thought of as coming from fits of a linear statistical model to experimental data measuring IP costs over a range of parasite genotypes varying in virulence (ε) and host genotypes varying in recovery rate (c) as was done recently to estimate how IP costs depend on parasite exploitation and the immune response in rodent malaria [21].

To understand how these costs shape host evolution, we take an invasion analysis approach [22]. Consider the invasion of a rare mutant host into a resident population that has reached its epidemiological equilibrium. Assuming that the mutant's abundance is low enough that its effects on epidemiological dynamics can be ignored, we derive an expression for invasion fitness by considering the expected reproductive output of a mutant individual across its life. Born into the susceptible class, the individual has birth rate b_Sm, where the subscript m denotes a parameter that may differ between the resident and invader population and suppressing, for now, any dependence of b_Sm on c_m, the invader recovery rate. The individual is expected to remain in the susceptible class for 1/(βI* + μ) units of time, where βI* is the infection risk at the resident equilibrium. With probability βI*/(βI* + μ), it becomes infected rather than dies, and its birth rate is then b_Im. The individual is expected to remain in the infected class for 1/(μ + α + c_m) units of time. With probability c_m/(μ + α + c_m), the individual recovers and returns to the susceptible class, beginning the cycle anew. This gives a recursion equation for total reproductive output, R:

This can be solved for R, where R > 1 implies mutant invasion. The same expression can be obtained using the next-generation matrix approach [23]. Rewriting R > 1 by separating I* from the terms involving the invader traits, we find that invasion requires

The expression on the left is the size of the infected class at the equilibrium set by the invader. Therefore, evolution maximizes the number of infected hosts at equilibrium, analogous to the result in community ecology that when two prey species (or, in this case, hosts) share a predator (or, in this case, parasite), the prey that can sustain a higher predator population will competitively exclude the other [24]. Thus, the ESS host strategy maximizes H, given by

2.1

Note that, in the absence of any resource or IP costs, evolution would drive recovery rate to infinity.

3. Results

The direction of evolution is determined by the sign of the selection gradient ∂H/∂c. To begin, we consider how constitutive versus facultative resource costs affect the evolution of recovery rate c. Possible endpoints of evolution are given by values of c that cause the selection gradient to vanish (i.e. ∂H/∂c = 0). After substituting the appropriate expressions for b_S and b_I, differentiating and rearranging the terms, the sign of the selection gradient for the facultative and constitutive cost cases is determined by the signs of the following expressions:

3.1

and

3.2

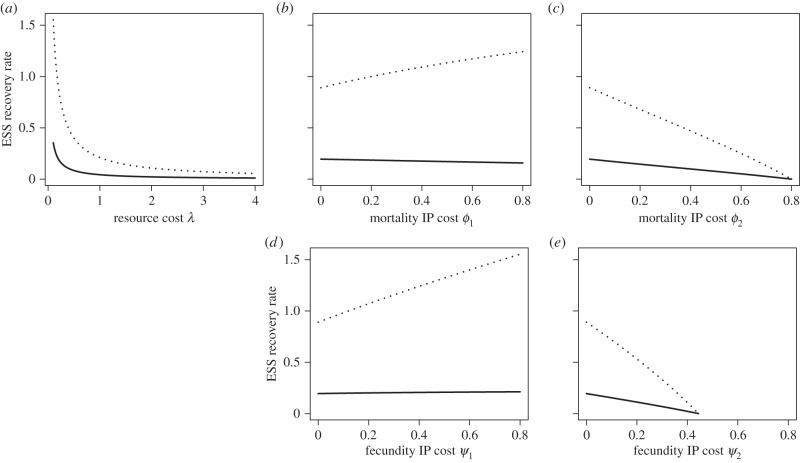
Here, ρ = (α + μ)/(α + μ + c) is the probability of dying while infected and R_I = (b − h(c))/(α + μ + c) is the expected reproductive output while infected. Thus, equation (3.1) predicts that a high probability of dying while infected will select for increased recovery rate, whereas a high reproductive output while infected or a high sensitivity of resource costs to recovery rate (h’(c)) will select for decreased recovery rate. All of the terms of equation (3.1) are found in equation (3.2), but they are differentially weighted. The quantity ρ − R_I is weighted by the per capita growth rate (b − h(c) − μ), whereas h’(c) is weighted by the parasite-induced mortality rate α. Because stability of the epidemiological equilibrium requires b − h(c) < α + μ, we conclude that the ESS recovery rate will always be lower in the constitutive cost case (figure 1a). This prediction is biologically intuitive. Recovery only increases fitness if uninfected hosts have higher fecundity or lower mortality than infected hosts. When uninfected and infected hosts have the same fecundity, the strength of selection on recovery rate will be weaker.

Figure 1.

ESS recovery rates as either resource costs or IP cost are increased, when resource costs are constitutive (solid lines) versus facultative (dashed lines). (a) ESS recovery rate as resource costs increase and there are no IP costs. (b,c) ESS recovery rates as IP mortality cost increases. (d,e) ESS recovery rates as IP fecundity cost increases. In (b,d), IP costs are independent of recovery rate. In (c,e), IP costs depend on recovery rate. In (a), f(ε, c) = g(ε, c) = 0; in (b), f(ε, c) = ϕ₁ε; in (c), f(ε, c) = ϕ₂c; in (d), g(ε, c) = ψ₁ε and in (e), g(ε, c) = ψ₂c. Other parameter values were (b = 1.0, μ = 0.8, λ = 0.2, γ = ɛ = 1.0).

We can next derive the selection gradient equations for the four combinations of resource and immunopathological costs. For facultative resource costs and mortality IP, the sign of the selection gradient is given by the sign of

3.3

where ρ_f = (α + f(ε, c) + μ)/(α + f(ε, c) + μ + c) is the probability of death while infected and R_I,f = (b − h(c))/(α + f(ε, c) + μ + c) is the expected reproductive output while infected. If mortality IP is independent of recovery rate, immunopathology will increase the recovery rate compared with the no-IP case (because IP leads to ρ_f > ρ and R_I,f < R_I; figure 1b). If mortality IP depends on recovery rate; however, the ESS recovery rate can decrease. In particular, because ρ_f − R_I,f − 1 < 0, IP costs will tend to decrease recovery rate when these costs are small (so the difference between ρ_f − R_I,f and ρ − R_I is not large) but are very sensitive to changes in recovery rate (so ∂f/∂c is large). For example, if IP costs were an accelerating rather than linear function of recovery rate, then it is much more likely for these costs to decrease recovery rate.

For facultative resource costs and fecundity IP, the sign of the selection gradient is given by the sign of

3.4

where R_I,g = (b − h(c) − g(ε, c))/(α + μ + c) is the expected reproductive output while infected (which is reduced by fecundity IP). Again, if IP costs are independent of recovery rate, immunopathology will increase the recovery rate (figure 1d), but if they depend on recovery rate, the ESS recovery rate can decrease (figure 1e). This is especially true when cost magnitude is not too large, but costs are very sensitive to changes in recovery rate.

For constitutive resource costs and mortality IP, the sign of the selection gradient is given by the sign of

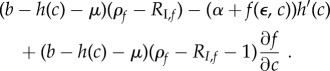3.5

Comparing equations (3.3) and (3.5) shows again that constitutive costs will reduce recovery rate compared with the facultative case. Moreover, even if IP cost is independent of recovery rate, immunopathology can decrease recovery rate from the no-IP expectation (3.2; figure 1b). In fact, there are few parameter combinations where IP costs will increase recovery rate if resource costs are constitutive.

For constitutive resource costs and fecundity IP, the sign of the selection gradient is given by the sign of

3.6

Again, constitutive costs decrease recovery rate relative to the facultative case and will tend to decrease it relative to the no-IP case (figure 1d,e).

Figure 1 also reveals that the evolution of recovery rate is much less sensitive to changes in IP cost when resource costs are constitutive. When costs are facultative, we would expect differences in IP cost to produce very large differences in recovery rate, whereas when costs are constitutive, recovery rate may be quite insensitive to changes in IP. Figure 1 also shows that increasing immunopathology can lead to the evolution of chronic infection (as recovery rate approaches zero).

Variability in immunopathological costs can also obscure the true relationship between recovery rate and fecundity. Figure 2a,c shows the ESS recovery rates as IP costs are increased when (a) IP cost is independent of recovery rate (g(ε, c) = ψ₀), or (c) IP cost depends on recovery rate (g(ε, c) = ψ₂c). Figure 2b,d shows the reproductive rates for each of the ESS recovery rates indicated by the solid points in figure 2a and c, respectively. The grey lines in the background show the reproductive rates (b_I = b − λc² − g(ε, c)) for each of the different values of cost. If one attempted to quantify the ‘cost of resistance’ by sampling from one or more populations where there was variation in cost and measuring the relationship between recovery and reproductive rate, the estimate of these costs would be very different. When IP costs are independent of recovery rate, there is a negative relationship between recovery and reproduction across a range of costs (figure 2b). When IP costs depend on recovery, however, the relationship between recovery and reproduction could appear negative, positive or non-significant, depending on the range of costs captured.

Figure 2.

ESS recovery rates as fecundity IP costs are increased when IP is independent of recovery (a) or depends on recovery (c). (b,d) Reproductive rates at the ESS recovery rates. The grey lines show g(ε, c) for each of the cost cases and for each level of IP cost. Other parameter values were (b = 1.0, μ = 0.8, λ = 0.2, γ = 2.0, ɛ = 1.0), and resource costs were assumed to be facultative.

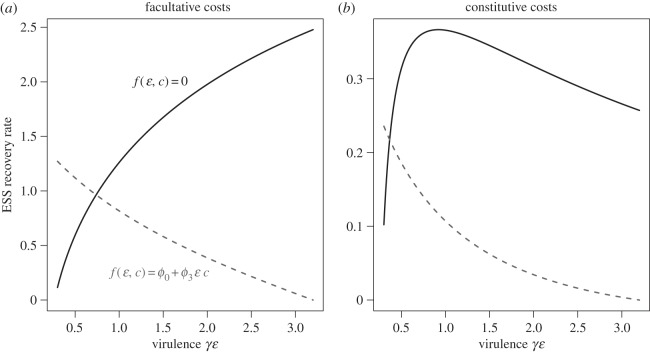
Immunopathology can also change the response of recovery rate to changes in other parameters, for example, baseline reproductive rate b_S, background mortality rate μ, or, most interestingly, parasite virulence α = γɛ. In the absence of immunopathology, the effect of increasing virulence on ESS recovery rate depends on whether resource costs are constitutive or facultative (figure 3). If costs are facultative, increasing virulence always increases recovery rate (black line, figure 3a); if costs are constitutive, increasing virulence can increase or decrease recovery rate, depending on whether virulence is low or high (black line, figure 3b). This result can be understood by comparing equations (3.1) and (3.2). ρ − R_I is an increasing function of α, so increasing virulence necessarily increases recovery rate in the facultative cost case. In the constitutive cost case, this increase is counterbalanced by the −αh‘(c) term. In particular, because ρ − R_I is a saturating function of virulence, it is assured that at some level of α, increasing virulence will increase a αh′(c) more than it increases (b − h(c) − μ)(ρ − R_I).

Figure 3.

ESS recovery rate as virulence is increased when physiological costs are facultative (a) versus constitutive (b), and when mortality IP costs are not present (black lines) or depend on the interaction between recovery and exploitation (grey dashed lines). Other parameter values were (b = 1.0, μ = 0.8, λ = 0.2, γ = 0.75, ϕ₀ = ϕ₃ = 1.0).

The response of recovery rate to increasing virulence can be very different if IP costs depend on an interaction between recovery rate and exploitation level ɛ, however (i.e. ϕ₃, ψ₃ > 0). In this case, even if resource costs are facultative, increasing virulence will drive an evolutionary decrease in recovery rate (grey lines in figure 3a,b). This would lead to the evolution of low resistance when hosts evolve in response to virulent parasites, and high resistance when hosts evolve in response to avirulent parasites.

4. Discussion

Host evolution is shaped by many factors, including the manifold costs of mounting an immune response. While previous theory has indicated that the magnitude and form of these costs can affect defence evolution [19,25–35], to the best of our knowledge, this is the first study that has examined the evolutionary consequences of changing the physiological cost structure (facultative versus constitutive resource costs, in the presence of immunopathological costs of varied magnitude and type) in a single modelling framework. We show that these costs qualitatively affect defence evolution, often leading to predictions that are the opposite of the expectation from previous theory. We discuss our results in the context of two general questions: how does variability in the source and magnitude of costs affect variability in immune defence and host life history? And when should a host mount a vigorous defence against parasitism?

(a). How does variability in cost affect recovery rate and host life history?

Models of host evolution typically assume that increased investment in defence reduces fecundity (e.g. table 2 in [30]). Constitutive costs of immunity are those incurred in the development and maintenance of the immune system, whereas facultative costs are those incurred in the deployment of the immune system (or indeed any inducible defence system [36]). The vast majority of models for the evolution of host recovery rate, in particular have assumed that increased recovery rate carries a constitutive cost—both susceptible and infected hosts have lower reproductive rates ([25,28,29,31], but see [27]). In reality, of course, organisms invest in both constitutive and facultative defences. Previous theory has investigated the optimal investment into constitutive and facultative defences at an individual scale [16,17]. In general, this theory has suggested that constitutive defences are almost always optimal. Investment in inducible defences tends to increase when these defences are relatively cheap, the probability of infection is low, and parasite virulence is high but unpredictable [16,17].

Our results indicate that ESS recovery rate is more sensitive to changes in cost magnitude when physiological costs are dependent on recovery rate, and when those costs are facultative (figure 1). If immune investment incurs a constitutive resource cost, in fact, changing the magnitude of costs can have almost no effect on the ESS recovery rate, especially if those costs are manifested as increased mortality (figure 1b,d). This result suggests that high variability in recovery rate among individuals or populations should only be expected when costs are facultative.

This result may help explain the otherwise peculiar empirical finding that constitutive costs of immune defence are detected less often than facultative costs (see [20] for a review of studies). To the extent that experimental efforts have focused on systems where individuals (or populations) are known to vary in immune defence, our results suggest that this may confer a bias towards systems where costs are facultative rather than constitutive.

However, our results suggest that immunopathology may complicate any effort to detect the costs of immune investment, especially if immunopathology affects fecundity. Such an example comes from studies of a rodent model of urogenital chlamydiosis. Data from this system suggest that CD4⁺ T-cells promote bacterial clearance but are also positively associated with CD8⁺ T-cells that scar the fallopian tubes [15,37]. Thus, those females that clear bacteria most quickly suffer the steepest declines in fertility, an effect that is enhanced by repeated exposure [37]. These costs, which are clearly detectable at the individual level, may be obscured in population-level comparisons if populations vary in the magnitude of the immunopathological cost. Figure 2 shows that, in this circumstance, populations with higher resistance can also have higher fecundity. The variation in IP cost obscures the true negative relationship between resistance and fecundity. This would operate in addition to other difficulties in detecting costs, like those noted above and the potential for varied condition among organisms to obscure negative correlations among life-history traits [38,39].

(b). When should hosts invest in a strong immune response to parasites?

Theory comparing the joint evolution of resistance and tolerance typically finds that tolerance is favoured over resistance whenever transmission rates are very high, leading to the evolution of chronic infections [29,33]. Our results (figure 1a,c,e) accord with this theory and with a conceptual model of chronic nematode infections [40]: when the cost of recovery is very high, it is better to simply tolerate infection by minimizing the cost of infection to fecundity. However, our results also suggest that the source of immune costs plays an important role in determining how investment in immune defence will change across environments.

For example, you might expect organisms living in resource-rich environments to invest more in defence. Increased resource abundance will increase the baseline fecundity b and reduce the background mortality μ. Our results suggest that the effect of these changes on immune investment depends on whether resource costs are facultative or constitutive. If the costs of recovery are facultative, organisms in the resource-rich environment will have a lower recovery rate; if the costs of recovery are constitutive, organisms in the resource-rich environment will have a higher recovery rate.

Similarly, it is intuitive to expect heavy investment in defence in response to highly virulent parasites. However, theory has shown that the evolutionary response of host defence to increased parasite virulence is varied: increased virulence can increase investment in resistance [27–29], but several studies have made the opposite prediction [26,31] or shown that host defence exhibits a unimodal response to increased virulence [25,32,33]. Our results suggest IP costs can also lead to host defence peaking at intermediate virulence (figure 3). In the most extreme case, IP can lead to the evolution of chronic infection with highly virulent pathogens [33]. Interestingly, the high virulence case, which favours investment in both constitutive and inducible defence, is also the case where the predictions for host evolution are most sensitive to the type and magnitude of costs (figure 2).

Kraaijeveld & Godfray [41] explored the relationship between the ability of Drosophila from different populations to survive parasitoid attack (‘resistance’) and the ability of sympatric parasitoid populations to evade the immune system and thus kill the larvae (‘virulence’) across Europe. The observed pattern did not present a simple relationship between resistance and virulence. In particular, many geographical locations where parasites had high virulence had Drosophila with low resistance. The authors suggested that some of the mismatch may be explained by changes in the presence of alternative hosts. However, immunopathology may also be playing a role in generating these patterns. Indeed, insects appear susceptible to immunopathology mediated by the phenoloxidase cascade [42] essential to parasitoid resistance [43]. Empirical studies that quantify virulence as well as manifold costs of defence may be essential to improve understanding of heterogeneity in the strength of immune responses.

(c). Outlook

Here, we studied the evolution of host recovery rate under manifold costs of defence: constitutive and facultative resource costs as well as immunopathological costs affecting mortality and fecundity. Immunopathology is a significant cost to immune activation that has received relatively little theoretical attention (but see [11,12,44]). As in Day et al. [11], we considered that immunopathology might depend on host recovery rate and/or parasite exploitation. There is empirical support for this: clinical and experimental data, for example, demonstrate that hosts mounting potent immune responses clear parasites but are more likely to exhibit lethal immunopathology (reviewed in [13]). Furthermore, Long & Graham [21] used a simple linear model [11] to statistically estimate the contributions of exploitation and recovery rate to immunopathological virulence in a rodent malaria system. Using peak within-host density as a proxy for exploitation and peak immune activation as a proxy for recovery rate, virulence attributable to immunopathology was found to increase with recovery rate [21]. There are also examples of immunopathological mortality dependent on exploitation or its interaction with recovery rate (e.g. mortality owing to avian influenza arising from strong inflammatory responses to high viral densities [45]). The generality of the dependence of immunopathology upon recovery rate and/or exploitation [37,45], however, remains to be assessed with suitable data from a wider variety of systems, including those restricted to the urogenital tract. Moreover, the probability of infection will affect optimal investment into defence, via feedback loops between individual and population scales [30]. Clearly, more theoretical and empirical work is needed, to better understand host evolution in a world of costly and complex defensive demands.