A GIS based spatially-explicit sensitivity and uncertainty analysis approach for multi-criteria decision analysis

Abstract

GIS multicriteria decision analysis (MCDA) techniques are increasingly used in landslide susceptibility mapping for the prediction of future hazards, land use planning, as well as for hazard preparedness. However, the uncertainties associated with MCDA techniques are inevitable and model outcomes are open to multiple types of uncertainty. In this paper, we present a systematic approach to uncertainty and sensitivity analysis. We access the uncertainty of landslide susceptibility maps produced with GIS-MCDA techniques. A new spatially-explicit approach and Dempster–Shafer Theory (DST) are employed to assess the uncertainties associated with two MCDA techniques, namely Analytical Hierarchical Process (AHP) and Ordered Weighted Averaging (OWA) implemented in GIS. The methodology is composed of three different phases. First, weights are computed to express the relative importance of factors (criteria) for landslide susceptibility. Next, the uncertainty and sensitivity of landslide susceptibility is analyzed as a function of weights using Monte Carlo Simulation and Global Sensitivity Analysis. Finally, the results are validated using a landslide inventory database and by applying DST. The comparisons of the obtained landslide susceptibility maps of both MCDA techniques with known landslides show that the AHP outperforms OWA. However, the OWA-generated landslide susceptibility map shows lower uncertainty than the AHP-generated map. The results demonstrate that further improvement in the accuracy of GIS-based MCDA can be achieved by employing an integrated uncertainty–sensitivity analysis approach, in which the uncertainty of landslide susceptibility model is decomposed and attributed to model's criteria weights.

Highlights

• •Sensitivity and uncertainty analysis for GIS-Multicriteria Decision Making is underdeveloped in GIScience.
• •Uncertainties associated with GIS-Multicriteria for landslide susceptibility mapping are systematically explored.
• •We develop a novel spatially-explicit approach and combine it with Dempster–Shafer Theory.
• •The results demonstrate that the accuracy of GIS-Multicriteria can be improved through this spatially-explicit approach.

1. Introduction

GIS based multicriteria decision analysis (MCDA) is primarily concerned with combining the information from several criteria to form a single index of evaluation (Chen et al., 2010a). The GIS-MCDA methods provide a framework for handling different views and compositions of the elements of a complex decision problem, and for organizing them into a hierarchical structure, as well as studying the relationships among the components of the problem (Malczewski, 2006). MCDA procedures utilizing geographical data consider the user's preferences, manipulate the data, and combine preferences with the data according to specified decision rules (Malczewski, 2004; Rahman et al., 2012). MCDA involves techniques, which have received increased interest for their capabilities of solving spatial decision problems and supporting analysts in addressing complex problems involving conflicting criteria (Kordi and Brandt, 2012). The integration of MCDA techniques with GIS has considerably advanced the traditional data combination approaches for Landslide Susceptibility Mapping (LSM). In analyzing natural hazards with GIS-MCDA, the LSM is considered to be one of the important application in domains (Feizizadeh and Blaschke, 2013a). A number of direct and indirect models have been developed in order to assess landslide susceptibility, and these maps were produced by using deterministic and non-deterministic (probabilistic) models (Yilmaz, 2010). In creating a susceptibility map, the direct mapping method involves identifying regions susceptible to slope failure, by comparing detailed geological and geomorphological properties with those of landslide sites. The indirect mapping method integrates many factors and weighs the importance of different variables using subjective decision-making rules, based on the experience of the geoscientists involved (Lei and Jing-feng, 2006; Feizizadeh and Blaschke, 2013a). Among the proposed methods, GIS-MCDA provides a rich collection of techniques and procedures for structuring decision problems and designing, evaluating and prioritizing alternative decisions for LSM. Thus, GIS-MCDA methods are increasingly being used in LSM for the prediction of future hazards, decision making, as well as hazard mitigation plans (Feizizadeh and Blaschke, 2013a). However, due to the multiple approach nature of natural hazard modeling (e.g LSM) the problems related to natural hazards cannot usually be handled without considering inherent uncertainty (Nefeslioglu et al., 2013). Such uncertainties may have significant impacts on the results, which may sometimes lead to inaccurate outcomes and undesirable consequences (Feizizadeh and Blaschke, 2013b).

GIS-MCDA based LSM methods are often applied without any indication of error or confidence in the results (Feizizadeh and Blaschke, 2012; Feizizadeh et al., 2012; Feizizadeh and Blaschke, 2013a). The uncertainties associated with MCDA techniques applied to LSM are due to incomplete and inaccurate data on landslide contributing factors, rules governing how the input data are combined into landslide susceptibility values and parameters used in the combination rules (Ascough et al., 2008). In the context of GIS-MCDA uncertainty, there is a strong relationship between data uncertainty and parameter uncertainty, since model parameters are obtained directly from measured data, or indirectly by calibration (Ascough et al., 2008). Due to a potentially large number of parameters and the heterogeneity of data sources, the uncertainty of the results is difficult to quantify. Even small changes in data and parameter values may have a significant impact on the distribution of landslide susceptibility values. Therefore, MCDA techniques in general, and in the domain of hazard mapping in particular, should be thoroughly evaluated to ensure their robustness under a wide range of possible conditions, where robustness is defined as a minimal response of model outcome to changing inputs (Ligmann-Zielinska and Jankowski, 2012).

In an effort to address the uncertainty associated with data and parameters of GIS-MCDA we use a unified approach to uncertainty and sensitivity analysis, in which uncertainty analysis quantifies outcome variability, given model input uncertainties, followed by sensitivity analysis that subdivides this variability and apportions it to the uncertain inputs. Conceptually, uncertainty and sensitivity analysis represent two different, albeit complementary approaches to quantify the uncertainty of the model (Tenerelli and Carver, 2012). Uncertainty analysis: (a) helps to reduce uncertainties in how a MCDA method operates, and (b) parameterizes the stability of its outputs. This is typically achieved by introducing small changes to specific input parameters and evaluating the outcomes (Crosetto et al., 2000; Eastman, 2003). This process provides the possibility of measuring the level of confidence in decision making and in the decision maker (Chen et al., 2011). Uncertainty analysis aims to identify and quantify confidence intervals for a model output by assessing the response to uncertainties in the model inputs (Crosetto et al., 2000). Meanwhile sensitivity analysis technically explores the relationships between the inputs and the output of a modeling application (Chen et al., 2010b). Sensitivity analysis is the study of how the variation in the output of a model (numerical or otherwise) can be apportioned, qualitatively or quantitatively, to different sources of variation, and how the model depends upon the information fed into it (Saltelli et al., 2000). Sensitivity and uncertainty analyses together contribute to understanding the influence of the assumptions and input parameters on the model of evaluation (Crosetto et al., 2000). They are crucial to the validation and calibration of MCDA (Chen et al., 2010b). Hereby, handling errors and uncertainty in GIS-MCDA plays a considerable role in decision-making when it is important to base decisions on probabilistic ranges rather than deterministic results (Tenerelli and Carver, 2012). In the context of applying GIS-MCDA to LSM we already compared different MCDA methods and their capabilities (see Feizizadeh et al., 2012, 2013; Feizizadeh and Blaschke, 2013a, 2013b). Building on this earlier work, in the remainder of this paper, we carry out a GIS-MCDA study for LSM with emphasis on the uncertainty and sensitivity analysis in order to improve the accuracies of the results by means of identifying and minimizing the uncertainties associated with the respective MCDA methods.

2. Study area and data

The study area is the Tabriz basin which is a sub-basin of the Urmia Lake basin in Northwest Iran (Fig. 1). The study area encompasses 5378 km² and has about 2 million inhabitants. It is important for the East Azerbaijan province in terms of housing, industrial and agricultural activities. In the Tabriz basin the elevation increases from 1260 m in the lowest part at the Urmia Lake, to 3680 m above sea level in the Sahand Mountains (Feizizadeh and Blaschke, 2013a). Landslides are common in the Urmia lake basin and the complexity of the geological structure in the associated lithological units, comprised of several formations, causes volcanic hazards, earthquakes, and landslides (Feizizadeh and Blaschke, 2012). A landslide inventory database for the East Azerbaijan Province lists 132 known landslide events (Feizizadeh and Blaschke, 2013a). The geophysical setting makes the slopes of this area potentially vulnerable to mass movements such as rock fall, creeps, flows, topples and landslides (Feizizadeh and Blaschke, 2013a). In addition, the geotechnical setting and its impacts in the form of earthquakes as well as volcanic activities in the Sahand Mountains affect many human activities. Such hazards are sometimes limiting factors in respect to land use intensity in the Tabriz basin. As already indicated in the introduction section, in the remainder of this paper we focus on the sensitivity and uncertainty analysis for GIS-MCDA. For more detailed information regarding the physical properties and the geological setting of the study area the reader is referred to Feizizadeh and Blaschke (2011, 2013b, 2013a) and Feizizadeh et al. (2012).

Fig. 1.

Urmia lake basin (right).

In order to develop a landslide susceptibility map of the area, we used nine factors (evaluation criteria) contributing to landslide vulnerability. They include topographic, geological, climatic, and socioeconomic characteristics, which were selected based on our previous studies in this area (see Feizizadeh et al., 2012, 2013; Feizizadeh and Blaschke, 2013a for criteria selection and justification). In the data preparation phase, topographic maps at the scale of 1:25,000 were used to extract road and drainage layers. The topographic maps were also used to generate a digital elevation model (DEM), as well as slope and aspect terrain derivatives. The lithology and fault maps were derived from geological maps at the scale of 1:100,000. A precipitation map was created through the interpolation of data gathered by meteorological stations in East Azerbaijan province over the time period of 30-years. A detailed land use/land cover map was derived from SPOT satellite images with 10 m spatial resolution using image processing techniques. In addition, a landslide inventory database including 112 landslide events was used for the validation of the results. In the final data pre-processing step, all vector layers were converted into raster format layers with 5 m spatial resolution.

3. Methods

The research methodology is designed to evaluate the sensitivity and uncertainty of GIS-MCDA for LSM through the GIS-based spatially explicit uncertainty analysis method (GISPEX) and Dempster–Schafer Theory (DST) methods in order to: (a) compare two MCDM techniques: Analytical Hierarchy Process (AHP) and Ordered Weighted Averaging (OWA) in terms of the uncertainty of generated landslide susceptibility maps and (b) demonstrate how a unified approach to uncertainty and sensitivity analysis can be used to help interpret the results of landslide susceptibility mapping. In order to achieve these objectives, the methodology is composed of following steps:

• (1)Compute landslide susceptibility maps using AHP and OWA.
• (2)Compute measures of uncertainty for both maps with Monte Carlo Simulation (MCS).
• (3)Run Global Sensitivity Analysis (GSA).
• (4)Access the uncertainty of LSM maps in light of MCS and Average Shift in Ranks (ASR) results.
• (5)Assess the robustness of weights in both MCDM techniques in light of GSA results.
• (6)Validate the landslide susceptibility maps without and with uncertainty metrics using the DST technique.

Fig. 2 depicts the three phases comprising this methodology. The first phase applies the AHP and OWA methods for producing the landslide susceptibility maps without accounting for uncertainty of criteria weights. This phase, called the “Conventional approach”, is based on a Spatial Multiple Criteria Evaluation (S-MCE) which assesses the landslide susceptibility by considering nine causal and diagnostic criteria. S-MCE methods allow multiple and often conflicting criteria to be taken into account and weights to be applied to input criteria depending on the level of importance ascribed to these by the user (Carver, 1991; Tenerelli and Carver, 2012). The second phase involves the uncertainty analysis using the GISPEX to simulate the error propagation. In this phase we employ the MCS to assess the uncertainty weight space, where weights are expressed using probability density functions. Within this phase we aim to produce the landslide susceptibility maps of the ‘Novel approach’, based on the outcome of sensitivity analysis and the revised weights. The third and last phase includes the validation of results using the landslide inventory database and applying the DST for calculating the certainty of the results. In this phase we aim to compare the accuracy of the two approaches in LSM.

Fig. 2.

Methodology scheme and workflow.

3.1. Training data and standardization

As the basis for the GISPEX approach we generated a set of random points serving as input training data. Specifically, we generated 300 random locations within the study area (Arc GIS 10.1; Create Random function). Within each of these 300 locations we generated multiple points resulting in a total of 6714 random points distributed across 300 random locations. These training data were assigned the attribute data and spatial characteristics of the nine criteria used in the GISPEX approach through standard GIS overlay techniques. In our LSM decision model each criterion is represented by a map. This includes categorical data maps (e.g. land use or geology), as well as ratio-level data maps (e.g. slope or elevation). Hence, for the purpose of decision analysis, the values and classes need to be converted into a common scale to overcome the incommensurability of data (Azizur Rahman et al., 2012). Such conversion is called standardization (Sharifi and Retsios, 2004; Azizur Rahman et al., 2012). The standardization transforms and rescales the original raster cell values into the [0–1] value range, and thus enables combining various raster layers regardless of their original measurement scales (Gorsevski et al., 2012). The function is chosen in such a way that cells in a rasterized map that are highly suitable in terms of achieving the analysis objective obtain high standardized values and less suitable cells obtain low values (Azizur Rahman et al., 2012). Accordingly the standardization was performed based on the benefit or cost contribution of each criterion to landslide susceptibility.

3.2. Criteria weights and AHP

One of the most widely used methods in spatial multicriteria decision analysis is the AHP, introduced and developed by Saaty (1977). As a multicriteria decision-making method, the AHP has been applied for solving a wide variety of problems that involve complex criteria across different levels, where the interaction among criteria is common (Tiwari et al., 1999; Nekhay et al., 2008; Feizizadeh et al., 2012). Since in any MCDA the weights are reflective of the relative importance of each criterion, they need to be carefully selected. In this regard, the AHP (Saaty, 1977) can be applied to help decision-makers make pairwise comparisons between the criteria and thus reduce the cognitive burden of evaluating the relative importance of many criteria at once. It derives the weights by comparing pairwise the relative importance of criteria, taken two at a time. Through a pairwise comparison matrix, the AHP calculates the weighting for each criterion (wi) by taking the eigenvector corresponding to the largest eigenvalue of the matrix, and then normalizing the sum of the components to unity as:

$$\sum _{i=1}^{n}wi=1$$ (1)

The overall importance of each of the individual criteria is then calculated. An importance scale is proposed for these comparisons through of AHP approach from 1 to 9 (see Table 1). The basic input is the pairwise comparison matrix, A, of n criteria, established on the basis of Saaty's scaling ratios, which is of the order (n×n) as defined in Eq. (2) below (Chen et al., 2010a; Feizizadeh and Blaschke, 2013c):

$$A=\left[aij\right],i,j=1,2,3,\dots ,n$$ (2)

in which A is a matrix with elements aij. The matrix generally has the property of reciprocity, expressed mathematically as:

$$aij=1/aji$$ (3)

Table 1.

Scales for pairwise AHP comparisons (Saaty and Vargas, 1991).

Intensity of importance	Description
1	Equal importance
3	Moderate importance
5	Strong or essential importance
7	Very strong or demonstrated importance
9	Extreme importance
2,4,6,8	Intermediate values
Reciprocals	Values for inverse comparison

After generating this matrix it is then normalized as a matrix B:

$$B=\left[bij\right],i,j=1,2,3,\dots ,n$$ (4)

in which B is the normalized matrix of A, with elements bij defined as:

$$bij=aij/\sum _{i=1}^{n}aij=1,2,3,\dots ,n$$ (5)

Each weight value wi is computed as:

$$wi=\frac{{\sum }_{j=1}^{n}bij}{{\sum }_{i=1}^n{\sum }_{j=1}^{n}bij},i,j=1,2,3,\mathrm{..}.,n$$ (6)

Eqs. (7)–(9) represent the relationships between the largest Eigenvalue (λ_max) and corresponding Eigenvector (W) of the matrix B (Xu, 2002; Chen et al., 2010a; Feizizadeh and Blaschke, 2013c):

$$BW={\lambda }_{\max }W$$ (7)

In AHP application it is important that the weights derived from pairwise comparison matrix be consistent, therefore one of the strengths of AHP is that it allows for inconsistent relationships while, at the same time, providing a Consistency Ratio (CR) as an indicator of the degree of consistency or inconsistency (Feizizadeh and Blaschke 2013c; Chen et al., 2010a). CR is used to indicate the likelihood that the matrix judgments were generated randomly (Saaty, 1977; Park et al., 2011).

$$CR=\frac{CI}{RI}$$ (8)

where the random index (RI) is the average of the resulting consistency index depending on the order of the matrix given by Saaty (1977), and the consistency index (CI) can be expressed as:

$$CI=\frac{({\lambda }_{\max -n})}{n-1}$$ (9)

where λ_max is the largest or principal eigenvalue of the matrix, and n is the order of the matrix. A CR on the order of 0.10 or less is a reasonable level of consistency (Saaty, 1977; Park et al., 2011). The determination of CR value is critical. It is computed in order to check the consistency of the conducted comparisons (Gorsevski et al., 2006). Based on (Saaty, 1977), if the CR<0.10 then the pairwise comparison matrix has an acceptable consistency and the weight values are valid and can be utilized. Otherwise, if the CR≥0.10 then the pairwise comparisons are lacking consistency and the matrix needs to be adjusted and the element values should be modified (Feizizadeh and Blaschke, 2013c). In our study the CR value for pairwise matrix was 0.053 (see Table 2 for weights of criteria and Table 4 for weights of sub-criteria).

Table 2.

Pairwise comparison matrix for dataset layers of landslide analysis.

Factors	1	2	3	4	5	6	7	8	9	Eigen values
(1) Aspect	1									0.025
(2) Distance to road	1/5	1								0.036
(3) Elevation	1/2	1/3	1							0.02
(4) Distance to stream	1/3	1/3	1/3	1						0.112
(5) Distance to fault	1/3	1/5	1/5	1/3	1					0.124
(6) Slope	7	1/5	9	1/3	1/4	1				0.141
(7) Land use	8	6	1/5	1/5	1/3	1/3	1			0.16
(8) Precipitation	8	6	7	7	4	3	1/5	1		0.172
(9) lithology	9	7	1/3	8	7	4	1/5	8	1	0.21
Consistency ratio: 0.053

Table 4.

Pairwise comparison matrix, factor weights and consistency ratio of the data layers used.

Factors	1	2	3	4	5	Eigen values	(H) observed landslide	(I)' area of landslides M2
Lithology
(1) Altered zone	1					0.09
(2) Metamorphic-Plutonic	1	1				0.12
(3) Plutonic	3	3	1			0.18	31	47,321
(4) Volcanic	6	5	7	1		0.27	43	107,568
(5) Metamorphic-volcanic	6	5	4	4	1	0.34	38	70,011
Consistency ratio: 0.061
Precipitation (mm)
(1) 250>	1					0.17
(2) 251–300	3	1				0.32	111	223,664
(3) 301–350	4	3	1			0.51	1	1236
Consistency ratio: 0.075
Land use/cover
(1) Settlement	1					0.053
(2) Orchard and croplands	3	1				0.067
(3) Dry-Farming & pasture lands	8	7	1			0.235	1	983
(4) Bare soil	9	8	3	1		0.325	111	223,917
(5) Rock bodies	9	8	3	3	1	0.32
Consistency ratio: 0.054
Slope (%)
(1) 0–10	1					0.09	33	37,873
(2) 10.1–20	3	1				0.18	15	18,345
(3) 20.1–30	4	3	1			0.47	25	29,876
(4) 30.1–40	3	3	1/3	1		0.15	18	110,242
(5) 40.1<	1/3	1/4	1/6	1/4	1	0.11	21	28,564
Consistency ratio: 0.083
Distance to fault (m)
(1) 0–1000	1					0.515	102	203,560
(2) 1001–2000	1/3	1				0.224	8	6762
(3) 2001–3000	1/5	1/3	1			0.126
(4) 3001–4000	1/7	1/5	1/2	1		0.085
(5) 4000<	1/5	1/2	2	3	1	0.05	2	14,578
Consistency ratio: 0.024
Distance to stream (m)
(1) 0–50	1					0.51	19	43,412
(2) 51–100	1/3	1				0.21	16	29,543
(3) 101–150	1/5	1/3	1			0.11	20	44,152
(4) 151–200	1/7	1/5	1/2	1		0.091	15	20,928
(5) 200<	1/5	1/2	1/6	1/4	1	0.079	42	86,865
Consistency ratio: 0.024
Distance to roads (m)
(1) 0–25	1					0.269
(2) 26–50	4	1				0.255
(3) 51–75	4	2	1			0.249	1	751
(4) 76–100	4	2	1	1		0.135	2	1569
(5) 100<	3	2	1	1	1	0.092	109	222,580
Consistency ratio: 0.002
Aspect
(1) Flat	1					0.046	19	56,345
(2) North	9	1				0.059	16	33,654
(3) East	1	1/8	1			0.109	10	16,789
(4) West	4	1/7	3	1		0.269	52	93,514
(5) South	9	7	7	7	1	0.517	15	24,598
Consistency ratio: 0.061
Elevation (m)
(1) 1260–1400	1					0.076	1	512
(2) 1401–1800	9	1				0.239	43	82,456
(3) 1801–2500	9	8	1			0.393	68	141,932
(4) 2501–3000	8	7	7	1		0.173
(5) 3001–3680	7	1/7	1/6	1/5	1	0.119
Consistency ratio: 0.072

3.3. Sensitivity and uncertainty in AHP weights

The uncertainty of weights lies in the subjective expert or stakeholder judgement of the relative importance of different attributes, given the range of their impacts (Chen et al., 2011). As we discussed in Section 3.2, the AHP's pairwise comparison is the most widely used technique for criteria weighting in MCDA processes. However, since the pairwise comparison of criteria is based on expert opinions, it is open to subjectivity in making the comparison judgements. As a result, any incorrect perception on the role of the different land-failure criteria can be easily conveyed from the expert's opinion into the weight assignment (Kritikos and Davies, 2011; Feizizadeh and Blaschke, 2013a). This expert subjectivity, particularly in pairwise comparisons, constitutes the main drawback of the AHP technique (Nefeslioglu et al., 2013). Furthermore, the AHP is coarse in finalizing the rankings of competing candidates when used to identify major contributors to the particular problems in question. The main difficulty associated with AHP application is centred on the decision regarding the priorities of all alternatives involved in the decision-making process (Hus and Pan, 2009). Traditionally, Eigen values from the AHP computation have been used as the basis for ranking, yet the absence of the probability of individual alternatives tends to confuse decision-makers, particularly for the alternatives that are similar (Hus and Pan, 2009). In an effort to deal with subjectivity in criterion weights contributing to potential uncertainty of model outcomes previous studies (e.g. Hus and Pan, 2009; Benke and Pelizaro, 2010; Feizizadeh and Blaschke 2013a) have suggested integrating the Monte Carlo Simulation (MCS) with conventional AHP in order to enhance the screening capability when there is a need to identify a reliable decision alternative (model outcome) (Hus and Pan, 2009).

The AHP-MCS approach takes the probabilistic characterization of the pairwise comparisons into account (Bemmaor and Wagner, 2000; Hahn, 2003). This approach is based on the associate with probability distributions which is sufficient to confirm that one alternative is preferred to another (in the sense of maximizing expected utility) provided that certain constraints on the underlying utility function are satisfied (Durbach and Stewart, 2012). Consider the pairwise comparison ratio (C_ij) where i≠j, that has resulted from the pairwise comparison of two and only two alternatives O_i and O_j with weights w_i and w_j. For the moment, take w_i≥w_j, so that C_ij={1, 2, …, 9}. Then C_ij expresses the amount by which O_i is preferred to O_j. Specifically, for every outcome of preference for O_j, there are C_ij outcomes of preference for O_i. We assume this to be the ratio of successful outcomes and failure outcomes in a binomial process. As such, the pairwise comparison ratios can be used to obtain the components of a binomial process in which w_i successes have been observed in (w_i+w_j) trials subject to an unobserved preference parameter, p_i. With no loss of generality, we can divide the numerator and the denominator of C_ij by the sum of the weights to obtain (Hahn, 2003).

$$C_{ij}=\frac{W_i}{W_j}=\frac{W_i/(W_i+W_j)}{W_j/(W_i+W)}=\frac{P_i}{1-P_i}$$ (10)

where p_i/(1−p_i) is the ratio of preferences and constitutes the stochastically derived priority. The priority p_i is such that 0<p_i<1 in the present context, since by definition the act of pairwise comparison requires the presence of non-zero weights w_i and w_j associated with O_i and O_j respectively. Again, we assume that w_i has a binomial distribution with parameters w_i+w_j and p_i, which we write as w_i~Binomial (w_i+w_j, p_i). Note that in the cases where w_i<w_j, it remains true that w_i~Binomial (w_i+w_j, p_i) (Hahn, 2003).

Many times a decision maker will be faced with more than two alternatives. In this case, the underlying process is multinomial by extension. If there are K alternatives O₁, O₂, …, O_K with weights w₁, w₂, …, w_K, then the ith row of the pairwise comparison matrix has a multinomial distribution. That is,

$$(w_{i1},w_{i2},\dots ,w_{iK})~Multinomial(w_{i1}+w_{i2}+\dots +w_{iK},p_i)$$ (11)

where p_i is a vector of preference parameters or priorities as following:

$$\sum _{k=1}^k{p}_{ik}=1$$ (12)

since all K alternatives are present by definition, it must be true that 0<p_ik<1. With K alternatives, the matrix of pairwise comparisons will contain K multinomial trials. Thus, the matrix of pairwise comparisons is square with K columns, each one corresponding to an alternative, and K rows, each one corresponding to a different trial. Having supplied a probabilistic characterization of the pairwise comparison process and the resulting matrix of pairwise comparisons, it is possible to specify statistical models for the prediction of outcomes. Of primary interest is p, the vector of marginal priorities for the alternatives. A natural model for the problem of interest is the multinomial logit model (e.g., McFadden, 1973). Using this general model, a Bayesian perspective will be adopted for inference on p, and estimation will be conducted using a MCS method (Hahn, 2003).

3.4. Implementation of AHP-Monte Carlo simulation

Simulation is one of the most appropriate approaches to analyze the uncertainty propagation of a GIS model, without knowing the functional form of the errors (Eastman, 2003; Tenerelli and Carver, 2012). The MCS technique is the most widely used statistical sampling method in the uncertainty analysis of a decision making system. It can be applied to complex systems, where it is allowed to vary possible variables jointly, and to check their synthetic effect through sampling input values repeatedly from their respective probability distributions (Chen et al., 2011). Sample-based uncertainty analysis, via MCS approaches, plays a central role in this characterization and quantification of uncertainty (Helton, 2004; Janssen, 2013), since the uncertainty of attribute values and weights can be represented as a probability distribution or a confidence interval (Chen et al., 2011). In our research we use the statistical analysis capability of MCS to carry out the uncertainty analysis associated with AHP weights. For this to happen, our research methodology makes use of the concept of AHP-MCS, where we take into account the criteria weights derived from the AHP pairwise matrix for the uncertainty analysis using MCS. In the context of AHP-MCS it should be notated that the traditional AHP approach lacks probability values to distinguish adjacent alternatives in the final ordering. In response to this specific problem, Rosenbloom (1997) suggested that, in the distribution of 1/9 and 9, where a_j,i=1/a_i,j and a_i,i=1, the pairwise values could be viewed as random variables a_i,j. This means that every paired matrix will be symmetrically complementary. The value of a random variable a_j,i will be the reciprocal of a_i,j. Therefore, it is reasonable to assume that {a_i,j|i>j} is independent, and the final scores S₁, S₂,…, S_n will be stochastic as well. In the case of Si>Sj, alternative i is superior to alterative j at a certain level of error (a). To obtain the probability information for a_i,j in the context of multiple decision-makers, we assume that the probability of evaluations made by all experts regarding a_i,j are equal. This will convert every a_i,j into a discrete random variable. In the case of one decision-maker, on the other hand, the judgment made regarding each paired uncertainty will become a continuous random variable (Rosenbloom, 1997; Hus and Pan, 2009).

The AHP-MCS approach in our research is based on sampling the vector of the input parameters in a random sequence in order to get a corresponding statistical sample of the vector of the output variables, and then estimate the characteristics of these output variables using the output samples. This approach makes use of the MCS method by estimating distributions of the output variables (Espinosa-Paredes et al., 2012). We performed AHP-MCS to model the error propagation from the input data to the model output (the landslide susceptibility surface) according to the following steps:

• (I)Generating a random uniformly distributed dataset using a random function as training data for calculating the uncertainty analysis.
• (II)Using the AHP based criteria weights as reference weights of MCS (see Table 2).
• (III)Running the simulation N times: practically the number of simulations (N) vary from 100 to 10,000 according to the computational load, the complexity of the model, and the desired accuracy.
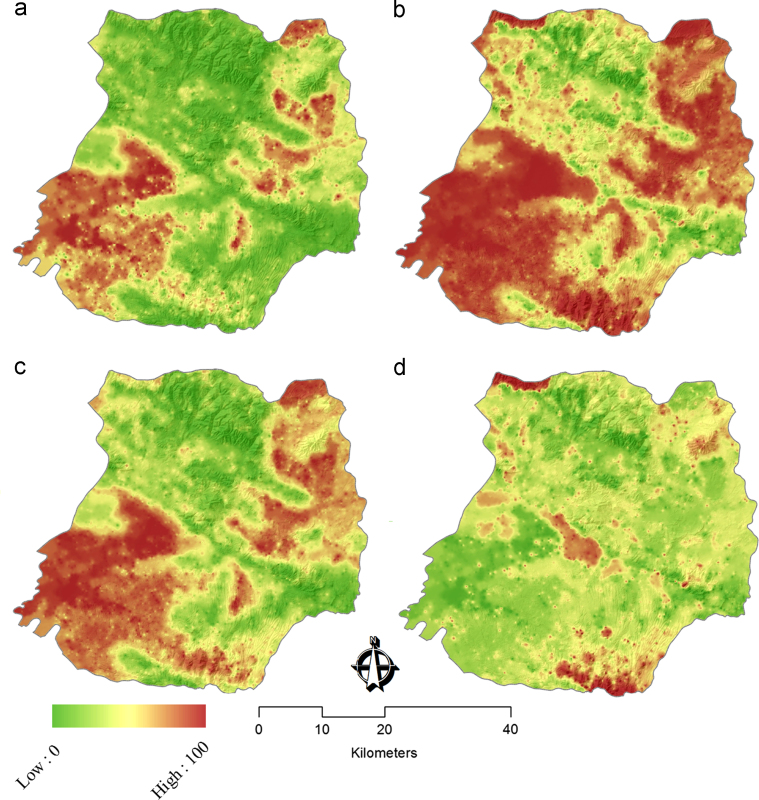
• (IV)Analyzing the results, producing statistics and mapping the spatial distribution of the computed errors including: the minimum rank (Fig. 3a), maximum rank (Fig. 3b), average rank (Fig. 3c), and standard deviation rank (Fig. 3d).

Fig. 3.

Results of MCS: (a) minimum rank, (b), maximum rank, (c) average rank and (d) standard deviation rank.

3.5. Variance-based global sensitivity analysis

Global Sensitivity Analysis (GSA) subdivides the variability and apportions it to the uncertain inputs (Ha et al., 2012). GSA is based on perturbations of the entire parameter space, where input factors are examined both individually and in combination (Ligmann-Zielinska, 2013). This algorithm has been developed for solving the real-value numerical optimization problems (Civicioglu, 2012). So far only a few methods have been proposed to use the capability of GSA for spatial decision making and modeling (Ligmann-Zielinska, 2013). In this regard, Lilburne and Tarantola (2009) categorized the methods based on their model dependence, computational efficiency, and algorithmic complexity. Ligmann-Zielinska (2013) also proposed a model-independent variance-based GSA, which obviates the assumptions of model linearity and offers an acceptable compromise in computational efficiency. Variance based GSA has been used in sensitivity analysis and this approach is identified as one of the most appropriate techniques for GSA (Saltelli et al., 2000; Saisana et al., 2005). The goal of variance-based GSA is to quantitatively determine the weights that have the most influence on model output, in this instance on the landslide susceptibility value computed for each cell of a landslide susceptibility layer. With this method we aim to generate two sensitivity measures: first order (S) and total effect (ST) sensitivity index. The importance of a given input factor X_i can be measured via the so-called sensitivity index, which is defined as the fractional contribution to the model output variance due to the uncertainty in X_i. For k independent input factors, the sensitivity indices can be computed by using the following decomposition formula for the total output variance V (Y) of the output Y (Saisana et al., 2005):

$$V(Y)=\sum _i{V}_i+\sum _i\sum _{j>i}{V}_{ij}+\dots +V_{12\dots k}$$ (13)

$$V_i=V_{Xi}\{E_{X-i}(Y|X_i)\},$$ (14)

$$V_{ij}=V_{XiXj}\{E_{X-ij}(Y|X_i,X_j)\}-V_{Xi}\{E_{X-i}(Y|X_i)\}-V_{Xj}\{E_{X-j}(Y|X_j)\}$$ (15)

and so on. In computing V_Xi{E_X−i(Y|X_i)}, the expectation E_X−i would call for an integral over X−i, i.e. over all factors except X_i, including the marginal distributions for these factors, whereas the variance V_xi would imply a further integral over X_i and its marginal distribution. A first measure of the fraction of the unconditional output variance V(Y) that is accounted for by the uncertainty in X_i is the first-order sensitivity index for the factor X_i defined as (Saisana et al., 2005):

$$S_i=V_i/V$$ (16)

Eq. (16) is the first term in Eq. (13) and is known as interactions. A model without interactions among its input factors is considered as additive. In this case, ${\sum }_{i=1}^{k}S=1$, and the first-order conditional variances of Eq. (14) are necessary in order to decompose the model output variance (Saisana et al., 2005). For a non-additive model, higher order sensitivity indices, which are responsible for interaction effects among sets of input factors, must be computed. However, higher order sensitivity indices are usually not estimated, as in a model with k factors the total number of indices (including the S_is) that should be estimated is as high as 2^k−1. For this reason, a more compact sensitivity measure is used. This is the total effect sensitivity index, which concentrates all the interactions involving a given factor X_i in one single term. For example, for a model of k=3 independent factors, the three total sensitivity indices would be as follows (Saisana et al., 2005):

$$S_{T1}=\frac{V(Y)-V_{X_2{X}_3}\{E_{X_1}(Y|X_2,X_3)\}}{V(Y)}=S_1+S_{12}+S_{13}+S_{123}$$ (17)

Analogously:

$$S_{T2}=S_2+S_{12}+S_{23}+S_{123}{S}_{T3}=S_3+S_{13}+S_{23}+S_{123.}$$ (18)

In other words, the conditional variance in Eq. (17) can be generally written as $V_{X-i\{E_{X-i}(Y|X-i)\}}$ (Homma and Saltelli, 1996). It expresses the total contribution to the variance of Y due to non-X_i, i.e. to the k−1 remaining factors, hence V(Y)−V_X−i{E_X−i(Y|X−i)} includes all terms, i.e. a first-order term as well as interactions in Eq. (13), which involve factor X_i. In general, ${\sum }_{i=1}^k{S}_{Ti}\ge 1$, with equality if there are no interactions. For a given factor X_i a notable difference between S_Ti and S_i flags an important role of interactions for that factor in Y. Highlighting interactions between input factors helps us to improve our understanding of the model structure (Saisana et al., 2005). In the context of variance-based GSA we continued the analysis by calculating the importance of spatial bias in determining option rank order by means of Average Shift in Ranks (ASR) as follows (Saisana et al., 2005; Ligmann-Zielinska and Jankowski, 2012):

$$ASR=\frac{1}{n}\sum _{a=1}^n|a_{-}ran{k}_{ref}–a_{-}rank|$$ (19)

where ASR is the average shift in ranks, a_rank_ref is the rank of option A in the reference ranking (e.g. equal weight case), and a_rank is the current rank of option A. ASR captures the relative shift in the position of the entire set of options and quantifies it as the sum of absolute differences between the current option rank (a_rank) and the reference rank (a_rank_ref), divided by the number of all options (Ligmann-Zielinska and Jankowski, 2012). In the first step of the analysis, we selected the AHP weight to arrive at the reference ranking (See column a in the Table 3). We also used maximum weights for the criteria which are assessed based on the importance of each criterion in the AHP pairwise matrix (see column b in Table 3). The results of GSA are presented in Table 3, columns c–f.

Table 3.

Results of GSA.

Factor	(a) Reference weights	(b) Maximum weights	(c) S	(d) ST	(e) S%	(f) ST %
Aspect	0.025	0.2	0.172	0.183	17.2	14.8
Distance to road	0.036	0.5	0.001	0.006	0.1	0.5
Elevation	0.02	0.55	0	0.01	0	0.8
Distance to stream	0.112	0.6	0.091	0.238	9.1	19.3
Distance to fault	0.124	0.7	0.176	0.286	17.6	23.2
Slope	0.141	0.75	0.012	0.058	1.2	4.7
Land use	0.16	0. 65	0.048	0.083	4.8	6.8
Precipitation	0.172	0.6	0.002	0.001	0.2	0.1
lithology	0.21	0.95	0.286	0.368	28.6	29.8

3.6. Dempster–Shafer theory

The DST, based on evidence proposed by Shafer (1976), has been regarded as an effective spatial data integration model. The DST is a well-known evidence theory and provides a mathematical framework for information representation and combination (Carranza, 2009; Althuwaynee et al., 2012; Feizizadeh et al., 2012). The DST is considered to be correct for the representation of the epistemic uncertainty affecting the expert knowledge of the probability P (M_l) that the alternative model M_l, l=$1$,…,n. In the DST framework, a lower and an upper bound are introduced for representing the uncertainty associated with P (M_l). The lower bound, called belief, Bel (M_l), represents the amount of belief that directly supports M_l at least in part, whereas the upper bound, called plausibility, P_l (M_l), measures the fact that M_l could be the correct model ‘up to that value’ because there is only so much evidence that contradicts it. From a general point of view, contrary to the probability theory, which assigns the probability mass to individual elementary events, the theory of evidence makes basic probability assignments (bpa) m (A) on sets A (the focal sets) of the power set P(Z) of the event space Z, i.e., on sets of outcomes rather than on single elementary events. In more detail, M(A) express the degree of belief that a specific element x belongs to the set A only, and not to any subset of A. the bpa satisfies the following requirements (Baraldi and Zio, 2010):

$$m:P(Z)\to [0,1],m(0)=0;\sum _{A\in (Z)}m(A)=1$$ (20)

The belief function denotes the lower bound for an (unknown) probability function, whereas the plausibility function denotes the upper bound for an (unknown) probability function. The difference between the plausibility (Pls) and the belief (Bel) function represents a measure of uncertainty. The belief function measures the amount of belief in the hypothesis on the basis of observed evidence. It represents the total support for the hypothesis that is drawn from the BPAs for all subsets of that hypothesis (i.e. belief in [A, B] will be calculated as the sum of the BPAs for [A, B], [A], and [B]) and it is defined as (Gorsevski and Jankowski, 2005):

$$Bel(A)=\sum _{B\subseteq A}m(B)$$ (21)

The plausibility represents the maximum level of belief possible, or the degree to which a hypothesis cannot be disbelieved, given the amount of evidence negating the hypothesis. Specifically, the plausibility is obtained by subtracting the BPAs associated with all subsets of the complement of the hypothesis (A) (Gorsevski and Jankowski, 2005). Plausibility is the sum of the probability masses assigned to all sets whose intersection with the proposition is not empty (Baraldi and Zio, 2010). The plausibility function is defined as follows (Gorsevski and Jankowski, 2005):

$$Pls(A)=\sum _{B\cap A=\varnothing }m(B)$$ (22)

when two masses m₁ and m₂ for Θ are obtained as a result of two pieces of independent information, they can be combined using Dempster's rule of combination in order to yield new BPAs (m₁⊕m₂). This combination of m₁ and m₂ is defined as:

$$(m_1\oplus m_2)(A)=\frac{\sum _{\mathbf{B}\cap C=A}{m}_1(B)m_2(C)}{1-\sum _{B\cap C=\varphi }{m}_1(B)m_2(C)}$$ (23)

where the combination operator “⊕” is called “orthogonal summation”, A≠∅, and the denominator, which represents a normalization factor (one minus the BPAs associated with empty intersection), is determined by summing the products of the BPAs of all sets where the intersection is null. When the normalization factor equals 0, the two items of evidence are not combinable. The order of applying the orthogonal summation does not affect the final results since Dempster's rule of combination is commutative and associative (Gorsevski and Jankowski, 2005). Since DST is able to unravel certainties of results we applied it in a spatially explicit manner to visualize the resulting certainties of the different approaches as discussed in Section 4.2.

4. Results

4.1. Initial results of the landslide susceptibility mapping

In order to assess the efficacy of the methods presented in Section 3, we employed a twofold analysis. First, the LSM criteria and sub-criteria are ranked based on the AHP pairwise matrix (see Tables 2 and 4 for criteria and sub-criteria, respectively).

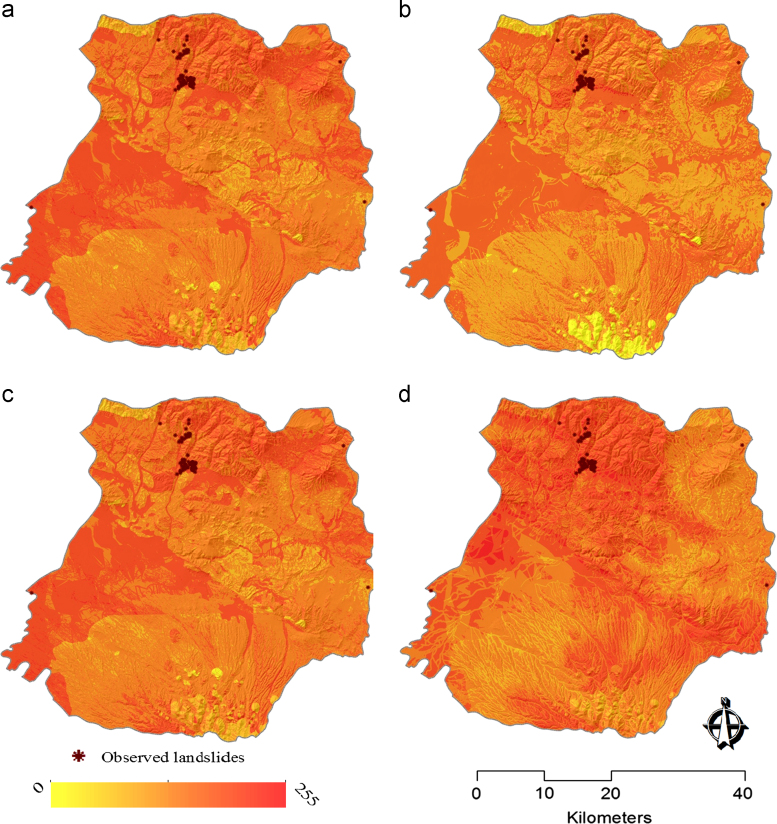
In the next step these criteria were combined and landslide susceptibility maps were produced (see Fig. 4a and b for the results of OWA and AHP, respectively). The conventional approach is based on the application of the S-MCE standard methodology for producing MCDA base maps and comparing them to the results of the new GISPEX approach for evaluating whether the accuracies are improved after applying GSA. Hence, in the following computation of two baseline landslide susceptibility maps, an alternative pair of landslide susceptibility maps is computed by using revised weights obtained from GSA (see Table 3 columns c–e). In doing so, the criteria and revised weights were combined and the landslide susceptibility maps were produced using OWA and AHP (See Fig. 4c and d). Finally in order to validate the results, all four landslide susceptibility maps derived from both of the approaches were classified into four groups, namely high, moderate, low and no susceptibility to landslides, using the natural breaks classification method in ArcGIS (see Table 5).

Fig. 4.

Results of LSM: Landslide susceptibility maps derived from S-MCE approach including (a) OWA, (b) AHP, and landslide susceptibility maps derived from GISPEX approach including: (c) GSA-OWA and (d) GSA-AHP.

Table 5.

Results of LSM.

MCDA	Susceptibility category	A⁎	B⁎	C⁎ (M2)		D⁎ (M2)
OWA	High susceptibility	1,079,741	12,342,873	3	1245	5	1675
	Moderate susceptibility	74,620,238	69,459,118	33	74,100	53	127,925
	Low susceptibility	118,844,521	105,535,783	76	149,555	54	95,300
	No susceptibility	16,223,918	23,430,644
	Sum	210,768,418	210,768,418	112	224,900	112	224,900
AHP	High susceptibility	1,706,322	6,005,410	20	44,825	25	57,200
	Moderate susceptibility	112,532,591	85,215,611	81	169,475	87	167,700
	Low susceptibility	91,194,144	102,953,641	11	10,600
	No susceptibility	5,335,361	16,593,756
	Sum	210,768,418	210,768,418	112	224,900	112	224,900

A^⁎=Number of pixels in the landslide susceptibility maps derived from the S-MEC approach (classical approach).

B^⁎=Number of pixels in the landslide susceptibility maps derived from the GISPEX approach (alternative approach).

C^⁎=Number of observed landslides and validation of the results for the S-MEC approach by comparing LSM results with the landslide inventory dataset and delimited landslides from OBIA.

D^⁎=Number of observed landslides and validation of the results for the GISPEX approach by comparing LSM results with the landslide inventory dataset and delimited landslides from OBIA.

4.2. DST for representation the certainty of result

The belief function in the IDRISI software was used to carry out the spatial distribution of the S-MCE and GISPEX approaches certainties. Three decision support indicators including plausibility, belief interval and belief were generated (see Figs. 5–7). Fig. 7 shows the resulting certainties for both of the S-MCE and GISPEX approaches based on the belief function. Based on the DST (belief) approach, the ignorance value can be used to represent the lack of evidence (complete ignorance is represented by 0). Thus, the belief and plausibility function values all lie between 0 and 1 (Althuwaynee et al., 2012; Feizizadeh et al., 2012). In our application of OWA (S-MCE approach), the belief function reveals certainty ranges between 0.46 and 0.81, however, it significantly increases to 0.71–0.96 when OWA is employed in conjunction with GSA-derived criterion weights in the second approach (GISPEX approach). For the AHP method, results show certainty ranges of 0.21–0.66 for the conventional approach and an increased range of 0.63–0.90 when integrating the AHP with GSA (novel approach). Detailed results of DST based uncertainty representation are listed in the Table 6.

Fig. 5.

Results of spatial distribution of the plausibility for the landslide susceptibility maps derived from S-MCE approach including: (a) OWA, (b) AHP and the landslide susceptibility maps derived from GISPEX approach including: (c) GSA-OWA and (d) GSA-AHP.

Fig. 6.

Results of spatial distribution of the belief interval for landslide susceptibility maps derived from S-MCE approach including: (a) OWA, (b) AHP and the landslide susceptibility maps derived from GISPEX approach including: (c) GSA-OWA and (d) GSA-AHP.

Fig. 7.

Results of the uncertainty representation based belief function for the landslide susceptibility maps derived from S-MCE approach including: (a) OWA, (b) AHP and the landslide susceptibility maps derived from GISPEX approach including: (c) GSA-OWA, and (d) GSA-AHP.

Table 6.

Representation certainty and validation of results by DST and ROC.

MCDA		Plausibility	Belief interval	Belief	ROC
Classical approach	OWA	0.04–0.29	0.06–0.42	0.46–0.81	0.15629
	AHP	0.55–0.68	0.10–0.37	0.21–0.66	0.75415
Alternate approach	GSA- OWA	0.26–0.81	0.19–54	0.71–0. 96	0.45565
	GSA- AHP	0.34–0.79	0.32–0.45	0.63–0.90	0.90557

4.3. Validation of results

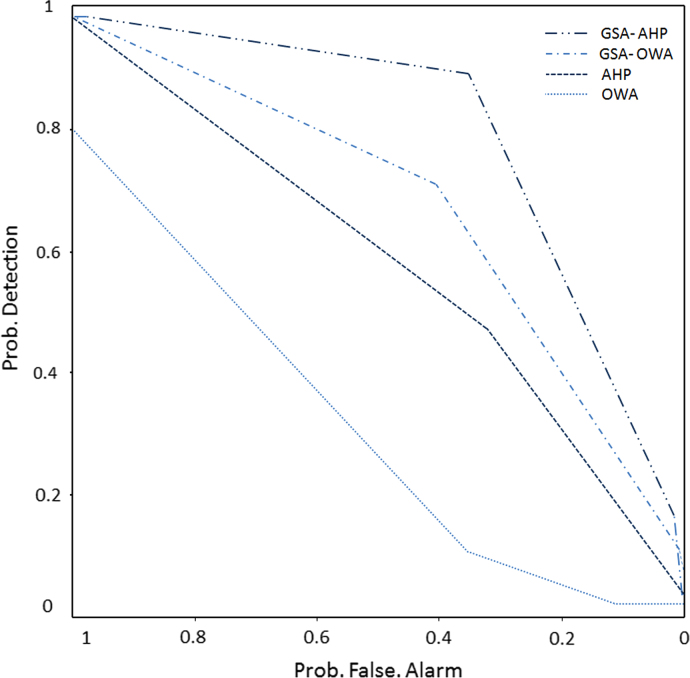
Validation is a fundamental step in the development of a susceptibility map and determination of its prediction ability (Pourghasemi et al., 2012). The purpose of the validation algorithm is to statistically evaluate the accuracy of the results (Sousa et al., 2004). The prediction capability of LSM and its resulting output is usually estimated by using independent information (i.e. landslide inventory map). In our research the accuracy of the obtained landslide susceptibility maps was evaluated by calculating Relative Operating Characteristics (ROC) (Fawcett, 2006; Nandi and Shakoor, 2009), and numbers of known landslides were observed in various categories of the landslide susceptibility maps. The ROC curve is a plot of the probability of having a true positive (correctly predicted event response) versus the probability of a false positive (falsely predicted event response) as the cut-off probability varies (Gorsevski et al., 2006).

A landslide inventory database was used to perform a validation of results. This database includes the occurrences of 112 landslide events for the Tabriz basin study area. This landslide inventory data consists of point data, which were collected in field surveys using GPS. We also use the results of delineated landslides from IRS-ID satellite images (with 5.8 m spatial resolution) through the Object Based Image Analysis (OBIA) method, which we determined in one of our previous researches in this area (Blaschke et al., in preparation). Respectively, these landslide areas (22.49 ha) were used to assess the accuracy of results through the ROC curve. In the ROC curve the ideal model shows a value close to 1.0 (Fawcett, 2006; Nandi and Shakoor, 2009). The results of the ROC method for four landslide susceptibility maps are shown in Fig. 8 and Table 5. In addition columns H and I in Table 3 shows the number and area of observed landslides in sub-criteria of our S-MEC and GISPEX models for LSM.

Fig. 8.

Validation of results using ROC curves for the landslide susceptibility maps derived from S-MCE and GISPEX approaches.

5. Discussion

We started with the hypothesis that uncertainty is associated with GIS-MCDA, and that applying uncertainty and sensitivity analysis using the GISPEX approach leads to an improved accuracy of the results. Results of this research indicated that the integration of spatially explicit analysis and MCDA supports to improve accuracy of the results significantly. As the validation of the results using ROC curves shows, increasing the accuracy from 0.1563 to 0.456 in the OWA method, and respectively from 0.754 to 0.906 in the AHP method, clearly offers the possibility of improving the accuracy of MCDA by means of taking into account the results of variance decomposition in GSA. In this regard we may emphasis that the GISPEX approach introduces the spatial heterogeneity of preferences in calculating the attractiveness and the subsequent ranking of decision options. Within this approach the decision-makers not only place a particular importance on a given criterion, but also pay attention to how an option is situated with respect to this criterion (Ligmann-Zielinska and Jankowski, 2012).

When comparing the accuracies of GIS-MCDA methods, the results indicate that the AHP method outperformes the OWA method. However, a cross-comparison of the uncertainty assessment using the DST shows that OWA yields the greatest certainty range. We should note that the differing accuracies are due to different decision rules of the respective MCDA operators. Naturally, different decision rules will result in various accuracies (Feizizadeh and Blaschke, 2013b). When using GIS-MCDA methods, it is evident that each method has its advantages and inherent limitations, which must be fully understood and accepted by the decision-maker before applying it (Kritikos and Davies, 2011; Feizizadeh and Blaschke, 2013b).

Obviously, MCDA is based on a number of pivotal evaluation criteria, defined according to the conditions of the problem being considered. In most decision-making problems, the management team already has a well-defined goal. In order to reach this goal, it is necessary to choose from a number of options or alternatives. The potential alternatives have different attributes and characteristics. The decision-makers try to choose the best among them by considering the effects these alternatives have on the quality of the final result. Such relative importances depend on different criteria. Decision-makers rank these criteria over each other in order to determine a weight for each criterion (Kordi and Brandt, 2012). In the traditional MCDA approach preferences relate to criteria rather than options themselves. Typically, weights are assumed to be homogeneous over the geographical space and no attention is given to how they might vary spatially. This homogeneous treatment of criterion preferences across a geographical decision space may result in solutions that only partially reflect the decision maker's preferences. Further, this approach leads to a loss of information, which may be critical in solving spatially explicit problems and may result in a choice of recommendations that are subsequently rejected due to their incongruence with the preference structure of the decision-maker (Ligmann-Zielinska and Jankowski, 2012).

In terms of using AHP as method of criteria weighting, the results pointed out this technique is not free of criticisms and it has limitations. It may suffer from sensitivity in decision making. In this regard the main potential problems associated with this technique include rank consistency and the time it takes to make judgments in a complex decision problem especially in cases when the number of decision alternatives to be addressed is large (Mamat and Daniel, 2007). Technically, AHP is used to evaluate complex multi-attribute alternatives among one or more decision makers. It imposes a hierarchical structure on any complex multi-criterion problem (Carmone et al., 1997). However, a major drawback of the AHP is that a large number of pairwise comparisons is needed to calibrate the hierarchy. When there are a few levels and sublevels, the AHP can be applied in a straightforward manner to derive the weights (Carmone et al., 1997). Naturally, as the size of the hierarchy increases, the number of pairwise comparisons increases rapidly which leads a degree of sensitivity and subsequently influence the pairwise comparisons. In order to deal with these issues, the results of our research demonstrate that one way of mitigating the limitations of the AHP technique is to apply AHP through the MCS that characterizes the multi-criteria procedural rationality paradigm. The improved accuracy of MCDA in the ‘alternative approach’ by using the revised weights from AHP-MCA clearly approved leads to improvements in the accuracy and reliability of LSM studies.

In the context of uncertainty analysis for GIS-MCDA based on DST approach, our research results showed that the DST can be used to evaluate the reliability of the whole system. The DST allows a flexible representation of uncertainty for data sources of different types and expert judgement in particular. Moreover, multiple experts' knowledge can provide more reliable information for an observation (e.g. the failure probability of a component) than a single expert can. As the results of our conventional approach (S-MCE, see Section 4.1) indicated, the expert judgment can often suffer from subjectivity of judgement, which affects the uncertainty of MCDA results. The DST addresses these issues effectively and is able to combine multi-expert knowledge by taking into account ignorance and conflicts through a belief structure (Sallak et al., 2010). The DST of evidence provides an explicit mechanism by replacing subjective probabilities with ‘degrees of belief’ that can be used to represent the extent to which a decision maker believes a specific proposition to be true. The degrees of belief assigned to a set of collectively exhaustive and mutually exclusive hypotheses (by a so-called ‘belief function’) are allowed to sum to less than one, with the difference revealing the degree of ignorance. Such ignorance may be due to a lack of data or familiarity with the problem at hand, imprecision in assessment, or the absence of certain stakeholders in a group decision (Durbach and Stewart, 2012). The DST representation is proposed as an attractive way of dealing with the issue at hand (expert judgment) (Sallak et al., 2010). The DST confirmed that the output results of belief, disbelief, uncertainty (doubt), and plausibility have to be defined as precisely as possible, in order to obtain a reasonable result (Carranza, 2009; Althuwaynee et al., 2012; Feizizadeh et al., 2012). In our research, the uncertainty assessment using the DST also confirmed the possibility of improving the accuracy of MCDA by means of integrating sensitivity analysis through GISPEX. The certainties measured by DST are significantly increased for both MCDA methods when GSA is performed in the GISPEX approach, (see Table 6).

6. Conclusion and future work

GIS-MCDA is complex due to the intricacy of the systems considered and the competing interests of multiple stakeholders. Further research in MCDA is needed to acquire better understanding of factors and mechanisms contributing to uncertainty in a decision-making system, and how the uncertainty affect the quality of the decisions rendered. Developing acceptable and efficacious decision-making approaches requires an improvement of uncertainty analysis techniques, concepts, and assumptions in pertinent research, with subsequent verification of LSM results (Ascough et al., 2008). In this paper, we focussed on applying the GISPEX approach for uncertainty and sensitivity analysis in GIS-MCDA, integrating the AHP and MCS, and assessing the certainty of the resulting outcomes through ROC and DST approaches. Based on our results, further improvement of the accuracy of GIS-based MCDA can be achieved by employing GSA of weights used in MCDA techniques. This study demonstrates the efficacy of the GISPEX approach to assessing the uncertainty of results produced by GIS-based MCDA models. Furthermore, the results of this research reveal that it is possible to enhance LSM by providing information about the uncertainty of its estimates.

This research and other studies demonstrate that MCDA methods can provide an effective tool for spatial decision making systems when the resulting accuracies are improved (Boroushaki and Malczewski, 2008; Azizur Rahman et al., 2012; Feizizadeh and Blaschke, 2013a, 2013b, 2013c). Building on these results, future research should focus on integration of decision rules in GIS-MCDA (e.g. AHP-OWA operators) with uncertainty analysis methods (e.g. spatially explicit-DST) in order to provide a comprehensive approach to deal with imprecision of input data and subjectivity of human judgement such research may include the integration of a fuzzy set with GIS-MCDA (Fuzzy-AHP) for improving the decision rule of the AHP – in particular the pairwise matrix of the AHP. In this study we attempted to improve the accuracy of GIS-MCDA based LSM in an effort to provide the bases for decision making plans for reducing and mitigating the landslide hazard. We conclude that the resulting landslide prediction maps were not only accomplished for the sake of comparison. The results of this study will be given to the responsible authorities in the East Azerbaijan province for risk management. The information provided by these maps shall help planners and engineers to reduce losses caused by future landslides through prevention, mitigation and avoidance. We will monitor whether or not the results described in this article will be utilized for supporting the mitigation of future landslide hazards in the Tabriz basin.