Prediction of the Fate of Organic Compounds in the Environment From Their Molecular Properties: A Review

Abstract

A comprehensive review of quantitative structure-activity relationships (QSAR) allowing the prediction of the fate of organic compounds in the environment from their molecular properties was done. The considered processes were water dissolution, dissociation, volatilization, retention on soils and sediments (mainly adsorption and desorption), degradation (biotic and abiotic), and absorption by plants. A total of 790 equations involving 686 structural molecular descriptors are reported to estimate 90 environmental parameters related to these processes. A significant number of equations was found for dissociation process (pK_a), water dissolution or hydrophobic behavior (especially through the K_OW parameter), adsorption to soils and biodegradation. A lack of QSAR was observed to estimate desorption or potential of transfer to water. Among the 686 molecular descriptors, five were found to be dominant in the 790 collected equations and the most generic ones: four quantum-chemical descriptors, the energy of the highest occupied molecular orbital (E_HOMO) and the energy of the lowest unoccupied molecular orbital (E_LUMO), polarizability (α) and dipole moment (μ), and one constitutional descriptor, the molecular weight. Keeping in mind that the combination of descriptors belonging to different categories (constitutional, topological, quantum-chemical) led to improve QSAR performances, these descriptors should be considered for the development of new QSAR, for further predictions of environmental parameters. This review also allows finding of the relevant QSAR equations to predict the fate of a wide diversity of compounds in the environment.

1. INTRODUCTION

The high number and the wide diversity of manmade organic compounds (e.g., pesticides, pharmaceuticals, polycyclic aromatic hydrocarbons (PAH), polychlorinated biphenyls (PCB)) that have been or will be released in the environment constitute the most important challenge for research on the fate and effects of these contaminants. About 100,000 substances have been registered for use in United States or Europe over the past 30 years (Hansen et al., ^1999b; Muir and Howard, ²⁰⁰⁶). However, they cannot be studied on a case-by-case basis, in particular because experimental studies are time-consuming and/or cost prohibitive (Reddy and Locke, ^1994a; Russom et al., ²⁰⁰³; Sabljic, ¹⁹⁸⁹; Türker Saçan and Balcioğlu, 1996). Therefore, the vast majority of existing and new chemical substances are not monitored in environmental media, and their fate and effects remain unknown, so that regulators face the task of reviewing the potential risk for chemicals having little or no empirical data (Muir and Howard, 2006; Russom et al., ²⁰⁰³).

Reliable environmental fate and risk assessment procedures strongly rely on the ability to accurately measure or estimate various environmental parameters and molecular properties of chemicals (Sabljic, 2001). Therefore, the development of in silico methods of prediction based on quantitative structure activity relationships (QSAR) or quantitative structure property relationships (QSPR) has received an increasing interest for many years (Cronin et al., 2003; Hermens et al., ¹⁹⁹⁵; Mackay et al., ²⁰⁰¹; Sabljic, ¹⁹⁹¹; Walker et al., ²⁰⁰²). The QSAR approach is based on the assumptions that the structure of a molecule contains the features responsible for its physical, chemical, and biological properties, and that variations in the fate within a series of similar structures can be correlated with changes in descriptors that reflect their molecular properties (Reddy and Locke, ^1994a; Sabljic, ²⁰⁰¹; Walker et al., ²⁰⁰³). The QSAR have the potential to estimate the risks of chemicals for environment and human health, for example, while reducing time, monetary cost, and animal testing currently needed for ecological risk assessment of chemicals (Organization for Economic Cooperation and Development, 2013; Reddy and Locke, ^1994a).

The QSAR can be based on (a) physicochemical properties that can be determined experimentally (e.g., water solubility, octanol-water partition coefficient) or (2) structural molecular descriptors that include constitutional (number of atoms, atom types), geometric (e.g., surface, volume), topological (connectivity indices), and quantum-chemical (dipole moment, polarizability, energies) properties (Doucette, 2003; Sabljic, ²⁰⁰¹; Tao et al., ¹⁹⁹⁹; Todeschini et al., ¹⁹⁹⁶). However, approaches based on experimental properties, such as water solubility or octanol-water distribution coefficient, are prone to experimental errors in the input variables, which may result in some severe statistical problems (Lohninger, 1994; Nguyen et al., ²⁰⁰⁵; Sabljic, ¹⁹⁹¹; Sabljic and Piver, ¹⁹⁹²). Therefore, some of the advantages of the exclusive use of structural molecular descriptors are that they are free of the uncertainty of experimental measurements and that they can be calculated for organic compounds under development, not yet synthesized (Gramatica and Di Guardo, 2002; Karelson et al., 1996).

The objective of this work was thus to do the first comprehensive review of QSAR allowing the prediction of the fate of organic compounds in the environment from their structural molecular properties. The major processes that were considered are water dissolution, dissociation, volatilization, retention, degradation, and absorption by higher plants. The reviewed QSAR were analyzed according to two criteria: the frequency of the use of one descriptor in all reviewed equations, and the generic character of one descriptor (i.e., if it is involved in the assessment of a high diversity of processes). In addition, the physical meaning of the structural molecular descriptors was considered. This allowed the identification of the most relevant descriptors for the assessment of the environmental parameters related to the considered processes.

The different types and categories of molecular descriptors are first presented followed by the review of the QSAR equations for each selected process, and by the synthesis and discussion of the results.

2. STRUCTURAL MOLECULAR DESCRIPTORS USED FOR ENVIRONMENTAL CONCERNS

The central axiom of QSAR is that the activity of molecules is reflected in their structures (Organization for Economic Cooperation and Development, 2013). The structure of a molecule (e.g., its geometric or quantum properties) can be represented by several structural molecular descriptors, and the information contained in the descriptors reflects the nature of the molecular representation used. For example, a graph theoretical representation describes the molecule as a set of vertices (atoms) and edges (bonds). This allows the estimation of topological descriptors. A more sophisticated representation views a molecule as a collection of nuclei bound together by overlapping electron orbitals. Such representation can be used to derive descriptors such as atomic charge and dipole moment. Another type of structural representation characterizes the molecule as a set of hard spheres connected by bonds possessing specific stretching, bending, and torsion energies. The shape of the molecule is determined by the strain placed on the bonds as the spheres are allowed to interact. Information that is related to the geometry of the molecule (size and shape) can be obtained from such representation. A realistic representation of a molecule must lie in the combination of these representations (Stanton and Jurs, 1990). A lot of structural molecular descriptors that take into account different aspects of chemical information have been proposed and reviewed by Todeschini and Consonni (2000). This section is focused on concise presentation of the 686 descriptors (Table S1) that were found in the 790 equations reported in this work allowing the assessment of 90 environmental parameters (Table S2). The descriptors were classified in seven categories: constitutional, geometric, geometric-topological, geometric-electronic, topological, electro-topological, and quantum-chemical. The review of the different QSAR will be then organized and discussed according to these seven categories. All structural molecular descriptors can be calculated with different softwares such as ChemOffice (2009), comprehensive descriptors for structural and statistical analysis PRO (CODESSA PRO) (Katritzky et al., 2005), Dragon (2007), Gaussian 09 (Frisch et al., 2009), HyperChem (2007) or parameter estimation for the treatment of reactivity applications (PETRA) (TORVS Research Team, 1999).

2.1. Constitutional Descriptors

Constitutional descriptors reflect the molecular composition of a compound without any information about its molecular geometry (Ma et al., 2010). One hundred and forty one descriptors were used in the reviewed equations. The simplest constitutional descriptors are the molecular weight or the number of atoms, bonds, functional groups, and rings (Table S1).

Several other constitutional descriptors were found such as indicators of the presence of different chemical groups (e.g., ester, epoxide, nitro group), H attached to heteroatom (H-050), the hydrophilic factor (HY), or the gravitation index (IG; Table S1). H-050 is one of the atom-centered fragment descriptors that describe each atom by its own atom type, and the bond types and atom types of its first neighbors. It represents the first neighbor (hydrogen) of heteroatom (Habibi-Yangjeh et al., 2009). The HY is based on atom and group counting (e.g., number of hydrophilic groups [‒OH, ‒NH, ‒SH], number of carbon atoms, and number of non-hydrogen atoms). It is related to the presence of hydroxyl groups in the molecule (Gramatica and Di Guardo, 2002; Gramatica et al., ^1999b). The gravitation index IG reflects the effective mass distribution within the molecule and depicts the molecular dispersion forces in a bulk liquid media (Estrada et al., 2004; Katritzky et al., ¹⁹⁹⁸).

In the fragment approaches, a molecular structure is divided into fragments (atom or larger functional groups), and values of each atom or group are summed together to give the estimate of one environmental parameter. The polarity of organic compounds can be taken into account through polarity correction factors (Meylan et al., 1992; Müller and Kördel, ¹⁹⁹⁶; Sabljic, ¹⁹⁸⁷; Tao and Lu, ¹⁹⁹⁹). There are two types of fragment approaches: the constructionist approach (Hansch and Leo, 1979; Meylan and Howard, 1995) and the reductionist approach. The constructionist approach consists of determining the environmental parameter values of a set of small molecules very accurately and then calculating fundamental chemical fragments from these values: single fundamental fragments consist of (a) isolated carbons or (b) a hydrogen or heteroatom plus multiple atom (e.g., ‒CN) with correction factors. The reductionist approach assumes the deduction of coefficients for individual fragments derived by statistical relationships between the molecular properties and individual constitutive fragments. However, there are two main limits of the fragment approaches: first, they require a large data set to obtain a contribution of each functional group or fragment; second, there can be missing fragment, which means that if a compound contains a missing fragment, the parameter cannot be precisely predicted (Hou et al., 2004; Leo, 1975; Meylan and Howard, ¹⁹⁹⁵; Schüürmann et al., ²⁰⁰⁶; Sun et al., ¹⁹⁹⁶; Tao et al., ¹⁹⁹⁹).

2.2. Geometric Descriptors

Geometric descriptors give information about molecular size and shape, thus require accurate three-dimensional coordinates of the optimized geometry of the compounds (McElroy and Jurs, 2001). In this review, 77 different geometric descriptors were inventoried (Table S1).

The simplest geometric descriptors are related to the dimensions of atoms or molecules: radius, diameter, length, perimeter, ovality, thickness, surface, and volume (Table S1). Among the 15 descriptors related to the surface, the FOSA (hydrophobic component of the total solvent accessible surface area) is a measure of the hydrophobic property of a molecule and as it increases, the polarity of the molecule will decrease. The FISA is the hydrophilic component of the total solvent accessible surface area, and the PSA is the Van der Waals surface area of polar nitrogen and oxygen atoms. Both PSA and FISA give measures of hydrophilic properties. As they increase, the polarity of the molecules will rise (Cao et al., 2009). For the molecular volume, 13 descriptors were found. Among them, the parachor (P) relates the surface tension to the molecular volume, allowing the comparison of molecular volumes under conditions such that surface tensions are equivalent (Zhao et al., 2003). The McGowan volume (V_x) is derived from the parachor and is calculated by a method of group contribution (Abraham and McGowan, 1987). For a molecule, the van der Waals volume (VdW) is the volume enclosed by the van der Waals surface, it is usually calculated with software through the estimation of the van der Waals radius. It was shown that the McGowan volumes are equivalent to computer-calculated van der Waals volumes (Reddy and Locke, ^1994a; Zhao et al., ²⁰⁰³). The Le Bas molar volume (V_LB) is based on the summation of atomic volumes with adjustment for the volume decrease arising from ring formation (Cousins and Mackay, 2000).

VolSurf is a computational program that generates 2D molecular descriptors from 3D molecular interaction energy grid maps (Cruciani et al., ^2000a; Cruciani et al., ^2000b). The base of VolSurf is to compress the information present in 3D maps into a few 2D numerical descriptors that are simple to understand and to interpret. These descriptors quantitatively characterize the size, shape, polarity, and hydrophobicity of molecules as well as the balance between them. Molecular shape, which affects packing and solvent interactions, can be described through geometry dependent descriptors such as SHDW, GEOM, and GRAV (McElroy and Jurs, 2001; Table S1). The VolSurf BV31OH2, as for it, is the volume descriptor representing one of the best hydrophilic volumes generated by a water probe calculated at –1 kcal mol⁻¹ energy level (Bordás et al., 2011; Cruciani et al., ^2000a; Cruciani et al., ^2000b).

Weighted holistic invariant molecular (WHIM) descriptors form another group of geometric descriptors (Todeschini and Gramatica, ^1997a, 1997b; Todeschini et al., ¹⁹⁹⁶). They are built to capture the relevant molecular 3D information regarding the molecular size, shape, symmetry, and atom distribution with respect to some invariant reference frames. WHIM descriptors are obtained from the molecular coordinates of the 3D structure of the molecule (i.e., from its spatial conformation). The algorithm consists in performing a principal component analysis on the centered molecular coordinates by using six different weighting schemes: unweighted (u), weighted by the atomic mass (m), by the van der Waals volume (v), by the Mulliken atomic electronegativity (e), by the atomic polarizabilities (p), or by the electro-topological index of Hall et al. (1991; s). For each weighting scheme, a set of statistical indices is calculated on the atoms projected onto each principal component (1, 2, and 3). The WHIM approach can be viewed as a generalization searching for the principal axes with respect to a defined atomic property (the weighting scheme). Unlike topological descriptors (see section 2.5), the WHIM descriptors are able to distinguish different conformations of the same molecule and different geometric isomers. There are a total of 66 directional WHIM descriptors, and 33 global WHIM descriptors: directional descriptors related to size (λ), shape (θ), symmetry (γ), and atom distribution and density around the origin (κ); and nondirectional descriptors related to the total dimension of the molecule (T(λ) and A(λ) related to linear and quadratic contribution to the total molecular size, and V(λ) being the complete expression), its shape (K(λ)), the total molecular symmetry (G(γ)), and its total density (D(η), with η being related to the quantity of unfilled space per projected atom; Todeschini and Gramatica, ^1997a, 1997b; Todeschini et al., ¹⁹⁹⁶).

3D molecule representation of structures based on electron diffraction (3D-MoRSE) descriptors and 2D autocorrelation descriptors were also involved in some QSAR (Tables S3, S4, S6, S7, and S9). The 3D-MoRSE descriptors are derived from infrared spectra simulation using a generalized scattering function (Habibi-Yangjeh et al., 2009; Todeschini and Consonni, ²⁰⁰⁰). The Mor(12p) and Mor(31)v descriptors relate to polarizabilities and van der Waals volumes of the atoms, respectively (Habibi-Yangjeh et al., 2009). The 2D autocorrelation descriptors are calculated from molecular graph by summing the products of atom weights of the terminal atoms of all the paths of the considered path length (the lag). For example, the GATS1p, Geary autocorrelation lag 1, weighted by atomic polarizabilities (Table S1), is one of the 2D autocorrelation descriptors. The Geary coefficient is a distance-type function, a function being any physicochemical property calculated for each atom of the molecule, such as atomic mass and polarizability. For GATS1p, the function is the polarizability. Therefore, the molecule atoms represent the set of discrete points in space, and the atomic property the function evaluated at those points (Habibi-Yangjeh et al., 2009).

Finally, some other miscellaneous geometric descriptors were used: the summation of the steric factors of the additional substituents (E_s; Peijnenburg et al., ¹⁹⁹²); the molecular refraction (MR), which affords information about the molecular volume and polarizability (Kim et al., 2007); the excess molar refraction (R₂; Abraham, ¹⁹⁹³); steric parameters, ΣD and ΣS, that reflect the overall dimension of the molecule (Chaumat et al., 1992); and the sum of the core count for non-hydrogen vertex (Σα_H) that may be taken as a measurement of the molecular bulk (Roy et al., 2007).

2.3. Geometric-Topological Descriptors

The geometry, topology, and atom-weights assembly (GETAWAY) descriptors include the geometric information given by the influence molecular matrix, and the topological information given by the molecular graph, weighted by chemical information encoded in selected atomic weightings (Consonni et al., 2002). Two sets of molecular descriptors have been devised: H-GETAWAY descriptors have been calculated from the molecular influence matrix H, while R-GETAWAY descriptors are from the influence/distance matrix R where the elements of the molecular influence matrix are combined with those of the geometry matrix. The molecular influence matrix H contains some useful information on the molecular geometry, and especially the diagonal elements (leverages) of the matrix allow discrimination among the atoms according to their position in the 3D molecular space with respect to the molecule center (Consonni et al., 2002). In the equations reviewed in this work, five GETAWAY descriptors were found: H4p, H5e, HATS7p, HTp, and R3e (Bordás et al., 2011; Gramatica et al., ²⁰⁰³; Table S1). The number of donatable hydrogens, count of all donatable hydrogens (CTDH), and the accessibility of the acidic oxygen atom in a molecule (A_access,O (2D)) can also be classified as combined geometric-topological descriptors (McElroy and Jurs, 2001; Zhang et al., 2006; Table S1).

2.4. Geometric-Electronic Descriptors

The geometric-electronic descriptors mainly belong to the charged partial surface area (CPSA) descriptors, which combine molecular surface area and partial atomic charge information. They encode features responsible for polar interactions between molecules. The molecular representation views a molecule as having a surface defined by the overlap of hard spheres, defined by the van der Waals radii of the atoms, which is traced by a sphere representing a solvent molecule (water by default). The surface traced out by the center of the solvent sphere has been termed the solvent-accessible surface. The molecule is further defined as having a specific electron distribution, thus yielding a representation of a charged contact surface where polar intermolecular interactions can take place. Depending on the method used to combine the surface area and the charge information, there are different kinds of descriptors such as three partial positive surface area descriptors (PPSA-1, PPSA-2, PPSA-3), and an equal number of the partial negative surface area descriptors (PNSA-1, PNSA-2, PNSA-3). Also, there is a set of three differences in partial surface area descriptors (DPSA-1, DPSA-2, DPSA-3), six fractional charged surface area descriptors (three positive: FPSA-1, FPSA-2, FPSA-3, and three negative: FNSA-1, FNSA-2, FNSA-3), and a similar set of six total surface weighted partial positively (WPSA-1, WPSA-2, WPSA-3) or negatively (WNSA-1, WNSA-2, WNSA-3) charged surface area descriptors (Stanton and Jurs, 1990). In addition to the charged surface area descriptors, the relative influence of the most highly charged (positive and negative) atom on the overall charge of the molecule can be taken into account. This information is combined with the accessible surface area of the most highly charged atoms to obtain the relative positive and the relative negative charged surface area descriptors (RPCS and RNCS, respectively; Stanton and Jurs, ¹⁹⁹⁰). From these CPSA descriptors, new descriptors were created to account for hydrogen bonding effects: the SAAA-i (i = 1 – 3), which is the summation of the surface area of atoms that are capable of accepting hydrogen bonding interactions; and the CHAA-i (i = 1 – 3), which is the sum of charges on acceptor atoms, which encodes similar information as SAAA-i (Bakken and Jurs, 1999; Sutter and Jurs, ¹⁹⁹⁶; Table S1).

Two VolSurf descriptors can also be classified as geometric-electronic (Table S1): the H-bonding capacity derived with the CO probe (HB5O), a hydrogen bond descriptor calculated with carboxyl oxygen probe; and the high values of the hydrophilic region of the hydrogen bond acceptor probe (W4O), which accounts for polarizability (Bordás et al., 2011). The last geometric-electronic descriptor is the hydrogen bonding parameter, HB₁, which was used to estimate the vapor pressure (Basak et al., 1997; Table S6).

2.5. Topological Descriptors

Topological descriptors encode information about the atom types, bond types, and connectivity of the molecule without the need for optimized geometry (McElroy and Jurs, 2001; Sabljic, 1991; Sabljic and Trinajstic, ¹⁹⁸¹). They describe both the size and shape of molecules (Organization for Economic Cooperation and Development, 1993). One hundred and forty one topological descriptors were found in the different equations (Table S1).

The best known topological descriptors are the molecular connectivity indices (MCI); (symbol: χ), which characterize the degree of the molecular branching (Randic, 1975). The molecule is considered to be a sum of parts, namely, the bonds connecting pairs of atoms. Each atom in a molecule is represented by a cardinal number, δ, the count of all bonded atoms other than hydrogen. The molecule is dissected into fragments or bonds, each retaining the δ values assigned in the original graph. This decomposition produces a set of fragments encoded by the two δ values of the atoms comprising each bond (Kier and Hall, 2000). The MCI encode, in the various indices, information on molecular size, branching, cyclization, unsaturation, and heteroatom content. Four types of MCI exist: path (χ), cluster (χ_c), path-cluster (χ_pc), and chains (χ_ch; Gerstl and Helling, ¹⁹⁸⁷; Sabljic, ¹⁹⁹¹). Zero-order path-type index (⁰χ) defines individual atom (vertices), first-order (¹χ) deals with single-bond length, and so on. The first-order MCI (¹χ) correlates extremely well with the molecular surface area (Sabljic, 1991; Sabljic and Horvatic, ¹⁹⁹³; Sabljic and Piver, ¹⁹⁹²). In addition, Kier and Hall (2002) demonstrated that the ¹χ is the contribution of one molecule to the bimolecular interactions arising from encounters of all bonds among two molecules. From order 3, as the order of path index goes higher, MCI describe some local structural properties and possibly long-range interactions. The main characteristic of cluster-type indices is that all bonds are connected to the common, central atom (star-type structure). The third-order cluster molecular connectivity index (³χ_c) is the first, simplest member of the cluster-type indices where three bonds are joined to the common central atom. For this kind of index, orders higher than four do not have much chemical and structural sense for organic chemicals (Sabljic, 1991). The fourth-order path-cluster molecular connectivity index (⁴χ_pc) is the first, simplest member of the path-cluster type indices. It refers to subgraphs consisting of four adjacent bonds between non-hydrogen atoms, three of which are joined to the same non-hydrogen atom. Orders higher than six do not have much chemical and structural sense either. The cluster and path-cluster indices describe local structural properties, mainly the extent or degree of branching in a molecule. They are very useful as steric descriptors (Sabljic, 1991; Sabljic and Piver, ¹⁹⁹²). The chain type molecular connectivity indices (χ_ch) describe the type of rings that are present in a molecule as well as the substitution patterns on those rings. Thus, chain type indices also describe more local-type properties. The lowest order for the chain type index is third order, and increases up to the largest ring in any particular molecule (Sabljic, 1991). In the valence approximation, non-hydrogen atoms are described by their atomic valence values calculated from their electron configuration (Kier and Hall, 1986, in Sabljic and Piver, 1992). For example, the zero-order valence MCI, ⁰χ^v, is a simple and good approximation for the molecular volume (Sabljic, 1991; Sabljic and Piver, ¹⁹⁹²).

Based on MCI, several descriptors were then developed: the polarity index (¹ _Fχ^v), which is the ¹χ^v normalized to the number of discrete functional groups (Sekusak and Sabljic, 1992), and the ith order (i = 0 or 1) valence nondispersive factor (Δⁱχ^v), which is equal to the difference between the MCI for the nonpolar molecular structure and the same-order MCI (Bahnick and Doucette, 1988). To account for negative and positive contribution of individual atoms to the modeled property within the same molecule, Pompe and Randic (2007) developed modified variable connectivity indices (¹χ^f and ¹χ^fλ). As classical MCI were shown to be not applicable to organometallic compound, Sun et al. (1996) introduced the radius-corrected MCI (¹χ^r) and the bond-length-corrected MCI (ⁱχ^b, i = 1 – 6; Table S1).

A second important group of topological descriptors is related to the information indices such as complementary information content (CIC), information content (IC), or structural information content (SIC), which quantify the degree of heterogeneity and redundancy of topological neighborhoods of atoms in a molecule (Basak, 1999; Basak et al., ¹⁹⁹⁶, 1997; Estrada et al., ²⁰⁰⁴; Gramatica and Di Guardo, 2002; Gramatica et al., ²⁰⁰¹; Gramatica et al., ^1999a; Gramatica et al., ²⁰⁰⁰; Huibers and Katritzky, ¹⁹⁹⁸; Katritzky et al., ¹⁹⁹⁸; Ma et al., ²⁰¹¹; Niemi et al., ¹⁹⁹²; Table S1). These descriptors view the molecular graph as a source of different probability distributions to which the Shannon's entropy and related expressions can be applied. They are insensitive to molecular geometry, accounting for structural characteristics such as size, branching patterns, bonding types, and cyclicity (Gramatica et al., 2000).

A set of weighted path descriptors (WTPT) was also used (Bakken and Jurs, 1999; Mitchell and Jurs, ¹⁹⁹⁸; Randic, ¹⁹⁸⁴; Sutter and Jurs, ¹⁹⁹⁶; Table S1). They are based on the molecular identification number (ID) that combines features of connectivity indices and path counts, and characterize molecular branching (Randic, 1984). Each contiguous path in the molecule can be assigned a weight based on the number of atoms adjacent to the atoms in the path. The molecular ID is the summation of all paths of the compound.

Four Moran autocorrelation descriptors (MATS6e, MATS7e, MATS4p, and MATS1v) were found in the equations (Bhhatarai and Gramatica, 2011; Goudarzi et al., ²⁰⁰⁹; Gramatica et al., ²⁰⁰³). The structural variables introduced by Moran correspond to bidimensional autocorrelations between pairs of atoms in the molecule, and are defined to quantify the contribution of a considered atomic property to the analyzed property. These can be readily calculated by summing products of terms including the atomic weights for the terminal atoms in all of the paths of a prescribed length. For example, for MATS6e, the path connecting a pair of atoms has a length of 6 and involves the atomic Sanderson electronegativities as weighting scheme (Goudarzi et al., 2009).

Liu et al. (1998) developed a molecular distance-edge between carbon atoms vector (MDE) based on two fundamental structural variables: one for distance between atoms in the molecular graph, and one for edges of the adjacency in the graph. In these descriptors, carbon atoms are divided into four types: (a) primary (‒CH₃), (b) secondary (>CH₂), (c) ternary (>CH-), and (d) quaternary (>C<). A distance edge term is computed for all pairwise combinations of carbon types, for a total of 10 descriptors. For example, MDE-13 represents the distance edge descriptor between primary and ternary carbons. In addition to describing carbon bonding, these descriptors include information regarding distance between atoms (Bakken and Jurs, 1999).

Several other miscellaneous topological descriptors were found in the equations listed in Tables S3–S10. Among BCUT descriptors (Burden - CAS - University of Texas eigen-values; Burden, 1989), BEHe7 brings 2D information which takes into account the weight of different atoms in the structure (Burden matrix) and their electronegativities (Papa et al., 2009). The DELS could be a measure of total charge transfer in the molecule (Gramatica et al., 2000). The group philicity (ω_g ⁺) is a descriptor of reactivity that allows a quantitative classification of the global electrophilic nature (electron accepting capacity) of a molecule within a relative scale (Parthasarathi et al., 2006). The Lu index is interpreted as a parameter characterizing molecular size, and the DAI characterizes the degree of branching on aromatic ring (Lu et al., 2006). The sum of topological distances between oxygen and bromine atoms (T(O…Br)) gives a double structural information: its values increases according to both the number and the distance of bromine substituents, thus T(O…Br) also takes into account the information related to the position of the bromine atoms on the phenyl rings (Papa et al., 2009). The eccentric connectivity index (ξ^C) is a topological index accounting for both size and branching of compounds (Sharma et al., 1997), and the bond connectivity index (ϵ) can be understood as molecular size corrected for geometric accessibility with respect to van der Waals contact (Schüürmann et al., 2006). The Kapa index (³κ), which is based on path lengths, is a shape index (Bakken and Jurs, 1999; Dunnivant et al., ¹⁹⁹²; Kier, ¹⁹⁸⁶). The numbers of different sp hybridized orbitals between carbon atoms were also used: 1SP2, 2SP2, 3SP2. They encode information concerning attack sites for the radical (Bakken and Jurs, 1999). The Wiener index (W) is defined as the number of bonds between all pairs of atoms in an acyclic molecule. It measures the compactness of the molecule (Bogdanov et al., 1989). The calculation of the 3D Wiener index for the hydrogen-suppressed geometric distance matrix (^3DW) consists in summing the entries in the upper triangular submatrix of the topographic Euclidean distance matrix for a molecule (Basak et al., 1996). This index is considered as a measure of molecular shape (Consonni and Todeschini, 2010). The characteristic root index (CRI) is the sum of the positive characteristic roots obtained from the characteristic polynomial of the matrix with the entries calculated from the electronic input information. It was shown that it is correlated to the molecular surface area (Türker Saçan and Balcioğlu, 1996; Türker Saçan and Inel, 1995). MAXDN represents the maximum negative intrinsic state difference in the molecule and can be related to the nucleophilicity of the molecule, while MAXDP represents the maximum positive intrinsic state difference and can be related to the electrophilicity of the molecule (Gramatica et al., 2000). The superpendentic index (PND) can be calculated from the pendent matrix, a submatrix of distance matrix. This index takes into consideration all pendent vertexes, and its value changes significantly with a small change in the branching of a molecule (Gupta et al., 1999). Finally, the Kier symmetry index (S0K) is used to encode the shape contribution due to symmetry (Todeschini and Consonni, 2000). The lower the S0K of a compound, the greater the topological symmetry, and thus the lower the change in molecular freedom (Ding et al., 2006).

2.6. Electro-Topological Descriptors

Electro-topological state (E-state) is a method for describing and encoding molecular structure at the atom level. In the E-state formalism, each atom is viewed as having an intrinsic state which is perturbed by every other atom in the molecule. The intrinsic state combines valence state electronegativity with the local topology of the atom. Perturbation is dependent on the difference between intrinsic state values, and diminishes as the square of the graph distance between atoms. The result is that the E-state index, S, for an atom represents electron accessibility at that site. There are several extensions of the E-state concept. E-states indices may be computed separately for hydrogen atoms, the hydrogen E-state indices. Also E-state indices may be summed for all atoms of a given type in a molecule. These atom type E-state indices encode electron accessibility, presence or absence of groups, and count of groups (Hall and Story, 1996; Hall et al., ¹⁹⁹¹; Huuskonen et al., ¹⁹⁹⁹; Kier and Hall, ¹⁹⁹⁹).

The E-state index for a given atom (or atom type) varies from molecule to molecule, and depends on the detailed structure of the molecule. In the different atom-type E-state index, the set of bonds to a skeletal atom is given by a chain of lowercase letters: s (single), d (double), t (triple), and a (aromatic). The element is given by its symbol together with the number of hydrogen atoms. For example, SdCH₂ represents the S values for a terminal CH₂ group on a double bond, while SssCH₂ represents the methylene group with two single bonds; SaasC stands for an aromatic carbon to which a substituent is bonded (Hall and Story, 1996; Huuskonen, ^2001a, 2001b; Huuskonen et al., ¹⁹⁹⁹). As indicated previously, E-state index can also be calculated for group or molecule by adding the contributions of the single atoms present in the group or the molecule: to each atom is ascribed an index encoding the intrinsic electronic and topological state of the atom as well as the effect of the molecular environment in which the atom under study resides (Gombar and Enslein, 1996; Thomsen et al., ¹⁹⁹⁹).

Finally, the mean E-state (Ms), the average E-state value over all heteroatoms (EAVE-2), and the sum of E-state values over all heteroatoms (ESUM-2) can also be calculated (Habibi-Yangjeh et al., 2009; McElroy and Jurs, 2001; Table S1).

2.7. Quantum-Chemical Descriptors

Two hundred and forty eight quantum-chemical descriptors were inventoried in this review, representing the highest number of descriptors for one category (Tables S1 and S3–S10).

The most well-known quantum-chemical molecular descriptors are related to energies, and in particular to the energies of the highest occupied molecular orbital (E_HOMO) and lowest unoccupied molecular orbital (E_LUMO). Orbitals play a major role in most of chemical reactions, they are particularly involved in the formation of covalent bonds and thus of many charge-transfer complexes. The E_HOMO is directly related to the ionization potential and characterizes the susceptibility of the molecule toward attack by electrophiles (Karelson et al., 1996). The E_LUMO measures the ability of a molecule to accept electrons in intermolecular interactions (Chen et al., ^2002a). E_HOMO represents the proton acceptance ability in forming hydrogen bond, while E_LUMO represents the proton donation ability in formation of hydrogen bond (Zhou et al., 2005). Two descriptors are derived from E_HOMO and E_LUMO (Table S1): the absolute electronegativity (EN), which provides insight into the energetics of the reactant molecule (Bakken and Jurs, 1999; Hu et al., ²⁰⁰⁰; Müller and Klein, ¹⁹⁹¹), and the hardness (Hard; Bakken and Jurs, 1999). The HOMO and LUMO are generally the most important orbitals, but in cases where lower-energy occupied orbitals are close in energy to the HOMO, and higher-energy orbitals are close in energy to the LUMO, other orbitals may also play a role (Brown and Mora-Diez, ^2006b; Table S1).

Klamt (1993) defined a new set of descriptors called local frontier orbital descriptors: the charge-limited effective HOMO energy at H atom (ECH^H (q)), which is the weighted average of the orbital energies starting with the HOMO and extending to lower orbitals until the amount of charge taken into account reaches q; the energy-weighted effective HOMO energy (EEH^H (ϵ)), which is similar to an effective E_HOMO of the electrons of atom H calculated with an energetic penetration length ϵ; and the energy limited effective frontier orbital charges QL^A (E), where QL^A (E) is the amount of electronic charge available at atom A in the lower unoccupied orbitals down to an energy limit E.

In contrast to conventional molecular orbital based descriptors such as the E_HOMO and E_LUMO, local quantum-chemical molecular descriptors are designed to extract, from the delocalized molecular orbital wavefunctions and energies, energy and charge information that reflects the local characteristics of a given atomic site in the molecular environment. The energy-weighted donor energy (EE_occ) describes the electron donor ability of a molecule at an atomic site, and is constructed through a sum of occupied molecular orbital energies Ei, weighted by exponential terms involving reference energy E_ref. EE_occ ranges between the E_HOMO as delocalized limit (for E_ref close to 0) and the sum of the orbital energies weighted only by pi (for E_ref close to ∞). The energy-weighted acceptor energy (EE_vac) is defined accordingly through unoccupied molecular orbitals. It characterizes the capability of the molecule to accept additional electron charge at an atomic site, and thus represents a localized generalization of the E_LUMO. Another local reactivity parameter is the charge-limited acceptor energy (EQ_vac (q, r)). It characterizes the energy gain upon accepting charge q at atomic site r, and can be understood as a further local generalization of the E_LUMO. As a general trend, EQ_vac (q, r) becomes increasingly local with increasing amount of the charge penetration depth q. A complementary approach is to evaluate, for a given energy loss or gain, the associated amount of charge released from or taken up at site r. Therefore, an energy-limited donor charge QE_occ (ϵ, r) can be defined as amount of charge being removed from center r when offering the energy ϵ. Atomic sites with high electron donor ability are characterized by large values for QE_occ. The defined energy-limited acceptor charge QE_vac involves unoccupied molecular orbitals and quantifies the amount of accepted electron charge that is associated with a predefined energy gain ϵ (Yu et al., 2011). The electron affinity (EA) represents the energy difference associated with the gain of an electron, which should correlate with the ease or difficulty of the reduction of a compound (Colón et al., 2006).

In addition to E_HOMO and E_LUMO and the derived energies, the number of descriptors related to energy is very large (Table S1). As most of these energy descriptors are well-known—total energy (TE, TE2), torsional energy (TOE), electronic energy (EE), attraction (EN1, EN1c, EN1x) or repulsion (CCR, EE1, EE1c, NN2, NRE) energies, resonance energy (J, MinOH), Gibbs energy (G, ΔG_aq, ΔG_diss)—no detailed description is given here.

The interaction process between an acid and a base can be dissected into two steps: a charge transfer process resulting in a common chemical potential describing the strengths of the acid and the base, at a fixed external potential, followed by a reshuffling process at a fixed chemical potential. The fractional number of electron transfer, ΔN, and the associated energy change in the charge transfer, ΔEe, depend on the interplay between electronegativity and hardness of the acid and the base. The ΔEe is the energy lowering due to this electron transfer from a species of higher chemical potential (base) to that of a lower chemical potential (acid; Gupta et al., ²⁰⁰⁷). The inclusion of pi-electronegativity of the α carbon atom, EN_π,αC, can represent the different hybridization states (i.e., sp, sp², and sp³) of the α carbon atom in an acid, and EN_σ,O is the σ-electronegativity for the oxygen atom in the acidic hydroxyl group (Zhang et al., 2006).

Several descriptors related to the electronegativity were also used, such as the molecular electronegativity distance vector (MEDV). The properties of a molecule mainly depend on various interactions between its atoms. These interactions vary with the electronegativity of the atoms and the distances of chemical bonds formed between atoms. To describe an organic molecule and to construct its MEDV, the atomic types of all non-hydrogen atoms in the molecule have to be specified. If an atom is linked to k non-hydrogen atoms through chemical bonds, then the atom belongs to the k atomic type. There are at best four atomic types (considering the non-hydrogen atoms are often carbon, oxygen, nitrogen, or halogen atoms) and, therefore, to express the approximate interactions, MEDV include a maximum of 10 elements (e.g., M₁₁, M₁₂, M₁₃, M₁₄, M₂₂, M₂₃, M₂₄, M₃₃, M₃₄, M₄₄). These ten elements combine atomic attributes (both the chemical element type and the chemical bond type of each atom), bond length, relative distance between atoms, and their relative electronegativities. The relative electronegativity of a non-hydrogen atom is defined as the ratio of Pauling's electronegativity of the non-hydrogen atom to Pauling's electronegativity of a carbon atom, and the relative distance or relative bond length of a chemical bond is defined as the ratio of the length of this bond to the bond length of the C-C bond (Liu et al., 2002; Sun et al., ²⁰⁰⁷).

Sixty-four of the 248 quantum-chemical descriptors that were found in the equations are related to the charges of atoms or molecules. Others are related to the dipole moment, polarizability, superdelocalizability, electrostatic potential, moments, and bond order (Table S1).

In addition to the dipole moment μ, two descriptors derived from μ were found useful: the Z-component of the dipole moment (Bordás et al., 2011), and the total local dipole, μ_tot. The latter is defined as the difference in charges of each atom in the bond, divided by the length of the bond, and summed over all bonds in the molecule. The resulting μ_tot describes the dipolarity as a single number independent of direction, and alleviates some of the problems encountered in using the dipole moment μ (Famini and Wilson, 1997).

The polarizability α was involved in many equations (Tables S3, S4, S6 to S9), but the atom self-polarizability (ALP_ij; Berger et al., 2001; Berger et al., ²⁰⁰²; Tehan et al., ^2002b; Von Oepen et al., 1991), the second (α₂) and third (α₃) principal polarizabilities (Dunnivant et al., 1992), and the polarizability of the hydroxyl oxygen atom in an acid (α_O) were also used. Other polarizability terms are specially used in linear solvation energy relationships (LSER) equations (see section 2.8).

The superdelocalizability of an atom is a measure of its available electron density. It is calculated by the sum over all orbitals of the ratio between orbital densities and the corresponding orbital energies. The superdelocalizability of the HOMO (S_HOMO) and of the LUMO (S_LUMO), and the electrophilic (SE) and nucleophilic superdelocalizabilities (SN) can also be calculated (Reddy and Locke, 1996). The SE has been designed to quantify the susceptibility of a molecule for an electrophilic attack (Tehan et al., ^2002b).

Concerning the electrostatic potential, the most used descriptors are the molecular electrostatic potential minima (V_min), the surface molecular electrostatic potential maxima (V_S,max) and minima (V_S,min), and the sum of the surface maxima (ΣV⁺ _s) or minima (ΣV⁻ _s) values of the electrostatic potential. The ΣV⁻ _s should not be viewed as a hydrogen bond basicity descriptor but one reflecting nonspecific intermolecular interactions despite the fact that similarities exist between each other. V_min measures the hydrogen bond-accepting tendency or hydrogen bond basicity of a molecule, whereas V_S,max measures the hydrogen bond-donating tendency or hydrogen bond acidity of a molecule. The electrostatic potential V(r) is created in the space surrounding a molecule by its nuclei and electrons. The electrostatic potential surrounding spherically symmetric, neutral atoms is positive everywhere. However, when atoms combine to form molecules, regions of negative potential develop. These are usually in regions surrounding electronegative atoms, above and below multiple carbon-carbon bonds and aromatic rings, and along the outer edges of strained carbon-carbon bonds. Each such negative region has one or more spatial minima, V_min, associated with it. These V_min, as well as surface minima, V_S,min, have served as a mean for ranking sites for susceptibility toward electrophilic attack (Gross et al., 2001; Ma et al., ²⁰⁰⁴; Xu et al., ²⁰⁰⁷; Zou et al., ²⁰⁰²). Other descriptors related to the electrostatic potential are indicated in Table S1, such as molecular electrostatic potential (MEP) on the acidic atom N, O, or S (Liu and Pedersen, 2009); highest hydrogen bond acceptor potential (V_HHA); and highest hydrogen bond donor potential (V_HHD; Yan and Gasteiger, 2003).

Another group of quantum-chemical descriptors is related to the moments (Table S1): σ-moments are derived from quantum chemical density functional calculations combined with the continuum solvation model (COSMO). The zero-moment M₀ is identical with the molecular surface, the second moment M₂ is a measure of the overall electrostatic polarity of the solute, the third moment M₃ is a measure of the asymmetry of the polarization charge density profile, and the hydrogen-bond moments M_acc and M_don are quantitative measures of the acceptor and donor capacities of the compound, respectively (Klamt et al., 2002). The second principal moment of inertia (SMI) is derived from 3D representations of the molecules (Dunnivant et al., 1992). The magnitude of the principal moments of inertia of a molecule (PMI) encodes information about spatial distribution of mass and its rotational properties. It also expresses the role of molecular size and volume in occupying the space between water molecules (Dimitriou-Christidis et al., 2008). The quadrupole moment (in particular Qzz) was also found in some equations (Staikova et al., 2004; Zeng et al., ²⁰¹²; Table S6).

Several descriptors related to bond order were useful for some environmental parameters (Tables S4, S5, and S10): the bond order of the carbon-halogen bonds (BO; Chen et al., ^1998b; Chen et al., ^2001c; Zhao et al., ²⁰⁰¹); the OH bond order (BO_OH), which is a measure of the strength of OH bond (Citra, 1999; Hollingsworth et al., ²⁰⁰²); the average bond order (ABO(N)), which is a term to correct the deficiency of the electrostatic or hydrogen-bonding parameter for the N-atom containing compounds (Katritzky et al., 1998); and the minimum bond order of an atom C (MinC; Pompe and Veber, 2001). The bond strength (BS) of the carbon-halogen bond to be broken enables the differentiation between the reactivity of the various halogen atoms (F, Br, Cl, and I; Peijnenburg et al., ¹⁹⁹²).

Some descriptors are defined by using a combination of topological invariants, such as interatomic connectivity, and quantum-chemical information, such as atomic charges and bond orders: the atom quantum-connectivity index of path type of the order 2 defined on the basis of graphs weighted by charge density (2ΩpC(q)), and the bond quantum-connectivity index of chain type of the order 6 based on graph weighted by bond orders (6ϵRg(ρ); Table S1). The 2ΩpC(q) accounts for the topological structural features of the sequence of three consecutive atoms (order 2), and includes quantum chemical information through the use of atomic charge densities. It controls the influence of the number of substitutions at different sites in the molecule. The 6ϵRg(ρ), as for it, accounts for the influence of bond order weighted cyclic fragments of six bonds, that is, six-atom rings (Estrada et al., 2004).

Several other miscellaneous descriptors were found (Table S1) such as the hydrogen bonding donor charged surface area, (HDCA(2)), which is connected with the hydrogen-bonding ability of compounds (Katritzky et al., 1998); and the hydrogen acceptor dependent hydrogen donors surface area-2 (HDSA(2)), based on quantum chemical partial charge, which is also directly related to hydrogen-bond acceptor capability of a molecule (Modarresi et al., 2007). The D3DRY and D6DRY, that are VolSurf descriptors, represent the hydrophobic energy calculated with the hydrophobic probes (Bordás et al., 2011). The spin density (SD) is a measure of free spin concentrated on the benzylic carbon after hydrogen atom abstraction (Beasley et al., 2009).

Finally, some quantum-chemical descriptors were specially used with the LSER approach, their description is given in the next section.

2.8. Descriptors Related to the Solvation Energy

Linear solvation energy relationships (LSER) are a part of the wider field of linear free energy relationships (LFER; Platts et al., 1999). LSER use a mechanistic understanding of the partition process, which considers the interaction energies that contribute to the overall free energy of the transfer process (Abraham and McGowan, 1987; Goss and Schwarzenbach, ²⁰⁰¹; Kamlet et al., ¹⁹⁸⁸). It takes into account the energy term for cavity formation (proportional to the size of the molecule which can be related to the geometric descriptors V_i or V_x), and the interaction terms that can be decomposed in four terms as follows: (a) the induction of dipoles within the solutes (London dispersive forces, Debye forces) represented by the excess molar refraction (R₂), (b) electrostatic interactions represented by dipolarity/polarizability term (π*), (c) overall hydrogen bond donor acidity Σα₂ ^H (H-donor or electron-acceptor), and (d) overall hydrogen bond acceptor basicity Σβ₂ ^H (H acceptor or electron donor; Gawlik et al., ¹⁹⁹⁷; Nguyen et al., ²⁰⁰⁵; Platts et al., ²⁰⁰⁰; Van Noort et al., 2010; Wauchope et al., ²⁰⁰²). For transfer between water and wet solvents, such as wet octanol or ethyl acetate, the Σα₂ ^H and Σβ₂ ^H are replaced by Σα₂ ^O and Σβ₂ ^O for certain functional groups (e.g., pyridines, sulfoxides), whose basicity is found to change substantially between wet and dry solvents (Platts et al., 1999 and 2000).

In theoretical LSER (TLSER), the energy term for cavity formation is the molar volume (Vm). The hydrogen bond acceptor basicity is represented by two terms: the covalent basicity (ϵ_β), based on E_HOMO, and the solute electrostatic basicity (largest negative net atomic charge on an atom q⁻). The hydrogen bond acidity is similarly divided into a covalent acidity (ϵ_α), which is a function of the E_LUMO, and the solute electrostatic acidity (most positive atomic net charge on a hydrogen atom Q_H ⁺; Cramer et al., ¹⁹⁹³; Famini and Wilson, ¹⁹⁹⁷; Wilson and Famini, ¹⁹⁹¹)

To simplify the TLSER equation, Chen et al. (1996a) developed a modified TLSER (MTLSER): the equation only depends on the polarizability (α), the dipole moment (μ), the E_HOMO and E_LUMO, Q_H ⁺, and q⁻. These descriptors were presented in the previous section (2.7).

3. PARAMETERS FOR PROCESSES GOVERNING THE FATE OF ORGANIC COMPOUNDS IN THE ENVIRONMENT

The fate of organic compounds in the environment is mainly regulated by their behavior in the soils on which they might be applied directly (i.e., after application of pesticides) or indirectly through rain and water leaching, atmospheric deposition or organic waste amendments. In soils, organic compounds are affected by various physicochemical and biological processes conditioning their biotic and abiotic degradation, their retention (adsorption, desorption); their transfer toward groundwater, surface water, plant, and atmosphere; and consequently their bioavailability and potential side effects on the organisms living in the contaminated environment. The organic compounds also undergo adsorption phenomena in sediments, and degradation in water, sediments, and atmosphere (Katayama et al., 2010).

From QSAR that are reviewed in this work, we propose to classify the processes governing the fate of organic compounds in the environment in six main categories (Table S2): water dissolution, dissociation, volatilization, retention, degradation, and absorption by higher plants. These processes are represented by 90 different environmental parameters. Their description and their relationships to the structural molecular descriptors are included in the following sections.

3.1. Water Dissolution Process

The physicochemical properties of substances related to their dissolution in water control their partitioning between air, water, soils, sediments, and biota, and thus the accumulation and the rates of transfer between these different compartments. The key parameters include water solubility (S_W) and octanol-water partition coefficient (K_OW; Shiu et al., 1988; Table S2). A review of the QSAR allowing, in particular, the prediction of S_W and K_OW was written by Katritzky et al. (2000). In the following paragraphs, we have completed and updated this review by considering the results that have been published since then.

3.1.1. Water Solubility

Water solubility, S_W, plays an important role in the fate of organic compounds in the environment. One of the routes of transport of contaminants in the environment is water, therefore S_W affects the ability of a compound to be transported as well as its rates of transfer between water and other environmental compartments (Kühne et al., 1995). Table S3 summarizes the 65 QSAR found for the prediction of S_W. They are classified in three parts: relationships with one descriptor, with one category of descriptors, and with several descriptors and categories. The equations involve from 1 to 30 descriptors (excluding the equations based on the fragment approach), but most of them involve 1–3 descriptors. The QSAR were developed for a wide diversity of organic compounds (Table S3).

Several of the one-descriptor relationships involved descriptors related to the molecular surface and volume (Cao et al., 2009; Huibers and Katritzky, ¹⁹⁹⁸; Katritzky et al., ²⁰⁰⁰; Puzyn et al., ²⁰⁰⁹; Shiu et al., ¹⁹⁸⁸; Table S3). For 13 androgens, the S_W were moderately correlated with the hydrophobic component of the total solvent accessible surface area (FOSA), the hydrophilic component of the total solvent accessible surface area (FISA) or the van der Waals surface area of polar nitrogen and oxygen atoms PSA (r² < 0.55; Table S3). As FISA and PSA increase, the polarity of the molecules rises and the aqueous solubility should rise (Cao et al., 2009). For 10 chloronaphthalenes, a relationship between S_W and the solvent accessible molecular volume (SAVw) in the water SAVw was proposed. The correlation coefficient is good (r² = 0.950; Table S3), however, the number of compounds used to develop the QSAR is low, therefore giving uncertainty on its robustness. The SAVw is directly related to the cavitation, and formation of cavitation in the solvent plays a critical role in dissolving highly hydrophobic compounds. In the case of chloronaphthalenes, the SAVw mainly depends on the chlorination degree: it increases from mono- to octa-chloronaphthalenes. The influence of the substitution pattern on S_W is less pronounced. The electrostatic and dispersive interactions occurring between the solvent and solute after formation of the caves are less important for the dissolving process. However, for chloronaphthalenes, those factors become significant when comparing each other congeners with the same number of chlorine substituents (Puzyn et al., 2009). The molecular volume Vm was a good descriptor to estimate the S_W of 241 hydrocarbons and halogenated hydrocarbons (r² = 0.904; Table S3; Huibers and Katritzky, ¹⁹⁹⁸), but also of 15 polychlorinated dibenzo-p-dioxins (PCDD; Shiu et al., 1988). Water as a solvent would much prefer to interact with itself or other hydrogen bonding or ionic species than with a nonpolar solute, so there is a lower S_W for larger hydrocarbon solutes. However, the major problem with Vm as the sole descriptor for S_W is that it does not take into account steric interactions or conformational effects (Huibers and Katritzky, 1998). For 209 polybrominated diphenyl ethers (PBDE) and hexabromobenzenes (HBB), there was a good correlation between S_W and the 3D-MoRSE-signal 23 weighted by atomic masses, Mor23m (r² = 0.918; Table S3). Mor23m brings complex 3D information related to the weights of the atoms in the structure, as viewed by an angular scattering function (Papa et al., 2009). Topological descriptors were involved in several relationships: the Lu index (Lu, 2009), and four different MCI: ⁰χ^v, ¹χ^v, ³χ^v or ⁵χ^v. The best correlations were obtained with ¹χ^v and ³χ^v: r² > 0.933, but the number of compounds considered is low (Table S3; Gerstl and Helling, 1987). Using constitutional descriptors, relationships were found between S_W and the molecular weight (MW) for only six PBDE (Wania and Dugani, 2003), or with the number of chlorine atoms n _Cl for 15 PCDD (Shiu et al., 1988). For each chlorine added, there is a 5× drop in solubility. Finally, the polarizability α allowed good estimate of the S_W of 20 substituted phenols (r² = 0.951; Table S3; Xie et al., ²⁰⁰⁸), and 75 PCDD (r² = 0.978; Table S3; Yang et al., ²⁰⁰⁷). S_W is inversely proportional to α mainly because α is correlated with the molecular volume. Indeed, the molecular volume can reflect the absorbed energy during the formation of cavity in the solvent (Yang et al., 2007).

Table S3 reports 21 QSAR developed with descriptors belonging to the same category. Chen et al. (2007) used the positions of Cl substitution method to predict the S_W of 107 polychlorinated diphenyl ethers (PCDE; Table S3). The best model involved four descriptors relative to the positions of chlorine atoms in the compound—N₂₍₆₎, N₃₍₅₎, N₄, N_m—but the effect of N₃₍₅₎ on S_W was the most important one. For 53 miscellaneous compounds, the quantum-chemical descriptors atom quantum-connectivity index of path type of the order 2 defined on the basis of graphs weighted by charge density (2ΩpC(q)), and bond quantum-connectivity index of chain type of the order 6 based on graph weighted by bond orders (6ϵRg(ρ)) were better descriptors to predict S_W than constitutional (n _C, and gravitation index (IG)), geometric (molecular surface S, molecular volume divided by xyz box Vxyz), or topological ones (³χ, average structural information content index of order two I² _av), and better descriptors than the quantum-chemical descriptors minimal net atomic charge Q_min, and α (Estrada et al., 2004). Three equations were based on electro-topological descriptors (Huuskonen, ^2001a; Thomsen et al., ¹⁹⁹⁹; Table S3). Two of them were obtained by Huuskonen (2001a) for 674 compounds: one only with atom-type E-state index, and one with E-state index and three simple indicator variables that are applied, for example, to compounds containing only aliphatic C and H, or to pyridines and their alkyl derivatives. Then, the S_W of up to six carbon atoms phthalates in the alkyl chain was moderately reproduced with electro-topological descriptors related to polar/hydrophilic (S_ester) and polar/hydrophobic (S_alkyl) characters (r² = 0.574; Table S3). For high molecular weight phthalates, other processes such as the formation of micro-droplets prevail, leading to unexpected high apparent water solubility (Thomsen et al., 1999). Several MCI (⁰χ^v, ¹χ,¹χ^v, ³χ, ³χ^v, ³χ^v _pc, ⁵χ^v, ⁶χ^v _c, or ⁶χ^v _pc) were used to predict the S_W of 50 alcohols, 14 derivates of benzanilides, and miscellaneous compounds (Dai et al., 1998; Gerstl and Helling, ¹⁹⁸⁷; Nirmalakhandan and Speece, ^1988a): the best correlations were obtained for alcohols (r² = 0.961) and the worst for pesticides (r² = 0.389; Table S3). The S_W of 107 PCDE was correlated to six quantum molecular electronegativity-distance vectors (M₁₁, M₁₂, M₁₃, M₂₂, M₂₃, M₃₃; Sun et al., ²⁰⁰⁷). The combination of the polarizability α and the total energy TE was found useful to estimate the S_W of 20 substituted phenols (r² = 0.980; Xie et al., ²⁰⁰⁸), and of 107 PCDE (r² = 0.956; Yang et al., ²⁰⁰³). The addition of the most positive atomic net charge on a hydrogen atom (Q_H ⁺) to the equation allowed to improve the correlation for the substituted phenols (r² = 0.985; Xie et al., ²⁰⁰⁸; Table S3). For these phenols, S_W increases with the increase in TE, because TE can be related to molecular volume. The molecule tends to be more hydrophobic and the substituted phenol has thus difficulty in entering water phase, resulting in low S_W (Xie et al., 2008). Similar results were found for the 107 PCDE (Yang et al., 2003). For 27 halogenated anisoles, S_W increases with E_LUMO and Qyy, and conversely with the decrease in Q_H ⁺. The effect of Qyy was the most remarkable (r² = 0.980; Table S3; Zeng et al., ²⁰¹²). Some relations based on the fragment approach were successfully developed for high number of compounds (Clark, 2005; Hou et al., ²⁰⁰⁴; Kühne et al., ¹⁹⁹⁵; Table S3).

The number of descriptors involved in the several descriptors and categories equations ranged from 2 to 30 (Table S3). The combination of different categories of descriptors improved the estimation of S_W (increase in r²; Huibers and Katritzky, ¹⁹⁹⁸), probably because it allows considering simultaneously different representations and properties of the molecule. Constitutional descriptors (C/H, MW, number of double bonds (NBD), number of single bonds (NSB), n _C, n _Cl, n _H, n _O, N_Cl) were used in more than half of the equations, combined either with topological (mainly MCI but also MDE, WTPT, or CIC), quantum-chemical (α, number of independent points of the positive electrostatic potentials on molecular surface N⁺ _v, charges) and/or geometric (GEOM, GRAV) descriptors (Bhhatarai and Gramatica, 2011; Huuskonen, ²⁰⁰⁰; McElroy and Jurs, 2001; Müller and Klein, ¹⁹⁹²; Nirmalakhandan and Speece, ^1988a, 1989, 1990; Patil, ¹⁹⁹⁴; Sutter and Jurs, ¹⁹⁹⁶; Xu et al., ²⁰¹⁰; Table S3). For 107 PCDE, S_W depended on the N_Cl because the larger PCDE molecules would yield stronger dispersion-type interactions between them and tend to be excluded from water (i.e., the S_W value becomes smaller). PCDE congener with smaller N⁺ _v will likely have stronger interaction with the water, and thus produce higher S_W. The introduction of σ² _tot in the equation indicates that the uniformity of electrostatic potential distribution has effect on aqueous solubility of PCDE (Xu et al., 2010). For 52 pesticides, acceptable correlation between S_W and C/H, ⁰χ, ⁰χ^v and α was found (r² = 0.810; Table S3), but this relationship cannot be suitably used for O-analogues and compounds with C/H ratio higher or equal to 2 (Patil, 1994). The QSAR developed by Sutter and Jurs (1996) to estimate the S_W of 123 organic compounds relied on nine descriptors: two constitutional (n _C, n _O), one geometric (GEOH), three geometric-electronic (SAAA-1, SAAA-2, FNSA-3), two topological (WTPT-1, WTPT-2), and one quantum-chemical (Q_SUM). The n _O, Q_SUM, and FNSA-3 descriptors could encode dipole interactions; n _C, GEOH, WTPT-1, and WTPT-2 could have been responsible for London dispersion forces; and SAAA-1 and SAAA-2 were probably encoding the hydrogen bonding interactions between the molecules and solvent (Sutter and Jurs, 1996).

Combination of quantum-chemical descriptors (bond order of nitrogen atom ABO(N), E_HOMO, E_LUMO, fractional area-weighted surface charge of hydrogen bonding donor atoms FHDSA(2), number of electron N_el, minimal net atomic charge Q_min, Q_H ⁺, electronic spatial extent R_e, TE or solvation free energy ΔGs) with geometric (molecular contact surface area CSA, largest bond length between two carbon atoms L_cc), geometric-electronic relative negative charged surface area (RNCS), or topological structural information content of zeroth order (⁰SIC) descriptors allowed good estimate of the S_W of various compounds (Katritzky et al., 1998; Lu et al., ²⁰⁰⁸; Schüürmann, ¹⁹⁹⁵; Table S3). For 411 organic compounds, the two most important descriptors were the number of electrons (N_el) and the most negative partial charge in the molecule (Q_min). The N_el can be related to cavity-size effects (dispersion and cavity formation), and the Q_min can be related to one specific type of solute-solvent interaction, as solute-solvent interaction is a major determining factor for the S_W of compounds. Among the other descriptors involved in the relationship, the structural information content of a graph based on zero-order neighborhood of vertices (⁰SIC) describes the atomic connectivity in the molecule and encodes the size and the degree of branching in the compound. The size and the shape of the molecule also directly affect the intermolecular interaction. The average bond order of nitrogen atom (ABO(N)) seems to correct the deficiency of the electrostatic or hydrogen-bonding parameter for the N-atom containing compounds (Katritzky et al., 1998).

Some equations were found combining geometric (magnitude of the third geometric moment GEOM-3, shadow area SHDW-i, Vm), topological (total weighted number of paths in the molecule divided by the total number of atoms ALLP-4, structural information content of zero-order ⁰SIC, average structural information content index of order zero I⁰ _av, MDE-i, WTPT-2, ¹χ^v _rc), electro-topological (average E-state value over all heteroatoms (EAVE-2), sum of E-state values over all heteroatoms (ESUM-2)), quantum-chemical (sum of charges on all donatable hydrogens (CHDH), electrostatic hydrogen bonding basicity (EHBB), maximum partial charge for a hydrogen atom Q_max(H), average surface area times charge on donatable hydrogen (SCDH-2)), and/or several geometric-electronic (sum of charges on acceptor atoms (CHAA-2), difference in partial surface areas (DPSA-i), fractional positively charged partial surface areas (FPSA-1), partial negative surface area (PNSA-i), partial positive surface area (PPSA-1), sum of the surface area of acceptor atoms (SAAA-3), surface weighted negatively charged partial surface area (WNSA-1), surface weighted positively charged partial surface area (WPSA-2)) descriptors (Estrada et al., 2004; Huibers and Katritzky, ¹⁹⁹⁸; McElroy and Jurs, 2001; Mitchell and Jurs, ¹⁹⁹⁸; Table S3). For 241 hydrocarbons and halogenated hydrocarbons, the molecular volume Vm was nevertheless the most performing descriptor (high t test value; Huibers and Katritzky, ¹⁹⁹⁸). As indicated previously, in order for a solute to enter into aqueous solution, a cavity must be formed in the solvent for the solute molecule. For 265 miscellaneous compounds, Mitchell and Jurs (1998) developed a nonlinear model involving nine descriptors: SHDW-3 and GRAV, which are geometry-based descriptors, three geometric-electronic descriptors (PPSA-1, FPSA-3, WPSA-3), three topological descriptors (2SP3, ALLP-3, WTPT-4) that contained information about weighted paths and carbon types, and one quantum-chemical descriptor (q⁻). This nonlinear model provided better estimate of S_W (r² = 0.974) than the linear one (r² = 0.931; Table S3).

Atom type E-state index and topological descriptors (essentially MCI) were correlated to the S_W of pharmaceuticals and miscellaneous compounds (Huuskonen, 2000; Huuskonen et al., ¹⁹⁹⁷, 1998). However, the model gave poor predictions for the subgroup of pesticides containing phosphate or thiophosphate group and polychlorinated hydrocarbons (Huuskonen et al., 1998).

The LSER and TLSER approaches were used successfully to estimate the S_W of numerous compounds (Famini and Wilson, 1997; Feng et al., ¹⁹⁹⁶; Hickey and Passino-Reader, ¹⁹⁹¹; Xie et al., ²⁰⁰⁸; Table S3). Finally, for 797 miscellaneous compounds, the development of a relationship based on the 3D structure of the molecules and eight descriptors: five constitutional (AROM, ALIF, n _H, n _O, n _HG), and three quantum-chemical (highest hydrogen bond acceptor potential V_HHA, highest hydrogen bond donor potential V_HHD, and α) allowed good estimate of the S_W (Yan and Gasteiger, 2003).

As a conclusion, the descriptors related to the surface (CSA, FISA, FOSA, PSA, S) and volume (SAVw, V_i, Vm, Vxyz) of molecules seem to be the most appropriate ones to estimate the S_W of organic compounds, but descriptors such as ⁰χ, ⁰χ^v, the number of chlorine atoms n _Cl, and the polarizability α (which can be related to the volume) also play an important role. All categories of descriptors were used in the equations.

3.1.2. Octanol-Water Partition Coefficient

The octanol-water partition coefficient, K_OW, is the most frequently used parameter to characterize the hydrophobicity (or lipophilicity) of chemicals, which is a very important property in environmental sciences (Katritzky et al., 2000). Therefore, a high number of QSAR were developed to predict the K_OW. The 115 equations that are reported in Table S4 contain from 1 to 19 molecular descriptors, most of them relying on one, three, or four descriptors, and they were developed for a wide diversity of organic compounds.

As for S_W, the prediction of K_OW with only one descriptor mainly involved geometric descriptors related to the molecular surface or volume (Table S4). Indeed, the size of the molecule is a major factor in determining its solubility and partition behavior (Doucette and Andren, 1988). The FOSA, FISA, or the PSA (Table S1) of polar nitrogen and oxygen atoms allowed good estimates of the K_OW of several hormones (r² > 0.782; Table S4; Cao et al., ²⁰⁰⁹). The FPSA-3 was not well correlated to the K_OW of 133 PCB (r² = 0.251; Table S4; Lü et al., ²⁰⁰⁷), but the total surface area (TSA) was very well correlated with the K_OW of PCB and several miscellaneous compounds (r² > 0.870; Table S4; Doucette and Andren, ¹⁹⁸⁸; Hansen et al., ^1999a; Hawker and Connell, ¹⁹⁸⁸; Lü et al., ²⁰⁰⁷), and the SAS with the K_OW of 139 PCB (r² = 0.898; Table S4; Makino, ¹⁹⁹⁸). The volume, as for it, was used to predict the K_OW of 15 PCDD (Shiu et al., 1988), and of 142 compounds including haloalkanes, aromatics, haloaromatics, and alkenes (Bodor and Buchwald, 1997). Then, some relationships were found with MW for 139 PCB, only six PBDE or 64 aromatic compounds (Doucette and Andren, 1988; Makino, ¹⁹⁹⁸; Wania and Dugani, ²⁰⁰³), the maximum valency of C atom (MVC) for 133 PCB (Lü et al., 2007), n _Br for only nine PBDE (Braekevelt et al., 2003), and n _Cl for 15 PCDD (Shiu et al., 1988). The addition of chlorine substituents results in an increase in the K_OW. In general, topological descriptors such as MCI (Dai et al., 1999; Doucette and Andren, ¹⁹⁸⁸; Gerstl and Helling, ¹⁹⁸⁷; Güsten et al., ¹⁹⁹¹; Sabljic, ²⁰⁰¹), CRI (Türker Saçan and Inel, 1995), the Lu index (Lu, 2009), and T(O…Br) (Papa et al., 2009) allowed good estimate of the K_OW of various compounds (HBB, PAH, and their alkyl derivatives, PBDE, PCB, polychlorinated organic compounds (PCOC), and phthalates; Table S4). In particular, ⁰χ^v, which is a simple and acceptable approximation for the molecular volume, was found to be a good descriptor for the K_OW of PAH and their alkyl derivatives (Güsten et al., 1991; Sabljic, ¹⁹⁹¹, 2001; Sabljic and Piver, ¹⁹⁹²) but not for that of nonacid pesticides and miscellaneous organic compounds (Gertsl and Helling, 1987). Among the quantum-chemical descriptors involved in one-descriptor relationships, the ionization potential (IP) and the dipole moment (μ) were used to estimate the K_OW of 139 PCB, however, the correlations were very bad (r² < 0.340; Makino, ¹⁹⁹⁸). Yang et al. (2007) modeled K_OW using the polarizability α of 75 PCDD and dibenzo-p-dioxins: the greater the α is, the larger the K_OW is, suggesting that PCDD molecule with large α possesses great dispersion force and can easily enter the octanol phase. Similarly, the K_OW of 133 PCB was correlated with α (Lü et al., 2007). Finally, the electron affinity (EA) and the final heat of formation (HOF) were satisfactorily correlated with the K_OW of 139 PCB (r² = 0.743 and 0.870, respectively; Makino, ¹⁹⁹⁸), and the total energy (TE) with the K_OW of 20 substituted phenols (r² = 0.843; Xie et al., ²⁰⁰⁸; Table S4).

Using several descriptors of the same category, it was shown that constitutional descriptors based on the numbers of chlorine atoms (N₂₍₆₎, N₃₍₅₎, N₄) allowed good prediction of the K_OW of 107 PCDE (r² = 0.983) and of 209 PCB (r² = 0.949; Chen et al., ²⁰⁰⁷; Han et al., ²⁰⁰⁶). As observed before for PCDD (Shiu et al., 1988), the higher the number of substituted chlorine atom is, the larger the K_OW value of PCDE is. For 22 polychlorinated diphenyl sulfides (PCDPS), the pairwise of Cl atoms at meta position N_m was added to N₂₍₆₎, N₃₍₅₎, and N₄, and K_OW was shown to increase with N_m for compounds with the same number of chlorine substituents (Shi et al., 2012). But, these equations were only developed for organochlorines, therefore their applicability domain remains limited. Atom/fragment contribution approaches were used successfully for high number of compounds (Clark, 2005; Katritzky et al., ²⁰⁰⁰; Meylan and Howard, ¹⁹⁹⁵; Table S4). However, the fragment constant approach leads to oversimplification of steric and conformational effects of complex structures. In addition, there is a need for correctional factors, and it is not possible to estimate K_OW for uncorrelated or unknown fragments. Some equations were based on several topological descriptors: MCI, the number of path length (P₇, P₁₀), the Balaban index based on distance (J_b), the Wiener index (W), and information indices (CIC, IC, SIC) led to good estimate of K_OW of various organic compounds (r² > 0.652; Table S4; Basak et al., ¹⁹⁹⁶; Dai et al., ¹⁹⁹⁸; Niemi et al., ¹⁹⁹²). However, for pesticides and miscellaneous compounds, the K_OW were not well correlated to MCI (r² < 0.425; Table S4; Gerstl and Helling, ¹⁹⁸⁷). For 50 aromatic hydrocarbons, 300 pharmaceutical compounds and 14 phthalates, the K_OW were correlated to E-state indices (Gombar and Enslein, 1996; Huuskonen et al., ¹⁹⁹⁹; Thomsen et al., ¹⁹⁹⁹), but these indices cannot account for 3D and conformational effects, which may play a major role for solubility properties of chemical compounds. The polarizability α was combined with μ to predict the K_OW of 22 PCDPS (Shi et al., 2012); with μ and the superdelocalizability of the highest unoccupied molecular orbital (S_HOMO) to predict the K_OW of 17 ureas (Reddy and Locke, 1996); with μ, E_LUMO and the largest negative net atomic charge on an atom (q⁻) for 28 alkyl (1-phenylsulfonyl) cycloalkane-carboxylates (Chen et al., ^1996a); with E_HOMO and E_LUMO for 209 PCB (Zhou et al., 2005); and with the partial atomic charge on nitrogen (q²N) and the partial atomic charge on oxygen (q²O) to predict the K_OW of 592 miscellaneous compounds (Xing and Glen, 2002). As indicated before, the bigger the α, the more hydrophobic the molecule is predicted to be: molecules which require a bigger cavity are predisposed to move into the octanol layer. The μ relating with the intermolecular dipole-dipole and dipole-induced dipole interactions also plays a role in the variations of K_OW because molecules with larger μ also tend to transfer from octanol phase to water phase (Shi et al., 2012). Finally, the atomic charges q²N and q²O are derived from computed charge densities of nitrogen and oxygen atoms of the molecule, which is a measure of their ability to form hydrogen bonds with the solvent molecules (Xing and Glen, 2002). For the 209 PCB, E_HOMO had the most important influence on K_OW. Large values of E_HOMO and E_LUMO would result in small values of K_OW for PCB because E_HOMO represents the proton acceptance ability in forming hydrogen bond, while E_LUMO represents the proton donation ability in formation of hydrogen bond. Therefore, the compounds with large values of E_HOMO and E_LUMO tend to donate or accept protons easily (Zhou et al., 2005). The K_OW of 49 halogenated anisoles was correlated to E_LUMO, the most positive atomic net charge on a hydrogen atom (Q_H ⁺), and the quadrupole moment (Qzz). The K_OW increases with increasing Q_H ⁺, which suggests intermolecular electrostatic interactions between halogenated anisoles and octanol molecules, with the carbon atoms in halogenated anisoles to accept electrons and the oxygen atoms in octanol molecules to donate electrons. On the contrary, K_OW increases with decreasing E_LUMO (see previous) and Qzz (Zeng et al., 2012). Finally, quantum-chemical (E_HOMO, q⁻, Q_H ⁺, TE, μ) descriptors allowed the estimate of the K_OW of 70 PCOC (r² = 0.931; Table S4; Dai et al., ¹⁹⁹⁹), and for 107 PCDE, the equation was based on the interactions between non-hydrogen atoms M₁₁, M₁₃, M₂₂, and M₃₃ (r² = 0.984; Table S4; Sun et al., ²⁰⁰⁷).

In general, as for S_W, the combination of descriptors of several categories improved the quality of the prediction of the K_OW (Dai et al., 1998; Güsten et al., ¹⁹⁹¹; Lü et al., ²⁰⁰⁷; Makino, ¹⁹⁹⁸; Xie et al., ²⁰⁰⁸; Table S4). Numerous relationships were based on the molecular volume (V, VdW, VdW_A, V_i, Vm) and/or surface (CSA, PSA, S, SAS, TSA), associated with several constitutional (I_alkane, Iv, MW, Np), topological (MCI, CIC_i, IC_i, P₁₀, ^3DW), or quantum-chemical (EA, E_HOMO, E_LUMO, HOF, IP, Q_N, qO, Q_O, Q_ON, S_HOMO, S_N, TE, V_S,max, V_min, ΔGs, μ, μ_tot, ΣV⁻ _s) descriptors (Basak et al., 1996; Bodor and Buchwald, ¹⁹⁹⁷; Bodor et al., ¹⁹⁸⁹; Edward, ¹⁹⁹⁸; Famini and Wilson, ¹⁹⁹⁷; Li et al., ²⁰⁰⁸; Makino, ¹⁹⁹⁸; Nandihalli et al., ¹⁹⁹³; Reddy and Locke, ^1994b, 1996; Schüürmann, ¹⁹⁹⁵; Xie et al., ²⁰⁰⁸; Zou et al., ²⁰⁰²; Table S4). The molecular volume was a key descriptor because molecules with larger size would tend to distribute into octanol: it is much easier to open a cavity in octanol than in water (fewer hydrogen bonds) therefore larger molecules will preferentially solvate in the octanol layer (Famini and Wilson, 1997). For 118 compounds, including basic heterocycles, halogenated compounds, multiple substituted benzenes derivatives, and pharmaceuticals, the geometric descriptors, surface S (indirectly, the volume), and ovality O, but also the MW, which is also a volume-related descriptor, were the most significant descriptors. The need to include I_alkane (classifier indicator for alkane) in the relationship may arise from the different nature of partition of alkanes: they cannot participate in any special interaction, such as hydrogen bonding and electrostatic effect with the surrounding solvent molecules; therefore, the alkanes cannot account for a quasi-structured hydrate environment. All the remaining descriptors are derived from computed charge densities of nitrogen and oxygen atoms of the molecules, these elements being capable of forming hydrogen bonding with the solvent molecule (Bodor et al., 1989).

As indicated previously, the polarizability α plays an important role in the prediction of K_OW (the greater the α is, the larger the K_OW is) and it was involved in several equations (but never in equations containing descriptors related to surface or volume; Table S4). The polarizability α with FPSA-3 and/or MVC, allowed good prediction of the K_OW of 133 PCB (r² = 0.928; Table S4; Lü et al., ²⁰⁰⁷), and with MW and ΔH_f it provided satisfactory estimate of the K_OW of 106 PCDE (r² = 0.976; Table S4; Yang et al., ²⁰⁰³). The relationship obtained by Patil (1994) for 55 pesticides, and based on carbon to hydrogen ratio C/H, α, and two MCI (⁰χ and ⁰χ^v), cannot be used acceptably for O-analogues and compounds with C/H ratio higher or equal to 2.

Constitutional descriptors, such as the number of the chlorine atoms on phenyl rings N_Cl, the number of ortho-chlorine substituents normalized to the molecular weight of the compound NrCl₀, the number of meta-chlorine substituents Cl_META, the number of meta/para pairs of chlorine substituents Cl_MP-PAIR or the number of branching points in the carbon skeleton NoB₃ were combined to MCI to estimate the K_OW of chlorinated compounds and of PAH and their alkyl derivatives (Güsten et al., 1991; Sabljic et al., ¹⁹⁹³), or to quantum-chemical descriptors (the number of independent points of the positive electrostatic potentials on molecular surface N⁺ _v, and the average of the sum of the surface minima values of the electrostatic potential V⁻ _s,av) to estimate the K_OW of 107 PCDE (Xu et al., 2010). For PCDE, the N_Cl term was introduced in the equations because the larger PCDE molecule would yield stronger dispersion-type interaction between the octanol molecule (i.e., the K_OW value becomes higher), and tend to be excluded from water. As V⁻ _s,av can be viewed as a descriptor reflecting nonspecific intermolecular interactions, the introduction of this descriptor in the equation reveals that nonspecific intermolecular interaction is statistically significant to K_OW (Xu et al., 2010). For 64 benzotriazoles, the geometric descriptor Geary autocorrelations-lag 3 weighted by atomic masses (GATS3m) was combined with two topological descriptors (2D binary fingerprint that takes into account the presence of C-C (C-C single bond) at a topological distance 8B08[C-C], and Moran autocorrelations lag (1) weighted by atomic van der Waals volume MATS1v), and n _N to give correct estimate of the K_OW (r² = 0.886; Table S4; Bhhatarai and Gramatica, ²⁰¹¹). With global descriptors, constituted by 19 constitutional and quantum-chemical descriptors, Cheu et al. (1996) modeled the K_OW of 30 phenylthio, phenylsufinyl, and phenylsulfonyl acetates. E-state indices associated to MW or to several topological descriptors were used successfully to estimate the K_OW of miscellaneous organic compounds (Gombar and Enslein, 1996; Tetko et al., ²⁰⁰¹) but the results were not good for drug compounds (Huuskonen et al., 1999; Table S4). Finally, for 122 nonionic organic compounds, the use of several functionality index [η‘_F] allowed good estimate of the K_OW (r² = 0.960; Table S4; Roy et al., ²⁰⁰⁷).

Some relationships were developed using LSER, TLSER, and MTLSER approaches (Chen et al., ^1996a; Dai et al., ¹⁹⁹⁸; Kamlet et al., ¹⁹⁸⁸; Katritzky et al., ²⁰⁰⁰; Xu et al., ²⁰⁰²). In general, the molecular volume was again the most significant descriptor (Famini and Wilson, 1997; Feng et al., ¹⁹⁹⁶; He et al., ¹⁹⁹⁵; Xie et al., ²⁰⁰⁸; Xu et al., ²⁰⁰²). The coefficient was positive, indicating an endoergic effect consistent with most cavity/bulk effects. As indicated previously, cavity effects are critical, and therefore larger molecules will preferentially solvate in the octanol layer (Famini and Wilson, 1997). For 28 alkyl(1-phenylsulfonyl)cycloalkane-carboxylates, the polarizability α was the most significant descriptor, but it is in direct proportion to the intrinsic molecular volume (Chen et al., ^1996a). TLSER equation was also combined with a fragment approach to estimate the K_OW of 148 various organic compounds (Platts et al., 1999 and 2000).

Considering all the results that are summarized in this section, it appeared that the molecular descriptors related to the volume (V, VdW, VdW_A, V_i, Vm, V_x) were the most relevant ones to assess the K_OW of organic compounds, but MW, ⁰χ^v, ¹χ^v, α, μ, E_HOMO and E_LUMO were also frequently involved in the equations and found to allow good estimate of the K_OW. All categories of descriptors were used in the equations, except geometric-topological descriptors.

3.2. Dissociation Process

The dissociation constant, pK_a, which describes the extent to which a compound dissociates in solution, is a fundamental physical property of a chemical. It is a key feature, which governs the chemical reactivity of the substances with other compounds in any solvent, and also the interaction with the solvent itself, and thus its hydrophobicity and water solubility (Citra, 1999; Jover et al., ²⁰⁰⁸). Lee and Crippen (2009) focused on the description of the methods used to predict the pK_a (e.g., quantum chemical and continuum electrostatic methods or artificial neural networks), rather than to review the different descriptors used in the relationships. This section is therefore different and complementary to the work of Lee and Crippen.

A very high number (145) of QSAR were developed to estimate the pK_a of organic compounds (Table S5). Most of these relationships use only one molecular descriptor but they can use up to eight descriptors, and most of the descriptors are quantum-chemical descriptors (the pK_a values themselves reflect electronic properties in a direct manner). Few constitutional, geometric, and topological descriptors have been also involved (Table S5). The QSAR were developed for several specific classes of organic compounds but not, for example, for pesticides (Table S5).

The estimation of the pK_a using one descriptor mostly involves the electrophilic superdelocalizability (SE) of the atoms N, C or O. The best correlations were found for anilines and amines, and ortho phenols (r² > 0.900), and the worst for heterocycles, pyridines and tertiary amines (r² < 0.570; Tehan et al., ^2002a; Tehan et al., ^2002b; Yu et al., ²⁰¹⁰; Table S5). SE quantifies the susceptibility of a molecule for an electrophilic attack. The negative value of SE indicates that increasing SE correlates with increasing pK_a and thus decreasing acidity (Yu et al., 2010; Table S5). The charges of atoms or groups were also involved in numerous equations: the atomic partial charges of carbon connected to hydroxyl or carboxyl groups (apc(C)), the atomic partial charges of hydrogen of the hydroxyl group (apc(H)), the atomic partial charges of oxygen of the hydroxyl group (apc(O)) (Hanai, 2003), the natural charge on the amino nitrogen (Q_n(N)) (Gross and Seybold, 2000; Gross et al., ²⁰⁰¹), the natural charge on the neutral amino group (Q(NH₂)), the natural charge on the cationic ammonium group (Q(NH₃ ⁺)) (Seybold, 2008), the natural charge on the phenoxide oxygen (Q_n(O⁻)) and the natural charge on the phenolic hydrogen (Q_n(H)) (Gross and Seybold, 2001), the Mulliken charge of COO⁻ group (Q_M(COO⁻)), the Löwdin charge of hydrogen (Q_L(H)) and of COOH (Q_L(COOH)), the AIM charge of hydrogen (Q_A(H)), the natural population analysis charge of COOH group (Q_n(COOH)) (Hollingsworth et al., 2002), the charge on the acidic hydrogen (Q^acid _H) and the charge on the basic nitrogen (Q^base _N) (Brown and Mora-Diez, ^2006b), and the charge on phenolic O or phenolate O atoms, (d_Ophenolic or d_Ophenolate) (Grüber and Buß, 1989). In general, the correlation coefficients were high (r² > 0.810), except for protonated benzimidazoles (r² = 0.644), but the number of compounds used to develop the QSAR were sometimes very low, in particular for fluorinated ethylamines (Table S5). For phenols, the significant correlation between pK_a and d_Ophenolic (r² = 0.810; Table S5) can be explained by the heterocyclic dissociation of the OH bond that should be facilitated by a positive charge on O, both by polarizing the bond and by accommodating the developing negative charge. The correlation with d_Ophenolate was nevertheless better: the charge distribution of the anion, especially at the acidic center, is an indicator of the ability of the system to accommodate excess negative charge and as such should correlate with acid strength (Grüber and Buß, 1989). The Q_n(H) and the Q_n(O⁻) should serve as good measures of acidity, more acidic hydrogens having lower electron densities. In the same manner, delocalization of the phenoxide oxygen negative charge is expected to impart stability to the phenoxide, favoring its formation and lowering the pK_a (Gross and Seybold, 2001). The Q^acid _H is related to the delocalization of charge over the molecule and in turn to the acidity: a lower value of Q^acid _H indicates good delocalization and should produce a higher pK_a. The higher pK_a could also be explained by stating that the lower the positive charge on the acidic hydrogen, the less polarized the N-H bond and the less acidic the compound. The values of Q^base _N become more negative with increasing pK_a which indicates that the larger the negative charge on the basic nitrogen of the neutral molecular form, the stronger it will be as a base, hence a weaker acid once protonated; that is well illustrated in the case of the benzimidazole (Brown and Mora-Diez, ^2006b). Hanai (2003) developed another approach to estimate the pK_a: the pK_a is the sum of the pK_a (base compounds) derived from the atomic partial charge (apc) of basic compounds, and of ΔpK_a (substitute effect) derived from the difference in the atomic partial charge between derivatized and base compounds. Good correlations between the partial charges apc(H), and apc(O) were obtained, but again the number of data is very low (r² > 0.864; Table S5). The substitute effect on atomic partial charge Δpc was balanced between the atomic partial charge of the substituted phenol and phenol, and was well correlated with ΔpK_a (r² > 0.900; Table S5; Hanai, ²⁰⁰³).

Equations were also developed with the molecular electrostatic potential minima (V_min), the surface molecular electrostatic potential minima (V_S,min) or the surface molecular electrostatic potential maxima (V_S,max) for phenols, phenolates, benzoic acids, benzoates and anilines. In any case, the correlation coefficients were very good (r² > 0.868; Table S5). V_min and V_S,min are related to the initial attraction that brings the proton into the vicinity of the amino group. When the V_S,min values are more negative, the anionic conjugate base is more attractive to the approach of an electrophile, and the acidity is lower. V_S,min indicates how negative is the electrostatic potential of the oxygen, and V_S,max how positive is the electrostatic potential of the hydrogen. The V_S,min values of the conjugate bases reflect the tendencies of electrophiles to approach the anions to reform the acids; the V_S,max values of the acids are good indicators of the ease of proton loss (Gross et al., 2001; Ma et al., ²⁰⁰⁴). Some equations were found with the molecular electrostatic potential on the acidic atom (MEP) for amines, anilines, carboxylic acids, alcohols, sulfonic acids, and thiols (r² > 0.878; Table S5). The pK_a of these compounds were also correlated to ΔMEP (i.e., the MEP evaluated for the isolated neutral acidic atom subtracted from the MEP value on the acidic nucleus for each category of compounds; Liu and Pedersen, 2009).

Several QSAR were developed using the energies of orbitals (E_HOMO, E^acid _HOMO−1, E^acid _HOMO, E^base _HOMO-2, E^base _HOMO-1, E^base _HOMO, E_LUMO, E^acid _LUMO, E^acid _LUMO+2, E^base _LUMO; Brown and Mora-Diez, ^2006b; Gross and Seybold, ²⁰⁰¹; Grüber and Buß, ¹⁹⁸⁹; Soscún Machado and Hinchliffe, 1995; Tehan et al., ^2002a; Yu et al., ²⁰¹⁰; Table S5). For 18 protonated benzimidazoles, the E^acid _LUMO+2 showed the strongest correlation to the experimental data (r² = 0.843; Table S5), followed by E^base _HOMO-2 (r² = 0.768; Table S5): an empty orbital of an acid will be more involved in its deprotonation process, while an occupied orbital of the base will be more involved in its protonation process. The energy of the LUMO of the protonated species is related to the formation of hydrogen bonds with the solvent molecules and the subsequent deprotonation. A lower value for E^acid _LUMO means that hydrogen bonds will form with greater ease, and allows for easier deprotonation and a lower pK_a (Brown and Mora-Diez, ^2006b). Among the other quantum-chemical descriptors, the sum of the valence p natural atomic orbitals of the atom (NAO) was correlated to the pK_a of amines, anilines, carboxylic acids, alcohols, sulfonic acids, and thiols (r² > 0.905; Table S5; Liu and Pedersen, 2009). For 17 benzoic acids and benzoates, 19 phenols and phenolates, and 36 anilines, pK_a values increase as the minimum molecular surface local ionization energy (I_S,min) values decrease. The I_S,min is related to the subsequent charge sharing or charge transfer. When the I_S,min values are low, there is a greater tendency for a proton to transfer back to form the neutral acid, leading to a lower acidity and a higher pK_a (Gross et al., 2001; Ma et al., ²⁰⁰⁴). Finally, some relationships were found using (a) the OH bond order (BO_OH): the pK_a of 17 substituted benzoic acids are proportional to the strength of the bond between hydrogen and oxygen in the carboxylic acid group (Hollingsworth et al., 2002); (b) the energy difference between acid and conjugated base (H_f) for phenols (Grüber and Buß, 1989); (c) the energy difference in aqueous phase between the neutral amines and their cationic forms (ΔE_aq) for 26 amines (Seybold, 2008); (d) the energy difference in gas phase between the neutral amines and their cationic forms (ΔEd) for four fluorinated ethylamines and 28 amines (Seybold, 2008); (e) the relative proton transfer energy (ΔE_prot) for 17 substituted benzoic acids or 19 phenols derivatives, or the relative proton transfer enthalpy (ΔH_prot) for 36 anilines (Gross and Seybold, 2001; Gross et al., ²⁰⁰¹; Hollingsworth et al., ²⁰⁰²): a positive value of ΔE_prot indicates that the substituted phenol is less acidic than phenol itself, and a negative ΔE_prot suggests the substituted phenol is more acidic; (f) the aqueous Gibbs free energy (ΔG_aq) for benzimidazoles (Brown and Mora-Diez, ^2006a, 2006b); (g) the Gibbs free energy of dissociation (ΔG_diss) for 64 organic and inorganic acids (Klamt et al., 2003); (h) the standard free energy (ΔG^O) for 12 aliphatic, alicyclic, and aromatic amines (Kallies and Mitzner, 1997); (i) the fractional number of electron transfer (ΔN), or the associated energy change (ΔEe) for 58 acids (Gupta et al., 2007): a larger ΔEe value denotes a stronger Lewis acid and that corresponds to a smaller pK_a value implying a stronger Brønsted acid. A larger value of ΔN indicates a greater amount of electron transfer and hence a better Lewis acid-base pair. Since the base remains the same for all the acid-base pairs studied, a larger ΔN would indicate a stronger acid and a smaller pK_a value (stronger Brønsted acid).

With topological descriptors, relationships were developed with the group philicity (ω_g ⁺) for small number of compounds: nine substituted phenols, nine alcohols or 14 substituted anilines and phosphoric acids, but also for 31 substituted carboxylic acids (r² > 0.722; Table S5; Parthasarathi et al., ²⁰⁰⁶), and with two modified MCI, ¹χ^f and ¹χ^fλ, for 31 carboxylic and halogenated carboxylic acids (Pompe and Randic, 2007; Table S5). For 18 benzimidazoles, Brown and Mora-Diez (2006b) tried to develop a relationship with the change in the volume of the solvent cavity going from the protonated to the neutral species (ΔV_SC), but the correlation was poor (r² = 0.269; Table S5).

The QSAR based on several descriptors of the same category only involve quantum-chemical descriptors. Ten equations combine self-polarizability (e.g., ALP_C1, ALP_C2, ALP_C4, ALP_O3, and ALP_N1), partial atomic charges of atom N or O at position 1 (e.g., AQ_N1, AQ_O1, AQ_O2, AQ_O3), superdelocalizability (e.g., SE_C1, SE_C2, SE_C4, SE_N, SE_N1, SE_O, and SE_O3), charge descriptors (e.g., Coulson net atomic charge of the nitrogen atom Q_C(N), net atomic charge at the carbonyl O of the carboxylic group Q _{= O}), the nucleophilic frontier electron density of atom N at position 1 (FN_N1), the electrophilic frontier electron density of atom O at position 1 or 3 (e.g., FE_O1, FE_O3), and E_LUMO (r² > 0.690; Table S5; Tehan et al., ^2002a; Tehan et al., ^2002b; Yu et al., ²⁰¹⁰). One relationship was based on four charges of carbon at different positions (d_C4, d_C12, d_C16, d_C18), and one charge of oxygen (d_O11) for 48 benzoic acids (r² = 0.880; Table S5; Grüber and Buß, ¹⁹⁸⁹). For phenols, and aromatic and aliphatic carboxylic acids, E_HOMO, H_f and charges play an important role in the prediction of pK_a. The other descriptors, relying on atomic charges, enter the regression equations with negative signs showing that the acid strength increases as excess negative charge decreases. For phenols, the high regression coefficient of the meta-carbon (d_C15) seems to indicate that resonance effects which are primarily related to ortho- and para-positions do not play a dominant role in differentiating acid strength (Grüber and Buß, 1989). Three relationships contained different combinations of two of the following descriptors (Yu et al., 2011): the energy-weighted acceptor energy (EE_vac), the energy-weighted donor energy (EE_occ), the charge-limited acceptor energy (EQ_vac), the energy-limited acceptor charge (QE_vac), and the energy-limited donor charge (QE_occ). The correlations were good (r² > 0.820; Table S5). For 29 phenols with intramolecular H bonding, the pK_a was correlated to the EE_vac evaluated at the acidic H atom, and EE_occ evaluated at the oxygen atom bonded to this H atom. The EE_vac increases with increasing electron acceptor strength of H, indicating a larger energy demand for ionizing H to become H⁺. Thus, EE_vac increases with decreasing acidity and accordingly increasing pK_a, which is reflected by its positive regression coefficient. The EE_occ evaluated at the oxygen bonded to H increases with increasing oxygen donor strength, which in turn reflects an increasing OH bond strength and thus a lower tendency for bond fission. Accordingly, EE_occ correlates with decreasing acidity and thus with increasing pK_a. EE_vac evaluated at H is also used as local reactivity parameter of the pK_a prediction models calibrated for the 190 aliphatic carboxylic acids. For this compound class, the QE_occ is used as second molecular descriptor. QE_occ increases with increasing amount of loose electron charge ready for donation, which stabilizes the carboxylic O-H bond. QE_occ increases with decreasing acidity (decreasing O-H bond fission tendency) and thus with increasing pK_a (Yu et al., 2011). The pK_a of 19 phenols and phenolates was well correlated to I_S,min and V_S,max (r² = 0.908; Table S5; Ma et al., ²⁰⁰⁴), and that of 13 benzimidazoles was found to depend on the difference in molar energies of the ground states of the product and reactants at 0 K (ΔEo), molecular partition functions (q_fi), and the stoichiometric coefficient (ν_i) of each species (Brown and Mora-Diez, ^2006a; Table S5). Other equations involve the gas-phase free energy of the proton abstraction (ΔG_g) and the solvation free energy (ΔGs) for only eight weak acids (Topol et al., 2000); or the charge on hydrogen atom (qH) and the net atomic charges on the oxygen atom (qO) combined with BO_OH for various compounds (Citra, 1999; Table S5).

There is no result allowing the comparison of equations using one category of descriptors and several categories of descriptors (Table S5). Using constitutional descriptors such as I_ortho associated with EE_vac, Yu et al. (2011) found good pK_a predictions for 150 aromatic carboxylic acids (r² = 0.820; Table S5). The I_ortho has a negative regression coefficient, indicating an increased acidity for ortho-substituted compounds. Ortho substitution might destabilize the molecular ground state as compared to meta and para substitution, and the associated steric repulsion decreases upon dissociation, thus supporting the cleavage of H⁺. For 190 phenols without intramolecular H bonding, the pK_a was correlated to EQ_vac, QE_vac, and I_ortho (r² = 0.900; Table S5). The H atoms with a large EQ_vac prefer more strongly to retain electron charge and accordingly provide more resistance in donating charge to their bonding partner in order to become dissociated. Larger QE_vac values reflect larger amounts of electron charge per unit energy transferred to H and thus a larger polarizability of H in its bonding situation. Because increasing polarizability indicates a decreasing resistance to changing local electron density, QE_vac increases with increasing readiness of the acidic H atom to become ionized upon dissociation. Accordingly, QE_vac increases with increasing acidity and thus with decreasing pK_a as indicated by the negative sign of its regression coefficient. For 288 alcohols, the pK_a was correlated to the inductive descriptor of the acidic oxygen atom in an acid (Q_σ,O), the pi-electronegativity for the α carbon atom in an acid (EN_π,αC), I_carboxy, and I_amino (Zhang et al., 2006). The negative coefficient sign for the atomic inductive descriptor Q_σ,O is consistent with the physical meaning of this descriptor, as a large Q_σ,O value means a large inductive effect of the substituent. For 1122 aliphatic carboxylic acids, the best multiple linear-regression equation is obtained with five molecular descriptors: the accessibility of the acidic oxygen atom in an acid (A_access,O (2D)), EN_π,αC, I_amino, Q_σ,O, and α_O (Zhang et al., 2006). As for alcohols, there is a small pK_a value if there is a large Q_σ,O value. The positive sign for A_access,O (2D) means that a large steric hindrance will increase the pK_a and therefore decrease the acidity of the acid, as access of water to take up the proton is hindered (Zhang et al., 2006). The geometric descriptor ΔV_SC combined with E^acid _LUMO+2 and Q^acid _H provided excellent results to estimate the pK_a of benzimidazoles (r² = 0.990; Table S5) however the number of data used for the correlation was not indicated in the study (Brown and Mora-Diez, ^2006b). For 15 imidazol-1-yl alcanoic compounds, there was a good correlation between pK_a and E_LUMO, n _ester, and Q_N3 (r² = 0.978; Table S5). For the protonated species, LUMO is located over the azole ring. A low E_LUMO would suggest an easy formation of a hydrogen bond with the water molecule and donation of a proton by overlapping with the HOMO of water, namely, a low pK_a (Soriano et al., 2004). Finally, the charges on hydrogen (q_Hδ+) and on oxygen (q_Oδ-) atoms combined with the change in O-H bond length (bl(OH)) provided good assessment of the pK_a of 74 aromatic acids derivatives (r² = 0.988; Table S5). Increasing q_Oδ- on the hydroxyl oxygen induces more hard characteristics to oxygen and consequently lowers the tendency for dissociation: this causes the molecule to be a weaker acid (Ghasemi et al., 2007).

Using artificial neural network methodology, Jover et al. (2007, 2008) introduced, in addition to five descriptors relative to the solute, two descriptors relative to the solvent. For 136 benzoic acids, they found good correlations between the pK_a and the FPSA-2, the maximum electron-electron repulsion for an O atom (MaxeeO), the minimum resonance energy for O-H bond (MinOH) the maximum valency of C atom (MVC) and the maximum partial charge for a hydrogen atom (Q_max(H)) (in all cases, the involved hydrogen atom corresponds to the carboxylic group) for the solute, and the hydrogen bond donor acidity (α_m) and the standard internal energy of vaporization (Δ_vapU^O) for the solvent (Jover et al., 2008). Thus, four solute descriptors of this model are related to the stability, reactivity, or the tendency to dissociate the carboxylic group. The Q_max(H) reflects the polarity of the OH bond that is cleaved in the dissociation process. Also, the MinOH descriptor is related to the energy of the bond that dissociates, and MaxeeO and MVC account for the reactivity of the atoms, respectively. On the other hand, the fifth solute descriptor, FPSA-2, represents a density of charge of the solute and explains the intermolecular interactions, in this case those between the benzoic acid and the solvent. All these solute descriptors can be associated to the nonspecific solute/solvent interactions. Of the two solvent descriptors, the Δ_vapU^O indicates the energy involved in the solute cavity formation in the bulk of the solvent in the dissolution process and can also be associated to the nonspecific solute/solvent interactions. The α_m is associated to the specific hydrogen-bonding interactions and stands for the hydrogen-bond donor properties of the solvents. Similarly, for 199 phenols, the pK_a was correlated to E_LUMO+1, the maximum electron-neutron attraction for a C-O bond (MaxenC-O), the maximum partial charge for a hydrogen atom (Q_max(H)), the relative positive charged surface area (RPCS), and the polarizability α for the solute; and α_m and μ for the solvent. The dipole moment μ of the solvent, and the solute descriptors MaxenC-O, RPCS, and α contain information related to the nonspecific solute/solvent interactions. On the other hand, the E_LUMO+1 and α_m encode information related to the specific interactions (Jover et al., 2007).

Methods such as principal component-genetic algorithm-multiparameter linear regression (PC-GA-MLR) and principal component-genetic algorithm-artificial neural network (PC-GA-ANN) models were employed to predict the pK_a of miscellaneous organic compounds (Habibi-Yangjeh et al., 2009; Lee and Crippen, 2009). For 282 nitrogen-containing compounds, 15 principal components were first selected by PC-GA-MLR, then descriptors having the highest correlations with the principal components were retained, leading to a selection of eight descriptors: two constitutional (H attached to heteroatom H-050, number of total primary C(sp³) nCp), three geometric (Geary autocorrelation-lag 1 weighted by atomic polarizabilities GATS1p; 3D-MoRSE-signal 12 weighted by atomic polarizabilities Mor(12)p; 3D-MoRSE-signal 31 weighted by atomic van der Waals volumes Mor(31)v), two topological (mean information content index based on the zero-order neighborhood of vertices in a graph IC₀, structural information content of a graph based on one-order neighborhood of vertices SIC₁) and one electro-topological (constitutional descriptor of the mean E-state of the molecule related to the polarizability, Ms). The Mor(12p) and Mor(31)v descriptors relate to polarizabilities and van der Waals volumes of the atoms, respectively, whereas IC₀ and SIC₁ are related to information content, which is a measure of the degree of diversity of the elements in the set. The Ms gives information related to the electronic and topological state of the atom in the molecule. Therefore, it is concluded that polarizabilities and van der Waals volumes of the atoms, diversity of the elements in compounds, electronic state of the atoms in the molecule, and the number of first neighbor (hydrogen) of heteroatom play main roles in the pK_a of the compounds. With the same 15 principal components, the PC-GA-ANN method gave higher correlations (Habibi-Yangjeh et al., 2009; Table S5). Finally, some relationships can take into account the temperature (Brown and Mora-Diez, ^2006a; Topol et al., ²⁰⁰⁰).

In summary, the most efficient descriptors to predict the pK_a were related to the superdelocalizability, the charges and to E_HOMO. No geometric-topological and no geometric-electronic descriptors were used in the equations, and contrary to S_W and K_OW, no MCI was involved.

3.3. Volatilization Process

Volatilization from soil and volatilization from leaf surfaces are distinguished as the factors that are involved may be different. Indeed, trying to correlate observed volatilization fluxes with physicochemical properties of the compounds, the vapor pressure alone (liquid vapor pressure P_L, solid vapor pressure P_S) and the Henry's law constant (K_H) divided by the adsorption coefficient are often found to give the best fit when considering volatilization from leaves and from soil, respectively (e.g., Woodrow et al., ¹⁹⁹⁷). The octanol-air partition coefficient (K_OA) is also thought to be a key descriptor of the distribution of semi-volatile compounds between the atmosphere and terrestrial organic phase (Zhao et al., 2005). Finally, a volatility index (VIN) can also be used to differentiate between volatile and nonvolatile compounds (Gramatica and Di Guardo, 2002).

3.3.1. Vapor Pressure

The 40 equations allowing the estimate of vapor pressure involve from 1 to 12 descriptors, and more than half of them are only based on one descriptor. The QSAR were developed for a wide diversity of organic compounds, but not for pesticides (Table S6).

In contrast to other environmental relevant compounds properties such as water solubility or lipophilicity, vapor pressure is highly dependent on temperature. Therefore the temperature was introduced in a few number of QSAR (Ding et al., 2006; Kühne et al., ¹⁹⁹⁷).

The prediction of the liquid vapor pressure (P_L) of organic compounds with one descriptor mainly involved the polarizability α, and correlations were good (r² > 0.731; Table S6; Liang and Gallagher, ¹⁹⁹⁸; Staikova et al., ²⁰⁰⁴). In any case, an increase in α led to a decrease in P_L. Indeed, α is related to dispersion forces or induced dipole-induced dipole interactions, which are the main component of the intermolecular forces in nonpolar compounds. On the other hand, polarizability α showed lower correlations for relatively polar compounds, such as the alcohols, amines, and halogenated ketones. This may be due to the potential for hydrogen bonding and/or dipole interactions which are not adequately accounted for by α (Liang and Gallagher, 1998; Table S6). Other equations involve n _Cl, MW, Vm, or T(O…Br) as single descriptor (Papa et al., 2009; Shiu et al., ¹⁹⁸⁸; Wania and Dugani, ²⁰⁰³). P_L tends to fall by a factor of eight per chlorine atom added (Shiu et al., 1988).

Using several topological descriptors, Basak et al. (1997) developed four relationships to estimate the P_L of 476 various organic compounds (Table S6). The efficiency of topological descriptors to estimate P_L (r² ranges from 0.515 to 0.804; Table S6) showed that adjacency and distance in chemical graphs, being general descriptors of molecular size, shape, and branching, are important in predicting this parameter. For 23 PBDE or 72 PCDE, P_L was very well related to three quantum-chemical descriptors: the largest negative net atomic charge on an atom (q⁻), α and μ (r² > 0.988; Table S6; Wang et al., ²⁰⁰⁸; Zeng et al., ²⁰⁰⁷). PCDE molecules with great absolute values of q⁻ tend to have great intermolecular electrostatic interactions and limited volatilization. The larger the value of μ is, the smaller the value of P_L is, because intermolecular interactions are in direct proportion to μ², therefore PCDE molecules with larger μ values tend to volatilize less. As indicated previously, increasing α value of the PCDE leads to decreasing P_L (Zeng et al., 2007). For 15 PCDD, P_L was also very well correlated to α and to the most positive atomic net charge on a hydrogen atom (Q_H ⁺; r² = 0.985; Table S6). Again, the PCDD with larger α values tend to have lower P_L values. The more chlorine atoms present in the parent structures, the greater α is, and thus the lower the P_L value is. Increasing Q_H ⁺ values leads to a decrease in P_L values because PCDD molecules with great Q_H ⁺ values also tend to have great intermolecular interactions that reduce volatilization (Zeng et al., 2013). The P_L of 11 chlorinated compounds was again well correlated to α, and Qzz (r² = 0.952; Table S6) but it has to be noticed that the number of data used to develop the equation is low (Staikova et al., 2004). For 72 PCDE, the relationship involved the number of chlorine atoms at different positions: the more the number of substituted chlorine atoms is, the lower the P_L value of PCDE is. Furthermore, P_L decreases with the different chlorine positions: N₂₍₆₎ < N₃₍₅₎ < N₄. This indicates that congeners with Cl substitutions in the ortho positions to the etherlink, that is, the (2, 6, 2, 6′) positions, have higher vapor pressures compared to those with Cl substitutions in the nonortho positions to the ether-link, that is, the (3, 5, 3, 5’) and (4, 4’) positions. Furthermore, for compounds with the same number of chlorine substitution, the values of P_L increases with the increase in pairwise of Cl atoms at meta position (N_m; Zeng et al., ²⁰⁰⁷). Finally, P_L of 107 PCDE was correlated to five quantum-chemical molecular electronegativity-distance vectors (M₁₁, M₁₂, M₁₃, M₂₃, M₃₃): M₁₁, M₁₃, and M₃₃ increase with the degree of chlorination, but M₂₂ decreases with increasing degree of chlorination. PCDE congeners with higher chlorination have lower P_L (Sun et al., 2007).

As observed in previous sections for S_W and K_OW, the combination of descriptors of different categories allows improvement in the assessment of P_L (Basak et al., 1997; Liang and Gallagher, ¹⁹⁹⁸; Table S6). Quantum-chemical descriptors were involved in almost all equations, combined with constitutional and/or geometric descriptors (Table S6). For 22 PBDE, P_L was well correlated to the molecular volume V, and to the sum of the surface maxima values of the electrostatic potential ΣV_s ⁺ (r² = 0.981; Table S6). Indeed, the larger PBDE molecule would yield stronger dispersion-type interaction between each other (lowering the volatility and liquid vapor pressure; Xu et al., ²⁰⁰⁷). For 107 PCDE, P_L can be estimated with N_Cl, ΣV_s ⁺, and σ² _tot (Xu et al., 2010), but also with MW, TE, α, and ΔH_f (Yang et al., 2003). Based on these descriptors, it can be concluded that P_L of PCDE congeners are mainly governed by the intermolecular dispersive interactions (Yang et al., 2003). The dispersion forces are a function of the molecule's polarizability, while hydrogen bonding can be facilitated by the presence of ‒OH, ‒NH, or ‒SH groups. Indeed, the addition of the number of polar functional groups ‒OH (n _OH), ‒C = O (n _{C = O}), ‒NH (n _NH), ‒COOH (n _COOH), ‒NO₂ (n _NO2), and ‒C≡N (n _C≡N) to the polarizability α allowed improvement of the estimate of P_L (r² = 0.960; Table S6; Liang and Gallagher, ¹⁹⁹⁸). The P_L of 17 benzenes was correlated to the molecular contact surface area (CSA) and to the solvation free energy (ΔGs): positive ΔGs coefficient and negative CSA coefficient agree with theory because increasing (negative) electrostatic interactions and increasing (positive) dispersion interactions both lead to decreasing P_L and thus decreasing volatilization (Schüürmann, 1995). For 411 compounds, a five-descriptor performing relationship (r² = 0.949; Table S6) was developed: the most important descriptor was the gravitation index (IG), and the second most important descriptor was the hydrogen-bonding donor charged surface area (HDCA(2)). The combination of IG and HDCA(2) adequately represents the forces of intermolecular attraction: IG is connected with the dispersion and cavity-formation effects in liquid, and HDCA(2) is connected with the hydrogen-bonding ability of compounds. The three additional descriptors were the maximum net atomic charge for a chlorine atom (MNAC(Cl)), the sum of the surface area of fluorine atoms (SA-2(F)), and the surface area of nitrogen atoms (SA(N)). The inclusion of these three descriptors in the model shows that the IG and HDCA(2) could not describe adequately the intermolecular interactions with solute molecules containing fluorine, chlorine, or nitrogen atoms (Katritzky et al., 1998). Finally, for 33 benzotriazoles, Bhhatarai and Gramatica (2011) developed a relationship based on combination of one constitutional number of rotatable bonds (RBN), and two topological descriptors (BCUT 2D descriptor encoding the lowest eigenvalue number 2 of the Burden matrix weighted by atomic polarizabilities, BELp2; and 2D binary fingerprint that corresponds to the presence of a N-Cl bond at topological distance 9, B09[N-Cl]). They found good results (r² = 0.809; Table S6).

Only two relationships were reported to estimate the solid vapor pressure P_S of 257 PCDD and PCDF, they involve the temperature (Ding et al., 2006; Table S6). The main factors governing P_S values, from important to less important, are temperature, intermolecular dispersive interactions (through α), entropic factor (through the Kier index S0K), and intermolecular dipole-dipole and dipole-induced dipole interactions (through μ).

The synthesis of these results shows that the polarizability α is a fundamental descriptor to explain the vapor pressure range of organic compounds and to estimate this parameter. No geometric-topological and no electro-topological descriptors were used in the equations.

3.3.2. Henry's Law Constant

Henry's law constant, K_H, is a physical property of a chemical that is a measure of its partitioning between two phases, air and water. Chemicals with low K_H will tend to stay in the aqueous phase, while those with high K_H will partition more into the gas phase. As air and water are the major compartments of the environment, and water is considered to act as a vector among air, soil, sediment, and biota, the knowledge of K_H is very important in assessing environmental risks associated with a chemical (Nirmalakhandan and Speece, ^1988b). Dearden and Schüürmann (2003) reviewed some of the methods developed for the estimation of K_H. This review is completed and updated in this section. The 17 equations reported in Table S6 involve from 1 to 10 descriptors. As for vapor pressure, the QSAR were developed for a wide diversity of organic compounds but not for pesticides.

Seven one-descriptor equations are reported in Table S6 to estimate K_H. For 15 PCDD, K_H was correlated to n _Cl: K_H tend to fall by a factor of 1.6 per chlorine added (Shiu et al., 1988). K_H was also correlated to geometric descriptors such as the molecular volume Vm for 15 PCDD (Shiu et al., 1988), or the TSA for 58 PCB (Brunner et al., 1990). With topological descriptors, QSAR were based on ⁴χ_pc for 58 PCB (Brunner et al., 1990), and on the highest eigenvalue number 7 of Burden matrix, weighted by Sanderson electronegativities (BEHe7) for 209 PBDE and HBB (Papa et al., 2009). BEHe7 brings 2D information which takes into account the weight of different atoms in the structure (Burden matrix) and their electronegativities (Papa et al., 2009). The quantum-chemical descriptor average of the sum of the surface minima values of the electrostatic potential (V⁻ _s,av) provided correct prediction of the K_H of 7 PBDE but based on a low number of compounds (r² = 0.929; Table S6; Xu et al., ²⁰⁰⁷). Finally, for 17 benzenes, a relationship was developed using the solvation free energy (ΔGs). An incomplete account of the cavity formation energy in water in the ΔGs term could have lowered the regression coefficient, which is nevertheless good (r² = 0.830; Table S6; Schüürmann, ¹⁹⁹⁵).

QSAR with several constitutional descriptors (n _Cl and n _{ortho Cl}) or with several MCI (⁴χ, ⁴χ_pc, or ⁶χ_pc) allowed good estimate of K_H of PCB (r² > 0.908; Table S6; Brunner et al., ¹⁹⁹⁰; Sabljic and Güsten, ¹⁹⁸⁹). Sabljic and Güsten showed that the degree of ortho-substitution was the major factor that governs the magnitude of K_H. In their model, this structural feature is described by ⁴χ whose size is proportional to the number of ortho-chlorine atoms. Its positive regression coefficient indicates that the PCB with the greatest ortho-substitution have higher K_H and show tendency to stay in the air. The second structural property that controls the K_H is the relative position of chlorine substituents (i.e., their distribution between two phenyl rings and their relative position within each ring). The accumulation of chlorine atoms on one phenyl ring in di- and trichlorinated biphenyls tends to increase the value of corresponding K_H. This structural feature is in part described by the ⁴χ_c whose size is proportional to the extent of adjacent substitution. Congeners which have chlorine substituents together have smaller K_H. The third structural feature identified to influence the K_H is the degree of branching. This feature is also described by ⁴χ_c, which is highly sensitive to changes in branching. The negative regression coefficient indicates that branching lowers the magnitude of K_H. Unfortunately, branching overlaps, to a certain degree, some of the structural features described previously (i.e., the extent of adjacent substitution; Sabljic, ¹⁹⁹¹; Table S6). For seven PBDE, K_H was correlated to two quantum-chemical descriptors: V⁻ _s,av and the equilibrium parameter of electrostatic potentials on molecular surface (ν). The correlation coefficient is high (r² = 0.998; Table S6), but the number of data points submitted to the regression is low. The larger ν value is, the better the balance between positive and negative electrostatic potentials is, and the smaller K_H is (Xu et al., 2007).

Meylan and Howard (1991) developed a bond contribution method based on 345 compounds to estimate K_H. The advantage of the bond contribution method is its ability to estimate K_H for many types of chemical structures. It is relatively accurate for predicting K_H for hydrocarbons, monofunctional compounds, and many multifunctional compounds. The major disadvantage is that inaccuracy is introduced by the occurrence of multiple polarizable groups. As chemical structures become more complex, the bond contribution method is more likely to become inaccurate. Comparing several methods of K_H estimation (experimental, bond contribution, MCI, and LSER), Brennan et al. (1998) found that the bond contribution method of Meylan and Howard (1991), and the use of MCI as done by Nirmalakhandan and Speece (1988b; see next paragraph), were the most performing ones.

As for vapor pressure, the combination of descriptors of different categories improves the estimate of K_H (Schüürmann, 1995; Table S6); and quantum-chemical descriptors were involved in almost all equations. Modarresi et al. (2007) developed a performing 10-descriptor QSAR for a wide set of 770 organic compounds (r² = 0.925; Table S6): the model involved four constitutional, one geometric, one geometric-electronic, and four quantum-chemical descriptors. The four constitutional descriptors were n _F, n _NO2, n _OH, and n_R6. The n _NO2 most probably represents hydrogen-bond acceptor ability, and the n _OH reflects molecular capability for hydrogen-bond acceptance or donation. The quantum-chemical descriptors, sum of absolute Ca and Cd values (hydrogen-bond free energy acceptor and donor factors, respectively) for all H-bond donor and acceptor atoms in molecule (ΣC_ad(o)), and largest Ca (hydrogen-bond free energy acceptor) factor value in molecule (Max(C_a(o))), demonstrated marked influences on the performance of the QSAR model. Inclusion of hydrogen bonding descriptors reveals that hydrogen bonding is the most important molecular feature of solvent-solute interaction in governing K_H of organic compounds in the air-water system. These results are consistent with the nature of water molecules as solvent, as they are very good hydrogen-bond acceptors and donors. Electrostatic intermolecular forces between solute and solvent molecules are characterized by the Geary autocorrelation-lag 1 weighted by atomic Sanderson electronegativities (GATS1e), the partial negative surface area (PNSA-1), and the relative positive charge based on quantum chemical partial charge (RPCG; Modarresi et al., 2007). For 31 PCB, Dunnivant et al. (1992) related K_H to two topological descriptors (path-three κ index ³κ, and ⁴χ) and three quantum-chemical descriptors (second moment of inertia SMI, second- and third-principal polarizability α₂ and α₃; r² = 0.899; Table S6). For 17 benzenes, K_H was found to be correlated to ΔGs and CSA (r² = 0.870; Table S6; Schüürmann, ¹⁹⁹⁵), and for 180 miscellaneous organic compounds K_H was correlated to α and MCI (⁰χ and/or ¹χ^v; r² > 0.932; Table S6; Nirmalakhandan and Speece, ^1988b). Finally, Goss (2006) used the TLSER equation to estimate the K_H of 408 miscellaneous organic compounds and obtained very good results (r² = 0.998; Table S6).

The temperature dependency of K_H was only taken into account in one model, developed from 456 miscellaneous organic compounds. This model is based on 45 parameters: 18 fragments, 26 correction factors, and 1 indicator (presence of halogen in 2-position to ring O as in polychlorinated dibenzodioxins or -furans). The correlation coefficient was found to be good (r² = 0.810; Kühne et al., ²⁰⁰⁵).

It has to be noticed that, after reviewing a large number of calculation schemes focusing on the K_H, Dearden and Schüürmann (2003) concluded that the prediction capability of the tested methods was found inferior to the expected one.

As a conclusion, no particular descriptor appeared to be more relevant than another one to estimate K_H. No geometric-topological and no electro-topological descriptors were used in the equations.

3.3.3. Octanol-Air Partition Coefficient

As indicated previously, the environmental fate of semivolatile organic compounds depends strongly on their distribution between different environmental compartments. Thus, accurate estimation and/or prediction of environmental distribution coefficients are essential. The octanol-air partition coefficient, K_OA, is a key descriptor of the distribution of semi-volatile organic compounds between the atmosphere and terrestrial organic phase (Zhao et al., 2005). Twenty-one QSAR allowing the assessment of K_OA are reported in Table S6, they involve from 1 to 16 descriptors. As for vapor pressures and Henry's constant, the QSAR were developed for a wide diversity of organic compounds but not for pesticides.

Four of the eight one-descriptor relationships involved topological descriptors (Table S6): MCI (¹χ^v, ²χ, ²χ^v), but the numbers of compounds used to develop the QSAR were very low (Zhao et al., 2005), or sum of topological distances between oxygen and bromine atoms (T(O…Br)) for 209 PBDE and HBB (Papa et al., 2009). The T(O…Br) descriptor gives a double structural information: its value increases according to both the number and the distance of bromine substituents, on each phenyl ring, from the oxygen ether. Thus, T(O…Br) also takes into account the information related to the position of the bromine atoms on the phenyl rings. For only six PBDE, K_OA was correlated to MW (Wania and Dugani, 2003), and for 22 phthalates, K_OA was correlated to the Le Bas molar volume (V_LB; Cousins and Mackay, ²⁰⁰⁰; Table S6). Then, for 82 chlorinated organic compounds, good estimate of K_OA was found using the polarizability α (r² = 0.979; Table S6; Staikova et al., ²⁰⁰⁴); and similarly good correlation was found with α for a low number of PCDD (r² = 0.983; Table S6; Zeng et al., ²⁰¹³). Increasing α value of PCDD molecule leads to increasing the K_OA values. Molecules with great α values may have great intermolecular dispersive forces with octanol molecules thus favoring partitioning into the octanol phase (Zeng et al., 2013). This is consistent with the previous results showing that P_L decreases when α increases (Liang and Gallagher, 1998; Table S6).

Combination of several topological (¹χ^v, ²χ, ³χ^v) or several quantum-chemical (largest negative net atomic charge on an atom q⁻, quadrupole moment Qzz, α, μ) descriptors led to good estimate of K_OA of PBDE, polychlorinated naphthalenes and chlorinated organic compounds (r² > 0.927; Table S6; Staikova et al., ²⁰⁰⁴; Wang et al., ²⁰⁰⁸; Zhao et al., ²⁰⁰⁵).

All the equations based on descriptors of different categories involved quantum-chemical descriptors (Table S6). It is not possible to determine if the combination of several descriptors of several categories improved the prediction of K_H as no result has been published to allow a rigorous comparison. For 22 PBDE, K_OA was very well correlated to the molecular volume V and to the sum of the surface maxima values of the electrostatic potential (ΣV_s ⁺; r² = 0.976; Table S6). The V term means that the larger PBDE molecule would yield stronger dispersion-type interactions with the octanol molecule (i.e., the K_OA value becomes larger; Xu et al., ²⁰⁰⁷). For 16 hydroxylated polybrominated diphenyl ethers (OH-PBDE) and eight methoxylated polybrominated diphenyl ethers (MeO-PBDE), K_OA was estimated with six descriptors: electronic energy (EE), E_LUMO, MW, the largest positive atomic charge on a bromine atom (Q_Br+), the most positive atomic net charge on a hydrogen atom (Q_H ⁺), and μ. The descriptors MW and E_LUMO were the two most important factors governing K_OA values. Increasing MW, Q_Br ⁺, Q_H ⁺, and μ of OH-PBDE and MeO-PBDE led to the increase in K_OA. On the contrary, increasing E_LUMO and EE can lead to the decrease in K_OA (Chen et al., ^2001d; Chen et al., ^2003a; Zhao et al., ²⁰¹⁰). Similarly, for 209 PCB, increasing CCR, MW, most positive net atomic charge on a chlorine atom (q_Cl), and α values of the PCB led to increasing K_OA, whereas increasing EE, total energy (TE), and standard heat of formation (ΔH_f) values of the PCB led to decreasing K_OA. In this case, the α was the most significant descriptor. The more chlorines in PCB molecules, the larger the size of PCB molecules, the greater the MW, and the greater the α and K_OA values. E_LUMO was also a significant descriptor, and increasing E_LUMO of the PCB leads to decreasing K_OA. E_LUMO measures the ability of a molecule to accept electrons in intermolecular interactions: molecules with a low E_LUMO tend to easily accept electrons. So the lower the E_LUMO values, the greater the tendency of PCB molecules to accept electrons in intermolecular interactions, the greater the intermolecular interactions between PCB and octanol molecules, and thus the greater the K_OA values (Chen et al., ^2002a).

Some relationships were developed taking into account the temperature (Chen et al., ^2002b; Chen et al., ^2003b; Chen et al., ^2003c; Chen et al., ²⁰⁰⁴; Table S6). Very good results were obtained for both correlations done with a small and a high number of compounds (r² > 0.918; Table S6). The most significant descriptors were still E_LUMO, MW, TE, and α. As observed previously, increasing α and MW leads to increasing K_OA values, while increasing TE, and E_LUMO leads to decreasing K_OA.

As for the vapor pressure, the polarizability α is the descriptor that explains the best the variation of K_OA. The molecular weight MW, the dipole moment μ, and the E_LUMO and EE energies also play an important role. No geometric-topological, no geometric-electronic, and no electro-topological descriptors were used in the equations.

3.3.4. Potential of Transfer to the Atmosphere

Only one equation was found to estimate the potential of transfer of organic compounds to the atmosphere (Table S6). For 135 pesticides, Gramatica and Di Guardo (2002) developed a VIN allowing a preliminary ranking of the pesticides according to their tendency to distribute in the atmosphere. The VIN was well correlated (r² = 0.771) to three constitutional descriptors (HY, number of multiple bonds (nBM), number of rings No^RING), two topological descriptors (⁰χ^v, mean information content index on vertex degree equality I^E _deg) and one geometric descriptor asphericity (ASP) (Table S6). The most important descriptor is HY, which is related to the presence of hydroxyl groups in the molecule. Then, the next most important descriptors are ⁰χ^v and nBM, whereas the least important one is I^E _deg.

3.4. Retention Processes

The mobility of organic compounds in the environment mainly depends on their retention on soils and sediments, which is essentially determined by adsorption. Therefore, retention is one of the most important processes that control the fate of organic compounds in the environment because it regulates their availability for degradation, absorption by plants and for transfer toward ground and surface water, and air. In this section, only the adsorption of organic compounds at the liquid-solid interface, the most important retention process, is considered (Katayama et al., 2010).

A total of 102 QSAR are inventoried for adsorption on soils, and 38 QSAR for the adsorption on sediments. The nonlinearity and nonequilibrium of adsorption, and the desorption were rarely studied by QSAR approaches: only 18 equations were found for these phenomena (Table S7). Finally, a small number of equations (6) has been published to estimate the potential of transfer of organic compounds to groundwater, and no equation has been published concerning the potential of transfer to surface water (Table S7).

3.4.1. Adsorption Processes

3.4.1.1. Adsorption on Soils

To estimate the adsorption of organic compounds on soils, the QSAR were generally developed for Koc (adsorption coefficient normalized to soil organic carbon content; e.g., Doucette, ²⁰⁰³; Gawlik et al., ¹⁹⁹⁷; Wauchope et al., ²⁰⁰²), and few of them were developed for Kom (adsorption coefficient normalized to soil organic matter content; Briggs, ¹⁹⁸¹; Sabljic, ¹⁹⁸⁷ and 1989; Sabljic and Piver, ¹⁹⁹²), Kf (Freundlich adsorption coefficient; Hance, 1969; Jin et al., ¹⁹⁹⁷), Kd (linear adsorption coefficient; Hansen et al., ^1999a; Hu et al., ¹⁹⁹⁵), or K_L (Langmuir adsorption coefficient; Mon et al., 2006; Table S2). The reviews of Doucette (2003), Gawlik et al. (1997), and Wauchope et al. (2002) are completed and updated in this section. In addition, the present review is focused on QSAR only based on structural molecular descriptors.

The number of descriptors used for the estimation of adsorption coefficients ranged from 1 to 11, excluding QSAR based on the fragment approach (Table S7). The increase in the number of descriptors does not improve the significance of the QSAR but the degree of correlation rather decreases with increasing heterogeneity of the training set (Reddy and Locke, ^1994a, 1994b; Wauchope et al., ²⁰⁰²). The QSAR equations that are reported in Table S7 were developed for a wide diversity of organic compounds.

The prediction of the adsorption with only one descriptor mainly involved the MCI (Table S7), and in particular a lot of equations involved ¹χ and ¹χ^v to estimate the Koc, Kom, or Kd of many organic chemicals (Bahnick and Doucette, 1988; Baker et al., ¹⁹⁹⁷; Baker et al., ²⁰⁰¹; Dai et al., ¹⁹⁹⁹; Doucette, ²⁰⁰³; Gawlik et al., ¹⁹⁹⁷; Gerstl and Helling, ¹⁹⁸⁷; Gerstl, ¹⁹⁹⁰; Hu et al., ¹⁹⁹⁵; Liu and Yu, ²⁰⁰⁵; Meylan et al., ¹⁹⁹²; Müller and Kördel, ¹⁹⁹⁶; Sabljic, ¹⁹⁸⁴, 1987, 1989, 2001; Sabljic et al., ¹⁹⁹⁵; Sabljic and Piver, ¹⁹⁹²; Thomsen et al., ¹⁹⁹⁹; Von Oepen et al., 1991; Wauchope et al., ²⁰⁰²). The r² are highly variable depending on the classes and on the number of compounds used to develop the relationship (r² ranges from 0.006 to 0.973; Table S7), and it seems that the inclusion of polar compounds in the dataset led to a decrease in r². Some correlations were also found between the Koc and ⁰χ, ⁰χ^v, ²χ, ²χ^v, ³χ^v, or ⁵χ^v for different classes of organic compounds (pesticides, alcohols; Baker et al., 1997; Gerstl and Helling, ¹⁹⁸⁷; Müller and Kördel, ¹⁹⁹⁶), and between the K_L and ⁹χ for only nine dye tracers (Mon et al., 2006). Indeed, MCI encode intermolecular accessibility, and, for example, ¹χ correlates very well with the molecular surface, and also represents the contribution of one molecule to the bimolecular interactions arising from encounters of bonds among two molecules (Kier and Hall, 2000; Sabljic and Piver, ¹⁹⁹²). Other topological descriptors were used successfully to estimate the Koc: the CRI for 36 various compounds (r² = 0.964; Türker Saçan and Balcioğlu, 1996), and the Lu index for only 11 phthalates (r² = 0.788; Lu, ²⁰⁰⁹; Table S7). The Koc could also be estimated using MW (Kanazawa, 1989; Liu and Yu, ²⁰⁰⁵), the TSA (Doucette, 2003; Hansen et al., ^1999a), and the volume of the molecules: molar volume Vm (Von Oepen et al., 1991); parachor P (Hance, 1969; Briggs, ¹⁹⁸¹) or van der Waals volume VdW (Hu et al., 1995). A larger molecular volume is unfavorable for partitioning to the aqueous phase where strong hydrogen bonds have to be broken to create room for the solute molecule (Baker et al., 1997; Briggs, ¹⁹⁸¹). However, the correlations with Vm were not good in some soils for acids and amines (r² < 0.360; Von Oepen et al., 1991). Finally, Baker et al. (1997), Liu and Yu (2005), and Von Oepen et al. (1991) tried to establish correlations with only one topological (second- (Δ²χ) or third-order (Δ³χ) simple nondispersive force factor), or one quantum-chemical descriptor (self-polarizability ALP, probability of nucleophilic attack D^N, E_HOMO, E_LUMO, MR, net negative atomic charges on atom N in anilines or atom O in phenols q, average charge of molecule Q_ave, total charge of molecule Q_tot, α, and μ) but the correlation coefficients were sometimes very low, and depended on soil characteristics (Table S7).

The combination of several MCI allowed acceptable estimates of Koc (r² ranges from 0.575 to 0.905; Table S7; Baker et al., ²⁰⁰¹; Gerstl, ¹⁹⁹⁰; Gerstl and Helling, ¹⁹⁸⁷; Tao and Lu, ¹⁹⁹⁹; Uddameri and Kuchanur, ²⁰⁰⁴). Nevertheless, the QSAR only based on MCI were not suitable for polar organic chemicals, and polarity correction factors have to be introduced in the equations to improve the prediction (Meylan et al., 1992; Müller and Kördel, ¹⁹⁹⁶; Sabljic, ¹⁹⁸⁷; Tao and Lu, ¹⁹⁹⁹). The results may be erroneous if an estimate is desired for a compound that has a polar group for which there was not enough data to develop a polarity correction factor (Baker et al., 1997). Good correlations were also found between the Koc and several topological indices (¹χ and sum over all atoms of the intrinsic state differences DELS, Lu index, and different distance-based atom-type topological index DAI; r² > 0.900; Table S7; Gramatica et al., ²⁰⁰⁰; Lu et al. ²⁰⁰⁶). To take into account the nonhydrophobic contribution to Koc, Bahnick and Doucette (1988) included, in addition to ¹χ, a first-order valence nondispersive force factor (Δ¹χ^v). The two descriptors relate to intermolecular interactions due to molecular size and nondispersive effects, and are important in predicting Koc for molecules exhibiting substantial hydrophilicity. These nondispersive factors were also used by Baker et al. (1997) for 14 miscellaneous compounds (Table S7). A relationship based on constitutional descriptors, 24 structural correction factors (e.g., number of triple bond or number of quaternary carbon) and 74 group fragments, allowed a robust assessment of the Koc of a wide variety of organic compounds (r² = 0.969; Table S7). These results confirmed the ability of the fragment approach to predict Koc of untested chemicals (Tao et al., 1999). Thomsen et al. (1999) developed a concept of grouped E-state index, and in particular, they showed that the Koc of eight phthalates is correlated to S_ester and S_alkyl that consider the polar/hydrophilic and nonpolar/hydrophobic effects, respectively (r² = 0.822; Table S7). However, the number of data used to develop the relationship was low. Finally, for 387 miscellaneous compounds, the Koc was estimated using several moment descriptors (M₀, M₂, M₃, M_acc, M_don; Klamt et al., 2002), and for 65 PCOC, the relationship based on several quantum-chemical descriptors such as E_HOMO, TE or μ showed good results (r² = 0.854; Table S7; Dai et al., ¹⁹⁹⁹; Table S7).

As observed for S_W, K_OW, P_L, and K_H in previous sections, when several descriptors of different categories are used together, the assessment of the adsorption coefficients is improved (Reddy and Locke, ^1994a). Reddy and Locke (1994a) obtained better correlations between Koc and E_HOMO, VdW, α and μ for 71 herbicides than with the volume alone (Table S7). The combination of some constitutional descriptors (MW, structural fragments) and topological (MCI, bond connectivity index) and/or electro-topological descriptors led to correct estimations of Koc for a lot of organic compounds (r² > 0.772; Table S7; Huuskonen, ²⁰⁰³; Lohninger, ¹⁹⁹⁴; Schüürmann et al., ²⁰⁰⁶). Sekusak and Sabljic (1992) introduced the number of polar (No^PP) and nonpolar parts (No^NP) in a molecule, the number of rings (No^RING), and the polarity index (¹ _Fχ^v), and found good correlations for 11 amides, 15 triazole, 16 dinitroanilines, and 21 acetalinides (r² > 0.846; Table S7). For 44 substituted phenylureas, the estimation of Koc based on VdW, μ and E_LUMO was correct (r² = 0.700; Table S7) but the range of experimental data and/or structural differences among substituted phenylureas in terms of substitution on N3 atom was narrow (Reddy and Locke, ^1994b).

Gramatica et al. (2000) developed several equations based on a representation of molecular structure by different types of descriptors, such as count descriptors, topological indices, information indices, fragment-based descriptors, and WHIM descriptors. For example, the Koc of 29 carbamates was correlated to the presence of electronegative atoms in the molecules: the greater the number of electronegative atoms in the molecule, the higher the probability of H-bonding with water, leading to a decrease in soil adsorption; and to the eccentric connectivity index (ξ_C): the size increase leads to increased hydrophobic effects and compound tendency to bind with the soil organic matter. The Koc of 43 phenylureas were well correlated to the MW, n _Cl, and No^RING, and to two directional WHIM descriptors (r² = 0.911; Table S7). Most of these descriptors indicated that an increase in phenylurea size favors their adsorption.

Several other relationships were established with various descriptors: scanning a very large number of molecular descriptors (1,457), Goudarzi et al. (2009) identified seven descriptors leading to accurate prediction of the Koc of 62 pesticides: three 2D descriptors (one BCUT index: BEHm2, and two Moran autocorrelation descriptors: MATS6e and MATS4p) and four 3D descriptors (one GETAWAY: HTp, one MoRSE: Mor(05)m, and two WHIM: G1m and G3v; Table S7). Winget et al. (2000) developed a set of effective solvent descriptors that characterize the organic carbon component of soil, and combined these descriptors with solute atomic surface tension parameters to predict the Koc of any solutes composed of H, C, N, O, F, P, S, Cl, Br, and I. However, the errors in predicting experimental data were greater than those resulting from other methods. Nevertheless, the developed models do not use different parameter sets for different classes of solutes, and thus are applicable to totally new classes of molecules. In addition, no experimental data are needed for a new compound once the molecular structure is known, and since the resulting solvent descriptors have reasonable values, it is possible to understand the sources of different partitioning phenomena in cases where the results exhibit significant fragment interactions.

Finally, the LSER and TLSER approaches, based on a mechanistic understanding of the partition process (section 2.8), were also efficient for the estimation of the Koc (r² > 0.720; Table S7; Baker et al., ¹⁹⁹⁷; Famini and Wilson, ¹⁹⁹⁷; Feng et al., ¹⁹⁹⁶; Poole and Poole, ¹⁹⁹⁹; Xu et al., ²⁰⁰²). In any case, the leading terms in the equations were those that measure cavity formation (the intrinsic volume V_i or the McGowan characteristic molecular volume V_x), and the overall or summation solute hydrogen bond basicity (Σβ₂ ^H or Σβ₂ ^O). The correlation coefficient seems to decrease with the heterogeneity of the compounds in the dataset (Table S7).

As a conclusion, it was shown that the prediction of adsorption of organic compounds in soils mainly depends on MCI and especially on ¹χ, ¹χ^v, and ³χ^v, but also on MW and on descriptors related to the volume (P, V_i, Vm, VdW). Indeed, compounds with high branching properties and high volume are less susceptible to partition in the aqueous phase. No geometric-electronic descriptor was used in the equations.

3.4.1.2. Adsorption on Sediments

The 38 QSAR equations reported in Table S7 allow the assessment of seven parameters related to the measurement of the adsorption on sediments: the association coefficient between PCB and humic marine substances (K_h), the Freundlich adsorption coefficient (Kf_s), the linear adsorption coefficient (Kd_s), the adsorption coefficient normalized to sediment organic carbon content (Koc_s; or total organic carbon normalized sediment-porewater distribution coefficient K_TOC), the sediment water partition coefficient (K_S/W), and the maximum concentration of the compound that can be adsorbed (C_sm; Tables S2 and S7). The equations involve from one to four descriptors, the majority of them involve one or two descriptors. Contrary to adsorption on soils, there is notably no QSAR for pesticides (Table S7). In general, the number of compounds used for the QSAR development was very low.

The 28 one-descriptor equations developed to estimate the adsorption on sediments involve constitutional, geometric, topological, or quantum-chemical descriptors (Table S7). For chlorobenzenes, PCDD and PCDF, Arp et al. (2009) found correlations between the K_TOC and n _Cl, and for PAH, they found a relation between the K_TOC and n _aromatic-C. However, the number of compounds used in these QSAR was not indicated in their study. The Koc_s and C_sm of 5 chlorobenzenes on sediment was very well correlated to the molar volume Vm (r² > 0.890; Table S7), but the number of chemicals used to develop this relationship was low (Von Oepen et al., 1991). Similarly, Vm was well correlated to the Koc_s of esters, acids, and amides (not with that of amines), but the number of data was also very low (Djohan et al., 2005). For 26 PCB, Lara and Ernst (1989) found better correlation between the K_h and the TSA calculated for the planar configuration (r² = 0.954) of the PCB than with the nonplanar configuration (r² = 0.919; with phenyl rings perpendicular to each other; Table S7). However, a disadvantage of using molecular surface areas as structural descriptors is that the molecular geometry has to be well known (Sabljic et al., 1989) and, indeed, bad correlations were found between the Kf_s of eight organotin (organometallic species) and the TSA (r² = 0.095; Table S7; Sun et al., ¹⁹⁹⁶). Bad correlations were also obtained with several MCI or the Leo fragment constant (π; r² < 0.135; Table S7; Sun et al., ¹⁹⁹⁶), and, similarly, there was no good correlation between MCI and the Kd_s of 11 naphthoic acids and five quinoline compounds (r² < 0.220; Table S7; Burgos and Pisutpaisal, ²⁰⁰⁶). The authors rather observed that the adsorption of naphthoic acids increased with the addition of ortho-substituent groups and with increasing chain length of the acid group, and that the adsorption of quinoline decreased with substituent group addition (except for nitro group) and with additional heterocyclic N atoms, but they did not develop any QSAR. On the contrary, for several esters, acids, amides and amines, Von Oepen et al. (1991) found some satisfactory correlations between Koc_s and ¹χ, ¹χ^v, self-polarizability (ALP), probability of nucleophilic attack (D^N), average charge of molecule (Q_ave), or total charge of molecule (Q_tot), but it depended on the soil and the number of data was low (Table S7).

The seven equations developed with several descriptors of the same category involved constitutional, topological, or quantum-chemical descriptors (Table S7). For PCB, the K_TOC was correlated to n _Cl and to n _{ortho Cl}. Orthochlorine atoms cause the planar conformation of PCB to be energetically unfavorable, which in turn causes lower adsorption (Arp et al., 2009; Hawthorne et al., ²⁰¹¹). Using MCI, Sabljic et al. (1989) found good correlations between the K_h of 26 PCB and ¹χ, following a quadratic function (r² = 0.948; Table S7). These results show that the adsorption of PCB on marine humic substances is primarily influenced by the size of molecule which is described by ¹χ: the larger PCB molecules showed a higher affinity for humic Q_tot substances than smaller ones. For 11 alcohol ethoxylates (Kiewiet et al., 1996) and for 31 alcohol ethoxylates and four other alcohols (Van Compernolle et al., 2006), the Kd_s was found to be correlated to the ethoxylate chain length (#EO), and to the alkyl chain length (#C). The dominant influence of the alkyl chain suggests a hydrophobic adsorption mechanism (Table S7).

For 26 PCB, the addition of the number of orthochlorine substituents (n _oCl) to MCI improved the prediction of K_h (r² = 0.990; Table S7; Sabljic et al., ¹⁹⁸⁹). The negative regression coefficient of n _oCl indicates that the adsorption decreases with the degree of ortho substitution: n _oCl provides an estimate for the extent of nonplanarity of PCB. Thus, it may be viewed as third dimension corrections for the ¹χ index that is unable to completely handle 3D situations (stereochemistry). However, this term limits the value in modeling the adsorption for other classes of nonionic chemicals with dissolved humic substances, as the n _oCl is specific for PCB. The quadratic relationship also indicates that each new chlorine substituent increases the extent of adsorption less than the previous one (Sabljic, 1991, 2001). Combining topological and quantum-chemical descriptors, Dai et al. (2000) showed that the Koc_s of 14 substituted benzaldehydes was well predicted with Q_H ⁺, μ, ²χ^v and ³χ_pc (r² = 0.922; Table S7). The dipole moment μ was the most significant descriptor.

He et al. (1995) used the LSER approach to estimate the Koc_s of 28 phenylsulfonyl acetates, and found excellent results (r² = 0.976; Table S7). The intrinsic volume V_i was a leading term in the adsorption of these compounds on sediments. Finally, with the MTLSER approach, Chen et al. (1996a) showed, for 22 alkyl(1-phenylsulfonyl)cycloalkane-carboxylates, that α and μ were leading terms influencing the Koc_s. The polarizability α is in direct proportion to the intrinsic molecular volume, and therefore it increases the Koc_s since the larger molecules would tend to be excluded from the water and be adsorbed on the sediments. The dipole term decreases the Koc_s probably because greater dipole would increase interactions between the solutes and more polar water, increasing solubility in water.

As for the adsorption on soils, the variations of the adsorption of organic compounds on sediments are mainly represented by MCI (mainly ¹χ, and ¹χ^v). No geometric-topological, no geometric-electronic, and no electro-topological descriptors were used in the equations.

3.4.1.3. Nonlinearity of Adsorption

The nonlinearity of adsorption is indirectly taken into account in the QSAR designed to assess the Kf or K_L. However, there is no estimation of the parameters such as n_f, the Freundlich exponent.

Only Droge et al. (2009) tried to develop QSAR describing the nonlinearity of adsorption. They proposed to consider the nonlinear adsorption of nine alcohol ethoxylates into the illite clays and sediments using a dual-model combining a Langmuir (K_Ls) and a linear (K_II) adsorption term. They showed that both adsorption coefficients are correlated to the ethoxylate chain length #EO and to the alkyl chain length #C (r² > 0.910; Table S7). The K_Ls increases with both chain lengths, on the contrary, the K_II slightly decreases with #EO. This probably results from the increased solubility with longer ethoxylate chains and because sorbate-sorbate interactions mainly occur via the alkyl chain, leaving the ethoxylate chains solvated with water. For illite, the increase in K_Ls with both chain lengths is consistent with adsorption mechanism that depends on both hydrophobic properties and polar interactions with the surface. The enhanced nonlinearity of isotherms with longer ethoxylate chains is explained by both an increasing adsorption coefficient and a decreasing bilayer formation affinity with additional ethoxylate units (Droge et al., 2009).

3.4.1.4. Nonequilibrium Adsorption and Desorption

Very few results have been published concerning the nonequilibrium adsorption and the desorption of organic compounds, and only 14 equations were found: 13 for nonequilibrium adsorption and one for desorption (Table S7).

Brusseau (1993) and Hu et al. (1995) demonstrated that the nonequilibrium adsorption in soils of several classes of compounds (PAH, pesticides), measured through a mass transfer coefficient (MT), was correlated to ¹χ^v (r² > 0.830), and to a lesser extent to the VdW (r² > 0.700). Indeed, most of the rate-limited adsorption behavior can be explained by accounting for the size and structure of the solute molecule. However, it has to be noticed that few compounds were used to develop the QSAR (Table S7).

Colón et al. (2002) studied the adsorption kinetics in sediment slurries of 21 anilines with substituents in the ortho, meta or para positions. They introduced fast and slow rates of adsorption (k_fast, k_slow) because the adsorption kinetics of the substituted anilines were characterized by an initial, rapid adsorption process followed by a much slower adsorption process. The rates of adsorption were correlated to the E_HOMO or to the one electron oxidation potentials (E₁), however the correlation coefficients were not very high (r² < 0.598; Table S7).

Only one equation was found for the desorption (Table S7): assuming a reversible adsorption, Hsieh and Mukherjee (2003) showed that the desorption of six halogenated aliphatic hydrocarbons from biosolids was very well related to ¹χ (r² = 0.979; Table S7), but the number of data is low. There is no result concerning the estimation of the desorption when the adsorption is partially irreversible.

3.4.2. Potential of Transfer to Ground and Surface Waters

Transfer of organic compounds to ground and surface waters first depends on their availability to be leached through the soil profile or to be mobilized by runoff water. This availability for water extraction changes with time since the compound has reached the soils either directly or indirectly, due to retention and degradation processes, and to climatic and soil conditions that enhance or inhibit these two processes (Louchart and Voltz, 2007; Sharer et al., ²⁰⁰³; Walker et al., ²⁰⁰⁵). It is therefore difficult to derive organic compound transfer properties on the basis of time-variable environmental parameters such as Koc and half-life (DT50). A few authors defined time-varying environmental parameters equivalent to Koc, taking into account a reference Koc, and either the time (Beigel et al., 1997; Renaud et al., ²⁰⁰⁴) or the cumulative rainfall (Louchart and Voltz, 2007), as organic compound application. Nevertheless, a few indicator or parameter of the potential for organic compound to be transferred toward water bodies have been developed on the basis of constant Koc and DT50 values (Gustafson, 1989; Rao et al., ¹⁹⁸⁵).

The occurrence of organic compound in both ground and surface waters also depends on the water fluxes through the soil and at the soil surface, respectively. In fact, water fluxes are driven by meteorological conditions, soil hydrodynamics and initial soil water profile, and soil surface characteristics. This occurrence is classically estimated by means of complex mathematical fate models that take into account these water fluxes, and the environmental parameters such as DT50 and Koc, that can be derived from QSAR models. But the use of such model is time consuming and do not permit to simulate the occurrence of each organic compound in water bodies easily. Another approach is to use QSAR to estimate the occurrence of organic compounds in groundwater (Worrall, 2001; Worrall and Thomsen, ²⁰⁰⁴). However, the number of QSAR that have been developed is very low: only six equations were found to estimate the potential of transfer to groundwater (Table S7), and no relationship was found to estimate the potential of transfer to surface water. In addition, these QSAR were only built with pesticides data, no equation has been developed for other organic compounds that are susceptible to reach groundwater (e.g., pharmaceuticals, PCB).

To assess the potential transfer of pesticides to groundwater, the leaching index (LIN) was developed by Gramatica and Di Guardo (2002) in order to give a preliminary ranking of these compounds according to their tendency to distribute in different environmental media. For 135 pesticides, LIN was correlated to three constitutional (n _X, n _NO2, n _S), one topological radial centric information index (ICR), and one electro-topological (constitutional descriptor of the mean E-state of the molecule related to the polarizability, Ms) descriptors with satisfactory model performance (r² = 0.870; Table S7).

To distinguish polluting from nonpolluting compounds, only on the basis on molecular topology and/or quantum-chemical descriptors, Worrall (2001) and Worrall and Thomsen (2004) used a dataset of 56 pesticides monitored in 303 boreholes across 12 states in the midwestern United States during 1991–1992. With logistic regression, they estimated the probability of finding these pesticides at a level concentration > 0.1μg L⁻¹, θ, using ⁶χ^v and ⁷χ^v _pc, the hydration energy ΔH_hyd, and the dipole moment μ, which gave good results (r² = 0.910; Table S7). Furthermore, they obtained more than 85% of variance explanation by considering the rule that a compound can be found in groundwater if ⁶χ^v < 0.55 (Worrall, 2001) or if 0.28 μ < ⁶χ^v (Worrall and Thomsen, 2004). They concluded that the dependence of leaching potential on the descriptors that control solubility (μ and ΔH_hyd) indicates that predictions of environmental fate based on this approach may represent a strong alternative to the use of adsorption and degradation parameters.

3.5. Degradation Processes

Degradation is one of the key processes governing the fate of organic compounds in the environment as it determines their removal and/or transformation to metabolites, conditioning their persistence and transfer to different components of the environment (soil, water, sediment, plant, or air). The degradation can be biotic (following degradation by living organisms including microorganisms) or abiotic (hydrolysis, photolysis). The QSAR that have been found to assess both types of degradation processes are reviewed here.

3.5.1. Biodegradation

The structure of this section is slightly different from the structure of the others because, contrary to other processes, the biodegradation of organic compounds can be estimated using a wide range of environmental parameters (Table S2), and nonetheless few QSAR equations were developed for each parameter (Table S8). Indeed, as explained in the following paragraphs, the measurement of the biodegradation of organic compounds can be done according to different methods and in different experimental conditions relying on the use of artificial media to test degrading activity of pure bacterial cultures under laboratory conditions or of more complex natural matrices such as soils, sediments, or water, or man-made matrices such as wastewater or activated sludge incubated under controlled conditions; leading to the determination of different kinds of QSAR. A total of 75 equations is reported in Table S8 for a wide diversity of compounds.

Microbial biodegradation is often considered as the major driving force of the fate of organic compounds in the environment. It is the result of aerobic or anaerobic enzymatic activities of microorganisms. Biodegradation acts on the transformation of organic compounds (primary degradation with production of metabolites), and on their removal (mineralization or ultimate degradation refers to the complete degradation of an organic species to stable inorganic species) from the environment as well. Consequently, biodegradation determines the persistence of organic compounds. Persistence is defined by the length of time a compound remains in an environmental compartment before it is transported to another one or is chemically or biologically transformed. As persistence is a usual criteria used in regulatory bodies, the estimation of the biodegradability (ability of a compound to be biodegraded), which is one way to define such criteria (a substance that is easily degraded is considered non persistent) is fully developed particularly with in silico models such as QSAR. The biodegradation ability can be experimentally determined by measuring half-lives of organic compounds in experimental tests conducted under environmental conditions. The main guidelines are given by Organization for Economic Cooperation and Development (e.g., Organization for Economic Cooperation and Development, 1992, 2009). These experimental results are highly dependent on the environmental conditions found in the matrix (temperature, water content, pH, redox potential, oxygen, substrates, salinity, trace element type, and concentration), on the nature of the microbial community (diversity, density, activity), and on the tested chemicals (structure, concentration). All these aspects are fully discussed in Howard (2000). Some of the available sources of biodegradation databases are given by Pavan and Worth (2008). The two most famous databases used in recent QSAR development are the MITI-I database made of the information on more than 1000 chemicals from one uniform biodegradation test, and the BIODEG database developed by the U.S. Environmental Protection Agency (EPA) and Syracuse Research Corporation (SRC) containing biodegradation information on 815 chemicals.

From these databases, the training sets used in QSAR development are more qualitative data than those issued from the standardized OECD tests. These tests measure either oxygen consumption, or CO₂ production, or disappearance of dissolved carbon by comparison to that resulting from easily mineralized compound such as sodium acetate. This type of test results in the classification of chemicals into two main categories readily biodegradable and not readily biodegradable. These categories can be divided to give biodegrades fast, biodegrades fast after acclimation, biodegrades slowly, biodegrades slowly even after acclimation or biodegrades sometimes (Rücker and Kümmerer, 2012). Each classification is rated according to the quality of the summarized data on one chemical, with rate 1 (three consistent results), 2 (at least two consistent results), and 3 (one result only or severely conflicting results). This results in two types of data used in QSAR development: either quantitative data such as half-lives (DT50), biodegradation rates, or kinetic constants (BS, k, K, k_b, k_x/k_h, RC), theoretical oxygen demand (%ThOD), biological oxygen demand (BOD), or qualitative data using Boolean-type logic (BM; 1 for readily biodegradable and 0 for not readily biodegradable; Table S2).

The first QSAR and quantitative structure biodegradability relationship (QSBR) models were developed in the 1980s on chemicals with similar structure (homologous models). They were based on octanol/water partition coefficients, Hammett constants or alkaline hydrolysis rate constants not considered there (Peijnenburg, 1994; Yonezawa and Urushigawa, ¹⁹⁷⁹), or on molecular descriptors such as MW (Boethling, 1986), van der Waals radius (Y_VdW; Paris and Wolfe, ¹⁹⁸⁷; Paris et al., ¹⁹⁸³), MCI (²χ, ²χ^v, ³χ, ³χ_c, ³χ^v, ³χ^v _c, ⁴χ, ⁴χ_c; Boethling, ¹⁹⁸⁶), and charge difference in the modulus charges on the atom of specified bonds (Δδ_x−y; Dearden and Nicholson, ¹⁹⁸⁶, 1987) that were well correlated to biodegradability endpoints (r² > 0.722; Table S8). Some equations were also found using E_HOMO, E_LUMO, IP, μ, and charges (Peijnenburg, 1994). However, these models were often limited in terms of applicability, prediction (class specific compounds and few numbers of compounds) and quality of datasets.

The construction of the two high-quality biodegradation datasets in the 1990s (BIODEG and MITI databases) led to the development of more reliable and accurate biodegradation prediction models. This was also facilitated by the application of new and advanced modeling approaches such as multivariate techniques such as principal component analysis (PCA) and partial least square analysis (PLS), nonlinear neural network, artificial intelligence, computer-automated structure evaluation (CASE), or empirical knowledge. These allowed the development of heterologous models describing the degradability of compounds displaying varying chemical structures.

The majority of these models are based on one category of descriptors which are functional groups or structural composition of chemicals combined or not with the molecular weight MW: indeed the so-called group contribution models (OECD hierarchical approach, Biodegradation Probability Program-Biowin 1–7 models) are based on the counts of structural/substructural fragments (number of carboxyl, hydroxyl, unsubstituted aromatic, phosphate ester). The 40-year work of Howard, Boethling, and collaborators (Table S8) contributed to the development of the most used models in predicting aerobic degradation in water, the Biowin models, that are based on constitutional descriptors: MW and 36 or 42 defined chemical substructures (Boethling, 1986; Boethling et al., ¹⁹⁹⁴; Howard, ²⁰⁰⁰, 2008; Howard et al., ¹⁹⁹¹; Howard et al., ¹⁹⁹²; Howard et al., ²⁰⁰⁵; Meylan et al., ²⁰⁰⁷; Sabljic and Peijnenburg, ²⁰⁰¹; Tunkel et al., ²⁰⁰⁰). Loonen et al. (1996, 1999) proposed a similar ready/nonready aerobic categorization but using a PLS model based on a bigger training set (894 substances) and 127 predefined substructures. All these group contribution models present an acceptably accurate prediction with only a single set of chemical substructures (for models performances comparison, see Pavan and Worth, ²⁰⁰⁸; Raymond et al., ²⁰⁰¹; Rorije et al., ¹⁹⁹⁹; Rücker and Kümmerer, ²⁰¹²). As indicated in the previous sections, the main drawback of this method is the nonprediction for compounds that did not contain any of the substructures. In order to overcome this drawback, models (MultiCASE approach) were developed based on the random generation of all fragments (all linear and terminally branched substructures), and the most significant ones were statistically correlated to the endpoint (Klopman, 1992). The fragments that activate the aerobic degradation were called biophores (aliphatic, carboxyl substructures) and the ones that inactivate biophobes (aromatic substructures). It was successfully applied on N-heterocycles compounds by Philipp et al. (2007) with 99% of correct classification.

Various statistical techniques were used to correlate descriptors to biodegradation data, including linear, multilinear, and nonlinear (e.g., neural networks) regressions; classification tools; and expert system based on if-then-else rules and artificial intelligence (Baker et al., 2004; Blockeel et al., ²⁰⁰⁴; Cuissart et al., ²⁰⁰²; Gamberger et al., ¹⁹⁹⁶; Tabak and Govind, ¹⁹⁹³). If the most used endpoints are the data from MITI-I and BIODEG databases (qualitative), other quantitative endpoints were also used, such as the percentage of theoretical biological oxygen demand achieved in five days (BOD; Sedykh and Klopman, ²⁰⁰⁷), first-order biodegradation constants (k; Desai et al., ¹⁹⁹⁰; Tabak and Govind, ¹⁹⁹³), or Monod constants (Tabak et al., 1992). To go further than predicting the extent of biodegradation, other models (META/MultiCASE and CATABOL/CATALOGIC) were developed to predict possible degradation products and pathways based on either expert system or machine-learning systems. The META/MultiCASE approach is an expert system that can predict the metabolic transformation thanks to hierarchized metabolic rules defined by constitutional descriptors. Indeed the 70 general rules are based on a set of MultiCASE biophores (fragments that activate biodegradation), the weights of the fragments being used to define the hierarchy of transformation rules for a given chemical structure (Klopman et al., 1994; Klopman et al., ¹⁹⁹⁵). CATABOL is a hybrid system predicting the extent of degradation through BOD evaluation, and biotransformation pathways through an expert knowledge-based system (Jaworska et al., 2002). The BOD of one compound is there considered as a complex sequence of reaction steps occurring spontaneously (abiotic) or being catalyzed by enzymes: BOD is thus modeled by a sum of terms, each term being the product of the BOD of one step multiplied by the probability of the step to occur. The set of reactions (550) were extracted from the literature and were based on constitutional descriptors of the parent and daughter molecule taking into account the presence/absence of inhibiting fragments for each transformation reaction.

All these models, from the first ones of Geating (1981) and Boethling and Howard's (Boethling et al., 1994; Howard et al., ¹⁹⁹¹; Howard et al., ¹⁹⁹²; Howard et al., ²⁰⁰⁵) to the following ones, are based on the common assumption that attack by microorganisms takes place at a specific functional group of the molecular skeleton and that the presence of a particular fragment may enhance or delay the degradation. This assumption of similar structure-similar microbial metabolism is a strong hypothesis, not always verified. For example, E_HOMO-E_LUMO gap and ionization potential (IP) may be useful descriptors to describe redox behavior (Rücker and Kümmerer, 2012). But, consequently to this assumption, other descriptors, such as constitutional or topological descriptors, that take into account the global structure of chemicals, were assumed not to describe this microbial ability, particularly if the models are used for compound sets of highly diverse structure. Nevertheless, some models were developed using these descriptors: constitutional such as MW or number of rotatable bonds RBN, geometric such as solvent accessible surface area SAS, or topological such as MCI or Wiener index W, alone (Boethling, 1986; Boethling and Sabljic, ¹⁹⁸⁹; Dearden and Nicholson, ¹⁹⁸⁶; Kim et al., ²⁰⁰⁷; Li and Xi, ²⁰⁰⁷; Lindner et al., ²⁰⁰³), or in combination with other constitutional descriptors such as the number of chlorine atoms (n _Cl), geometric descriptors such as the MR, quantum-chemical descriptors such as the charge on the substituted carbon (C12), E_HOMO, the sum of charges on all carbons on the substituted benzene ring C8-C12 (SUMC8:C12) and μ (Boethling and Sabljic, 1989; Gombar and Enslein, ¹⁹⁹¹; Kim et al., ²⁰⁰⁷; Li and Xi, ²⁰⁰⁷; Lindner et al., ²⁰⁰³) for a series of similar compounds (Greaves et al., 2001; Kompare, ¹⁹⁹⁸), but also for compounds with varying structures (Delisle and Dixon, 2004; Jaworska et al., ²⁰⁰³; Okey and Stensel, ¹⁹⁹⁶; Table S8). Boethling and Sabljic (1989) observed that the structural features found to have a major influence on ultimate biodegradation of chemicals were size and shape, degree of chlorination, and degree of branching. The size and shape of chemicals accounted for the major part of the variation in the biodegradation data. In the model, this structural feature is described by ²χ^v, the magnitude of which is directly proportional to the size and shape of the chemical. Its positive regression coefficient indicates that microbial biodegradation will be slower for the bigger and more extended chemicals than for the smaller and more compact ones. The second structural property that controls the biodegradation rate of chemicals was the degree of chlorination (halogenation). The relative importance of this structural feature decreases with the size of the chemical. The third structural feature influencing the biodegradation is the degree of branching. It is described by ⁴χ_pc, which is highly sensitive to changes in branching, and its value rapidly increases with the degree of branching. The positive regression coefficient of ⁴χ_pc indicates that the degree of branching increases the period required for ultimate biodegradation. The relative importance of this structural feature decreases with the size of the chemical. It can be concluded that the ultimate biodegradation rate of a chemical will be a balance between the global structural features and some local structural features, the presence of particular functional groups (Sabljic, 1991).

Some models were developed without constitutional descriptors but based on the combined use of geometric (molecular diameter D, solvent accessible surface area SAS; Kim et al., 2007; Yang et al., ²⁰⁰⁴), topological MCI (Huuskonen, ^2001b, Yang et al., 2004, 2006), and/or quantum-chemical descriptors (E_HOMO, E_LUMO, repulsion energy NRE, q⁻, natural charge on the NH group Q(NH), spin density SD, α, ΔGs, μ; Beasley et al., ²⁰⁰⁹; Berger et al., ²⁰⁰²; Kim et al., ²⁰⁰⁷; Yang et al., ²⁰⁰⁴; Table S8). They were, however, developed on a small set of similar compounds. Finally, for 18 PAH, the biotransformation affinity coefficient (K_s) and the maximal specific biotransformation rate (q_max) were well correlated to geometric (radius of gyration (RadOfGyration), fraction of the area of the projection of a molecule on the y,z-plane divided by the area of the rectangle enclosing the projection of the molecule SHDW-Yzfrac, length of the projection of the molecule on the y axis SHDW-Ylength), topological (Kier flexibility index ø), geometric-electronic (PNSA-1) and quantum-chemical (final heat of formation (HOF), magnitude of the principal moment of inertia [PMI]) descriptors (r² > 0.821; Table S8; Dimitriou-Christidis et al., ²⁰⁰⁸). Descriptors related to 3D shape of the molecules were found essential. Indeed, PMI and RadOfGyration encode information about spatial distribution of mass and rotational properties of a molecule. The SHDW-Yfrac and SHDW-Ylength encode information about size, shape and orientation, and ø expresses the conformational flexibility of a molecule (Dimitriou-Christidis et al., 2008). Wammer et al. (2005) did not find any reliable QSAR to estimate the first-order biomass-normalized rate coefficients of 22 PAH, however their study did not include a comprehensive analysis of all possible molecular descriptors.

As for other environmental parameters (see previous subsections), it was observed that the combination of several categories of descriptors improves the prediction of B, BOD, COD, and AERUD (Boethling and Sabljic, 1989; Kim et al., ²⁰⁰⁷; Li and Xi, ²⁰⁰⁷; Tables S2 and S8). We finally ended up with the concept that the combination of descriptors may be the best option: group contribution models may be good for initial screening of the chemicals, but adding other descriptors than fragments may be good to better understand the biodegrading mechanisms.

As a conclusion, although the existence of an important number of studies, it remains difficult to identify descriptors explaining the huge variations in biodegradation of organic compounds. However, MCI were involved in almost half of the reviewed equations (33 over 75), especially ²χ^v and ⁴χ_c, and they provided satisfactory results. MW was also involved in 11 equations, and E_HOMO and E_LUMO in eight equations. No geometric-topological and no geometric-electronic descriptors were used.

3.5.2. Abiotic Degradation

Among the abiotic degradation processes, the chemical degradation occurring in soil, water, and sediment is the most studied for the development of QSAR (84 equations), followed by the degradation in atmosphere (35 equations; Table S9). Few QSAR were developed to estimate the degradation of organic compounds at the surface of the leaves of plants (2 equations). Most of the equations involve one or two descriptors to estimate the different abiotic degradation processes (i.e., hydrolysis, photolysis, reduction, and oxidation), but the number of descriptors can reach a maximum of 26 (photolysis, reduction; Table S9). The environmental parameters that are considered are essentially the degradation rates and the half-lives of the compounds, but several relationships were also developed using the quantum yield of the reactions Φ, the one-electron reduction potential E^o _H, and the activation energy Ea (Tables S2 and S9).

A number of reviews were written concerning the photooxidation processes (Mill, 1989), the tropospheric degradation (Güsten et al., 1995), the radical reactions of benzene derivatives (Hansch and Gao, 1997), the photoreaction rates in surface waters (Mill, 1999), and the atmospheric oxidation of chemicals (Meylan and Howard, 2003). However, almost all the reviewed QSAR are not based on structural molecular descriptors.

3.5.2.1. Abiotic Degradation in Soils, Water, and Sediments

Among the fate processes essentially occurring in natural surface, ground and interstitial water, and sediment, hydrolysis is one of the most important; however, only 12 QSAR equations have been found (Table S9). These equations only involved just one or two quantum-chemical descriptors, and were only developed for a small number of phenylurea and sulfonylurea herbicides. There was no QSAR for other types of organic compounds.

The pseudo-first-order reaction rate constant, k_hy, of six sulfonylureas herbicides decreased significantly with higher E_LUMO (r² > 0.702; Table S9). This is related to electron affinity and thereby reflects the energy for the uptake of electrons (Berger and Wolfe, 1996). In general, the self-polarizability of the carbonyl carbon (ALP_CO) and self-polarizability at the heterocycle atom 4 (ALP_{Heterocycle atom, 4}), or the superdelocalizability of the carbonyl carbon (SE(CO)) and at the heterocycle atom 4 (SE(4)) allowed correct prediction of the k_hy of 11 sulfonylureas in buffer, sterile soil and sterile sediment (Berger et al., 2002). The carbonyl group drives the hydrolysis at the sulfonylurea bridge, and the carbon 4 of the heterocycle part of the molecule is the atom where the substitution reaction takes place (hydrolysis of the methoxy group). The ALP_CO describes the reactivity of the pi electron system, reflecting the higher reactivity at the carbonyl-carbon of methylmethoxy-substituted compared with dimethyl-substituted phenylureas.

The transformation rates T of 10 phyenylureas in sterile soil and water can be well estimated with ALP_ij (r² > 0.745; Table S9; Berger et al., ²⁰⁰¹).

The 39 QSAR that are summarized in Table S9 to estimate the photolysis of organic compounds were mainly developed for the quantum yield φ, and more rarely for the degradation rates k_p or for the half-life T_1/2ph (Table S9). The equations are mostly based on one descriptor, but they can involve up to 27 descriptors. They were developed for several compounds but neither for PCB or pesticides, for example.

Twenty-four one-descriptor QSAR are reported to estimate the quantum yield φ of various aromatic halides. The equations mostly involved quantum-chemical descriptors (bond order for the carbon-halogen bonds BO, bond strength of the carbon-halogen bond to be broken BS, electronic energy EE, E_HOMO, E_LUMO, electron-nuclear attraction energy of the one-center term for the halogen atoms EN1, electron-nuclear attraction energy of the two-center term of the weakest carbon-halogen bond EN2, nuclear-nuclear repulsion energy of the two-center term of the weakest carbon-halogen bond NN2, net atomic charges on the carbon atoms in the benzene ring that are connected with the halogen atoms qc, net atomic charges on the halogen atoms q_x, total of electronic and nuclear energy of the two-center term of the weakest carbon-halogen bond TE2, α, μ), but also constitutional (MW) or geometric (summation of the steric factors of the additional substituents E_s) descriptors (Chen et al., ^1998b; Peijnenburg et al., ¹⁹⁹²; Table S9). The best correlations were found with q_x for 15 substituted chlorobenzenes (r² = 0.829) and E_s for 12 substituted aromatic halides (r² = 0.810), and the worst with BS for 12 substituted aromatic halides (r² = 0.000), μ for 17 substituted bromo- and iodobenzenes (r² = 0.242), and EN2 for 15 substituted chlorobenzenes (r² = 0.267; Table S9). E_s was one of the most efficient descriptor showing that steric effects seem to play a dominant role during the rate-limiting step of photolysis. However, the number of data used to develop the QSAR was low (Peijnenburg et al., 1992).

All equations based on descriptors of the same categories used quantum-chemical descriptors, and in particular E_HOMO and E_LUMO. The absolute electronegativity was a common descriptor able to predict the quantum yields of different substituted aromatic halides (bromo-, iodo-, chloro-, and fluorobenzenes) showing φ are dependent on the overall character of the halides, the character of carbon-halogen bond to be broken, and/or the nature of halogen atoms to be replaced. Considering each group of substituted aromatic halides independently, EN1 was the best descriptor for chlorobenzenes; and E_HOMO for fluorobenzenes (Chen et al., ^1998b). Similarly, the quantum yield of 41 substituted halides was correlated to EN2 and E_LUMO (r² = 0.807; Table S9; Chen et al., ^1998a). For 11 PBDE, the quantum yields (in methanol/water) increased with E_HOMO, E_LUMO, q_C− and Q_H ⁺, and decrease with CCR, Q_Br+, and Q_O− (r² = 0.982; Table S9; Niu et al., ²⁰⁰⁶).

Using a number of molecular descriptors of different categories, Chen et al. (1998a) developed some relationships to predict the quantum yields of several classes of organic compounds (Table S9). The quantum yields of 41 substituted aromatic halides can be well predicted from EE2, E_LUMO, and MW (r² = 0.848; Table S9). Compounds with higher E_LUMO and EE2 could have a higher probability of intersystem crossing, a higher probability of formation of excited triplet state, and thus a higher probability of photochemical reaction. A relationship was also developed using four factors condensing different types of information: (a) the strength of the carbon-halogen bonds, (b) the most positive or negative net atomic charges on an atom, (c) molecular ability to be oxidized or reduced, and (d) structural information related to polarizability α. This may imply that the weaker the carbon-halogen bonds are, the higher the quantum yields are. Thus, the compounds with higher polarizability tend to have smaller quantum yields. Because the electrons in the molecules of the compounds with higher polarizability can relatively move easily, both excited singlet and triplet states of the molecules of such compounds may be unstable (i.e., they may easily undergo processes such as internal conversion and fluorescence) resulting in smaller quantum yield (Chen et al., ^1998a). The quantum yields in water/acetonitrile of PCDD, as for it, mainly depended on core-core repulsion energy (CCR), EE, electron-electron repulsion energy of the one-center term for the oxygen atoms (EE1-O), E_HOMO, E_LUMO, electron-nuclear attraction energy of the one-center term for the oxygen atoms (EN1-O), HOF, MW, largest negative atomic charge on a carbon atom (q_C-), largest positive atomic charge on a chlorine atom (q_Cl), net atomic charges on the oxygen atom (qO), TE, and α. The correlation coefficient was good (r² = 0.972; Table S9), but the number of data used for the regression is small. Increasing bulkiness and polarity of PCDD led to decrease in quantum yield values; increasing E_LUMO, E_HOMO, and HOF values led to increase in quantum yield. EE1-O, EN1-O, and qO describe the character of the oxygen atoms and play an important role in the relation. This supports the suggestion that fission of the ether bond in the dioxin ring is the most likely route for direct photolysis (Chen et al., ^2001c). The combination of MW and bond order of the carbon-halogen bonds (BO) led to correct estimate of φ of 17 substituted bromo and iodobenzenes (r² = 0.789; Table S9; Chen et al., ^1998b), and the quantum yield of 12 substituted aromatic halides was best correlated with BS and Es (r² = 0.940; Table S9; Peijnenburg et al., ¹⁹⁹²). Finally, PAH with large average polarizability α, HOF and MW values tend to have smaller quantum yield, and PAH with great E_LUMO and E_LUMO/E_HOMO values, and small E_HOMO values tend to have great φ (Chen et al., 2000).

For 11 PBDE, CCR, MW, TE, and E_LUMO or E_HOMO were common descriptors to estimate their photolysis rate constants k_p in different solutions. As all PBDE congeners have a same parent diphenyl ether, it can be concluded that the more bromine atoms in the parent molecule, the higher the photolysis rate. Because a nucleophile reacts by means of its E_HOMO values, the compound with higher E_HOMO values will be a better nucleophile and will generate more stable. Similarly, PBDE with big absolute E_HOMO – E_LUMO values tend to be more stable. This result implies that photolysis rates of PBDE are also affected by the characteristics of solution in which they take place (Niu et al., 2006). E_HOMO and E_LUMO were also good descriptors for the assessment of k_p of 17 PAH (r² = 0.848; Table S9; Chen et al., ^1996b).

The direct photolysis (in water) half-lives T_1/2ph of 13 PAH under irradiation of sunlight was mainly correlated to E_LUMO + E_HOMO and E_LUMO – E_HOMO, but also to α (r² = 0.912; Table S9; Chen et al., ^2001e): the half-lives decrease when E_HOMO and α increase, but they increase with E_LUMO – E_HOMO gap and E_LUMO. As indicated before, chemical structures tend to be more stable at larger values of the E_LUMO – E_HOMO gap. In sunlight, E_LUMO – E_HOMO was presumed to be an indicator of the wavelengths absorbed, and therefore of the energy of the intermediate excited state. The half-lives also decreased with MW therefore it can be concluded that the larger the PAH molecules, the faster the degradation rate. This is probably mainly caused by enhanced spectral overlap of the absorption spectra of the high molecular weight PAH with solar radiation. In methanol/water solution, it was shown that PAH with larger E_LUMO – E_HOMO gap absorbs light with small wavelengths and may exhibit greater photolysis rate (Chen et al., ^1996b).

The most relevant descriptors to explain the variability of the photolysis of organic compounds were found to be E_HOMO and E_LUMO. The molecular weight MW, and the quantum-chemical descriptors α and μ were also relevant. Only constitutional, geometric, and quantum-chemical descriptors were used in the equations.

Reductive transformation is the dominant reaction pathway for many organic compounds in anoxic environments, and reducing environments abound in nature (e.g., subsurface waters and soils, aquatic sediments, sewage sludge, oxygen-free segments of eutrophic rivers). Most of the research in reductive transformations of chemicals focuses on dehalogenation of chlorinated aliphatic or aromatic contaminants, and on the reduction of nitroaromatic compounds (Tratnyek et al., 2003). Only nine QSAR were found to estimate three parameters related to reduction processes: rate constants k_red, k for dechlorination, and one-electron reduction potential E^O _H, which quantifies the tendency for a reduction reaction to occur (Tables S2 and S9). The diversity and number of organic compounds from which the equations were developed is low: only nitroaromatics, chlorinated aliphatics and halogenated aliphatic hydrocarbons.

The E_LUMO was the best descriptor to explain the variability in the reactivity data for the reduction of six nitroaromatics (r² = 0.990; Table S9) and 12 chlorinated aliphatics (r² = 0.832; Table S9; Colón et al., ²⁰⁰⁶; Scherer et al., ¹⁹⁹⁸). E_LUMO characterizes the tendency of a compound to accept electrons or to be reduced: the greater the E_LUMO values are, the lower the tendency of a compound to accept electrons is. Correlations were also found with electron affinity EA (r² = 0.834) and one-electron reduction potential E1 (r² = 0.810). EA represents the energy difference associated with the gain of an electron, which should correlate with the ease or difficulty in the reduction of a compound (Colón et al., 2006). E1 is a promising descriptor for dechlorination as it represents the potential of the rate limiting initial electron-transfer step (Scherer et al., 1998).

The k_red of 13 halogenated aliphatic hydrocarbons can be correctly estimated using a combination of constitutional (MW), and of several quantum-chemical (BO, C, CCR, EE, EE1c, EE1x, EE2, E_HOMO, E_LUMO, EN1c, EN1x, EN2, HOF, J, K, NN2, q⁻, q-cx, Q_H ⁺, q_xc, TE, TE2, α, and μ; Table S1) descriptors (r² = 0.808; Table S9). As for nitroaromatics and chlorinated aliphatics, the greater the E_LUMO values, the lower the dehalogenation rate constants of halogenated aliphatic hydrocarbons. Increasing the values of Q_H ⁺ led to decreasing values of k_red, and the higher the BO, the lower the k_red, which implies that the stronger carbon-halogen bond, the slower the dehalogenation rate. Halogenated aliphatic compounds with great BO, EE, E_LUMO, Q_H ⁺, and TE tend to be dehalogenated slowly, whereas halogenated aliphatic compounds with high values of CCR, MW, and α values tend to be dehalogenated fast (Zhao et al., 2001).

The E^O _H of 20 nitroaromatics can be estimated with one of these three quantum-chemical descriptors: EA, E_LUMO in aqueous or gas phase, or vertical detachment energy (VDE). E_LUMO and VDE are alternative measures used to approximate the energy change accompanying the transfer of one electron. EA value incorporates the effect of changes in geometry between the (gas-phase) anion and neutral species, whereas E_LUMO and VDE do not account for geometry changes. All correlations have similarly high predictive capabilities (r² ranges from 0.913 to 0.940; Table S9) suggesting that any reasonable measure of the energy change accompanying the one-electron reduction process will be highly correlated with the reduction potential (Phillips et al., 2010).

As a conclusion, E_LUMO was found to be the most fundamental descriptor allowing the prediction of the reduction of organic compounds in the environment. Only constitutional, and quantum-chemical descriptors were used, but the number of equations is low.

Oxidation, along with hydrolysis and reduction, accounts for the vast majority of chemical reactions that result in degradation of organic contaminants, especially in aquatic systems. Oxidation of organics can occur by a wide variety of mechanisms: the main ones are loss of electrons or hydrogen atoms (abstraction by the oxidant), addition of an oxidant (OH, ¹O₂, manganese (III/IV) oxides), or substitution of a hydrogen atom by an electron-withdrawing atom or functional group (Canonica and Tratnyek, 2003; Rorije and Peijnenburg, ¹⁹⁹⁶). Oxidation by ozone (ozonation) is also considered in this review as it is an effective method for removing residual pollutants such as pesticides and other hazardous chemicals from water during drinking water treatment (Hu et al., 2000; Sudhakaran and Amy, ²⁰¹³). Twenty-four QSAR allowing the prediction of oxidation rates are reported in Table S9. They mainly involve one descriptor (with a maximum of three descriptors) and were developed for several classes of organic compounds (Table S9).

E_HOMO was the best descriptor to estimate the oxidation of substituted phenols by singlet oxygen, manganese (III/IV) oxides, chlorine dioxide, peroxydisulfate, and potassium dichromate in the aqueous phase (r² > 0.750; Table S9), and the oxidation reactivity decreases with increasing E_HOMO. Indeed, an electron from the HOMO with a large ionization potential has to overcome a larger energy barrier before it can be removed from its orbital (Rorije and Peijnenburg, 1996). E_HOMO was also strongly related to the reaction rates k_HOCl of eight organophosphorous pesticides in the presence of chlorine (r² > 0.950; Table S9; Duirk et al., ²⁰⁰⁹), and with reaction rates with ozone k_O3 for different pesticides (r² > 0.840; Table S9; Hu et al., ²⁰⁰⁰), but k_O3 increases with E_HOMO. However, the number of compounds used for the development of these QSAR was very small (from three to a marginal maximum of 24; Table S9). For eight phenoxyalkylacetic pesticides, the rate constant k_O3 was very well predicted by a two-parameter QSAR model that used E_HOMO and the absolute electronegativity (EN) as predictors (r² = 0.970; Table S9), but the number of data for the regression was also low. The dependence of rate constants of pesticides on E_HOMO shows that the reaction between pesticides and ozone was controlled by the frontier orbital effect connected with partly covalent bonding in the transition state (Hu et al., 2000; Ljubic and Sabljic, ²⁰⁰²). For 55 miscellaneous compounds, some correlations between k_OH and constitutional descriptors such as n_{C = C} or double bond equivalence (DBE), geometric such as SAS, and quantum-chemical such as α were found. With one descriptor, the best estimates of k_OH of 55 miscellaneous organic compounds were found with DBE or the number of ring atoms (NR; r² = 0.767 and 0.902, respectively; Table S9), but the greatest correlation was obtained with a combination of DBE and the weakly polar component of SAS (WPSA; r² = 0.918; Table S9). Similarly, for 27 organic compounds, the best estimate of k_O3 used DBE, WPSA, and IP (r² = 0.832; Table S9). DBE focuses on the double bond nature of the organic compounds which enhances ozonation efficiency. WPSA focuses on the surface area occupied by halogens, and IP represents the energy required to remove an electron from a neutral atom. An increase in both WPSA and IP decreases ozonation efficiency (Sudhakaran and Amy, 2013). For 60 aromatic compounds, two models were found to give good estimate of k_OH (r² > 0.735; Table S9). The four-descriptors model involves E_HOMO, the Geary autocorrelation-2 lag weighted by atomic polarizabilities (GATS2p), the leverage-weighted autocorrelation of lag 7 weighted by atomic polarizabilities (HATS7p) and the number of path of length 8 (P₈), whereas the five-descriptors model involves E_HOMO, MW, P₉, and two 3D MoRSE-signal descriptors (Mor(02)e and Mor(26)p). In both cases, the main contribution to the degradation rate was obtained from E_HOMO. Indeed, as stated before, E_HOMO determines the nucleophilic ability of compound and hence the possibility of reaction by attack of such a strong electrophile as the OH radical. Thus, compounds with higher value of E_HOMO are more reactive with OH radical (Kušić et al., 2009).

Considering these results, E_HOMO was the most used and the most useful descriptor to estimate the oxidation of organic compounds in the environment. Only constitutional, geometric, geometric-topological, and quantum-chemical descriptors were used, but the number of equations is low.

3.5.2.2. Abiotic Degradation in the Atmosphere

Organic compounds emitted or formed in the troposphere are removed by physical processes such as wet and dry deposition, and by chemical transformation processes that include reaction with photochemically generated oxidants such as hydroxyl radicals and ozone at day time, and nitrate radicals at night time (Güsten, 1999; Meylan and Howard, ²⁰⁰³; Pompe and Veber, ²⁰⁰¹). Reaction with chlorine atoms can also be significant due to their high concentrations in the atmosphere (Long and Niu, 2007; Meng et al., ²⁰⁰⁵). Güsten et al. (1995) reviewed the tropospheric degradation of chemicals and found that the great majority of published models were only developed for single chemical class and a small number of chemicals.

Only four equations were found to predict the persistence of several persistent organic pollutants (POP) in the atmosphere, and they are related to four different environmental parameters (Table S9).

Atmospheric half-life (T_1/2) is one of the criteria commonly used to study air persistence and long-range transport (LRT) potentials of organic compounds. The mean atmospheric half-lives (Mean T_1/2) of 59 POP were satisfactorily correlated (r² = 0.841; Table S9) to two global WHIM descriptors (Ku and Tu), and to two topological descriptors (mean information content index on the distance degree equality I^E _D,deq and Kier flexibility index ø). The WHIM descriptors were the most relevant ones, highlighting that 3D size Tu, and shape Ku have opposite role in determining the persistence of compounds (Tu has a negative sign in the regression and Ku has a positive sign). The same relationship was obtained for the maximum half-lives (Max T_1/2), but the results were slightly less satisfactory than for mean half-lives (mean T_1/2; r² = 0.826; Table S9; Gramatica et al., ²⁰⁰¹).

A principal component analysis performed on the same data allowed the development of an atmospheric persistence index (API), and a LRT index. The API was correlated to n _H (this highlights the importance of the number of hydrogen atoms in the molecule influencing the hydroxyl-radical reaction), and to three WHIM descriptors (Ve, η2e and θ2e; r² = 0.897; Table S9). The LRT index was well correlated to MW and to two directional WHIM (λ2e and λ1p; r² = 0.952; Table S9; Gramatica et al., ²⁰⁰¹).

Only two equations were found to estimate the photodegradation of PAH, PCDD, and PCDF in the atmosphere (Table S9). The predicted photodegradation half-lives T_1/2p of 11 PAH on aerosols (r² = 0.960; Chen et al., ^2001b), and 75 PCDD and PCDF on fly ashes (r² = 0.704; Niu et al., ²⁰⁰⁴) were mainly correlated to E_HOMO, E_LUMO, MW, and α (Table S9). Increasing MW values of the PCDD and PCDF leads to increase half-life values; on the contrary, PAH with great MW values tend to photolyze fast. The PAH, PCDD, and PCDF with small absolute electronegativity (EN) values and large absolute (E_HOMO – E_LUMO) values tend to have lower T_1/2p (Chen et al., ^2001b; Niu et al., ²⁰⁰⁴).

In the atmosphere, the oxidation of organic compounds is mainly due to reactions with OH, O₃, NO₃, and Cl atoms, and in particular, the reaction with the OH radical is the major chemical loss process for the majority of organic compounds emitted into the troposphere (Medven et al., 1996; Sabljic and Peijnenburg, ²⁰⁰¹). Twenty-nine equations were found to estimate the oxidation reaction rate constants of organic compounds in the atmosphere, the highest number being for reaction with OH (Table S9). The equations involve from 1 to 10 descriptors, and were developed for miscellaneous organic compounds, but not, for example, for PCB or pesticides.

Among the 15 QSAR related to the reaction rates with OH in the atmosphere, k_A,OH, eight relationships were developed using only one descriptor (Table S9). The E_HOMO allowed good estimate of k_A,OH of various compounds (r² > 0.749; Bartolotti and Edney, ¹⁹⁹⁴; Güsten et al., ¹⁹⁹⁵), and the ionization potential IP was well correlated to the k_A,OH of 15 hydrocarbons and fluorinated hydrocarbons (r² = 0.846; Percival et al., ¹⁹⁹⁵), and of aromatic and aliphatic compounds (r² > 0.902; Güsten et al., ¹⁹⁸⁴; Table S9). Oberg (2005) found that the main sources of variation of k_A,OH were directly linked to four constitutional descriptors: number of aromatic bonds (NAB), NDB, n _H, and n _X. For Bakken and Jurs (1999), the rate constants k_A,OH of 52 unsaturated hydrocarbons were estimated using five topological descriptors: number of sp² hybridized carbon atoms (2SP2, 3SP2) and molecular distance edge (MDE-13, MDE-23, MDE-34), encoding information concerning attack sites for the radical, branching information, and steric considerations (r² = 0.868; Table S9). This is consistent with the reaction center for radical reactions which is often an unsaturated carbon. Then, they developed a second relation using computational neural networks (CNN). It showed correlation with miscellaneous descriptors: one constitutional (number of multiple-multiple carbon bonds MCB), one topological (PND), one geometric-electronic (FPSA-3), and two quantum-chemical (E_LUMO and EN). PND encodes information on branching of the molecules, and quantum-chemical descriptors encode the energetics of the reactant molecular orbitals that will be involved in the reaction. Then, using a very large dataset of 281 miscellaneous compounds, they found a ten-descriptor linear relationship involving two constitutional (NAB, number of lone pairs (NLP)), six topological (3SP2, MDE-14, PND, sum of weighted paths starting from heteroatoms WTPT-3, path-three κ index ³κ, ³χ), and two quantum-chemical descriptors (E_LUMO, EN). The CNN model involved three constitutional (n _C, NDB, NSB), three topological (1SP2, MDE-33, WTPT-3), one geometric (GEOM-3), one geometric-electronic (CHAA-3), and two quantum-chemical (E_HOMO, Hard) descriptors (r² = 0.876; Table S9). Using descriptors of the different categories, k_A,OH of various organic chemicals was correctly correlated to some constitutional (MW, number of atoms in the molecule (NAT), n _C, n _HD, n _OH, No^RING, unsaturation index (UI)), and geometric (WHIM descriptors) and/or topological (information index) descriptors (r² > 0.733; Table S9; Gramatica et al., ^1999a). The rate constants of 14 alkylnaphthalene, as for it, depended on MW, and on quantum-chemical (CCR, EE, E_HOMO, E_LUMO, Q_Cave, Q_H ⁺, TE, μ, α) descriptors (r² = 0.879; Table S9; Long and Niu, ²⁰⁰⁷). Finally, using PLS regression, Medven et al. (1996) showed that five descriptors had more pronounced influence than the others on the k_A,OH of 57 unsaturated hydrocarbons: E_HOMO, E_LUMO, Hard, average number of alkyl substituents per unsaturated bond (n _Alk), and number of carbon atoms in unsaturated bonds (n _Cub). Among these, E_HOMO was the most influential, which is in accordance with the assumed mechanism of electrophilic addition to multiple bonds in which the singly occupied molecular orbital (SOMO) of the electrophilic radical predominantly interacts with the HOMO of the unsaturated chemical, which means that chemicals with low values of E_HOMO are more reactive. Two other descriptors, Hard and E_LUMO, have a strong influence on the reactivity of unsaturated compounds with hydroxyl radical. Again, chemicals with lower values of both descriptors are more reactive. Thus a small HOMO-LUMO energy gap has a positive effect on the reactivity of unsaturated chemicals with hydroxyl radical. This result can be rationalized within the framework of the frontier molecular orbital theory: the SOMO of the electrophilic radical also interacts with the LUMO of unsaturated chemicals, and this interaction has a significant effect on reactivity. As expected, the reactivity of unsaturated chemicals increases with the number of carbon atoms in unsaturated bonds or potential reactive centers. Furthermore, the degree of alkyl substitution on unsaturated bonds (n _Alk) also has a positive effect on reactivity.

Klamt (1993) proposed to divide the rate constants of degradation of various organic compounds by hydroxyl radicals considering three subreactions: (a) the OH addition to carbon-carbon double bonds (k_add ^C), which depended on the charge-limited effective HOMO energy at H atom (ECH^H); (b) the addition to aromatic rings (k_ar ^C), which depended on the energy-weighted effective HOMO energy at atom H (EEH^H) and on the energy required to deform the molecule in a way to enable the OH-addition (Δ_def ^C); and (c) the hydrogen abstraction from aliphatic carbon atoms (k_abs ^H), which depended on ECH^H. They obtained very good results (r² > 0.954; Table S9). For 13 halogenated compounds, an hologram method was used to predict half-life of the hydroxyl radical with substituted aromatic compounds: the generated fragments include atoms, bonds, connections, hydrogen atoms, donor and acceptor atoms, and the chiral center (Vrtacnik and Voda, 2003).

The QSAR developed by Atkinson (1987), though widely used to estimate the OH reaction rates, were not considered in this study, as they involve an experimental descriptor: the sum of the electrophilic substituent constants.

Two equations are reported for the reaction rates with ozone, k_A,O3, and quantum-chemical descriptors were found to be the best predictors in both cases (Table S9). For 117 miscellaneous compounds, all descriptors of the QSAR were quantum-chemical (average electrophilic reaction index for a C atom AER_C, E_HOMO, fractional hydrogen bonding donor ability of the molecule FHDCA(1), maximum exchange energy for a C‒C bond MaxC‒C, maximum electron-electron repulsion for a C‒C bond MaxeeC-C, minimum (> 0.1) bond order of a C atom MinC; r² = 0.870; Table S9). The relationship encodes chemical features which are important in the reaction of organic compounds with ozone, that is, information about formation of transition state, cleavage of the chemical bonds, and different conformational changes. The MaxC-C and MaxeeC-C characterize intramolecular energy distribution and may be related to the conformational changes or atomic reactivity in the molecule (Pompe and Veber, 2001). The other quantum-chemical descriptors that were used to predict k_A,O3 were E_HOMO, AER_C which represents the interactions between the frontier orbitals of the reacting compounds, and the MinC that relates to the strength of intramolecular bonding interactions, and therefore to the stability of the molecule or its conformational flexibility (Sannigrahi, 1992). The FHDCA(1) can describe polar interactions between molecules as well as their chemical reactivity (Pompe and Veber, 2001). Among the quantum-chemical (E_HOMO – E_LUMO gap), constitutional (MW, number of conjugated double bonds n _AB, number of isolated double bonds n _DB), topological (Moran autocorrelation lag (7) weighted by atomic Sanderson electronegativities (MATS7e), and geometric-electronic (R autocorrelation of lag 3 weighted by atomic Sanderson electronegativities (R3e)) descriptors that allow the prediction of k_A,O3 of 125 miscellaneous compounds, the best descriptor was the E_HOMO – E_LUMO gap. As stated before, this is an important stability index reflecting molecule reactivity as well as polarization: the more reactive chemicals have a smaller gap. The information regarding attack sites for ozone is provided by the constitutional descriptors highlighting the relevance of the double bonds for the molecular cleavage by ozone. Charge distribution factors, in addition to dimensional aspects, are encoded by the different kinds of autocorrelation descriptors selected, all weighted by the atomic electronegativity of Sanderson (Gramatica et al., 2003; Table S9).

Eight equations allowing estimate of the rate constants for the reaction with NO₃, k_NO3, were inventoried in Table S9. The k_NO3 are essentially and correctly predicted by E_HOMO and/or E_LUMO (r² > 0.677; Table S9; Güsten et al., ¹⁹⁹⁵; Long and Niu, ²⁰⁰⁷; Müller and Klein, ¹⁹⁹¹), though the mechanism of NO₃ radical addition is complex and that it's maybe not possible to model its reactivity by one single descriptor (Güsten et al., 1995). The relationship developed by Long and Niu (2007) for 14 alkylnaphthalene involved, in addition to E_LUMO and E_HOMO, constitutional (MW) and quantum-chemical (Q_Cave, Q_H ⁺, total energy TE, standard heat of formation ΔH_f, μ) descriptors (r² = 0.817; Table S9). For 58 aliphatic compounds, the k_NO3 is correlated to constitutional (NAT, nHD, UI), and geometric WHIM (Du, λ1s) descriptors (r² = 0.840), and for 16 aromatics, k_NO3 was correlated to two constitutional (MW, hydrophilic factor (HY)), and one topological (mean information content index on the distance degree equality I^E _D,deq) descriptors (r² = 0.978; Table S9; Gramatica et al., ^1999a). Sabljic and Güsten (1990) developed two relationships linking k_NO3 to the ionization potential (IP): one for 62 aliphatic compounds and one for seven benzene derivatives. For the aliphatic compounds, the correlation was significant (r² = 0.927; Table S9) but chloroalkenes compounds needed to be approximate by the parent hydrocarbon molecule because of lack of ionization energy in the study. For benzene derivatives, good correlation (r² = 0.883; Table S9) was found excluding two outliers (tetraline and methoxybenzene), however the dataset was limited.

Only one equation was found to estimate the reaction rate of organic compounds with chlorine k_Cl (Table S9). For 14 alkylnaphthalene, k_Cl was again mainly found to depend on energies of orbital (E_HOMO, E_LUMO), but also on Q_Cave, Q_H ⁺, and μ (r² = 0.944; Table S9; Long and Niu, ²⁰⁰⁷).

As a summary, E_HOMO was the most relevant descriptor to estimate the oxidation of organic compounds in the atmosphere. No geometric-topological and no electro-topological descriptors were involved in the equations.

3.5.2.3 Abiotic Degradation on Vegetation.

Few QSAR studies are related to the degradation of organic compounds on the surface of plants, and only two equations were found for PCDD and PCDF (Table S9). The photodegradation half-lives T_1/2v of 42 PCDF adsorbed to spruce needle surfaces (Niu et al., 2005) was mainly correlated to E_HOMO, E_LUMO, MW, TE, and α (r² = 0.740; Table S9). But, the stability of PCDF was also shown to increase with the increase in chlorine atoms in the parent molecules, and PCDF with high (E_LUMO – E_HOMO) values tend to be more stable and difficult to be degraded. For 10 PCDD and PCDF dissolved in cuticular wax from Prunus laurocerasus leaves exposed to sunlight, the degradation rates k_v mainly depended on q_Cl, but the rates also increased with MW and α. PCDD and PCDF with large values of E_LUMO, E_HOMO, and E_LUMO – E_HOMO tend to have low k_v, however the dataset was limited (r² = 0.958; Table S9; Chen et al., ^2001a).

3.6. Absorption by Plants Processes

Organic compounds present in soil, water and air may be taken up by plants (Paterson et al., 1994). The chemical can be transferred to the vegetation from the soil and/or water by uptake through the roots (i.e., symplastic way), from the atmosphere by their aboveground parts after wet or dry deposition, or following rain-splash in which soil particles are dispersed onto the leaf surfaces following the impact of raindrops on the soil surface (Hiatt, 1998; McKone and Maddalena, 2007; Paterson et al., ¹⁹⁹⁴; Sabljic et al., ¹⁹⁹⁰). For atmospheric contaminants, the predominant initial site of interception is the plant cuticle, and the adsorption on the cuticles is the first step of the transfer of volatile and nonvolatile organic compounds to plant (Chaumat et al., 1992; Hiatt, ¹⁹⁹⁸; Welke et al., ¹⁹⁹⁸).

Twenty-six QSAR allowing the estimation of the parameters describing the absorption of organic compounds by plants are reported in Table S10. The absorption can be estimated with the bioconcentration factor BCF (ratio between the contaminant concentration in the plant tissue and the concentration in soil), the bioconcentration ratio BCR (the ratio of a tissue concentration to the concentration in a relevant exposure medium), the cuticle-air partition coefficient Kca, the cuticle-water partition coefficient K_CW, the polymer matrix membrane-water partition coefficient K_MXw, the permeability of the cuticle P, and the sorbed amount by the plant cuticle Q. In most cases, a single descriptor was used to predict these environmental parameters, the maximum being five descriptors. The equations were developed for a wide diversity of organic compounds but mainly with very limited datasets (Table S10).

The BCF (in zucchini) of several POP were correlated to n _Cl (except for PCB), which is related to the hydrophobicity of the molecule. However, the best correlations were found using combinations of GETAWAY, VolSurf, and quantum-chemical descriptors (r² > 0.918; Table S10; Bordás et al., ²⁰¹¹): POP taken up preferentially from soil are characterized by high values of E_LUMO – E_HOMO, VOH2 and HB5O (two VolSurf descriptors), and low values of Z-component, GETAWAY (H4p and H5e), and VolSurf (BV31OH2, D3DRY, D6DRY, H5e, W4O) descriptors.

The MCI were involved in six of the 26 relationships: the BCR of several miscellaneous compounds for aboveground plant-soil bioconcentration, root-soil bioconcentration, and plant-air bioconcentration were well correlated with ¹χ and the polar correction factors of Meylan et al. (1992; r² > 0.780; Table S10; Dowdy and McKone, ¹⁹⁹⁷). Similarly, for 14 alcohols, the Kca (of tomato cuticle) was well correlated to ¹χ (r² = 0.868; Table S10; Welke et al., ¹⁹⁹⁸). For 47 organic chemicals, the K_CW was correctly estimated using ³χ^v and n _OHaliph (r² = 0.984; Table S10). The K_CW are primarily influenced by the size of the molecule, which is described by ³χ^v: larger molecules show a higher affinity for cuticles than smaller ones. However, it has to be underlined that not all parts of a molecule contribute equally to its affinity for plant cuticles. The major contribution is from chlorine substituents, hydrocarbon chains, and benzene rings. Another factor controlling the magnitude of K_CW is the presence of aliphatic hydroxy groups. The negative regression coefficient of n _OHaliph shows that the association with cuticles decreases with the presence of aliphatic hydroxy groups. Compared with the main factor, the size of the molecule, n _OHaliph can be viewed only as a fine-tuning element for the affinity of organic chemicals for plant cuticles (Sabljic, 1991; Sabljic et al., ¹⁹⁹⁰).

For 5 phenylurea herbicides, significant relationships between K_CW, Q, or P (for tomato and pepper), and the steric descriptors ΣD and ΣS were found (r² > 0.943; Table S10), but the number of data used in the regression is very low. As observed for the 47 organic chemicals (Sabljic et al., 1990), the overall dimension of the phenylurea molecules reflected by the steric descriptors is an important factor for cuticular adsorption. Within the same chemical family, penetration in plant tissues is greater for chemicals well adsorbed to cuticles (Chaumat et al., 1992).

Platts and Abraham (2002) used the LSER approach to estimate the K_MXw for tomato of 62 volatile organic compounds, and found very good result (r² = 0.981; Table S10). They concluded that the cuticular matrix interacts more through pi- and n-electron pairs, is rather less polar/polarizable and basic, and much less acidic than bulk water, and that cavities are much more easily formed in cuticle than in water.

Finally, a PLS analysis was performed to determine the main descriptors involved in the estimation of the Rhizopus oryzae cell-wall water partition coefficients of only 3 PAH. MW was the principal contributing descriptor, followed by the total information content index with neighborhood symmetry of one-order TIC₁ (Ma et al., 2011).

As a conclusion, descriptors related to the size of the organic compounds (³χ^v, steric descriptors such as ΣS and ΣD, and the number of chlorine atoms) were the most relevant ones to estimate their absorption by plants.

4. SYNTHESIS AND DISCUSSION

For the first time, a comprehensive review of QSAR focused on several processes driving the fate of organic compounds in the environment was done. Six main processes were considered: water dissolution, dissociation, volatilization, retention, degradation, and absorption by higher plants. These main processes were then subdivided in 23 environmental subprocesses as shown in Table S2. We chose to focus our work on QSAR based on structural molecular descriptors because QSAR based on K_OW or S_W, for example, are prone to experimental errors in the input variables, which can result in some statistical problems (Lohninger, 1994; Nguyen et al., ²⁰⁰⁵; Sabljic and Piver, ¹⁹⁹²). Overall, 790 QSAR equations involving 686 different molecular descriptors allowing the assessment of 90 environmental parameters are presented here (Tables S1–S10). The equations were developed for a wide diversity of organic compounds including pesticides, PAH, PCB, PCDD, pharmaceuticals, and hormones. However it has to be underlined that almost no pesticide was up to now included in the development of QSAR for pK_a, vapor pressures, K_H, K_OA, or adsorption on sediments. Similarly, most of the QSAR related to abiotic degradation were developed for restricted classes of organic compounds (Tables S3–S10).

Figure 1 shows the number of equations found for each of the 23 environmental processes (Table S2). The highest number of equations, 145 equations (i.e., 18.3% of the total number of equations), was developed to predict the dissociation of organic compounds (pK_a). A fairly large number of equations were found to predict the K_OW (115; i.e., 14.5%), and the adsorption of compounds on the soils (102; i.e., 12.9%) as well. The number of equations to predict biodegradation and solubility in water (S_W) were also important, being 75 (i.e., 9.5%) and 65 (i.e., 8.2%), respectively. On the contrary, there were only one equation for the soil desorption of organic compounds, two equations for the degradation of compounds on vegetation, four equations for the nonlinear adsorption, and six equations to predict the potential of transfer to groundwater. To the best of our knowledge, there is neither QSAR to estimate the formation of nonextractable (bound) residues, known as an important dissipation route of pesticides and other organic compounds in soil matrices (Barriuso et al., 2008), nor to estimate the potential of transfer of organic compounds to surface water. This might be explained by the fact that the estimation of the transfer of organic compounds to ground and surface water is often addressed by mass balance models, which are mechanistic (Mackay et al., 2003).

Figure 1 . Number of equations found for the main processes governing the fate of organic compounds in the environment (see Table S2).

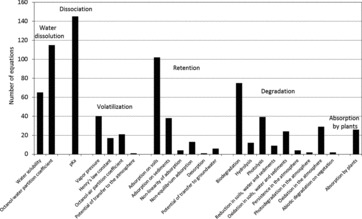
The descriptors that were the most used in the 790 equations are summarized in Figure 2. Twenty-two descriptors were involved in more than 10 equations: nine were quantum-chemical descriptors related to the energies (CCR, EE, E_HOMO, E_LUMO, q⁻, Q_H ⁺, TE, α, μ), eight were topological and they were all MCI (⁰χ, ⁰χ^v, ¹χ, ¹χ^v, ²χ, ²χ^v, ³χ^v, ³χ^v _c), three were geometric related to the surface and the volume of the compounds (TSA, VdW, Vm), and two were constitutional (MW and n _Cl). The most used descriptor is E_HOMO, which is involved in 80 (i.e., 10%) equations, followed by α in 68 (i.e., 8.6%) equations, E_LUMO in 58 (i.e., 7.3%) equations, MW in 57 (i.e., 7.2%) equations, μ in 46 (i.e., 5.8%) equations, and ¹χ^v in 44 (i.e., 5.6%) equations. The n _Cl, VdW, Vm, TSA, ⁰χ, ⁰χ^v, ¹χ, ²χ, ²χ^v, ³χ^v, ³χ^v _c, CCR, EE, q⁻, Q_H ⁺, and TE descriptors were included in 11–41 (i.e., 1.4 to 5.4%) equations (Figure 2). The remaining descriptors of Table S1 were mainly found only in one or two equations.

Figure 2 . Molecular descriptors that are the most frequently used to assess the parameters related to the main processes governing the fate of organic compounds in the environment (see Tables S1 and S2).

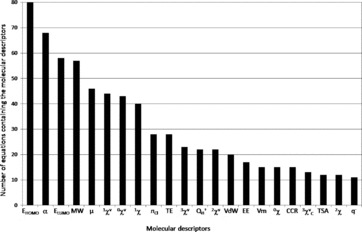
Finally, the descriptors the most frequently used to estimate environmental processes are summarized in Figure 3 (a descriptor involved in several different process will be considered as generic). Nineteen descriptors were found to be involved in six or more processes (Figure 3): twelve were quantum-chemical (EE, E_HOMO, E_LUMO, HOF, q⁻, q_C, Q_H ⁺, TE, α, ΔGs, ΔH_f, μ), four were topological (¹χ, ¹χ^v, ²χ^v, ³χ^v), two were constitutional (MW, n _Cl) and one was geometric (Vm). Fifteen of these 19 descriptors were among the 22 most used descriptors (Table S1, Figure 1); the four remaining descriptors are HOF, q_C-, ΔGs, and ΔH_f. In particular, the five most generic descriptors were also the five most used descriptors: E_HOMO, α, E_LUMO, μ, and MW, and among them, E_HOMO was the most used descriptor and one of those that allowed the assessment of the highest diversity of environmental processes (Figures 2 and 3).

Figure 3 . Molecular descriptors allowing the assessment of the highest diversity of environmental processes (see Tables S1–S10).

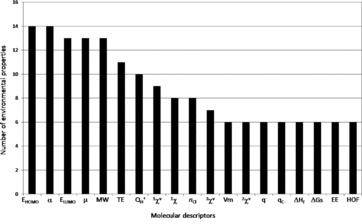
The overall synthesis of the results that are reviewed in this work showed that, in general, an increase in the absolute values of E_HOMO led to a decrease in K_OW, adsorption on soils, redox reactions in soils, water and sediments, photodegradation in the atmosphere, and degradation on the vegetation. On the contrary an increase in the absolute values of E_HOMO led to an increase in biodegradation and BCF (Tables S3–S10). Similar results were found for E_LUMO, except that an increase in the absolute values of E_LUMO involved an increase in photolysis and atmospheric oxidation of organic compounds (there was no clear relationship between E_LUMO and biodegradation or BCF; Tables S3–S10). Orbitals play a major role in a lot of chemical reactions and they are also responsible for the formation of many charge-transfer complexes. The E_HOMO is directly related to the ionization potential and characterizes the susceptibility of the molecule toward electrophilic attack (Karelson et al., 1996). E_HOMO also represents the proton acceptance ability in forming hydrogen bond, while E_LUMO represents the proton donation ability in forming hydrogen bond. Therefore, the compounds with large value of E_HOMO and E_LUMO tend to donate or accept protons easily (Chen et al., ^2002a; Colón et al., ²⁰⁰⁶; Zhou et al., ²⁰⁰⁵). This could explain why E_HOMO and E_LUMO were rather good descriptors for estimating several processes such as adsorption, biodegradation, photolysis, redox reactions, and degradation in the atmosphere.

The two quantum-chemical descriptors, α and μ, also allowed the estimate of a wide diversity of environmental processes (Figure 3; Table S2). They were especially used to assess partition properties such as S_W, K_OW, P_L, P_S, K_H, K_OA, and adsorption on soils and sediments (Tables S3, S4, S6, and S7). An increase in α was related to an increase in K_OW, K_OA, redox reactions and degradation on vegetation; and to a decrease in S_W, vapor pressure and photodegradation in the atmosphere (Tables S3 to S10). The bigger the α is, the more hydrophobic the molecules are (Chen et al., 1996; Katritzky et al., 1998; Shi et al., ²⁰¹²; Yang et al., ²⁰⁰⁷). An increase in μ was found to increase K_OA, COD, atmospheric photodegradation, and degradation on the vegetation, but to decrease K_OW, vapor pressure, adsorption and reduction reactions. As indicated before, molecules with larger μ tend to transfer from octanol phase to water phase, to volatilize and to sorb less because intermolecular dipole-dipole interactions and dipole-induced dipole interactions are in direct proportion to μ². A larger dipole would imply greater dipole interactions with the polar water molecules (Chen et al., ^1996a; Dai et al., ²⁰⁰⁰; Shi et al., ²⁰¹²; Zeng et al., ²⁰⁰⁷).

The last of the five most used and generic descriptor is MW (Figures 2 and 3; Tables S3, S4, S6–S9). An increase in MW is correlated with an increase in K_OW, K_OA, adsorption on soils, reduction reactions, degradation on vegetation, and to a decrease in S_W, vapor pressure, biodegradation, photolysis, and persistence in the atmosphere.

Finally, the MCI ¹χ^v was also a useful descriptor (Tables S3, S4, S6 to S8). Solubility in water and vapor pressure decrease when ¹χ^v increases. On the contrary, K_OW, K_OA, and adsorption on soils increase with ¹χ^v. Several other MCI (⁰χ, ²χ^v, ³χ^v) were involved in the estimate of partition properties and biodegradation (Tables S3, S4, S6–S8, S10).

This review also showed that the combination of descriptors belonging to different categories improves the estimate of the different environmental parameters, probably because it allows to consider simultaneously different representations and properties of the molecule (Basak et al., 1997; Boethling and Sabljic, ¹⁹⁸⁹; Güsten et al., ¹⁹⁹¹; Huibers and Katritzky, ¹⁹⁹⁸; Kim et al., ²⁰⁰⁷; Liang and Gallagher, ¹⁹⁹⁸; Lü et al., ²⁰⁰⁷; Makino, ¹⁹⁹⁸; Reddy and Locke, ^1994a; Sabljic et al., ¹⁹⁸⁹; Schüürmann, ¹⁹⁹⁵; Sudhakaran and Amy, ²⁰¹³; Xie et al., ²⁰⁰⁸; Tables S3–S9). Therefore, one could hypothesize that the combination of the five descriptors that were identified as the most used and most generic ones will be pretty much helpful to develop the next generation of QSAR to predict a range of environmental parameters for a wide diversity of organic compounds.

5. CONCLUSION

A tremendously high number of organic compounds having a wide diversity are still released in the environment. Although it is well known that some of them will cause environmental and health problems in a near future, they cannot be studied on a case by case basis because it is time consuming and cost prohibitive. Therefore, in order to overcome this problem, a lot of QSAR allowing the prediction of the fate of organic compounds in the environment from their molecular properties were developed. This review is the first comprehensive synthesis of QSAR focused on the principal processes governing the behavior of organic compounds in the different compartments of the environment, and using only structural molecular descriptors.

The most important numbers of equations were found for pK_a, K_OW, adsorption to soils and biodegradation parameters. A lack of QSAR was observed to estimate the desorption, nonequilibrium adsorption, adsorption nonlinearity, potential of transfer to water (especially surface water), or nonextractable residues formation. Five molecular descriptors (energies of orbitals EHOMO and ELUMO, polarizability α, dipole moment μ and molecular weight (MW)) were especially used in the 790 equations, and also involved in the assessment of the highest diversity of environmental processes. Further QSAR development should therefore pay a particular attention to these descriptors. In addition, the combination of descriptors belonging to different categories (e.g., constitutional, topological, quantum-chemical) was generally found to improve the predictions of the environmental parameters as it simultaneously considers different representations and properties of the molecule.

In order to facilitate the broader application of the QSAR in organic compounds risks assessment, it is important to define criteria of acceptability of these predicting models, improving their validation, defining their accuracy, and defining and checking their applicability domain (range of cases for which prediction can be made; Boethling and Costanza, ²⁰¹⁰; Gramatica, ²⁰⁰⁷; Hermens et al., ¹⁹⁹⁵; Jaworska et al., ²⁰⁰⁵). The use of QSAR for regulatory purposes has been increasing steadily (Cronin et al., 2003; Mackay et al., ²⁰⁰³). This review is delivering relevant QSAR equations to predict the fate of a wide diversity of compounds in the environment. In a near future the development and the implementation of highly powerful QSAR may offer an invaluable insight in various stages of the hazard and risk assessment processes.

ACKNOWLEDGMENTS

The authors acknowledge the anonymous reviewers for their constructive comments.

SUPPLEMENTAL MATERIAL

Supplemental data for this article can be accessed on the publisher*s website.