A computational modelling approach combined with cellular electrophysiology data provides insights into the therapeutic benefit of targeting the late Na⁺ current

Abstract

Selective inhibition of the slowly inactivating or late Na⁺ current (I_NaL) in patients with inherited or acquired arrhythmia syndrome may confer therapeutic benefit by reducing the incidence of triggers for arrhythmia and suppressing one component of arrhythmia-promoting cardiac substrates (e.g. prolonged refractoriness and spatiotemporal dispersion of action potential duration). Recently, a novel compound that preferentially and potently reduces I_NaL, GS-458967 (IC₅₀ for block of I_NaL = 130 nm) has been studied. Experimental measurements of the effects of GS-458967 on endogenous I_NaL in guinea pig ventricular myocytes demonstrate a robust concentration-dependent reduction in action potential duration (APD). Using experimental data to calibrate I_NaL and the rapidly activating delayed rectifier K⁺ current, I_Kr, in the Faber–Rudy computationally based model of the guinea pig ventricular action potential, we simulated effects of GS-458967 on guinea pig ventricular APD. GS-458967 (0.1 μm) caused a 28.67% block of I_NaL and 12.57% APD shortening in experiments, while the model predicted 10.06% APD shortening with 29.33% block of I_NaL. An additional effect of I_NaL block is to reduce the time during which the membrane potential is in a high resistance state (i.e. the action potential plateau). To test the hypothesis that targeted block of I_NaL would make ventricular myocytes less susceptible to small electrical perturbations, we used the computational model to test the degree of APD prolongation induced by small electrical perturbations in normal cells and in cells with simulated long QT syndrome. The model predicted a substantial dose-dependent reduction in sensitivity to small electrical perturbations as evidenced by action potential duration at 90% repolarization variability in the presence of GS-458967-induced I_NaL block. This effect was especially potent in the ‘disease setting’ of inherited long QT syndrome. Using a combined experimental and theoretical approach, our results suggest that I_NaL block is a potent therapeutic strategy. This is because reduction of I_NaL stabilizes the action potential waveform by reducing depolarizing current during the plateau phase of the action potential. This reduces the most vulnerable phase of the action potential with high membrane resistance. In summary, by reducing the sensitivity of the myocardial substrate to small electrical perturbations that promote arrhythmia triggers, agents such as GS-458967 may constitute an effective antiarrhythmic pharmacological strategy.

Key points

• The ventricular action potential plateau is a phase of high resistance, which makes ventricular myocytes vulnerable to small electrical perturbations.

• We developed a computationally based model of GS-458967 interaction with the cardiac Na+ channel, informed by experimental data recorded from guinea pig isolated single ventricular myocytes.

• The model predicts that the therapeutic potential of GS-458967 derives largely from the designed property of significant potent selectivity for INaL.

Introduction

The plateau phase of the cardiac action potential results from precisely tuned fluxes of Na⁺ and Ca²⁺ into the myocyte balanced by efflux of potassium ions (Luo & Rudy, 1994; Zeng et al. 1995; Viswanathan et al. 1999). The ventricular action potential lasts several hundred milliseconds, and this is critical to allow required intracellular Ca²⁺-triggered release from intracellular stores and diffusion of Ca²⁺ to contractile elements, both of which synchronize the electrical signal to the mechanical elements that produce cell shortening (Grant, 2009). While this long action potential allows for effective excitation–contraction coupling, it is well known that the currents that maintain the plateau are very small. Thus, the cardiac action potential plateau is a phase of high resistance. This renders the myocyte action potential duration vulnerable to even very small perturbations. Indeed, even normal healthy cardiac ventricular myocytes, when isolated and then paced at a constant frequency, display marked beat-to-beat variability (Zaniboni et al. 2000). Under physiological conditions cardiac ventricular electrical activity is a highly synchronized process due to the strong electrotonic coupling between myocytes. In contrast, disease states (e.g. regional ischaemia and concomitant fibrosis) lead to reduced coupling between distinct spatial regions in ventricle and even between adjacent cells (de Bakker et al. 1993; Kumar & Joyner, 1995; Miragoli et al. 2007; Zlochiver et al. 2008; Pedrotty et al. 2009; Ashihara et al. 2012; Nguyen et al. 2014). As a result, in pathological settings, weakly coupled cells can oscillate out of phase, resulting in spatial heterogeneity of repolarization. Thus, adjacent ventricular regions may exhibit spatially discordant alternans, an extension of beat-to-beat variability at the tissue level (Qu et al. 2004; Nguyen et al. 2012).

Recently a novel compound, GS-458967, that potently reduces late Na⁺ current (I_NaL) was developed (Belardinelli et al. 2013; Antzelevitch et al. 2014). Experimental measurements of the effects of GS-458967 on endogenous I_NaL in guinea pig ventricular myocytes demonstrate a concentration-dependent reduction in action potential duration (APD). Because GS-458967 block of endogenous late I_Na shortens the plateau and APD, it also reduces the time during which the myocyte exists in a high resistance state. As a result, it is plausible that targeted inhibition of I_NaL would make cells less susceptible to small electrophysiological perturbations. These may arise from spatial and temporal dispersion of repolarization, electrical and/or mechanical remodelling resulting from paracrine, autonomic or inflammatory stress during disease progression, electrotonic influences of the surrounding tissue, and arrhythmia triggers in the form of early and delayed afterdepolarizations (Liu et al. 1992; Ver Donck et al. 1993; Bennett et al. 1995; Le Grand et al. 1995; Song et al. 2006, 2008).

In order to evaluate the potential for GS-458967-induced block of I_NaL to reduce APD and incr-ease susceptibility to APD variability induced by small electrical perturbations, we have adapted and applied a computationally based multiscale modelling approach. The starting point was based on our recently developed model for simulating the interaction kinetics of the anti-arrhythmic drugs with cardiac Na⁺ channels and their emergent effects on cardiac ventricular electrical activity (Moreno et al. 2011, 2013).

The emergent effects of a drug on the electrical activity of a cardiac myocyte derive from the kinetics of the drug-affected current. This results in changed voltage profile of the action potential plateau. Thus, we also used the computational approach to determine whether different methods of APD shortening can reduce myocyte sensitivity to perturbation. We did this by first testing inhibition of late I_Na, which is essentially ‘kineticless’: it resembles a time-independent current during the plateau of the action potential (AP). Thus, reducing late I_Na results in a fairly uniform reduction of inward current throughout the duration of the plateau. We also evaluated enhancing activation of the rapidly activating delayed rectifier K⁺ current, I_Kr. Even though both treatments could be adjusted in silico so that they result in identical shortening of APD, I_Kr has kinetics that result in a steep increase in current late during the late plateau phase of the AP. Our simulations suggest that preferentially enhancing I_Kr late in the plateau phase to reduce APD results in a steeper repolarization phase that is more sensitive to applied electrophysiological perturbations than comparable APD shortening resulting from block of I_NaL.

This paper explores the promising concept of the potential for a drug to reduce sensitivity to electrophysiological perturbation. It is based on experimental findings in guinea pig ventricular cell preparations and insights gained from a mathematical model of the guinea pig ventricular action potential and Ca²⁺ homeostasis. Consideration of the mechanisms for the high resistance of the plateau phase of the action potential, in combination with the pharmacological inhibition of I_NaL yield important new physiological insights and illustrate fundamental relationships between a molecular pharmacology effect and changes to the action potential waveform.

Methods

Experimental methods in MICEE reporting standard www.micee.org.

Material

Type

Isolated cardiac ventricular myocytes.

Ethical approval

Animal use was approved by the Institutional Animal Care and Use Committee, and conformed to the Guide for the Care and Use of Laboratory Animals (National Research Council, 2011).

Sex

Either sex.

Weight

301–350 g.

Species

Hartley guinea pig.

Supplier

Charles River (Wilmington, MA, USA).

Isolation procedure

Use of animals was in accordance with the Guide for the Care and Use of Laboratory Animals (NIH Publication 86-23, 1985) and was approved by the Institutional Animal Care and Use Committee of the University of Florida. Adult Hartley guinea pigs of either sex were anesthetized with inhalant isoflurane delivered through a vaporizer. Hearts were surgically isolated and perfused via the aorta with warm (35°C) and oxygenated solutions as follows: (1) Tyrode solution containing (in mmol l⁻¹) 135 NaCl, 4.6 KCl, 1.8 CaCl₂, 1 MgCl₂, 10 glucose and 10 Hepes, pH 7.4, for 5 min; (2) Ca²⁺-free solution containing (in mmol l⁻¹) 100 NaCl, 30 KCl, 2 MgCl₂, 10 glucose, 10 Hepes, 15 taurine, and 5 pyruvate, pH 7.4, for 5 min; and (3) Ca²⁺-free solution containing collagenase (120 units ml⁻¹) and albumin (2 mg ml⁻¹), for 20 min. At the end of the perfusion, the ventricles were minced and gently shaken for 10 min in No. 3 solution to release single cells. Only the quiescent myocytes with clear striations were used for this study.

Electrophysiological recordings

Transmembrane voltages and currents were determined using the whole-cell patch-clamp technique. Data were acquired and analysed with an Axopatch 200 amplifier, a Digidata 1440A digitizer and pCLAMP 10 software. All experiments were performed at 36°C. Series resistance compensation of 80–90% was applied in these experiments.

For measurements of action potentials, cells were incubated in the Tyrode solution (bath solution). The recording pipettes were filled with a solution containing (in mmol l⁻¹) 120 potassium aspartate, 20 KCl, 1 MgSO₄, 4 Na₂ATP, 0.1 Na₃GTP, and 10 Hepes, pH 7.3. A depolarizing pulse was applied every 6 s to elicit action potentials. The APD was determined from the beginning of depolarization to the time when 50% of repolarization was completed.

For measurements of late I_Na, myocytes were superfused with a bath solution containing (in mmol l⁻¹) 135 NaCl, 1.8 CaCl₂, 1 MgCl₂, 10 glucose, 10 Hepes, 4.6 CsCl, 0.05 NiCl₂, and 0.01 nitrendipine, pH 7.4. The recording pipettes were filled with a solution containing (in mmol l⁻¹) 120 caesium aspartate, 20 CsCl, 1 MgSO₄, 4 Na₂ATP, 0.1 Na₃GTP, and 10 Hepes, pH 7.2. Sodium current was activated by 200 ms voltage-clamp pulses applied every 10 s, from a holding potential of −90 mV to a test potential of −30 mV. The amplitude of late I_Na was calculated as the average amplitude of current during the last 100 ms of a depolarizing pulse.

Measurements of ionic currents during the guinea pig plateau (as in Fig.2) were made using the methods described in (Horvath et al. 2013).

Figure 2.

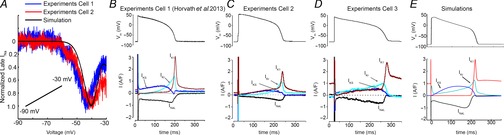
Predictions of the model compared to experiments

A shows the superimposition of model-predicted and experimentally recorded current in response to a slow depolarizing ramp voltage protocol. B, C and D, experimentally recorded transmembrane ionic currents (I_Ks, I_Kr, I_K1 and I_NaL) during the guinea pig ventricular action potential compared to the simulated current profiles during the AP in the Faber–Rudy model (Faber & Rudy, 2000) in E. (B is reproduced from Horvath et al. 2013.)

Model development

Full computational methods are contained in an online supplement. A package consisting of source code and all related components required to generate each simulation result in each figure is also included in the supplemental materials.

Results

As an initial step we calibrated a computer model of the wild-type cardiac Na⁺ current (Moreno et al. 2011) by optimizing the model parameters to reproduce the timecourse and amplitude of I_Na that was experimentally recorded from guinea pig ventricular myocytes. In Fig.1, the adjusted, post-optimized, model-generated I_Na (black) is shown superimposed on experimental records (colours) at low gain (left panels) and high gain (corresponding data in right panels) in the absence of drug (A and B; n = 30 experiments from 30 cells shown) and presence of 0.3 μm GS-458967 (C and D; n = 10 experiments from 10 cells) and 1 μm GS-458967 (E and F; n = 10 experiments shown from 10 cells). Current records were normalized to the peak I_Na value.

Figure 1.

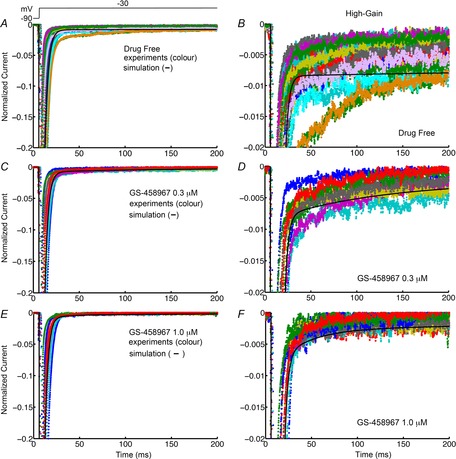
Simulated and experimentally recorded I_Na data from isolated guinea pig ventricular myocytes

Model-generated I_Na in guinea pig ventricular myocytes (black) is shown superimposed on experimental I_Na records. The right panels show late I_Na at high gain. Currents were normalized to peak values. Normalized I_Na is shown in the absence of GS-458967 (A, n = 30 for experiments) and presence of 0.3 μm (B, n = 10) and 1 μm (C, n = 10) GS-458967.

Following calibration of the timecourse and amplitude of I_Na, we subjected the model to a validation test by simulating a slow depolarizing ramp and comparing the simulated current to an experimentally measured current recorded during the same protocol Fig.2A). The model-generated inward current was comparable to experimentally measured current.

We next adjusted other key ionic currents in the Faber–Rudy guinea pig ventricular action potential model (Faber & Rudy, 2000) by comparing the simulated current profiles during the AP to those experimentally recorded from individual guinea pig ventricular myocytes using the self AP-clamp sequential dissection technique under physiological conditions (Horvath et al. 2013) (Fig.2B–E). The Faber–Rudy model output was in good agreement with the experimentally recorded currents, with the exception of the rapidly activating delayed rectifier K⁺ current, I_Kr. I_Kr exhibited slower kinetics than the experimental data for I_Kr (Supplemental Figure S1). Thus we evaluated I_Kr models from other ventricular myocyte models. This revealed that the kinetics of I_Kr from ten Tusscher & Panfilov (2006) closely reproduced the experimental I_Kr shown in Fig.2. The maximum conductances of other currents were also tuned to better approximate the experimentally measured current amplitude during the action potential and generate an action potential duration within the experimental range (see Supplemental Table 1).

Although the currents that are active during the plateau are of small amplitude, each exhibits distinct kinetics. I_NaL has very little time dependence and thus it has nearly constant amplitude throughout the plateau of the AP. This is in contrast to I_Kr, which has distinct kinetics resulting from very rapid inactivation upon depolarization followed by subsequent recovery from inactivation. The latter leads to a transition to the open state prior to slow deactivation that results in a steep increase in current late in the plateau of the AP, where it surpasses the amplitude of the slowly activating component of the delayed rectifier current I_Ks. The final repolarization phase of the AP is marked by a sharp rise in the inwardly rectifying K⁺ current (I_K1) current.

GS-458967 causes marked concentration-dependent shortening of APD

GS-458967 has been shown to selectively inhibit endogenous late I_Na and cause a marked dose-dependent shortening of APD in ventricular myocytes (Song et al. 2012; Belardinelli et al. 2013; Sicouri et al. 2013). We have used these experimental data from guinea pig ventricular myocytes (Song et al. 2012) as the basis for a validation and testing of the model to accurately predict the effects of GS-458967 on simulated guinea pig APs. We incorporated our calibrated Na⁺ channel model from Fig.1 and recalibrated I_Kr from Fig.2 into the Faber–Rudy model of the cardiac ventricular action potential. The results are shown in Fig.3. Panel A shows the simulated effects of 10-fold changes in doses of GS-458967 to shorten the guinea pig APD. As was observed experimentally, the model accurately predicts marked dose-dependent shortening of the APD. The summary comparison in Fig.3B shows that predicted (line) dose-dependent APD shortening by GS-458967 corresponds to that observed experimentally (symbols). The degree of endogenous I_NaL reduction predicted by the model simulations after selected doses of GS-458967 (Fig.3C) also corresponds closely to the experimentally measured reductions in current in guinea pig ventricular myocytes (Fig.3D).

Figure 3.

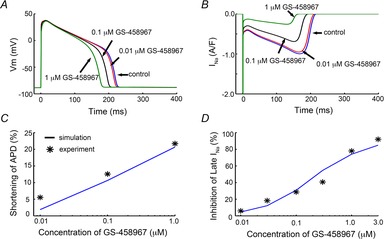
GS-458967 (that specifically targets endogenous late I_Na) causes dose-dependent shortening of the experimental and computed APD in guinea pig ventricular myocytes

A, simulated effects of GS-458967 on guinea pig APD. B, the timecourse of I_Na during the AP. C, experimentally measured and model-predicted GS-458967-induced concentration-dependent reduction in APD. D, experimentally measured and model-predicted effects of GS-458967 on the amplitude of late I_Na.

Membrane resistance during the action potential

In order to further develop the quantitative assessment of the effect of GS-458967 block of endogenous late I_Na on the sensitivity of action potentials to perturbations, we next quantified the membrane resistance in the model ventricular myocyte, and compared our predictions to experimental measurements of membrane resistance from Zaniboni et al. (2000) (Fig.4). A detailed assessment of membrane resistance (R_m) was performed at various time points (Fig.4A–F) in the guinea pig ventricular action potential in experiments (Fig.4A) and in the computational model with no drug (Fig.4B) and with 1 μm GS-458967 (Fig.4C) as indicated by the arrows. Figure 4D, E and F shows experimentally recorded and simulated instantaneous currents generated by clamping the membrane voltage −10 mV or +10 mV with reference to the action potential plateau voltage, at selected points in time during the action potential (see Supplemental Figure S7). From these instantaneous currents, instantaneous I–V relationships were constructed both experimentally (Fig.4E) and in the simulations (Fig.4F). Figure 4G and H shows experimental and simulated membrane resistance values computed from the slopes (dV/dI) of the instantaneous I–V relationships at points in time along the action potential plateau. Note the sharp rise in R_m during the action potential plateau in Fig.4J–L. The points in Fig.4K and L were chosen at the times of the most comparable instantaneous current–voltage relationships. Because GS-458967 block of endogenous I_NaL shortens the APD, it also reduced the time during which the membrane resides in a high resistance state as shown in Fig. 4L.

Figure 4.

Simulated and experimentally measured membrane resistance at selected points in time during the action potential plateau in a guinea pig ventricular myocyte

All experimental data are from Zaniboni et al. (2000). Experimentally recorded (A) and simulated drug-free (B) or in the presence of 1 μm GS-458967 (C) guinea pig ventricular action potentials with arrows indicating time-points during the action potential plateau when experimental (D) and simulated drug free (E) and in the presence of 1 μm GS-458967 (F) instantaneous currents were recorded during the action potential. At each time, current changes in response to voltage steps −10 mV or +10 mV relative to the plateau action potential voltage. Experimental (G) and simulated drug-free (H) and 1 μm GS-458967 (I) instantaneous current–voltage relationships were constructed from the currents in D, E and F at times indicated by arrows in A, B and C. R_m was superimposed on the AP waveforms from experimental (J), and drug-free (K) and 1 μm GS-458967 (L) model-generated reproduction of membrane resistance at the same points in time computed from slopes of the instantaneous I–V curves in G, H and I. Membrane resistance R_m² (dV/dI) at indicated voltages and points in time along the action potential plateau. Note the rapid and substantial rise in R_m values during the AP plateau.

Effects of reduction of I_NaL on sensitivity of cells to small electrophysiological perturbations

A quantitative exploration of the effect of reducing I_NaL on the sensitivity of action potential waveforms to small electrophysiological perturbations was performed using the computational guinea pig ventricular myocyte model to test the degree of action potential duration at 90% repolarization (APD₉₀) prolongation induced by small electrical perturbations. Our approach included small perturbations that are present in any noisy physiological system, or that may result from an ectopic beat or triggered depolarization in nearby cells. To simulate these perturbations, we applied small amplitude inward square wave currents that were varied randomly for each action potential between −0.1 and −0.2 pA pF⁻¹ for 50 ms over the course of the action potential plateau at a pacing cycle length of 1 Hz. The small inward current was also applied randomly in time between 30 and 200 ms on the plateau phase for 1000 beats. APD was recorded in the simulations as the difference between the time from the maximum velocity of the action potential upstroke (dV/dt_max) until the time of 90% repolarization. As shown in Fig.5, our modified model predicted a marked reduction in sensitivity of the APD to small electrical perturbations. Note that the APD₉₀ variability is reduced in response to progressive levels of I_NaL block: no I_NaL block (Fig.5A), low dose (0.1 μm) GS-458967 I_NaL block (Fig.5B), and high dose (1.0 μm) GS-458967 I_NaL block (Fig.5C).

Figure 5.

Systematic comparison of sensitivity of simulated guinea pig cardiac ventricular action potentials to small perturbations before and after application the selective blocker of I_NaL GS-458967

A small inward current (between 0.1 and 0.2 pA pF⁻¹ for 50 ms) was applied randomly during the AP plateau between 30 and 200 ms after AP initiation for no I_NaL block (A), and I_NaL block via 0.1 μm GS-458967 (B) and 1.0 μm GS-458967 (C). Lower panels show the timecourse and amplitude of the associated APD₉₀ variability.

Effects of reduction of I_NaL in the setting of long QT syndrome type 1

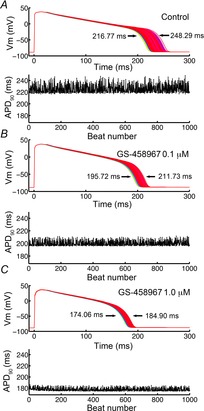
Having shown that reduction of I_NaL via GS-458967 block can be protective against APD variability arising from small electrical perturbations in normal myocytes, we next simulated the pathological situation of inherited long QT syndrome type 1 (LQT1) (Splawski et al. 2000). LQT1 is a congenital disease that arises from a mutation-induced loss of function in the slowly activating component of the voltage-dependent delayed rectifier K⁺ current, I_Ks. Simulation results are shown in Fig.6, where LQT1 action potentials were simulated by reducing the conductance of the slow delayed rectifier K⁺ current, I_Ks, to 50% of normal in the absence of drugs (Fig.6A), or the presence of 0.1 μm GS-458967 (Fig.6B) or 1.0 μm GS-458967 (Fig.6C). In this simulated pathological situation, we observed a marked reduction of APD variability in myocytes pretreated with GS-458967.

Figure 6.

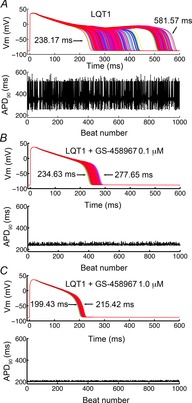
Sensitivity of 1000 simulated LQT1 action potentials to electrophysiological perturbations as indicated by APD variability (protocol as in Fig.5)

Model predictions of sensitivity to these rectangular current stimuli (as evidenced by APD₉₀ variability) are illustrated as follows: A, no I_NaL block; B, I_NaL block by 0.1 μm GS-458967; C, block by 1.0 μm GS-458967. In each panel the data in the bottom row shows the timecourse and amplitude of APD variability.

It is well documented that individual cardiac cells differ in their specific cellular electrophysiology, i.e. there is variability in the cellular action potential duration and morphology. These differences arise from variability in the underlying currents as can be seen in the experimental measurements of ionic currents recorded during the dynamic action potential clamp as shown in Fig.2.

Effects of reduction of I_NaL in the setting of cell variability

To study drug effects on ‘natural’ cell-to-cell variability, we applied a physiological noisy current during the following simulations to allow for efficient construction of 1000 distinct cell action potentials (see Supplemental Figure S8) (Sato et al. 2006, 2013; Tanskanen & Alvarez, 2007). The noisy current was generated as described in Tanskanen & Alvarez (2007) and in the supplemental methods. Following pacing to steady state at a cycle length of 1 Hz, the physiological noise was applied throughout the duration of the ensuing simulation of 1000 paced beats. The action potentials for each beat during the noise protocol were recorded. An additional reason for including noise-induced variability is to allow us to conduct a ‘computational experiment’ in a cell population that generates data sets that can be compared and are not overly sensitive to, or reliant, on the specific set of model parameters.

Figure7A shows the results from our computational experiment. In a population of 1000 ‘normal’ simulated ventricular myocytes (Fig.7A), beat-to-beat APD variability was increased compared with cells from the population pretreated with 0.025 μm GS-458967 (Fig.7B). Note that this dose resulted in exactly the same degree of APD shortening as the converse approach: applying an I_Kr activator that increased I_Kr by 12% (Fig.7C). The middle row of panels A, B and C are Poincaré plots showing sequential AP variability (APDⁱ versus APD_i+1) and the bottom row of panels shows the histogram distributions of the action potential durations for each case. While the drug-free model action potentials exhibited marked beat-to-beat variability (Fig.7A, mean = 220.74 ms, standard deviation = 5.2 ms, maximum (max) APD₉₀ = 240.45 ms, minimum (min) APD₉₀ = 204.83 ms), the model predicts that 0.025 μm GS-458967 is slightly better at reducing the cell-to-cell variability (P = 0.0093) via reduction in late I_Na (Fig.7B, mean = 211.43 ms, standard deviation = 4.17 ms, max APD₉₀ = 224.98 ms, min APD₉₀ = 197.58 ms) than I_Kr activation (increase I_Kr by 12%) (Fig.7C, mean = 211.95 ms, standard deviation = 4.66 ms, max APD₉₀ = 227.8 ms, min APD₉₀ = 200.00 ms), even though the I_Kr activator caused the same extent of APD shortening (note increased APD variability in larger area of Poincaré plot and APD histogram in Fig.7C compared to GS-458967).

Figure 7.

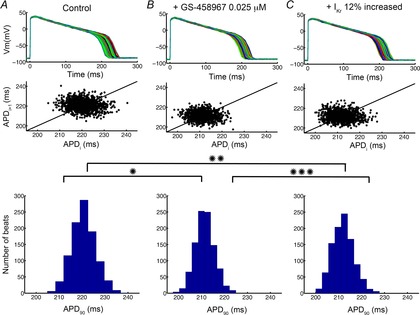
Predicted sensitivity of APD₉₀ of 1000 action potentials to drug treatment in the presence of a physiological noise current

Graphs show drug-free (A), 0.025 μm GS-458967 (B) or I_Kr activator (I_Kr increased by 12%) (C) conditions. Poincaré plots of sequential APD pairs indicating beat-to-beat variability are shown in the middle row for each selected condition. Histogram distributions of APD are shown in the bottom row. *P = 1.9 × 10⁻²⁹⁷, **P = 1.2 × ⁻²⁵⁵, ***P = 0.0093.

We then tested these same interventions in the setting of reduced I_Ks to mimic LQT1. As shown in Fig.8A our simulations revealed pronounced cell-to-cell variability in LQT1 ventricular myocytes accompanied by induction of early afterdepolarizations (EADs; mean = 369.89 ms, standard deviation = 113.46 ms, max APD₉₀ = 718.02 ms, min APD₉₀ = 199.06 ms). We then compared 0.035 μm GS-458967 (Fig.8B), which resulted in identical APD shortening to an I_Kr activator (Fig.8C; increase I_Kr by 17%) to normalize EADs and reduce the cell-to-cell variability. Note that GS-458967 was again more effective as judged by reduction of cell-to-cell variability as indicated by the reduced area of the Poincaré plot and histogram distribution in Fig.8B (mean = 272.44 ms, standard deviation = 13.54 ms, max APD₉₀ = 370.99 ms, min APD₉₀ = 240.74 ms) compared to I_Kr activator in Fig.8C (mean = 276.59 ms, standard deviation = 16.54 ms, max APD₉₀ = 412.76 ms, min APD₉₀ = 237.11 ms).

Figure 8.

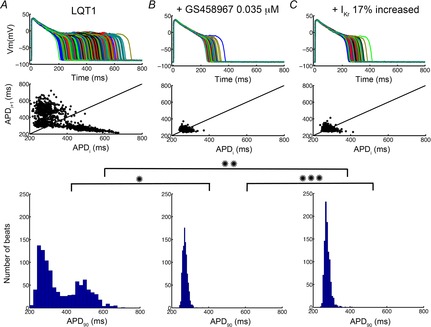
Predicted sensitivity of 1000 ‘diseased’ LQT1 cell action potentials incorporating physiological noise to induce beat-to-beat variability in response to drug treatment

1000 individual LQT1 model cells are shown. Data in A correspond to baseline LQT1 conditions. B shows the effects of the presence of 0.035 μm GS-458967. C indicates the predicted effects of an I_Kr activator. Poincaré plots of sequential APD pairs indicating beat-to-beat variability are shown in the middle panel for each case. Histogram distributions of APD are shown in the bottom row. *P = 6.6 × ⁻¹³⁷, **P = 2.3 × ⁻¹²⁶, ***P = 9.6 × ⁻¹⁰.

Discussion

The long cardiac ventricular action potential allows for effective excitation–contraction coupling. However, the ventricular action potential plateau is a phase of high resistance, which makes ventricular myocytes vulnerable to small electrical perturbations that may arise from spatial and temporal dispersion of repolarization, electrical and/or mechanical remodelling resulting from stress or disease, the existence of distinct cell populations, or electrotonic influences of the surrounding tissue and arrhythmia triggers in the form of early and delayed afterdepolarizations.

In an earlier study, Noble & Noble (2006) utilized a computational modelling and simulation approach to predict that specific block of I_NaL could mitigate repolarization failure induced by I_Kr block. Like most modelling and simulation studies, these simulations captured the concept of idealized drugs by reducing channel conductances in the model and suggested general mechanisms of cardiac action potential plateau behaviour. The plateau reflects a balance of depolarizing and repolarizing current and Noble and Noble showed that changes in one current may alter or prevent action potential repolarization, but that these disruptions can be alleviated by additional current perturbation(s) that counterbalance the original change.

In this study, we sought to use a computationally based approach to predict if the candidate drug GS-458967 can prevent emergent arrhythmogenic activity in virtual ventricular myocytes in response to small electrical perturbations. In order to do so, we developed a computationally based model of GS-458967 interaction with the cardiac Na⁺ channel, informed by experimental data recorded from guinea pig isolated single ventricular myocytes (Fig.1). We also modelled the drug effect as a linear reduction of ‘late G_Na’ (GNa is maximal conductance of the Na channel; shown in Supplemental Figure S6), but the simplified approach failed to reproduce the kinetics of the timecourse of current reduction. We integrated the optimized model of the drug–channel interaction into the Faber–Rudy model of the guinea pig ventricular action potential, which was also recalibrated to reproduce experimental currents measured during the guinea pig plateau (Fig.2). The simulations predicted GS-458967 dose-dependent shortening of the APD, and that was validated by experimental data (Fig.3) (Song et al. 2012). The cellular-level model simulations also predicted a drug-induced reduction in the duration of the high resistance phase of the action potential plateau and consequently, reduced sensitivity of the APD to small electrical perturbations as evidenced by reduced APD₉₀ variability in the presence of GS-458967-mediated I_NaL block. The model simulations predicted only nominal changes to intracellular Na⁺ concentration and consequently to the amplitudes of the Na/Ca2⁺ exchanger and Na/K⁺ ATPase currents during the action potential (Supplemental Figure S4). These results are not surprising. Previous studies have suggested that even pathological increases in late I_Na are not sufficient to account for substantial Na⁺ loading and that other mechanisms must also be contributing to Na⁺ loading (Grandi et al. 2007; Wagner et al. 2011; Moreno et al. 2013).

As it becomes increasingly clear that the most commonly used surrogate marker of arrhythmia (i.e. the corrected QT interval) is insufficient to accurately predict arrhythmia risk (Hondeghem, 2006), alternative approaches to assess arrhythmia vulnerability need to be developed and validated. For example, it is well documented that spatial and temporal variability in action potential repolarization in the heart is a precursor to ventricular arrhythmias (Antzelevitch & Fish, 2001; Lankipalli et al. 2005). Dispersion of repolarization promotes arrhythmia because myocytes that exhibit prolonged repolarization can serve as depolarizing current sources for downstream myocytes. In the electrotonically coupled myocardium, such current sources may lead downstream myocytes to give rise to triggered arrhythmias. But, this can only occur if those downstream cells are vulnerable to the electrical perturbation. In terms of therapeutic approaches, two targets exist; either the ‘source’ of the current can be extinguished by preventing or reducing dispersion of repolarization, or the ‘sink’ for the current can be rendered insensitive to the perturbations. Our simulations predict that pretreatment with GS-458967 is an effective approach to modify the ‘sink’ and thereby reduce its sensitivity to the arrhythmogenic sources.

During the cardiac action potential plateau, the membrane current becomes increasingly small and the membrane resistance rises sharply. This is qualitatively reproduced in the computational model, where the resistance approaches infinity as current approaches zero towards the end of the AP plateau, a point at which the membrane is expected to be most sensitive to small changes in current. This can be very clearly seen in the instantaneous I–V relationship that is generated by clamping the membrane voltage to +10 mV or −10 mV with reference to the action potential plateau voltage, during the action potential (see Supplemental Figure S7). Throughout most of the plateau the current elicited by a +10 mV clamp is outward while the −10 mV voltage clamp initiates an inward current. Late in the action potential plateau there is a switch, as inward currents inactivate and the I_K1 current activates. At the crossover point, the membrane resistance rises sharply as the difference in current at the crossover point is zero, so the limit in the computational model of dV/dI → ∞. This can also be observed as the flattening of the instantaneous I–V curves in Fig.4G for point E. In the computational model, we can get extremely close to this point of crossover because we can compute the instantaneous I–V curve with extremely high temporal fidelity. This is not the case experimentally, where just a few milliseconds on either side of the crossover point will have a major impact on the dV/dI calculation. This is also the reason why the membrane resistance in the model simulation appears to be so much higher than in the experiment – we can compute the instantaneous I–V at a point in time that is very near to the crossover point.

We have also compared the efficacy of GS-458967 with a simulated I_Kr activator, which has been suggested as a novel drug class for treating channelopathies (Seebohm, 2005; Zhou et al. 2005). These simulations suggest that activation of I_Kr is not as effective as block of I_NaL, judged in terms of reducing the sensitivity of cells to small perturbations. This is the case even when the I_Kr activator was titrated so that the degree of APD shortening was identical to that caused by GS-458967. I_Kr has intrinsic kinetics that result in an increase in the current late in the plateau phase of the action potential, that is, during the period of highest membrane resistance. The steep increase in I_Kr late in the action potential plateau is even more pronounced with the application of an ‘activator’ (leading to a steepening of repolarization slope). The model predicts that, as a result, I_Kr activation is a less effective approach to reduce the membrane sensitivity to small perturbations than targeted block of I_NaL.

In our model predictions in simulated guinea pig ventricular myocytes, the therapeutic effect of GS-458967 was amplified when we simulated pathological inherited long QT syndrome type 1 (LQT1). The first LQT syndrome locus (LQT1) was linked to mutations in KCNQ1, a gene coding for the α subunit of the voltage-gated potassium channel, the slowly activating delayed rectifier potassium current, I_Ks (Splawski et al. 2000; Clancy et al. 2003). In the guinea pig ventricle, I_Ks plays a critical role in cardiac repolarization as well as the characteristic rate-dependent shortening of the action potential in response to increases in heart rate (Lu et al. 2001; Silva & Rudy, 2005; Terrenoire et al. 2005). LQT1 action potentials were generically simulated in the model by reducing I_Ks in accordance with experiments. In this setting of LQT1, we observed differences in the reduction of EADs and APD variability in cells pretreated with GS-458967 versus an I_Kr activator.

There are some limitations of our study that should be noted. First, it is important to state that we have not developed a detailed model of a hERG activator, rather we used a simplified approach by increasing the maximal conductance of the channel. Because individual I_Kr activators have specific and distinct kinetic interactions with the channel, we may predict different effects by simulating specific activators (Casis et al. 2006; Guo et al. 2014). For example, many I_Kr activators that reduce inactivation would be expected to augment the steep current increase during the plateau phase of the action potential and perform more similarly to GS-458967 than we predict in this study.

Another important limitation of our study, and indeed all modelling and simulation studies, is determining when a model is ‘good enough’ and captures the general but essential behaviour of the system. There may be limited value in some cases to developing a model that is very tightly informed by a single experimental data set, especially if the model predictions are sensitive to the specific parameter set. Experimentally recorded currents from individual myocytes vary from cell to cell, and so variability may need to be considered in a model when threshold responses such as EADs are observed. We have tried to account for variability by building sensitivity tests into our models, which allows for a test of robustness of the results of the simulation to changes in parameters. We have done this by applying random perturbations during the plateau phase of the action potential and also by applying a continuous stream of physiological noise in other simulations (Fox & Lu, 1994; Tanskanen & Alvarez, 2007; Sato et al. 2013). Doing so increases our confidence that the model predictions are robust and not overly sensitive to small perturbations.

By targeting I_NaL, which is increased in a number of pathological settings, GS-458967 shows promise for treatment of triggered arrhythmias. Notably, GS-458967 was very effective in reducing cell-to-cell variability in normal cells and especially in the setting of LQT1. The model thus predicts multiple therapeutic effects of an I_NaL inhibitor: (1) shortening of APD, (2) prevention of emergent EADs and (3) marked reduction in cell-to-cell variability.

In summary, we applied a computational model of normal myocytes and computational models of LQT1 to specifically test a therapeutic intervention that targets the aberrant molecular mechanism of persistent I_NaL. The results of our study suggest that the therapeutic potential of GS-458967 derives largely from the designed property of significant potent selectivity for I_NaL.

This study represents one step toward construction of an in silico high throughput preclinical drug testing system that can be used to compare various therapies in normal ventricular myocytes and also in myocytes with simulated gene defects that alter transmembrane current. This framework can be readily extended to myriad disease states, genotypes and drugs.

Supporting information for this study is available including expanded methodology, parameters and validation. Also available as online supporting information for each published figure, is a package of model components (fully documented source code), modeling parameters (and initial conditions) and associated datasets used for comparison or optimization. This bundle contains all necessary information to allow any user to reproduce the published figure. The packages available in C source code.

Glossary

AP

action potential

APD

action potential duration

APD₉₀

action potential duration at 90% repolarization

EAD

early afterdepolarization

I_K1

inwardly rectifying K⁺ current

I_Kr

rapidly activating delayed rectifier K⁺ current

I_Ks

slowly activating component of the delayed rectifier current

I_NaL

late Na⁺ current

LQT1

long QT syndrome type 1

R_m

membrane resistance

Additional information

Competing interests

C.E.C. and Y.C.-I. have significant grant support from Gilead Sciences.

Author contributions

P.-C.Y. designed and performed simulations, optimizations, and prepared the manuscript; W.R.G., S.R. and L.B. designed experiments and simulations, analyzed data and prepared the manuscript; Y.S., B.H. and Y.C.-I. designed and performed experiments; C.E.C. designed simulations and experiments, analyzed data, coordinated and oversaw the project, and prepared the manuscript. All authors approved the final submitted version.

Funding

This work was supported by the American Heart Association (GIA 13GRNT14370019, Western States Affiliate), National Institutes of Health R01GM101928, R01HL105242, and Gilead Sciences.

Supporting Information

Disclaimer: Supporting information has been peer-reviewed but not copyedited.