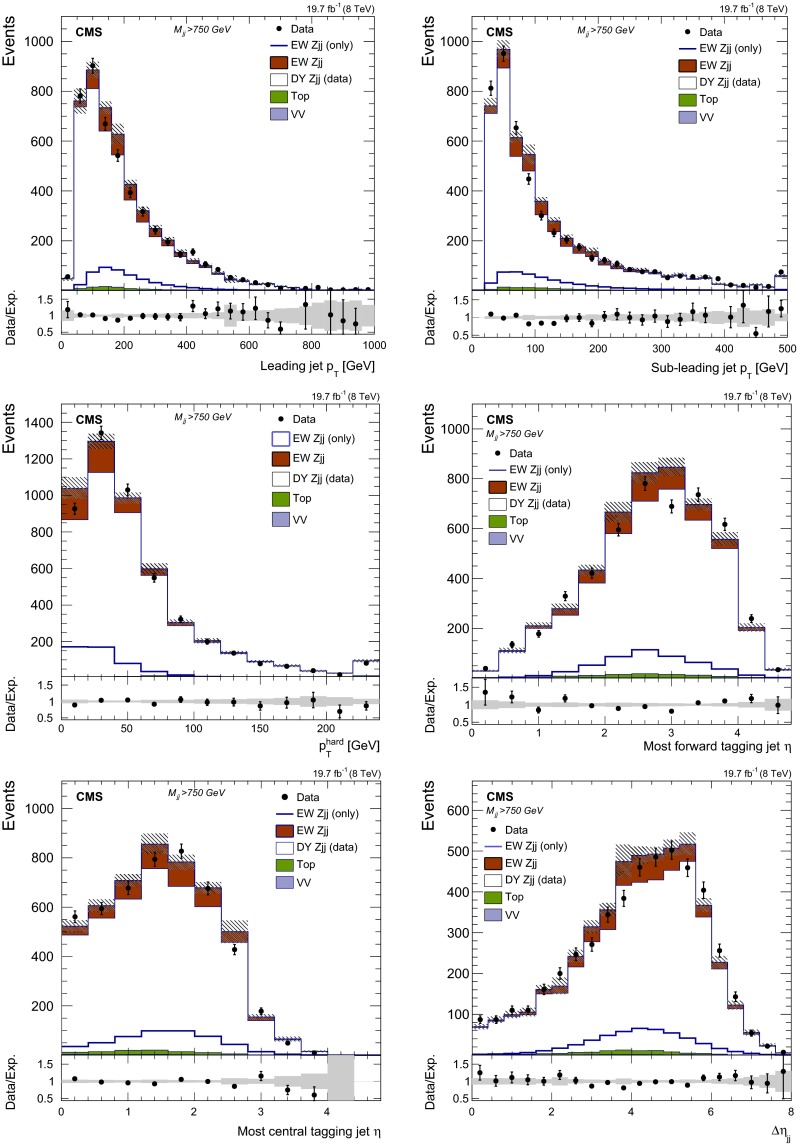
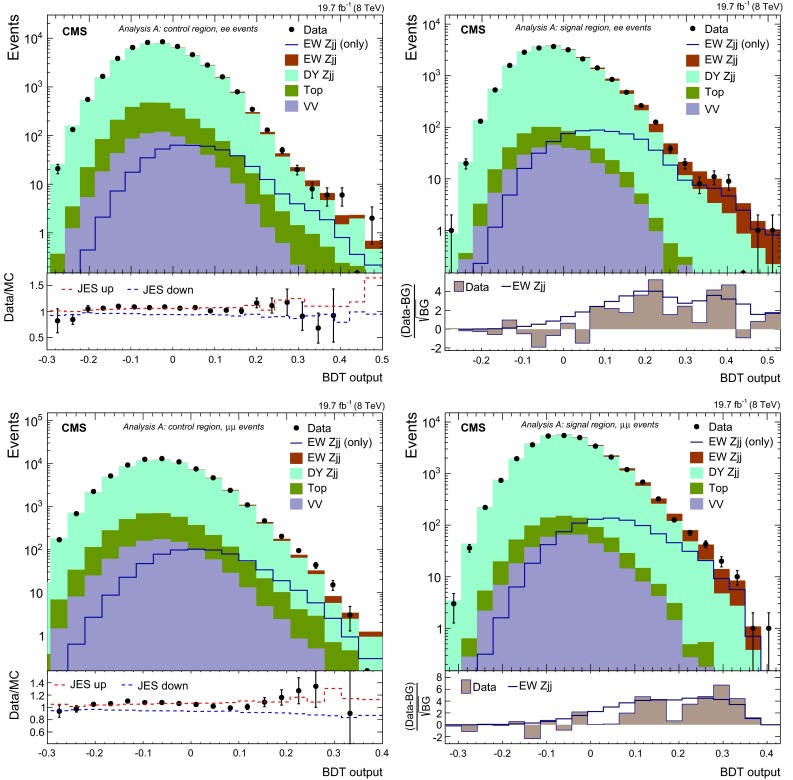
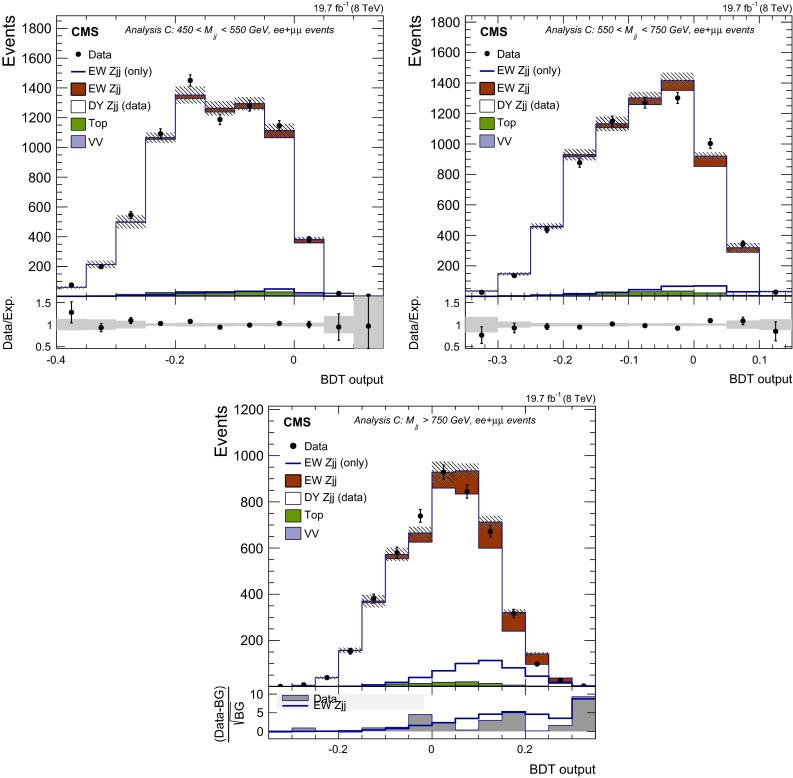
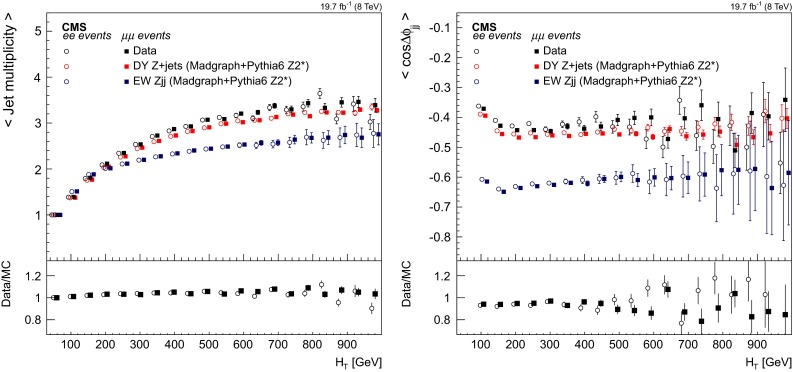
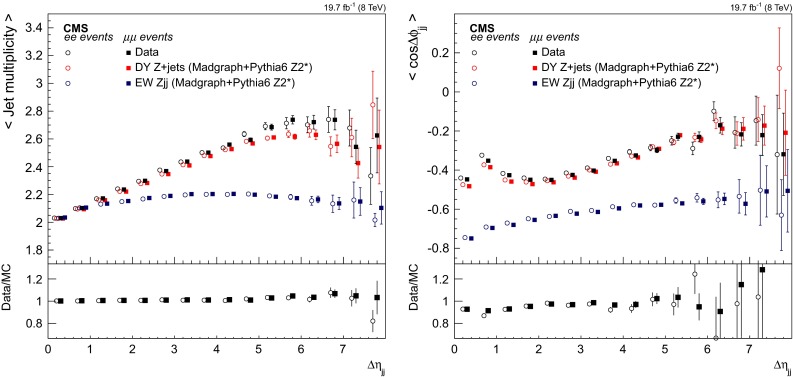
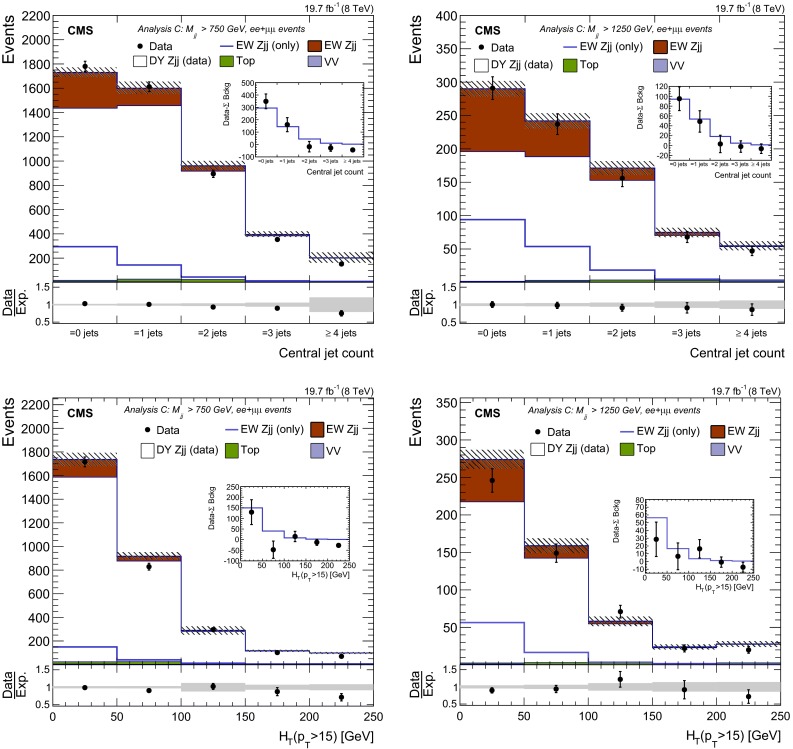
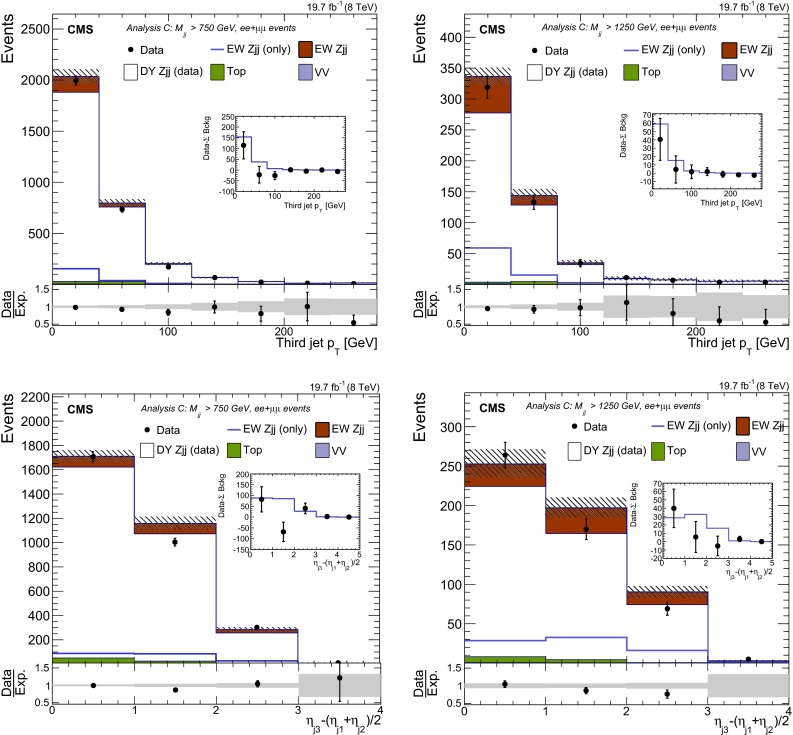
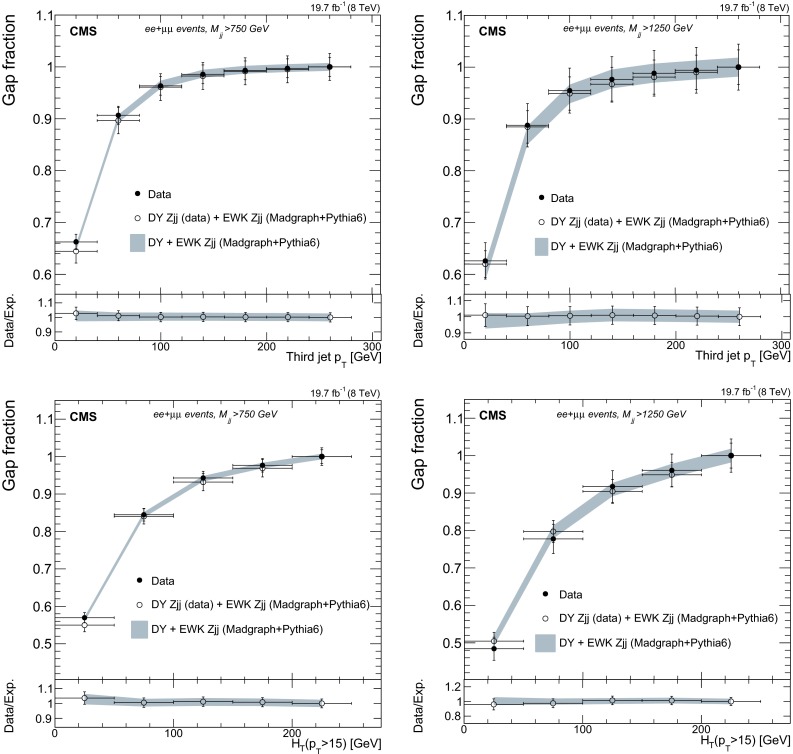
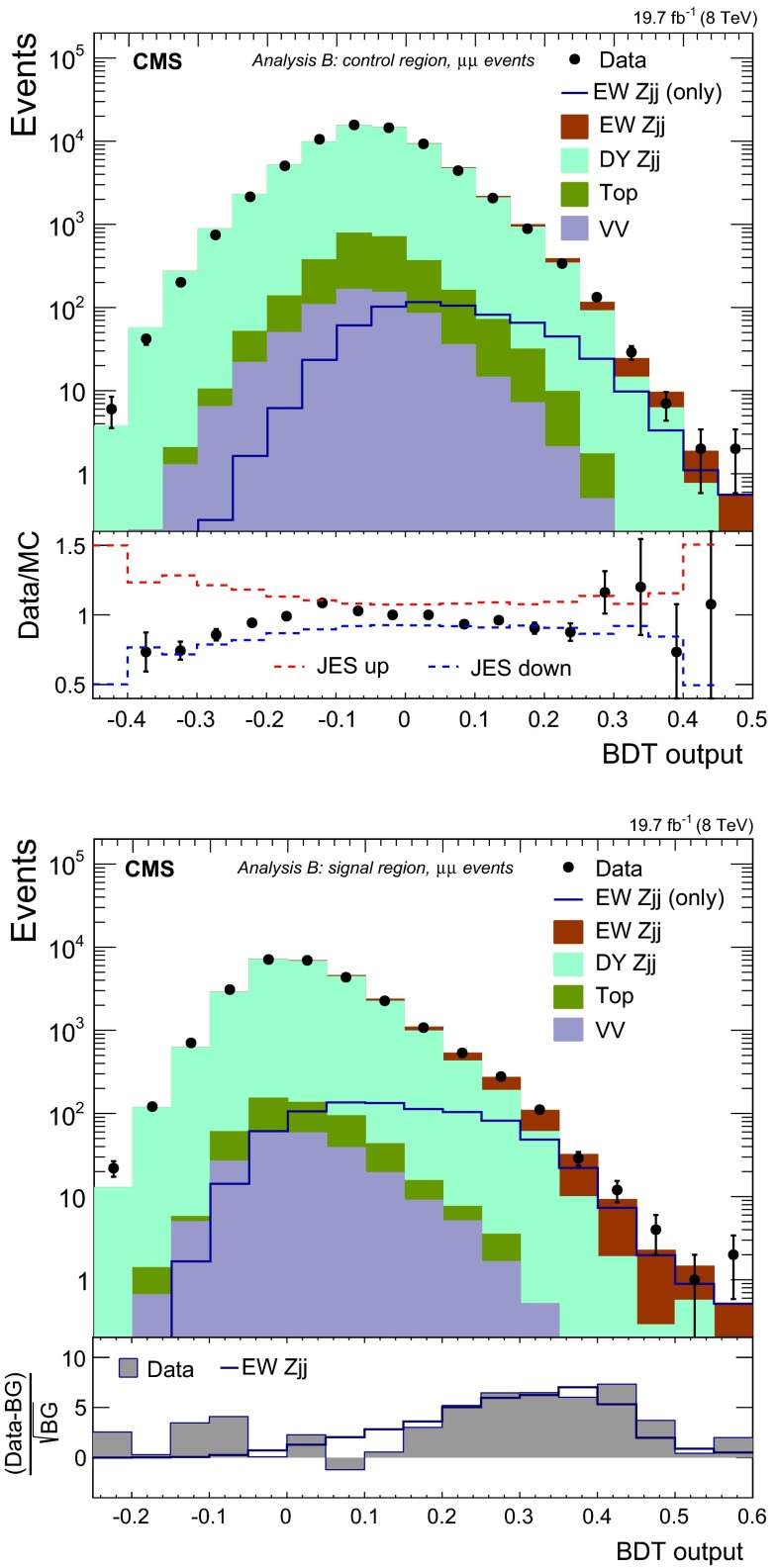
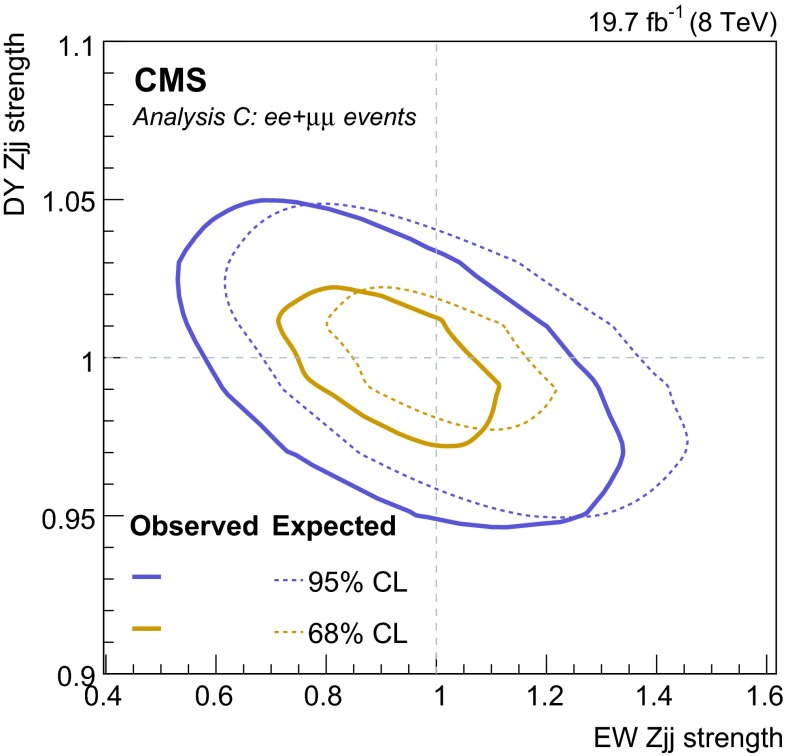
V Khachatryan
V Khachatryan
1Yerevan Physics Institute, Yerevan, Armenia
1,
A M Sirunyan
A M Sirunyan
1Yerevan Physics Institute, Yerevan, Armenia
1,
A Tumasyan
A Tumasyan
1Yerevan Physics Institute, Yerevan, Armenia
1,
W Adam
W Adam
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
T Bergauer
T Bergauer
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
M Dragicevic
M Dragicevic
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
J Erö
J Erö
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
C Fabjan
C Fabjan
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
M Friedl
M Friedl
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
R Frühwirth
R Frühwirth
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
V M Ghete
V M Ghete
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
C Hartl
C Hartl
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
N Hörmann
N Hörmann
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
J Hrubec
J Hrubec
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
M Jeitler
M Jeitler
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
W Kiesenhofer
W Kiesenhofer
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
V Knünz
V Knünz
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
M Krammer
M Krammer
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
I Krätschmer
I Krätschmer
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
D Liko
D Liko
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
I Mikulec
I Mikulec
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
D Rabady
D Rabady
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
B Rahbaran
B Rahbaran
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
H Rohringer
H Rohringer
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
R Schöfbeck
R Schöfbeck
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
J Strauss
J Strauss
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
A Taurok
A Taurok
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
W Treberer-Treberspurg
W Treberer-Treberspurg
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
W Waltenberger
W Waltenberger
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
C-E Wulz
C-E Wulz
2Institut für Hochenergiephysik der OeAW, Wien, Austria
2,
V Mossolov
V Mossolov
3National Centre for Particle and High Energy Physics, Minsk, Belarus
3,
N Shumeiko
N Shumeiko
3National Centre for Particle and High Energy Physics, Minsk, Belarus
3,
J Suarez Gonzalez
J Suarez Gonzalez
3National Centre for Particle and High Energy Physics, Minsk, Belarus
3,
S Alderweireldt
S Alderweireldt
4Universiteit Antwerpen, Antwerpen, Belgium
4,
M Bansal
M Bansal
4Universiteit Antwerpen, Antwerpen, Belgium
4,
S Bansal
S Bansal
4Universiteit Antwerpen, Antwerpen, Belgium
4,
T Cornelis
T Cornelis
4Universiteit Antwerpen, Antwerpen, Belgium
4,
E A De Wolf
E A De Wolf
4Universiteit Antwerpen, Antwerpen, Belgium
4,
X Janssen
X Janssen
4Universiteit Antwerpen, Antwerpen, Belgium
4,
A Knutsson
A Knutsson
4Universiteit Antwerpen, Antwerpen, Belgium
4,
S Luyckx
S Luyckx
4Universiteit Antwerpen, Antwerpen, Belgium
4,
S Ochesanu
S Ochesanu
4Universiteit Antwerpen, Antwerpen, Belgium
4,
B Roland
B Roland
4Universiteit Antwerpen, Antwerpen, Belgium
4,
R Rougny
R Rougny
4Universiteit Antwerpen, Antwerpen, Belgium
4,
M Van De Klundert
M Van De Klundert
4Universiteit Antwerpen, Antwerpen, Belgium
4,
H Van Haevermaet
H Van Haevermaet
4Universiteit Antwerpen, Antwerpen, Belgium
4,
P Van Mechelen
P Van Mechelen
4Universiteit Antwerpen, Antwerpen, Belgium
4,
N Van Remortel
N Van Remortel
4Universiteit Antwerpen, Antwerpen, Belgium
4,
A Van Spilbeeck
A Van Spilbeeck
4Universiteit Antwerpen, Antwerpen, Belgium
4,
F Blekman
F Blekman
5Vrije Universiteit Brussel, Brussel, Belgium
5,
S Blyweert
S Blyweert
5Vrije Universiteit Brussel, Brussel, Belgium
5,
J D’Hondt
J D’Hondt
5Vrije Universiteit Brussel, Brussel, Belgium
5,
N Daci
N Daci
5Vrije Universiteit Brussel, Brussel, Belgium
5,
N Heracleous
N Heracleous
5Vrije Universiteit Brussel, Brussel, Belgium
5,
J Keaveney
J Keaveney
5Vrije Universiteit Brussel, Brussel, Belgium
5,
S Lowette
S Lowette
5Vrije Universiteit Brussel, Brussel, Belgium
5,
M Maes
M Maes
5Vrije Universiteit Brussel, Brussel, Belgium
5,
A Olbrechts
A Olbrechts
5Vrije Universiteit Brussel, Brussel, Belgium
5,
Q Python
Q Python
5Vrije Universiteit Brussel, Brussel, Belgium
5,
D Strom
D Strom
5Vrije Universiteit Brussel, Brussel, Belgium
5,
S Tavernier
S Tavernier
5Vrije Universiteit Brussel, Brussel, Belgium
5,
W Van Doninck
W Van Doninck
5Vrije Universiteit Brussel, Brussel, Belgium
5,
P Van Mulders
P Van Mulders
5Vrije Universiteit Brussel, Brussel, Belgium
5,
G P Van Onsem
G P Van Onsem
5Vrije Universiteit Brussel, Brussel, Belgium
5,
I Villella
I Villella
5Vrije Universiteit Brussel, Brussel, Belgium
5,
C Caillol
C Caillol
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
B Clerbaux
B Clerbaux
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
G De Lentdecker
G De Lentdecker
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
D Dobur
D Dobur
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
L Favart
L Favart
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
A P R Gay
A P R Gay
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
A Grebenyuk
A Grebenyuk
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
A Léonard
A Léonard
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
A Mohammadi
A Mohammadi
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
L Perniè
L Perniè
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
T Reis
T Reis
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
T Seva
T Seva
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
L Thomas
L Thomas
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
C Vander Velde
C Vander Velde
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
P Vanlaer
P Vanlaer
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
J Wang
J Wang
6Université Libre de Bruxelles, Bruxelles, Belgium
6,
V Adler
V Adler
7Ghent University, Ghent, Belgium
7,
K Beernaert
K Beernaert
7Ghent University, Ghent, Belgium
7,
L Benucci
L Benucci
7Ghent University, Ghent, Belgium
7,
A Cimmino
A Cimmino
7Ghent University, Ghent, Belgium
7,
S Costantini
S Costantini
7Ghent University, Ghent, Belgium
7,
S Crucy
S Crucy
7Ghent University, Ghent, Belgium
7,
S Dildick
S Dildick
7Ghent University, Ghent, Belgium
7,
A Fagot
A Fagot
7Ghent University, Ghent, Belgium
7,
G Garcia
G Garcia
7Ghent University, Ghent, Belgium
7,
J Mccartin
J Mccartin
7Ghent University, Ghent, Belgium
7,
A A Ocampo Rios
A A Ocampo Rios
7Ghent University, Ghent, Belgium
7,
D Ryckbosch
D Ryckbosch
7Ghent University, Ghent, Belgium
7,
S Salva Diblen
S Salva Diblen
7Ghent University, Ghent, Belgium
7,
M Sigamani
M Sigamani
7Ghent University, Ghent, Belgium
7,
N Strobbe
N Strobbe
7Ghent University, Ghent, Belgium
7,
F Thyssen
F Thyssen
7Ghent University, Ghent, Belgium
7,
M Tytgat
M Tytgat
7Ghent University, Ghent, Belgium
7,
E Yazgan
E Yazgan
7Ghent University, Ghent, Belgium
7,
N Zaganidis
N Zaganidis
7Ghent University, Ghent, Belgium
7,
S Basegmez
S Basegmez
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
C Beluffi
C Beluffi
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
G Bruno
G Bruno
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
R Castello
R Castello
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
A Caudron
A Caudron
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
L Ceard
L Ceard
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
G G Da Silveira
G G Da Silveira
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
C Delaere
C Delaere
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
T du Pree
T du Pree
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
D Favart
D Favart
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
L Forthomme
L Forthomme
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
A Giammanco
A Giammanco
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
J Hollar
J Hollar
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
P Jez
P Jez
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
M Komm
M Komm
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
V Lemaitre
V Lemaitre
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
C Nuttens
C Nuttens
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
D Pagano
D Pagano
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
L Perrini
L Perrini
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
A Pin
A Pin
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
K Piotrzkowski
K Piotrzkowski
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
A Popov
A Popov
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
L Quertenmont
L Quertenmont
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
M Selvaggi
M Selvaggi
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
M Vidal Marono
M Vidal Marono
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
J M Vizan Garcia
J M Vizan Garcia
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
N Beliy
N Beliy
9Université de Mons, Mons, Belgium
9,
T Caebergs
T Caebergs
9Université de Mons, Mons, Belgium
9,
E Daubie
E Daubie
9Université de Mons, Mons, Belgium
9,
G H Hammad
G H Hammad
9Université de Mons, Mons, Belgium
9,
W L Aldá Júnior
W L Aldá Júnior
9Université de Mons, Mons, Belgium
9,
G A Alves
G A Alves
10Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
10,
L Brito
L Brito
10Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
10,
M Correa Martins Junior
M Correa Martins Junior
10Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
10,
T Dos Reis Martins
T Dos Reis Martins
10Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
10,
C Mora Herrera
C Mora Herrera
10Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
10,
M E Pol
M E Pol
10Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
10,
W Carvalho
W Carvalho
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
J Chinellato
J Chinellato
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
A Custódio
A Custódio
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
E M Da Costa
E M Da Costa
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
D De Jesus Damiao
D De Jesus Damiao
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
C De Oliveira Martins
C De Oliveira Martins
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
S Fonseca De Souza
S Fonseca De Souza
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
H Malbouisson
H Malbouisson
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
D Matos Figueiredo
D Matos Figueiredo
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
L Mundim
L Mundim
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
H Nogima
H Nogima
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
W L Prado Da Silva
W L Prado Da Silva
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
J Santaolalla
J Santaolalla
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
A Santoro
A Santoro
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
A Sznajder
A Sznajder
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
E J Tonelli Manganote
E J Tonelli Manganote
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
A Vilela Pereira
A Vilela Pereira
11Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
11,
C A Bernardes
C A Bernardes
12Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
12,
S Dogra
S Dogra
12Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
12,
T R Fernandez Perez Tomei
T R Fernandez Perez Tomei
12Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
12,
E M Gregores
E M Gregores
12Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
12,
P G Mercadante
P G Mercadante
12Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
12,
S F Novaes
S F Novaes
12Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
12,
Sandra S Padula
Sandra S Padula
12Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
12,
A Aleksandrov
A Aleksandrov
13Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
13,
V Genchev
V Genchev
13Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
13,
P Iaydjiev
P Iaydjiev
13Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
13,
A Marinov
A Marinov
13Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
13,
S Piperov
S Piperov
13Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
13,
M Rodozov
M Rodozov
13Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
13,
S Stoykova
S Stoykova
13Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
13,
G Sultanov
G Sultanov
13Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
13,
V Tcholakov
V Tcholakov
13Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
13,
M Vutova
M Vutova
13Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
13,
A Dimitrov
A Dimitrov
14University of Sofia, Sofia, Bulgaria
14,
I Glushkov
I Glushkov
14University of Sofia, Sofia, Bulgaria
14,
R Hadjiiska
R Hadjiiska
14University of Sofia, Sofia, Bulgaria
14,
V Kozhuharov
V Kozhuharov
14University of Sofia, Sofia, Bulgaria
14,
L Litov
L Litov
14University of Sofia, Sofia, Bulgaria
14,
B Pavlov
B Pavlov
14University of Sofia, Sofia, Bulgaria
14,
P Petkov
P Petkov
14University of Sofia, Sofia, Bulgaria
14,
J G Bian
J G Bian
15Institute of High Energy Physics, Beijing, China
15,
G M Chen
G M Chen
15Institute of High Energy Physics, Beijing, China
15,
H S Chen
H S Chen
15Institute of High Energy Physics, Beijing, China
15,
M Chen
M Chen
15Institute of High Energy Physics, Beijing, China
15,
R Du
R Du
15Institute of High Energy Physics, Beijing, China
15,
C H Jiang
C H Jiang
15Institute of High Energy Physics, Beijing, China
15,
S Liang
S Liang
15Institute of High Energy Physics, Beijing, China
15,
R Plestina
R Plestina
15Institute of High Energy Physics, Beijing, China
15,
J Tao
J Tao
15Institute of High Energy Physics, Beijing, China
15,
X Wang
X Wang
15Institute of High Energy Physics, Beijing, China
15,
Z Wang
Z Wang
15Institute of High Energy Physics, Beijing, China
15,
C Asawatangtrakuldee
C Asawatangtrakuldee
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
Y Ban
Y Ban
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
Y Guo
Y Guo
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
Q Li
Q Li
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
W Li
W Li
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
S Liu
S Liu
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
Y Mao
Y Mao
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
S J Qian
S J Qian
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
D Wang
D Wang
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
L Zhang
L Zhang
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
W Zou
W Zou
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
C Avila
C Avila
17Universidad de Los Andes, Bogota, Colombia
17,
L F Chaparro Sierra
L F Chaparro Sierra
17Universidad de Los Andes, Bogota, Colombia
17,
C Florez
C Florez
17Universidad de Los Andes, Bogota, Colombia
17,
J P Gomez
J P Gomez
17Universidad de Los Andes, Bogota, Colombia
17,
B Gomez Moreno
B Gomez Moreno
17Universidad de Los Andes, Bogota, Colombia
17,
J C Sanabria
J C Sanabria
17Universidad de Los Andes, Bogota, Colombia
17,
N Godinovic
N Godinovic
18University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
18,
D Lelas
D Lelas
18University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
18,
D Polic
D Polic
18University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
18,
I Puljak
I Puljak
18University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
18,
Z Antunovic
Z Antunovic
19University of Split, Faculty of Science, Split, Croatia
19,
M Kovac
M Kovac
19University of Split, Faculty of Science, Split, Croatia
19,
V Brigljevic
V Brigljevic
20Institute Rudjer Boskovic, Zagreb, Croatia
20,
K Kadija
K Kadija
20Institute Rudjer Boskovic, Zagreb, Croatia
20,
J Luetic
J Luetic
20Institute Rudjer Boskovic, Zagreb, Croatia
20,
D Mekterovic
D Mekterovic
20Institute Rudjer Boskovic, Zagreb, Croatia
20,
L Sudic
L Sudic
20Institute Rudjer Boskovic, Zagreb, Croatia
20,
A Attikis
A Attikis
21University of Cyprus, Nicosia, Cyprus
21,
G Mavromanolakis
G Mavromanolakis
21University of Cyprus, Nicosia, Cyprus
21,
J Mousa
J Mousa
21University of Cyprus, Nicosia, Cyprus
21,
C Nicolaou
C Nicolaou
21University of Cyprus, Nicosia, Cyprus
21,
F Ptochos
F Ptochos
21University of Cyprus, Nicosia, Cyprus
21,
P A Razis
P A Razis
21University of Cyprus, Nicosia, Cyprus
21,
M Bodlak
M Bodlak
22Charles University, Prague, Czech Republic
22,
M Finger
M Finger
22Charles University, Prague, Czech Republic
22,
M Finger Jr
M Finger Jr
22Charles University, Prague, Czech Republic
22,
Y Assran
Y Assran
23Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
23,
A Ellithi Kamel
A Ellithi Kamel
23Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
23,
M A Mahmoud
M A Mahmoud
23Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
23,
A Radi
A Radi
23Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
23,
M Kadastik
M Kadastik
24National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
24,
M Murumaa
M Murumaa
24National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
24,
M Raidal
M Raidal
24National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
24,
A Tiko
A Tiko
24National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
24,
P Eerola
P Eerola
25Department of Physics, University of Helsinki, Helsinki, Finland
25,
G Fedi
G Fedi
25Department of Physics, University of Helsinki, Helsinki, Finland
25,
M Voutilainen
M Voutilainen
25Department of Physics, University of Helsinki, Helsinki, Finland
25,
J Härkönen
J Härkönen
26Helsinki Institute of Physics, Helsinki, Finland
26,
V Karimäki
V Karimäki
26Helsinki Institute of Physics, Helsinki, Finland
26,
R Kinnunen
R Kinnunen
26Helsinki Institute of Physics, Helsinki, Finland
26,
M J Kortelainen
M J Kortelainen
26Helsinki Institute of Physics, Helsinki, Finland
26,
T Lampén
T Lampén
26Helsinki Institute of Physics, Helsinki, Finland
26,
K Lassila-Perini
K Lassila-Perini
26Helsinki Institute of Physics, Helsinki, Finland
26,
S Lehti
S Lehti
26Helsinki Institute of Physics, Helsinki, Finland
26,
T Lindén
T Lindén
26Helsinki Institute of Physics, Helsinki, Finland
26,
P Luukka
P Luukka
26Helsinki Institute of Physics, Helsinki, Finland
26,
T Mäenpää
T Mäenpää
26Helsinki Institute of Physics, Helsinki, Finland
26,
T Peltola
T Peltola
26Helsinki Institute of Physics, Helsinki, Finland
26,
E Tuominen
E Tuominen
26Helsinki Institute of Physics, Helsinki, Finland
26,
J Tuominiemi
J Tuominiemi
26Helsinki Institute of Physics, Helsinki, Finland
26,
E Tuovinen
E Tuovinen
26Helsinki Institute of Physics, Helsinki, Finland
26,
L Wendland
L Wendland
26Helsinki Institute of Physics, Helsinki, Finland
26,
J Talvitie
J Talvitie
27Lappeenranta University of Technology, Lappeenranta, Finland
27,
T Tuuva
T Tuuva
27Lappeenranta University of Technology, Lappeenranta, Finland
27,
M Besancon
M Besancon
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
F Couderc
F Couderc
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
M Dejardin
M Dejardin
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
D Denegri
D Denegri
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
B Fabbro
B Fabbro
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
J L Faure
J L Faure
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
C Favaro
C Favaro
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
F Ferri
F Ferri
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
S Ganjour
S Ganjour
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
A Givernaud
A Givernaud
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
P Gras
P Gras
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
G Hamel de Monchenault
G Hamel de Monchenault
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
P Jarry
P Jarry
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
E Locci
E Locci
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
J Malcles
J Malcles
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
J Rander
J Rander
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
A Rosowsky
A Rosowsky
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
M Titov
M Titov
28DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
28,
S Baffioni
S Baffioni
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
F Beaudette
F Beaudette
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
P Busson
P Busson
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
C Charlot
C Charlot
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
T Dahms
T Dahms
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
M Dalchenko
M Dalchenko
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
L Dobrzynski
L Dobrzynski
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
N Filipovic
N Filipovic
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
A Florent
A Florent
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
R Granier de Cassagnac
R Granier de Cassagnac
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
L Mastrolorenzo
L Mastrolorenzo
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
P Miné
P Miné
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
C Mironov
C Mironov
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
I N Naranjo
I N Naranjo
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
M Nguyen
M Nguyen
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
C Ochando
C Ochando
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
P Paganini
P Paganini
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
S Regnard
S Regnard
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
R Salerno
R Salerno
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
J B Sauvan
J B Sauvan
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
Y Sirois
Y Sirois
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
C Veelken
C Veelken
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
Y Yilmaz
Y Yilmaz
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
A Zabi
A Zabi
29Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
29,
J-L Agram
J-L Agram
30Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
30,
J Andrea
J Andrea
30Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
30,
A Aubin
A Aubin
30Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
30,
D Bloch
D Bloch
30Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
30,
J-M Brom
J-M Brom
30Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
30,
E C Chabert
E C Chabert
30Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
30,
C Collard
C Collard
30Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
30,
E Conte
E Conte
30Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
30,
J-C Fontaine
J-C Fontaine
30Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
30,
D Gelé
D Gelé
30Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
30,
U Goerlach
U Goerlach
30Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
30,
C Goetzmann
C Goetzmann
30Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
30,
A-C Le Bihan
A-C Le Bihan
30Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
30,
P Van Hove
P Van Hove
30Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
30,
S Gadrat
S Gadrat
31Centre de Calcul de l’Institut National de Physique Nucleaire et de Physique des Particules, CNRS/IN2P3, Villeurbanne, France
31,
S Beauceron
S Beauceron
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
N Beaupere
N Beaupere
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
G Boudoul
G Boudoul
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
E Bouvier
E Bouvier
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
S Brochet
S Brochet
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
C A Carrillo Montoya
C A Carrillo Montoya
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
J Chasserat
J Chasserat
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
R Chierici
R Chierici
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
D Contardo
D Contardo
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
P Depasse
P Depasse
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
H El Mamouni
H El Mamouni
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
J Fan
J Fan
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
J Fay
J Fay
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
S Gascon
S Gascon
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
M Gouzevitch
M Gouzevitch
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
B Ille
B Ille
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
T Kurca
T Kurca
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
M Lethuillier
M Lethuillier
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
L Mirabito
L Mirabito
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
S Perries
S Perries
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
J D Ruiz Alvarez
J D Ruiz Alvarez
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
D Sabes
D Sabes
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
L Sgandurra
L Sgandurra
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
V Sordini
V Sordini
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
M Vander Donckt
M Vander Donckt
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
P Verdier
P Verdier
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
S Viret
S Viret
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
H Xiao
H Xiao
32Institut de Physique Nucléaire de Lyon, Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Villeurbanne, France
32,
Z Tsamalaidze
Z Tsamalaidze
33Institute of High Energy Physics and Informatization, Tbilisi State University, Tbilisi, Georgia
33,
C Autermann
C Autermann
34RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
34,
S Beranek
S Beranek
34RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
34,
M Bontenackels
M Bontenackels
34RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
34,
M Edelhoff
M Edelhoff
34RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
34,
L Feld
L Feld
34RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
34,
O Hindrichs
O Hindrichs
34RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
34,
K Klein
K Klein
34RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
34,
A Ostapchuk
A Ostapchuk
34RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
34,
A Perieanu
A Perieanu
34RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
34,
F Raupach
F Raupach
34RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
34,
J Sammet
J Sammet
34RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
34,
S Schael
S Schael
34RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
34,
H Weber
H Weber
34RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
34,
B Wittmer
B Wittmer
34RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
34,
V Zhukov
V Zhukov
34RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
34,
M Ata
M Ata
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
M Brodski
M Brodski
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
E Dietz-Laursonn
E Dietz-Laursonn
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
D Duchardt
D Duchardt
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
M Erdmann
M Erdmann
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
R Fischer
R Fischer
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
A Güth
A Güth
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
T Hebbeker
T Hebbeker
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
C Heidemann
C Heidemann
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
K Hoepfner
K Hoepfner
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
D Klingebiel
D Klingebiel
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
S Knutzen
S Knutzen
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
P Kreuzer
P Kreuzer
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
M Merschmeyer
M Merschmeyer
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
A Meyer
A Meyer
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
P Millet
P Millet
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
M Olschewski
M Olschewski
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
K Padeken
K Padeken
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
P Papacz
P Papacz
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
H Reithler
H Reithler
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
S A Schmitz
S A Schmitz
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
L Sonnenschein
L Sonnenschein
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
D Teyssier
D Teyssier
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
S Thüer
S Thüer
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
M Weber
M Weber
35RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
35,
V Cherepanov
V Cherepanov
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
Y Erdogan
Y Erdogan
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
G Flügge
G Flügge
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
H Geenen
H Geenen
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
M Geisler
M Geisler
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
W Haj Ahmad
W Haj Ahmad
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
A Heister
A Heister
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
F Hoehle
F Hoehle
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
B Kargoll
B Kargoll
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
T Kress
T Kress
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
Y Kuessel
Y Kuessel
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
J Lingemann
J Lingemann
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
A Nowack
A Nowack
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
I M Nugent
I M Nugent
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
L Perchalla
L Perchalla
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
O Pooth
O Pooth
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
A Stahl
A Stahl
36RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
36,
I Asin
I Asin
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
N Bartosik
N Bartosik
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
J Behr
J Behr
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
W Behrenhoff
W Behrenhoff
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
U Behrens
U Behrens
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
A J Bell
A J Bell
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
M Bergholz
M Bergholz
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
A Bethani
A Bethani
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
K Borras
K Borras
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
A Burgmeier
A Burgmeier
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
A Cakir
A Cakir
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
L Calligaris
L Calligaris
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
A Campbell
A Campbell
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
S Choudhury
S Choudhury
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
F Costanza
F Costanza
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
C Diez Pardos
C Diez Pardos
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
S Dooling
S Dooling
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
T Dorland
T Dorland
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
G Eckerlin
G Eckerlin
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
D Eckstein
D Eckstein
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
T Eichhorn
T Eichhorn
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
G Flucke
G Flucke
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
J Garay Garcia
J Garay Garcia
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
A Geiser
A Geiser
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
P Gunnellini
P Gunnellini
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
J Hauk
J Hauk
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
M Hempel
M Hempel
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
D Horton
D Horton
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
H Jung
H Jung
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
A Kalogeropoulos
A Kalogeropoulos
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
M Kasemann
M Kasemann
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
P Katsas
P Katsas
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
J Kieseler
J Kieseler
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
C Kleinwort
C Kleinwort
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
D Krücker
D Krücker
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
W Lange
W Lange
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
J Leonard
J Leonard
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
K Lipka
K Lipka
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
A Lobanov
A Lobanov
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
W Lohmann
W Lohmann
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
B Lutz
B Lutz
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
R Mankel
R Mankel
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
I Marfin
I Marfin
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
I-A Melzer-Pellmann
I-A Melzer-Pellmann
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
A B Meyer
A B Meyer
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
G Mitta
G Mitta
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
J Mnich
J Mnich
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
A Mussgiller
A Mussgiller
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
S Naumann-Emme
S Naumann-Emme
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
A Nayak
A Nayak
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
O Novgorodova
O Novgorodova
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
F Nowak
F Nowak
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
E Ntomari
E Ntomari
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
H Perrey
H Perrey
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
D Pitzl
D Pitzl
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
R Placakyte
R Placakyte
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
A Raspereza
A Raspereza
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
P M Ribeiro Cipriano
P M Ribeiro Cipriano
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
E Ron
E Ron
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
M Ö Sahin
M Ö Sahin
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
J Salfeld-Nebgen
J Salfeld-Nebgen
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
P Saxena
P Saxena
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
R Schmidt
R Schmidt
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
T Schoerner-Sadenius
T Schoerner-Sadenius
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
M Schröder
M Schröder
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
C Seitz
C Seitz
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
S Spannagel
S Spannagel
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
A D R Vargas Trevino
A D R Vargas Trevino
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
R Walsh
R Walsh
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
C Wissing
C Wissing
37Deutsches Elektronen-Synchrotron, Hamburg, Germany
37,
M Aldaya Martin
M Aldaya Martin
38University of Hamburg, Hamburg, Germany
38,
V Blobel
V Blobel
38University of Hamburg, Hamburg, Germany
38,
M Centis Vignali
M Centis Vignali
38University of Hamburg, Hamburg, Germany
38,
A R Draeger
A R Draeger
38University of Hamburg, Hamburg, Germany
38,
J Erfle
J Erfle
38University of Hamburg, Hamburg, Germany
38,
E Garutti
E Garutti
38University of Hamburg, Hamburg, Germany
38,
K Goebel
K Goebel
38University of Hamburg, Hamburg, Germany
38,
M Görner
M Görner
38University of Hamburg, Hamburg, Germany
38,
J Haller
J Haller
38University of Hamburg, Hamburg, Germany
38,
M Hoffmann
M Hoffmann
38University of Hamburg, Hamburg, Germany
38,
R S Höing
R S Höing
38University of Hamburg, Hamburg, Germany
38,
H Kirschenmann
H Kirschenmann
38University of Hamburg, Hamburg, Germany
38,
R Klanner
R Klanner
38University of Hamburg, Hamburg, Germany
38,
R Kogler
R Kogler
38University of Hamburg, Hamburg, Germany
38,
J Lange
J Lange
38University of Hamburg, Hamburg, Germany
38,
T Lapsien
T Lapsien
38University of Hamburg, Hamburg, Germany
38,
T Lenz
T Lenz
38University of Hamburg, Hamburg, Germany
38,
I Marchesini
I Marchesini
38University of Hamburg, Hamburg, Germany
38,
J Ott
J Ott
38University of Hamburg, Hamburg, Germany
38,
T Peiffer
T Peiffer
38University of Hamburg, Hamburg, Germany
38,
N Pietsch
N Pietsch
38University of Hamburg, Hamburg, Germany
38,
J Poehlsen
J Poehlsen
38University of Hamburg, Hamburg, Germany
38,
T Poehlsen
T Poehlsen
38University of Hamburg, Hamburg, Germany
38,
D Rathjens
D Rathjens
38University of Hamburg, Hamburg, Germany
38,
C Sander
C Sander
38University of Hamburg, Hamburg, Germany
38,
H Schettler
H Schettler
38University of Hamburg, Hamburg, Germany
38,
P Schleper
P Schleper
38University of Hamburg, Hamburg, Germany
38,
E Schlieckau
E Schlieckau
38University of Hamburg, Hamburg, Germany
38,
A Schmidt
A Schmidt
38University of Hamburg, Hamburg, Germany
38,
M Seidel
M Seidel
38University of Hamburg, Hamburg, Germany
38,
V Sola
V Sola
38University of Hamburg, Hamburg, Germany
38,
H Stadie
H Stadie
38University of Hamburg, Hamburg, Germany
38,
G Steinbrück
G Steinbrück
38University of Hamburg, Hamburg, Germany
38,
D Troendle
D Troendle
38University of Hamburg, Hamburg, Germany
38,
E Usai
E Usai
38University of Hamburg, Hamburg, Germany
38,
L Vanelderen
L Vanelderen
38University of Hamburg, Hamburg, Germany
38,
C Barth
C Barth
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
C Baus
C Baus
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
J Berger
J Berger
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
C Böser
C Böser
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
E Butz
E Butz
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
T Chwalek
T Chwalek
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
W De Boer
W De Boer
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
A Descroix
A Descroix
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
A Dierlamm
A Dierlamm
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
M Feindt
M Feindt
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
F Frensch
F Frensch
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
M Giffels
M Giffels
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
F Hartmann
F Hartmann
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
T Hauth
T Hauth
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
U Husemann
U Husemann
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
I Katkov
I Katkov
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
A Kornmayer
A Kornmayer
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
E Kuznetsova
E Kuznetsova
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
P Lobelle Pardo
P Lobelle Pardo
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
M U Mozer
M U Mozer
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
Th Müller
Th Müller
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
A Nürnberg
A Nürnberg
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
G Quast
G Quast
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
K Rabbertz
K Rabbertz
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
F Ratnikov
F Ratnikov
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
S Röcker
S Röcker
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
H J Simonis
H J Simonis
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
F M Stober
F M Stober
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
R Ulrich
R Ulrich
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
J Wagner-Kuhr
J Wagner-Kuhr
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
S Wayand
S Wayand
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
T Weiler
T Weiler
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
R Wolf
R Wolf
39Institut für Experimentelle Kernphysik, Karlsruhe, Germany
39,
G Anagnostou
G Anagnostou
40Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
40,
G Daskalakis
G Daskalakis
40Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
40,
T Geralis
T Geralis
40Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
40,
V A Giakoumopoulou
V A Giakoumopoulou
40Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
40,
A Kyriakis
A Kyriakis
40Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
40,
D Loukas
D Loukas
40Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
40,
A Markou
A Markou
40Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
40,
C Markou
C Markou
40Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
40,
A Psallidas
A Psallidas
40Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
40,
I Topsis-Giotis
I Topsis-Giotis
40Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
40,
A Panagiotou
A Panagiotou
41University of Athens, Athens, Greece
41,
A Agapitos
A Agapitos
41University of Athens, Athens, Greece
41,
S Kesisoglou
S Kesisoglou
41University of Athens, Athens, Greece
41,
N Saoulidou
N Saoulidou
41University of Athens, Athens, Greece
41,
E Stiliaris
E Stiliaris
41University of Athens, Athens, Greece
41,
X Aslanoglou
X Aslanoglou
42University of Ioánnina, Ioánnina, Greece
42,
I Evangelou
I Evangelou
42University of Ioánnina, Ioánnina, Greece
42,
G Flouris
G Flouris
42University of Ioánnina, Ioánnina, Greece
42,
C Foudas
C Foudas
42University of Ioánnina, Ioánnina, Greece
42,
P Kokkas
P Kokkas
42University of Ioánnina, Ioánnina, Greece
42,
N Manthos
N Manthos
42University of Ioánnina, Ioánnina, Greece
42,
I Papadopoulos
I Papadopoulos
42University of Ioánnina, Ioánnina, Greece
42,
E Paradas
E Paradas
42University of Ioánnina, Ioánnina, Greece
42,
G Bencze
G Bencze
43Wigner Research Centre for Physics, Budapest, Hungary
43,
C Hajdu
C Hajdu
43Wigner Research Centre for Physics, Budapest, Hungary
43,
P Hidas
P Hidas
43Wigner Research Centre for Physics, Budapest, Hungary
43,
D Horvath
D Horvath
43Wigner Research Centre for Physics, Budapest, Hungary
43,
F Sikler
F Sikler
43Wigner Research Centre for Physics, Budapest, Hungary
43,
V Veszpremi
V Veszpremi
43Wigner Research Centre for Physics, Budapest, Hungary
43,
G Vesztergombi
G Vesztergombi
43Wigner Research Centre for Physics, Budapest, Hungary
43,
A J Zsigmond
A J Zsigmond
43Wigner Research Centre for Physics, Budapest, Hungary
43,
N Beni
N Beni
44Institute of Nuclear Research ATOMKI, Debrecen, Hungary
44,
S Czellar
S Czellar
44Institute of Nuclear Research ATOMKI, Debrecen, Hungary
44,
J Karancsi
J Karancsi
44Institute of Nuclear Research ATOMKI, Debrecen, Hungary
44,
J Molnar
J Molnar
44Institute of Nuclear Research ATOMKI, Debrecen, Hungary
44,
J Palinkas
J Palinkas
44Institute of Nuclear Research ATOMKI, Debrecen, Hungary
44,
Z Szillasi
Z Szillasi
44Institute of Nuclear Research ATOMKI, Debrecen, Hungary
44,
P Raics
P Raics
45University of Debrecen, Debrecen, Hungary
45,
Z L Trocsanyi
Z L Trocsanyi
45University of Debrecen, Debrecen, Hungary
45,
B Ujvari
B Ujvari
45University of Debrecen, Debrecen, Hungary
45,
S K Swain
S K Swain
46National Institute of Science Education and Research, Bhubaneswar, India
46,
S B Beri
S B Beri
47Panjab University, Chandigarh, India
47,
V Bhatnagar
V Bhatnagar
47Panjab University, Chandigarh, India
47,
R Gupta
R Gupta
47Panjab University, Chandigarh, India
47,
U Bhawandeep
U Bhawandeep
47Panjab University, Chandigarh, India
47,
A K Kalsi
A K Kalsi
47Panjab University, Chandigarh, India
47,
M Kaur
M Kaur
47Panjab University, Chandigarh, India
47,
M Mittal
M Mittal
47Panjab University, Chandigarh, India
47,
N Nishu
N Nishu
47Panjab University, Chandigarh, India
47,
J B Singh
J B Singh
47Panjab University, Chandigarh, India
47,
Ashok Kumar
Ashok Kumar
48University of Delhi, Delhi, India
48,
Arun Kumar
Arun Kumar
48University of Delhi, Delhi, India
48,
S Ahuja
S Ahuja
48University of Delhi, Delhi, India
48,
A Bhardwaj
A Bhardwaj
48University of Delhi, Delhi, India
48,
B C Choudhary
B C Choudhary
48University of Delhi, Delhi, India
48,
A Kumar
A Kumar
48University of Delhi, Delhi, India
48,
S Malhotra
S Malhotra
48University of Delhi, Delhi, India
48,
M Naimuddin
M Naimuddin
48University of Delhi, Delhi, India
48,
K Ranjan
K Ranjan
48University of Delhi, Delhi, India
48,
V Sharma
V Sharma
48University of Delhi, Delhi, India
48,
S Banerjee
S Banerjee
49Saha Institute of Nuclear Physics, Kolkata, India
49,
S Bhattacharya
S Bhattacharya
49Saha Institute of Nuclear Physics, Kolkata, India
49,
K Chatterjee
K Chatterjee
49Saha Institute of Nuclear Physics, Kolkata, India
49,
S Dutta
S Dutta
49Saha Institute of Nuclear Physics, Kolkata, India
49,
B Gomber
B Gomber
49Saha Institute of Nuclear Physics, Kolkata, India
49,
Sa Jain
Sa Jain
49Saha Institute of Nuclear Physics, Kolkata, India
49,
Sh Jain
Sh Jain
49Saha Institute of Nuclear Physics, Kolkata, India
49,
R Khurana
R Khurana
49Saha Institute of Nuclear Physics, Kolkata, India
49,
A Modak
A Modak
49Saha Institute of Nuclear Physics, Kolkata, India
49,
S Mukherjee
S Mukherjee
49Saha Institute of Nuclear Physics, Kolkata, India
49,
D Roy
D Roy
49Saha Institute of Nuclear Physics, Kolkata, India
49,
S Sarkar
S Sarkar
49Saha Institute of Nuclear Physics, Kolkata, India
49,
M Sharan
M Sharan
49Saha Institute of Nuclear Physics, Kolkata, India
49,
A Abdulsalam
A Abdulsalam
50Bhabha Atomic Research Centre, Mumbai, India
50,
D Dutta
D Dutta
50Bhabha Atomic Research Centre, Mumbai, India
50,
S Kailas
S Kailas
50Bhabha Atomic Research Centre, Mumbai, India
50,
V Kumar
V Kumar
50Bhabha Atomic Research Centre, Mumbai, India
50,
A K Mohanty
A K Mohanty
50Bhabha Atomic Research Centre, Mumbai, India
50,
L M Pant
L M Pant
50Bhabha Atomic Research Centre, Mumbai, India
50,
P Shukla
P Shukla
50Bhabha Atomic Research Centre, Mumbai, India
50,
A Topkar
A Topkar
50Bhabha Atomic Research Centre, Mumbai, India
50,
T Aziz
T Aziz
51Tata Institute of Fundamental Research, Mumbai, India
51,
S Banerjee
S Banerjee
51Tata Institute of Fundamental Research, Mumbai, India
51,
S Bhowmik
S Bhowmik
51Tata Institute of Fundamental Research, Mumbai, India
51,
R M Chatterjee
R M Chatterjee
51Tata Institute of Fundamental Research, Mumbai, India
51,
R K Dewanjee
R K Dewanjee
51Tata Institute of Fundamental Research, Mumbai, India
51,
S Dugad
S Dugad
51Tata Institute of Fundamental Research, Mumbai, India
51,
S Ganguly
S Ganguly
51Tata Institute of Fundamental Research, Mumbai, India
51,
S Ghosh
S Ghosh
51Tata Institute of Fundamental Research, Mumbai, India
51,
M Guchait
M Guchait
51Tata Institute of Fundamental Research, Mumbai, India
51,
A Gurtu
A Gurtu
51Tata Institute of Fundamental Research, Mumbai, India
51,
G Kole
G Kole
51Tata Institute of Fundamental Research, Mumbai, India
51,
S Kumar
S Kumar
51Tata Institute of Fundamental Research, Mumbai, India
51,
M Maity
M Maity
51Tata Institute of Fundamental Research, Mumbai, India
51,
G Majumder
G Majumder
51Tata Institute of Fundamental Research, Mumbai, India
51,
K Mazumdar
K Mazumdar
51Tata Institute of Fundamental Research, Mumbai, India
51,
G B Mohanty
G B Mohanty
51Tata Institute of Fundamental Research, Mumbai, India
51,
B Parida
B Parida
51Tata Institute of Fundamental Research, Mumbai, India
51,
K Sudhakar
K Sudhakar
51Tata Institute of Fundamental Research, Mumbai, India
51,
N Wickramage
N Wickramage
51Tata Institute of Fundamental Research, Mumbai, India
51,
H Bakhshiansohi
H Bakhshiansohi
52Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
52,
H Behnamian
H Behnamian
52Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
52,
S M Etesami
S M Etesami
52Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
52,
A Fahim
A Fahim
52Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
52,
R Goldouzian
R Goldouzian
52Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
52,
A Jafari
A Jafari
52Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
52,
M Khakzad
M Khakzad
52Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
52,
M Mohammadi Najafabadi
M Mohammadi Najafabadi
52Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
52,
M Naseri
M Naseri
52Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
52,
S Paktinat Mehdiabadi
S Paktinat Mehdiabadi
52Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
52,
F Rezaei Hosseinabadi
F Rezaei Hosseinabadi
52Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
52,
B Safarzadeh
B Safarzadeh
52Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
52,
M Zeinali
M Zeinali
52Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
52,
M Felcini
M Felcini
53University College Dublin, Dublin, Ireland
53,
M Grunewald
M Grunewald
53University College Dublin, Dublin, Ireland
53,
M Abbrescia
M Abbrescia
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
L Barbone
L Barbone
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
C Calabria
C Calabria
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
S S Chhibra
S S Chhibra
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
A Colaleo
A Colaleo
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
D Creanza
D Creanza
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
N De Filippis
N De Filippis
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
M De Palma
M De Palma
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
L Fiore
L Fiore
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
G Iaselli
G Iaselli
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
G Maggi
G Maggi
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
M Maggi
M Maggi
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
S My
S My
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
S Nuzzo
S Nuzzo
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
A Pompili
A Pompili
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
G Pugliese
G Pugliese
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
R Radogna
R Radogna
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
G Selvaggi
G Selvaggi
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
L Silvestris
L Silvestris
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
G Singh
G Singh
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
R Venditti
R Venditti
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
P Verwilligen
P Verwilligen
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
G Zito
G Zito
54INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
54,
G Abbiendi
G Abbiendi
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
A C Benvenuti
A C Benvenuti
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
D Bonacorsi
D Bonacorsi
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
S Braibant-Giacomelli
S Braibant-Giacomelli
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
L Brigliadori
L Brigliadori
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
R Campanini
R Campanini
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
P Capiluppi
P Capiluppi
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
A Castro
A Castro
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
F R Cavallo
F R Cavallo
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
G Codispoti
G Codispoti
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
M Cuffiani
M Cuffiani
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
G M Dallavalle
G M Dallavalle
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
F Fabbri
F Fabbri
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
A Fanfani
A Fanfani
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
D Fasanella
D Fasanella
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
P Giacomelli
P Giacomelli
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
C Grandi
C Grandi
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
L Guiducci
L Guiducci
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
S Marcellini
S Marcellini
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
G Masetti
G Masetti
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
A Montanari
A Montanari
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
F L Navarria
F L Navarria
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
A Perrotta
A Perrotta
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
F Primavera
F Primavera
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
A M Rossi
A M Rossi
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
T Rovelli
T Rovelli
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
G P Siroli
G P Siroli
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
N Tosi
N Tosi
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
R Travaglini
R Travaglini
55INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
55,
S Albergo
S Albergo
56INFN Sezione di Catania, Università di Catania, CSFNSM, Catania, Italy
56,
G Cappello
G Cappello
56INFN Sezione di Catania, Università di Catania, CSFNSM, Catania, Italy
56,
M Chiorboli
M Chiorboli
56INFN Sezione di Catania, Università di Catania, CSFNSM, Catania, Italy
56,
S Costa
S Costa
56INFN Sezione di Catania, Università di Catania, CSFNSM, Catania, Italy
56,
F Giordano
F Giordano
56INFN Sezione di Catania, Università di Catania, CSFNSM, Catania, Italy
56,
R Potenza
R Potenza
56INFN Sezione di Catania, Università di Catania, CSFNSM, Catania, Italy
56,
A Tricomi
A Tricomi
56INFN Sezione di Catania, Università di Catania, CSFNSM, Catania, Italy
56,
C Tuve
C Tuve
56INFN Sezione di Catania, Università di Catania, CSFNSM, Catania, Italy
56,
G Barbagli
G Barbagli
57INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
57,
V Ciulli
V Ciulli
57INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
57,
C Civinini
C Civinini
57INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
57,
R D’Alessandro
R D’Alessandro
57INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
57,
E Focardi
E Focardi
57INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
57,
E Gallo
E Gallo
57INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
57,
S Gonzi
S Gonzi
57INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
57,
V Gori
V Gori
57INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
57,
P Lenzi
P Lenzi
57INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
57,
M Meschini
M Meschini
57INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
57,
S Paoletti
S Paoletti
57INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
57,
G Sguazzoni
G Sguazzoni
57INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
57,
A Tropiano
A Tropiano
57INFN Sezione di Firenze, Università di Firenze, Firenze, Italy
57,
L Benussi
L Benussi
58INFN Laboratori Nazionali di Frascati, Frascati, Italy
58,
S Bianco
S Bianco
58INFN Laboratori Nazionali di Frascati, Frascati, Italy
58,
F Fabbri
F Fabbri
58INFN Laboratori Nazionali di Frascati, Frascati, Italy
58,
D Piccolo
D Piccolo
58INFN Laboratori Nazionali di Frascati, Frascati, Italy
58,
F Ferro
F Ferro
59INFN Sezione di Genova, Università di Genova, Genoa, Italy
59,
M Lo Vetere
M Lo Vetere
59INFN Sezione di Genova, Università di Genova, Genoa, Italy
59,
E Robutti
E Robutti
59INFN Sezione di Genova, Università di Genova, Genoa, Italy
59,
S Tosi
S Tosi
59INFN Sezione di Genova, Università di Genova, Genoa, Italy
59,
M E Dinardo
M E Dinardo
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
S Fiorendi
S Fiorendi
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
S Gennai
S Gennai
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
R Gerosa
R Gerosa
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
A Ghezzi
A Ghezzi
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
P Govoni
P Govoni
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
M T Lucchini
M T Lucchini
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
S Malvezzi
S Malvezzi
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
R A Manzoni
R A Manzoni
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
A Martelli
A Martelli
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
B Marzocchi
B Marzocchi
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
D Menasce
D Menasce
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
L Moroni
L Moroni
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
M Paganoni
M Paganoni
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
D Pedrini
D Pedrini
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
S Ragazzi
S Ragazzi
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
N Redaelli
N Redaelli
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
T Tabarelli de Fatis
T Tabarelli de Fatis
60INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
60,
S Buontempo
S Buontempo
61INFN Sezione di Napoli, Università di Napoli ’Federico II’, Università della Basilicata (Potenza), Università G. Marconi (Roma), Naples, Italy
61,
N Cavallo
N Cavallo
61INFN Sezione di Napoli, Università di Napoli ’Federico II’, Università della Basilicata (Potenza), Università G. Marconi (Roma), Naples, Italy
61,
S Di Guida
S Di Guida
61INFN Sezione di Napoli, Università di Napoli ’Federico II’, Università della Basilicata (Potenza), Università G. Marconi (Roma), Naples, Italy
61,
F Fabozzi
F Fabozzi
61INFN Sezione di Napoli, Università di Napoli ’Federico II’, Università della Basilicata (Potenza), Università G. Marconi (Roma), Naples, Italy
61,
A O M Iorio
A O M Iorio
61INFN Sezione di Napoli, Università di Napoli ’Federico II’, Università della Basilicata (Potenza), Università G. Marconi (Roma), Naples, Italy
61,
L Lista
L Lista
61INFN Sezione di Napoli, Università di Napoli ’Federico II’, Università della Basilicata (Potenza), Università G. Marconi (Roma), Naples, Italy
61,
S Meola
S Meola
61INFN Sezione di Napoli, Università di Napoli ’Federico II’, Università della Basilicata (Potenza), Università G. Marconi (Roma), Naples, Italy
61,
M Merola
M Merola
61INFN Sezione di Napoli, Università di Napoli ’Federico II’, Università della Basilicata (Potenza), Università G. Marconi (Roma), Naples, Italy
61,
P Paolucci
P Paolucci
61INFN Sezione di Napoli, Università di Napoli ’Federico II’, Università della Basilicata (Potenza), Università G. Marconi (Roma), Naples, Italy
61,
P Azzi
P Azzi
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
N Bacchetta
N Bacchetta
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
M Bellato
M Bellato
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
M Biasotto
M Biasotto
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
A Branca
A Branca
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
M Dall’Osso
M Dall’Osso
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
T Dorigo
T Dorigo
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
U Dosselli
U Dosselli
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
M Galanti
M Galanti
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
F Gasparini
F Gasparini
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
P Giubilato
P Giubilato
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
A Gozzelino
A Gozzelino
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
K Kanishchev
K Kanishchev
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
S Lacaprara
S Lacaprara
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
M Margoni
M Margoni
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
A T Meneguzzo
A T Meneguzzo
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
J Pazzini
J Pazzini
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
N Pozzobon
N Pozzobon
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
P Ronchese
P Ronchese
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
F Simonetto
F Simonetto
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
E Torassa
E Torassa
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
M Tosi
M Tosi
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
A Trioss
A Trioss
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
S Vanini
S Vanini
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
S Ventura
S Ventura
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
P Zotto
P Zotto
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
A Zucchetta
A Zucchetta
62INFN Sezione di Padova, Università di Padova, Università di Trento (Trento), Padua, Italy
62,
M Gabusi
M Gabusi
63INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
63,
S P Ratti
S P Ratti
63INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
63,
C Riccardi
C Riccardi
63INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
63,
P Salvini
P Salvini
63INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
63,
P Vitulo
P Vitulo
63INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
63,
M Biasini
M Biasini
64INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
64,
G M Bilei
G M Bilei
64INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
64,
D Ciangottini
D Ciangottini
64INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
64,
L Fanò
L Fanò
64INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
64,
P Lariccia
P Lariccia
64INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
64,
G Mantovani
G Mantovani
64INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
64,
M Menichelli
M Menichelli
64INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
64,
F Romeo
F Romeo
64INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
64,
A Saha
A Saha
64INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
64,
A Santocchia
A Santocchia
64INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
64,
A Spiezia
A Spiezia
64INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
64,
K Androsov
K Androsov
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
P Azzurri
P Azzurri
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
G Bagliesi
G Bagliesi
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
J Bernardini
J Bernardini
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
T Boccali
T Boccali
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
G Broccolo
G Broccolo
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
D Caiulo
D Caiulo
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
R Castaldi
R Castaldi
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
M A Ciocci
M A Ciocci
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
R Dell’Orso
R Dell’Orso
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
S Donato
S Donato
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
F Fiori
F Fiori
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
L Foà
L Foà
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
A Giassi
A Giassi
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
M T Grippo
M T Grippo
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
F Ligabue
F Ligabue
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
T Lomtadze
T Lomtadze
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
L Martini
L Martini
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
A Messineo
A Messineo
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
C S Moon
C S Moon
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
F Palla
F Palla
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
A Rizzi
A Rizzi
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
A Savoy-Navarro
A Savoy-Navarro
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
A T Serban
A T Serban
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
P Spagnolo
P Spagnolo
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
P Squillacioti
P Squillacioti
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
R Tenchini
R Tenchini
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
G Tonelli
G Tonelli
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
A Venturi
A Venturi
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
P G Verdini
P G Verdini
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
C Vernieri
C Vernieri
65INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
65,
L Barone
L Barone
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
F Cavallari
F Cavallari
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
G D’imperio
G D’imperio
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
D Del Re
D Del Re
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
M Diemoz
M Diemoz
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
M Grassi
M Grassi
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
C Jorda
C Jorda
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
E Longo
E Longo
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
F Margaroli
F Margaroli
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
P Meridiani
P Meridiani
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
F Micheli
F Micheli
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
S Nourbakhsh
S Nourbakhsh
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
G Organtini
G Organtini
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
R Paramatti
R Paramatti
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
S Rahatlou
S Rahatlou
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
C Rovelli
C Rovelli
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
F Santanastasio
F Santanastasio
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
L Soffi
L Soffi
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
P Traczyk
P Traczyk
66INFN Sezione di Roma, Università di Roma, Rome, Italy
66,
N Amapane
N Amapane
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
R Arcidiacono
R Arcidiacono
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
S Argiro
S Argiro
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
M Arneodo
M Arneodo
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
R Bellan
R Bellan
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
C Biino
C Biino
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
N Cartiglia
N Cartiglia
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
S Casasso
S Casasso
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
M Costa
M Costa
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
A Degano
A Degano
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
N Demaria
N Demaria
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
L Finco
L Finco
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
C Mariotti
C Mariotti
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
S Maselli
S Maselli
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
E Migliore
E Migliore
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
V Monaco
V Monaco
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
M Musich
M Musich
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
M M Obertino
M M Obertino
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
G Ortona
G Ortona
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
L Pacher
L Pacher
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
N Pastrone
N Pastrone
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
M Pelliccioni
M Pelliccioni
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
G L Pinna Angioni
G L Pinna Angioni
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
A Potenza
A Potenza
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
A Romero
A Romero
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
M Ruspa
M Ruspa
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
R Sacchi
R Sacchi
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
A Solano
A Solano
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
A Staiano
A Staiano
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
U Tamponi
U Tamponi
67INFN Sezione di Torino, Università di Torino, Università del Piemonte Orientale (Novara), Torino, Italy
67,
S Belforte
S Belforte
68INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
68,
V Candelise
V Candelise
68INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
68,
M Casarsa
M Casarsa
68INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
68,
F Cossutti
F Cossutti
68INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
68,
G Della Ricca
G Della Ricca
68INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
68,
B Gobbo
B Gobbo
68INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
68,
C La Licata
C La Licata
68INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
68,
M Marone
M Marone
68INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
68,
D Montanino
D Montanino
68INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
68,
A Schizzi
A Schizzi
68INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
68,
T Umer
T Umer
68INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
68,
A Zanetti
A Zanetti
68INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
68,
S Chang
S Chang
69Kangwon National University, Chunchon, Korea
69,
A Kropivnitskaya
A Kropivnitskaya
69Kangwon National University, Chunchon, Korea
69,
S K Nam
S K Nam
69Kangwon National University, Chunchon, Korea
69,
D H Kim
D H Kim
70Kyungpook National University, Daegu, Korea
70,
G N Kim
G N Kim
70Kyungpook National University, Daegu, Korea
70,
M S Kim
M S Kim
70Kyungpook National University, Daegu, Korea
70,
D J Kong
D J Kong
70Kyungpook National University, Daegu, Korea
70,
S Lee
S Lee
70Kyungpook National University, Daegu, Korea
70,
Y D Oh
Y D Oh
70Kyungpook National University, Daegu, Korea
70,
H Park
H Park
70Kyungpook National University, Daegu, Korea
70,
A Sakharov
A Sakharov
70Kyungpook National University, Daegu, Korea
70,
D C Son
D C Son
70Kyungpook National University, Daegu, Korea
70,
T J Kim
T J Kim
71Chonbuk National University, Jeonju, Korea
71,
J Y Kim
J Y Kim
72Chonnam National University, Institute for Universe and Elementary Particles, Kwangju, Korea
72,
S Song
S Song
72Chonnam National University, Institute for Universe and Elementary Particles, Kwangju, Korea
72,
S Choi
S Choi
73Korea University, Seoul, Korea
73,
D Gyun
D Gyun
73Korea University, Seoul, Korea
73,
B Hong
B Hong
73Korea University, Seoul, Korea
73,
M Jo
M Jo
73Korea University, Seoul, Korea
73,
H Kim
H Kim
73Korea University, Seoul, Korea
73,
Y Kim
Y Kim
73Korea University, Seoul, Korea
73,
B Lee
B Lee
73Korea University, Seoul, Korea
73,
K S Lee
K S Lee
73Korea University, Seoul, Korea
73,
S K Park
S K Park
73Korea University, Seoul, Korea
73,
Y Roh
Y Roh
73Korea University, Seoul, Korea
73,
M Choi
M Choi
74University of Seoul, Seoul, Korea
74,
J H Kim
J H Kim
74University of Seoul, Seoul, Korea
74,
I C Park
I C Park
74University of Seoul, Seoul, Korea
74,
S Park
S Park
74University of Seoul, Seoul, Korea
74,
G Ryu
G Ryu
74University of Seoul, Seoul, Korea
74,
M S Ryu
M S Ryu
74University of Seoul, Seoul, Korea
74,
Y Choi
Y Choi
75Sungkyunkwan University, Suwon, Korea
75,
Y K Choi
Y K Choi
75Sungkyunkwan University, Suwon, Korea
75,
J Goh
J Goh
75Sungkyunkwan University, Suwon, Korea
75,
D Kim
D Kim
75Sungkyunkwan University, Suwon, Korea
75,
E Kwon
E Kwon
75Sungkyunkwan University, Suwon, Korea
75,
J Lee
J Lee
75Sungkyunkwan University, Suwon, Korea
75,
H Seo
H Seo
75Sungkyunkwan University, Suwon, Korea
75,
I Yu
I Yu
75Sungkyunkwan University, Suwon, Korea
75,
A Juodagalvis
A Juodagalvis
76Vilnius University, Vilnius, Lithuania
76,
J R Komaragiri
J R Komaragiri
77National Centre for Particle Physics, Universiti Malaya, Kuala Lumpur, Malaysia
77,
M A B Md Ali
M A B Md Ali
77National Centre for Particle Physics, Universiti Malaya, Kuala Lumpur, Malaysia
77,
H Castilla-Valdez
H Castilla-Valdez
78Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
78,
E De La Cruz-Burelo
E De La Cruz-Burelo
78Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
78,
I Heredia-de La Cruz
I Heredia-de La Cruz
78Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
78,
R Lopez-Fernandez
R Lopez-Fernandez
78Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
78,
A Sanchez-Hernandez
A Sanchez-Hernandez
78Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
78,
S Carrillo Moreno
S Carrillo Moreno
79Universidad Iberoamericana, Mexico City, Mexico
79,
F Vazquez Valencia
F Vazquez Valencia
79Universidad Iberoamericana, Mexico City, Mexico
79,
I Pedraza
I Pedraza
80Benemerita Universidad Autonoma de Puebla, Puebla, Mexico
80,
H A Salazar Ibarguen
H A Salazar Ibarguen
80Benemerita Universidad Autonoma de Puebla, Puebla, Mexico
80,
E Casimiro Linares
E Casimiro Linares
81Universidad Autónoma de San Luis Potosí, San Luis Potosí, Mexico
81,
A Morelos Pineda
A Morelos Pineda
81Universidad Autónoma de San Luis Potosí, San Luis Potosí, Mexico
81,
D Krofcheck
D Krofcheck
82University of Auckland, Auckland, New Zealand
82,
P H Butler
P H Butler
83University of Canterbury, Christchurch, New Zealand
83,
S Reucroft
S Reucroft
83University of Canterbury, Christchurch, New Zealand
83,
A Ahmad
A Ahmad
84National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
84,
M Ahmad
M Ahmad
84National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
84,
Q Hassan
Q Hassan
84National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
84,
H R Hoorani
H R Hoorani
84National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
84,
S Khalid
S Khalid
84National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
84,
W A Khan
W A Khan
84National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
84,
T Khurshid
T Khurshid
84National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
84,
M A Shah
M A Shah
84National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
84,
M Shoaib
M Shoaib
84National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
84,
H Bialkowska
H Bialkowska
85National Centre for Nuclear Research, Swierk, Poland
85,
M Bluj
M Bluj
85National Centre for Nuclear Research, Swierk, Poland
85,
B Boimska
B Boimska
85National Centre for Nuclear Research, Swierk, Poland
85,
T Frueboes
T Frueboes
85National Centre for Nuclear Research, Swierk, Poland
85,
M Górski
M Górski
85National Centre for Nuclear Research, Swierk, Poland
85,
M Kazana
M Kazana
85National Centre for Nuclear Research, Swierk, Poland
85,
K Nawrocki
K Nawrocki
85National Centre for Nuclear Research, Swierk, Poland
85,
K Romanowska-Rybinska
K Romanowska-Rybinska
85National Centre for Nuclear Research, Swierk, Poland
85,
M Szleper
M Szleper
85National Centre for Nuclear Research, Swierk, Poland
85,
P Zalewski
P Zalewski
85National Centre for Nuclear Research, Swierk, Poland
85,
G Brona
G Brona
86Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
86,
K Bunkowski
K Bunkowski
86Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
86,
M Cwiok
M Cwiok
86Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
86,
W Dominik
W Dominik
86Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
86,
K Doroba
K Doroba
86Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
86,
A Kalinowski
A Kalinowski
86Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
86,
M Konecki
M Konecki
86Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
86,
J Krolikowski
J Krolikowski
86Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
86,
M Misiura
M Misiura
86Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
86,
M Olszewski
M Olszewski
86Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
86,
W Wolszczak
W Wolszczak
86Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
86,
P Bargassa
P Bargassa
87Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
87,
C Beirão Da Cruz E Silva
C Beirão Da Cruz E Silva
87Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
87,
P Faccioli
P Faccioli
87Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
87,
P G Ferreira Parracho
P G Ferreira Parracho
87Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
87,
M Gallinaro
M Gallinaro
87Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
87,
F Nguyen
F Nguyen
87Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
87,
J Rodrigues Antunes
J Rodrigues Antunes
87Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
87,
J Seixas
J Seixas
87Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
87,
J Varela
J Varela
87Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
87,
P Vischia
P Vischia
87Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
87,
S Afanasiev
S Afanasiev
87Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
87,
P Bunin
P Bunin
88Joint Institute for Nuclear Research, Dubna, Russia
88,
M Gavrilenko
M Gavrilenko
88Joint Institute for Nuclear Research, Dubna, Russia
88,
I Golutvin
I Golutvin
88Joint Institute for Nuclear Research, Dubna, Russia
88,
I Gorbunov
I Gorbunov
88Joint Institute for Nuclear Research, Dubna, Russia
88,
A Kamenev
A Kamenev
88Joint Institute for Nuclear Research, Dubna, Russia
88,
V Karjavin
V Karjavin
88Joint Institute for Nuclear Research, Dubna, Russia
88,
V Konoplyanikov
V Konoplyanikov
88Joint Institute for Nuclear Research, Dubna, Russia
88,
A Lanev
A Lanev
88Joint Institute for Nuclear Research, Dubna, Russia
88,
A Malakhov
A Malakhov
88Joint Institute for Nuclear Research, Dubna, Russia
88,
V Matveev
V Matveev
88Joint Institute for Nuclear Research, Dubna, Russia
88,
P Moisenz
P Moisenz
88Joint Institute for Nuclear Research, Dubna, Russia
88,
V Palichik
V Palichik
88Joint Institute for Nuclear Research, Dubna, Russia
88,
V Perelygin
V Perelygin
88Joint Institute for Nuclear Research, Dubna, Russia
88,
S Shmatov
S Shmatov
88Joint Institute for Nuclear Research, Dubna, Russia
88,
N Skatchkov
N Skatchkov
88Joint Institute for Nuclear Research, Dubna, Russia
88,
V Smirnov
V Smirnov
88Joint Institute for Nuclear Research, Dubna, Russia
88,
A Zarubin
A Zarubin
88Joint Institute for Nuclear Research, Dubna, Russia
88,
V Golovtsov
V Golovtsov
89Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
89,
Y Ivanov
Y Ivanov
89Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
89,
V Kim
V Kim
89Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
89,
P Levchenko
P Levchenko
89Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
89,
V Murzin
V Murzin
89Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
89,
V Oreshkin
V Oreshkin
89Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
89,
I Smirnov
I Smirnov
89Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
89,
V Sulimov
V Sulimov
89Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
89,
L Uvarov
L Uvarov
89Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
89,
S Vavilov
S Vavilov
89Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
89,
A Vorobyev
A Vorobyev
89Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
89,
An Vorobyev
An Vorobyev
89Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
89,
Yu Andreev
Yu Andreev
90Institute for Nuclear Research, Moscow, Russia
90,
A Dermenev
A Dermenev
90Institute for Nuclear Research, Moscow, Russia
90,
S Gninenko
S Gninenko
90Institute for Nuclear Research, Moscow, Russia
90,
N Golubev
N Golubev
90Institute for Nuclear Research, Moscow, Russia
90,
M Kirsanov
M Kirsanov
90Institute for Nuclear Research, Moscow, Russia
90,
N Krasnikov
N Krasnikov
90Institute for Nuclear Research, Moscow, Russia
90,
A Pashenkov
A Pashenkov
90Institute for Nuclear Research, Moscow, Russia
90,
D Tlisov
D Tlisov
90Institute for Nuclear Research, Moscow, Russia
90,
A Toropin
A Toropin
90Institute for Nuclear Research, Moscow, Russia
90,
V Epshteyn
V Epshteyn
91Institute for Theoretical and Experimental Physics, Moscow, Russia
91,
V Gavrilov
V Gavrilov
91Institute for Theoretical and Experimental Physics, Moscow, Russia
91,
N Lychkovskaya
N Lychkovskaya
91Institute for Theoretical and Experimental Physics, Moscow, Russia
91,
V Popov
V Popov
91Institute for Theoretical and Experimental Physics, Moscow, Russia
91,
G Safronov
G Safronov
91Institute for Theoretical and Experimental Physics, Moscow, Russia
91,
S Semenov
S Semenov
91Institute for Theoretical and Experimental Physics, Moscow, Russia
91,
A Spiridonov
A Spiridonov
91Institute for Theoretical and Experimental Physics, Moscow, Russia
91,
V Stolin
V Stolin
91Institute for Theoretical and Experimental Physics, Moscow, Russia
91,
E Vlasov
E Vlasov
91Institute for Theoretical and Experimental Physics, Moscow, Russia
91,
A Zhokin
A Zhokin
91Institute for Theoretical and Experimental Physics, Moscow, Russia
91,
V Andreev
V Andreev
92P. N. Lebedev Physical Institute, Moscow, Russia
92,
M Azarkin
M Azarkin
92P. N. Lebedev Physical Institute, Moscow, Russia
92,
I Dremin
I Dremin
92P. N. Lebedev Physical Institute, Moscow, Russia
92,
M Kirakosyan
M Kirakosyan
92P. N. Lebedev Physical Institute, Moscow, Russia
92,
A Leonidov
A Leonidov
92P. N. Lebedev Physical Institute, Moscow, Russia
92,
G Mesyats
G Mesyats
92P. N. Lebedev Physical Institute, Moscow, Russia
92,
S V Rusakov
S V Rusakov
92P. N. Lebedev Physical Institute, Moscow, Russia
92,
A Vinogradov
A Vinogradov
92P. N. Lebedev Physical Institute, Moscow, Russia
92,
A Belyaev
A Belyaev
93Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
93,
E Boos
E Boos
93Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
93,
A Ershov
A Ershov
93Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
93,
A Gribushin
A Gribushin
93Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
93,
L Khein
L Khein
93Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
93,
V Klyukhin
V Klyukhin
93Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
93,
O Kodolova
O Kodolova
93Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
93,
I Lokhtin
I Lokhtin
93Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
93,
O Lukina
O Lukina
93Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
93,
S Obraztsov
S Obraztsov
93Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
93,
S Petrushanko
S Petrushanko
93Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
93,
V Savrin
V Savrin
93Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
93,
A Snigirev
A Snigirev
93Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
93,
I Azhgirey
I Azhgirey
94State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
94,
I Bayshev
I Bayshev
94State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
94,
S Bitioukov
S Bitioukov
94State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
94,
V Kachanov
V Kachanov
94State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
94,
A Kalinin
A Kalinin
94State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
94,
D Konstantinov
D Konstantinov
94State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
94,
V Krychkine
V Krychkine
94State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
94,
V Petrov
V Petrov
94State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
94,
R Ryutin
R Ryutin
94State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
94,
A Sobol
A Sobol
94State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
94,
L Tourtchanovitch
L Tourtchanovitch
94State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
94,
S Troshin
S Troshin
94State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
94,
N Tyurin
N Tyurin
94State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
94,
A Uzunian
A Uzunian
94State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
94,
A Volkov
A Volkov
94State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
94,
P Adzic
P Adzic
95University of Belgrade, Faculty of Physics and Vinca Institute of Nuclear Sciences, Belgrade, Serbia
95,
M Ekmedzic
M Ekmedzic
95University of Belgrade, Faculty of Physics and Vinca Institute of Nuclear Sciences, Belgrade, Serbia
95,
J Milosevic
J Milosevic
95University of Belgrade, Faculty of Physics and Vinca Institute of Nuclear Sciences, Belgrade, Serbia
95,
V Rekovic
V Rekovic
95University of Belgrade, Faculty of Physics and Vinca Institute of Nuclear Sciences, Belgrade, Serbia
95,
J Alcaraz Maestre
J Alcaraz Maestre
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
C Battilana
C Battilana
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
E Calvo
E Calvo
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
M Cerrada
M Cerrada
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
M Chamizo Llatas
M Chamizo Llatas
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
N Colino
N Colino
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
B De La Cruz
B De La Cruz
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
A Delgado Peris
A Delgado Peris
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
D Domínguez Vázquez
D Domínguez Vázquez
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
A Escalante Del Valle
A Escalante Del Valle
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
C Fernandez Bedoya
C Fernandez Bedoya
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
J P Fernández Ramos
J P Fernández Ramos
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
J Flix
J Flix
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
M C Fouz
M C Fouz
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
P Garcia-Abia
P Garcia-Abia
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
O Gonzalez Lopez
O Gonzalez Lopez
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
S Goy Lopez
S Goy Lopez
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
J M Hernandez
J M Hernandez
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
M I Josa
M I Josa
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
G Merino
G Merino
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
E Navarro De Martino
E Navarro De Martino
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
A Pérez-Calero Yzquierdo
A Pérez-Calero Yzquierdo
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
J Puerta Pelayo
J Puerta Pelayo
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
A Quintario Olmeda
A Quintario Olmeda
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
I Redondo
I Redondo
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
L Romero
L Romero
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
M S Soares
M S Soares
96Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
96,
C Albajar
C Albajar
97Universidad Autónoma de Madrid, Madrid, Spain
97,
J F de Trocóniz
J F de Trocóniz
97Universidad Autónoma de Madrid, Madrid, Spain
97,
M Missiroli
M Missiroli
97Universidad Autónoma de Madrid, Madrid, Spain
97,
D Moran
D Moran
97Universidad Autónoma de Madrid, Madrid, Spain
97,
H Brun
H Brun
98Universidad de Oviedo, Oviedo, Spain
98,
J Cuevas
J Cuevas
98Universidad de Oviedo, Oviedo, Spain
98,
J Fernandez Menendez
J Fernandez Menendez
98Universidad de Oviedo, Oviedo, Spain
98,
S Folgueras
S Folgueras
98Universidad de Oviedo, Oviedo, Spain
98,
I Gonzalez Caballero
I Gonzalez Caballero
98Universidad de Oviedo, Oviedo, Spain
98,
L Lloret Iglesias
L Lloret Iglesias
98Universidad de Oviedo, Oviedo, Spain
98,
J A Brochero Cifuentes
J A Brochero Cifuentes
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
I J Cabrillo
I J Cabrillo
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
A Calderon
A Calderon
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
J Duarte Campderros
J Duarte Campderros
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
M Fernandez
M Fernandez
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
G Gomez
G Gomez
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
A Graziano
A Graziano
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
A Lopez Virto
A Lopez Virto
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
J Marco
J Marco
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
R Marco
R Marco
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
C Martinez Rivero
C Martinez Rivero
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
F Matorras
F Matorras
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
F J Munoz Sanchez
F J Munoz Sanchez
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
J Piedra Gomez
J Piedra Gomez
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
T Rodrigo
T Rodrigo
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
A Y Rodríguez-Marrero
A Y Rodríguez-Marrero
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
A Ruiz-Jimeno
A Ruiz-Jimeno
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
L Scodellaro
L Scodellaro
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
I Vila
I Vila
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
R Vilar Cortabitarte
R Vilar Cortabitarte
99Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
99,
D Abbaneo
D Abbaneo
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
E Auffray
E Auffray
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
G Auzinger
G Auzinger
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
M Bachtis
M Bachtis
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
P Baillon
P Baillon
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
A H Ball
A H Ball
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
D Barney
D Barney
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
A Benaglia
A Benaglia
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
J Bendavid
J Bendavid
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
L Benhabib
L Benhabib
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
J F Benitez
J F Benitez
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
C Bernet
C Bernet
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
G Bianchi
G Bianchi
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
P Bloch
P Bloch
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
A Bocci
A Bocci
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
A Bonato
A Bonato
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
O Bondu
O Bondu
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
C Botta
C Botta
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
H Breuker
H Breuker
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
T Camporesi
T Camporesi
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
G Cerminara
G Cerminara
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
S Colafranceschi
S Colafranceschi
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
M D’Alfonso
M D’Alfonso
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
D d’Enterria
D d’Enterria
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
A Dabrowski
A Dabrowski
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
A David
A David
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
F De Guio
F De Guio
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
A De Roeck
A De Roeck
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
S De Visscher
S De Visscher
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
M Dobson
M Dobson
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
M Dordevic
M Dordevic
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
N Dupont-Sagorin
N Dupont-Sagorin
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
A Elliott-Peisert
A Elliott-Peisert
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
J Eugster
J Eugster
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
G Franzoni
G Franzoni
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
W Funk
W Funk
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
D Gigi
D Gigi
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
K Gill
K Gill
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
D Giordano
D Giordano
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
M Girone
M Girone
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
F Glege
F Glege
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
R Guida
R Guida
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
S Gundacker
S Gundacker
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
M Guthoff
M Guthoff
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
R Guida
R Guida
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
J Hammer
J Hammer
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
M Hansen
M Hansen
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
P Harris
P Harris
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
J Hegeman
J Hegeman
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
V Innocente
V Innocente
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
P Janot
P Janot
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
K Kousouris
K Kousouris
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
K Krajczar
K Krajczar
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
P Lecoq
P Lecoq
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
C Lourenço
C Lourenço
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
N Magini
N Magini
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
L Malgeri
L Malgeri
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
M Mannelli
M Mannelli
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
J Marrouche
J Marrouche
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
L Masetti
L Masetti
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
F Meijers
F Meijers
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
S Mersi
S Mersi
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
E Meschi
E Meschi
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
F Moortgat
F Moortgat
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
S Morovic
S Morovic
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
M Mulders
M Mulders
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
P Musella
P Musella
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
L Orsini
L Orsini
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
L Pape
L Pape
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
E Perez
E Perez
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
L Perrozzi
L Perrozzi
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
A Petrilli
A Petrilli
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
G Petrucciani
G Petrucciani
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
A Pfeiffer
A Pfeiffer
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
M Pierini
M Pierini
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
M Pimiä
M Pimiä
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
D Piparo
D Piparo
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
M Plagge
M Plagge
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
A Racz
A Racz
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
G Rolandi
G Rolandi
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
M Rovere
M Rovere
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
H Sakulin
H Sakulin
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
C Schäfer
C Schäfer
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
C Schwick
C Schwick
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
A Sharma
A Sharma
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
P Siegrist
P Siegrist
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
P Silva
P Silva
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
M Simon
M Simon
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
P Sphicas
P Sphicas
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
D Spiga
D Spiga
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
J Steggemann
J Steggemann
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
B Stieger
B Stieger
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
M Stoye
M Stoye
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
Y Takahashi
Y Takahashi
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
D Treille
D Treille
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
A Tsirou
A Tsirou
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
G I Veres
G I Veres
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
J R Vlimant
J R Vlimant
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
N Wardle
N Wardle
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
H K Wöhri
H K Wöhri
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
H Wollny
H Wollny
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
W D Zeuner
W D Zeuner
100CERN, European Organization for Nuclear Research, Geneva, Switzerland
100,
W Bertl
W Bertl
101Paul Scherrer Institut, Villigen, Switzerland
101,
K Deiters
K Deiters
101Paul Scherrer Institut, Villigen, Switzerland
101,
W Erdmann
W Erdmann
101Paul Scherrer Institut, Villigen, Switzerland
101,
R Horisberger
R Horisberger
101Paul Scherrer Institut, Villigen, Switzerland
101,
Q Ingram
Q Ingram
101Paul Scherrer Institut, Villigen, Switzerland
101,
H C Kaestli
H C Kaestli
101Paul Scherrer Institut, Villigen, Switzerland
101,
D Kotlinski
D Kotlinski
101Paul Scherrer Institut, Villigen, Switzerland
101,
U Langenegger
U Langenegger
101Paul Scherrer Institut, Villigen, Switzerland
101,
D Renker
D Renker
101Paul Scherrer Institut, Villigen, Switzerland
101,
T Rohe
T Rohe
101Paul Scherrer Institut, Villigen, Switzerland
101,
F Bachmair
F Bachmair
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
L Bäni
L Bäni
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
L Bianchini
L Bianchini
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
P Bortignon
P Bortignon
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
M A Buchmann
M A Buchmann
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
B Casal
B Casal
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
N Chanon
N Chanon
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
A Deisher
A Deisher
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
G Dissertori
G Dissertori
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
M Dittmar
M Dittmar
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
M Donegà
M Donegà
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
M Dünser
M Dünser
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
P Eller
P Eller
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
C Grab
C Grab
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
D Hits
D Hits
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
W Lustermann
W Lustermann
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
B Mangano
B Mangano
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
A C Marini
A C Marini
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
P Martinez Ruiz del Arbol
P Martinez Ruiz del Arbol
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
D Meister
D Meister
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
N Mohr
N Mohr
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
C Nägeli
C Nägeli
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
F Nessi-Tedaldi
F Nessi-Tedaldi
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
F Pandolfi
F Pandolfi
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
F Pauss
F Pauss
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
M Peruzzi
M Peruzzi
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
M Quittnat
M Quittnat
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
L Rebane
L Rebane
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
M Rossini
M Rossini
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
A Starodumov
A Starodumov
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
M Takahashi
M Takahashi
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
K Theofilatos
K Theofilatos
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
R Wallny
R Wallny
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
H A Weber
H A Weber
102Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
102,
C Amsler
C Amsler
103Universität Zürich, Zurich, Switzerland
103,
M F Canelli
M F Canelli
103Universität Zürich, Zurich, Switzerland
103,
V Chiochia
V Chiochia
103Universität Zürich, Zurich, Switzerland
103,
A De Cosa
A De Cosa
103Universität Zürich, Zurich, Switzerland
103,
A Hinzmann
A Hinzmann
103Universität Zürich, Zurich, Switzerland
103,
T Hreus
T Hreus
103Universität Zürich, Zurich, Switzerland
103,
B Kilminster
B Kilminster
103Universität Zürich, Zurich, Switzerland
103,
C Lange
C Lange
103Universität Zürich, Zurich, Switzerland
103,
B Millan Mejias
B Millan Mejias
103Universität Zürich, Zurich, Switzerland
103,
J Ngadiuba
J Ngadiuba
103Universität Zürich, Zurich, Switzerland
103,
P Robmann
P Robmann
103Universität Zürich, Zurich, Switzerland
103,
F J Ronga
F J Ronga
103Universität Zürich, Zurich, Switzerland
103,
S Taroni
S Taroni
103Universität Zürich, Zurich, Switzerland
103,
M Verzetti
M Verzetti
103Universität Zürich, Zurich, Switzerland
103,
Y Yang
Y Yang
103Universität Zürich, Zurich, Switzerland
103,
M Cardaci
M Cardaci
104National Central University, Chung-Li, Taiwan
104,
K H Chen
K H Chen
104National Central University, Chung-Li, Taiwan
104,
C Ferro
C Ferro
104National Central University, Chung-Li, Taiwan
104,
C M Kuo
C M Kuo
104National Central University, Chung-Li, Taiwan
104,
W Lin
W Lin
104National Central University, Chung-Li, Taiwan
104,
Y J Lu
Y J Lu
104National Central University, Chung-Li, Taiwan
104,
R Volpe
R Volpe
104National Central University, Chung-Li, Taiwan
104,
S S Yu
S S Yu
104National Central University, Chung-Li, Taiwan
104,
P Chang
P Chang
105National Taiwan University (NTU), Taipei, Taiwan
105,
Y H Chang
Y H Chang
105National Taiwan University (NTU), Taipei, Taiwan
105,
Y W Chang
Y W Chang
105National Taiwan University (NTU), Taipei, Taiwan
105,
Y Chao
Y Chao
105National Taiwan University (NTU), Taipei, Taiwan
105,
K F Chen
K F Chen
105National Taiwan University (NTU), Taipei, Taiwan
105,
P H Chen
P H Chen
105National Taiwan University (NTU), Taipei, Taiwan
105,
C Dietz
C Dietz
105National Taiwan University (NTU), Taipei, Taiwan
105,
U Grundler
U Grundler
105National Taiwan University (NTU), Taipei, Taiwan
105,
W-S Hou
W-S Hou
105National Taiwan University (NTU), Taipei, Taiwan
105,
K Y Kao
K Y Kao
105National Taiwan University (NTU), Taipei, Taiwan
105,
Y J Lei
Y J Lei
105National Taiwan University (NTU), Taipei, Taiwan
105,
Y F Liu
Y F Liu
105National Taiwan University (NTU), Taipei, Taiwan
105,
R-S Lu
R-S Lu
105National Taiwan University (NTU), Taipei, Taiwan
105,
D Majumder
D Majumder
105National Taiwan University (NTU), Taipei, Taiwan
105,
E Petrakou
E Petrakou
105National Taiwan University (NTU), Taipei, Taiwan
105,
Y M Tzeng
Y M Tzeng
105National Taiwan University (NTU), Taipei, Taiwan
105,
R Wilken
R Wilken
105National Taiwan University (NTU), Taipei, Taiwan
105,
B Asavapibhop
B Asavapibhop
106Chulalongkorn University, Faculty of Science, Department of Physics, Bangkok, Thailand
106,
N Srimanobhas
N Srimanobhas
106Chulalongkorn University, Faculty of Science, Department of Physics, Bangkok, Thailand
106,
N Suwonjandee
N Suwonjandee
106Chulalongkorn University, Faculty of Science, Department of Physics, Bangkok, Thailand
106,
A Adiguzel
A Adiguzel
107Cukurova University, Adana, Turkey
107,
M N Bakirci
M N Bakirci
107Cukurova University, Adana, Turkey
107,
S Cerci
S Cerci
107Cukurova University, Adana, Turkey
107,
C Dozen
C Dozen
107Cukurova University, Adana, Turkey
107,
I Dumanoglu
I Dumanoglu
107Cukurova University, Adana, Turkey
107,
E Eskut
E Eskut
107Cukurova University, Adana, Turkey
107,
S Girgis
S Girgis
107Cukurova University, Adana, Turkey
107,
G Gokbulut
G Gokbulut
107Cukurova University, Adana, Turkey
107,
E Gurpinar
E Gurpinar
107Cukurova University, Adana, Turkey
107,
I Hos
I Hos
107Cukurova University, Adana, Turkey
107,
E E Kangal
E E Kangal
107Cukurova University, Adana, Turkey
107,
A Kayis Topaksu
A Kayis Topaksu
107Cukurova University, Adana, Turkey
107,
G Onengut
G Onengut
107Cukurova University, Adana, Turkey
107,
K Ozdemir
K Ozdemir
107Cukurova University, Adana, Turkey
107,
S Ozturk
S Ozturk
107Cukurova University, Adana, Turkey
107,
A Polatoz
A Polatoz
107Cukurova University, Adana, Turkey
107,
K Sogut
K Sogut
107Cukurova University, Adana, Turkey
107,
D Sunar Cerci
D Sunar Cerci
107Cukurova University, Adana, Turkey
107,
B Tali
B Tali
107Cukurova University, Adana, Turkey
107,
H Topakli
H Topakli
107Cukurova University, Adana, Turkey
107,
M Vergili
M Vergili
107Cukurova University, Adana, Turkey
107,
I V Akin
I V Akin
108Physics Department, Middle East Technical University, Ankara, Turkey
108,
B Bilin
B Bilin
108Physics Department, Middle East Technical University, Ankara, Turkey
108,
S Bilmis
S Bilmis
108Physics Department, Middle East Technical University, Ankara, Turkey
108,
H Gamsizkan
H Gamsizkan
108Physics Department, Middle East Technical University, Ankara, Turkey
108,
G Karapinar
G Karapinar
108Physics Department, Middle East Technical University, Ankara, Turkey
108,
K Ocalan
K Ocalan
108Physics Department, Middle East Technical University, Ankara, Turkey
108,
S Sekmen
S Sekmen
108Physics Department, Middle East Technical University, Ankara, Turkey
108,
U E Surat
U E Surat
108Physics Department, Middle East Technical University, Ankara, Turkey
108,
M Yalvac
M Yalvac
108Physics Department, Middle East Technical University, Ankara, Turkey
108,
M Zeyrek
M Zeyrek
108Physics Department, Middle East Technical University, Ankara, Turkey
108,
E Gülmez
E Gülmez
109Bogazici University, Istanbul, Turkey
109,
B Isildak
B Isildak
109Bogazici University, Istanbul, Turkey
109,
M Kaya
M Kaya
109Bogazici University, Istanbul, Turkey
109,
O Kaya
O Kaya
109Bogazici University, Istanbul, Turkey
109,
K Cankocak
K Cankocak
110Istanbul Technical University, Istanbul, Turkey
110,
F I Vardarlı
F I Vardarlı
110Istanbul Technical University, Istanbul, Turkey
110,
L Levchuk
L Levchuk
111National Scientific Center, Kharkov Institute of Physics and Technology, Kharkov, Ukraine
111,
P Sorokin
P Sorokin
111National Scientific Center, Kharkov Institute of Physics and Technology, Kharkov, Ukraine
111,
J J Brooke
J J Brooke
112University of Bristol, Bristol, UK
112,
E Clement
E Clement
112University of Bristol, Bristol, UK
112,
D Cussans
D Cussans
112University of Bristol, Bristol, UK
112,
H Flacher
H Flacher
112University of Bristol, Bristol, UK
112,
R Frazier
R Frazier
112University of Bristol, Bristol, UK
112,
J Goldstein
J Goldstein
112University of Bristol, Bristol, UK
112,
M Grimes
M Grimes
112University of Bristol, Bristol, UK
112,
G P Heath
G P Heath
112University of Bristol, Bristol, UK
112,
H F Heath
H F Heath
112University of Bristol, Bristol, UK
112,
J Jacob
J Jacob
112University of Bristol, Bristol, UK
112,
L Kreczko
L Kreczko
112University of Bristol, Bristol, UK
112,
C Lucas
C Lucas
112University of Bristol, Bristol, UK
112,
Z Meng
Z Meng
112University of Bristol, Bristol, UK
112,
D M Newbold
D M Newbold
112University of Bristol, Bristol, UK
112,
S Paramesvaran
S Paramesvaran
112University of Bristol, Bristol, UK
112,
A Poll
A Poll
112University of Bristol, Bristol, UK
112,
S Senkin
S Senkin
112University of Bristol, Bristol, UK
112,
V J Smith
V J Smith
112University of Bristol, Bristol, UK
112,
T Williams
T Williams
112University of Bristol, Bristol, UK
112,
K W Bell
K W Bell
113Rutherford Appleton Laboratory, Didcot, UK
113,
A Belyaev
A Belyaev
113Rutherford Appleton Laboratory, Didcot, UK
113,
C Brew
C Brew
113Rutherford Appleton Laboratory, Didcot, UK
113,
R M Brown
R M Brown
113Rutherford Appleton Laboratory, Didcot, UK
113,
D J A Cockerill
D J A Cockerill
113Rutherford Appleton Laboratory, Didcot, UK
113,
J A Coughlan
J A Coughlan
113Rutherford Appleton Laboratory, Didcot, UK
113,
K Harder
K Harder
113Rutherford Appleton Laboratory, Didcot, UK
113,
S Harper
S Harper
113Rutherford Appleton Laboratory, Didcot, UK
113,
E Olaiya
E Olaiya
113Rutherford Appleton Laboratory, Didcot, UK
113,
D Petyt
D Petyt
113Rutherford Appleton Laboratory, Didcot, UK
113,
C H Shepherd-Themistocleous
C H Shepherd-Themistocleous
113Rutherford Appleton Laboratory, Didcot, UK
113,
A Thea
A Thea
113Rutherford Appleton Laboratory, Didcot, UK
113,
I R Tomalin
I R Tomalin
113Rutherford Appleton Laboratory, Didcot, UK
113,
W J Womersley
W J Womersley
113Rutherford Appleton Laboratory, Didcot, UK
113,
S D Worm
S D Worm
113Rutherford Appleton Laboratory, Didcot, UK
113,
M Baber
M Baber
114Imperial College, London, UK
114,
R Bainbridge
R Bainbridge
114Imperial College, London, UK
114,
O Buchmuller
O Buchmuller
114Imperial College, London, UK
114,
D Burton
D Burton
114Imperial College, London, UK
114,
D Colling
D Colling
114Imperial College, London, UK
114,
N Cripps
N Cripps
114Imperial College, London, UK
114,
M Cutajar
M Cutajar
114Imperial College, London, UK
114,
P Dauncey
P Dauncey
114Imperial College, London, UK
114,
G Davies
G Davies
114Imperial College, London, UK
114,
M Della Negra
M Della Negra
114Imperial College, London, UK
114,
P Dunne
P Dunne
114Imperial College, London, UK
114,
W Ferguson
W Ferguson
114Imperial College, London, UK
114,
J Fulcher
J Fulcher
114Imperial College, London, UK
114,
D Futyan
D Futyan
114Imperial College, London, UK
114,
A Gilbert
A Gilbert
114Imperial College, London, UK
114,
G Hall
G Hall
114Imperial College, London, UK
114,
G Iles
G Iles
114Imperial College, London, UK
114,
M Jarvis
M Jarvis
114Imperial College, London, UK
114,
G Karapostoli
G Karapostoli
114Imperial College, London, UK
114,
M Kenzie
M Kenzie
114Imperial College, London, UK
114,
R Lane
R Lane
114Imperial College, London, UK
114,
R Lucas
R Lucas
114Imperial College, London, UK
114,
L Lyons
L Lyons
114Imperial College, London, UK
114,
A-M Magnan
A-M Magnan
114Imperial College, London, UK
114,
S Malik
S Malik
114Imperial College, London, UK
114,
B Mathias
B Mathias
114Imperial College, London, UK
114,
J Nash
J Nash
114Imperial College, London, UK
114,
A Nikitenko
A Nikitenko
114Imperial College, London, UK
114,
J Pela
J Pela
114Imperial College, London, UK
114,
M Pesaresi
M Pesaresi
114Imperial College, London, UK
114,
K Petridis
K Petridis
114Imperial College, London, UK
114,
D M Raymond
D M Raymond
114Imperial College, London, UK
114,
S Rogerson
S Rogerson
114Imperial College, London, UK
114,
A Rose
A Rose
114Imperial College, London, UK
114,
C Seez
C Seez
114Imperial College, London, UK
114,
P Sharp
P Sharp
114Imperial College, London, UK
114,
A Tapper
A Tapper
114Imperial College, London, UK
114,
M Vazquez Acosta
M Vazquez Acosta
114Imperial College, London, UK
114,
T Virdee
T Virdee
114Imperial College, London, UK
114,
S C Zenz
S C Zenz
114Imperial College, London, UK
114,
J E Cole
J E Cole
115Brunel University, Uxbridge, UK
115,
P R Hobson
P R Hobson
115Brunel University, Uxbridge, UK
115,
A Khan
A Khan
115Brunel University, Uxbridge, UK
115,
P Kyberd
P Kyberd
115Brunel University, Uxbridge, UK
115,
D Leggat
D Leggat
115Brunel University, Uxbridge, UK
115,
D Leslie
D Leslie
115Brunel University, Uxbridge, UK
115,
W Martin
W Martin
115Brunel University, Uxbridge, UK
115,
I D Reid
I D Reid
115Brunel University, Uxbridge, UK
115,
P Symonds
P Symonds
115Brunel University, Uxbridge, UK
115,
L Teodorescu
L Teodorescu
115Brunel University, Uxbridge, UK
115,
M Turner
M Turner
115Brunel University, Uxbridge, UK
115,
J Dittmann
J Dittmann
116Baylor University, Waco, USA
116,
K Hatakeyama
K Hatakeyama
116Baylor University, Waco, USA
116,
A Kasmi
A Kasmi
116Baylor University, Waco, USA
116,
H Liu
H Liu
116Baylor University, Waco, USA
116,
T Scarborough
T Scarborough
116Baylor University, Waco, USA
116,
O Charaf
O Charaf
117The University of Alabama, Tuscaloosa, USA
117,
S I Cooper
S I Cooper
117The University of Alabama, Tuscaloosa, USA
117,
C Henderson
C Henderson
117The University of Alabama, Tuscaloosa, USA
117,
P Rumerio
P Rumerio
117The University of Alabama, Tuscaloosa, USA
117,
A Avetisyan
A Avetisyan
118Boston University, Boston, USA
118,
T Bose
T Bose
118Boston University, Boston, USA
118,
C Fantasia
C Fantasia
118Boston University, Boston, USA
118,
P Lawson
P Lawson
118Boston University, Boston, USA
118,
C Richardson
C Richardson
118Boston University, Boston, USA
118,
J Rohlf
J Rohlf
118Boston University, Boston, USA
118,
D Sperka
D Sperka
118Boston University, Boston, USA
118,
J St John
J St John
118Boston University, Boston, USA
118,
L Sulak
L Sulak
118Boston University, Boston, USA
118,
J Alimena
J Alimena
119Brown University, Providence, USA
119,
E Berry
E Berry
119Brown University, Providence, USA
119,
S Bhattacharya
S Bhattacharya
119Brown University, Providence, USA
119,
G Christopher
G Christopher
119Brown University, Providence, USA
119,
D Cutts
D Cutts
119Brown University, Providence, USA
119,
Z Demiragli
Z Demiragli
119Brown University, Providence, USA
119,
N Dhingra
N Dhingra
119Brown University, Providence, USA
119,
A Ferapontov
A Ferapontov
119Brown University, Providence, USA
119,
A Garabedian
A Garabedian
119Brown University, Providence, USA
119,
U Heintz
U Heintz
119Brown University, Providence, USA
119,
G Kukartsev
G Kukartsev
119Brown University, Providence, USA
119,
E Laird
E Laird
119Brown University, Providence, USA
119,
G Landsberg
G Landsberg
119Brown University, Providence, USA
119,
M Luk
M Luk
119Brown University, Providence, USA
119,
M Narain
M Narain
119Brown University, Providence, USA
119,
M Segala
M Segala
119Brown University, Providence, USA
119,
T Sinthuprasith
T Sinthuprasith
119Brown University, Providence, USA
119,
T Speer
T Speer
119Brown University, Providence, USA
119,
J Swanson
J Swanson
119Brown University, Providence, USA
119,
R Breedon
R Breedon
120University of California, Davis, USA
120,
G Breto
G Breto
120University of California, Davis, USA
120,
M Calderon De La Barca Sanchez
M Calderon De La Barca Sanchez
120University of California, Davis, USA
120,
S Chauhan
S Chauhan
120University of California, Davis, USA
120,
M Chertok
M Chertok
120University of California, Davis, USA
120,
J Conway
J Conway
120University of California, Davis, USA
120,
R Conway
R Conway
120University of California, Davis, USA
120,
P T Cox
P T Cox
120University of California, Davis, USA
120,
R Erbacher
R Erbacher
120University of California, Davis, USA
120,
M Gardner
M Gardner
120University of California, Davis, USA
120,
W Ko
W Ko
120University of California, Davis, USA
120,
R Lander
R Lander
120University of California, Davis, USA
120,
T Miceli
T Miceli
120University of California, Davis, USA
120,
M Mulhearn
M Mulhearn
120University of California, Davis, USA
120,
D Pellett
D Pellett
120University of California, Davis, USA
120,
J Pilot
J Pilot
120University of California, Davis, USA
120,
F Ricci-Tam
F Ricci-Tam
120University of California, Davis, USA
120,
M Searle
M Searle
120University of California, Davis, USA
120,
S Shalhout
S Shalhout
120University of California, Davis, USA
120,
J Smith
J Smith
120University of California, Davis, USA
120,
M Squires
M Squires
120University of California, Davis, USA
120,
D Stolp
D Stolp
120University of California, Davis, USA
120,
M Tripathi
M Tripathi
120University of California, Davis, USA
120,
S Wilbur
S Wilbur
120University of California, Davis, USA
120,
R Yohay
R Yohay
120University of California, Davis, USA
120,
R Cousins
R Cousins
121University of California, Los Angeles, USA
121,
P Everaerts
P Everaerts
121University of California, Los Angeles, USA
121,
C Farrell
C Farrell
121University of California, Los Angeles, USA
121,
J Hauser
J Hauser
121University of California, Los Angeles, USA
121,
M Ignatenko
M Ignatenko
121University of California, Los Angeles, USA
121,
G Rakness
G Rakness
121University of California, Los Angeles, USA
121,
E Takasugi
E Takasugi
121University of California, Los Angeles, USA
121,
V Valuev
V Valuev
121University of California, Los Angeles, USA
121,
M Weber
M Weber
121University of California, Los Angeles, USA
121,
J Babb
J Babb
122University of California, Riverside, Riverside, USA
122,
K Burt
K Burt
122University of California, Riverside, Riverside, USA
122,
R Clare
R Clare
122University of California, Riverside, Riverside, USA
122,
J Ellison
J Ellison
122University of California, Riverside, Riverside, USA
122,
J W Gary
J W Gary
122University of California, Riverside, Riverside, USA
122,
G Hanson
G Hanson
122University of California, Riverside, Riverside, USA
122,
J Heilman
J Heilman
122University of California, Riverside, Riverside, USA
122,
M Ivova Rikova
M Ivova Rikova
122University of California, Riverside, Riverside, USA
122,
P Jandir
P Jandir
122University of California, Riverside, Riverside, USA
122,
E Kennedy
E Kennedy
122University of California, Riverside, Riverside, USA
122,
F Lacroix
F Lacroix
122University of California, Riverside, Riverside, USA
122,
H Liu
H Liu
122University of California, Riverside, Riverside, USA
122,
O R Long
O R Long
122University of California, Riverside, Riverside, USA
122,
A Luthra
A Luthra
122University of California, Riverside, Riverside, USA
122,
M Malberti
M Malberti
122University of California, Riverside, Riverside, USA
122,
H Nguyen
H Nguyen
122University of California, Riverside, Riverside, USA
122,
M Olmedo Negrete
M Olmedo Negrete
122University of California, Riverside, Riverside, USA
122,
A Shrinivas
A Shrinivas
122University of California, Riverside, Riverside, USA
122,
S Sumowidagdo
S Sumowidagdo
122University of California, Riverside, Riverside, USA
122,
S Wimpenny
S Wimpenny
122University of California, Riverside, Riverside, USA
122,
W Andrews
W Andrews
123University of California, San Diego, La Jolla, USA
123,
J G Branson
J G Branson
123University of California, San Diego, La Jolla, USA
123,
G B Cerati
G B Cerati
123University of California, San Diego, La Jolla, USA
123,
S Cittolin
S Cittolin
123University of California, San Diego, La Jolla, USA
123,
R T D’Agnolo
R T D’Agnolo
123University of California, San Diego, La Jolla, USA
123,
D Evans
D Evans
123University of California, San Diego, La Jolla, USA
123,
A Holzner
A Holzner
123University of California, San Diego, La Jolla, USA
123,
R Kelley
R Kelley
123University of California, San Diego, La Jolla, USA
123,
D Klein
D Klein
123University of California, San Diego, La Jolla, USA
123,
M Lebourgeois
M Lebourgeois
123University of California, San Diego, La Jolla, USA
123,
J Letts
J Letts
123University of California, San Diego, La Jolla, USA
123,
I Macneill
I Macneill
123University of California, San Diego, La Jolla, USA
123,
D Olivito
D Olivito
123University of California, San Diego, La Jolla, USA
123,
S Padhi
S Padhi
123University of California, San Diego, La Jolla, USA
123,
C Palmer
C Palmer
123University of California, San Diego, La Jolla, USA
123,
M Pieri
M Pieri
123University of California, San Diego, La Jolla, USA
123,
M Sani
M Sani
123University of California, San Diego, La Jolla, USA
123,
V Sharma
V Sharma
123University of California, San Diego, La Jolla, USA
123,
S Simon
S Simon
123University of California, San Diego, La Jolla, USA
123,
E Sudano
E Sudano
123University of California, San Diego, La Jolla, USA
123,
M Tadel
M Tadel
123University of California, San Diego, La Jolla, USA
123,
Y Tu
Y Tu
123University of California, San Diego, La Jolla, USA
123,
A Vartak
A Vartak
123University of California, San Diego, La Jolla, USA
123,
C Welke
C Welke
123University of California, San Diego, La Jolla, USA
123,
F Würthwein
F Würthwein
123University of California, San Diego, La Jolla, USA
123,
A Yagil
A Yagil
123University of California, San Diego, La Jolla, USA
123,
J Yoo
J Yoo
123University of California, San Diego, La Jolla, USA
123,
D Barge
D Barge
124University of California, Santa Barbara, Santa Barbara, USA
124,
J Bradmiller-Feld
J Bradmiller-Feld
124University of California, Santa Barbara, Santa Barbara, USA
124,
C Campagnari
C Campagnari
124University of California, Santa Barbara, Santa Barbara, USA
124,
T Danielson
T Danielson
124University of California, Santa Barbara, Santa Barbara, USA
124,
A Dishaw
A Dishaw
124University of California, Santa Barbara, Santa Barbara, USA
124,
K Flowers
K Flowers
124University of California, Santa Barbara, Santa Barbara, USA
124,
M Franco Sevilla
M Franco Sevilla
124University of California, Santa Barbara, Santa Barbara, USA
124,
P Geffert
P Geffert
124University of California, Santa Barbara, Santa Barbara, USA
124,
C George
C George
124University of California, Santa Barbara, Santa Barbara, USA
124,
F Golf
F Golf
124University of California, Santa Barbara, Santa Barbara, USA
124,
L Gouskos
L Gouskos
124University of California, Santa Barbara, Santa Barbara, USA
124,
J Incandela
J Incandela
124University of California, Santa Barbara, Santa Barbara, USA
124,
C Justus
C Justus
124University of California, Santa Barbara, Santa Barbara, USA
124,
N Mccoll
N Mccoll
124University of California, Santa Barbara, Santa Barbara, USA
124,
J Richman
J Richman
124University of California, Santa Barbara, Santa Barbara, USA
124,
D Stuart
D Stuart
124University of California, Santa Barbara, Santa Barbara, USA
124,
W To
W To
124University of California, Santa Barbara, Santa Barbara, USA
124,
C West
C West
124University of California, Santa Barbara, Santa Barbara, USA
124,
A Apresyan
A Apresyan
125California Institute of Technology, Pasadena, USA
125,
A Bornheim
A Bornheim
125California Institute of Technology, Pasadena, USA
125,
J Bunn
J Bunn
125California Institute of Technology, Pasadena, USA
125,
Y Chen
Y Chen
125California Institute of Technology, Pasadena, USA
125,
E Di Marco
E Di Marco
125California Institute of Technology, Pasadena, USA
125,
J Duarte
J Duarte
125California Institute of Technology, Pasadena, USA
125,
A Mott
A Mott
125California Institute of Technology, Pasadena, USA
125,
H B Newman
H B Newman
125California Institute of Technology, Pasadena, USA
125,
C Pena
C Pena
125California Institute of Technology, Pasadena, USA
125,
C Rogan
C Rogan
125California Institute of Technology, Pasadena, USA
125,
M Spiropulu
M Spiropulu
125California Institute of Technology, Pasadena, USA
125,
V Timciuc
V Timciuc
125California Institute of Technology, Pasadena, USA
125,
R Wilkinson
R Wilkinson
125California Institute of Technology, Pasadena, USA
125,
S Xie
S Xie
125California Institute of Technology, Pasadena, USA
125,
R Y Zhu
R Y Zhu
125California Institute of Technology, Pasadena, USA
125,
V Azzolini
V Azzolini
126Carnegie Mellon University, Pittsburgh, USA
126,
A Calamba
A Calamba
126Carnegie Mellon University, Pittsburgh, USA
126,
B Carlson
B Carlson
126Carnegie Mellon University, Pittsburgh, USA
126,
T Ferguson
T Ferguson
126Carnegie Mellon University, Pittsburgh, USA
126,
Y Iiyama
Y Iiyama
126Carnegie Mellon University, Pittsburgh, USA
126,
M Paulini
M Paulini
126Carnegie Mellon University, Pittsburgh, USA
126,
J Russ
J Russ
126Carnegie Mellon University, Pittsburgh, USA
126,
H Vogel
H Vogel
126Carnegie Mellon University, Pittsburgh, USA
126,
I Vorobiev
I Vorobiev
126Carnegie Mellon University, Pittsburgh, USA
126,
J P Cumalat
J P Cumalat
127University of Colorado at Boulder, Boulder, USA
127,
W T Ford
W T Ford
127University of Colorado at Boulder, Boulder, USA
127,
A Gaz
A Gaz
127University of Colorado at Boulder, Boulder, USA
127,
E Luiggi Lopez
E Luiggi Lopez
127University of Colorado at Boulder, Boulder, USA
127,
U Nauenberg
U Nauenberg
127University of Colorado at Boulder, Boulder, USA
127,
J G Smith
J G Smith
127University of Colorado at Boulder, Boulder, USA
127,
K Stenson
K Stenson
127University of Colorado at Boulder, Boulder, USA
127,
K A Ulmer
K A Ulmer
127University of Colorado at Boulder, Boulder, USA
127,
S R Wagner
S R Wagner
127University of Colorado at Boulder, Boulder, USA
127,
J Alexander
J Alexander
128Cornell University, Ithaca, USA
128,
A Chatterjee
A Chatterjee
128Cornell University, Ithaca, USA
128,
J Chu
J Chu
128Cornell University, Ithaca, USA
128,
S Dittmer
S Dittmer
128Cornell University, Ithaca, USA
128,
N Eggert
N Eggert
128Cornell University, Ithaca, USA
128,
N Mirman
N Mirman
128Cornell University, Ithaca, USA
128,
G Nicolas Kaufman
G Nicolas Kaufman
128Cornell University, Ithaca, USA
128,
J R Patterson
J R Patterson
128Cornell University, Ithaca, USA
128,
A Ryd
A Ryd
128Cornell University, Ithaca, USA
128,
E Salvati
E Salvati
128Cornell University, Ithaca, USA
128,
L Skinnari
L Skinnari
128Cornell University, Ithaca, USA
128,
W Sun
W Sun
128Cornell University, Ithaca, USA
128,
W D Teo
W D Teo
128Cornell University, Ithaca, USA
128,
J Thom
J Thom
128Cornell University, Ithaca, USA
128,
J Thompson
J Thompson
128Cornell University, Ithaca, USA
128,
J Tucker
J Tucker
128Cornell University, Ithaca, USA
128,
Y Weng
Y Weng
128Cornell University, Ithaca, USA
128,
L Winstrom
L Winstrom
128Cornell University, Ithaca, USA
128,
P Wittich
P Wittich
128Cornell University, Ithaca, USA
128,
D Winn
D Winn
129Fairfield University, Fairfield, USA
129,
S Abdullin
S Abdullin
130Fermi National Accelerator Laboratory, Batavia, USA
130,
M Albrow
M Albrow
130Fermi National Accelerator Laboratory, Batavia, USA
130,
J Anderson
J Anderson
130Fermi National Accelerator Laboratory, Batavia, USA
130,
G Apollinari
G Apollinari
130Fermi National Accelerator Laboratory, Batavia, USA
130,
L A T Bauerdick
L A T Bauerdick
130Fermi National Accelerator Laboratory, Batavia, USA
130,
A Beretvas
A Beretvas
130Fermi National Accelerator Laboratory, Batavia, USA
130,
J Berryhill
J Berryhill
130Fermi National Accelerator Laboratory, Batavia, USA
130,
P C Bhat
P C Bhat
130Fermi National Accelerator Laboratory, Batavia, USA
130,
K Burkett
K Burkett
130Fermi National Accelerator Laboratory, Batavia, USA
130,
J N Butler
J N Butler
130Fermi National Accelerator Laboratory, Batavia, USA
130,
H W K Cheung
H W K Cheung
130Fermi National Accelerator Laboratory, Batavia, USA
130,
F Chlebana
F Chlebana
130Fermi National Accelerator Laboratory, Batavia, USA
130,
S Cihangir
S Cihangir
130Fermi National Accelerator Laboratory, Batavia, USA
130,
V D Elvira
V D Elvira
130Fermi National Accelerator Laboratory, Batavia, USA
130,
I Fisk
I Fisk
130Fermi National Accelerator Laboratory, Batavia, USA
130,
J Freeman
J Freeman
130Fermi National Accelerator Laboratory, Batavia, USA
130,
Y Gao
Y Gao
130Fermi National Accelerator Laboratory, Batavia, USA
130,
E Gottschalk
E Gottschalk
130Fermi National Accelerator Laboratory, Batavia, USA
130,
L Gray
L Gray
130Fermi National Accelerator Laboratory, Batavia, USA
130,
D Green
D Green
130Fermi National Accelerator Laboratory, Batavia, USA
130,
S Grünendahl
S Grünendahl
130Fermi National Accelerator Laboratory, Batavia, USA
130,
O Gutsche
O Gutsche
130Fermi National Accelerator Laboratory, Batavia, USA
130,
J Hanlon
J Hanlon
130Fermi National Accelerator Laboratory, Batavia, USA
130,
D Hare
D Hare
130Fermi National Accelerator Laboratory, Batavia, USA
130,
R M Harris
R M Harris
130Fermi National Accelerator Laboratory, Batavia, USA
130,
J Hirschauer
J Hirschauer
130Fermi National Accelerator Laboratory, Batavia, USA
130,
B Hooberman
B Hooberman
130Fermi National Accelerator Laboratory, Batavia, USA
130,
S Jindariani
S Jindariani
130Fermi National Accelerator Laboratory, Batavia, USA
130,
M Johnson
M Johnson
130Fermi National Accelerator Laboratory, Batavia, USA
130,
U Joshi
U Joshi
130Fermi National Accelerator Laboratory, Batavia, USA
130,
K Kaadze
K Kaadze
130Fermi National Accelerator Laboratory, Batavia, USA
130,
B Klima
B Klima
130Fermi National Accelerator Laboratory, Batavia, USA
130,
B Kreis
B Kreis
130Fermi National Accelerator Laboratory, Batavia, USA
130,
S Kwan
S Kwan
130Fermi National Accelerator Laboratory, Batavia, USA
130,
J Linacre
J Linacre
130Fermi National Accelerator Laboratory, Batavia, USA
130,
D Lincoln
D Lincoln
130Fermi National Accelerator Laboratory, Batavia, USA
130,
R Lipton
R Lipton
130Fermi National Accelerator Laboratory, Batavia, USA
130,
T Liu
T Liu
130Fermi National Accelerator Laboratory, Batavia, USA
130,
J Lykken
J Lykken
130Fermi National Accelerator Laboratory, Batavia, USA
130,
K Maeshima
K Maeshima
130Fermi National Accelerator Laboratory, Batavia, USA
130,
J M Marraffino
J M Marraffino
130Fermi National Accelerator Laboratory, Batavia, USA
130,
V I Martinez Outschoorn
V I Martinez Outschoorn
130Fermi National Accelerator Laboratory, Batavia, USA
130,
S Maruyama
S Maruyama
130Fermi National Accelerator Laboratory, Batavia, USA
130,
D Mason
D Mason
130Fermi National Accelerator Laboratory, Batavia, USA
130,
P McBride
P McBride
130Fermi National Accelerator Laboratory, Batavia, USA
130,
K Mishra
K Mishra
130Fermi National Accelerator Laboratory, Batavia, USA
130,
S Mrenna
S Mrenna
130Fermi National Accelerator Laboratory, Batavia, USA
130,
Y Musienko
Y Musienko
130Fermi National Accelerator Laboratory, Batavia, USA
130,
S Nahn
S Nahn
130Fermi National Accelerator Laboratory, Batavia, USA
130,
C Newman-Holmes
C Newman-Holmes
130Fermi National Accelerator Laboratory, Batavia, USA
130,
V O’Dell
V O’Dell
130Fermi National Accelerator Laboratory, Batavia, USA
130,
O Prokofyev
O Prokofyev
130Fermi National Accelerator Laboratory, Batavia, USA
130,
E Sexton-Kennedy
E Sexton-Kennedy
130Fermi National Accelerator Laboratory, Batavia, USA
130,
S Sharma
S Sharma
130Fermi National Accelerator Laboratory, Batavia, USA
130,
A Soha
A Soha
130Fermi National Accelerator Laboratory, Batavia, USA
130,
W J Spalding
W J Spalding
130Fermi National Accelerator Laboratory, Batavia, USA
130,
L Spiegel
L Spiegel
130Fermi National Accelerator Laboratory, Batavia, USA
130,
L Taylor
L Taylor
130Fermi National Accelerator Laboratory, Batavia, USA
130,
S Tkaczyk
S Tkaczyk
130Fermi National Accelerator Laboratory, Batavia, USA
130,
N V Tran
N V Tran
130Fermi National Accelerator Laboratory, Batavia, USA
130,
L Uplegger
L Uplegger
130Fermi National Accelerator Laboratory, Batavia, USA
130,
E W Vaandering
E W Vaandering
130Fermi National Accelerator Laboratory, Batavia, USA
130,
R Vidal
R Vidal
130Fermi National Accelerator Laboratory, Batavia, USA
130,
A Whitbeck
A Whitbeck
130Fermi National Accelerator Laboratory, Batavia, USA
130,
J Whitmore
J Whitmore
130Fermi National Accelerator Laboratory, Batavia, USA
130,
F Yang
F Yang
130Fermi National Accelerator Laboratory, Batavia, USA
130,
D Acosta
D Acosta
131University of Florida, Gainesville, USA
131,
P Avery
P Avery
131University of Florida, Gainesville, USA
131,
D Bourilkov
D Bourilkov
131University of Florida, Gainesville, USA
131,
M Carver
M Carver
131University of Florida, Gainesville, USA
131,
T Cheng
T Cheng
131University of Florida, Gainesville, USA
131,
D Curry
D Curry
131University of Florida, Gainesville, USA
131,
S Das
S Das
131University of Florida, Gainesville, USA
131,
M De Gruttola
M De Gruttola
131University of Florida, Gainesville, USA
131,
G P Di Giovanni
G P Di Giovanni
131University of Florida, Gainesville, USA
131,
R D Field
R D Field
131University of Florida, Gainesville, USA
131,
M Fisher
M Fisher
131University of Florida, Gainesville, USA
131,
I K Furic
I K Furic
131University of Florida, Gainesville, USA
131,
J Hugon
J Hugon
131University of Florida, Gainesville, USA
131,
J Konigsberg
J Konigsberg
131University of Florida, Gainesville, USA
131,
A Korytov
A Korytov
131University of Florida, Gainesville, USA
131,
T Kypreos
T Kypreos
131University of Florida, Gainesville, USA
131,
J F Low
J F Low
131University of Florida, Gainesville, USA
131,
K Matchev
K Matchev
131University of Florida, Gainesville, USA
131,
P Milenovic
P Milenovic
131University of Florida, Gainesville, USA
131,
G Mitselmakher
G Mitselmakher
131University of Florida, Gainesville, USA
131,
L Muniz
L Muniz
131University of Florida, Gainesville, USA
131,
A Rinkevicius
A Rinkevicius
131University of Florida, Gainesville, USA
131,
L Shchutska
L Shchutska
131University of Florida, Gainesville, USA
131,
M Snowball
M Snowball
131University of Florida, Gainesville, USA
131,
J Yelton
J Yelton
131University of Florida, Gainesville, USA
131,
M Zakaria
M Zakaria
131University of Florida, Gainesville, USA
131,
S Hewamanage
S Hewamanage
132Florida International University, Miami, USA
132,
S Linn
S Linn
132Florida International University, Miami, USA
132,
P Markowitz
P Markowitz
132Florida International University, Miami, USA
132,
G Martinez
G Martinez
132Florida International University, Miami, USA
132,
J L Rodriguez
J L Rodriguez
132Florida International University, Miami, USA
132,
T Adams
T Adams
133Florida State University, Tallahassee, USA
133,
A Askew
A Askew
133Florida State University, Tallahassee, USA
133,
J Bochenek
J Bochenek
133Florida State University, Tallahassee, USA
133,
B Diamond
B Diamond
133Florida State University, Tallahassee, USA
133,
J Haas
J Haas
133Florida State University, Tallahassee, USA
133,
S Hagopian
S Hagopian
133Florida State University, Tallahassee, USA
133,
V Hagopian
V Hagopian
133Florida State University, Tallahassee, USA
133,
K F Johnson
K F Johnson
133Florida State University, Tallahassee, USA
133,
H Prosper
H Prosper
133Florida State University, Tallahassee, USA
133,
V Veeraraghavan
V Veeraraghavan
133Florida State University, Tallahassee, USA
133,
M Weinberg
M Weinberg
133Florida State University, Tallahassee, USA
133,
M M Baarmand
M M Baarmand
134Florida Institute of Technology, Melbourne, USA
134,
M Hohlmann
M Hohlmann
134Florida Institute of Technology, Melbourne, USA
134,
H Kalakhety
H Kalakhety
134Florida Institute of Technology, Melbourne, USA
134,
F Yumiceva
F Yumiceva
134Florida Institute of Technology, Melbourne, USA
134,
M R Adams
M R Adams
135University of Illinois at Chicago (UIC), Chicago, USA
135,
L Apanasevich
L Apanasevich
135University of Illinois at Chicago (UIC), Chicago, USA
135,
V E Bazterra
V E Bazterra
135University of Illinois at Chicago (UIC), Chicago, USA
135,
D Berry
D Berry
135University of Illinois at Chicago (UIC), Chicago, USA
135,
R R Betts
R R Betts
135University of Illinois at Chicago (UIC), Chicago, USA
135,
I Bucinskaite
I Bucinskaite
135University of Illinois at Chicago (UIC), Chicago, USA
135,
R Cavanaugh
R Cavanaugh
135University of Illinois at Chicago (UIC), Chicago, USA
135,
O Evdokimov
O Evdokimov
135University of Illinois at Chicago (UIC), Chicago, USA
135,
L Gauthier
L Gauthier
135University of Illinois at Chicago (UIC), Chicago, USA
135,
C E Gerber
C E Gerber
135University of Illinois at Chicago (UIC), Chicago, USA
135,
D J Hofman
D J Hofman
135University of Illinois at Chicago (UIC), Chicago, USA
135,
S Khalatyan
S Khalatyan
135University of Illinois at Chicago (UIC), Chicago, USA
135,
P Kurt
P Kurt
135University of Illinois at Chicago (UIC), Chicago, USA
135,
D H Moon
D H Moon
135University of Illinois at Chicago (UIC), Chicago, USA
135,
C O’Brien
C O’Brien
135University of Illinois at Chicago (UIC), Chicago, USA
135,
C Silkworth
C Silkworth
135University of Illinois at Chicago (UIC), Chicago, USA
135,
P Turner
P Turner
135University of Illinois at Chicago (UIC), Chicago, USA
135,
N Varelas
N Varelas
135University of Illinois at Chicago (UIC), Chicago, USA
135,
E A Albayrak
E A Albayrak
136The University of Iowa, Iowa City, USA
136,
B Bilki
B Bilki
136The University of Iowa, Iowa City, USA
136,
W Clarida
W Clarida
136The University of Iowa, Iowa City, USA
136,
K Dilsiz
K Dilsiz
136The University of Iowa, Iowa City, USA
136,
F Duru
F Duru
136The University of Iowa, Iowa City, USA
136,
M Haytmyradov
M Haytmyradov
136The University of Iowa, Iowa City, USA
136,
J-P Merlo
J-P Merlo
136The University of Iowa, Iowa City, USA
136,
H Mermerkaya
H Mermerkaya
136The University of Iowa, Iowa City, USA
136,
A Mestvirishvili
A Mestvirishvili
136The University of Iowa, Iowa City, USA
136,
A Moeller
A Moeller
136The University of Iowa, Iowa City, USA
136,
J Nachtman
J Nachtman
136The University of Iowa, Iowa City, USA
136,
H Ogul
H Ogul
136The University of Iowa, Iowa City, USA
136,
Y Onel
Y Onel
136The University of Iowa, Iowa City, USA
136,
F Ozok
F Ozok
136The University of Iowa, Iowa City, USA
136,
A Penzo
A Penzo
136The University of Iowa, Iowa City, USA
136,
R Rahmat
R Rahmat
136The University of Iowa, Iowa City, USA
136,
S Sen
S Sen
136The University of Iowa, Iowa City, USA
136,
P Tan
P Tan
136The University of Iowa, Iowa City, USA
136,
E Tiras
E Tiras
136The University of Iowa, Iowa City, USA
136,
J Wetzel
J Wetzel
136The University of Iowa, Iowa City, USA
136,
T Yetkin
T Yetkin
136The University of Iowa, Iowa City, USA
136,
K Yi
K Yi
136The University of Iowa, Iowa City, USA
136,
B A Barnett
B A Barnett
137Johns Hopkins University, Baltimore, USA
137,
B Blumenfeld
B Blumenfeld
137Johns Hopkins University, Baltimore, USA
137,
S Bolognesi
S Bolognesi
137Johns Hopkins University, Baltimore, USA
137,
D Fehling
D Fehling
137Johns Hopkins University, Baltimore, USA
137,
A V Gritsan
A V Gritsan
137Johns Hopkins University, Baltimore, USA
137,
P Maksimovic
P Maksimovic
137Johns Hopkins University, Baltimore, USA
137,
C Martin
C Martin
137Johns Hopkins University, Baltimore, USA
137,
M Swartz
M Swartz
137Johns Hopkins University, Baltimore, USA
137,
P Baringer
P Baringer
138The University of Kansas, Lawrence, USA
138,
A Bean
A Bean
138The University of Kansas, Lawrence, USA
138,
G Benelli
G Benelli
138The University of Kansas, Lawrence, USA
138,
C Bruner
C Bruner
138The University of Kansas, Lawrence, USA
138,
R P Kenny III
R P Kenny III
138The University of Kansas, Lawrence, USA
138,
M Malek
M Malek
138The University of Kansas, Lawrence, USA
138,
M Murray
M Murray
138The University of Kansas, Lawrence, USA
138,
D Noonan
D Noonan
138The University of Kansas, Lawrence, USA
138,
S Sanders
S Sanders
138The University of Kansas, Lawrence, USA
138,
J Sekaric
J Sekaric
138The University of Kansas, Lawrence, USA
138,
R Stringer
R Stringer
138The University of Kansas, Lawrence, USA
138,
Q Wang
Q Wang
138The University of Kansas, Lawrence, USA
138,
J S Wood
J S Wood
138The University of Kansas, Lawrence, USA
138,
A F Barfuss
A F Barfuss
139Kansas State University, Manhattan, USA
139,
I Chakaberia
I Chakaberia
139Kansas State University, Manhattan, USA
139,
A Ivanov
A Ivanov
139Kansas State University, Manhattan, USA
139,
S Khalil
S Khalil
139Kansas State University, Manhattan, USA
139,
M Makouski
M Makouski
139Kansas State University, Manhattan, USA
139,
Y Maravin
Y Maravin
139Kansas State University, Manhattan, USA
139,
L K Saini
L K Saini
139Kansas State University, Manhattan, USA
139,
S Shrestha
S Shrestha
139Kansas State University, Manhattan, USA
139,
N Skhirtladze
N Skhirtladze
139Kansas State University, Manhattan, USA
139,
I Svintradze
I Svintradze
139Kansas State University, Manhattan, USA
139,
J Gronberg
J Gronberg
140Lawrence Livermore National Laboratory, Livermore, USA
140,
D Lange
D Lange
140Lawrence Livermore National Laboratory, Livermore, USA
140,
F Rebassoo
F Rebassoo
140Lawrence Livermore National Laboratory, Livermore, USA
140,
D Wright
D Wright
140Lawrence Livermore National Laboratory, Livermore, USA
140,
A Baden
A Baden
141University of Maryland, College Park, USA
141,
A Belloni
A Belloni
141University of Maryland, College Park, USA
141,
B Calvert
B Calvert
141University of Maryland, College Park, USA
141,
S C Eno
S C Eno
141University of Maryland, College Park, USA
141,
J A Gomez
J A Gomez
141University of Maryland, College Park, USA
141,
N J Hadley
N J Hadley
141University of Maryland, College Park, USA
141,
R G Kellogg
R G Kellogg
141University of Maryland, College Park, USA
141,
T Kolberg
T Kolberg
141University of Maryland, College Park, USA
141,
Y Lu
Y Lu
141University of Maryland, College Park, USA
141,
M Marionneau
M Marionneau
141University of Maryland, College Park, USA
141,
A C Mignerey
A C Mignerey
141University of Maryland, College Park, USA
141,
K Pedro
K Pedro
141University of Maryland, College Park, USA
141,
A Skuja
A Skuja
141University of Maryland, College Park, USA
141,
M B Tonjes
M B Tonjes
141University of Maryland, College Park, USA
141,
S C Tonwar
S C Tonwar
141University of Maryland, College Park, USA
141,
A Apyan
A Apyan
142Massachusetts Institute of Technology, Cambridge, USA
142,
R Barbieri
R Barbieri
142Massachusetts Institute of Technology, Cambridge, USA
142,
G Bauer
G Bauer
142Massachusetts Institute of Technology, Cambridge, USA
142,
W Busza
W Busza
142Massachusetts Institute of Technology, Cambridge, USA
142,
I A Cali
I A Cali
142Massachusetts Institute of Technology, Cambridge, USA
142,
M Chan
M Chan
142Massachusetts Institute of Technology, Cambridge, USA
142,
L Di Matteo
L Di Matteo
142Massachusetts Institute of Technology, Cambridge, USA
142,
V Dutta
V Dutta
142Massachusetts Institute of Technology, Cambridge, USA
142,
G Gomez Ceballos
G Gomez Ceballos
142Massachusetts Institute of Technology, Cambridge, USA
142,
M Goncharov
M Goncharov
142Massachusetts Institute of Technology, Cambridge, USA
142,
D Gulhan
D Gulhan
142Massachusetts Institute of Technology, Cambridge, USA
142,
M Klute
M Klute
142Massachusetts Institute of Technology, Cambridge, USA
142,
Y S Lai
Y S Lai
142Massachusetts Institute of Technology, Cambridge, USA
142,
Y-J Lee
Y-J Lee
142Massachusetts Institute of Technology, Cambridge, USA
142,
A Levin
A Levin
142Massachusetts Institute of Technology, Cambridge, USA
142,
P D Luckey
P D Luckey
142Massachusetts Institute of Technology, Cambridge, USA
142,
T Ma
T Ma
142Massachusetts Institute of Technology, Cambridge, USA
142,
C Paus
C Paus
142Massachusetts Institute of Technology, Cambridge, USA
142,
D Ralph
D Ralph
142Massachusetts Institute of Technology, Cambridge, USA
142,
C Roland
C Roland
142Massachusetts Institute of Technology, Cambridge, USA
142,
G Roland
G Roland
142Massachusetts Institute of Technology, Cambridge, USA
142,
G S F Stephans
G S F Stephans
142Massachusetts Institute of Technology, Cambridge, USA
142,
F Stöckli
F Stöckli
142Massachusetts Institute of Technology, Cambridge, USA
142,
K Sumorok
K Sumorok
142Massachusetts Institute of Technology, Cambridge, USA
142,
D Velicanu
D Velicanu
142Massachusetts Institute of Technology, Cambridge, USA
142,
J Veverka
J Veverka
142Massachusetts Institute of Technology, Cambridge, USA
142,
B Wyslouch
B Wyslouch
142Massachusetts Institute of Technology, Cambridge, USA
142,
M Yang
M Yang
142Massachusetts Institute of Technology, Cambridge, USA
142,
A S Yoon
A S Yoon
142Massachusetts Institute of Technology, Cambridge, USA
142,
M Zanetti
M Zanetti
142Massachusetts Institute of Technology, Cambridge, USA
142,
V Zhukova
V Zhukova
142Massachusetts Institute of Technology, Cambridge, USA
142,
B Dahmes
B Dahmes
143University of Minnesota, Minneapolis, USA
143,
A De Benedetti
A De Benedetti
143University of Minnesota, Minneapolis, USA
143,
A Gude
A Gude
143University of Minnesota, Minneapolis, USA
143,
S C Kao
S C Kao
143University of Minnesota, Minneapolis, USA
143,
K Klapoetke
K Klapoetke
143University of Minnesota, Minneapolis, USA
143,
Y Kubota
Y Kubota
143University of Minnesota, Minneapolis, USA
143,
J Mans
J Mans
143University of Minnesota, Minneapolis, USA
143,
N Pastika
N Pastika
143University of Minnesota, Minneapolis, USA
143,
R Rusack
R Rusack
143University of Minnesota, Minneapolis, USA
143,
A Singovsky
A Singovsky
143University of Minnesota, Minneapolis, USA
143,
N Tambe
N Tambe
143University of Minnesota, Minneapolis, USA
143,
J Turkewitz
J Turkewitz
143University of Minnesota, Minneapolis, USA
143,
J G Acosta
J G Acosta
144University of Mississippi, Oxford, USA
144,
L M Cremaldi
L M Cremaldi
144University of Mississippi, Oxford, USA
144,
R Kroeger
R Kroeger
144University of Mississippi, Oxford, USA
144,
S Oliveros
S Oliveros
144University of Mississippi, Oxford, USA
144,
L Perera
L Perera
144University of Mississippi, Oxford, USA
144,
D A Sanders
D A Sanders
144University of Mississippi, Oxford, USA
144,
D Summers
D Summers
144University of Mississippi, Oxford, USA
144,
E Avdeeva
E Avdeeva
145University of Nebraska-Lincoln, Lincoln, USA
145,
K Bloom
K Bloom
145University of Nebraska-Lincoln, Lincoln, USA
145,
S Bose
S Bose
145University of Nebraska-Lincoln, Lincoln, USA
145,
D R Claes
D R Claes
145University of Nebraska-Lincoln, Lincoln, USA
145,
A Dominguez
A Dominguez
145University of Nebraska-Lincoln, Lincoln, USA
145,
R Gonzalez Suarez
R Gonzalez Suarez
145University of Nebraska-Lincoln, Lincoln, USA
145,
J Keller
J Keller
145University of Nebraska-Lincoln, Lincoln, USA
145,
D Knowlton
D Knowlton
145University of Nebraska-Lincoln, Lincoln, USA
145,
I Kravchenko
I Kravchenko
145University of Nebraska-Lincoln, Lincoln, USA
145,
J Lazo-Flores
J Lazo-Flores
145University of Nebraska-Lincoln, Lincoln, USA
145,
S Malik
S Malik
145University of Nebraska-Lincoln, Lincoln, USA
145,
F Meier
F Meier
145University of Nebraska-Lincoln, Lincoln, USA
145,
G R Snow
G R Snow
145University of Nebraska-Lincoln, Lincoln, USA
145,
J Dolen
J Dolen
146State University of New York at Buffalo, Buffalo, USA
146,
A Godshalk
A Godshalk
146State University of New York at Buffalo, Buffalo, USA
146,
I Iashvili
I Iashvili
146State University of New York at Buffalo, Buffalo, USA
146,
S Jain
S Jain
146State University of New York at Buffalo, Buffalo, USA
146,
A Kharchilava
A Kharchilava
146State University of New York at Buffalo, Buffalo, USA
146,
A Kumar
A Kumar
146State University of New York at Buffalo, Buffalo, USA
146,
S Rappoccio
S Rappoccio
146State University of New York at Buffalo, Buffalo, USA
146,
G Alverson
G Alverson
147Northeastern University, Boston, USA
147,
E Barberis
E Barberis
147Northeastern University, Boston, USA
147,
D Baumgartel
D Baumgartel
147Northeastern University, Boston, USA
147,
M Chasco
M Chasco
147Northeastern University, Boston, USA
147,
J Haley
J Haley
147Northeastern University, Boston, USA
147,
A Massironi
A Massironi
147Northeastern University, Boston, USA
147,
D Nash
D Nash
147Northeastern University, Boston, USA
147,
T Orimoto
T Orimoto
147Northeastern University, Boston, USA
147,
D Trocino
D Trocino
147Northeastern University, Boston, USA
147,
R -J Wang
R -J Wang
147Northeastern University, Boston, USA
147,
D Wood
D Wood
147Northeastern University, Boston, USA
147,
J Zhang
J Zhang
147Northeastern University, Boston, USA
147,
A Anastassov
A Anastassov
148Northwestern University, Evanston, USA
148,
K A Hahn
K A Hahn
148Northwestern University, Evanston, USA
148,
A Kubik
A Kubik
148Northwestern University, Evanston, USA
148,
L Lusito
L Lusito
148Northwestern University, Evanston, USA
148,
N Mucia
N Mucia
148Northwestern University, Evanston, USA
148,
N Odell
N Odell
148Northwestern University, Evanston, USA
148,
B Pollack
B Pollack
148Northwestern University, Evanston, USA
148,
A Pozdnyakov
A Pozdnyakov
148Northwestern University, Evanston, USA
148,
M Schmitt
M Schmitt
148Northwestern University, Evanston, USA
148,
S Stoynev
S Stoynev
148Northwestern University, Evanston, USA
148,
K Sung
K Sung
148Northwestern University, Evanston, USA
148,
M Velasco
M Velasco
148Northwestern University, Evanston, USA
148,
S Won
S Won
148Northwestern University, Evanston, USA
148,
A Brinkerhoff
A Brinkerhoff
149University of Notre Dame, Notre Dame, USA
149,
K M Chan
K M Chan
149University of Notre Dame, Notre Dame, USA
149,
A Drozdetskiy
A Drozdetskiy
149University of Notre Dame, Notre Dame, USA
149,
M Hildreth
M Hildreth
149University of Notre Dame, Notre Dame, USA
149,
C Jessop
C Jessop
149University of Notre Dame, Notre Dame, USA
149,
D J Karmgard
D J Karmgard
149University of Notre Dame, Notre Dame, USA
149,
N Kellams
N Kellams
149University of Notre Dame, Notre Dame, USA
149,
K Lannon
K Lannon
149University of Notre Dame, Notre Dame, USA
149,
W Luo
W Luo
149University of Notre Dame, Notre Dame, USA
149,
S Lynch
S Lynch
149University of Notre Dame, Notre Dame, USA
149,
N Marinelli
N Marinelli
149University of Notre Dame, Notre Dame, USA
149,
T Pearson
T Pearson
149University of Notre Dame, Notre Dame, USA
149,
M Planer
M Planer
149University of Notre Dame, Notre Dame, USA
149,
R Ruchti
R Ruchti
149University of Notre Dame, Notre Dame, USA
149,
N Valls
N Valls
149University of Notre Dame, Notre Dame, USA
149,
M Wayne
M Wayne
149University of Notre Dame, Notre Dame, USA
149,
M Wolf
M Wolf
149University of Notre Dame, Notre Dame, USA
149,
A Woodard
A Woodard
149University of Notre Dame, Notre Dame, USA
149,
L Antonelli
L Antonelli
150The Ohio State University, Columbus, USA
150,
J Brinson
J Brinson
150The Ohio State University, Columbus, USA
150,
B Bylsma
B Bylsma
150The Ohio State University, Columbus, USA
150,
L S Durkin
L S Durkin
150The Ohio State University, Columbus, USA
150,
S Flowers
S Flowers
150The Ohio State University, Columbus, USA
150,
C Hill
C Hill
150The Ohio State University, Columbus, USA
150,
R Hughes
R Hughes
150The Ohio State University, Columbus, USA
150,
K Kotov
K Kotov
150The Ohio State University, Columbus, USA
150,
T Y Ling
T Y Ling
150The Ohio State University, Columbus, USA
150,
D Puigh
D Puigh
150The Ohio State University, Columbus, USA
150,
M Rodenburg
M Rodenburg
150The Ohio State University, Columbus, USA
150,
G Smith
G Smith
150The Ohio State University, Columbus, USA
150,
B L Winer
B L Winer
150The Ohio State University, Columbus, USA
150,
H Wolfe
H Wolfe
150The Ohio State University, Columbus, USA
150,
H W Wulsin
H W Wulsin
150The Ohio State University, Columbus, USA
150,
O Driga
O Driga
151Princeton University, Princeton, USA
151,
P Elmer
P Elmer
151Princeton University, Princeton, USA
151,
P Hebda
P Hebda
151Princeton University, Princeton, USA
151,
A Hunt
A Hunt
151Princeton University, Princeton, USA
151,
S A Koay
S A Koay
151Princeton University, Princeton, USA
151,
P Lujan
P Lujan
151Princeton University, Princeton, USA
151,
D Marlow
D Marlow
151Princeton University, Princeton, USA
151,
T Medvedeva
T Medvedeva
151Princeton University, Princeton, USA
151,
M Mooney
M Mooney
151Princeton University, Princeton, USA
151,
J Olsen
J Olsen
151Princeton University, Princeton, USA
151,
P Piroué
P Piroué
151Princeton University, Princeton, USA
151,
X Quan
X Quan
151Princeton University, Princeton, USA
151,
H Saka
H Saka
151Princeton University, Princeton, USA
151,
D Stickland
D Stickland
151Princeton University, Princeton, USA
151,
C Tully
C Tully
151Princeton University, Princeton, USA
151,
J S Werner
J S Werner
151Princeton University, Princeton, USA
151,
A Zuranski
A Zuranski
151Princeton University, Princeton, USA
151,
E Brownson
E Brownson
152University of Puerto Rico, Mayaguez, USA
152,
H Mendez
H Mendez
152University of Puerto Rico, Mayaguez, USA
152,
J E Ramirez Vargas
J E Ramirez Vargas
152University of Puerto Rico, Mayaguez, USA
152,
V E Barnes
V E Barnes
153Purdue University, West Lafayette, USA
153,
D Benedetti
D Benedetti
153Purdue University, West Lafayette, USA
153,
G Bolla
G Bolla
153Purdue University, West Lafayette, USA
153,
D Bortoletto
D Bortoletto
153Purdue University, West Lafayette, USA
153,
M De Mattia
M De Mattia
153Purdue University, West Lafayette, USA
153,
Z Hu
Z Hu
153Purdue University, West Lafayette, USA
153,
M K Jha
M K Jha
153Purdue University, West Lafayette, USA
153,
M Jones
M Jones
153Purdue University, West Lafayette, USA
153,
K Jung
K Jung
153Purdue University, West Lafayette, USA
153,
M Kress
M Kress
153Purdue University, West Lafayette, USA
153,
N Leonardo
N Leonardo
153Purdue University, West Lafayette, USA
153,
D Lopes Pegna
D Lopes Pegna
153Purdue University, West Lafayette, USA
153,
V Maroussov
V Maroussov
153Purdue University, West Lafayette, USA
153,
P Merkel
P Merkel
153Purdue University, West Lafayette, USA
153,
D H Miller
D H Miller
153Purdue University, West Lafayette, USA
153,
N Neumeister
N Neumeister
153Purdue University, West Lafayette, USA
153,
B C Radburn-Smith
B C Radburn-Smith
153Purdue University, West Lafayette, USA
153,
X Shi
X Shi
153Purdue University, West Lafayette, USA
153,
I Shipsey
I Shipsey
153Purdue University, West Lafayette, USA
153,
D Silvers
D Silvers
153Purdue University, West Lafayette, USA
153,
A Svyatkovskiy
A Svyatkovskiy
153Purdue University, West Lafayette, USA
153,
F Wang
F Wang
153Purdue University, West Lafayette, USA
153,
W Xie
W Xie
153Purdue University, West Lafayette, USA
153,
L Xu
L Xu
153Purdue University, West Lafayette, USA
153,
H D Yoo
H D Yoo
153Purdue University, West Lafayette, USA
153,
J Zablocki
J Zablocki
153Purdue University, West Lafayette, USA
153,
Y Zheng
Y Zheng
153Purdue University, West Lafayette, USA
153,
N Parashar
N Parashar
154Purdue University Calumet, Hammond, USA
154,
J Stupak
J Stupak
154Purdue University Calumet, Hammond, USA
154,
A Adair
A Adair
155Rice University, Houston, USA
155,
B Akgun
B Akgun
155Rice University, Houston, USA
155,
K M Ecklund
K M Ecklund
155Rice University, Houston, USA
155,
F J M Geurts
F J M Geurts
155Rice University, Houston, USA
155,
W Li
W Li
155Rice University, Houston, USA
155,
B Michlin
B Michlin
155Rice University, Houston, USA
155,
B P Padley
B P Padley
155Rice University, Houston, USA
155,
R Redjimi
R Redjimi
155Rice University, Houston, USA
155,
J Roberts
J Roberts
155Rice University, Houston, USA
155,
J Zabel
J Zabel
155Rice University, Houston, USA
155,
B Betchart
B Betchart
156University of Rochester, Rochester, USA
156,
A Bodek
A Bodek
156University of Rochester, Rochester, USA
156,
R Covarelli
R Covarelli
156University of Rochester, Rochester, USA
156,
P de Barbaro
P de Barbaro
156University of Rochester, Rochester, USA
156,
R Demina
R Demina
156University of Rochester, Rochester, USA
156,
Y Eshaq
Y Eshaq
156University of Rochester, Rochester, USA
156,
T Ferbel
T Ferbel
156University of Rochester, Rochester, USA
156,
A Garcia-Bellido
A Garcia-Bellido
156University of Rochester, Rochester, USA
156,
P Goldenzweig
P Goldenzweig
156University of Rochester, Rochester, USA
156,
J Han
J Han
156University of Rochester, Rochester, USA
156,
A Harel
A Harel
156University of Rochester, Rochester, USA
156,
A Khukhunaishvili
A Khukhunaishvili
156University of Rochester, Rochester, USA
156,
G Petrillo
G Petrillo
156University of Rochester, Rochester, USA
156,
D Vishnevskiy
D Vishnevskiy
156University of Rochester, Rochester, USA
156,
R Ciesielski
R Ciesielski
157The Rockefeller University, New York, USA
157,
L Demortier
L Demortier
157The Rockefeller University, New York, USA
157,
K Goulianos
K Goulianos
157The Rockefeller University, New York, USA
157,
G Lungu
G Lungu
157The Rockefeller University, New York, USA
157,
C Mesropian
C Mesropian
157The Rockefeller University, New York, USA
157,
S Arora
S Arora
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
A Barker
A Barker
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
J P Chou
J P Chou
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
C Contreras-Campana
C Contreras-Campana
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
E Contreras-Campana
E Contreras-Campana
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
D Duggan
D Duggan
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
D Ferencek
D Ferencek
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
Y Gershtein
Y Gershtein
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
R Gray
R Gray
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
E Halkiadakis
E Halkiadakis
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
D Hidas
D Hidas
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
S Kaplan
S Kaplan
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
A Lath
A Lath
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
S Panwalkar
S Panwalkar
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
M Park
M Park
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
R Patel
R Patel
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
S Salur
S Salur
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
S Schnetzer
S Schnetzer
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
S Somalwar
S Somalwar
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
R Stone
R Stone
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
S Thomas
S Thomas
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
P Thomassen
P Thomassen
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
M Walker
M Walker
158Rutgers, The State University of New Jersey, Piscataway, USA
158,
K Rose
K Rose
159University of Tennessee, Knoxville, USA
159,
S Spanier
S Spanier
159University of Tennessee, Knoxville, USA
159,
A York
A York
159University of Tennessee, Knoxville, USA
159,
O Bouhali
O Bouhali
160Texas A&M University, College Station, USA
160,
A Castaneda Hernandez
A Castaneda Hernandez
160Texas A&M University, College Station, USA
160,
R Eusebi
R Eusebi
160Texas A&M University, College Station, USA
160,
W Flanagan
W Flanagan
160Texas A&M University, College Station, USA
160,
J Gilmore
J Gilmore
160Texas A&M University, College Station, USA
160,
T Kamon
T Kamon
160Texas A&M University, College Station, USA
160,
V Khotilovich
V Khotilovich
160Texas A&M University, College Station, USA
160,
V Krutelyov
V Krutelyov
160Texas A&M University, College Station, USA
160,
R Montalvo
R Montalvo
160Texas A&M University, College Station, USA
160,
I Osipenkov
I Osipenkov
160Texas A&M University, College Station, USA
160,
Y Pakhotin
Y Pakhotin
160Texas A&M University, College Station, USA
160,
A Perloff
A Perloff
160Texas A&M University, College Station, USA
160,
J Roe
J Roe
160Texas A&M University, College Station, USA
160,
A Rose
A Rose
160Texas A&M University, College Station, USA
160,
A Safonov
A Safonov
160Texas A&M University, College Station, USA
160,
T Sakuma
T Sakuma
160Texas A&M University, College Station, USA
160,
I Suarez
I Suarez
160Texas A&M University, College Station, USA
160,
A Tatarinov
A Tatarinov
160Texas A&M University, College Station, USA
160,
N Akchurin
N Akchurin
161Texas Tech University, Lubbock, USA
161,
C Cowden
C Cowden
161Texas Tech University, Lubbock, USA
161,
J Damgov
J Damgov
161Texas Tech University, Lubbock, USA
161,
C Dragoiu
C Dragoiu
161Texas Tech University, Lubbock, USA
161,
P R Dudero
P R Dudero
161Texas Tech University, Lubbock, USA
161,
J Faulkner
J Faulkner
161Texas Tech University, Lubbock, USA
161,
K Kovitanggoon
K Kovitanggoon
161Texas Tech University, Lubbock, USA
161,
S Kunori
S Kunori
161Texas Tech University, Lubbock, USA
161,
S W Lee
S W Lee
161Texas Tech University, Lubbock, USA
161,
T Libeiro
T Libeiro
161Texas Tech University, Lubbock, USA
161,
I Volobouev
I Volobouev
161Texas Tech University, Lubbock, USA
161,
E Appelt
E Appelt
162Vanderbilt University, Nashville, USA
162,
A G Delannoy
A G Delannoy
162Vanderbilt University, Nashville, USA
162,
S Greene
S Greene
162Vanderbilt University, Nashville, USA
162,
A Gurrola
A Gurrola
162Vanderbilt University, Nashville, USA
162,
W Johns
W Johns
162Vanderbilt University, Nashville, USA
162,
C Maguire
C Maguire
162Vanderbilt University, Nashville, USA
162,
Y Mao
Y Mao
162Vanderbilt University, Nashville, USA
162,
A Melo
A Melo
162Vanderbilt University, Nashville, USA
162,
M Sharma
M Sharma
162Vanderbilt University, Nashville, USA
162,
P Sheldon
P Sheldon
162Vanderbilt University, Nashville, USA
162,
B Snook
B Snook
162Vanderbilt University, Nashville, USA
162,
S Tuo
S Tuo
162Vanderbilt University, Nashville, USA
162,
J Velkovska
J Velkovska
162Vanderbilt University, Nashville, USA
162,
M W Arenton
M W Arenton
163University of Virginia, Charlottesville, USA
163,
S Boutle
S Boutle
163University of Virginia, Charlottesville, USA
163,
B Cox
B Cox
163University of Virginia, Charlottesville, USA
163,
B Francis
B Francis
163University of Virginia, Charlottesville, USA
163,
J Goodell
J Goodell
163University of Virginia, Charlottesville, USA
163,
R Hirosky
R Hirosky
163University of Virginia, Charlottesville, USA
163,
A Ledovskoy
A Ledovskoy
163University of Virginia, Charlottesville, USA
163,
H Li
H Li
163University of Virginia, Charlottesville, USA
163,
C Lin
C Lin
163University of Virginia, Charlottesville, USA
163,
C Neu
C Neu
163University of Virginia, Charlottesville, USA
163,
J Wood
J Wood
163University of Virginia, Charlottesville, USA
163,
C Clarke
C Clarke
163University of Virginia, Charlottesville, USA
163,
R Harr
R Harr
164Wayne State University, Detroit, USA
164,
P E Karchin
P E Karchin
164Wayne State University, Detroit, USA
164,
C Kottachchi Kankanamge Don
C Kottachchi Kankanamge Don
164Wayne State University, Detroit, USA
164,
P Lamichhane
P Lamichhane
164Wayne State University, Detroit, USA
164,
J Sturdy
J Sturdy
164Wayne State University, Detroit, USA
164,
D A Belknap
D A Belknap
165University of Wisconsin, Madison, USA
165,
D Carlsmith
D Carlsmith
165University of Wisconsin, Madison, USA
165,
M Cepeda
M Cepeda
165University of Wisconsin, Madison, USA
165,
S Dasu
S Dasu
165University of Wisconsin, Madison, USA
165,
L Dodd
L Dodd
165University of Wisconsin, Madison, USA
165,
S Duric
S Duric
165University of Wisconsin, Madison, USA
165,
E Friis
E Friis
165University of Wisconsin, Madison, USA
165,
R Hall-Wilton
R Hall-Wilton
165University of Wisconsin, Madison, USA
165,
M Herndon
M Herndon
165University of Wisconsin, Madison, USA
165,
A Hervé
A Hervé
165University of Wisconsin, Madison, USA
165,
P Klabbers
P Klabbers
165University of Wisconsin, Madison, USA
165,
A Lanaro
A Lanaro
165University of Wisconsin, Madison, USA
165,
C Lazaridis
C Lazaridis
165University of Wisconsin, Madison, USA
165,
A Levine
A Levine
165University of Wisconsin, Madison, USA
165,
R Loveless
R Loveless
165University of Wisconsin, Madison, USA
165,
A Mohapatra
A Mohapatra
165University of Wisconsin, Madison, USA
165,
I Ojalvo
I Ojalvo
165University of Wisconsin, Madison, USA
165,
T Perry
T Perry
165University of Wisconsin, Madison, USA
165,
G A Pierro
G A Pierro
165University of Wisconsin, Madison, USA
165,
G Polese
G Polese
165University of Wisconsin, Madison, USA
165,
I Ross
I Ross
165University of Wisconsin, Madison, USA
165,
T Sarangi
T Sarangi
165University of Wisconsin, Madison, USA
165,
A Savin
A Savin
165University of Wisconsin, Madison, USA
165,
W H Smith
W H Smith
165University of Wisconsin, Madison, USA
165,
C Vuosalo
C Vuosalo
165University of Wisconsin, Madison, USA
165,
N Woods
N Woods
165University of Wisconsin, Madison, USA
165;
The CMS Collaboration166