Computational Modeling of Pathophysiologic Responses to Exercise in Fontan Patients

Abstract

Reduced exercise capacity is nearly universal among Fontan patients. Although many factors have emerged as possible contributors, the degree to which each impacts the overall hemodynamics is largely unknown. Computational modeling provides a means to test hypotheses of causes of exercise intolerance via precisely controlled virtual experiments and measurements. We quantified the physiological impacts of commonly encountered, clinically relevant dysfunctions introduced to the exercising Fontan system via a previously developed lumped-parameter model of Fontan exercise. Elevated pulmonary arterial pressure was observed in all cases of dysfunction, correlated with lowered cardiac output, and often mediated by elevated atrial pressure. Pulmonary vascular resistance was not the most significant factor affecting exercise performance as measured by cardiac output. In the absence of other dysfunctions, atrioventricular valve insufficiency alone had significant physiological impact, especially under exercise demands. The impact of isolated dysfunctions can be linearly summed to approximate the combined impact of several dysfunctions occurring in the same system. A single dominant cause of exercise intolerance was not identified, though several hypothesized dysfunctions each led to variable decreases in performance. Computational predictions of performance improvement associated with various interventions should be weighed against procedural risks and potential complications, contributing to improvements in routine patient management protocol.

INTRODUCTION

Single ventricle congenital heart defects, characterized by the presence of a single functional systemic ventricle, are among the most challenging forms of congenital heart disease for clinicians to treat. Surgical palliation for these patients typically culminates in a Fontan operation, which separates the pulmonary and systemic circulations, resulting in complex circulatory physiology and a host of ensuing clinical complications.

While survival rates following the Fontan procedure have been increasing, numerous morbidities are associated with Fontan physiology, including protein losing enteropathy, arteriovenous malformations, arrhythmias, thrombosis, and decreased cardiac function. A nearly universal finding among Fontan patients is reduced exercise capacity^7,8, although the causes of exercise intolerance are not fully understood^9,12. A recent multi-center study involving 321 patients demonstrated that less than 5% of Fontan patients have normal (>90% of predicted peak VO₂) or borderline normal (80%–90% of predicted peak VO₂) exercise capacity⁷. Several factors have emerged as possible contributors to reduced exercise capacity, including performance of the single ventricle, pulmonary vascular resistance, valvular function, and chronotropic response^6,11. However, the relative contribution of each of these to the overall physiologic performance remains largely unknown¹⁰. The myriad abnormalities often existing in each Fontan patient make it difficult to isolate and quantify physiological impacts of specific abnormalities without confounding factors and complicate decision-making for the appropriateness and timing of interventions. Furthermore, clinical measurements of these factors in exercising Fontan patients are challenging, often requiring invasive methods and thus are not adopted as standard of care. The realities of these clinical limitations have contributed to relatively slow progress in increasing understanding of Fontan exercise physiology. For the design and execution of patient management decisions, there are numerous potential benefits associated with the ability to systematically investigate mechanisms of exercise intolerance and quantitatively evaluate potential efficacy of clinical interventions.

Computational modeling has been used to provide insights into surgical planning, physiologic response, and hemodynamics in a range of cardiovascular treatments^24,29,36. Computational models that can reasonably approximate underlying physiologic mechanisms offer a powerful means to carry out precisely controlled “virtual” experiments, targeted perturbations to the modeled system, and detailed “virtual probing” of the resulting hemodynamics. Prior modeling efforts to describe Fontan hemodynamics have mainly focused on the effects of varying Fontan connection geometries^27,33. Coupled multi-scale and closed-loop modeling approaches have been used to obtain realistic local and global hemodynamic interactions, and extract detailed physiologic information to compare hemodynamic changes resulting from virtual surgeries^19,22,39. Prior studies that have attempted to simulate exercise conditions have primarily adopted open loop models, requiring numerous assumptions for increasing flow rates, changing waveform shapes, and prescribing changes in vascular resistances^2,23,33,41. These approaches tend to restrict the investigation to local 3D hemodynamics in isolation from the systemic physiologic response.

By considering a combination of physiological responses occurring during exercise, we recently developed a comprehensive closed-loop lumped-parameter modeling technique to simulate Fontan exercise hemodynamics²⁰. In the present study, we employ this model to investigate and compare the simulated physiologic impacts of several hypothesized etiologies of Fontan exercise intolerance. By virtually introducing a set of commonly encountered and clinically relevant pathophysiological conditions into the exercising Fontan system via a computational model, we quantify the relative physiologic significance of each dysfunction on the overall exercise hemodynamics, and identify possible mechanisms delineating exercise intolerance. The use of a computational model allows for a controlled “virtual experiment” in which one can systematically examine these effects independently from other confounding clinical variables.

METHODS

The computational modeling of Fontan exercise in this study is based on our previously published modeling protocol for holistically simulating Fontan lower-body exercise²⁰. The protocol enables the derivation of a full set of parameters necessary to model a typical Fontan patient of a given body size at various physiologic exercise intensities defined by metabolic equivalent (MET). This computational model is a closed-loop lumped-parameter network (LPN) using a circuit analogy to represent the Fontan circulation. The LPN consists of several major blocks describing the atrium, ventricle, upper body, lower body, and pulmonary circuits. The heart blocks and the intrathoracic pressure generate active pressure sources in the system, where the rest of the circuit is made up of passive elements including resistances, compliances, inertances, and diodes. We implemented a time-varying elastance approach³¹ to describe the pressure-volume relationship in the ventricle, with the parameters E_max and E_offset reflecting measures of contractility and ventricular filling, respectively. More specifically, E_max and E_offset define the amplitude and the vertical offset, respectively, of the elastance function used in a simulation. In the case of simulating valve insufficiency, the regurgitant flow through a valve is described by a non-linear resistance with a resistance value in units of mmHg s² mL⁻². To run an exercise simulation, the inputs to the modeling protocol are patient weight, height, and desired exercise MET. Based on the analyses of a set of clinical data measured in a cohort of 9 exercising Fontan patients, and a comprehensive literature compilation of exercise physiology, the LPN parameters are prescribed for each simulation according to the patient body size and target exercise intensity. The online supplemental materials detail the implementation of the Fontan LPN framework, governing equations, and the protocol for prescribing exercise parameter values, with additional details provided in our previous work. The outputs of the model are pulsatile and time-varying pressure, flow, and volume waveforms at various locations in the circulation including the upper and lower body, pulmonary circulation, abdominal organs, atrium, and ventricle.

In this study we investigate several commonly observed dysfunctions in Fontan patients by incorporating them into our previously established computational model. The novelty of this study is the ability to isolate and examine specific combinations of dysfunctions and how they impact a dynamic exercising Fontan system. The specific incorporation of each dysfunction into the modeling context is based on estimates of realistic moderate degrees of dysfunction as observed by our clinical co-authors in their patient populations, as well as reported in the literature. The particular dysfunctions we investigate are:

• Abnormal pulmonary vascular response (APVR): Absence of normal decrease in pulmonary vascular resistance (PVR) during exercise^28,32. This is modeled as a non-changing PVR that remains fixed at the resting value during exercise.

• Disordered respiration (DR): Impaired movement of the thoracic cavity caused by common or potential complications of multiple sternotomy incisions, including diaphragm plication. The changes in thoracic volume and pressure amplitude due to respiration are reduced³⁵. This is modeled as a 40% decrease in thoracic pressure amplitude¹³.

• Diastolic dysfunction (DiasD): Impaired ventricular relaxation during exercise¹. This is modeled as a non-changing E_offset parameter, which stays at the resting value during exercise.

• Systolic dysfunction (SysD): Impaired ability to increase ventricular contractility during exercise⁴⁰ (baseline, or resting state, systolic function is normal). This is modeled as a non-changing E_max parameter, which stays at the resting value during exercise.

• Systolic dysfunction (SysD2): Baseline decrease in ventricular systolic function¹ (resting ejection fraction = 0.44), while contractility remains reactive to exercise. This is modeled as a 30% decrease in E_max³⁴.

• Atrial-ventricular valve insufficiency (AVVI): This is modeled with a regurgitation valve resistance of 0.015 mmHg s² mL⁻², which produces a 30% regurgitant fraction under resting conditions³⁷.

• 1st degree AV block (AVB): The AV activation synchronization is delayed. In this case, we model a time delay increase amounting to 20% of the cardiac cycle in the AV activation⁵.

• Chronotropic Insufficiency/Incompetence (ChI): Inability to attain a normal peak heart rate at maximal exercise²⁶. This is modeled as a maximum heart rate limitation of 120 beats per minute.

We also investigate the effects of graded severities of AVVI, AV activation delay, and thoracic pressure impairment (defined as the percent decrease in thoracic pressure amplitude). For the 7 levels of severity in AVVI examined in this study, the regurgitation valve resistances used in the model were 0.35, 0.12, 0.06, 0.03, 0.015, 0.008, and 0.004 mmHg s² mL⁻², from the least to the most severe. This represents a range of minor to severe AVVI characterized by regurgitant fractions of up to 0.47 at resting condition.

In this paper all results presented correspond to an example patient with a weight of 70 kg and height of 160 cm. Simulations of patients with different body sizes do not produce significantly different results regarding the relative effects of dysfunctions. The system of algebraic and ordinary differential equations of the LPN model was solved using a 4th order Runge–Kutta method for time integration in a custom solver written in Fortran. All simulations were run with 20 microsecond time steps for 12 seconds of simulated time. The last 4 cardiac cycles (one respiration cycle) of data, after stable periodicity was established, was used in the analysis. Note that each simulation is setup to directly simulate only one specific steady exercise state, and does not simulate the transient transition from a different exercise or resting state. Exercise performance is quantified via the resulting cardiac output (CO). Aortic, pulmonary, and atrial pressures are also examined to reveal additional physiological impacts.

RESULTS

Dysfunctions in isolation

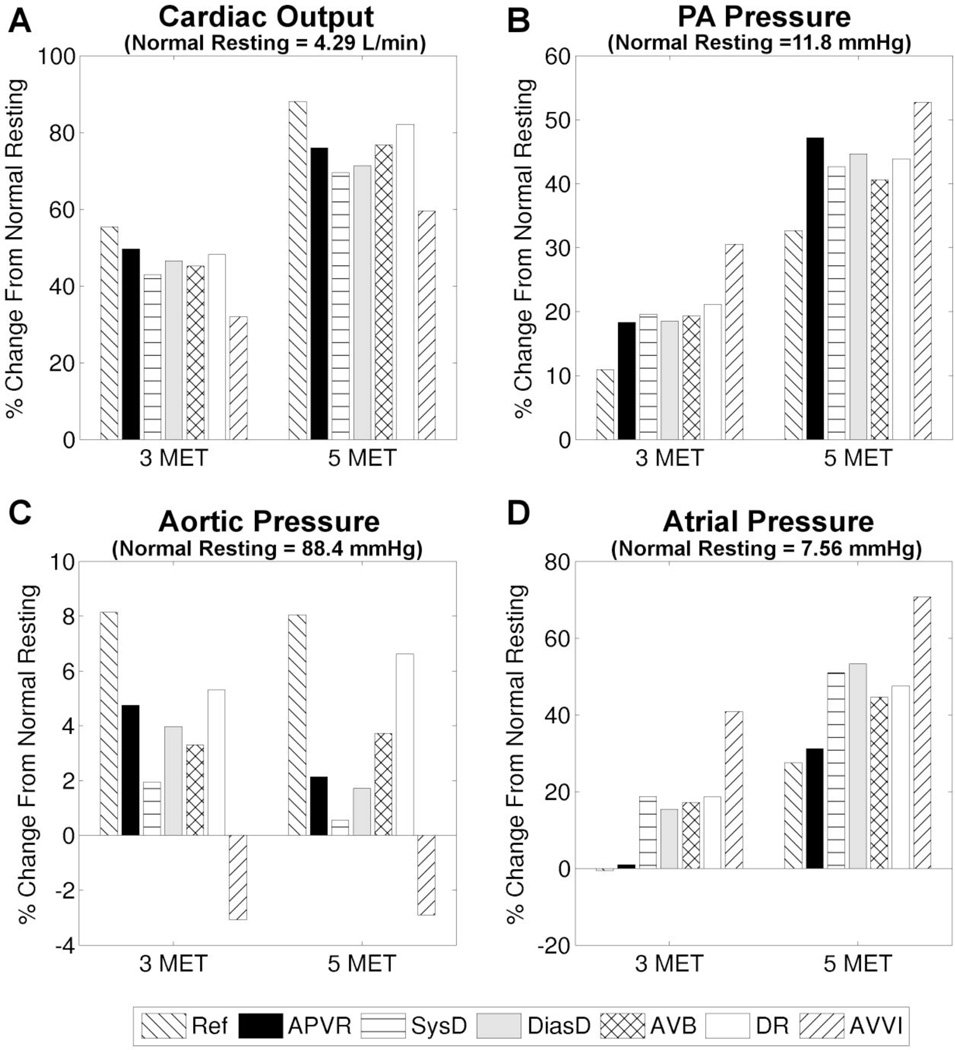
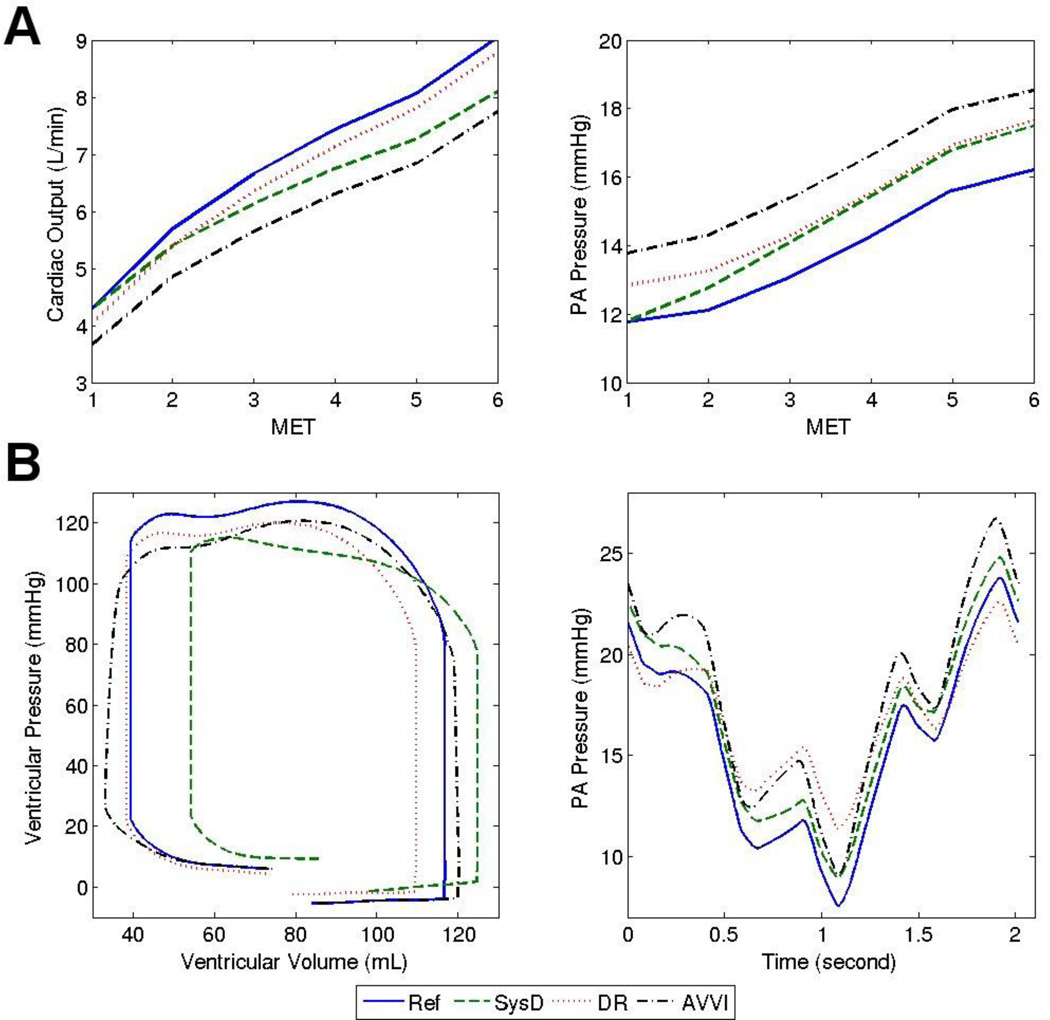
We first examine the impacts of isolated dysfunctions on the physiologic response to exercise. For reference, Table 1 presents the mean parameter values for the normal non-dysfunction reference case. Figure 1 illustrates that relative to the reference case, the presence of any single dysfunction leads to a decrease in CO and aortic pressure, as well as increases in atrial and pulmonary arterial (PA) pressure. For example, Figure 1A shows that at 5 MET, the CO increases ~90% from the normal resting value (4.29 L/min) in the reference case, but only ~60% in the case of AVVI. In Figure 2B, the PA pressure time-tracings provide detailed temporal information showing that for the case of DR, the peak PA pressure remains lower than the reference even though the mean PA pressure value is higher (Figure 2A right). The ventricular pressure-volume loop shows a right-ward shift, which is manifested more in the phase of iso-volumetric relaxation than in the phase of iso-volumetric contraction, indicating decreased ejection fraction and contractility in the case of SysD. In the case of DR, the decreased end-diastolic volume is likely caused by the slight increase in diastolic ventricular pressure. In the case of AVVI, ventricular volume load is clearly increased. Impaired filling is also evident in the cases of APVR, DiasD, and AVB, although the associated ventricular pressure-volume plots are not presented here.

Table 1.

Reference values of heart rate (HR) in beats/min, cardiac output (CO) in L/min, stroke volume (SV) in mL, ejection fraction (EF), and aortic, atrial, and PA pressures (Pao, Psa, Ppul) in mmHg for the normal case (no dysfunctions) at different MET intensities

MET	HR	CO	SV	EF	Pao	Psa	Ppul
1	73	4.29	58.4	0.520	88.4	7.56	11.8
2	91	5.70	62.7	0.560	93.7	7.03	12.1
3	102	6.66	65.8	0.599	95.5	7.51	13.1
4	112	7.43	66.6	0.617	95.9	8.46	14.3
5	119	8.06	67.6	0.638	95.5	9.64	15.6
6	126	9.04	71.6	0.662	97.6	9.90	16.2

Figure 1.

Percent change from the normal case resting value during exercise, for the reference case (Ref) and various cases of isolated dysfunctions. A) cardiac output, B) PA pressure, C) aortic pressure, and D) atrial pressure.

Figure 2.

Reference case and selected cases of isolated dysfunctions: A) Trends in cardiac output and PA pressure with increasing exercise. B) Tracings of Ventricular pressure-volume loop (one cardiac cycle) and PA pressure (4 cardiac cycles / 1 breathing cycle) at 5 MET.

The physiological significance of one dysfunction relative to the others may change at different exercise intensities. For example, Figure 1 shows that at 3 MET the dysfunction AVB has more detrimental impacts on all of the 4 examined parameters (larger differences from the reference case) compared to DiasD, whereas at 5 MET the reverse is true. The impact of SysD on CO (Figure 2A left) and PA pressure (Figure 2A right) also becomes larger relative to that of DR as exercise intensity increases. Among the isolated dysfunctions investigated, AVVI has the largest impact on exercise parameters, and effects of APVR are generally not larger than other dysfunctions.

To analyze the effects of respiratory-rate, we varied the ratio of respiratory-to-cardiac cycles, and found no notable differences in the mean values of physiological parameters with ratios of 1:4, 1:3, and 1:2.

Varying severities of dysfunctions

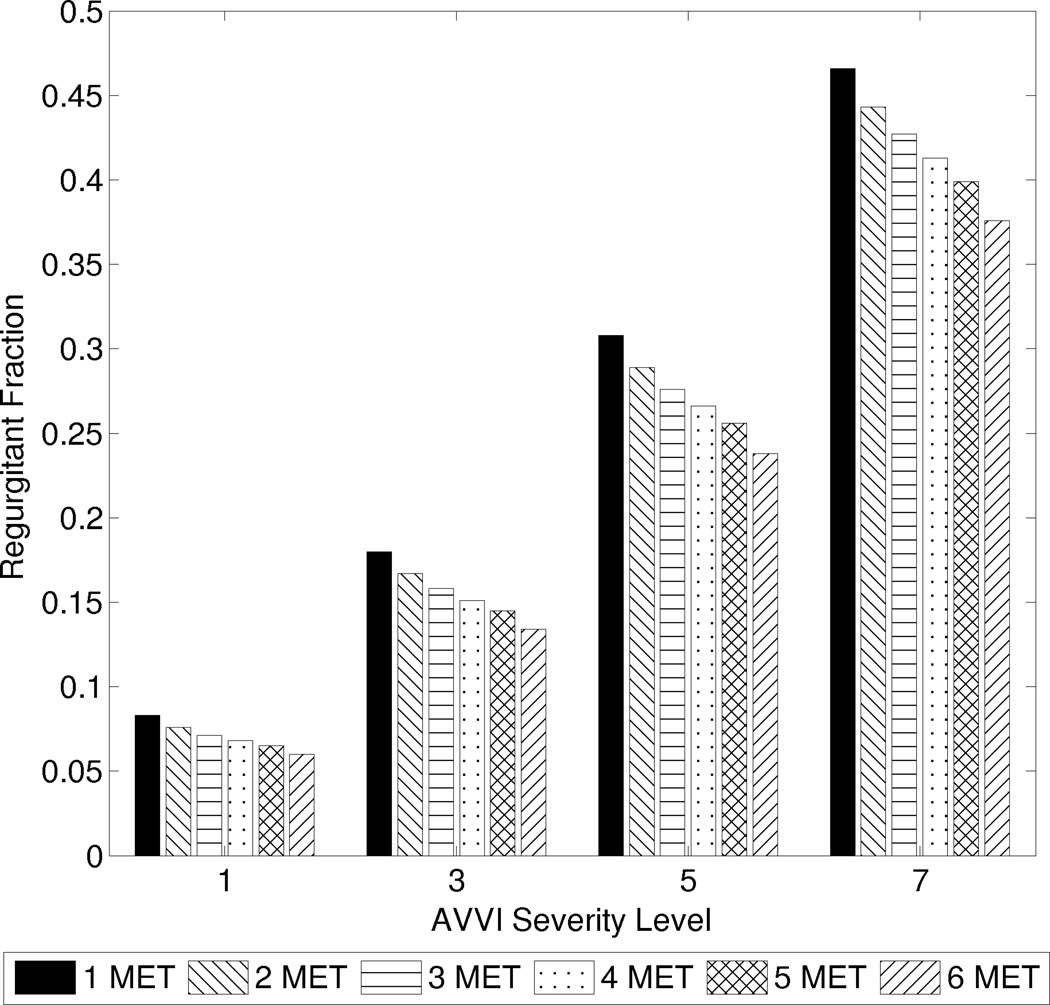
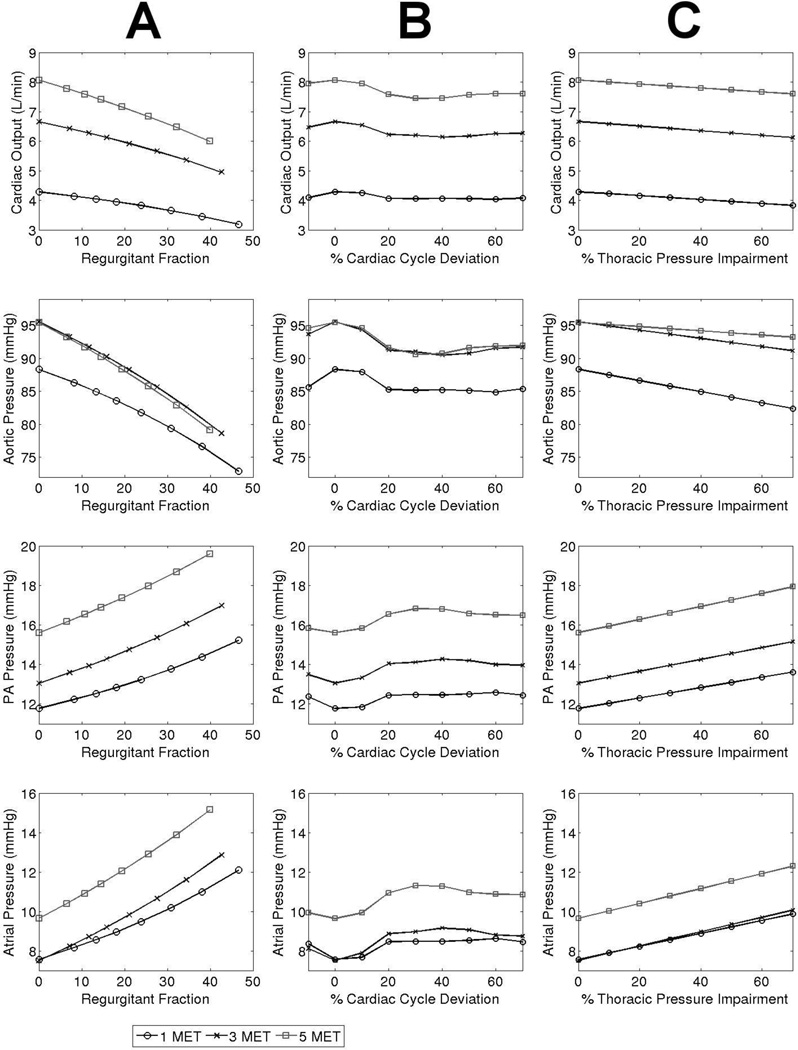
For a given severity of AVVI, the regurgitant fraction decreases with increasing exercise (Figure 3). This does not imply that less total blood is regurgitated at exercise, but rather that the amount of regurgitated blood is proportionally less as CO increases. At high severity of AVVI, the regurgitant fraction could decrease by as much as from 0.47 to 0.38 between rest and 6 MET. The slopes of the plots in Figure 4a demonstrate that CO is negatively affected by regurgitation, with slightly higher sensitivity at higher exercise intensities.

Figure 3.

Regurgitant fraction at different exercise intensities for graded severities of AV valve insufficiency.

Figure 4.

Trends in cardiac output, and aortic, PA, and atrial pressures in varying levels of A) AV regurgitation, B) AV activation delay deviation from optimal, and C) Disordered respiration.

Figure 4b shows that an AV delay deviation from normal in either direction (shortening or lengthening) incurs performance penalties in the system. The CO sensitivity to abnormal AV delay gradually increases with increasing exercise intensity, however, the maximum CO penalty from any level of AV delay is always less than 9%. We also observe that the worst performance occurs when the atrial contraction falls entirely within the ventricular relaxation period. Some overlap between atrial and ventricular contractions leads to improved performance. The optimal performance occurs when the AV delay length is such that the atrial contraction peaks at the onset of systole.

When varying the severity of impaired thoracic pressure amplitude, the rates of change (sensitivity) of physiologic parameters were generally independent of the severity level, as demonstrated by the constant slopes in Figure 4c.

Examining effects on CO and pressures, Figure 4 demonstrates that even mild or moderate AVVI is at least as detrimental as severe degrees of AVB or DR, and that higher exercise intensity exacerbates the relative impact of AVVI. Figure 4 also reveals that changes in PA pressure generally correlate with similar magnitude changes in atrial pressure.

Combinations of dysfunctions

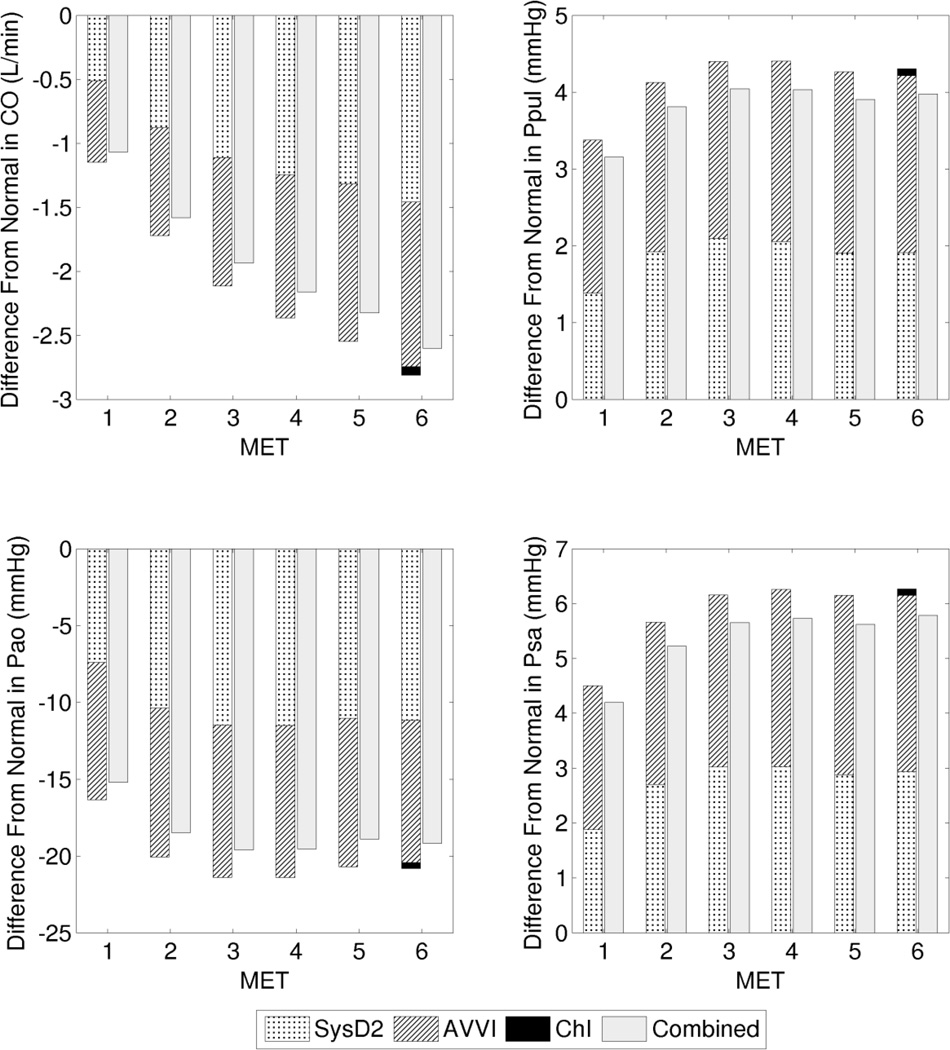
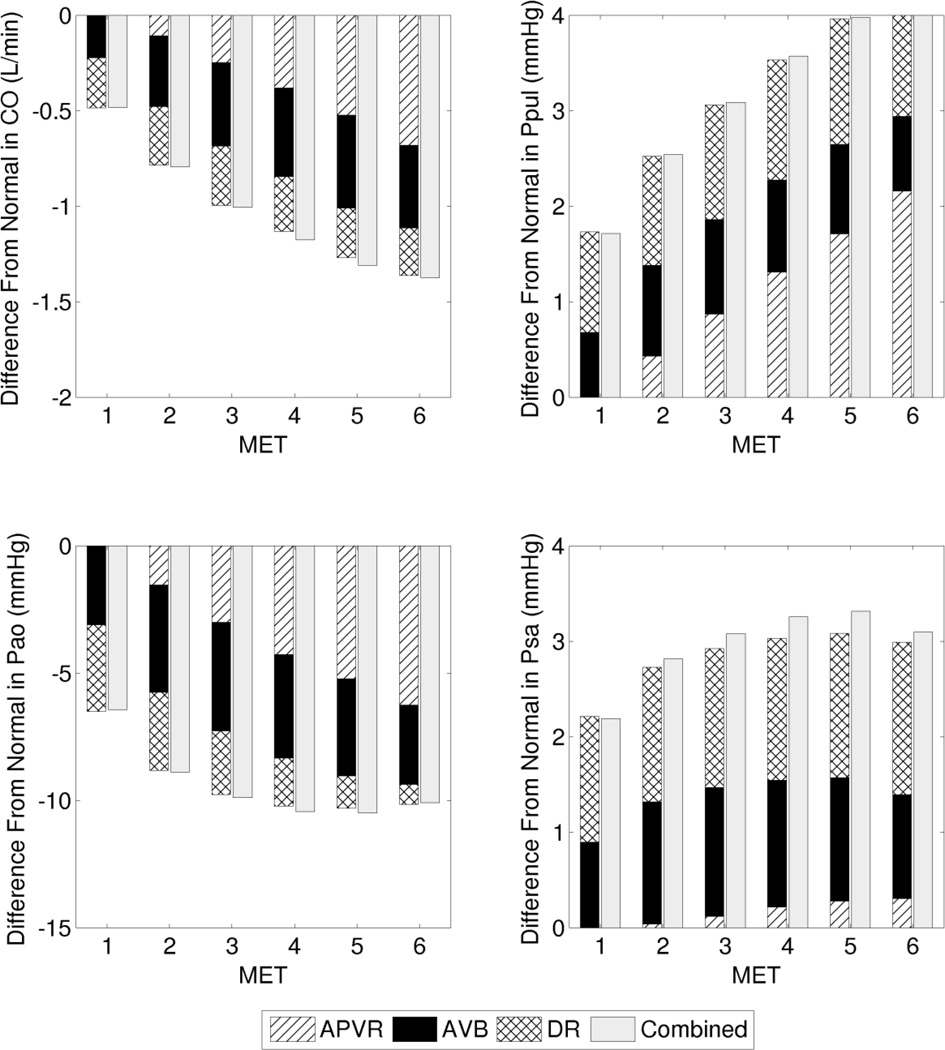
We present two case studies comparing the effects of several dysfunctions in isolation and combination, and examine the changes in output parameters (relative to their corresponding reference values at the particular MET intensity) resulting from each dysfunction in isolation, and from all dysfunctions combined in the same system. Case study 1 represents a clinical scenario in which a patient exhibits a combination of AVVI, SysD2, and ChI (Figure 5). Case study 2 represents a scenario with a combination of APVR, AVB, and DR (Figure 6). In both case studies, the combined effect was nearly linear, such that the physiological impact of the combined dysfunctions is close to the sum of the impact of each dysfunction in isolation. The combined impact can be either slightly less (case study 1) or more (case study 2) than the sum of the isolated impacts.

Figure 5.

Case study 1: Deviation from the normal reference (at each particular exercise intensity) contributed by cases of isolated and combined dysfunctions. Cardiac output (CO), PA pressure (Ppul), aortic pressure (Pao), and atrial pressure (Psa).

Figure 6.

Case study 2: Deviation from the normal reference (at each particular exercise intensity) contributed by cases of isolated and combined dysfunctions. Cardiac output (CO), PA pressure (Ppul), aortic pressure (Pao), and atrial pressure (Psa).

Table 2 shows the O₂ extraction requirements for the reference case and the two case studies. When dysfunctions are present and the CO is reduced at a particular MET, the O₂ extraction requirement increases in order to meet metabolic demand. In both combined dysfunction cases, intensities beyond 3 MET results in O₂ extraction that reaches or exceeds that of a higher MET level of the reference case. The O₂ extraction requirement at 4 MET in case study 1 exceeds the O₂ extraction requirement at 6 MET in the reference case by 14%.

Table 2.

O₂ extraction (L-O₂/L-CO) requirements at different exercise intensities in various cases of isolated and combined dysfunctions

		1 MET	2 MET	3 MET	4 MET	5 MET	6 MET
Reference		0.057	0.086	0.110	0.132	0.152	0.163
Case Study 1
SysD2		0.065	0.102	0.132	0.159	0.182	0.194
AVVI		0.067	0.101	0.130	0.155	0.179	0.190
ChI		0.057	0.086	0.110	0.132	0.152	0.164
Combined		0.076	0.119	0.156	0.186	0.214	0.228
Case Study 2
APVR		0.057	0.088	0.115	0.139	0.163	0.176
AVB		0.060	0.092	0.118	0.141	0.162	0.171
DR		0.061	0.091	0.116	0.137	0.157	0.167
Combined		0.064	0.100	0.130	0.157	0.181	0.192

Sensitivity Analysis

Beyond the input parameters examined in Figure 4, additional sensitivity analysis was performed to determine effects of PVR, E_offset, E_max, and HR on model predictions. These input parameters were varied incrementally from −60% to +60% and the model was re-run to quantify changes in outputs. Results are shown in the supplemental materials. Around the model reference operating points, we observed approximately linear relationships between input (PVR, E_offset, E_max) and output (CO, PA pressure, aortic pressure, atrial pressure) parameters, except for the input parameter HR. When examined in terms of percent changes, CO is most sensitive to E_offset at resting condition (with a slope of ~0.67), and most sensitive to PVR at 5 MET (with a slope of ~0.33).

DISCUSSION

The goal of this study was to isolate and quantify the hemodynamic impacts, relative to a reference normal, of a set of dysfunctions introduced to the exercising Fontan system under the controlled conditions of a computational model. Starting from a previously developed computational protocol, we performed simulations of Fontan lower-body exercise using a closed-loop LPN. We demonstrated the utility of the computational model to pose and virtually test a series of hypotheses on causes of Fontan exercise intolerance. By creating a number of clinical scenarios in a “virtual patient,” we isolated and examined the effects of a set of commonly encountered, clinically relevant pathophysiological conditions among Fontan patients.

In all cases of dysfunction examined in this study, increased PA pressure is correlated with decreased performance (decreased CO). However, in case study 1, while the effect of the combined dysfunctions on CO increases steadily with exercise intensity, the effect on PA pressure does not. This suggests that changes in PA pressure may not always be the most direct indicator of exercise performance at higher intensities. Contrary to common speculation, the model showed that the impact of APVR is not generally greater than that of other dysfunctions of similar clinical severity. Our analysis shows that elevated PA pressure can often be mediated by elevated atrial pressure, rather than by increased PVR; we observed elevated PA pressure in all cases of dysfunctions investigated, even when there was no PVR dysfunction.

The elevation of atrial pressure in the dysfunctions we examined is likely due to a combination of several mechanisms. In the cases where a dysfunction involves cardiac function, the impairment in forward blood propagation may lead to a “backup” of blood in the atrium that raises atrial pressure. For example, elevated ventricular diastolic pressure resulting from either impaired contractility and reduced stroke volume, or impaired ventricular relaxation, could impede ventricular filling and lead to elevated atrial pressure. In other words, the forward blood movement produced by the ventricle provides a sink for the atrium and keeps the atrial pressure low. In the case of DR, in which the amplitude of the negative thoracic pressure is diminished, the decreased trans-myocardial pressure difference could also contribute to elevated atrial pressure. In the case of APVR, there is almost no increase in atrial pressure compared to normal (only 3% at peak exercise), possibly due to the increased pressure loss in the pulmonary vasculature.

The ratio between respiratory cycle and cardiac cycle lengths may vary under different physiological conditions. However, we found that this ratio had little impact on system performance. The effect of respiration on the simulated hemodynamics is principally mediated by the thoracic pressure amplitude.

Hardt et al. found a ~7% increase in 6-min walking distance performance with AV delay optimization in patients under cardiac resynchronization therapy whose reference AV delay differed >20ms from the optimal¹⁶. Our modeling prediction produced similar results and showed that at peak exercise the CO performance penalty from an unfavorable AV delay can approach ~9%. Using our computational model, we systematically showed that deviations from the optimal AV delay, either by shortening or lengthening, compromise ventricular filling and negatively impact system performance.

AVVI has been correlated with clinical outcomes^14,18, and even mild regurgitation has been correlated with noticeably worse outcomes^15,21,30. This study quantifies the hemodynamic impact of a clinically moderate AVVI relative to other dysfunctions. In previous clinical studies, there had been no clear indication whether poor patient outcome with AVVI was primarily related to valvular dysfunction, or whether it was a surrogate manifestation of other co-morbidities such as ventricular dysfunctions. The modeling approach allowed for a controlled experiment, not possible in the clinical setting, showing that in the absence of other morbidities, AVVI alone can significantly impact hemodynamics, especially under the demands of exercise.

Thoracic pressure variations have been shown to affect venous return as well as CO^4,17,25. While there have been no studies (to our knowledge) that directly record changes in hemodynamics due to graded impairment in thoracic pressure variation amplitude, Buda et al. showed that Valsalva and Muller maneuvers (both exhibiting zero thoracic pressure variation) lead to a decrease in CO⁴. Statistically significant decreases in end diastolic volume have also been documented during Valsalva maneuvers^3,4. Our results from investigations of the DR dysfunction are consistent with these previous findings. The simulated ventricular pressure-volume loop reveals the mechanism in which the lack of proper negative thoracic pressure provided by respiration increased diastolic ventricular pressure, leading to impaired filling, lowered end-diastolic volume, and eventually reduced stroke volume and CO.

Many of the dysfunctions examined in this work have hemodynamic impacts that are comparable, and the impacts of dysfunctions combined appear to be approximately equal to the sum of the impact of each isolated dysfunction involved. This suggests that for many clinical cases of exercise intolerance, one should consider a variety of dysfunctions equally rather than focusing on any single dysfunction that is traditionally associated with exercise intolerance (ie. APVR).It is also important to note that a single clinical diagnosis can be associated with multiple dysfunctions which all affect exercise performance. For example, a diagnosis of heart failure is often associated with various levels of multiple systolic and diastolic dysfunctions.

The modeling results demonstrating the relative significances of different dysfunctions are critically dependent on the definitions of how each dysfunction affects the relevant parameter in the computational model. The linear relationships between several input and output parameters shown in the sensitivity analysis provide means to estimate how these relative significances may change, if varying severities of dysfunctions result in different parameter variations. Based on the slopes of the sensitivities, we can evaluate the general importance of a dysfunction according to the potential it possesses to impact the system. Comparisons of the modeling results in this study to clinical data which may become available in the future will provide further insights and validation to the behaviour of the exercising Fontan system as predicted by the model.

The O₂ extraction requirement for meeting metabolic demands provides insight into how dysfunctions may limit exercise capacity. Typically a reserve in O₂ extraction ratio allows the body to cope with a drop in delivered O₂ (relative to O₂ demand) without compromising aerobic respiration. When dysfunctions lead to a decreased CO, in order to meet the peripheral tissue oxygen demand, higher O₂ extraction must be achieved by drawing from the reserve. In the theoretical scenario presented in this study, if the patient’s O₂ extraction reserve is capable of handling up to 6 MET exercise under normal physiology, when a combination of dysfunctions corresponding to case study 1 is present, the O₂ extraction reserve is exhausted just beyond 3 MET.

Limitations

The overall structure of the computational model is to simulate physiology based on reductionist exercise response mechanisms, while the specific model tuning is based on population trends from the literature and clinical data available during model development. Therefore, for the purposes of this particular study, the comparisons of relative differences between dysfunctions are more meaningful than the predictions of absolute output parameter values. In addition to previous validation against clinical data, we have also seen that the exercise response mechanisms incorporated in the model produced exercise hemodynamic features that serendipitously aligned with many clinical observations, suggesting that the model captures a good estimation of underlying mechanisms and interactions. While this provides a powerful tool to investigate the impacts of specific changes in the system, there are currently no clinical data to directly confirm the model predictions of the newly analyzed scenarios in this study. We must remember that the computational model is a simplified representation of physiology and is meant to be used in combination with other tools and clinical observations to gain further insights into Fontan exercise hemodynamics. The model is meant to provide a baseline performance without accounting for inter-patient variability. Furthermore, while the power of the model is the ability to isolate the effects of each dysfunction, one must take care to consider the possibility of associated auto-regulation responses. For example, compensatory mechanisms in the body may decrease the systemic vascular resistance in response to an elevated PVR as an attempt to maintain CO. The results we present are meant to correspond to the worst-case scenario where such compensatory mechanisms in the patient have already been exhausted. Inclusion of auto-regulatory effects is a promising area of future research that would enhance the capabilities of our models. Lastly, our analysis does not explain why the dysfunctions occur, or the likelihood of their occurrences in a given patient, but only their resulting impacts.

Future work

The exercise model upon which this study is based was developed using reasonable assumptions from literature and clinical data that were translated into a modeling context. Additional clinical information could provide further quantifications to improve the modeling protocol, for example, increased model complexity and specificity may be achieved by integrating new clinical exercise data as it is acquired and made available³⁸. In this study, we modeled a set of dysfunctions using reasonable assumptions to prescribe changes to model input parameters. Future improvements could be made by modeling combinations of dysfunctions with severity levels that are correlated to each other. For example, in patients with cardiac insufficiency, there are often correlations between the severities of systolic and diastolic dysfunctions which can be incorporated. The 0D lumped-parameter model can be coupled to 3D anatomical models to achieve multi-scale computational fluid dynamic simulations accounting for patient-specific anatomy. Finally, validation of simulation results against clinical measurements in patients with corresponding combinations of dysfunctions will provide confidence in model predictions.

Ultimately, modeling allows not only the hope of eventual patient-specific predictive forecasts of therapeutic interventions, but more importantly can also serve as a tool to influence routine care. For example, the benefits of pacing can be assessed for cases of ChI, AVB, or AV dyssynchrony, and weighed against the procedural risks and potential complications. The influence of peripheral vascular responses on performance during exercise can also be quantified and contribute to the consideration of vasodilator administration. These are two examples of the many potential clinical utilities of the modeling approach presented in this study.

Summary

The power of the computational approach in this study is the ability to perform controlled experiments, which are not possible clinically, to systematically investigate the consequences of isolated or combined dysfunctions of various severities on Fontan exercise performance. We quantified the effects of dysfunctions on relevant clinical parameters, and provided insights on their relative impacts on the overall exercise physiology. The detailed “virtual probing” of the simulated physiology allowed identification of possible mechanisms of exercise dysfunctions. This study quantified the contribution of several dysfunctions isolated and in combination towards the multiple potential etiologies for decreased exercise performance in Fontan patients.

Conclusions derived from the simulation results complement previous clinical observations. Elevated PA pressure is a consistent indication of sub-optimal physiology. Increased O₂ extraction requirements calculated from the decreased CO in dysfunctions can be used as a surrogate for quantifying the relative impairment of peak exercise. In the context of patient management strategies, this study reveals two interesting findings. First, in the case of multiple dysfunctions, palliation of AVVI may yield the largest improvement in exercise tolerance. Second, palliation of other dysfunctions could each provide incremental improvements, meaning that the priority for palliation may simply depend on the severity of each dysfunction. To obtain more patient-specific information regarding any particular clinical case, additional simulations can be performed using the specific combination and severities of dysfunctions representing the patient, and predictions made regarding the expected relative performance improvement associated with various palliation decisions. Employing a computational approach, this study offers clinically useful insights of sub-optimal Fontan exercise physiology and intolerance etiologies.

ABBREVIATIONS

APVR

Abnormal pulmonary vascular response

AV

Atrio-ventricular

AVB

1st degree AV block

AVVI

AV valve insufficiency

ChI

Chronotropic insufficiency

CO

Cardiac output in L/min

DR

Disordered respiration

DiasD

Diastolic dysfunction

MET

Metabolic equivalent in units of 3.5mL O₂·kg⁻¹·min⁻¹

PA

Pulmonary arterial

PVR

Pulmonary vascular resistance

SysD

Systolic dysfunction