Abstract
It has been argued that, to ensure accurate spectral feature estimates for sibilants, the spectral estimation method should include a low-variance spectral estimator; however, no empirical evaluation of estimation methods in terms of feature estimates has been given. The spectra of /s/ and /ʃ/ were estimated with different methods that varied the pre-emphasis filter and estimator. These methods were evaluated in terms of effects on two features (centroid and degree of sibilance) and on the detection of four linguistic contrasts within these features. Estimation method affected the spectral features but none of the tested linguistic contrasts.
1. Introduction
In many studies of /s/ and /ʃ/, these fricatives are analyzed by estimating some of their spectral features—such as their spectral moments, peaks, and troughs—and then testing these feature estimates for significant linguistic contrasts—such as differences due to consonant place, or to how this place contrast is realized across genders or age groups. These feature estimates are typically computed from the spectrum that results from applying the discrete Fourier transform (DFT) to an acoustic waveform. Because a sibilant fricative is generated by turbulence noise sources, its waveform fluctuates randomly; thus, in this setting, the DFT is used as a spectral estimator—a method for transforming random data (i.e., a waveform) into a multivariate statistic (i.e., a spectral estimate).
A spectral estimator can be evaluated by considering it as a sequence of point estimators, each of which estimates the amplitude of a particular frequency component. Each point estimator is then assessed in terms of its mean squared error (MSE)—i.e., the sum of its bias and variance. As bias increases, accuracy decreases; as variance increases, precision decreases. Despite its widespread use, the DFT is known to have undesirably large variance and, by extension, poor precision and high MSE: If f(ω) denotes the amplitude of a spectrum f at frequency ω, then the asymptotic distribution of the DFT's estimator for f(ω) has variance equal to f2(ω) (Shumway and Stoffer, 2011, p. 193).
As an alternative to the DFT, Blacklock (2004) and Shadle (2006) have suggested the multitaper spectrum (MTS) (Thomson, 1982), which is equivalent to the pointwise average of some number K of statistically independent estimators based on the DFT. Because of this averaging, the point estimators of the MTS have (1/K)th the variance as those of the DFT (Percival and Walden, 1993, p. 343; cf. the confidence intervals in Fig. 1). The reduced variance of the MTS has led to claims that only it will yield accurate and precise estimates for a sibilant's spectral features. For example, Shadle (2006, p. 456) argues that “[i]deally, a low-variance spectral estimate would be used” to estimate spectral features since they “depend greatly on the particular spectral representation” from which they are computed.
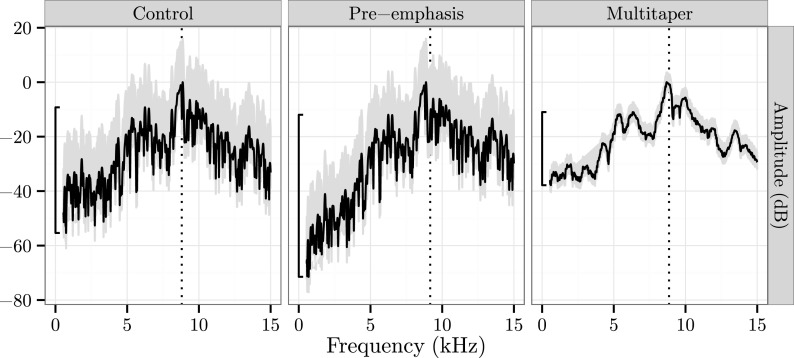
Fig. 1.
Spectral estimates (black lines) for /s/ under the control (left), pre-emphasis (center), and multitaper (right) strategies, with 95% confidence intervals (gray ribbons), centroid frequency (dotted line) and AmpDM-LMin (solid bracket) also shown.
While the reduced variance of the MTS is an unassailable fact, there are three reasons to suspect that the spectral estimator's variance or other distributional properties may not greatly affect a linguistic analysis. First, the spectral estimator is just one component in a series of transformations applied to a waveform in order to compute a spectral representation; below, such a series is referred to as a “spectral estimation method.” Another component that affects the values of the computed spectral estimate is an optional pre-emphasis filter that damps low-frequency oscillations in the waveform before the spectral estimator is applied. Thus, the spectral estimator does not necessarily determine all properties of the spectral representation from which spectral features are computed.
Second, a linguistic analysis typically does not end with the estimation of a spectrum, but proceeds from there to the computation of spectral features. As a transformation of a spectral estimate, the accuracy and precision of a spectral feature estimator will be affected by the bias and variance of the spectral estimator; however, this propagation of bias and variance will not be uniform across all spectral features. For example, since centroid frequency (see Sec. 2.2) involves the sum of amplitude estimates, the variance of the spectral estimator will directly affect the precision of the centroid estimator, but it is not obvious whether the accuracy of the centroid estimator will be affected. Alternatively, the variance of the spectral estimator will affect the excursiveness of the spectral estimate, which in turn may affect the accuracy of estimators for peak or trough amplitudes, but how it might affect the precision of such estimators is unclear.
Finally, the endpoint of a linguistic analysis is, almost always, the test for linguistic contrasts within the spectral feature estimates. So, while it is possible that different spectral estimators will reveal different linguistic contrasts, the importance of spectral estimator—or, more generally, any component of a spectral estimation method—should be considered with respect to linguistic contrasts, not the asymptotic distributional properties of the estimator.
This research note quantitatively evaluates the effects of two components of a spectral estimation method—spectral estimator and pre-emphasis filter—in terms of two spectral features—centroid frequency and degree of sibilance. Since the actual expected value of either feature is unknown, the feature estimates under either estimation method are compared to those computed with a control method. Additionally, the effects of estimation method are assessed in terms of linguistic contrasts revealed within these spectral features.
2. Methods
2.1. Sibilant production data
Target productions of /s/ and /ʃ/ were drawn from the English portion of the Paidologos corpus (Edwards and Beckman, 2008). These productions were elicited from native English-acquiring children aged between two and five years old (N = 64; 33 females) and native English-speaking adults (N = 20; 10 females) using a picture-prompted, word-repetition task. The materials for this task comprised 30 real English words, in which one of the target sibilants occurred in initial position and was followed immediately by a vowel. Half of these words began with /s/; the other half, with /ʃ/. The target productions were recorded using a Marantz PMD660 flash card recorder with a sampling frequency of 44.1 kHz.
The recorded productions of target /s/ and /ʃ/ were transcribed phonemically by a trained, native English-speaking phonetician. Only phonemically correct tokens were analyzed. This criterion left a total of 893 /s/ tokens (297 from adults) and 1048 /ʃ/ tokens (300 from adults). For each token, a trained native English speaker manually marked the onset and offset of frication after inspecting the spectrogram and waveform.
2.2. Spectral estimation and spectral features
For each phonemically correct production, the frication onset and offset were used to define a 20-ms analysis interval that was center-aligned with the temporal midpoint of frication. The spectrum of the waveform within each interval was estimated using three different methods (see Fig. 1), which were implemented with custom R scripts. Under the control method, the waveform was shaped by a Hamming window, and then its spectrum was estimated with the DFT. Under the pre-emphasis method, the waveform was first pre-emphasized according to the difference equation Y[n] = X[n] − αX[n − 1], where α = 0.98. The pre-emphasized waveform Y was then shaped by a Hamming window, and the DFT was used to estimate its spectrum. Under the multitaper method, the spectrum was estimated by the MTS (with parameters K = 8 and NW = 4) without preprocessing the waveform. The values for the parameters α, K, and NW were chosen to match previous studies of sibilants (cf. Jongman et al., 2000, who pre-emphasized with α = 0.98; Romeo et al., 2013, who computed MT spectra with K = 8 and NW = 4). From each spectral estimate, two spectral features were computed to assess how estimation method reveals different aspects of a spectrum's shape.
Compared to /ʃ/, /s/ is articulated with a more anterior lingual constriction and a smaller front cavity, whose resonances are concentrated at relatively higher frequencies (Narayanan et al., 1995). This difference in the broadband distribution of energy has commonly been measured with centroid frequency, which, in the current study, was computed within the interval Iω = [0.55, 15] kHz of a spectral estimate , following the method of Forrest et al. (1988):
| (1) |
During the time-course of a sibilant fricative, the spectral balance shifts such that the mid-frequency resonances and the low-frequency anti-resonances are more pronounced at frication midpoint than onset. To quantify a spectrum's mid- to low-frequency spectral balance, Koenig et al. (2013, p. 1180) proposed a measure, AmpDM-LMin, of the spectrum's “degree of sibilance,” which they computed as follows. Given a spectral estimate , whose amplitude values have been transformed to the decibel scale, let Il = [0.55, 3] kHz and Im = [3,7] kHz denote the low- and mid-frequency ranges of , respectively. Then, AmpDM-LMin is the difference in amplitude between the mid-frequency peak and the low-frequency trough (cf. the solid bracket at left in each panel of Fig. 1):
| (2) |
2.3. Statistical analyses
The effects of the pre-emphasis and multitaper methods on centroid and AmpDM-LMin were investigated through two types of analysis. The first analysis considered the effect of estimation method on either spectral feature. For this analysis, the estimates of a given spectral feature were pooled across place, age, gender, and estimation method, and then entered as the dependent variable in a linear mixed-effects (LME) model that included a fixed effect for spectral estimation method and random intercepts by subject. The parameters of the fitted model corresponded to the treatment mean of the control method and the differences between the pre-emphasis or the multitaper method, respectively, and the control. Coefficients and Wald confidence intervals, using the Bonferroni-adjusted confidence level 1 – (0.05/3) were estimated for these parameters, and the effect of either the pre-emphasis or multitaper method was considered significant if the corresponding confidence interval did not cover zero.
The second analysis investigated whether the estimation methods differentially detected linguistic contrasts within measures of a given spectral feature. For this analysis, six LME models were built—one for each combination of estimation method and spectral feature. Each of the models included fixed effects for consonant place (/s/ or /ʃ/), age (adult or child), and gender (female or male), as well as all interactions between these factors; and random intercepts by subject.
For each fitted model, the treatment mean for each combination of the place, age, and gender factors was estimated. Four linguistic contrasts among these treatment means, which indicate how a given spectral feature differentiates /s/ and /ʃ/, were of interest: Place (P) indicates the overall difference in how the /s/–/ʃ/ distinction is reflected in the spectral feature; Place:Age (P:A), the difference in how well adults, as opposed to children, distinguish /s/ from /ʃ/; Place:Gender (P:G), the difference in how well females, as opposed to males, distinguish /s/ from /ʃ/; and Place:Age:Gender (P:A:G), the difference in the P:G contrast across age groups. These contrasts are defined formally below, where μs,a,f denotes the treatment mean for female adults' /s/ productions, and so on:
| (3) |
| (4) |
| (5) |
| (6) |
For each estimation method, means and Wald confidence intervals for these linguistic contrasts were estimated at the adjusted level 1 − (0.05/4). An estimation method was considered to have detected a linguistic contrast in a given spectral feature, if the corresponding confidence interval did not cover zero.
3. Results
The spectral feature analysis for centroid found that relative to the control ( = 6789.64 Hz, SE = 110.55 Hz, CI = [6524.98,7054.31] Hz), the pre-emphasis method produced significantly greater values ( = 1198.64 Hz, SE = 62.55 Hz, CI = [1048.90, 1348.39] Hz); however, the difference between the multitaper and control methods was not significant ( = −12.83 Hz, SE = 61.96 Hz, CI = [−161.16 135.50] Hz). Mean centroid estimates for each estimation strategy, sibilant, and speaker group are shown in Table 1. The results of the linguistic contrast analysis for centroid are shown in the top row of Fig. 2. Under the control method, the P (M = 3438.25 Hz, SE = 132.28 Hz) and P:G (M = 1240.56 Hz, SE = 264.56 Hz) contrasts were detected, but the P:A and P:A:G contrasts were not. The pre-emphasis and multitaper methods detected the same linguistic contrasts as the control.
Table 1.
Mean centroid and AmpDM-LMin estimates for each sibilant, speaker group, and estimation method. Within each cell, the value above the dashed line refers to /s/; below, to /∫/.
| Children | Adults | ||||
|---|---|---|---|---|---|
| Females | Males | Females | Males | ||
| Centroid (Hz) | Control | 9296.7 | 8424.5 | 8903.8 | 6849.3 |
| 5540.5 | 5544.7 | 4496.2 | 4056.3 | ||
| Pre-emphasis | 10 396.8 | 9497.0 | 9518.1 | 7993.8 | |
| 6909.2 | 6972.7 | 5533.3 | 5554.9 | ||
| Multitaper | 9261.4 | 8432.0 | 8907.7 | 6846.8 | |
| 5521.3 | 5538.2 | 4463.3 | 4049.4 | ||
| AmpDM-LMin (dB) | Control | 52.6 | 53.5 | 56.7 | 59.8 |
| 58.7 | 56.4 | 63.1 | 58.1 | ||
| Pre-emphasis | 65.1 | 66.2 | 69.8 | 72.5 | |
| 70.5 | 68.3 | 75.2 | 70.1 | ||
| Multitaper | 23.3 | 24.4 | 26.2 | 30.0 | |
| 29.7 | 27.6 | 33.9 | 29.9 | ||
Fig. 2.
Means and Wald confidence intervals for the linguistic contrasts, involving place (P), age (A), and gender (G), in centroid (top) and AmpDM-LMin (bottom) estimates computed under the control (left), pre-emphasis (center), and multitaper (right) methods.
Relative to the control ( = 56.43 dB, SE = 0.43 dB, CI = [55.39, 57.47] dB), the spectral feature analysis for AmpDM-LMin found that the pre-emphasis method had a significant positive effect ( = 12.26 dB, SE = 0.28 dB, CI = [11.59, 12.92] dB), yielding greater AmpDM-LMin values. Conversely, the effect of the multitaper method was significant but negative ( = −29.06 dB, SE = 0.29 dB, CI = [−29.76, −28.37] dB), which produced lower AmpDM-LMin estimates. Mean AmpDM-LMin estimates are displayed in Table 1. The bottom row of Fig. 2 displays the results of the linguistic contrast analysis for AmpDM-LMin. The control method detected only the P (M = −3.54 dB, SE = 0.71) and P:G (M = −5.78 dB, SE = 1.43) contrasts. The pre-emphasis and multitaper methods detected the same contrasts as the control.
4. Discussion
Relative to the MTS, the DFT yields spectral estimates with more excursive amplitude fluctuations. Furthermore, both centroid and AmpDM-LMin depend on the amplitude values of the spectral estimate from which they are computed; however, the spectral feature analyses for the multitaper method found that only AmpDM-LMin was sensitive to spectral estimator. One possible explanation for this asymmetry is that within a narrow frequency band, some of the DFT-estimates' amplitude values will be greater than those of the MTS-estimate at the same frequency, and others will be less. Since centroid is a weighted sum of frequency, where the weights are scaled amplitude values, the narrowband amplitude fluctuations of a DFT-estimate will end up averaging out across a large number of frequency components. This would also explain why higher moments (variance, skewness, kurtosis) have been found to be insensitive to spectral estimator (Reidy, 2013). On the other hand, AmpDM-LMin directly measures the amplitude drop across just two components: the mid-frequency peak and the low-frequency trough. Thus, AmpDM-LMin would be expected to be more sensitive to the excursiveness of the spectral estimate, and by extension the variance of the spectral estimator.
By damping the low-frequency components, a pre-emphasis filter depresses the low-frequency trough and increases the proportion of energy concentrated in the mid- and high-frequency ranges. Therefore, AmpDM-LMin and centroid would both be expected to be greater under the pre-emphasis method, relative to the control, as was observed. While these differences due to pre-emphasis filter were predictable, they nonetheless show that the spectral estimator does not, in all cases, fully determine the properties of a spectral representation; and that when comparing the values of spectral feature estimates across studies, the effects of transformations other than spectral estimator may need to be borne in mind.
While the pre-emphasis method increased estimates of both features, and while the multitaper method decreased estimates of AmpDM-LMin, neither method detected different linguistic contrasts than the control did in either centroid or AmpDM-LMin. The results of the linguistic contrast detection analyses underscore this note's thesis that despite two spectral estimators having markedly different asymptotic variance, such a difference in their distributional properties may not alter the detection of linguistically meaningful contrasts, which are often the goal of such an analysis.
The analyses presented here demonstrated that the effects of a given component of a spectral estimation method on downstream analyses are in some cases quite small; however, the results should of course be interpreted within the limited scope of the spectral features and linguistic contrasts considered. Other contrasts that are relevant for sibilants include vowel context (e.g., Koenig et al., 2013) and hearing status of the speaker (e.g., Todd et al., 2011). It remains an open question whether other contrasts such as these are sensitive to spectral estimation method; however, the broader point of this research note still holds—that this question should be settled empirically, in terms of estimates of these contrasts, rather than analytically, in terms of the asymptotic variance of the spectral estimator. Furthermore, different spectral estimation methods may be of use for the development of novel spectral features. For example, minor peaks are more apparent within MTS than DFT estimates (cf. right and left panels of Fig. 1).
5. Conclusion
This research note compared the effects of spectral estimation method on estimates of centroid frequency and of the degree of sibilance, and on the detection of four linguistic contrasts within either of these features. Pre-emphasis was found to increase estimates of both features, while the MTS decreased estimates of the degree of sibilance but had no effect on centroid. Despite their effects on the spectral features, all the methods detected only Place and Place:Gender contrasts within either feature, suggesting that estimation strategy is un-likely to affect conventional analyses of sibilants, but it may facilitate the development of novel spectral features for these consonants.
Acknowledgments
The author was supported by a Distinguished University Fellowship (Ohio State University Graduate School) and by a Raymond H. Stetson Scholarship (Acoustical Society of America). Data collection was supported by NIDCD grant R01-02932 to Jan Edwards (University of Wisconsin, Madison, WI).
References and links
- 1.Blacklock, O. S. (2004). “ Characteristics of variation in production of normal and disordered fricatives, using reduced-variance spectral methods,” Ph.D. thesis, University of Southampton, Southampton, UK. [Google Scholar]
- 2.Edwards, J. , and Beckman, M. E. (2008). “ Some cross-linguistic evidence for modulation of implicational universals by language-specific frequency effects in the acquisition of consonant phonemes,” Lang. Learn. Dev. 4(2), 122–156 10.1080/15475440801922115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Forrest, K. , Weismer, G. , Milenkovic, P. , and Dougall, R. N. (1988). “ Statistical analysis of word-initial voiceless obstruents: Preliminary data,” J. Acoust. Soc. Am. 84, 115–124 10.1121/1.396977 [DOI] [PubMed] [Google Scholar]
- 4.Jongman, A. , Wayland, R. , and Wong, S. (2000). “ Acoustic characteristics of English fricatives,” J. Acoust. Soc. Am. 108(3), 1252–1263 10.1121/1.1288413 [DOI] [PubMed] [Google Scholar]
- 5.Koenig, L. L. , Shadle, C. H. , Preston, J. L. , and Mooshammer, C. R. (2013). “ Toward improved spectral measures of /s/: Results from adolescents,” J. Speech Lang. Hear. Res. 56(4), 1175–1189 10.1044/1092-4388(2012/12-0038) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Narayanan, S. S. , Alwan, A. A. , and Haker, K. (1995). “ An articulatory study of fricative consonants using magnetic resonance imaging,” J. Acoust. Soc. Am. 93(3), 1325–1347 10.1121/1.413469 [DOI] [Google Scholar]
- 7.Percival, D. B. , and Walden, A. T. (1993). Spectral Analysis for Physical Applications ( Cambridge University Press, Cambridge, UK: ). [Google Scholar]
- 8.Reidy, P. F. (2013). “ The (null) effect of spectral estimator on the estimation of spectral moments,” J. Acoust. Soc. Am. 134(5), 4238. 10.1121/1.4831579 [DOI] [Google Scholar]
- 9.Romeo, R. , Hazan, V. , and Pettinato, M. (2013). “ Developmental and gender-related trends in intra-talker variability in consonant production,” J. Acoust. Soc. Am. 134(5), 3781–3792 10.1121/1.4824160 [DOI] [PubMed] [Google Scholar]
- 10.Shadle, C. H. (2006). “ Acoustic phonetics,” in Encyclopedia of Language and Linguistics, edited by Brown K., 2nd ed. ( Elsevier, Oxford, UK: ), Vol. 9, pp. 442–460. [Google Scholar]
- 11.Shumway, R. H. , and Stoffer, D. S. (2011). Time Series Analysis and Its Applications, 3rd ed. ( Springer, New York: ). [Google Scholar]
- 12.Thomson, D. J. (1982). “ Spectrum estimation and harmonic analysis,” Proc. IEEE 70, 1055–1096 10.1109/PROC.1982.12433 [DOI] [Google Scholar]
- 13.Todd, A. E. , Edwards, J. R. , and Litovsky, R. Y. (2011). “ Production of contrast between sibilant fricatives by children with cochlear implants,” J. Acoust. Soc. Am. 130(6), 3969–3979 10.1121/1.3652852 [DOI] [PMC free article] [PubMed] [Google Scholar]