Robust Hadley Circulation changes and increasing global dryness due to CO₂ warming from CMIP5 model projections

Significance

In spite of increasing research efforts, global warming signals of the Hadley Circulation (HC) and its dynamical linkages to water cycle changes remain largely unknown. Here, from model projections, we find robust signals of both strengthening and weakening components of the HC induced by CO₂ warming. These changes in the HC drive a pattern of global dryness featuring widespread reduction of tropospheric humidity and increased frequency of dry months, particularly over subtropical and tropical land regions. We also find that global warming signal in increased dryness is the most detectable among numerous water-cycle quantities examined. Our results provide a scientific basis for inferring that greenhouse warming is likely to contribute to the observed prolonged worldwide droughts in recent decades.

Abstract

In this paper, we investigate changes in the Hadley Circulation (HC) and their connections to increased global dryness (suppressed rainfall and reduced tropospheric relative humidity) under CO₂ warming from Coupled Model Intercomparison Project Phase 5 (CMIP5) model projections. We find a strengthening of the HC manifested in a “deep-tropics squeeze” (DTS), i.e., a deepening and narrowing of the convective zone, enhanced ascent, increased high clouds, suppressed low clouds, and a rise of the level of maximum meridional mass outflow in the upper troposphere (200−100 hPa) of the deep tropics. The DTS induces atmospheric moisture divergence and reduces tropospheric relative humidity in the tropics and subtropics, in conjunction with a widening of the subsiding branches of the HC, resulting in increased frequency of dry events in preferred geographic locations worldwide. Among various water-cycle parameters examined, global dryness is found to have the highest signal-to-noise ratio. Our results provide a physical basis for inferring that greenhouse warming is likely to contribute to the observed prolonged droughts worldwide in recent decades.

The Hadley Circulation (HC), the zonally averaged meridional overturning motion connecting the tropics and midlatitude, is a key component of the global atmospheric general circulation. How the HC has been or will be changed as a result of global warming has tremendous societal implications on changes in weather and climate patterns, especially the occurrences of severe floods and droughts around the world (1, 2). Recent studies have suggested that the global balance requirement for water vapor and precipitation weakens the tropical circulation in a warmer climate (3, 4). So far, the most robust signal of weakening of tropical circulation from models appears to come from the Walker circulation but not from the HC, possibly because of the large internal variability in the latter (5, 6). Observations based on reanalysis data have shown weak signals of increasing, decreasing, or no change in HC strength in recent decades, with large uncertainties depending on the data source and the period of analyses (7–10). Meanwhile, studies have also shown that even though water vapor is increased almost everywhere as global temperature rises, increased dryness (lack of rainfall and reduced surface relative humidity) is found in observations and in model projections, especially in many land regions around the world (11–13). Reduction in midtropospheric relative humidity and clouds in the subtropics and midlatitude under global warming have also been noted in models and observations, suggesting the importance of cloud feedback and circulation changes (14–16). Even though robust global warming signals have been found in changing rainfall characteristics (2, 17, 18), in the widening of the subtropics, and in the relative contributions of circulation and surface warming to tropical rainfall from climate model projections and observations (19–24), the dynamical linkages between HC changes and global patterns of moistening and drying have yet to be identified and understood. In this paper, we aim at establishing a baseline understanding of the dynamics of changes in the HC and relationships with increased global dryness based on monthly outputs from 33 Coupled Model Intercomparison Project Phase 5 (CMIP5) 140-y projection experiments under a scenario of a prescribed 1% per year CO₂ emission increase. The baseline developed here hopefully will provide guidance for future observational studies in the detection and attribution of climate change signals in atmospheric circulation and in the assessment of risk of global droughts. Consistent with previous studies (3, 4, 17, 24), we find that under the prescribed emission scenario, global rainfall increases at a muted rate of 1.5 ± 0.1% K⁻¹, much slower than that for saturated water vapor as governed by the Clausius−Clapeyron relationship (∼6.5% K⁻¹). In the following, the responses of various quantities related to the climatology and anomaly of the HC, rainfall, tropical convection, global dryness, and their interrelationships are discussed. For definitions of climatology and anomaly, see Methods and Materials.

Rainfall and Vertical Motions

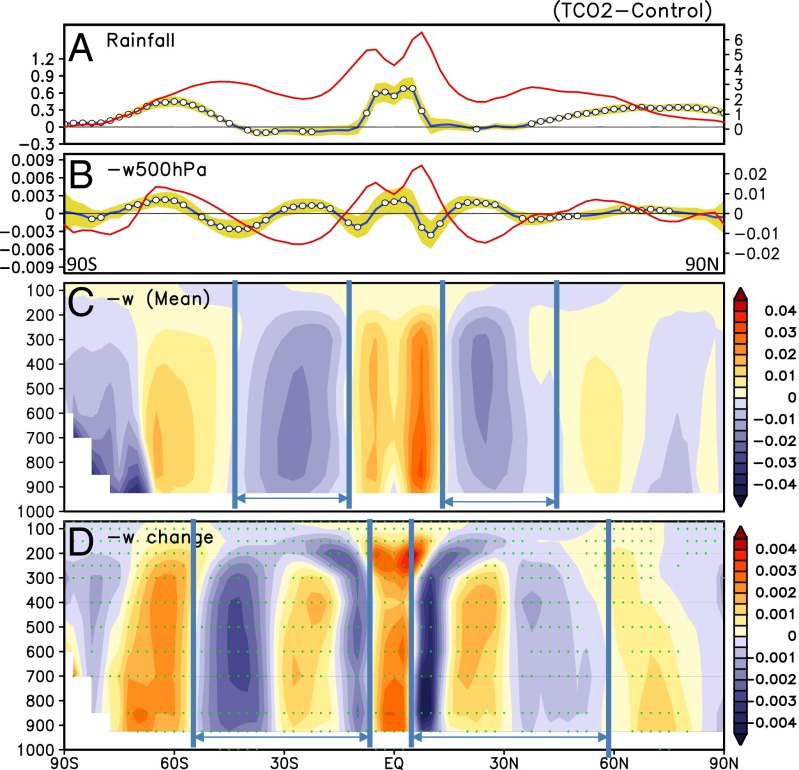
First, we examine the relationship between zonally averaged rainfall and vertical motions (Fig. 1). Both the climatological Multi-Model Mean (MMM) rainfall and 500-hPa pressure velocity (Fig. 1 A and B) show double maxima in the tropics, consistent with the observed off-equatorial positions of the Inter-Tropical Convergence Zones (ITCZs) (25). Both show the well-known double-ITCZ model bias, i.e., excessive rainfall and too strong rising motions in the southern hemisphere deep tropics (26). The MMM anomalous rainfall shows pronounced increase between 10°S and 10°N, a slight drying in the subtropics, and increased rainfall in the extratropics of both hemispheres (Fig. 1A). The anomalous pressure velocity profile (Fig.1B) shows wavelike perturbations that generally vary inversely with the climatology, featuring enhanced rising motion coinciding with increased rainfall in the deep tropics. Strong compensating anomalous sinking motions are found centered near 10°S and 10°N. Subsiding motions in the subtropics appears to be weakened. Comparing Fig. 1 C and D, a structural change in the vertical motion field can be perceived as a shift of the ITCZs of both hemispheres toward the equator, in the form of a narrowing and strengthening of anomalous ascent throughout the troposphere in the equatorial region, flanked on both sides by equally strong anomalous descent centered near 10°S and 10°N. The climatological equatorial minimum appears to be filled in by a “squeeze” of the ascending branch of the HC toward the equator from both hemispheres. This “deep-tropics squeeze” (DTS) appears to be coupled to positive anomalies, i.e., weakened sinking motions, near the center of the climatological subsiding branches of the HC. A widening of the subtropics is achieved via the DTS together with a poleward extension (marked by zero-wind contours) of the sinking branch of the HC, and poleward shift of the Ferrel and polar cells in both hemispheres (21, 22). These changes in the HC and related global signals are robust in the sense that more than two thirds (25/33) of the models agree on the sign of the anomalies (grid points highlighted by a green dot in Fig. 1D) almost everywhere. Time series of zonally averaged mean vertical motion clearly show steadily increasing rising motion in the ascending branch of the HC in the deep tropics, throughout the entire 140-y integration (Fig. S1 and SI Text).

Fig. 1.

Latitudinal profile of MMM (A) rainfall and (B) 500-hPa vertical motion. Climatology is indicated by red line, and anomaly is indicated by black line. Open circles indicate where more than 75% (25/33) of models agree in the sign of the anomalies. Latitude−height profile of MMM 500-hPa vertical motion for (C) climatology and (D) anomaly. The width of the subsidence zones are indicated by the vertical blue lines. Grid points where more than 25 models agree in the sign of the anomaly are indicated by green dots. Rainfall is in units of millimeters per day, and vertical motion is in units of negative pascal per second. Different unit scales are used for climatology and anomalies.

Tropical Convection

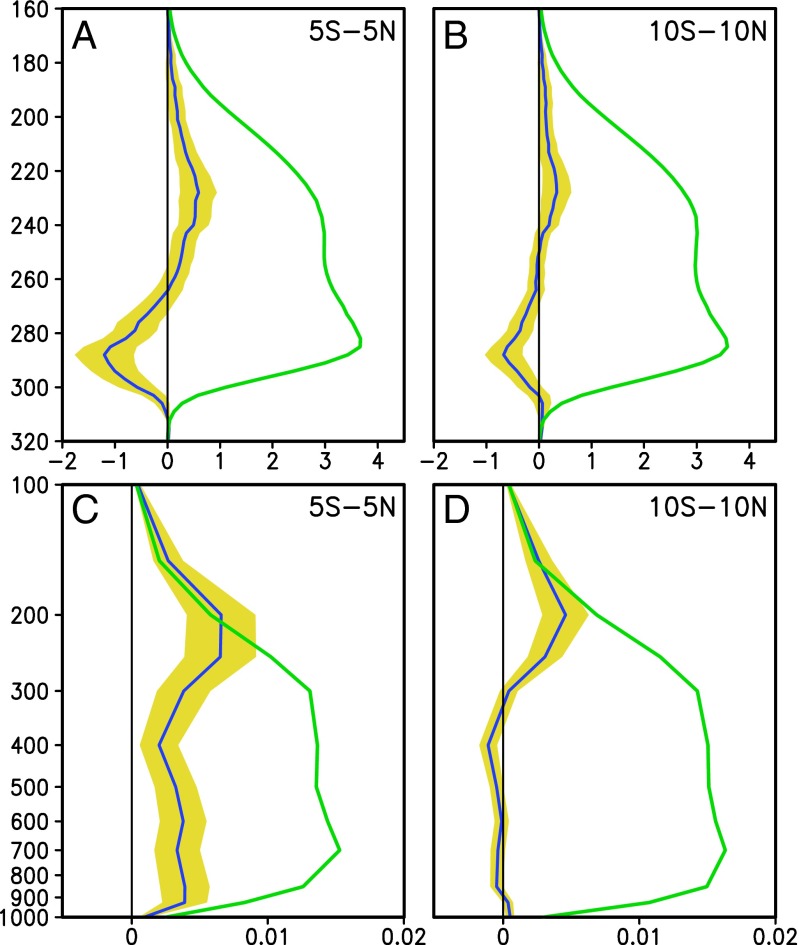
To better understand the nature of the DTS, we examine the changes in tropical convection and the large-scale tropical circulation. Here, as a proxy for tropical convection, monthly outgoing longwave radiation (OLR) is used. Based on a comparison of observations between monthly OLR from National Oceanic and Atmospheric Administration Advanced Very High Resolution Radiometer, and daily brightness temperature from Tropical Rainfall Measuring Mission (Fig. S2), and findings from previous studies (27–29), we identify a high monthly OLR (>270 W⋅m⁻²) with low clouds; a moderate OLR (270–220 W⋅m⁻²) with middle clouds, and a low OLR (<220 W⋅m⁻²) with high clouds associated with deep convection. We have computed the MMM climatological probability distribution functions (pdf) of OLR and their changes due to global warming. The climatological OLR pdf (Fig. 2 A and B) indicates a weak bimodal distribution of convection in the deep tropics, with an abundance of low to middle clouds, as well as high clouds associated with deep convection (OLR < 220 W⋅m⁻²). Near the equator (Fig. 2A), the anomalous OLR profile indicates a shift toward deeper convection, as evident in the pronounced increase in the frequency of lower OLR (colder cloud top) and decrease in higher OLR (warmer cloud top) by 5–15%. At 10°S−10°N (Fig. 2B), similar shift toward deeper convection can be seen, although the signal is weaker (<10%) compared with near the equator, due to suppression of deep convection by the anomalous subsidence near 10°S and 10°N (see Fig. 1). In conjunction with deepening clouds, the anomalous ascent near the equator (Fig. 2C) is enhanced at all levels, most pronounced (up to ∼30–40% increase) at upper levels, signaling an upward shift of maximum ascent from the lower to middle troposphere (700−400 hPa) to the upper troposphere (300−150 hPa). Averaged over 10°S−10°N (Fig. 2D), the enhanced ascent in the upper troposphere remains strong (∼30%), but the anomalous vertical motion below 300 hPa is slightly negative due to strong anomalous sinking motions found near 10°S and 10°N, associated with the DTS.

Fig. 2.

MMM outgoing longwave radiation (OLR) probability distribution function as a function of OLR flux (in watts per square meter on y axis) averaged over (A) 5°S−5°N, and (B) 10°S−10°N. Vertical profile of mean vertical motion averaged over (C) 5°S−5°N, and (D) 10°S−10°N. Climatology is indicated by green line, and anomaly is indicated by blue line. The model spread is shown as yellow shading. The magnitudes of the anomalies have been doubled to enhance clarity. Vertical motion is in units of negative pascals per second. OLR pdf is nondimensional.

Meridional Outflow and Relative Humidity

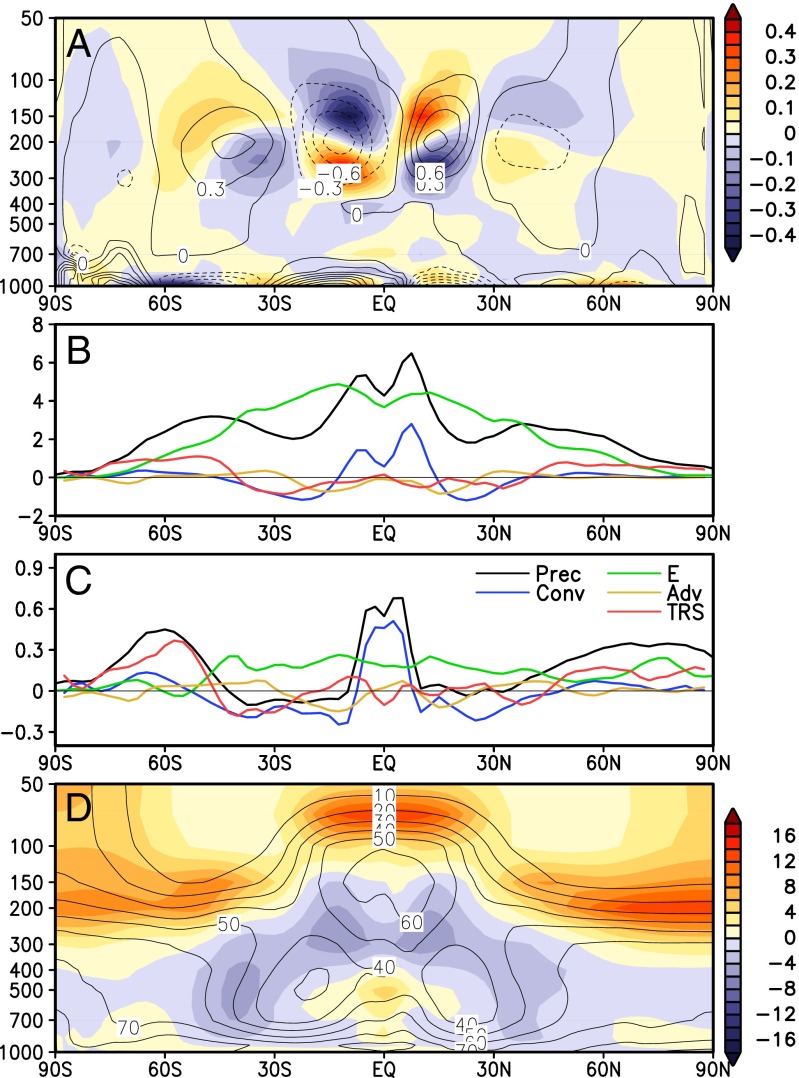
The DTS is closely linked to changes in meridional winds of the HC (Fig. 3A). Here, the most prominent feature is a vertical dipole wind anomaly in the tropics, with opposite signs in each hemisphere, i.e., a quadruple pattern, with enhanced outflow away from the equator in the 200- to 100-hPa layer, and increased inflow between 400 hPa and 200 hPa, toward the equator. Compared to the control, this indicates a rise in the maximum outflow region in the upper branch of the HC from its climatological maximum level near 200 hPa to 150 hPa. Note that at 200 hPa, the anomaly is near zero. A conventional measure of the strength of the HC based on mass outflow at 200 hPa (9) would have yielded no significant change in the HC. An examination of the anomalous meridional wind profiles for each model (Fig. S3) indicates that the rise of the maximum outflow region of the HC under global warming is very robust, with all 33 models showing the characteristic quadruple pattern, albeit with varying magnitudes. Time−height cross sections of the MMM meridional wind profile at 10°S and 10°N (Fig. S4) show clearly a steady rise of the region of maximum outflow as the atmospheric CO₂ loading increases. The meridional outflow mass flux at the upper troposphere (200−150 hPa) out of the 10°S−10°N zone is estimated to be intensifying at a rate of +13.2 ± 1.34% K⁻¹, consistent with an enhancement of the upward motions in the ascending branch of the HC. The effect of the rise in the region of maximum outflow is also evident in the meridional mass streamfunction and zonal winds profile (Fig. S5 and SI Text), reflecting a rise of the center of mass of the entire HC, a poleward expansion of the subtropical subsidence zone (Fig. S5A), in conjunction with an upward shift of the westerly zonal wind maxima in the subtropics and midlatitudes (Fig. S5B). The rise in the region of maximum outflow of the HC is also consistent with the increase in tropopause height in the tropics under global warming reported in past studies (30, 31). Note that even though the strongest meridional divergent wind is in the upper troposphere, the strongest moisture convergence is confined to the lower and middle troposphere (Fig. S6), where most of the atmospheric moisture is concentrated.

Fig. 3.

Latitude−height cross section of (A) anomalous meridional zonal mean winds (meter per second) and (D) anomalous humidity (percent). The climatological mean is shown in contour, and anomaly is shown in color. Latitudinal profiles of components of moisture budget for (B) the control and (C) the anomaly. See Eq. 1 for explanation of symbols. Units in millimeters per day.

The roles of atmospheric moist processes and surface evaporation in contributing to the changes in precipitation anomalies are evaluated from the following moisture budget analysis:

$$\langle \overline{P}\rangle =\langle \overline{E}\rangle +\text{ADV}+\text{CONV}+\text{TRS}$$ [1]

where $\overline{P}$ and $\overline{E}$ are monthly mean precipitation and surface evaporation, and $\text{ADV}=-\langle \overline{\mathit{V}}\mathrm{\cdot }\nabla \overline{\text{q}}\rangle ,\text{CONV}=\mathrm{-}\langle \overline{\text{q}}\nabla \cdot \overline{\mathit{V}}\rangle ,\text{and}\hspace{0.17em}\text{TRS}=-\langle \overline{\mathbf{V}\prime \cdot \nabla q\prime }\rangle -\langle q\prime \nabla \cdot \mathbf{V}\prime \rangle$ represent, respectively, the contribution from moisture advection, dynamic convergence, and transients on shorter time scales; $\langle \rangle$ denotes vertical average, the overbar denotes monthly mean, and $\left(\right)\prime$ denotes deviation from the mean. Here, the transients are computed as the residual from Eq. 1. Each term in Eq. 1 has been computed for the control and for the anomaly. In the control (Fig. 3B), clearly, surface evaporation in the tropics and subtropics contributes to a large portion of the moisture available for precipitation. However, the structure of the precipitation profile in the tropics and subtropics are dominated by CONV and, to a smaller extent, by ADV. The effect of TRS appears to be largely in transporting available precipitable water from the subtropics to higher latitudes. Under global warming (Fig. 3C), anomalous evaporation contributes ∼10–15% of the increased precipitation in the deep tropics but remains relatively constant in latitude, except falling off sharply in the southern hemisphere extratropics. Precipitation anomaly in the deep tropics associated with DTS is dominated by CONV. Between 10° and 30° latitudes, both CONV and ADV contribute substantially to the precipitation deficit. The contribution from TRS is relatively small in the tropics but large outside the tropics (>30° latitudes), and dominant at higher latitudes (>50° latitudes). In the northern hemisphere extratropics, precipitation anomalies are contributed almost equally by evaporation and TRS, with decreasing contributions from ADV and CONV at higher latitudes. In the southern hemisphere extratropics, TRS contributes to large fraction (>50%) of the precipitation changes. The TRS has been identified with increased eddy heat and momentum fluxes associated with a poleward shift of the storm tracks (21, 32, 33). A more detailed discussion of regional contributions by the various processes in Eq. 1 can be found in Fig. S7.

The aforementioned changes in HC, and related changes in moisture balance have strong influence on the relative humidity (RH) of the troposphere. The zonally averaged RH anomalous pattern (Fig. 3D) shows a 5–10% reduction, i.e., increased relative dryness, throughout most of the troposphere, except in the lower and middle troposphere of the deep tropics, and in the lower troposphere of the extratropics and the polar region. This pattern of RH anomaly has been reported in previous studies in the context of cloud radiation feedback and vertical mixing under global warming (15, 34). In this work, we emphasize the physical connection of the RH pattern to changes in the HC. The anomalous RH pattern stems from the different rates of response of moisture convergence and temperature as a function of height and latitude. As a result of CO₂-induced warming, both tropospheric temperature and moisture increase everywhere (Fig. S8). In the deep tropics, below 400 hPa, RH is enhanced because of strong CONV (Fig. 3C). However, in the layer from 400 hPa to 150 hPa, RH is reduced. This is due to a faster warming rate in the upper troposphere compared with the lower troposphere, as a result of the moist adiabatic constraint (Fig. S8A). Here, high RH air transported from below by CONV encounters regions of warmer temperature in the upper troposphere, resulting in a deficit of RH. Near 10°S and 10°N, the upper troposphere RH deficit is strongly enhanced by increased subsidence associated with negative CONV and ADV (see Fig. 3C), as evident in the two RH minima in the upper troposphere, which coincide with the regions of maximum anomalous downward motion at 10°S and 10°N (see Fig. 1). In the subtropical mid-to-lower troposphere, the widening of the subsidence zone associated with the DTS brings more dry air from above, increasing the RH deficit. This is reflected in the expanding region of reduced RH from the midtroposphere to the surface in the poleward flank of the climatological dry zones (regions with RH < 40), where the RH deficit is at a maximum. The increased RH near the tropopause and lower stratosphere is associated with the cooling from increased longwave radiative loss to space under global warming (35, 36). Even a small increase in moisture due to enhanced vertical transport will result in a large increase in RH in these regions.

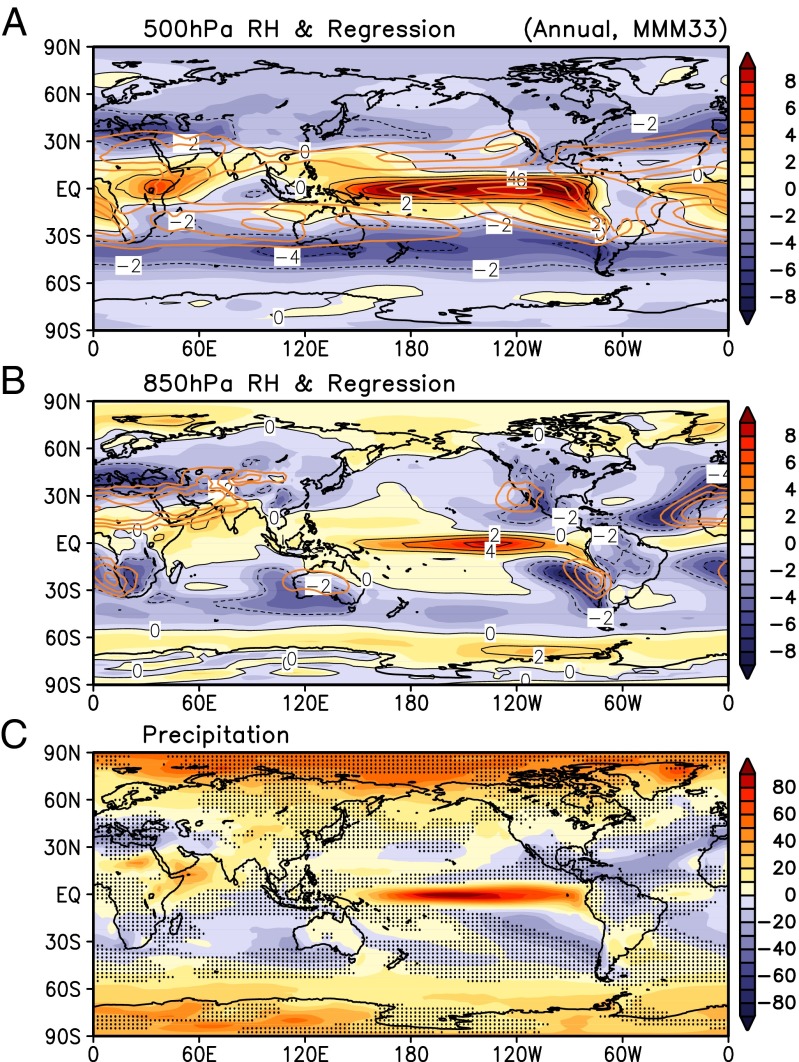
The association of DTS with the RH changes in the middle and lower troposphere is further examined by regression analysis. The regression map of the 200- to 150-hPa mass outflow at 10°S and 10°N with the 500-hPa RH field (Fig. 4A) shows a quasi-zonal symmetry pattern, indicating that positive mass outflow of the HC is associated with increased RH in a narrow swath in the deep tropics along the equator, with the most pronounced signal over the near-equatorial regions of the central and eastern Pacific, the Indian Ocean, and the Atlantic. Elsewhere globally, RH is mostly reduced, with strong signals found at the poleward flank of the climatological subtropical dry zones (RH < 40 in Fig. 4A). The RH deficit is especially pronounced over the southern hemisphere, appearing as a continuous belt around 30°S−60°S. Significant RH reduction is also found over the western Indian Ocean/eastern Maritime continent in connection with increased subsidence associated with a weakened climatological Walker Circulation (see also Fig. 4C). At 850 hPa (Fig. 4B), the RH regression pattern displays more regional characteristics. Over the longitude sector (160°W–0°W), the squeeze by the RH deficit zones in the subtropics of both hemispheres toward the strongly increased RH narrow regions of the equatorial central and eastern Pacific and the equatorial Atlantic is very pronounced. The 850-hPa RH deficit pattern corresponds well with regions of large fractional rainfall reduction and enhanced subsidence in the expanded descending branch of the HC (Fig. 4C). Fig. 4C also shows that the DTS is not apparent in the rainfall pattern over the tropical western Pacific and Indian Ocean, where widespread anomalous subsidence dominates, reflecting a weakening of the Walker Circulation under global warming (4, 5). The RH 500-hPa and 850-hPa anomaly patterns have also been computed, and are found to be very similar to Fig. 4 A and B. At the action centers in the polar flank of the subtropical descending zones, the maximum RH deficits are ∼8–10% (Fig. S9).

Fig. 4.

Spatial pattern of regression of meridional mass flux in the upper troposphere (200−150 hPa) at 10°S−10°N with 500-hPa RH anomaly (A) and 850-RH anomaly (B). Climatological dry zones (RH < 40 for 500 hPa, and RH < 50 for 850 hPa) are indicated by orange contours. Also shown are anomaly rainfall pattern (C), with regions of anomalous downward motion stippled. Unit of unit of regression is in percentage change per kilogram per meter. Unit of rainfall is in percentage.

DTS and Global Dryness

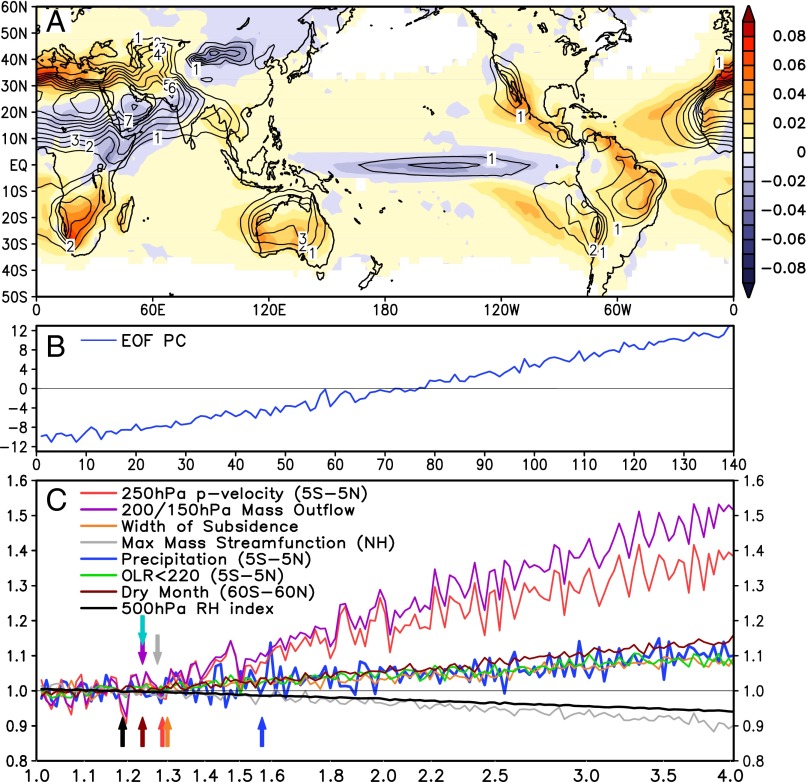
To further explore the relationship of HC changes and increased global dryness, we define an extreme dry month at any grid point as a month where the monthly rainfall is less than 0.1 mm/d, and compute the global dryness index (GDI) as the frequency of the occurrence of dry months at every grid point within 60°S−60°N, for all simulated years. The 0–0.1 mm/d range corresponds well with the driest bin in the monthly rainfall pdf of the CMIP5 models (17). The results shown here are not sensitive to a reasonable range of threshold values used. As shown in Fig. 5A, the climatological GDI pattern matches well with regions of low RH in the climatological 850-hPa RH field (Fig. 4B), which can be identified with major regions of deserts and arid zones around the world. The dominant pattern of anomalous GDI is obtained using empirical orthogonal function (EOF) decomposition applied to the yearly GDI anomalies. The principal component of the first EOF, which explains a large fraction of the variance (>48%), shows a steady increase in GDI (Fig. 5B) as the CO₂ burden in the atmosphere increases. Region of negative GDI in the tropics appears as a narrow tongue in the equatorial Pacific, coinciding well with regions of RH surplus and maximum rainfall increase (Fig. 4). Regions of increased GDI are concentrated in preferred geographic locations, i.e., the polar flank of the climatological subtropics of southern Europe and western Asia, South Africa, Australia, and southern Chile and the marginal convective zones over the tropical land regions of southwestern North America, central and northern South America and northeastern Brazil. The concentration of pronounced GDI over land regions is likely related to positive feedback from atmosphere−land interactions, arising from large-scale dynamical forcing associated with changes in the HC (37, 38). The strong east−west asymmetry in the GDI is likely related to changes in rainfall, wind, and moist stability in the tropics associated with a weakened Walker Circulation and an altered land−sea thermal contrast between the western and eastern hemisphere (38).

Fig. 5.

(A) Spatial distribution of eigenfunction of first empirical orthogonal mode of global drought index (GDI), (B) principal component of first EOF of GDI, and (C) time series of HC circulation and related quantities. See DTS and Global Dryness for detailed definition. Magnitudes are scaled to the mean value in the control (first 27 y of integration), and time is scaled to total CO₂ emission relative to the first year of the integration, with 1% per year increase.

As a summary analysis, the temporal changes of aforementioned key circulation parameters related to DTS, and global dryness expressed in percentage change relative to the control as a function of CO₂ loading, are shown in Fig. 5C. Relevant statistics of each parameter, including climate sensitivity, R² values with respect to DTS outflow are shown in Table 1. The responses seem to fall into three groups. First is the rapid response group consisting of the 150- to 200-hPa meridional mass outflow and the 250-hPa vertical motion in the ascending branch of the HC, which increase at a rate of 13.2 ± 1.34% K⁻¹ and 9.9 ± 1.31% K⁻¹, respectively, with respect to increase in global mean surface temperature. Second is the slower response group with positive trend, including width of the subsidence region (2.3 ± 0.3% K⁻¹), precipitation (3.6 ± 0.3% K⁻¹), and increased high clouds as indicated by frequency of OLR < 220 W⋅m⁻² (2.4 ± 0.82% K⁻¹) in the deep tropics, and the GDI (3.6 ± 0.45% K⁻¹). Third is the slower response group with negative trends, showing decreasing midtropospheric RH in the subtropics (−3.1 ± 0.17% K⁻¹), and an apparent overall weakening (−2.4 ± 0.26% K⁻¹) of the HC according to the conventional measure, i.e., the maximum value of the meridional mass streamfunction in the subtropics (6). The fractional variance of the aforementioned variables explained by DTS mass outflow in the upper troposphere as shown by the R² values in Table 1 is uniformly high, in the range 0.83–0.98, indicating strong coherence with the HC outflow, except for precipitation, which shows less coherence, with R² = 0.52.

Table 1.

Climate sensitivity (ΔX/X) in percentage change per degree global surface temperature rise, R² value with respect to HC outflow in upper troposphere in the deep tropics, and detectability level (DL) for HC outflow, 250-hPa p-velocity, OLR, and precipitation in the deep tropics, width of the subsidence zone, GDI, Maximum Ψ (subtropical maximum in zonally averaged mass streamfunction), and 500-hPa RH in the subtropics

	HC outflow	250-hPa p-velocity	OLR	Precipitation	Width of subtropics	GDI	Maximum Ψ	500-hPa RH
ΔX/X	13.2 ± 1.34	9.9 ± 1.36	2.4 ± 0.82	3.6 ± 0.30	2.3 ± 0.30	3.6 ± 0.45	−2.4 ± 0.26	−3.1 ± 0.17
R2	1.00	0.98	0.91	0.52	0.83	0.92	0.85	0.95
DL	1.23	1.28	1.23	1.56	1.30	1.23	1.27	1.18

See DTS and Global Dryness for detailed explanation of symbol.

Fig. 5C offers additional information regarding the detectability of global warming signals in HC and water cycle. To estimate detectability, we first construct the 27-y running mean of all of the variables examined so far. The global warming signal is then obtained as the difference of the 27-y running mean with respect to the mean of the first 27-y of the integration, for each quantity we have so far examined. The noise is computed based on the intermodel variability from the MMM. We define the detectability level (DL) as the level of CO₂ in the atmosphere (in percentage) with respect to the control (preindustrial) at which the signal first becomes statistically significant at 99% statistical confidence based on a Student’s t test. The DL is meaningful only because of the quasi-linear nature of the responses. Based on the experimental design of 1% per year increase of CO₂, a lower DL represents a more robust signal (higher signal-to-noise ratio) detectable earlier at weaker CO₂ forcing compared with a higher DL. From Fig. 5C and Table 1, in order of increasing DL, the lowest (most detectable) is at 1.18 times the preindustrial CO₂, for subtropical 500 RH deficit. The next group with DL ∼1.23 consists of GDI, the upper tropospheric outflow and cloudiness change (OLR) in the deep tropics. This is followed by the next higher DL group at 1.27–1.30, associated with the overall weakening of the HC, enhanced ascent in the rising branch of the HC, and the widening of the subsidence zone. The highest DL (least detectable signal) is found at 1.56 for precipitation in the deep tropics. This is not surprising, because tropical precipitation has the least coherent variability with the DTS signal (lowest R² value) and is likely the most difficult to detect due to its inherent noisy nature. Noting that the current climate is at about 1.40 times the preindustrial CO₂ loading, the DLs estimated here seem to be in broad agreement with numerous published reports of observations of strong signals of midtropospheric RH deficit, upper tropospheric moistening, widening of the subtropics, and expansion of global dry lands over subtropical land (11–13, 37–39). Nonetheless, it is important to point out that the DL cannot be equated with actual detectability, because of the presence of strong interannual to multidecadal natural variability in the real world. The DL computed here is for MMM, where the natural variability has been minimized. Additionally, estimating detectability from observations has its own practical limitations from lack of reliable long-term global data. Hence, actual detectability of global warming signal in the HC and global water cycle is likely to be at higher CO₂ level than estimated here. At best, DL can only provide relative detectability of the different parameters examined in this paper.

Discussion

In this work, we report new findings regarding robust responses of the HC and their physical linkages to global dryness. Based on analyses of outputs of 33 CMIP5 coupled models, we find both strengthening and weakening signals in the HC responses to a prescribed 1% per year increase in CO₂ emission. The strengthening is associated with a DTS, manifested in the near-equatorial regions in the form of a deepening and narrowing of the convective zone, enhanced ascent, increased high clouds, suppressed low clouds, and increased meridional mass outflow (13.2 ± 1.34% K⁻¹) in the upper troposphere (200−150 hPa), away from the deep tropics. The DTS is coupled to an upward shift of the region of maximum outflow of the HC, a widening of the subtropical subsidence zone, and weakened return inflow of the HC in the lower troposphere. These changes in the large-scale circulation are closely linked to an overall deficit in relative humidity in the upper troposphere of the tropics, and in the middle and lower troposphere of the subtropics, and likely to cloud radiative feedback processes (16, 34). Increasing tropospheric and surface dryness is found at the poleward flank of the climatological dry zones of Africa−Eurasia, and over subtropical land of southwest North America and Mexico and northeastern Brazil. Our results further show that among the various atmospheric water cycle quantities associated with changes in the HC, global warming signal in tropospheric dryness is most likely to be among the first to be detected, manifesting in increased risks of drought in subtropical and tropical land regions.

Methods and Materials

To establish the baseline response of the HC to global warming, we used monthly outputs from a 140-y integration of 33 CMIP5 models forced by 1% increase per year CO₂ emission (for details, see SI Text, Model Experiment and Background). The control, also referred to as climatology, is defined as the first 27-y of the model simulation. By the midpoint of the integration, i.e., 27 y centered at year 70 of the integration, the CO₂ level is nearly doubled, and by the last 27 y, the mean CO₂ level is nearly tripled (TCO₂) compared with the control mean. In this work, we only focused on the forced response, as represented by the MMM of monthly data, defined as the average of all 33 models interpolated on a common grid resolution of 2.5 by 2.5 degrees latitude−longitude, and 17 vertical levels. Anomalies are defined as the MMM differences between TCO₂ and the control. The uncertainties of the MMM are estimated from the spread of the individual model means about the MMM, based on calculation of the mean square errors.