Triassic–Jurassic climate in continental high-latitude Asia was dominated by obliquity-paced variations (Junggar Basin, Ürümqi, China)

Significance

Geological records of paleoclimate provide the only constraints on Solar System orbital solutions extending beyond the ∼50-Ma limit imposed by chaotic diffusion. Examples of such constraints are coupled high and low latitude, Triassic–Jurassic (∼198–202 Ma) sedimentary cyclicity in coal-bearing outcrops from the ∼60° N-paleolatitude Junggar Basin (Western China), and contemporaneous tropical basins. Analysis reveals climate variability dominated by obliquity-scale cyclicity in the Junggar Basin and precession-scale cyclicity in the tropics. Together, these geological records empirically constrain orbital solutions by providing joint g4 − g3 and s4 − s3 secular frequency estimates of the Earth–Mars orbital resonance. These results demonstrate the opportunity for developing a new class of solutions grounded by geological data extending hundreds of millions of years into the geologic past.

Abstract

Empirical constraints on orbital gravitational solutions for the Solar System can be derived from the Earth’s geological record of past climates. Lithologically based paleoclimate data from the thick, coal-bearing, fluvial-lacustrine sequences of the Junggar Basin of Northwestern China (paleolatitude ∼60°) show that climate variability of the warm and glacier-free high latitudes of the latest Triassic–Early Jurassic (∼198–202 Ma) Pangea was strongly paced by obliquity-dominated (∼40 ky) orbital cyclicity, based on an age model using the 405-ky cycle of eccentricity. In contrast, coeval low-latitude continental climate was much more strongly paced by climatic precession, with virtually no hint of obliquity. Although this previously unknown obliquity dominance at high latitude is not necessarily unexpected in a high CO₂ world, these data deviate substantially from published orbital solutions in period and amplitude for eccentricity cycles greater than 405 ky, consistent with chaotic diffusion of the Solar System. In contrast, there are indications that the Earth–Mars orbital resonance was in today’s 2-to-1 ratio of eccentricity to inclination. These empirical data underscore the need for temporally comprehensive, highly reliable data, as well as new gravitational solutions fitting those data.

Our understanding of Triassic and Early Jurassic high-latitude climate, biotic evolution, mass extinction, and geochronology is very poor in contrast to that of the contemporaneous tropics (1, 2). This poor resolution impairs an elucidation of the basic patterns of Earth system function during the early Mesozoic, notably the high-latitude climatic response to orbital forcing, as well as the effects of the eruption of the Triassic–Jurassic Central Atlantic Igneous Province (CAMP) (3). The former issue bears on the stability of the Solar System, in which determining variations in orbital eccentricity (via climatic precession) and inclination (via obliquity) figure as crucial (4–6), and the latter bears on the causes, effects, and recovery from the end-Triassic mass extinction (ETE) (e.g., ref. 2). Here, we describe results of a cyclostratigraphic investigation of lithologic variations in the paleo-high latitude, lacustrine, Late Triassic–Early Jurassic Haojiagou and Badaowan formations of the Junggar Basin, China representing, to our knowledge, the first analysis of orbital cyclicity from a high-latitude, early Mesozoic continental sequence, and a step toward development of an empirical basis for evaluating numerical solutions of Solar System chaotic behavior.

Junggar Basin, Ürümqi, Western China

The thick, nonmarine, early Mesozoic sequence of the Junggar Basin of Western China (Fig. 1 and Figs. S1 and S2) comprises >11 km of largely nonmarine Late Paleozoic to Cenozoic strata deposited in the northwestern-most of the “walled basins” of China (7). It is a collisional successor basin, established during the Late Permian, 50–75 My after the cessation of subduction and complex amalgamation of microplates and ocean basins. Triassic and Early Jurassic age strata amount to 3,600 m in the interior, subsurface region of the basin (7) but outcrop extensively in several areas. One of the largest outcrops is the Haojiagou section located about 50 km southwest of Ürümqi City on the southern margin of the Junggar Basin of northern Xinjiang Uygur (Uighur) Autonomous Region, Northwestern China (Fig. 1 and Fig. S1) that forms the basis for this report. There, the 1,050 m of the nonmarine Haojiagou and coal-bearing Badaowan formations are continuously exposed and only slightly deformed (Fig. S2). The section has been studied in various aspects (e.g., see SI Text), but only one summary on the cyclostratigraphy has been published to date (8).

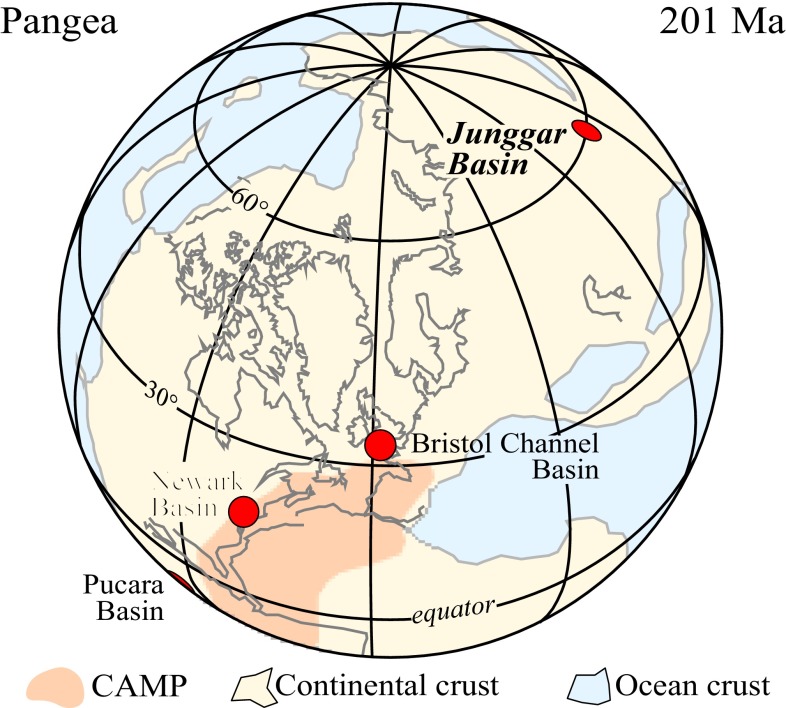
Fig. 1.

Position of the Triassic–Jurassic Junggar Basin at 201 Ma and other basins discussed in SI Text. CAMP is the Central Atlantic Magmatic Province (3).

The paleolatitude of the Junggar Basin for the Triassic–Jurassic is most parsimoniously placed at about 60° N (Fig. 1), constrained by paleomagnetic data (9) interpreted in light of the effects of compaction-induced inclination error (10) and plate-tectonic context (e.g., ref. 7; see SI Text). It is the highest latitude continental basin in which Triassic–Jurassic orbitally paced cyclicity has been quantitatively examined.

In contrast to the present, Late Triassic–Early Jurassic high-latitude regions had warm, humid climates according to the presence of broad-leaf gymnosperm macrofossil assemblages from both formations (SI Text) and the presence of coal, consistent with many early Mesozoic northern hemisphere high-latitude sedimentary basins (11).

The Haojiagou section exposes 350 m of Haojiagou Formation and 700 m of Badaowan Formation. The lower and upper members have a significant fluvial component with coal beds, and the middle member consists of largely lacustrine deposits with coal seams (8) (SI Text). The termination of the end-Triassic extinction (ETE) interval is placed at the last appearance datum of the sporomorph Lunatisporites rhaeticus in bed 52 and is used as a tie point to pin the latest Rhaetian end of the ETE within the studied successions (Fig. 2, Fig. S3, and SI Text). In eastern North America, the last appearance of this pollen taxon occurs in strata about 60 ky younger than the initiation of the initial ETE, constrained by both U-Pb dates and astrochronology (2, 12), and the Triassic–Jurassic boundary occurs about 40 ky after that based on extrapolation and correlation with United Kingdom sections (12).

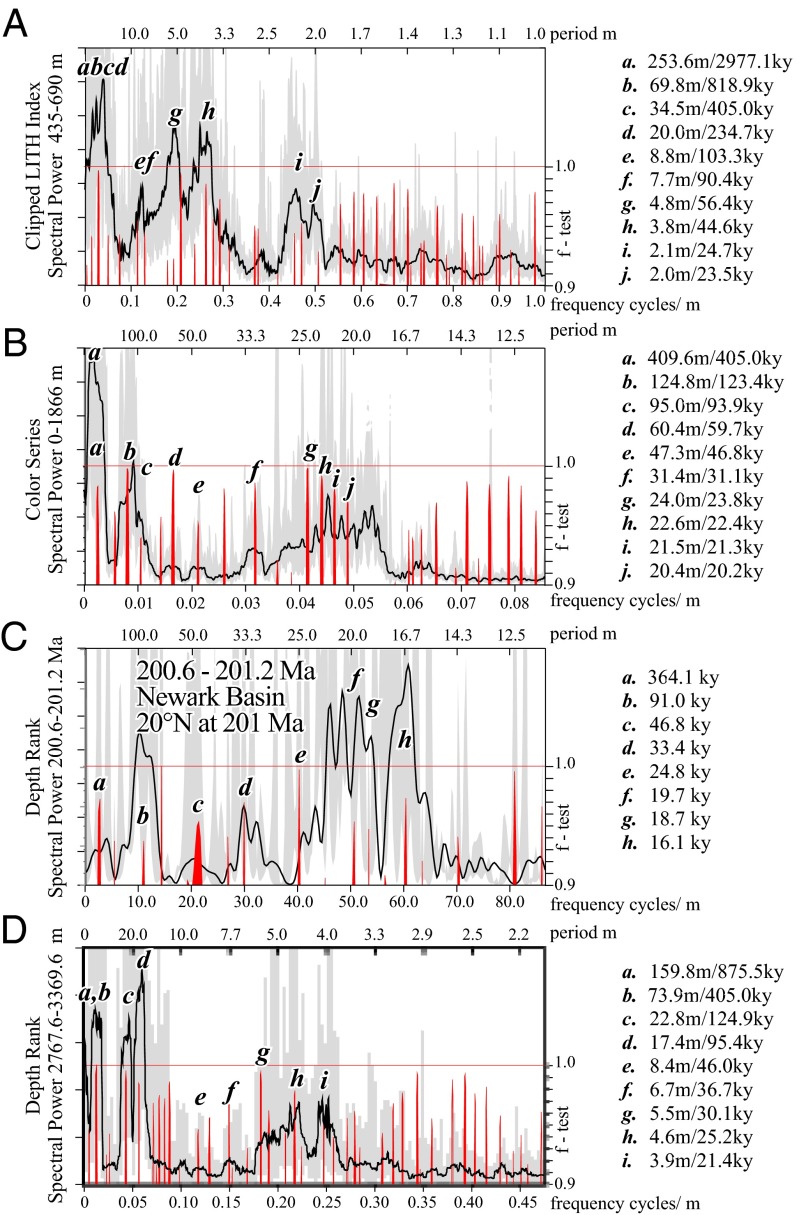
Fig. 2.

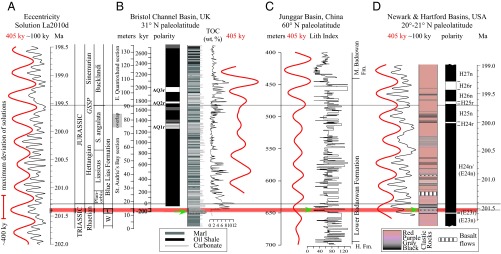
LITH Index data (C) and correlative sections: (A) Laskar 2010d solution (21); (B) Bristol Channel (United Kingdom); (C) Junggar Basin (China); (D) the Newark–Hartford astrochronology and geomagnetic polarity time scale (APTS). The thick red bar indicates the interval of extinctions and uncertainty of correlations between the sections, and the green arrows indicate the last appearance of L. rhaeticus (SI Text). A and B are adapted from refs. 19 and 31 (potential error added from ref. 21); D is modified from refs. 25 and 26. Note the difference in phase between the phasing eccentricity cycles in the La2010d solution (selected by ref. 31 for comparison with B) and the geological data that we attribute to chaotic drift; therefore, we have retained the independent times scales for both A and D.

LITH Index

Cyclicity is visually evident at multiple scales in the Haojiagou and Badaowan formations in outcrop as alternations of organic-rich mudstones with sandstone and conglomerate beds (Fig. S2). To quantify this cyclicity and examine its possible periodicity in thickness, we constructed a scale of lithologies based largely on grain size (Fig. 2, Figs. S3 and S4, and Table S1) termed the LITH index, which, in a broad way, can be interpreted as a proxy of the degree of flooding of the land surface during deposition. At low LITH values, coals and organic-rich black mudstones represent the most flooded environment (analogous to certain Neogene lake cycles) (e.g., ref. 13) and high LITH values, predominately conglomerates, the least flooded, with unimpeded fluvial systems flowing toward the basin depocenter. Many of the organic-poor, poorly bedded mudstones and sandstones with intermediate LITH values are pedogenically modified. The fluctuations in LITH index are thus a proxy for climatic variability in precipitation and evaporation, ultimately driven by insolation changes.

Carroll et al. (7) classify the lacustrine environment for both the Haojiagou and Badaowan formations as “overfilled” freshwater lakes, and the lake level variations are typical of “forced regressions” in a sequence stratigraphic framework (14). The upper Haojiagou Formation is characterized dominantly by largely lake margin and fluvial environments for the interbedded mudstone, sandstones, and coal. The muted lake level fluctuations of the Haojiagou Formation are followed by an increase in the magnitude of fluctuations in the Badaowan Formation, marked by an increase in coal thickness and sandstone abundance comprising braided fluvial systems feeding into the lake. This relationship suggests increased clastic input to the basin associated with an increase in humidity and intensification of the hydrological cycle into the earliest Jurassic, as inferred for other parts of the world for the Triassic–Jurassic transition (15). Overall the general facies interpretation of the Haojiagou and Badaowan formations is similar to the Triassic–Jurassic Kap Stewart Formation of Jamesonland, Greenland, the latter also interpreted in terms of lacustrine forced regressions compatible with a Milankovitch interpretation of the thickness periodicities (16).

Thickness Periodicities in the Junggar Basin

We chose four methods of examining the thickness periodicities of the Haojiagou and Badaowan formations (see Methods and SI Text): (i) multitaper method (MTM) spectral estimates that include an f-test for significance (Fig. 3 and Figs. S4 and S5); (ii) evolutive wavelet spectra (Fig. 4); (iii) simple periodograms [fast Fourier transforms (FFTs)] (Fig. S4); and (iv) Blackman–Tukey spectra with cross-spectral coherence (Fig. S5). The LITH index has significant variance symmetrical around the mean, and, because all three of these methods are insensitive to such variance, the LITH data were clipped at a value of 60, with the lower values being used for this analysis (the high values give the same results—see SI Text and Fig. S5). Because of the lack of temporal constraints on the middle and upper Badaowan Formation and its less obvious periodicities, we focused on the lower Badaowan and upper Haojiagou formations.

Fig. 3.

MTM spectra from high and low Triassic–Jurassic latitudes: (A) high-latitude Badaowan Formation, Junggar Basin, China; (B) contemporaneous low-latitude Portland Formation, Hartford Basin, eastern United States; (C) contemporaneous low-latitude Newark Basin Towaco and Boonton formations, eastern United States; and (D) equatorial Lockatong Formation, Newark Basin, eastern United States (modified from ref. 22), showing that the low-latitude low obliquity signal is not limited to the Triassic–Jurassic boundary interval. Spectra are lined up by time based on the 405-ky cycle. Highlighted spectral peaks are only those with both high amplitude and high f-test significance (>0.9) (red). The area between the upper and lower confidence limits is shaded gray. Note that, for A, B, and D, accumulation rate is based on setting a specific spectral peak to 405 ky whereas, in C, accumulation rate is derived from U-Pb dates and tuning to a 20-ky average climatic precession cycle (2). See SI Text for details.

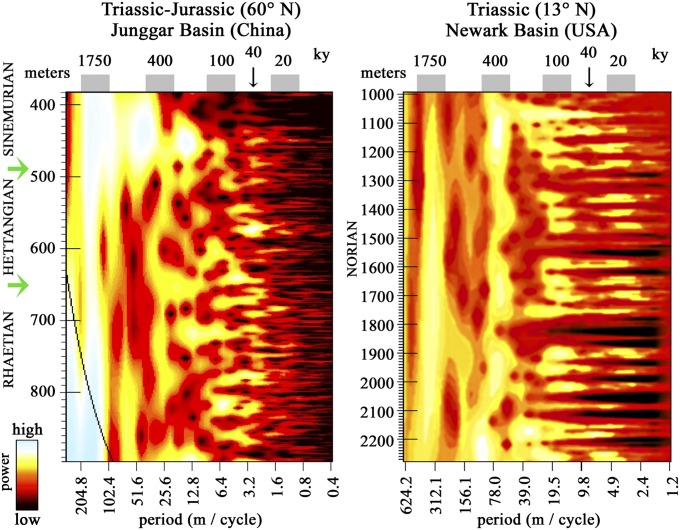
Fig. 4.

Untuned (depth) wavelet spectra of the LITH data of high-latitude Haojiagou and Badaowan formations of Rhaetian to Sinemurian age (Late Triassic–Early Jurassic, Junggar Basin) with strong power in the obliquity band (∼40 ky) and low power in the climatic precession (∼20 ky) band compared with the low-latitude Lockatong Formation of Norian (depth rank, Late Triassic, Newark Basin) (from ref. 28). Spectra are lined up along the frequency modulations (in thickness) of the 405-ky cycle. Similar continuous data for the Rhaetian–Sinemurian of eastern North America are not available. Lower and upper green arrows for the Junggar Basin indicate the end-Triassic extinction (201.6 Ma) and the Hettangian–Sinemurian boundary (199.7 Ma), respectively (Figs. S3 and S4).

Using these methods, a periodic signal was most clearly apparent between 450 m and 950 m in the upper Haojiagou and lower Badaowan formations, with a prominent continuously fluctuating thickness period of between 20 m and 40 m (Figs. 3 and 4 and Figs. S4 and S5). Periodicities were revealed in more detail by the FFT and MTM analyses (Fig. 4 and Figs. S4 and S5), with the strongest and most significant thickness periodicities at around 3–6 m and 20–40 m (Figs. 3 and 4 and Figs. S4 and S5) although other important periodicities are present and discussed below.

Eccentricity and Obliquity Cyclicity in the Junggar Basin

The biostratigraphic constraints (see SI Text and Fig. S3) on the Badaowan Formation suggest that the lower to middle Badaowan should span the entire Hettangian age and part of the Sinemurian. Because the duration of the Hettangian Age is about 2.0 ± 0.1 My (12, 17–19), the 300-m-thick lower to middle Badaowan should span ∼2–4 My. Given these constraints, the 20- to 40-m-thick cycle should have a period between 133 ky and 533 ky. Given that the highest amplitude astronomical cycle is the 405-ky eccentricity cycle, the 20- to 40-m-thick cycles of the Haojiagou and Badaowan formations are most simply interpreted as sedimentological expressions of that cycle. The 405 ky is the most stable of the orbital cycles over geological time and is the most appropriate term for the calibration of Mesozoic astrochronological age models (20, 21). Not only is it unimodal in value, it is the least effected by chaotic diffusion of the gravitation system of the Solar System (20, 21) and is a prominent feature of many deep-time sequences (21), particularly in the Triassic and Jurassic (22–26). Therefore, we calibrate the prominent 34.5 m and 37.2 m MTM periodicities of the Haojiagou and lower Badaowan formations, respectively, at 405 ky to obtain an age model for the LITH index. These thickness periodicities are near the middle of the 20- to 40-m range of the fluctuating band of high amplitude in the wavelet spectra (Fig. 4 and Fig. S4).

Assuming that we have correctly identified the 405-ky cycle in the LITH index depth series, the most prominent higher frequency cycles of the Haojiagou and lower Badaowan formations have spectral peaks with periods of between 30 ky and 60 ky, with the median periods most strongly at 42.5 and 44.6 ky. These periods are close to what would be expected for the obliquity periods, which for the Triassic–Jurassic should be 36.6 and 46.7 ky (6, 27, 28), assuming a constant rate of recession of the moon and constant dynamic ellipticity of the Earth, with the former period being of much higher magnitude. The shift to lower frequencies from the expected precession and obliquity periods is also observed in the precession band in the eastern North American Triassic Lockatong Formation where the shift has been interpreted as a consequence of accumulation rate variability (22, 24). The most dramatic expression of such a frequency-modulated shift would be occasional and perhaps periodically spaced hiatuses as might be present in the fluvial portions of the Junggar sequences. However, it is not impossible that the unexpectedly low frequencies could be real, caused by nonlinear changes through time in dynamic ellipticity that could produce occasional decreases in precession rate (20, 29). Nonetheless, because the independently U-Pb–calibrated (2) periods of Newark Basin latest Triassic–Early Jurassic precession-band cycles are compatible with an average period of about 20 ky, spectral distortion from frequency modulation is the simpler explanation for the apparent discrepancy. Relatively less important in the analysis are periods that could be assigned to climatic precession although significant periods are present in the MTM analyses. The weakness in amplitude at precessional periods could be a real feature of the climate system of the Mesozoic (see Mesozoic High- vs. Low-Latitude Cyclicity) or it could be due to accumulation rate noise at the precessional frequencies. Periods at about 100 ky, although present, are weak, consistent with the low power of the assumed precession periods, but, because we seem to be able to recognize the 405-ky cycle, some climatic precession signal is evidently present.

Based on our analysis of thickness periodicities, the sedimentary cycles attributed to climatic precession, obliquity, and eccentricity cycles correspond to the microcycles and different scales of mesoscale cycles of Hornung and Hinderer (14). These Junggar Basin strata are similar to what Olsen and Kent (30) termed Kap Stewart-type lacustrine sequences, named after the eponymous gray and black cyclical strata of Jamesonland East Greenland (16). We propose that the cycles in these sequences fit into a continuum of orbitally forced lacustrine sedimentary cycles extending from the tropics to the high latitudes, with the Haojiagou and Badaowan cycles in Kap Stewart-type lacustrine sequences representing the humid high latitude end member of the cyclicity (30). This type of lacustrine sequence and cycles may well extend to the paleo-north pole, for which there is obviously no sedimentary analog today.

Testing the Junggar Basin Age Model

Direct age calibration of the section by radiometric or paleomagnetic means does not yet exist for the Triassic–Jurassic of the Junggar Basin; however, the age model may be at least partially tested by its consistency with contemporaneous records from elsewhere, specifically the Newark–Hartford basins of eastern North America, the Bristol Channel Basin of the United Kingdom, and the Pucara Basin of Peru (Fig. 1, Fig. S3, and Table 1).

Table 1.

U-Pb and astrochronological ages compared

Boundary or unit	Newark igneous*	Newark–Hartford*	Pucara Basin	Bristol Channel† Pucara‡/Newark§
Hettangian–Sinemurian boundary	—	199.70 ± 0.02	199.46 ± 0.17	199.61/199.66
Hook Mountain Basalt	200.916 ± 0.064	200.93 ± 0.02	—	—
Preakness Basalt	201.274 ± 0.032	201.28 ± 0.02	—	—
Rhaetian–Hettangian boundary	—	201.42 ± 0.022	201.36 ± 0.14‡	201.32/201.37
Orange Mountain Basalt	201.520 ± 0.034	201.52 ± 0.02	—	—
End-Triassic extinction	201.564 ± 0.015	201.56 ± 0.02	201.51 ± 0.15	201.51/201.56

^*See ref. 2 for ages. Details in Table S2.

^†See refs. 19 and 31 for ages. Details in Table S2.

^‡See refs. 12 and 17 for ages. Details in Table S2.

^§See ref. 15 for ages. Details in Table S2.

To compare the obliquity-dominated successions of the Junggar Basin with the precession-dominated eastern North American lacustrine sequences and the contemporaneous marine section at St. Audrie’s Bay in the United Kingdom (Bristol Channel Basin), we compared the filtered 405-ky cycle from the three sections (SI Text) and correlated them using the last appearance of Lunatisporites rhaeticus (green arrows in Fig. 2). Using the latter datum results in the encouraging observation that the 405-ky cycles are in phase and that the interval of low variance interpreted as a minimum in the long eccentricity g4 − g3 cycle (2, 19, 31) occurs in same relative position (Fig. 2).

The Newark–Hartford astronomical calibration was independently corroborated using U-Pb dates from interbedded lavas (2) and could be confidently and tightly correlated to marine sections. Tying the Newark–Hartford and Bristol Channel Basin astrochronologies at the biostratigraphic ETE with a U-Pb–determined age of its base at 201.564 ± 0.015 Ma (2) (from the Newark–Hartford section) provided near perfect agreement between the magnetostratigraphy of the two areas, as well as with the astrochronological ages of the Hettangian–Sinemurian boundary, the formal definition of which (GSSP, global boundary stratotype section and point) is within the Bristol Channel sequence (31) (Table 1). The Pucara Basin section contains multiple dated ashes (ref. 17 and references therein, allowing further testing of the astrochronologies, with the marine ammonite-based ETE and Hettangian–Sinemurian boundary in complete agreement (within tight error) with the Newark–Hartford and Bristol Channel astrochronologies (Fig. 2 and Table 1). This framework of multiple independent constraints strongly supports the Junggar Basin astrochronology.

Mesozoic High- vs. Low-Latitude Cyclicity

The Haojiagou and Badaowan formations are, to our knowledge, the first high-latitude early Mesozoic continental sequences for which astronomical forcing has been quantitatively explored, and, unlike contemporaneous lower-latitude analyses, obliquity-paced cyclicity is a dominant high-frequency component of the variability. A comparison of MTM spectra and wavelet spectra from the high-latitude Badaowan Formation and the lower latitude continental sequences in eastern North America shows this difference dramatically (Fig. 4). The lower latitude records for both Triassic and Jurassic have little obliquity signal and are strongly dominated by climatic precession corroborated by the independent U-Pb and magnetostratigraphic tests (2, 31) (Fig. 2 and Table 1).

Obliquity-related insolation variation is greatest at high latitudes, but dominance of obliquity in climate is not necessarily expected as a consequence. In theory, interannual insolation forcing at a given calendar day or yearly average is dominated by precessional cycles at all latitudes, even at the poles where the obliquity effect on insolation variation is the greatest (32). However, obliquity dominance in high-latitude climate is by no means without precedent, the most spectacular example of which is the dominance of 41-ky glacial cycles of all but the last 0.8 million y (3.0–0.8 Ma) of the Neogene (33) and is also an important component of variability in the high-latitude (∼52–55° N) Lake Baikal sedimentary record (34) situated at a similar latitude to the Junggar Basin deposits.

Differences between the Late Neogene world and that of the Triassic–Jurassic are vast, including but not limited to continental configuration with Pangea straddling the equator, a lack of polar glaciers (35), and very high CO₂ (approximate background at between 1,000 and 2,000 ppm and maxima of >6,000 ppm) (36)—a world without modern analog. Therefore, explanations of obliquity dominance due to fluctuations of high-latitude glaciers are difficult to support for the early Mesozoic. However, some aspects of these explanations might still be pertinent to the Haojiagou and Badaowan formations. In particular, integrated summer insolation is directly controlled by obliquity and has been proposed as a cause of the late Neogene obliquity dominance in glacial fluctuations (32), and it is possible that the highly vegetated Triassic–Jurassic high latitudes were similarly sensitive to the length of the growing season and associated timing and magnitude of precipitation and evaporation.

Implications for Chaotic Evolution of the Solar System and Astronomical Solutions

Since Poincaré’s (37) contribution to dynamical systems, it has been recognized that the Solar System has chaotic properties. Chaos significantly limits the accuracy of numerical solutions of planetary behavior, including the frequency and phases of climatically important orbital cycles (4–6), and impedes understanding of the general problem of the stability of the Solar System (5, 13). At time scales of hundreds of millions of years, chaotic diffusion of the gravitational system of the Solar System results in an inability to recognize accurate solutions of planetary orbital and axial behavior (4).

Integral to the long-term chaotic behavior of the Solar System are the secular resonances of the planets, particularly for the inner Solar System. Particularly important are those of Earth and Mars (4), affecting modulations of eccentricity and obliquity with present periods of 2.4 and 1.2 My (g4 − g3 and s4 − s3, respectively, where g4 and g3 are related to the precession of the orbital perihelia of Mars and Earth and s4 and s3 are related to orbital inclination). However, due to chaotic diffusion of the gravitational system, these periods are expected to change through time. Presently, there is a two-to-one ratio of the eccentricity modulator (2.4 My) to the obliquity modulator (1.2 My), reflecting the secular resonant argument 2(s4 − s3) − (g4 − g3) = 0, which is currently in libration. However, there are expected to be important transitions in the chaotic behavior of the gravitational system from libration to circulation so that the eccentricity and obliquity modulators are equal (s4 − s3) − (g4 − g3) = 0 (38). Because both the period and state of these modulating cycles have varied in an unknown way in deep time, strict interpretation of insolation curves are unreliable beyond about 50 Ma (20, 21). This uncertainty is most obviously reflected in the eccentricity and obliquity modulating cycles with periods longer than 405 ky and the long-term phase relationships of all of the cycles. Without geological data with a long obliquity record, it is not possible to determine when these transitions in the Earth–Mars resonances occur or even if they occur, or what the periods of the long eccentricity or inclination cycles should be.

In addition to being a celestial mechanical problem, chaotic drift in the gravitational solutions also poses fundamental Earth science problems because it limits tuning of geological records to insolation curves and our ability to use astrochronologies to assess and improve the accuracy of important isotopic dating systems (e.g., ref. 39). Empirical, deep-time geological data have the potential to allow us to determine which solutions best fit the actual history of the Solar System.

To quantify the actual behavior of the celestial mechanical gravitational system, precession-related (eccentricity) and obliquity-related cycles need to be isolated in geological records. Continental records, which tend to be tightly coupled to local forcing, provide a possible mechanism to isolate precession-related eccentricity cycles, dominant at low latitudes, from the obliquity-related cyclicity important at higher latitudes.

Previous quantitative investigations of long Late Triassic–Early Jurassic records have been limited to the lower latitudes, largely the tropics and subtropics in eastern North America (2, 22, 24, 25) and the United Kingdom (e.g., refs. 19 and 40). In these areas (20°–30° N) (10), the effects of obliquity on local climate forcing would be expected to be small compared with the higher latitudes, as predicted by basic astronomical theory, although precessional effects should always be greatest in insolation at all latitudes, and that is what is observed for the Triassic–Jurassic in the records described thus far. In the case of the tropical records in eastern North America, obliquity was barely detected (22, 24), but a strong 1.6- to 1.8-My cycle in eccentricity (g4 − g3) is present, differing from the present 2.4 My presumably because of chaotic diffusion (6, 24). More or less the same value of the g4 − g3 cycle, in the same phase, is present in the contemporaneous tropical pelagic cherts from the Panthalassic Ocean at Inuyama, Japan (41).

Until now, there have been no long Triassic–Jurassic, high-latitude records that have been quantitatively analyzed, and therefore we have had little knowledge of what the quantitative obliquity behavior was, especially with regard to their modulating cycles. Importantly, there is a strong suggestion of modulation of the obliquity by an ∼819-ky (∼70-m) cycle in the upper Haojiagou and lower Badaowan, visible in the wavelet spectrum (Fig. 3 and Fig. S4) where it is evident as a modulation in the strength of obliquity cycle (Fig. S4), both as filtered and demodulated data (Figs. S5–S7), and also as period in its own right (Fig. S4). This period is missing or extremely weak in the tropical continental records (22, 24). Together, the data from the Junggar Basin, Newark–Hartford basins, and St. Audrie’s Bay section suggest the present-day two-to-one ratio (Early Jurassic, ∼1.6–0.8 My) of orbital eccentricity to inclination for the state of the Earth–Mars resonance, but with different periods and phases not seen in existing orbital solutions (21) (Fig. 2).

Conclusions

Analysis of the LITH proxy of environmental change shows that an astronomical signal in which obliquity is dominant can be extracted from lacustrine strata of the high-latitude (∼60° N) Junggar Basin straddling the end-Triassic extinction and Triassic–Jurassic boundary. Constrained by fixing the accumulation rate to the 405-ky eccentricity cycle, data show that the main periods of obliquity for the Late Triassic–Early Jurassic are present and were dominant components of high-latitude Early Mesozoic climate, dramatically different from the climatic precession-dominated continental tropics. In combination, the data are incompatible with published astronomical solutions for the Triassic–Jurassic in phase and amplitude, consistent with chaotic behavior of the Solar System whereas, at the same time, the Earth–Mars orbital resonance seems to have been in today’s two-to-one ratio of eccentricity to inclination, providing a constraint for the Earth–Mars secular resonance for around 201 Ma. With the prospect of the acquisition of better temporally resolved records from deeper lake settings in the Junggar and other basins, the use of more directly climate-sensitive proxies, and additional exploration of the paleobiological context of the strata, it will be possible to test these findings, constraining the history of Solar System chaos, during this transitional time in Earth history.

Methods

LITH index data were recorded during the 1996, 1998, and 2008 field seasons using standard descriptive field methods. Standard preparation procedures were used to prepare the palynological slides, archived at the Department of Geology, Lund University, Sweden. The evolutive FFT and MTM spectra were developed using Analyseries (2.0) (42), and the evolutive wavelet spectra were computed using the Matlab script of Torrence and Compo (43). See SI Text for additional methodological details.