Exponential synchronization of discontinuous neural networks with time-varying mixed delays via state feedback and impulsive control

Abstract

This paper investigates drive-response synchronization for a class of neural networks with time-varying discrete and distributed delays (mixed delays) as well as discontinuous activations. Strict mathematical proof shows the global existence of Filippov solutions to neural networks with discontinuous activation functions and the mixed delays. State feedback controller and impulsive controller are designed respectively to guarantee global exponential synchronization of the neural networks. By using Lyapunov function and new analysis techniques, several new synchronization criteria are obtained. Moreover, lower bound on the convergence rate is explicitly estimated when state feedback controller is utilized. Results of this paper are new and some existing ones are extended and improved. Finally, numerical simulations are given to verify the effectiveness of the theoretical results.

Introduction

Although neural networks with piecewise-linear neuron activation or continuously differentiable strictly increasing sigmoid activation have important applications in signal and image processing (Di Marco et al. 2010, 2005; Kamel and Xia 2009; Cao and Wan 2014; Zhang et al. 2014), it is reported that neural networks with discontinuous (or non-Lipschitz) neuron activations are an ideal model for neuron amplifiers with very high gain (Forti et al. 2005). For example, the sigmoidal neuron activations of the classical Hopfield network with high-gain amplifiers would approach a discontinuous hard-comparator function (Li et al. 1989). The high-gain hypothesis is crucial to make negligible the contribution to the network energy function of the term depending on the neuron self-inhibitions, and to favor binary output formation (Li et al. 1989; Forti and Nistri 2003). When dealing with neural networks possessing high-slope nonlinear activations it is often advantageous to model them with a system of differential equations with discontinuous neuron activations, rather than studying the case where the slope is high but of finite value. So far many results have been published on the convergence of periodic (almost) periodic solutions or equilibrium point of neural networks with discontinuous activations (Forti et al. 2005, 2006; Liu et al. 2011, 2012, 2014; Lu and Chen 2008, 2006; Wang et al. 2009; Cai and Huang 2011; Haddad 1981) since the global convergence criteria of this class of neural networks was firstly researched in Forti and Nistri (2003), nevertheless, synchronization result on this class of neural networks is seldom.

Since the pioneering work of Pecora and Carrol (1990), much attention have been attracted to synchronization due to its wide applications in engineering such as secure communication, biological systems, information processing (Yan and Wang 2014; Yang et al. 2011b, 2014; Liao and Huang 1999; Cao et al. 2013; Li et al. 2013; Rigatos 2014; Xu 2014. In Pecora and Carroll (1990), complete synchronization (synchronization for brief) was proposed, the mechanism of which is this: a chaotic system, called the driver (or master), generates a signal sent over a channel to a responder (or slave) which is identical with the driver, then the responder uses this signal to control itself so that it oscillates in a synchronized manner with the driver. By far many effective control methods have been proposed to realize synchronization, such as state feedback control, intermittent control, impulsive control, etc. Recently, by using the state feedback control technique, several quasi-synchronization criteria were obtained in Liu et al. (2011) for neural networks with discontinuous activations and parameters mismatches. Results in Liu et al. (2011) show that, under the linear state feedback controller as usual, complete synchronization cannot be realized even without parameter mismatches between the drive and response systems due to the discontinuity of activation function. Afterwards, by using a class of discontinuous state feedback control, authors in Yang and Cao (2013) considered exponential synchronization of neural networks with time-varying delays and discontinuous activations. However, authors of Yang and Cao (2013) did not consider distributed delay.

As a matter of fact, a realistic neural network should involve both discrete and distributed delays (Liao and Lu 2011). It is well known that discrete time-delays are introduced in neural networks due to the finite speed of switching of the amplifiers and transmissions of signal in the network, while distributed delays correspond to the presence of an amount of parallel pathways with a variety of axon sizes and lengths. The distributed delay is usually bounded since the signal propagation is distributed during a certain time period. The application of distributed delay can be found in Tank and Hopfield (1987), where a neural circuit with bounded distributed delays has been designed to solve a general problem of recognizing patterns in a time-dependent signal. Although there were many results on synchronization of continuous neural networks with discrete and distributed delays (mixed delays) (Cao et al. 2007; Yang et al. 2013; Wang et al. 2010; Yang et al. 2011a), as far as we know, result on synchronization of neural networks with discontinuous activations and mixed delays is few.

On the other hand, impulsive control technique has got the favor of many researchers because it needs small control gains and acts only at discrete time instants. These special characters of impulsive control can reduce control cost drastically (Yang et al. 2011b). However, result on synchronization of neural networks with discontinuous activations under impulsive control has not yet been reported in the literature.

Motivated by the above analysis, this paper aims to investigate global exponential synchronization of neural networks with discontinuous activation functions and time-varying mixed delays via two kinds of control technique: state feedback control and impulsive control. The bounded distributed delay is related to delay kernel, which makes the considered model more general. Unlike Lu and Chen (2008), Liu et al. (2012), Lu and Chen (2006), and Haddad (1981), in which constructing method was utilized to get approximate Filippov solutions of neural networks with discontinuous activations and mixed delays, we show the global existence of Filippov solutions through strict mathematical proof. Then, by using the sign function, novel state feedback controller and impulsive controller are designed to guarantee the synchronization goal. Moreover, the lower bound on the convergence rate is explicitly estimated when state feedback controller is utilized. Numerical simulations show the effectiveness of the theoretical results.

Notations

In the sequel, if not explicitly stated, matrices are assumed to have compatible dimensions. ${\mathbb{N}}_{+}$ is the set of positive integers, $I_m$ denotes the identity matrix of $m$-dimension. $\mathbb{R}$ is the space of real number. The Euclidean norm in ${\mathbb{R}}^m$ is denoted as $\Vert ·\Vert$, accordingly, for vector $x\in {\mathbb{R}}^m$, $\Vert x\Vert =\sqrt{x^{T}x}$, where $T$ denotes transposition. $x=0$ represents each component of $x$ is zero. $A={(a_{ij})}_{m\times m}$ denotes a matrix of $m$-dimension, $\Vert A\Vert =\sqrt{{\mathit{\lambda }}_{\max }(A^{T}A)}$. $\overline{co}[E]$ stands for the closure of the convex hull of the set $E$.

The rest of this paper is organized as follows. In section “Model description and some preliminaries”, model of discontinuous neural networks with mixed delays is described. Some necessary assumptions, definitions and lemmas are also given in this section. Exponential synchronization of the considered model under state feedback control and impulsive control are studied in sections “Synchronization under state feedback control” and “Synchronization under impulsive control”, respectively. In section “Examples and simulations”, two examples with their numerical simulations verify the effectiveness of our results. conclusions and future research interest are given in section “Conclusion”. At last, acknowledgments are presented.

Model description and some preliminaries

In this paper, we consider the neural network with time-varying discrete and distributed delays which is described as follows:

$$\begin{array}{cc}\hfill \dot{x}(t)& =-Cx(t)+Af(x(t))+Bf(x(t-\mathit{\tau }(t)))\hfill \\ \hfill & +D{\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)f(x(s))\mathrm{d}s+I,\hfill \end{array}$$ 1

where $x(t)=(x_1(t),x_2(t),\dots ,x_n(t))\in {\mathbb{R}}^n$ is the state vector; $C=\mathrm{diag}(c_1,c_2,\dots ,c_n)$, in which $c_i>0,i=1,2,\dots ,n$, are the neuron self-inhibitions; $A={(a_{ij})}_{n\times n}$, $B={(b_{ij})}_{n\times n}$ and $D={(d_{ij})}_{n\times n}$ are the connection weight matrices; the activation function $f(x(t))={(f_1(x_1(t)),f_2(x_2(t)),\dots ,f_n(x_n(t)))}^T$ represents the output of the network; $I=(I_1,I_2,\dots ,I_n)$ is the external input vector; the bounded functions $\mathit{\tau }(t)>0$ and $\mathit{\theta }(t)>0$ (They can be different) represent unknown time-varying discrete and distributed delays, respectively; $K(u)$ is a non-negative bounded scalar function for $u\ge 0$ describing the delay kernel.

The trajectory of the solution $x(t)$ of neural network (1) can be any desired state: equilibrium point, a nontrivial periodic or almost periodic orbit, or even a chaotic orbit. In this paper, we suppose that the activation function $f(x(t))$ is not continuous on ${\mathbb{R}}^n$. Hence, the system (1) becomes a differential equation with discontinuous right-hand side. In this case, the uniqueness of the solution of (1) might be lost, and at the worst case, one can not define a solution in the conventional sense.

In order to study the dynamics of a system of differential equation with discontinuous right-hand side, we first transform it into a differential inclusion (Filippov 1960) by using Filippov regularization, then by the measurable selection theorem in Aubin and Cellina 1984 we reach an uncertain differential equation. Thus, studying the dynamics of the system of differential equation with discontinuous right-hand side has at last been transformed into considering the same problem of the uncertain differential equation. The Filippov regularization is defined as follows.

Definition 1

Filippov (1960) (Filippov regularization). The Filippov set-valued map of $f(x)$ at $x\in {\mathbb{R}}^n$ is defined as follows:

$$\begin{array}{c}\hfill F(x)=\bigcap _{\mathit{\delta }>0}\bigcap _{\mathit{\mu }(\mathrm{\Omega })=0}\overline{co}[f(B(x,\mathit{\delta })\backslash \mathrm{\Omega })],\end{array}$$

where $B(x,\mathit{\delta })=\{y:\Vert y-x\Vert \le \mathit{\delta }\}$, and $\mathit{\mu }(\mathrm{\Omega })$ is the Lebesgue measure of set $\mathrm{\Omega }$.

By Definition 1, the Filippov set-valued map gives the convex hull of $f(·)$ at the discontinuity points (ignoring sets of measure zero) when applied to the discontinuity points, but is otherwise the same as $f(·)$ at continuous points.

For example, consider the following initial value problem (IVP):

$$\begin{array}{c}\hfill \dot{x}(t)=f(x(t)),x(0)=x_0,t\in [0,T],\end{array}$$ 2

where

$$\begin{array}{c}\hfill f(x)=\left\{\begin{array}{c}x,x<1,\hfill \\ x+1,x>1.\hfill \end{array}\right.\end{array}$$ 3

According to Definition 1, the differential inclusion of the system (2) is as follows:

$$\begin{array}{c}\hfill \dot{x}(t)\in F(x)=\left\{\begin{array}{cc}& x,x<1,\hfill \\ \hfill & [1,2],x=1,\hfill \\ \hfill & x+1,x>1.\hfill \end{array}\right.\end{array}$$ 4

Function $f(x)$ in (3) and its convex hull $F(x)$ are shown in Fig. 1. Note that convex hull $F(x)$ is not related to the values of $f(x)$ at the discontinuous points.

Fig. 1.

Function $f(x)$ in (3) (left) and convex hull $F(x)$ for the $f(x)$ (right)

A vector-value function $x(t)$ defined on the interval $[0,T]$ is called a Filippov solution of (2) if it is absolutely continuous on $[0,T]$ and satisfies the differential inclusion $\dot{x}(t)\in F(x(t))$ for $t\in [0,T]$. By the measurable selection theorem in Aubin and Cellina (1984), we can find a measurable function $\mathit{\gamma }:[0,T]\to {\mathbb{R}}^n$ such that $\mathit{\gamma }(t)\in F(x(t))$ for almost all (a.a.) $t\in [0,T]$ and $\dot{x}(t)=\mathit{\gamma }(t)$ for a.a. $t\in [0,T]$.

The following properties hold Forti and Nistri (2003): $\overline{co}[\mathit{\alpha }E]=\mathit{\alpha }\overline{co}[E]$ for any $\mathit{\alpha }\in \mathbb{R}$ and $E\subset {\mathbb{R}}^n$; $\overline{co}[E_1+E_2]=\overline{co}[E_1]+\overline{co}[E_2]$ for any $E_1,E_2\subset {\mathbb{R}}^n$. A set-valued map $F$ with nonempty values is said to be upper semicontinuous at $x_0\in E$ if, for any open set $\mathcal{N}$ containing $F(x_0)$, there exists a neighborhood $\mathcal{M}$ of $x_0$ such that $F(\mathcal{M})\subset \mathcal{N}$. If $E$ is closed, $F$ has nonempty closed values, and $F$ is bounded in a neighborhood of each point $x\in E$, then $F$ is upper semicontinuous on $E$ if and only if its graph $\{(x,y)\in E\times {\mathbb{R}}^n:y\in F(x)\}$ is closed (Forti and Nistri 2003).

From the above discussion, we give the following definition, which specifies what a Filippov solution of the system (1) is.

Definition 2

Cai and Huang (2011). A function $x:[-\mathit{\vartheta },T]\to {\mathbb{R}}^n$, $T\in (0,+\infty ]$, is a solution (in the sense of Filippov) of the discontinuous system (1) on $[-\mathit{\vartheta },T]$ if:

• (i)$x$ is continuous on $[-\mathit{\vartheta },T]$ and absolutely continuous on $[0,T]$;
• (ii)
  $x(t)$ satisfies

  $$\begin{array}{cc}\hfill \dot{x}(t)& \in -Cx(t)+AF(x(t)+BF(x(t-\mathit{\tau }(t)))\hfill \\ \hfill & +D{\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)F(x(s))\mathrm{d}s\hfill \\ \hfill & +I,t\in [0,T].\hfill \end{array}$$ 5

or equivalently, by the measurable selection theorem in Aubin and Cellina (1984),

• (ii’)
  There exists a measurable function $\mathit{\gamma }(t)=({\mathit{\gamma }}_1,{\mathit{\gamma }}_2,\dots ,$${{\mathit{\gamma }}_n)}^T:[-\mathit{\vartheta },T]\to {\mathbb{R}}^n$, such that $\mathit{\gamma }(t)\in F(x(t))$ for a.a. $t\in [-\mathit{\vartheta },T]$ and

  $$\begin{array}{cc}\hfill \dot{x}(t)=& -Cx(t)+A\mathit{\gamma }(t)+B\mathit{\gamma }(t-\mathit{\tau }(t))\hfill \\ \hfill & +D{\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)\mathit{\gamma }(s)\mathrm{d}s+I,\hfill \\ \hfill & \mathrm{for}\mathrm{a}.\mathrm{a}.t\in [0,T].\hfill \end{array}$$ 6

The next definition is the initial value problem (IVP) associated to system (1).

Definition 3

(IVP) Forti et al. (2005). For any continuous function $\mathit{\varphi }:[-\mathit{\vartheta },0]\to {\mathbb{R}}^n$ and measurable selection $\mathit{\psi }:[-\mathit{\vartheta },0]\to {\mathbb{R}}^n$ such that $\mathit{\psi }(s)\in F(\mathit{\varphi }(s))$ for a.a. $s\in [-\mathit{\vartheta },0]$ by an initial value problem associated to (6) with initial condition $(\mathit{\varphi },\mathit{\psi })$, we mean the following problem: find a couple of functions $[x(t),\mathit{\gamma }(t)]:[-\mathit{\vartheta },T]\to {\mathbb{R}}^n\times {\mathbb{R}}^n$, such that $x(t)$ is a solution of (6) on $[-\mathit{\vartheta },T]$ for some $T>0$, $\mathit{\gamma }(t)$ is an output associated to $x(t)$, and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{x}(t)=-Cx(t)+A\mathit{\gamma }(t)+B\mathit{\gamma }(t-\mathit{\tau }(t))\hfill \\ +D{\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)\mathit{\gamma }(s)\mathrm{d}s+I,\hfill \\ \mathrm{for}\mathrm{a}.\mathrm{a}.t\in [0,T],\hfill \\ \mathit{\gamma }(t)\in F(x(t)),\mathrm{for}\mathrm{a}.\mathrm{a}.t\in [0,T],\hfill \\ x(s)=\mathit{\varphi }(s),\forall s\in [-\mathit{\vartheta },0],\hfill \\ \mathit{\gamma }(s)=\mathit{\psi }(s),\mathrm{for}\mathrm{a}.\mathrm{a}.s\in [-\mathit{\vartheta },0].\hfill \end{array}\right.\end{array}$$ 7

Throughout this paper, we assume that

(${\mathrm{H}}_1$)

For every $i=1,2,\dots ,n$, $f_i:\mathbb{R}\to \mathbb{R}$ is continuous except on a countable set of isolate points $\{{\mathit{\rho }}_k^i\}$, where there exist finite right and left limits $f_i^{+}({\mathit{\rho }}_k^i)$ and $f_i^{-}({\mathit{\rho }}_k^i)$, respectively. Moreover, $f_i$ has at most a finite number of jump discontinuities in every compact interval of $\mathbb{R}$;

(${\mathrm{H}}_2$)

There exist nonnegative constants $\tilde{L}$ and $\tilde{P}$ such that

$$\begin{array}{c}\hfill \Vert \mathit{\xi }\Vert \le \tilde{L}\Vert u\Vert +\tilde{P},\end{array}$$ 8

$\forall u\in {\mathbb{R}}^n$, where $\mathit{\xi }\in F(u)$, $F(u)=(F_1(u_1),F_2(u_2),$$\dots ,F_n{(u_n))}^T$, $F_i(u_i)=[min\{f_i^{-}(u_i),f_i^{+}(u_i)\},$$max\{f_i^{-}(u_i),f_i^{+}(u_i)\}]$ for $i=1,2,\dots ,n$;

(${\mathrm{H}}_3$)

There exist nonnegative constants $L$ and $P$ such that

$$\begin{array}{c}\hfill \Vert \mathit{\xi }-\mathit{\eta }\Vert \le L\Vert u-v\Vert +P\end{array}$$ 9

$\forall u,v\in {\mathbb{R}}^n$, where $\mathit{\xi }\in F(u)$, $\mathit{\eta }\in F(v)$;

(${\mathrm{H}}_4$)

There exists constant $h$ and positive constants $\mathit{\tau }$ and $\mathit{\theta }$ such that $0<\mathit{\tau }(t)\le \mathit{\tau }$, $0\le \mathit{\theta }(t)\le \mathit{\theta }$, and $\dot{\mathit{\tau }}(t)\le h<1$. Let $\mathit{\vartheta }=max\{\mathit{\tau },\mathit{\theta }\}$.

(${\mathrm{H}}_5$)

There are positive function $q(t)$ and positive constant $q$ such that $q(t)\le q$ and ${\int }_0^{\mathit{\theta }(t)}K(s)\mathrm{d}s=q(t)\le q$.

Remark 1

If there exists even one discontinuous point defined in (${\mathrm{H}}_1$), the constant $P$ in (9) is positive. When the function $f_i(u_i)$ is continuous on $\mathbb{R}$, then $P=0$. Hence, the above assumptions include continuous activation function $f_i(u_i)$ as a special case. This implies that results of this paper are also applicable to corresponding models with continuous function.

Remark 2

Generally, it is difficult to determine the exact value of $\mathit{\gamma }(t)$ at the discontinuous points of $f(x(t))$. What we only know is that $\mathit{\gamma }(t)\in F(x(t))$ is a bounded measurable function from the condition (${\mathrm{H}}_1$). In order to realize complete synchronization of neural networks with discontinuous activations, the effects of the uncertainties of the measurable function must be surmounted. Obviously, the paper Liu et al. (2011) did not solve this problem.

In the literature, there were many results on the existence of solutions of differential inclusions with and without delays (Benchohra and Ntouyas 2000; Balasubramaniam et al. 2005). The main tool for proving the existence of solutions of differential inclusions is a fixed point theorem for condensing map due to Martelli (1975). Inspired by Benchohra and Ntouyas (2000) and Balasubramaniam et al. (2005), we shall prove that, under the above conditions, the neural network (1) exists solutions globally in the sense of Filippov. Before starting our proof, we first introduce the fixed point theorem for condensing map developed in Martelli (1975).

Lemma 1

Martelli (1975). Let $X$ be a Banach space and $G:X\to BCC(X)$ a condensing map. If the set $\mathrm{\Gamma }=\{x\in X:\mathit{\lambda }x\in \mathit{\lambda }G(x),\mathit{\lambda }>1\}$ is bounded, then $G$ has a fixed point, where $BCC(X)$ denotes the set of all nonempty bounded closed and convex subsets of $X$.

By using Lemma 1, we get the following Lemma 2. The analysis techniques is similar to those used in Benchohra and Ntouyas (2000), Balasubramaniam et al. (2005). In order to deal with the distributed delay, the method of exchanging integral order is utilized in (14).

Lemma 2

Suppose that $({\mathrm{H}}_1$– ${\mathrm{H}}_5)$ are satisfied. Then, there exists at least one solution $x(t)$ of discontinuous neural network (1) on $[0,+\infty )$ in the sense of Eq. (7).

Proof

Transform the problem in (7) into a fixed point problem. Consider the multi-valved map $G:C([-\mathit{\vartheta },T],{\mathbb{R}}^n)\to C([-\mathit{\vartheta },T],{\mathbb{R}}^n)$ defined by

$$\begin{array}{c}\hfill G(x)(t)=\left\{\begin{array}{c}x(0)e^{-Ct}+{\int }_0^t{e}^{-C(t-s)}\{AF(x(s))\hfill \\ +BF(x(s-\mathit{\tau }(s)))\hfill \\ +D{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)F(x(u))\mathrm{d}u\hfill \\ +I\}\mathrm{d}s\mathrm{for}t\in [0,T],\hfill \\ \mathit{\varphi }(s),\forall s\in [-\mathit{\vartheta },0],\hfill \end{array}\right.\end{array}$$ 10

where $C([-\mathit{\vartheta },T],{\mathbb{R}}^n)$ is the Banach space of continuous functions from $[-\mathit{\vartheta },T]$ into ${\mathbb{R}}^n$ normed by ${\Vert \mathit{\xi }\Vert }_{\infty }=sup\{\Vert \mathit{\xi }(t)\Vert ,t\in [-\mathit{\vartheta },T]\}$.

It is clear that the fixed points of $G$ are solutions to the IVP of (7).

It should be remarked that a completely continuous multi-valued map is the easiest example of a condensing map. By the similar process of the steps 1–4 in the proof of theorem 3.2 in Balasubramaniam et al. (2005) and the steps 1–4 in the proof of theorem 3.1 in Benchohra and Ntouyas (2000), it is easy to get that, under the assumptions $({\mathrm{H}}_1$–${\mathrm{H}}_5)$, $G$ is a completely continuous multi-valued map, upper semi-continuous with convex closed values.

Now we prove that the set $\mathrm{\Gamma }=\{x\in C([-\mathit{\vartheta },T],{\mathbb{R}}^n):\mathit{\lambda }x\in G(x),\mathit{\lambda }>1\}$ is bounded.

Let $x\in \mathrm{\Gamma }$, then $\mathit{\lambda }x\in G(x)$ for some $\mathit{\lambda }>1$. Thus there exists $\mathit{\gamma }(t)\in F(x(t))$ such that

$$\begin{array}{cc}\hfill x(t)& ={\mathit{\lambda }}^{-1}\{x(0)e^{-Ct}+{\int }_0^t{e}^{-C(t-s)}\{A\mathit{\gamma }(s)\hfill \\ \hfill & +B\mathit{\gamma }(s-\mathit{\tau }(s))\hfill \\ \hfill & +D{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)\mathit{\gamma }(u)\mathrm{d}u+I\}\mathrm{d}s\}\hfill \\ \hfill & \mathrm{for}\mathrm{a}.\mathrm{a}.t\in [0,T].\hfill \end{array}$$ 11

Denote $c=min\{c_i,i=1,2,\dots ,n\}$. For any $t\in [0,T]$, one has from $({\mathrm{H}}_2)$ and (11) that

$$\begin{array}{cc}& \Vert x(t)\Vert \hfill \\ \hfill & \le \Vert x(0)\Vert e^{-ct}+{\int }_0^t{e}^{-c(t-s)}\Vert A\mathit{\gamma }(s)\hfill \\ \hfill & +B\mathit{\gamma }(s-\mathit{\tau }(s))+D{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)\mathit{\gamma }(u)\mathrm{d}u\hfill \\ \hfill & +I\Vert \mathrm{d}s\hfill \\ \hfill & \le e^{-ct}[\Vert x(0)\Vert +{\int }_0^t{e}^{cs}\Vert A\Vert \Vert \mathit{\gamma }(s)\Vert \mathrm{d}s\hfill \\ \hfill & +{\int }_0^t{e}^{cs}\Vert B\Vert \Vert \mathit{\gamma }(s-\mathit{\tau }(s))\Vert \mathrm{d}s\hfill \\ \hfill & +{\int }_0^t{e}^{cs}\Vert D\Vert {\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)\Vert \mathit{\gamma }(u)\Vert \mathrm{d}u\mathrm{d}s\hfill \\ \hfill & +{\int }_0^t{e}^{cs}\Vert I\Vert \mathrm{d}s]\hfill \\ \hfill & \le e^{-ct}[\Vert x(0)\Vert +e^{-ct}\tilde{L}\Vert A\Vert {\int }_0^t{e}^{cs}\Vert x(s)\Vert \mathrm{d}s\hfill \\ \hfill & +\tilde{L}\Vert B\Vert {\int }_0^t{e}^{cs}\Vert x(s-\mathit{\tau }(s))\Vert \mathrm{d}s\hfill \\ \hfill & +{\int }_0^t{e}^{cs}\Vert D\Vert {\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)\Vert \mathit{\gamma }(u)\Vert \mathrm{d}u\mathrm{d}s]\hfill \\ \hfill & +\frac{1}{c}(\Vert I\Vert +\tilde{P}(\Vert A\Vert +\Vert B\Vert ))(1-e^{-ct}).\hfill \end{array}$$ 12

It is easy to get that

$$\begin{array}{cc}& e^{-ct}\tilde{L}\Vert B\Vert {\int }_0^t{e}^{cs}\Vert x(s-\mathit{\tau }(s))\Vert \mathrm{d}s\hfill \\ \hfill & \le e^{-ct}\tilde{L}\Vert B\Vert {\int }_{-\mathit{\tau }(0)}^{t-\mathit{\tau }(t)}\frac{e^{c(s+\mathit{\tau })}\Vert x(s)\Vert }{1-\dot{\mathit{\tau }}({\mathit{\phi }}^{-1}(s))}\mathrm{d}s\hfill \\ \hfill & \le e^{c(\mathit{\tau }-t)}\tilde{L}\Vert B\Vert {\int }_{-\mathit{\tau }(0)}^{t-\mathit{\tau }(t)}\frac{e^{cs}\Vert x(s)\Vert }{1-h}\mathrm{d}s,\hfill \end{array}$$ 13

where ${\mathit{\phi }}^{-1}$ is the inverse function of $\mathit{\phi }(t)=t-\mathit{\tau }(t)$.

Since $K(·)$ is a non-negative bounded scalar function, there exists a positive constant $\overline{k}$ such that $K(t)\le \overline{k}$ for $\forall t\in \mathbb{R}$. It can be derived from $({\mathrm{H}}_2)$ and $({\mathrm{H}}_5)$ that

$$\begin{array}{cc}& e^{-ct}{\int }_0^t\Vert D\Vert e^{cs}{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)|\mathit{\gamma }(u)\Vert \mathrm{d}u\mathrm{d}s\hfill \\ \hfill & \le e^{-ct}\Vert D\Vert \tilde{L}{\int }_0^t{\int }_{s-\mathit{\theta }}^s{e}^{cs}K(s-u)\Vert x(u)\Vert \mathrm{d}u\mathrm{d}s\hfill \\ \hfill & +\frac{1}{c}\Vert D\Vert \tilde{P}q(1-e^{-ct})\hfill \\ \hfill & \le \overline{k}\Vert D\Vert \tilde{L}{e}^{-ct}{\int }_0^t{\int }_{s-\mathit{\theta }}^s{e}^{cs}\Vert x(u)\Vert \mathrm{d}u\mathrm{d}s\hfill \\ \hfill & +\frac{1}{c}\Vert D\Vert \tilde{P}q(1-e^{-ct})\hfill \\ \hfill & =\overline{k}\Vert D\Vert \tilde{L}{e}^{-ct}({\int }_{-\mathit{\theta }}^0{\int }_0^{u+\mathit{\theta }}{e}^{cs}\Vert x(u)\Vert \mathrm{d}s\mathrm{d}u\hfill \\ \hfill & +{\int }_0^{t-\mathit{\theta }}{\int }_{\mathit{\theta }}^{u+\mathit{\theta }}{e}^{cs}\Vert x(u)\Vert \mathrm{d}s\mathrm{d}u\hfill \\ \hfill & +{\int }_{t-\mathit{\theta }}^t{\int }_{\mathit{\theta }}^t{e}^{cs}\Vert x(u)\Vert \mathrm{d}s\mathrm{d}u)+\frac{1}{c}\Vert D\Vert \tilde{P}q(1-e^{-ct})\hfill \\ \hfill & =\Vert D\Vert \tilde{L}\frac{\overline{k}}{c}{e}^{-ct}({\int }_{-\mathit{\theta }}^0(e^{c(u+\mathit{\theta })}-1)\Vert x(u)\Vert \mathrm{d}u\hfill \\ \hfill & +{\int }_0^{t-\mathit{\theta }}(e^{c(u+\mathit{\theta })}-e^{c\mathit{\theta }})\Vert x(u)\Vert \mathrm{d}u\hfill \\ \hfill & +{\int }_{t-\mathit{\theta }}^t(e^{ct}-e^{c\mathit{\theta }})\Vert x(u)\Vert \mathrm{d}u)+\frac{1}{c}\Vert D\Vert \tilde{P}q(1-e^{-ct})\hfill \\ \hfill & \le \Vert D\Vert \tilde{L}\frac{\overline{k}}{c}{e}^{-ct}({\int }_{-\mathit{\theta }}^0(e^{c(s+\mathit{\theta })}-1)\Vert x(s)\Vert \mathrm{d}s\hfill \\ \hfill & +{\int }_0^t(e^{ct}-e^{c\mathit{\theta }})\Vert x(s)\Vert \mathrm{d}s)\hfill \\ \hfill & +\frac{1}{c}\Vert D\Vert \tilde{P}q(1-e^{-ct}).\hfill \end{array}$$ 14

Therefore, it can be obtained from $({\mathrm{H}}_4)$, (12), (13), and (14) that

$$\begin{array}{cc}\hfill \Vert x(t)\Vert & \le \Vert x(0)\Vert e^{-ct}+e^{-ct}\tilde{L}\Vert A\Vert {\int }_0^t{e}^{cs}\Vert x(s)\Vert \mathrm{d}s\hfill \\ \hfill & +e^{c(\mathit{\tau }-t)}\tilde{L}\Vert B\Vert {\int }_{-\mathit{\tau }(0)}^{t-\mathit{\tau }(t)}\frac{e^{cs}\Vert x(s)\Vert }{1-h}\mathrm{d}s\hfill \\ \hfill & +e^{-ct}\Vert D\Vert \tilde{L}\frac{\overline{k}}{c}({\int }_{-\mathit{\theta }}^0(e^{c(s+\mathit{\theta })}-1)\Vert x(s)\Vert \mathrm{d}s\hfill \\ \hfill & +{\int }_0^t(e^{ct}-e^{c\mathit{\theta }})\Vert x(s)\Vert \mathrm{d}s)\hfill \\ \hfill & +\frac{1}{c}\Vert D\Vert \tilde{P}q(1-e^{-ct})+\frac{1}{c}(\Vert I\Vert +\tilde{P}(\Vert A\Vert \hfill \\ \hfill & +\Vert B\Vert ))(1-e^{-ct})\hfill \\ \hfill & =\Vert x(0)\Vert e^{-ct}+\frac{1}{c}\Vert D\Vert \tilde{P}q(1-e^{-ct})\hfill \\ \hfill & +\frac{1}{c}(\Vert I\Vert +\tilde{P}(\Vert A\Vert +\Vert B\Vert ))(1-e^{-ct})\hfill \\ \hfill & +e^{c(\mathit{\tau }-t)}\tilde{L}\Vert B\Vert {\int }_{-\mathit{\tau }(0)}^0\frac{e^{cs}\Vert x(s)\Vert }{1-h}\mathrm{d}s\hfill \\ \hfill & +e^{-ct}\Vert D\Vert \tilde{L}\frac{\overline{k}}{c}{\int }_{-\mathit{\theta }}^0(e^{c(s+\mathit{\theta })}-1)\Vert x(s)\Vert \mathrm{d}s\hfill \\ \hfill & +e^{-ct}\tilde{L}\Vert A\Vert {\int }_0^t{e}^{cs}\Vert x(s)\Vert \mathrm{d}s\hfill \\ \hfill & +e^{c(\mathit{\tau }-t)}\tilde{L}\Vert B\Vert {\int }_0^t\frac{e^{cs}\Vert x(s)\Vert }{1-h}\mathrm{d}s\hfill \\ \hfill & +e^{-ct}\Vert D\Vert \tilde{L}\frac{\overline{k}}{c}{\int }_0^t(e^{ct}-e^{c\mathit{\theta }})\Vert x(s)\Vert \mathrm{d}s\hfill \\ \hfill & \le \Vert x(0)\Vert e^{-ct}+\frac{1}{c}\Vert D\Vert \tilde{P}q(1-e^{-ct})\hfill \\ \hfill & +\frac{1}{c}(\Vert I\Vert +\tilde{P}(\Vert A\Vert +\Vert B\Vert ))(1-e^{-ct})\hfill \\ \hfill & +e^{c(\mathit{\tau }-t)}\tilde{L}\Vert B\Vert {\int }_{-\mathit{\tau }(0)}^0\frac{e^{cs}\Vert x(s)\Vert }{1-h}\mathrm{d}s\hfill \\ \hfill & +e^{-ct}\Vert D\Vert \tilde{L}\frac{\overline{k}}{c}{\int }_{-\mathit{\theta }}^0(e^{c(s+\mathit{\theta })}-1)\Vert x(s)\Vert \mathrm{d}s\hfill \\ \hfill & +\tilde{L}\Vert A\Vert {\int }_0^t\Vert x(s)\Vert \mathrm{d}s+e^{c\mathit{\tau }}\tilde{L}\Vert B\Vert {\int }_0^t\frac{\Vert x(s)\Vert }{1-h}\mathrm{d}s\hfill \\ \hfill & +\Vert D\Vert \tilde{L}\frac{\overline{k}}{c}{\int }_0^t\Vert x(s)\Vert \mathrm{d}s\hfill \\ \hfill & \le \tilde{a}+{\int }_0^{t}m\Vert x(s)\Vert \mathrm{d}s,\hfill \end{array}$$

where $\tilde{a}=\Vert x(0)\Vert +\frac{1}{c}\Vert D\Vert \tilde{P}q+\frac{1}{c}(\Vert I\Vert +\tilde{P}(\Vert A\Vert +\Vert B\Vert ))+e^{c\mathit{\tau }}\tilde{L}\Vert B\Vert {\int }_{-\mathit{\tau }(0)}^0\frac{e^{cs}\Vert x(s)\Vert }{1-h}\mathrm{d}s+\Vert D\Vert \tilde{L}\frac{\overline{k}}{c}{\int }_{-\mathit{\theta }}^0(e^{c(s+\mathit{\theta })}-1)\Vert x(s)|\mathrm{d}s$, $m=\tilde{L}\Vert A\Vert +\frac{e^{c\mathit{\tau }}\tilde{L}\Vert B\Vert }{1-h}+\Vert D\Vert \tilde{L}\frac{\overline{k}}{c}$.

Utilizing the Gronwall inequality yields:

$$\begin{array}{c}\hfill \Vert x(t)\Vert \le \tilde{a}{e}^{mt}\le \tilde{a}{e}^{mT},\mathrm{for}\mathrm{a}.\mathrm{a}.t\in [0,T].\end{array}$$ 15

It is obvious that $\Vert x(t)\Vert =\Vert \mathit{\varphi }(t)\Vert \le \tilde{a}{e}^{mT}$ for $t\in [-\mathit{\vartheta },0]$. Considering the inequality (15), we have ${\Vert x(t)\Vert }_{\infty }\le \tilde{a}{e}^{mT}$, which implies that $\mathrm{\Gamma }$ is bounded. As a consequence of Lemma 1, we deduce that $G$ has a fixed point which is a solution of (7).

From the above derivation process we also know that $x(t)$ is bounded for any positive time, and hence it is defined on $[0,+\infty )$. This completes the proof.$\square$

Remark 3

By exchanging the integral order and using the integration by substitution, Lemma 1 gives sufficient conditions on the existence of Filippov solution $x(t)$ to the neural network with time-varying mixed delays. It is easy prove the existence of Filippov solution $x(t)$ to the neural network with time-varying discrete delay and unbounded distributed delay by using the same analysis technique as that in the proof of Lemma 1. As fa as we know, no published paper give strict mathematical proof for the existence of Filippov solution to neural networks with discontinuous activation functions and mixed delays. Although many attempts have been made by researchers, to the best of our knowledge, this problem has not been solved in the literature so far. Recently, the authors of Cai and Huang (2011) had to deal with the distributed delay as discrete delay [see the proof of Lemma 3.1 in Cai and Huang (2011)], authors in Lu and Chen (2008), Liu et al. (2012), Lu and Chen (2006), and Haddad (1981) only got approximate Filippov solutions to such discontinuous neural networks with mixed delays by constructing a sequence of continuous delay differential equations with high–slope right–hand sides. Moreover, the conditions on the discontinuous activation functions in Lemma 1 are very general. However, the discontinuous activation functions in Lu and Chen (2008), Liu et al. (2012), Lu and Chen (2006), and Haddad (1981) were monotonically nondecreasing or uniformly locally bounded. This is another reason for giving Lemma 1.

Based on the drive-response concept for synchronization proposed by Pecora and Carrol Pecora and Carroll (1990), we consider the neural network model (1) as the drive system, the controlled response system is given in the following form:

$$\begin{array}{cc}\hfill \dot{y}(t)=& -Cy(t)+Af(y(t))+Bf(y(t-\mathit{\tau }(t)))\hfill \\ \hfill & +D{\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)f(y(s))\mathrm{d}s\hfill \\ \hfill & +I+u(t),\hfill \end{array}$$ 16

where $y(t)={(y_1(t),y_2(t),\dots ,y_n(t))}^T$ is the state of the response system, $u(t)={(u_1(t),u_2(t),\dots ,u_n(t))}^T$ is the controller to be designed, the other parameters are the same as those defined in system (1).

In view of Definitions 2, 3 and Lemma 2, the initial value problem of system (16) is

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{y}(t)=-Cy(t)+A\mathit{\delta }(t)+B\mathit{\delta }(t-\mathit{\tau }(t))\hfill \\ +D{\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)\mathit{\delta }(s)\mathrm{d}s\hfill \\ +I+u(t),\mathrm{for}\mathrm{a}.\mathrm{a}.t\in [0,+\infty ),\hfill \\ \mathit{\delta }(t)\in F(y(t)),\mathrm{for}\mathrm{a}.\mathrm{a}.t\in [0,+\infty ),\hfill \\ y(s)=\mathit{\upsilon }(s),\forall s\in [-\mathit{\vartheta },0],\hfill \\ \mathit{\delta }(s)=\mathit{\omega }(s),\mathrm{for}\mathrm{a}.\mathrm{a}.s\in [-\mathit{\vartheta },0].\hfill \end{array}\right.\end{array}$$ 17

According to Pecora and Carroll (1990), if ${lim}_{t\to +\infty }y(t)=x(t)$, then (17) is said to be synchronized with (1) under the controller $u(t)$.

Remark 4

Since the measurable functions $\mathit{\gamma }(t)$ and $\mathit{\delta }(t)$ are uncertain at the discontinuous points of activation function $f(x)$, the usual state feedback controller and impulsive controller as those in Liu et al. (2011) and Yang et al. (2011b) can not realize synchronization between systems (1) and (17). Results of Liu et al. (2011) shows that only quasi-synchronization can be achieved when the usual linear state feedback controllers are added to systems with discontinuous right-hand side and discrete time delays. As for synchronization of neural networks with discontinuous activations or other systems with discontinuous right-hand side, we do not find any similar result in the literature, let alone result on synchronization of neural networks with time-varying mixed delays via impulsive control. This fact implies that realizing synchronization of neural networks with discontinuous activations and time-varying mixed delays is not an easy work.

Remark 5

Although achieving synchronization of neural networks with discontinuous activations under control is difficult, the stability of neural networks with discontinuous activations as (1) without control can be realized by designing special connection weight matrices, for instance, the matrices $-A,-B,-D$ should satisfy the Lyapunov Diagonal Stable (LDS) condition (Forti et al. 2006) or other linear matrix inequalities (LMIs) (Lu and Chen 2008; Wang et al. 2009; Liu et al. 2012; Cai and Huang 2011). In this paper, we shill study the exponential synchronization of (16) and (1) without using these special and strict conditions.

In this paper, we study exponential synchronization between the neural networks (16) and (1), i.e., by adding suitable controller $u(t)$ to (16), the state of (16) can be exponentially synchronized onto the state of (1). Based on the discussion above, if the state $y(t)$ of (17) is exponentially synchronized onto the state $x(t)$ of (7), then our synchronization goal can be realized. Let $e(t)=y(t)-x(t)$. Substituting (7) from (17) yields the following error system:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{e}(t)=-Ce(t)+A\mathit{\beta }(t)+B\mathit{\beta }(t-\mathit{\tau }(t))\hfill \\ +D{\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)\mathit{\beta }(s)\mathrm{d}s+u(t),\hfill \\ e(s)=\mathit{\upsilon }(s)-\mathit{\varphi }(s),\forall s\in [-\mathit{\vartheta },0],\hfill \end{array}\right.\end{array}$$ 18

where $\mathit{\beta }(t)=\mathit{\delta }(t)-\mathit{\gamma }(t)$.

Now we introduce the definition of exponential synchronization, which is used in this paper.

Definition 4

The controlled neural network (16) with discontinuous activations is said to be exponentially synchronized with system (1) if there exist positive constants $M>1,\mathit{\alpha }>0$ such that

$$\begin{array}{c}\hfill \Vert e(t)\Vert \le M{\sup }_{-\mathit{\vartheta }\le s\le 0}\Vert \mathit{\upsilon }(s)-\mathit{\varphi }(s)\Vert \exp (-\mathit{\alpha }t)\end{array}$$

hold for $t\ge 0$.

Obviously, $e(t)=0$ is the equilibrium point of the error system (18) when $u(t)=0$. If system (18) realizes global exponential stability at the origin for any given initial condition, then the global exponential synchronization between (16) and (1) [or (17) and (7)] is achieved.

Let $V:{\mathbb{R}}^n\to \mathbb{R}$ be a locally Lipschitz continuous function. The Clarke’s generalized gradient of $V$ at $x\in {\mathbb{R}}^n$ Clarke (1983) is defined by $\mathit{\partial }V(x)=\overline{co}[lim\mathrm{\nabla }V(x_i):x_i\to x,x_i\notin \mathrm{\Omega }\cup \mathcal{N}]$, where $\mathrm{\Omega }\subset {\mathbb{R}}^n$ is the set of Lebesgue measure zero where $\mathrm{\nabla }V$ does not exist, and $\mathcal{N}\subset {\mathbb{R}}^n$ is an arbitrary set with measure zero.

The next lemma will be useful to compute the time derivative along solutions (18) of the Lyapunov function designed in the later sections.

Lemma 3

(Chain rule) Clarke (1983). If $V(x):{\mathbb{R}}^n\to \mathbb{R}$ is C-regular Clarke (1983), and $x(t)$ is absolutely continuous on any compact subinterval of $[0,+\infty )$. Then, $x(t)$ and $V(x(t)):[0,+\infty )\to \mathbb{R}$ are differentiable for a.a. $t\in [0,+\infty )$ and

$$\begin{array}{c}\hfill \frac{\mathrm{d}}{\mathrm{d}t}V(x(t))=\mathit{\gamma }(t)\dot{x}(t),\forall \mathit{\gamma }(t)\in \mathit{\partial }V(x(t)),\end{array}$$ 19

where $\mathit{\partial }V(x(t))$ is the Clark generalized gradient of $V$ at $x(t)$.

The next two lemmas will be utilized in this paper.

Lemma 4

Wang et al. (1992). If $X,Y$ are real matrices with appropriate dimensions, then there exist number $\mathit{\epsilon }>0$ such that

$$\begin{array}{c}\hfill X^{T}Y+Y^{T}X\le \mathit{\epsilon }{X}^{T}X+\frac{1}{\mathit{\epsilon }}{Y}^{T}Y.\end{array}$$

Lemma 5

Yang et al. (2011a). Suppose $K(t)$ is a non-negative bounded scalar function defined on $[0,+\infty )$ and ${\int }_0^{+\infty }K(u)\mathrm{d}u=k$. For any constant matrix $D\in {\mathbb{R}}^{n\times n}$, $D>0$, and vector function $x:(-\infty ,t]\to {\mathbb{R}}^n$ for $t\ge 0$, one has

$$\begin{array}{cc}& k{\int }_{-\infty }^{t}K(t-s)x^T(s)Dx(s)\mathrm{d}s\ge \hfill \\ \hfill & {\left({\int }_{-\infty }^{t}K(t-s)x(s)\mathrm{d}s\right)}^{T}D{\int }_{-\infty }^{t}K(t-s)x(s)\mathrm{d}s\hfill \end{array}$$

provided the integrals are all well defined.

Synchronization under state feedback control

In the literature, there are many results concerning exponential synchronization of continuous neural networks with discrete or/and distributed delays. However, there is seldom published result on exponential synchronization of discontinuous neural networks with discrete or/and distributed delays. The main difficulty in studying the exponential synchronization comes from the discontinuous activations, which result in non-zero uncertain measurable selections $\mathit{\gamma }(t)$ and $\mathit{\delta }(t)$ in the drive and response systems. In order to overcome this difficulty, in this section, we shall design a novel state feedback controller $u(t)$ such that the uncertainty can be well dealt with and the controlled neural networks (16) can realize global exponential synchronization with system (1).

The following Theorem 1 is our first result.

Theorem 1

Suppose that the assumptions $({\mathrm{H}}_1$–${\mathrm{H}}_5)$ are satisfied. Then the neural networks (1) and (16) can achieve global exponential synchronization under the following controller:

$$\begin{array}{c}\hfill u(t)=-Re(t)-\mathit{\eta }\mathrm{sign}(e(t)),\end{array}$$ 20

where $R=\mathrm{diag}(R_1,R_2,\dots ,R_n)$, $R_i\ge -c_i+L\Vert A\Vert +\frac{2-h}{2(1-h)}L\Vert B\Vert +\frac{1}{2}L\Vert D\Vert (q^2+1)+\mathit{\alpha }$, $\mathit{\alpha }$ is a positive constant, $\mathit{\eta }$ is a constant satisfying

$$\begin{array}{c}\hfill \mathit{\eta }\ge P(\Vert A\Vert +\Vert B\Vert +q\Vert D\Vert ),\end{array}$$ 21

$\mathrm{sign}(e(t))={(\mathrm{sign}(e_1(t)),\mathrm{sign}(e_2(t)),\dots ,\mathrm{sign}(e_n(t)))}^T$, $\mathrm{sign}(·)$ is the sign function. Moreover, the lower bound on the convergence rate is $\mathit{\alpha }$.

Proof

Define the following Lyapunov functional candidate:

$$\begin{array}{cc}\hfill \overline{V}(t)& =\frac{1}{2}{e}^T(t)e(t)+\frac{L\Vert B\Vert }{2(1-h)}{\int }_{t-\mathit{\tau }(t)}^t{e}^T(s)e(s)\mathrm{d}s\hfill \\ \hfill & +\frac{1}{2}qL\Vert D\Vert {\int }_{-\mathit{\theta }}^0{\int }_{t+u}^{t}K(-u)e^T(s)e(s)\mathrm{d}s\mathrm{d}u.\hfill \end{array}$$

In view of $({\mathrm{H}}_3)$, one has $\Vert \mathit{\beta }(t)\Vert \le L\Vert e(t)\Vert +P$. Computing the derivative of $\overline{V}(t)$ along trajectories of error system (18), we get from $({\mathrm{H}}_4)$, Lemma 2, and the calculus for differential inclusion in Paden and Sastry (1987) that:

$$\begin{array}{cc}\hfill \dot{\overline{V}}(t)& =e^T(t)[-Ce(t)+A\mathit{\beta }(t)+B\mathit{\beta }(t-\mathit{\tau }(t))\hfill \\ \hfill & +D{\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)\mathit{\beta }(s)\mathrm{d}s\hfill \\ \hfill & -Re(t)-\mathit{\eta }\mathrm{sign}(e(t))]+\frac{L\Vert B\Vert }{2(1-h)}{e}^T(t)e(t)\hfill \\ \hfill & -\frac{L\Vert B\Vert }{2(1-h)}(1-\dot{\mathit{\tau }}(t))e^T(t-\mathit{\tau }(t))e(t-\mathit{\tau }(t))\hfill \\ \hfill & +\frac{1}{2}qL\Vert D\Vert {\int }_{-\mathit{\theta }}^{0}K(-u)e^T(t)e(t)\mathrm{d}u\hfill \\ \hfill & -\frac{1}{2}qL\Vert D\Vert {\int }_{t-\mathit{\theta }}^{t}K(t-u)e^T(u)e(u)\mathrm{d}u\hfill \\ \hfill & \le -e^T(t)(C+R)e(t)+{L\Vert A\Vert \Vert e(t)\Vert }^2\hfill \\ \hfill & +L\Vert B\Vert \Vert e(t)\Vert \Vert e(t-\mathit{\tau }(t))\Vert \hfill \\ \hfill & +L\Vert e(t)\Vert \Vert D\Vert {\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)\Vert e(s)\Vert \mathrm{d}s\hfill \\ \hfill & -e^T(t)\mathit{\eta }\mathrm{sign}(e(t))+\frac{1}{2}{q}^{2}L\Vert D\Vert e^T(t)e(t)\hfill \\ \hfill & +\frac{L\Vert B\Vert }{2(1-h)}{e}^T(t)e(t)\hfill \\ \hfill & -\frac{1}{2}L\Vert B\Vert e^T(t-\mathit{\tau }(t))e(t-\mathit{\tau }(t))\hfill \\ \hfill & +P\Vert e(t)\Vert (\Vert A\Vert +\Vert B\Vert +q\Vert D\Vert )\hfill \\ \hfill & -\frac{1}{2}qL\Vert D\Vert {\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)e^T(s)e(s)\mathrm{d}s.\hfill \end{array}$$ 22

It can be get from Lemma 3 that

$$\begin{array}{cc}& L\Vert B\Vert \Vert e(t)\Vert \Vert e(t-\mathit{\tau }(t))\Vert \hfill \\ \hfill & \le \frac{1}{2}{L\Vert B\Vert \Vert e(t)\Vert }^2+\frac{L\Vert B\Vert }{2}{\Vert e(t-\mathit{\tau }(t))\Vert }^2,\hfill \end{array}$$ 23

and

$$\begin{array}{cc}& L\Vert e(t)\Vert \Vert D\Vert {\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)\Vert e(s)\Vert \mathrm{d}s\hfill \\ \hfill & \le \frac{1}{2}{L\Vert D\Vert \Vert e(t)\Vert }^2\hfill \\ \hfill & +\frac{1}{2}L\Vert D\Vert {\left({\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)\Vert e(s)\Vert \mathrm{d}s\right)}^2.\hfill \end{array}$$ 24

By virtue of Lemma 4, it can be obtained from $({\mathrm{H}}_5)$ that

$$\begin{array}{cc}& {\left({\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)\Vert e(s)\Vert \mathrm{d}s\right)}^2\hfill \\ \hfill & \le q{\int }_{t-\mathit{\theta }(t)}^{t}K(t-s){\Vert e(s)\Vert }^2\mathrm{d}s.\hfill \end{array}$$ 25

On the other hand, it is easy to get that

$$\begin{array}{cc}& P\Vert e(t)\Vert (\Vert A\Vert +\Vert B\Vert +q\Vert D\Vert )\hfill \\ \hfill & \le P(\Vert A\Vert +\Vert B\Vert +q\Vert D\Vert )\sum _{i=1}^n|e_i(t)|.\hfill \end{array}$$ 26

Therefore, it follows from (21) and (26) that

$$\begin{array}{cc}& -e^T(t)\mathit{\eta }\mathrm{sign}(e(t))\hfill \\ \hfill & +P\Vert e(t)\Vert (\Vert A\Vert +\Vert B\Vert +q\Vert D\Vert )\le 0.\hfill \end{array}$$ 27

Substituting (23–27) into (22) produces that

$$\begin{array}{c}\hfill \dot{\overline{V}}(t)+\mathit{\alpha }{e}^T(t)e(t)\le e^T(t)\mathrm{\Xi }e(t),\end{array}$$ 28

where $\mathrm{\Xi }=-C+(L\Vert A\Vert +\frac{2-h}{2(1-h)}L\Vert B\Vert +\frac{1}{2}L\Vert D\Vert (q^2+1)+\mathit{\alpha })I_n-R$.

By virtue of $R_i\ge -c_i+L\Vert A\Vert +\frac{2-h}{2(1-h)}L\Vert B\Vert +\frac{1}{2}L\Vert D\Vert (q^2+1)+\mathit{\alpha }$, one gets that

$$\begin{array}{c}\hfill \dot{\overline{V}}(t)+\mathit{\alpha }{e}^T(t)e(t)\le 0.\end{array}$$ 29

Hence, it is followed from (22) and (29) that

$$\begin{array}{cc}& e^T(t)e(t)\le 2\overline{V}(t)=2\overline{V}(0)+2{\int }_0^t\dot{\overline{V}}(s)\mathrm{d}s\hfill \\ \hfill & \le 2\overline{V}(0)-2\mathit{\alpha }{\int }_0^t{e}^T(s)e(s)\mathrm{d}s.\hfill \end{array}$$ 30

According to Gronwall inequality, one derives from (30) that

$$\begin{array}{c}\hfill e^T(t)e(t)\le 2\overline{V}(0)\exp (-2\mathit{\alpha }t),\end{array}$$

which implies the following inequality:

$$\begin{array}{c}\hfill \Vert e(t)\Vert \le \sqrt{\mathit{\rho }}{\sup }_{-\mathit{\vartheta }\le s\le 0}\Vert \mathit{\varphi }(s)-\mathit{\upsilon }(s)\Vert \exp (-\mathit{\alpha }t),\end{array}$$

where $\mathit{\rho }=1+\frac{\mathit{\tau }L\Vert B\Vert }{1-h}+\mathit{\theta }{q}^{2}L\Vert D\Vert$.

According to Definition 4, the neural networks (1) and (16) achieve global exponential synchronization. This completes the proof.$\square$

Remark 6

According to Theorem 1, the designed state feedback controller (20) can realize global exponential synchronization between the discontinuous neural networks (1) and (16). According to the definition of sign function ($\mathrm{sign}(e_i)=1$ if $e_i>0$, $\mathrm{sign}(e_i)=-1$ if $e_i<0$, and $\mathrm{sign}(e_i)=0$ if $e_i=0$), the controller (20) becomes $u_i(t)=-R_i{e}_i(t)-\mathit{\eta }<0$ if $e_i(t)>0$, $u_i(t)=-R_i{e}_i(t)+\mathit{\eta }>0$ if $e_i(t)<0$, and $u_i(t)=0$ if $e_i(t)=0$, $i=1,2,\dots ,n$. Hence, the role of the controller is: it decreases ${\dot{e}}_i(t)$ when $e_i(t)>0$, it increases ${\dot{e}}_i(t)$ when $e_i(t)<0$, and the controller is not needed when $e_i(t)=0$. From the inequality (27) one can see that the term $-\mathit{\eta }\mathrm{sign}(e(t))$ in the controller (20) plays the role of dealing with the uncertainties of the measurable selections. To the best of our knowledge, no result concerning complete synchronization of discontinuous neural networks with time-varying mixed delays is published in the literature, let alone exponential synchronization of discontinuous neural networks with time-varying mixed. Recently, in Liu et al. (2011), the synchronization issue of coupled discontinuous neural networks and other chaotic systems were investigated by using the classical state feedback controller, i.e., controller (20) without the term $-\mathit{\eta }\mathrm{sign}(e(t))$, however, only quasi-synchronization criteria were derived due to its disability in coping with the uncertainties of the uncertain measurable selections in the drive and response systems. Moreover, authors in Liu et al. (2011) did not consider distributed delay. Therefore, Theorem 1 in this paper is new and improve the corresponding results in Liu et al. (2011).

Remark 7

In the proof of Theorem 1, we do not use the well known Halanay inequality. One of the advantages using the method in the proof is that the relationship between the control gain $R$ and the convergence rate $\mathit{\alpha }$ is obvious. However, it is not so obvious by using Halanay inequality. Moreover, the utilized Lyaponov functional (22) is simple and does not include the exponential function $e^{\mathit{\alpha }t}$. In sum, by using the simple Lyaponov functional and the new proving method, we simplify the proof process.

Synchronization under impulsive control

In the above section, the designed state feedback controller leads to the global exponential synchronization between (1) and (16). However, the corresponding control cost may be high. It is well known that it is better that designed controller can not only realize the synchronization goal but also reduce the control cost. Impulsive control, as an effective and ideal control technique, is activated only at some isolated points. Obviously, the control cost can be drastically reduced if the response system can be synchronized with the drive system under impulsive control. Until now, impulsive control has been extensively utilized to study synchronization (Yang et al. 2011b), but result on synchronization of neural networks with discontinuous activations via impulsive control is seldom, let alone the same result of discontinuous neural networks with mixed delays. Hence, in the present section, a novel impulsive controller shall be designed such that the system (16) can globally exponentially synchronize with system (1). Furthermore, a useful corollary will be given such that the given synchronization criterion reduces conservativeness as much as possible.

The impulsive controller $u(t)$ is designed as

$$\begin{array}{c}\hfill u_i(t)=\sum _{k=1}^{\infty }{E}_i{e}_i(t)\mathit{\varrho }(t-t_k)-\mathit{\eta }\mathrm{sign}(e_i(t)),\end{array}$$ 31

where $k\in {\mathbb{N}}_{+}$, $E_i,i=1,2,\dots ,n,$ are constants to be determined, $\mathit{\eta }$ and $\mathrm{sign}(·)$ are defined in Theorem 1, the time sequence $\{t_k,k\in {\mathbb{N}}_{+}\}$ satisfies $0=t_0<t_1<t_2<\dots <t_{k-1}<t_k<\dots$, and ${lim}_{k\to +\infty }{t}_k=+\infty$, $\mathit{\varrho }(·)$ is the Dirac impulsive function.

With the impulsive controller (31), the synchronization error system (18) turns out to the following hybrid impulsive system:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{e}(t)=-Ce(t)+A\mathit{\beta }(e(t))\hfill \\ +B\mathit{\beta }(e(t-\mathit{\tau }(t)))\hfill \\ +D{\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)\mathit{\beta }(e(s))\mathrm{d}s\hfill \\ -\mathit{\eta }\mathrm{sign}(e(t)),t\ne t_k,\hfill \\ \mathrm{\Delta }e(t_k)=e(t_k)-e(t_k^{-})=Ee(t_k^{-}),t=t_k,\hfill \end{array}\right.\end{array}$$ 32

where $E=\mathrm{diag}(E_1,E_2,\dots ,E_n)$, $e(t_k)=e(t_k^{+})={lim}_{t\to t_k^{+}}e(t)$, $e(t_k^{-})={lim}_{t\to t_k^{-}}e(t)$.

The following Theorem 2 states the sufficient conditions guaranteeing the global exponential synchronization between (1) and (16) under the impulsive controller (32).

Theorem 2

Suppose that the assumptions $({\mathrm{H}}_1$–${\mathrm{H}}_5)$ are satisfied. Then the neural networks (1) and (16) can achieve global exponential synchronization under the impulsive controller (31), if there exist positive constants $\mathit{\alpha },\mathit{\beta }$ such that the following inequalities hold:

$$\begin{array}{cc}& P(\Vert A\Vert +\Vert B\Vert +q\Vert D\Vert )<\mathit{\eta },\hfill \end{array}$$ 33

$$\begin{array}{cc}& \Vert I_n{+E\Vert }^2\le d<1,k\in {\mathbb{N}}_{+},\hfill \end{array}$$ 34

$$\begin{array}{cc}& -2c+2L\Vert A\Vert +L\Vert B\Vert \mathit{\alpha }+L\Vert D\Vert \mathit{\beta }\hfill \\ \hfill & +\frac{lnd}{T_m}+d^{-1}(\frac{L\Vert B\Vert }{\mathit{\alpha }}+\frac{qL\Vert D\Vert }{\mathit{\beta }})<0,\hfill \end{array}$$ 35

where $c=min\{c_i,i=1,2,\dots ,n\}$, $T_m=max\{t_{k+1}-t_k,k\in {\mathbb{N}}_{+}\}$.

Proof

Define the following Lyapunov functional candidate:

$$\begin{array}{c}\hfill V(t)=\frac{1}{2}{e}^T(t)e(t).\end{array}$$ 36

Computing the derivative of $V(t)$ along trajectories of error system (32) for $t\in [t_{k-1},t_k)$ yields:

$$\begin{array}{cc}& \dot{V}(t)\hfill \\ \hfill & =e^T(t)[-Ce(t)+A\mathit{\beta }(e(t))+B\mathit{\beta }(e(t-\mathit{\tau }(t)))\hfill \\ \hfill & +D{\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)\mathit{\beta }(e(s))\mathrm{d}s-\mathit{\eta }\mathrm{sign}(e(t))]\hfill \\ \hfill & \le -e^T(t)Ce(t)+\Vert e^T(t)\Vert \Vert A\Vert \Vert \mathit{\beta }(e(t))\Vert \hfill \\ \hfill & +\Vert e^T(t)\Vert \Vert B\Vert \Vert \mathit{\beta }(e(t-\mathit{\tau }(t)))\Vert \hfill \\ \hfill & +\Vert e^T(t)\Vert \Vert D\Vert {\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)\Vert \mathit{\beta }(e(s))\Vert \mathrm{d}s\hfill \\ \hfill & -e^T(t)\mathit{\eta }\mathrm{sign}(e(t))\hfill \\ \hfill & \le -e^T(t)Ce(t)+{L\Vert A\Vert \Vert e(t)\Vert }^2\hfill \\ \hfill & +L\Vert B\Vert \Vert e(t)\Vert \Vert e(t-\mathit{\tau }(t))\Vert \hfill \\ \hfill & +L\Vert e(t)\Vert \Vert D\Vert {\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)\Vert e(s)\Vert \mathrm{d}s\hfill \\ \hfill & -e^T(t)\mathit{\eta }\mathrm{sign}(e(t))\hfill \\ \hfill & +P\Vert e(t)\Vert (\Vert A\Vert +\Vert B\Vert +q\Vert D\Vert ).\hfill \end{array}$$ 37

For constants $\mathit{\alpha }>0,\mathit{\beta }>0$, one has from Lemma 3 that

$$\begin{array}{cc}& L\Vert B\Vert \Vert e(t)\Vert \Vert e(t-\mathit{\tau }(t))\Vert \hfill \\ \hfill & \le \frac{1}{2}{L\Vert B\Vert \mathit{\alpha }\Vert e(t)\Vert }^2+\frac{L\Vert B\Vert }{2\mathit{\alpha }}{\Vert e(t-\mathit{\tau }(t))\Vert }^2,\hfill \end{array}$$ 38

and

$$\begin{array}{cc}& L\Vert e(t)\Vert \Vert D\Vert {\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)\Vert e(s)\Vert \mathrm{d}s\hfill \\ \hfill & \le \frac{1}{2}{L\mathit{\beta }\Vert D\Vert \Vert e(t)\Vert }^2\hfill \\ \hfill & +\frac{1}{2\mathit{\beta }}L\Vert D\Vert {\left({\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)\Vert e(s)\Vert \mathrm{d}s\right)}^2.\hfill \end{array}$$ 39

Substituting (25), (27), (38) and (39) into (37) produces that

$$\begin{array}{cc}\hfill \dot{V}(t)& \le (-2c+2L\Vert A\Vert +L\Vert B\Vert \mathit{\alpha }+L\Vert D\Vert \mathit{\beta })V(t)\hfill \\ \hfill & +\frac{L\Vert B\Vert }{\mathit{\alpha }}V(e(t-\mathit{\tau }(t)))\hfill \\ \hfill & +\frac{qL\Vert D\Vert }{\mathit{\beta }}{\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)V(e(s))\mathrm{d}s.\hfill \end{array}$$ 40

On the other hand, when $t=t_k,k\in {\mathbb{N}}_{+}$, it is obtained from inequality (34) and the second equation of (32) that

$$\begin{array}{cc}\hfill V(t_k)& =\frac{1}{2}{e}^T(t_k)e(t_k)\hfill \\ \hfill & =\Vert I_n{+E\Vert }^2\frac{1}{2}{e}^T(t_k^{-})e(t_k^{-})\le dV(t_k^{-}).\hfill \end{array}$$ 41

For any $\mathit{ϵ}>0$, let $v(t)$ be the unique solution of the following impulsive delay system:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{v}(t)=av(t)+bv(e(t-\mathit{\tau }(t)))+\mathit{ϵ}\hfill \\ +\overline{c}{\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)v(e(s))\mathrm{d}s,t\ne t_k,\hfill \\ v(t_k)=dv(t_k^{-}),t=t_k,k\in {\mathbb{N}}_{+},\hfill \\ v(s)=\frac{1}{2}{\Vert e(s)\Vert }^2,s\in [-\mathit{\vartheta },0].\hfill \end{array}\right.\end{array}$$ 42

where $a=-2c+2L\Vert A\Vert +L\Vert B\Vert \mathit{\alpha }+L\Vert D\Vert \mathit{\beta }$, $b=\frac{L\Vert B\Vert }{\mathit{\alpha }}$, $\overline{c}=\frac{qL\Vert D\Vert }{\mathit{\beta }}$.

For $t\in [0,t_1)$, using the ordinary differential equation theory, one gets

$$\begin{array}{cc}\hfill v(t)& =e^{at}v(0)+{\int }_0^t{e}^{a(t-s)}[bv(s-\mathit{\tau }(s))\hfill \\ \hfill & +\overline{c}{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)v(e(u))\mathrm{d}u+\mathit{ϵ}]\mathrm{d}s.\hfill \end{array}$$ 43

For $t\in [t_1,t_2)$, one obtains from (43) and the second equation of (42) that

$$\begin{array}{cc}\hfill v(t_1^{+})& =d{e}^{a{t}_1}v(t_1^{+})+d{\int }_0^{t_1}{e}^{a(t_1-s)}[bv(s-\mathit{\tau }(s))\hfill \\ \hfill & +\overline{c}{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)v(e(u))\mathrm{d}u+\mathit{ϵ}]\mathrm{d}s,\hfill \end{array}$$ 44

and

$$\begin{array}{cc}\hfill v(t)& =e^{a(t-t_1)}v(t_1^{+})+{\int }_{t_1}^t{e}^{a(t-s)}[bv(s-\mathit{\tau }(s))\hfill \\ \hfill & +\overline{c}{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)v(e(u))\mathrm{d}u+\mathit{ϵ}]\mathrm{d}s.\hfill \end{array}$$ 45

It is followed that

$$\begin{array}{cc}\hfill v(t_2^{+})& =d{e}^{a(t_2-t_1)}v(t_1^{+})+d{\int }_{t_1}^{t_2}{e}^{a(t_2-s)}[bv(s-\mathit{\tau }(s))\hfill \\ \hfill & +\overline{c}{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)v(e(u))\mathrm{d}u+\mathit{ϵ}]\mathrm{d}s\hfill \\ \hfill & =d^2{e}^{a{t}_2}v(0)+d^2{e}^{a(t_2-t_1)}{\int }_0^{t_1}{e}^{a(t_1-s)}\hfill \\ \hfill & \times [bv(s-\mathit{\tau }(s))+\overline{c}{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)v(e(u))\mathrm{d}u\hfill \\ \hfill & +\mathit{ϵ}]\mathrm{d}s+d{\int }_{t_1}^{t_2}{e}^{a(t_2-s)}[bv(s-\mathit{\tau }(s))\hfill \\ \hfill & +\overline{c}{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)v(e(u))\mathrm{d}u+\mathit{ϵ}]\mathrm{d}s.\hfill \end{array}$$

By induction, we can derive that, for $t\in [t_k,t_{k+1})$,

$$\begin{array}{cc}\hfill v(t)& =d^k{e}^{at}v(0)+{\int }_0^{t_1}{e}^{a(t-s)}{d}^k[bv(s-\mathit{\tau }(s))\hfill \\ \hfill & +\overline{c}{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)v(e(u))\mathrm{d}u\hfill \\ \hfill & +\mathit{ϵ}]\mathrm{d}s+{\int }_{t_1}^{t_2}{e}^{a(t-s)}{d}^{k-1}[bv(s-\mathit{\tau }(s))\hfill \\ \hfill & +\overline{c}{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)v(e(u))\mathrm{d}u\hfill \\ \hfill & +\mathit{ϵ}]\mathrm{d}s+\cdots +{\int }_{t_{k-1}}^{t_k}{e}^{a(t-s)}d[bv(s-\mathit{\tau }(s))\hfill \\ \hfill & +\overline{c}{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)v(e(u))\mathrm{d}u\hfill \\ \hfill & +\mathit{ϵ}]\mathrm{d}s+{\int }_{t_k}^t{e}^{a(t-s)}[bv(s-\mathit{\tau }(s))\hfill \\ \hfill & +\overline{c}{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)v(e(u))\mathrm{d}u+\mathit{ϵ}]\mathrm{d}s\hfill \\ \hfill & =\prod _{0\le t_k\le t}d{e}^{at}v(0)+{\int }_0^t{e}^{a(t-s)}\prod _{s\le t_k\le t}d[bv(s-\mathit{\tau }(s))\hfill \\ \hfill & +\overline{c}{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)v(e(u))\mathrm{d}u+\mathit{ϵ}]\mathrm{d}s.\hfill \end{array}$$ 46

It is derived from $d<1$ that

$$\begin{array}{cc}& e^{a(t-s)}\prod _{s\le t_k\le t}d\le e^{a(t-s)}{d}^{\frac{t-s}{T_m}-1}\hfill \\ \hfill & =d^{-1}{e}^{-\mathit{\sigma }(t-s)},t\ge s\ge 0,\hfill \end{array}$$ 47

where $\mathit{\sigma }=-(a+\frac{lnd}{T_m})>0$.

It follows from (46) and (47) that

$$\begin{array}{cc}\hfill v(t)& \le \mathrm{\Delta }{e}^{-\mathit{\sigma }t}+{\int }_0^t{d}^{-1}{e}^{-\mathit{\sigma }(t-s)}[bv(s-\mathit{\tau }(s))\hfill \\ \hfill & +\overline{c}{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)v(u)\mathrm{d}u+\mathit{ϵ}]\mathrm{d}s,\hfill \end{array}$$ 48

where $\mathrm{\Delta }=\frac{1}{2}{d}^{-1}{sup}_{-\mathit{\vartheta }\le s\le 0}{\Vert e(s)\Vert }^2$. Now define

$$\begin{array}{c}\hfill h(\mathit{\nu })=\mathit{\nu }-\mathit{\sigma }+d^{-1}b{e}^{\mathit{\nu }\mathit{\tau }}+d^{-1}\overline{c}{\int }_0^{\mathit{\theta }(t)}K(s)e^{\mathit{\nu }s}\mathrm{d}s.\end{array}$$

It can be derived from $({\mathrm{H}}_4)$ and (35) that

$$\begin{array}{cc}\hfill h_l(0)& =-\mathit{\sigma }+d^{-1}b+d^{-1}\overline{c}{\int }_0^{\mathit{\theta }(t)}K(s)\mathrm{d}s\hfill \\ \hfill & \le -\mathit{\sigma }+d^{-1}b+d^{-1}\overline{c}q<0.\hfill \end{array}$$

Since $h(+\infty )=+\infty$ and $h(\mathit{\nu })$ is continuous on $[0,+\infty )$, there exists an unique constant $\overline{\mathit{\nu }}>0$ such that

$$\begin{array}{c}\hfill \overline{\mathit{\nu }}-\mathit{\sigma }+d^{-1}b{e}^{\overline{\mathit{\nu }}\mathit{\tau }}+d^{-1}\overline{c}{\int }_0^{\mathit{\theta }(t)}K(s)e^{\overline{\mathit{\nu }}s}\mathrm{d}s=0.\end{array}$$ 49

It is obvious that

$$\begin{array}{cc}\hfill v(t)& =\frac{1}{2}{\Vert e(t)\Vert }^2\le \mathrm{\Delta }\hfill \\ \hfill & <\mathrm{\Delta }{e}^{-\overline{\mathit{\nu }}t}+\frac{\mathit{ϵ}}{\mathit{\sigma }d-b-\overline{c}q},-\mathit{\vartheta }\le t\le 0.\hfill \end{array}$$

We claim that the inequality

$$\begin{array}{c}\hfill v(t)<\mathrm{\Delta }{e}^{-\overline{\mathit{\nu }}t}+\frac{\mathit{ϵ}}{\mathit{\sigma }d-b-\overline{c}q},\end{array}$$ 50

holds for $t\ge 0$. If it is not true, there exists a point $t^{\ast }>0$ such that

$$\begin{array}{c}\hfill v(t^{\ast })\ge \mathrm{\Delta }{e}^{-\overline{\mathit{\nu }}{t}^{\ast }}+\frac{\mathit{ϵ}}{\mathit{\sigma }d-b-\overline{c}q},\end{array}$$ 51

and

$$\begin{array}{c}\hfill v(t)<\mathrm{\Delta }{e}^{-\overline{\mathit{\nu }}t}+\frac{\mathit{ϵ}}{\mathit{\sigma }d-b-\overline{c}q},t<t^{\ast }.\end{array}$$ 52

Then one has from (48) and (52) that

$$\begin{array}{cc}\hfill v(t^{\ast })& \le \mathrm{\Delta }{e}^{-\mathit{\sigma }{t}^{\ast }}+{\int }_0^{t^{\ast }}{d}^{-1}{e}^{-\mathit{\sigma }(t^{\ast }-s)}[bv(s-\mathit{\tau }(s))\hfill \\ \hfill & +c{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)v(u)\mathrm{d}u+\mathit{ϵ}]\mathrm{d}s\hfill \\ \hfill & <e^{-\mathit{\sigma }{t}^{\ast }}\{\mathrm{\Delta }+\frac{\mathit{ϵ}}{\mathit{\sigma }d-b-\overline{c}q}+{\int }_0^{t^{\ast }}{d}^{-1}{e}^{\mathit{\sigma }s}\hfill \\ \hfill & \times [b(\mathrm{\Delta }{e}^{-\overline{\mathit{\nu }}(s-\mathit{\tau }(s))}+\frac{\mathit{ϵ}}{\mathit{\sigma }d-b-\overline{c}q})\hfill \\ \hfill & +c{\int }_{s-\mathit{\theta }(s)}^{s}K(s-u)(\mathrm{\Delta }{e}^{-\overline{\mathit{\nu }}u}\hfill \\ \hfill & +\frac{\mathit{ϵ}}{\mathit{\sigma }d-b-\overline{c}q})\mathrm{d}u+\mathit{ϵ}]\mathrm{d}s.\hfill \end{array}$$ 53

By simple computation, one can get

$$\begin{array}{cc}& \frac{b\mathit{ϵ}}{d(\mathit{\sigma }d-b-\overline{c}q)}+\frac{ck\mathit{ϵ}}{d(\mathit{\sigma }d-b-\overline{c}q)}+d^{-1}\mathit{ϵ}\hfill \\ \hfill & =\frac{\mathit{ϵ}\mathit{\sigma }}{\mathit{\sigma }d-b-\overline{c}q}.\hfill \end{array}$$ 54

Noticing $0\le \mathit{\tau }(t)\le \mathit{\tau }$, one derives from (49), (53), and (54) that

$$\begin{array}{cc}\hfill v(t^{\ast })& <e^{-\mathit{\sigma }{t}^{\ast }}\{\mathrm{\Delta }+\frac{\mathit{ϵ}}{\mathit{\sigma }d-b-\overline{c}q}+d^{-1}\mathrm{\Delta }(b{e}^{\overline{\mathit{\nu }}\mathit{\tau }}\hfill \\ \hfill & +\overline{c}{\int }_0^{\mathit{\theta }(t)}K(s)e^{\overline{\mathit{\nu }}s}\mathrm{d}s){\int }_0^{t^{\ast }}{e}^{(\mathit{\sigma }-\overline{\mathit{\nu }})s}\mathrm{d}s\hfill \\ \hfill & +\frac{\mathit{ϵ}\mathit{\sigma }}{\mathit{\sigma }d-b-\overline{c}q}{\int }_0^{t^{\ast }}{e}^{\mathit{\sigma }s}\mathrm{d}s\hfill \\ \hfill & =\mathrm{\Delta }{e}^{-\overline{\mathit{\nu }}{t}^{\ast }}+\frac{\mathit{ϵ}}{\mathit{\sigma }d-b-\overline{c}q},\hfill \end{array}$$

which contradicts (51). So (50) holds. Letting $\mathit{ϵ}\to 0$, one gets from the lemma 3 in Yang et al. (2011a) that

$$\begin{array}{c}\hfill V(t)\le v(t)\le \mathrm{\Delta }{e}^{-\overline{\mathit{\nu }}t},t\ge 0,\end{array}$$

which implies $\Vert e(t)\Vert \le \frac{1}{\sqrt{d}}{sup}_{-\mathit{\vartheta }\le s\le 0}\Vert \mathit{\upsilon }(s)-\mathit{\varphi }(s)\Vert \exp (-\frac{\overline{\mathit{\nu }}}{2}t)$ for $t\ge 0$. According to Definition 4, the neural networks (1) and (16) realize global exponential synchronization under the (31). This completes the proof.$\square$

In Theorem 2, for given $\mathit{\eta }$ and $d$, different values of $\mathit{\alpha },\mathit{\beta }$ lead to different value of $T_m$. It is well known that larger $T_m$ can further reduce the control cost. In order to enlarge the value of $T_m$, appropriate values of $\mathit{\alpha }$ and $\mathit{\beta }$ in (35) should be taken. The following Corollary 1 solves this problem.

Corollary 1

Suppose that the assumptions $({\mathrm{H}}_1)$-$({\mathrm{H}}_5)$ are satisfied. Then the neural networks (1) and (16) can achieve global exponential synchronization under the impulsive controller (31), if the inequalities (33), (34) and the following inequality hold:

$$\begin{array}{c}\hfill -c+L\Vert A\Vert +\frac{L\Vert B\Vert }{\sqrt{d}}+\sqrt{\frac{q}{d}}L\Vert D\Vert +\frac{lnd}{2T_m}<0,\end{array}$$ 55

where $c$ and $T_m$ are defined in Theorem 2.

Proof

Define the function $g(\mathit{\alpha },\mathit{\beta })$ with variables $\mathit{\alpha }>0,\mathit{\beta }>0$ as

$$\begin{array}{cc}\hfill g(\mathit{\alpha },\mathit{\beta })& =-2c+2L\Vert A\Vert +L\Vert B\Vert \mathit{\alpha }+L\Vert D\Vert \mathit{\beta }\hfill \\ \hfill & +\frac{lnd}{T_m}+d^{-1}(\frac{L\Vert B\Vert }{\mathit{\alpha }}+\frac{qL\Vert D\Vert }{\mathit{\beta }}).\hfill \end{array}$$

In order to reduce the conservativeness of (35) holds, we only need to find a point $(\overline{\mathit{\alpha }},\overline{\mathit{\beta }})$ such that $g(\overline{\mathit{\alpha }},\overline{\mathit{\beta }})$ takes the minimum value and $g(\overline{\mathit{\alpha }},\overline{\mathit{\beta }})<0$. By simple computation, one has $\frac{\mathit{\partial }g}{\mathit{\partial }\mathit{\alpha }}=L\Vert B\Vert -\frac{L\Vert B\Vert }{d{\mathit{\alpha }}^2}$ and $\frac{\mathit{\partial }g}{\mathit{\partial }\mathit{\beta }}=L\Vert D\Vert -\frac{PL\Vert D\Vert }{d{\mathit{\beta }}^2}$. Let $\frac{\mathit{\partial }g}{\mathit{\partial }\mathit{\alpha }}=\frac{\mathit{\partial }g}{\mathit{\partial }\mathit{\beta }}=0$, one gets $(\overline{\mathit{\alpha }},\overline{\mathit{\beta }})=(\frac{1}{\sqrt{d}},\sqrt{\frac{q}{d}})$. Since $\frac{{\mathit{\partial }}^{2}g}{\mathit{\partial }{\mathit{\alpha }}^2}{|}_{(\overline{\mathit{\alpha }},\overline{\mathit{\beta }})}\frac{{\mathit{\partial }}^{2}g}{\mathit{\partial }{\mathit{\beta }}^2}{|}_{(\overline{\mathit{\alpha }},\overline{\mathit{\beta }})}-{\left(\frac{{\mathit{\partial }}^{2}g}{\mathit{\partial }\mathit{\alpha }\mathit{\partial }\mathit{\beta }}{|}_{(\overline{\mathit{\alpha }},\overline{\mathit{\beta }})}\right)}^2=\frac{4}{\sqrt{q}}d{L}^2\Vert B\Vert \Vert D\Vert >0$ and $\frac{{\mathit{\partial }}^{2}g}{\mathit{\partial }{\mathit{\alpha }}^2}{|}_{(\overline{\mathit{\alpha }},\overline{\mathit{\beta }})}=2\sqrt{d}L\Vert B\Vert >0$, $g(\mathit{\alpha },\mathit{\beta })$ takes the minimum value at the point $(\overline{\mathit{\alpha }},\overline{\mathit{\beta }})=(\frac{1}{\sqrt{d}},\sqrt{\frac{q}{d}})$. Let $g(\frac{1}{\sqrt{d}},\sqrt{\frac{P}{d}})<0$, one derives (28). This completes the proof.$\square$

Remark 8

When the activation function $f(x)$ is continuous, the constant $P$ becomes zero. In this case, the state feedback controller (20) and impulsive controller (31) are also effective, and the constant $\mathit{\eta }$ can be chosen as $\mathit{\eta }\ge 0$. When $\mathit{\eta }=0$, the controllers (20) and (31) become the classical the state feedback (Liu et al. 2011) and impulsive controllers (Yang et al. 2011b), respectively. Moreover, the bounded distributed delay becomes the usual one when the delay kernel $K(t)=1$. It is obvious from Lemma 4 and the proofs of Theorems 1 and 2 that the distributed delay can be extended to the unbounded case. Hence, the results of this paper are general and are applicable to neural networks with both discontinuous and continuous activations.

Remark 9

In this paper, the existence of Filippov solutions to a class of discontinuous neural networks with time-varying mixed delays is solved, analysis technology is different from those in Liu et al. (2012) and Cai and Huang (2011). One may think that whether the existence of the solution of (17) is guaranteed when the controller is added to the system. This problem can still be solved in this paper. In the case that $u(t)$ is state feedback controller (20), the existence of the solution of (17) is guaranteed by using the same analysis technique in the proof of Lemma 1. In the case of impulsive controller (31), one can first translate (17) into the form of (46) by using the similar the method in (43–46), then apply the same analysis technique in the proof of Lemma 1. In order to avoid tedious repetition, we do not give all the proofs in this paper.

Examples and simulations

In this section, numerical examples and figures are given to show the theoretical results obtained above. Consider the following delayed neural networks:

$$\begin{array}{cc}\hfill \dot{x}(t)& =-Cx(t)+Af(x(t))+Bf(x(t-\mathit{\tau }(t)))\hfill \\ \hfill & +D{\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)f(x(s))\mathrm{d}s+I,\hfill \end{array}$$ 56

where $x(t)={(x_1(t),x_2(t))}^T$, $\mathit{\tau }(t)=0.8-0.2sint$, $\mathit{\theta }(t)=0.3$, $K(t)=4^{-0.2t}$, $C=\mathrm{diag}(1.2,1)$, $I={(1.5,0.5)}^T$, and

$$\begin{array}{c}\hfill A=\left(\begin{array}{cc}3& -0.3\\ 8& 5\end{array}\right),B=\left(\begin{array}{cc}-1.4& 0.1\\ 0.3& -7\end{array}\right),D=\left(\begin{array}{cc}-1.2& 0.1\\ -2.8& -1\end{array}\right),\end{array}$$

the activation function is $f(x)=(f_1(x_1),f_2(x_2))$ with

$$\begin{array}{c}\hfill f_i(x_i)=\left\{\begin{array}{c}\hfill tanh(x_i)+0.05,x_i>0,i=1,2,\\ \hfill tanh(x_i)-0.05,x_i<0,i=1,2.\end{array}\right.\end{array}$$

Figure 2 shows the trajectory of (56) with initial condition $x(t)={(0.4,0.6)}^T,t\in [-1,0]$.

Fig. 2.

Trajectory of system (56) with initial value $x(t)={(0.4,0.6)}^T,t\in [-1,0]$

Obviously, neural network (56) satisfies $({\mathrm{H}}_1$–${\mathrm{H}}_5)$ with $\mathit{\tau }=1,\mathit{\theta }=0.3$, $h=0.2$, $L=1$, $P=0.1$, $q=0.2879$. Now consider the following controlled response system of system (56):

$$\begin{array}{cc}\hfill \dot{y}(t)& =-Cy(t)+Af(y(t))+Bf(y(t-\mathit{\tau }(t)))\hfill \\ \hfill & +D{\int }_{t-\mathit{\theta }(t)}^{t}K(t-s)f(y(s))\mathrm{d}s+I+u(t),\hfill \end{array}$$ 57

When no controller is added to the response system (57), the systems (56) and (57) can not realize synchronization, see Fig. 3.

Fig. 3.

Time response of the trajectory error $e(t)=y(t)-x(t)$ between systems (56) and (57) without control

In the first case, we use the state feedback controller (20). Take $\mathit{\alpha }=0.1$. By simple computation, we get $R_1\ge 18.2444$, $R_2\ge 18.4444$, $P(\Vert A\Vert +\Vert B\Vert +q\Vert D\Vert )=1.8664$. Take $R_1=18.2444$, $R_2=18.4444$, $\mathit{\eta }=1.9662$. According to Theorem 1, system (57) can be exponentially synchronized with (56) under the state feedback controller (20) and the convergence rate is $\mathit{\alpha }=0.1$.

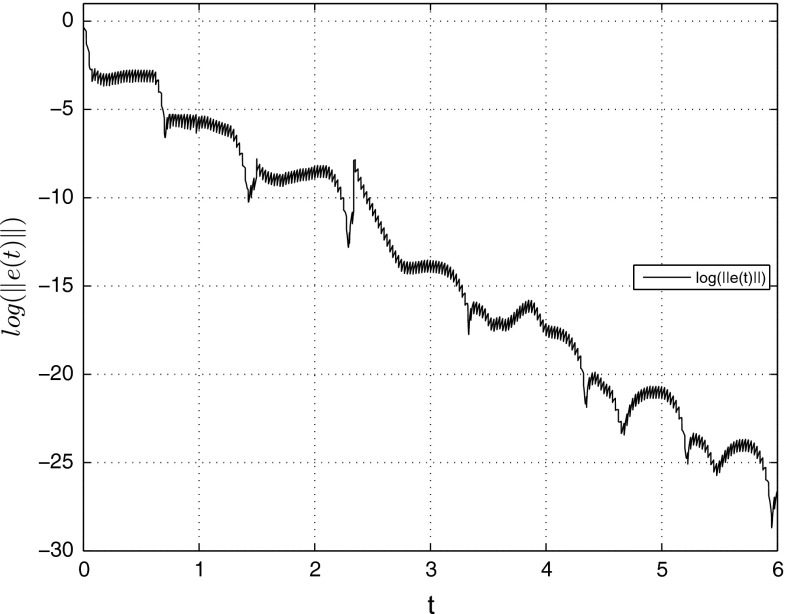
In the numerical simulations, we use the forward Euler method, which was used in Danca (2004) to obtain numerical solution of differential inclusions. The parameters in the simulations are taken as: step-length is 0.0005, $y(t)={(-0.1,1.1)}^T$ for $t\in [-1,0]$. The trajectory of $log(\Vert e(t)\Vert )=log(\Vert y(t)-x(t)\Vert )$ is presented in Fig. 4, from which one can see that $log(\Vert e(t)\Vert )\le \mathit{\omega }(t)=-4.9t+0.5$, so the convergence rate of $\Vert e(t)\Vert$ is larger than 4.9, which is larger than $\mathit{\alpha }=0.1$. Therefore, the results in Theorem 1 are verified.

Fig. 4.

Time response of $log(\Vert e(t)\Vert )$ between systems (56) and (57) via state feedback controller (20)

Now we construct impulsive controllers. Taking $E=-0.5I_2$, $k\in {\mathbb{N}}_{+}$, $t_k-t_{k-1}=T_m=0.025$, it is obtained that $d=0.25<1$ and

$$\begin{array}{cc}& -c+L\Vert A\Vert +\frac{L\Vert B\Vert }{\sqrt{d}}+\sqrt{\frac{q}{d}}L\Vert D\Vert \hfill \\ \hfill & +\frac{lnd}{2T_m}=-1.562<0,\hfill \end{array}$$

According to the above computation in the first case, we still take $\mathit{\eta }=1.9662$. Then the inequalities (33), (34) and (55) are satisfied. According to Corollary 1, system (57) can be exponentially synchronized with (56) under the impulsive controller (31).

In the numerical simulations, the other parameters and initial values of $y(t)$ are the same as those in the first case. The trajectory of $log(\Vert e(t)\Vert )=log(\Vert y(t)-x(t)\Vert )$ are presented in Fig. 5, which verify the effectiveness of Corollary 1, and hence the Theorem 2 is also effective.

Fig. 5.

Time response of $log(\Vert e(t)\Vert )$ between systems (56) and (57) via impulsive controller (31)

Remark 10

Numerical examples and simulations specify the effectiveness of the designed controllers and the obtained results. However, results and numerical simulations in Liu et al. (2011) only get quasi-synchronization for systems with discontinuous right-hand side under the linear state feedback controller $u_i(t)=-k_i{e}_i(t),i=1,2,\dots ,n$ (for instance see Remark 6, Corollary 2, and Figs. 8–10 in Example 3 in the reference Liu et al. (2011)). From the proofs of Theorems 1–2 and and Corollary 1 and the numerical simulations one can see that the term $-\mathit{\eta }\mathrm{sign}(e_i(t))$ in the controllers plays a key role in dealing with the uncertain measurable functions $\mathit{\gamma }(t)\in F(x(t))$ and $\mathit{\delta }(t)\in F(y(t))$ between the drive and response systems. Therefore, theoretical results and numerical simulations in this paper improve those in Liu et al. (2011).

Conclusion

The issue of controlled synchronization of neural networks with discontinuous activations has intrigued increasing interests of researchers from different fields. However, few published paper considered complete synchronization control of such system with mixed delays. Hence, this paper study the exponential synchronization of neural networks with discontinuous activations with mixed delays. Strict mathematical proof guaranteeing the global existence of Filippov solutions to neural networks with discontinuous activation functions and mixed delays has been given. Both state feedback control and impulsive control techniques have been considered. The designed controllers are simple and can be applied to neural networks with discontinuous and continuous activations. Compared with existing results which only quasi-synchronization can be realized, the obtained results of this paper are better. Numerical simulations show that the theoretical results are effective.

It is well known that finite-time synchronization means the optimality in convergence time Yang and Cao (2010). Recently, authors in Forti et al. (2005) investigated the global convergence in finite time for a subclass of neural networks with discontinuous activations and constant delay. However, finite-time synchronization in an array of coupled general neural networks with discontinuous activations and time-varying mixed delays has not been considered in the literature, this is an interesting and challenging problem to be considered in our future research.