A HIERARCHICAL MULTI-UNIDIMENSIONAL IRT APPROACH FOR ANALYZING SPARSE, MULTI-GROUP DATA FOR INTEGRATIVE DATA ANALYSIS

Abstract

The present paper proposes a hierarchical, multi-unidimensional two-parameter logistic item response theory (2PL-MUIRT) model extended for a large number of groups. The proposed model was motivated by a large-scale integrative data analysis (IDA) study which combined data (N = 24,336) from 24 independent alcohol intervention studies. IDA projects face unique challenges that are different from those encountered in individual studies, such as the need to establish a common scoring metric across studies and to handle missingness in the pooled data. To address these challenges, we developed a Markov chain Monte Carlo (MCMC) algorithm for a hierarchical 2PL-MUIRT model for multiple groups in which not only were the item parameters and latent traits estimated, but the means and covariance structures for multiple dimensions were also estimated across different groups. Compared to a few existing MCMC algorithms for multidimensional IRT models that constrain the item parameters to facilitate estimation of the covariance matrix, we adapted an MCMC algorithm so that we could directly estimate the correlation matrix for the anchor group without any constraints on the item parameters. The feasibility of the MCMC algorithm and the validity of the basic calibration procedure were examined using a simulation study. Results showed that model parameters could be adequately recovered, and estimated latent trait scores closely approximated true latent trait scores. The algorithm was then applied to analyze real data (69 items across 20 studies for 22,608 participants). The posterior predictive model check showed that the model fit all items well, and the correlations between the MCMC scores and original scores were overall quite high. An additional simulation study demonstrated robustness of the MCMC procedures in the context of the high proportion of missingness in data. The Bayesian hierarchical IRT model using the MCMC algorithms developed in the current study has the potential to be widely implemented for IDA studies or multi-site studies, and can be further refined to meet more complicated needs in applied research.

1. Introduction

Combining data in meaningful ways and making more robust inferences using all available data are important scientific goals in many disciplines, including psychology. In particular, meta-analysis utilizing individual participant-level data (IPD) or integrative data analysis (IDA), in which raw data from multiple studies are combined for a consolidated analysis, provides a tool to improve our understanding in ways that individual studies are not well equipped to accomplish. However, as pointed out by Curran and Hussong (2009), IDA projects face unique challenges that are different from those encountered in independent, single studies. One such challenge is to establish common metrics for a pooled data set combined from multiple independent studies that are similar in key research designs but do not have identical measures. Thus, the challenge of establishing commensurate metrics across different studies and samples, and across time, is a critical first step for IDA studies. Several approaches to this measurement challenge have been utilized in the literature. For example, Curran et al. (2008) utilized a unidimensional, two-parameter logistic (2PL) IRT model, and Bauer and Hussong (2009) utilized moderated nonlinear factor analysis (MNLFA). Others utilized a longitudinal invariant Rasch test (LIRT) and simultaneously estimated both latent traits and latent growth curve parameters (McArdle, Grimm, Hamagami, Bowles, & Meredith, 2009). Although these existing approaches extend the boundary of our capacity in the field of psychological assessment, they can be rather limited when one wants to estimate latent traits from multiple related dimensions or to establish latent trait scores to be more widely used for other subsequent investigations. Furthermore, when multiple, independent studies are involved, it is of value to model different sample/study characteristics more explicitly, when calculating individual-level trait scores. Finally, the existing studies developed their approaches to integrate data across just a few studies (i.e., two or three). Given the many promising utilities of IDA (see Curran & Hussong, 2009), it is important to establish a method that can be utilized more generally with a large number of independent studies.

The current study was motivated by a large-scale IDA study, Project INTEGRATE (Mun et al., 2011), which combined data (N = 24,336) from 24 independent alcohol intervention studies. We proposed a hierarchical, two-parameter multi-unidimensional logistic item response theory (2PL-MUIRT) model extended for multiple groups (or studies) and developed new Markov chain Monte Carlo (MCMC) algorithms from a hierarchical Bayesian perspective, which is an extension from the existing work by de la Torre and Patz (2005) on the 3PL-MUIRT model. In particular, the current MCMC algorithms were designed specifically to handle multiple groups (i.e., studies in the context of IDA), which is an important theoretical extension to the literature. We modified and expanded the MCMC algorithms used in a previous study (e.g., de la Torre & Patz, 2005) to estimate the correlation matrix of an anchor group (in the multiple-group situation, a group for which constraints are imposed is called the anchor group) and covariance matrices of the remaining groups. Existing algorithms typically imposed constraints on the item parameters to allow for estimation of the covariance matrices (e.g., Fox & Glas, 2001). The algorithms developed in the current paper are more consistent with the tradition of constraining the latent distribution (i.e., structural parameters), rather than the existing approach of constraining the item parameters, to deal with IRT model indeterminacies. The selection of an anchor group was based on several criteria and is described in section 6. With this modification, the current algorithms can simultaneously estimate latent traits, item parameters, and hierarchical model parameters (the mean vector, correlation/covariance matrices). In subsequent sections, we explain the conceptual and mathematical foundations of this new MUIRT model in greater detail. We then present findings from a simulation study. We provide a real data analysis, in which we applied this flexible IRT approach to the IDA data set mentioned above. Finally, we show the results from an additional simulation study to examine robustness of the MCMC procedures against the high proportion of missingness in the real data set.

2. Item Response Theory

Item response theory (IRT), also known as latent trait theory (Lazarsfeld & Henry, 1968; Lord & Novick, 1968), is a psychometric framework that has been extensively used in the area of educational testing and measurement. Traditionally, IRT has provided a single measure of a latent trait, or ability, θ. As an extension of the unidimensional IRT, multidimensional IRT (MIRT) models can model participants’ performance while taking multiple abilities, θs, into account. As a result, MIRT has the potential to offer richer and more nuanced information than unidimensional IRT. In the past several decades, to meet the increasing need to describe the complex interactions between test takers (or survey participants) and test items (or scale items) from more than one dimension, numerous MIRT models have been developed and applied to real data (e.g., see Reckase, 2009; van der Linden & Hambleton,1997), such as the two-parameter and three-parameter logistic multidimensional models (Reckase, 1996) and the normal-ogive multidimensional model (Adams, Wilson, & Wang, 1997; McDonald, 1997).

The multidimensionality considered by the MIRT models can be classified by the within-item and between-item types (Adams et al., 1997; Hartig&Höhler, 2009;Millsap&Maydeu-Olivares, 2009). In a within-item multidimensionality model each item is designed to measure multiple ability dimensions simultaneously, whereas models with between-item multidimensionality contain items that measure only one of multiple abilities. The latter is a special type of MIRT, also known as the multi-unidimensional IRT (MUIRT) model, which is equivalent to an overall test, consisting of multiple unidimensional subtests (e.g., de la Torre & Patz, 2005; Sheng & Wikle, 2007). In general, the within-item model is appropriate for analyzing a test or questionnaire in which each item measures two or more latent traits that can explicitly be defined, whereas the between-item model is appropriate for analyzing a test that measures several subsets or domains (Oshima, Raju, & Flowers, 1997; Wang, Wilson, & Adams, 1995).

In the present study, we utilize the Bayesian estimation framework via MCMC to estimate a between-item MUIRT model. MCMC is well suited for complex models that cannot be estimated easily using traditional estimating algorithms, such as the expectation-maximization algorithm (EM; Dempster, Laird, & Rubin, 1977). In recent years, MCMC has received greater attention from researchers and practitioners in the areas of psychology, measurement, and educational testing. Particularly, MCMC has broadly been applied to the estimation of MIRT models, which is generally assumed to be challenging and complex (e.g., see Béguin & Glas, 2001; Bolt & Lall, 2003; de la Torre & Patz, 2005; Sheng & Wikle, 2008). In contrast to the traditional estimation procedures, such as the EM algorithm, MCMC is relatively easy to implement because it does not require knowing the exact form of the joint posterior distribution or obtaining mathematical derivatives. From a Bayesian perspective, MCMC is a class of simulation algorithms that iteratively draw samples from probability distributions (typically, joint posterior distributions and/or full conditional distributions) based on a stochastic process of Markov chains, in which the current state depends only on the immediately preceding value of the chain and is thus conditionally independent of all other previous values (Gill, 2002). Two MCMC approaches commonly used in practice are Gibbs (Casella&George, 1992) and Metropolis–Hastings (M–H;Chib&Greensberg, 1995) sampling algorithms. In the current study, we used both MCMC sampling procedures.

3. Hierarchical 2PL-MUIRT Model

De la Torre and Patz (2005) simplified the compensatory MIRT model proposed by Reckase (1996) into the 3PL-MUIRT model by providing a restriction that each item measures only one latent trait dimension. The MUIRT model proposed by de la Torre and Patz can be extended for multiple groups. We express this extension in the 2PL-MUIRT form because the 2PL model is a special case of the 3PL model and it is of the central interest in our study:

$$P(X_{gij(d)}=1|{\theta }_{gi(d)},{\alpha }_{j(d)},{\beta }_{j(d)})=\frac{\text{exp}[{\alpha }_{j(d)}({\theta }_{gi(d)}-{\beta }_{j(d)})]}{1+\text{exp}[{\alpha }_{j(d)}({\theta }_{gi(d)}-{\beta }_{j(d)})]},$$ (1)

where X_gij(d) is the response of respondent i in group g to the j th item of dimension d; θ_gi(d) is the dth component of vector θ _gi (i.e., θ _gi = {θ_gi(d)}); α_{j (d)} and β_{j (d)} are the discrimination and difficulty parameters, respectively, of the j th item of dimension, d = 1, …, D; and j (d) = 1 (d), …, J (d); and ${\sum }_{d=1}^{D}J(d)=J$.

A hierarchical structure on the latent trait means and covariances across groups is imposed on this model so that θ _gi is assumed to have a multivariate normal distribution characterized by its higher-level parameters, namely the mean vector and covariance structure. In other words, θ _gi ~ N(μ_g, Σ_g). Here, we use the term, hierarchical structure to describe the multi-layer structure of the MUIRT model of interest, and this is different from the higher-order IRT model (de la Torre & Hong, 2009; de la Torre & Song, 2009), in which a higher-order overall latent trait is formulated to subsume several lower-level domain abilities. Although a higher-order structure can be added to the current model, we focus on a more general case, that is, latent trait domains are fully characterized by their means and covariance structures in the present study for the purpose of illustration.

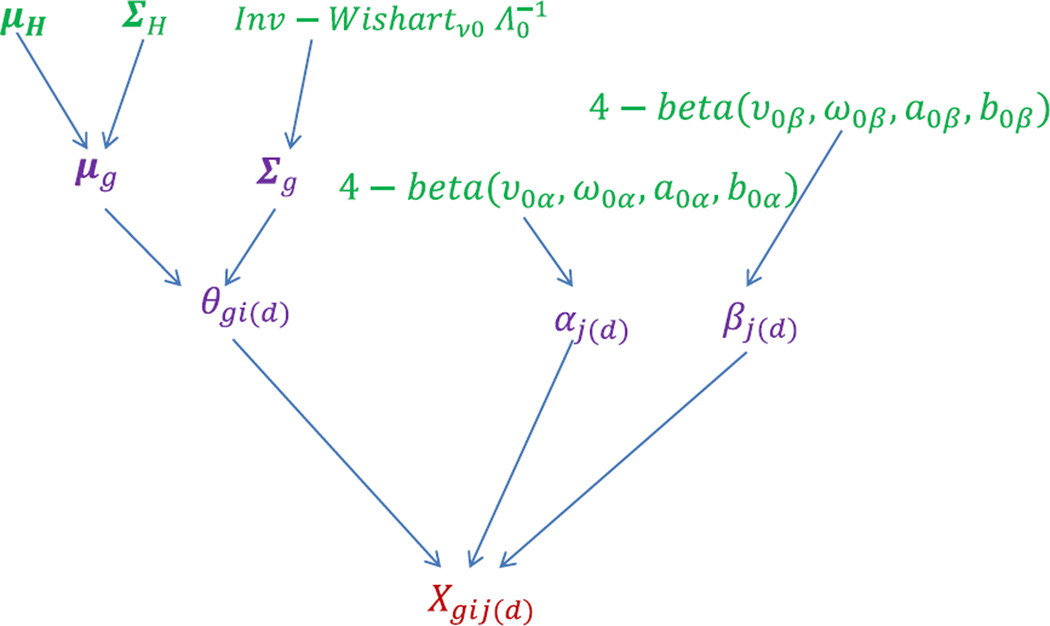
A graphical representation of the hierarchical structure of the MUIRT model for multiple groups is presented in Figure 1. Figure 1 shows how the response by respondent i in group g on item j measuring dimension d, X_{gi j (d)} can be modeled using item parameters, α_{j (d)} and β_{j (d)}, as well as latent trait parameters, θ_gi(d), which are characterized by their mean vector μ_g and covariance structure Σ_g in a hierarchical fashion.

Figure 1.

A directed acyclic graph of the MUIRT model for multiple groups.

The likelihood of the data matrix X_g (g = 1, …, G) is given by

$$L({\mathit{X}}_g|{\mathit{\theta }}_g,{\mathit{\mu }}_g,{\mathbf{\Sigma }}_g,\mathit{\alpha },\mathit{\beta })=\prod _{d=1}^D\prod _{i=1}^I\prod _{j(d)=1(d)}^{J(d)}{[P_{gij(d)}({\theta }_{gi(d)})]}^{X_{gij(d)}}{[1-P_{gij(d)}({\theta }_{gi(d)})]}^{1-X_{gij(d)}}.$$ (2)

The model formulation shown above is open and flexible to incorporate additional estimation components of parameters if necessary. Note that the response matrix is assumed to be complete, and it contains no missing data. When this model is applied to real data, however, the issue of missingness needs to be addressed. We will discuss this in greater detail in the application section.

The approach taken in the present study to accommodate multiple groups differs from those utilized in a few existing MCMC algorithms for multiple-group MIRT applications. In contrast to the existing MCMC algorithms (e.g., Fox & Glas, 2001) that estimate covariance matrices for all groups and address model indeterminacies by constraining item parameters (e.g., fixing one discrimination parameter to 1 and one difficulty parameter to 0), we estimate the correlation matrix for the anchor group as well as the covariance matrices for all other remaining groups by constraining the means and the variances of the anchor group to be 0s and 1s, respectively, and then estimating the correlation matrix for the anchor group. This approach is consistent with the IRT tradition of constraining the latent distribution in dealing with model indeterminacies (e.g., see Cai, Thissen, & du Toit, 2011; Chalmers, 2012). To directly estimate the correlation matrix, we adapted the relevant MCMC algorithms (Liu, 2008; Liu&Daniels, 2006). More detailed steps are explained in the section below. All the estimation codes were written and implemented in the Ox program (Doornik, 2009). Readers who are interested in the estimation codes can contact the authors for further information.

4. Markov Chain Monte Carlo Estimation

4.1. Prior, Posterior, and Conditional Distributions

For the hierarchical Bayesian formulation illustrated in Figure 1, the following prior distributions were used for the estimation of all parameters of interest. Note that the informativeness of the prior for the covariance matrix is determined by the degrees of freedom of the Inverse–Wishart distribution. In the present study, a small df (i.e., D + 2) was used to make the priors relatively uninformative.

$${\mathit{\mu }}_g~\mathrm{M}\mathrm{V}\mathrm{N}({\mathit{\mu }}_H,{\mathbf{\Sigma }}_H);$$

where μ_H was set to 0s and Σ_H was a correlation matrix with the off-diagonal elements set to 0.5s.

$${\mathit{\theta }}_{gi}~\mathrm{M}\mathrm{V}\mathrm{N}({\mathit{\mu }}_g,{\mathbf{\Sigma }}_g);{\mathbf{\Sigma }}_g~\text{Inv}-{\text{Wishart}}_{\nu 0}({\mathrm{\Lambda }}_0^{-1}),$$

where ν₀ = D + 2 and the diagonal and off-diagonal elements of Λ₀ were set to 1s and 0.5s, respectively;

$${\alpha }_{j(d)}~4-\text{Beta}({\upsilon }_{0\alpha },{\omega }_{0\alpha },a_{0\alpha },b_{0\alpha });\text{and}{\beta }_{j(d)}~4-\text{Beta}({\upsilon }_{0\beta },{\omega }_{0\beta },a_{0\beta },b_{0\beta }).$$

The 4-Beta distribution is the four-parameter beta distribution, that is, Beta (υ, ω, a, b), where, in addition to the shape parameters υ and ω, a and b are the location parameters defining the support of the distribution. With additional parameters a and b, the support of the Beta distribution is extended from (0, 1) to (a, b), therefore, the 4-Beta distribution can be used to specify more flexibly different supports for the prior distributions of the discrimination and difficulty parameters in the MCMC estimation. It is more convenient than specifying the lognormal and normal distributions for the discrimination and difficulty parameters, respectively, to bound the supports.

The joint posterior distribution of interest is:

$$P({\mathit{\mu }}_g,{\mathbf{\Sigma }}_g,{\mathit{\theta }}_{gi},\mathit{\alpha },\mathit{\beta }|{\mathit{X}}_g)\propto P({\mathit{X}}_g|{\mathit{\theta }}_{gi},\mathit{\alpha },\mathit{\beta })\times P({\mathit{\theta }}_{gi}|{\mathit{\mu }}_g,{\mathbf{\Sigma }}_g)\times P({\mathbf{\Sigma }}_g|{\mathit{\nu }}_0,{\mathbf{\Lambda }}_0)\times P({\mathit{\mu }}_g|{\mathit{\mu }}_H,{\mathbf{\Sigma }}_H)\times P(\mathit{\alpha }|{\upsilon }_{0\alpha },{\omega }_{0\alpha },a_{0\alpha },b_{0\alpha })\times P(\mathit{\beta }|{\upsilon }_{0\beta },{\omega }_{0\beta },a_{0\beta },b_{0\beta }).$$ (3)

The joint distribution above cannot be fully simplified into an explicit and exact distribution for samples to be drawn. Therefore, we decompose the joint posterior distribution above into several full conditional distributions so that samples can be drawn relatively more easily.

The full conditional distribution of θ _gi is:

$$P({\mathit{\theta }}_{gi}|{\mathit{X}}_g,{\mathit{\mu }}_g,{\mathbf{\Sigma }}_g,\mathit{\alpha },\mathit{\beta })\propto P({\mathit{X}}_g|{\mathit{\theta }}_{gi},\mathit{\alpha },\mathit{\beta })\times P({\mathit{\theta }}_{gi}|{\mathit{\mu }}_g,{\mathbf{\Sigma }}_g).$$ (4)

Because there is no closed form solution to express the full conditional distribution of θ _gi, it is impossible to evaluate the distribution and draw samples directly from it within the MCMC sampling process. However, the Metropolis–Hastings (M–H) algorithm (e.g., Chib&Greensberg, 1995) can be applied to draw samples indirectly from the distribution.

The full conditional distribution of μ_g is a multivariate distribution, denoted as $\mathrm{M}\mathrm{V}\mathrm{N}({\mathit{\mu }}_{(g)}^{(1)},{\mathbf{\Sigma }}_{(g)}^{(1)})$. The two parameters of the distribution can be expressed in explicit forms, that is, ${\mathit{\mu }}_g~\mathrm{M}\mathrm{V}\mathrm{N}(\frac{{\mathrm{\Lambda }}_0^{-1}{\mu }_0+n{\mathrm{\Sigma }}^{-1}\mathrm{\theta ̄}}{{\mathrm{\Lambda }}_0^{-1}+n{\mathrm{\Sigma }}^{-1}},{(\frac{1}{{\mathrm{\Lambda }}_0}+\frac{n}{\mathrm{\Sigma }})}^{-1})$. The Gibbs algorithm (Casella & George, 1992) can be used to draw samples directly from this known distribution.

The full conditional distribution of Σ_g is P(Σ_g|θ _gi) ∝ P(Σ_g)P(θ _gi |Σ_g,μ_g). This full conditional distribution can be written as an Inv-Wishart_νl $({\mathrm{\Lambda }}_I^{-1})$, where ν_I = ν₀ + I and ${\mathrm{\Lambda }}_I={\mathrm{\Lambda }}_0+\mathbf{\Sigma }{\mathit{\theta }}_i{\mathit{\theta }}_i^{\prime }$, and thus can be directly sampled using the Gibbs approach.

Instead of drawing Σ_g, sometimes it is necessary to draw the correlation matrix R. For example, when the covariance structure is assumed to be common across different groups, the common covariance structure is often constrained as the correlation matrix to avoid estimation indeterminacy. If the covariance structures are allowed to vary across groups, the covariance structure of the anchor group becomes equivalent to the correlation matrix R. In the current simulation study, three groups are allowed to have different covariance structures. Therefore, the correlation matrix for the anchor group and the two covariance matrices for the remaining two groups need to be estimated. With regard to drawing R, first, samples are drawn from the conditional distribution of Σ, which is the Inverse-Wishart distribution, and the sampled Σ is then transformed into the corresponding R. The provisional R is accepted based on a Metropolis– Hastings (M–H) acceptance probability, that is, the probability calculated from comparing the determinant of the correlation matrix obtained from the previous draw and current draw. For the more detailed description of the procedures of sampling the correlation matrix R, see Liu (2008), and Liu and Daniels (2006).

The full conditional distribution of the item parameters (i.e., α and β) is $P(\mathbf{\alpha },\mathbf{\beta })\propto \prod _{d=1}^D\prod _{j(d)=1(d)}^{J(d)}P({\mathbf{X}}_{gi(d)}|{\mathit{\theta }}_{gi})P({\alpha }_{j(d)})P({\beta }_{j(d)})$. The M–Halgorithm is used to indirectly draw samples from this distribution.

4.2. MCMC Algorithms

Below we describe a procedure for sampling the parameters of interest from their full conditional distributions. Assume that g = G is the anchor group. At iteration t,

• Step 1: Draw ${\mathbf{\Sigma }}_g^{(t)}$ conditionally on ${\mathit{\theta }}_g^{(t-1)}$ and ${\mathit{\mu }}_g^{(t-1)}$, for g = 1, 2, …, G − 1, and R^(t) conditionally on ${\mathit{\theta }}_G^{(t-1)}$ and μ_G = 0;

• Step 2: Draw ${\mathit{\mu }}_g^{(t)}$ conditionally on ${\mathbf{\Sigma }}_g^{(t)}$ and ${\mathit{\theta }}_g^{(t-1)}$, for g = 1, 2, …, G − 1;

• Step 3: Draw ${\mathit{\theta }}_g^{(t)}$ conditionally on ${\mathit{\mu }}_g^{(t)},{\mathbf{\Sigma }}_g^{(t)}$, and α^{(t − 1)} and β^{(t − 1)}, for g = 1, 2, …, G − 1, and ${\mathit{\theta }}_G^{(t)}$ conditionally on μ_G = 0, R^(t), α^{(t − 1)} and β^{(t − 1)}; and

• Step 4: Draw α^(t) and β^(t) conditionally on θ, where $\mathit{\theta }=\{{\mathit{\theta }}_g^{(t)}\}$, g = 1, 2, …, G.

The procedure above can easily be adapted for a situation with a common mean and/or a common covariance structure, where common μ and/or R are estimated across multiple groups.

Multiple chains (e.g., four chains) with different initial values can be run to monitor the convergence of the algorithm. Each chain can have m iterations, and the first n iterations of each chain can be discarded as the burn-in period. The convergence for the structural parameters (i.e., the item parameters, mean matrix and covariance matrix) was determined using the Gelman–Rubin (G–R) diagnostic (Gelman & Rubin, 1992). The G–R diagnostic compares the ratio of the weighted average of the within-chain variance and between-chain variance to the within-chain variance. If this ratio is close to 1 (e.g., less than 1.1 or 1.2; Gelman, Carlin, Stern, & Rubin, 2004), it indicates that the chains have reached the stationary distribution.

The parameter estimates of interest are based on the posterior mean (i.e., expected a posteriori; EAP) across multiple chains, and relevant formulas are shown below:

$${\mathbf{\Sigma }}_g\approx \frac{1}{m-n}\sum _{t=n+1}^m{\mathbf{\Sigma }}^{(t)};\mathit{\rho }\approx \frac{1}{m-n}\sum _{t=n+1}^m{\mathit{\rho }}^{(t)};{\mathit{\theta }}_g\approx \frac{1}{m-n}\sum _{t=n+1}^m{\mathit{\theta }}^{(t)};{\mathit{\mu }}_g\approx \frac{1}{m-n}\sum _{t=n+1}^m{\mathit{\mu }}^{(t)};{\alpha }_{j(d)}\approx \frac{1}{m-n}\sum _{t=n+1}^m{\alpha }_{j(d)}^{(t)}\text{and}{\beta }_{j(d)}\approx \frac{1}{m-n}\sum _{t=n+1}^m{\beta }_{j(d)}^{(t)}.$$

To fully utilize the results obtained from multiple chains with different starting values, the formulas above yield averaged values across multiple chains. Four chains with the length of 75,000 with the first 10,000 as burn-in were used in both the simulation study and the real data analysis.

5. A Simulation Study

5.1. Simulation Design

The implementation of the MCMC algorithm for the hierarchical 2PL-MUIRT model with multiple groups is illustrated using a simulation study in this section. The simulation design in the current study contains three groups, with each group consisting of 1,000 individuals. The respondents in each group were assumed to come from a multivariate normal distribution with five dimensions. Group 1 was the anchor group and consequently the mean vector of Group 1 was set to 0. The covariance matrix of Group 1 became essentially the correlation matrix. The off-diagonal elements of the correlation matrix of Group 1 were set to 0.4. The remaining Groups 2 and 3 were set to be heterogeneous in terms of different scaling constants, i.e., Σ₂ = 0.75 × Σ₁ and Σ₃ = 1.25 × Σ₁, respectively. The values of the mean vectors in Group 2 were 0.3, 0.4, 0.5, 0.6, and 0.7, for the five dimensions. The values of the mean vectors in Group 3 had the same values as those in Group 2 with opposite signs, that is, −0.3, −0.4, −0.5, −0.6, and −0.7. Thirty items were randomly drawn from a pool of 80 2PL IRT item parameters. Their discrimination and difficulty parameters are presented in Table 1. To ensure identical item quality across dimensions, these 30 items were repeated five times and used in the simulation phase as a 150-item test, measuring five correlated traits. All three groups (a total sample size of 3,000) had complete responses on the 150 items. The model formulation and the MCMC algorithms followed those given in the previous sections. A total of 25 replication data sets were generated and analyzed.

Table 1.

Item parameters used in the simulation study (first 30 items).

Item	Discrimination	Difficulty	Item	Discrimination	Difficulty
1	1.288	0.193	16	1.554	0.693
2	1.320	−0.080	17	1.390	1.076
3	1.260	0.881	18	0.930	−0.668
4	1.092	1.300	19	0.906	−0.028
5	1.120	0.164	20	1.366	1.852
6	0.995	1.096	21	1.258	1.821
7	1.010	0.562	22	0.919	1.797
8	1.366	1.488	23	0.944	1.751
9	1.110	−1.351	24	1.253	−0.654
10	0.956	1.557	25	0.910	−1.013
11	1.050	0.134	26	0.977	−0.942
12	0.937	−0.408	27	0.974	−0.244
13	0.682	1.503	28	1.231	−0.604
14	1.125	1.504	29	0.780	−1.236
15	1.105	1.746	30	1.099	−1.162

5.2. Results

The G–R diagnostic values calculated for the mean vectors, covariance structures, and item parameters showed that the chain had reached convergence (i.e., the G–R diagnostic values across all parameters were less than 1.1).¹ Table 2 presents the MCMC estimates and the true values of the mean vectors in Groups 2 and 3. In general, the MCMC estimates of the means of the five dimensions in Groups 2 and 3 were close to their true values. Note that all the MCMC parameter estimates were averaged across the 25 replications.

Table 2.

MCMC estimates of mean vectors in Groups 2 and 3.

Dimension	Group 2		Group 3
	True value	Estimate	True value	Estimate
1	0.300	0.297	−0.300	−0.306
2	0.400	0.398	−0.400	−0.392
3	0.500	0.492	−0.500	−0.497
4	0.600	0.593	−0.600	−0.601
5	0.700	0.687	−0.700	−0.690

The correlation matrix of Group 1 and the covariance matrices of Groups 2 and 3 had 5 × 5 dimensional spaces. The true values of the off-diagonal correlation elements were 0.4 and the diagonal elements of the covariance matrices were 0.75 and 1.25, for Groups 2 and 3, respectively. The off-diagonal elements of the covariance matrices of Group 2 and Group 3 were 0.3 and 0.5, respectively. The bias and root mean square error (RMSE) for the off-diagonal and diagonal elements in the different groups are summarized in Table 3. The correlation matrix of Group 1 was very accurately recovered; the values of bias and RMSE were all essentially 0. The values of bias and RMSE of the off-diagonal and diagonal elements of the covariance matrices in Groups 2 and 3were extremely small, indicating that all elements of the covariance matrices were essentially accurately estimated.

Table 3.

The bias and RMSE of the MCMC estimates of the correlation/covariance matrix in Groups 1–3.

		Group 1	Group 2	Group 3
Bias	Off-diagonal	−0.004	−0.005	−0.005
	Diagonal		−0.011	−0.020
RMSE	Off-diagonal	0.005	0.005	0.006
	Diagonal		0.014	0.023

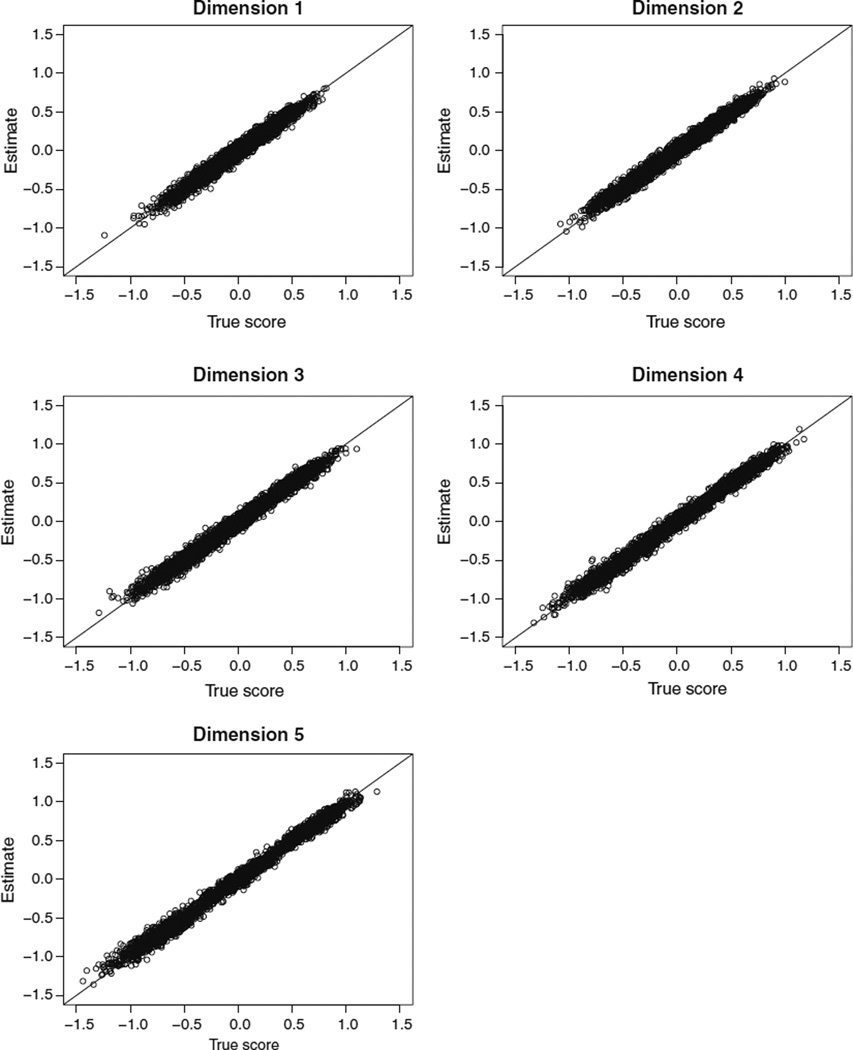
Figure 2 shows the scatter plots of the true and estimated latent trait scores on the five dimensions for 3,000 respondents (from all three groups) averaged over 25 replications. All five plots show that the true and estimated trait scores were highly correlated (Pearson’s r ≥ .98 across all five dimensions).

Figure 2.

Scatter plots of true and estimated latent traits from all three groups for five dimensions.

Table 4 shows bias and RMSE of the discrimination and difficulty parameters across the five dimensions, as well as for each dimension. Overall, the values of bias and RMSE of the discrimination and difficulty parameter estimates were very small, which indicates that these item parameters were accurately recovered. Note also that the discrimination and difficulty parameters measuring different dimensions were comparatively estimated despite that different levels existed across different dimensions.

Table 4.

Bias and RMSE of the discrimination and difficulty parameter estimates of the 150 items.

	Bias		RMSE
Dimension	Discrimination	Difficulty	Discrimination	Difficulty
1	0.007	−0.005	0.013	0.009
2	0.014	−0.002	0.017	0.012
3	0.011	−0.002	0.014	0.009
4	0.012	−0.004	0.018	0.012
5	0.019	−0.007	0.022	0.018
Overall	0.013	−0.004	0.017	0.012

De la Torre and Patz (2005) showed that taking into account associations across different dimensions as auxiliary information can help derive better latent trait estimates. We adopted this approach and extended it further in two major aspects. First, the current MCMC algorithms incorporated more estimation components, such as mean parameters of the latent traits and the item parameters. The simulation results showed that they could be estimated accurately along with other parameters. Second, the current MCMC algorithms were extended for the use with multiple groups. In conclusion, the MCMC algorithms developed in the present study show that it is feasible for the proposed 2PL-MUIRT model with multiple groups to accurately estimate the parameters of interest.

6. Application of the New MCMC Algorithms to the Project INTEGRATE Data

6.1. Basic Description

As we briefly discussed earlier, we developed the 2PL-MUIRT model to establish a commensurate metric across different studies pooled for Project INTEGRATE (Mun et al., 2011). Project INTEGRATE was launched to overcome existing methodological limitations of individual studies, such as lack of sufficient sample size and homogeneous samples, in the field of college alcohol intervention research. Project INTEGRATE combined data across 24 independent studies, which had several key design features in common across the studies, all of which utilized a variant of brief motivational interventions (BMI; e.g., the Brief Alcohol Screening and Intervention for College Students [BASICS; Dimeff, Baer, Kivlahan, & Marlatt, 1999]) to reduce risky drinking and harmful consequences, but differed in measures, longitudinal follow-up designs, and sample characteristics. Thus, establishing common metrics across the studies was a first critical step toward analyzing the pooled data as a single data set. In the present study, we focus on alcohol-related problems data as an example. The ultimate goal of this application was to derive valid latent trait scores for all individuals across the studies, which are based on common metrics and thus are commensurate.

We analyzed a total of 69 items assessed in 20 out of total 24 studies. Items for alcohol-related problems came from the Rutgers Alcohol Problem Index (RAPI; White & Labouvie, 1989), the Young Adult Alcohol Problems Screening Test (YAAPST;Hurlbut&Sher, 1992), the Brief Young Adult Alcohol Consequences Questionnaire (BAACQ;Kahler, Strong,&Read, 2005), the Alcohol Use Disorders Identification Test (AUDIT; Saunders, Aasland, Babor, De La Fuente, & Grant, 1993), and the Alcohol Dependence Scale (ADS; Skinner & Allen, 1982; Skinner & Horn, 1984). For each item, responses were dichotomized to indicate 1 = Yes; 0 = No, because this response format was the common denominator across studies. When someone did not drink during the time frame referenced (e.g., in the past month), their score was coded as zero. Based on the literature, we conceptualized the alcohol-related problems trait as constituting the following four dimensions: responsibility (dimension 1); interpersonal (dimension 2); dependence-like symptoms (dimension 3); and acute heavy-drinking (dimension 4).

6.2. Data Structure and Missingness

Some of the challenges we encountered were that the overall structure for the combined data was very sparse (i.e., high rate of missing data), and that the items were sometimes slightly differently worded across the studies. We had two types of missing data: participant-level missing data (i.e., participants did not answer) and study-level missing data (i.e., items were not assessed). Table 5 provides a glimpse of the missing patterns at the item level. It presents the number of participants who answered the 13 items from Dimension 1 across the 20 studies that assessed items in this dimension. In Table 5, zero indicates study-level missing data. The different numbers within rows are due to participant-level missing data. The missing pattern shown in Table 5 clearly reveals that the merged data set had a large portion of missingness. Overall, the proportion of missing data in the entire data set (N = 22, 608) was approximately 0.57. In addition, studies had different follow-up schedules and follow-up rates across time and discrepant sample sizes at baseline. For example, Studies 8a through 8c each had participants in thousands, whereas Studies 5, 6, and 17 had no more than 200 participants each.

Table 5.

The missingness pattern of 13 items in dimension 1: responsibility.

Study	Item
	1	2	3	4	5	6	7	8	9	10	11	12	13
1	0	0	0	0	348	347	344	347	0	0	0	0	0
2	0	0	0	0	230	230	230	230	0	0	0	0	0
3	225	0	225	0	0	0	0	0	225	225	225	225	225
4	0	0	0	0	707	706	707	707	707	707	707	0	707
5	0	0	0	0	167	167	167	167	0	0	0	0	0
6	111	0	0	0	111	111	111	111	0	0	0	0	0
8a	0	0	0	0	6385	6385	6383	6370	6374	6385	6381	0	6378
8b	0	0	0	0	4977	4972	4972	4970	4976	4980	4978	0	4968
8c	0	0	0	0	2813	2813	2813	2810	2819	2823	2823	0	2810
9	0	0	0	0	830	830	829	830	1379	1379	1379	0	1377
10	452	0	0	0	453	455	455	454	0	0	0	0	0
11	383	0	0	0	383	383	383	383	0	0	0	0	0
12	0	0	334	0	0	0	0	0	334	334	334	333	335
15	246	0	0	0	246	246	246	246	0	0	0	0	0
16	0	0	0	0	287	287	287	287	181	0	0	0	182
17	0	0	0	0	120	120	120	120	0	0	0	0	0
18	0	328	329	328	0	0	0	0	0	0	0	0	0
19	0	0	0	0	1188	1189	1186	1186	0	0	0	0	0
20	0	0	302	0	944	939	943	945	672	704	705	301	698
21	288	0	0	0	288	288	288	288	0	0	0	0	0

The sparsity shown in Table 5 resulted in isolated situations where overlap in items across the studies was weak, especially when slightly differently worded items were treated differently. We identified three pairs of items that were highly similar in wording and collapsed each pair into one single item after consulting with experts in the alcohol research field. Examples of similarly worded items are “I have not gone to work or missed classes at school because of drinking, a hangover, or an illness caused by drinking.” versus “Have you not gone to work or missed classes at school because of drinking, a hangover, or an illness caused by drinking?” This collapsing step reduced the total number of unique items from 69 to 66.2 This step of collapsing similarly worded items met the following two goals: (1) to reduce the proportion of missing data and (2) to increase common linkages among different studies. Although IRT allows that items come from different tests and different scales, IRT modeling needs an adequate number of linking (i.e., common) items to bridge multiple tests to establish a common metric for data from multiple sources. In practice, people need to be cautious to collapse similarly worded items because the process of collapsing items requires an assumption that the items have identical parameters. It should be noted that different wordings can result in differences in item parameters. However, in combining different scales into one big data structure, the pooled data set inevitably became very sparse. To address issues related to data sparsity, it is sometimes necessary to collapse highly similar items to enhance item coverage across different studies. In this project, the pairs of items eligible for item collapsing were identified by a group of the domain experts in the alcohol research field, who determined that valid conceptual evidence allowed for such collapsing. Although item collapsing is not a standard procedure in many IRT applications, we chose this option to arrive at a practical solution that allowed us to carry out the real data analysis.

Sparse data matrices can lead to ill-conditioned covariance matrices, which in turn cause estimation problems for methods relying on them, such as factor analysis. This is because estimation methods under the factor analysis framework are based on the covariance structure of data, therefore, an effective estimation requires the minimum coverage of the covariance matrix (i.e., overlap of items across observations). Although this can be relaxed somewhat, the highly sparse data that we had, due to the pooling of data across the studies, could not fulfill this relaxed requirement. As an alternative, one could use commercially available IRT software programs, which can estimate model parameters based on the original response matrix rather than the covariance matrix computed from the raw data, and thus can be better suited for sparse data. However, the hierarchical formulation of our problem was uniquely complex for such programs. Although there are many popular commercial IRT software packages that can handle missing data or multiple groups, etc., no commercially available program exists that could be tailored enough to sufficiently meet our needs to fit the hierarchical model in a multiple-group situation. Programming our own MCMC algorithm gave us maximal control and full flexibility for the estimation purpose.³ Therefore, we implemented the MCMC algorithms, as illustrated in the previous sections, that were more flexible to deal with the specific problems that emerged from the current data set. The goal of the real data analysis was to apply the 2PL-MUIRT model to the current data set.

The missing data patterns (Table 5) show that the majority of the missing patterns were due to the design factor created when the 20 studies were combined into one data set. Since there is no systematic, unobserved reason to cause missing data as noted by Schafer (1997), we deemed that missing at random (MAR) was a reasonable assumption for our data and that any inference bias would be ignorable. Béguin and Glas (2001) illustrated how MCMC procedures for complete data can be adapted to incomplete data designs. The key for this adaptation is to create a matrix that differentiates the missing and nonmissing data using binary entries so that the MCMC estimation can skip the missing data and use only the nonmissing data. This procedure is commonly called “not presented” (NP) and is available in many standard statistical software packages, such as BILOGMG (Zimowski, Muraki, Mislevy, & Bock, 2003). Finch (2008) investigated multiple methods dealing with missing data for IRT item parameter estimation and showed that NP is one of the three methods that effectively limit item parameter estimation bias due to missing responses.

6.3. MCMC Estimation and Algorithms

The earlier simulation section that illustrated the MCMC algorithms gives the general modeling framework for the 2PL-MUIRT model with multiple groups that was developed for the present study. In principle, the MCMC algorithms can be modified in a number of ways to meet various needs in applied research. Specifically, for the alcohol-related problems data, we applied the following approach within this framework: the different-μ with the common covariance approach. Although estimating different covariance matrices can be implemented as demonstrated in the simulation study, it could be unstable compared to estimating the common covariance structure due to the sparse nature of the given data. As a result, choosing the common covariance structure solution is a more feasible approach in the current application. Choice of the anchor group was guided by (1) moderate sample size, (2) not too extreme response means, and (3) fairly good item coverage. Study 4 was selected as the anchor group because both its sample size and parameter estimates were not extreme and it had fairly good item coverage.

To improve estimation accuracy, another hierarchical component was included to estimate the means of μ_g across different groups (g = 1, …, G), denoted as μ_H. It should be noted that μ_H is a vector of length D and μ_g is also a vector for group g. Combining μ_g for all groups together resulted in a mean matrix in G × D dimensions. The prior distribution of each element of μ_H is $N(0,{\tau }_H^2)$.

The joint posterior distribution including μ_H can be expressed as:

$$P({\mathit{\mu }}_g,{\mathit{\mu }}_H,{\mathbf{\Sigma }}_g,{\mathit{\theta }}_{gi},\mathit{\alpha },\mathit{\beta }|{\mathit{X}}_g)\propto P({\mathit{X}}_g|{\mathit{\theta }}_{gi},\mathit{\alpha },\mathit{\beta })\times P({\mathit{\theta }}_{gi}|{\mathit{\mu }}_g,{\mathbf{\Sigma }}_g)\times P({\mathbf{\Sigma }}_g)\times P({\mathit{\mu }}_g|{\mathit{\mu }}_H,{\mathbf{\Sigma }}_H)\times P({\mathit{\mu }}_H|{\tau }_H^2·\mathit{I})\times P(\mathit{\alpha }|{\upsilon }_{0\alpha },{\omega }_{0\alpha },a_{0\alpha },b_{0\alpha })\times P(\mathit{\beta }|{\upsilon }_{0\beta },{\omega }_{0\beta },a_{0\beta },b_{0\beta }).$$ (5)

Accordingly, the full conditional distribution of μ_H is $MVN({\mathit{\mu }}_H^{(1)},{\mathbf{\Sigma }}_H^{(1)})$. μ_g was drawn from its full distribution, but each element was drawn differently and contingent on whether this element was missing or nonmissing. If μ_g(d) was nonmissing, drawing this element was based on θ_gi(d) and μ_H(d). Otherwise, drawing this element was based on μ_H(d) only. Reciprocally, μ_H was drawn based only on nonmissing μ_g(d). The remaining aspects of the MCMC algorithms were basically identical to those in the simulation study except that a common correlation matrix across the different groups was assumed and estimated.

The entire MCMC procedure proceeded in two stages: (1) calibration and (2) scoring. In the calibration stage essential model parameters were estimated and subsequently used in the scoring stage, in which latent trait scores for the entire sample were estimated.⁴ Because Studies 8a, 8b, and 8c had considerably larger samples than others, only 10 % of the sample from Studies 8a, 8b, and 8c were randomly selected to compose the calibration sample. As a result, the size of the calibration sample was 9,798, consisting of a random sample of 10 % of the sample from these three studies and all participants from the rest of the studies. Therefore, all studies were included in the calibration stage and the complexity and characteristics of the entire data set were preserved in the reduced calibration sample, with the only difference being the reduced number of participants in the calibration stage. In a pilot study, the estimation results obtained from the calibrated sample and from the entire sample were very similar. Based on this pilot study finding, we chose to use the reduced sample in the calibration stage. Compared to using the entire sample (N = 22,608), it was more efficient to use a relatively smaller calibration sample for estimating the structural parameters of the model. In the calibration stage, the MCMC procedures simultaneously estimated μ_g, μ_H, Σ_g, α, β, and the latent trait scores for the reduced sample. Because μ_H was not directly related to the latent trait scores (i.e., θ _gi), only the estimates of μ_g, Σ_g, α, and β were employed in the scoring stage to estimate the latent trait scores on the four dimensions for all eligible participants in the entire sample. In other words, μ_g, Σ_g, α, and β were treated as the “known parameters” in the scoring stage, which allowed us to estimate θ _gi through the MCMC procedures without the need to estimate them again.

A total of four chains with different starting values were implemented for the calibration stage. Each chain had 75,000 draws and the initial 10,000 iterations were considered as the burn-in phase. The G–R diagnostic values computed for all of the parameters in the μ_g,μ_H, α, and β were less than 1.12, which indicated convergence was reached.

6.4. Missing Data and MCMC Estimation: Simulation Results

An additional simulation study was conducted upon completion of the calibration stage. Unlike the simulation study reported in the previous section, the purpose of this simulation was to examine whether the large proportion of missing data would cause biased parameter estimation. This simulation study proceeded as follows. First, a new data set with the same sample size as the calibration sample was generated using the parameter estimates (i.e., mean, correlation and item parameter estimates) obtained from the calibration stage. Second, this generated data set was converted to an incomplete data set with the exactly same pattern of missingness as the calibration sample. The calibration procedure detailed in the previous section was then applied to the generated calibration sample to estimate the model parameters. If the MCMC estimation procedure is robust to missing data, the parameter estimates from the simulated data should be close to the true values obtained from the calibration sample. Good quality θ scores depend mostly on the accuracy of the model parameter estimates from the calibration stage. We used “bias” to measure the difference between the two sets of values: the “known” true values of the generated calibration sample and their estimates.

Table 6 presents the bias values of μs. The magnitudes of the bias of μ varied across the different studies and dimensions, but they were in general small. The largest absolute bias was no greater than 0.2 and the smallest bias was essentially 0.⁵ Given the missingness that existed in the generated calibration sample, the estimated μs for different studies and dimensions were reasonably close to the estimated μs in the calibration sample. As shown in Table 7, the values of bias of the off-diagonal elements of the correlation matrix were essentially equal to 0s, which indicated that the missingness had very little effect on the estimation of the correlation matrix of the real data. Table 8 presents the average bias of the item discrimination and difficulty parameters on the four dimensions and the average bias across the four dimensions. Based on the sizes of bias, the discrimination parameter was affected less by the missingness than the difficulty parameter. The largest bias was observed for the difficulty parameter estimates of Dimension 1, which was −0.088, and the overall bias of the difficulty parameter estimates across the four dimensions was −0.053.

Table 6.

Bias of µ_g on different dimensions.

Study	Dimension
	1	2	3	4
1	−0.080	−0.015	0.002	−0.105
2	−0.065	−0.092	0.028	−0.057
3	−0.009	−0.061	−0.063	−0.030
4	–	–	–	–
5	−0.031	0.021	0.003	−0.086
6	−0.198	−0.113	−0.126	−0.184
8a	−0.103	−0.058	−0.024	−0.038
8b	−0.105	−0.079	−0.018	−0.111
8c	−0.098	−0.004	0.014	−0.036
9	−0.078	−0.102	0.020	−0.068
10	−0.113	−0.062	0.001	−0.070
11	−0.081	−0.064	0.001	−0.114
12	−0.065	−0.098	−0.061	−0.027
15	−0.007	−0.011	−0.030	−0.113
16	−0.060	−0.124	−0.060	0.014
17	−0.043	0.122	0.02	−0.177
18	−0.182	−0.188	−0.054	−0.023
19	−0.086	−0.051	−0.042	−0.087
20	−0.095	−0.037	−0.043	−0.057
21	−0.067	0.013	−0.089	−0.060
Overall	−0.078	−0.050	−0.026	−0.071

Table 7.

Bias of Σ_g.

	Dimension
Dimension	1	2	3	4
1	0.000
2	0.003	0.000
3	0.003	0.011	0.000
4	0.009	0.018	0.004	0.000

Table 8.

Average bias of the discrimination and difficulty parameter estimates.

	Bias
Dimension	Discrimination	Difficulty
1	0.017	−0.088
2	−0.035	−0.043
3	0.006	−0.045
4	−0.042	−0.042
Overall	−0.005	−0.053

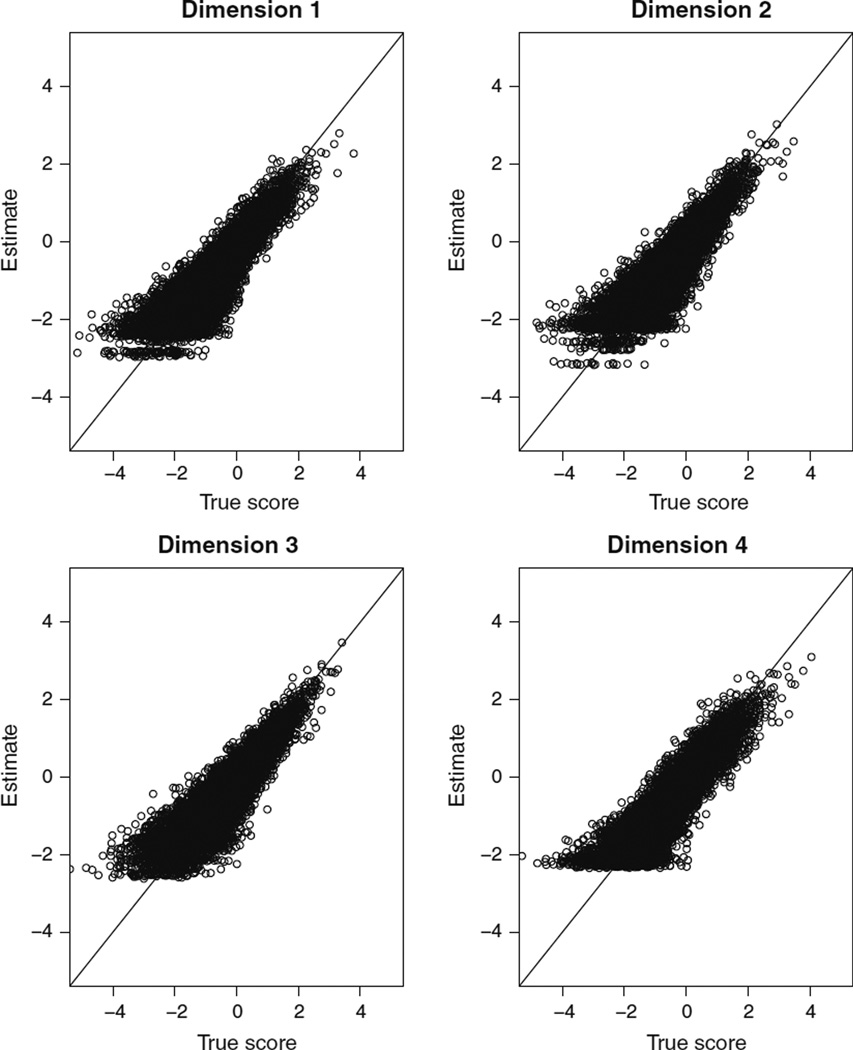
Table 9 shows the correlations of the θ estimates of the calibration sample and the generated calibration sample. The X-axis of the scatter plots in Figure 3 represents the θ estimates of the calibration sample and they were the true values of the θs of the generated calibration sample. The correlations on the four dimensions were generally high, ranging from 0.873 to 0.894. Moreover, overestimation was observed at the lower end of the θ scale. The minor distortion indicates estimation shrinkage, and it is probably due to the fact that items are difficult relative to the population/s of interest. The θ estimates are a function of the test information and the prior distribution. In general, a test that contains a few relatively “easy” items will be more informative for respondents with low latent trait scores, whereas a test with relatively “difficult” items is less informative for those respondents. In the latter case, the test will not be able to discriminate among respondents at the lower end of the latent trait distribution so that the prior distribution tends to dominate the scores of these examinees. Thus, even though their latent trait scores are different, their response patterns, and consequently, their estimated scores are not. The lack of gradient in the estimated scores of examinees with low latent trait scores can be deemed a floor effect. The items for alcohol-related problems had many zero responses. Consequently, there was not a lot of useful information in data for those at the lower end of the latent trait scale. With less information, the estimates shrank to the means of the distributions, which were close to zero.

Table 9.

Correlations of the theta estimates of the calibration sample and generated calibration sample.

	Dimension 1	Dimension 2	Dimension 3	Dimension 4
Correlation	0.881	0.873	0.882	0.894

Figure 3.

Scatter plots of theta estimates in the calibration sample and the generated calibration sample.

In sum, the current simulation study showed that the MCMC procedure could achieve relatively reasonable parameter estimates even with the huge proportion of missingness (0.57) in the real data set. Therefore, we concluded that the parameter estimates obtained from the calibration stage could be applied to the subsequent scoring stage and that θs could accurately be estimated.

6.5. Posterior Predictive Model Check

The general idea of posterior predictive model check (PPMC) is to simulate data with sufficient replications using the estimates of the item parameters and person parameters of a model. A number of PPMC discrepancy measures are generally drawn based on the comparison between the generated and observed data. Commonly utilized discrepancy measures are observed score distributions, proportion correctness, correlations, and log ratios of item pairs. For these discrepancy measures, the posterior predictive p value (ppp; Meng, 1994) can be used to evaluate the model fit (see Béguin & Glas, 2001; Sinharay, Johnson, & Stern, 2006 for PPMC application examples in IRT). The ppp can be understood as a Bayesian counterpart of the significance probability from a frequentist perspective. It indicates that the probability of the discrepancy measure of the simulated data is different from that of the observed data. A moderate ppp (i.e., 0.025 < ppp < 0.975) suggests good fit, whereas an extreme ppp-value (close to 1 or 0) indicates poor fit.

The discrepancy measure used for the PPMC procedure in the present study was the proportion correct (i.e., the proportion of responses endorsing the “correct” or “agree” answers). In the current different-μ with the common correlation approach for the data analysis, the ppp showed that the model fit all items quite well (i.e., all ppp values were between 0.025 and 0.975).

6.6. Associations Between Latent Trait Scores and Original Scale Scores

To validate the newly derived latent trait scores estimated in the scoring stage of the MCMC procedure, we compared these scores with the original sum scores for the original scales used in each study. The averaged correlations between the theta dimensional scores and the original dimensional scores are presented in Table 10. The correlations between the MCMC scores and original scores were overall quite high (0.737–0.818). These results provided some evidence of the construct validity of the newly derived latent trait scores from the MCMC procedure.

Table 10.

Average correlations between the MCMC scores and the original scale scores for dimensions 1–4.

Dimension	Scale	Averaged correlation across studies
1	Responsibility	0.785
2	Interpersonal	0.766
3	Dependence-like symptoms	0.737
4	Acute Heavy-drinking	0.818

7. Discussion

The present study was aimed at developing a general IRT approach with the practical goal of developing commensurate measures across independent studies to be analyzed as a single data set for an IDA study, Project INTEGRATE. To be more specific, this present study extended the 2PL-MUIRT model into the multiple-group scenario, and developed the comprehensive MCMC algorithms to simultaneously estimate model parameters in the hierarchical Bayesian framework. The model proposed in the present study contains a large number of parameters to be estimated. Bayesian MCMC algorithms were developed for the model in the present study. The feasibility and effectiveness of the MCMC algorithms were examined using a simulation study. The simulation results showed that the item parameters and ability (i.e., severity or proficiency) scores, as well as the parameters of the hierarchical structures (i.e., the means and correlation/covariance structures for multiple groups), were accurately estimated. Furthermore, our study illustrated how the correlation matrix of an anchor group can be estimated. Many existing algorithms typically impose constraints on the item parameters and, therefore, estimate only covariance matrices. Our algorithm provides an alternative, i.e., constraining the mean and covariance of the anchor group, to deal with estimation indeterminacy that commonly exists in multiple-group situations.

In addition to our technical contributions, this study underscores the possibility of using the extended 2PL-MUIRT model with multiple groups as an IDA approach. This model and its MCMC algorithms can be used together as a general IRT approach to analyze data pooled from multiple independent studies. As demonstrated in the real data analysis, the algorithms developed in the present study have several advantages in analyzing pooled data sets. First, the developed algorithms can straightforwardly handle missing data, which is a common design artifact. The additional simulation study showed that the algorithms were robust against missingness. Second, the algorithms have significant flexibility to accommodate several key adaptations under the proposed framework. For example, an additional hierarchical structure, the higher-level mean, can be added to improve estimation of the mean part. The mean vectors/covariance matrices can be set to be identical or different across different groups. Third, although not shown in the present study, one potential advantage of the MCMC algorithms is that it is possible to obtain latent trait estimates for the dimensions that were systematically missing. It can be achieved through borrowing information from internal ancillary information (i.e., the estimates of the covariance structure and the mean vector of latent traits) as long as at least one of the dimensions had informative responses for a given group. As a result, it is possible for the MCMC algorithms to provide complete estimates on all dimensions of the latent traits, if at least one dimension is not missing. This feature may have important implications for IDA studies because for some studies some dimensions may have no responses at all. For those dimensions, the additional hierarchical structure can provide auxiliary information to allowestimation of latent traits not available through the traditional estimation approach.

Combining multiple groups in IDA results in increased sample sizes, which reduce measurement errors. In addition, increased sample sizes help estimate low-base rate item parameters. In the present study, due to the small sample sizes in some studies and data sparseness, some groups could not be analyzed by themselves for calibration of item parameters. Some of the items were endorsed too infrequently to estimate the item parameters in small samples and pooling data sets increased the number of observations for the low-frequency items, making it feasible to reasonably estimate the low-base rate item parameters. This is one additional, important benefit of pooling data sets from multiple sources.

Several studies have been conducted with respect to inferring latent traits in the presence of missing data. Mislevy (1991) adapted the multiple-imputation procedure (Rubin, 1987) to obtain latent traits in complex surveys. Thomas (2002) included covariates, in addition to the basic demographic variables, to improve the precision of inferring latent traits. Zeger and Thomas (1997) studied how information from some measured traits can improve the precision of the estimates of the means of other correlated traits using different matrix sampling designs. De la Torre (2009) used auxiliary information and correlational structure to improve multidimensional ability scoring. Unlike these previous approaches, the MCMC algorithms in the current study estimated the latent traits on the missing dimensions through the information from the mean vectors and covariance matrices. More thorough theoretical consideration and simulation studies are needed to further investigate the extent to which the structure of the latent traits can lead to precise estimation of latent traits not directly measured in the multiple-group IRT model.

Overall, the present study developed a new IRT approach to calibrate model parameters and score latent traits for the 2PL-MUIRT model with multiple groups in the Bayesian hierarchical fashion. From the IRT perspective, the present study, especially the real data analysis that involved different sets of items for different groups, was essentially about linking, i.e., the concurrent calibration for multiple groups in order to establish a common scale for model parameters and latent traits. Moreover, the present study went much beyond the scope of linking in that it utilized the core techniques of IRT as tools to tackle IDA challenges encountered by pooling a large number of alcohol intervention studies. Furthermore, to better serve the purpose of the present study, the MCMC algorithms were developed to make the complex model developed in the present study more feasible and applicable for IDA applications in the alcohol intervention research area as demonstrated here and potentially for other applied psychological research areas as well.

The present study had several limitations. First, we made an assumption that the same items administered in different studies had the same item parameters as specified in the item response function. We think that this is a reasonable, as well as practical, assumption. This assumption may be justified because all participants were college students (48 % first-year or incoming students; 76 %White; 40 % men). For many groups, these demographic and alcohol-related characteristics were similar. We did not have particular reasons to assume that participants in one university campus may react differently to the items compared to those in other university campuses. Thus, we assumed that item parameters would be the same across different groups. In addition, there was a limited number of common items that could be linked across groups. The assumption that common items were identical across different groups made it easier to construct test linkage. Given the challenging nature of our data (i.e., sparse data with the necessity of linking items across groups), this assumption simplified our tasks. With more complete data and more common items, DIF analysis could have been accommodated by the proposed model to better capture if there are any subtle differences across different groups (studies). Second, our two-stage approach may have introduced extra “noise” compared to one integrated, single-step approach in which latent trait scores are estimated along with all other model parameters. The added estimation errors may be the cost we pay for enhancing computational efficiency. Given the huge and complex data set to deal with, we chose the two-stage procedure as a practical solution specifically tailored for the challenges we had.

Last but not least, the algorithms developed in the present study can be further refined and modified. For example, the 2PL-MUIRT model with multiple groups can be extended to the generalized partial credit model in the multi-unidimensional framework for polytomous response data. In addition, this work can be extended to higher-order IRT models. De la Torre and his collaborators (de la Torre & Hong, 2009; de la Torre & Song, 2009) developed a higher-order IRT model, which addressed the linear relationship among multiple, multi-unidimensional abilities, and modeled it as the higher-order ability. Future research can take the higher-order IRT model into consideration to explore the linear relationship among the multi-unidimensional abilities and to construct their higher-order ability.