Processing scalar implicature: a Constraint-Based approach

Abstract

Three experiments investigated the processing of the implicature associated with some using a “gumball paradigm”. On each trial participants saw an image of a gumball machine with an upper chamber with 13 gumballs and an empty lower chamber. Gumballs then dropped to the lower chamber and participants evaluated statements, such as “You got some of the gumballs”. Experiment 1 established that some is less natural for reference to small sets (1, 2 and 3 of the 13 gumballs) and unpartitioned sets (all 13 gumballs) compared to intermediate sets (6–8). Partitive some of was less natural than simple some when used with the unpartitioned set. In Experiment 2, including exact number descriptions lowered naturalness ratings for some with small sets but not for intermediate size sets and the unpartitioned set. In Experiment 3 the naturalness ratings from Experiment 2 predicted response times. The results are interpreted as evidence for a Constraint-Based account of scalar implicature processing and against both two-stage, Literal-First models and pragmatic Default models.

1. Introduction

Successful communication requires readers and listeners (hereafter, listeners) to infer a speaker's intended meaning from an underspecified utterance. To this end listeners make use of the semantic and pragmatic information available in the linguistic input and the discourse context. However, it is an open question whether semantic information takes a privileged position in this reasoning process. In recent years, scalar implicatures as in (1) have served as an important testing ground for examining the time course of integration of semantic and pragmatic information in inferring a speaker’s intended meaning.

• (1)You got some of the gumballs.

  ⤹ You got some, but not all, of the gumballs.

The semantic content of the utterance in (1) is that the listener got at least one gumball (lower-bound meaning of some). Under some conditions, however, the listener is also justified in taking the speaker to implicate that he, the listener, did not get all of the gumballs (upper-bound meaning of some). This is a case of scalar implicature. The term “scalar” is used because the inference that gives rise to the upper-bound interpretation is assumed to depend upon a highly accessible set of alternatives that are ordered on a scale by asymmetrical entailment (Horn, 2004), and that the speaker could have selected but didn’t (e.g., <all, some>).

1.1. Overview

The current article focuses on how listeners compute the upper-bound interpretation, sometimes called pragmatic some. We first discuss the classic distinction between Generalized and Particularized Conversational Implicature, originally introduced by Grice (1975) to distinguish relatively context-dependent from relatively context-independent inferences. We then describe two processing hypotheses, the Default hypothesis and the two-stage, Logical/Semantic/Literal-First hypothesis, that have played a central role in guiding experimental investigations of how listeners arrive at an interpretation of pragmatic some. In doing so, we flesh out some of the assumptions that underlie these approaches. We propose a probabilistic Constraint-Based framework in which naturalness and availability of alternatives (along with other factors) play a central role in computing pragmatic some. We then focus on two superficially similar visual world experiments that test the two-stage hypothesis, finding strikingly different data patterns and arriving at opposite conclusions. We argue that the differences arise because of the naturalness and availability of other lexical alternatives to some besides the stronger scalar alternative all, in particular the effects of intermixing some and exact number with small set sizes. We test this claim in three experiments using a “gumball” paradigm.

1.2. Generalized and Particularized Conversational Implicatures

According to Grice (1975), scalar implicatures are an instance of Generalized Conversational Implicature (GCI). These are implicatures that are assumed to arise in the same systematic way regardless of context. In the case of scalar implicature, the speaker is taken to convey the negation of a stronger alternative statement that she could have made (and that would have also been relevant) but chose not to. Instead of (1), the speaker could have said, You got all of the gumballs, which would have also been relevant and more informative. Together with the additional assumption that the speaker is an authority on whether or not the stronger statement is true (the Competence Assumption, Sauerland, 2004; van Rooij & Schulz, 2004), the listener may infer that the speaker is conveying that the listener in fact got some, but not all, of the gumballs.

Generalized Conversational Implicatures are distinguished from Particularized Conversational Implicatures (PCI) which are strongly dependent on specific features of the context such as, the nature of the Question Under Discussion or QUD (Roberts, 1996). For example, if the sentence in (1) was uttered in a context in which the listener - say, a little boy - was complaining that he did not get any candy, the speaker – say, his mother - may be taken to implicate that he should stop complaining. However, this implicature does not arise if the context is modified slightly; for example, if uttered in a context where the child can’t see which objects came out of a prize machine and asks his parents whether he got all of the gumballs, the scalar implicature that he did not get all of the gumballs will presumably arise, whereas the implicature that he should stop complaining does not.

Although it is sometimes claimed that scalar implicatures arise in nearly all contexts (Levinson, 2000), scalar implicatures can, in fact, be canceled not only explicitly as in (2), but also implicitly as in (3).

• (2)You got some of the gumballs. In fact, you got all of them.
• (3)
  1. Did I get anything from the prize machine?
  2. You got some of the gumballs.

In (2) the implicature is explicitly canceled because it is immediately superseded by assertion of the stronger alternative. In (3) it is canceled implicitly because the preceding context makes the stronger alternative with all irrelevant. What matters to A in (3) is not whether he got all versus some but all of the gumballs, but whether he got any items at all (e.g. gumballs, rings, smarties) from the machine. This feature of implicit cancelability has played a crucial role in experimental studies of implicatures (e.g. Bott & Noveck, 2004; Breheny, Katsos, & Williams, 2006) because hypotheses about the time course of scalar implicature processing make different claims about the status of implicit implicature cancelation.

1.3. Processing frameworks

Formal accounts of conversational implicatures typically do not specify how a listener might compute an implicature as an utterance unfolds in a specific conversational context (e.g., Gazdar, 1979; Horn, 1984). Recently, however, there has been increased interest in how listeners compute scalar implicatures in real-time language comprehension. Most of this work has focused on distinguishing between two alternative hypotheses.

The first hypothesis is that implicatures are computed immediately and effortlessly due to their status as default inferences (Levinson, 2000; see also Chierchia, 2004 for a related account under which scalar implicatures are taken to arise by default in upward-entailing, but not in downward-entailing contexts). Under this Default account, scalar implicatures do not incur the usual processing costs associated with generating an inference. Only cancelation of an implicature takes time and processing resources. This view is motivated by considerations about communicative efficiency. Rapid, effortless inference processes for deriving GCIs are proposed as a solution to the problem of the articulatory bottleneck: while humans can only produce a highly limited number of phonemes per second, communication nevertheless proceeds remarkably quickly.

The inferences that allow listeners to derive context-dependent interpretations, such as those presumably involved in computing particularized implicatures, are assumed to be slow and resource-intensive, in the sense of classic two-process models of attention that distinguish between automatic processes, which are fast, require few resources and arise independent of context and controlled processes, which are slow, strategic and resource demanding (Neely, 1977; Posner & Snyder, 1975; Shiffrin & Schneider, 1977; also see Kahneman, 2011 for a related framework). In contrast, a scale containing a small set of lexical alternatives – like <all, some> - could be pre-compiled and thus automatically accessed, regardless of context. Because the default interpretation arises automatically, there will be a costly interpretive garden-path when the default meaning has to be overridden. Therefore the default model predicts that in all contexts, a default, upper-bound interpretation will precede a possible lower-bound interpretation.

The second hypothesis, also termed the Literal-First hypothesis (Huang & Snedeker, 2009), assumes that the lower-bound semantic interpretation is computed rapidly, and perhaps automatically, as a by-product of basic sentence processing. All inferences, including generalized implicatures require extra time and resources. Therefore the Literal-First hypothesis predicts that in all contexts a lower-bound interpretation will be computed before an upper-bound interpretation is considered. For proponents of the Literal-First hypothesis this follows from the traditional observation in the linguistic literature (e.g., Horn, 2004) that the semantic interpretation of simple declaratives containing some is in an important sense more basic than the pragmatic interpretation: the upper-bound interpretation some but not all always entails the lower-bound interpretation at least one¹. The pragmatic interpretation cannot exist without the semantic one, which translates into a two-stage processing sequence: upon encountering a scalar item like some, the semantic interpretation is necessarily constructed before the pragmatic one. To the extent that there is a processing distinction between generalized and particularized implicatures, it is that the relevant dimensions of the context and the interpretations that drive the inference are more circumscribed and thus perhaps more accessible for generalized implicatures.

The Default and two-stage models make straightforward predictions about the time course of the implicature associated with the upper-bound interpretation of utterances containing some. The Default hypothesis predicts that logical/semantic some should be more resource-intensive and slower than upper-bound, pragmatic some, whereas the two-stage model makes the opposite prediction.

There are, however, alternative Context-Driven frameworks in which the speed with which a scalar implicature is computed is largely determined by context (e.g., Breheny et al., 2006). For example, Relevance Theory (Sperber & Wilson, 1995), like the Literal-First hypothesis, assumes that the semantic interpretation is basic. In Relevance Theory the upper-bound meaning is only computed if required to reach a certain threshold of relevance in context. In contrast to the Literal-First hypothesis, however, Relevance Theory does not necessarily assume a processing cost for the pragmatic inference. If the context provides sufficient support for the upper-bound interpretation, it may well be computed without incurring additional processing cost. However, a processing cost will be incurred if the upper-bound interpretation is relevant but the context provides less support.

The Constraint-Based framework, which guides our research, is also Context-Driven. It falls most generally into the class of generative (i.e. data explanation) approaches to perception and action (Clark, 2013) which view perception as a process of probabilistic, knowledge-driven inference. Our approach is grounded in three related observations. First, as an utterance unfolds listeners rapidly integrate multiple sources of information. That is, utterance comprehension is probabilistic and constraint-based (MacDonald, Pearlmutter, & Seidenberg, 1994; Seidenberg & Macdonald, 1999; Tanenhaus & Trueswell, 1995). Second, listeners generate expectations of multiple types about the future, including the acoustic/phonetic properties of utterances, syntactic structures, referential domains, and possible speaker meaning (Chambers, Tanenhaus, & Magnuson, 2004; Chang, Dell, & Bock, 2006; Kutas & Hillyard, 1980; Levy, 2008; Tanenhaus, Spivey-Knowlton, Eberhard & Sedivy, 1995; Trueswell, Tanenhaus, & Kello, 1993). Third, interlocutors can rapidly adapt their expectations to different speakers, situations, etc. (Bradlow & Bent, 2008; Clayards, Tanenhaus, Aslin, & Jacobs, 2008; Fine, Jaeger, Farmer, & Qian, under review; Grodner & Sedivy, 2011; Kurumada, Brown, & Tanenhaus, 2012). Given these assumptions, standard hierarchical relations among different types of representations need not map onto temporal relationships in real-time processing. We illustrate these points with three examples grounded in recent results in the language processing literature.

The first example involves the mapping between speech perception, spoken word recognition, parsing and discourse. Consider a spoken utterance that begins with “The lamb… As the fricative at the onset of “the” unfolds, the acoustic signal provides probabilistic evidence for possible words, modulated by the prior expectations of these possible words, e.g., their frequency, likely conditioned on the position in the utterance. Thus, after hearing only the first 50 to 100 ms of the signal, the listener has partial evidence that “the” is likely to be the word currently being uttered. Put differently, the hypothesis that the speaker intended to say “the” begins to provide an explanation for the observed signal. In addition, there is evidence for a likely syntactic structure (noun phrase) and evidence that the speaker intends (for some purpose) to refer to a uniquely identifiable entity (due to presuppositions associated with the definite determiner the, Russell, 1905). Thus referential constraints can be available to the listener before any information in the speech signal associated with the production of the noun is available.

The second example focuses on the interpretation of referential expressions in context. Consider the instruction in (4):

• (4)Put the pencil below the big apple.

Assume that the addressee is listening to the utterance in the context of a scene with a large apple, a smaller apple, a large towel, and a small pencil. According to standard accounts of scalar adjectives, a scalar dimension can only be interpreted with respect to a reference class given by the noun it modifies (e.g. what counts as big for a building differs from what counts as big for a pencil). Translating this directly into processing terms, when the listener encounters the scalar adjective big, interpretation should be delayed because the reference class has not yet been established. However, in practice the listener’s attention will be drawn to the larger of the two apples before hearing the word apple because use of a scalar adjective signals a contrast among two or more entities of the same semantic type (Sedivy, Tanenhaus, Chambers, & Carlson, 1999). Thus, apple will be immediately interpreted as the larger of the two apples. More generally, addressees circumscribe referential domains on the fly, taking into account possible actions as well as the affordances of objects (Chambers, et al., 2004; Chambers, Tanenhaus et al., 2002; Tanenhaus et al., 1995).

Finally listeners rapidly adjust expectations about the types of utterances that speakers will produce in a particular situation. After brief exposure to a speaker who uses scalar adjectives non-canonically, e.g., a speaker who frequently overmodifies, an addressee will no longer assume that a pre-nominal adjective will be used contrastively (Grodner & Sedivy, 2011). Likewise, the utterance, It looks like a zebra is most canonically interpreted to mean The speaker thinks it’s a zebra (with noun focus), or You might think it’s a zebra, but it isn’t (with contrastive focus on the verb), depending on the context, the prosody, and the knowledge of the speaker and the addressee (Kurumada et al., 2012). Crucially, when a stronger alternative is sometimes used by the speaker, e.g., It is a zebra, then the interpretation of It looks like a zebra with noun focus is more likely to receive the but it’s not interpretation (Kurumada et al., 2012). Again an utterance is interpreted with respect to the context and the set of likely alternatives to the observed utterance.

When we embed the issue of when, and how quickly, upper- and lower-bound some are interpreted within a Constraint-Based approach with expectations and adaptation, then questions about time course no longer focus on distinguishing between the claim that scalar implicatures are computed by default and the claim that they are only computed after an initial stage of semantic processing. When there is more probabilistic support from multiple cues, listeners will compute scalar inferences more quickly and more robustly. Conversely, when there is less support, listeners will take longer to arrive at the inference, and the inference will be weaker (i.e. more easily cancelable). Under the Constraint-Based account, then, the research program becomes one of identifying the cues that listeners use in service of the broader goal of understanding the representations and processes that underlie generation of implied meanings.

1.4. Cues under investigation

We focus on two types of cues, both of which are motivated by the notion that speakers could have produced alternative utterances. The first cue is the partitive of, which marks the difference between (5) and (6).

• (5)Alex ate some cookies.
• (5)Alex ate some of the cookies.

While it may seem intuitively clear to the reader that (6) leads to a stronger implicature than (5), this intuition has not previously been tested. Moreover, researchers have used either one or the other form in their experimental stimuli without considering the effect this might have on processing. For example, some researchers who find delayed implicatures and use some form of the Literal-First hypothesis to explain these findings have consistently used the non-partitive form (Bott, Bailey, & Grodner, 2012; Bott & Noveck, 2004; Noveck & Posada, 2003). The absence of the partitive may provide weaker support for the implicature than use of the partitive form would have provided. Under a Constraint-Based account, this should result in increased processing effort.

The second cue is the availability of lexical alternatives to some that listeners assume are available to the speaker. In general the alternatives to some will be determined by the context in which an utterance occurs. We assume that lexical items that are part of a scale will generally be available as alternatives.² However, in a given context, other lexical items may be introduced that become salient alternatives. In the current studies we focus on the effects of number terms as alternatives, and the effects of intermixing some with exact number terms, e.g., You got two of the gumballs vs. You got some of the gumballs. The motivation for using exact number terms as a case study comes from two studies (Grodner, Klein, Carbary, & Tanenhaus, 2010; Huang & Snedeker, 2009), which used similar methods but found different results.

Both Huang and Snedeker (2009, 2011) and Grodner et al. (2010) used the visual world eye-tracking paradigm (Cooper, 1974; Tanenhaus et al., 1995). In Huang & Snedeker 's (2009, 2011) experiments participants viewed a display with four quadrants, with the two left and the two right quadrants containing pictures of children of the same gender, with each child paired with objects. For example, on a sample trial, the two left quadrants might each contain a boy: one with two socks and one with nothing. The two right quadrants might each contain a girl: one with two socks (pragmatic target) and one with three soccer balls (literal target). A preamble established a context for the characters in the display. In the example, the preamble might state that a coach gave two socks to one of the boys and two socks to one of the girls, three soccer balls to the other girl, who needed the most practice, and nothing to the other boy.

Participants were asked to follow instructions such as Point to the girl who has some of the socks. Huang & Snedeker (2009) reasoned that if the literal interpretation is computed prior to the inference, then, upon hearing some, participants should initially fixate both the semantic and pragmatic targets equally because both are consistent with the literal interpretation. If, however, the pragmatic inference is immediate, then the literal target should be rejected as soon as some is recognized, resulting in rapid fixation of the pragmatic target. The results strongly indicated that the literal interpretation was computed first. For commands with all (e.g., Point to the girl who has all of the soccer balls) and commands using number (e.g., Point to the girl who has two/three of the soccer balls), participants converged on the correct referent 200–400 ms after the quantifier. In contrast, for commands with some, target identification did not occur until 1000–1200 ms after the quantifier onset. Moreover, participants did not favor the pragmatic target prior to the noun’s phonetic point of disambiguation (POD; e.g., -ks of socks). Huang and Snedeker concluded that ‘‘even the most robust pragmatic inferences take additional time to compute” (Huang & Snedeker, 2009, p. 408).

The Huang and Snedeker results complement previous response time (Bott & Noveck, 2004; Noveck & Posada, 2003) and reading-time experiments (Breheny, Katsos, & Williams, 2006). In these studies, response times associated with the pragmatic inference are longer than both response times to a scalar item's literal meaning and to other literal controls (typically statements including all). Moreover, participants who interpret some as some and possibly all, so-called logical responders (Noveck & Posada, 2003), have faster response times than pragmatic responders who interpret some as some but not all.

In contrast, Grodner, Klein, Carbary, & Tanenhaus (2010) found evidence for rapid interpretation of pragmatic some, using displays and a logic similar to that used by Huang & Snedeker (2009). Each trial began with three boys and three girls on opposite sides of the display and three groups of objects in the center. A prerecorded statement described the total number and type of objects in the display. Objects were then distributed among the participants. The participant then followed a pre-recorded instruction, of the form Click on the girl who has summa/nunna/alla/ the balloons.

Convergence on the target for utterances with some was just as fast as for utterances with all. Moreover, for trials on which participants were looking at the character with all of the objects at the onset of the quantifier summa) participants began to shift fixations away from that character and to the character(s) with only some of the objects (e.g., the girl with the balls or the girl with the balloons) within 200–300ms after the onset of the quantifier. Thus participants were immediately rejecting the literal interpretation as soon as they heard summa. If we compare the results for all and some in the Huang and Snedeker and Grodner et al. experiments, the time course of all is similar but the upper-bound interpretation of partitive some is computed 600–800ms later in Huang and Snedeker.

Why might two studies as superficially similar as Huang & Snedeker (2009) and Grodner et al. (2010) find such dramatically different results? In Degen & Tanenhaus (to appear), we discuss some of the primary differences between the two studies, concluding that only the presence or absence of number expressions might account for the conflicting results. Huang and Snedeker included stimuli with numbers, whereas Grodner et al. did not. In Huang and Snedeker (2009) a display in which one of the girls had two socks was equally often paired with the instruction, Point to the girl who has some of the socks and Point to the girl who has two of the socks. In fact, Huang, Hahn, & Snedeker (2010) have shown that eliminating number instructions reduces the delay between some and all in their paradigm and Grodner (personal communication) reports that including instructions with number results in a substantial delay for summa relative to alla in the Grodner et al. paradigm.

Why might instructions with exact number delay upper-bound interpretations of partitive some? Computation of speaker meaning takes into account what the speaker could have, but did not say, with respect to the context of the utterance. Recall that the upper-bound interpretation of some is licensed when the speaker could have, but did not say all, because all would have been more informative. More generally, it would be slightly odd for a speaker to use some when all would be the more natural or typical description. We propose that in situations like the Huang and Snedeker and Grodner et al. experiments, exact number is arguably more natural than some. In fact, intuition suggests that mixing some and exact number makes some less natural.

Consider a situation where there are two boys, two girls, four socks, three soccer balls and four balloons. One girl is given two of the four socks, one boy the four balloons and the other boy, two of the three soccer balls. Assuming the speaker knows exactly who got what, the descriptions in (7) and (8) seem natural, compared to the description in (9):

• (7)One of the girls got some of the socks and one of the boys got all of the balloons.
• (8)One of the girls got two of the socks and one of the boys got all of the balloons.
• (9)One of the girls got two of the socks and one of the boys got some of the soccer balls.

Grodner et al. (2010) provided some empirical support for these intuitions. They collected naturalness ratings for their displays and instructions, both with and without exact number included in the instruction set. Including exact number lowered the naturalness ratings for partitive some but not for all. However, even without exact number instructions, some was rated as less natural than all. One reason might be that in most situations, pragmatic some is relatively infelicitous when used to describe small sets. Again, intuition suggests that using some is especially odd for sets of one and two. Consider a situation where there are three soccer balls and John is given one ball and Bill two. John got one of the soccer balls seems a more natural description than John got some of the soccer balls and Bill got two of the soccer balls seems more natural than Bill got some of the soccer balls.

These observations suggest an alternative hypothesis for why responses to pragmatic some are delayed when intermixed with exact number for small set sizes. Most generally we suggest that some will compete with other rapidly available contextual alternatives. In particular, we hypothesize that the mapping between an utterance with some and an interpretation of that utterance is delayed when there are rapidly available, more natural alternatives to describe the state of the world. This seems likely to be the case for exact number descriptions with small sets because the more natural number alternative is also a number in the subitizing range where number terms become rapidly available and determining the cardinality of a set does not require counting (Atkinson, Campbell, & Francis, 1976; Kaufman, Lord, Reese, & Volkman, 1949; Mandler, Shebo, & Vol, 1982). In situations where exact number is available as a description, the number term is likely to become automatically available, thus creating a more natural, more available interpretation of the scene.

In Gricean terms, we are proposing that delays in response times (to press a button or to fixate a target) that have previously been argued to be due to the costly computation of the Quantity implicature from some to not all, might in fact be due to interference from lexical alternatives to some. In the Huang and Snedeker studies, in particular, there may be interference from number term alternatives that, while scalar in nature, function on a different scale than some. In Gricean terms, the motivation for this interference comes from the maxim of Manner: if there is a less ambiguous quantifier (e.g., two) that could have been chosen to refer to a particular set size, the speaker should have used it. If she didn’t, it must be because she meant something else. Finally arriving at the implicature from some to not all when there are more natural lexical alternatives to some that the speaker could have used but didn’t, thus may involve both reasoning involving the Quantity maxim (standard scalar implicature) and the Manner maxim (inference that the speaker must have not meant the partitioned set which could have more easily and naturally been referred to by two). If this is indeed the case, this would have serious implications for the interpretation of response time results on scalar implicature processing across the board: previously, delays in computing pragmatic some have been associated with the costly computation of the scalar implicature itself, taking into account only the competition of some with its scalemate all. What we are proposing here is that this view is too narrow – rather than competing only with its lexicalized scalemate, some contextually competes with many other alternatives, like number terms, which are not lexicalized alternatives. Thus, observed delays in the processing of scalar implicatures might be at least partly due to costly reasoning about unnatural, misleading quantifier choices.

1.5. The gumball paradigm

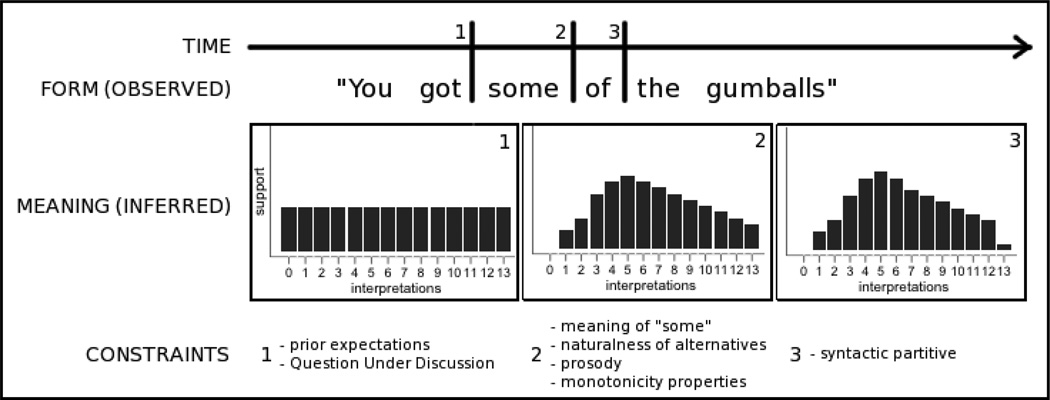
The current experiments examine the role of contextual alternatives within the Constraint-Based framework using the case of exact number. Our specific hypothesis is that number selectively interferes with some – both in processing the upper-bound and the lower-bound interpretation - where naturalness of some is low and number terms are rapidly available. We evaluate this hypothesis in a series of experiments using a “gumball paradigm”. We begin with an example to illustrate how likely interpretations might change over time. Suppose that there is a gumball machine with 13 gumballs in the upper chamber. Alex knows that this gumball machine has an equal probability of dispensing 0 – 13 gumballs. His friend, Thomas, inserts a quarter and some number of gumballs drops to the lower chamber but Alex cannot see how many have dropped. Thomas, however, can, and he says You got some of the gumballs.

Before the start of the utterance Alex will have certain prior expectations about how many gumballs he got – in fact, in this case there is an equal probability of 1/14 that Alex got any number of gumballs. This is shown in the first panel of Fig. 1. Once Alex hears You got some, he has more information about how many gumballs he got. First, the meaning of some constrains the set to be larger than 0. However, Alex also has knowledge about how natural it would be for Thomas to utter some instead of, for example, an exact number term, to inform him of how many gumballs he got. Fig. 1 illustrates how this knowledge might shift his subjective belief probabilities for having received specific numbers of gumballs.

Fig. 1.

Possible constraint-based update of most likely intended interpretation at different incremental time points. Interpretations are represented as set sizes. Bars represent the amount of probabilistic support provided for each interpretation, given the constraints at each point.

Alex is now more certain that he has received an intermediate set size rather than a small set (where Thomas could have easily said one or two instead of some) or a large set (where Thomas could have said most, or even all). Finally, once Alex hears the partitive of, his expectations about how many gumballs he got might shift even more (for example because Alex knows that the partitive is a good cue to the speaker meaning to convey upper-bound some), as shown in the third panel³. Thus, by the end of the utterance Alex will be fairly certain that he did not get all of the gumballs, but he will also expect to have received an intermediate set size, as there would have been more natural alternative utterances available to pick out either end of the range of gumballs.

Note that without additional assumptions, neither the Default nor the Literal-First model make gradient predictions about expected set size. Under the Default model, the distribution on states would be uniform until the word some is encountered, at which point both the zero-gumball and all-gumball state would be excluded as potential candidates, leaving a uniform distribution over states 1 – 12. In contrast, the Literal-First model predicts that upon encountering some, only the zero-gumball state should be excluded. Both models predict that over time, the integration of further contextual information may require re-including the all-state in the set of possible states (Default), or excluding the all-state from said set (Literal-First). However, neither of these models directly predicts variability in naturalness of partitive vs. non-partitive some for any set size, nor variability in the naturalness of some used with different set sizes. Moreover, adding probabilistic assumptions that would map onto the time course of initial processing of some would be inconsistent with the fundamental assumptions of each of these models.

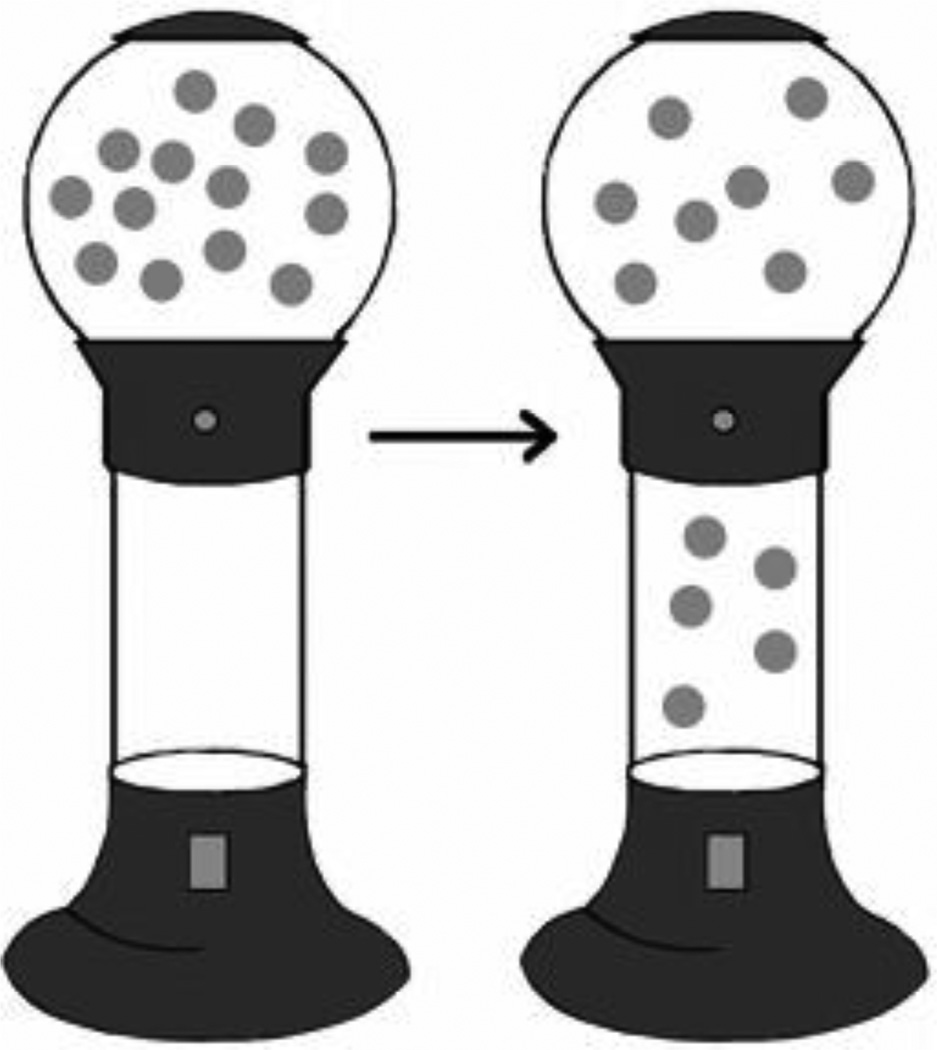
We developed a gumball paradigm based on this scenario in order to investigate whether listeners are sensitive to the partitive and to the naturalness and availability of number descriptions as lexical alternatives to some in scalar implicature processing using a range of different set sizes. On each trial the participant sees a gumball machine with an upper chamber and a lower chamber, as illustrated in Fig. 2. All of the gumballs begin in the upper chamber. After a brief delay, some number of gumballs drops to the lower chamber. The participant then responds to a statement describing the scene, either by rating the statement’s naturalness or judging whether they agree or disagree with the statement. We can thus obtain information about participants’ judgments while at the same time recording response times as a measure of their interpretation of different quantifiers with respect to different visual scenes.

Fig. 2.

Sample displays in the gumball paradigm. Left: initial display. Right: sample second display with dropped gumballs.

The rationale for the rating studies is that we need to establish the relative naturalness of alternative descriptions for particular set sizes. These data are crucial for generating time course predictions that distinguish the Default, Literal-First and Constraint-Based approaches. Crucially, naturalness data are essential for evaluating the time course claims of the Constraint-Based approach. In two rating studies in which the upper chamber begins with 13 gumballs, we establish the naturalness of some for different set sizes of interest, in particular small sets (1 – 3), intermediate sets (6 – 8), and for the unpartitioned set (all 13 gumballs). In addition, we investigate the relative naturalness of simple some vs. partitive some of for the unpartitioned set. We further investigate the effect of including exact number descriptions on naturalness ratings for some and some of used with different set sizes in Experiment 2. These results allow us to make specific predictions about response times that are tested in Experiment 3.

2. Experiment 1

Experiment 1 was conducted to determine the naturalness of descriptions with some, some of (henceforth summa), all of (henceforth all) and none of (henceforth none) for set sizes ranging from 0 to 13.

2.1. Methods

2.1.1. Participants

Using Amazon’s Mechanical Turk, 120 workers were paid $0.30 to participate. All were native speakers of English (as per requirement) who were naïve as to the purpose of the experiment.

2.1.2. Procedure and materials

On each trial, participants saw a display of a gumball machine with an upper chamber filled with 13 gumballs and an empty lower chamber (Fig. 2). After 1.5 seconds a new display was presented in which a certain number of gumballs had dropped to the lower chamber. Participants heard a pre-recorded statement of the form You got X gumballs, where X was a quantifier. They were then asked to rate how naturally the scene was described by the statement on a seven point Likert scale, where seven was very natural and one was very unnatural. If they thought the statement was false, they were asked to click a FALSE button located beneath the scale. We varied both the size of the set in the lower chamber (0 to 13 gumballs) and the quantifier in the statement (some, summa, all, none). Some trials contained literally false statements. For example, participants might get none of the gumballs and hear You got all of the gumballs. These trials were interspersed in order to have a baseline against which to compare naturalness judgments for some (of the) used with the unpartitioned set. If interpreted semantically (as You got some and possible all of the gumballs), the some statement is true (however unnatural) for the unpartitioned set. However, if it is interpreted pragmatically as meaning You got some but not all of the gumballs, it is false and should receive a FALSE rating.

Participants were assigned to one of 24 lists. Each list contained 6 some trials, 6 summa trials, 2 all trials, and 2 none trials. To avoid an explosion of conditions, each list sampled only a subset of the full range of gumball set sizes in the lower chamber. The quantifiers some and summa occurred once each with 0 and 13 gumballs. In addition, none occurred once (correctly) with 0 gumballs and all once (correctly) with 13 gumballs. Each of all and none also occurred once with an incorrect number of gumballs. The remaining some and summa trials sampled two data points each per quantifier from the subitizing range (1 – 4 gumballs), one from the mid range (5 – 8 gumballs), and one from the high range (9 – 12 gumballs). For an overview, see Table. See Appendix A, Table 5, for the set sizes that were sampled on each list. From each of twelve base lists, one version used a forward order and the other a reverse order. Five participants were assigned to each list.

Table 1.

Distribution of the 16 experimental trials over quantifiers and set sizes. See Appendix A for the exact set sizes that were sampled on different lists in the subitizing (sub), mid, and high range.

	Set size
Quantifier	0	Sub	Mid	High	13
Some	1	2	1	1	1
Summa	1	2	1	1	1
None	1		1
All			1		1

2.2. Results and discussion

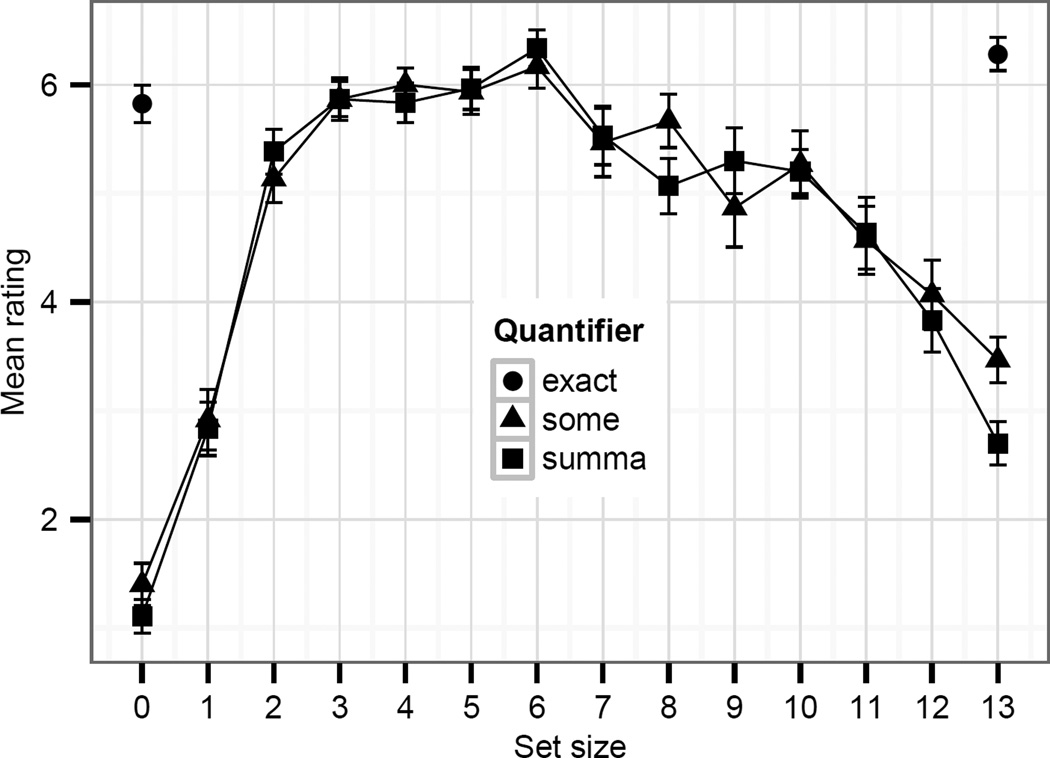
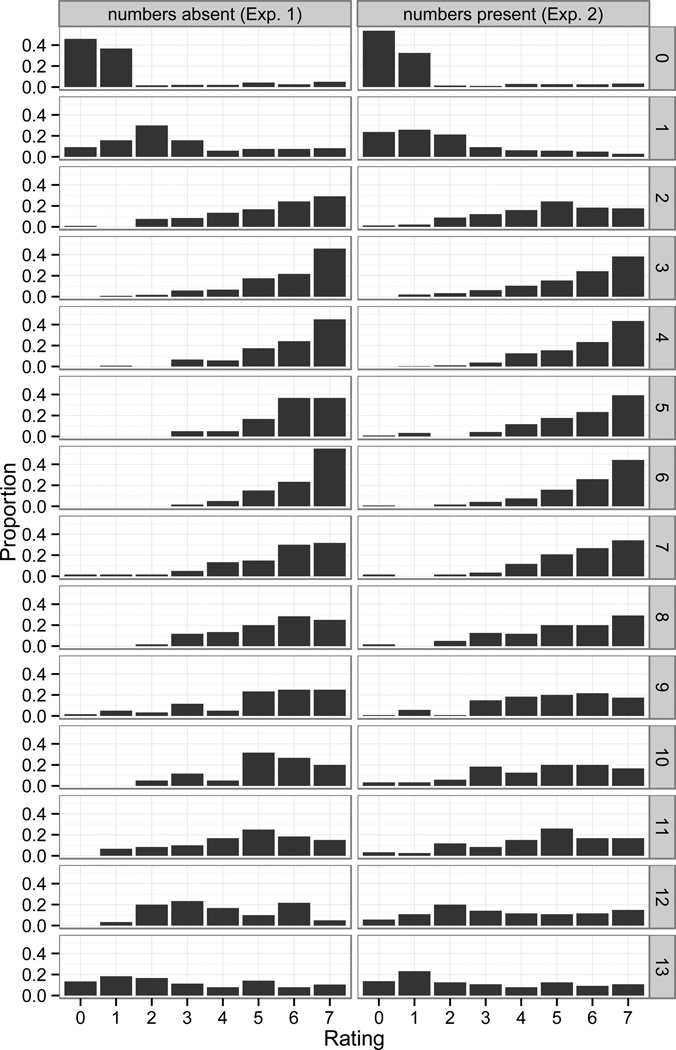
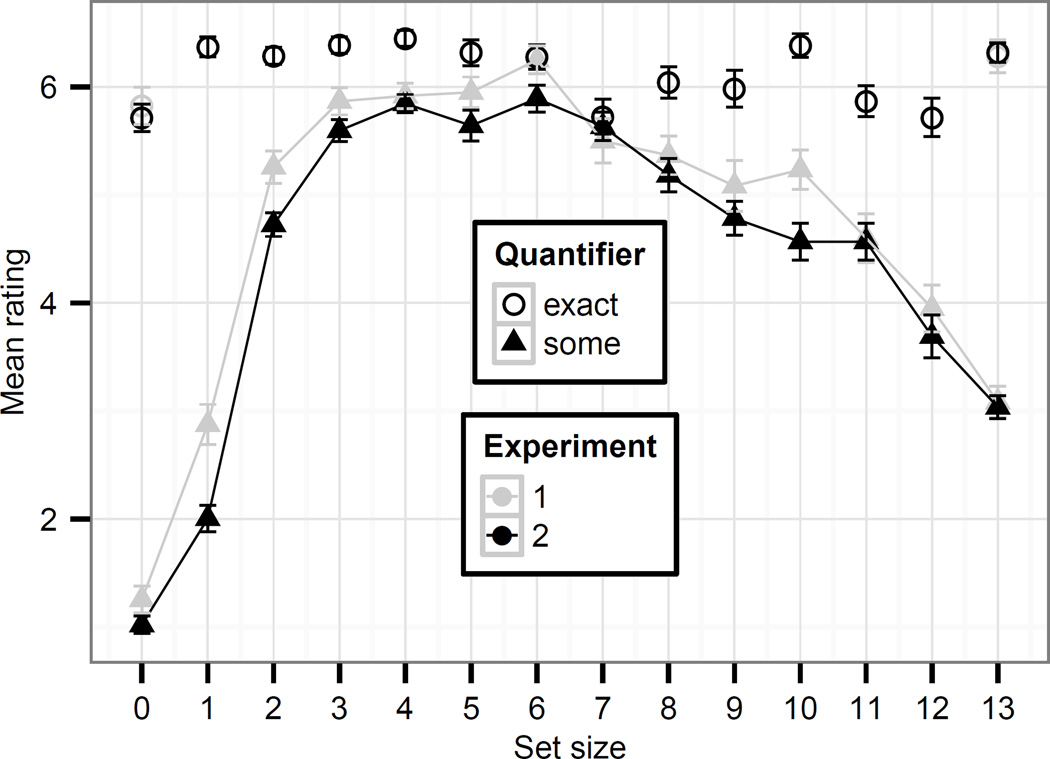
Mean ratings for each quantifier for the different set sizes are presented in Fig. 3. Clicks of the FALSE button were coded as 0. This was motivated by many participants’ use of the lowest point on the scale to mean FALSE (see the histogram of responses to some/summa in Fig. 4). We thus treated all responses on a single, continuous dimension. Mean ratings were 5.83 for none (0 gumballs) and 6.28 for all (13 gumballs) and close to 0 otherwise. Mean ratings for some/summa were lowest for 0 gumballs (1.4/1.1), increased to 2.7 and 5.2 for 1 and 2 gumballs, respectively, peaked in the mid range (5.81/5.73), decreased again in the high range (4.69/4.74), and decreased further at the unpartitioned set (3.47/2.7).

Fig. 3.

Mean ratings for simple “some”, partitive “some of the”, and the exact quantifiers “none” and “all”. Means for the exact quantifiers “none” and “all” are only shown for their correct set size.

Fig. 4.

Proportion of ratings (where FALSE responses are coded as 0 ratings) for “some”/”summa” in Exps. 1 and 2. Rows represent number of gumballs in the lower chamber. Note that some participants consistently gave the lowest rating on the scale (1) instead of clicking the FALSE button.

Our analyses were designed to address the following three questions: a) for which set size ranges some and summa are deemed most natural; b) whether some and summa differ in naturalness, and c) whether the naturalness of some and summa differs for different set sizes (or ranges of set sizes).

The data were analyzed using a series of mixed effects linear regression models with by-participant random intercepts to predict ratings. P-values were obtained using MCMC sampling (Baayen, Davidson, & Bates, 2008). For some/summa used with each unique set size in the lower chamber (0 – 13), we fit one model each to each subset of the data corresponding to that set size in addition to trials where all and none were used with their correct set size (13 and 0, respectively). Each model included a centered fixed effect of quantifier (some/summa vs. all/none). Some and summa were most natural in the mid range (numerically peaked when used with 6 gumballs), where ratings did not differ from ratings for none and all used with their correct set size (β=0.2, SE=0.24, t=0.81, p < .42). Mean ratings for some and summa did not differ for any set size except at the unpartitioned set, where some was more natural than summa (β=−0.77, SE=0.19, t=−4.07, p < .01). This naturalness difference between some and summa used with the unpartitioned set suggests that summa is more likely to give rise to a scalar implicature than some and is thus dispreferred with the unpartitioned set. Because ratings for some and summa did not differ anywhere except for the unpartitioned set, we henceforth report collapsed results for some and summa.

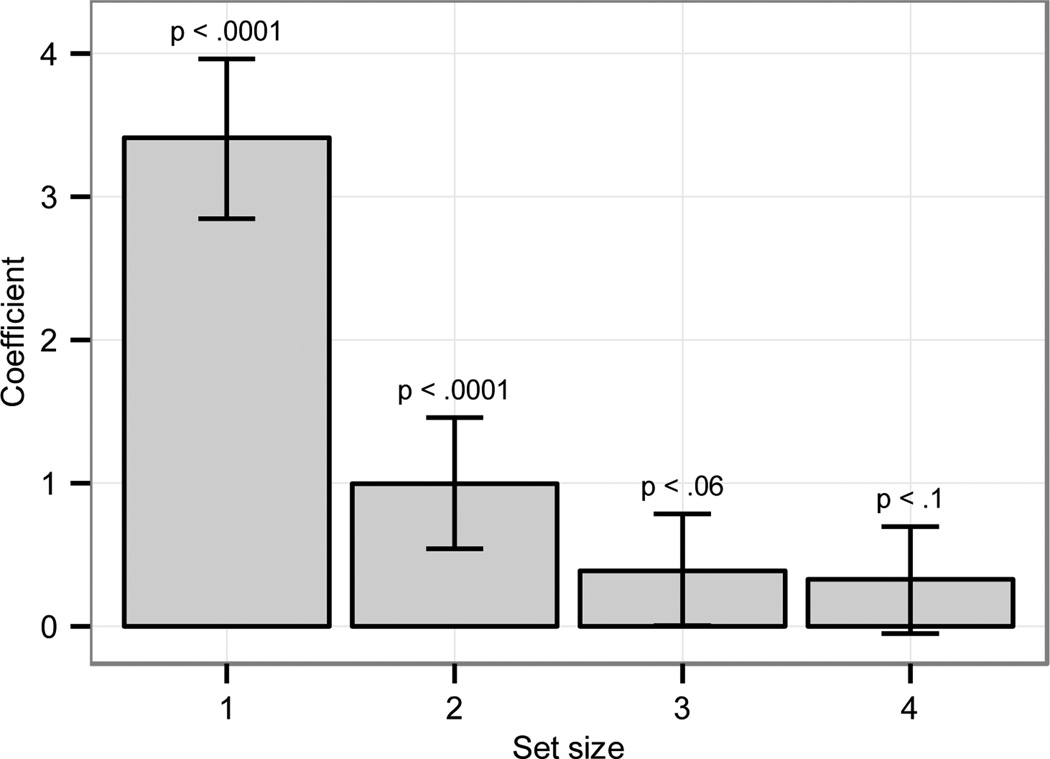
To test the hypothesis that naturalness for some varies with set size, we fit a mixed effects linear model predicting mean naturalness rating from range (subitizing (1–4 gumballs) or mid range (5–8 gumballs)) to the subset of the some cases in each range. As predicted, naturalness was lower in the subitizing range than in the mid range (β=−0.79, SE=0.13, t=−6.01, p < .001). Similarly, naturalness ratings for some were lower for the unpartitioned set than in the mid range (β=−2.68, SE=0.15, t=−17.82, p < .001). However, Fig. 3 suggests that the naturalness ratings differed for set sizes within the subitizing range (1–4). Performing the analysis on subsets of the data comparing each set size with naturalness of some/summa used with the preferred set size (6 gumballs) yields the following results. Collapsing over some and summa, we coded small set versus 6 gumballs as 0 and 1 respectively and subsequently centered the predictor. The strongest effect is observed for one gumball (β=2.95, SE=0.17, t=14.28, p < .0001). The effect is somewhat weaker for two (β=1.0, SE=0.22, t=4.47, p < .0001), even weaker for three (β=.36, SE=0.2, t=1.81, p = .05), and only marginally significant for four (β=0.29, SE=0.19, t=1.52, p < .1).⁴ The coefficients for the set size predictor for each subset model are plotted in Fig. 5. Given these results we will refer to “small set size” effects rather than “subitizing” effects.

Fig. 5.

Set size model coefficient for each set size in the subitizing range. Error bars represent one standard error.

In sum, some and summa were both judged to be quite unnatural for set sizes of 1 and 2, and more natural but not quite as natural as for the preferred set size (6 gumballs) for 3. Naturalness also decreased after the mid-range (5 – 8 gumballs) and was low at the unpartitioned set. In addition, the partitive, some of, was less natural to refer to the unpartitioned set than simple some.

Finally, we note that naturalness ratings for some/summa gradually decreased for set sizes above 6. This is probably due to there being other more natural, salient alternatives for that range: many and most. It is striking that these alternatives seem to affect the naturalness of some just as much as number terms for small set sizes.

The naturalness results from this study point to an interesting fact about the meaning of some. The linguistic literature standardly treats the semantics of some as proposed in Generalized Quantifier Theory (Barwise & Cooper, 1981) as the existential operator (corresponding to at least one). Under this view, as long as at least one gumball dropped to the lower chamber, participants should have rated the some statements as true (i.e., not clicked the FALSE button). However, this was not the case: some received 12% FALSE ratings for one gumball and 9% FALSE ratings for the unpartitioned set; summa statements were rated FALSE in 7% of cases for one gumball and 18% of cases for the unpartitioned set. For comparison, rates of FALSE responses to some/summa for all other correct set sizes were 0%.

In addition, treating some as simply the existential operator does not allow a role for the naturalness of quantifiers. What matters is that a statement with some is true or false. Differences in naturalness are not predicted. Whether this means that language users’ underlying representation of some is more complex than the existential operator (and similarly for other quantifiers) is an open question. One could argue for an analogy to the distinction between the underlying category and what affects categorization (for discussion of this perspective, see Armstrong, Gleitman, & Gleitman, 1983). However, our preferred view is that for the purposes of formalizing truth conditions, the existential operator is useful as an abstraction over the possible contexts in which a simple statement with some could be true. The underlying cognitive representations, on the other hand, are likely to involve mappings onto expectations of usage in specific contexts.

One way of conceptualizing these naturalness results is that we have obtained probability distributions over set sizes for different quantifiers, where the relevant probabilities are participants’ subjective probabilities of expecting a speaker to use a particular quantifier with a particular set size. Thus, a vague quantifier like some, where naturalness is high for intermediate sets and gradually drops off at both ends of the spectrum, has a very wide distribution, with probability mass distributed over many set sizes. In contrast, for a number term like two one would expect naturalness to be very high for a set size of two and close to 0 for all other cardinalities, and thus the distribution would be very narrow and peaked around 2.

According to the Constraint-Based account that allows for parallel processing of multiple sources of information, distributions of quantifiers over set sizes (or in other words listeners’ expectations about speakers’ quantifier use) are a function of at least two factors: a) set size and b) awareness of contextual availability of alternative quantifiers. If no lexical alternative is available, listeners will have some expectations about the use of some with different set sizes. We propose that the distribution of ratings obtained in Exp. 1a reflects just these expectations. For some, naturalness is highest for intermediate set sizes and drops off at both ends of the tested range. That is, listeners’ expectation for some to be used is highest in the mid range. The Constraint-Based account predicts that listeners’ expectations about quantifier use are sensitive to alternatives. Including number terms among the experimental items, thus making participants aware that number terms are contextually available alternatives to some, should change this distribution. In particular, the prediction is that due to subitizing processes, which allow number terms to become rapidly available as labels for small sets, the naturalness of some should decrease for small sets when number terms are included. In other words, participants’ expectations that a small set will be referred to by some should decrease. This prediction is tested in Experiment 2.

3. Experiment 2

Experiment 2 tested the hypothesis that when number terms are included as alternatives within the context of an experiment, the naturalness of some will be reduced when it is used with small set sizes. Using the same paradigm as in Experiment 1, we included number terms among the stimuli to test the hypothesis that the naturalness of some/summa would be reduced when used with small set sizes, where number terms are hypothesized to be most natural.

3.1. Methods

3.1.1. Participants

Using Amazon’s Mechanical Turk, 240 workers were paid $0.75 to participate. All were native speakers of English (as per requirement) who were naïve as to the purpose of the experiment.

3.1.2. Procedure and materials

The procedure was the same as that described for Experiment 1 with one difference; the number terms one of the through twelve of the were included among the stimuli. Each participant rated naturalness of statements with quantifiers as descriptions of gumball machine scenes on 32 trials. Participants were assigned to one of 48 lists. As in Experiment 1, each list contained 6 some trials, 6 summa trials, 2 all trials, and 2 none trials (see Table for an overview of these 16 trials). In addition, 4 number terms were included on each list. Each number term occurred once with its correct set size, once with a wrong set size that differed from the correct set size by one gumball, and once with a wrong set size that differed from the correct set size by at least 3 gumballs. The lists were created from the same base lists used in Experiment 1. See Appendix A for the set sizes that were sampled on each list. Four versions of each of the twelve base lists were created. On half of the lists, some/summa occurred before the correct number term for each set size, on the other half it occurred after the correct number term. Half of the lists sampled wrong set sizes that were one bigger than the correct set size for the number terms employed, and half sampled set sizes that were one smaller.

Table 2.

Distribution of the 80 trials each participant saw, over quantifiers and set sizes.

	Set Size
Quantifier	0	1	2	3	4	10	11	12	13
Some	10	2	2	1	1	1	1	2	4
Summa	10	2	2	1	1	1	1	2	4
None	8	2	2
One		4
Two			4
All							2	2	8

3.2. Results

As in Experiment 1, clicks of the FALSE button were coded as 0 and ratings treated as continuous values (see Fig. 4 for a histogram of the distribution of ratings for each number of gumballs). Mean ratings were 5.71 for none with 0 gumballs and 6.31 for all with 13 gumballs, and close to 0 otherwise. Mean ratings for some/summa were lowest for 0 gumballs (1.08/0.96), increased from 2.02/1.99 to 4.91/4.54 in the small set range peaked in the mid range at 6 gumballs (5.82/5.97), decreased again in the high range (4.33/4.47), and decreased further at the unpartitioned set (3.42/2.65), replicating the general shape of the curve obtained in Experiment 1.

Again, some and summa were most natural when used with 6 gumballs. As in Experiment 1, mean ratings for some and summa did not differ for any set size except at the unpartitioned set, where some was more natural than summa (β=−0.77, SE=0.13, t=−4.07, p < .001).

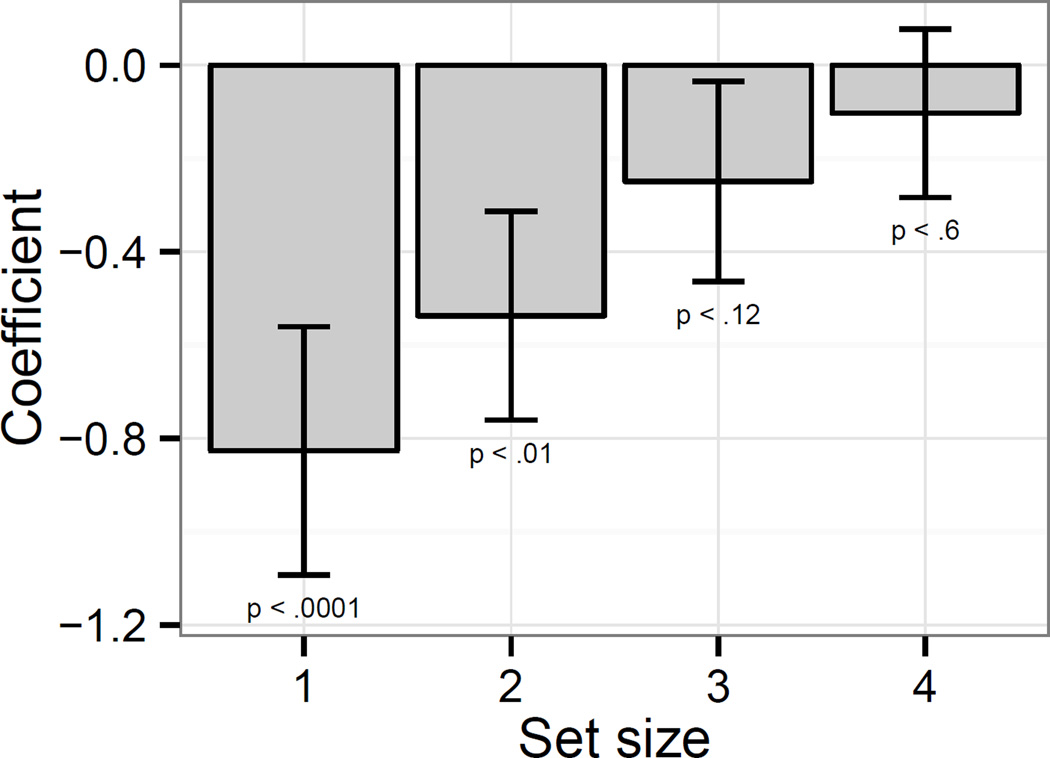
To test the hypothesis that adding number terms decreases the naturalness for some/summa in the small set range but nowhere else, we fit a series of mixed effects linear models with random by-participant intercepts, predicting mean naturalness rating from number term presence for each range (no gumballs, small, mid, high, unpartitioned set). The models were fit to the combined datasets from Experiment 1 (numbers absent) and Experiment 2 (numbers present). As predicted, naturalness was lower for both some and summa when numbers were present in the small set range (β=−0.49, SE=0.16, t=−3.13, p < .002), but not for 0 gumballs (β=−0.19, SE=0.17, t=−1.11, p < .28), in the mid range (β=−0.14, SE=0.14, −0.99, p = .13), in the high range (β=−0.38, SE=0.23, t=−1.37, p < .12), or with the unpartitioned set (β=−0.11, SE=0.23, t=−0.49, p <.71). Fig. 6 presents the mean naturalness ratings when numbers were present (Experiment 2) and absent (Experiment 1).

Fig. 6.

Mean ratings for “some” (collapsing over simple and partitive “some”) and exact quantifiers/number terms when number terms are present (Experiment 2) vs. absent (Experiment 1). Means for the exact quantifiers are only shown for their correct set size.

Performing each analysis individually for each set size in the subitizing range shows that the strength of the number presence effect in the small set range differed for different set sizes. It was strongest for one gumball (β=−0.83, SE=0.27, t=−3.12, p < .0001), less strong for two (β=−0.54, SE=0.22, t=−2.4, p < .01), trending for three gumballs (β=−0.27, SE=0.2, t=−1.16, p < .12), and non-significant for four gumballs (β=−0.1, SE=0.18, t=−0.57, p < .61). We provide a coefficient plot for the effect of number presence for different set sizes in Fig. 7. Therefore, naturalness effects are not due to subitizing per se, as we had initially hypothesized. Rather, subitizing might interact with naturalness to determine the degree to which number alternatives compete with some.

Fig. 7.

Model coefficients for number term presence predictor for each set size in the subitizing range. Error bars represent one standard error.

Number terms did not reduce naturalness for none (β=−0.1, SE=0.22, t=−0.47, p < .6) and all (β=−0.02, SE=0.17, t=0.14, p < .84) when used with their correct set sizes. Finally, although ratings for number term ratings are extremely high throughout when used with their correct set size and close to floor otherwise, number terms are judged as more natural when used with small set sizes than when used with large ones as determined in a model predicting mean naturalness rating from a continuous set size predictor (β=−0.05, SE=0.01, p < .001). The exception is ten, which is judged to be slightly more natural than the surrounding terms.

3.3. Discussion

The results of the two rating studies suggest that a listener’s perception of an expression’s naturalness is directly affected by the availability of lexical alternatives. With the exception of 6 and 7 (around half of the original set size), numbers are always judged to be more natural than some/summa when they are intermixed. This difference, however, is largest for the smallest set sizes. As predicted, the reduced naturalness of some/summa used with small sets, established in Experiment 1, decreased further when number terms were added to the stimuli. Therefore, at least in off-line judgments, listeners take into account what the speaker could have said, but didn’t. The results of Experiments 1 and 2 establish that the naturalness of descriptions with some varies with set size and for small set sizes is affected by the inclusion of number. Note, as mentioned in the Introduction, that these patterns are not predicted by the Literal-First and Default models. However, because these models focus on differences in the time-course of processing, these results cannot be taken as evidence against these models. Crucially, we use the obtained naturalness ratings to test the Default, Literal-First, and Constraint-Based model in Experiment 3, which evaluated competing predictions about time course using response times as the primary dependent measure.

4. Experiment 3

Experiment 3 was designed to test whether the effect of available natural alternatives is reflected in response times. Using the same paradigm and stimuli, we recorded participants’ judgments and response times to press one of two buttons (YES or NO) depending on whether they agreed or disagreed with the description. Based on the naturalness results from Experiments 1 and 2, the Constraint-Based account predicts that participants’ YES responses should be slower for more unnatural statements. Specifically, for some and summa response times are predicted to be slower compared to their more natural alternatives when used with a) the unpartitioned set, where all is a more natural alternative and b) in the small set range, where number terms are more natural and more rapidly available. Based on the naturalness data, the largest effect is expected for a set size of one, a somewhat smaller effect for two, and a still smaller effect for three. Response times for some/summa with these set sizes should be slower than when some and summa are used in the preferred range (4 – 7 gumballs).

In Experiments 1 and 2 we also observed a difference in naturalness of simple vs. partitive some for the unpartitioned set. This difference should be reflected both in the number of YES responses (more YES responses to some than to summa) and in response times (faster YES responses for some than for summa).

Note that neither the Default nor the Literal-First model predict response time differences based on naturalness of alternatives – regardless of set size, processing of a statement with some should take the same amount of time, except for the unpartitioned set, where the Default model predicts longer response times for semantic YES responses and the Literal-First model predicts longer response times for pragmatic NO responses. In addition, neither of these models predicts when a statement with some should result in a pragmatic NO judgment despite being semantically true. In contrast, the Constraint-Based account predicts the proportion of NO judgments to be proportional to the naturalness of some used with that set size.

The conditions in which some/summa are used with the unpartitioned set are of additional interest because they can be linked to the literature using sentence-verification tasks. In these conditions, enriching the statement to You got some but not all (of the) gumballs via scalar implicature makes it false. However, if no such pragmatic enrichment takes place, it is true. That is, YES responses reflect the semantic, at least, interpretation of the quantifier, whereas NO responses reflect the pragmatic, but not all, interpretation. Noveck and Posada (2003) and Bott and Noveck (2004) called the former logical responses and the latter pragmatic responses; we will make the same distinction but use the terms semantic and pragmatic and in addition characterize responders by how consistent they were in their responses. Analysis of semantic and pragmatic response times will allow us to test the predictions of the Constraint-Based, Literal-First, and Default account.

In Bott and Noveck’s sentence verification paradigm participants were asked to perform a two alternative forced choice task. Participants were asked to respond TRUE or FALSE to clearly true, clearly false, and underinformative items (e.g., Some elephants have trunks). Bott and Noveck found that: a) pragmatic responses reflecting the implicature were slower than semantic responses; and b) pragmatic responses were slower than TRUE responses to all for the unpartitioned set. If processing of the scalar item some proceeds similarly in our paradigm, we would expect to replicate Bott and Noveck’s pattern of results for the unpartitioned set with YES responses to some being faster than NO responses, and NO responses to some being slower than YES responses to all.

4.1. Methods

4.1.1. Participants

Forty-seven undergraduate students from the University of Rochester were paid $7.50 to participate.

4.1.2. Procedure and materials

The procedure was the same as in Experiments 1 and 2, except that: a) participants heard a “ka-ching” sound before the gumballs moved from the upper to the lower chamber and; b) participants responded by pressing one of two buttons to indicate that YES, they agreed with, or NO, they disagreed with, the spoken description. Participants were asked to respond as quickly as possible. If they did not respond within four seconds of stimulus onset, the trial timed out and the next trial began. Participants' judgments and response times were recorded.

Participants were presented with the same types of stimuli as in Experiments 1 and 2. Because this experiment was conducted in a controlled laboratory setting rather than over the web, we were able to gather more data from each participant. However, even in the lab setting we could not collect judgments from each participant for every quantifier / set size combination; that would have required 224 trials to collect a single data point for each quantifier / set size combination (14 set sizes and the 16 quantifiers from Experiment 2). Instead, we sampled a subset of the space of quantifier / set size combinations with each participant. Each participant received 136 trials. Of those, 80 were the same across participants and represented the quantifier / set size combinations that were of most interest. (see Table).

The remaining 56 trials were pseudo-randomly sampled combinations of quantifier and set size, with only one trial per sampled combination. Trials were sampled as follows. For some and summa, four set sizes were randomly sampled from the mid range (5–8) gumballs. For all, four set sizes were randomly sampled from 0 to 10 gumballs. For none, four set sizes were randomly sampled from 3 to 13 gumballs. For both one and two, four additional incorrect set sizes were sampled, one each from the small set range (1–4 gumballs, excluding the correct set size), the mid range (5–8 gumballs), the high range (9–12 gumballs) and one of 0 or 13 gumballs. Finally, four additional number terms were sampled (one each) from the set of three or four, five to seven, eight or nine, and ten to twelve. This ensured that number terms were not all clustered at one end of the full range. Each number term occurred four times with its correct set size and four times with an incorrect number, one each sampled from the small set range, the mid range, the high range, and one of 0 or 13 gumballs, excluding the correct set size. For example, three could occur 4 times with 3 gumballs, once with 4, once with 7, once with 11, and once with 13 gumballs. The reason we included so many false number trials was to provide an approximate balance of YES and NO responses to avoid inducing an overall YES bias that might influence participants’ response times.

To summarize, there were 28 some and summa trials each, 16 all trials, 16 none trials, 8 one trials, 8 two trials, and 8 trials each for four additional number terms. Of these, 64 were YES trials, 60 were NO trials, and 12 were critical trials – cases of some/summa used with the unpartitioned set, where they were underinformative, and some/summa used with one gumball, where a NO response is expected if the statement triggers a plural implicature (at least two gumballs, Zweig, 2009) and a YES response if it does not. Finally, there were three different versions of each image, with slightly different arrangements of gumballs to discourage participants from forming quantifier – image associations.

4.2. Results

A total of 6392 responses were recorded. Of those, 26 trials were excluded because participants did not respond within the four seconds provided before the trial timed out. These were mostly cases of high number terms occurring with big set sizes that required counting (e.g. 11 eleven trials, 8 twelve trials, 5 ten trials). Further 33 cases with response times above or below 3 standard deviations from the grand mean of response times were also excluded. Finally, 254 cases of incorrect responses were excluded from the analysis. These were mostly cases of quantifier and set size combinations where counting a large set was necessary and the set size differed only slightly from the correct set size (e.g., ten used with a set size of 9). In total, 4.9% of the initial dataset was excluded from the analysis.

We organize the results as follows. We first report the proportion of YES and NO responses, focusing on the relationship between response choice and the naturalness ratings. These judgments will not allow us to tease apart the predictions of the Default and Literal-First model because these models do not make any predictions about response choices. However, they will allow us to test whether the naturalness differences between all, some, and summa are reflected in participants binary response choices.

We then turn to the relationship between response times and naturalness ratings, testing the predictions we outlined earlier. Finally, we examine judgments and response times for pragmatic and semantic responses, relating our results to earlier work by Bott and Noveck (2004) and Noveck and Posada (2003). The results will be discussed with respect to the predictions made by the Default, Literal-First, and Constraint-Based models.

Judgments

All statistical analyses were obtained from mixed effects logistic regressions predicting the binary response outcome (YES or NO) from the predictors of interest. All models were fitted with the maximal random effects structure with by-participant random slopes for all within-participant factors of interest unless mentioned otherwise, following the guidelines in Barr, Levy, Scheepers, & Tily (2013).

We first examine the unpartitioned some/summa conditions, which are functionally equivalent to the underinformative conditions from Noveck and Posada (2003) and Bott and Noveck (2004). Recall that under a semantic interpretation of some (You got some, and possibly all of the gumballs), participants should respond YES when they get all of the gumballs, while a pragmatic interpretation (You got some, but not all of the gumballs) yields a NO response. The judgment data qualitatively replicates the findings from the earlier studies: 100% of participants’ responses to all were YES, compared with 71% YES responses to partitive some. Judgments for simple some were intermediate between the two, with 82% YES responses. The difference between some and summa was significant in a mixed effects logistic regression predicting the binary response outcome (YES or NO) from quantifier (some or summa). The log odds of a YES response are lower for summa than some (β = −1.18, SE = 0.34, p < .001), reflecting the naturalness results obtained in Experiments 1 and 2, where summa was judged as less natural than some when used with the unpartitioned set. Thus both the word some and its use in the partitive construction increase the probability and/or strength of generating an implicature, consistent with the naturalness-based predictions of the Constraint-Based account.

Response time analysis of naturalness effects on YES responses

Response times ranged from 577 to 3574ms (mean: 1420ms, SD: 444ms). Results of statistical analyses were obtained from mixed effects linear regression models predicting log-transformed response times from the predictors of interest. As with the judgment data, all models were fitted with the maximal random effects structure with by-participant random slopes for all within-participant factors of interest. Significance of predictors was confirmed by performing likelihood ratio tests, in which the deviance (−2LL) of a model containing the fixed effect is compared to another model without that effect that is otherwise identical. This is one of the procedures recommended by Barr et al. (2013) for models containing random correlation parameters, as MCMC sampling (the approach recommended by Baayen, Davidson, and Bates (2008)) is not implemented in the R lme4 package.

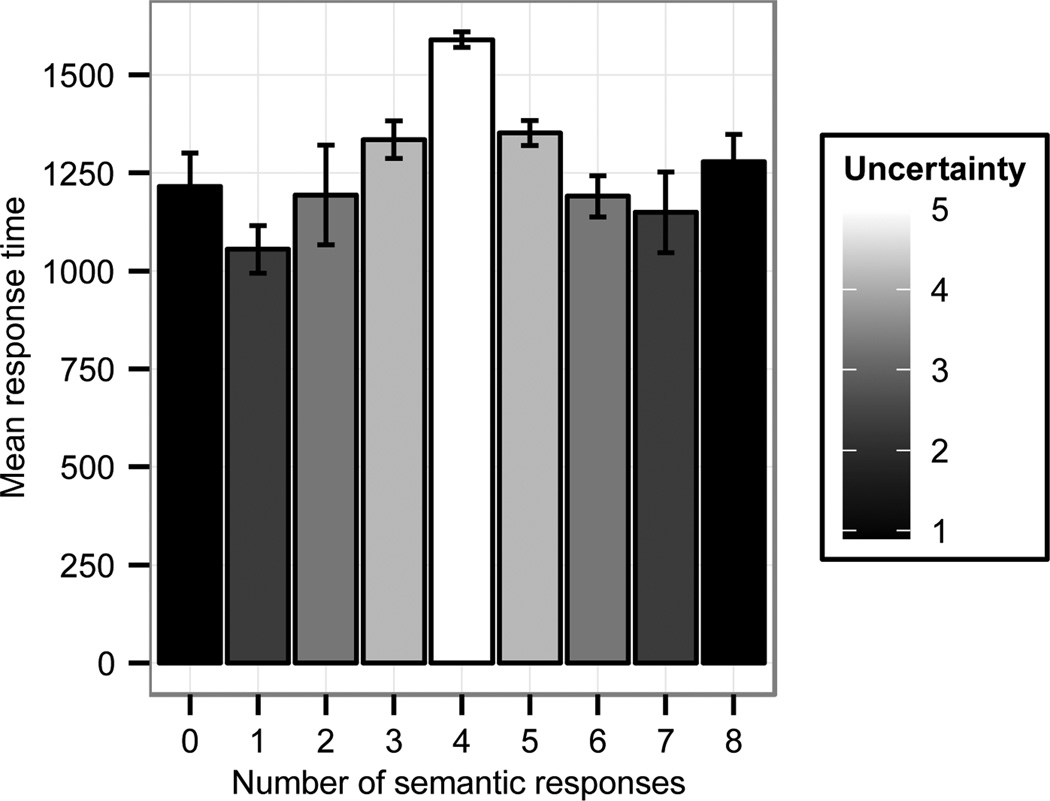
For YES responses at the unpartitioned set, quantifier was Helmert-coded. Two Helmert contrasts over the three levels of quantifier were included in the model, comparing each of the more natural levels against all less natural levels (all vs. some/summa, some vs. summa). YES responses to all were faster than /some/summa (β = −.26, SE = .02, t = −10.79) and YES responses to some were faster than to summa (β = −0.09, SE = .03, t = −3.24). YES responses to some and summa were slower for the unpartitioned set than in the most natural range determined in Experiments 1 and 2, 4 – 7 gumballs, (β = .09, SE = .03, t = 3.44).

A similar pattern holds in the small set range for the comparison between some/summa and number terms: responses to both some (β = 0.12, SE = .02, t = 5.7) and summa (β = .12, SE = .02, t = 5.8) were slower than number terms. Response times in the small set range did not differ for some and summa, as determined in model comparison between a model with and without a quantifier predictor (β = .02, SE = .02, t = 1.4), so we collapse them in further analysis.

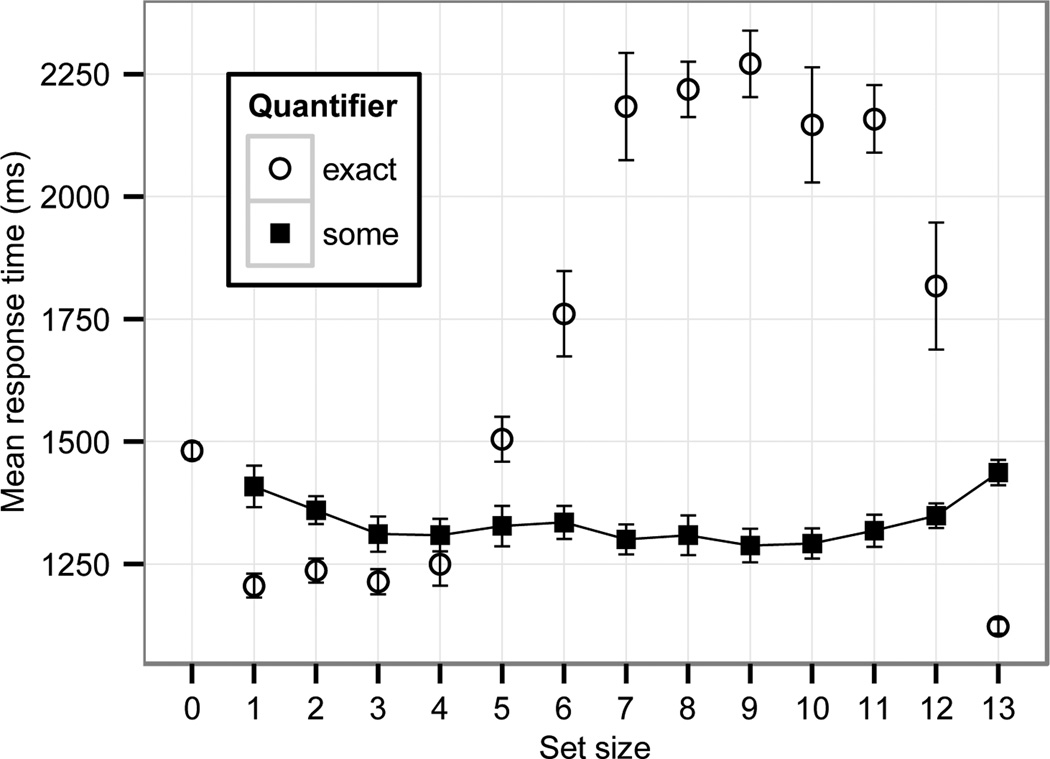
There was a main effect of set size in the small set range: responses were faster as set size increased (β = −0.02, SE = .009, t = −2.54). The interaction between set size and quantifier (number term vs. some) was also significant (β = −0.08, SE = .02, t = −4.32), such that there was no difference in response times for number terms used with different set sizes in the subitizing range, but response times decreased for some/summa with increasing set size. That is, the difference in response time between some/summa and number terms is largest for one gumball, somewhat smaller for two gumballs, and smaller still for three gumballs. This mirrors the naturalness data obtained in Experiments 1 and 2 (see Fig. 6). Comparing response times for some/summa in the small set range to those in the preferred range (4–7), the results are similar: responses in the small set range are slower than in the preferred range (β = 0.04, SE = .02, t = 2.3). Mean response times for YES responses are shown in Fig. 8 (response times for some and summa are collapsed as they did not differ).

Fig. 8.

Mean response times of YES responses to “some” (collapsed over simple and partitive use) and for exact quantifiers and number terms. For exact quantifiers, only the response time for their correct cardinality is plotted.

Analyzing the overall effect of naturalness on response times (not restricted to some/summa) yields the following results. The Spearman r between log-transformed response times and mean naturalness for a given quantifier and set size combination was −0.1 for YES responses overall (collapsed over quantifier). This value increased to −0.3 upon exclusion of cases of number terms used outside the subitizing range, where counting is necessary to determine set size. This correlation was significant in a model predicting log-transformed response time from a centered naturalness predictor and a centered control predictor coding cases of number terms used outside the small set range as 1 and all other cases as 0. The main effect of naturalness was significant in the predicted direction, such that more natural combinations of quantifiers and set sizes were responded to more quickly than less natural ones (β = −.04, SE = .01, t = −9.3). In addition, a main effect of the control predictor revealed that number terms used outside the subitizing range are responded to more slowly than cases that don’t require counting (β = .44, SE = .02, t = 18.6).

Judgments and YES response times analyzed by pragmatic and semantic responders

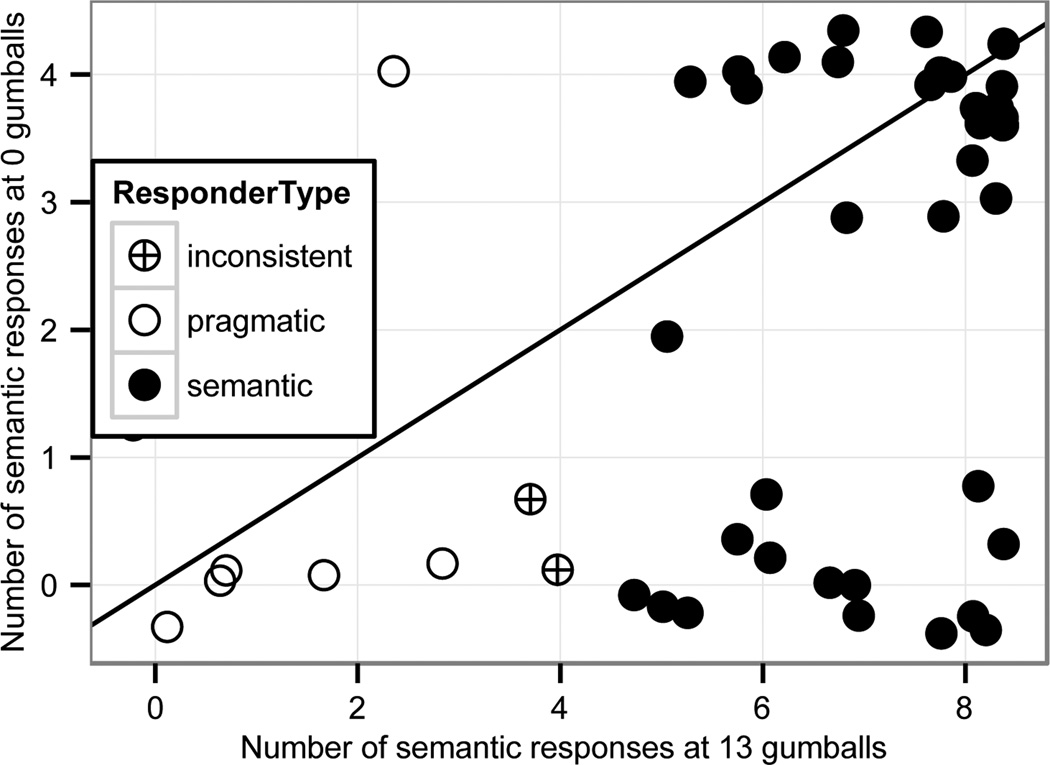
Table shows the distribution of participants over number of semantic responses to some/summa at the unpartitioned set. Noveck and Posada (2003) and Bott and Noveck (2004) found that individual participants had a strong tendency to give mostly pragmatic or mostly semantic responses at the unpartitioned set⁵. Therefore they conducted sub-analyses comparing pragmatic and semantic responders. Our participants were less consistent. Rather than two groups of responders clustered at either end of the full range, we observe a continuum in participants’ response behavior, with more participants clustered at the semantic end. 42% of the participants gave 100% (8) semantic responses. Dividing participants into two groups, semantic and pragmatic responders, where pragmatic responders are defined as those participants who gave pragmatic responses more than half of the time and semantic responders as those who responded semantically more than half of the time yields a large group of semantic responders (38 participants, 81%) and a smaller group of pragmatic responders (7 participants, 15%). Two participants (4%) gave an equal number of semantic and pragmatic responses.

Table 3.

Distribution of participants over number of semantic responses given.

Number of semantic responses	0	1	2	3	4	5	6	7	8
Number of participants	2	2	2	1	2	5	6	6	21

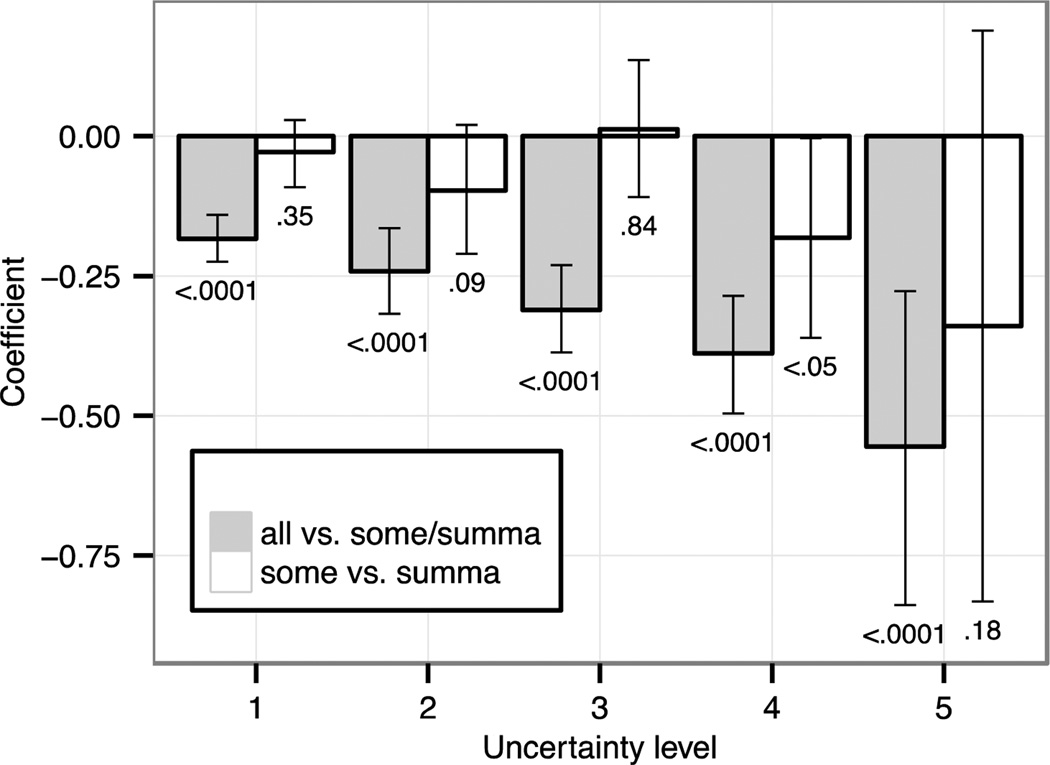
Given the nature of the distribution, rather than analyzing response times for semantic and pragmatic responders separately, we included a continuous predictor of responder type (degree of “semanticity” as determined by number of semantic responses) as a control variable in the analyses.⁶ That is, a participant with 1 semantic response was treated as a more pragmatic responder than a participant with 5 semantic responses. We analyzed the effect of (continuous) responder type on the response time effects reported above, specifically a) the naturalness effect at the unpartitioned set and b) the naturalness effect for small sets. First, we included centered continuous responder type as interaction terms with the Helmert contrasts for quantifier (all vs. some/summa, some vs. summa) for the unpartitioned set. In this model both interactions were significant: the difference between some and summa was more pronounced for more pragmatic responders (β = 0.05, SE = .02, t = 2.5), while the difference between all and some/summa was significantly different for different responder types (β = 0.04, SE = .01, t = 3.97) but seems to be better accounted for by participants’ response consistency (see below). This suggests that more pragmatic responders are more sensitive to the relative naturalness of simple and partitive some used with an unpartitioned set. We return to this finding in the discussion.

An analysis of responder type for the naturalness effects for small set sizes yielded no significant results. That is, responder type did not interact with the quantifier by set size interaction reported above.

Response time analysis for semantic vs. pragmatic responses to some/summa

Recall that the Default model predicts pragmatic NO responses to some/summa with the unpartitioned set to be faster than semantic YES responses, while the reverse is the case for the Literal-First hypothesis. The latter has found support in a similar sentence verification task as the one reported here (Bott & Noveck, 2004). We thus attempted to replicate Bott and Noveck’s finding that pragmatic NO responses are slower than semantic YES responses. To this end we conducted four different analyses. All were linear regression models predicting log-transformed response time from response and quantifier predictors and their interaction (the interaction terms were included to test for whether NO and YES responses were arrived at with different speed for some and summa): in model 1, we compared all YES responses to all NO responses. Then we performed the Bott and Noveck between-participants analysis comparing only responses from participants who responded entirely consistently to some/summa (i.e. either 8 or 0 semantic responses in total) in model 2. In a very similar between-participants analysis, we compared response times from participants who responded entirely consistently to either some or summa (i.e. either 4 or 0 semantic responses to either quantifier) in model 3. Finally, again following Bott and Noveck, we compared response times to YES and NO responses within participants, excluding the consistent responders that entered model 2 from model 4. Results are summarized in Table.

Table 4.

Model coefficients, standard error, t-value, and p-value for the three predictors (quantifier, response, and their interaction) in each of four different models9.

		Quantifier (some, summa)				Response (no, yes)				Quantifier:Response interaction
Model	Obs.	β	SE	t	p	β	SE	t	p	β	SE	t	p
1. Overall	375	0.06	0.02	2.69	<.05	0.01	0.04	0.25	0.86	−0.05	0.06	−0.88	0.23
2. Consistent	184	0.03	0.03	0.95	.38	−0.19	0.15	−1.25	<0.09	0.23	0.1	0.24	0.83
3. Consistent within quantifier	256	0.01	0.03	0.50	.92	−0.12	0.08	−1.51	<0.06	−0.02	0.09	−0.23	0.52
4. Inconsistent	191	0.1	0.04	2.78	<.05	0.03	0.04	0.76	.53	−0.04	0.08	−0.56	.33

The interaction between quantifier and response was not significant in any of the models, suggesting there was no difference between some and summa in the speed with which participants responded YES or NO. The main effect of quantifier reached significance in both model 1 (all responses to some/summa at unpartitioned set) and model 4 (including only inconsistent responders), such that responses to summa were generally slower than those to some (see Table for coefficients). Finally, the main effect of response was marginally significant in models 2 and 3 (including only consistent responders, either overall or within quantifier condition), such that YES responses were marginally faster than NO responses.

Response times as a function of response inconsistency

We conducted a final response time analysis that was motivated by the overall inconsistency in participants’ response behavior at the unpartitioned set. Rather than analyzing only how participants’ degree of semanticity impacted their response times, we analyzed the effect of within-participant response inconsistency on response times. Five levels of inconsistency were derived from the number of semantic responses given. Participants with completely inconsistent responses (4 semantic and 4 pragmatic responses) were assigned the highest inconsistency level (5). Participants with a 3:5 or 5:3 distribution were assigned level 4, a 2:6 or 6:2 distribution were assigned level 3, a 1:7/7:1 distribution level 2, and a 0:8/8:0 distribution (participants who gave only semantic or only pragmatic responses) level 1.

There is a clear non-linear effect of inconsistency on YES responses for the unpartitioned set (see Fig. 9).

Fig. 9.

Mean response times to YES responses at the unpartitioned set (collapsed across quantifiers) as a function of responder uncertainty.

Model comparison of models with polynomial terms of different orders for inconsistency and their interactions with naturalness reveal that there is a significant main effect of naturalness (as observed before, β = −0.07, SE = .01, t = −11.0), a significant effect of the second-order inconsistency term (β = 1.62, SE = 0.6, t = 2.7), and a significant interaction of naturalness and the first-order inconsistency term (β = −0.65, SE = 0.17, t = −3.78). That is, those participants who responded most inconsistently also responded most slowly to some, summa, and all when used with the unpartitioned set. Response times decreased as inconsistency increased, but both completely pragmatic and completely semantic responders showed a slight but significant increase in response times (as revealed in the significant second-order term).

As we did for responder type, we analyzed the effect of inconsistency on the naturalness effect at the unpartitioned set by including centered inconsistency level as interaction terms with the Helmert contrasts for quantifier (all vs. some/summa, some vs. summa).

This yields a strong interaction of inconsistency with the all vs. some/summa contrast (β = −0.08, SE = .02, t = −3.36) and a weak trend for the interaction with the some vs. summa contrast (β = −0.06, SE = .03, t = 1.42) in the same direction. The effect of the difference between the different levels of the quantifier predictor on log response times is larger for more inconsistent responders. This is visualized in Fig. 10, where the coefficients of the two contrasts are plotted for models run on subsets of the data depending on inconsistency level. As with responder type, letting the inconsistency term interact with quantifier (some/summa or number) for small sets replicates the effects reported previously, but there are no significant interactions with inconsistency.

Fig. 10.

Model coefficients obtained from models predicting YES response times from Helmert-coded quantifier contrasts at the unpartitioned set. Coefficients are plotted as a function of responder consistency. Numbers below the bars indicate that coefficient’s p-value.

4.3. Discussion

In Experiment 3 we found that the mean naturalness of the quantifier some for different set sizes predicted response times. In particular, YES responses were processed more slowly with decreasing naturalness. This effect was particularly strong where the more natural alternative was very rapidly available due to subitizing processes (e.g., two). In addition, responders who gave many pragmatic responses to some/summa were more sensitive to the naturalness difference between some and summa when used with the unpartitioned set, whereas less consistent participants were more sensitive to the naturalness difference between all and some/summa. The main result of Bott and Noveck’s, namely that pragmatic NO responses to some/summa are slower than semantic ones, was replicated marginally in a subset of analyses we conducted. We discuss both the responder type / inconsistency effects and the implications of the partial replication of Bott and Noveck’s results in more detail here and defer discussion of the more general theoretical implications until the General Discussion.

Response inconsistency as uncertainty about the Question Under Discussion

The difference in naturalness effects for pragmatic and semantic responders raises two questions. First, why do more pragmatic responders exhibit a stronger naturalness effect than more semantic responders? Second, why do more inconsistent responders exhibit a stronger sensitivity to the difference between all and some/summa? Here we draw upon the notion of the Question Under Discussion (QUD, Roberts, 1996), which is becoming increasingly influential within formal pragmatics. The QUD is the question that a participant in a discourse is trying to answer at the point of an utterance. Depending on what the QUD is, an utterance of the same sentence in different contexts may lead to different implicatures. Zondervan (2008) has shown that the QUD can affect how reliably an implicature is drawn: more exclusivity implicatures were triggered by the scalar item or when it was in a focused constituent.

Many researchers have noted that scalar implicatures arise only when the stronger alternative is contextually relevant (e.g. Carston, 1998; Green, 1995; Levinson, 2000). Thus, for example, (6) in response to (5a) is taken to implicate that not all of their documents are forgeries, whereas the same implicature does not arise if (6) is uttered in response to (5b) (Levinson, 2000).

• (5a)Are all of their documents forgeries?
• (5b)Is there any evidence against them?
• (6)Some of their documents are forgeries.

Similarly, there are many different potential QUDs that the utterance You got some of the gumballs might be interpreted relative to, as is illustrated in the examples in (7):

• (7a)Did I get all of the gumballs?
• (7b)How many gumballs did I get?
• (7c)Did I get any of the gumballs?

Intuitively, You got some of the gumballs implicates that you did not get all of them if it is an answer to the question in (7a), but not to the question in (7c), and more weakly to the question in (7b). This is compatible with the probabilistic account of scalar implicatures proposed by (Benjamin Russell, 2012), where the strength of a scalar implicature depends on the relative relevance to the QUD of the stronger and weaker alternatives. For space reasons we cannot work this out formally here, but the relative difference in relevance between the all and the some alternative is greatest for the QUD in (7a) (where the all alternative completely resolves the QUD but the some alternative does not), smallest for the QUD in (7c) (where both the some and the all alternative resolve the QUD), and intermediate for (7b) (where all resolves the QUD and some at least reduces the uncertainty about the number of gumballs received).

In a particular context, the QUD is sometimes established explicitly e.g. by asking a question. However, the QUD is often a matter of negotiation between interlocutors. That is, at a particular point in discourse interlocutors may have uncertainty about the actual QUD. One way to view the inconsistency results above is that participants in our experiment had different amounts of uncertainty about the QUD when they observed an utterance of You got some (of the) gumballs with the unpartitioned set. Under this view, participants who consistently responded either semantically or pragmatically had little uncertainty about the QUD: semantic responders consistently adopted the QUD in (7c) whereas pragmatic responders consistently adopted the QUD in (7a). The distributions of participants’ responses who were intermediate between the two extremes reflect their increased uncertainty about the actual QUD and it is may have been this uncertainty that resulted in slower response times. This explanation is also consistent with the result that more inconsistent/uncertain responders are more sensitive to the difference between all and some/summa than to the difference between some and summa: You got all of the gumballs is true for the unpartitioned set regardless of the QUD, thus the difference between more and less certain responders should be small in their response times to all, and it was. Uncertainty about the QUD should have a much larger effect on responses to some/summa, as the truth or falsity of You got some (of the) gumballs with the unpartitioned set depends on the QUD. Greater uncertainty about the QUD should result in slower responses. This is just the pattern that we observed.

We acknowledge that our appeal to the uncertainty of the QUD to explain response time patterns is necessarily post-hoc because we did not manipulate the QUD. In future research it will be important to investigate the effect of QUD uncertainty on response times by explicitly manipulating the (implicit or explicit) QUD that statements containing scalar items are interpreted relative to. We are currently developing paradigms to pursue this line of inquiry.

The second interesting difference in responder type was that participants who gave more pragmatic responses to some/summa at the unpartitioned set were more sensitive to the naturalness difference between some and summa; when compared to semantic responders, they responded YES more slowly to summa relative to some.

It is possible that there was a difference in our participant population between listeners who are generally more sensitive to naturalness differences between different utterance alternatives and those less sensitive to naturalness differences. The more sensitive ones should have responded more pragmatically overall because the naturalness of some/summa is generally rated lower than the naturalness of all for the unpartitioned set. Therefore, participants who are more sensitive to naturalness are likely to make more pragmatic responses. It is plausible to assume that participants who are more sensitive to the naturalness difference between all and some/summa with the unpartitioned set (as reflected in judgments), are also more sensitive to the difference between some and summa. If this difference as reflected in response times, it would result in the pattern of results we observe.

Implications of the response time analysis of pragmatic vs. semantic judgments

Recall that Bott & Noveck (2004) found that pragmatic responses to some were slower than semantic responses both between and within participants. They interpreted this as evidence that the interpretation of the semantic some and possibly all interpretation comes for free and is more basic than the some but not all interpretation, which is assumed to be computed only if the semantic interpretation does not suffice to meet expectations of relevance in context and incurs additional processing cost.

We partly replicated this result: in the analysis comparing semantic and pragmatic responses between participants who were entirely consistent in their judgments to some/summa used with the unpartitioned set, semantic responses were marginally faster than pragmatic responses. The weakness of the effect may have been due to data sparseness as there were relatively few pragmatic responders overall. However, the result did not hold up within participants, where more data were available. Moreover, for all set sizes, consistently pragmatic responders were marginally slower to respond to some/summa than consistently semantic responders (β = −0.02, SE = .01, p < .09). Proponents of the Literal-First hypothesis might interpret this as compatible with their claims: by generally taking more time to reach an interpretation of an utterance containing a quantifier, pragmatic responders could be giving themselves the time necessary to generate the scalar inference once they encounter some with an unpartitioned set. Some support from this interpretation comes from Bott and Noveck (2004), who showed that participants were more likely to draw a scalar inference when they were given more time to make their judgment. Similarly, De Neys and Schaeken (2007) found that placing participants under increased cognitive load led to fewer scalar implicatures.

However, there is an alternative interpretation. The delay might not be caused by the computation of an interpretation, but rather by the time it takes to verify that interpretation in the relevant context. That is, pragmatic responders might be investing more effort in carefully evaluating whether the observed utterance is true in the visual context. We cannot tease apart these two different explanations in our dataset, but see Degen and Tanenhaus (to appear) for evidence that semantic and pragmatic responders have different verification strategies.

A further alternative explanation for the pragmatic delay effect may be that giving the pragmatic response is confounded with giving a NO response. If participants are slower to reject a statement than they are to accept it, this would predict NO responses to be slower than YES responses. While it is indeed the case that in our dataset NO responses were generally slower than YES responses⁷, there were multiple quantifiers for which NO responses were faster than YES responses or did not differ in response time (e.g., none, five to twelve, some). Thus, it is unlikely that a response bias was fully responsible for the delay in pragmatic over semantic responses.

5. General discussion

Motivated by the observation that the presence of exact number as an alternative seems to result in delayed responses to the pragmatic interpretation of partitive some for small sets, we developed a gumball paradigm to explore the relative naturalness of quantifiers and number terms across set sizes ranging from zero to thirteen. We begin by summarizing the pattern of results across the three experiments. We then discuss the most important theoretical and methodological implications of these results for an understanding of the processing of scalar implicatures.

5.1. Summary of results

In rating studies in which the upper chamber began with 13 gumballs, we found the following results: (1) some was less natural for small sets (1 – 3) than for intermediate size sets (6–8); (2) exact number was more natural than some, with the effect being most pronounced for small and large set sizes; (3) descriptions with some were less natural than descriptions with all for the unpartitioned set, with the effect more pronounced for partitive some of the than for simple some; (4) intermixing exact number descriptions further lowered naturalness ratings for small sets (1, 2, and 3 gumballs) but not for intermediate size sets.

Result (3) was replicated in a two alternative sentence verification task: the greatest number of YES responses occurred when utterances with all were used with the unpartitioned set, fewer with simple some, and fewer yet with partitive some of the.

Response times in the sentence verification task reflected the patterns from the naturalness rating studies. For YES responses, both response times for participants who on average interpreted some semantically (as meaning some and possibly all) and response times for participants who interpreted some pragmatically increased when some was used to refer to the unpartitioned set and to small sets. In addition, response time increased with greater uncertainty about the QUD, which was defined as the consistency with which a participant interpreted some semantically or pragmatically. Finally, pragmatic responses to some were marginally slower than semantic responses on the subset of the data that included only consistent responders.

5.2. Conclusions

Our results are incompatible with both of the most influential approaches to the processing of scalar implicatures. According to the Literal-First hypothesis the implicature for the upper-bound interpretation of some is computed only after the semantic interpretation of some, predicting that NO responses to some with the unpartitioned set should always be slower than YES responses. This was indeed the marginally significant result we observed when comparing YES and NO responses between (entirely consistent) participants. Crucially, however, it was not reliable within participants. This cannot be attributed to lack of power. There were three times as many NO judgments in the within-participants analysis compared to the between-participants analysis. Moreover, we cannot rule out the possibility that participants took longer to respond pragmatically than semantically because they are more careful in verifying the utterance in context. The fact that pragmatic responders are generally slower (even in YES responses) than semantic responders is more consistent with a verification hypothesis.

The Literal-First account has trouble explaining the naturalness effects we observed for the YES responses, in particular the slower response time for YES responses to some/summa at the unpartitioned set compared to the preferred range. The Literal-First hypothesis predicts that as soon as the first stage of semantic processing is complete and the lower bound verified, a YES response can be made. Thus, according to this account, there should be no difference in YES response times to some/summa from 1 to 13 gumballs, where the semantic interpretation holds. Yet we observed clear response time differences.

Proponents of the Literal-First hypothesis might argue that the slowdown effect at the unpartitioned set is due to participants having initially computed the semantic interpretation and then the pragmatic interpretation, before reverting to the semantic interpretation. That is, rather than the semantic response itself taking longer to compute, it is the integration with context that might result in an intermediate computation and subsequent cancelation of the implicature that led to the delayed YES response. However, this type of explanation cannot account for the slowdown effects observed for the small sets. For small sets, YES responses to some/summa were again slower than responses to number times. Moreover, the difference in response times was as function of their naturalness relative to number terms. Thus the more parsimonious explanation is to assume that the effects in both cases arise from the same underlying cause: there is a more natural alternative to some that the speaker could have used, but didn’t.

Our results are also incompatible with the Default model, which assumes that scalar implicatures are computed by default, upon encountering some. The Default approach also cannot account for effects of naturalness. Under the Default model, contextual factors like the naturalness of an utterance with a particular quantifier should only come into play when the participant is deciding whether to cancel the already computed implicature. That is, YES responses to the unpartitioned set should be the only set size where naturalness of some affects response times. To see this, consider what interpretation is necessary for each set size to arrive at a YES response. For the unpartitioned set, only the semantic some and possibly all interpretation yields a YES response. In contrast, for set sizes 1 – 12, both the semantic and the pragmatic interpretation yield YES responses. Thus, under the Default model YES responses to some should have been equally long for set sizes 1 – 12, and a slowdown is expected only for the unpartitioned set, where an additional cost for canceling the implicature is incurred.

The Default account correctly predicts the slowdown effect for YES responses to some with the unpartitioned set compared to its most preferred range. However, it cannot explain a) the slowdown effect for small sets and b) the fact that pragmatic NO responses to the unpartitioned set are also slower compared to YES responses in the preferred range.

We thus believe that the pattern of results we obtained in Experiments 1 – 3 is most compatible with a Constraint-Based account in which the speed and robustness of an implicature is determined by the probabilistic support it receives from multiple cues available in the linguistic and discourse context, including the task/goal relevant information. In this paper we investigated the effect of alternatives on processing some and the scalar inference from some to not all. In particular, we investigated a) the syntactic partitive as a cue to the implicature and b) the naturalness and availability of lexical alternatives to some as inhibitory cues to arriving at an interpretation for some.

Some observations on the naturalness/availability of lexical alternatives are in order. While linguists and logicians treat the meaning of some, all, and other quantifiers as set-theoretically well-defined as for example in Generalized Quantifier Theory (Barwise & Cooper, 1981), the naturalness results from Experiments 1 and 2 show that not only are quantifiers like some more natural for some set sizes than others, but that their naturalness depends crucially on alternative lexical items that the speaker might have used. That is, while there may be ways to unambiguously define quantifier meanings, quantifier interpretation is a matter of degree. Some set sizes (e.g. 6 or 7 out of 13 gumballs) are better fits for some than others (e.g. 2 or 13 out of 13 gumballs) and introducing alternatives can change the goodness of fit. This is paralleled in the concepts and categories literature, where typicality influences categorization even for logically well-defined concepts such as parity (Armstrong et al., 1983). Some numbers are judged as better instances of an odd or an even number than others. Similarly, in our studies some is judged as a more or less natural label for different sizes (and processed more or less quickly accordingly), despite its logical definition unambiguously assigning a TRUE or FALSE value for any given set size.

The effects of naturalness and availability are also compatible with accounts that treat the meaning of quantifiers as distributions over quantities. These distributions reflect listener beliefs about the probability of a particular quantifier being uttered given a particular set size. Listener beliefs are updated by different contextual factors, among them the availability of alternatives. That is, the distributions may shift contextually depending on the available alternatives. Mapping this onto our naturalness results for small sets: the posterior probability of observing an utterance of some to refer to a set of size 2 given that number terms are contextually available is lower than when they are not.

Methodologically, this means that it is important for researchers to be aware of the relative naturalness of the quantifiers under investigation, i.e. which range of the interpretive distribution one is sampling from. For example, in light of the intrusion effects we have shown, delays in the processing of some observed by Huang and Snedeker (2009) could have an explanation that is unrelated to the processing of implicatures per se: not only did they use a set size that is relatively unnatural for some for (two), but two was also explicitly included as a lexical alternative among the experimental items. Therefore some may have been a dispreferred label for referring to the set size it was used for and thus caused the delay. Note that Huang and Snedeker did not find a similar delay for all⁸, which was used with a larger set size (3). Based on our finding we would predict a delay for 'all' if it had been paired with a set size of 2, a prediction that was confirmed by Degen & Tanenhaus (to appear).

Another important factor that is likely to affect the speed and robustness of scalar implicatures is the QUD. While the QUD was not explicitly manipulated in our studies, it may have played a substantial role in participants’ response behavior. In Experiment 3, we interpreted participants’ response consistency to some used with the unpartitioned set as indicative of how much uncertainty they had about the QUD. Our reasoning was that an implicature from You got some of the gumballs to You got some, but not all of the gumballs should be more likely if the assumed QUD is Did I get all of the gumballs? rather than Did I get any gumballs? (see Zondervan (2008) for evidence that both implicit and explicit QUDs affect implicature rates). Thus, we took within-participant distributions over semantic and pragmatic responses to reflect the uncertainty that participants had about the QUD – more skewed distributions, whether skewed towards semantic or pragmatic responses, were taken to indicate less uncertainty. We found that participants with less uncertainty were faster to respond, regardless of whether they responded semantically or pragmatically. This provides an interesting further testing ground for the Constraint-Based account, which predicts that given a QUD that makes the stronger alternative You got all of the gumballs particularly relevant, the implicature should be more rapidly available than in the neutral case (as in our Experiment 3) and in turn the implicature should be even less rapidly available in a lower-bound context. We are currently exploring this hypothesis. More generally, our results suggest that it will be important for future research to explicitly manipulate the QUD.

While in this paper we have focused on the naturalness and availability of some and its alternatives (partitive vs. non-partitive, some vs. other quantifiers), and to some extent on the QUD, there are many other cues that listeners are likely to take into consideration when making an interpretive choice about an utterance with some, some of which have been previously been shown to affect the rate and processing speed of scalar implicatures. Among them are cognitive load (De Neys & Schaeken, 2007), threat of loss of face (Bonnefon, Feeney, & Villejoubert, 2009), speaker competence and reliability (Grodner & Sedivy, 2011), average informativeness of the stronger alternative (Stiller, Goodman, & Frank, 2011), semantic context (Chierchia, 2004) and prosody (Schwarz, Clifton, & Frazier, 2010).

Taken together, then, the evidence suggests that listeners, upon encountering a scalar item, simultaneously consider information from multiple cues in the linguistic and discourse context in determining whether an implicature is likely, and if so, what form it should take in a particular context. Rather than granting privileged status to the semantic interpretation of some, under a Constraint-Based account the research program becomes one of identifying and quantifying the cues that listeners use in computing scalar implicatures. The goal, then, is to provide a unified account of why in many situations this computation appears to be delayed and to come at a cost, whereas in others situations, it is more rapid, and less resource-intensive. The work reported here is a first step in that direction.

We conclude with two observations, one theoretical and one methodological. The theoretical observation is that the perspective we are pursuing presents a challenge to the classic distinction between generalized and particularized implicatures. If we are correct about the context dependency of generalized implicatures, then they no longer have a special status relative to other conversational implicatures. This is analogous to related claims in the literature, for example, the view that lexical representations are distributed and processing a word always involves a context-dependent computation, rather than retrieving a "core" meaning (Elman, 2004; MacDonald & Seidenberg, 2006).

The methodological observation concerns the relationship between formal theories and research in Experimental Pragmatics. We strongly endorse the view that Experimental Pragmatics must be informed by formal theories. However, research in Experimental Pragmatics requires grounding the experimental work in a task, which necessarily involves mapping utterances onto specific contexts. Experimental tests of those theories will often result in novel observations and new data that are central to understanding pragmatics, but might be orthogonal to our current theories. We view this as part of the challenge and excitement of current work in the field.

Indeed, the effects of numbers statements on upper-bound some is an example of a specific result that arises in particular experimental contexts. However, it has more general implications for the importance of the availability and naturalness of alternatives in guiding implicature and, more generally, for the hypothesis that generalized implicatures differ in kind from particularized implicatures.

Appendix A

Table 5.

Set sizes sampled by the twelve base lists used in Experiments 1 and 2.

List	Set sizes	List	Set sizes
1	1, 2, 5, 9	7	2, 3, 5, 9
2	1, 2, 6, 10	8	2, 3, 6, 10
3	1, 3, 5, 9	9	2, 4, 7, 11
4	1, 3, 7, 11	10	2, 4, 8, 12
5	1, 4, 6, 10	11	3, 4, 7, 11
6	1, 4, 8, 12	12	3, 4, 8, 12

Appendix B

We observed an interesting correlation between participants’ response behavior to some/summa used with the unpartitioned set (upper bound) versus when it was used for one gumball (lower bound). At the lower bound, the sentences You got some (of the) gumballs are strictly speaking true but often trigger a multiplicity implicature, whereby the cardinality of the set denoted by some (of the) gumballs is expected to be greater than one (Zweig, 2009). We observe response behavior to some at the lower bound similar to that at the upper bound: 52% of responses were YES responses, while 48% were NO responses. Of these, 38 participants (81%) were completely consistent, 8 participants (17%) gave one response that was different from the rest, and only one participant gave 50% pragmatic and 50% semantic responses at the lower bound. Interestingly, 88% of participants who responded pragmatically at the upper bound also responded pragmatically at the lower bound. In addition, 40% of participants who had responded semantically or inconsistently at the upper bound responded pragmatically at the lower bound. That is, most participants who responded pragmatically at the upper bound also responded pragmatically at the lower bound, and most people who responded semantically at the lower bound also responded semantically at the upper bound (see Fig. 11). The correlation between the number of semantic responses a participant gave at the upper bound vs. at the lower bound is .45.

Fig. 11. Jittered scatterplot of participants' response behavior at the upper and lower bound. Each point represents one participant. Horizontal line represents the perfect correlation line.