Abstract
Image-guided radiotherapy (IGRT) requires fast and accurate localization of the prostate in 3-D treatment-guided radiotherapy, which is challenging due to low tissue contrast and large anatomical variation across patients. On the other hand, the IGRT workflow involves collecting a series of computed tomography (CT) images from the same patient under treatment. These images contain valuable patient-specific information yet are often neglected by previous works. In this paper, we propose a novel learning framework, namely incremental learning with selective memory (ILSM), to effectively learn the patient-specific appearance characteristics from these patient-specific images. Specifically, starting with a population-based discriminative appearance model, ILSM aims to “personalize” the model to fit patient-specific appearance characteristics. The model is personalized with two steps: backward pruning that discards obsolete population-based knowledge and forward learning that incorporates patient-specific characteristics. By effectively combining the patient-specific characteristics with the general population statistics, the incrementally learned appearance model can localize the prostate of a specific patient much more accurately. This work has three contributions: 1) the proposed incremental learning framework can capture patient-specific characteristics more effectively, compared to traditional learning schemes, such as pure patient-specific learning, population-based learning, and mixture learning with patient-specific and population data; 2) this learning framework does not have any parametric model assumption, hence, allowing the adoption of any discriminative classifier; and 3) using ILSM, we can localize the prostate in treatment CTs accurately (DSC ∼0.89) and fast (∼4 s), which satisfies the real-world clinical requirements of IGRT.
Index Terms: Anatomy detection, image-guided radiotherapy (IGRT), incremental learning, machine learning, prostate segmentation
I. Introduction
IMAGE-guided radiotherapy (IGRT) is a newly developed technology for prostate cancer radiation treatment. It is usually recommended when patients are diagnosed with prostate cancer by biospy [1], [2] in the early stage. IGRT consists of a planning stage followed by a treatment stage (Fig. 1). In the planning stage, a planning computed tomography (CT) scan is acquired from the patient and radiation oncologists then manually delineate the prostate for treatment planning. These steps are the same as in conventional radiotherapy. The novelty of IGRT lies in the treatment stage. To account for daily prostate motions, a CT scan called the treatment image is acquired at each treatment day right before the radiation therapy. Since the treatment image captures a present snapshot of the patient's anatomy, radiation oncologists are able to adapt the treatment plan to precisely target the radiation dose to the current positions of tumors and avoid neighboring healthy tissues. Consequently, IGRT increases the probability of tumor control and typically shortens radiation therapy schedules [3], [4]. In order to effectively adapt the treatment plan, it is critical to localize the prostate in the daily treatment images fast and accurately. Thus, an automatic prostate localization algorithm would be a valuable asset in IGRT.
Fig. 1.
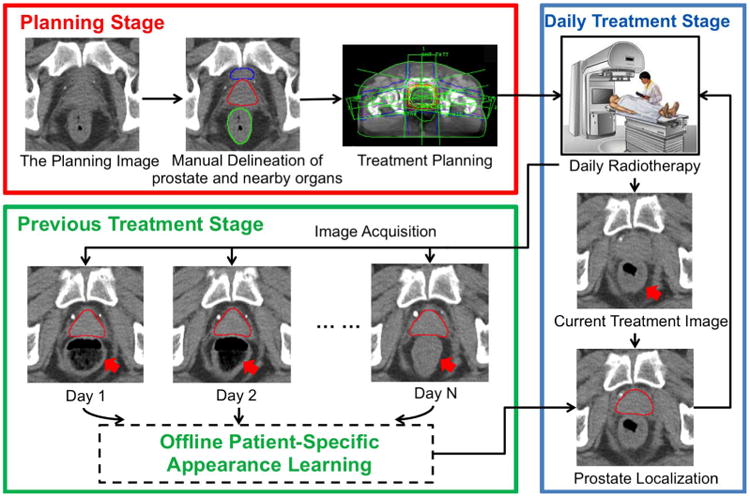
Illustration of IGRT.
However, prostate localization in treatment CT images is quite challenging for three reasons. First, unlike the planning CT image, the treatment CT images are typically acquired with low dose protocols, in order to reduce unnecessary radiation exposure to patients during treatment. As a result, the image contrast of treatment CT is relatively lower compared to other modalities (e.g., MR and regular CT). Fig. 1 shows several typical treatment CTs and their prostate contours (red). Second, due to the existence of bowel gas and filling (pointed to by red arrows in Fig. 1), the image appearance of treatment CTs can change dramatically. Third, unpredicted daily prostate motion [5] further complicates the prostate localization procedure.
Many methods have been proposed to address the aforementioned challenges (for example, deformable models [6], [7], and deformable registration [8]). While such methods exhibit some effectiveness in CT prostate localization, their localization accuracy is often limited because they overlook a remarkable opportunity that is inherent in the IGRT workflow. In fact, at each treatment day, several CT scans of the patient have already been acquired and segmented in the planning day and previous treatment days. If the prostate appearance characteristics of this specific patient can be learned from these patient-specific images, an algorithm could exploit this information to localize the prostate much more effectively. Recently Li [9], Liao [10], and Gao [11] proposed different methods that use patient-specific information for CT prostate localization and have achieved promising results. However, their methods require at least three manually segmented patient-specific images available for patient-specific training, which imposes two major limitations: 1) there may not be sufficient patient-specific data available, especially in the beginning treatment days when only planning CT is available; and 2) manual segmentation of patient-specific images is time consuming (11 min) even for experienced physicians. Additionally, these methods typically need minutes or even longer to localize the prostate due to the computationally expensive methodologies adopted (i.e., sparse coding, iterative voxel-wise classification, deformable registration). If the prostate unexpectedly moves during the long localization procedure, the localization result might become meaningless for IGRT.
To this end, we propose a novel learning scheme, namely incremental learning with selective memory (ILSM), for fast and accurate localization of the prostate in treatment CTs. Compared with previous prostate localization methods, the contributions of our work are two-fold: 1) by leveraging the large amount of population data (that is, CT scans of other patients) and the very limited amount of patient-specific data, ILSM is able to learn patient-specific characteristics from only one image of the patient and apply the learned model to the localization of beginning treatment CTs; 2) our method can obtain comparable (if not better) localization accuracy to the state-of-the-art methods while substantially reducing the computational time to 4 s. To the best of our knowledge, this is the first prostate localization method that can satisfy both accuracy and efficiency requirements in the IGRT workflow. Also, compared to previous methods [9]–[11] that require manual annotation of the entire prostate on the patient-specific training images, our method only needs the annotations of seven prostate anatomical landmarks, thus significantly reducing the labor required for manual annotations.
To leverage both population and patient-specific data, our learning framework (ILSM) starts with learning a population-based discriminative appearance model. This model is then “personalized” according to the appearance information from CTs of the specific patient under treatment. Instead of either preserving or discarding all knowledge learned from the population, our method selectively inherits the part of population-based knowledge that is in accordance with the current patient, and at the same time incrementally learns the patient-specific characteristics. This is where the name “incremental learning with selective memory” comes from. Once the population-based discriminative appearance model is personalized, it can be used to detect distinctive anatomical landmarks in new treatment images of the same patient for fast prostate localization. Compared with traditional learning schemes, such as pure patient-specific learning, population-based learning, and mixture learning with patient-specific and population data, ILSM exhibits better capability to capture the patient-specific characteristics embedded in the data. We note that the preliminary version of our method was previously reported in a conference paper [12]. The present paper extends the method by using multi-atlas RANSAC for prostate localization, and further evaluates the performance with much more comprehensive experiments and on a larger dataset.
The rest of the paper is organized as follows. Section II gives an overview of related methods on both CT prostate localization and incremental learning. Section III presents our ILSM framework and the prostate localization procedure. The experimental results are provided in Section IV. Finally, Section V presents the conclusion.
II. Related Works
As mentioned, we employ incremental learning to localize the prostate in CT images. The following literature review will cover CT prostate localization and incremental learning, respectively.
A. CT Prostate Localization
Many methods have been proposed to address the challenging prostate localization problem in CT images. Most of them can be categorized into three groups: deformable models, deformable registration, and pixel-wise classification/labeling.
Deformable models are popular in medical image segmentation [13], [14], and widely adopted in CT prostate localization. For example, Pizer [15] proposed a medial shape model named M-reps for joint segmentation of bladder, rectum, and prostate. Freedman [16] proposed to segment the CT prostate by matching the probability distributions of photometric variables. Costa et al. [6] proposed coupled 3-D deformable models by considering the nonoverlapping constraint from bladder. Feng et al. [17] proposed to selectively combine the gradient profile features and region-based features to guide the deformable segmentation. Although deformable models have shown their robustness in many medical image segmentation problems, their performance highly depends on good initialization of the model, which is difficult to obtain in CT prostate localization since the daily prostate motion is unpredictable and sometimes can be very large due to the bowel gas and filling.
Deformable Registration [18]–[21] has been investigated in the community for many years as a way to align the corresponding structures between two images. It can also be used to localize the CT prostate by warping the previous treatment CTs (with the prostate segmented) of the same patient to the current treatment CT. For example, Foskey et al. [8] proposed a deflation method to explicitly eliminate bowel gas before 3-D deformable registration. Liao et al. [22] proposed a feature-guided deformable registration method by exploiting patient-specific information. Compared to deformable models, deformable registration takes into account global appearance information and is thus more robust to prostate motion. However, the nonrigid registration procedure is often time-consuming and typically takes minutes or even longer to localize the prostate, which is problematic if the prostate moves during the long localization procedure.
Pixel-wise classification/labeling is a recently proposed method for precise prostate segmentation. The basic idea is to enhance the indistinct prostate in CT scans through pixel-wise labeling. Li et al. [9] proposed to utilize image context information to assist the pixel-wise classification, and level-set was used to segment the prostate based on the classification response map. Gao et al. [23] proposed a sparse representation based classifier with a discriminative learned dictionary and further employed multi-atlas labeling for prostate segmentation. Liao et al. [10] proposed a sparse patch-based label propagation framework that effectively transfers the labels from previous treatment CTs of the patient for pixel-wise labeling. Shi et al. [24] proposed a semi-automated prostate segmentation method by designing spatial-constrained transductive lasso for multi-atlas based label fusion. Despite the high accuracy of these methods (mean DSC ≈ 0.9), in general, they suffer from two limitations: 1) as in deformable registration, pixel-wise labeling is usually time consuming; 2) in order to learn statistically reliable patient-specific appearance information, these methods require a sufficient number of manually segmented patient-specific images (i.e., at least three images). In practice, one may not be able to collect enough patient-specific images, especially in the beginning of radiotherapy when only the planning CT image is available.
Besides the aforementioned methods, Haas et al. [25] used 2-D flood fill with the shape guidance to localize the prostate in CT images. Ghosh et al. [26] proposed a genetic algorithm with prior knowledge in the form of texture and shape. Although these approaches adopted novel methodologies, their localization accuracies were very limited.
There are also many methods published for prostate segmentation in other modalities (e.g., MR [27], [28], ultrasound [29]–[31]). However, due to various reasons, most of these methods cannot be readily adapted for fast prostate localization in CT images. For example, conventional multi-atlas methods (e.g., [27]) often require nonrigid registration to align each atlas with the image to be segmented. This procedure is quite time consuming (e.g., 15 min per registration) and thus not suitable for fast prostate localization. Methods such as [29], [30] utilized the existence of diagnostic probe in ultrasound images for feature design and prostate localization. Due to lack of such structure in CT images, these kinds of methods are no longer applicable. Other methods (e.g., [28], [30]) are not considered because they are either semi-automatic or only applicable to 2-D segmentation.
B. Incremental Learning
Incremental learning has been extensively investigated in the area of machine learning area. The key objective of incremental learning is to adapt previously learned models (e.g., classifiers) to new data without retraining from scratch. Polikar et al. [32] proposed Learn++, an algorithm for incremental training of neural network (NN) classifiers. By assembling previously learned classifiers with incrementally trained classifiers, Learn++ is able to adapt the trained classifiers to incoming data. Diehl et al. [33] proposed an incremental learning algorithm for adapting the support vector machine (SVM) classifier. Ross et al. [34] proposed an incremental learning algorithm for online updating of the Gaussian appearance model for visual tracking. While these methods share some similarities with our framework in terms of incremental learning, there are three main differences between previous incremental learning approaches and our method: 1) instead of preserving all previously learned knowledge [32], ILSM selectively discards some learned population characteristics if they are no longer applicable to the patient-specific data; 2) in contrast to [34], which assumes image appearance follows Gaussian distribution, ILSM doesn't impose any assumption on appearance distribution, as prostate appearance often follows a complex non-Gaussian distribution (demonstrated in Fig. 3); 3) different from [33], which only focuses on the incremental learning of a specific classifier (i.e., SVM), ILSM provides a general learning framework for effective combination of large population data and the limited patient-specific data, hence allowing for the adoption of any classifier. To the best of our knowledge, this is the first work that employs the concept of incremental learning to effectively combine the appearance statistics from large population data and the limited patient-specific data.
Fig. 3.
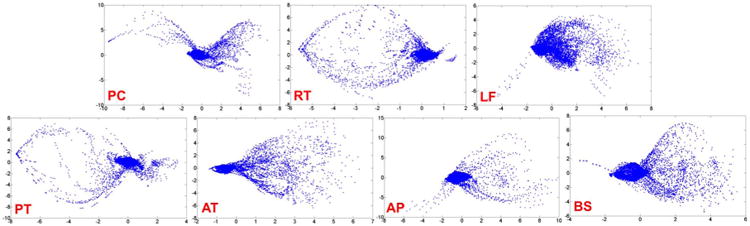
Non-Gaussianity of local appearance distribution of the seven landmarks in Fig. 2. Given all prostate CT scans, we ask an expert to annotate the seven landmarks on the images. For each landmark, we extract its local patches (size 9 × 9 × 9 mm3) from all annotated CT scans and perform a PCA analysis on the extracted patches. Figures are plotted using the first two principal components. Each point in the figure denotes a local patch represented by the first two principal component scores. To take annotation error into account, we randomly perturb the annotated landmarks by at most 1 mm to generate additional samples. Clearly, none of these distributions follow the Gaussian distribution.
III. Methodology
Our method aims to localize the prostate in daily treatment images via learning a set of local discriminative appearance models. Specifically, these models are used as anatomy detectors to detect distinctive prostate anatomical landmarks as shown in Fig. 2. Based on the detected landmarks, multiple patient-specific shape atlases (i.e., prostate shapes in planning and previous treatment stages) can be aligned onto the treatment image space by RANSAC [35]. Finally, majority voting is adopted to fuse the labels from different shape atlases.
Fig. 2.
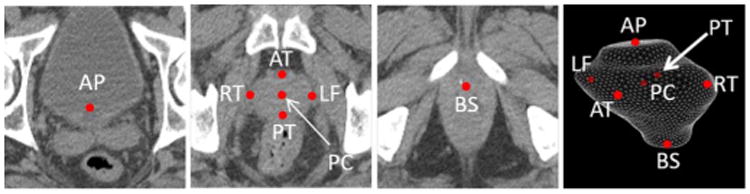
Seven prostate anatomical landmarks used in our study: prostate center (PC), right lateral point (RT), left lateral point (LF), poterior point (PT), anterior point (AT), base center (BS), and apex center (AP).
As shown in Fig. 4, our method consists of three components, 1) cascade detector learning, 2) incremental learning with selective memory, and 3) robust prostate localization by multi-atlas RANSAC, which will be detailed in the following subsections.
Fig. 4.

Flowchart of our CT prostate localization method.
A. Cascade Learning for Anatomy Detection
Our prostate localization method relies on several anatomical landmarks of the prostate. Inspired by Viola's face detection work [36], we adopt a learning-based detection method, which formulates landmark detection as a classification problem. Specifically, for each image, the voxel of the specific landmark is positive and all others are negatives. In the training stage, we employ a cascade learning framework that aims to learn a sequence of classifiers to gradually separate negatives from positives (Fig. 5). Compared to learning only a single classifier, cascade learning has shown better classification accuracy and runtime efficiency [36], [37]. Mathematically, cascade learning can be formulated as follows.
Fig. 5.

Illustration of cascade learning.
Input: Positive voxel set X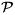 , negative voxel set X
, negative voxel set X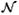 , and label set ℒ = {+1,−1}.
, and label set ℒ = {+1,−1}.
Classifier: C(x) :
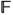 (x) →ℒ,
(x) →ℒ,
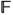 (x) denotes the appearance features of a voxel x.
(x) denotes the appearance features of a voxel x.
Initial Set: X0 = X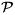 ∪ X
∪ X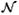 .
.
Objective: Optimize Ck, k = 1, 2,…, K, such that
where Xk = {x|x ∈ Xk−1 and Ck(x) = +1}, and τ controls the tolerance ratio of false positives.
The cascade classifiers Ck, k = 1, 2,…, K, are optimized sequentially. As shown in (1), Ck is optimized to minimize the false positives left over by the previous k − 1 classifiers
| (1) |
where ‖·‖ denotes the cardinality of a set. It is worth noting that the constraint in (1) can be simply satisfied by adjusting the threshold of classifier Ck [36] to make sure that all positive training samples are correctly classified. This cascade learning framework is general to any image feature and classifier. Extended Haar wavelets [38], [39] and the Adaboost [36] classifier are employed in our study.
Once the cascade classifiers {Ck(x)} are learned, they have captured the appearance characteristics of the specific anatomical landmark. Given a testing image, the learned cascade is applied to each voxel. The voxel with the highest classification score after going through the entire cascade is selected as the detected landmark. To increase the efficiency and robustness of the detection procedure, a multi-scale scheme is further adopted. Specifically, the detected landmark in the coarse resolution serves as the initialization for landmark detection in a following finer resolution, in which the landmark is only searched in a local neighborhood centered by the initialization. In this way, the search space is largely reduced and the detection procedure is more robust to local minima.
B. Incremental Learning With Selective Memory (ILSM)
1) Motivation
Using cascade learning, one can learn anatomy detectors from training images of different patients (population-based learning). However, since intra-patient anatomy variations are much less pronounced than inter-patient variations (Fig. 6), patient-specific appearance information available in the IGRT workflow should be exploited in order to improve the detection accuracy for an individual patient. Unfortunately, the number of patient-specific images is often very limited, especially in the beginning of IGRT. To overcome this problem, one may apply random spatial/intensity transformations to produce more “synthetic” training samples with larger variability. However, these artificially created transformations may not capture the real intra-patient variations, e.g., the uncertainty of bowel gas and filling (Fig. 6). As a result, cascade learning using only patient-specific data (pure patient-specific learning) often suffers from overfitting. One can also mix population and patient-specific images for training (mixture learning). However, since patient-specific images are the “minority” in the training samples, detectors trained by mixed samples might not capture patient-specific characteristics very well. To address this problem, we propose a new learning scheme, ILSM, to combine the general information in the population images with the personal information in the patient-specific images. Specifically, population-based anatomy detectors serve as an initial appearance model and are subsequently “personalized” by the limited patient-specific data. ILSM consists of backward pruning to discard obsolete population appearance information and forward learning to incorporate the online-learned patient-specific appearance characteristics.
Fig. 6.
Inter- and intra-patient prostate shape and appearance variations. Red points denote the prostate center. Each row represents prostate shapes and images from the same patient.
2) Notations
Denote as the population-based anatomy detector (learned as outlined in Section III-A), which contains a cascade of classifiers. and are positives and negatives from the patient-specific training images, respectively. D(x) denotes the class label (landmark versus nonlandmark) of voxel x predicted by detector D.
3) Backward Pruning
The general appearance model learned from the population is not necessarily applicable to the specific patient. More specifically, the anatomical landmarks in the patient-specific images (positives) may be classified as negatives by the population-based anatomy detectors, i.e., . In order to discard these parts of the population appearance model that do not fit the patient-specific characteristics, we propose backward pruning to tailor the population-based detector. As shown in Algorithm 1, in backward pruning, the cascade is pruned from the last level until all patient-specific positives successfully pass through the cascade. This is equivalent to searching for the maximum number of cascade levels that could be preserved from the population-based anatomy detector
|
|
| Algorithm 1 Backward pruning algorithm. |
|
|
| Input: |
| - the population-based detector |
| - patient-specific positive samples |
| Output: Dbk - the tailored population-based detector |
| Init: k = Kpop, Dbk = Dpop. |
| while do |
| k = k − 1 |
| end while |
| Kbk = k |
| return |
|
|
|
| ||
| Algorithm 2 Forward learning algorithm. | ||
|
| ||
| Input: | ||
| - the tailored population-based detector | ||
| - patient-specific positive samples | ||
| - patient-specific negative samples | ||
| Output: Dpat - the patient-specific detector | ||
| Init: k = 1, Dpat = Dbk | ||
| while do | ||
| Train the classifier by minimizing Eq. 3 below | ||
| ||
| k = k + 1 | ||
| end while | ||
| Kpat = k − 1 | ||
| return | ||
| ‖·‖ denotes the cardinality of a set. τ is the parameter controlling the tolerance ratio of false positives. | ||
|
|
| (2) |
4) Forward Learning
Once the population cascade has been tailored, the remaining cascade of classifiers encodes the population appearance information that is consistent with the patient-specific characteristics. Yet, until now no real patient-specific information has been incorporated into the cascade. More specifically, false positives might exist in the patient-specific samples, i.e., . In the forward learning stage, we use the remaining cascade from the backward pruning algorithm as an initialization and reapply the cascade learning to eliminate the patient-specific false positives left over by the previously inherited population classifiers. As shown in Algorithm 2, a greedy strategy is adopted to sequentially optimize a set of additional patient-specific classifiers .
After backward pruning and forward learning, the personalized anatomy detector includes two groups of classifiers (Fig. 7). While encode patient-specific characteristics, contain population information that is applicable to this specific patient. This information effectively remedies the limited variability from the small number of patient-specific training images.
Fig. 7.

Incrementally learned anatomy detector.
5) Insight of ILSM
In fact, pure patient-specific learning (PPAT) and traditional incremental learning (IL) can also be employed to incorporate the patient-specific information. It is interesting to compare ILSM with PPAT and IL. PPAT only uses patient-specific data for training. In other words, it completely discards all knowledge learned from population, which is known as “catastrophic forgetting” [32]. The method is prone to over-fitting if the patient-specific data is very limited. On the other hand, IL aims to gradually adapt the classifiers with new data. It assumes the previously learned knowledge is always applicable for the new incoming data and tries to “remember” all of them. Consequently, the incrementally learned patient-specific knowledge can be impaired by incompatible population-based knowledge. In fact, in the context of cascade learning, IL can be regarded as the proposed method without backward pruning. In contrast to PPAT and IL, ILSM aims to “selectively” remember the subset of pre-learned knowledge consistent with the characteristics in the new data. ILSM's “selective memory” helps to overcome the limitations of the other two methods.
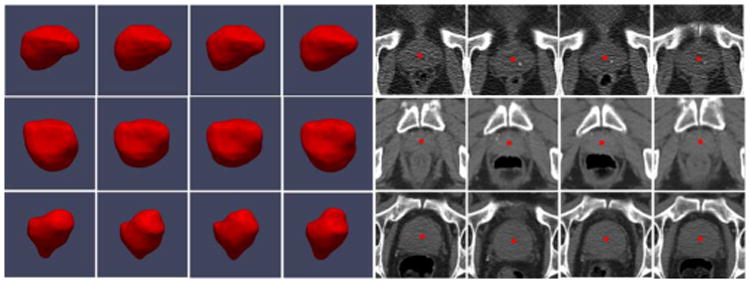
Fig. 8 schematically explains the differences among PPAT, IL, and ILSM from the perspective of decision boundary refinement. Fig. 8(a) shows the sample distribution in a 2-D feature space. Star and circle represent positive and negative samples, respectively. Blue stars/circles are population training samples, and green ones denote patient-specific samples. The orange star is a testing sample.
Fig. 8.
Schematic illustration of differences among PPAT, IL, and ILSM.
As shown in Fig. 8(b), since PPAT only uses patient-specific samples (stars/circles in green), the generated decision boundaries (green lines) closely encompass the positive patient-specific training samples (green stars). These decision boundaries might overfit the very limited number of patient-specific samples. As a result, a testing sample [the orange star in Fig. 8(b)], having slight differences from these training samples, is misclassified.
IL derives the decision boundaries in two steps. First, as shown in Fig. 8(c), it learns the decision boundaries using population samples (blue stars/circles). Second, these boundaries are adapted to accommodate patient-specific samples. For example, in Fig. 8(d), an additional purple line is generated to separate patient-specific positives (green stars) and negatives (green circles). Since IL aims to preserve all pre-learned population-based boundaries (blue and red lines), some patient-specific data [circled in red in Fig. 8(d)] are still misclassified due to the “unforgettable” decision boundary [the red line in Fig. 8(d)].
Similar to IL, ILSM also starts from a population-based learning [Fig. 8(c)]. However, in adapting the decision boundaries to patient-specific samples, it is able to “forget” some pre-learned knowledge that is not applicable to the patient-specific data. Specifically, the obsolete decision boundary [red line in Fig. 8(d)] can be discarded in the “backward prunning” step of ILSM. Hence, ILSM can correctly classify all patient-specific data [Fig. 8(e)]. In addition, by reusing some applicable population-based decision boundaries (blue lines), the overfitting risks are also highly reduced. In this way, ILSM can address the limitations of both PPAT and IL.
In fact, ILSM can be considered as a more general learning framework, of which IL and PPAT are just two special cases. In Algorithm 1, if all positive samples from patient-specific images can be correctly classified by Dpop, the backward pruning will stop at the first place, i.e., Kbk = Kpop (Algorithm 1). The learned patient-specific detector will then preserve all population characteristics, which is the same as IL. At the other extreme, if the population-based detector is completely incompatible with patient-specific samples, the backward pruning will not stop until Dbk = ∅ (Algorithm 2), which means all population-based classifiers will be discarded. In such cases, the forward learning will start from scratch with patient-specific samples and ILSM becomes equivalent to PPAT. In practice, this situation rarely happens. We manually checked all these cases in our trained detectors and found that they all happened when sufficient patient-specific images (≥ 5) had already been collected. In such situation, PPAT is capable to obtain similar performance with ILSM.
C. Robust Prostate Localization by Multi-Atlas RANSAC
Once the population-based anatomy detectors are “personalized” by ILSM, they are used to detect the corresponding prostate anatomical landmarks (Fig. 2) in new treatment images. Based on the detected landmarks, any patient-specific prostate shape model (e.g., the prostate shape delineated in the planning stage) can be aligned onto the treatment image space for fast localization. For robust performance against wrongly detected landmarks, the RANSAC algorithm [35] is used to estimate the optimal transformation that fits the shape model onto the detected landmarks (Algorithm 3). Considering the limited number of anatomical landmarks (seven), as well as in the interest of computational efficiency, rigid transformation is used in our work.
One can simply align the planning prostate shape onto the treatment image for localization, which is referred as single-atlas RANSAC. However, due to the daily shape variations under radiotherapy, the performance of using a single shape model is usually limited. To overcome this limitation, we propose a multi-atlas RANSAC for robust prostate localization. Instead of using a single shape model, we utilize all patient-specific shape models available in both planning and previous treatment stages for multi-atlas labeling of a new treatment image. In other words, each patient-specific shape model is treated as a shape atlas. Once anatomical landmarks are detected in the new treatment image, all available shape atlases can be independently aligned onto the new treatment image space by RANSAC (Algorithm 3). Then, majority voting is adopted to fuse the labels from different shape atlases. Thus, by integrating all patient-specific shape information into a multi-atlas scheme, the localization procedure is more robust to daily shape variations than single-atlas RANSAC. Fig. 9 illustrates the multi-atlas model fitting process.
Fig. 9.

Illustration of multi-atlas RANSAC. First row shows aligned patient-specific shape models (denoted by different colors) in a new treatment CT. Second row shows the prostate likelihood map by averaging all aligned prostate masks. Third row shows the final segmentation (red contours) overlaid by the ground truth (blue contours). Three columns are the middle slices in transverse, sagittal, and coronal views, respectively.
|
|
| Algorithm 3 Robust Surface Transformation by RANSAC |
|
|
| Definition: ℕ = 7 - number of anatomical landmarks |
| Input: pk, k = 1, 2, ⋯, ℕ - landmarks in one patient-specific training image Ipat |
| mk, k = 1, 2, ⋯, ℕ - detected landmarks in the treatment image Itreat |
| ℳ - minimum number of landmarks required for transformation estimation |
| η - threshold to determine whether a landmark agrees on the transformation |
| Output: Topt - optimal transformation between prostate shapes in Ipat and Itreat |
| Init: Topt = nil, εopt = infinity |
| for each landmark subset S of {1, 2, ⋯, ℕ} with ‖S‖ ≥ ℳ do |
| for any k not in S do |
| if then |
| add k into S |
| end if |
| end for |
| if then |
| end if |
| end for |
| return Topt |
|
|
IV. Experimental Results
A. Data Description
Our experimental data consists of two datasets acquired at the University of North Carolina Cancer Hospital. In total, our data consists of 32 patients with 478 images. Every patient has one planning scan and multiple treatment scans. The prostates in all CT images have been manually delineated by an experienced expert to serve as ground-truth. The planning images in dataset A were scanned by a Siemens Somatom CT scanner, while the planning images in dataset B were scanned by a Philips Big bore scanner. The treatment images in both dataset A and dataset B were collected on a Siemens Somatom CT-on-rails scanner. The typical dose was 200–300 cGy for planning imaging and less than 2 cGy for treatment imaging. The field-of-view (FOV) is 50 cm for planning images in dataset A, 60 cm for planning images in dataset B, and 40 cm for treatment images in both datasets. For other information (e.g., spacing, image size), please refer to Table I. Fig. 10 shows the histogram of number of treatment scans per patient.
Table I. Parameters of Two CT Prostate Datasets.
| Dataset A | Dataset B | |
|---|---|---|
| Planning Resolution (mm) | 0.98 × 0.98 × 3 | 1.24 × 1.24 × 3 |
| Treatment Resolution (mm) | 0.98 × 0.98 × 3 | |
| Image Size | 512 × 512 × 30 ∼ 120 | |
| Number of patients | 25 | 7 |
| Number of images | 349 | 129 |
Fig. 10.
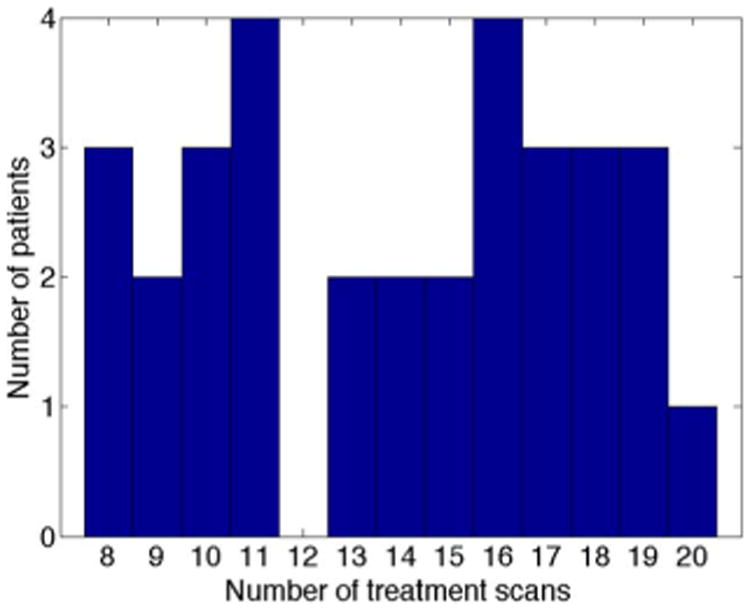
Histogram of number of treatment scans per patient.
B. Accuracy Measurements
To quantitatively evaluate the proposed method, we adopt the following four measurements.
Dice Similarity Coefficient (DSC) measures the overlap ratio between automatic and manual segmentation. It is defined as (2 ×‖Vs ∩ Vm‖)/(‖Vs‖ + ‖Vm‖), where Vs and Vm are the prostate-labelled voxel sets automatically segmented by our method and manually segmented by a clinical expert, respectively, and ‖·‖ denotes the cardinality of a set.
Average Surface Distance (ASD) measures the surface distance between automatically and manually segmented prostate volumes. To compute this measure, we first sample a number of directions (i.e., 360 × 180 = 64800 directions) from the uniform spherical distribution. Then, for each sampled direction, we cast a ray originating from the ground truth centroid and compute the surface distance along this ray. Finally, the surface distances over all sampled directions are averaged to obtain the average surface distance.
Sensitivity (Sen.) is defined as ‖Vs ∩ Vm‖/‖Vm‖, which measures the percentage of manually segmentation that overlaps with automatic segmentation.
Positive Predictive Value (PPV.) is defined as ‖Vs ∩ Vm‖/‖Vs‖, which measures the percentage of automatic segmentation that overlaps with manual segmentation.
C. Accuracy and Efficiency Requirement for Image Guided Radiation Therapy
As indicated by an experienced clinician, a localization algorithm with average surface distance less than 3 mm, DSC greater than 0.80 and runtime less than 2 min would be acceptable for standard conventional radiation therapy. For Stereotactic Body Radiation Therapy (SBRT), which delivers much higher dose per fraction (800 cGy) than conventional radiation therapy, it is desirable to track the intra-fraction prostate motion during the radiation treatment to reduce the chances of missing the target. Thus, a localization algorithm with higher efficiency is often required. According to the clinician, in order to track the intra-fraction prostate motion in SBRT, the time for the entire prostate localization procedure should be controlled within 1 min, including the time for review and manual adjustment. Since the time for manual adjustment heavily depends on the segmentation quality, it is difficult to give a quantitative acceptable threshold for the algorithm speed. In principle, a faster algorithm would save more time for better quality control, and in the meanwhile minimizes the discomfort of the patients when they are fixed in the treatment bed.
D. Parameter and Experimental Setting
We use three scales (coarse, middle, and fine) in population-based learning. Table II lists the training parameters of landmark detection at different scales, which will be elaborated in the following paragraphs.
Table II. Training Parameters for Multi-Scale Landmark Detection.
| Scale | Spacing (mm) | W (mm) | dn (mm) |
|---|---|---|---|
| Coarse | 4 | 80 | 400 |
| Middle | 2 | 40 | 200 |
| Fine | 1 | 20 | 100 |
In the training of each cascade, positive training samples X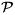 are the voxels annotated as landmarks. The negative training sample set X
are the voxels annotated as landmarks. The negative training sample set X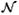 consists of all voxels whose distances are within dn from the annotated landmarks. At every cascade level k, if ‖X
consists of all voxels whose distances are within dn from the annotated landmarks. At every cascade level k, if ‖X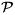 ‖/‖Xk–1∩X
‖/‖Xk–1∩X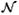 ‖ < τ, we randomly sample a portion of negatives from Xk–1∩X
‖ < τ, we randomly sample a portion of negatives from Xk–1∩X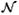 such that the positive/negative ratio is equal to τ (in this paper, τ = 1/5). Otherwise, if ‖X
such that the positive/negative ratio is equal to τ (in this paper, τ = 1/5). Otherwise, if ‖X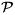 ‖/‖Xk–1 ∩ X
‖/‖Xk–1 ∩ X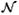 ‖ ≥ τ, we use all samples in Xk–1∩X
‖ ≥ τ, we use all samples in Xk–1∩X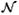 as negative samples. τ is also used as a relative threshold for stopping cascade learning and forward learning when the false positive/positive ratio is less than τ. In this way, we can restrict the positive/negative ratio between τ and 1/τ at every cascade level, thus avoiding the problems introduced by the imbalanced training dataset.
as negative samples. τ is also used as a relative threshold for stopping cascade learning and forward learning when the false positive/positive ratio is less than τ. In this way, we can restrict the positive/negative ratio between τ and 1/τ at every cascade level, thus avoiding the problems introduced by the imbalanced training dataset.
Each training voxel is represented by a set of extended Haar wavelet features [38], which are computed by convoluting the Haar-like kernels with the original image. The Haar-like kernels are generated by scaling predefined Haar-like templates. Each Haar-like template consists of one or more 3-D rectangle functions with different polarities
| (4) |
| (5) |
where Z is the number of 3-D rectangle functions (in our case, Z ∈ {1, 2}) and pi ∈ {−1, 1} and ai are the polarity and translation of the ith 3-D rectangle function, respectively. Fig. 11 shows the 14 Haar-like templates used in this paper. The coefficients for scaling the Haar-like templates are 3 and 5. For each training voxel, we compute the extended Haar wavelet features in its W × W × W local neighborhood. Then, all these computed features are concatenated to form a patch-based feature representation for the voxel. The training parameters are listed in Table II. In the cascade learning step, we employ the Adaboost classifier as cascade classifier. The Adaboost classifier training stops when 20 weak classifiers are obtained.
Fig. 11.
14 Haar templates used in the paper. Blue and red cubes are 3-D rectangle functions with positive and negative polarities, respectively. Cubes with dashed borders are the empty areas which are only shown for purpose of visualization.
In the multi-atlas RANSAC, ℳ (the minimum number of landmarks required for transformation estimation) is set to 3 since only 3-D rigid transformation needs to be estimated, and η (the threshold to determine whether a landmark agrees on the transformation) is set to 5 mm. In the remainder of this section, all results from ILSM are generated with the same parameter settings.
We used five-fold cross validation on dataset A to evaluate our method. In this approach, the population-based landmark detectors of one fold are trained using CT scans of patients from the other four folds. For each fold, about 250 CT images were used in the training of population-based detectors. For the experiments on dataset B, the population-based detectors are trained using all CT scans of dataset A. In this way, we can validate the generalization of our method to dataset acquired by different scanners and protocols.
To emulate the real clinical setting, for prostate localization in treatment day N + 1, we use the previous N treatment images and the planning image as patient-specific training data (Fig. 1). From our observations, we found that, when N reaches 4, there is negligible accuracy gained from performing additional ILSMs. Therefore, after treatment day 4, we do not perform ILSM to further refine the patient-specific landmark detectors; instead, we directly adopt the existing detectors for prostate localization. If not explicitly mentioned, all the reported performances of ILSM are computed using up to five patient-specific training images (four treatment images +1 planning image).
E. Number of Cascade Classifiers
To gain an insight on the number of cascade classifiers remaining after backward pruning or appended by forward learning, we summarize the statistics of Kpop, Kbk, and Kpat in Table III. As we can see, the majority of population cascade classifiers in coarse and middle scale are retained after backward pruning (i.e., Kbk is close to Kpop). However, when it comes to the fine scale, many population cascade classifiers are discarded. The reason for this might be related to the fact that individual differences are embodied in the fine scale but not evident in the coarse and middle scale. Finally, for the number of patient-specific cascade classifiers appended in the forward learning stage, experimental results show that usually 2–3 classifiers are sufficient.
Table III. Statistics of Numbers of Cascade Classifiers.
| Scale | Kpop | Kbk | Kpat |
|---|---|---|---|
| Coarse | 13.1 ± 1.2 | 12.6 ± 3.4 | 2.1 ± 1.3 |
| Middle | 13.5 ± 0.6 | 12.7 ± 2.8 | 2.5 ± 1.6 |
| Fine | 15.5 ± 2.1 | 6.3 ± 2.8 | 2.9 ± 0.1 |
F. Comparison Studies
1) Comparison With Traditional Learning-Based Approaches
To illustrate the effectiveness of our learning framework, we compared ILSM with four other learning-based approaches on dataset A. All of these methods localize the prostate through learning-based anatomy detection with the same features, classifiers and cascade framework (as described in Section III-A). Their differences lie at the training images and learning strategies, which are shown in Table IV. Note that for all patient-specific training images, artificial transformations are applied to increase the variability.
Table IV. Differences Between ILSM and Four Learning-Based Methods. (POP: Population-Based Learning; PPAT: Pure Patient-Specific Learning; MIX: Population and Patient-Specific Mixture Learning; IL: Incremental Learning Without Backward Pruning; ILSM: Proposed Incremental Learning With Selective Memory).
| POP | PPAT | MIX | IL | ILSM | ||
|---|---|---|---|---|---|---|
| Training images | Population | ✓ | ✓ | ✓ | ✓ | |
| Patient-specific | ✓ | ✓ | ✓ | ✓ | ||
| Learning strategies | Cascade Learning | ✓ | ✓ | ✓ | ✓ | ✓ |
| Backward Pruning | ✓ | |||||
| Forward Learning | ✓ | ✓ | ||||
Table V compared the four learning-based approaches with ILSM on landmark detection errors. To exclude the influence from other components of our method, the reported landmark detection error is directly measured without using RANSAC for outlier detection and correction. We can see that ILSM outperforms other four learning-based approaches on all seven anatomical landmarks. In order to better interpret the landmark detection accuracies of our method, we further conducted an experiment to assess the inter-operator annotation variability on CT prostate landmarks. Specifically, we asked four different operators to independently annotate the seven antomical landmarks on 19 CT scans of one patient. Then, the landmark annotation differences between any pair of operators were calculated. Finally, all pair-wise landmark annotation differences were averaged to obtain the inter-operator annotation variability (listed in Table VI). From Table VI, we can see that on average ILSM achieves comparable (if not better) accuracy to the inter-operator annotation variability, exhibiting better mean error but slightly worse standard deviation. A two sample t-test shows that the difference between ILSM and inter-operator variability is statistically significant (p < 0.05).
Table V. Quantitative Comparisons on Landmark Detection Error (mm) Between ILSM and Four Learning-Based Methods on Dataset A. Landmark Error Reported Here is Calculated Without Using RANSAC for Outlier Detection and Correction. The Last Row Shows the P-Values of Two-Sample T-Test When Comparing Landmark Errors of Four Learning-Based Methods With That of ILSM.
| POP | PPAT | MIX | IL | ILSM | |
|---|---|---|---|---|---|
| PC | 6.69 ± 3.65 | 4.89 ± 5.64 | 6.03 ± 3.03 | 5.87 ± 4.01 | 4.73 ± 2.69 |
| RT | 7.85 ± 8.44 | 6.09 ± 9.00 | 5.72 ± 4.04 | 6.33 ± 4.82 | 3.76 ± 2.80 |
| LF | 6.89 ± 4.63 | 5.39 ± 7.61 | 5.61 ± 3.63 | 5.90 ± 4.54 | 3.69 ± 2.69 |
| PT | 7.04 ± 5.04 | 8.66 ± 13.75 | 6.18 ± 4.76 | 6.74 ± 5.05 | 4.78 ± 4.90 |
| AT | 6.60 ± 4.97 | 4.54 ± 5.06 | 5.38 ± 4.55 | 5.68 ± 4.97 | 3.54 ± 2.19 |
| BS | 6.12 ± 2.97 | 5.63 ± 7.44 | 6.63 ± 3.98 | 5.61 ± 2.94 | 4.68 ± 2.71 |
| AP | 10.42 ± 6.03 | 8.94 ± 16.07 | 8.77 ± 5.00 | 9.50 ± 7.17 | 6.28 ± 4.60 |
| Average | 7.37 ± 5.52 | 6.31 ± 10.13 | 6.33 ± 4.32 | 6.52 ± 5.09 | 4.49 ± 3.49 |
| p-value | < 10−5 | < 10−5 | < 10−5 | < 10−5 | n/a |
Table VI. Quantitative Comparison Between Landmark Detection Error (mm) of ILSM and Inter-Rater Annotation Variability on 19 Treatment Scans of One Patient. Landmark Error Reported Here Is Calculated Without Using RANSAC for Outlier Detection and Correction. The P-Value Reported Here Is Computed by Two-Sample T-Test.
| PC | RT | LF | |
|---|---|---|---|
| ILSM | 4.72 ± 1.42 | 3.03 ± 1.75 | 3.17 ± 1.61 |
| Inter-rater | 4.50 ± 1.22 | 5.25 ± 1.27 | 5.77 ± 1.49 |
| PT | AT | BS | |
| ILSM | 2.45 ± 1.00 | 3.24 ± 1.28 | 5.57 ± 1.98 |
| Inter-rater | 5.71 ± 2.85 | 4.44 ± 3.09 | 4.63 ± 1.32 |
| AP | Average | p-value | |
| ILSM | 7.18 ± 4.17 | 4.20 ± 2.65 | n/a |
| Inter-rater | 4.44 ± 1.05 | 4.96 ± 2.00 | 0.01 |
Table VII compares the four learning-based approaches with ILSM on overlap ratios (DSC). To exclude the influence of multi-atlas RANSAC, only a single shape atlas (i.e., the planning prostate shape) is used for localization. Here, “Acceptance Rate” denotes the percentage of images where an algorithm performs with higher accuracy than inter-operator variability (DSC = 0.81) [8]. According to our experienced clinician, these results can be accepted without manual editing. We can see that ILSM achieves the best localization accuracy among all methods. Not surprisingly, by utilizing patient-specific information, all three methods (i.e., PPAT, MIX, and IL) outperform POP. However, their performances are still inferior to ILSM, which shows the effectiveness of ILSM in combining both population and patient-specific characteristics.
Table VII. Quantitative Comparisons on Overlap Ratios (DSC) Between ILSM and Four Learning-Based Methods in Dataset A. (S) and (M) Indicate Single-Atlas and Multi-Atlas RANSAC, Respectively.
| POP (S) | PPAT (S) | MIX (S) | IL (S) | ILSM (S) | ILSM (M) | |
|---|---|---|---|---|---|---|
| Mean DSC | 0.81 ± 0.10 | 0.84 ± 0.15 | 0.83 ± 0.09 | 0.83 ± 0.09 | 0.87 ± 0.06 | 0.88 ± 0.06 |
| Acceptance Rate | 66% | 85% | 74% | 77% | 90% | 91% |
Fig. 12 shows the differences in localization accuracy between ILSM and PPAT with respect to the number of patient-specific training images. We can see that when the number of patient-specific training images is limited (< 3), the performance of PPAT is very poor, even with aritifical transformations to increase the variability in training samples. This is especially the case when only one patient-specific training image is used. Due to the limited patient-specific patterns observed, PPAT suffers from severe overfitting and results in high failure rates for some patients. In such cases, ILSM significantly outperforms PPAT by 40%–70% DSC, as shown in Fig. 12(a). The main reason why simple artificial transformations (e.g., rotation, translation) fail to improve the performance of PPAT is that generally they cannot well capture intra-patient anatomical appearance variations such as bowel gas and filling (Fig. 1). This also explains why previous pure patient-specific learning algorithms [9], [10], [23] often start with three patient-specific training images. By leveraging both population and patient-specific data, ILSM can achieve DSC 0.85 ± 0.06 on the first two treatment images using only a single planning CT as patient-specific training data, while in the same setting PPAT only obtained DSC 0.79 ± 0.15. As the number of patient-specific training images increases, the performance difference between ILSM and PPAT gradually decreases. Ideally, when sufficient patient-specific data is collected, the performance of ILSM and PPAT should converge. However, by using up to 13 patient-specific training images, we still observe that ILSM is slightly better than PPAT (1.5% DSC difference), which implies the effectiveness of the general appearance characteristics learned from the population.
Fig. 12.
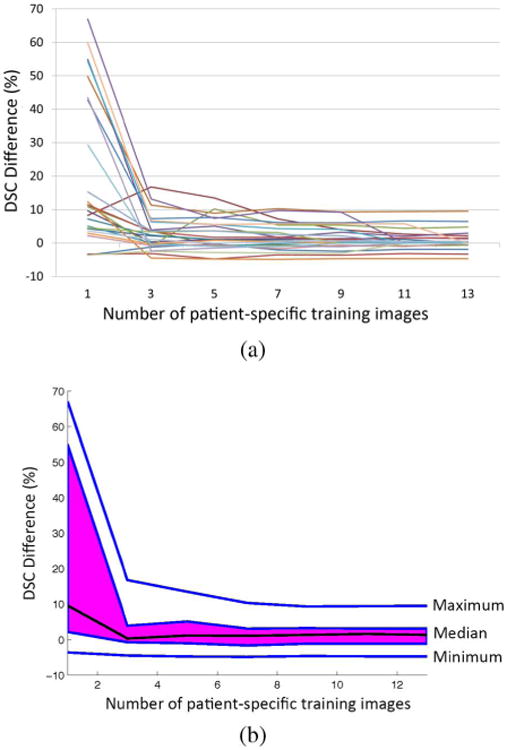
Function boxplot [40] of DSC difference curves between ILSM and PPAT for convergence analysis on dataset A. Each DSC difference curve is a function of DSC difference between ILSM and PPAT with respect to the number of patient-specific training images. Image (a) shows 25 DSC difference curves, each of which corresponds to one patient. Image (b) shows the function boxplot of 25 curves in (a). Black curve in (b) corresponds to the median curve, the magenta area covers the central 50% of the curves, and two outmost blue curves are the extreme maximum and minimum curve, respectively.
2) Comparison With Single-Atlas RANSAC
Fig. 13 shows the average DSCs of all 25 patients in Dataset A with single-atlas RANSAC and multi-atlas RANSAC. For single-atlas RANSAC, we use the planning prostate shape as the shape atlas. For multi-atlas RANSAC, we use not only the planning prostate shape but also previously segmented prostate shapes of the patient as shape atlases. We can see that in almost all patients, multi-atlas RANSAC achieves better localization accuracy than single-atlas RANSAC. Table VII also compares single-atlas and multi-atlas RANSAC on average DSC and acceptance rate. It shows that the localization accuracy of ILSM can be further boosted by using multi-atlas RANSAC (1% improvement on both average DSC and acceptance rate).
Fig. 13.
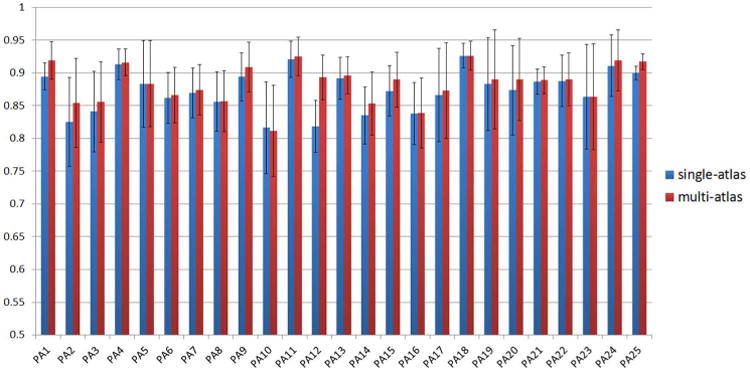
Comparison between single-atlas and multi-atlas RANSAC on dataset A using overlap ratio (DSC).
3) Comparison With Traditional Bone Alignment
Bone alignment is usually adopted as a standard preprocessing step in many prostate localization methods [8]–[10], [23]. The basic idea is to register the current treatment CT scan with the previous one of the same patient by aligning pelvic bones. The prostate mask in the previous CT can thereby be transformed to the current treatment CT. In the bone alignment, the pelvic bones in two CT scans are first segmented by thresholding. Based on the segmented binary bone images, the optimal rigid transformation is estimated and used to co-align two scans. Since prostate is very close to pelvic bone, bone alignment usually achieves satisfactory overlap ratios of the prostate. For fair comparison, we adopted the same multi-atlas scheme as described in Section III-A to evaluate the performance gain of the proposed method over bone alignment. We used the FLIRT toolkit [41] for bone alignment as previous methods. Fig. 14 visually shows the overlapping degree of prostate after bone alignment for 12 typical patients. The DSC obtained by bone alignment on our dataset is 0.78 ± 0.12, which is significantly lower than the DSC achieved by the proposed method (0.89 ± 0.06). In addition, bone alignment takes more computational time than the proposed method. To align two CT scans of image size 512 × 512 × 60, bone alignment typically takes 5 min, while the proposed method only takes 4 s on the same image size.
Fig. 14.

Prostate contours of treatment CTs from 12 typical patients after bone alignment. Contours in the figure are from the middle transversal slices of the prostates after bone alignment.
To consider the local intensity information around the prostate in the alignment procedure, we further conducted an experiment to compare a local intensity-based rigid registration method with the proposed method. In the former method, bone alignment is first performed to align a previous CT scan with the current treatment CT based on the pelvic bone. Then, a tight bounding box is determined using the prostate mask of the previous CT scan. Based on the determined bounding box, the two CT scans are further registered using an intensity-based rigid registration method as implemented in FLIRT using correlation ratio as the cost function. Finally, given the estimated rigid transformation, the prostate mask in the previous CT scan is transformed onto the current treatment CT for localization. Following the same multi-atlas scheme (Section III-C), we found that compared to bone alignment, local intensity-based rigid registration improves the localization accuracy from mean DSC 0.78 to 0.80. However, the standard deviation of DSC also increases from 0.12 to 0.14 due to some failure cases caused by the bad initialization of bone alignment. In contrast, the proposed method achieves much higher accuracy (0.89 ± 0.06) with faster localization speed (4 s).
4) Comparison With Other CT Prostate Localization Methods on the Same Dataset
Our method can achieve localization accuracy at DSC 0.89 ± 0.06 and average surface distance 1.72 ± 1.00 mm on 446 treatment CT scans of 32 patients. Table VIII quantatively compares the performance of our method with five other state-of-the-art methods on the same dataset, which employ deformable model [17], registration [22], multi-atlas based segmentation [10] and classification [9], [23] to localize the prostate on treatment CTs. We can see that our method achieves comparable accuracy to the state-of-the-art methods, while substantially reduces the localization time to just 4 s. This fast localization speed helps overcome the limitation of previous localization methods: if the prostate unexpectedly moves during the long localization procedure, their method has to be performed again. It is also worth noting that [9], [10], [23] require at least three patient-specific training images for initialization due to the nature of pure patient-specific learning, which indicates such methods cannot be adopted to segment the first two treatment CTs. By effectively combining both population and patient-specific information, even with only one planning CT, our method can still achieve reasonably accurate localization results on the first two treatment CTs (DSC 0.85 ± 0.06).
Table VIII. Quantitative Comparison With Other CT Prostate Localization Methods on the Same Dataset (DSC: Dice Similarity Coefficient, ASD: Average Surface Distance, Sen.: Sensitivity, PPV.: Positive Predictive Value).
| Method | Deformable | Registration | Multi-atlas | Classification | ILSM | |
|---|---|---|---|---|---|---|
|
| ||||||
| Feng [17] | Liao [22] | Liao [10] | Li [9] | Gao [23] | ||
|
| ||||||
| Automaticity | Fully | Fully | Fully | Fully | Semi | Fully |
| Mean DSC | 0.89 | 0.90 | 0.91 | 0.91 | 0.91 | 0.89 |
| Mean ASD | 2.08 | 1.08 | 0.97 | 1.40 | 1.24 | 1.72 |
| Median Sen. | n/a | 0.89 | 0.90 | 0.90 | 0.92 | 0.89 |
| Median PPV. | n/a | 0.89 | 0.92 | 0.90 | 0.92 | 0.92 |
| Speed (sec.) | 96 | 228 | 156 | 180 | 600 | 4 |
5) Comparison With Other CT Prostate Localization Methods on the Different Datasets
Table IX lists the performance of other CT prostate localization methods for reference. Due to the fact that neither their data nor the source codes of these methods are publicly available, we only cite the numbers reported in their publications. Based on the reported numbers, we can see that our method has been evaluated on the largest dataset and achieves the best localization accuracy.
Table IX. Comparison With Other CT Prostate Localization Methods on Different Datasets for Reference (DSC: Dice Similarity Coefficient, Sen.: Sensitivity, PPV.: Positive Predictive Value).
G. Algorithm Performance
In this section, we report the performance of the proposed algorithm in terms of localization accuracy, robustness to unsupervised annotation, generalization, sensitivity to landmark selection, temporal accuracy, and speed.
1) Accuracy
Table X shows the localization accuracy of our method on dataset A and dataset B. We can see that our method is able to achieve more consistent and accurate localizations (DSC 0.89 ± 0.06) than inter-operator variability (DSC 0.81 ± 0.06) [8]. This indicates that our method in fact well satisfies the accuracy requirement of IGRT and can be adopted in the clinical setting. To assess the lower and upper bound accuracy of our localization method, we further conducted two experiments. In the first experiment, we detected only one anatomical landmark (prostate center) and used only one shape atlas (planning prostate shape) for localization. The performance under this setting is regarded as the lower bound of the accuracy of the landmark-based prostate localization. In the second experiment, we performed the landmark-based prostate localization using manually annotated landmarks and multiple shape atlases (prostate shapes in planning and previous treatment images). This accuracy represents the upper bound of the landmark-based prostate localization. Table XI lists the lower and upper bound accuracies on different quantitative measures. It should be noted that the only difference between upper-bound accuracy (shown in Table XI) and the reported accuracy of our method (shown in Table X) is on the landmark localization. Upper bound accuracy is calculated using the manually annotated landmarks, and the performance of our method is obtained using automatically detected landmarks. By comparing two, we can see that the performance of our method is quite close to the upper bound, which indicates that through ILSM we can achieve accurate automatic landmark detection. On the other hand, by using only one anatomical landmark and a single shape atlas, the localization accuracy is still comparable to the inter-operator variability (DSC 0.81 ± 0.06), which shows the effectiveness of ILSM in CT prostate localization.
Table X. Localization Accuracy of ILSM on Two Datasets (DSC: Dice Similarity Coefficient, ASD: Average Surface Distance, Sen: Sensitivity, PPV: Positive Predictive Value).
| DSC | ASD (mm) | Sen. | PPV. | |
|---|---|---|---|---|
|
| ||||
| Dataset A | 0.88±0.06 | 1.89±0.98 | 0.87±0.06 | 0.89±0.06 |
| Dataset B | 0.91±0.05 | 1.27±0.90 | 0.88±0.05 | 0.93±0.06 |
| All | 0.89±0.06 | 1.72±1.00 | 0.88±0.06 | 0.90±0.06 |
Table XI. Lower and Upper Bound Accuracy of ILSM in CT Prostate Localization. Reported Values Are Calculated on Both Dataset A and Dataset B.
| DSC | ASD (mm) | Sen. | PPV. | |
|---|---|---|---|---|
|
| ||||
| UpperBound | 0.92±0.03 | 1.00±0.60 | 0.91±0.05 | 0.94±0.03 |
| LowerBound | 0.81±0.09 | 3.01±2.01 | 0.80±0.10 | 0.83±0.10 |
2) Robustness to Unsupervised Annotation
As shown in Fig. 4, in order to incorporate patient-specific characteristics, ILSM requires annotations in planning and previous treatment images. Annotations in planning images are always provided by physicians. Afterward, there are two ways to obtain annotations in treatment images. 1) Supervised annotation. In this scenario, detectors trained by planning and previous treatment images are applied to localize the landmarks in current treatment images. The detection results need to be reviewed and corrected by physicians before being used to train detectors for the next treatment days. 2) Unsupervised annotation. The auto-detected results are considered as ground truth and used to train detectors for the next treatment days without manual review/corrections. Although the first scenario guarantees all training data are correctly annotated, the second scenario has the advantage in less manual operations (i.e., no manual operation, except the annotation in the planning CT) as long as the uncorrected annotation errors do not significantly degrade the localization accuracy.
We validated ILSM in both scenarios on Dataset A. To simulate the supervised annotation, we directly used the manually annotated landmarks as the corrected landmarks for training. Compared with the average DSC 0.88 ± 0.06% achieved using supervised annotation, our method can achieve average DSC 0.85 ± 0.06% using unsupervised annotation. This is still more accurate than the inter-operator variability (0.81 ± 0.06%). Therefore, if some specific IGRT workflows require very limited manual operations, our method can be employed in the unsupervised annotation mode yet still with acceptable accuracy.
It is worth noting that compared with previous methods [9], [10], [23], which require precise manual segmentation of the entire prostate in the training treatment images, our method only requires the annotations of at most seven anatomical landmarks, which dramatically reduces physicians' efforts on manual annotation. To be precise, we recorded the annotation time of an experienced radiation oncologist on the 19 treatment scans of one patient. It takes 11.7 ± 2.5 min to manually segment the entire prostate, while it only takes 1.2 ± 0.3 min to annotate seven anatomical landmarks. If the proposed method is used to automatically detect the seven landmarks and radiation oncologists are only asked to verify and edit the detected landmarks, the landmark annotation time can be further reduced to 8.3 ± 1.3 s.
3) Generalization
A learning-based algorithm has to have good generalization in order to be applied on data from various institutions and scanners. To evaluate the generalization of ILSM, we tested our localization algorithm on Dataset B, which is acquired under a different scanner from that of Dataset A. We used all CT scans of Dataset A (349 scans) to train the population-based landmark detectors for Dataset B. The localization accuracy is shown in Table X, which indicates the good generalization of our method. This is mainly due to the “selective memory” nature of ILSM. Even when the population landmark detectors are trained using a dataset with slightly different scanning protocols, after “personalized” by ILSM, the portion of the population-based appearance knowledge that is not in accordance with the current patient-specific characteristics will be discarded. By preserving only the applicable knowledge learned from population data, the generalization of the learned detectors is improved. Table X summarizes the overall performance of our method on total 32 patients.
4) Sensitivity to Landmark Selection
To assess the sensitivity of our method to landmark selection, we tested the performance of our algorithm by alternatively excluding one of the seven landmarks. Table XII lists the DSCs of our method on Dataset A by excluding any of the seven landmarks. Overall, the performance is quite consistent no matter which subset of six landmarks is picked. Further, it is surprising to see that by excluding any of landmarks in {PC, BS, AP}, the localization accuracy can actually be increased, compared to the performance of DSC 0.88±0.06 obtained by using all landmarks. The reason for this can be inferred from Table V. That is, compared with other landmarks, the landmark detections of PC, BS and AP are less accurate due to the indistinct image appearance in those regions. Therefore, removing any of them helps improve the overall localization accuracy. For more thorough discussion in landmark selection, please refer to Section V.
Table XII. Sensitivity to Landmark Selection. The Table Below Shows the Localization Accuracies of Six Landmarks by Excluding Any of The Seven Landmarks Used in the Paper. Reported Values Are Computed on Dataset A.
| Excluded | PC | RT | LF | PT |
|---|---|---|---|---|
| DSC | 0.89±0.05 | 0.88±0.06 | 0.88±0.06 | 0.88±0.06 |
| Excluded | AT | BS | AP | |
| DSC | 0.88±0.05 | 0.89±0.05 | 0.89±0.05 |
5) Temporal Analysis of Localization Accuracy
Fig. 15 shows the localization accuracy curve with respect to the number of patient-specific training images used. Not surprisingly, the localization accuracy of the proposed method increases as more patient-specific training data (i.e., image and shape) is available. The most significant improvement happens when the number of patient-specific training images increases from 1 to 3. As the number of patient-specific training images increases to 5, the localization accuracy levels off, which indicates that after the fourth treatment day, the patient-specific landmark detectors are sufficiently accurate, and thus there is no need to do additional incremental learning. That is, the existing landmark detectors can be directly applied to localize the prostate in the future treatment images. In practice, considering that the period of radiation treatment typically takes 35 days, the ILSM procedure is only needed in the first four treatment days (about 4/35 ≈ 11% fraction of the entire treatment course).
Fig. 15.
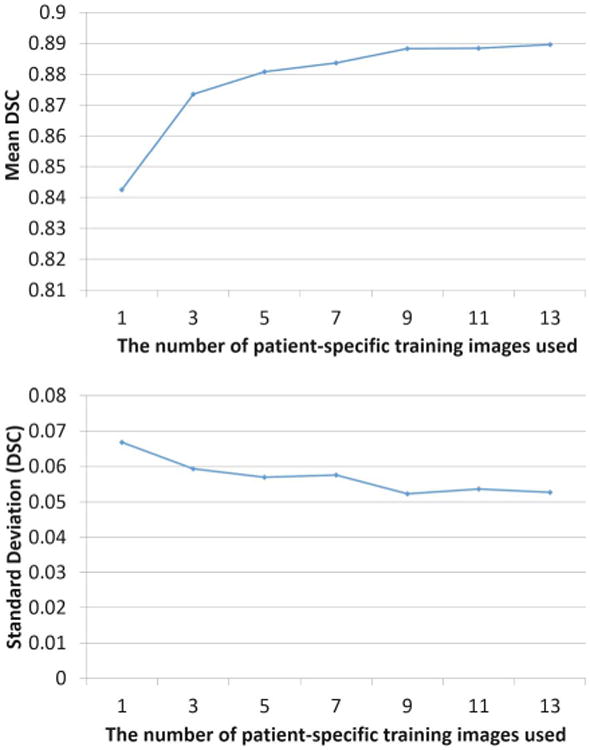
Temporal analysis of localization accuracy on dataset A.
6) Speed
The typical runtime for our method to localize the prostate is around 4 s (on an Intel Q6600 2.4 GHz desktop with 4 GB memory), which is almost real-time compared to previous methods. Thanks to incremental learning, the training time is reduced from 3–4 h (traditional population-based training) to 30 min/landmark detector. Each landmark detector is independent and thus can be trained in parallel. It is also worth noting that the incremental learning process can be completed overnight before the treatment day. Therefore, the learning step does not take any additional time when the patients are receiving treatment.
H. Experiment Summary
In summary, our experiments show the following.
Compared to traditional learning schemes, ILSM shows better landmark detection and prostate localization accuracy.
Compared to other state-of-the-art methods, 1) our method can achieve comparable accuracy with much faster speed; 2) our method can be applied on any treatment day of radiotherapy since it is still reasonably accurate (DSC ∼0.85) even with only one patient-specific training image (i.e., the planning CT); 3) our method only requires annotations of seven anatomical landmarks, thus significantly reducing physicians' manual efforts (from 11 min to 1 min).
Validated on 446 treatment CTs, we achieved average DSC 0.89±0.06 in 4 s, which indicates that our method is well-suited for the accuracy and speed requirements of IGRT.
V. Conclusion and Discussion
In this paper, we propose a novel learning scheme, namely ILSM, which can take both generalization and specificity into account by leveraging the large amount of population data and the limited amount of patient specific data. It is applied to extract the patient-specific appearance information in IGRT for anatomical landmark detection. Once the anatomical landmarks on the new treatment CT are accurately localized, a multi-atlas RANSAC is applied to align previous patient-specific shape atlases for prostate localization. Validated on a large dataset (446 CT scans), ILSM shows comparable accuracy (0.89 ± 0.06) to the state-of-the-art methods, while significantly reducing the runtime to 4 s. Moreover, in comparisons with traditional learning-based schemes (e.g., population learning, pure patient-specific learning, and mixture learning with population and patient-specific data), ILSM shows better capability to capture patient-specific appearance characteristics from limited patient-specific data.
To boost the performance, our method could be combined with other sophisticated segmentation methods (e.g., deformable model [14], [42]) for better accuracy. However, using more sophisticated methods increases accuracy at the expense of run-time efficiency. Since our method obtains much more accurate localization than inter-operator variability, it actually satisfies for both the efficiency and accuracy requirements of IGRT. The comparison experiment with conventional bone alignment-based prostate localization also suggests that our landmark-based alignment is better in terms of both efficiency and accuracy. Therefore, we can use our method to replace bone alignment—the standard preprocessing step for most CT prostate segmentation methods, thus further improving their performance.
Another problem that may be interesting to investigate is landmark selection. In the current application, it is relatively easy to select landmarks due to the ellipsoid-like shape of prostate. However, in other applications dealing with organs of complex shapes (e.g., the rectum), it may be not intuitive to decide which landmarks are good for organ localization. In general, we suggest two basic principles that should be followed in selecting a set of good landmarks for organ localization: 1) the image appearance of a selected landmark should be distinct within its neighborhood and consistent across the training images; 2) selected landmarks should be sparsely distributed on the organ boundary. The distinctness and consistency in principle 1) aims to achieve accurate landmark detection, while principle; 2) ensures the selected landmarks are able to represent the overall organ shape. In practice, given a set of training images with manual labeling of organ of interest, we can first generate a surface mesh using the label map for each image. Then, surface registration can be used to build the correspondence between any two surface meshes. Once the correspondences are known, we can select a set of landmarks that satisfy the two aforementioned principles. The quantification of the two stated principles and the formulation of landmark selection as an optimization problem will be the focus of future work.
To apply our method in clinical practice, we suggest three workflows to satisfy different speed and accuracy requirements of prostate localization as illustrated in Fig. 16. Among them, workflow 1 has the advantage of fully automaticity but moderate localization accuracy (DSC 0.85 ± 0.06). Workflow 2 involves minimal manual efforts to adjust the automatically detected landmarks after treatment (8.3 ± 1.3 s for quick verification), but is capable to obtain high localization accuracy (DSC 0.89 ± 0.06). Compared with workflow 1 and 2, workflow 3 can achieve the near-optimal localization accuracy (DSC 0.92 ± 0.03), but requires clinicians to verify the landmarks during the treatment period. In both workflow 2 and workflow 3, we provide clinicians the option to edit the automatic localization results. However, since both workflow 2 and 3 can obtain quite high localization accuracy, there is rarely any need for clinicians to manually edit the localization results.
Fig. 16.
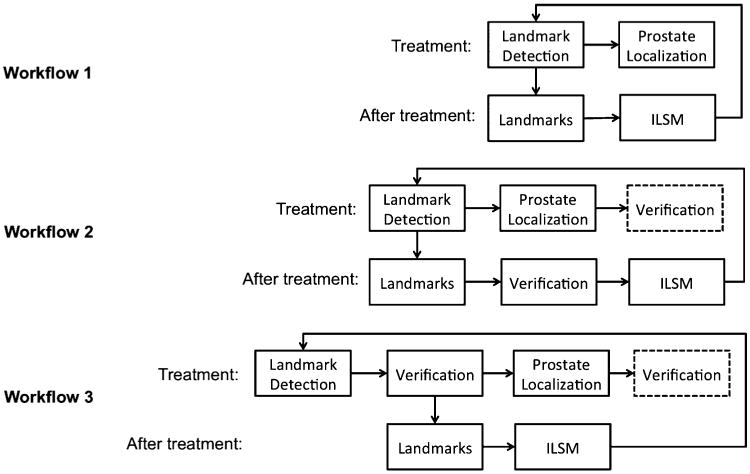
Three possible clinical workflows. Box with dash line is an optional step in the workflow.
Acknowledgments
This work was supported in part by the National Institutes of Health (NIH) under Grant CA140413 and Grant DE022676. This work was also supported in part by the National Research Foundation under Grant 2012-005741, funded by the Korean government.
Footnotes
Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.
Digital Object Identifier 10.1109/TMI.2013.2291495
Contributor Information
Yaozong Gao, Email: yzgao@cs.unc.edu, Department of Computer Science and the Department of Radiology, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599 USA.
Yiqiang Zhan, Email: yiqiang@gmail.com, SYNGO Division, Siemens Medical Solutions, Malvern, PA 19355 USA.
Dinggang Shen, Email: dgshen@med.unc.edu, Biomedical Research Imaging Center, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599 USA, and also with the Department of Brain and Cognitive Engineering, Korea University, Seoul 136-701, Korea.
References
- 1.Shen D, Lao Z, Zeng J, Zhang W, Sesterhenn IA, Sun L, Moul JW, Herskovits EH, Fichtinger G, Davatzikos C. Optimized prostate biopsy via a statistical atlas of cancer spatial distribution. Med Image Anal. 2004;8(2):139–150. doi: 10.1016/j.media.2003.11.002. [DOI] [PubMed] [Google Scholar]
- 2.Zhan Y, Shen D, Zeng J, Sun L, Fichtinger G, Moul J, Davatzikos C. Targeted prostate biopsy using statistical image analysis. IEEE Trans Med Imag. 2007 Jun;26(6):779–788. doi: 10.1109/TMI.2006.891497. [DOI] [PubMed] [Google Scholar]
- 3.Xing L, Thorndyke B, Schreibmann E, Yang Y, Li TF, Kim GY, Luxton G, Koong A. Overview of image-guided radiation therapy. Med Dosimetry. 2006;31(2):91–112. doi: 10.1016/j.meddos.2005.12.004. [DOI] [PubMed] [Google Scholar]
- 4.Dawson L, Jaffray D. Advances in image-guided radiation therapy. J Clin Oncol. 2007;25(8):938–946. doi: 10.1200/JCO.2006.09.9515. [DOI] [PubMed] [Google Scholar]
- 5.Liu W, Qian J, Hancock SL, Xing L, Luxton G. Clinical development of a failure detection-based online repositioning strategy for prostate IMRT—Experiments, simulation, and dosimetry study. Med Phys. 2010;37(10):5287–5297. doi: 10.1118/1.3488887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Costa MJ, Delingette H, Novellas S, Ayache N. Automatic segmentation of bladder and prostate using coupled 3-D deformable models. Med Image Comput Comput Assist Interv. 2007;10(Pt 1):252–60. doi: 10.1007/978-3-540-75757-3_31. [DOI] [PubMed] [Google Scholar]
- 7.Chen S, Lovelock DM, Radke RJ. Segmenting the prostate and rectum in CT imagery using anatomical constraints. Med Image Anal. 2011;15(1):1–11. doi: 10.1016/j.media.2010.06.004. [DOI] [PubMed] [Google Scholar]
- 8.Foskey M, Davis B, Goyal L, Chang S, Chaney E, Strehl N, Tomei S, Rosenman J, Joshi S. Large deformation three-dimensional image registration in image-guided radiation therapy. Phys Med Biol. 2005;50(24):5869. doi: 10.1088/0031-9155/50/24/008. [DOI] [PubMed] [Google Scholar]
- 9.Li W, Liao S, Feng Q, Chen W, Shen D. Learning image context for segmentation of prostate in CT-guided radiotherapy. 2011:570–578. doi: 10.1007/978-3-642-23626-6_70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Liao S, Gao Y, Lian J, Shen D. Sparse patch-based label propagation for accurate prostate localization in CT images. IEEE Trans Med Imag. 2013 Feb;32(2):419–434. doi: 10.1109/TMI.2012.2230018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gao Y, Liao S, Shen D. Prostate segmentation by sparse representation based classification. In: Ayache N, Delingette H, Golland P, Mori K, editors. Medical Image Computing and Computer-Assisted Intervention MICCAI 2012. Vol. 7512. Berlin, Germany: Springer; 2012. pp. 451–458. Lecture Notes Computer Science. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gao Y, Zhan Y, Shen D. Incremental learning with selective memory (ILSM): Towards fast prostate localization for image guided radiotherapy. In: Mori K, Sakuma I, Sato Y, Barillot C, Navab N, editors. Medical Image Computing and Computer-Assisted Intervention MICCAI 2013. Vol. 8150. Berlin, Germany: Springer; 2013. pp. 378–386. Lecture Notes Computer Science. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shi Y, Qi F, Xue Z, Chen L, Ito K, Matsuo H, Shen D. Segmenting lung fields in serial chest radiographs using both population-based and patient-specific shape statistics. IEEE Trans Med Imag. 2008 Apr;27(4):481–494. doi: 10.1109/TMI.2007.908130. [DOI] [PubMed] [Google Scholar]
- 14.Zhang S, Zhan Y, Dewan M, Huang J, Metaxas DN, Zhou XS. Towards robust and effective shape modeling: Sparse shape composition. Med Image Anal. 2012;16(1):265–277. doi: 10.1016/j.media.2011.08.004. [DOI] [PubMed] [Google Scholar]
- 15.Pizer S, Fletcher P, Joshi S, Gash A, Stough J, Thall A, Tracton G, Chaney E. A method and software for segmentation of anatomic object emsembles by deformable m-reps. Med Phys. 2005;32(5):1335–1345. doi: 10.1118/1.1869872. [DOI] [PubMed] [Google Scholar]
- 16.Freedman D, Radke RJ, Tao Z, Yongwon J, Lovelock DM, Chen GTY. Model-based segmentation of medical imagery by matching distributions. IEEE Trans Med Imag. 2005 Mar;24(3):281–292. doi: 10.1109/tmi.2004.841228. [DOI] [PubMed] [Google Scholar]
- 17.Feng Q, Foskey M, Tang S, Chen W, Shen D. Segmenting CT prostate images using population and patient-specific statistics for radiotherapy. 2009:282–285. doi: 10.1109/ISBI.2009.5193039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wu G, Qi F, Shen D. Learning-based deformable registration of MR brain images. IEEE Trans Med Imag. 2006 Sep;25(9):1145–1157. doi: 10.1109/tmi.2006.879320. [DOI] [PubMed] [Google Scholar]
- 19.Yang J, Shen D, Davatzikos C, Verma R. Diffusion tensor image registration using tensor geometry and orientation features. In: Metaxas D, Axel L, Fichtinger G, Szkely G, editors. Medical Image Computing and Computer-Assisted Intervention MICCAI 2008. Vol. 5242. Berlin, Germany: Springer; 2008. pp. 905–913. Lecture Notes Computer Science. [DOI] [PubMed] [Google Scholar]
- 20.Shen D, Wong W, Ip H. Affine-invariant image retrieval by correspondence matching of shapes. 1999 May;:489–499. [Google Scholar]
- 21.Zhan Y, Ou Y, Feldman M, Tomaszeweski J, Davatzikos C, Shen D. Registering histologic and MR images of prostate for image based cancer detection. Acad Radiol. 2007;14(11):1367–1381. doi: 10.1016/j.acra.2007.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liao S, Shen D. A feature-based learning framework for accurate prostate localization in CT images. IEEE Trans Image Process. 2012 Aug;21(8):3546–3559. doi: 10.1109/TIP.2012.2194296. [DOI] [PubMed] [Google Scholar]
- 23.Gao Y, Liao S, Shen D. Prostate segmentation by sparse representation based classification. Med Phys. 2012;39(10):6372–6387. doi: 10.1118/1.4754304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Shi Y, Liao S, Gao Y, Zhang D, Gao Y, Shen D. Prostate segmentation in CT images via spatial-constrained transductive lasso. Proc 2013 IEEE Conf Comput Vis Pattern Recognit. 2013:2227–2234. doi: 10.1109/CVPR.2013.289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Haas B, Coradi T, Scholz M, Kunz P, Huber M, Oppitz U, Andr L, Lengkeek V, Huyskens D, Esch AV, Reddick R. Automatic segmentation of thoracic and pelvic CT images for radiotherapy planning using implicit anatomic knowledge and organ-specific segmentation strategies. Phys Med Biol. 2008;53(6):1751. doi: 10.1088/0031-9155/53/6/017. [DOI] [PubMed] [Google Scholar]
- 26.Ghosh P, Mitchell M. Segmentation of medical images using a genetic algorithm. Proc 8th Annu Conf Genetic Evolut Computat. 2006:1171–1178. [Google Scholar]
- 27.Klein S, van der Heide UA, Lips IM, van Vulpen M, Staring M, Pluim JPW. Automatic segmentation of the prostate in 3-D MR images by atlas matching using localized mutual information. Med Phys. 2008;35(4):1407–1417. doi: 10.1118/1.2842076. [DOI] [PubMed] [Google Scholar]
- 28.Toth R, Madabhushi A. Multifeature landmark-free active appearance models: Application to prostate MRI segmentation. IEEE Trans Med Imag. 2012 Aug;31(8):1638–1650. doi: 10.1109/TMI.2012.2201498. [DOI] [PubMed] [Google Scholar]
- 29.Zhan Y, Shen D. Deformable segmentation of 3-d ultrasound prostate images using statistical texture matching method. IEEE Trans Med Imag. 2006 Mar;25(3):256–272. doi: 10.1109/TMI.2005.862744. [DOI] [PubMed] [Google Scholar]
- 30.Yan P, Xu S, Turkbey B, Kruecker J. Adaptively learning local shape statistics for prostate segmentation in ultrasound. IEEE Trans Biomed Eng. 2011 Mar;58(3):633–641. doi: 10.1109/TBME.2010.2094195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zhan Y, Shen D. Automated segmentation of 3-D us prostate images using statistical texture-based matching method. In: Ellis R, Peters T, editors. Medical Image Computing and Computer-Assisted Intervention-MICCAI 2003. Vol. 2878. Berlin, Germany: Springer; 2003. pp. 688–696. Lecture Notes Computer Science. [Google Scholar]
- 32.Polikar R, Upda L, Upda SS, Honavar V. Learn++: An incremental learning algorithm for supervised neural networks. IEEE Trans Syst, Man, Cybern Part C: Appl Rev. 2001 Nov;31(4):497–508. [Google Scholar]
- 33.Diehl CP, Cauwenberghs G. SVM incremental learning, adaptation and optimization. Proc Int Joint Conf Neural Netw. 2003;4:2685–2690. [Google Scholar]
- 34.Ross D, Lim J, Lin RS, Yang MH. Incremental learning for robust visual tracking. Int J Comput Vis. 2008;77(1):125–141. [Google Scholar]
- 35.Fischler M, Bolles R. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun ACM. 1981;24(6):381–395. [Google Scholar]
- 36.Viola P, Jones M. Robust real-time face detection. Int J Comput Vis. 2004;57(2):137–154. [Google Scholar]
- 37.Zhan Y, Dewan M, Zhou XS. Auto-alignment of knee MR scout scans through redundant, adaptive and hierarchical anatomy detection. Proc 22nd Int Conf Inf Process Med Imag. 2011:111–122. doi: 10.1007/978-3-642-22092-0_10. [DOI] [PubMed] [Google Scholar]
- 38.Zhan Y, Dewan M, Harder M, Krishnan A, Zhou XS. Robust automatic knee MR slice positioning through redundant and hierarchical anatomy detection. IEEE Trans Med Imag. 2011 Dec;30(12):14. doi: 10.1109/TMI.2011.2162634. [DOI] [PubMed] [Google Scholar]
- 39.Zhan Y, Zhou X, Peng Z, Krishnan A. Active Scheduling of Organ Detection and Segmentation in Whole-Body Medical Images. Vol. 5241. Berlin, Germany: Springer; 2008. pp. 313–321. Lecture Notes Computer Science, ch. 38. [DOI] [PubMed] [Google Scholar]
- 40.Sun Y, Genton M. Functional boxplots. J Computat Graph Stat. 2011;20(2):316–334. [Google Scholar]
- 41.Fischer B, Modersitzki J. FLIRT: A Flexible Image Registration Toolbox Biomedical Image Registration. Vol. 2717. Berlin, Germany: Springer; 2003. pp. 261–270. Lecture Notes in Computer Science. [Google Scholar]
- 42.Zhang S, Zhan Y, Metaxas DN. Deformable segmentation via sparse representation and dictionary learning. Med Image Anal. 2012;16(7):1385–1396. doi: 10.1016/j.media.2012.07.007. [DOI] [PubMed] [Google Scholar]


