Crystal Structure Prediction from First Principles: The Crystal Structures of Glycine

Abstract

Here we present the results of our unbiased searches of glycine polymorphs obtained using the Genetic Algorithms search implemented in Modified Genetic Algorithm for Crystals coupled with the local optimization and energy evaluation provided by Quantum Espresso. We demonstrate that it is possible to predict the crystal structures of a biomedical molecule using solely first principles calculations. We were able to find all the ambient pressure stable glycine polymorphs, which are found in the same energetic ordering as observed experimentally and the agreement between the experimental and predicted structures is of such accuracy that the two are visually almost indistinguishable.

Introduction

More than a decade ago Professor Desiraju published¹ a critical article identifying crystal structure prediction from first principles as one of the most important unsolved problems in computational material science and questioned if this problem could ever be solved. Since 1997 there has been much effort towards the goal of being able to readily and reliably predict, by computational methods alone, the crystal structure of a molecule based only on its chemical diagram.^2–5 The process to do this is depicted in Figure 1.

Figure 1.

Overview of the Crystal Structure Prediction (CSP) process, which attempts to predict the structure or structures (when polymorphs exists) of a molecular entity based solely in its chemical diagram. The prediction of these structures directly from first principles has been identified a one of the greatest challenges remaining in computational molecular sciences.

The ability to accomplish this goal has far reaching implications well beyond just intellectual curiosity. On a basic science level, this can lead to an understanding of the principles that control crystal growth, by providing accurate information on the crystal energetics necessary for any further dynamical model of aggregation. More practically, the ability to successfully predict crystal structures based on computation alone will have a significant impact in many industries for which crystal structure and stability plays a critical role in product formulation and manufacturing, including pharmaceuticals, agrochemicals, pigments, dyes and explosives.⁶

The current status of crystal structure prediction (CSP) can be evaluated by the performance of the participants in the periodic blind tests that have been organized by the Cambridge Crystallographic Data Centre (CCDC).^4,7,8 The results of the last two blind tests showed the advantage of using dispersion corrected density functional theory (DFT-D)^9–11 to create a tailored molecule specific force field that is used to generate trial structures and to reorder a subset of the trial structures in search of the lowest energy crystal structures.^12–16 The software used in this approach is proprietary. There has also been an attempt to utilize first principle calculations to predict the crystal structure of organic crystals,¹⁷ in which the authors used a two-step approach optimizing the crystal structures with constrained molecular geometries in the initial stages and allowing full relaxation in the final stages. In this approach the authors used a combination of open source and proprietary software tools for the constrained and fully relaxed optimizations.

These results lend promise to using DFT-D methods to completely replace molecular mechanics and/or multistep optimization approaches as the method of choice for the evaluation of the energies of the trial crystal structures in CSP. To the authors knowledge there are no reports of any open source software capable of successfully predict crystal structures of molecules of biomedical interest directly from first principles without using either common or tailored potentials as intermediate steps and/or multistep optimization strategies.

It is important to realize that local optimization of plausible crystal structures is not a feasible approach for CSP. We have recently demonstrated,¹⁸ using a set of drug like molecules, that local optimization using full DFT-D results in near experimental structures only when the starting point is quite close to the experimental one. Therefore global optimization with a reliable and universal energy function is necessary for accurate CSP.

The MGAC (Modified Genetic Algorithm for Crystals) package has been developed in our lab over the last decade.^19–23 MGAC is capable of doing CSP for any space group, any number of molecules per asymmetric unit, and can take into account the conformational flexibility of the molecule both at the local and global optimization levels. This allows an efficient, GA (Genetic Algorithms) based, global exploration of the crystal energy landscape. The previously released versions of MGAC relied on the use of the CHARMM ^24,25 molecular mechanics program using the Generalized Atomic Force Field (GAFF) ²⁶ for the energy evaluation and local minimization of the GA trial structures.

Previously, we used the set of molecules present in the Karamertzanis and Price (K&P) paper,²⁷ to demonstrate the capabilities of the MGAC-CHARMM program.²³ These results demonstrated that the implementation of the GA in MGAC was effective and was always able to find the correct experimental structures provided that the GAFF potential energy represented the experimental energy landscape with sufficient fidelity. However, the matches to the experimental structure ranged from rank 1 to rank 1182 in terms of energy, highlighting the second issue with the use of the generic force field, namely the unreliability of the energy ranking.

Our more recent work¹⁸ has demonstrated that when using Quantum Espresso (QE) to locally optimize the experimental structures in the K&P set the calculated local minima structure compares well with the experimental structure in all 32 of the molecules, with RMS differences ranging from 0.056 to 0.459 Å. This implies that for unknown structures, an approach which couples the use of MGAC with energy evaluation using QE will be successful in finding the “true” experimental structures.

In this article we report the results of our unbiased searches for glycine polymorphs obtained using the global GA search implemented in MGAC coupled with local optimizations and energetics provided by QE (MGAC-QE). To our knowledge here we demonstrate for the first time that it is possible to predict the crystal structure of a molecule of biomedical interest, glycine, using solely first principles calculations (DFT-D) of the crystal energetics without using any intermediate steps, such as constructing special interatomic potentials, reordering the structures found by the search algorithm and/or using multistep search strategies with nonuniform approximations for the energy calculations. The only difference in the calculations presented here and a complete blind CSP search is that we only performed searches in the known space groups of each of the three stable polymorphs of glycine.

Methods

Using the existing MGAC framework we have integrated the QE calculation of the energy and local optimizations into the framework as well as reworked the way in which the initial populations are selected and how the genetic algorithms were implemented (MGAC-QE). A full account of the technical and computational details of the integration of QE into the MGAC framework will be presented in detail elsewhere, along with the documentation and instructions on how to use the software that we will make available as an open source tool.

Glycine’s biological interest, relatively small size and polymorphic characteristics make it a good case to demonstrate the ability of MGAC-QE to predict the crystal structures of biomedical relevant compounds. Glycine is a precursor to the synthesis of proteins, a building block to numerous natural products, and provides the central C₂N subunit of all purines. It is a relatively small, semi rigid molecule, for which polymorphism is well establish in the literature. The existence of polymorphism is critical to demonstrate the usefulness of MGAC-QE to successfully predict crystal structures of biomedical interest for which the existence of polymorphism is prevalent.⁶

Glycine has three room temperature and atmospheric pressure polymorphs: α-glycine (P2_1/c),²⁸ β-glycine (P2₁),²⁹ and γ-glycine (P3₁/P3₂) ³⁰ (stability order: γ-glycine > α-glycine > β-glycine), as well as two high pressure polymorphs, δ-glycine (high pressure of the β-glycine form),²⁹ and ε-glycine (the high pressure form of the γ-glycine form).³¹ For the purpose of comparison of our results we used the following glycine reference structures from the Cambridge Structural Database (CSD): GLYCIN98 for α-glycine,²⁸ GLYCIN71 for β-glycine,²⁹ and GLYCIN33 for γ-glycine.³⁰ These three experimental structures were locally optimized using the QE vc-relax option, which allows for optimization of the unit cell parameters along with all atomic coordinates, with the same QE parameters used in our previous work (see below).¹⁸ In all cases the experimental structures converged to local minima in close proximity to the experimental structures. The QE energies for these local minima structures are E_α-glycine = −147,662.07 kJ/mol, E_β-glycine= −147,659.78 kJ/mol, and E_γ-glycine = −147,663.10 kJ/mol, which reproduce the experimental stability order: γ-glycine > α-glycine > β-glycine.

Following these preliminary tests we conducted unbiased global searches for crystal structures in the following space groups, with a number of molecules per unit cell given in parenthesis: P2_1/c (4), P2₁ (2) and P3₁ (3). All calculations were performed using a population size of 120 individuals, a replacement rate of 1.0 per generation, and the searches were run for 50 generations. The probability of an individual being mutated was 0.01, and the probability of a crossover occurring between two individuals was 1. The selection method was a roulette wheel, using linear scaling of the energy, with the lowest energy structure having the largest selection probability. The optimization parameters for the QE optimization were again identical to those used by Lund et. al.¹⁸ The DFT functional used was the Perdew-Burke-Ernzerhof generalized gradient approximation.³² The dispersion correction method selected was the semi-empirical D2 method proposed by Grimme as implemented in Quantum Espresso.¹⁰ The self-consistency threshold was set to 10⁻⁷ Ry and the plane wave cutoff energy was set to 55 Ry per the recommendation of the pseudopotentials creators. The pseudopotentials used for glycine were the Rappe-Rabe-Kaxiras-Joannopoulos-Ultrasoft pseudopotentials provided at the QE website, http://www.quantum-espresso.org/.

Calculations were performed on a LINUX cluster using six 16-core nodes (2x8-core Intel Xeon E5-2670 processors clocked at 2.60 GHz), with 64 GB memory per node and Mellanox FDR Infiniband for node interconnectivity. The total number of core hours for each run was: α-glycine: 10,238 core hours; β-glycine: 7,174 core hours; and γ-glycine: 9,518 core hours. Therefore the total number of core hours used for these three searches was 26,930, which represent a total elapsed time of approximately 12 days.

Results and Discussion

The results of the analysis of the populations generated by the MGAC-QE runs described above are presented in Figure 2. This Figure presents, as suggested by Price,³³ the distribution of the energies of crystals in the MGAC populations as function of their volume. As expected when polymorphism is present, the plot shows a great deal of crowding and the volume energy pairs of the different polymorphs are not well separated.³³ This clustering of the three polymorphs reinforces that glycine is a challenging case for CSP and therefore a stringent test for the MGAC-QE method. From the Figure it is also apparent that the structures found by MGAC-QE (solid symbols) for each of the symmetry groups studied here closely match the experimental ones (hatched symbols) corresponding to the most stable polymorphs, in the same space group.

Figure 2.

The distribution of the energies of crystals in the MGAC-QE populations as a function of the molecular volume. The crystals structures corresponding to the P2_1/c, P2₁, and P3₁ GA runs are represented by squares, circles and triangles, respectively. The hatched markers correspond to the experimental structures and the solid ones to the lowest energy structures found by MGAC-QE. For the experimental structures the volumes are those from the original reference and the energies correspond to the energy of the local minima obtained by QE when starting the minimization at the experimental energy.

Notably, in some initial generations we observed structures where the protonation state of glycine was altered and the non-zwitterionic form was adopted. This is made possible by the unconstrained optimization algorithm in QE. These structures were typically much higher in energy (by >80 kJ/mol) than structures remaining in the zwitterionic form, and were therefore eliminated rapidly from the population. The conclusion drawn from this is that one must be careful to identify low energy structures where the protonation state (and in general, bonding state) might be altered.

In Table 1 the crystallographic parameters and the calculated energies of the best structures found by MGAC-QE for each of the space groups considered here along with the RMS between them and the corresponding experimental structures are given. The results in Table 1 show an excellent agreement between the MGAC-QE predicted structures and the experimental ones; the agreement is apparent in both in the cell parameters as well as the RMS difference between the experimental and predicted structures. The RMS values can be compared to the RMS values observed when comparing different experimental structures of the same polymorphs reported in the CSD; for instance the RMS between α-glycine structures GLYCINE89 and GLYCINE17 is 0.026 Å, for β-glycine structures GLYCIN74 and GLYCINE25 is 0.114 Å and for γ-glycine structures GLYCIN65 and GLYCIN15 is 0.07 Å.

Table 1.

Comparison of the energies and geometries of the a-glycine, P-glycine and y-glycine structures found by MGAC-QE with the reference experimental structures.

Polymorph		SPG	Energyd	Cell Parameterse						RMSf
				a	b	c	α	β	γ
α-glycine	MGAC-QE	P21/c	−147,663.00	5.0517	11.7146	5.7965	90.0	120.3102	90.0	0.097
	Expa			5.0874	11.7817	5.4635	90.0	112.0530	90.0
β-glycine	MGAC-QE	P21	−147,661.12	5.6840	6.0727	5.0305	90.0	119.8711	90.0	0.199
	Expb			5.3880	6.2760	5.0905	90.0	113.1200	90.0
γ-glycine	MGAC-QE	P31	−147,663.07	6.9166	6.9166	5.4983	90.0	90.0	120.0	0.087
	Expc			7.0383	7.0383	5.4813	90.0	90.0	120.0

^aStructure GLYCIN98 (10 K) from Ref. 28.

^bStructure GLYCIN71 (room temperature) from Ref. 29.

^cStructure GLYCIN33 (room temperature) from Ref. 30.

^dEnergy in kJ/mol for the lowest energy found by MGAC-QE in the corresponding space group.

^eCrystallographic axis in Å, cell angles in degrees.

^fComputed using the Solid Form Crystal Packing Similarity method in Mercury CSD with 15 molecules for comparison and ignoring hydrogen atoms.³⁵

The energies of the MGAC-QE predicted structures follow the experimental stability order: E_γ-glycine < E_α-glycine < E_β-glycine, with α-glycine and β-glycine 70 J/mol and 1,950 J/mol, respectively, less stable than γ-glycine. These values can be compared with recent values from the literature³⁴ of 962 J/mol and 1,506 J/mol, respectively, obtained using the DFT method plus many body dispersion correction and zero point energy corrections (PBeh + MBD +ZPE).³⁴

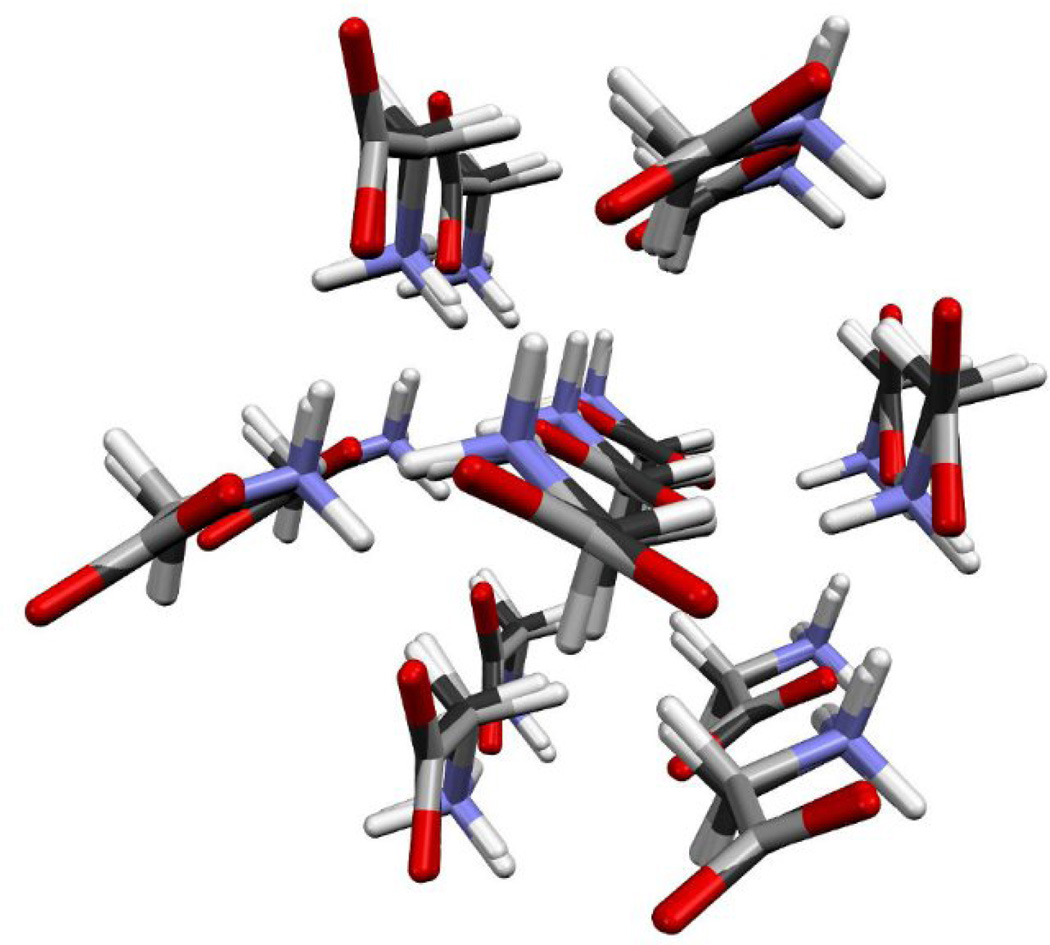
The graphical comparison between the experimental and the best MGAC-QE structures is presented in Figs. 3–5. This comparison does not require additional discussion, as it is apparent that the agreement is of such quality that the two structures are almost indistinguishable.

Figure 3.

Comparison of the experimental structure of the α-glycine CSD structure GLYCIN98 from Ref. 28 (black) with the lowest energy structure found by MGAC-QE in the P2_1/c space group (green).

Figure 5.

Comparison of the experimental structure of the γ-glycine CSD structure GLYCIN33 from Ref. 30 (black) with the lowest energy structure found by MGAC-QE in the P3₁ space group (white).

In conclusion, using MGAC-QE we were able to find each of the ambient pressure stable polymorphs of glycine when searching in their corresponding space group. The match to the experimental structure was the lowest energy structure found in each of the three searches. The polymorphs encountered by MGAC-QE are energetically ordered in agreement with experimental results and the comparison of the experimental and predicted structure is of such accuracy that the two are visually almost indistinguishable. When the success of MGAC-QE is compared with the results for glycine in Ref. 17, it becomes apparent that allowing the full relaxation of both molecular and crystal structural parameters as well as using a single approach for the calculation of the crystal energies at all stages of the global optimization is critical for successful CSP. However, there is already enough evidence in the literature that current functional and dispersion correction lattice energies may not be adequate for all crystals, particularly disordered ones, therefore new DFT approaches may be needed to address those systems.

The computer times required by the calculations reported here are significant, but manageable. Computer times for larger system will be a significant challenge, but we are confident that we will be able to greatly improve performance once we better understand the optimal GA parameters like population size, replacement and number of generations and area able to make use of emerging computer technologies like GPU accelerators. A truly blind test of the method, exploring most common space groups and/or using searches in P1 with different number of molecules per unit cell is the next goal. The exact search strategies will be defined by studies that are underway in our laboratory to establish the most efficient search protocols for blind test CSP. The results of this exploration will be used to participate in the current sixth CSP blind test, and our results will be presented at the 2015 CCDC meeting in the fall of 2015.

Conclusions

The results presented here show that it is possible to predict the crystal structures of molecules of biomedical interest from first principles without using any intermediate potentials, energy reordering strategies and/or step wise optimization strategies. With these results we believe that we can answer Professor Desiraju’s question with an unquestionable yes! Crystal structures can be predicted from first principles and with existing computational resources and appropriate optimization of our methods, CSP can become a standard tool for material design.

Figure 4.

Comparison of the experimental structure of the β-glycine CSD structure GLYCIN71 from Ref. 29 (black) with the lowest energy structure found by MGAC-QE in the P2₁ space group (blue).

Crystal Structure Prediction from First Principles

MGAC-QE predicts all atmospheric pressure glycine polymorphs

The Crystal Structures of Glycine polymorphs predicted in the correct energetic order