Discovering dynamic patterns from infectious disease data using dynamic mode decomposition

Abstract

Background

The development and application of quantitative methods to understand disease dynamics and plan interventions is becoming increasingly important in the push toward eradication of human infectious diseases, exemplified by the ongoing effort to stop the spread of poliomyelitis.

Methods

Dynamic mode decomposition (DMD) is a recently developed method focused on discovering coherent spatial-temporal modes in high-dimensional data collected from complex systems with time dynamics. The algorithm has a number of advantages including a rigorous connection to the analysis of nonlinear systems, an equation-free architecture, and the ability to efficiently handle high-dimensional data.

Results

We demonstrate the method on three different infectious disease sets including Google Flu Trends data, pre-vaccination measles in the UK, and paralytic poliomyelitis wild type-1 cases in Nigeria. For each case, we describe the utility of the method for surveillance and resource allocation.

Conclusions

We demonstrate how DMD can aid in the analysis of spatial-temporal disease data. DMD is poised to be an effective and efficient computational analysis tool for the study of infectious disease.

Introduction

The rapid increase in surveillance systems for infectious disease, capacity for digital storage, and computational resources better positions the scientific community to understand and, more importantly, combat the spread of infectious disease in human populations. A stronger understanding of the underlying process of infectious disease spread has the potential to shape intervention efforts such as multi-billion dollar campaigns on vaccination and vector-control programs. The strengthening focus on measuring the spread of disease and collecting data has created a set of new computational challenges for analyzing large amounts of infectious disease data. This big-data regime requires data-driven analysis methods that can both mitigate the difficulties of high-dimensional measurements and maintain the fundamentally dynamic nature of disease spread. In this manuscript, we demonstrate how one such method, dynamic mode decomposition (DMD), can help in the analysis of infectious disease data.

Modeling the spread of infectious disease can be challenging given the complexity and heterogeneity of the unknown, underlying system. DMD is fundamentally equation-free operating solely on snapshots in time of measurements, thus alleviating the need for a set of governing equations; further, the required input data can be generated from simulations, experiments, or historical data.^1–3 In addition, the method contains the advantageous properties of two traditional and transformative data analysis methods: principal component analysis (PCA) for the reduction of high-dimensional (possibly redundant) measurements and spectral time-series analysis for identifying the frequency content of a time-varying signal. DMD is a powerful method, developed in the fluid dynamics community, with the ability to find coherent spatial-temporal patterns in data arising from large-scale, nonlinear systems.^1–4

The equation-free and adaptable architecture of DMD has also led to a number of exciting modifications that are relevant to the study of infectious disease data. The method can be modified to evaluate a limited, sparse number of measurements in either space or time while still recovering the underlying dynamics, based on compressive sensing.^5–7 For surveillance of infectious disease data, the full state of the system will rarely be available, thus methods able to handle a sparse set of measurements will be integral for future applications. Other challenges facing disease surveillance for high-burden areas include not having reliable diagnostic tools, prevalence of asymptomatic infections, and disorganized health information systems. The adaptable architecture of DMD is well posed to mitigate these data-challenges; for example, DMD has been recently modified to evaluate data from complex systems that have had external forcing such as interventions.⁸

The outline of this manuscript includes a background on the theory for DMD. The subsequent section demonstrates the application of DMD on three data examples, including Google Flu, pre-vaccination measles in the UK, and polio cases in Nigeria. We follow up with a discussion and future extensions of DMD for mathematical modeling.

Materials and methods

This section describes the DMD method.^1–4 To precede the mathematical description of DMD, a brief subsection is included about processing raw disease data into a standard spatial-temporal data framework.

Infectious disease data and dynamical systems

DMD is a method that analyzes the relationship between pairs of measurements. In the case of spatial-temporal infectious disease data, these pairs consist of a future measurement ${\mathrm{x}}_{\mathrm{k}+1}$ and a previous measurement ${\mathrm{x}}_{\mathrm{k}}$, where $\mathrm{x}\in {\mathbb{R}}^n$.³ For all pairs of data, a linear operator $\mathrm{A}\in {\mathbb{R}}^{\mathrm{n}\times \mathrm{n}}$ can be assumed to provide the following relationship:

$${\mathrm{x}}_{\mathrm{k}+1}=\mathrm{A}{\mathrm{x}}_{\mathrm{k}},$$ (1)

where the operator A is constructed by seeking the best-fit solution for all pairs. The relationship in (1) does not need to hold exactly. Previous work has demonstrated the theoretical justification between using this approximating operator on data generated by nonlinear systems (see Supplementary Materials: Section 3 for more detail). Further, most applications of DMD are on data collected from complex, nonlinear systems.^1,3,6,9

Data collected from numerical simulations, laboratory experiments, and historical records are most often measured at discrete instances in time, which we will denote as ${\mathrm{x}}_{\mathrm{k}}\mathrm{\forall }\mathrm{k}\in [1,\mathrm{m}]$ and call each of the m observations snapshots.¹⁰ In other scientific applications, such as fluid dynamics, the measured state ${\mathrm{x}}_{\mathrm{k}}$ is clearly defined i.e., the velocity field at each spatial grid point measured at equal temporal intervals $\mathrm{\Delta }\mathrm{t}$. Well-curated infectious disease data often arrives in a similar form with, for example, the number of infections (or cases) in each of a set of particular geo-spatial location over a period of time. More care is required if the data is in the form of individual patient records. In order to utilize DMD, an aggregation step is required to sum across spatial and temporal scales. See Schmid PJ¹ for an informative example about choosing the correct $\mathrm{\Delta }\mathrm{t}$ for a fluid dynamics problem.

Once the data have been aggregated, each pair of state snapshots ${\mathrm{x}}_{\mathrm{k}}$ and ${\mathrm{x}}_{\mathrm{k}+1}$ can be collected. Then, two data matrices can be constructed given by the following:

$$\begin{array}{c}\mathrm{X}=\left[\begin{array}{c}|\hfill \\ {\mathrm{x}}_1\hfill \\ |\hfill \end{array}\begin{array}{c}|\hfill \\ {\mathrm{x}}_2\hfill \\ |\end{array}\cdots \begin{array}{c}|\\ {\mathrm{x}}_{\mathrm{m}-1}\\ |\end{array}\right],\hfill \\ {\mathrm{X}}^{\mathrm{\prime }}=\left[\begin{array}{c}|\\ {\mathrm{x}}_2\\ |\end{array}\begin{array}{c}|\\ {\mathrm{x}}_3\\ |\end{array}\cdots \begin{array}{c}|\\ {\mathrm{x}}_{\mathrm{m}}\\ |\end{array}\right],\end{array}$$ (2)

where X and X′ are $\in {\mathbb{R}}^{\mathrm{n}\times \mathrm{m}-1}$. Note, the general case of DMD does not require sequential time-series data only that the pairs of data (column j of X and column j of X′) are related. Combining (1) and (2), the following relationship between pairs of states ${\mathrm{x}}_{\mathrm{k}}$ and ${\mathrm{x}}_{\mathrm{k}+1}$ can be more generally described in matrix form:

$${\mathrm{X}}^{\mathrm{\prime }}\approx \mathrm{AX}.$$ (3)

The next section describes the process of solving (3).

Dynamic mode decomposition

In this section, we define the DMD and describe the method. The DMD of the measurement pair X and X′ is the eigendecomposition of the matrix A from (3). The approximating operator is defined by the following:

$$\mathrm{A}={\mathrm{X}}^{\mathrm{\prime }}{\mathrm{X}}^{†},$$ (4)

where † is the Moore-Penrose pseudoinverse.³ The pseudoinverse can be efficiently and accurately solved by the singular value decomposition (SVD). The well-known SVD of a matrix X, truncated at r singular values, is given by the following:

$$\mathrm{X}\approx \tilde{\mathrm{U}}\tilde{\mathrm{\Sigma }}{\tilde{\mathrm{V}}}^{\ast },$$ (5)

where $\tilde{\mathrm{U}}\in R^{\mathrm{n}\times \mathrm{r}}$, $\tilde{\mathrm{\Sigma }}\in {\mathbb{R}}^{\mathrm{r}\times \mathrm{r}}$, ${\tilde{\mathrm{V}}}^{\mathbf{\ast }}\in {\mathbb{R}}^{\mathrm{r}\times \mathrm{m}-1}$, and * denotes the complex conjugate transpose. The SVD provides a principled method for reducing the dimension of the data matrix. For more details on the SVD and the truncation value see the Supplementary Materials: Section 1. Also, Figure 1 shows an illustration of truncating an SVD based on the singular value magnitudes.

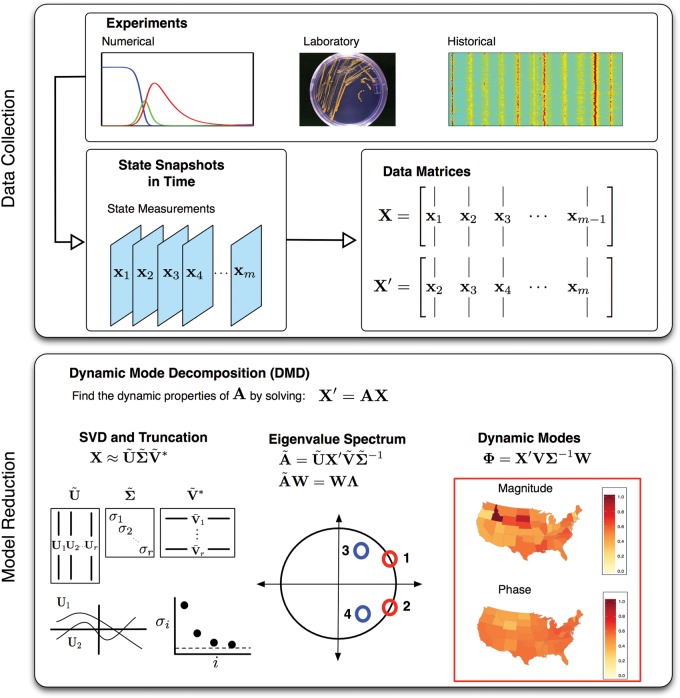
Figure 1.

An illustration of the data collection and the dynamic mode decomposition (DMD) method. In the top panel, an illustration of how to construct the data matrices from numerical, laboratory, or historical data sources. The historical data illustration is of flu data for the US according to the Google Flu Trends tool. A longer description of the data is described in the Results section. The bottom panel illustrates the key components of solving for A: the singular value decomposition (SVD), the eigenvalue spectrum, and the dynamic modes. For infectious disease data, each of the elements of a dynamic mode will typically represent a specific geo-spatial location. The magnitude and phase of the element describes how the geo-spatial locations are related to each within that mode. If the mode has an associated eigenvalue with a nonzero imaginary component, indicating oscillatory behavior, then the angle of each element represents the relative phase of the location's oscillation relative to the other locations for that dynamic mode. This representation allows for a direct interpretation of the DMD output for disease spread: each dynamic mode identifies the locations involved in that dynamic pattern of disease spread as well as the relative phase of that location's peak infection time.

An approximation of the operator A can be found using (4) and (5) and choosing a truncation value r given by the following:

$$\mathrm{A}\approx \overline{\mathrm{A}}={\mathrm{X}}^{\mathrm{\prime }}\tilde{\mathrm{V}}{\tilde{\mathrm{\Sigma }}}^{-1}{\tilde{\mathrm{U}}}^{\ast }.$$ (6)

Note the size of matrix $\overline{\mathrm{A}}$ is n×n. A more computationally efficient method for computing both an approximation of A and the dynamic characteristics of $\overline{\mathrm{A}}$ is reducing the dimension of the operator. This is efficiently performed by projecting on to the lower-dimensional subspace defined by the first r left singular vectors represented by Ũ. The following is the reduced order operator:

$$\tilde{\mathrm{A}}={\tilde{\mathrm{U}}}^{\ast }{\mathrm{X}}^{\mathrm{\prime }}\tilde{\mathrm{V}}{\tilde{\mathrm{\Sigma }}}^{-1}.$$ (7)

Computing the eigendecomposition of $\tilde{\mathrm{A}}$ can be substantially more efficient and crucial when considering the memory footprint of $\overline{\mathrm{A}}$ when $n\gg 1$. A similar observation was made earlier by Sirovich and the method of snapshots.¹⁰ The dynamic characteristics can be found by the well-known eigendecomposition: $\tilde{\mathrm{A}}\mathrm{W}=\mathrm{W}\mathrm{\Lambda }$ where W contains the eigenvectors and Λ the eigenvalues.

The relationship between the dynamic characteristic of the reduced-order model of $\tilde{\mathrm{A}}$ and $\overline{\mathrm{A}}$ can be exactly recovered through the method described by Tu JH et al.³ The following are called dynamic modes of the full system.

$$\varphi ={\mathrm{X}}^{\mathrm{\prime }}\tilde{\mathrm{V}}{\tilde{\mathrm{\Sigma }}}^{-1}\text{w}.$$ (8)

If $\lambda \ne 0$, then this is the DMD mode for λ. If the eigenvalue is 0, then the dynamic mode is computed using $\varphi =\tilde{\mathrm{U}}\mathrm{w}.$

The collection of dynamic modes and their respective eigenvalues are the low-dimensional coherent spatial-temporal patterns within the dataset. The eigenvalues describe the growth/decay and oscillatory characteristics of each dynamic mode. Figure 1 illustrates an example eigenvalue spectrum with two pairs of complex conjugate eigenvalues. The red pair indicates a purely oscillatory mode since they lie on the unit circle, whereas the blue pair lie within the unit circle and thus have a decaying dynamic characteristic. The oscillatory frequency of each eigenvalue of the map $\tilde{\mathrm{A}}$ can be converted in to the continuous time frequency with the following relationship:

$$\text{frequenc}{\text{y}}_j=\frac{\text{imag}(\log ({\lambda }_j)/\mathrm{\Delta }t)}{2\pi }$$ (9)

This relationship allows for each discrete eigenvalue to be examined based on the more intuitive and interpretable continuous time frequencies, i.e., per year frequency.

The dynamic modes describe how spatial locations (each element of the measurement vector x_k) are related. Within a single dynamic mode, each element in the vector ${\varphi }_j$ has two important pieces of information: the magnitude of the element (absolute value) provides a measure of the spatial location's participation in the mode; the angle between the real and imaginary component of the element provides a measure of a location's phase of oscillation relative to others for that mode's frequency. Figure 1 shows how a dynamic mode from DMD can be represented on a geo-spatial map in terms of both the magnitude and phase. This data is from the Google Flu Trends data described in the first part of the Results section and the mode being examined is the one-year frequency. A discussion about picking relevant dynamic modes is included in the Supplementary Materials: ‘Picking relevant dynamic modes’.

Results

Example 1: Google Flu Trends

The first example of infectious disease data comes from Google's Flu Trends tool. Google has investigated how certain search terms are indicators of flu activity within a country. By using aggregated Google search data and historical flu data, they have constructed a method for determining the current state of flu activity.¹¹ Despite recent scientific discussions about the validity of the Google Trends predictions, this dataset is a relevant spatial-temporal data set of infectious disease.¹² Here, we use flu activity data from the US generated by their tool.

In the top panel of Figure 2, four traces of the raw (unprocessed data) from Alaska (black), California (red), Texas (green) and New York (blue) are shown for comparison. The Google Flu Trends tool provides data for every seven days; this is the Δt value for DMD. Also for visualization, the complete set of spatial locations is included (states, cities, and the health-human-services regional breakdown) in time. In order to visually compare each location with potentially different order of magnitude of infection value, each location's time series (each row of the data matrix X) is normalized. The mean is subtracted and the variance of the time series is set to one. The normalization helps to account for larger population centers. Note the clear seasonality of the flu activity, in addition to the larger peaks in 2010 and 2013. For a number of the states and cities, non-zero entries of the data do not begin until 2007; for the analysis with DMD, we take the dates from June 2007 to July 2014. Also, we focus solely on the state information in order to visualize every element of the dynamic mode on the map of the US.

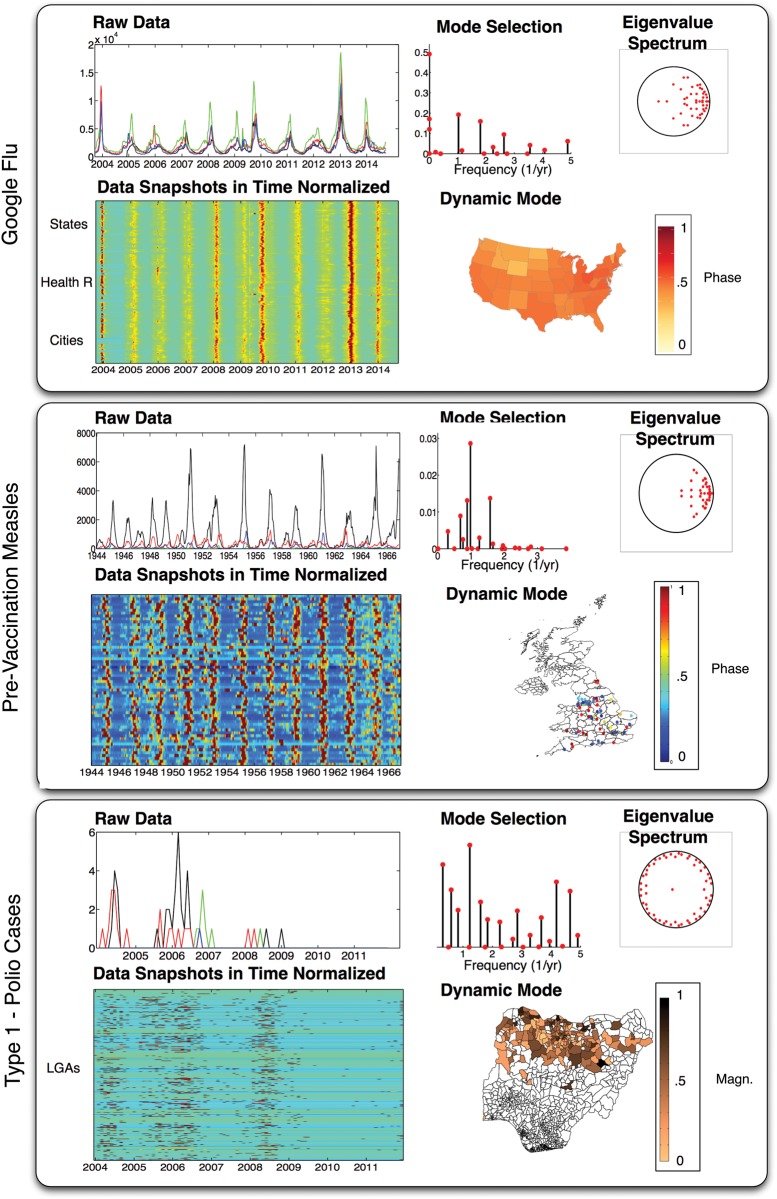
Figure 2.

The panels describe the data and output of the dynamic mode decomposition (DMD) on three examples: Google Flu, pre- vaccination measles in the UK, and type 1 paralytic polio cases. In each panel, two plots are included to visualize the data: the top left plot shows four time-histories from different locations; the bottom left is a visualization of all the locations in time. The time histories in the bottom left are normalized, described in the text. The three plots illustrate the output of DMD: how to select the mode based on a power calculation, the eigenvalue spectrum of $\tilde{\mathrm{A}}$, a dynamic mode ϕ plotted as a map.

The output of DMD is included to the right of the data visualizations. The eigenvalue spectrum indicates a number of modes that are well-within the unit circle indicating fast decaying eigenvalues and modes that do not contribute to the broader structure of the dynamics. The Mode Selection plot illustrates this point by examining the dynamic modes that have greater power ${\lambda }_j^p∥{\varphi }_j∥$ vs their frequency, defined in Supplementary Materials: Section 2, where p=20 and the energy truncation of the SVD is 99%. Note the clear yearly frequency mode. The phase of the dynamic mode associated with the one year frequency is plotted on the US map. The phase is defined between 0 and 1 for both this example and the next. Note, since the phase value exists on the circle, the color values near 0 and 1 are actually close in phase. The phase difference found by DMD between Ohio and North Dakota (states with larger color difference) is approximately 0.25 (or 3 months). Also, a general grouping of states emerges from mapping the phase difference; the northwest states generally group together as well as the northeast. A smooth transition also occurs traveling north from California to Washington on the western coast.

Example 2: pre-vaccination measles in the UK

In this example, we look at the well-known infectious disease data-set of pre-vaccination measles cases in the UK. The data has been previously examined with classical methods like Fourier decomposition.¹³ In the middle panel of Figure 2, four traces of the raw (unprocessed data) from four cities in the UK: London (black), Liverpool (red), Colchester (green) and Cardiff (blue), are shown for comparison. Sixty cities are included in the dataset. The measles cases are reported every 2 weeks for 22 years.

Each location's time series is normalized both in mean and variance in order to allow visual comparison. Note the clear seasonality with dramatic fluctuations. Here, we take the first 10 years of data for all cities to be used in the DMD analysis.

Similar to above, the output of DMD is shown to the right of the plots. The Mode Selection plot illustrates the dynamic modes that have a greater ${\lambda }_j^p∥{\varphi }_j∥$ with p=50 and the energy truncation of the SVD is 95%. The visually appealing seasonality is captured by the close to one-year frequency ≈ 0.98. Also, strong peaks exist near the twice a year and close to every two years frequency. These peaks are weaker than the one-year frequency, but indicate other modes of oscillation that may account for the fluctuation observed in the visualized data. The phase of the one-year periodic dynamic mode is plotted on the map of the UK. Instead of coloring in the states according to the phase, individual markers are placed down at each city's latitude and longitude with the color indicating the phase. The phase differences for measles in the UK span a larger range than the previous example, as seen with locations spanning the color bar. For example, the difference between London and Warrington is approximately 0.39, almost five months. This is in contrast to Bournemouth, which is tied closely to London with a phase difference of 0.02, about two weeks. Groupings of locations also share similar phase differences near London. As mentioned in the previous section, the phase values near 0 and 1 (dark red and dark blue) are actually close in phase. Thus, a set of locations in the north and south are similar in phase for the yearly dynamic mode.

Example 3: Type 1 polio in Nigeria

The final example involves the analysis of data about wild type 1 polio paralytic cases from Nigeria. The eradication of polio has been an ongoing and difficult campaign for a number of decades. Substantial success has been demonstrated in eradicating polio from most of the world's countries except for three: Afghanistan, Pakistan, and Nigeria. Polio has proven to be a difficult disease to eradicate in these countries due to a broad number of reasons, including poor health infrastructure, war-time interruption of vaccination campaigns, and even violence against vaccinators. Another challenge, especially for analysis, is a fundamental characteristic of the disease: the case-to-infection ratio. For type 1 polio, the ratio is approximately 1:200, meaning that for every detected paralytic case there are approximately 200 unobserved infections. As the push toward eradication is more successful, the detection and measurement of polio becomes more difficult and less probable. Despite being in the eradication regime, we apply DMD on this more difficult, but relevant dataset in the global health community.

The lower panel of Figure 2 shows raw data traces, as well as a visualization of all of the sub-province (LGA) level spatial divisions. The four LGAs plotted are Kano (black), Katsina (red), Akko (green), and Funakaye (blue). The data come from the Nigerian Acute Flaccid Paralysis (AFP) surveillance database curated by the Nigerian WHO. The same dataset was used recently to construct a risk model for polio in Nigeria.¹⁴ For the subsequent DMD analysis, we take only LGAs with more than five cases. Also, we focus on the five years of data from 2004–2009. Here, we aggregate paralytic cases in time by month.

The output of the DMD analysis is shown to the right of the data visualizations. The eigenvalue spectrum is substantially different than the previous two examples with more eigenvalues near the unit circle and evenly spaced. This is characteristic of a signal decomposition with a broad frequency content. The mode selection plot also illustrates this point with a less-clear dominant set of modes. Here, p=70 and the truncation energy value is set at 99%. We select the large magnitude norm at approximately f ≈ 1.2 per year. In contrast with the previous two examples, the magnitude of the dynamic mode is plotted on top of the Nigerian map. Note, the darker areas in the center of northern Nigeria, called Kano state, is historically known to be a hot-spot for polio cases. By illustrating the magnitude of the dynamic mode, dark versus light areas indicate the strength of membership of specific LGAs for this particular dynamic mode. For example, the dark areas emanating along spatially connected LGAs from Kano indicate these LGAs have been dynamically linked to flare-ups in Kano state.

Discussion

The epidemiological interpretation of DMD modes

The dynamic modes of DMD allow for epidemiological interpretation of large-scale dynamic patterns within the data examples. In both the flu and measles examples, DMD automatically identifies the yearly cycle as clearly important. The dynamic mode associated with this yearly cycle provides the phase relationship among the locations. The phase information can be used to interpret how that dynamic pattern spreads across a spatial domain; for the flu example, moving north along the west coast shows a smooth change of phase for the peak time of flu indicating the spread of disease. This information can be particularly useful for planning the annual resource allocation of vaccines, surveillance and monitoring teams, and delivery timing of interventions especially if the interventions are time sensitive.

In addition, DMD and the dynamic modes offer insight in to the epidemiological connectedness of spatial locations. The spatial locations described within most infectious disease datasets are often politically defined boundaries and do not necessarily reflect the epidemiological connectedness of spatial areas. Both the magnitude and phase information of the dynamic mode can provide a measure of connectedness. In the flu and measles examples, similar phase information can indicate well-connected areas, such as the Montana, Washington, Idaho and Wyoming grouping or the states in New England as seen in Figure 2. Note, DMD is not given a model about the spatial location of these states, the groupings are automatically discovered. Also, epidemiologically connected areas do not necessarily need to be neighbors. Long-distance migration routes can connect them by air or train; this could be the case for the matching phase of cities like London with cities in the north of the UK and links between New York and California from air travel.

The polio example illustrates how the magnitude (versus the phase discussed for the previous two examples) of the dynamic mode can illuminate which locations are active for that dynamic pattern. The LGAs (the darker colored locations in Figure 2) are significantly more active for this dynamic mode indicating an epidemiological link. For campaign planning, such as the country-wide vaccine campaigns called supplementary immunization activities (SIAs) in Nigeria, this epidemiological connectedness of spatial locations can help with the logistical planning of intervention campaigns. The understanding of historical connectedness can help in planning which LGAs will receive SIAs if cases are detected, especially given the current low level of infections and the low case-to-infection ratio in Nigeria. Further, an understanding of historical connectedness can allow for better planning of surveillance teams and sites, minimizing redundant measurements. The characteristic speed of the dynamic mode given by the eigenvalue also offers direct relevant information for campaigns. If a set of cases occur activating the dynamic mode, the eigenvalue (the decay rate and the oscillatory frequency) will indicate whether that mode can be affected by a mop-up campaign due to the fixed time-delay from campaign logistics.

Another important output of DMD is the ability to better inform mechanistic models of infectious disease spread. Parameter estimation can make mechanistic modeling intractable when the spatial discretization of the model is finely grained. The dynamic modes of DMD offer a way to reduce the dimension of these models (through understanding the epidemiologically connected areas) allowing for better estimation of model structure and features.

Connections to other methods

This subsection explores the connection of DMD to other methods typically applied to spatial-temporal data. The Fourier decomposition, a spectral time-series method, can find the frequency content and phase information for each spatial location's time-series. Each location's time-series can be summed to form a single-channel signal allowing the Fourier decomposition to discover the frequency content from data representing all locations,¹³ but the phase information between locations is lost. The principal components analysis (PCA) is a standard model reduction technique that provides an optimal subspace to describe the data with fewer modes (linear combinations of spatial locations), without regard for temporal characteristics. PCA is also known as proper orthogonal decomposition (POD),^15–17 the Hotelling transform,¹⁸ empirical orthogonal functions (EOF),^19,20 and/or the Karhunen–Loéve (KL) decomposition.²¹ DMD combines the advantageous properties of both methods while also allowing for the dynamic characteristic of growth and decay. In addition, the dynamic modes discovered from DMD can be substantially different from the principal component modes.²²

DMD has connections to other methods such as linear inverse modeling (LIM) from the atmospheric science community and eigensystem realization algorithm (ERA) and the observer Kalman identification (OKId) from the control theoretic literature; under certain theoretical conditions, the methods become equivalent.^3,8 Autoregressive-moving-average (ARMA) Models are also utilized to analyze spatial-temporal data, but fundamentally differ from DMD in the method for discovering a reduced-order model from the data. DMD uses the truncation threshold of the SVD whereas reducing the dimension of an ARMA model typically requires fitting linear models of various dimensions and evaluating a model-fit measure like the Akaike information criteria (AICc).

Limitations

Data-driven, equation-free methods like DMD suffer from a limitation stemming from the quality and quantity of data. In the elimination or eradication regimes of an infectious disease, the number of disease cases, and thus the signal, decrease substantially. Other data-driven methods also suffer from this limitation. DMD, though, has been shown to perform well even with sparse data collection.^5–7

Conclusions

The application of DMD on infectious disease data can help inform epidemiologically relevant actions such as allocating intervention resources, avoiding redundancy in surveillance team deployment, and designing effective mop-up immunization campaigns. Quantitative modeling and analysis will play a key role in understanding disease spread and optimally applying intervention resources to maximize the probability of success for eradication. With increased investment in surveillance systems, the magnitude and heterogeneity of measurements requires the development and adaptation of analysis tools for this big-data regime. DMD is one such analysis tool that can aid in the analysis and understanding of infectious disease spread in parallel with other existing approaches.

Supplementary data

Supplementary data are available at International Health Online (http://inthealth.oxfordjournals.org/).